How the formation of amyloid plaques and neurofibrillary tangles may be related: a mathematical modelling study

Abstract

We develop a mathematical model that enables us to investigate possible mechanisms by which two primary markers of Alzheimer's disease (AD), extracellular amyloid plaques and intracellular tangles, may be related. Our model investigates the possibility that the decay of anterograde axonal transport of amyloid precursor protein (APP), caused by toxic tau aggregates, leads to decreased APP transport towards the synapse and APP accumulation in the soma. The developed model thus couples three processes: (i) slow axonal transport of tau, (ii) tau misfolding and agglomeration, which we simulated by using the Finke–Watzky model and (iii) fast axonal transport of APP. Because the timescale for tau agglomeration is much larger than that for tau transport, we suggest using the quasi-steady-state approximation for formulating and solving the governing equations for these three processes. Our results suggest that misfolded tau most likely accumulates in the beginning of the axon. The analysis of APP transport suggests that APP will also likely accumulate in the beginning of the axon, causing an increased APP concentration in this region, which could be interpreted as a ‘traffic jam’. The APP flux towards the synapse is significantly reduced by tau misfolding, but not due to the APP traffic jam, which can be viewed as a symptom, but rather due to the reduced affinity of kinesin-1 motors to APP-transporting vesicles.

1. Introduction

Extracellular amyloid plaques and intracellular neurofibrillary tangles (NFTs) are known to be hallmarks of Alzheimer's disease (AD). The amyloid plaques are produced by aggregation of β-amyloid peptide (Aβ) that is generated by the cleavage of amyloid precursor protein (APP) due to the proteolytic action of β- and γ-secretases, while normal processing of APP involves α- and γ-secretases [1–3]. NFTs are composed of misfolded tau protein, a microtubule (MT)-associated protein that normally binds to MTs. In AD, tau becomes hyperphosphorylated, detaches from MTs, and aggregates to form intra-neuronal deposits [4–7].

The AD field is dominated by the amyloid cascade hypothesis, which postulates that the deposition of amyloid-β in the brain initiates a cascade of events (including tau pathology) that leads to AD [8]. However, due to the failure of several anti-Aβ directed therapeutics in Phase III clinical trials, this hypothesis was criticized by some researchers [9,10]. An alternative hypothesis that has recently gained popularity is the tau hypothesis, which assumes that tau agglomeration begins before Aβ agglomeration and that tau misfolding is the main driver of disease development. For example, the pattern of pathology developed during AD suggests that it is unlikely that amyloid-β is produced by neurons that do not have tau pathology [11]. The tau hypothesis is also supported by the observation that a reduction of tau protein prevents amyloid-β accumulation [12].

In this paper, we concentrate on the tau hypothesis. We simulate the situation in which tau begins to agglomerate in the axon. We examine where in the axon tau agglomeration begins and how it can potentially affect APP transport.

Aggregated forms of tau protein are reported to appear in the proximal axon. Large insoluble tau aggregates, which contain irreversibly phosphorylated tau species, do not move in the axon [13]. The production of toxic tau species may damage the transport system in the axon, reduce APP transport towards the synapse, cause APP accumulation in the soma, and thus lead to Aβ aggregation. In support of this hypothesis, Kamal et al. [14] hypothesized that abnormal interaction between kinesin-1 motors and APP could be a factor in AD.

The exact mechanism of interaction between motor proteins, kinesin-1 and dynein, and APP is a subject of a debate. Several mechanisms of APP interaction with kinesin-1 have been discussed. Some authors investigated the possibility of direct interaction between kinesin-1 light chain subunit and APP [14]. Protein JIP1b has been suggested as a possible scaffold protein, which binds to both APP and kinesin light chain KLC1 [15]. However, results reported in ref. [16] do not support direct interaction of kinesin-1 with APP. According to an alternative point of view, APP, together with other membrane proteins, is transported anterogradely in presynaptic vesicles towards the acceptor membrane in the presynaptic terminal by kinesin-1C motors. The number of APP molecules in one vesicle could exceed several hundred [17]. In our model, we will use the latter hypothesis, assuming that APP is transported in presynaptic vesicles.

Despite the significance of tau and APP transport in AD, very little has been done in terms of developing mathematical models that could help in understanding the transport and aggregation of these two proteins in axons. A phenomenological model of AD that simulates various processes that occur in the brain during this disease was developed [18]. Various mathematical models of neurodegeneration were reviewed in ref. [19] and the need for further progress in this area was pointed out. However, to the best of our knowledge, mechanistic models explaining the relation between tau and Aβ aggregation are still lacking.

Here, by means of mathematical modelling, we investigated the possibility that the formation of toxic tau aggregates may cause the formation of amyloid plaques. According to our hypothesis, the formation of toxic tau oligomers may lead to decreased anterograde transport of APP, thus causing APP accumulation in the soma, which is known to be a locus for the generation of Aβ peptides [20]. Investigating possible links between tau and APP agglomeration is important for better understanding processes leading to the onset of AD at a mechanistic level.

2. Methods and models

(a). Governing equations simulating slow axonal transport and diffusion of tau protein

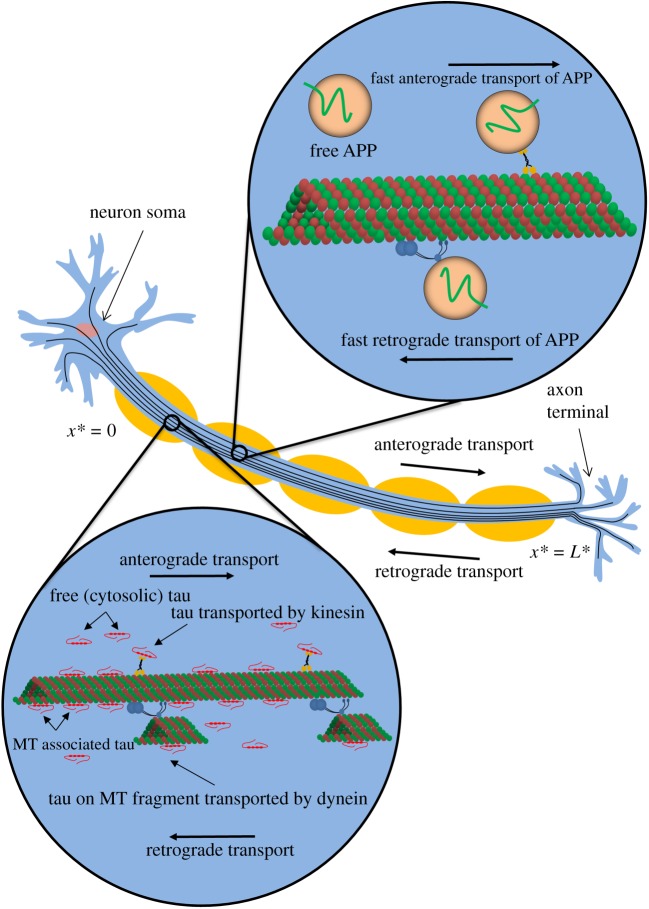
Experimental research suggests that tau is transported in axons by a combination of active (driven by molecular motors) and passive (diffusion) transport mechanisms. The motor-driven pathway was established in refs. [21–23]. Tau can be either pulled by a motor directly or reside on a small piece of an MT which is pulled by a molecular motor [24]. In terms of passive transport, tau can diffuse in the cytosol [25–27]. Also, some of MT-bound tau can be transported by one-dimensional diffusion along the MTs [28]. According to our numerical study [29], both motor-driven and diffusion-driven mechanisms contribute to tau transport in axons, with motor-driven mechanisms becoming more important for transport at longer distances (figure 1).

Figure 1.

A diagram of a neuron showing various modes of slow axonal transport of tau protein and fast axonal transport of APP. In displaying possible mechanisms of tau transport, we followed ref. [24] (see fig. 3 in ref. [24]). (Online version in colour.)

In ref. [30], we suggested a model of tau transport in the axon, which simulates slow axonal transport of tau protein due to motor-driven transport of tau (by kinesin and dynein motors), diffusion of free cytosolic tau, and transport of a sub-population of MT-bound tau due to its diffusion along the MT lattice. The model depends on 24 parameters, six of which were estimated from the literature. In ref. [30], we estimated the remaining 18 parameters by minimizing the discrepancy between the model predictions and experimental results for the total tau concentration, reported in ref. [31], and for the tau average velocity, reported in ref. [32]. Here, we extend our previous model by simulating agglomeration of misfolded tau. We formulate the model under the quasi-steady-state approximation (QSSA) [33,34], when agglomeration of the misfolded tau is assumed to be sufficiently slow so that tau concentrations in all kinetic states, with the exception of misfolded tau, assume their steady-state distributions along the axon. This allows us to investigate the consequences of possible coupling between tau and APP transport, as well as to investigate in what region of the axon the largest tau agglomeration is expected to occur. Dependent variables characterizing tau transport are summarized in electronic supplementary material, table S1, independent variables are summarized in electronic supplementary material, table S2, and parameters for the tau transport model are given in electronic supplementary material, table S3. All tables are given in the electronic supplementary material. The proposed model is as follows.

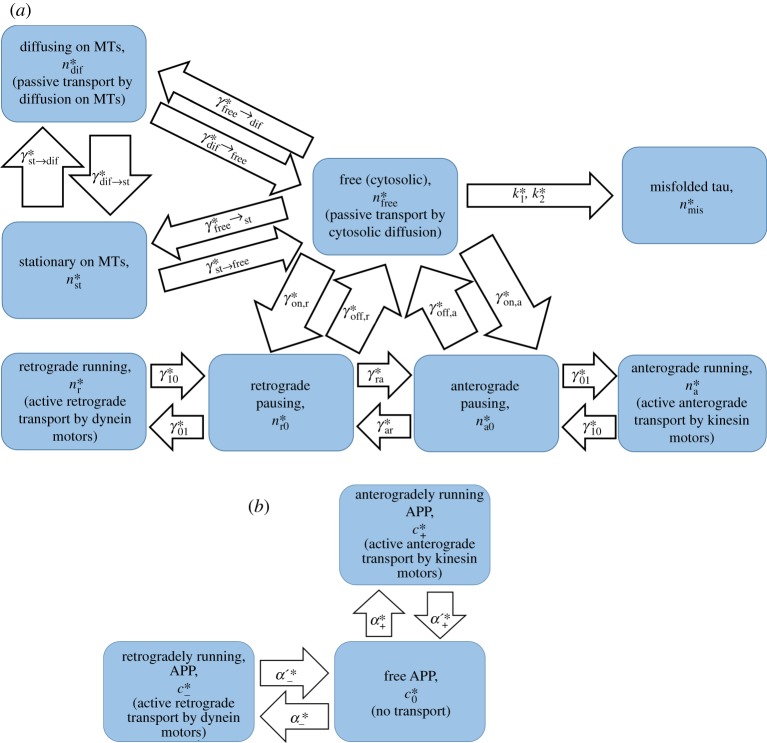
The model includes two motor-driven states for tau protein (figure 2a), which simulate populations of tau that are pulled anterogradely by kinesin motors (with a velocity $v_{\mathrm{a}}^{\ast }$) and retrogradely by dynein motors (with a velocity $v_{\mathrm{r}}^{\ast }$). Tau concentrations in these kinetic states are $n_{\mathrm{a}}^{\ast }$ and $n_{\mathrm{r}}^{\ast }$. Because the axon is extended in one direction, we characterize the tau concentration in any kinetic state by its linear number density, which is the number of tau molecules per unit length of the axon. The conservation of tau in these kinetic states gives the following equations:

$$-v_{\mathrm{a}}^{\ast }\frac{\mathrm{\partial }{n}_{\mathrm{a}}^{\ast }}{\mathrm{\partial }{x}^{\ast }}-{\gamma }_{10}^{\ast }{n}_{\mathrm{a}}^{\ast }+{\gamma }_{01}^{\ast }{n}_{\mathrm{a}0}^{\ast }=0$$ 2.1

and

$$v_{\mathrm{r}}^{\ast }\frac{\mathrm{\partial }{n}_{\mathrm{r}}^{\ast }}{\mathrm{\partial }{x}^{\ast }}-{\gamma }_{10}^{\ast }{n}_{\mathrm{r}}^{\ast }+{\gamma }_{01}^{\ast }{n}_{\mathrm{r}0}^{\ast }=0.$$ 2.2

The first terms in equations (2.1) and (2.2) describe the change of tau concentrations due to anterograde and retrograde motor-driven transport, respectively. Parameters $v_{\mathrm{a}}^{\ast }$ and $v_{\mathrm{r}}^{\ast }$ should be understood as average instantaneous velocities of rapid motions of tau on MTs when tau is propelled by kinesin and dynein motors, respectively. These are effective properties because the velocity of cargo that is propelled by molecular motors may depend on the number of motors, whether there is coordination between the motors or a tug-of-war between them [35], how crowded the MT is [36,37], and many other factors [38,39]. Coordination means that while a cargo is transported by one group of motors, the opposing motors are deactivated. A tug-of-war means that groups of anterograde and retrograde motors are in competition [40].

Figure 2.

(a) A kinetic diagram showing various kinetic states for simulating slow axonal transport of tau protein. A kinetic state corresponding to misfolded (aggregated) tau protein is also shown. (b) A kinetic diagram showing various kinetic states for simulating fast axonal transport of APP. (Online version in colour.)

The second and third terms in equations (2.1) and (2.2), which involve various kinetic constants (γs), simulate transitions between motor-driven and pausing populations of tau (figure 2a). According to the data reported in ref. [22], tau spends much more time (73%) in the pausing states, which is typical for slow axonal transport. This fact is manifested by a large value of the ratio ${\gamma }_{10}^{\ast }/{\gamma }_{01}^{\ast }$ in our model (electronic supplementary material, table S3).

It should be noted that equations for MT-bound tau (running on MTs, pausing, stationary, and diffusing along the MT lattice) do not contain any terms describing tau degradation. This is because tau's degradation occurs primarily through the proteolytic pathway [41,42]. We assume that tau must be detached from MTs in order to enter a proteasome's proteolytic chamber. Therefore, tau in any of the MT-bound states is protected from degradation.

The model also includes two kinetic states for pausing tau (figure 2a), describing tau protein that is ready to resume its anterograde or retrograde motion. Tau concentrations in these kinetic states are $n_{\mathrm{a}0}^{\ast }$ and $n_{\mathrm{r}0}^{\ast }$. It should be noted that our model is a cargo-level model; it describes the behaviour of tau protein rather than the behaviour of molecular motors propelling tau protein. We do not simulate particular events causing cargo pausing [43]; this would require going one level higher in complexity and simulating detachment and reattachment of motors to MTs as well as whether the motors are coordinated or there is a tug-of-war between the motors [40]. The conservation equations for the pausing tau are

$$-({\gamma }_{01}^{\ast }+{\gamma }_{\mathrm{ar}}^{\ast }+{\gamma }_{\mathrm{off},\mathrm{a}}^{\ast })n_{\mathrm{a}0}^{\ast }+{\gamma }_{10}^{\ast }{n}_{\mathrm{a}}^{\ast }+{\gamma }_{\mathrm{ra}}^{\ast }{n}_{\mathrm{r}0}^{\ast }+{\gamma }_{\mathrm{on},\mathrm{a}}^{\ast }{n}_{\mathrm{free}}^{\ast }=0$$ 2.3

and

$$-({\gamma }_{01}^{\ast }+{\gamma }_{\mathrm{ra}}^{\ast }+{\gamma }_{\mathrm{off},\mathrm{r}}^{\ast })n_{\mathrm{r}0}^{\ast }+{\gamma }_{10}^{\ast }{n}_{\mathrm{r}}^{\ast }+{\gamma }_{\mathrm{ar}}^{\ast }{n}_{\mathrm{a}0}^{\ast }+{\gamma }_{\mathrm{on},\mathrm{r}}^{\ast }{n}_{\mathrm{free}}^{\ast }=0.$$ 2.4

Note that various terms in equations (2.3) and (2.4) describe transitions between the pausing states and other kinetic states (figure 2a). This is because in the pausing states, tau protein does not move.

Free tau (having a concentration $n_{\mathrm{free}}^{\ast }$) is tau protein detached from molecular motors and suspended in the cytosol (figure 2a). In this kinetic state, tau can move by diffusion, the energy-independent process that is described by the first term on the left-hand side of equation (2.5). The last term in equation (2.5) describes tau proteolytic degradation in proteasomes. Other terms in equation (2.5) describe transitions between free tau and tau in other kinetic states.

$$\begin{array}{rl}& D_{\mathrm{free}}^{\ast }\frac{{\mathrm{\partial }}^2{n}_{\mathrm{free}}^{\ast }}{\mathrm{\partial }{x^{\ast }}^2}+{\gamma }_{\mathrm{off},\mathrm{a}}^{\ast }{n}_{\mathrm{a}0}^{\ast }+{\gamma }_{\mathrm{off},\mathrm{r}}^{\ast }{n}_{\mathrm{r}0}^{\ast }-({\gamma }_{\mathrm{on},\mathrm{a}}^{\ast }+{\gamma }_{\mathrm{on},\mathrm{r}}^{\ast }+{\gamma }_{\mathrm{free}\to \mathrm{st}}^{\ast }+{\gamma }_{\mathrm{free}\to \mathrm{dif}}^{\ast })n_{\mathrm{free}}^{\ast }+{\gamma }_{\mathrm{st}\to \mathrm{free}}^{\ast }{n}_{\mathrm{st}}^{\ast }\\ & +{\gamma }_{\mathrm{dif}\to \mathrm{free}}^{\ast }{n}_{\mathrm{dif}}^{\ast }-k_1^{\ast }{n}_{\mathrm{free}}^{\ast }-k_2^{\ast }{n}_{\mathrm{free}}^{\ast }{n}_{\mathrm{mis}}^{\ast }-\frac{n_{\mathrm{free}}^{\ast }\ln (2)}{T_{1/2,\mathrm{free}}^{\ast }}=0.\end{array}$$ 2.5

In AD, tau is hyperphosphorylated; it detaches from MTs and agglomerates into neurofibrillary tangles (NFTs). Recent studies suggest that tau oligomers, the intermediates of the tau aggregation process, may be the true toxic species [44]. In order to model tau aggregation, we used the minimalistic 2-step Finke–Watzky (F-W) model. We assumed that monomeric, cytosolic tau (having a concentration $n_{\mathrm{free}}^{\ast }$) can form a polymeric aggregate (having a concentration $n_{\mathrm{mis}}^{\ast }$). In the F-W model, the aggregate is interpreted as an average tau polymer, representing many different fibril sizes. The model includes only two kinetic constants, $k_1^{\ast }$ and $k_2^{\ast }$, which are average rate constants describing nucleation and autocatalytic growth, respectively. The F-W model was shown to fit protein aggregation data in various neurological systems [45,46]. The use of the F-W model to simulate aggregation of tau protein in vitro was reported in ref. [47]. The F-W model provides an approximate representation of tau aggregation, but, counting for the lack of tau aggregation data in vivo and the lack of understanding of which tau intermediates are the exact toxic species, it is the best approach.

We interpret $n_{\mathrm{mis}}^{\ast }$ as the concentration of insoluble tau aggregates, which contain irreversibly phosphorylated tau species that do not move in the axon [13]. This is different from infectious seeds of aggregated tau that may move from cell to cell and act as prions [48–50]. It should also be noted that the exact identity of tau protein species that may be transmitted among neurons has not been identified yet [51].

Tau aggregation is a very slow process that may take years. Therefore, we assume that there are two timescales in our problem: a timescale of tau transport from the soma to the synapse (may be weeks) and the timescale for NFT formation (probably years). Owing to the long timescale for tau aggregation, we assume that the concentrations of tau protein in various kinetic states approximately reach their steady-state distributions along the axon. The only transient term that we keep in the model is the term on the left-hand side of equation (2.6), which describes accumulation of aggregated tau:

$$\frac{\mathrm{\partial }{n}_{\mathrm{mis}}^{\ast }}{\mathrm{\partial }{t}^{\ast }}=k_1^{\ast }{n}_{\mathrm{free}}^{\ast }+k_2^{\ast }{n}_{\mathrm{free}}^{\ast }{n}_{\mathrm{mis}}^{\ast }-\frac{n_{\mathrm{mis}}^{\ast }\ln (2)}{T_{1/2,\mathrm{mis}}^{\ast }}.$$ 2.6

The last term on the right-hand side of equation (2.6) describes degradation of the misfolded tau.

MT-bound tau is not all stationary, according to [28] approximately half of it can diffuse along MTs. We hypothesize that the ability to diffuse along the MT lattice exhibited by a sub-population of MT-bound tau can be explained by the different conformations that the MT-bound tau can take due to attachment through multiple weak binding sites [52]. The concentration of a sub-population of MT-bound tau that can diffuse is $n_{\mathrm{dif}}^{\ast }$. Stating its conservation gives the following equation:

$$D_{\mathrm{mt}}^{\ast }\frac{{\mathrm{\partial }}^2{n}_{\mathrm{dif}}^{\ast }}{\mathrm{\partial }{x^{\ast }}^2}-({\gamma }_{\mathrm{dif}\to \mathrm{free}}^{\ast }+{\gamma }_{\mathrm{dif}\to \mathrm{st}}^{\ast })n_{\mathrm{dif}}^{\ast }+{\gamma }_{\mathrm{free}\to \mathrm{dif}}^{\ast }{n}_{\mathrm{free}}^{\ast }+{\gamma }_{\mathrm{st}\to \mathrm{dif}}^{\ast }{n}_{\mathrm{st}}^{\ast }=0.$$ 2.7

The first term in equation (2.7) describes the effect of tau diffusion along the MT lattice; all other terms describe tau transitions between various kinetic states.

Finally, the conservation requirement for a sub-population of stationary MT-bound tau, which has concentration $n_{\mathrm{st}}^{\ast }$, gives the following equation:

$$-({\gamma }_{\mathrm{st}\to \mathrm{free}}^{\ast }+{\gamma }_{\mathrm{st}\to \mathrm{dif}}^{\ast })n_{\mathrm{st}}^{\ast }+{\gamma }_{\mathrm{free}\to \mathrm{st}}^{\ast }{n}_{\mathrm{free}}^{\ast }+{\gamma }_{\mathrm{dif}\to \mathrm{st}}^{\ast }{n}_{\mathrm{dif}}^{\ast }=0.$$ 2.8

The only reason for $n_{\mathrm{st}}^{\ast }$ to change is tau transition to/from a different kinetic state. Therefore, equation (2.8) contains only kinetic terms.

In order to find the total concentration of tau protein, we calculated the sum of tau concentrations over all eight kinetic states displayed in figure 2a, which also includes the concentration of misfolded tau $(n_{\mathrm{mis}}^{\ast })$:

$$n_{\mathrm{tot}}^{\ast }=n_{\mathrm{a}}^{\ast }+n_{\mathrm{r}}^{\ast }+n_{\mathrm{a}0}^{\ast }+n_{\mathrm{r}0}^{\ast }+n_{\mathrm{free}}^{\ast }+n_{\mathrm{st}}^{\ast }+n_{\mathrm{dif}}^{\ast }+n_{\mathrm{mis}}^{\ast }.$$ 2.9

We then used equation (2.9) to find the percentage of tau bound to MTs at a particular location in the axon (the numerator in equation (2.10) excludes concentrations of free (cytosolic) and misfolded tau):

$$\mathrm{\%}\mathrm{bound}=\frac{n_{\mathrm{a}}^{\ast }+n_{\mathrm{r}}^{\ast }+n_{\mathrm{a}0}^{\ast }+n_{\mathrm{r}0}^{\ast }+n_{\mathrm{st}}^{\ast }+n_{\mathrm{dif}}^{\ast }}{n_{\mathrm{tot}}^{\ast }}(100\mathrm{\%}).$$ 2.10

The total flux of tau, transported by diffusion-driven (both in the cytosol and on MTs) and motor-driven (on MTs) mechanisms, is given by the following equation:

$$j_{\mathrm{tot},\mathrm{tau}}^{\ast }=-D_{\mathrm{free}}^{\ast }\frac{\mathrm{\partial }{n}_{\mathrm{free}}^{\ast }}{\mathrm{\partial }{x}^{\ast }}-D_{\mathrm{mt}}^{\ast }\frac{\mathrm{\partial }{n}_{\mathrm{dif}}^{\ast }}{\mathrm{\partial }{x}^{\ast }}+v_{\mathrm{a}}^{\ast }{n}_{\mathrm{a}}^{\ast }-v_{\mathrm{r}}^{\ast }{n}_{\mathrm{r}}^{\ast }.$$ 2.11

As suggested in ref. [29], the average velocity of tau can be found as the ratio of the total flux of tau to its total concentration. This definition accounts for contributions of both diffusion-driven and motor-driven mechanisms to tau transport:

$$v_{\mathrm{av}}^{\ast }=\frac{j_{\mathrm{tot},\mathrm{tau}}^{\ast }}{n_{\mathrm{tot}}^{\ast }}.$$ 2.12

Note that $v_{\mathrm{av}}^{\ast }$ depends on x*.

Equations (2.1)–(2.8) require six boundary conditions and an initial condition for $n_{\mathrm{mis}}^{\ast }$. The following boundary conditions were postulated at the axon hillock.

At x* = 0:

$$\begin{array}{rl}{n}_{\mathrm{free}}^{\ast }& =n_{\mathrm{free},x=0}^{\ast },\end{array}$$ 2.13a

$$\begin{array}{rl}{j}_{\mathrm{tot},\mathrm{tau}}^{\ast }& =j_{\mathrm{tot},\mathrm{tau},x=0}^{\ast }\end{array}$$ 2.13b

$$\begin{array}{rl}\mathrm{and}{n}_{\mathrm{dif}}^{\ast }& =n_{\mathrm{dif},x=0}^{\ast }.\end{array}$$ 2.13c

Equation (2.13b) postulates the flux at which tau, synthesized in the soma, enters the axon. Values of parameters $n_{\mathrm{free},x=0}^{\ast }$, $j_{\mathrm{tot},\mathrm{tau},x=0}^{\ast }$, and $n_{\mathrm{dif},x=0}^{\ast }$ are found by determining the best-fit values that minimize the discrepancy between the model predictions and published experimental data. The best-fit values are given in electronic supplementary material, table S3. For details of how the discrepancy between the model predictions and experimental results is minimized see [30]. It is likely that in the beginning of AD, tau aggregation into NFTs plays a neuroprotective role by sequestering toxic tau oligomers [53,54]. Therefore, we assumed that slow accumulation of aggregated tau is not going to influence tau production in the soma for many years, until later stages of the disease. This justifies the use of steady-state values in equation (2.13).

At the axon terminal, we postulated the following boundary conditions.

At x* = L*.

$$\begin{array}{rl}& \frac{\mathrm{\partial }{n}_{\mathrm{free}}^{\ast }}{\mathrm{\partial }{x}^{\ast }}=0,\end{array}$$ 2.14a

$$\begin{array}{rl}& j_{\mathrm{tot},\mathrm{tau}}^{\ast }=j_{\mathrm{tot},\mathrm{tau},x=L}^{\ast }\end{array}$$ 2.14b

$$\begin{array}{rl}\mathrm{and}& \frac{\mathrm{\partial }{n}_{\mathrm{dif}}^{\ast }}{\mathrm{\partial }{x}^{\ast }}=0.\end{array}$$ 2.14c

Equation (2.14b) postulates that some of tau that enters the axon terminal is eventually destroyed there. The rest of tau is re-routed back by retrograde transport. This is consistent with published data indicating that tau is required for the maintenance of the synapse [55]. In ref. [30], we suggested the following expanded form of equation (2.14b):

$$-D_{\mathrm{free}}^{\ast }\frac{\mathrm{\partial }{n}_{\mathrm{free}}^{\ast }}{\mathrm{\partial }{x}^{\ast }}-D_{\mathrm{mt}}^{\ast }\frac{\mathrm{\partial }{n}_{\mathrm{dif}}^{\ast }}{\mathrm{\partial }{x}^{\ast }}+v_{\mathrm{a}}^{\ast }{n}_{\mathrm{a}}^{\ast }-v_{\mathrm{r}}^{\ast }{n}_{\mathrm{r}}^{\ast }=A\left(1-\exp \left[-\frac{\ln (2)}{T_{1/2}^{\ast }}\frac{1}{{\gamma }_{\mathrm{ar}}^{\ast }}\right]\right)v_{\mathrm{a}}^{\ast }{n}_{\mathrm{a}}^{\ast }.$$ 2.15

The left-hand side of equation (2.15) was obtained using equation (2.11). To obtain the right-hand side of equation (2.15), we used the argument suggested in ref. [56]. Tau enters the terminal moving anterogradely and in order to leave the terminal it must change the motors that propel it. We estimated the percentage of tau that is destroyed in the terminal while the motors are being switched. The right-hand side of equation (2.15) involves a dimensionless constant A that is determined by fitting model predictions with experimental results. The estimated value of A is given in electronic supplementary material, table S3.

The initial condition for the misfolded tau protein is:

At t* = 0:

$$n_{\mathrm{mis}}^{\ast }=0.$$ 2.16

(b). Governing equations simulating fast axonal transport of amyloid precursor protein

Because APP is transported by fast axonal transport, there are no pausing kinetic states in the kinetic diagram that is used to develop the model of APP transport (figure 2b). We consider the concentration of anterogradely transported APP, $c_{+}^{\ast }$, the concentration of retrogradely transported APP, $c_{-}^{\ast }$, and the concentration of free APP, $c_0^{\ast }$, which is not actively transported by molecular motors (figure 2b). Similar to tau, we characterize APP concentrations in these three kinetic states by their linear number densities, the number of APP molecules per unit length of the axon.

In order to simulate APP transport, we used the model of fast axonal transport [57,58]. Dependent variables are given in electronic supplementary material, table S4, independent variables are given in electronic supplementary material, table S2, and model parameters are given in electronic supplementary material, table S5. The conservation of anterogradely transported APP leads to the following equation:

$$-v_{+}^{\ast }\frac{\mathrm{d}{c}_{+}^{\ast }}{\mathrm{d}{x}^{\ast }}+{\alpha }_{+}^{\ast }{c}_0^{\ast }-{\alpha }_{+}^{\mathrm{\prime }\ast }{c}_{+}^{\ast }=0.$$ 2.17

The first term in equation (2.17) simulates the change of APP concentration because of kinesin-driven anterograde transport of APP, and the second and third terms describe transitions between anterogradely running and free kinetic states (figure 2b).

The conservation of retrogradely transported APP is represented by the following equation:

$$v_{-}^{\ast }\frac{\mathrm{d}{c}_{-}^{\ast }}{\mathrm{d}{x}^{\ast }}+{\alpha }_{-}^{\ast }{c}_0^{\ast }-{\alpha }_{-}^{\mathrm{\prime }\ast }{c}_{-}^{\ast }=0.$$ 2.18

The first term in equation (2.18) describes the change of APP concentration because of dynein-driven retrograde transport of APP, and the second and third terms describe transitions between retrogradely running and free kinetic states (figure 2b).

Parameters $v_{+}^{\ast }$ and $v_{-}^{\ast }$ in equations (2.17) and (2.18) denote APP velocities when APP-transporting vesicles are pulled by kinesin and dynein motors, respectively. These parameters are effective properties, and they are not necessarily the same as $v_{\mathrm{a}}^{\ast }$ and $v_{\mathrm{r}}^{\ast }$ in the model for tau transport.

APP is assumed to move in the axon in APP-transporting vesicles whose diffusivity is assumed negligible. The conservation of free APP gives the following equation:

$$-{\alpha }_{+}^{\ast }{c}_0^{\ast }-{\alpha }_{-}^{\ast }{c}_0^{\ast }+{\alpha }_{+}^{\mathrm{\prime }\ast }{c}_{+}^{\ast }+{\alpha }_{-}^{\mathrm{\prime }\ast }{c}_{-}^{\ast }=0,$$ 2.19

where $c_0^{\ast }$ is the concentration of free APP. All terms in equation (2.19) are kinetic terms describing transitions between anterogradely running, retrogradely running, and free kinetic states (figure 2b).

The APP half-life is estimated to be 4 h. As it would take longer to reach the synapse in long axons, it is logical to assume that APP, like many other cargos, is protected from degradation in the ubiquitin proteasome system during the transport [59]. The protection may be provided by a membrane of the vesicle in which APP is transported. Also, APP cleavage does not occur on vesicles during transport [17]. For this reason, we have not included any terms describing APP degradation in equations (2.17)–(2.19).

The total concentration of APP is the sum of APP concentrations in three kinetic states displayed in figure 2b:

$$c_{\mathrm{tot}}^{\ast }=c_{+}^{\ast }+c_{-}^{\ast }+c_0^{\ast }.$$ 2.20

The fluxes of anterogradely and retrogradely transported APP are given by the following equations, respectively:

$$j_{+,\mathrm{APP}}^{\ast }=v_{+}^{\ast }{c}_{+}^{\ast }$$ 2.21

and

$$j_{-,\mathrm{APP}}^{\ast }=v_{-}^{\ast }{c}_{-}^{\ast }.$$ 2.22

According to fig. 5a of ref. [60], approximately 50% of APP vesicles move anterogradely, 20% move retrogradely and 30% are stationary. Because $v_{+}^{\ast }$ and $v_{-}^{\ast }$ are constant in our model, if $j_{+,\mathrm{APP}}^{\ast }$ and $j_{-,\mathrm{APP}}^{\ast }$ are constant, then concentrations of anterogradely and retrogradely running APP, $c_{+}^{\ast }$ and $c_{-}^{\ast }$, are constant . We therefore searched for a solution of equations (2.17)–(2.19) with constant concentrations of APP in its three different kinetic states (figure 2b). We found the following solution:

$$c_{-}^{\ast }=\frac{{\alpha }_{-}^{\ast }{\alpha }_{+}^{\mathrm{\prime }\ast }}{{\alpha }_{+}^{\ast }{\alpha }_{-}^{\mathrm{\prime }\ast }}{c}_{+}^{\ast }$$ 2.23

and

$$c_0^{\ast }=\frac{{\alpha }_{+}^{\mathrm{\prime }\ast }}{{\alpha }_{+}^{\ast }}{c}_{+}^{\ast }.$$ 2.24

This solution is expected to hold for a healthy axon.

Using equations (2.21) and (2.22), and the percentage of anterogradely and retrogradely transported APP reported in ref. [60], we obtained that

$$\frac{c_{-}^{\ast }}{c_{+}^{\ast }}=0.4\frac{v_{+}^{\ast }}{v_{-}^{\ast }}.$$ 2.25

By comparing equation (2.23) and equation (2.25), we concluded that in order for the APP concentrations to be constant along the axon length, the following relation between the kinetic constants must be satisfied:

$$\frac{{\alpha }_{-}^{\ast }{\alpha }_{+}^{\mathrm{\prime }\ast }}{{\alpha }_{+}^{\ast }{\alpha }_{-}^{\mathrm{\prime }\ast }}=0.4\frac{v_{+}^{\ast }}{v_{-}^{\ast }}.$$ 2.26

Equation (2.25) suggests that if $c_{+}^{\ast }$ satisfies the following boundary condition:

$$c_{+}^{\ast }(0)=c_{+,x=0}^{\ast }$$ 2.27

then $c_{-}^{\ast }$ satisfies the following boundary condition:

$$c_{-}^{\ast }(L^{\ast })=0.4\frac{v_{+}^{\ast }}{v_{-}^{\ast }}{c}_{+,x=0}^{\ast }.$$ 2.28

Because equation (2.22) establishes a direct relation between $j_{-,\mathrm{APP}}^{\ast }$ and $c_{-}^{\ast }$, equation (2.28) postulates a retrograde flux of APP from the synapse back to the axon. The retrograde flux postulated by equation (2.28) is supported by the observation that some vesicles transporting APP can fuse with the acceptor membrane at the presynaptic terminal [61]. A fraction of anterogradely transported APP protein is then returned to the soma by retrograde transport [61,62].

Note that the boundary condition for $c_{+}^{\ast }$ must be imposed in the beginning of the axon, at x* = 0, while the boundary condition for $c_{-}^{\ast }$ must be imposed at the end of the axon, at x* = L*. These boundary conditions can be used for solving equations (2.17)–(2.19) when conditions in the axon deviate from a healthy axon and the APP concentrations along the axon are not constant.

The total APP flux towards the synapse (anterograde minus retrograde flux) can be calculated as follows:

$$j_{\mathrm{tot},\mathrm{APP}}^{\ast }=v_{+}^{\ast }{c}_{+}^{\ast }-v_{-}^{\ast }{c}_{-}^{\ast }.$$ 2.29

(c). Numerical solution of differential equations

Equations (2.1)–(2.5), (2.7), (2.8), (2.17)–(2.19) include ordinary differential (containing various derivatives with respect to x*) and algebraic equations. The algebraic equations were used to eliminate $n_{\mathrm{a}0}^{\ast }(x^{\ast })$, $n_{\mathrm{r}0}^{\ast }(x^{\ast })$, $n_{\mathrm{st}}^{\ast }(x^{\ast })$, and $c_0^{\ast }(x^{\ast })$, and the boundary value problem for the remaining equations was solved using Matlab's BVP4C solver (Matlab R2016b, MathWorks, Natick, MA, USA). Equation (2.6) is an ordinary differential equation containing a derivative of the concentration of misfolded tau, $n_{\mathrm{mis}}^{\ast }$, with respect to t*. As the production of misfolded tau occurs very slowly, we can use the QSSA and separate the timescales, postulating that for each moment of time equations (2.1)–(2.5), (2.7), (2.8), (2.17)–(2.19) can be solved assuming that $n_{\mathrm{mis}}^{\ast }$ depends only on x*. The change of $n_{\mathrm{mis}}^{\ast }$ with time was then found by integrating equation (2.6) with respect to time. At t* = 0, there is no misfolded tau, which allows finding tau concentrations in all other kinetic states by solving equations (2.1)–(2.5), (2.7), (2.8), (2.17)–(2.19). Time was advanced by a timestep Δt*, $n_{\mathrm{mis}}^{\ast }(x^{\ast })$ was obtained for a new time, and the steady-state problem given by equations (2.1)–(2.5), (2.7), (2.8), (2.17)–(2.19) was solved again. This procedure was repeated until $n_{\mathrm{mis}}^{\ast }(x^{\ast })$ reached a steady-state distribution when the production of misfolded tau is balanced by its destruction due to a finite half-life of misfolded tau, see equation (2.6). We found that under physiologically reasonable conditions (see the explanation before equation (3.5) for how we selected values of $k_1^{\ast }$ and $k_2^{\ast }$), the rate of production of misfolded tau is so small that the remaining concentrations do not visibly deviate from their steady-state distributions at any time (figures 3 and 4). We used the default settings of BVP4C solver and we checked that our numerical solution is not affected by reducing values of error tolerance parameters of the solver and the chosen value of Δt*.

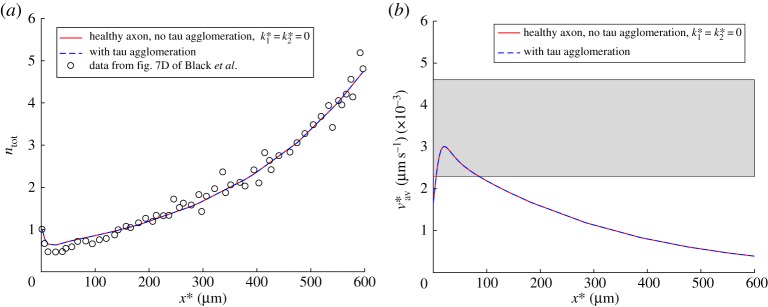
Figure 3.

(a) A comparison between model predictions and experimental results reported in fig. 7D of ref. [31] for the dimensionless total concentration of tau protein, $n_{\mathrm{tot}}=n_{\mathrm{tot}}^{\ast }/n_{\mathrm{tot},x=0}^{\ast }$. Experimental data were rescaled such that n_tot at x* = 0 was equal to unity. (b) A comparison between model predictions of the average tau velocity, defined by equation (2.12), and the experimental range for this quantity reported in ref. [32] (shown by a horizontal band). To demonstrate that even for the case with tau agglomeration, all components of the total tau concentration, except for n_mis, can be computed from steady-state equations (see equations (2.1)–(2.5), (2.7) and (2.8)), we show computational results for a healthy axon (with no tau agglomeration) and for an axon with tau agglomeration. Results with tau agglomeration are shown at the time when n_mis(x*) reaches its steady-state distribution. (Online version in colour.)

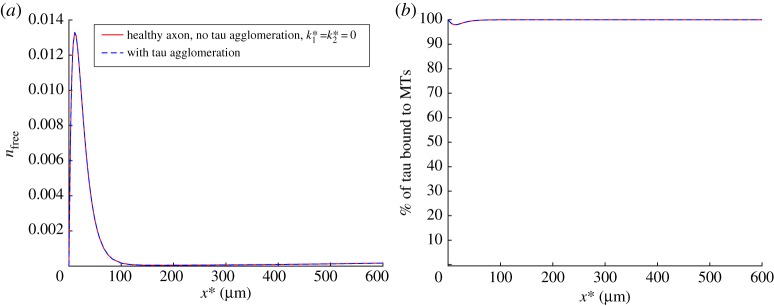
Figure 4.

(a) Dimensionless concentration of free cytosolic tau, $n_{\mathrm{free}}=n_{\mathrm{free}}^{\ast }/n_{\mathrm{tot},x=0}^{\ast }$, versus position in the axon. Free tau can polymerize and be converted to the misfolded tau, see equation (2.6). (b) Percentage of MT-bound tau, defined by equation (2.10), versus position in the axon. Modelling results without tau agglomeration and with tau agglomeration are shown to validate the QSSA for computing distributions of tau concentrations in various kinetic states along the axon. Results with tau agglomeration are shown at the time when n_mis(x*) reaches its steady-state distribution. (Online version in colour.)

3. Results

(a). Simulating the effect of tau agglomeration on amyloid precursor protein transport. Estimating values of rate constants $k_1^{\ast }$ and $k_2^{\ast }$ in the F-W model for simulating tau agglomeration

Equation (2.6) can be re-written using the dimensionless concentrations:

$$\frac{\mathrm{\partial }{n}_{\mathrm{mis}}}{\mathrm{\partial }{t}^{\ast }}=k_1^{\ast }{n}_{\mathrm{free}}+(k_2^{\ast }{n}_{\mathrm{tot},x=0}^{\ast })n_{\mathrm{free}}{n}_{\mathrm{mis}}-\frac{n_{\mathrm{mis}}\ln (2)}{T_{1/2,\mathrm{mis}}^{\ast }},$$ 3.1

where $n_{\mathrm{mis}}=n_{\mathrm{mis}}^{\ast }/n_{\mathrm{tot},x=0}^{\ast }$ and $n_{\mathrm{free}}=n_{\mathrm{free}}^{\ast }/n_{\mathrm{tot},x=0}^{\ast }$.

As explained in footnote ‘c’ after electronic supplementary material, table S5, to simulate a healthy axon (no misfolded tau), we set kinetic constants ${\alpha }_{-}^{\ast }$, ${\alpha }_{+}^{\ast }$, and ${\alpha }_{-}^{\mathrm{\prime }\ast }$ to 1 s⁻¹ and we set ${\alpha }_{+}^{\mathrm{\prime }\ast }$ to 0.4609 s⁻¹ to satisfy equation (2.26). Although the precise mechanism of regulation of APP transport is a subject of a debate [63], there are published data that suggest that the formation of tau oligomers may inhibit anterograde transport. The inhibition involves the following steps. Filamentous tau activates protein phosphatase 1, which dephosphorylates and activates glycogen synthase kinase-3β (GSK-3β). This, in turn, leads to phosphorylation of kinesin-1 light chain, which facilitates kinesin-1 detachment from its cargos [64,65]. In our model, this effect can be simulated by the increase of ${\alpha }_{+}^{\mathrm{\prime }\ast }$, a kinetic constant that simulates the detachment of APP-transporting vesicles from MTs. Because it was reported that membrane association of kinesin-1 could be reduced by 50% [64], we estimated that tau agglomeration could increase a value of ${\alpha }_{+}^{\mathrm{\prime }\ast }$ by at most a factor of two. In order to simulate the effect of misfolded tau on APP transport, we assumed a simple linear correlation between ${\alpha }_{+}^{\mathrm{\prime }\ast }$ and $n_{\mathrm{mis}}^{\ast }$:

$${\alpha }_{+}^{\mathrm{\prime }\ast }=(0.4609\hspace{0.17em}{\mathrm{s}}^{-1})(1+\beta n_{\mathrm{mis}}).$$ 3.2

Note that tau inhibits dynein to a much lesser extent than it inhibits kinesin-1 [66–68]; therefore, any effects of tau on dynein are neglected in this study.

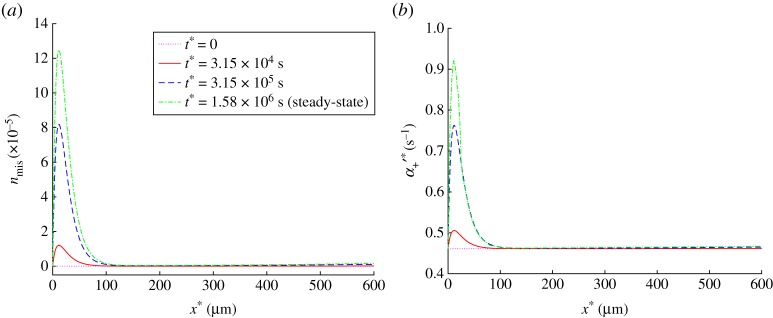
A value of $\beta =8\times {10}^3$ in equation (3.2) was found by performing numerical experiments so that the ratio of a steady-state value of ${\alpha }_{+}^{\mathrm{\prime }\ast }$ to the initial value of ${\alpha }_{+}^{\mathrm{\prime }\ast }$ would be equal to two at the location in the axon where most of misfolded tau accumulates at steady-state (compare figure 5a and 5b).

Figure 5.

(a) Dimensionless concentration of the misfolded tau protein, $n_{\mathrm{mis}}=n_{\mathrm{mis}}^{\ast }/n_{\mathrm{tot},x=0}^{\ast }$, versus position in the axon. At steady state, the production of misfolded tau is balanced by its destruction. (b) Kinetic constant describing the probability of APP transition from the anterograde running state to the free state versus position in the axon. Equation 3.2 was used to simulate the dependence of ${\alpha }_{+}^{\mathrm{\prime }\ast }$ on n_mis. Results are shown at the initial (t* = 0) and steady-state conditions as well as at two intermediate times. (Online version in colour.)

The neural concentration of tau is estimated to be 2 µM [47,69]. Neurofibrillary tangles appear years (possibly 10–20 years) before the onset of clinically detectable symptoms of AD [70].

The initial rescaled concentration of monomeric tau is $A_0/(1\hspace{0.17em}\mu \mathrm{M})$, where A₀ is measured in μM and the rescaled concentration is dimensionless. Then the half-time, at which half of monomeric tau is converted to the misfolded tau aggregate, can be calculated from the following equation [46]:

$$t_{50}=\ln \left(2+\frac{k_2^{\ast }{n}_{\mathrm{tot},x=0}^{\ast }}{k_1^{\ast }}\frac{A_0}{1\hspace{0.17em}\mu \mathrm{M}}\right){\left[k_1^{\ast }+k_2^{\ast }{n}_{\mathrm{tot},x=0}^{\ast }\frac{A_0}{1\hspace{0.17em}\mu \mathrm{M}}\right]}^{-1}.$$ 3.3

The maximum slope of the misfolded protein concentration, denoted by B(t*), can be found from the following equation [71]:

$${\left(\frac{1}{1\hspace{0.17em}\mu \mathrm{M}}\frac{\mathrm{d}B}{\mathrm{d}{t}^{\ast }}\right)}_{max}={\left(k_1^{\ast }+k_2^{\ast }{n}_{\mathrm{tot},x=0}^{\ast }\frac{A_0}{1\hspace{0.17em}\mu \mathrm{M}}\right)}^2{[4k_2^{\ast }{n}_{\mathrm{tot},x=0}^{\ast }]}^{-1}.$$ 3.4

In order to obtain estimates of $k_1^{\ast }$ and $(k_2^{\ast }{n}_{\mathrm{tot},x=0}^{\ast })$, we assumed the following. The initial concentration of tau monomer is assumed to be 2 µM. If all tau in a single neuron is converted into its aggregated form in one year, then t₅₀ = 0.5 year. Also, if all tau (2 µM) is converted into a polymer within one year, it is reasonable to assume that ${(\mathrm{d}B/\mathrm{d}{t}^{\ast })}_{max}=2\hspace{0.17em}\mu \mathrm{M}\hspace{0.17em}{\mathrm{yr}}^{-1}$. This can be restated as $((\mathrm{d}B/{(1\hspace{0.17em}\mu \mathrm{M}))/\mathrm{d}{t}^{\ast })}_{max}=2\hspace{0.17em}\mathrm{yr}{\hspace{0.17em}}^{-1}$. Converting years into seconds and solving equations (3.3) and (3.4) for $k_1^{\ast }$ and $k_2^{\ast }$ gives that

$$k_1^{\ast }=3.011\times {10}^{-8}\hspace{0.17em}{\mathrm{s}}^{-1},(k_2^{\ast }{n}_{\mathrm{tot},x=0}^{\ast })=2.727\times {10}^{-8}\hspace{0.17em}{\mathrm{s}}^{-1}.$$ 3.5

The concentration of misfolded tau protein will continue growing until the rate of its production becomes equal to the rate of its destruction due to the assumed finite half-life of misfolded tau. The steady-state concentration can be found by setting the right-hand side of equation (3.1) to zero:

$$n_{\mathrm{mis},\mathrm{ss}}=\frac{k_1^{\ast }{n}_{\mathrm{free}}{T}_{1/2,\mathrm{mis}}^{\ast }}{-(k_2^{\ast }{n}_{\mathrm{tot},x=0}^{\ast })n_{\mathrm{free}}{T}_{1/2,\mathrm{mis}}^{\ast }+\ln (2)}.$$ 3.6

For n_free, we used its maximum value of 0.013 from figure 4a. Taking values of other parameters in equation (3.6) from electronic supplementary material, table S3, we obtained $n_{\mathrm{mis},\mathrm{ss}}=12.2\times {10}^{-5}$, which corresponds to the maximum steady-state value in figure 5a.

(b). Quantifying the effect of tau agglomeration on amyloid precursor protein transport

In this paper, we have explored the possibility of using a steady-state solution describing tau protein distribution along the axon, which we reported in ref. [30], in order to simulate tau transport for the situation when there is agglomeration of misfolded tau protein. The idea is that tau agglomeration is a very slow process, which usually takes years [72], and therefore tau transport in an axon can be modelled as quasi-steady, where various components of the total tau concentration (except for the misfolded tau) are found from corresponding steady-state equations (see equations (2.1)–(2.5), (2.7) and (2.8)). To validate this idea, we compared distributions of the total tau concentration (figure 3a) and the average tau velocity (figure 3b) computed with and without tau agglomeration. We measured the distance between distributions computed with and without tau agglomeration by using the L² distance [73], see equation (S1) in the electronic supplementary material. The case with no tau agglomeration was computed by setting both $k_1^{\ast }$ and $k_2^{\ast }$ in equation (2.6) equal to zero, which resulted in n_mis= 0. We also compared the distributions of the free (cytosolic) tau (figure 4a) and the percentage of MT-bound tau (figure 4b) computed with and without tau agglomeration. The results displayed in figures 3 and 4 suggest that tau agglomeration, at low physiological rates typical for AD, does not cause any deviation of the quantities characterizing tau transport (such as the concentrations of tau in various kinetic states displayed in figure 2a, and the average tau velocity) from their steady-state distributions computed without tau agglomeration.

The concentration of misfolded tau (figure 5a) increases in the beginning of the axon until it reaches the steady-state distribution, at which production of misfolded tau (described by the first two terms on the right-hand side of equation (2.6)) is balanced by destruction of misfolded tau (described by the third term on the right-hand side of equation (2.6)). Tau aggregates at small distances from the cell body because this is the region of the axon where free (cytosolic) tau is present (figure 4a). In our model, we assumed that only free tau is converted into misfolded tau aggregate (equation (2.6)), because tau must be able to move in the cytosol in order to agglomerate. The result in figure 5a is supported by observations that initially aggregated forms of hyperphosphorylated tau appear in the proximal axon [13,74]. Infectious seeds of misfolded tau protein may enter a neuron and move in it by using cellular transport machinery, but it is more likely that they will start growing by attaching more tau molecules in the proximal axon due to the high concentration of free tau in this region.

In order to simulate the effect of tau agglomeration on APP transport, we assumed that the presence of misfolded tau increases the probability of detachment of APP-transporting vesicles from kinesin-1. This detachment process is modelled by the kinetic constant ${\alpha }_{+}^{\mathrm{\prime }\ast }$, which we assumed to be linearly correlated with n_mis (equation (3.2)). The distributions of ${\alpha }_{+}^{\mathrm{\prime }\ast }(x^{\ast })$ (figure 5b) suggest that agglomeration of misfolded tau in the beginning of the axon leads to the increased likelihood of APP being released by kinesin-1 motors in this region.

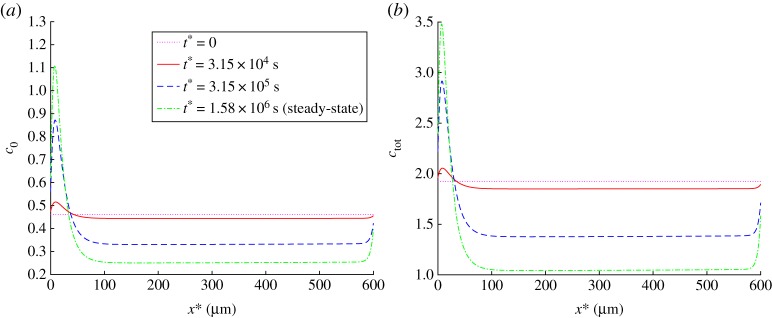
Tau agglomeration in the beginning of the axon results in an increased concentration of APP in the beginning of the axon and in a decreased concentration of APP in the rest of the axon. This applies to APP concentrations in various kinetic states (c₊, c₋ and c₀, see figures 6a,b and 7a) and to the total APP concentration (figure 7b). Because we simulated steady-state APP transport in the axon, and there is no APP destruction during its transport in the axon, the flux of APP is independent of x*. However, tau agglomeration in the beginning of the axon (figure 5a) results, due to APP release by kinesin-1, in increased APP concentration in the beginning of the axon (figure 7b). This leads to a significant reduction of the APP flux towards the synapse (by approximately a factor of two, figure 8).

Figure 6.

(a) Dimensionless concentration of anterogradely running APP, $c_{+}=c_{+}^{\ast }/c_{+,x=0}^{\ast }$. (b) Dimensionless concentration of retrogradely running APP, $c_{-}=c_{-}^{\ast }/c_{+,x=0}^{\ast }$. Results are shown at the initial (t* = 0) and steady-state conditions as well as at two intermediate times. (Online version in colour.)

Figure 7.

(a) Dimensionless concentration of free APP, $c_0=c_0^{\ast }/c_{+,x=0}^{\ast }$. (b) Dimensionless total concentration of APP (anterogradely running plus retrogradely running plus free APP), $c_{\mathrm{tot}}=c_{\mathrm{tot}}^{\ast }/c_{+,x=0}^{\ast }$. Results are shown at the initial (t* = 0) and steady-state conditions as well as at two intermediate times. (Online version in colour.)

Figure 8.

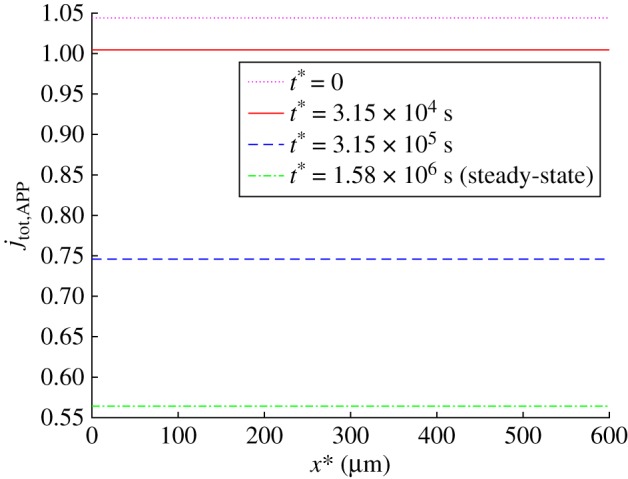
Dimensionless total flux of APP towards the synapse, $j_{\mathrm{tot},\mathrm{APP}}=j_{\mathrm{tot},\mathrm{APP}}^{\ast }/(c_{+,x=0}^{\ast }{v}_{+}^{\ast })$. Results are shown at the initial (t* = 0) and steady-state conditions as well as at two intermediate times. (Online version in colour.)

The results displayed in figures 7b and 8 suggest that tau agglomeration can lead to the axon losing APP. This seems to be in line with an experimentally observed trend reported in ref. [20], where it was noted that tau enrichment leads to the axon becoming depleted of APP vesicles, which causes an increase of APP concentration in the cell body, leading to APP cleavage and aggregation in the extracellular space. The reason for the axon becoming depleted of APP vesicles is the reduced APP flux in the axon (figure 8). If APP production in the soma is not reduced, the produced APP must accumulate in the soma where it could be cleaved by β- and γ-secretases and then assembled in amyloid-β. It is possible that the reduction of APP flux to the synapse (figure 8) can be sensed by the synapse and stimulate even more APP production in the soma via retrograde signalling.

The observed increase of APP concentration in the beginning of the axon (figure 7b) can be interpreted as a traffic jam (blockage). The question is whether such traffic jams, which may appear as swellings and can mark early AD [75,76], can be causative for the axonal transport deficits and thus lead to ‘dying back’ axonal degeneration. Indeed, the results reported in ref. [75] suggest that axonal swellings may precede amyloid deposition. An alternative hypothesis is that traffic jams associated with axonal swellings are merely symptoms of axonal transport failure. In support of the later hypothesis, direct observations have shown that various organelles, such as mitochondria, could move vigorously within such traffic jam regions and could also pass through them [77].

Although our results show that an APP traffic jam (figure 7b) is associated with a reduction of APP flux (figure 8), our model suggests that the traffic jam is merely a symptom rather than a cause for the reduction of the APP flux towards the synapse. The cause is toxicity of tau oligomers, which lead to kinesins releasing their cargos. In our model, the released APP cargos, which accumulate in the beginning of the axon, do not do anything to prevent APP transport towards the synapse, they simply indicate that there is weak association between kinesin-1 motors and kinesin cargo. The reduction of cargo transport towards the synapse is caused by weakening the affinity between kinesin motors and their cargo rather than by cargo accumulation in a certain location in the axon.

4. Conclusion and future directions

We developed a model that describes the effects of tau transport and agglomeration in the axon on APP transport in the axon. Because the timescale for tau agglomeration (years) is much larger than the timescale for tau transport in the axon (weeks), we proposed to use the QSSA in order to formulate and solve governing equations for our model. This approximation implies that tau agglomeration occurs so slowly that tau concentrations in all other kinetic states (figure 2a) have steady-state distributions.

Our results suggest that tau would initially aggregate in the beginning of the axon. Toxic tau species would cause kinesin-1 motors to release their APP cargos in that region. The APP concentration in the beginning of the axon would also increase. This increased APP concentration could be interpreted as a traffic jam (blockage). However, our model suggests that rather than being the cause of the axonal transport deficiency in AD, traffic jams (blockages) of FAT cargos may be merely symptoms of this deficiency. The real cause may be the effect of toxic tau products on interactions between the APP-transporting vesicles and kinesin motors. This theoretical prediction should be taken cautiously and more research addressing the effects of traffic blockages is needed before mechanisms of Aβ production and dying back axonal degeneration are fully elucidated. Investigating causative factors for axonal transport deficiencies in AD is important for determining therapeutic interventions that could stop or postpone the development of the disease.

In future research, the model should be expanded to include a possible dependence of APP metabolic processing on Aβ deposition, which may lead to enhanced Aβ production [62,78]. A model of APP cleavage and Aβ aggregation should also be developed.

Data accessibility

Additional data accompanying this paper are available in the electronic supplementary material.

Authors' contributions

I.A.K. and A.V.K. contributed equally to the performing of computational work and article preparation.

Competing interests

We declare we have no competing interests.

Funding

A.V.K. acknowledges funding from the National Science Foundation (award no. CBET-1642262).