Microstructural origin of resistance–strain hysteresis in carbon nanotube thin film conductors

Significance

An essential building block for stretchable electronics, the enabler of novel wearable and biological technologies, is stretchable conductors that can maintain good electrical conductivity under large deformation. A widely used approach to meet this need is to use a network of 1D nanomaterials, such as carbon nanotubes, as a thin film on a stretchable substrate. When these networks are subjected to stretching and unloading cycles, electrical resistance shows a hysteretic dependence on strain, but the underlying mechanism is poorly understood. We have answered this question by combining computer simulations, analytic modeling, and experiments, finding that the hysteretic resistance–strain relationship is controlled by a single microstructural parameter ξ, the ratio of the mean projected carbon nanotube length over the film length.

Abstract

A basic need in stretchable electronics for wearable and biomedical technologies is conductors that maintain adequate conductivity under large deformation. This challenge can be met by a network of one-dimensional (1D) conductors, such as carbon nanotubes (CNTs) or silver nanowires, as a thin film on top of a stretchable substrate. The electrical resistance of CNT thin films exhibits a hysteretic dependence on strain under cyclic loading, although the microstructural origin of this strain dependence remains unclear. Through numerical simulations, analytic models, and experiments, we show that the hysteretic resistance evolution is governed by a microstructural parameter $\xi$ (the ratio of the mean projected CNT length over the film length) by showing that $\xi$ is hysteretic with strain and that the resistance is proportional to ${\xi }^{-2}$. The findings are generally applicable to any stretchable thin film conductors consisting of 1D conductors with much lower resistance than the contact resistance in the high-density regime.

Stretchable electronic devices are in great demand in wearable and biomedical electronics (1–3). However, electronic materials are usually not intrinsically stretchable. The common strategies to endow electronics with the capability of large deformation include isolating the active components from a large external strain by rigid island designs, fabricating interconnects into tortuous shapes, and making electronic components in a buckled pattern using surface instability (1–6). Networks of one-dimensional (1D) materials, such as carbon nanotubes (CNTs) (7–18) or silver nanowires (19–22), on top of a stretchable substrate offer an alternative way to realize stretchability of electronic materials. They have been widely used for stretchable transistors (8, 23), sensors (9), and actuators (24). The electrical resistance of a thin CNT film has been found to increase with increasing strain but remains almost constant as strain is released, forming a hysteresis between loading and unloading (8, 9, 15, 16, 22, 25). However, the microstructural origin of this strain dependence remains unclear (26–30). In this paper, we investigate the relation among the loading and unloading cycles, the network morphological evolution, and the resistance change via coarse-grained molecular statics (CGMS) simulations, analytic modeling, and experiments. Through this combined approach, we successfully identify a single microstructural parameter that governs the resistance–strain hysteresis of CNT thin film conductors.

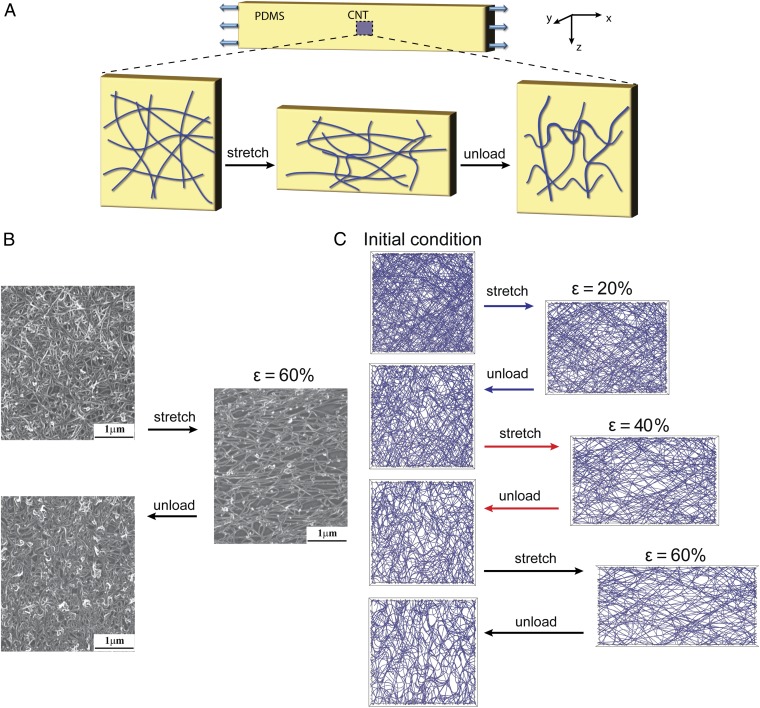
We fabricate conducting CNT thin films by spray coating a well-dispersed solution of single-wall CNTs with diameters 1.2–1.7 nm in N-methyl-2-pyrrolidone (NMP) solvent onto a polydimethylsiloxane (PDMS) substrate (Methods and Fig. 1A). The PDMS substrate is then repeatedly stretched to increasing levels of strain followed by unloading to zero strain. Fig. 1B shows the morphology of the CNT films before, during, and after the stretching by in situ scanning electron microscopy (SEM).

Fig. 1.

Morphology of a thin film CNT network under a cyclical loading. (A) Schematics of the experiment. A PDMS substrate with a CNT thin film sprayed undergoes stretching and unloading cycles. During stretching, the CNTs reorient to the stretching direction and slide between each other, while during unloading, the CNTs buckle in the stretching direction and bundle with each other. (B) SEM images showing the morphology of a CNT conductor spray coated on a PDMS substrate before, during, and after a 60% strain. (C) CGMS simulation results of the morphology of a CNT network under three sequentially increasing strain cycles of 20, 40, and 60%. The CNT network is composed by $N_{CNT}=135$ CNTs with length $l_{CNT}=\mathrm{2,400}\hspace{0.17em}\text{nm}$ and diameter $d_{CNT}=1\hspace{0.17em}\text{nm}$, each discretized by $N_{\text{node}}=120$ nodes, in a simulation cell with $H_x=H_z=\mathrm{1,200}\hspace{0.17em}\text{nm}$.

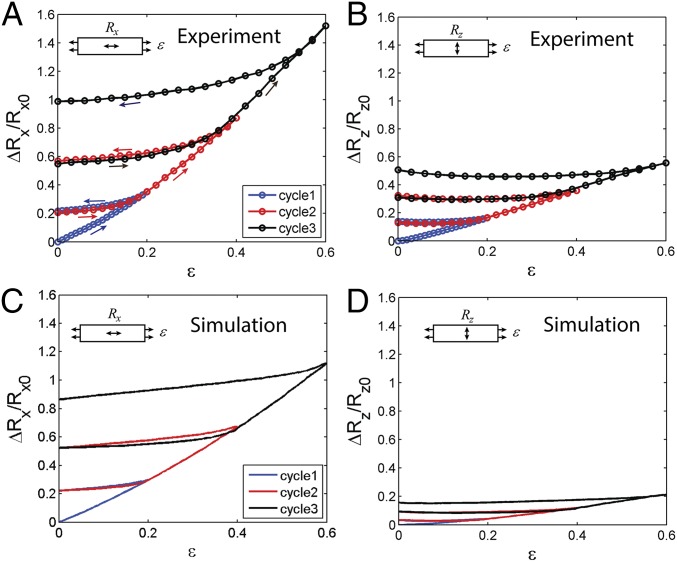
Fig. 2 A and B plot the measured resistance change $\mathrm{\Delta }R$ normalized by the initial resistance $R_0,$ $\mathrm{\Delta }R/R_0$, as a function of the strain in the stretching (x) direction and the in-plane transverse (z) direction, respectively (SI Appendix, Fig. S1 shows the experimental setup). The resistances in both x and z directions increase during the initial loading and remain almost constant during the unloading, forming a hysteresis loop, as indicated by arrows in Fig. 2A. When the sample is reloaded, the resistance stays near the same constant value until the previous maximal strain is reached. When the loading strain exceeds the previous maximal strain, the resistance increases again with the strain. The relative resistance change in the z direction $\mathrm{\Delta }{R}_z/R_{z0}$ (Fig. 2B) is smaller than that in the x direction $\mathrm{\Delta }{R}_x/R_{x0}$ (Fig. 2A). These observations are consistent with previous reports (8, 9, 15, 16), but here, the resistances in both in-plane directions are measured under multiple strain cycles.

Fig. 2.

Resistance change as a function of strain under a cyclical loading. Experimental (A and B) and CGMS simulation (C and D) results of the resistance change in the stretching direction $\mathrm{\Delta }{R}_x/R_{x0}$ (A and C) and transverse direction $\mathrm{\Delta }{R}_z/R_{z0}$ (B and D) under three sequentially increasing strain cycles of 20, 40, and 60%. The CNT network is composed of $N_{CNT}=135$ CNTs with length $l_{CNT}=\mathrm{2,400}\hspace{0.17em}\text{nm}$ and diameter $d_{CNT}=1\hspace{0.17em}\text{nm}$, each discretized by $N_{\text{node}}=120$ nodes, in a simulation cell with $H_x=H_z=\mathrm{1,200}\hspace{0.17em}\text{nm}$. The contact resistance is set as $R_{\text{contact}}=200\hspace{0.17em}\text{k}\mathrm{\Omega }$, and the resistance of a single CNT is set as $R_{CNT}=17.3\hspace{0.17em}\text{k}\mathrm{\Omega }$.

The evolution of the electrical resistance with strain means that the morphology of the CNT network must have been changed by the stretching of the film. However, is it possible to pinpoint a quantifiable microstructure feature that explains the resistance dependence on strain? A satisfactory answer to this question must meet two conditions. First, we must explain why the identified microstructure feature evolves with strain in a hysteretic manner. Second, we must explain how the identified microstructure feature controls the electrical resistance. Accomplishing these tasks would represent a significant advance in understanding the microstructural origin of the resistance in stretchable conductors and will enable rational design of materials for stretchable electronics that may be subjected to complex loading paths during fabrication and usage.

To answer this question, we start by constructing a CGMS model of a thin film single-wall CNT network, in which each CNT is discretized into a series of nodes connected by straight segments. Nodes on the same CNT interact with their neighbors through a bond potential that represents the stretching and bending stiffness of the CNT. Nodes on different CNTs interact with each other through van der Waals interactions represented by a Lennard–Jones potential (17, 31–33) (Methods and SI Appendix, section S1). The long-range attraction and short-range repulsion of the substrate are modeled by an external potential applied to all nodes (SI Appendix, section S1). Periodic boundary conditions are applied in the x and z directions (i.e., within the plane of the CNT film) (Fig. 1A). For simplicity, the initial configurations of the CNTs were created as randomly oriented straight lines parallel to the substrate surface. Stretching of the CNT film is simulated by elongating the simulation cell in the x direction and contracting in the z direction in small increments, allowing all nodes to relax to a local energy minimum after each increment based on the conjugate–gradient algorithm. Fig. 1C shows an example of the morphology change of the CNT film during cyclic loading from the CGMS simulations. The initial simulation cell has in-plane dimensions of $H_x=H_z=\mathrm{1,200}\hspace{0.5em}\text{nm}$ and contains $N_{CNT}=135$ CNTs, each with length $l_{CNT}=\mathrm{2,400}\hspace{0.5em}\text{nm}$ and diameter $d_{CNT}=1\hspace{0.17em}\text{nm}$. It is interesting to note that, after a few strain cycles, the predicted CNT network structure becomes progressively more similar to the SEM observations (Fig. 1B). In particular, the CNTs become more curved and form thicker bundles. We observe that, during loading, some CNT bundles that are well-aligned to the x direction break apart through an unzipping process, allowing the CNTs to move away from each other (SI Appendix, Fig. S2)—for brevity, we shall refer to this mechanism as sliding between CNTs. During unloading, these CNTs buckle (Movie S1). When the CNT film is stretched again in the x direction, the CNTs first straighten out (i.e., undoing the buckling that occurred during the unloading phase). Sliding between CNTs previously within the same bundle occurs again when the strain exceeds the maximal strain in the previous loading cycle.

The CGMS model allows us to predict the resistance evolution with strain by considering the relaxed CNT structure after each strain increment as a network of resistors and computing the overall resistance R. Specifically, charge transport along each CNT is described by assigning a resistance $R_{\text{node}}$ between neighboring nodes on the same CNT. Charge transport between CNTs is described by assigning a (much larger) contact resistance $R_{\text{contact}}$ between nodes on different CNTs that are within a contact radius $r_{\text{contact}}$ (SI Appendix, section S2). Although the CNT network in the experiments contains both metallic and semiconducting tubes, the above approximation is still reasonable for the following reasons. If the semiconducting CNTs are highly doped in an ambient environment, their properties become comparable with those of metallic ones (34, 35). Semiconducting CNTs on nonpolar substrates, such as the PDMS used in this work, typically exhibit minimal doping and consequently, have much higher tube resistance and contact resistance (36, 37). In this case, their contribution to the conductance can be neglected. In both situations, the CNTs can be modeled as a uniform network of resistors. Here, we assume that the end-to-end resistance of a single CNT is $R_{CNT}=17.3\hspace{0.17em}\text{k}\mathrm{\Omega }$ (38–40), and therefore, the resistance between neighboring nodes is $R_{\text{node}}={R_{CNT}/N}_{\text{node}}$, with N_node being the number of nodes on each CNT. The contact resistance is assumed to be $R_{\text{contact}}=200\hspace{0.17em}\text{k}\mathrm{\Omega }$ (40–42). (We find that the overall resistance of the CNT film is insensitive to the exact value of R_CNT as long as it is much lower than R_contact.) Fig. 2 C and D plot the predicted relative change of resistance, $\mathrm{\Delta }R/R_0$, in x and z directions, respectively, for the same CNT structures shown in Fig. 1C. We have verified that the result is not sensitive to the simulation cell size (SI Appendix, Fig. S3) and contact radius $r_{\text{contact}}$ (SI Appendix, Fig. S4). Most CGMS results, including ones shown in Fig. 2 C and D, are the average of around 10 simulations to eliminate any possible nonuniformity from a single simulation. A typical result of the resistance evolution from a single simulation is shown in SI Appendix, Fig. S5. The CGMS predictions and the experimental results are plotted together in SI Appendix, Fig. S6. The evolution of the relative sheet resistance is shown in SI Appendix, Fig. S7.

The predicted resistance–strain curves (Fig. 2 C and D and SI Appendix, Fig. S6) show striking resemblance with the experimental data (Fig. 2 A and B) in both x and z directions. The remaining differences between the CGMS predictions and experimental results (e.g., in the transverse direction) can be attributed to the idealizations in the simulation model, including straight CNTs as initial configurations, uniform length of CNTs, and the simplified description of the CNT–substrate interaction.

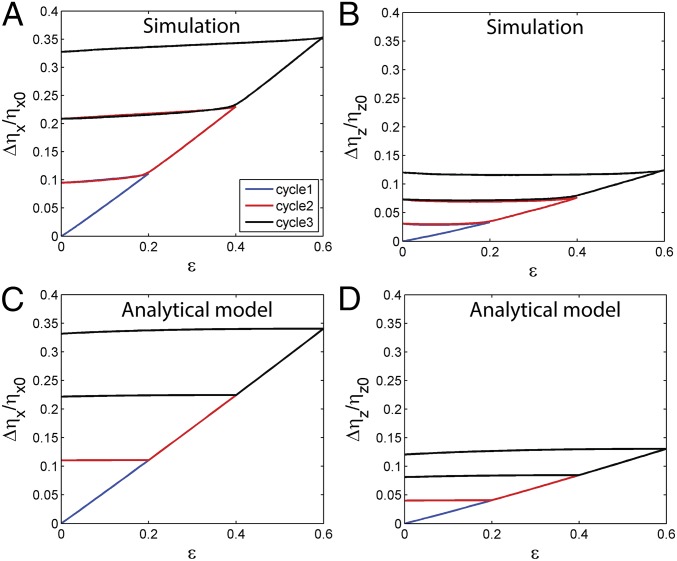
The close agreement between the predictions and measurements, especially in the longitudinal direction, suggests that the microstructural feature controlling the resistance–strain evolution can be determined by analyzing the simulation results. To pinpoint the controlling microstructural feature, we examined a large number of candidate features of the predicted CNT network, such as mean orientation, mean bending (SI Appendix, Fig. S8), number of contacts per CNT (SI Appendix, Fig. S9), etc. The parameters that show the strongest correlation with the resistances are the mean relative lengths of CNTs projected in the x direction ${\xi }_x=\langle l_x\rangle /h_x$ and in the z direction ${\xi }_z=\langle l_z\rangle /h_z$, respectively (SI Appendix, Fig. S10 C and D), where $\langle \rangle$ means average over all CNTs. For convenience, it is also useful to consider their inverse: ${\mathit{\eta }}_x=1/{\xi }_x$ and ${\mathit{\eta }}_z=1/{\xi }_z$. Fig. 3 A and B show that the relative changes of ${\mathit{\eta }}_x$ and ${\mathit{\eta }}_z$ with strain exhibit hysteresis and closely resemble the resistance–strain curves. Both ${\mathit{\eta }}_x$ and ${\mathit{\eta }}_z$ exhibit strong correlation with the resistances $R_x$ and $R_z$, respectively (SI Appendix, Fig. S11). This strongly suggests that ${\xi }_x$ and ${\xi }_z$ are the controlling microstructural parameters for which we are looking.

Fig. 3.

Change of the microstructural parameter $\eta$ as a function of strain under a cyclical loading. (A and B) The change of the microstructural parameters $\mathrm{\Delta }{\eta }_x/{\eta }_{x0}$ and $\mathrm{\Delta }{\eta }_z/{\eta }_{z0}$ of the CNT network obtained by CGMS simulations under three sequentially increasing strain cycles of 20, 40, and 60%; ${\eta }_x$ and ${\eta }_z$ are the inverse of the mean relative projected length of CNTs in x and z directions defined as ${\eta }_x=h_x/\langle l_x\rangle$ and ${\eta }_z=h_z/\langle l_z\rangle$, respectively. (C and D) The change of the microstructural parameters $\mathrm{\Delta }{\eta }_x/{\eta }_{x0}$ and $\mathrm{\Delta }{\eta }_z/{\eta }_{z0}$ obtained by the analytic model.

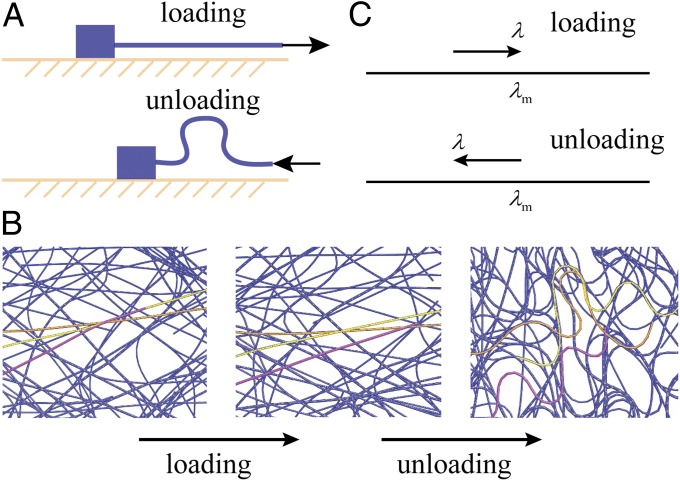
To prove the hypothesis that ${\xi }_x$ and ${\xi }_z$ (or equivalently, ${\mathit{\eta }}_x$ and ${\mathit{\eta }}_z$) are indeed the microstructural features responsible for the hysteretic resistance–strain behavior, we need to explain (i) why they exhibit hysteresis in cyclic loading and (ii) how they control electrical resistance. To answer the first question, we note that, during the first loading phase, $\langle l_x\rangle$ increases with the strain due to CNT reorientation (SI Appendix, Fig. S10 A and C). However, the amount of increase is not as large as that of the film size $h_x$, so that ${\mathit{\eta }}_x$ increases with strain (Fig. 3A). During unloading, the CNTs buckle (Fig. 4 A and B), and $l_x$ decreases in proportion to that of the film size h_x, so that ${\mathit{\eta }}_x$ stays nearly constant. The hysteresis of ${\mathit{\eta }}_x$ is due to the asymmetric behavior of CNTs between reorientation and sliding during loading and buckling during unloading (Fig. 4 A and B). A similar trend is observed in the z direction, although the amplitude of ${\mathrm{\Delta }{\mathit{\eta }}_z/\mathit{\eta }}_{z0}$ is much smaller than that of ${\mathrm{\Delta }{\mathit{\eta }}_x/\mathit{\eta }}_{x0}$ (SI Appendix, Fig. S10 B and D).

Fig. 4.

Schematic and results of the CNTs morphology during loading and unloading. (A) Schematic of the asymmetric behavior of the CNTs between reorientation and sliding during loading and buckling during unloading. This leads to the hysteretic microstructural parameter $\xi$ and therefore, resistance of CNTs between loading and unloading. (B) CGMS simulation results showing CNTs reorienting and sliding during loading and buckling during unloading in the same region. (C) In the analytic model of the evolution of $\xi$ (Eqs. 1 and 2), during loading and subsequent loading beyond the maximal stretch reached before, the maximal stretch ${\lambda }_{\text{m}}$ equals $\lambda$, while during unloading, ${\lambda }_{\text{m}}$ is the maximal stretch ever reached and $\lambda <{\lambda }_{\text{m}}$.

To be more quantitative, we construct an analytic model for the evolution of the $\mathit{\eta }$ parameters with strain. For simplicity, we consider a collection of CNTs in which the end-to-end vector of each CNT has an orientation angle $\mathrm{\Theta }$ (relative to the x axis) that is randomly distributed. We first consider how the end-to-end vectors of all CNTs would vary if they deform affinely as the film is stretched along x by a stretching ratio λ and compressed along z by a factor of $1/\sqrt{\lambda }$. In this case, the end-to-end vectors with an initial orientation angle above a critical angle ${\mathrm{\Theta }}_c=\arccos \left(1/\left({\lambda }^2+\lambda +1\right)\right)$ would become shorter, and the vectors with initial orientation angle below the critical angle would become longer. We assume that CNTs can easily accommodate a reduction of end-to-end distance by buckling, so that CNTs oriented above the critical angle would indeed deform affinely. However, CNTs oriented below the critical angle would not deform affinely, because doing so would require their end-to-end distance to become longer. Instead, we assume that the end-to-end vectors for these CNTs will only rotate to the new orientation $\mathit{\theta }\mathrm{=}\arctan \left(\tan \left(\mathrm{\Theta }\right){\lambda }^{-3/2}\right)$ but that their lengths will remain unchanged. This will cause sliding between CNTs previously in the same bundle. During unloading, after reaching the maximal stretch ${\lambda }_{\text{m}}$, the CNTs with $\mathrm{\Theta }>{\mathrm{\Theta }}_c$ reversibly recover from the buckling, while the CNTs with $\mathrm{\Theta }<{\mathrm{\Theta }}_c$ buckle. Based on these assumptions, we obtain analytic expressions of ${\xi }_x$ and ${\xi }_z$ as a function of strain

$${\mathit{\xi }}_x=\frac{2}{\pi h_x}\left(l_{CNT}{\displaystyle {\int }_0^{{\mathrm{\Theta }}_c}\cos {\mathit{\theta }}_{\text{m}}\frac{\lambda }{{\lambda }_{\text{m}}}\hspace{0.17em}d\mathrm{\Theta }}+l_{aff}{\displaystyle {\int }_{{\mathrm{\Theta }}_c}^{\mathit{\pi }/2}\cos \mathit{\theta }d\mathrm{\Theta }}\right),$$ [1]

$${\mathit{\xi }}_z=\frac{2}{\mathit{\pi }{h}_z}\left(l_{CNT}{\displaystyle {\int }_0^{{\mathrm{\Theta }}_c}\sin {\mathit{\theta }}_{\text{m}}\sqrt{\frac{{\lambda }_{\text{m}}}{\lambda }}\hspace{0.17em}d\mathrm{\Theta }}+l_{aff}{\displaystyle {\int }_{{\mathrm{\Theta }}_c}^{\mathit{\pi }/2}\sin \mathit{\theta }d\mathrm{\Theta }}\right),$$ [2]

where $l_{aff}=l_{CNT}\sqrt{{\lambda }^2{\cos }^2\mathrm{\Theta }+{\sin }^2\mathrm{\Theta }/\lambda }$ is the length of the CNTs under affine deformation following the substrate. During the initial loading as well as the subsequent loadings beyond the previous maximal stretch, the maximal stretch equals the current stretch (i.e., ${\lambda }_m=\lambda$) (Fig. 4C). However, during unloading, $\lambda$ decreases, while ${\lambda }_{\text{m}}$ stays at the maximal stretch value, so that ${\lambda }_m>\lambda$ (Fig. 4C); ${\theta }_{\text{m}}$ is the new orientation angle under ${\lambda }_{\text{m}}$: ${\theta }_{\text{m}}=\arctan \left(\tan \left(\mathrm{\Theta }\right){\lambda }_{\text{m}}^{-3/2}\right)$ (SI Appendix, section S3). Fig. 3 C and D shows the evolution of $\mathrm{\Delta }{\eta }_x/{\eta }_{x0}$ and $\mathrm{\Delta }{\eta }_z/{\eta }_{z0}$ during three loading and unloading cycles predicted by these analytic expressions. The analytic results are in excellent agreement with the data extracted from the CGMS simulations, which are shown in Fig. 3 A and B (SI Appendix, Fig. S12).

We now address the second question of how ${\eta }_x$ and ${\eta }_z$ control the resistances $R_x$ and $R_z$. We note that, in this case, where the contact resistance $R_{\text{contact}}$ is much higher than the intrinsic CNT resistance $R_{CNT}$, the CGMS model shows that resistance of the film is very well-described by the following expressions:

$$R_x=\alpha R_{\text{contact}}{\eta }_x^2/N_{CNT},$$ [3]

$$R_z=\alpha R_{\text{contact}}{\eta }_z^2/N_{CNT},$$ [4]

where $\alpha$ is a dimensionless variable related to the morphology of the CNT network (SI Appendix, section S3). The quadratic dependence of resistance R on parameter η can be qualitatively understood using the following model. Since the overall resistance is dominated by contact resistance, for simplicity, we assume that the electrical resistance along each CNT is zero. In other words, a charge can travel over an average distance of $\langle l_x\rangle$ in the x direction without experiencing any resistance. In this limit, the dimensionless parameter ${\xi }_x=\langle l_x\rangle /h_x$ is analogous to the Knudsen number in fluid mechanics. For a charge to travel from one end to the other end of the film in the x direction, the least resistance path that it can take should contain ${\eta }_x=h_x/\langle l_x\rangle$ CNTs on average. The resistance of this path is $R_{\text{contact}}{\eta }_x$. Given a total number of $N_{CNT}$ nanotubes, we can consider the entire CNT network consisting of $N_{CNT}/{\eta }_x$ parallel paths, each consuming ${\eta }_x$ nanotubes. As a result, the overall resistance of the CNT film is $R_{\text{contact}}{\eta }_x/\left(N_{CNT}/{\eta }_x\right)=R_{\text{contact}}{\eta }_x^2/N_{CNT}$. This is very similar to Eq. 3, in which a dimensionless parameter α is introduced to account for the error induced by replacing the CNT network with a collection of parallel paths (SI Appendix, section S3).

The CGMS simulation results of the resistance $R$ in both the stretching and transverse directions show linear correlation with ${\eta }^2/N_{CNT}$, with the fitting coefficient α = 0.125 (Fig. 5 A and B). Combining Eqs. 1–4, we arrive at an analytic model for the evolution of the resistance in both the stretching and transverse directions: $R_x$ and $R_z$. The relative change of the resistance $\mathrm{\Delta }{R}_x/R_{x0}$ and $\mathrm{\Delta }{R}_z/R_{z0}$ (Fig. 5 C and D) predicted by the analytic model shows good agreement with the CGMS simulation results in Fig. 2 C and D.

Fig. 5.

Resistance evolution based on the analytic model. (A and B) Linear correlations between $R$ and ${\eta }^2/N_{CNT}$ in both x and z directions are shown based on the CGMS simulation results. The simulation results are for $N_{CNT}=135$ CNTs with length $l_{CNT}=\mathrm{2,400}\hspace{0.17em}\text{nm}$ and diameter $d_{CNT}=1\hspace{0.17em}\text{nm}$, each discretized by $N_{\text{node}}=120$ nodes, in a simulation cell with $H_x=H_z=\mathrm{1,200}\hspace{0.17em}\text{nm}$. The dashed lines are fitting curves $R=0.125R_{\text{contact}}{\eta }^2/N_{CNT}$. (C and D) Analytic results of the evolution of the relative change of resistances $\mathrm{\Delta }{R}_x/R_{x0}$ and $\mathrm{\Delta }{R}_z/R_{z0}$ under three sequentially increasing strain cycles of 20, 40, and 60% based on Eqs. 1–4. The analytic results are for $N_{CNT}=135$ CNTs corresponding to the CGMS simulation in Fig. 2 C and D.

Based on the good agreement between the experimental data, CGMS model, and analytic theory, we conclude that ${\eta }_x$ and ${\eta }_z$ are indeed the controlling microstructural parameters for the hysteretic resistance–strain behavior. Intuitively, we might expect the number of contacts between CNTs to be an important microstructural parameter for resistance. However, the CNT films in this study are well above the percolation limit, so that the contacts between CNTs are redundant. This is why considering the CNT network as parallel and isolated paths (and significantly reducing the number of contact points in this process) still captures the relative resistance change of the film very well. Indeed, our simulation results do not show a good correlation between the number of contacts and resistance (SI Appendix, Fig. S9). Varying the density of CNTs also has a negligible effect on the relative resistance change–strain curves (SI Appendix, Fig. S13).

Using the CGMS model, we can also predict the effect of CNT length on the resistance change of the network under cyclic loading. Fig. 6 shows the resistance change–strain relation in the stretching direction for CNTs with lengths (i) 800, (ii) 1,600, and (iii) 2,400 nm. Here, we assume that the CNT resistance depends linearly on its length, $R_{CNT}=R_B+R_C{l}_{CNT}/\mathrm{1,000}$, where $R_B=6.5\hspace{0.17em}\text{k}\mathrm{\Omega }$ is the ballistic resistance of single-wall CNTs, $R_C=4.5\hspace{0.17em}\text{k}\mathrm{\Omega }$, and $l_{CNT}$ is in the units of nanometers (38–40). We find that, for shorter CNTs, the slope of the resistance change–strain curve in unloading becomes nonzero and that the hysteresis between the loading and unloading becomes smaller. This occurs because shorter CNTs are less susceptible to buckling, so that sliding between CNTs in the reverse direction can occur during the unloading phase. Similarly, our CGMS model also predicts that CNTs with larger diameters show smaller hysteresis of the resistance change (SI Appendix, Fig. S14), where for simplicity, we neglect the variation of CNT and contact resistances with respect to the CNT diameter. Therefore, if the CNT film is intended to be used as stretchable interconnects, longer CNTs are preferred, because the resistance would stay nearly constant as long as the strain does not exceed a previously applied maximal strain. However, if shorter CNTs are used, the CNT film can potentially function as a strain sensor.

Fig. 6.

Effect of the CNT length on the resistance change: (A) $l_{CNT}$ = 800 nm, (B) $l_{CNT}$ = 1,600 nm, and (C) $l_{CNT}$ = 2,400 nm (same data as in Fig. 2C). For all cases, the density of CNTs is kept constant, and the CNTs have diameter $d_{CNT}=1\hspace{0.17em}\text{nm}$, contact resistance $R_{\text{contact}}=200\hspace{0.17em}\text{k}\mathrm{\Omega }$, and resistance of a single CNT $R_{CNT}=R_B+R_C{l}_{CNT}\text{/}1,000$, with $R_B=6.5\hspace{0.17em}\text{k}\mathrm{\Omega }$, $R_C=4.5\hspace{0.17em}\text{k}\mathrm{\Omega }$, and $l_{CNT}$ in units of nanometers.

In summary, we have shown that the hysteretic resistance–strain behavior of the CNT films is controlled by the microstructure parameter $\xi$, the mean relative projected length of CNTs. This conclusion is supported by the excellent agreement between experiments, CGMS simulations, and analytic theories. The decrease of $\xi$ during loading is caused by the combination of CNT reorientation and sliding, and the tendency for long CNTs to buckle causes $\xi$ to stay nearly constant during unloading. In the limit of high contact resistance, the electrical resistance of the film is proportional to ${\xi }^{-2}$, where $\xi$ acts as a “mean free path” relative to the film dimension along which the charge can travel without experiencing Ohmic loss at the CNT contacts. Our simulations further predict that CNTs with smaller lengths or larger diameters exhibit smaller hysteresis of resistance change on a loading and unloading cycle. However, the CNT density itself has a minimal effect on the relative resistance change with strain when the CNT network is far above the percolation threshold. We believe that these conclusions are not limited to CNT films but are generally applicable to stretchable conductors consisting of a network of 1D tubes or wires with individual resistance that is much lower than the contact resistance. Furthermore, our numerical (CGMS) model has even broader applicability and is not limited by the relative magnitude of the two resistances. Our predictions on the microstructural origin of resistance hysteresis can potentially be validated more directly if several existing experimental challenges can be overcome, such as the identification of individual CNTs in an SEM image to measure the end-to-end distances of CNTs and the fabrication of long CNTs with more precisely controlled lengths and diameters.

Methods

Spray Coating CNT Films.

We created a conducting thin film of CNTs by spray coating a well-dispersed CNT solution onto a PDMS substrate. The PDMS (Dow Corning Sylgard 184) with 15:1 base to cross-linker ratio was mixed, degassed, and cured overnight at 80 °C. The PDMS substrate had thickness around 1 mm and was cut into rectangles with dimensions 7.62 × 1.27 cm.

To prepare the CNT solution, arc discharge single-wall P2 CNTs (Carbon Solution, Inc.) of diameters 1.2–1.7 nm were ultrasonicated in NMP (Fisher Scientific) with a Cole Parmer 750-W tip sonicator at 30% power for 30 min. The solution was then centrifuged (Sorvall Lynx 4000, Fiberlite F21-8*50y Roter, Thermo Fisher Scientific) for 30 min at 8,000 rpm to remove large bundles and amorphous carbon. The top 75% of the solution was used for spray coating.

The CNT solution was spray coated with a commercial airbrush (Master Airbrush; model SB844-SET). Before the spray coating, the PDMS substrates were activated with UV ozone for 20 min. During the spray coating, the hot plate underneath the PDMS was held at 200 °C so that the solvent (boiling point ∼ 180 °C) evaporates during deposition. We patterned the CNT film into a small square with dimension 0.51 × 0.51 cm in the center of the substrate by using a mask cut with the Silhouette Cameo 3 machine (Sihouette America, Inc.). Multiple passes of airbrush (∼50–100 times) were performed to spray CNTs until the two-point resistance reached around $5\hspace{0.17em}\text{k}\mathrm{\Omega }$.

Measuring Resistance of CNT Films.

Two 30-nm-thick gold stripes were patterned and evaporated onto the two opposite edges of the CNT film to ensure a good electrical contact (43). We tested the resistance measurement of CNT films with different lengths between the two gold stripes and found that the resistance almost linearly scaled with the length; therefore, the contact resistance was negligible. Then, the patterned gold patches were connected to an Agilent E4980A LCR meter (Agilent Technologies, Inc.) via liquid metal EGaIn forming a stretchable conductive path (SI Appendix, Fig. S1). We applied loading and unloading cycles to the PDMS substrate with a home-built mechanical strain platform and in situ measured the resistance in the stretching and transverse directions using the LCR meter. In a typical experiment, we stretched the sample along the length direction to 20% strain, fully unloaded it, and then repeated this process for another two cycles, with the maximal strains being 40 and 60%, respectively.

Observing CNT Films Under SEM.

In situ SEM strain measurements were conducted in the FEI Magellan Scanning Electron Microscope at 1 kV with a 13-pA beam current. The sample was clamped down with clips and measured before, during, and after stretching the sample. Due to the insulating nature of the flexible substrates, scan times were adjusted to prevent deformation of the CNT network caused by localized heating of the PDMS substrate from the electron beam.

CGMS Simulation of CNT Films.

We used the CGMS method to simulate the morphology change of CNTs under cyclic loading with increasing levels of strain with a molecular dynamics package MD++. A thin sheet of single-wall CNTs was simulated by a collection of CNTs interacting with each other and with the substrate. Each CNT was represented by a series of nodes (on the order of 100) connected by linear segments. The interactions between nodes were introduced to reproduce the stretching and bending stiffness of the CNTs and van der Waals interactions between CNTs (SI Appendix, section S1). The interactions between the CNTs and the substrate were modeled as an external potential with a long-range attraction and a short-range repulsion applied to all nodes (SI Appendix, section S1).

For simplicity, the initial configurations of the CNTs were created as randomly oriented straight lines parallel to the substrate surface. This structure was then relaxed to a local energy minimum using the conjugate–gradient algorithm, so that the CNTs form a thin sheet on the substrate. The simulation cell sizes in the x and z directions were allowed to adjust during the relaxation, so that a zero-stress state was reached. The initial simulation cell had the sizes of $H_x$, $H_y$, and $H_z$ in the x, y, and z directions, respectively. Stretching was simulated by elongating the simulation cell size in the x direction to $h_x=H_x\lambda =H_x\left(1+\epsilon \right)$ in small increments (0.1% strain for each increment), allowing all nodes to relax to a local energy minimum after each increment. The simulation cell size in the z direction was adjusted in each strain increment to $h_z=H_z{\left(1+\epsilon \right)}^{-1/2}$ to ensure the uniaxial loading condition of the incompressible PDMS substrate (SI Appendix, section S1).

The simulation cell is subjected to the same loading and unloading cycles as in the experiments. The simulation example that we show in Fig. 1C has the initial size of simulation cell as $H_x=H_z=\mathrm{1,200}\hspace{0.17em}\text{nm}$ and $H_y=100\hspace{0.17em}\text{nm}$. The convergence of the simulation with respect to the simulation cell size is shown in SI Appendix, Fig. S3.