Origami-inspired, on-demand deployable and collapsible mechanical metamaterials with tunable stiffness

Significance

Origami has been employed to build deployable mechanical metamaterials through folding and unfolding along the crease lines. These deployable structures are flexible in their deployment direction so that they can be easily collapsed along the same path they are deployed. Here we create an origami-inspired mechanical metamaterial with on-demand deployability and selective collapsibility: autonomous deployability from the collapsed state and selective collapsibility along two different paths, with low stiffness for one path and substantially high stiffness for another path. The created mechanical metamaterial yields load-bearing capability in the deployed direction while still possessing great deployability and collapsibility. The principle in this work can be utilized to design and create versatile origami-inspired mechanical metamaterials that can find many applications.

Abstract

Origami has been employed to build deployable mechanical metamaterials through folding and unfolding along the crease lines. Deployable metamaterials are usually flexible, particularly along their deploying and collapsing directions, which unfortunately in many cases leads to an unstable deployed state, i.e., small perturbations may collapse the structure along the same deployment path. Here we create an origami-inspired mechanical metamaterial with on-demand deployability and selective collapsibility through energy analysis. This metamaterial has autonomous deployability from the collapsed state and can be selectively collapsed along two different paths, embodying low stiffness for one path and substantially high stiffness for another path. The created mechanical metamaterial yields load-bearing capability in the deployed direction while possessing great deployability and collapsibility. The principle in this work can be utilized to design and create versatile origami-inspired mechanical metamaterials that can find many applications.

A deployable structure is a structure that can reconfigure and change shape/size mainly from folding and unfolding, and has many applications from daily essentials (e.g., umbrella), vascular stents (1), to solar panels (2) for spacecraft. Origami, the art of paper folding, thus naturally provides inspirations for deployable structures. In addition to deployable structures, origami recently has gained much attention as it has offered an appealing strategy on the development of 3D architectures across different length scales (3–5) and metamaterials with tunable properties (6–12). Many origami-inspired deployable structures are based on rigid origami patterns, in which the kinematic deformation is solely limited to the folding lines while the panels remain undeformed. Well-known representatives of deployable rigid origami patterns are the Miura folding (2) and its derivates (6, 13). In addition to rigid origami, another type is deformable origami, where the panels and the folding lines all bear deformation, such as the twisted square pattern (14). Due to the simplicity of the kinematics of rigid origami, much attention has been focused on this type.

Despite recent active research in origami and related deployable structures, a critical aspect of the origami research that has been overlooked is whether the deployed structure remains in a deployed state under loading, such as vibration experienced by a deployed structure used in spacecraft. From the perspective of mathematics of origami, deployability means the kinematics of the pattern geometry to deploy and collapse. Since this is a pure mathematical point of view, there is no energy associated with the deployability and collapsibility of the structure. Therefore, a deployable structure at the same time also allows it to collapse through which it deploys. Thus, easy deployment, one of the many attractive attributes of some origami patterns (e.g., Miura pattern and its derivates), also indicates that the structure can be easily collapsed. In addition to utilizing mechanical mechanisms to lock the deployed state, the discovery of deployable and yet stiff origami patterns, such as zipper-coupled tubes (6), has gained attention. However, the stiffness along the deploying direction of the structure is not enhanced to ensure that the deployed structure can be readily retracted to its collapsed state in the same way it deploys. To fully harness the exemplar properties of origami in terms of its deployability and tunable properties, it is essential to create a deployable structure with on-demand deployability and collapsibility, i.e., keeping the easy deployment and selectively controlling the path by which the structure collapses.

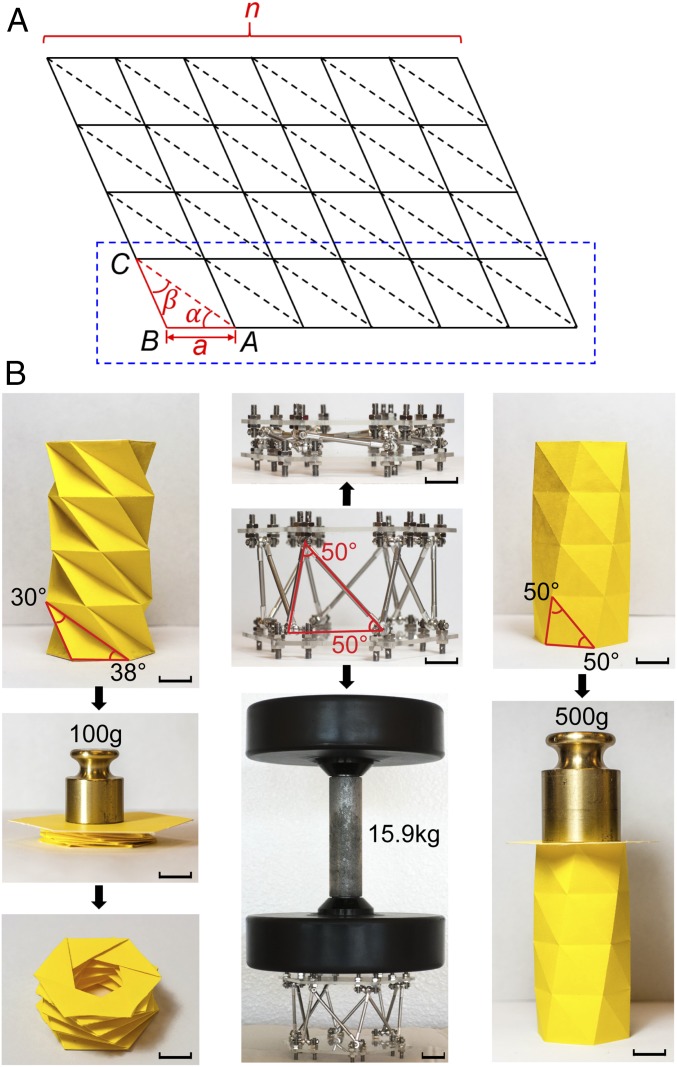
Here in this paper, an origami-inspired mechanical metamaterial was created with on-demand deployability, collapsibility, and tunable stiffness, where the deploy and collapse can follow two paths. Thus, easy deploy and hard collapse, seemly contradictory attributes, are achieved simultaneously. The metamaterial is inspired by a triangulated cylinder pattern (15, 16) that has been studied as one type of deformable origami pattern. Its crease pattern is shown in Fig. 1A. By altering the angles α and β, two distinct cylinders can be folded (Fig. 1B). For α = 38° and β = 30° (Fig. 1B, Left), a construction-paper–folded triangulated cylinder can be deployed in the axial direction (Movie S1) but at the same time a small compressive load (e.g., a 100-g weight) will collapse it along the same way. This suggests an “easy deploy and easy collapse” structure. For α = 50° and β = 50° (Fig. 1B, Right), the construction-paper–folded cylinder is not deployable (or collapsible) and can bear much larger compressive load (e.g., a 500-g weight). This pattern is “hard deploy and hard collapse.” For this paper we combined these two patterns and created an on-demand “easy deploy and selective collapse” origami-inspired truss structure, as illustrated by Fig. 1B (Middle). To create such a metamaterial, we first analyzed the deformation energy of triangulated cylinder patterns and elucidated the deployability and collapsibility from the energy and strain perspectives. This provides an inspiration to develop this metamaterial by employing a member with an asymmetric tensile and compressive behavior and leads to distinct deploy and collapse paths. A representative model was then built and its on-demand deployability and collapsibility along with tunable stiffness were characterized. This work provides an unprecedented and unappreciated perspective to achieve truly deployable and stiff origami-inspired mechanical metamaterial with great on-demand tunability, which can find tremendous applications in many fields.

Fig. 1.

Origami and origami-inspired structures based on the triangulated cylinder patterns with different deployability and collapsibility. (A) Crease pattern of a triangulated cylinder. $\mathrm{\Delta }ABC$ is the unit cell. (B, Left) Construction-paper–folded triangulated cylinder with n = 6, $\alpha ={38}^{°}$, and $\beta ={30}^{°}$, which is easily deployable but also easily collapsible. (B, Right) Construction-paper–folded triangulated cylinder with n = 6, $\alpha ={50}^{°}$, and $\beta ={50}^{°}$, which is not deployable or collapsible but can bear load. (B, Middle) Created origami-inspired mechanical metamaterial that is deployable but can also carry load, which demonstrates the on-demand deployability and collapsibility with tunable stiffness. (Scale bar, 1 cm.)

Results

Deformation Energy Analysis of Triangulated Cylinder Patterns.

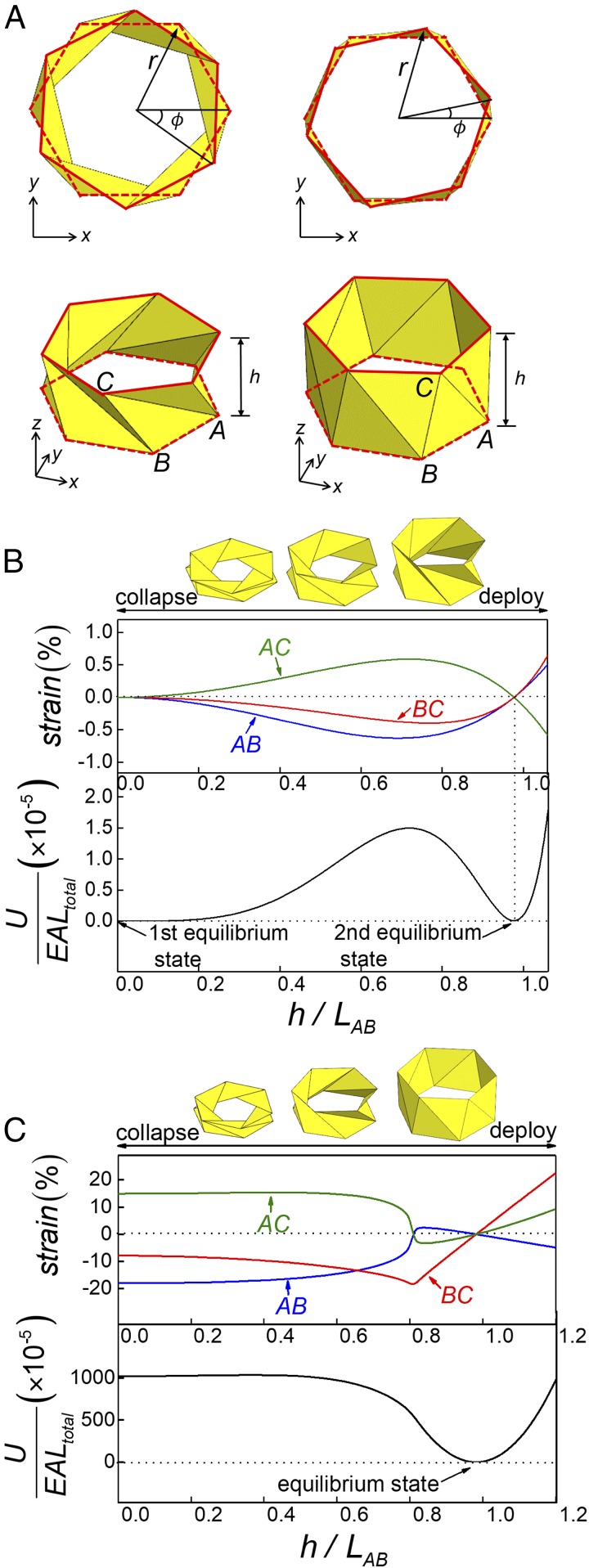
The triangulated cylinder has many identical triangles; its unit cell is highlighted in Fig. 1A and can be characterized by three parameters, namely one side, a and two angles, α and β. The lengths of three folding lines at the planar state are given by $L_{AB}=a$, $L_{BC}=a\sin \alpha /\sin \beta$, and $L_{AC}=a\sin \left(\alpha +\beta \right)/\sin \beta$. n is the number of triangles to sew the right and left boundaries for a closed cylinder, i.e., n = 6 for Fig. 1A. At the folded cylindrical state (Fig. 2A), the positions of the representative unit cell $\mathrm{\Delta }ABC$ are characterized by the height h and twist angle ϕ between two neighboring lines in the vertical direction, as well as the radius r of the triangulated cylinder. Thus, the lengths of the three folding lines at the folded state are given by $l_{AB}=2r\sin \left(\pi /n\right)$, $l_{BC}=\sqrt{h^2-2r^2\cos \varphi +2r^2}$, and $l_{AC}=\sqrt{h^2-2r^2\cos \left(2\pi /n+\varphi \right)+2r^2}$. As illustrated by Fig. 2A and Movie S1, there are many folded cylindrical states characterized by different height h, twist angle ϕ, and radius r, which apparently cannot be determined by three constants a, α, and β. Strains ${\epsilon }_{AB}$, ${\epsilon }_{BC}$, and ${\epsilon }_{AC}$ are thus introduced as variables to link these three variables (h, ϕ, and r) to three constants (a, α, and β), e.g., ${\epsilon }_{AB}=\left(l_{AB}-L_{AB}\right)/L_{AB}$. For the sake of simplicity, the deformation of the panel (i.e., $\mathrm{\Delta }ABC$) is solely concentrated at the three folding lines, AB, BC, and AC. In other words, the unit cell is represented by a three-member truss structure. As detailed in SI Appendix, Fig. S1, the truss structure can capture the featured deformation characteristics of origami structures, including in-plane stretching, shearing, and bending (17). Moreover, the triangulated cylinder patterns have been modeled as truss structures and the strain energy has been characterized by experiments (18). Thus, the deformation energy stored in one strip as marked in Fig. 1A is given by $U=nEA/2\left(L_{AB}{\epsilon }_{AB}^2+L_{BC}{\epsilon }_{BC}^2+L_{AC}{\epsilon }_{AC}^2\right)$, where EA is the tensile rigidity of the truss. At a given height h, i.e., a prescribed deploy/collapse height, minimization of the deformation energy U with respect to twist angle ϕ and radius r gives the folded states. The detailed derivations are provided in SI Appendix.

Fig. 2.

Energy landscapes and strain variations of two triangulated cylinder patterns during the deploy and collapse processes. (A) Geometrical parameters, namely height h, relative angle ϕ, and radius r, to define the folded states of two patterns (Left: n = 6, $\alpha ={38}^{°}$, and $\beta ={30}^{°}$; Right: n = 6, $\alpha ={50}^{°}$, and $\beta ={50}^{°}$). (B) Energy landscapes and strain variations during the deploy and collapse processes for a pattern with n = 6, $\alpha ={38}^{°}$, and $\beta ={30}^{°}$. (C) Energy landscapes and strain variations during the deploy and collapse processes for a pattern with n = 6, $\alpha ={50}^{°}$, and $\beta ={50}^{°}$.

Fig. 2B shows the variation of normalized deformation energy $U/EA{L}_{total}$ and strains in AB, BC, and AC members during the deploy and collapse processes for the triangulated cylinder in Fig. 1B (Left) ($\alpha ={38}^{°}$ and $\beta ={30}^{°}$), characterized by normalized height $h/L_{AB}$ with $h/L_{AB}=0$ for a completely collapsed state. Here $L_{total}=n\left(L_{AB}+L_{BC}+L_{AC}\right)$ is the total length of the truss members. The 3D illustrations were generated using the calculated results. The deformation energy suggests an apparent bistable states, where both the completed collapsed state and deployed state have the minimum energy. An energy barrier exists between these two equilibrium states, which indicates that this energy barrier needs to be overcome during deploy and collapse. It is observed that the strains are vanishing at the two equilibrium states and the maximum strain during the processes of deploy and collapse is ∼1%, which is within the fracture strain of construction papers (19, 20). The triangulated cylinder is thus clearly a deformable origami. The same deploy and collapse paths indicate this pattern does not possess on-demand or selective deployability and collapsibility.

For another triangulated cylinder shown in Fig. 1B (Right) (with $\alpha ={50}^{°}$ and $\beta ={50}^{°}$), as shown in Fig. 2C, qualitatively distinct deformation energy and strains present. Instead of a bistable state as in Fig. 2B, the completed collapsed state is no longer an equilibrium state but rests at an elevated energy state, and only the deployed state remains at the equilibrium configuration. This energy landscape indicates that the deploy process can be autonomous since there is no energy barrier, and during collapse there is an energy barrier to overcome. Moreover, this energy barrier is about 600× higher than that in Fig. 2A. However, this origami pattern cannot be claimed as an easy deploy but hard collapse pattern because of the large strain. The maximum strain exceeds 10%, which in fact explains the reason construction-paper–folded pattern cannot be collapsed (Fig. 1B, Right) because a construction paper cannot bear this large strain. This pattern has been considered as nonfoldable origami. However, the energy landscape indicates that this origami pattern is in fact foldable, but the required strain cannot be achieved using paper as the folding materials. Another distinct feature of this pattern is that the strain for the members varies between tension and compression. For example, AC truss is in tension during most of the deploy process and turns compressive right before reaching the deployed state. For collapse, AC member needs to be compressed and then stretched.

The distinct strain variations between Fig. 2B (for $\alpha ={38}^{°}$ and $\beta ={30}^{°}$) and Fig. 2C (for $\alpha ={50}^{°}$ and $\beta ={50}^{°}$) are attributed to the measure of another angle $\angle ABC$ in the unit triangle (Fig. 1A). When $\angle ABC>{90}^{°}$, the strain in each member remains tension or compression throughout the deploy and collapse processes (e.g., in Fig. 2B). When $\angle ABC<{90}^{°}$, the strain may vary between tension and compression (e.g., in Fig. 2C). The threshold is $\angle ABC=\alpha +\beta ={90}^{°}$, which is a catastrophic point that governs the strain variations in AC and AB trusses (21). Nonenergy barrier, and particularly strain variation between tension and compression, together suggest an origami-inspired mechanical metamaterial to achieve “on-demand deploy and selective collapse.”

Rationale of Origami-Inspired Mechanical Metamaterials with On-Demand Deploy and Collapse.

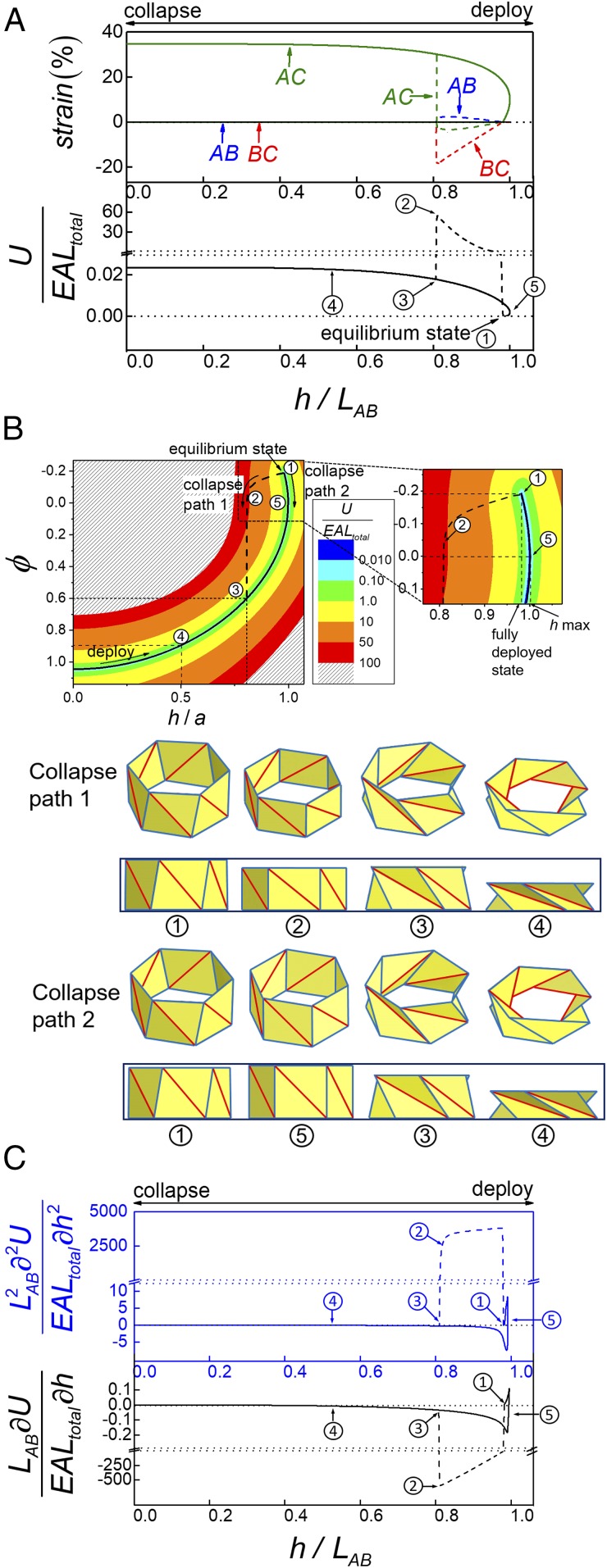
An on-demand deploy and collapse needs easy deploy and selective collapse. In other words, distinct and selective deploy and collapse paths are necessary. The strain paths of AC and AB trusses that vary between tension and compression suggest such a possibility: If the AC truss is easy to be stretched and hard to be compressed, or the AB truss is easy to be compressed and hard to be stretched, the desired distinct and selective deploy and collapse paths should become possible. For the same triangulated cylinder pattern with $\alpha =50°$ and $\beta =50°$, we have studied three combinations with asymmetric tension/compression behavior for just AC, just AB, and both AC and AB (SI Appendix, Fig. S3). The details of the AC truss are provided here because it offers the most desired energy landscape and is experimentally achievable. AC truss is assigned an asymmetric tension/compression behavior. Its tensile rigidity is four orders of magnitude smaller than its compressive rigidity, which is the same as that for AB and BC trusses. Now the deformation energy and strain variation are shown in Fig. 3A. In addition to the similar energy landscape where the collapsed state has an elevated energy and the deployed state is at equilibrium, an apparently distinct feature for the deformation energy is that during collapse, a different path appears ($➀$ → $➁$ → $➂$ → $➃$) with a much higher energy barrier for collapse. Thus, during deploy, the energy decreases and the collapsed state autonomously deploys; the AC truss experiences large strain while other members barely deform because of the low tensile rigidity of the AC truss. During collapse through path $➀$ → $➁$ → $➂$ → $➃$, in which the strain variations are marked as the dashed lines, the energy barrier can be very high because of the high compressive rigidity. It is noted that the strain in the BC member during collapse (dashed line) is too high to be practically achievable and thus the high-energy barrier just represents an ideal limit.

Fig. 3.

On-demand deployability and selective collapsibility of an origami-inspired mechanical metamaterial. (A) Energy landscapes and strain variations during the deploy and collapse processes for a mechanical metamaterial inspired by a triangulated cylinder with n = 6, $\alpha =50°$, and $\beta =50°$, and an asymmetric tension/compression behavior for the AC member. The dashed lines are strain variations when collapsed along the path $➀$ → $➁$ → $➂$ → $➃$, i.e., hard collapse path. (B) Energy contour showing two collapse paths, hard collapse path $➀$ → $➁$ → $➂$ → $➃$ and easy collapse path $➀$ → $➄$ → $➂$ → $➃$, which suggests a selective collapse. (C) Tunable reaction force and stiffness of the origami-inspired mechanical metamaterial during deploy and collapse (along two paths). The dashed lines are for the hard collapse path.

At the completely deployed state, a subtle feature that the height h is not at its extrema in fact defines two selective collapse paths. The first collapse path is distinct from the deploy path (i.e., $➀$ → $➁$ → $➂$ → $➃$). It starts by directly compressing the structure, i.e., decreasing height h, and leads to a much higher energy barrier. The second collapse path (i.e., $➀$ → $➄$ → $➂$ → $➃$) is by firstly increasing the height h ($➀$ → $➄$) followed by a compression ($➄$ → $➂$ → $➃$), which leads to the same path as deploy. Consequently, an on-demand deploy and collapse origami-inspired mechanical metamaterial is just created that can always be autonomously deployed and selectively collapsed, hard or easy, depending on two different paths.

This deploy and collapse property can be further shown in the contour plot of the deformation energy as a function of height h and twisting angle ϕ (Fig. 3B). The deploy path is along the minimum energy “valley” from the collapsed state to the deployed state (i.e., an equilibrium state). The zoom-in near the deployed state (marked as $➀$ in Fig. 3B) shows that the deployed state does not have an extreme height h. The first collapse path ($➀$ → $➁$ → $➂$ → $➃$) involves directly decreasing the height h and thus experiences a very high energy barrier, i.e., hard collapse. The second collapse path ($➀$ → $➄$ → $➂$ → $➃$) needs to increase the height h to pass the extrema ($➄$) and then decrease, which leads to the same path as deploy. To pass the extrema from the deployed state, i.e., $➀$ → $➄$, a tensile load in the axial direction (i.e., along the deploy direction) or a torque to change the twisting angle ϕ needs to be applied. The 3D configurations (i.e., $➀$ to $➄$) are based on the calculated results. It is noted that the relationship between the twisting angle ϕ and the tension or compression for this origami-inspired metamaterial is different from the triangulated cylinder structure (as shown in Movie S1). For the origami structure, tension and compression lead to opposite twisting direction. However, for the origami-inspired metamaterial, twisting angle varies monotonically during tension and compression, which can be seen from the side view of the collapse path 2 in Fig. 3B. From $➄$ to $➀$, the metamaterial is under compression and the line in blue (i.e., the BC truss) rotates clockwise to achieve a stable deployed state. From $➄$ to $➂$, the metamaterial is also under compression, but the BC truss rotates counterclockwise. Thus, the BC truss rotates monotonically when the metamaterial is under tension (from $➀$ to $➄$) and under compression (from $➄$ to $➂$). This characteristic indeed leads to selective collapsibility. Movie S2 demonstrates the synchronized evolution of deformation energy and configurations, showing on-demand and selective deploy and collapse paths of this origami-inspired mechanical metamaterial.

This structure also has tunable axial reaction force and stiffness. The normalized axial reaction force $L_{AB}/EA{L}_{total}\partial U/\partial h$ and stiffness $L_{AB}^2/EA{L}_{total}{\partial }^{2}U/\partial h^2$ are provided in Fig. 3C. At the collapsed state, both the reaction force and the stiffness are infinitesimal, which suggests just a vanishing force is needed to hold the collapsed structure. At the deployed state, for the easy collapse path ($➀$ → $➄$ → $➂$ → $➃$), a very small axial force, in tension and then in compression is needed to collapse the structure. The corresponding stiffness is also low. It is apparently different from that for the hard collapse path ($➀$ → $➁$ → $➂$ → $➃$), a compressive axial force with magnitude $\left|L_{AB}/EA{L}_{total}\partial U/\partial h\right|\approx \mathrm{12,000}$ (2,000× higher than that for the easy deploy path) needs to be applied to collapse the structure. The corresponding stiffness is also three orders of magnitude higher than that for the easy deploy path.

As can be imagined, the variation of deformation energy strongly depends on the geometry of the crease patterns, specifically, the number of triangles in the circumferential direction n, and angles α and β. As detailed in SI Appendix, another pattern was also studied, with n = 4, $\alpha =50°$, and $\beta =50°$. Similar to Fig. 2C, as shown in SI Appendix, Fig. S4, this pattern has a collapsed state with elevated energy and an equilibrium state for a deployed configuration. Also, distinct deploy and collapse paths also present when the asymmetric tension/compression behavior is prescribed (SI Appendix, Fig. S5). It also confirms that the condition $\alpha +\beta \ge 90°$ leads to this behavior and n does not play an important role. Thus, these two structures all suggest an on-demand deployability and collapsibility: autonomous deployability and selective collapsibility.

Experimental Realization of On-Demand Deployable and Collapsible Origami-Inspired Mechanical Metamaterials.

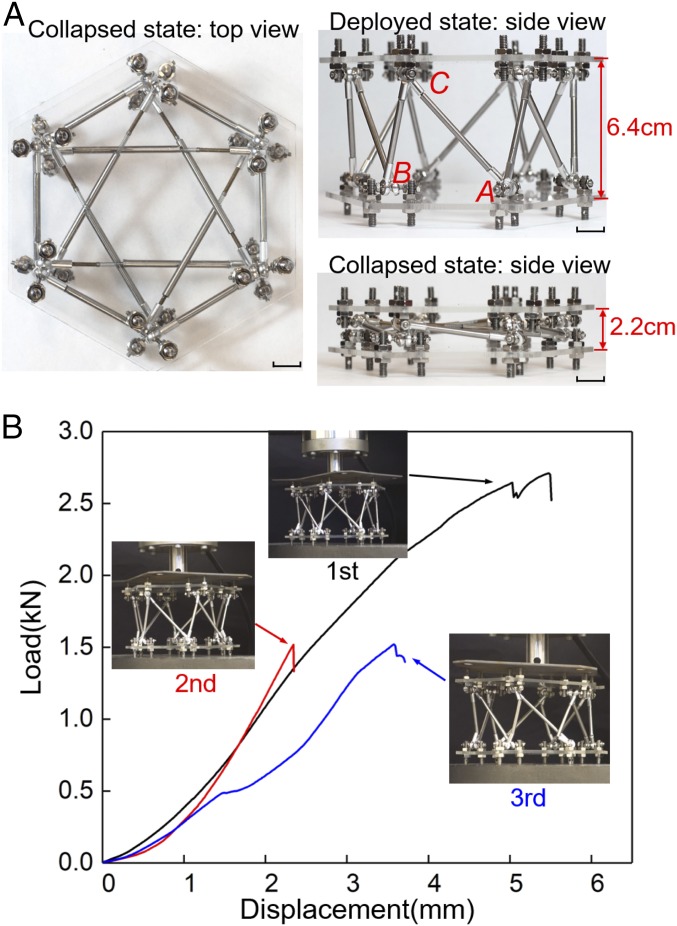
To realize the merit of on-demand deployability and collapsibility, models were built using standard components, such as bolts, rod end bearing, springs, tubes, and acrylic plates. Fig. 4A shows the deployed and collapsed states. The list and details of the components are provided in SI Appendix, Fig. S6 and the design of the metamaterial is in SI Appendix, Fig. S7. The key component to achieve the tension/compression asymmetrical behavior is AC, consisting of a spring inside a tube (SI Appendix, Fig. S8), where the spring bears tension while the tube resists compression. Rod end bearing enables smooth rotation at the joints (SI Appendix, Fig. S9). Movie S3 demonstrates the deployability and selective collapsibility yet strong load-bearing capability of the mechanical metamaterial. We characterized the load-bearing capability of this origami-inspired mechanical metamaterial by directly placing the deployed structure between two plates of a uniaxial compression machine, and the load/displacement curve is shown in Fig. 4B, provided with a few representative snapshots of the metamaterial during compression. For the first compression, the maximum load approached 2,700 N, more than 1,600× of the weight of this metamaterial (∼160 g). Beyond the peak compressive load, a few BC members fractured and the load dropped. SI Appendix, Fig. S10 shows the fractured members after compression. This observation is consistent with the strain variation in Fig. 3A where the BC member bears larger strain while being collapsed along path 2, i.e., hard collapse path. As shown in SI Appendix, Fig. S11, after the first compression, the structure can still be deployed and collapsed, although with a few BC members fractured. Then, the deployed structure with a few fractured BC members after the first compression was subjected to the second compression. The peak load can achieve ∼1,500 N, which is still 900× its weight. This defected structure is still deployable and collapsible as shown in SI Appendix, Fig. S12, although the collapsed configuration is not perfect. A third compression was run and again this very damaged structure could still carry significant load ∼1,500 N. With more BC members fractured after the third compression, the on-demand deployability and collapsibility still present (SI Appendix, Fig. S13). These observations confirm this origami-inspired metamaterial possesses on-demand and defect insensitive deployability and collapsibility. The load-bearing capability leads to more practical applications.

Fig. 4.

Experimental characterizations of the deployability and load-bearing capability of the origami-inspired mechanical metamaterial. (A) Photos of the structure at the deployed and collapsed states before the compression load is applied. (B) Load versus displacement curve for the metamaterial under compression. Three consecutive compression tests were conducted. The representative snapshots were included.

A simpler version of this origami-inspired mechanical metamaterial can be built by just using construction papers and rubber bands. A rubber band inside of a tube made of construction paper functions as the asymmetric tension/compression member. As detailed in SI Appendix, Fig. S14 and Movie S4), the similar load bearing and on-demand deployability and selective collapsibility have been achieved.

Discussion

We have introduced an on-demand deployable and selectively collapsible origami-inspired mechanical metamaterial whose configurations and stiffness are greatly tunable, depending on different states and loading paths, which leads to many applications as reconfigurable and stiff mechanical metamaterials. The principle discovered in this work can be readily applied to other metamaterials. Still taking triangulated cylinder as an example, one can simply increase the number of triangles (i.e., n) to create a deployable cylinder or tube with great axial stiffness. By altering the angles α and β with $\alpha +\beta \ge 90°$, the strains can be designed eventually across AB, BC, and AC members during the hard collapse path and all strains do not exceed the fracture threshold of the constitutive materials; thus, one can create on-demand deployable and very stiff mechanical metamaterials. The lesson to create such a metamaterial can be greatly extended to other structures by achieving nonmonotonic strain path, or in other words, deformable origami with interesting strain path. The key requirement for a general design principle would be two aspects, deformable origami and nonmonotonic strain path. Although deformable origami was not extensively studied or discovered, one can create deformable origami patterns using rigid origami as the building block. For example, two Miura unit cells can be brought together to form composite, deformable origami patterns. A similar approach has been utilized to create a Miura tube (6), although this tube is a rigid origami because it satisfies certain constraints. Without these constraints, the formed composited origami patterns are in general deformable. It is expected that a large family of deformable origami patterns can be created this way (22). The second requirement, i.e., nonmonotonic strain path, would be a bit challenging as it needs thorough searching. Intuitively, triangle patterns may tend to exhibit this property more than quadrilateral patterns. Another option is to consider not only axial deformation but also rotation or twist, although special treatment should be adopted at the joints to allow combined deformations. By finding potential patterns that satisfy these two requirements, it is expected that this work can be employed to create more versatile mechanical metamaterials with tunable deployability and stiffness.

This work explores the on-demand deployability and collapsibility and achieves these characteristics manually. Various type of automatic actuations, including pneumatic force (7, 23), heat (24–28), light (29–32), swelling (29, 33), and magnetic forces (34, 35), can be considered in the future to develop responsive, self-deploy/collapse, and stiff metamaterials. Although the structure we built in this work is on the centimeter scale, the principle we discovered can be applied to make a miniaturized structure. Moreover, by connecting the metamaterials in series with each metamaterial with different stiffness at the deployed state, one can make a mechanical metamaterial with continuously tunable stiffness.

In summary, we believe that this work represents an innovative approach to create a mechanical metamaterial with on-demand and selective deployability and collapsibility, and great stiffness and load-bearing capability. The principle in this work can be utilized to design and create versatile origami-inspired mechanical metamaterials that can find many applications, ranging from deployable structures for aerospace, civil applications, implantable medical devices, daily essentials, and toys, to bistable states for vibration isolations, to continuous tunable stiffness for wearable robotics.

Materials and Methods

Folding Origami Structures.

The models in Fig. 1 were created from precreased construction paper (90 g/m²). To make uniform creases on the paper, Silhouette Cameo cutting plotter was used to pattern the construction paper along the folding lines with cuts of 1 mm in length and 1 mm in spacing between the cuts. Once folded to a cylindrical tube, tapes were used to adhere them together along the commensurate edges.

Assembly of the Origami-Inspired Metamaterials.

The list of all components is provided in SI Appendix, Fig. S6. Their detailed geometries and series are also given. The rod end bearing was customized (FXB) with the detailed geometry in SI Appendix, Figs. S6 and S8. By following the design blueprint (SI Appendix, Fig. S7), the origami-inspired metamaterials can be assembled using standard tools.

Compression Tests.

We characterized the load-bearing capability of the metamaterial using a single-axis Instron (model 4411; Instron). The samples were placed between two flat plates of the compression machine. The load cell is 5,000 N and the displacement rate is 1 mm min⁻¹. Multiple runs were conducted to achieve average measurement.