Abstract
Maternally inherited symbionts such as Wolbachia have long been seen mainly as reproductive parasites, with deleterious effects on host fitness. It is becoming clear, however, that, frequently, these symbionts also have beneficial effects on host fitness, either along with reproductive parasitism or not. Using the examples of cytoplasmic incompatibility (CI) and male-killing (MK), we here analyze the effect of direct fitness benefits on the evolution of reproductive parasites. By means of a simple theoretical framework, we synthesize and extend earlier modeling approaches for CI and MK, which usually ignore fitness benefits. Moreover, our framework is not restricted to a particular mechanism underlying the fitness benefit (e.g., protection against pathogens). We derive invasion conditions and equilibrium frequencies for the different infection scenarios. Our results demonstrate the importance of a symbiont’s “effective fecundity” (i.e., the product of the relative fecundity of an infected female and her transmission efficiency) for a symbiont’s invasion success. In particular, we adopt the concept of effective fecundity to scenarios where CI and MK co-occur in one host population. We confirm that direct fitness benefits substantially facilitate the invasion and spread of infections (for example, by lowering or removing the invasion threshold) or even make invasion possible in the first place (for example, if reproductive parasitism is weak or absent). Finally, we discuss the role of direct fitness benefits in long-term evolutionary dynamics of reproductive phenotypes and highlight their potential to resolve genetic conflicts between maternally inherited symbionts and their hosts.
Introduction
Most heritable bacterial symbionts of arthropods are transmitted through females only. Maternally inherited symbionts are therefore under selection to increase the proportion of infected females. An obvious way to do so is to directly increase the fitness of infected females—the strategy chosen by mutualistic symbionts. A less obvious way is to manipulate host reproduction in ways that increase the proportion of infected females somewhat more indirectly. The strategy of manipulating host reproduction likewise enhances symbiont transmission, even though it can be detrimental to host fitness (that is why this strategy is also called reproductive parasitism).
Reproductive parasites are extremely widespread among arthropods: Wolbachia, the most famous one, probably infects about half of all terrestrial arthropod species alone, but other symbionts have their share, too (Zug and Hammerstein 2012; Weinert et al. 2015). Phenotypes of reproductive parasitism have profound effects on host development, ecology, and evolution (Engelstädter and Hurst 2009; Hurst and Frost 2015). In detail, these phenotypes include feminization, induction of thelytokous parthenogenesis, male-killing (MK), and cytoplasmic incompatibility (CI). The adaptive rationale behind the former two phenotypes is straightforward: converting non-transmitting males into transmitting females. MK is advantageous to symbionts when infected sisters of killed males benefit from their brothers’ death through some form of fitness compensation, for example, resource reallocation. CI-inducing symbionts, lastly, exert a form of conditional sterility on their hosts: uninfected females suffer high offspring mortality when mating with infected males. By contrast, infected females can mate successfully with both infected and uninfected males. CI thus benefits infected females and favors the spread of symbionts through host populations. The functioning of CI is usually conceptualized by a modification/rescue model: symbionts modify the sperm (the mod function), and the same strain must be present in the egg to rescue this modification (the resc function) (Werren 1997). Interestingly, mod and resc are functionally independent, illustrated by the existence of the mod − resc + phenotype, which is unable to induce CI but capable of rescuing it (Poinsot et al. 2003). Recently, putative bacterial genes responsible for the mod function have been identified (LePage et al. 2017; Beckmann et al. 2017). Nevertheless, the exact mechanism of CI, and of the resc function in particular, remains elusive.
In light of these drastic manipulations, it is not surprising that there has been a historical tendency to separate symbionts into mutualists and reproductive parasites. This view, however, neglects the fact that both strategies are not mutually exclusive: reproductive parasites can also have direct beneficial effects on host fitness, in addition to fitness effects that are due to reproductive parasitism (Harris et al. 2010; Himler et al. 2011; Zhang et al. 2012; Elnagdy et al. 2013; Xie et al. 2014; Zug and Hammerstein 2015 and references therein; Okayama et al. 2016; Xie et al. 2016). Instances of reproductive parasitism with direct fitness benefits have been termed “Jekyll and Hyde” infections (Jiggins and Hurst 2011; Zug and Hammerstein 2015).
There is a long history of population genetic models describing the infection dynamics of reproductive parasites, and of CI and MK in particular, as these are the two most commonly observed reproductive phenotypes. However, and although CI and MK are known to coexist in some populations, most models consider only invasion scenarios involving either of them. To our knowledge, only two studies have investigated theoretically the coexistence of CI and MK symbionts in an unstructured host population, but without explicit consideration of direct fitness benefits (Freeland and McCabe 1997; Engelstädter et al. 2004). Indeed, many models investigating the evolution of reproductive parasites either ignore direct fitness effects altogether or consider only fitness costs of infection. For example, MK models usually lack a term describing direct fitness effects, and most CI models consider direct fitness effects only in terms of reduced fecundity of infected females (but see Randerson et al. 2000; Dobson et al. 2002). Only recently have researchers begun to include the possibility of direct fitness benefits when modeling the invasion and spread of reproductive parasites. However, such fitness benefits have mostly been modeled in the form of symbiont-mediated protection against pathogens (Fenton et al. 2011; Xie et al. 2014; Souto-Maior et al. 2015). Such models usually involve many specific assumptions and parameters concerning pathogen infection, e.g., virulence, susceptibility, or parasitism rate. Hence, these models are not applicable to cases where symbiont-induced fitness benefits do not stem from protective effects. Moreover, the significance of symbiont-mediated protection in nature is still under debate (Zug and Hammerstein 2015). Therefore, we think that a modeling approach involving a more general conception of direct fitness benefits will complement more specific models and thus advance our understanding of “Jekyll and Hyde” infection dynamics.
Last but not least, direct fitness benefits are also crucial for understanding the prevalence of infections where reproductive parasitism is weak or absent (so-called “stand-alone benefit” infections; Giordano et al. 1995; Hoffmann et al. 1996, 1998; Vavre et al. 1999; Perrot-Minnot et al. 2002; Charlat et al. 2003, 2004; Zabalou et al. 2004; Kageyama et al. 2006; Jaenike et al. 2010; Zhang et al. 2010; Bouwma and Shoemaker 2011; Ventura et al. 2012; Kriesner et al. 2013; Hamm et al. 2014; Xie et al. 2015; Zug and Hammerstein 2015 and references therein; Cattel et al. 2016a, b; Cooper et al. 2017). Theory suggests that in these cases, and if transmission is not perfect, symbionts should increase host fitness in order to be maintained (Hoffmann and Turelli 1997).
In this paper, we analyze the effects of direct fitness benefits on the dynamics of both “stand-alone benefit” and “Jekyll and Hyde” infections, in the latter case focusing on CI and MK. First, we outline the basic structure of our modeling framework and review the infection dynamics involving one symbiont (beneficial, CI, or MK). We then investigate infection dynamics involving two symbionts with distinct phenotypes and also consider the possibility of doubly infected host individuals. In doing so, we synthesize former theoretical studies on CI and MK symbionts and extend them to include mutualistic effects. Finally, we discuss our findings in the light of relevant theoretical and empirical research.
Theoretical framework
Consider a single panmictic host population with discrete, non-overlapping generations. Host individuals are haploid and reproduce sexually with the primary sex ratio being 1:1. Individuals are sufficiently described by two parameters: their infection status and their sex. Regarding their infection status, individuals can be uninfected, infected with CI symbionts, with MK symbionts, or with both. Depending on infection status and sex, individuals can be grouped into different classes. We denote by p the frequency of females of a given infection status, as a fraction of the whole population (for reasons of comprehensibility, however, frequencies depicted in the figures are those of all individuals of a given infection status, i.e., males and females). We derive difference equations describing the frequency changes of the different classes of individuals from one generation to the next. Building upon standard replicator dynamics, frequencies of the offspring classes can be calculated from frequencies of parental classes, maternal transmission efficiency, and fitness-related effects of infection.
Symbionts are maternally inherited with transmission efficiency t, i.e., the proportion of infected offspring produced by an infected female (see Table 1 for all parameters used). Transmission efficiency is assumed to be unaffected by the presence or absence of symbiont-induced fitness effects. Regarding double infections, transmission of CI is assumed to be independent of transmission of MK.
Table 1.
Glossary of notation
| Symbol | Definition |
|---|---|
| β | Resource reallocation efficiency (proportion of the resources the killed males would have used that is reallocated to the surviving siblings) |
| F | Relative fecundity of infected females |
| l CI | CI level (proportion of offspring killed in incompatible matings) |
| p | Frequency of females of a given infection status |
| Equilibrium infection frequency | |
| p ⊕ | Beneficial infection frequency |
| p CI | CI infection frequency |
| p CI+MK | CI+MK double-infection frequency |
| p MK | MK infection frequency |
| p U | Frequency of uninfected females |
| p ini | Initial infection frequency |
| p thr | Threshold infection frequency |
| R | Fitness compensation (surviving offspring’s fitness increase through resource reallocation) |
| t | Maternal transmission efficiency (proportion of infected offspring produced by an infected female) |
| v | Male viability in the face of MK |
Symbiont-induced fitness effects can be partitioned into two components: those due to reproductive parasitism (CI and/or MK in this paper); and those directly affecting host fitness. Both fitness effects are assumed to be independent of each other (as are direct fitness effects of each symbiont in doubly infected hosts). In the spirit of the classical CI models by Hoffmann and Turelli (Hoffmann et al. 1990; Turelli 1994; Hoffmann and Turelli 1997), we denote by the parameter F the relative fecundity of an infected female. In principle, however, F also approximates other fitness effects such as viability, growth, and performance, each of which are known to be affected by reproductive parasites (Dobson et al. 2002; Gavotte et al. 2010; Xue et al. 2012). For example, when thinking of F as lifetime fecundity, then the parameter also captures effects on longevity or development time. Such a general conception of F is also advocated in other recent theoretical studies of the infection dynamics of reproductive parasites (e.g., Turelli and Barton 2017). Moreover, this approach is independent of the particular mechanism underlying the fitness effect, e.g., anti-pathogenic protection (Zélé et al. 2012), nutritional provisioning (Brownlie et al. 2009), or manipulation of host plant physiology (Kaiser et al. 2010). Importantly, fitness effects that are due to reproductive manipulations are not measured by F.
Following Turelli (1994), we refer to Ft (i.e., the product of an infected female’s relative fecundity and her transmission efficiency) as the “effective fecundity” of an infected female. In other words, effective fecundity is a measure of the number of infected eggs laid by an infected female (relative to the number of uninfected eggs laid by an uninfected female). Therefore, the term can be used not only as an attribute of the female host but also of the symbiont (because symbiont transmission depends directly on the number of infected eggs).
“Stand-alone benefit” infection dynamics
In the absence of reproductive manipulations and without perfect maternal transmission, symbionts must confer a fitness benefit to the host in order to be able to spread (“stand-alone benefit” infections). In describing the infection dynamics of facultative beneficial symbionts, at least two parameters are necessary: the transmission efficiency t ⊕; and the relative fecundity of infected females F ⊕. The proportion of infected and uninfected females in the population (p ⊕ and p U, respectively) then changes from one generation to the next by
| 1a |
| 1b |
where
The resulting stable equilibrium frequency of beneficial symbionts is
| 2 |
This equilibrium frequency is precisely analogous to mutation-selection balance for haploids (Hoffmann and Turelli 1997). The “transmission-selection balance” described by Eq. (2) is the simplest means by which a polymorphism for a beneficial symbiont infection can be maintained (Jaenike 2012; Kriesner et al. 2016).
The condition for the spread of beneficial symbionts is
| 3 |
We see that for beneficial symbionts to spread, their effective fecundity must be >1. This reflects the simple fact that maternally inherited symbionts will spread if infected females produce more infected daughters than uninfected females produce uninfected daughters. If, on the other hand, F ⊕ t ⊕ < 1, symbionts will not spread by benefits alone. They then have to resort to some kind of reproductive manipulation such as CI or MK in order to persist.
CI infection dynamics
In describing the infection dynamics of CI-inducing symbionts, we follow earlier models (Hoffmann et al. 1990; Turelli 1994; Hoffmann and Turelli 1997). Under CI, uninfected females suffer offspring loss when mating with infected males. This fitness reduction is depicted as the CI level l CI, i.e., the proportion of offspring killed in incompatible matings. The proportion p of infected and uninfected females in the population changes from one generation to the next by
| 4a |
| 4b |
where
In the numerator of Eqs. (4a) and (4b), the first term (in round brackets) denotes the maternal contribution and the second term (in square brackets) denotes the paternal contribution. Note that under CI, the proportion of infected and uninfected individuals among males equals that among females, hence it is possible to express the paternal contribution in terms of female frequencies.
Equation (4a) has two nontrivial equilibria, given by
| 5a |
| 5b |
where
The first equilibrium is stable and defines the CI equilibrium frequency. The second equilibrium is unstable and defines the threshold frequency below which the infection will disappear from the population. The CI threshold exists whenever F CI t CI < 1 and can take values of substantial magnitude, particularly under low transmission efficiency and high costs of infection, i.e., reduced fitness (Fig. 1a). By contrast, if a symbiont’s effective fecundity is >1 (F CI t CI > 1), there is no invasion threshold (Fig. 1a,b). The crucial effect of effective fecundity on the CI equilibrium frequency is shown in Fig. 3a. If F CI t CI < 1, CI dynamics are bistable; there is an unstable equilibrium that separates two stable equilibria, one at zero and the other being . Invasion is only possible if the initial frequency exceeds the threshold frequency . If F CI t CI > 1, CI can invade and spread from any initial frequency, however small it may be, and will eventually reach .
Fig. 1.
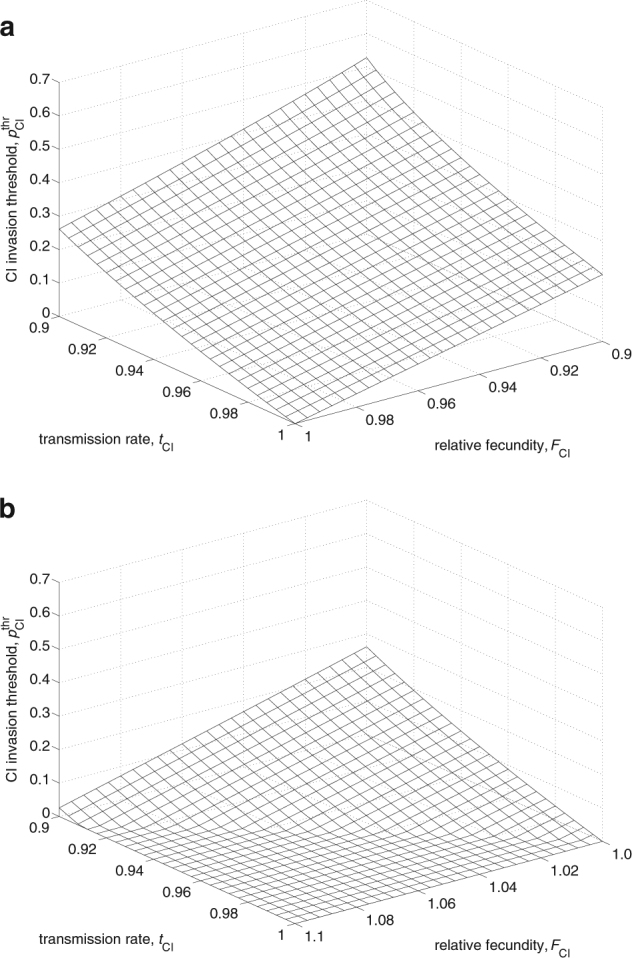
Direct fitness benefits facilitate invasion of CI by lowering or removing the CI invasion threshold. Behavior of the CI invasion threshold in dependence of the relative fecundity of infected females, F CI, and the transmission rate, t CI, for F CI < 1 (a) and F CI > 1 (b). The CI threshold disappears if F CI t CI > 1. l CI = 0.5
Fig. 3.
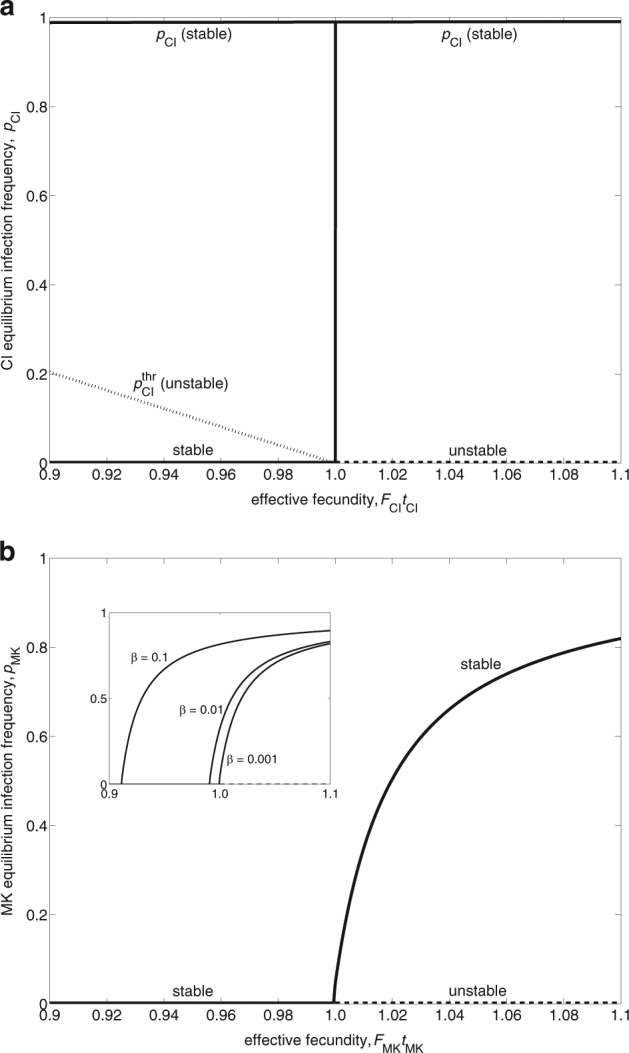
The effect of effective fecundity on the equilibrium infection frequency of CI (a) and MK (b). a Due to frequency-dependent selection, CI dynamics exhibit cβ if F CI t CI < 1. In this case, an unstable equilibrium, which defines the CI threshold frequency , separates two stable equilibria, one at 0 and the other defining the CI equilibrium frequency . Invasion is possible only if the initial frequency exceeds the threshold frequency. At F CI t CI = 1, there is a fold bifurcation. If F CI t CI > 1, there is only one stable equilibrium so that invasion is possible for arbitrarily low initial frequencies. Parameters take the values t CI = 0.99 and l CI = 0.5. b MK dynamics lack frequency-dependent selection, and hence do not exhibit bistability. The critical resource reallocation efficiency β crit (below which invasion is not possible) exists whenever F MK t MK < 1. At F MK t MK = 1, there is a transcritical bifurcation. However, the fact that the bifurcation point lies at F MK t MK = 1 only becomes obvious for very small β values, because β crit is easily exceeded if β values are larger (see inset). Parameters take the values t MK = 0.99, β = 0.001, and v = 0
It has been stated that changes in F CI have little impact on (Weeks et al. 2007). However, this is only correct as long as the initial frequency exceeds the threshold frequency . If the initial frequency lies below the threshold frequency, changes in F CI have a huge effect on (Supplementary Figure S1). For a large part of the range of the CI level l CI, the relationship between F CI and exhibits a switch-like behavior at the point where the initial frequency equals the threshold frequency. Above this point, the positive effect of F CI on is extremely small for a large part of the l CI range, but becomes strong for small l CI values. The switch-like behavior only vanishes for very small l CI values close to zero, where increases gradually with increasing F CI.
MK infection dynamics
In describing the infection dynamics of MK-inducing symbionts, we follow earlier models, in particular Hurst (1991b), Randerson et al. (2000), and Normark (2004). Under MK, male offspring is killed during embryogenesis. However, a fraction v of the male offspring is assumed to survive the male-killing. A proportion β of the resources the killed males would have used is reallocated to the surviving siblings and distributed equally among them. The relative fitness of the surviving offspring from infected females is increased by a factor R, which is given by
| 6 |
For the derivation of this fitness compensation term, see for example Normark (2004) and Engelstädter and Hurst (2006). The proportion p of infected and uninfected females in the population changes from one generation to the next by
| 7a |
| 7b |
where
In Eqs. (7a) and (7b), the numerator denotes only the maternal contribution (as the paternal contribution cancels out in both equations). The nontrivial equilibria of these equations are
| 8a |
| 8b |
where
In contrast to CI, MK distorts offspring sex ratios, and therefore the proportion of infected females differs from that of infected males (that are scarce or absent under MK). To derive the equilibrium frequency of infected males, one has to multiply with v.
The MK equilibrium is positive if
| 9 |
Since this is also the condition for to be stable (not shown), condition (9) is a necessary and sufficient condition for male-killing bacteria to invade and persist in a population. Hence, male-killers can invade if the product of their effective fecundity (F MK t MK) and the fitness compensation through resource reallocation (R) is >1.
It is convenient to solve this invasion condition for β, the resource reallocation efficiency (Hurst 1991b; Normark 2004). Doing this yields
| 10 |
If the resource reallocation efficiency β is greater than a critical value β crit (given by condition 10), then the male-killer will invade and finally reach the equilibrium frequency given in Eq. (8a). If MK bacteria have a negative fitness effect on infected females (F MK < 1), then β crit can take quite high values, particularly if there is considerable male survival under MK (Fig. 2a). The ability of male-killers to induce a fitness benefit (F MK > 1) substantially facilitates their invasion by lowering the critical resource reallocation efficiency β crit (Fig. 2b). Therefore, even if the resource reallocation efficiency β is very low, a small fitness benefit is sufficient to reduce the critical value β crit so that the male-killer can invade. The critical value β crit exists whenever F MK t MK < 1. That is the same condition as for the existence of the CI invasion threshold (Eq. (5b)). This again emphasizes the importance of a symbiont’s effective fecundity for its invasion potential. The effect of effective fecundity on the MK equilibrium frequency is shown in Fig. 3b. In contrast to CI, MK dynamics are never bi-stable. If F MK t MK < 1, there is only one stable equilibrium at 0, and if F MK t MK > 1, MK can invade from arbitrarily low frequencies and will reach the stable equilibrium . However, the threshold behavior at F MK t MK = 1 only becomes obvious for very small β values, because β crit is easily exceeded if β values are larger.
Fig. 2.
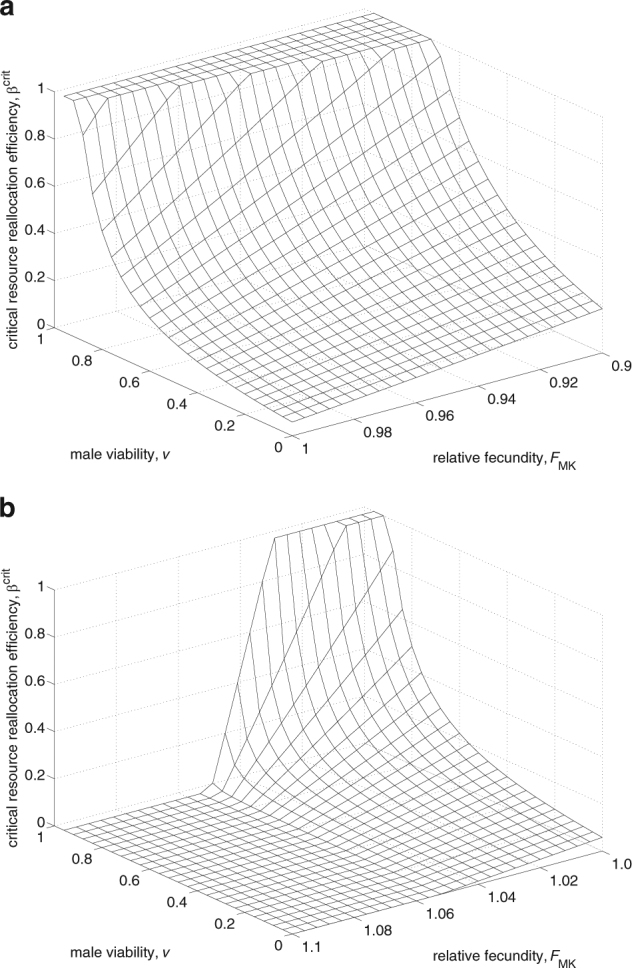
Direct fitness benefits facilitate invasion of male-killers by lowering or removing the critical resource reallocation efficiency. Behavior of the critical resource reallocation efficiency, β crit, in dependence of the relative fecundity of infected females, F MK, and the viability of males under MK, v, for F MK < 1 (a) and F MK > 1 (b). β crit disappears if F MK t MK > 1. t MK = 0.95
Results
The theoretical framework outlined above also allows for the analysis of infection dynamics involving two symbionts with distinct phenotypes (beneficial, CI, or MK). In the main text, we present invasion conditions (and equilibrium frequencies where double infections occur) and their biological implications; the difference equations and the derivation of the invasion conditions can be found in the Supplementary Information 1 and 2.
Infection dynamics with two symbionts, but without doubly infected hosts
Two symbionts: beneficial vs. CI
Invasion of a beneficial symbiont into a CI population
The condition for an initially rare beneficial symbiont to increase in a population where a CI symbiont is at equilibrium is
| 11 |
F ⊕ t ⊕ is the effective fecundity of the beneficial symbiont, and F CI t CI is the effective fecundity of the CI symbiont. The term describes the CI-associated offspring loss in females not infected with the CI symbiont. Thus, in order to invade, a beneficial symbiont must not only exhibit a larger effective fecundity than the resident CI symbiont but also compensate for the fitness loss due to incompatible matings with CI-infected males (Turelli 1994). The latter is only possible with low CI levels. If condition (11) is fulfilled, the beneficial symbiont will invade and drive the CI symbiont to extinction. For biologically reasonable parameter values (F CI, t CI > 0.9), the term is always >1 (not shown). Hence, if condition (11) is satisfied, it also implies that F ⊕ t ⊕ > 1; therefore, the beneficial symbiont will finally reach the equilibrium frequency given by Eq. (2).
If the beneficial symbiont is able to rescue CI (i.e., if it is a mod − resc + strain), the invasion condition is simply
| 12 |
Whether the ability to rescue CI influences the invasion probability of a beneficial symbiont depends on which of the conditions (11) and (12) are fulfilled. If both are satisfied, the beneficial symbiont will invade and reach , regardless of whether it is able to rescue CI or not. Importantly, however, insensitivity to CI significantly accelerates the time it takes for the beneficial symbiont to invade the population and replace the CI symbiont (not shown). If neither condition is satisfied, infection will go extinct in both cases. Finally, if condition (12) is satisfied, but condition (11) is not, it is crucial whether the beneficial symbiont is able to rescue CI or not. If not (i.e., if it is mod − resc −), it will go extinct. However, if the beneficial symbiont is mod − resc +, it will invade the population, drive the resident CI symbiont to extinction, and, if F ⊕ t ⊕ > 1, finally reach the equilibrium frequency . The fact that neither l CI nor enters condition (12) implies that a mod − resc + beneficial symbiont is able to invade a CI population even if CI levels are very high and CI is essentially fixed in the population (Fig. 4).
Fig. 4.
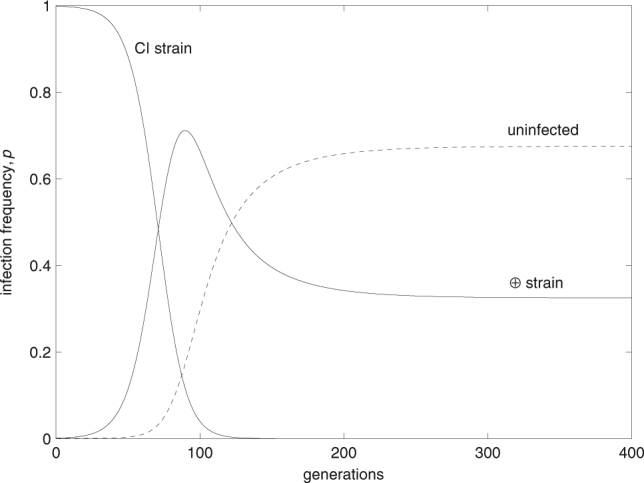
A beneficial symbiont that is able to rescue CI can invade even into populations fixed for CI. Such invasion is possible if condition (12) is fulfilled. Parameters take the values F ⊕ = 1.08, t ⊕ = 0.95, F CI = 0.95, t CI = 0.98, and l CI = 0.98
Theory suggests that with imperfect maternal transmission and without any fitness benefits, mod − resc + strains can only spread in the presence of a mod + resc + strain, but their spread eventually leads to the extinction of both infections (Hurst and McVean 1996). Beneficial mod − resc + strains, by contrast, can easily spread in a CI-infected population and outcompete the resident strain.
Invasion of a CI symbiont into a beneficial population
The condition for a rare CI symbiont to invade a population in which a beneficial infection is at equilibrium was derived by Kriesner et al. (2013) and is given by
| 13 |
Because essentially no CI occurs when the CI symbiont is very rare, the incompatibility does not enter this condition. Hence, for a CI symbiont to invade a population at equilibrium with a beneficial symbiont it is sufficient that it has a larger effective fecundity (obviously, this also holds for a beneficial symbiont invading a population infected with another beneficial symbiont). However, a beneficial symbiont can reach its equilibrium frequency in the first place only if F ⊕ t ⊕ > 1. Without direct fitness benefits, the CI symbiont’s effective fecundity cannot exceed 1, and it is therefore only able to invade a population infected at equilibrium with a beneficial symbiont if it confers a direct benefit.
Two symbionts: beneficial vs. MK
Invasion of a beneficial symbiont into a MK population
The condition for an initially rare beneficial symbiont to increase in a population where a MK symbiont is at equilibrium is
| 14 |
Thus, in order to invade, a beneficial symbiont’s effective fecundity must exceed the MK symbiont’s effective fecundity multiplied by the fitness compensation factor R.
Invasion of a MK symbiont into a beneficial population
The condition for an initially rare MK symbiont to invade into a population infected at equilibrium with a beneficial symbiont is
| 15 |
Above we showed that a CI symbiont without direct fitness benefits is not able to invade a beneficial population. By contrast, a MK symbiont without direct benefits is able to do so if the fitness compensation due to MK is sufficiently high.
Two symbionts: CI vs. MK
Invasion of a MK symbiont into a CI population
The condition for an initially rare MK symbiont to increase in a population where a CI symbiont is at equilibrium is
| 16 |
The invading MK symbiont faces the risk of high offspring mortality due to CI prevailing in the population. Therefore, invasion is only possible with low CI levels (Fig. 5). In addition to low CI levels, invasion is also facilitated by high fitness compensation through male-killing (R) and direct fitness benefits of the MK symbiont. A strong male-killer (with low v and high β values, leading to high fitness compensation) might be able to invade into a CI population even without conferring direct fitness benefits. However, as shown above, fitness benefits strongly enhance the invasion potential of weak male-killers (high v and low β). In particular, if a male-killer’s resource reallocation efficiency β is low, the symbiont will only be able to invade when conferring a direct fitness benefit.
Fig. 5.
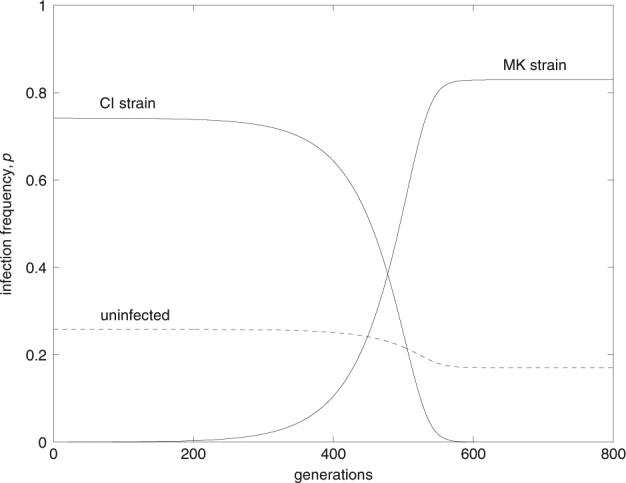
A male-killing symbiont invades into a population at equilibrium with a CI-inducing symbiont. Such invasion is possible if condition (16) is fulfilled. Parameters take the values F MK = 1.02, t MK = 0.99, β = 0.1, v = 0, F CI = 1.04, t CI = 0.97, and l CI = 0.1
If the MK symbiont is mod − resc +, the invasion condition simplifies to
| 17 |
If condition (17) is fulfilled, the mod − resc + MK symbiont will invade the population, drive the resident CI symbiont to extinction, and, if RF MK t MK > 1, finally reach the equilibrium frequency . Given that the mod − resc + MK symbiont is insensitive to CI, it can invade even in populations fixed for CI.
So far, we have considered fitness compensation only in the case of male-killing. However, fitness compensation could also occur in broods where offspring is killed not because of MK, but CI (Freeland and McCabe 1997). Interestingly, when vertical transmission is high (which holds true throughout this paper), such compensation cannot aid the spread of CI, but only increases the average fitness of uninfected offspring, and may thus even impede the spread of CI (Freeland and McCabe 1997). In our model, we also find this impeding effect of CI-associated fitness compensation: when we allow for fitness compensation not only for MK but also for CI, we find that invasion of a MK symbiont into a CI population is accelerated significantly (not shown). Therefore, the possibility of CI-associated fitness compensation does not prevent CI symbionts from being replaced by MK symbionts (given that condition (16) or (17) is fulfilled).
Invasion of a CI symbiont into a MK population
Due to frequency-dependent selection, CI involves a minimum infection frequency below which it cannot establish. When introduced into a population infected with male-killers, this invasion threshold exists whenever F CI t CI < RF MK t MK (albeit we could not derive this threshold analytically). If, on the other hand, F CI t CI > RF MK t MK, there is no invasion threshold, and CI can establish no matter how low its initial frequency. Therefore, the condition for an initially arbitrarily rare CI symbiont to increase in a population where a MK symbiont is at equilibrium is
| 18 |
The fact that the invasion condition does not contain the CI level l CI implies that even symbionts with very low CI levels can invade. This is not surprising, however, since a symbiont with stand-alone benefits is also able to invade a MK population as long as its effective fecundity is large enough (see above). Further, remember that the condition for male-killers to invade an uninfected population is RF MK t MK > 1 (condition 9). Therefore, for a male-killer to reach the equilibrium, the right-hand side of condition (18) must be >1. From this, it is easy to see that an extremely rare CI symbiont without direct benefits cannot invade a population infected at equilibrium with a male-killer, because its effective fecundity never exceeds 1. Hence, invasion is only possible for a CI symbiont that additionally confers a direct fitness benefit (the same holds true for CI invasion into a population infected at equilibrium with a beneficial symbiont; see above).
Infection dynamics with two symbionts and doubly infected hosts
So far, we have not observed stable coexistence of CI and MK. Previous modeling has shown that stable coexistence of CI and MK symbionts is possible if doubly infected individuals exist within the population (Engelstädter et al. 2004). If doubly infected hosts occur, there are eight types of individuals, four of each sex. The corresponding equation system (Supplementary Information 2) has eight equilibrium sets, five of which are biologically plausible. These plausible sets are (i) the infection-free equilibrium, (ii) the CI equilibrium (stable), (iii) the CI threshold (unstable), (iv) the MK equilibrium, and (v) the equilibrium containing CI, MK, and the double infection CI+MK. In the latter case, all eight types of individuals are present in equilibrium, and the equilibrium frequencies of the four female types are given by
| 19a |
| 19b |
| 19c |
| 19d |
where
Note that the term inside the square root, C, is identical with the term inside the square root in the standard CI equilibria (Eqs. (5a) and (5b)), and the denominator, D, is half the product of the denominators in the standard CI and MK equilibria (Eqs. (5a) and (8a)). Accordingly, the equilibrium frequency of the double infection (Eq. (19a)) is twice the product of the equilibrium frequencies of the corresponding single infections (Eq. (5a)) and (Eq. (8a)) in the one-symbiont dynamics. Moreover, there is a structural similarity between and on the one hand, and between and on the other hand. One reason for this is that both uninfected females and females infected by a male-killer suffer from CI, whereas females infected by CI+MK and CI do not. Hence, if all four types are present in equilibrium, we can expect generally larger values for and than for and (Fig. 6b).
Fig. 6.
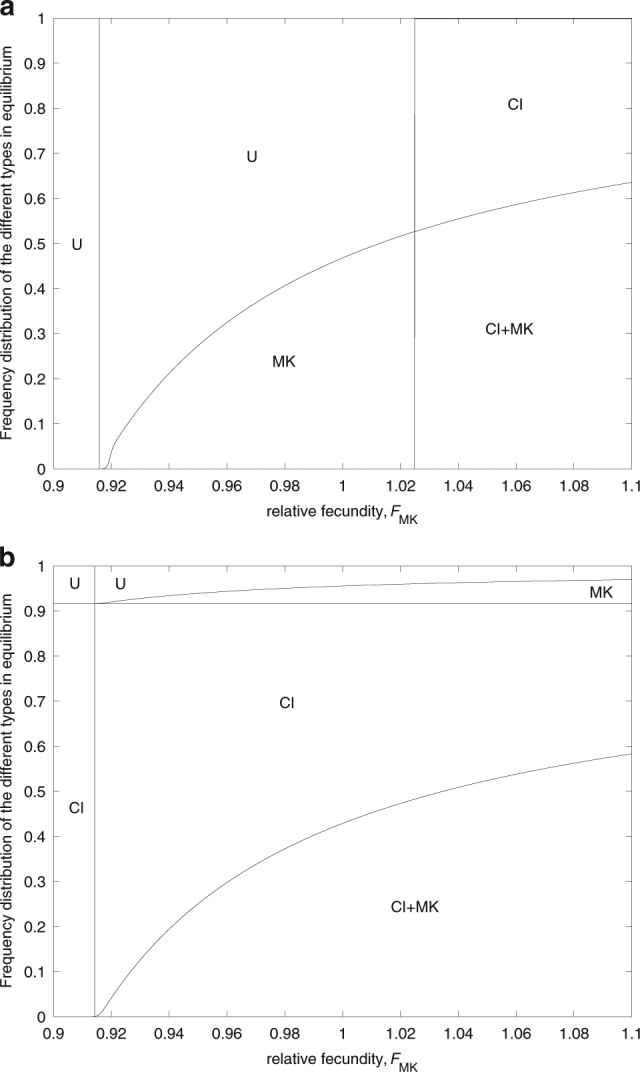
Frequency distribution of the different types in equilibrium after invasion of a CI+MK double infection into an uninfected population. Frequency distributions are shown in dependence of the relative fecundity of females infected with the male-killer, F MK, for F CI < 1 (a) and F CI > 1 (b). Parameters take the values F CI = 0.96, l CI = 0.9 (a), F CI = 1.02, l CI = 0.1 (b), t CI = 0.99, t MK = 0.95, β = 0.2, and v = 0.1
Invasion of a CI+MK double infection into an uninfected population
If we allow for the existence of doubly infected hosts, complex dynamics are possible. The condition for an initially rare double infection (CI+MK) to invade into an uninfected population and finally reach the stable equilibrium given by Eq. (19a) is
| 20 |
If this condition is not met, the double infection must exceed a threshold frequency in order to be able to invade (Engelstädter et al. 2004).
To see how condition (20) relates to the possible outcomes of the CI+MK introduction, let us term its left-hand part C 1 and partition it into two parts, C 2 and C 3, where and . Table 2 shows all possible outcomes of the introduction of a double infection into an uninfected population, dependent on which of the terms C 1, C 2, and C 3 are >1. Let us start with the obvious results. If none of the three conditions is fulfilled, there will be no infection (case I; Fig. 6a). If only C 3 > 1, only the male-killer will invade (case II; Fig. 6a), and if only C 2 > 1, only CI will establish (case IV; Fig. 6b). The double infection is stably maintained only if C 1 > 1, that is, if condition (20) is fulfilled (cases III and VI; Fig. 6). Importantly, however, this condition is necessary, but not sufficient for the stable existence of double infections. Even if condition (20) is fulfilled, it is possible that the double infection disappears, while either CI or MK prevails as a single infection (cases III and V).
Table 2.
Possible outcomes of the introduction of the CI+MK double infection
| C1 > 1? | C2 > 1? | C3 > 1? | Further conditions | Result (stable equilibria) | |
|---|---|---|---|---|---|
| I | No | No | No | U | |
| II | No | No | Yes | MK, U | |
| III | Yes | No | Yes | CI and MK parameters higha | CI+MK, CI, MK, Ub |
| Else | MK, U | ||||
| IV | No | Yes | No | CI, U | |
| V | Yes | Yes | No | CI, U | |
| VI | Yes | Yes | Yes | CI+MK, CI, MK, Ub |
aHere, CI parameters are F CI, l CI, and t CI, and MK parameters are F MK, t MK, and β
bFor most of the parameter range, CI+MK and CI dominate over MK and U (see main text)
The most interesting dynamics can be observed in case III. Here, RF MK t MK > 1, implying that MK will be present in equilibrium, be it as single or double infection. In contrast, the effective fecundity of the CI symbiont is <1. In the one-symbiont dynamics, this implies the existence of a threshold frequency so that no CI invasion is possible if the initial frequency is below this threshold (see above). The introduction of a double infection, by contrast, makes it possible for CI to establish in a population, even if extremely rare initially. To see this, let us have a closer look at the infection dynamics in case III. Due to imperfect maternal transmission (t CI, t MK < 1), the double infection also introduces both single infections into the population. Given that the CI-associated drive is frequency-dependent (being very weak when CI is rare), whereas the MK-associated drive is not, MK will initially increase more strongly than CI. Nevertheless, as long as the double infection increases, the single CI infection will also increase. With increasing CI+MK and CI frequencies, CI-associated positive frequency-dependent selection becomes stronger, so that it can happen that CI eliminates MK and becomes predominant, being present both as single and double infection. This happens if sufficient parameters underlying the success of CI and MK (F CI, l CI, t CI, F MK, t MK, and β) are large enough (while male viability v must not be too large). The crucial point is that CI benefits from a successful double infection, regardless of how this success is achieved. This leads to the counter-intuitive result that even an increase in F MK can result in the displacement of MK by the double infection and in fixation of CI (Fig. 6a).
Invasion of a CI+MK double infection into a CI population
The condition for an initially rare double infection (CI+MK) to increase in a population where CI is at equilibrium is
| 21 |
With the spread of the double infection, the single MK infection is also introduced into the population. The only exception is for l CI = 1: in a population fixed for CI, the double infection can invade, but there is no introduction of the single MK infection. Instead, CI stays fixed during the invasion process; before the invasion, the single CI infection was fixed, and after the invasion, there is a polymorphism of the single CI and the double infection.
If condition (21) is not met, the double infection will not be able to invade, however high its initial frequency may be. The reason is that it is only MK that must establish (CI is already at equilibrium), but MK is not frequency-dependent so that there is no extra benefit from a high initial frequency.
Invasion of a CI+MK double infection into a MK population
The condition for an initially rare double infection (CI+MK) to increase in a population where MK is at equilibrium is
| 22 |
With the spread of the double infection, the single CI infection is also introduced into the population. There is a tendency for the CI+MK infection to “replace” the MK infection, eventually reaching an equilibrium frequency very similar to the initial MK frequency, and equally for the CI infection to “replace” the uninfecteds. This tendency increases with increasing l CI, until replacement is perfect with complete CI (Fig. 7). That is because, for l CI = 1, (Eq. (19a)) = (Eq. (8a)), and (Eq. (19b)) = (Eq. (8b)). As a consequence, and not surprisingly for l CI = 1, CI becomes fixed in the population, being present as a single and a double infection.
Fig. 7.
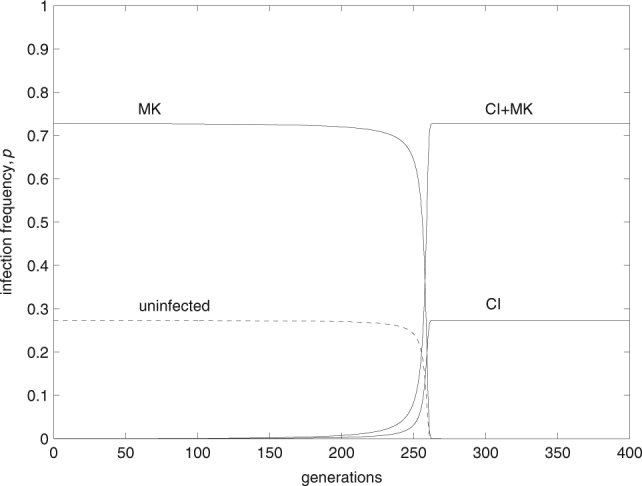
With complete CI, the invading double infection completely replaces the pre-existing MK infection. Simultaneously, CI is introduced as a single infection. As a consequence, CI becomes fixed in the population. Parameters take the values F CI = 1.04, t CI = 0.98, l CI = 1, F MK = 1.05, t MK = 0.97, β = 0.2, and v = 0.1
If condition (22) is not met, the double infection must again exceed a threshold frequency in order to be able to invade (Engelstädter et al. 2004).
Discussion
Reproductive parasitism constitutes a powerful means for maternally inherited symbionts to spread in host populations. However, evidence is accumulating that in a range of circumstances, reproductive manipulation alone is not sufficient to ensure symbiont invasion and spread. In these cases, direct positive effects on female fitness are predicted to enable symbionts to successfully invade host populations. This study investigates the effects of direct fitness benefits on the evolution of reproductive parasites, using the examples of CI and MK.
The key quantity in our paper is effective fecundity, i.e., the product of the relative fecundity of an infected female and her transmission efficiency. In a broader sense, however, effective fecundity also approximates more general fitness effects. Ever since Turelli (1994) established the concept of effective fecundity, theoretical studies have repeatedly proven its significance for the evolutionary success of microbes inducing CI or MK (Randerson et al. 2000; Egas et al. 2002; Vavre et al. 2003; Vautrin et al. 2007, 2008; Haygood and Turelli 2009; Kriesner et al. 2016). Our study supports these findings and at the same time extends them significantly: for the first time, we apply the concept of effective fecundity to a situation where different types of reproductive parasites co-occur, thus unifying earlier results. Here we discuss the major conclusions that can be drawn from this unifying framework.
One of the major gaps in our understanding of the infection dynamics of reproductive parasites is how they initially invade host populations. When introduced into a novel host, symbionts frequently perform poorly, for example, exhibiting low transmission efficiency (Clancy and Hoffmann 1997; Riegler et al. 2004; Russell and Moran 2005; Kageyama et al. 2006; Tinsley and Majerus 2007; Nakayama et al. 2015). Moreover, the benefits of reproductive parasitism are not unconditional. The drive associated with CI is frequency-dependent and hence very weak when infection is rare. As a result, CI-inducing symbionts face a threshold frequency below which infection cannot establish. Therefore, recently introduced CI infections, which usually exhibit low frequencies, should fail to invade (although, in principle, chance fluctuations might carry low initial frequencies above the threshold; Jansen et al. 2008). The drive associated with MK does not depend on infection frequency, but on the efficacy of the MK-associated fitness compensation, measured in terms of male-killing intensity and resource reallocation efficiency. This equally results in a threshold behavior: if fitness compensation is not effective enough, the male-killer will fail to invade. Indeed, survival of males despite infection with MK symbionts has been observed (Hurst et al. 2000; Dyer and Jaenike 2004; Charlat et al. 2005; Weinert et al. 2007; Watts et al. 2009; Bohacsova et al. 2016; Hayashi et al. 2016). In addition, it is unclear how efficient resource reallocation is in nature (Balas et al. 1996; Martins et al. 2010; Elnagdy et al. 2011; Unckless and Jaenike 2012). Accordingly, there has also been some debate in the theoretical literature on the range of values for the resource reallocation efficiency (Engelstädter and Hurst 2006; Úbeda and Normark 2006). In sum, invading symbionts face a range of obstacles when relying solely on reproductive parasitism. Our results show that direct fitness benefits easily overcome these obstacles by lowering or even removing invasion thresholds, thus confirming previous theoretical findings in the specific context of symbiont-induced protection (Fenton et al. 2011; Souto-Maior et al. 2015). Such net fitness advantages seem far more plausible than chance fluctuations to pass the invasion threshold (Turelli and Barton 2017). Lastly, reproductive parasitism may be weak or absent. Our findings confirm that in such cases, direct fitness benefits enable symbionts to invade host populations in the first place. Again, this is in line with recent theoretical results (Kriesner et al. 2013, 2016), and recent empirical studies corroborate that symbionts that do not show reproductive parasitism in novel hosts rapidly evolve to be benign (Veneti et al. 2012; Nakayama et al. 2015). Interestingly, another means of invasion and maintenance of weakly effective reproductive parasites is horizontal transmission among conspecific hosts (Parratt et al. 2016). Together, these findings indicate that in some cases, reproductive parasitism may be of secondary importance for symbiont invasion and spread. With regard to the evolutionary origins of reproductive parasitism, it is therefore important to consider the possibility that parasitic manipulation may evolve in addition to other, pre-existing phenotypic effects, e.g., mutualistic phenotypes (Engelstädter and Hurst 2009).
Direct fitness benefits also influence infection dynamics of different types of reproductive parasites within one host population. Engelstädter et al. (2004) showed that without direct benefits, threshold frequencies for CI symbionts tend to be highest if they are introduced as a single infection into a population infected with MK symbionts at equilibrium, and that the opposite invasion (MK symbionts into CI-infected population) is not possible under strong CI. Our results show that in the former case, direct benefits easily remove the invasion threshold, and that in the latter case, direct benefits considerably facilitate invasion of a male-killer, in particular if it is a weak one (low β and high v). Moreover, a mod − resc + male-killer can invade even in populations fixed for CI. Evidence of the existence of such a CI-insensitive MK symbiont comes from Drosophila pandora that carries both CI and MK Wolbachia. No incompatibility was detected in crosses between CI-infected males and MK-infected females, suggesting that these females can rescue CI (Richardson et al. 2016). Unfortunately, there is as yet not much empirical evidence for invasion scenarios involving CI and MK within one host population. The tropical butterfly Hypolimnas bolina might be a promising system to study the interactions between both reproductive phenotypes. In the South Pacific, this species harbors two strains of Wolbachia, one of which induces MK and the other one induces CI. Most populations are infected with either the MK strain or the CI strain only, suggesting that most often, populations infected by one strain are able to resist invasion by the other strain, and vice versa (Charlat et al. 2006). These findings are in line with the theoretical prediction that CI and MK cannot stably coexist in a single host population (if no doubly infected individuals occur; Engelstädter et al. 2004, 2008). In 3 out of 25 populations, however, co-occurrence of both strains was observed. The most likely explanation is that these populations are not at equilibrium, but rather represent transitional stages in which one strain (in this case, the CI strain) is about to invade and replace the other (Charlat et al. 2006). Given the existence of a threshold frequency for CI symbionts introduced into a population infected with a male-killer, it is quite possible that the invasion of CI into MK-infected H. bolina populations is facilitated by direct fitness benefits.
Theory suggests that CI and MK can coexist within a single unstructured host population in two different ways. First, both phenotypes can be expressed simultaneously by the same strain of reproductive parasite (Hurst et al. 2002). Alternatively, CI and MK are expressed by different strains of symbionts, and doubly infected host individuals exist (Freeland and McCabe 1997; Engelstädter et al. 2004). The latter situation was investigated in this paper. To the best of our knowledge, we present for the first time invasion conditions and equilibrium frequencies for the invasion of CI+MK double infections. Engelstädter et al. (2004) showed via simulations that the double infection must exceed a threshold frequency to invade a population that is uninfected or MK-infected, but that this threshold is lower than the threshold for CI as a single infection. In accordance with these results, we find that invasion conditions for the double infection are more relaxed than those for the single infections. Our results show that direct fitness benefits also facilitate invasion of double infections by reducing or removing the threshold. Evidence for the role of direct benefits in the invasion of double infections is scarce. Coexistence of CI and MK caused by two infections has been observed in a few cases, for example, in Drosophila pandora infected with two different Wolbachia strains, one inducing CI and the other MK (Richardson et al. 2016), or in Drosophila melanogaster infected with CI-inducing Wolbachia and MK-inducing Spiroplasma (Montenegro et al. 2006). In D. Melanogaster, however, Wolbachia induce only weak CI, suggesting direct fitness benefits of infection. Whereas no benefits were found in terms of larval competitiveness or adult fecundity (Montenegro et al. 2006), the fitness advantage probably stems from increased host survival in the presence of viruses (Chrostek et al. 2013). This not only suggests that fitness benefits may facilitate invasion of double infections but also emphasizes the importance of a general conception of direct fitness effects.
Lastly, we may take a look at how direct fitness benefits affect evolutionary dynamics of reproductive phenotypes in the long run. In particular, evolutionary dynamics of CI have been the focus of extensive research. Early models showed that the mod function is selectively neutral, predicting that a mod − resc + strain would spread if it raised effective fecundity (Prout 1994; Turelli 1994). Although these studies did not consider host population structure, which has been argued to engender selection for stronger CI through a kin selection process (Hurst 1991a; Frank 1997), a more recent model found that even in subdivided host populations, selection for increased CI levels is only weak and transient (Haygood and Turelli 2009). These findings have two major implications. First, regardless of whether host populations are panmictic or structured, selection on CI-inducing symbionts acts to maximize effective fecundity, and not the CI level itself. This has also been shown to hold for haplodiploid hosts (Egas et al. 2002; Vavre et al. 2003) and multiple infections (Vautrin et al. 2007, 2008). The fact that there is selection acting on effective fecundity, but not on CI intensity also implies that CI and direct fitness benefits are not correlated. Both predictions have been confirmed for CI-inducing Wolbachia in Drosophila simulans: in Californian fly populations, Wolbachia have evolved so that effective fecundity, but not CI intensity, has risen (Weeks et al. 2007). Moreover, recent experiments revealed that across multiple Wolbachia strains, CI and antiviral protection occur independently (Martinez et al. 2015). These observations are inconsistent with the view that CI is a pleiotropic byproduct of other bacterial traits that benefit hosts, as has been assumed by Prout (1994) and Turelli (1994). The second major implication concerns the possible extinction of CI-inducing symbionts. Given the lack of selection for the mod function, symbionts may lose their ability to induce CI and become extinct (Hurst and McVean 1996). Moreover, CI symbionts could go extinct due to evolution of host resistance (Koehncke et al. 2009). However, loss of infection is not expected if symbionts additionally have a beneficial effect on host fitness. In the presence of direct fitness benefits, symbionts may still lose the ability to induce CI, but probably won’t go extinct. In this scenario, symbionts that used to express CI subsequently lost this ability (either because of lacking positive selection or because the host evolved suppression) and now are maintained solely by beneficial effects.
In the case of MK, evolutionary pressures are somewhat different from those acting on CI-inducing symbionts. For male-killers, the primary target of selection is the product of effective fecundity and MK-associated fitness compensation. This was first shown by Randerson et al. (2000) who called the quantity the “Basic Rate of Increase”. Hence, and in contrast to CI, male-killers are under selection to increase not only effective fecundity, but also the efficiency of the reproductive phenotype itself. Nevertheless, male-killers also face the risk of extinction, and that is because of selection on hosts to counteract the sex ratio distortion (Hurst 1992; Randerson et al. 2000). Host suppression of MK has been observed in several species (Hornett et al. 2006; Kageyama et al. 2009; Majerus and Majerus 2010). Interestingly, however, suppression of the MK phenotype does not always lead to extinction of the male-killer (Charlat et al. 2005; Hornett et al. 2006). In one case, symbionts immediately express CI when MK is suppressed, which is sufficient to maintain the infection in the population (Hornett et al. 2008). Another possible reason is that symbionts confer a direct fitness benefit to the host. In this case, the bacteria are predicted to persist as well, even if the MK phenotype is suppressed. Direct fitness benefits therefore could explain the persistence of male-killing symbionts in populations where suppression of MK has presumably evolved (as deduced from the occurrence of infected males; e.g., Weinert et al. 2007; Hayashi et al. 2016). Eventually, populations once plagued by MK would end up harboring only “beneficial symbionts that are a peaceful resolution of an evolutionary arms race between a male-killer and a suppressor system” (Majerus and Majerus 2010).
In summary, our results demonstrate that direct fitness benefits have a strong effect on the invasion and persistence of reproductive parasites. Positive fitness effects enable or facilitate invasion into novel hosts and allow symbionts to persist even in the absence of reproductive manipulations. Beneficial effects also play an important role in infection dynamics involving more than one manipulation phenotype (both at the population and the individual level), but more empirical research is clearly needed in this respect. Our findings also point to the potential of direct fitness benefits to resolve genetic conflicts between maternally inherited symbionts and their hosts. As more and more beneficial aspects of reproductive manipulators are being discovered, their significance for the evolution of these symbionts and their hosts is increasingly acknowledged. It will be exciting to further elucidate the interaction of reproductive manipulations and mutualistic effects in ensuring the evolutionary success of CI- and MK-inducing symbionts.
Electronic supplementary material
Acknowledgements
We thank Greg Hurst and Arndt Telschow for valuable comments that improved the manuscript.
Compliance with ethical standards
Conflict of interest
The authors declare that they have no conflict of interests.
Footnotes
Electronic supplementary material
The online version of this article (10.1038/s41437-017-0022-5) contains supplementary material, which is available to authorized users.
References
- Balas MT, Lee MH, Werren JH. Distribution and fitness effects of the son-killer bacterium in Nasonia. Evol Ecol. 1996;10:593–607. doi: 10.1007/BF01237709. [DOI] [Google Scholar]
- Beckmann JF, Ronau JA, Hochstrasser M. A Wolbachia deubiquitylating enzyme induces cytoplasmic incompatibility. Nat Microbiol. 2017;2:17007. doi: 10.1038/nmicrobiol.2017.7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bohacsova M, Mediannikov O, Kazimirova M, Raoult D, Sekeyova Z. Arsenophonus nasoniae and Rickettsiae infection of Ixodes ricinus due to parasitic wasp Ixodiphagus hookeri. PLoS ONE. 2016;11:e0149950. doi: 10.1371/journal.pone.0149950. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bouwma AM, Shoemaker D. Wolbachia wSinvictaA infections in natural populations of the fire ant Solenopsis invicta: testing for phenotypic effects. J Insect Sci. 2011;11:11. doi: 10.1673/031.011.0111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brownlie JC, Cass BN, Riegler M, Witsenburg JJ, Iturbe-Ormaetxe I, Mcgraw EA, et al. Evidence for metabolic provisioning by a common invertebrate endosymbiont, Wolbachia pipientis, during periods of nutritional stress. PLoS Pathog. 2009;5:e1000368. doi: 10.1371/journal.ppat.1000368. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cattel J, Kaur R, Gibert P, Martinez J, Fraimout A, Jiggins F, et al. Wolbachia in European populations of the invasive pest Drosophila suzukii: regional variation in infection frequencies. PLoS ONE. 2016;11:e0147766. doi: 10.1371/journal.pone.0147766. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cattel J, Martinez J, Jiggins F, Mouton L, Gibert P. Wolbachia-mediated protection against viruses in the invasive pest Drosophila suzukii. Insect Mol Biol. 2016;25:595–603. doi: 10.1111/imb.12245. [DOI] [PubMed] [Google Scholar]
- Charlat S, Ballard JW, Merçot H. What maintains noncytoplasmic incompatibility inducing Wolbachia in their hosts: a case study from a natural Drosophila yakuba population. J Evol Biol. 2004;17:322–330. doi: 10.1046/j.1420-9101.2003.00676.x. [DOI] [PubMed] [Google Scholar]
- Charlat S, Engelstädter J, Dyson EA, Hornett EA, Duplouy A, Tortosa P, et al. Competing selfish genetic elements in the butterfly Hypolimnas bolina. Curr Biol. 2006;16:2453–2458. doi: 10.1016/j.cub.2006.10.062. [DOI] [PubMed] [Google Scholar]
- Charlat S, Hornett EA, Dyson EA, Ho PPY, Loc NT, Schilthuizen M, et al. Prevalence and penetrance variation of male-killing Wolbachia across Indo-Pacific populations of the butterfly Hypolimnas bolina. Mol Ecol. 2005;14:3525–3530. doi: 10.1111/j.1365-294X.2005.02678.x. [DOI] [PubMed] [Google Scholar]
- Charlat S, Le Chat L, Merçot H. Characterization of non-cytoplasmic incompatibility inducing Wolbachia in two continental African populations of Drosophila simulans. Heredity. 2003;90:49–55. doi: 10.1038/sj.hdy.6800177. [DOI] [PubMed] [Google Scholar]
- Chrostek E, Marialva MSP, Esteves SS, Weinert LA, Martinez J, Jiggins FM, Teixeira L. Wolbachia variants induce differential protection to viruses in Drosophila melanogaster: a phenotypic and phylogenomic analysis. PLoS Genet. 2013;9:e1003896. doi: 10.1371/journal.pgen.1003896. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clancy DJ, Hoffmann AA. Behavior of Wolbachia endosymbionts from Drosophila simulans in Drosophila serrata, a novel host. Am Nat. 1997;149:975–988. doi: 10.1086/286033. [DOI] [PubMed] [Google Scholar]
- Cooper BS, Ginsberg PS, Turelli M, Matute DR. Wolbachia in the Drosophila yakuba complex: pervasive frequency variation and weak cytoplasmic incompatibility, but no apparent effect on reproductive isolation. Genetics. 2017;205:333–351. doi: 10.1534/genetics.116.196238. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dobson SL, Marsland EJ, Rattanadechakul W. Mutualistic Wolbachia infection in Aedes albopictus: accelerating cytoplasmic drive. Genetics. 2002;160:1087–1094. doi: 10.1093/genetics/160.3.1087. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dyer KA, Jaenike J. Evolutionarily stable infection by a male-killing endosymbiont in Drosophila innubila: molecular evidence from the host and parasite genomes. Genetics. 2004;168:1443–1455. doi: 10.1534/genetics.104.027854. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Egas M, Vala F, Breeuwer JAJ. On the evolution of cytoplasmic incompatibility in haplodiploid species. Evolution. 2002;56:1101–1109. doi: 10.1111/j.0014-3820.2002.tb01424.x. [DOI] [PubMed] [Google Scholar]
- Elnagdy S, Majerus MEN, Gardener M, Lawson Handley LJ. The direct effects of male killer infection on fitness of ladybird hosts (Coleoptera: Coccinellidae) J Evol Biol. 2013;26:1816–1825. doi: 10.1111/jeb.12186. [DOI] [PubMed] [Google Scholar]
- Elnagdy S, Majerus MEN, Lawson Handley LJ. The value of an egg: resource reallocation in ladybirds (Coleoptera: Coccinellidae) infected with male-killing bacteria. J Evol Biol. 2011;24:2164–2172. doi: 10.1111/j.1420-9101.2011.02346.x. [DOI] [PubMed] [Google Scholar]
- Engelstädter J, Hurst GD. The ecology and evolution of microbes that manipulate host reproduction. Annu Rev Ecol Evol Syst. 2009;40:127–149. doi: 10.1146/annurev.ecolsys.110308.120206. [DOI] [Google Scholar]
- Engelstädter J, Hurst GDD. Can maternally transmitted endosymbionts facilitate the evolution of haplodiploidy? J Evol Biol. 2006;19:194–202. doi: 10.1111/j.1420-9101.2005.00974.x. [DOI] [PubMed] [Google Scholar]
- Engelstädter J, Telschow A, Hammerstein P. Infection dynamics of different Wolbachia-types within one host population. J Theor Biol. 2004;231:345–355. doi: 10.1016/j.jtbi.2004.06.029. [DOI] [PubMed] [Google Scholar]
- Engelstädter J, Telschow A, Yamamura N. Coexistence of cytoplasmic incompatibility and male-killing-inducing endosymbionts, and their impact on host gene flow. Theor Popul Biol. 2008;73:125–133. doi: 10.1016/j.tpb.2007.08.004. [DOI] [PubMed] [Google Scholar]
- Fenton A, Johnson KN, Brownlie JC, Hurst GDD. Solving the Wolbachia paradox: modeling the tripartite interaction between host, Wolbachia, and a natural enemy. Am Nat. 2011;178:333–342. doi: 10.1086/661247. [DOI] [PubMed] [Google Scholar]
- Frank SA. Cytoplasmic incompatibility and population structure. J Theor Biol. 1997;184:327–330. doi: 10.1006/jtbi.1996.0276. [DOI] [PubMed] [Google Scholar]
- Freeland SJ, McCabe BK. Fitness compensation and the evolution of selfish cytoplasmic elements. Heredity. 1997;78:391–402. doi: 10.1038/hdy.1997.62. [DOI] [Google Scholar]
- Gavotte L, Mercer DR, Stoeckle JJ, Dobson SL. Costs and benefits of Wolbachia infection in immature Aedes albopictus depend upon sex and competition level. J Invertebr Pathol. 2010;105:341–346. doi: 10.1016/j.jip.2010.08.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Giordano R, O’Neill SL, Robertson HM. Wolbachia infections and the expression of cytoplasmic incompatibility in Drosophila sechellia and D. mauritiana. Genetics. 1995;140:1307–1317. doi: 10.1093/genetics/140.4.1307. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hamm CA, Begun DJ, Vo A, Smith CCR, Saelao P, Shaver AO, et al. Wolbachia do not live by reproductive manipulation alone: infection polymorphism in Drosophila suzukii and D. subpulchrella. Mol Ecol. 2014;23:4871–4885. doi: 10.1111/mec.12901. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harris LR, Kelly SE, Hunter MS, Perlman SJ. Population dynamics and rapid spread of Cardinium, a bacterial endosymbiont causing cytoplasmic incompatibility in Encarsia pergandiella (Hymenoptera: Aphelinidae) Heredity. 2010;104:239–246. doi: 10.1038/hdy.2009.130. [DOI] [PubMed] [Google Scholar]
- Hayashi M, Watanabe M, Yukuhiro F, Nomura M, Kageyama D. A nightmare for males? A maternally transmitted male-killing bacterium and strong female bias in a green lacewing population. PLoS ONE. 2016;11:e0155794. doi: 10.1371/journal.pone.0155794. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haygood R, Turelli M. Evolution of incompatibility-inducing microbes in subdivided host populations. Evolution. 2009;63:432–447. doi: 10.1111/j.1558-5646.2008.00550.x. [DOI] [PubMed] [Google Scholar]
- Himler AG, Adachi-Hagimori T, Bergen JE, Kozuch A, Kelly SE, Tabashnik BE, et al. Rapid spread of a bacterial symbiont in an invasive whitefly is driven by fitness benefits and female bias. Science. 2011;332:254–256. doi: 10.1126/science.1199410. [DOI] [PubMed] [Google Scholar]
- Hoffmann AA, Clancy D, Duncan J. Naturally-occurring Wolbachia infection in Drosophila simulans that does not cause cytoplasmic incompatibility. Heredity. 1996;76:1–8. doi: 10.1038/hdy.1996.1. [DOI] [PubMed] [Google Scholar]
- Hoffmann AA, Hercus M, Dagher H. Population dynamics of the Wolbachia infection causing cytoplasmic incompatibility in Drosophila melanogaster. Genetics. 1998;148:221–231. doi: 10.1093/genetics/148.1.221. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoffmann AA, Turelli M. Cytoplasmic incompatibility in insects. In: O’Neill SL, Hoffmann AA, Werren JH, editors. Influential passengers. Inherited microorganisms and arthropod reproduction. Oxford: Oxford University Press; 1997. pp. 42–80. [Google Scholar]
- Hoffmann AA, Turelli M, Harshman LG. Factors affecting the distribution of cytoplasmic incompatibility in Drosophila simulans. Genetics. 1990;126:933–948. doi: 10.1093/genetics/126.4.933. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hornett EA, Charlat S, Duplouy AM, Davies N, Roderick GK, Wedell N, et al. Evolution of male-killer suppression in a natural population. PLoS Biol. 2006;4:e283. doi: 10.1371/journal.pbio.0040283. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hornett EA, Duplouy AM, Davies N, Roderick GK, Wedell N, Hurst GD, et al. You can’t keep a good parasite down: evolution of a male-killer suppressor uncovers cytoplasmic incompatibility. Evolution. 2008;62:1258–1263. doi: 10.1111/j.1558-5646.2008.00353.x. [DOI] [PubMed] [Google Scholar]
- Hurst GD, Frost CL. Reproductive parasitism: maternally inherited symbionts in a biparental world. Cold Spring Harb Perspect Biol. 2015;7:a017699. doi: 10.1101/cshperspect.a017699. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hurst GD, Jiggins FM, Pomiankowski A. Which way to manipulate host reproduction? Wolbachia that cause cytoplasmic incompatibility are easily invaded by sex ratio-distorting mutants. Am Nat. 2002;160:360–373. doi: 10.1086/341524. [DOI] [PubMed] [Google Scholar]
- Hurst GDD, Johnson AP, Von Der Schulenburg JHG, Fuyama Y. Male-killing Wolbachia in Drosophila: a temperature-sensitive trait with a threshold bacterial density. Genetics. 2000;156:699–709. doi: 10.1093/genetics/156.2.699. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hurst LD. The evolution of cytoplasmic incompatibility or when spite can be successful. J Theor Biol. 1991;148:269–277. doi: 10.1016/S0022-5193(05)80344-3. [DOI] [PubMed] [Google Scholar]
- Hurst LD. The incidences and evolution of cytoplasmic male killers. Proc R Soc Lond B. 1991;244:91–99. doi: 10.1098/rspb.1991.0056. [DOI] [Google Scholar]
- Hurst LD. Intragenomic conflict as an evolutionary force. Proc R Soc Lond B. 1992;248:135–140. doi: 10.1098/rspb.1992.0053. [DOI] [Google Scholar]
- Hurst LD, McVean GT. Clade selection, reversible evolution and the persistence of selfish elements: the evolutionary dynamics of cytoplasmic incompatibility. Proc R Soc Lond B. 1996;263:97–104. doi: 10.1098/rspb.1996.0016. [DOI] [Google Scholar]
- Jaenike J. Population genetics of beneficial heritable symbionts. Trends Ecol Evol. 2012;27:226–232. doi: 10.1016/j.tree.2011.10.005. [DOI] [PubMed] [Google Scholar]
- Jaenike J, Unckless R, Cockburn SN, Boelio LM, Perlman SJ. Adaptation via symbiosis: recent spread of a Drosophila defensive symbiont. Science. 2010;329:212–215. doi: 10.1126/science.1188235. [DOI] [PubMed] [Google Scholar]
- Jansen VAA, Turelli M, Godfray HCJ. Stochastic spread of Wolbachia. Proc R Soc B. 2008;275:2769–2776. doi: 10.1098/rspb.2008.0914. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jiggins FM, Hurst GDD. Rapid insect evolution by symbiont transfer. Science. 2011;332:185–186. doi: 10.1126/science.1205386. [DOI] [PubMed] [Google Scholar]
- Kageyama D, Anbutsu H, Shimada M, Fukatsu T. Effects of host genotype against the expression of Spiroplasma-induced male killing in Drosophila melanogaster. Heredity. 2009;102:475–482. doi: 10.1038/hdy.2009.14. [DOI] [PubMed] [Google Scholar]
- Kageyama D, Anbutsu H, Watada M, Hosokawa T, Shimada M, Fukatsu T. Prevalence of a non-male-killing Spiroplasma in natural populations of Drosophila hydei. Appl Environ Microbiol. 2006;72:6667–6673. doi: 10.1128/AEM.00803-06. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kaiser W, Huguet E, Casas J, Commin C, Giron D. Plant green-island phenotype induced by leaf-miners is mediated by bacterial symbionts. Proc R Soc B. 2010;277:2311–2319. doi: 10.1098/rspb.2010.0214. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koehncke A, Telschow A, Werren JH, Hammerstein P. Life and death of an influential passenger: Wolbachia and the evolution of CI-modifiers by their hosts. PLoS ONE. 2009;4:e4425. doi: 10.1371/journal.pone.0004425. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kriesner P, Conner WR, Weeks AR, Turelli M, Hoffmann AA. Persistence of a Wolbachia infection frequency cline in Drosophila melanogaster and the possible role of reproductive dormancy. Evolution. 2016;70:979–997. doi: 10.1111/evo.12923. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kriesner P, Hoffmann AA, Lee SF, Turelli M, Weeks AR. Rapid sequential spread of two Wolbachia variants in Drosophila simulans. PLoS Pathog. 2013;9:e1003607. doi: 10.1371/journal.ppat.1003607. [DOI] [PMC free article] [PubMed] [Google Scholar]
- LePage DP, Metcalf JA, Bordenstein SR, On J, Perlmutter JI, Shropshire JD, et al. Prophage WO genes recapitulate and enhance Wolbachia-induced cytoplasmic incompatibility. Nature. 2017;543:243–247. doi: 10.1038/nature21391. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Majerus TMO, Majerus MEN. Intergenomic arms races: detection of a nuclear rescue gene of male-killing in a ladybird. PLoS Pathog. 2010;6:e1000987. doi: 10.1371/journal.ppat.1000987. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martinez J, Ok S, Smith S, Snoeck K, Day JP, Jiggins FM. Should symbionts be nice or selfish? Antiviral effects of Wolbachia are costly but reproductive parasitism is not. PLoS Pathog. 2015;11:e1005021. doi: 10.1371/journal.ppat.1005021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martins AB, Ventura IM, Klaczko LB. Spiroplasma infection in Drosophila melanogaster: What is the advantage of killing males? J Invertebr Pathol. 2010;105:145–150. doi: 10.1016/j.jip.2010.06.002. [DOI] [PubMed] [Google Scholar]
- Montenegro H, Petherwick AS, Hurst GDD, Klaczko LB. Fitness effects of Wolbachia and Spiroplasma in Drosophila melanogaster. Genetica. 2006;127:207–215. doi: 10.1007/s10709-005-3766-4. [DOI] [PubMed] [Google Scholar]
- Nakayama S, Parratt SR, Hutchence KJ, Lewis Z, Price TAR, Hurst GDD. Can maternally inherited endosymbionts adapt to a novel host? Direct costs of Spiroplasma infection, but not vertical transmission efficiency, evolve rapidly after horizontal transfer into D. melanogaster. Heredity. 2015;114:539–543. doi: 10.1038/hdy.2014.112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Normark BB. Haplodiploidy as an outcome of coevolution between male-killing cytoplasmic elements and their hosts. Evolution. 2004;58:790–798. doi: 10.1111/j.0014-3820.2004.tb00412.x. [DOI] [PubMed] [Google Scholar]
- Okayama K, Katsuki M, Sumida Y, Okada K. Costs and benefits of symbiosis between a bean beetle and Wolbachia. Anim Behav. 2016;119:19–26. doi: 10.1016/j.anbehav.2016.07.004. [DOI] [Google Scholar]
- Parratt SR, Frost CL, Schenkel MA, Rice A, Hurst GDD, King KC. Superparasitism drives heritable symbiont epidemiology and host sex ratio in a wasp. PLoS Pathog. 2016;12:e1005629. doi: 10.1371/journal.ppat.1005629. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Perrot-Minnot MJ, Cheval B, Migeon A, Navajas M. Contrasting effects of Wolbachia on cytoplasmic incompatibility and fecundity in the haplodiploid mite Tetranychus urticae. J Evol Biol. 2002;15:808–817. doi: 10.1046/j.1420-9101.2002.00446.x. [DOI] [Google Scholar]
- Poinsot D, Charlat S, Merçot H. On the mechanism of Wolbachia-induced cytoplasmic incompatibility: confronting the models with the facts. Bioessays. 2003;25:259–265. doi: 10.1002/bies.10234. [DOI] [PubMed] [Google Scholar]
- Prout T. Some evolutionary possibilities for a microbe that causes incompatibility in its host. Evolution. 1994;48:909–911. doi: 10.1111/j.1558-5646.1994.tb01371.x. [DOI] [PubMed] [Google Scholar]
- Randerson JP, Smith NG, Hurst LD. The evolutionary dynamics of male-killers and their hosts. Heredity. 2000;84:152–160. doi: 10.1046/j.1365-2540.2000.00645.x. [DOI] [PubMed] [Google Scholar]
- Richardson KM, Schiffer M, Griffin PC, Lee SF, Hoffmann AA. Tropical Drosophila pandora carry Wolbachia infections causing cytoplasmic incompatibility or male killing. Evolution. 2016;70:1791–1802. doi: 10.1111/evo.12981. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Riegler M, Charlat S, Stauffer C, Merçot H. Wolbachia transfer from Rhagoletis cerasi to Drosophila simulans: investigating the outcomes of host-symbiont co-evolution. Appl Environ Microbiol. 2004;70:273–279. doi: 10.1128/AEM.70.1.273-279.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Russell JA, Moran NA. Horizontal transfer of bacterial symbionts: heritability and fitness effects in a novel aphid host. Appl Environ Microbiol. 2005;71:7987–7994. doi: 10.1128/AEM.71.12.7987-7994.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Souto-Maior C, Lopes JS, Gjini E, Struchiner CJ, Teixeira L, Gomes MGM. Heterogeneity in symbiotic effects facilitates Wolbachia establishment in insect populations. Theor Ecol. 2015;8:53–65. doi: 10.1007/s12080-014-0235-7. [DOI] [Google Scholar]
- Tinsley MC, Majerus ME. Small steps or giant leaps for male-killers? Phylogenetic constraints to male-killer host shifts. BMC Evol Biol. 2007;7:238. doi: 10.1186/1471-2148-7-238. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Turelli M. Evolution of incompatibility-inducing microbes and their hosts. Evolution. 1994;48:1500–1513. doi: 10.1111/j.1558-5646.1994.tb02192.x. [DOI] [PubMed] [Google Scholar]
- Turelli M, Barton NH. Deploying dengue-suppressing Wolbachia: robust models predict slow but effective spatial spread in Aedes aegypti. Theor Popul Biol. 2017;115:45–60. doi: 10.1016/j.tpb.2017.03.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Úbeda F, Normark BB. Male killers and the origins of paternal genome elimination. Theor Popul Biol. 2006;70:511–526. doi: 10.1016/j.tpb.2006.06.011. [DOI] [PubMed] [Google Scholar]
- Unckless RL, Jaenike J. Maintenance of a male-killing Wolbachia in Drosophila innubila by male-killing dependent and male-killing independent mechanisms. Evolution. 2012;66:678–689. doi: 10.1111/j.1558-5646.2011.01485.x. [DOI] [PubMed] [Google Scholar]
- Vautrin E, Charles S, Genieys S, Vavre F. Evolution and invasion dynamics of multiple infections with Wolbachia investigated using matrix based models. J Theor Biol. 2007;245:197–209. doi: 10.1016/j.jtbi.2006.09.035. [DOI] [PubMed] [Google Scholar]
- Vautrin E, Genieys S, Charles S, Vavre F. Do vertically transmitted symbionts co-existing in a single host compete or cooperate? A modelling approach. J Evol Biol. 2008;21:145–161. doi: 10.1111/j.1420-9101.2007.01460.x. [DOI] [PubMed] [Google Scholar]
- Vavre F, Fouillet P, Fleury F. Between- and within-host species selection on cytoplasmic incompatibility-inducing Wolbachia in haplodiploids. Evolution. 2003;57:421–427. doi: 10.1111/j.0014-3820.2003.tb00275.x. [DOI] [PubMed] [Google Scholar]
- Vavre F, Girin C, Boulétreau M. Phylogenetic status of a fecundity-enhancing Wolbachia that does not induce thelytoky in Trichogramma. Insect Mol Biol. 1999;8:67–72. doi: 10.1046/j.1365-2583.1999.810067.x. [DOI] [PubMed] [Google Scholar]
- Veneti Z, Zabalou S, Papafotiou G, Paraskevopoulos C, Pattas S, Livadaras I, et al. Loss of reproductive parasitism following transfer of male-killing Wolbachia to Drosophila melanogaster and Drosophila simulans. Heredity. 2012;109:306–312. doi: 10.1038/hdy.2012.43. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ventura IM, Martins AB, Lyra ML, Andrade CAC, Carvalho KA, Klaczko LB. Spiroplasma in Drosophila melanogaster populations: prevalence, male-killing, molecular identification, and no association with Wolbachia. Microb Ecol. 2012;64:794–801. doi: 10.1007/s00248-012-0054-6. [DOI] [PubMed] [Google Scholar]
- Watts T, Haselkorn TS, Moran NA, Markow TA. Variable incidence of Spiroplasma infections in natural populations of Drosophila species. PLoS ONE. 2009;4:e5703. doi: 10.1371/journal.pone.0005703. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weeks AR, Turelli M, Harcombe WR, Reynolds KT, Hoffmann AA. From parasite to mutualist: rapid evolution of Wolbachia in natural populations of Drosophila. PLoS Biol. 2007;5:e114. doi: 10.1371/journal.pbio.0050114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weinert LA, Araujo-Jnr EV, Ahmed MZ, Welch JJ. The incidence of bacterial endosymbionts in terrestrial arthropods. Proc R Soc. 2015;B282:20150249. doi: 10.1098/rspb.2015.0249. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weinert LA, Tinsley MC, Temperley M, Jiggins FM. Are we underestimating the diversity and incidence of insect bacterial symbionts? A case study in ladybird beetles. Biol Lett. 2007;3:678–681. doi: 10.1098/rsbl.2007.0373. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Werren JH. Biology of Wolbachia. Annu Rev Entomol. 1997;42:587–609. doi: 10.1146/annurev.ento.42.1.587. [DOI] [PubMed] [Google Scholar]
- Xie J, Butler S, Sanchez G, Mateos M. Male killing Spiroplasma protects Drosophila melanogaster against two parasitoid wasps. Heredity. 2014;112:399–408. doi: 10.1038/hdy.2013.118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xie J, Winter C, Winter L, Mateos M. Rapid spread of the defensive endosymbiont Spiroplasma in Drosophila hydei under high parasitoid wasp pressure. FEMS Microbiol Ecol. 2015;91:1–11. doi: 10.1093/femsec/fiu017. [DOI] [PubMed] [Google Scholar]
- Xie RR, Sun JT, Xue XF, Hong XY. Cytoplasmic incompatibility and fitness benefits in the two-spotted spider mite Tetranychus urticae (red form) doubly infected with Wolbachia and Cardinium. Syst Appl Acarol. 2016;21:1161–1173. doi: 10.11158/saa.21.9.1. [DOI] [Google Scholar]
- Xue X, Li SJ, Ahmed MZ, De Barro PJ, Ren SX, Qiu BL. Inactivation of Wolbachia reveals its biological roles in whitefly host. PLoS ONE. 2012;7:e48148. doi: 10.1371/journal.pone.0048148. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zélé F, Nicot A, Duron O, Rivero A. Infection with Wolbachia protects mosquitoes against Plasmodium-induced mortality in a natural system. J Evol Biol. 2012;25:1243–1252. doi: 10.1111/j.1420-9101.2012.02519.x. [DOI] [PubMed] [Google Scholar]
- Zhang H, Zhang KJ, Hong XY. Population dynamics of noncytoplasmic incompatibility-inducing Wolbachia in Nilaparvata lugens and its effects on host adult life span and female fitness. Environ Entomol. 2010;39:1801–1809. doi: 10.1603/EN10051. [DOI] [PubMed] [Google Scholar]
- Zhang XF, Zhao DX, Hong XY. Cardinium—the leading factor of cytoplasmic incompatibility in the planthopper Sogatella furcifera doubly infected with Wolbachia and Cardinium. Environ Entomol. 2012;41:833–840. doi: 10.1603/EN12078. [DOI] [Google Scholar]
- Zug R, Hammerstein P. Still a host of hosts for Wolbachia: analysis of recent data suggests that 40% of terrestrial arthropod species are infected. PLoS ONE. 2012;7:e38544. doi: 10.1371/journal.pone.0038544. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zug R, Hammerstein P. Bad guys turned nice? A critical assessment of Wolbachia mutualisms in arthropod hosts. Biol Rev. 2015;90:89–111. doi: 10.1111/brv.12098. [DOI] [PubMed] [Google Scholar]
- Zabalou S. Natural Wolbachia Infections in the Drosophila yakuba Species Complex Do Not Induce Cytoplasmic Incompatibility but Fully Rescue the wRi Modification. Genetics. 2004;167:827–834. doi: 10.1534/genetics.103.015990. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


