Abstract
Cellular cytoskeletal mechanics plays a major role in many aspects of human health from organ development to wound healing, tissue homeostasis and cancer metastasis. We summarize the state‐of‐the‐art techniques for mathematically modeling cellular stiffness and mechanics and the cytoskeletal components and factors that regulate them. We highlight key experiments that have assisted model parameterization and compare the advantages of different models that have been used to recapitulate these experiments. An overview of feed‐forward mechanisms from signaling to cytoskeleton remodeling is provided, followed by a discussion of the rapidly growing niche of encapsulating feedback mechanisms from cytoskeletal and cell mechanics to signaling. We discuss broad areas of advancement that could accelerate research and understanding of cellular mechanobiology. A precise understanding of the molecular mechanisms that affect cell and tissue mechanics and function will underpin innovations in medical device technologies of the future. WIREs Syst Biol Med 2018, 10:e1407. doi: 10.1002/wsbm.1407
This article is categorized under:
-
1
Models of Systems Properties and Processes > Mechanistic Models
-
2
Physiology > Mammalian Physiology in Health and Disease
-
3
Models of Systems Properties and Processes > Cellular Models
INTRODUCTION
It is well established that cellular mechanics plays a significant role in cellular and tissue biology, from tissue and organ development to wound healing and cancer cell metastasis and migration. Significant research has been conducted to develop an integrated understanding of cellular mechanics and biology. However, as with any complex system, these advances have only scratched the surface of a complete understanding of cellular mechanobiology.
In this on‐going pursuit of a comprehensive picture of the cell, mathematical models play a dual role: (1) as in silico hypothesis test models—not too dissimilar from experimental animal models—to discover new mechanisms from the experimental data that would otherwise have limited power in providing insights on the integrative biology of cell behavior; (2) as re‐usable and extensible repositories to integrate research findings from multiple and disparate reductionist experiments.
There are many excellent reviews that have covered all aspects of modeling cell and cytoskeletal mechanics. Lim et al.1 provide an elegant summary of continuum‐based models of the mechanical stiffness of cells. Reviews such as that of Sun et al.2 and others3, 4 discuss models in the context of cell migration. There are also reviews of specific aspects of cell mechanics such as the cytoskeleton,5, 6, 7 or actin protrusion,8 or cell signaling in cell shape and cell motility9 for example.
In light of these reviews and the advancements in our understanding of cell mechanics, the main aims of this review are as follows: (1) to provide an updated review of continuum and particle‐based models of cell and cytoskeletal mechanics, from bulk stiffness to cytoskeletal protein contributions and from actin protrusion to cell adhesion (thus advancing on Lim et al.1 and taking a broader perspective on cell mechanics, not just stiffness or just motility); and (2) to discuss our current understanding of cell signaling in relation to cell migration and cytoskeletal mechanics. In particular, this review will focus on how the field is moving towards understanding the feedback from mechanics to signaling. Finally, (3) we highlight key experimental results that have been or can be used to constrain and/or parameterize models of single cell and cytoskeletal mechanics. Throughout the sections we discuss drawbacks, advantages and challenges in the different modeling approaches that one can adopt to simulate different experimental observations of cell mechanics.
The structure of this review is as follows. We first provide a brief overview of the mathematical frameworks that are employed when simulating cell mechanics and associated signaling. We then discuss measurements and associated models of bulk single cell properties, followed by the contribution of the cytoskeletal network and its constituent cytoskeletal proteins. The contribution of the external surrounding environment in determining the emergent mechanical behavior of single cells is then discussed. We further review our current understanding of how biochemical signaling processes modulate cell and cytoskeletal mechanical behavior. We conclude with a discussion of what we believe are key areas of advancement that the community could target to further our understanding of cellular mechanobiology.
MATHEMATICAL TECHNIQUES FOR MODELING MECHANICS AND SIGNALING IN CELLULAR MECHANOBIOLOGY
An animal cell is a composite of soft biopolymers that is enclosed by a hydrophobic phospholipid bi‐layer. In Simulation Equations for Modelling Cellular Mechanics section we will discuss current computational approaches that are in use to capture the mechanical deformation of the cell. These approaches can be categorized into one of two broad approaches: (1) methods based on continuum approximations that discretize the cell into sub‐regions on which Newton's equations are applied; or (2) methods that discretize the cell into collections of particles that mechanically interact with each other on a point‐to‐point basis following Newton's laws. The stiffness and mechanical behavior of a cell is regulated by the quantity, spatial organization and interactions of different cytoskeletal proteins that make up the cell. These parameters are tight regulated by a myriad of interconnected biochemical processes. These processes are often described and depicted as signal pathway maps. In Simulation Equations for Modelling the Regulation of Cytoskeletal Mechanics by Signalling Pathways section we outline the most common mathematical techniques that are used to simulate these processes in the context of cell mechanics and mechanobiology.
Simulation Equations for Modeling Cellular Mechanics
Figure 1 highlights three models published in literature that use three different techniques to describe cell mechanics at three different spatial scales. These methods will be discussed in the following sections.
Figure 1.
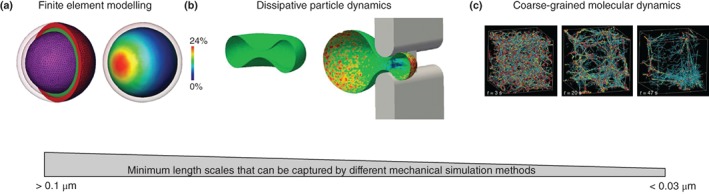
Mechanical modelling techniques across spatial scales. Each panel shows the unloaded, initial geometry, and simulated deformation of the cell or cytoskeleton. (a) a continuum mechanics model of an actin cytoskeleton cortex (red), intermediate vimentin filaments (green) and the nucleus (Reprinted with permission from Ref 10. Copyright 2011 Elsevier Ltd); (b) a dissipative particle dynamics simulation of a red blood cell passing through a narrow slit (Reprinted with permission from Ref 11. Copyright 2016 National Academy of Sciences); (c) a coarse‐grained brownian dynamics simulation of a small portion of the cell actin cytoskeleton to study the role of individual cytoskeletal proteins to the emergent mechanical behaviour of the cytoskeleton. The image shows snapshots of the cytoskeleton at different time points (Reprinted with permission from Ref 12. Copyright 2016 Nature Publishing Group).
Nonlinear Continuum Mechanics Simulation Equations
Continuum models seek to describe the bulk behavior of cellular materials without requiring a description of the molecular details of those materials. Nonlinear continuum mechanics theory is a natural fit for simulating bulk mechanics of cells undergoing large deformations. The theory is based on the principles of conservation of mass, conservation of linear momentum and conservation of angular momentum, described by canonical Eqs. (1), (2) and (3):
| (1) |
| (2) |
| (3) |
where ρ o and ρ represent the mass density in the undeformed and deformed geometries respectively; V o and V represent the volume of the material in the undeformed and deformed geometries; v k represents the velocity component of a moving body, τ k is the traction stress vector component, b k is the body force component, and t represents time. In Eq. (3) ɛijk represents the permutation symbol in tensor notation and xj represents the distance of each particle in the continuum from a point of reference about which the angular momentum is calculated. The consequence of Eq. (3) is that it imposes a symmetry condition on the stress tensor. Equation (1) is also converted into a constraint in simulations that assume volume is conserved. This leaves Eq. (2) as the primary nonlinear equation that must be solved computationally. The finite element method13 is the most popular method to numerically solve these equations.
Equations (1) and (2) represent the cell as a nonlinear elastic/viscoelastic solid. The quasi‐static approximation is routinely used to simulate deformations at iteratively increasing loads, thus removing the velocity and acceleration variables in the equations. In simulations of cell mechanics in contexts such as cell migration,14 the mass of the cell is small enough to neglect inertial forces (note, however, that a recent study showed that gravity affects some larger cells that are >10 μm in diameter15). However, a viscous component is typically introduced to simulate intracellular drag forces induced by a viscous cytoskeleton. Another valid extension of the representation of the cell is as a poroelastic system16, 17, 18, 19 consisting of polymer networks whose pores are filled by a viscous fluid. This representation of the cell is backed up by structural images of the cytoskeleton,20 confocal images of fluid flow in migrating cells21 and more recent experimental measurements of poroelastic behavior.22 Recently, more generalized versions of Eqs. (1) and (2), termed virtual power equations, have been employed.23 Virtual power equations reformulate the force equilibrium equations above in terms of velocities and power and enable the study of the mechanics of materials with evolving microstructure—such as a cell undergoing cytoskeletal remodeling.
Rather than track the individual polymers that make up the cytoskeleton, the continuum representation models regional variations in cytoskeletal distributions, which can be used to represent, for example, stiffness10 (see Figure 1(a)). Multi‐scale approaches can also be implemented whereby a constitutive equation is derived from the mechanics of a network microstructure24 but these methods have not been validated or adopted extensively (more details in Measurements and Models of the Bulk Mechanical Properties of Cells).
A major advantage of the continuum mechanics approach is that many of its parameters are physically measureable (such as stiffness and viscosity). Additionally, model predictions of deformation of the entire cell can be readily compared against microscopy images of cell shape. This approach incurs relatively little computational cost when compared to particle‐based methods. A disadvantage of this approach is that finite element implementations give rise to complications when simulating significant changes to cell shape; large deformations can distort element shapes and introduce numerical instabilities.
Particle‐Based Mechanics Simulation Equations
In these methods, a cell is represented by a collection of points, where each particle is subject to elastic, viscous/dissipative and stochastic forces (Figure 1(b) and (c)). These forces cause the particles to move in accordance with Newton's laws of motion:
| (4) |
where m i represents the mass of each particle, r i is the position vectors of each particle, is the elastic, conservative force that arises between particles, represents the dissipative forces acting on each particle and represents the stochastic, random forces that exert influence on each particle. There are several variations to Eq. (4) that depend on the assumptions made when representing the cell. Dissipative particle dynamics (DPD)25 treats the cell as a complex fluid where each particle can be considered as a particle of that fluid or a collection of physical particles of the fluid, depending on the spatial scale of interest. Smoothed particle hydrodynamics (SPH) represents length‐scales similar to continuum models,26 but with the advantage of being free of mesh topology constraints. Unlike DPD, SPH is derived from the Navier–Stokes equations and therefore the parameters have direct physical meaning.
In the broad sense of the term, coarse‐grained molecular dynamics (also termed Brownian dynamics) simulations27, 28, 29 are also particle‐based methods that have been successfully utilized to study the mechanical interactions between the proteins that compose the cytoskeleton.30, 31, 32 A key difference between DPD and coarse‐grained Brownian dynamics (BD) models is that the equations for DPD are more rigorously developed for the treatment of hydrodynamic properties than Brownian dynamics models.33 Readers can delve deeper into the theory and utility of different particle‐based methods by reading an excellent review by Ye et al.,26 albeit in the context of simulations of red blood cells.
An important advantage of the particle‐based methods is that points within a topology can move with more freedom—subject to mechanical equilibrium constraints—than those in mesh‐based methods. Mesh‐free methods like SPH are under active development34 and it is foreseeable that these methods will be adopted routinely in the future, much like mesh‐based methods such as finite elements. Coarse‐grained molecular dynamics simulations also provide a sense of the microstructural organization that continuum models cannot be provided. This can also provide additional insights into nanoscale mechanical forces that act between cell and cytoskeletal components, which cannot be captured in a continuum approximation.
On the other hand, DPD and SPH require all particles to be treated as fluid particles, which may not be the most appropriate description of the cellular environment in some circumstances. The choice of DPD equation parameters, such as the dissipative and stochastic forces, and the number of computational nodes (which are difficult to experimentally constrain) for each type of fluid in the simulation significantly affect the behavior of the simulation (in addition to the computational cost).26 This makes extrapolation of model predictions beyond the simulation's original purpose more challenging than those from classical methods such as finite element method (FEM); FEM simulation predictions of cell mechanics are only dependent on parameters such as cell stiffness once a sufficiently high density mesh has been defined. SPH is based on the Navier–Stokes equations and its parameters are not as arbitrary as those in the DPD equations. However, as the method also implicitly solves the Navier Stokes’ equations, representing viscoelastic and solid properties can be challenging.
The computational cost of tracking the motion and mechanics of thousands of particles (representing molecules or groups of molecules) also preclude coarse‐grained molecular dynamics simulations from simulating time scales longer than a few seconds or spatial scales larger than a few micrometers (one could consider each particle as representing a larger spatial scale as a trade‐off for computational cost). Mesh‐free methods such as DPD and SPH enable simulations at similar spatial scales to mesh‐based methods for solving continuum‐scale models, such as the FEM. The need to dynamically track the relationship between different computational nodes within a neighborhood however make these methods computationally more intensive than mesh‐based, continuum methods.
Simulation Equations for Modeling the Regulation of Cytoskeletal Mechanics by Signaling Pathways
Cells undergo cytoskeletal remodeling on the order of seconds, which affect measurements of mechanical stiffness.32, 35, 36, 37, 38, 39, 40 Hence, cellular mechanics must be measured and studied alongside biochemical signaling processes that regulate cytoskeletal organization. The general framework used to describe spatio‐temporal biochemical signaling processes are the reaction–diffusion (RD) equations:
| (5) |
where c is the concentration of a signaling module, D is the diffusivity of the environment in which the signaling molecules interact and R(c,t) represents the list of chemical reactions that represent a signal pathway. Analogous to particle‐based mechanical dynamics methods, particle‐type and Markov‐chain‐type methods41, 42 are available for simulating signaling as well. These methods are predominantly used to simulate conditions where there are few signaling molecules in a small domain and the stochastic nature of particle interactions become important. Such methods are rarely used in the cell mechanics context because signaling molecules are typically abundant.
Intracellular fluid flow plays a crucial part in transporting cytoskeletal proteins from the leading edge to the trailing edge (and back) in migrating cells,21, 43 thus reaction advection diffusion (RAD) equations can also be used in such contexts.14 As fluid pressure also plays a role in the temporal mechanical response of cells,22 some models incorporate equations for fluid flow18, 44 in the mechanical equilibrium equations. The fluid velocities are coupled to the advective terms in RAD models of signaling, thus incorporating a mechanism of coupling between cellular mechanics and cellular signaling. In a later section of this review we will explore how chemical signals can further modulate cytoskeleton composition, organization and hence cellular mechanics, as well as how mechanics can influence signaling.
Model Parameterization and Validation
Estimation of model parameters is an important yet infrequently discussed challenge in computational modeling of cells. Here we compare methods for parameterization of models across mechanics and signaling.
The continuum‐based solid mechanics Eqs. (1) and (2) can only be solved after prescribing the stress–strain relationship that describes the mechanical behavior of the cell. As alluded to in Simulation Equations for Modelling Cellular Mechanics, parameters of continuum‐based models are typically measurable experimentally. The values of these parameters are usually estimated by iteratively running finite element simulations with different parameter values until a match with an experimental metric (such as a reaction force, displacement or morphology) is achieved. This approach is particularly advantageous when some of the model parameters cannot be directly related to an experimental measure. This calibration is however only the first step. One should (when possible) validate the model and its parameters by making predictions beyond the initial calibration. For example, Zhou et al.45 estimated parameters based on creep tests during micropipette aspiration. This parameterized model was subsequently used to predict the effects of micropipette ramp tests, which compared well to predictions. Simulation results from models that do not have this additional check46 must be used with careful consideration.
As one increases the spatial resolution that the model represents, the parameters become more difficult to estimate and validate. Parameters for DPD, such as dissipative forces or stochastic forces cannot be measured experimentally but can be correlated to physical parameters if carefully addressed for each simulation.47 Coarse‐grained molecular dynamics simulations can suffer from a lack of experimental techniques to measure specific parameters with regards to the cross‐linking proteins but can provide insights if the model simulation is validated against bulk or segment rheology experimental data.31, 48
Fundamental measurements when modeling chemical signaling include concentration, diffusivity, and biochemical reaction rate constants. While diffusivity can be readily measured for regulators, their kinetic properties and even their concentration are significantly more difficult to quantify. Direct measurements of kinetic rate constants are not always feasible and are therefore often inferred from other experiments or estimates based on other indirect observations. Fluorescence images are routinely used to measure qualitative changes in cytoskeletal proteins within cells. Care must however be taken to account for properties of the fluorescent probe and optics if one is interested in quantifying signaling properties. Due to these difficulties, quantitative observations about spatial localization and temporal dynamics of regulators are lacking.
These challenges in parameter estimation make model validation and simulation reproducibility a challenge. While cell morphology and cytoskeletal protein distributions within the cell are relatively easy to acquire, the multitude of parameters in these multi‐component models of the cell have varying degrees of uncertainty associated with them. This challenge is compounded by cell to cell variability in mechanical response as well. Parameter sensitivity analysis provides some insights into the effect of this uncertainty. More high throughput measurements of cell to cell variability and more efficient methods for parameter sensitivity and variability analysis would help synthesize the wide variety of model parameters and results in the literature towards an integrated understanding of cell mechanics.
MEASUREMENTS AND MODELS OF THE BULK MECHANICAL PROPERTIES OF CELLS
Experimental measurements have shown that cells exhibit elastic and viscous behavior as they undergo large deformations in vivo.49, 50 Some early studies modeled the cell as a cytoplasmic liquid core encased in a cortical shell under tension.1 Although cells exhibit fluid‐like behavior during micropipette aspiration experiments at time scales greater than 10 seconds, these fluid‐based models could not capture the elastic behavior that was observed at the onset of aspiration. There are currently three classes of continuum‐scale constitutive equations (as illustrated in Figure 2) that have been successfully employed to characterize the bulk behavior of red blood cells,51 chondrocytes,52 neutrophils,18, 53, 54, 55 stem cells,56 and fibroblasts57, 58, 59 to name a few: (1) Hyperelastic and viscoelastic solid constitutive models; (2) Soft‐glassy rheology based constitutive models; (3) Poroelastic constitutive models.
Figure 2.
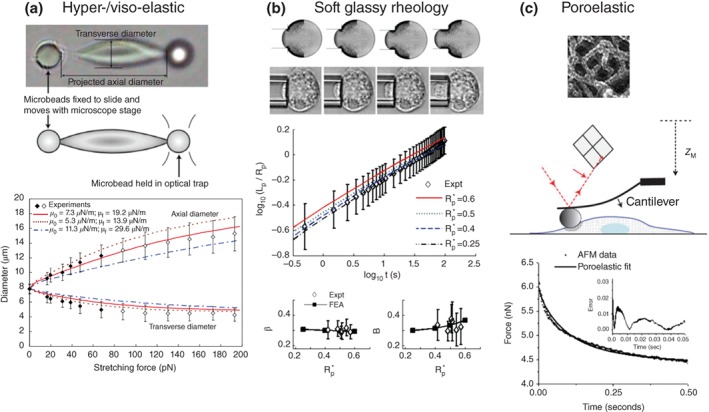
Examples of experimental measurements and mechanical models of bulk mechanical properties of cells. (a) Mills et al.51 used optical tweezers to perform uniaxial extension and relaxation experiments on red blood cell to parameterize hyperelastic and viscoelastic constitutive equations of its mechanical behavior (Reprinted with permission from Ref 51. Copyright 2004 Tech Science Press); (b) Zhou et al.45 implemented a finite element model (top image in (b)) with a power‐law rheology based constitutive equation to capture the long‐time‐range soft‐glassy like response of cells as measured by creep tests using micropipette aspiration (middle of panel) (Reprinted with permission from Ref 45. Copyright 2012 Springer); (c) Herant and Dembo18 used the poroelastic continuum mechanics equations to account for the porous nature of the cytoskeletal network (image shown in the top panel of (c), reprinted with permission from Ref 18. Copyright 2010, Elsevier Inc.) and the movement of fluid through these pores. The influence of fluid reorganization during mechanical perturbations and the poroelastic nature of the cell have been recently experimentally measured (and fitted with a poroelasitc model) by Moeenderbary et al. 22 (middle and bottom panels, reprinted with permission from Ref 22. Copyright 2013 Nature Publishing Group).
Red blood cells are made up of a liquid hemoglobin center encased in a cortical cytoskeleton and lipid‐bilayer membrane shell. By representing this membrane composite as a viscoelastic solid, parameters of high order hyperelastic and viscoelastic strain energy functions such as Yeoh (see Figure 2(a) and Eq. (6)) have been fitted successfully to micropipette and optical tweezer data.51 As shown in Figure 2(a), the hyperelastic component of the in‐plane membrane tension (T s) is scaled by the shear modulus (μ), the extension ratios in the orthogonal directions of the membrane (λ1 and λ2). The viscous nature of the membrane is accounted for in the second term and is dependent on the strain rate and the viscous co‐efficient (η). Linear viscoelastic models such as Maxwell, Kelvin or Voigt models have also been employed previously to capture the viscoelastic nature of the cytoplasm of cells which are richer in cytoskeletal proteins than red blood cells24, 52, 60, 61, 62; Gizzi et al.63 used a transverse‐isotropic hyperelastic law to model the mechanical properties of cardiac cells.
| (6) |
While viscoelastic models can characterize both solid and fluid like behavior of cells, another class of models represent the cell as a soft‐glassy material.45, 64, 65, 66, 67 Classical spring and dashpot viscoelastic models aim to attribute different time‐dependent transitions in cell mechanical behavior to different structural components of the cell, such as the membrane, cortex, and cytoplasm. While these models were found to be sufficient to capture viscoelastic behavior at time scales in the order of seconds, they failed to capture the viscoelastic behavior at extended timescales (10s and 100s of seconds).45, 66 It was shown that a power‐law model with a single exponent could adequately describe viscoelastic behavior over much wider timescales.66 Zhou et al.45 (Figure 2(b)) developed a power‐law model based on a Prony series expansion (see Eq. (7) below) and successfully replicated micropipette aspiration creep test data using a finite element model. They defined the relaxation modulus using a Prony series expansion as follows:
| (7) |
G 0 is the instantaneous shear modulus, and g i and λ i (i = 1,2,…, N) are material constants characterizing the relaxation spectrum. Experimental time scales of upto five orders of magnitude can be adequately described by a 5‐term (N = 5) Prony series expansion.
Although the aforementioned constitutive models have successfully reconstructed experimental conditions in silico, one of their drawbacks is that they are phenomenological equations, in which material parameters are chosen to ensure that the model simulation results fit the experimental data. To that extent, the parameter values quantify the bulk, emergent properties from several spatial and temporal interactions of the cell's constituents. The cell cytoskeleton is made up of a heterogeneous, porous network of cytoskeletal proteins and its cross‐linking proteins (see Figure 2(c)), immersed within a viscous fluid. A poroelastic framework (see Figure 2(c)) begins to account for how microstructural contributors give rise to emergent behavior of the cell.
As outlined in Eqs. (8), (9), (10) below, in the poroelastic treatment of the cell, spatially variable volume fractions of solid (θ s, such as the cytoskeletal network) and liquid phases (θ n water and solutes) are defined and at each point within the cell, the total volume must be conserved. The stress‐equilibrium equations (Eqs. (1), (2) and (3)) are used to solve for the equilibrium shape and stress of the solid phase. Fluid flow equations (typically based on Darcy's law) are used to describe the flow of fluid through the cell volume. In these equations p represents the fluid pressure and ζ represents the drag coefficient between the solid and fluid phases. Movement of this fluid is critical to blebbing‐based cell motility and cellular protrusions.21, 68 Continuum‐level, two‐phase or poroelastic models have been shown to successfully capture the mechanisms of cytoskeletal protein transport and intracellular pressure that these fluid movements provide.17, 18, 43, 55, 69 Recently Moeendarbary et al.22 experimentally tested the poroelastic nature of cells and showed that cells indeed behave like poroelastic materials at short timescales, and exhibits a power‐law response at long time scales.
| (8) |
| (9) |
| (10) |
When performing any experimental measurement to interrogate the mechanical behavior of the cell and its cytoskeleton, one must be acutely aware of the conditions under which the experiments are conducted. Temperature and pH are well known to affect many properties of cells but cell stiffness is also modulated by the density of adhesions and the cell's local environment.70, 71, 72, 73 In addition to these factors, the effects of cytoskeletal remodeling on apparent viscoelastic behavior should also be carefully considered. Cytoskeletal remodeling has been routinely observed within 10s of seconds of initiating a micropipette aspiration experiment, for example.32, 35, 36, 37, 38 Knight et al.39 showed that compression loads and hydrostatic pressure can induce cytoskeletal remodeling in chondrocytes. Song et al.56 elegantly used fluid flow to exert controlled strains and stresses on the surfaces of stem cells and correlated stress and strain data to measures of gene transcription that mark cell lineage commitment. Therefore, models that incorporate the microstructural arrangement and dynamic reorganization of cytoskeletal proteins, when subject to mechanical loads or chemical treatment, have the potential to give more integrative insights into cellular mechanics and cytoskeletal mechanobiology than continuum‐based phenomenological models discussed so far.
MEASUREMENTS AND MODELS OF THE CONTRIBUTION OF CYTOSKELETAL COMPONENTS TO BULK BEHAVIOR
The bulk mechanical behavior of the cell emerges from the organization and stiffness of the cell membrane, its interaction with its surroundings and the proteins that make up its cytoskeleton. This section summarizes the current understanding of how different cytoskeletal proteins contribute to the stiffness of the cell and how their contribution has been explicitly accounted for in computational models of cellular mechanics.
The Mechanics of Individual Filament Types
The cytoskeletal network is made up of three major classes of biopolymers: actin filaments microtubules and intermediate filaments.
Actin filaments have a double helical structure consisting of two strands that spiral around the axis of the polymer (see Figure 3(a)). The coiling occurs every 37 nm (nm) and the two strands span a width of 7 to 9 nm.
Figure 3.
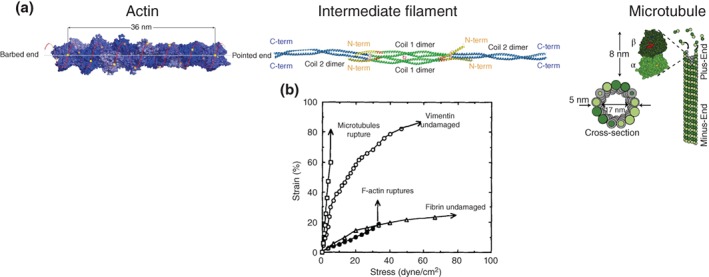
(a) Illustrates the fundamental structure of the three groups of filaments that constitute the cytoskeletal network (Reprinted with permission from Ref 83 and Ref 84. Copyright 2016 Cold Spring Harbor Laboratory Press and Copyright 2010 Elsevier Inc., respectively); (b) Stress‐strain relationship for reconstituted cytoskeletal networks purely made from one filament type (Reprinted with permission from Ref 85. Copyright 1991 Rockefeller University Press).
Central to understanding muscle biophysics, single actin filaments have been the subject of mechanical studies for several decades. Microneedle manipulation, x‐ray and laser techniques74, 75, 76 have been used to measure the axial spring stiffness of actin filaments to be between 11 and 44 pN/μm (piconewtons/μm) for every 1‐μm length of actin filament; the reported range of values can be attributed largely to the chemical environment in which the filamentous actin was pulled.77 The tensile strength of an actin filament—the force at which the filament breaks—is 108 pN, regardless of filament length.78 Measurement of thermal fluctuations of actin filaments have been used to estimate the bending stiffness, via flexural rigidity, of single actin filaments in the order of 7.5 × 10−26 Nm2.79, 80 Similar methods that observe torsional movement have been employed to estimate torsional stiffness of the order of 8.5 × 10−26 Nm2.81, 82
Microtubules are hollow polymeric structures that are constituted by alpha‐ and beta‐ isoforms of a heterodimer called tubulin (see Figure 3(a)). Larger than actin filaments (55 kDa, 25 nm external diameter, 17 nm internal diameter, and 50 nm long repeating unit), microtubules also provide rigidity to the cell, and play a central role in biological phenomena such as mitosis and cargo transport across the subcellular domain.86
Schaap et al.87 provide force‐displacement curves from atomic force microscopy (AFM) based cantilever indentation experiments that show that microtubules exhibit a linear elastic response. They showed that microtubules have a higher spring stiffness of ~74 nN/μm, bending stiffness 3 orders of magnitude higher than actin filaments (~22 × 1023 Nm2)80, 88 and deformations become irrecoverable after indentation strains exceed 15%. Hawkins et al.84 provide an excellent review of the experimental measurements on microtubule mechanics.
Intermediate filaments have been given their name because of their intermediary diameter (~10 nm) between actin filaments and microtubules. Unlike the other two classes of protein filaments, intermediary filaments are made from a more diverse range of proteins and have more varied functions. The wide range of intermediary filaments has been classified into six groups based on the similarity in amino acids.
Unlike microtubules and actin filaments, whose fundamental unit is a globular protein, all intermediate filaments have a distinctly organized, extended α‐helical conformation that forms two‐stranded coiled coils (Figure 3(a)).83, 89, 90 This fundamental difference grants individual intermediate filaments the ability to withstand strains much larger than 100% and a nonlinear stress–strain relationship91, 92, 93, 94, 95—actin filaments and microtubules exhibit linear stress–strain relationships and much lower yield strains (see Figure 3(b)). Readers are directed to several excellent reviews4, 7, 84, 89, 95, 96 for further detailed measurements and models of the mechanical behavior of the three filament types and their networks. Here, we summarize some key measurements of how the different components of the cytoskeleton contribute to the emergent mechanical behavior of the composite cytoskeleton and review models that account for these distinct contributions to cytoskeleton and cell mechanics.
Cytoskeletal Network Mechanics and the Role of Cross‐Linkers
Actin Cytoskeleton Mechanics
Actin and associated cross‐linking proteins are the most studied components of the cell cytoskeleton due to their role in many biological functions such as skeletal and cardiac muscle force generation,63 cell migration,4 cell shape97 as well as endo and exocytosis. Actin filament network stiffness increases with both filament lengths98 and density.99 Biochemical and mechanical signals regulate the lengths and density of the actin filaments within the cytoskeleton and create a wide variety of network morphologies, broadly categorized into branched, parallel and antiparallel bundles. These morphologies modulate the emergent mechanical behavior of the cytoskeleton composite.100 Families of actin cross‐linking proteins are employed by the cell to affect these modifications.
Fascin, filamin‐A, α‐actinin, and fimbrin are some of the more commonly utilized cross‐linking proteins in studies of cytoskeletal mechanics. Fimbrin and fascin are compact cross‐linking proteins that create parallel‐aligned actin networks that drive membrane protrusions such as filopodia.104 On the other hand α‐actinin and filamin‐A form networks with more widely spaced and orthogonally aligned actin filaments.102, 105 Studies have shown that these cross‐linking proteins can cooperatively enhance the mechanical behavior of the cytoskeletal network. Tseng et al.101 showed that fibroblast cells injected with α‐actinin alone exhibited a higher stiffness than a network cross‐linked by fascin alone; networks that included both cross‐linking proteins exhibited a higher stiffness compared to when the network was only crosslinked by one of them (see Figure 4(a)). Similar observations have been made about the stiffness of networks that contain both filamin‐A and α‐actinin102 (see Figure 4(b)). Fimbrin has been shown to make a moderate contribution, compared to α‐actinin, to cytoskeleton stiffness associated with the cell membrane as well32 but its tight bundling capability has been shown to play a more critical role in generating stronger acto‐myosin forces at the cortex for cytokinesis and endocytosis.106, 107
Figure 4.
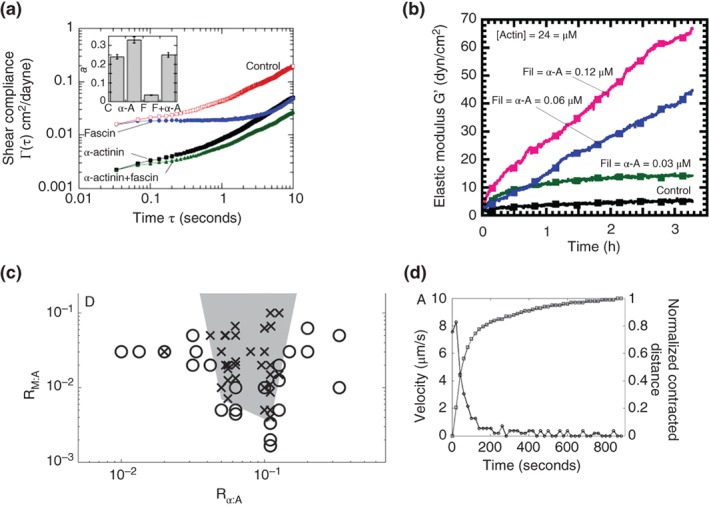
The role of cytoskeletal proteins and their cross‐linkers: (a, b) Cytoskeletal networks made from combinations of different cross‐linkers exhibit different emergent mechanical behaviour (Reprinted with permission from Ref 101 and 102. Copyright 2005 Elsevier Inc. and Copyright 2009 Public Library of Science, respectively). (c) Myosin‐contractility of the cytoskeletal network is ineffective at very low or very high cross‐linker concentrations (Reprinted with permission from Ref 103. Copyright 2008 Elsevier Inc.). The shaded region indicates the myosin contractility feasibility. (d) Myosin exerts contractile stresses on the cytoskeletal network that reaches equilibrium after approximately 800 ms (Reprinted with permission from Ref 103. Copyright 2008 Elsevier Inc.).
The enhanced stiffness or force generation capacity due to the use of a combination of cross‐linkers may suggest that all cross‐linkers act cooperatively but different combinations of cytoskeletal proteins also produce different network organizations. Recent studies on reconstituted networks show that cross‐linkers may repel other types of cross‐linkers and promote cooperative binding of actin to more cross‐linkers of the same kind.105, 108 Winkelman et al.105 showed that fascin and α‐actinin repelled each other and formed different actin network topologies—this was observed in the absence of any chemical signaling or local changes to the environment (such as pH). On the other hand, proteins that are similar to fascin, such as fimbrin, bind more cooperatively and in close proximity with fascin. This illustrates the fact that the combination of proteins may not just affect cell stiffness but will also affect the spatial assembly of the cytoskeleton.
Outside of pulling together actin filaments and increasing their stiffness, crosslinking proteins such as fascin, filamin, and α‐actinin are passive in nature. Myosin is a more dynamic crosslinker and plays a role not only in modulating cytoskeletal stiffness, but also viscoelasticity, migration, shape changes and apoptotic processes as well.109 Figure 4(c) and(d) show two key, bulk characteristics of acto‐myosin gels103: (1) myosin contraction is only effective within a short, middle range of actin cross‐linking protein densities (as shown in Figure 4(c)); (2) acto‐myosin contractions exhibit exponentially decaying contraction velocities lasting over several 100 s of seconds before reaching a steady state as shown in Figure 4(d). Contraction velocities are concentration dependent, with a one‐fold drop in myosin concentration causing an increase in the duration of contraction by an order of magnitude.
Mathematical Modeling of the Actin Cytoskeleton Network
Coarse‐grained Brownian dynamics models like Figure 1(c) have captured several features of the actin cytoskeleton behavior mentioned above and have also provided additional insights on the interactions between different cytoskeletal components that give rise to mechanical properties of actin cytoskeleton.12, 31, 110, 111 Actin cross‐linking proteins that promote orthogonal linkages between actin filaments contribute more to increasing stiffness than cross‐links that form parallel bundles.31 The energy from mechanical loads is absorbed within the network through actin filament bending, cross‐link protein bending and stretching of the proteins at much higher strains. More than protein unfolding, actin cross‐link protein unbinding regulates the cytoskeletal behavior during strain hardening and stress relaxation.110
Myosin also contributes to the emergent mechanical stiffness of the cell but its procession over the actin filaments that it binds to brings about a rich set of characteristics to the mechanical response of cells. Borau et al.112 showed that when a small cytoskeletal network with myosin motors is formed within a stiff surrounding, myosin motors exert maximal contractile force thus making the cytoskeleton stiffer. At lower levels of boundary stiffness, myosin motors do not reach maximal force as they are stalled by cross‐linking proteins at a sub‐maximal stress, making the cytoskeleton softer.
Luo et al.32 performed a comprehensive, single cell‐scale Brownian dynamics simulation coupled with an extensive experimental dataset of cytoskeletal distributions to investigate the mechanisms that govern cytoskeletal reorganization during micropipette aspiration. Localization of cytoskeletal proteins during micropipette aspiration was assessed using live imaging of GFP‐fusion proteins. They found that myosin II accumulation occurred at the pipetted tip of the membrane along with some passive cross‐linkers such as α‐actinin but some cross‐linkers such as filamin A accumulated at the neck region instead of the pipetted tip. Their model simulations suggest different cross‐linking proteins are more responsive to specific modes of deformation. For example, cross‐linking proteins such as α‐actinin respond more to dilatational stresses, while filamin‐A accumulated in regions of high shear stress. Luo et al.'s model simulation predictions of the localization of different cross‐linkers matched with their experimental measurements as well.
Mechanics of Microtubules and Intermediate Filament Networks
The mechanical and structural effects of crosslinking microtubules or intermediate filament networks have been explored less than the actin cytoskeletal network.
Microtubule networks can be crosslinked by a class of proteins called microtubule‐associated proteins (MAPs), such as Tau, MAP1, MAP1a, MAP1b, and MAP4.113 These proteins stabilize and promote the assembly of microtubules and have largely been reported to increase the stiffness of microtubule networks.84, 114 In vitro studies have shown that reconstituted microtubule networks made from purified microtubules alone form homogeneous networks, whereas more heterogeneous networks are formed when crosslinkers are added.114, 115, 116 The networks show a nonlinear stress–strain relationship, with an initial nonlinear stiffening at low strains/forces followed by softening at high forces due to crosslinker unbinding115, 116 (see Figure 5(a)).
Figure 5.
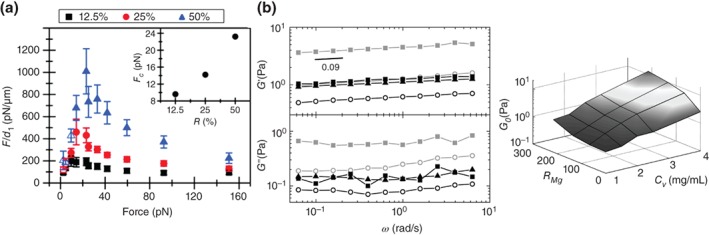
Stiffness of microtubule and intermediate filament networks as functions of cross‐linker density. (a) Plot of microtubule network stiffness, calculated by dividing force F by the initial elastic jump distance d1, with three different densities of cross‐linkers (12.5%, 25% and 50%). The plot shows network stiffening at low forces and softening at high forces. Inset shows the crossover force Fc from stiffening to softening reginmes increases with crosslinking density (Reprinted with permissions from Ref 115. Copyright 2012 RSC Publishing); (b) Plots of stiffness of vimentin intermediate filament networks cross‐linked by different divalent ions. Plot on the left shows linear viscoelastic moduli in the absence of divalent ions (with vimentin concentration c v = 1 mg/ml, black open circles; c v = 2.5 mg/ml, gray open circles) and in the presence of Mg2+ (with molar ratio, RMg = 215; c v = 1 mg/ml black squares; c v = 2.5 mg/ml, gray squares) and Ca2+ (with molar ratio, R Ca = 215; c v = 1 mg/ml, black triangles). G′ dominates over G″ and exhibits weak power‐law scaling with frequency, ω, having an exponent of 0.09. The networks in the presence of divalent ions are two to four times stiffer. Plot on the right summarizes the dependence of the elastic response, G o, of vimentin networks on R Mg and c v. (Reprinted with permissions from Ref 118. Copyright 2010 Elsevier Inc.).
Specific crosslinking proteins do not seem to be needed for intermediate filament network formation unlike the actin crosslinking proteins discussed in Actin Cytoskeleton Mechanics; divalent cations such as magnesium (Mg2+), calcium (Ca2+), and zinc (Zn2+) can act as crosslinkers of intermediate filament networks95, 117 (see Figure 5(b)). Some reports also suggest that subunits of the intermediate filaments may act as binding sites for other neighboring filaments.95
Mathematical Models of Microtubules and Intermediate Filament Networks
Microtubules can be well represented as slender beams or composite fiber reinforcements due to their very long persistence lengths, bending rigidity and structural dimensions relative to the rest of the cell. There are several continuum‐elasticity‐based computational models of individual microtubules that have been used to study microtubule mechanical properties,119 the buckling of microtubules due to deformations in the surrounding elastic matrix120 and vibration and wave‐propagation.121 Molecular dynamics and coarse‐grain techniques have also been used to study microtubule growth and instability.122 Despite the fact that microtubules are known to play a role in cell morphogenesis and cell migration mechanics,123 very few mechanical models of microtubule networks have been developed. Allain et al.124 used particles to define a discretized connected microtubule network and simulated their mechanical dynamics using Newtonian mechanics. Euler‐Bernouilli theory was used to derive an elastic force that is applied at each node to account for the rigidity of microtubules. Buxton et al.125 used a similar approach and although these models were mostly qualitative in their insights, they demonstrated the interplay between microtubule growth kinetics, network morphology and mechanics.
The ability of intermediate filament networks to sustain large deformations and self‐assemble into heterogeneous networks makes IF networks ideal for continuum mechanics treatment.10 Similar to microtubule network models, there are few models of intermediate filament networks. What models are present are mostly qualitative in their insights, using energy potentials to formulate the mechanical dynamics.126
New Frontiers for Computational Modeling of Cytoskeletal Mechanics
As outlined above, significant strides have been made to understand the effect of the different constituents of the cytoskeleton on the mechanical behavior of cells and reconstituted networks using a reductionist approach, more so of the actin cytoskeleton than the remaining two groups. Here we outline several additional aspects of mathematical modeling that are open for development and need attention in order to gain an integrative understanding of the emergent mechanical behavior of cells.
Coarse‐grained models of the actin cytoskeleton, while providing a framework to examine emergent behavior from the constituent parts, are computationally expensive for extensive use. Extending the Brownian dynamics framework that was used to model the membrane‐bound skeleton,32 to simulate the mechanics of the cytoskeleton of the entire cell volume, is computationally intractable. To this end, homogenization of the emergent properties of cytoskeletal networks in a continuum framework is much sought after. Studies by groups such as Muller et al.,111 Kwon et al.,127 and Fallqvist et al.128 developed microstructure based constitutive equations of the stiffness of actin cytoskeletal networks.
Fallqvist et al.128 formulated a thermodynamically consistent constitutive law that incorporates anisotropic properties and is based on a strain energy function that can be incorporated into the continuum‐based models. Starting with a 1‐dimensional (1D) strain energy function, W 1D for an individual filament within a network:
| (11) |
W f and W s are strain energies due to filament bending and stretching, respectively. μ f and μ s are stiffness parameters associated with filament bending and stretching. λ f and λ s are the magnitudes of bending and stretching of individual filaments. f s is a 1D constitutive force‐displacement relationship—to be chosen—to describe the mechanical behavior of individual filaments within the network. The 3D strain energy function contains isochoric (W isoch) and volumetric (W vol) components.
| (12) |
W a and W b are isochoric strain energies due to networks a and b and ω a and ω b are ‘damage’ variables that account for network filament rupture and debonding. One can represent anisotropic properties of a network by defining an orientation distribution function ρ. This function describes the distribution of filament directions in the network. Thus, the isochoric strain energy within a unit spherical domain, Ω, for a given network can be defined as:
| (13) |
This model was validated against existing rheological experiments on reconstituted cytoskeletal networks and found to be in good agreement with the data. Some aspects such as the effects of cross‐linker unbinding and binding on rheology could not be captured. With our understanding of cytoskeletal composition, organization and mechanics still incomplete, both particle‐based molecular dynamics and continuum‐based homogenized models of the cytoskeleton will need to develop in parallel for some time yet before any one model is adopted widely.
While there have been many studies that investigated the stiffness of intermediate filaments and microtubules,95, 96, 123 more experimental and computational studies are needed to understand the mechanisms that govern microtubule and intermediate filament network dynamics (as mentioned in Mechanics of Microtubules and Intermediate Filament Networks and Mathematical Models of Microtubules and Intermediate Filament Networks). Their contributions to the emergent behavior of the cell cytoskeleton have also only gained increased traction recently. Gladlin et al.10 developed a 3‐layered linear elastic shell model of a cell nucleus, a perinuclear intermediate filament network region and a cortical actin network region (see Figure 1(a)) and showed using the model and experiments that drugs that targeted perinuclear vimentin intermediate filaments caused a change to cytoskeletal network density. Mendez et al.129 showed that vimentin intermediate filaments contribute more to the increased stiffness of cells as their local environment becomes stiffer. Rajthe et al.130 showed that loss of microtubule integrity caused intermediate filaments to collapse near the nucleus. Guo et al.131 showed that intermediate filaments could be found in greater abundance within the cytoplasm than within the membrane‐bound cortex meshwork. More research into how and when the roles of these two classes of proteins become significant to cell stiffness and biology is a widely untapped opportunity.
Spatial heterogeneity of cell stiffness has also not been incorporated with sufficient accuracy into computational models. Most models have traditionally assumed that most of the relevant mechanics of the cell occurs at the boundary because the cell membrane and membrane associated cortical cytoskeleton is stiffer than the viscous interior. Considering the potential segregation of the highly stretchable intermediate filaments from the stiffer cortical actin, the spatial heterogeneity may in fact be very important when modeling large deformations of the cell. Incorporating the spatial heterogeneity is also important to develop an understanding of how the nucleus senses mechanical forces to send signals for remodeling.132 New advances in microrheology133 and non‐invasive Brillouin microscopy134 will provide richer datasets to advance this aspect of cell mechanics in future.
Measurements and Models of Protrusion Forces Due to Actin Polymerization, Depolymerization and Disassembly
Another important contributor to cytoskeletal mechanics and cell stiffness modulation is actin (de)polymerization. It plays a significant role in cell migration along with numerous other processes and the molecules that regulate its dynamics have been studied extensively in the literature.135, 136, 137 We provide a summary of these details within the signaling section of this review. Here, we discuss some key experiments and models that have been used to study the effect of actin polymerization and disassembly on single cell and cytoskeletal mechanics.
Actin polymerization against a membrane produces a force that pushes the membrane forward. Three experimental studies138, 139, 140 provide elegant measurements of the forces generated by actin polymerization. Parekh et al. promoted actin growth within an actin gel against an AFM cantilever tip (see Figure 6(a)) and used the deflection of the beam to measure the force during actin polymerization. Similarly, Marcy et al.140 promoted growth within an actin gel against an optical trap. Such experiments provide data similar to that shown in Figure 6(b) that relate the force measured at the optical trap or cantilever and the rate of growth of the actin gel.
Figure 6.
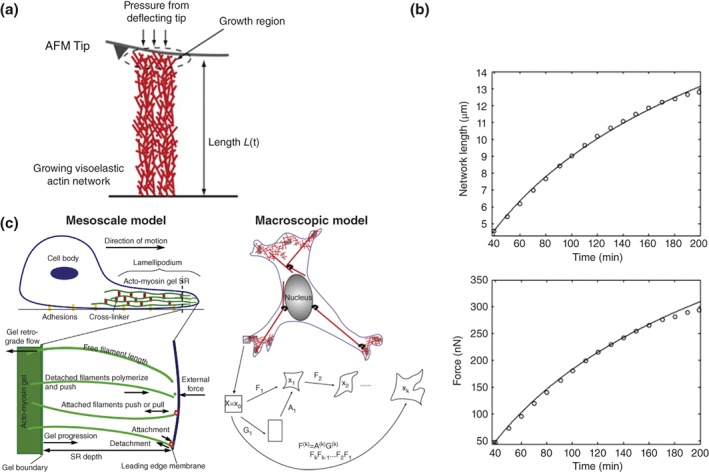
Measuring and modelling actin polymerisation mechanics. (a) A method of measuring the force produced by actin polymerisation where polymerisation is promoted near an AFM tip. The deflection of the tip and imaging the growing actin gel provide sufficient data to parameterise a model of actin gel growth from actin polymerisation. (b) Plots that relate growth rates and protrusion force that can be used to parameterise a model of actin protrusion. Circles represent the experimental data and the curves are predictions from a macroscopic growth‐tensor model of the leading edge. (c) Schematic of mesoscopic and macroscopic concepts of the interpretation of the force generation due to actin polymerisation. In the mesoscopic model, actin filaments push and pull the membrane depending on their kinetics. One approach to macroscopic modelling of the forces due to actin polymerisation is to treat the polymerisation as a cell growth strain, G, that is applied on top of any mechanical strains due to external loads. ((a), (b) and macroscopic model of (c) reprinted with permission from Ref 143. Copyright 2009 Elsevier Inc. Mescoscale schematic in (c) reprinted with permission from Ref 145. Copyright 2012 Elsevier Inc.)
Models of actin protrusion and migration vary in the spatial scales they represent. Models that explore the role of individual filaments at the leading edge8, 141, 142 simulate the attachment and detachment of collections of 1‐D actin spring‐like filaments against the cell membrane, each of which generates a pulling or pushing force against the leading edge (see Figure 6(c)). Models at this scale are termed mesoscopic. Kim et al.143 took a macroscopic approach and used a growth‐tensor continuum mechanics formulation to simulate cell growth144 at the leading edge due to actin polymerization. Namely, the mechanical strain is made up of two components: (1) a strain due to mechanical forces that are exerted on the cell and cytoskeleton (these can be due to external forces on the cell, or internal forces due to acto‐myosin contractions), which is modeled using a stress–strain constitutive relationship (such as those discussed in previous sections); (2) and a strain due to growth of a region, which in this context arises from actin polymerization (see Figure 6(c)).
Two mechanisms are thought to play major roles in reversing protrusions and local expansions of the actin network: (1) actin network disassembly by ADF/cofilin mediated actin filament severing; (2) and myosin‐induced actin network disassembly.146
ADF/cofilin is a family of proteins that promote actin network disassembly by local binding to actin filaments and consequently reducing the persistence length of actin filaments fivefold and increasing their bending and twisting compliance.147 This is thought to promote severing of filaments at the boundaries between compliant, ADF/cofilin‐decorated regions and stiffer, ADF/cofilin‐bare regions. On the other hand, acto‐myosin contractions induce stresses onto the actin filament network, which are thought to buckle and fragment the filaments.146, 148
Fragmentation and severing causes local changes to the actin cytoskeletal network density and its viscoelastic properties, while increasing the availability of actin monomers for reorganization of the cytoskeleton.146 Jung et al.149 used a coarse‐grained Brownian dynamics simulation of the actin cytoskeleton to demonstrate stress‐relaxation due to actin network buckling and fragmentation. Zhu et al.142 incorporated network disassembly in their node‐and‐spring model of the cell cytoskeleton by actively removing nodes and springs at a set disassembly rate; this effectively decreased network density and local network stiffness. These effects could be accounted for in the viscous and elastic parameters of coarser‐grained, continuum‐based models of the cell cytoskeleton.
The precise relationship between disassembly and cytoskeletal force and mechanics is yet to be fully realized. Rates of disassembly may be affected by two‐way feedback mechanisms between the local network morphology, the state of acto‐myosin contractions and density of cross‐linkers.146 As with all other aspects of cytoskeletal behavior that we have discussed in this section, unraveling the interplay between the spatio‐temporal forces and the dynamics of different aspects of the cytoskeletal is a major challenge. However, when reviewing the advances that have been made so far, these new advancements are sure to follow.
MEASUREMENTS AND MODELS OF THE CONTRIBUTION OF ADHESIONS AND THE SURROUNDING ENVIRONMENT ON SINGLE CELL AND CYTOSKELETAL MECHANICS
Every computational simulation must prescribe not just what happens in the interior of the cell but also the dynamics of the boundary. Mathematically, this involves prescribing Dirchlet or von Neumann boundary conditions for a computationally tractable simulation result. From this perspective adhesions to the extracellular matrix (ECM) or neighboring cells are where boundary tractions or displacement boundary conditions are specified. Proper prescription of these boundary conditions is not only important for tractable simulations but they are also critical to deciphering the biological mechanisms that are regulated through adhesions. Many studies have shown that mechanical interactions between cells and the ECM or other cells, via adhesions, play a fundamental role in biological processes such as migration, growth and morphogenesis.43, 150, 151, 152, 153, 154 Cell–ECM adhesions are formed by a major class of adhesion proteins called integrin receptors and cell–cell adhesions are formed by other classes of adhesion proteins such as cadherins and nectins. While biochemical regulation of adhesion formation and degradation is discussed in Adhesion Regulation, here we review measurements and models of the mechanics at the interface of the local environment, adhesions and the cell.
Traction force microscopy is the method of choice for tracking cell–ECM interactions.50, 155, 156, 157 The method typically involves tracking the movement of beads or extracellular matrix fibers (or liquid droplets between cell‐to‐cell adhesions50), near the vicinity of the cell when it generates contractile forces against adhesions. Figure 7(a) shows results of tracking beads in a ECM as a cell contracts and migrates through this 3D environment from Legant et al.157 The bead displacements can be post‐processed into strains, which show that cells generate significantly large deformations against the ECM (~30%). These bead displacements are further processed into traction stress/forces via a constitutive model. This invariably requires assumptions of the mechanical properties of the cell or ECM gel, typically as a linear elastic solid or the solution of the inverse problem whereby the traction strain data are used with a finite element model of the cell to estimate traction forces. Readers are directed to an excellent review by Schwarz et al.156 on traction force microscopy for further details on the different methods.
Figure 7.
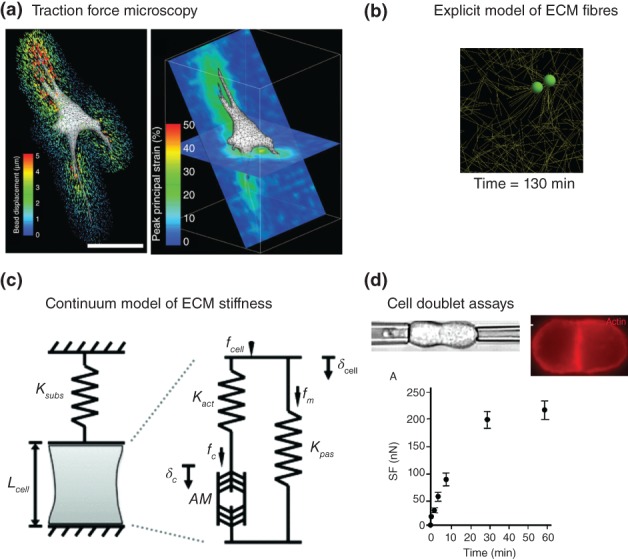
Measuring and modelling cell‐ECM tractions. (a) Measurement of bead displacements (left) and calculated peak strains (right) of a cell migrating inside a 3D ECM environment (Reprinted with permission from Ref 157. Copyright 2010 Nature Publishing Group Inc.). Scale bar represents 50 μm. (b) A simulation from a model of cell‐ECM interactions in which the ECM fibres are explicitly modelled as cylindrical segments (Reprinted with permission from Ref 160. Copyright 2012 Elsevier Inc.). The two spheres represent cells that are migrating through the ECM, remodelling the local ECM matrix in the process. (c) A conceptual diagram of a continuum model of a cell and its mechanical interaction with the ECM. The model incorporates the role of ECM stiffness in the traction forces felt at the cell adhesions (Reprinted with permission from Ref 161. Copyright 2013 Springer). (d) Cell doublet assays involve pulling two adhered cells apart using micropipette aspiration The fluorescence image shows cortical actin accumulation at the cell‐cell junction. The plot shows the temporal change in separation force as the cells are pulled apart (Reprinted with permission from Ref 162. Copyright 2004 Rockefeller University Press).
Using these approaches, several characteristics about the relationship between ECM density, adhesion size and traction forces have been elucidated. The local orientation of the ECM fibers has been implicated in guiding cell migration by restricting cell protrusions that come in contact with matrix fibers.158 Traction forces generated by the actomyosin contractions tend to increase in magnitude due to the cascading effect of increased ECM fiber density, causing an increased stiffness in the ECM and increased density of adhesions (and size of adhesion complexes) between cell and ECM. Coarse‐grained Brownian dynamics simulations of the actin cytoskeleton also suggest that the increased actomyosin contractions are due to increased processivity of myosin over actin filaments.112 Passive cross‐linkers also play a role at the cell–ECM interface. Both filamin‐A and α‐actinin have been experimentally observed to trigger maturation of adhesions by linking actin to integrin proteins.153, 159
Several mesoscopic and macroscopic models of cell‐ECM interactions have been used to study the interactions between the cell, adhesions and ECM. Schlutter et al.160 explored the role of ECM architecture remodeling by explicitly modeling collagen fibers as cylindrical rods that were oriented in ECM‐like configurations. The cell was modeled as a point mass whose mechanical cues were regulated by the intracellular acto‐myosin contractions and the external orientation and deformation of the fibers (see Figure 7(b)). The force balance between the cell and the ECM was modeled as:
| (14) |
where F drag is a macroscopic drag force on the cell that is balanced by the sum of the conservative forces between the cell and every ECM fiber, f, and a noise term f j(t) to account for other factors. The interaction forces between the cell and ECM fibers were weighted towards favoring cell migration along its direction of polarity. The re‐orientation of each fiber was computed using the concept that the fibers were levers that are rotated by the moment generated by the cellular contraction. Using this formulation, the study showed that ECM fiber re‐orientation reduced the persistence of the cell to move in a direction. As the model equations suggest, these observations are limited by the point‐wise representation of the cell and the simplified interaction force between cell and ECM.
Zhu et al.142 represented the cell acto‐myosin network and the ECM network as a collection of nodes and springs. This allows for incorporation of additional details such as protrusion forces and adhesion kinetics. Such spatially extended models163, 164 enable more detailed studies of the interactions between the ECM fibers and the cell intracellular machinery.
A continuum approach to modeling cell–ECM interactions is to incorporate the mechanical influence of the ECM into constitutive models of the whole cell. For example Borau et al.161 incorporated the influence of ECM stiffness on acto‐myosin contractility through a spring model (see Figure 7(c)). In this model, the substrate stiffness is represented by a single passive spring stiffness. The cell is modeled as a material with two springs in parallel: (1) K pas representing the passive mechanical properties of the cell that the microtubules, intermediate filaments and membrane contribute to and; (2) K act representing the stiffness of actin filaments which are in series with the acto‐myosin complex, AM. The model also incorporated the time‐dependent response of myosin motors,112 thus incorporating a viscoelastic component to the cell's response. While simple and more phenomenological in its detail, the model was successfully able to capture the dynamics of acto‐myosin contractile stiffness due to changes in ECM stiffness.
While we have discussed the mechanical interactions between the cell and ECM fibers above, interstitial fluid flow has also been demonstrated to trigger cytoskeletal remodeling.56, 165, 166 Song et al.56, 165 prescribed fluid flow through a tissue scaffold and applied fluid dynamics analysis techniques to compute micro‐scale particle image velocimetry (micro‐PIV) data. They also tracked the displacement of beads bound to cell membrane glycoproteins to compute a corresponding strain distribution for the prescribed fluid flow and tissue scaffold geometry. A combined computational fluid dynamics model of the fluid flow with measured strains and micro‐PIV data was used to estimate the stress distributions over the cell surface and to track the changing cell shape and stiffness. Although only a linear elastic model of the cell was used in these studies, they demonstrate the rich data that can be collected and analyzed using fluid‐induced cytoskeletal or cellular remodeling.
The forces in cell to cell interactions are transmitted through another class of adhesion receptors different to integrins, the most well‐studied being cadherins. These forces are of significant interest due to their implications in tissue development and tissue homeostasis. An in‐depth review of the measurements and models of cell–cell adhesions in tissue constructs are beyond the scope of this review on single‐cell mechanobiology and we encourage readers to refer to many excellent reviews of this field for more details.167, 168, 169, 170, 171 Nevertheless, these same forces affect the cytoskeleton and the mechanics of the individual cells that make up the tissue. Therefore, we present a brief summary of some pertinent information that can be used as a starting point for any computational study of the effect of cell–cell adhesions on single‐cell mechanobiology.
The actin cytoskeleton is connected to the cell–cell cadherin adhesions via a class of proteins called catenins. Acto‐myosin contractions play a critical role in immobilizing cadherin proteins during adhesion formation172 and the actin cytoskeleton transmits forces through these cadherin‐based adhesions to neighboring cells,168 which subsequently activate a wide range of signaling pathways that regulate cell shape, tissue morphogenesis and homeostasis. Micropipette based cell‐doublet experiments162, 172(see Figure 7(d)), liquid droplet assays,49 and laser ablation microscopy173 are some of the tools that can be used to estimate these forces. As an example, Campas et al.49 estimated acto‐myosin‐driven intercellular stresses at the cell–cell interface in the order of 1 nN/μm2 within embryonic tissues. Bambardekar et al.174 used optical trapping to pull on cell–cell adhesions and estimated forces in the order of 100 pN. Many computational modeling efforts are also underway to quantify relationships between cell–cell adhesions, tissue homeostasis and morphogenesis,167, 174, 175, 176 which can again be classified into particle‐based or continuum‐based models. For example, Bambardekar et al.174 proposed and validated a continuum viscoelastic constitutive equation to describe the force dynamics at epithelial cell–cell adhesions, while Coburn et al.176 used a particle‐based method, known as the vertex‐based method, to simulate the acto‐myosin contractile forces that transmit across the tissue through the cell–cell adhesions. Tightly coupled with experimental data, these models have helped to estimate tensions at the cell–cell adhesion interface167, 174, 175 and could therefore be adopted for studies on the role of cell–cell adhesions on single‐cell mechanobiology. Thanks to these many advances in measuring and modeling cell–cell adhesions and their acto‐myosin generated forces, research in this field is now focused on uncovering how these mechanical forces regulate cellular and tissue remodeling.
THE ROLE OF SIGNAL TRANSDUCTION PATHWAYS IN MODULATING CYTOSKELETAL MECHANICS
It is well established that numerous cellular processes ranging from cell motility177 to cell wound healing178 require coordinated action of acto‐myosin growth, contraction, and adhesion formation. For example, from a bulk perspective, motility requires three essential events, (1) protrusion of the cell front, (2) retraction of the cell rear, and (3) engagement of adhesions that serve as a molecular clutch to transmit these forces to the substrate. How though are these events coordinated? The historical view is that feed‐forward regulatory pathways that convert signaling information into action coordinate where and when these processes take place (Figure 8(a)). More recent observations and modeling however have suggested that complex feedbacks between cytoskeletal remodeling and its own regulation are at play (Figure 8(b)–(e)). Here we review how biochemical and biophysical events regulate cytoskeletal mechanics. This discussion will differ in nature from that in the preceding sections for two reasons. First, quantitative data of spatially localized signaling molecules (e.g., micromolar concentrations of Rac in a specific cell location) is not available. Second, mathematical models encoding signaling dynamics are predominantly described in the language of Reaction Diffusion Equations with models differing primarily in their molecular assumptions rather than mathematical formalisms. We chose here to focus on the role of signaling in cell behavior and why it is important to couple it to cell mechanics rather than the mathematical details of the myriad of associated models developed over recent decades. For comprehensive reviews of the mathematical modeling on this topic, see179, 180
Figure 8.
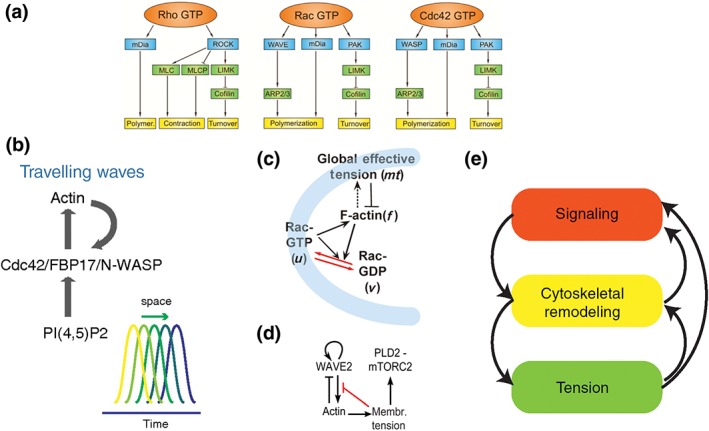
Signalling to cytoskeletal mechanics and back. (a) Well‐established biochemical pathways that link signalling molecules to the cytoskeletal machinery (Reprinted with permission from Ref 181. Copyright 2012 Frontiers) (b)‐(e) are new ideas of how cytoskeletal mechanics may feedback to signalling as well. The acronyms within each box refer to key signalling molecules involved in modulating cytoskeletal components such as actin (polymerisation, turnover) and myosin (contraction). ((b) reprinted with permission from Ref 182. Copyright 2013 National Academy of Sciences; (c) reprinted with permission from Ref 183. Copyright 2017 Public Library of Science; d reprinted with permission from Ref 184. Copyright 2016 Public Library of Congress).
Regulating Actin Growth and Protrusion
When discussing actin growth, it is important to distinguish between different populations of actin. Cortical actin forms part of the structural shell of the cell. Actin bundles, aligned arrays of actin filaments cross‐linked by, among other things, myosin motors, are responsible for contractile stresses in the cell and can generate protrusion in filapodia. Lamellipodial actin, located near the protrusive leading edge of a cell, is comprised of a dense, cross‐linked meshwork of filaments and is primarily responsible for broad lamellipodial protrusion at the leading edge of cells. While each of these structures contributes to force production in the cell, lamellipodial actin is the most studied and its regulation will be the focus here.
Numerous actin‐binding proteins regulate its nucleation and growth. In response to a signal, Arp2/3, formins, cofilin, and other actin binding proteins are recruited to the cell periphery.177 Their combined action increases the number of actin barbed ends and their rate of elongation, both of which contribute to force production. Arp2/3 in particular is critical to the generation of the highly branched, dendritic actin network found at the leading edge of motile cells. It is a dimer comprised of two sub‐units, Arp2 and Arp3, each of which closely resemble a G‐actin monomer.185 This close resemblance allows Arp2/3 to form a thermodynamically stable bond with an existing actin filament, generating a new growing filament branched from an existing filament at an angle of approximately 35°.186 It is thus a primarily regulator of the density of force producing filaments.
Cofilin, which binds to F‐actin and severs it into two new filaments, also serves to increase the number of growing barbed ends in this network. Spatial modeling has shown that Arp's preference for new actin filaments and cofilin's preference for older filaments leads to a synergy where they jointly produce more barbed ends than would be expected from simple addition of the two mechanisms.187 While these (and other) binding proteins increase the number of growing filaments, regulation of their growth rate, which depends on the availability of GTP G‐actin, also determines the potential for force production. Profilin, which catalyzes the exchange of GDP → GTP in monomeric G‐actin,188 has a critical role regulating this pool of polymerizable actin, and additional modeling has suggested that advective transport due to retrograde flow of actin can influence this pool as well.189
But how are these binding proteins recruited and restricted to the appropriate location? Upstream of these direct actin nucleators, the WASp (Wiskott–Aldrich Syndrome protein) family of proteins, including WASp, N‐WASp, SCAR/WAVE among others, regulate the recruitment of Arp2/3 to the cytoskeleton.190 While the mechanism of action differs among members of this family, each has domains that recruit Arp2/3 and G‐actin monomers, respectively. Moving another step up in the regulatory chain, the small Rho GTPases Rac and Cdc42, along with the phospholipids activate this family of proteins.191, 192 Cdc42 activates WASp193 while Rac in concert with PIP3 (and to a lesser extent PIP2194) activates WAVE. Thus, in response to external signaling, localization of the small GTPases and other signaling proteins leads to the activation of WASP/WAVE, which leads to recruitment of Arp2/3 and G‐actin.
While Arp2/3 is the star of the show in lamellipodial force production, it is dispensable for chemotaxis. Fibroblast cells depleted of Arp can still undergo chemotaxis, but with lower efficiency.195, 196 Formins appear to pick up the slack in the absence of Arp2/3. These actin‐binding proteins have an affinity for both barbed ends of filaments as well as profilin. They bring primed actin monomers into close proximity with barbed ends and increases the rate of filament elongation by a factor of up to 15.197 Unlike Arp2/3, which becomes incorporated into a filament, formins stay at the barbed end and continually add monomers, leading to linear growth. This promotes the formation of actin cables in yeast,198 stress fibers in HeLa cells,199 and filapodia in melanoma and HeLa cells.200 These filapodia, along with the myosin contractile arcs connecting them201 are thought to generate force production and protrusion in the absence of Arp2/3.196
The complexities of this regulation present a challenge for modeling and understanding how different pathways influence force generation. From a theoretical perspective, force generation is often associated with actin density. However, it is not the density of the actin network that is important, but rather how it grows. This growth depends on a number of interdependent factors including the type of actin (branched versus bundled), how new barbed ends are regulated (branching, severing, capping), and the speed of polymerization. Each of these factors is likely to have different influences on the broader behavior of cells.
Regulation of Myosin and its Interactions with Actin
A second important component in the migration of typical cells is the production of contractile forces behind the lamellipodium to aid retraction. As with F‐actin mediated protrusion, there are multiple contractile structures in the cell. Myosin can form filaments interleaved with actin filaments to produce contractile stress fibers.202 Alternatively, myosin can integrate into a dense, branched actin network resembling an active gel203 to generate a centripetal inward actin flow204 that both drives contraction of the rear as well as retrograde flow of actin. In either case, the central player in this process is the molecular motor myosin.
While there are numerous myosin isoforms, non‐muscle myosin II (conventional myosin, NMII) is the dominant form responsible for actin crosslinking and cytoskeletal contraction. NMII is found throughout the cell and can perform numerous actions. NMIIA promotes the formation of stress fibers in the lamella while NMIIB promotes the enlargement of those bundles.205 It has been shown to generate localized pockets of cell retraction at the leading edge of the cell201 and is known to be important for leading edge protrusion in Arp2/3 deficient cells.197 More generally however, it's action is primarily located in the rear of the cell206 where it promotes retraction.
Independent of its location of action, force generation by myosin requires its phosphorylation. Whereas there is a myriad of functionally different ways to regulate actin behavior (branching, severing, capping, etc.), regulation of NMII function appears converge on the phosphorylation of myosin light chain (MLC), which effectively activates NMII.
The two primary myosin binding proteins that phosphorylate MLC are Rho associated protein kinase (ROCK)207 and myosin light chain kinase (MLCK).208 ROCK's role in myosin regulation and migration is well established. The role of MLCK, which was first found to activate myosin in muscle cells, is still unclear. It was shown to modulate membrane tension in migratory smooth muscle cells, but was not required for migration.209 This is in line with observations in fibroblasts210 that MLCK is responsible for myosin activity at the cell periphery and influences membrane ruffling, while ROCK is responsible for myosin activity in the cell interior. Thus it is possible that ROCK plays a role in regulating retraction of the cell rear while, in some cases, MLCK regulates cell tension, which itself has a putative role as a mechanical signal regulating migration211, 212, 213). Whereas Ca+ signaling (more commonly associated with stimulating muscle contraction than cell migration) activates MLCK, the small GTPase Rho regulates ROCK.214 The mutual antagonism between Rho and protrusive regulators Rac and Cdc42 ensures spatial segregation myosin contraction to the rear of the cell.178, 215, 216, 217, 218
While signaling pathways primarily appear to converge on the activation of NMII, once activated, NMII appears to perform a number of different actions relevant to migration. Its role in leading retraction of the cell rear is clear. The potential of myosin in regulating tension however could be particularly significant as well given the suggested role of tension in regulating bulk cell behavior. Additionally, NMII has the capacity to generate either diffuse, isotropic stresses, if integrated homogeneously into an actin network, or more localized, anisotropic stresses if integrated into stress fibers.
Adhesion Regulation
The actions of protrusive and contractile force generation are not sufficient to generate translocation of the cell. It is well established that the pushing of growing actin filaments against the front of the cell drives retrograde flow from the front to the rear of the cell. Some friction or traction between the cell and its substrate is required to translate those forces into motion. This is where adhesions come into play. During migration, small nascent adhesions (NA) near the front edge (<0.5 μm) of the cell form. As the cell translocates forward these stay and place mature while they flow towards the interior of the cell. During this process, these NA's mature to form focal complexes (FC) which themselves mature into focal adhesions (FA).
The life cycle of a NA to a FA has been well studied. They are complex structures that are constructed in sequential fashion219 with over 500 proteins, kinases, motors, etc. found to associate with them.220 Rather than describe this molecular inventory and the undoubtedly long list of regulators involved in their assembly, we give an overview of the signaling pathways involved and discuss the role of FA's as regulators of the cytoskeleton themselves. It is well established that tension helps adhesions mature, but evidence also suggests that it is the structural formation of stress fibers rather than just tension that aids this process.221 Initial formation of a NA is independent of NMII,222 myosin generated tension and stress fiber formation, but maturation requires both. Furthermore, different myosins have different roles in their maturation with NMIIA responsible for the initial maturation and NMIIB responsible for further maturation.205
Given the role of stress fibers and myosin generated tension in adhesion maturation, it is unsurprising that the small GTPases have at least an indirect role in their formation.223, 224 Rho's function as a regulator of Myosin contractility makes it a natural candidate to regulate tension induced FA maturation. The role of Rac in FA regulation is less clear however. While it is required for efficient migration, evidence indicates it is not required for FA formation in fibroblast cells.225 In osteosarcoma cells on the other hand, Rac was recently found to phosphorylate and recruit NMIIA directly to the site of FA's,226 suggesting that NMIIA is a bona fida FA protein that is integrated in part through phosphorylation by Rac.
In addition to being the target of regulation, FA's have a role in regulating cytoskeletal dynamics as well. They provide a connection between the cell and the outside world, transducing both mechanical stresses as well as molecular signaling, both of which augment cytoskeletal dynamics. In fibroblasts, actin retrograde flow is fast in the lamellipodia and slower in the lamella, where FC and FA are present.227 When FA's are lost, the speed of retrograde flow becomes uniform due to the loss of traction to slow it. Furthermore, the formation of new NA's correlate with reduced retrograde velocity and advancement of the leading edge. Similarly in fast moving fish keratocytes, there is a gradient of flow velocity that decays away from the front and completely reverses from retrograde to anterograde206 as a result of the myosin generated centripetal flow in the rear.204 Thus, FA density and strength, which are modulated by a number of factors including ECM signaling density and mechanical stresses, modulates actin flows and force production within the cell.
They also have a role in molecular signaling to the cytoskeleton.228 Focal adhesion kinase (FAK) is a critical mechano‐sensor that translates integrin and ECM contacts into internal signaling. Among other functions, FAK activates PI3K, which in turn activates the small GTPase Rac,229 promoting actin growth. Similarly, deletion of FAK was shown to lead to increased Rho activity, cell rounding, and impaired motility.230 Through a parallel pathway, at sufficiently high levels, fibronectin has been observed to activate Rho with FA's as an intermediary.231, 232 Thus, FA's are a critical element in the signaling pathway, both receiving signals from and sending signals to the Rho GTPases and the cytoskeleton.
BROADER REGULATION OF CELL BULK BEHAVIOR THROUGH SIGNAL TRANSDUCTION PATHWAYS
While molecular interrogation has yielded extensive insights into the processes responsible for reorganization of the cytoskeleton during migration, one of the major challenges still to be addressed is to understand how these biophysical processes and their control contribute to broader morphology and migratory behavior of cells. In the context of migration, cells can exhibit different sensitivities to stimuli,233 different levels of persistence,234 and even different types of migration (amoeboid versus mesenchymal).235 Modeling has provided numerous insights into how various actin binding proteins interact with the cytoskeleton, and how the actions of those proteins coordinate different types of force production. But how do they contribute to the broader phenomenological behavior of cells?
Beyond controlling where and when acto‐myosin remodeling occurs, the Rho GTPases exert significant control over the broader type of motility cells exhibit. Evidence suggests Rho GTPase signaling provides cells with an intrinsic sensitivity to stimuli that can be modulated by either intrinsic or extrinsic factors.233 GTPase signaling has also been implicated in regulating the types of migration cells undergo. Enrichment of Rho was found to be associated with amoeboid migration, which is characterized by more rounded and contractile cells, while Rac enrichment is associated with mesenchymal migration, characterized by well‐defined protrusive lamellipodia.217, 235, 236 Similarly, expression levels of Rac and Rho were found to influence the morphology (large, small, polar, apolar) of cells.237 Cells also exhibit plasticity in these characteristics. Varying the levels of Rac and Rho expression toggle cells between amoeboid and mesenchymal migration238 and influence cell morphology,237 which were shown to be linked.239
In addition to modulating these features, interactions between GTPases and both upstream (ECM) and downstream (actin) signaling processes modulate bulk cell behavior. The feed‐forward model of regulation (depicted in Figure 8(a)) where ECM signaling initiates cascades involving GTPases and other signaling activity, which in turn regulates acto‐myosin remodeling (ECM → GTPases or other regulators → actin/myosin) is oversimplified. There are significant feedbacks between these regulatory layers that influence cell behavior. Dynamic feedbacks from actin back onto GTPase regulation lead to the generation of dynamic waves of actin polymerization that generate force upon colliding with the cell periphery240, 241, 242 (see, e.g., Figure 9(c)). Imaging studies have found that a number of actin binding proteins associate with these waves.243, 244 Furthermore, they exhibit excitable characteristics such as mutual annihilation (two waves converging suppress each other),245 with interactions between small GTPases and actin being reported to give rise to this excitability195 (Figure 9(d) for example depicts a relationship between waves of actin activity and FBP17 activity that are out of phase with FBP17 leading the actin wave). Mata240, 241 and Bernitt245 have further suggested that, in some cases, the unique nature of GTPases as a conserved excitable activator produces a global coupling between disparate regions of a wave. This type of ‘conserved excitable system’ has distinct wave propagation characteristics, such as size dependent propagation velocity, as observed in.245
Figure 9.
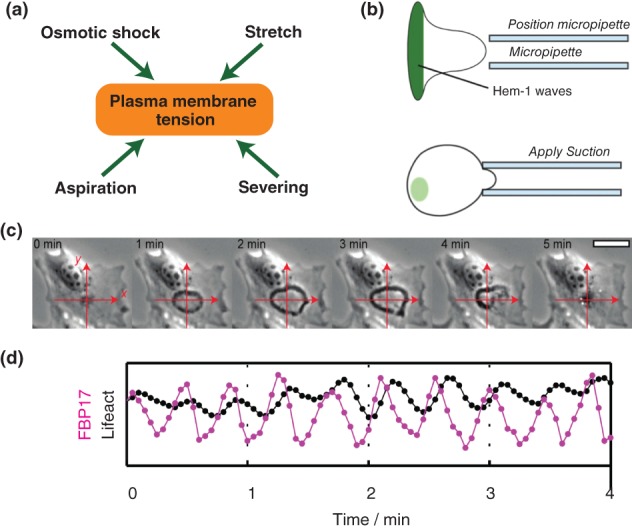
(a) Synopsis of some of the types of manipulations that have been performed to manipulate cell tension and investigate its effects. (b) Illustration of micropipette aspiration used to increase plasma membrane tension (Reprinted with permission from Ref 213. Copyright 2012 Elsevier Inc.). (c) Images of an actin wave (circular dorsal ruffle) expanding and subsequently contracting (scale bar corresponds to 25 μm, reprinted with permission from Ref 245. Copyright 2015 Public Library of Science). (d) Image depicting a phase relationship where actin waves are preceded by and appear to suppress FBP17 (a downstream effector of Cdc42) activity, suggesting a negative influence of actin on its own signaling (Reprinted with permission from Ref 182. Copyright 2013 National Academy of Sciences).
In addition to actin dependent feedbacks, substrate dependent feedbacks have been observed. While it is known that ECM signaling initiates a number of signaling cascades that regulate acto‐myosin reorganization, downstream growth or contraction of lamellipodia (which involve actin and myosin dynamics) influences the level of physical cell contact with the substrate and thus levels of ECM signaling. These feedbacks in turn influence the persistence of migration,246 which can be manipulated by augmenting the topography of the substrate or the density of fibronectin coating.
Feedbacks involving plasma membrane tension also have a role in regulating cell behavior. Physical manipulations such as stretch, osmotic shock, and aspiration have been applied to cells to assess its effects (Figure 9(a) and (b)). In one case, it was found that aspiration of one side of a cell by a micropipette very quickly suppresses polarity and signaling on the far side of the cell. A joint experiment and modeling study suggested this likely results from tension effects rather than chemical diffusion.213 The influence of tension on GTPase signaling has been further documented in muscle cells212 and neutrophil like HL‐60 cells.213
These feedbacks have been posited to play a role in helping cells navigate complex environments. In the case of wave like actin dynamics, it is proposed that the negative feedback associated with excitability helps cells navigate around barriers by extinguishing growth where there is contact with a barrier. Cell tension based feedbacks provide a potential mechanism for fast, long range communication that ensures only one protrusion is actively growing at a time.213 Mathematical modeling has also shown that tension mediated effects promote migratory persistence and make the cell more resistant to random perturbations.183 Thus, accounting for these mechanochemical feedbacks is necessary to account for real cell dynamics.
The challenge is that there are multiple locations in these signaling cascades that feedbacks could act. Tension could for example act at the level of regulators like GTPases or actin binding proteins. Furthermore, as is the case in actin regulation, there can be multiple qualitatively similar but quantitatively different ways to regulate force production. Finally, ECM mediated feedbacks require an accounting of the structure of ECM (particularly in 3D environments) and how cells interact with and perturb it. Addressing these challenges with a joint modeling and experimentation approach incorporating both mechanics and signaling will be required to link the molecular detail that has been uncovered in recent decades to cellular behavior.
DISCUSSION AND OUTLOOK
A variety of experimental techniques and mathematical models have advanced our understanding of single cell mechanics and cytoskeleton mechanobiology. While initially continuum, phenomenological models of the bulk mechanical properties were the norm, the availability of new, higher‐resolution experimental measurements are driving advances in mathematical modeling of cells that incorporate more microstructural details. Based on our extensive review of cell mechanobiology, we believe there are three broad directions in which to focus future efforts.
Microstructurally Informed Models of Cell Stiffness and Mechanics
While models of cell mechanics are prevalent, our understanding of and mathematical models of the contributions of microstructural components of the cell to its stiffness are far from complete. There are few studies that investigate the role of intermediate filaments or microtubules on bulk cell stiffness. Identifying and quantifying spatial heterogeneity in cell stiffness is critical to evaluating the mechanical stresses that the cell undergoes, which then feed signals to the nucleus.
One brute force approach involves identifying as many cytoskeletal proteins as possible and simulating their contributions to different cell contexts. Perhaps a more fruitful and less time‐consuming approach would be to develop a minimal model that includes several proteins that have been implicated in a relatively broad range of biological phenomena and to parameterize and validate the model with a wide range of experimental techniques. Certainly, the relative simplicity of the number of components that contribute to red blood cell mechanics has meant that such an approach has already proven successful.47 A more in‐depth understanding of the role of cytoskeletal components would also help identify and couple biochemical signal pathways to cytoskeletal mechanics remodeling.
Closer Ties between Signaling and Mechanics
As Figures 8 and 9 illustrate, cellular biology is regulated by continuous mechanistic links between biochemical signaling processes and cytoskeletal and cell‐wide mechanics. More often than one would like, mechanical and biochemical studies of cells are not performed in tandem. Disciplinary training is a limiting factor to more integrative studies but technological limitations also prevent tandem measurements of mechanical forces and chemical processes simultaneously. Some studies22, 32 show that cross‐disciplinary studies provide a more comprehensive picture of cellular mechanobiology than studies that only focus on one aspect.
There are several aspects of cell signaling to mechanics coupling that we have not discussed in this review that are worth mentioning here. A precise understanding of the ‘random’ myosin motor driven contractions of the cell require attention. Currently, microrheology methods are being used to measure these contractions and to remove them from analysis of cytoskeletal rheology.133 These processes have been suggested to play a role in sensing the local environment. An investigation into the role of biochemical processes, like calcium dynamics, could move us closer to determine the source of these random fluctuations. Another open question is how actin polymerization affects cell stiffness in single cell and tissue constructs.
Model Sharing and Standardization
Cellular mechanobiology is a burgeoning field of research with scientists across the STEM disciplines collaborating with biologists and life scientists to discover the fundamental laws that govern cell and tissue function. During the rapid growth of this field, many experimental measurement technologies and computational modeling methods have been brought to bear on a variety of biological contexts, such as the mechanobiology of malaria, cancer cell migration, stem cell differentiation and ostocyte and bone remodeling to name a few. The variety of models and parameters suggest that some efforts to consolidate these advances for future developments would be beneficial. Open‐source software packages exist for finite element models247 and particle based models.248 Model reproducibility and reuse has the enormous potential to accelerate our research by allowing colleagues to use our models as building blocks in their own research.
Towards Application
We have largely focused this review on the fundamental mechanisms that govern cellular and cytoskeletal mechanics. The motivation that underpins these advances is patient healthcare. Cellular mechanobiology regulates tissue function and therefore insights from our models must ultimately lead to clinical outcomes. While these are still early days, we anticipate that the insights we gain from our computational models will drive further development of new innovative technologies in drug testing and pharmacology. Indeed, as illustrated in Figure 2, experimental measurements need mathematical models to decipher the underlying mechanisms that regulate cell behavior. Models that are tightly coupled with experimental data will make the models more reliable and consequently accelerate innovations that are based on insights that can be gained from such models. When reviewing the modeling efforts to date it is clear that the field is already making advances in this direction.
Conflict of interest: The authors have declared no conflicts of interest for this article.
REFERENCES
- 1. Lim CT, Zhou EH, Quek ST. Mechanical models for living cells—a review. J Biomech 2006, 39:195–216. [DOI] [PubMed] [Google Scholar]
- 2. Sun M, Zaman MH. Modeling, signaling and cytoskeleton dynamics: integrated modeling‐experimental frameworks in cell migration. WIREs Syst Biol Med 2016, 9:e1365–e1313. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Mak M, Spill F, Kamm RD, Zaman MH. Single‐cell migration in complex microenvironments: mechanics and signaling dynamics. J Biomech Eng 2016, 138:021004–021008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Danuser G, Allard J, Mogilner A. Mathematical modeling of eukaryotic cell migration: insights beyond experiments. Annu Rev Cell Dev Biol 2013, 29:501–528. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Banerjee N, Park J. Modeling and simulation of biopolymer networks: classification of the cytoskeleton models according to multiple scales. Korean J Chem Eng 2015, 32:1207–1217. [Google Scholar]
- 6. Yamaoka H, Matsushita S, Shimada Y, Adachi T. Multiscale modeling and mechanics of filamentous actin cytoskeleton. Biomech Model Mechanobiol 2012, 11:291–302. [DOI] [PubMed] [Google Scholar]
- 7. Broedersz CP, MacKintosh FC. Modeling semiflexible polymer networks. Rev Mod Phys 2014, 86:995–1036. [Google Scholar]
- 8. Mogilner A. On the edge: modeling protrusion. Curr Opin Cell Biol 2006, 18:32–39. [DOI] [PubMed] [Google Scholar]
- 9. Holmes WR, Edelstein‐Keshet L. A Comparison of Computational Models for Eukaryotic Cell Shape and Motility. PLoS Comput Biol 2012, 8:e1002793. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Gladilin E, Gonzalez P, Eils R. Dissecting the contribution of actin and vimentin intermediate filaments to mechanical phenotype of suspended cells using high‐throughput deformability measurements and computational modeling. J Biomech 2014, 47:2598–2605. [DOI] [PubMed] [Google Scholar]
- 11. Pivkin IV, Peng Z, Karniadakis GE, Buffet PA, Dao M, Suresh S. Biomechanics of red blood cells in human spleen and consequences for physiology and disease. Proc Natl Acad Sci 2016, 113:7804–7809. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Mak M, Zaman MH, Kamm RD, Kim T. Interplay of active processes modulates tension and drives phase transition in self‐renewing, motor‐driven cytoskeletal networks. Nat Commun 2016, 7:10323. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Zienkiewicz OC, Taylor RL. The Finite Element Method: Solid Mechanics. Oxford, UK: Butterworth‐Heinemann; 2000. [Google Scholar]
- 14. Shao D, Levine H, Rappel W‐J. Coupling actin flow, adhesion, and morphology in a computational cell motility model. Proc Natl Acad Sci USA 2012, 109:6851–6856. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Feric M, Brangwynne CP. A nuclear F‐actin scaffold stabilizes ribonucleoprotein droplets against gravity in large cells. Nat Cell Biol 2013, 15:1253–1259. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Taber LA, Shi Y, Yang L, Bayly PV. A poroelastic model for cell crawling including mechanical coupling between cytoskeletal contraction and actin polymerization. J Mech Mater Struct 2011, 6:569–589. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Strychalski W, Copos CA, Lewis OL, Guy RD. A poroelastic immersed boundary method with applications to cell biology. J Comput Phys 2015, 282:77–97. [Google Scholar]
- 18. Herant M, Dembo M. Form and function in cell motility: from fibroblasts to keratocytes. Biophys J 2010, 98:1408–1417. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Bidhendi AJ, Korhonen RK. A finite element study of micropipette aspiration of single cells: effect of compressibility. Comput Math Methods Med 2012, 2012:192618–192619. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Carlsson AE. Actin dynamics: from nanoscale to microscale. Annu Rev Biophys 2010, 39:91–110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Keren K, Yam PT, Kinkhabwala A, Mogilner A, Theriot JA. Intracellular fluid flow in rapidly moving cells. Nat Cell Biol 2009, 11:1219–1224. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Moeendarbary E, Valon L, Fritzsche M, Harris AR, Moulding DA, Thrasher AJ, Stride E, Mahadevan L, Charras GT. The cytoplasm of living cells behaves as a poroelastic material. Nat Mater 2013, 12:253–261. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Knothe Tate ML, Gunning PW, Sansalone V. Emergence of form from function—Mechanical engineering approaches to probe the role of stem cell mechanoadaptation in sealing cell fate. BioArchitecture 2016, 6:85–103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Unterberger MJ, Schmoller KM, Wurm C, Bausch AR, Holzapfel GA. Viscoelasticity of cross‐linked actin networks: experimental tests, mechanical modeling and finite‐element analysis. Acta Biomater 2013, 9:7343–7353. [DOI] [PubMed] [Google Scholar]
- 25. Pivkin IV, Caswell B, Karniadakis GE. Dissipative particle dynamics. Rev Comput Chem 2011, 27:85–110. [Google Scholar]
- 26. Ye T, Phan‐Thien N, LIM CT. Particle‐based simulations of red blood cells—a review. J Biomech 2016, 49:2255–2266. [DOI] [PubMed] [Google Scholar]
- 27. Keaveny EE, Pivkin IV, Maxey M, Em Karniadakis G. A comparative study between dissipative particle dynamics and molecular dynamics for simple‐ and complex‐geometry flows. J Chem Phys 2005, 123:104107. [DOI] [PubMed] [Google Scholar]
- 28. Erban R. From molecular dynamics to Brownian dynamics. Proc R Soc A 2014, 470:20140036–20140036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Chen JC, Kim AS. Brownian dynamics, molecular dynamics, and Monte Carlo modeling of colloidal systems. Adv Colloid Interface Sci 2004, 112:159–173. [DOI] [PubMed] [Google Scholar]
- 30. Zhang Y, Huang C, Kim S, Golkaram M, Dixon MWA, Tilley L, Li J, Zhang S, Suresh S. Multiple stiffening effects of nanoscale knobs on human red blood cells infected with Plasmodium falciparum malaria parasite. Proc Natl Acad Sci 2015, 112:6068–6073. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Kim T, Hwang W, Lee H, Kamm RD. Computational analysis of viscoelastic properties of crosslinked actin networks. PLoS Comp Biol 2009, 5:e1000439. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Luo T, Mohan K, Iglesias PA, Robinson DN. Molecular mechanisms of cellular mechanosensing. Nat Mater 2013, 12:1064–1071. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Lei H, Caswell B, Karniadakis GE. Direct construction of mesoscopic models from microscopic simulations. Phys Rev E Stat Nonlin Soft Matter Phys 2010, 81:026704. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. Liu MB, Liu GR. Smoothed particle hydrodynamics (SPH): an overview and recent developments. Arch Computat Methods Eng 2010, 17:25–76. [Google Scholar]
- 35. Gokhin DS, Nowak RB, Khoory JA, Piedra ADL, Ghiran IC, Fowler VM. Dynamic actin filaments control the mechanical behavior of the human red blood cell membrane. Mol Biol Cell 2015, 26:1699–1710. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36. Knowles DW, Tilley L, Mohandas N, Chasis JA. Erythrocyte membrane vesiculation: model for the molecular mechanism of protein sorting. Proc Natl Acad Sci 1997, 94:12969–12974. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. Pravincumar P, Bader DL, Knight MM. Viscoelastic cell mechanics and actin remodelling are dependent on the rate of applied pressure. PLoS One 2012, 7:e43938. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38. Brugués J, Maugis B, Casademunt J, Nassoy P, Amblard F, Sens P. Dynamical organization of the cytoskeletal cortex probed by micropipette aspiration. Proc Natl Acad Sci USA 2010, 107:15415–15420. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39. Knight MM, Toyoda T, Lee DA, Bader DL. Mechanical compression and hydrostatic pressure induce reversible changes in actin cytoskeletal organisation in chondrocytes in agarose. J Biomech 2006, 39:1547–1551. [DOI] [PubMed] [Google Scholar]
- 40. Chang H, Tate M. Structure‐function relationships in the stem cell's mechanical world B: emergent anisotropy of the cytoskeleton correlates to volume and shape changing stress exposure. Mol Cell Biomech 2011, 8:297–318. [PMC free article] [PubMed] [Google Scholar]
- 41. Bressloff PC. Stochastic Processes in Cell Biology. Switzerland: Springer; 2014. [Google Scholar]
- 42. Rajagopal V, Bass G, Walker CG, Crossman DJ, Petzer A, Hickey A, Siekmann I, Hoshijima M, Ellisman MH, Crampin EJ, et al. Examination of the effects of heterogeneous organization of RyR clusters, myofibrils and mitochondria on Ca2+ release patterns in cardiomyocytes. PLoS Comp Biol 2015, 11:e1004417. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43. Barnhart EL, Lee KC, Keren K, Mogilner A. An adhesion‐dependent switch between mechanisms that determine motile cell shape. PLoS Biol 2011, 9:e1001059. https://doi.org/10.1371/journal.pbio.1001059.g011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44. Doubrovinski K, Kruse K. Cell motility resulting from spontaneous polymerization waves. Phys Rev Lett 2011, 107:258103. [DOI] [PubMed] [Google Scholar]
- 45. Zhou EH, Xu F, Quek ST, Lim CT. A power‐law rheology‐based finite element model for single cell deformation. Biomech Model Mechanobiol 2012, 11:1075–1084. [DOI] [PubMed] [Google Scholar]
- 46. Gladilin E, Micoulet A, Hosseini B, Rohr K, Spatz J, Eils R. 3D finite element analysis of uniaxial cell stretching: from image to insight. Phys Biol 2007, 4:104–113. [DOI] [PubMed] [Google Scholar]
- 47. Peng Z, Li X, Pivkin IV, Dao M, Karniadakis GE, Suresh S. Lipid bilayer and cytoskeletal interactions in a red blood cell. Proc Natl Acad Sci 2013, 110:13356–13361. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48. Kim T, Hwang W, Kamm RD. Computational analysis of a cross‐linked actin‐like network. Exp Mech 2009, 49:91–104. [Google Scholar]
- 49. Campàs O, Mammoto T, Hasso S, Sperling RA, O'Connell D, Bischof AG, Maas R, Weitz DA, Mahadevan L, Ingber DE. Quantifying cell‐generated mechanical forces within living embryonic tissues. Nat Methods 2013, 11:183–189. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50. Serwane F, Mongera A, Rowghanian P, Kealhofer DA, Lucio AA, Hockenbery ZM, Campàs O. vivo quantification of spatially varying mechanical properties in developing tissues. Nat Methods 2017, 14:181–186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51. Mills JP, Qie L, Dao M, Lim CT, Suresh S. Nonlinear elastic and viscoelastic deformation of the human red blood cell with optical tweezers. Mech Chem Biosyst 2004, 1:169–180. [PubMed] [Google Scholar]
- 52. Trickey WR, Lee GM, Guilak F. Viscoelastic properties of chondrocytes from normal and osteoarthritic human cartilage. J Orthop Res 2000, 18:891–898. [DOI] [PubMed] [Google Scholar]
- 53. Shirai A, Masuda S. Numerical simulation of passage of a neutrophil through a rectangular channel with a moderate constriction. PLoS One 2013, 8:e59416. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54. Teo SK, Parker KH, Chiam KH. Viscoelastic finite‐element modelling of neutrophil deformation in a tapered micropipette. In: ASME 2008 Summer Bioengineering Conference, Parts A and B 2008:183–184. https://doi.org/10.1115/SBC2008‐191099.
- 55. Herant M, Marganski WA, Dembo M. The mechanics of neutrophils: synthetic modeling of three experiments. Biophys J 2003, 84:3389–3413. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56. Song MJ, Brady‐Kalnay SM, McBride SH, Phillips‐Mason P, Dean D, Knothe Tate ML. Mapping the mechanome of live stem cells using a novel method to measure local strain fields In situ at the fluid‐cell interface. PLoS One 2012, 7:e43601. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57. Dokukina IV, Gracheva ME. A model of fibroblast motility on substrates with different rigidities. Biophys J 2010, 98:2794–2803. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58. Fernández P, Pullarkat PA, Ott A. A master relation defines the nonlinear viscoelasticity of single fibroblasts. Biophys J 2006, 90:3796–3805. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59. Stéphanou A, Chaplain MAJ, TRACQUI P. A mathematical model for the dynamics of large membrane deformations of isolated fibroblasts. Bull Math Biol 2004, 66:1119–1154. [DOI] [PubMed] [Google Scholar]
- 60. Cartagena A, Raman A. Local viscoelastic properties of live cells investigated using dynamic and quasi‐static atomic force microscopy methods. Biophys J 2014, 106:1033–1043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61. Milner JS, Grol MW, Beaucage KL, Dixon SJ, Holdsworth DW. Finite element modeling of viscoelastic cells during high‐frequency cyclic strain. JFB 2012, 3:209–224. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62. Karcher H, Lammerding J, Huang H, Lee RT, Kamm RD, Kaazempur‐Mofrad MR. A three‐dimensional viscoelastic model for cell deformation with experimental verification. Biophys J 2003, 85:3336–3349. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63. Gizzi A, Ruiz‐Baier R, Rossi S, Laadhari A, Cherubini C, Filippi S. A three‐dimensional continuum model of active contraction in single cardiomyocytes. Model Heart Circul Syst 2015, 14:157–176. [Google Scholar]
- 64. Hecht FM, Rheinlaender J, Schierbaum N, Goldmann WH, Fabry B, Schäffer T. Imaging viscoelastic properties of live cells by AFM: power‐law rheology on the nanoscale. Soft Matter 2015, 11:4584–4591. [DOI] [PubMed] [Google Scholar]
- 65. Cai P, Mizutani Y, Tsuchiya M, Maloney JM, Fabry B, Van Vliet KJ, Okajima T. Quantifying cell‐to‐cell variation in power‐law rheology. Biophys J 2013, 105:1093–1102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66. Kollmannsberger P, Fabry B. Linear and nonlinear rheology of living cells. Annu Rev Mat Res 2011, 41:75–97. [Google Scholar]
- 67. Fabry B, Maksym G, Butler J, Glogauer M, Navajas D, Fredberg J. Scaling the microrheology of living cells. Phys Rev Lett 2001, 87:148102. [DOI] [PubMed] [Google Scholar]
- 68. Shih W, Yamada S. Myosin IIA dependent retrograde flow drives 3D cell migration. Biophys J 2010, 98:L29–L31. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69. Alt W, Dembo M. Cytoplasm dynamics and cell motion: two‐phase flow models. Math Biosci 1999, 156:207–228. [DOI] [PubMed] [Google Scholar]
- 70. Théry M, Pépin A, Dressaire E, Chen Y, Bornens M. Cell distribution of stress fibres in response to the geometry of the adhesive environment. Cell Motil Cytoskeleton 2006, 63:341–355. [DOI] [PubMed] [Google Scholar]
- 71. Discher DE, Janmey P, Wang Y‐L. Tissue cells feel and respond to the stiffness of their substrate. Science 2005, 310:1139–1143. [DOI] [PubMed] [Google Scholar]
- 72. Doyle AD, Petrie RJ, Kutys ML, Yamada KM. Dimensions in cell migration. Curr Opin Cell Biol 2013, 25:642–649. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73. Friedl P, Sahai E, Weiss S, Yamada M. New dimensions in cell migration. Nat Rev Mol Cell Biol 2012, 13:743–747. [DOI] [PubMed] [Google Scholar]
- 74. Kojima H, Ishijima A, Yanagida T. Direct measurement of stiffness of single actin filaments with and without tropomyosin by in vitro nanomanipulation. Proc Natl Acad Sci 1994, 91:12962–12966. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75. Huxley HE, Stewart A, Sosa H, Irving T. X‐ray diffraction measurements of the extensibility of actin and myosin filaments in contracting muscle. Biophys J 1994, 67:2411–2421. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76. Higuchi H, Yanagida T, Goldman YE. Compliance of thin filaments in skinned fibers of rabbit skeletal muscle. Biophys J 1995, 69:1000–1010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77. Grazi E, Cintio O, Trombetta G. On the mechanics of the actin filament: the linear relationship between stiffness and yield strength allows estimation of the yield strength of thin filament in vivo. J Muscle Res Cell Motil 2004, 25:103–105. [DOI] [PubMed] [Google Scholar]
- 78. Kishino A, Yanagida T. Force measurements by micromanipulation of a single actin filament by glass needles. Nature 1988, 334:74–76. [DOI] [PubMed] [Google Scholar]
- 79. Dupuis DE, Guilford WH, Wu J, Warshaw DM. Actin filament mechanics in the laser trap. J Muscle Res Cell Motil 1997, 18:17–30. [DOI] [PubMed] [Google Scholar]
- 80. Gittes F, Mickey B, Nettleton J. Flexural rigidity of microtubules and actin filaments measured from thermal fluctuations in shape. J Cell Biol 1993, 120:923–934. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81. Yasuda R, Miyata H, Kinosita K. Direct measurement of the torsional rigidity of single actin filaments. J Mol Biol 1996, 263:227–236. [DOI] [PubMed] [Google Scholar]
- 82. Tsuda Y, Yasutake H, Ishijima A, Yanagida T. Torsional rigidity of single actin filaments and actin–actin bond breaking force under torsion measured directly by in vitro micromanipulation. Proc Natl Acad Sci 1996, 93:12937–12942. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83. Herrmann H, Aebi U. Intermediate filaments: structure and assembly. Cold Spring Harb Perspect Biol 2016, 8:a018242. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84. Hawkins T, Mirigian M, Selcuk Yasar M, Ross JL. Mechanics of microtubules. J Biomech 2010, 43:23–30. [DOI] [PubMed] [Google Scholar]
- 85. Janmey PA, Euteneuer U, Traub P, Schliwa M. Viscoelastic properties of vimentin compared with other filamentous biopolymer networks. J Cell Biol 1991, 113:155–160. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86. Fletcher DA, Mullins RD. Cell mechanics and the cytoskeleton. Nature 2009, 463:485–492. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87. Schaap IAT, Carrasco C, de Pablo PJ, MacKintosh FC, Schmidt CF. Elastic response, buckling, and instability of microtubules under radial indentation. Biophys J 2006, 91:1521–1531. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 88. Kikumoto M, Kurachi M, Tosa V, Tashiro H. Flexural rigidity of individual microtubules measured by a buckling force with optical traps. Biophys J 2006, 90:1687–1696. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 89. Buehler MJ. Mechanical players—The role of intermediate filaments in cell mechanics and organization. Biophys J 2013, 105:1733–1734. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 90. Qin Z, Buehler MJ, Kreplak L. A multi‐scale approach to understand the mechanobiology of intermediate filaments. J Biomech 2010, 43:15–22. [DOI] [PubMed] [Google Scholar]
- 91. Ackbarow T, Buehler MJ. Superelasticity, energy dissipation and strain hardening of vimentin coiled‐coil intermediate filaments: atomistic and continuum studies. J Mater Sci 2007, 42:8771–8787. [Google Scholar]
- 92. Kreplak L, Herrmann H, Aebi U. Tensile properties of single desmin intermediate filaments. Biophys J 2008, 94:2790–2799. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 93. Qin Z, Kreplak L, Buehler MJ. Nanomechanical properties of vimentin intermediate filament dimers. Nanotechnology 2009, 20:425101. [DOI] [PubMed] [Google Scholar]
- 94. Kreplak L, Bär H, Leterrier JF, Herrmann H, Aebi U. Exploring the mechanical behavior of single intermediate filaments. J Mol Biol 2005, 354:569–577. [DOI] [PubMed] [Google Scholar]
- 95. Charrier EE, Janmey PA. Mechanical properties of intermediate filament proteins. Methods Enzymol 2016, 568:35–57. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 96. Liew KM, Xiang P, Zhang LW. Mechanical properties and characteristics of microtubules: a review. Composit Struct 2015, 123:98–108. [Google Scholar]
- 97. Salbreux G, Charras G, Paluch E. Actin cortex mechanics and cellular morphogenesis. Trends Cell Biol 2012, 22:536–545. [DOI] [PubMed] [Google Scholar]
- 98. Janmey PA, Hvidt S, Käs J, Lerche D, Maggs A, Sackmann E, Schliwa M, Stossel TP. The mechanical properties of actin gels. Elastic modulus and filament motions. J Biol Chem 1994, 269:32503–32513. [PubMed] [Google Scholar]
- 99. Gardel ML, Kasza KE, Brangwynne CP, Liu J, Weitz DA. Mechanical response of cytoskeletal networks. Methods Cell Biol 2008, 89:487–519. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 100. Jensen MH, Morris EJ, Weitz DA. Mechanics and dynamics of reconstituted cytoskeletal systems. Biochim Biophys Acta 2015, 1853:3038–3042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 101. Tseng Y, Kole TP, Lee JSH, Fedorov E, Almo SC, Schafer BW, Wirtz D. How actin crosslinking and bundling proteins cooperate to generate an enhanced cell mechanical response. Biochem Biophys Res Commun 2005, 334:183–192. [DOI] [PubMed] [Google Scholar]
- 102. Esue O, Tseng Y, Wirtz D. α‐actinin and filamin cooperatively enhance the stiffness of actin filament networks. PLoS One 2009, 4:e4411. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 103. Bendix PM, Koenderink GH, Cuvelier D, Dogic Z, Koeleman BN, Brieher WM, Field CM, Mahadevan L, Weitz DA. A quantitative analysis of contractility in active cytoskeletal protein networks. Biophys J 2008, 94:3126–3136. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 104. Kamioka H, Sugawara Y, Honjo T, Yamashiro T, Takano‐Yamamoto T. Terminal differentiation of osteoblasts to osteocytes is accompanied by dramatic changes in the distribution of actin‐binding proteins. J Bone Miner Res 2004, 19:471–478. [DOI] [PubMed] [Google Scholar]
- 105. Winkelman JD, Suarez C, Hocky GM, Harker AJ, Morganthaler AN, Christensen JR, Voth GA, Bartles JR, Kovar DR. Fascin‐ and α‐actinin‐bundled networks contain intrinsic structural fatures that drive protein sorting. Curr Biol 2016, 26:2697–2706. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 106. Skau CT, Courson DS, Bestul AJ, Winkelman JD, Rock RS, Sirotkin V, Kovar DR. Actin filament bundling by fimbrin is important for endocytosis, cytokinesis, and polarization in fission yeast. J Biol Chem 2011, 286:26964–26977. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 107. Ding WY, Ong HT, Hara Y, Wongsantichon J, Toyama Y, Robinson RC, Nédélec F, Zaidel‐Bar R. Plastin increases cortical connectivity to facilitate robust polarization and timely cytokinesis. J Cell Biol 2017, 216:1371–1386. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 108. Michelot A, Drubin DG. Building distinct actin filament networks in a common cytoplasm. Curr Biol 2011, 21:R560–R569. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 109. Chen G, Hou Z, Gulbranson D, Thomson JA. Actin‐myosin contractility is responsible for the reduced viability of dissociated human embryonic stem cells. Cell Stem Cell 2010, 7:240–248. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 110. Kim T, Hwang W, Kamm RD. Dynamic role of cross‐linking proteins in actin rheology. Biophys J 2011, 101:1597–1603. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 111. Müller KW, Cyron CJ. Computational analysis of morphologies and phase transitions of cross‐linked, semi‐flexible polymer networks. Proc R Soc A 2015, 471:20150332–20150349. [Google Scholar]
- 112. Borau C, Kim T, Bidone T, García‐Aznar JM, Kamm RD. Dynamic mechanisms of cell rigidity sensing: insights from a computational model of actomyosin networks. PLoS One 2012, 7:e49174. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 113. Mandelkow E, Mandelkow EM. Microtubules and microtubule‐associated proteins. Curr Opin Cell Biol 1995, 7:72–81. [DOI] [PubMed] [Google Scholar]
- 114. Lopez BJ, Valentine MT. Molecular control of stress transmission in the microtubule cytoskeleton. Biochim Biophys Acta Mol Cell Res 2015, 1853:3015–3024. [DOI] [PubMed] [Google Scholar]
- 115. Yang Y, Bai M, Klug WS, Levine AJ, Valentine MT. Microrheology of highly crosslinked microtubule networks is dominated by force‐induced crosslinker unbinding. Soft Matter 2012, 9:383–393. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 116. Lin Y‐C, Koenderink GH, MacKintosh FC, Weitz DA. Viscoelastic properties of microtubule networks. Macromolecules 2007, 40:7714–7720. [Google Scholar]
- 117. Koester S, Lin Y‐C, Herrmann H, Weitz DA. Nanomechanics of vimentin intermediate filament networks. Soft Matter 2010, 6:1910–1914. [Google Scholar]
- 118. Lin Y‐C, Broedersz CP, Rowat AC, Wedig T, Herrmann H, MacKintosh FC, Weitz DA. Divalent Cations Crosslink Vimentin Intermediate Filament Tail Domains to Regulate Network Mechanics. J Mol Biol 2010, 399:637–644. [DOI] [PubMed] [Google Scholar]
- 119. Kasas S, Kis A, Riederer BM, Forró L, Dietler G, Catsicas S. Mechanical properties of microtubules explored using the finite elements method. Chemphyschem 2004, 5:252–257. [DOI] [PubMed] [Google Scholar]
- 120. Civalek Ö, Demir C. A simple mathematical model of microtubules surrounded by an elastic matrix by nonlocal finite element method. Appl Math Comput 2016, 289:335–352. [Google Scholar]
- 121. Daneshmand F, Farokhi H, Amabili M. A higher‐order mathematical modeling for dynamic behavior of protein microtubule shell structures including shear deformation and small‐scale effects. Math Biosci 2014, 252:67–82. [DOI] [PubMed] [Google Scholar]
- 122. Deriu MA, Soncini M, Orsi M, Patel M, Essex JW, Montevecchi FM, Redaelli A. Anisotropic Elastic Network Modeling of Entire Microtubules. Biophys J 2010, 99:2190–2199. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 123. Bouchet BP, Akhmanova A. Microtubules in 3D cell motility. J Cell Sci 2017, 130:39–50. [DOI] [PubMed] [Google Scholar]
- 124. Allain P, Kervrann C. Physical modeling of microtubules network. J Phys Conf Ser 2014, 542:012005. [Google Scholar]
- 125. Buxton GA, Siedlak SL, Perry G, Smith MA. Mathematical modeling of microtubule dynamics: insights into physiology and disease. Prog Neurobiol 2010, 92:478–483. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 126. Bertaud J, Qin Z, Buehler MJ. Intermediate filament‐deficient cells are mechanically softer at large deformation: a multi‐scale simulation study. Acta Biomater 2010, 6:2457–2466. [DOI] [PubMed] [Google Scholar]
- 127. Kwon RY, Lew AJ, Jacobs CR. A microstructurally informed model for the mechanical response of three‐dimensional actin networks. Comput Methods Biomech Biomed Engin 2008, 11:407–418. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 128. Fallqvist B, Kroon M. Constitutive modelling of composite biopolymer networks. J Theor Biol 2016, 395:51–61. [DOI] [PubMed] [Google Scholar]
- 129. Mendez MG, Restle D, Janmey PA. Vimentin enhances cell elastic behavior and protects against compressive stress. Biophys J 2014, 107:314–323. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 130. Rathje L‐SZ, Nordgren N, Pettersson T, Rönnlund D, Widengren J, Aspenström P, Gad AKB. Oncogenes induce a vimentin filament collapse mediated by HDAC6 that is linked to cell stiffness. Proc Natl Acad Sci 2014, 111:1515–1520. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 131. Guo M, Ehrlicher AJ, Mahammad S, Fabich H, Jensen MH, Moore JR, Fredberg JJ, Goldman RD, Weitz DA. The role of vimentin intermediate filaments in cortical and cytoplasmic mechanics. Biophys J 2013, 105:1562–1568. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 132. Swift J, Ivanovska IL, Buxboim A, Harada T, Dingal PCDP, Pinter J, Pajerowski JD, Spinler KR, Shin J‐W, Tewari M, et al. Nuclear lamin‐A scales with tissue stiffness and enhances matrix‐directed differentiation. Science 2013, 341:1240104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 133. Guo M, Ehrlicher AJ, Jensen MH, Renz M, Moore JR, Goldman RD, Lippincott Schwartz J, MacKintosh FC, Weitz DA. Probing the stochastic, motor‐driven properties of the cytoplasm using force spectrum microscopy. Cell 2014, 158:822–832. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 134. Scarcelli G, Polacheck WJ, Nia HT, Patel K, Grodzinsky AJ, Kamm RD, Yun SH. Noncontact three‐dimensional mapping of intracellular hydromechanical properties by Brillouin microscopy. Nat Methods 2015, 12:1132–1134. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 135. Münter S, Enninga J, Vazquez‐Martinez R, Delbarre E, David‐Watine B, Nehrbass U, Shorte SL. Actin polymerisation at the cytoplasmic face of eukaryotic nuclei. BMC Cell Biol 2006, 7:23. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 136. Wear MA, Schafer DA, Cooper JA. Actin dynamics: assembly and disassembly of actin networks. Curr Biol 2000, 10:R891–R895. [DOI] [PubMed] [Google Scholar]
- 137. Mogilner A, Keren K. The shape of motile cells. Curr Biol 2009, 19:R762–R771. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 138. Footer MJ, Kerssemakers JWJ, Theriot JA, Dogterom M. Direct measurement of force generation by actin filament polymerization using an optical trap. Proc Natl Acad Sci 2007, 104:2181–2186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 139. Parekh SH, Chaudhuri O, Theriot JA, Fletcher DA. Loading history determines the velocity of actin‐network growth. Nat Cell Biol 2005, 7:1219–1223. [DOI] [PubMed] [Google Scholar]
- 140. Marcy Y, Prost J, Carlier MF, Sykes C. Forces generated during actin‐based propulsion: a direct measurement by micromanipulation. Proc Natl Acad Sci 2004, 101:5992–5997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 141. Zhu J, Mogilner A. Mesoscopic model of actin‐based propulsion. PLoS Comput Biol 2012, 8:e1002764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 142. Zhu J, Mogilner A. Comparison of cell migration mechanical strategies in three‐dimensional matrices: a computational study. Interface Focus 2016, 6:20160040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 143. Kim JS, Sun SX. Continuum modeling of forces in growing viscoelastic cytoskeletal networks. J Theor Biol 2009, 256:596–606. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 144. Jones GW, Chapman SJ. Modeling growth in biological materials. SIAM Rev 2012, 54:52–118. [Google Scholar]
- 145. Zimmermann J, Brunner C, Enculescu M, Goegler M, Ehrlicher A, Käs J, Falcke M. Actin filament elasticity and retrograde flow shape the force‐velocity relation of motile cells. Biophys J 2012, 102:287–295. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 146. Blanchoin L, Boujemaa‐Paterski R, Sykes C, Plastino J. Actin dynamics, architecture, and mechanics in cell motility. Physiol Rev 2014, 94:235–263. [DOI] [PubMed] [Google Scholar]
- 147. De La Cruz EM, Martiel J‐L, Blanchoin L. Mechanical heterogeneity favors fragmentation of strained actin filaments. Biophys J 2015, 108:2270–2281. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 148. De La Cruz EM, Gardel ML. Actin mechanics and fragmentation. J Biol Chem 2015, 290:17137–17144. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 149. Jung W, Murrell MP, Kim T. F‐Actin fragmentation induces distinct mechanisms of stress relaxation in the actin cytoskeleton. ACS Macro Lett 2016, 5:641–645. [DOI] [PubMed] [Google Scholar]
- 150. Trichet L, Murrell MP, Kim T . Evidence of a large‐scale mechanosensing mechanism for cellular adaptation to substrate stiffness. Proc Natl Acad Sci 2012, 109:6933–6938. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 151. Gardel ML, Schneider IC, Aratyn‐Schaus Y, Waterman CM. Mechanical integration of actin and adhesion dynamics in cell migration. Annu Rev Cell Dev Biol 2010, 26:315–333. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 152. Yeung T, Schneider IC, Aratyn‐Schaus Y, Waterman CM . Effects of substrate stiffness on cell morphology, cytoskeletal structure, and adhesion. Cell Motil Cytoskeleton 2005, 60:24–34. [DOI] [PubMed] [Google Scholar]
- 153. Roca‐Cusachs P , Georges PC, Flanagan LA, Marg B, Ortiz M, Funaki M, Zahir N, Ming W, Weaver V, Janmey PA. Integrin‐dependent force transmission to the extracellular matrix by alpha‐actinin triggers adhesion maturation. Proc Natl Acad Sci 2013, 110:E1361–E1370. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 154. DiMilla PA, Barbee K, Lauffenburger DA. Mathematical model for the effects of adhesion and mechanics on cell migration speed. Biophys J 1991, 60:15–37. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 155. Colin‐York H, Eggeling C, Fritzsche M. Dissection of mechanical force in living cells by super‐resolved traction force microscopy. Nat Protoc 2017, 12:783–796. [DOI] [PubMed] [Google Scholar]
- 156. Schwarz US, Soiné JRD. Traction force microscopy on soft elastic substrates: a guide to recent computational advances. Biochim Biophys Acta 2015, 1853:3095–3104. [DOI] [PubMed] [Google Scholar]
- 157. Legant WR, Miller JS, Blakely BL, Cohen DM, Genin GM, Chen CS. Measurement of mechanical tractions exerted by cells in three‐dimensional matrices. Nat Methods 2010, 7:969–971. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 158. Ramirez‐San Juan GR, Oakes PW, Gardel ML. Contact guidance requires spatial control of leading‐edge protrusion. Mol Biol Cell 2017, 28:1043–1053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 159. Kim H, Sengupta A, Glogauer M, McCulloch CA. Filamin A regulates cell spreading and survival via beta1 integrins. Exp Cell Res 2008, 314:834–846. [DOI] [PubMed] [Google Scholar]
- 160. Schlüter DK, Ramis‐Conde I, Chaplain MAJ. Computational modeling of single‐cell migration: the leading role of extracellular matrix fibers. Biophys J 2012, 103:1141–1151. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 161. Borau C, Kamm RD, García‐Aznar JM. A time‐dependent phenomenological model for cell mechano‐sensing. Biomech Model Mechanobiol 2014, 13:451–462. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 162. Chu Y‐S, Thomas WA, Eder O, Pincet F, Perez E, Thiery JP, Dufour S. Force measurements in E‐cadherin–mediated cell doublets reveal rapid adhesion strengthened by actin cytoskeleton remodeling through Rac and Cdc42. J Cell Biol 2004, 167:1183–1194. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 163. Kim M‐C, Kim C, Wood L, Neal D, Kamm RD, Asada HH. Integrating focal adhesion dynamics, cytoskeleton remodeling, and actin motor activity for predicting cell migration on 3D curved surfaces of the extracellular matrix. Integr Biol 2012, 4:1386–1397. [DOI] [PubMed] [Google Scholar]
- 164. Borau C, Polacheck WJ, Kamm RD, García‐Aznar JM. Probabilistic Voxel‐Fe model for single cell motility in 3D. In Silico Cell Tissue Sci 2014, 1:1–17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 165. Song MJ, Dean D, Knothe Tate ML. Mechanical modulation of nascent stem cell lineage commitment in tissue engineering scaffolds. Biomaterials 2013, 34:5766–5775. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 166. Polacheck WJ, Charest JL, Kamm RD. Interstitial flow influences direction of tumor cell migration through competing mechanisms. Proc Natl Acad Sci 2011, 108:11115–11120. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 167. Xia S, Kanchanawong P. Nanoscale mechanobiology of cell adhesions. Semin Cell Dev Biol 2017, 71:53–67. https://doi.org/10.1016/j.semcdb.2017.07.029. [DOI] [PubMed] [Google Scholar]
- 168. Hoffman BD, Yap AS. Towards a dynamic understanding of cadherin‐based mechanobiology. Trends Cell Biol 2015, 25:803–814. [DOI] [PubMed] [Google Scholar]
- 169. Campbell HK, Maiers JL, DeMali KA. Interplay between tight junctions & adherens junctions. Exp Cell Res 2017, 358:39–44. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 170. Kourtidis A, Lu R, Pence LJ, Anastasiadis PZ. A central role for cadherin signaling in cancer. Exp Cell Res 2017, 358:78–85. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 171. Priest AV, Shafraz O, Sivasankar S. Biophysical basis of cadherin mediated cell‐cell adhesion. Exp Cell Res 2017, 358:10–13. [DOI] [PubMed] [Google Scholar]
- 172. Engl W, Arasi B, Yap LL, Thiery JP, Viasnoff V. Actin dynamics modulate mechanosensitive immobilization of E‐cadherin at adherens junctions. Nat Cell Biol 2014, 16:587–594. [DOI] [PubMed] [Google Scholar]
- 173. Wu SK, Gomez GA, Michael M, Verma S, Cox HL, Lefevre JG, Parton RG, Hamilton NA, Neufeld Z, Yap AS. Cortical F‐actin stabilization generates apical‐lateral patterns of junctional contractility that integrate cells into epithelia. Nat Cell Biol 2014, 16:167–178. [DOI] [PubMed] [Google Scholar]
- 174. Bambardekar K, Clément R, Blanc O, Chardès C, Lenne P‐F. Direct laser manipulation reveals the mechanics of cell contacts in vivo. Proc Natl Acad Sci USA 2015, 112:1416–1421. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 175. Schlüter DK, Ramis‐Conde I, Chaplain MAJ. Multi‐scale modelling of the dynamics of cell colonies: insights into cell‐adhesion forces and cancer invasion from in silico simulations. J R Soc Interface 2015, 12:20141080–20141080. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 176. Coburn L, Lopez H, Noppe A, Caldwell BJ, Moussa E, Yap C, Priya R, Lobaskin V, Roberts AP, Yap AS, et al. Contact inhibition of locomotion and mechanical cross‐talk between cell‐cell and cell‐substrate adhesion determines the pattern of junctional tension in epithelial cell aggregates. arXivorg 2016, 27:3436–3448. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 177. Pollard TD, Borisy GG. Cellular motility driven by assembly and disassembly of actin filaments. Cell 2003, 112:453–465. [DOI] [PubMed] [Google Scholar]
- 178. Holmes WR, Golding AE, Bement WM, Edelstein‐Keshet L. A mathematical model of GTPase pattern formation during single‐cell wound repair. Interface Focus 2016, 6:20160032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 179. Edelstein‐Keshet L, Holmes WR, Zajac M, Dutot M. From simple to detailed models for cell polarization. Philos Trans R Soc B Bioll Sci 2013, 368:20130003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 180. Jilkine A, Edelstein‐Keshet L. A comparison of mathematical models for polarization of single eukaryotic cells in response to guided cues. PLoS Comput Biol 2011, 7:e1001121. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 181. Dráber P, Sulimenko V, Dráberová E. Cytoskeleton in mast cell signaling. Front Immunol 2012, 3:130. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 182. Wu M, Wu X, De Camilli P. Calcium oscillations‐coupled conversion of actin travelling waves to standing oscillations. Proc Natl Acad Sci 2013, 110:1339–1344. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 183. Wang W, Tao K, Wang J, Yang G, Ouyang Q, Wang Y, Zhang L, Liu F. Exploring the inhibitory effect of membrane tension on cell polarization. PLoS Comput Biol 2017, 13:e1005354. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 184. Diz‐Muñoz A, Thurley K, Chintamen S, Altschuler SJ, Wu LF, Fletcher DA, Weiner OD. Membrane tension acts through PLD2 and mTORC2 to limit actin network assembly during neutrophil migration. PLoS Biol 2016, 14:e1002474–e1002430. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 185. Robinson RC, Turbedsky K, Kaiser DA, Marchand JB, Higgs HN, Choe S, Pollard TD. Crystal structure of Arp2/3 complex. Science 2001, 294:1679–1684. [DOI] [PubMed] [Google Scholar]
- 186. Mullins RD, Heuser JA, Pollard TD. The interaction of Arp2/3 complex with actin: nucleation, high affinity pointed end capping, and formation of branching networks of filaments. Proc Natl Acad Sci 1998, 95:6181–6186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 187. Tania N, Condeelis J, Edelstein‐Keshet L. Modeling the synergy of cofilin and Arp2/3 in lamellipodial protrusive activity. Biophys J 2013, 105:1946–1955. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 188. Goode BL, Eck MJ. Mechanism and function of formins in the control of actin assembly. Annu Rev Biochem 2007, 76:593–627. [DOI] [PubMed] [Google Scholar]
- 189. Novak IL, Slepchenko BM, Mogilner A. Quantitative analysis of G‐actin transport in motile cells. Biophys J 2008, 95:1627–1638. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 190. Dayel MJ, Mullins RD. Activation of Arp2/3 complex: addition of the first subunit of the new filament by a WASP protein triggers rapid ATP hydrolysis on Arp2. PLoS Biol 2004, 2:E91. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 191. Prehoda KE, Scott JA, Mullins RD, Lim WA. Integration of multiple signals through cooperative regulation of the N‐WASP‐Arp2/3 complex. Science 2000, 290:801–806. [DOI] [PubMed] [Google Scholar]
- 192. Chen Z, Borek D, Padrick SB, Gomez TS, Metlagel Z, Ismail AM, Umetani J, Billadeau DD, Otwinowski Z, Rosen MK. Structure and control of the actin regulatory WAVE complex. Nature 2010, 468:533–538. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 193. Abdul‐Manan N, Aghazadeh B, Liu GA, Majumdar A, Ouerfelli O, Siminovitch KA, Rosen MK. Structure of Cdc42 in complex with the GTPase‐binding domain of the ‘Wiskott‐Aldrich syndrome’ protein. Nature 1999, 399:379–383. [DOI] [PubMed] [Google Scholar]
- 194. Miki H, Suetsugu S, Takenawa T. WAVE, a novel WASP‐family protein involved in actin reorganization induced by Rac. EMBO J 1998, 17:6932–6941. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 195. Wu CY, Asokan SB, Berginski ME, Haynes EM, Sharpless NE, Griffith JD, Gomez SM, Bear JE. Arp2/3 is critical for lamellipodia and response to extracellular matrix cues but is dispensable for chemotaxis. Cell 2012, 148:973–987. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 196. Suraneni P, Rubinstein B, Unruh JR, Durnin M, Hanein D, Li R. The Arp2/3 complex is required for lamellipodia extension and directional fibroblast cell migration. J Cell Biol 2012, 197:239–251. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 197. Romero S, Le Clainche C, Didry D, Egile C, Pantaloni D, Carlier MF. Formin is a processive motor that requires profilin to accelerate actin assembly and associated ATP hydrolysis. Cell 2004, 119:419–429. [DOI] [PubMed] [Google Scholar]
- 198. Evangelista M, Pruyne D, Amberg DC, Boone C, Bretscher A. Formins direct Arp2/3‐independent actin filament assembly to polarize cell growth in yeast. Nat Cell Biol 2002, 4:260–269. [DOI] [PubMed] [Google Scholar]
- 199. Watanabe N, Kato T, Fujita A, Ishizaki T, Narumiya S. Cooperation between mDia1 and ROCK in Rho‐induced actin reorganization. Nat Cell Biol 1999, 1:136–143. [DOI] [PubMed] [Google Scholar]
- 200. Pellegrin S, Mellor H. The Rho family GTPase Rif induces filopodia through mDia2. Curr Biol 2005, 15:129–133. [DOI] [PubMed] [Google Scholar]
- 201. Suraneni P, Fogelson B, Rubinstein B, Noguera P, Volkmann N, Hanein D, Mogilner A, Li R. A mechanism of leading‐edge protrusion in the absence of Arp2/3 complex. Mol Biol Cell 2015, 26:901–912. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 202. Tojkander S, Gateva G, Lappalainen P. Actin stress fibers‐‐assembly, dynamics and biological roles. J Cell Sci 2012, 125:1855–1864. [DOI] [PubMed] [Google Scholar]
- 203. Prost J, Jülicher F, Joanny J‐F. Active gel physics. Nat Phys 2015, 11:111–117. [Google Scholar]
- 204. Rubinstein B, Fournier MF, Jacobson K, Verkhovsky AB, Mogilner A. Actin‐myosin viscoelastic flow in the keratocyte lamellipod. Biophys J 2009, 97:1853–1863. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 205. Vicente‐Manzanares M, Newell‐Litwa K, Bachir AI, Whitmore LA, Horwitz AR. Myosin IIA/IIB restrict adhesive and protrusive signaling to generate front‐back polarity in migrating cells. J Cell Biol 2011, 193:381–396. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 206. Schaub S, Bohnet S, Laurent VM, Meister JJ, Verkhovsky AB. Comparative maps of motion and assembly of filamentous actin and myosin II in migrating cells. Mol Biol Cell 2007, 18:3723–3732. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 207. Amano M, Ito M, Kimura K, Fukata Y, Chihara K, Nakano T, Matsuura Y, Kaibuchi K. Phosphorylation and activation of myosin by Rho‐associated kinase (Rho‐kinase). J Biol Chem 1996, 271:20246–20249. [DOI] [PubMed] [Google Scholar]
- 208. Kamm KE, Stull JT. The function of myosin and myosin light chain kinase phosphorylation in smooth muscle. Annu Rev Pharmacol Toxicol 1985, 25:593–620. [DOI] [PubMed] [Google Scholar]
- 209. Chen C, Tao T, Wen C, He WQ, Qiao YN, Gao YQ, Chen X, Wang P, Chen CP, Zhao W, et al. Myosin light chain kinase (MLCK) regulates cell migration in a myosin regulatory light chain phosphorylation‐independent mechanism. J Biol Chem 2014, 289:28478–28488. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 210. Totsukawa G, Wu Y, Sasaki Y, Hartshorne DJ, Yamakita Y, Yamashiro S, Matsumura F. Distinct roles of MLCK and ROCK in the regulation of membrane protrusions and focal adhesion dynamics during cell migration of fibroblasts. J Cell Biol 2004, 164:427–439. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 211. Diz‐Muñoz A, Fletcher DA, Weiner OD. Use the force: membrane tension as an organizer of cell shape and motility. Trends Cell Biol 2013, 23:47–53. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 212. Katsumi A, Milanini J, Kiosses WB, del Pozo MA, Kaunas R, Chien S, Hahn KM, Schwartz MA. Effects of cell tension on the small GTPase Rac. J Cell Biol 2002, 158:153–164. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 213. Houk AR, Jilkine A, Mejean CO, Boltyanskiy R, Dufresne ER, Angenent SB, Altschuler SJ, Wu LF, Weiner OD. Membrane tension maintains cell polarity by confining signals to the leading edge during neutrophil migration. Cell 2012, 148:175–188. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 214. Sandquist JC, Swenson KI, DeMali KA, Burridge K, Means AR. Rho kinase differentially regulates phosphorylation of nonmuscle myosin II isoforms A and B during cell rounding and migration. J Biol Chem 2006, 281:35873–35883. [DOI] [PubMed] [Google Scholar]
- 215. Parri M, Chiarugi P. Rac and Rho GTPases in cancer cell motility control. Cell Commun Signal 2010, 8:23. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 216. Nguyen LK, Kholodenko BN, von Kriegsheim A. Rac1 and RhoA: networks, loops and bistability. Small GTPases 2016:1–6. https://doi.org/10.1080/21541248.2016.1224399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 217. Byrne KM, Monsefi N, Dawson JC, Degasperi A, Bukowski‐Wills JC, Volinsky N, Dobrzynski M, Birtwistle MR, Tsyganov MA, Kiyatkin A, et al. Bistability in the Rac1, PAK, and RhoA signaling network drives actin cytoskeleton dynamics and cell motility switches. Cell Syst 2016, 2:38–48. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 218. Holmes WR, Edelstein‐Keshet L. Analysis of a minimal Rho‐GTPase circuit regulating cell shape. Phys Biol 2016, 13:046001. [DOI] [PubMed] [Google Scholar]
- 219. Zaidel‐Bar R, Cohen M, Addadi L, Geiger B. Hierarchical assembly of cell‐matrix adhesion complexes. Biochem Soc Trans 2004, 32:416–420. [DOI] [PubMed] [Google Scholar]
- 220. Geiger T, Zaidel‐Bar R. Opening the floodgates: proteomics and the integrin adhesome. Curr Opin Cell Biol 2012, 24:562–568. [DOI] [PubMed] [Google Scholar]
- 221. Oakes PW, Beckham Y, Stricker J, Gardel ML. Tension is required but not sufficient for focal adhesion maturation without a stress fiber template. J Cell Biol 2012, 196:363–374. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 222. Choi CK, Vicente‐Manzanares M, Zareno J, Whitmore LA, Mogilner A, Horwitz AR. Actin and alpha‐actinin orchestrate the assembly and maturation of nascent adhesions in a myosin II motor‐independent manner. Nat Cell Biol 2008, 10:1039–1050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 223. Ridley AJ, Hall A. The small GTP‐binding protein rho regulates the assembly of focal adhesions and actin stress fibers in response to growth factors. Cell 1992, 70:389–399. [DOI] [PubMed] [Google Scholar]
- 224. Chrzanowska‐Wodnicka M, Burridge K. Rho‐stimulated contractility drives the formation of stress fibers and focal adhesions. J Cell Biol 1996, 133:1403–1415. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 225. Steffen A, Ladwein M, Dimchev GA, Hein A, Schwenkmezger L, Arens S, Ladwein KI, Holleboom JM, Schur F, Small JV, et al. Rac function is crucial for cell migration but is not required for spreading and focal adhesion formation. J Cell Sci 2013, 126:4572–4588. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 226. Pasapera AM, Plotnikov SV, Fischer RS, Case LB, Egelhoff TT, Waterman CM. Rac1‐dependent phosphorylation and focal adhesion recruitment of myosin IIA regulates migration and mechanosensing. Curr Biol 2015, 25:175–186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 227. Alexandrova AY, Arnold K, Schaub S, Vasiliev JM, Meister JJ, Bershadsky AD, Verkhovsky AB. Comparative dynamics of retrograde actin flow and focal adhesions: formation of nascent adhesions triggers transition from fast to slow flow. PLoS One 2008, 3:e3234. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 228. Zhao X, Guan JL. Focal adhesion kinase and its signaling pathways in cell migration and angiogenesis. Adv Drug Deliv Rev 2011, 63:610–615. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 229. Kallergi G, Agelaki S, Markomanolaki H, Georgoulias V, Stournaras C. Activation of FAK/PI3K/Rac1 signaling controls actin reorganization and inhibits cell motility in human cancer cells. Cell Physiol Biochem 2007, 20:977–986. [DOI] [PubMed] [Google Scholar]
- 230. Chen BH, Tzen JT, Bresnick AR, Chen HC. Roles of Rho‐associated kinase and myosin light chain kinase in morphological and migratory defects of focal adhesion kinase‐null cells. J Biol Chem 2002, 277:33857–33863. [DOI] [PubMed] [Google Scholar]
- 231. Park JS, Holmes WR, Lee S‐H, Kim H‐N, Kim D‐H, Kwak MK, Wang CJ, Edelstein‐Keshet L, Levchenko A. Mechanochemical feedback underlies coexistence of qualitatively distinct cell polarity patterns within diverse cell populations. Proc Natl Acad Sci 2017, 114:E5750–E5759. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 232. Danen EHJ, Sonneveld P, Brakebusch C, Fässler R, Sonnenberg A. The fibronectin‐binding integrins α5β1 and αvβ3 differentially modulate RhoA–GTP loading, organization of cell matrix adhesions, and fibronectin fibrillogenesis. J Cell Biol 2002, 159:1071–1086. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 233. Lin B, Holmes WR, Wang CJ, Ueno T, Harwell A, Edelstein‐Keshet L, Inoue T, Levchenko A. Synthetic spatially graded Rac activation drives cell polarization and movement. Proc Natl Acad Sci 2012, 109:E3668–E3677. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 234. Abdul‐Manan N, Aghazadeh B, Liu GA, Majumdar A, Ouerfelli O, Siminovitch KA, Rosen MK. Structure of Cdc42 in complex with the GTPase‐binding domain of the ‘Wiskott‐Aldrich syndrome’ protein. Nature 1999, 399:379–383. [DOI] [PubMed] [Google Scholar]
- 235. Huang B, Lu MY, Jolly MK, Tsarfaty I, Onuchic J, Ben‐Jacob E. The three‐way switch operation of Rac1/RhoA GTPase‐based circuit controlling amoeboid‐hybrid‐mesenchymal transition. Sci Rep 2014, 4:1–11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 236. Martin E, Ouellette MH, Jenna S. Rac1/RhoA antagonism defines cell‐to‐cell heterogeneity during epidermal morphogenesis in nematodes. J Cell Biol 2016, 215:483–498. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 237. Sailem H, Bousgouni V, Cooper S, Bakal C. Cross‐talk between Rho and Rac GTPases drives deterministic exploration of cellular shape space and morphological heterogeneity. Open Biol 2014, 4:130132. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 238. Sanz‐Moreno V, Gadea G, Ahn J, Paterson H, Marra P, Pinner S, Sahai E, Marshall CJ. Rac activation and inactivation control plasticity of tumor cell movement. Cell 2008, 135:510–523. [DOI] [PubMed] [Google Scholar]
- 239. Cooper S, Sadok A, Bousgouni V, Bakal C. Apolar and polar transitions drive the conversion between amoeboid and mesenchymal shapes in melanoma cells. Mol Biol Cell 2015, 26:4163–4170. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 240. Mata MA, Dutot M, Edelstein‐Keshet L, Holmes WR. A model for intracellular actin waves explored by nonlinear local perturbation analysis. J Theor Biol 2013, 334:149–161. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 241. Holmes WR, Carlsson AE, Edelstein‐Keshet L. Regimes of wave type patterning driven by refractory actin feedback: transition from static polarization to dynamic wave behaviour. Phys Biol 2012, 9:046005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 242. Weiner OD, Marganski WA, Wu LF, Altschuler SJ, Kirschner MW. An actin‐based wave generator organizes cell motility. PLoS Biol 2007, 5:e221. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 243. Gerhardt M, Ecke M, Walz M, Stengl A, Beta C, Gerisch G. Actin and PIP3 waves in giant cells reveal the inherent length scale of an excited state. J Cell Sci 2014, 127:4507–4517. [DOI] [PubMed] [Google Scholar]
- 244. Bretschneider T, Anderson K, Ecke M, Muller‐Taubenberger A, Schroth‐Diez B, Ishikawa‐Ankerhold HC, Gerisch G. The three‐dimensional dynamics of actin waves, a model of cytoskeletal self‐organization. Biophys J 2009, 96:2888–2900. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 245. Bernitt E, Koh CG, Gov N, Dobereiner HG. Dynamics of actin waves on patterned substrates: a quantitative analysis of circular dorsal ruffles. PLoS One 2015, 10:e0115857. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 246. Holmes WR, Park J, Levchenko A, Edelstein‐Keshet L. A mathematical model coupling polarity signaling to cell adhesion explains diverse cell migration patterns. PLoS Comput Biol 2017, 13:e1005524. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 247. Bradley C, Bowery A, Britten R, Budelmann V, Camara O, Christie R, Cookson A, Frangi AF, Gamage TB, Heidlauf T, et al. OpenCMISS: a multi‐physics & multi‐scale computational infrastructure for the VPH/Physiome project. Prog Biophys Mol Biol 2011, 107:32–47. [DOI] [PubMed] [Google Scholar]
- 248. Plimpton S. Fast parallel algorithms for short‐range molecular dynamics. J Comput Phys 1995, 117:1–19. [Google Scholar]


