With or without you: predictive coding and Bayesian inference in the brain

Abstract

Two theoretical ideas have emerged recently with the ambition to provide a unifying functional explanation of neural population coding and dynamics: predictive coding and Bayesian inference. Here, we describe the two theories and their combination into a single framework: Bayesian predictive coding. We clarify how the two theories can be distinguished, despite sharing core computational concepts and addressing an overlapping set of empirical phenomena. We argue that predictive coding is an algorithmic / representational motif that can serve several different computational goals of which Bayesian inference is but one. Conversely, while Bayesian inference can utilize predictive coding, it can also be realized by a variety of other representations. We critically evaluate the experimental evidence supporting Bayesian predictive coding and discuss how to test it more directly.

Introduction

From very early work in neuroscience, it has been noted that neural systems rarely represent measured quantities directly, as a human engineer might [1]. For instance, a digital camera simply records and transmits the light intensity at each pixel [2]. In contrast, the human retina preprocesses the signal using the surrounding pixels [3], and the recent past [4]. Activity in the visual cortex is also strongly modulated by the spatial and temporal context of stimuli [5] – to the extent that, for example, neurons in primary visual cortex (V1) even respond to illusory contours, stimulus features that are not physically present in the input but must be inferred from context [6]. Overall, there is much evidence that perception and, correspondingly, neural responses in sensory cortical areas are as influenced by predictions and expectations about stimuli as by the actual stimuli themselves [7, 8]. Indeed, while ascending feed-forward connections convey stimulus-related information [9], long-range horizontal and feed-back connections within and between different cortical areas provide a natural anatomical substrate for conveying such “contextual” effects. The principles for how these contextual signals are computed, integrated with sensory information and represented in neural activities have been formalised in two different, though closely related theoretical frameworks: predictive coding and Bayesian inference.

Predictive coding

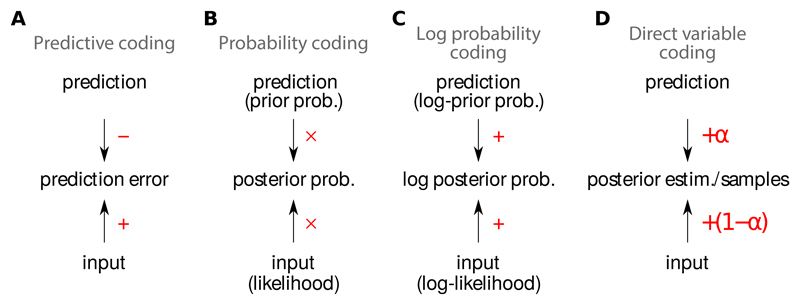
Predictive coding is based on the simple but powerful idea that instead of representing the input directly, it is often preferable to represent the prediction error, the difference (or sometimes the ratio [10]) between a sensory input and a prediction (Fig. 1A):

$$\text{prediction}\text{error}=\text{input}-\text{prediction}$$ (1)

One reason for doing so is that, if the prediction is correct, no costly spikes need to be transmitted, thus improving efficiency [1, 2]. The spatio-temporal receptive fields of retinal ganglion cells offer a classical example of this; they use the past and the surround to predict the current light intensity in the centre, and then transmit the prediction error, the difference between the measured light intensity and the prediction [11, 12].

Figure 1.

Neural arithmetics corresponding to different representational schemes. A. Predictive coding: the difference between the input and a prediction is computed, and the resulting prediction error is represented in the response of neurons. B. Probability coding: the response of each neuron represents the posterior probability associated with a particular value (or range of values) of the latent variable(s). Thus, to compute their firing rate, neurons need to multiply their inputs, representing the likelihood, and the prediction, representing the prior. C. Log-probability coding: the response of each neuron represents the logarithm of the posterior probability associated with a particular value of the latent variable(s), thus it needs to sum its inputs, representing the log likelihood, and the prediction, representing the log prior. D. Direct variable coding: the response of each neuron represents the value of a different latent variable. The resulting population codes typically interpolate between what would be dictated by inputs or predictions alone.

Bayesian inference

Uncertainty is a ubiquitous feature of neural processing: in many situations it is impossible to know the external, latent causes for incoming sensory stimuli. For example, when hearing leaves rustling in the night, it is vital to infer whether the latent cause was a dangerous predator, or simply the wind. The optimal strategy for computing such inferences is to follow the rules of probability, including Bayes’ rule [13]. Therefore, Bayesian inference of the latent causes of sensory inputs is one of the brain’s fundamental computational goals (in the sense of the first of Marr’s three levels [14]).

Formally, Bayesian inference uses the current input data to compute the posterior probability of each latent cause, P(latent|input), by multiplying the prior probability of each potential setting for the latents, P(latent), with the likelihood, P(input|latent), the probability of receiving the current sensory input under that setting of the latents:

$$P(\text{latent}|\text{input})\propto P(\text{input}|\text{latent})\times P(\text{latent})$$ (2)

There is considerable behavioural evidence that human and animal behaviour exploits Bayes’ theorem (Eq. 2) to achieve near-optimal performance in a variety of situations, from decision making [15], through cue combination [16], to motor control [17]. However, there is a much more limited understanding of how the dynamics of cortical (and potentially subcortical) circuits might implement Bayesian inference [18, 19].

Bayesian predictive coding

Although predictive coding and Bayesian inference agree upon the importance of combining external inputs with internal signals (predictions or priors), they are complementary in their focus and the type of data they naturally address. While predictive coding specifies that prediction errors, rather than raw predictions or inputs should be represented, it remains agnostic as to how predictions are computed in the first place and how prediction errors should ultimately be used. In contrast, Bayesian inference provides an optimal calculus for computing predictions, but does not specify the underlying neural representation. Experimentally, as the examples in the previous sections illustrate, predictive coding describes neural responses, while Bayesian inference describes the end-result of computation: behaviour.

It thus seems natural to combine the strength of these two theoretical ideas, and use the latent variables inferred by Bayes’ theorem (specifically, a setting of latent variables that is representative of the posterior distribution in Eq. 2) to provide the predictions about the (current or future) sensory input required by predictive coding, for example as the expectation of the input based on our current inferences about the latent variables:

$$\text{prediction}={\displaystyle \int \text{input}P(\text{input}|\text{latent})\mathit{d}\text{input}}$$ (3)

Neurons can then subtract this prediction from the actual input to form a prediction error, as suggested by Eq. 1. In turn, such a prediction error turns out to be a very useful input to a neural circuit implementing Bayesian inference, as it helps to guide network dynamics towards population activity patterns encoding values of the latent variables that better represent the sensory input [20]. A recent application of Bayesian predictive coding is the “free-energy principle” [21] which can be seen as a special case, using a specific class of dynamical probabilistic generative models, and a specific class of variational filtering inference algorithms.

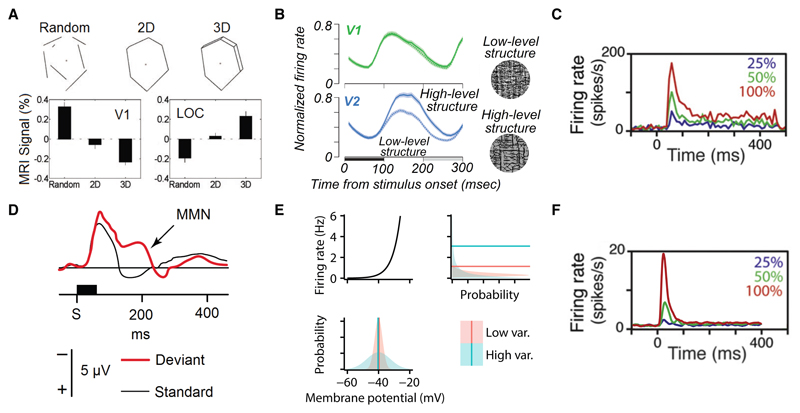
The most prominent experimental support for such a combined Bayesian predictive coding scheme comes from the relative suppression of responses in V1 by extra-classical receptive field stimuli [22]. First, as a bar is lengthened beyond a cell’s classical receptive field, its response falls [23, 20]. Second, the response to a grating presented in the classical receptive field depends on the presence of oriented structure in the surround: having the same orientation in the centre and surround suppresses the response [24, 20]. In both these cases, the centre and the surround form a coherent structure, which allows the inferred latent variables to better model the presented image stimulus, and so prediction errors at the lower levels become smaller – thus accounting for suppressed V1 activity.

At the level of BOLD signals, V1 was activated less strongly by a coherent line drawing, while higher order visual cortices (the lateral occipital complex, LOC) were more activated by the coherent than the incoherent stimuli (Fig. 2A) [25]. Predictive coding accounts for these effects by hypothesising that V1 represents the difference between sensory input and a higher-level prediction, whereas the LOC represents the predictions themselves. Thus, as above, when larger-scale structure is present, prediction errors are lower, implying suppressed activity in V1, whereas the increased activity in LOC may be a signature of the improved higher-level predictions [20, 25]. It is interesting to note, however, that more direct electrophysiological measurements of visual cortical responses, using stimuli with more carefully controlled statistics, found that activity in V1 remains largely unaffected by manipulations of the level of naturalistic structure in the stimulus [32], even as activity in V2 substantially increases for more naturalistic stimuli (Fig. 2B) [26].

Figure 2.

A. Stimuli having progressively more high-level structure (top) give rise to less BOLD activity in human V1 (bottom left), and more activity in higher-level visual areas (lateral occipital complex, LOC, bottom right). Adapted from [25]. B. Stimuli (right) matching low-level (frequency structure) and high-level structure in natural images [26, 27] evoke near-identical average responses in macaque V1 (top left; if anything, the stimuli with higher-level structure gave slightly higher responses), despite activity in V2 increasing substantially (bottom left). The horizontal black bar denotes stimulus presentation, the grey bar is a noise control. Adapted from [27]. C. Stimulus-induced transients in macaque V1 responses at the onset of a static visual stimulus presented between 0–400 ms. The magnitude of the transient scales with contrast (colour code). Adapted from [28]. D. Mismatch negativity (MMN) in human auditory cortex. Two types of auditory tones were presented, a standard stimulus at 1000 Hz that was presented 80% of the time, and a deviant stimulus at a variety of frequencies that was presented 20% of the time. The event-related potentials for the two stimuli (black: standard 1000 Hz, red: deviant 1032 Hz) diverge around 200 ms after stimulus onset (S, horizontal black bar). Adapted from [29] using data from [30]. E. Nonlinear signal transformations result in changes in mean output even when only the variance of the input changes. Bottom: two membrane potential distributions with identical means, but one with less variability (red) than the other (blue). Top-left: firing rate nonlinearity mapping from membrane potential (x-axis) to firing rate (y-axis). Right: the resulting distributions over firing rates, and their means (horizontal lines). Notably, while the mode of the broader (blue) distribution is smaller than the mode of the narrower (red) distribution, the long tail of the broader distribution increases the mean above that of the red distribution. F. Stimulus-induced transients in a sampling-based direct variable coding model of V1 using non-equilibrium dynamics. The magnitude of the transient scales with contrast (colour code). Adapted from [31], c.f. panel C.

Furthermore, in the temporal domain, in many brain areas including cortex and retina, there are large, brief “transient” increases in activity following unexpected changes (including stimulus onset, e.g. [28]; Fig. 2C). This has been most extensively studied in primary auditory cortex, using a series of tones of which most have the same frequency, with a few “oddballs” of a different frequency. Event related potentials measured using electroencephalography display mismatch negativity (MMN), an elongation of the response to these oddball stimuli (Fig. 2D) [33, 29]. Predictive coding accounts for these effects by noting that, at stimulus onset, the unexpected stimulus cannot be predicted, giving rise to a large prediction error. This prediction error is then rapidly eliminated as new observations are incorporated into the predictions [29, 34].

Predictive coding: an algorithmic motif, not a computational goal

While it is natural to combine predictive coding with Bayesian inference, whereby the prediction is based on an inferred latent variable and the resulting prediction error is used to improve further predictions, this is not the only way to compute a prediction and to make use of a prediction error signal. Indeed, using other types of prediction, predictive coding can yield a useful representation that can serve a multitude of other computational goals.

First, the retina is required to transmit the entire visual input through an extremely narrow bottleneck: only around 10⁶ cells [35] firing at only around 1 Hz [36]. As such, the retina must maximize the information about the image present in the output signal by reducing redundancy [11]. In certain regimes (though see below), this objective results in a predictive coding scheme, in which costly spikes are transmitted only when predictions based on the surround or recent past are violated, meaning that static scenes, or flat blocks of colour are encoded cheaply, thus reducing the high level of redundancy that is inherent in the similar responses of nearby photoreceptor cells [12].

Second, a critical problem faced by sensory systems is that self-generated signals (e.g. motion) can dramatically alter sensory input, swamping the more important externally generated signals. To compensate for these self-generated signals, it is suggested that an efference copy (i.e. a copy of motor commands) is sent to sensory areas, which allows the effect of self-generated signals to be predicted, and subtracted from the sensory signal, leaving only the externally generated signals [37]. These effects are particularly evident in the observation that one cannot tickle oneself [38], in the shift of visual receptive fields in anticipation of a saccade [22], and in the interaction between self-generated electrical signals and electrosensation in the mormyrid electric fish [39].

Third, cortical circuits must typically encode continuous quantities in the external world (such as trajectories of objects) using temporally punctate, all-or-none spikes. In order to make this analogue-to-digital conversion efficient, it has been suggested that the membrane potential dynamics of cortical neurons implement a predictive coding scheme, such that membrane potentials represent prediction errors and spikes are generated only when prediction errors exceed a threshold [40, 41, 42]. For self-consistency, the prediction error represented by membrane potentials is the difference between the continuous signal that needs to be represented and its representation in the spiking activity of the network itself. Such a predictive coding scheme results in biophysically plausible leaky integrate-and-fire membrane potential dynamics and Poisson-like spiking patterns often observed in cortex.

Fourth, animals need to learn to select actions that yield high long-term rewards (an objective formalised by reinforcement learning [43]). One powerful solution to this computationally challenging problem is to maintain predictions about expected rewards, and compute a reward prediction error, describing whether an action gave rise to more or less reward than expected. Such a prediction error can be used to increase the propensity to perform actions resulting in higher-than-expected rewards, and also to update future predictions [44, 45, 46]. Neurally, there is strong evidence that this reward prediction error is instantiated by dopamine [47], which has indeed been shown to be a potent modulator of synaptic plasticity [48].

In summary, predictive coding emerges and performs a useful function not only in the service of Bayesian inference, but also when achieving a wide variety of different computational goals: maximizing information transmission, cancelling the effects of self-generated actions, representing continuous quantities using spikes, and performing reinforcement learning. As such, we suggest that predictive coding should be understood not as a computational goal in and of itself, but as an algorithmic motif (i.e. at the second of Marr’s three levels [14]): a common pattern that can emerge in neural circuits subserving fundamentally different computations.

Even the computational goals for which predictive coding seems a natural fit are not always best served by it – and indeed, the brain often seems to use other strategies to achieve these goals. For instance, in retinal ganglion cells, predictive coding is the optimal strategy for transmitting information by reducing redundancy when light levels are high. However, when light levels are reduced and so the signal-to-noise ratio in the input is lower, the optimal strategy is the opposite: to sum the centre and surround [49]. This occurs because computing the prediction error by subtracting two noisy signals (from the centre and surround) increases the noise in the output signal. At high light levels, the effect of this increased noise is outweighed by the benefits of redundancy reduction given by predictive coding, while at low light levels it is more important to preserve whatever signal is there, and it is therefore detrimental to use a predictive coding strategy. Indeed, in low-light the retinal surround becomes facilitating, the opposite of a predictive coding strategy [50]. Similarly, the computational goal of reinforcement learning can be achieved by several algorithms that do not compute and represent prediction errors per se [51, 52], and whether prediction error-based or these other algorithms should be used depends on environmental and neural constraints [53].

Bayesian inference without predictive coding

Just as other computational goals, Bayesian inference can also be performed by many other neural algorithms and representations which do not use predictive coding (Fig. 1B-D). Perhaps the most obvious neural representation for probabilities is simply to use neural firing rates themselves, such that the firing rate of each neuron represents the posterior probability of one possible value (or a range of values) of the latent variables, which can be computed following Bayes’ rule (Eq. 2) by multiplying bottom-up inputs, representing the likelihood, with top-down biases, representing the prior (Fig. 1B) [19]. As multiplication is often thought to be an operation that is harder for neurons to implement than summation, it is preferable to work with a tightly related code in which firing rates represent log-probabilities [19] (Fig 1C). The best known example of such a log-probability representation is probabilistic population codes [54]. Both probability and log-probability codes are special cases of neural responses representing the parameters of the posterior probability distribution [18]. There are several other variants of such parametric representations (e.g. [55]), leading to different algebraic forms of integrating inputs with predictions, but they do not generally lend themselves to predictive coding.

An alternative approach is to use “direct variable coding”, whereby neural activity directly represents latent variables. For instance, in sparse coding models of visual images (or image patches), the latent variables typically correspond to the intensity with which a visual feature (such as an oriented Gabor filter) is present in the image [56]. Thus, in a direct variable coding representation, neural responses directly encode these intensities: no response implies the feature represented by the neuron is absent, a small or a large response means the feature’s intensity is low or high, respectively. (Note that predictive coding schemes also use a one-to-one correspondence between latent variables and neurons, but they define neural responses as representing differences between inferred and predicted variable values [20], rather than the inferred values directly.)

Neural responses in direct variable encoding schemes either deterministically converge to the single best setting of the latent variables [56], or stochastically sample multiple different plausible settings for the latents [18, 57, 58, 59] (Fig. 1D). Interestingly, a prediction error-like signal was first used for Bayesian inference in the context of such direct variable coding models. There, it was computed as part of the input to individual neurons and used to change their output iteratively so that they represented progressively better explanations of the current input [56]. Thus, merely computing prediction errors does not imply that there must be cells whose responses directly represent these prediction errors: in fact, self-consistent neural circuit dynamics can be constructed using pure direct variable coding [56]. In contrast, Bayesian predictive coding models rarely use purely prediction error-based representations, instead they typically use a hybrid scheme combining a population of direct coding neurons (which facilitate the computation of predictions), with an additional population of predictive coding neurons [20].

Pure direct coding models have enjoyed great success at a number of challenging supervised and unsupervised learning tasks, and their dynamics typically take a biologically plausible form, requiring neurons to integrate their inputs linearly and apply a spiking nonlinearity [60] or (a possibly stochastic) threshold [61, 62]. In line with the intuition that priors bias percepts towards expectations based on previous experience [63, 64], the resulting population activities exhibit an integration of top-down (conveying priors) and bottom-up inputs (conveying stimulus-related information) that often takes the form of a simple weighted average of the a priori expected value and that suggested by sensory evidence (Fig. 1D). The integration of different (independent) sensory sources of evidence can similarly result in a simple weighted averaging of inputs, again as has been observed at the level of perception [16].

Several predictions of direct variable coding models are well matched by experimental data. First, the weighted averaging of prior expectations and sensory information in population activity has been observed at the level of BOLD signals [65]. Second, the direct coding of sparse latent causes of natural images accounts for the localised and orientation-tuned receptive fields of V1 simple cells, with extensions of the same model – all using direct variable coding – also accounting for complex cell receptive fields [66, 67]. Third, as classical direct coding theories assume that neurons deterministically represent the single best setting of latent variables (the one that has the highest posterior probability), the responses they predict to any particular input are static (at least asymptotically) and thus cannot account for the ubiquitously observed variability of neural responses. However, a stochastic extension of these theories, in which the activity of neurons represents latent variable values that are sampled from the posterior distribution [18], accounts for task- [59] and stimulus-dependent variability [58] and for the similarity of evoked and spontaneous activities in V1 [57].

Finally, different combinations of these representations are also possible: for example, a generalisation of sampling-based stochastic dynamics with membrane-potential based predictive encoding of multiple simultaneous samples has been suggested to improve upon the time-efficiency of simple sampling-based direct variable codes [68].

Revisiting the evidence

Having understood the distinction between predictive coding and Bayesian inference, and the different features of experimental data they account for, it is useful to revisit the evidence that is traditionally considered to specifically support their combination. In particular, we ask whether these data exclude the possibility of Bayesian inference being implemented by a pure direct variable code.

A staple hallmark of predictive coding is that “interesting” or “surprising” stimuli evoke higher responses than expected ones [20, 29, 34]. However, some of these effects could be explained by attention instead, by which neural resources are directed towards more interesting or surprising stimuli, such that responses towards these stimuli are typically higher than towards unattended ones [69, 70]. Note that while attention and predictive coding may give rise to similar neural responses, they are fundamentally different in that top-down attention depends on, and can thus be modulated by the task, whereas prediction errors are part of a Bayesian computation so should not depend on the task (to the extent that the statistics of sensory inputs remain unchanged across tasks) [71]. Moreover, visual attention is focused at only one (or a very small number of) locations at a time [72], whereas prediction errors can be distributed arbitrarily across the visual field.

It may also be possible to account for these effects in Bayesian models using direct variable coding, rather than predictive coding, by noting that the same situations that result in higher prediction errors also typically evoke higher levels of uncertainty in the latent variables responsible for the predictions. Under a sampling-based direct coding scheme, this heightened uncertainty translates into higher levels of neural response variability [18, 58]. Indeed, less naturalistic images (due to the application of a small aperture, or phase-scrambling) evoke more unreliable responses in V1 [73, 32]. In turn, when a signal is passed through a non-linearity (in our case this could be the spiking non-linearity, Fig. 2F, or the BOLD response non-linearity [74]), an increase in the variance of the original signal will also change the mean of the transformed signal. Thus, the increased uncertainty due to an unexpected stimulus may also account for larger mean responses as measured electrophysiologically or in the BOLD signal.

While large transients following stimulus onset are commonly considered to be another signature of predictive coding [75], they have also been accounted for in a model using pure direct variable coding [31] (Fig. 2G). This model uses “non-equilibrium” (technically, “non-normal”) population dynamics that are particularly efficient for implementing sampling-based direct variable codes [76], and have been suggested to capture essential aspects of the dynamics of cortical circuits, due to the interactions between separate populations of excitatory and inhibitory neurons [77]. Large transient responses to any sharp transition (including stimulus onset) are a fundamental characteristic of such non-normal dynamics [78].

Finally, extra-classical receptive field effects, such as surround suppression, have also been explained in models using another canonical algorithmic motif: divisive normalization [79]. In divisive normalization, cells compute a ratio between their direct (bottom-up) inputs and the summed activity of a pool of neurons. (This is different from divisive predictive coding in that all neurons use a single global divisor, rather than each neuron’s activity being divided by its own specific prediction.) Divisive normalization can describe a range of effects, including saturation, cross-orientation suppression, and surround suppression [79], and it is modulated by attention [80], locomotion [81], and even disease [82]. In the context of Bayesian computations, divisive normalization implements inference in a powerful statistical model of natural images [83, 84, 85], which, critically, assumes a direct variable, rather than a predictive code. Indeed, inference in such a model not only accounts for the extra-classical receptive field effects commonly characterised by simple laboratory stimuli [84, 58], but also the degree of surround suppression observed in response to natural images [85].

In summary, while predictive coding is an attractive algorithmic idea that accounts for a remarkable range of phenomena, the experimental evidence for it seems inconclusive in the sense that it does not rule out Bayesian inference with a direct variable code, potentially in combination with a variety of non-probabilistic processes including attention and adaptation.

Conclusions

Our review suggests three major directions for future research. First, we have suggested that predictive coding, like divisive normalization, can be used to implement many different computations, and thus should be understood as a neural motif: an algorithmic step that emerges in a variety of different brain areas and computations. While the study of motifs is well-developed in molecular biology [86], it remains little studied in neuroscience suggesting a potentially fruitful direction for future research. Second, we have seen that while the evidence in favour of any particular implementation of Bayesian inference is inconclusive, these implementations do make different predictions that could be addressed experimentally. Examples include the singular focus of attention, compared to the potentially broad distribution of prediction errors, and the fact that predictive and direct coding make opposite predictions about the effect of prior expectations: with direct coding suggesting that a weighted average of expectations and sensory data is taken, and predictive coding suggesting they are subtracted. Third, in order for (pure) predictive coding to remain a viable candidate algorithm for Bayesian inference in the brain, it will be necessary to show that it can account for the data that direct variable codes have already successfully explained, such as the stimulus-dependent variability of cortical responses. Alternatively, if hybrid direct-predictive coding schemes are pursued, further work will need to identify phenomena that are specific to predictive coding neurons, and it will be necessary to clarify how the functional division between direct and predictive coding neurons maps on to anatomically and physiologically defined cell types in the cortex.

Highlights.

• –Predictive coding occurs in many different computations not just Bayesian inference
• –Bayesian inference can be, but does not need to be implemented by predictive coding
• –Data suggesting Bayesian inference is achieved by predictive coding is inconclusive
• –Making predictions does not necessarily imply predictive coding