Abstract
Pigs (Sus scrofa) originated in Southeast Asia and expanded to Europe and North Africa approximately 1 MYA. Analyses of porcine Y-chromosome variation have shown the existence of two main haplogroups that are highly divergent, a result that is consistent with previous mitochondrial and autosomal data showing that the Asian and non-Asian pig populations remained geographically isolated until recently. Paradoxically, one of these Y-chromosome haplogroups is extensively shared by pigs and wild boars from Asia and Europe, an observation that is difficult to reconcile with a scenario of prolonged geographic isolation. To shed light on this issue, we genotyped 33 Y-linked SNPs and one indel in a worldwide sample of pigs and wild boars and sequenced a total of 9903 nucleotide sites from seven loci distributed along the Y-chromosome. Notably, the nucleotide diversity per site at the Y-linked loci (0.0015 in Asian pigs) displayed the same order of magnitude as that described for autosomal loci (~0.0023), a finding compatible with a process of sustained and intense isolation. We performed an approximate Bayesian computation analysis focused on the paternal diversity of wild boars and local pig breeds in which we compared three demographic models: two isolation models (I models) differing in the time of isolation and a model of isolation with recent unidirectional migration (IM model). Our results suggest that the most likely explanation for the extensive sharing of one Y-chromosome haplogroup between non-Asian and Asian populations is a recent and unidirectional (non-Asian > Asian) paternal migration event.
Introduction
Sus scrofa emerged as a new species in the tropical forests of Southeast Asia during the Pliocene, 3–4 MYA (Frantz et al. 2016). Genomic analyses have demonstrated that there was an extensive and asymmetric hybridization of S. scrofa with other suid species (e.g., Sus verrucosus), an event that was facilitated by the existence of land bridges connecting the islands of Borneo, Java and Sumatra during the glacial periods of the Plio–Pleistocene (Frantz et al. 2016). For a period of approximately 1–2 MYA, S. scrofa migrated westward, colonizing Eurasia and North Africa and replacing local Sus species (e.g., Sus strozzi and Sus minor in Europe), which became extinct. This large-scale dispersal of S. scrofa left a durable genetic footprint in the form of much higher variation in Asian than in European wild and domestic porcine populations (Li et al. 2004; Larson et al. 2005; Ramirez et al. 2009). Approximately 10,000 YBP, pigs were independently domesticated in the Near East, China (Larson et al. 2005), and possibly other locations.
European and Asian wild boar and pig populations show strong genetic divergence that can be observed when comparing variation of their mitochondrial (Giuffra et al. 2000) and nuclear (Groenen et al. 2012; Frantz et al. 2015) genes. Comparative genomic studies have shown that specimens from these two pools (i.e., European and Asian wild boars) diverge, in terms of minimum allele frequencies or alternative allele fixation, at millions of polymorphic sites (Groenen 2016). This feature suggests that these two gene pools remained isolated for 0.8–1 MYA after the initial dispersal of S. scrofa across Eurasia. This inexistent or limited gene flow increased substantially when Chinese sows were massively imported into the United Kingdom two centuries ago, an historical event that resulted in European pigs exhibiting Asian mitochondrial (29% frequency) and autosomal (35%) haplotypes at considerable frequencies.
A puzzling observation that is difficult to reconcile with the scenario of prolonged geographic isolation depicted above has come from analyses of Y-chromosome diversity. Ramirez et al. (2009) identified two main Y-chromosome haplogroups whose presence has been confirmed in subsequent studies (Cliffe et al. 2010). In stark contrast to the autosomal and mitochondrial data (Giuffra et al. 2000; Groenen et al. 2012), one of these haplogroups is extensively shared by European and Asian wild boars and pigs. Conversely, the second highly divergent haplogroup is exclusively restricted to Asia. Similarly, analyses of a 48 Mb low-recombining region on the X-chromosome have shown that Northern Chinese haplotypes are more closely related to the European than the Southern Chinese ones (Ai et al. 2014; Groenen 2016). In this work, we aimed to compare, through an ABC approach, different demographic models that may explain the paradoxical patterns of Y-chromosome variation observed in wild and domestic pigs from Asia and Europe. To achieve this objective, we partially resequenced seven Y-linked genes and typed their variation in a worldwide sample of 236 S. scrofa specimens.
Materials and methods
Sequencing and genotyping of seven Y-chromosome-linked genes
A representative sample of 236 pigs (S. scrofa) with a worldwide distribution was used to characterize the variability of the Y chromosome (Table S1). The names, origins and breeds of the genotyped and sequenced samples (including outgroups) are shown in Table S2.
For the sequencing experiment, we used 51 S. scrofa individuals plus two outgroups. PCR primers from Ramirez et al. (2009) and several newly designed primers were used to amplify fragments of seven genes on the Y chromosome: SRY, AMELY, USP9Y, DBY, DDX3Y, UTY and EIFS3Y (Fig. 1). Table S3 shows the primers used for amplification. PCR amplification and sequencing conditions followed the amplification and sequencing procedures described by Ramirez et al. (2009) and Ojeda et al. (2011), respectively. The amplified products were sequenced using the BigDye Terminator version 3.1 Ready Reaction Cycle Sequencing Kit in an ABI PRISM 3730 (Applied Biosystems). The analysis of the sequences was performed with SeqScape version 2.5 software (Applied Biosystems) using standard filters, and the sequences were manually edited and verified. The sequenced regions for each locus and their functional annotations are shown in Table S4.
Fig. 1.
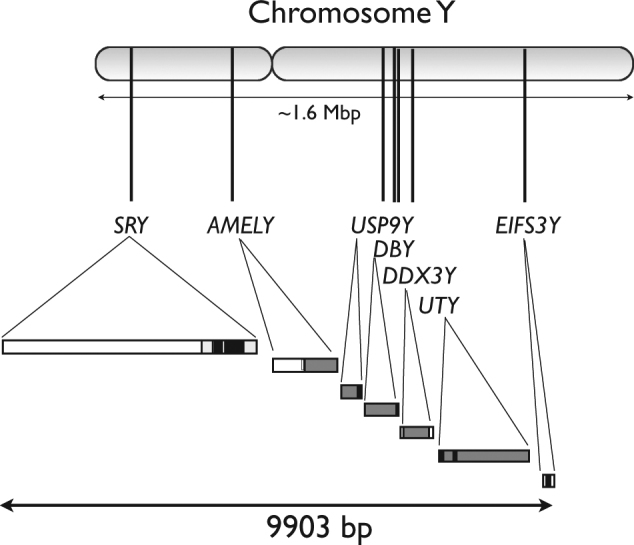
Graphic representation of the porcine Y-chromosome loci analyzed in the current work
Genomic DNA samples from 236 S. scrofa individuals and two outgroup specimens were submitted to the National Center of Genotyping (CeGen, http://www.usc.es/cegen) to be genotyped for 33 single-nucleotide polymorphisms (SNPs) and one indel using a SNPlex assay. The 22 SNPs and one indel located in the loci regions sequenced in this study are listed in Table S5. The remaining 11 SNPs that mapped to the Y-chromosome (CAHM0000165, CAHM0000167, CAHM0000169, CAHM0000170, CAHM0000171, CAHM0000172, CAHM0000173, CAHM0000180, CAHM0000185, CAHM0000187 and CAHM0000192) were obtained from the Porcine SNP60K BeadChip (Ramos et al. 2009).
Diversity analyses
Estimates of the number of haplotypes, heterozygosity (π, Tajima 1983) and population differentiation (Fst, Weir and Cockerham 1984; Hudson et al. 1992) were obtained with mstatspop (available from the authors, https://github.com/cragenomica/mstatspop). A haplotype network was calculated by means of the median-joining algorithm implemented in the Network 4.5 program (Bandelt et al. 1999). S. scrofa individuals were classified into ten different groups according to their geographical distribution and breed type. Two outgroup species (Sus celebensis and Sus cebifrons) were also included. The identification code for each individual and associated information about geographical location and breed type are presented in Table S2.
An analysis of nucleotide variation was performed by considering a 9903-bp-long fragment composed of seven concatenated Y-chromosome loci (SRY, AMELY, USP9Y, DBY, DDX3Y, UTY and EIFS3Y), as shown in Fig. 1. Statistics based on the frequency spectrum were used in these analyses because of the lack of complete information regarding linkage disequilibrium. Site-frequency spectrum statistics for sites, including missing values, were calculated by considering the number of real samples per site (Ferretti et al. 2012). Different estimates of nucleotide variation (θ, π; Watterson 1975; Tajima 1983), neutrality tests (Tajima’s D, Fu and Li’s D, Fay and Wu’s H; Tajima 1989; Fu and Li 1993; Fay and Wu 2000) and mismatch distribution statistics (standard deviation of π; Rogers and Harpending 1992) were calculated. Population differentiation among groups was estimated using Fst coefficients (Weir and Cockerham 1984; Hudson et al. 1992), and their respective P-values were calculated with a permutation test (Hudson et al. 1992) based on 1000 replicates. Fst analysis was performed separately using genotype and nucleotide sequence data and taking into account missing data. The numbers of different variant classes within and among groups, i.e., exclusive, shared, fixed, and other variant classes (Ramos-Onsins et al. 2004) were calculated. We used Babyrousa babyrussa as an outgroup to calculate the number of fixed variants. Note also that there are positions with missing values. This means that the number of variants do not correspond to Watterson’s theta estimation using a fixed sample size, since the number of samples per position is variable.
We estimated the confidence intervals (CI) for the ratio of Y-chromosome to Autosomal (Y/A) variability considering (i) all wild boars together, (ii) Asian wild boars and (iii) Non-Asian wild boars. Estimates were obtained performing a bootstrap analysis by randomly sampling (with replacement) the same number of nucleotide positions as in the empirical Y-chromosome data (Fig. S1). Then, we estimated the pair-wise nucleotide diversity (Tajima 1983) of this bootstrap data matrix and the nucleotide divergence (Nei 1987) using B. babyrussa as an outgroup. This was performed 10,000 times for each of the three main groups of wild boars described above. The obtained estimates of Y-chromosome variation were divided by the autosomal estimate previously obtained (Ojeda et al. 2011; Bosse et al. 2012). As this latter estimate was obtained using genome-wide data, it is considered here as a fixed value. We obtained the distributions and the confidence intervals for the ratio Y/A for the three groups. Difference in the ratio of Y/A for the Asian and non-Asian wild boars was tested using the bootstrap distributions of both Y/A ratios; specifically, we tested if the difference between the Y/A ratio for the Asian and non-Asian wild boars was significantly different from 0.
Approximate Bayesian computation analysis (ABC)
Demographic models
We investigated three alternative demographic scenarios (see Fig. 2 for details) that included two isolation models (I models): (i) model Irecent, which is characterized by a short period of isolation that began less than 0.1·4N e generations ago, and (ii) model Iold, with a longer period of isolation that began more than 0.1·4N e generations ago, and a model of isolation with recent unidirectional migration (model IM). Both I models assume an ancestral population that split T s generations ago into two populations, Asian and non-Asian (mostly European), and remained completely isolated after divergence. Model IM assumes that the Asian and non-Asian populations have been isolated most of the time since their split and that they recently experienced asymmetric gene flow (from the non-Asian into the Asian population). All models are characterized by an exponential change in N e in both Asian and non-Asian populations since their initial split/divergence. Population size changes were modeled by assuming that the population size of the ancestral and the non-Asian populations was a fraction f of the current Asian population. In model IM, we assumed a fixed starting time of migration of T M = 1E-03 (Table S6). This is an arbitrary value in order to reduce the number of parameters in the model. We selected a value of time, which, below this time and to the present, the probability of having new mutations was virtually 0 since the haplotypes of the Asian and non-Asian pigs belonging to the non-Asian haplogroup are highly similar. Note that this parameter is inversely associated with the migration parameter (as it also happens with the magnitude and the time of a bottleneck; Fay and Wu 1999), in the sense that larger T M values would imply smaller migration rates to produce the same observed variability pattern.
Fig. 2.
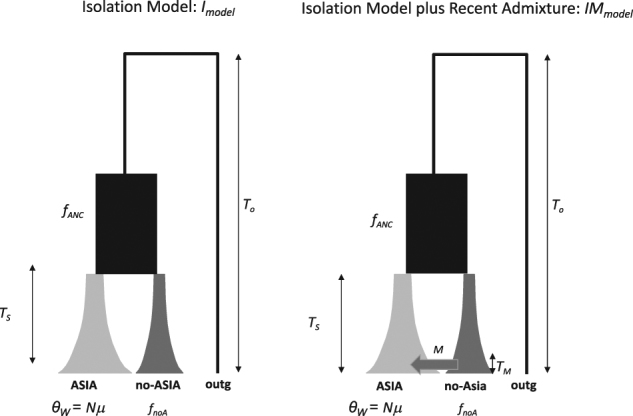
Plots of the two demographic models (I and IM) used in the ABC analysis. Extant populations (Asian and non-Asian) are represented by gray boxes, and the ancestral population is represented in black. Time is depicted on the y-axis (the present time is shown at the bottom of the figure). All parameters are reported in the Materials and Methods section
Prior distributions
The ranges of prior distributions (Table S6) were set according to realistic demographic parameters and to the history of wild boars, which considers what is already known from previous studies based on analyses of the autosomal genome (Groenen et al. 2012). We sampled parameter values from a log-uniform distribution because the range of our priors covered several orders of magnitude. We estimated demographic and mutation population parameters, i.e., the Asian population mutation parameter for the Y chromosome (θ W Asia = N 0 μ, where N 0 represents the current size of the Asian population and μ is the mutation rate), the population size of the non-Asian population relative to the Asian population (f noA), the population size of the ancestral population relative to the Asian population (f ANC), and the time (scaled in N 0 generations) of the split between the Asian and non-Asian populations (T s) and between the ancestral population and the outgroup (T o). For model IM, the migration parameter was modeled as a strong unidirectional population migration (m) from the non-Asian to the Asian population (M = N 0 m).
Simulated data and summary statistics
The ABC analysis was performed using nucleotide sequence data information. Porcine nucleotide sequences were grouped into Asian pigs with nine individuals (AWB = 3 and ALP = 6), non-Asian pigs with 19 individuals (EWB = 2, NEWB = 5, MEDLP = 7 and AFWB = 5) and one outgroup (B. babyrussa). For each demographic scenario, we ran one million simulations with the same sequence length and sample sizes employed in the analysis of the observed Y-chromosome data set. Coalescent simulations were run using the program ms (Hudson 2002). We summarized the observed and simulated nucleotide variation within and between populations in a vector of six summary statistics. This vector included the Watterson’s estimator (Watterson 1975) for the Asian and non-Asian populations, the nucleotide divergence (Nei 1987) between these two populations, the number of exclusive polymorphic sites in each population and the number of fixed mutations in the lineage leading to the outgroup (Wakeley and Hey 1997). We chose these statistics based on available information about frequency data containing missing positions. Summary statistics for the observed and simulated data were computed with the programs mstatspop and mlcoalsim, respectively.
Model choice and validation of posterior probabilities
Posterior probabilities for each demographic scenario were computed on 5000 retained simulations (from a total of 1 million) displaying the smallest Euclidean distances from the empirical observations. The post-sampling adjustment step based on the ABC-GLM method implemented in the ABC toolbox software (Wegmann et al. 2010) was applied in this analysis. The model choice was based on these estimated posterior probabilities. Given that ABC approximates the likelihood function, the impact of this approximation must be carefully evaluated. Hence, we assessed whether our results were robust to potential deviations. To validate the performance of our model choice analysis (i.e., the power of our method to distinguish between models), we generated a vector of summary statistics for 1000 pseudo-observed data sets (PODS) for each model that were identical to our observed dataset in terms of number of positions and sample sizes. Subsequently, we determined the number of times that our model choice procedure correctly identified the true model (e.g., how many times the posterior probability of the true model was higher than the posterior probability of the wrong model). The confusion matrix summarized the proportion of correctly and wrongly identified data sets under each model. We also assessed whether the estimated ABC posterior probabilities under the best model were unbiased (i.e., well calibrated) by comparing them with the empirical posterior probabilities estimated from PODS (Chu et al. 2013). Briefly, we generated 1000 new PODS using model IM and the parameters drawn from the posterior distributions obtained with the ABC analysis. Then, we calculated 1000 empirical posterior probabilities for each of the two competing models. These probabilities were sorted and binned in a list, and the empirical probability was calculated as the proportion of values of the best model for each bin along the list. We compared the empirical probabilities with those obtained using the ABC approach. If ABC probabilities are unbiased, we would expect similar probabilities from the two sources and for each bin.
Validation of parameters
The number of summary statistics is a fundamental aspect affecting the quality of an ABC analysis because a defect or an excess of such statistics may be associated with a substantial loss of information or with “curse of dimensionality” problems, respectively (Beaumont et al. 2002; Wegmann et al. 2010). To confirm that our vector of summary statistics was sufficient (e.g., the probability of the model given the data were the same as the probability of the model given the summary statistics), we evaluated the uniformity of the posterior quantiles for each parameter of the selected model using a Kolmogorov–Smirnov test, and its significance was calculated by applying the Bonferroni correction.
Posterior predictive simulations
We performed posterior predictive simulations to determine whether our best model was capable of reproducing the empirical data with a high probability (Gelman et al. 2003; Thornton and Andolfatto 2006; Ingvarsson 2008). Specifically, we sampled parameter values from the probability density functions of the marginal posterior distributions of the best model (IM) to simulate 1000 replicates with the same features of the observed Y-chromosome data (e.g., fragment length and sample sizes). We then determined whether the observed vector of summary statistics fell within the distribution of summary statistics of the vector of simulated data.
Coalescent simulations to study the behavior of the ratio of Y-chromosome to autosomal (Y/A) variability
We performed extra coalescent simulations using mlcoalsim v2 software (available at https://github.com/cragenomica/mlcoalsim-v2) to infer Y/A ratios under different demographic scenarios and to compare them with the ratios of the observed data. The coalescent algorithm in mlcoalsim corrects the population size of Y-linked loci to a factor of 0.25 of that of autosomal loci. Two main demographic scenarios were considered: Subdivision and Population Decline. For each one, we also considered a scenario in which selection is operating on Y-linked loci (see below). One million iterations were performed, and two loci (one Y-linked and one autosomal) and 20 samples per locus were simulated assuming a lack of recombination. The parameters used for each model were arbitrary but sufficiently informative to elucidate the behaviour of the Y/A ratio using different ranges of demographic parameters.
For the Subdivision scenario, we simulated an ancestral population of size N A that split at time T S into two descendant populations (populations 1 and 2) of sizes N 1 and N 2. The model had three parameters, N 2, N A and T S, because the size of the ancestral population and population 2 were relative to the size of population 1, which was fixed at N 1 = 1.0 for convenience. We set a population mutation rate of θ = 0.05. We drew the parameter values from uniform distributions ranging from 0.1 to 1.0 (for population 2), from 1.1 to 2.0 (for the ancestral population) and from 0.01 to 3.0 (for the split time). The size of population 2 and the split time parameters were plotted whereas the effective size of the ancestral population N e was considered as a nuisance parameter. For the population decline scenario, we simulated a single ancestral population of size N A that changed to a current size N 0 at time T D in the past. We used a lower level of variability (θ = 0.001) than in the previous scenario to simulate a broad range of decline intensities. Note that coalescent simulation scales parameters by the current population size and moves backward in time. Parameter values were sampled from log-uniform and uniform distributions for T D and N A, and their ranges were 0.0001–60 and 1–500, respectively. Time was expressed in 4N units in all cases. Selection on linked loci was simulated as a reduction in the population size at the Y-linked loci to emulate the effective reduction in variability caused by the action of linked selection (positive or negative).
It has been documented that for strong selection the levels of variability are reduced by a factor of around one order of magnitude (Wilson Sayres et al. 2014). In this article, Wilson Sayres et al. (2014) demonstrate that the low diversity observed in the human Y-chromosome is not consistent with a purely neutral model, and that purifying selection, removing harmful mutations, and possibly positive selection have played key roles in the evolution of Y-chromosome variation by erasing neutral polymorphisms. Given that selection could reduce drastically the Y/A ratio, we modeled selection simulating even a strongest effect (22×). Here, we did not intend to discern the nature of selection acting on the Y-chromosome (background or positive selection), we are just interested in testing whether such strong selective effect added to the underlying demographic scenarios could generate patters of variability compatible with our observed data. Intermediate patterns between no reduction and 22× reduction (e.g., 10×) are expected to be in the middle of these two conditions.
We also modeled LD (using the ZnS statistic, Kelly 1997) and nucleotide variability (Watterson 1975) to further elucidate the expected patterns of LD and variability under the IM scenario. This procedure was performed for both (i) the ratio Y/A (i.e., Y-linked loci vs. autosomal loci) in the Asian population and (ii) the ratio A noAsian /A Asia (i.e., non-Asian autosomal vs. Asian autosomal loci). We used arbitrary parameters that were compatible with previously described estimated parameters for the ABC analysis. The parameter values for these models are detailed in the Supplementary Information.
Results
The high genetic diversity at Y-linked loci is explained by the existence of two main haplogroups
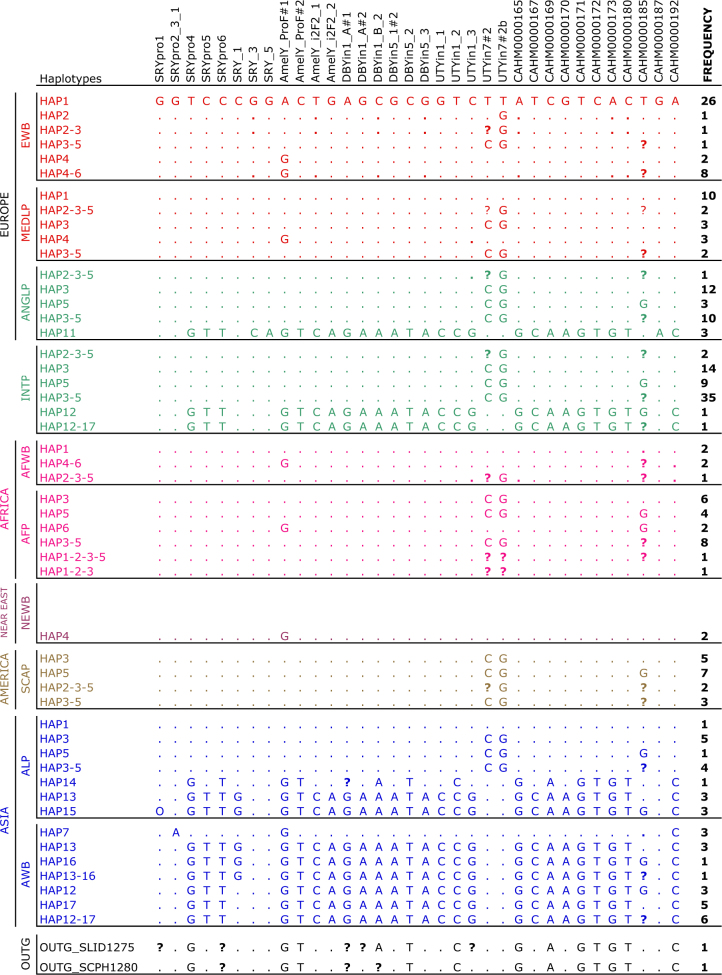
Two different haplogroups were observed in the 236 pigs genotyped for 33 SNPs and 1 indel: the Eurasian haplogroup, which includes haplotypes 1 to 6, and the Asian haplogroup, which includes haplotypes 11 to 17. These two haplogroups are highly divergent (Fig. 3; Table S7). Whereas the Asian haplogroup (see Fig. 4a) is confined to Asia (with the exception of Tamworth swine and minipigs), the Eurasian haplogroup is ubiquitous and can be found in the entire geographic area under study. Tamworth pigs (included in the ANGLP group) and several African pig samples exhibit the Asian haplogroup, a feature that might be the consequence of a recent introgression (Ramirez et al. 2009). The high genetic differentiation between both haplogroups is also reflected in the network shown in Fig. 4, which shows that the two haplogroups are separated by a long branch. The outgroup (Sus celebensis) and a wild boar sample from Indonesia are located in the middle of this branch. Interestingly, the outgroup species shows an intermediate haplotype between the two haplogroups of S. scrofa (i.e. a very short branch instead of a large branch proportional to the divergence time), possibly because the variants selected for genotyping were mostly exclusive to pigs.
Fig. 3.
Matrix representing the observed haplotypes inferred from Y-chromosome genotyping data. Each column represents a single SNP position. The number of different haplotypes observed in each group or population is also indicated. Haplotypes 1–6 and 11–17 belong to the Eurasian and Asian haplogroups, respectively. The absolute frequency of each haplotype is indicated on the right side of the figure. Dots indicate the presence of the same variant as the first sample on the top. O indicates a complex pattern (indel). A question mark indicates unknown data
Fig. 4.
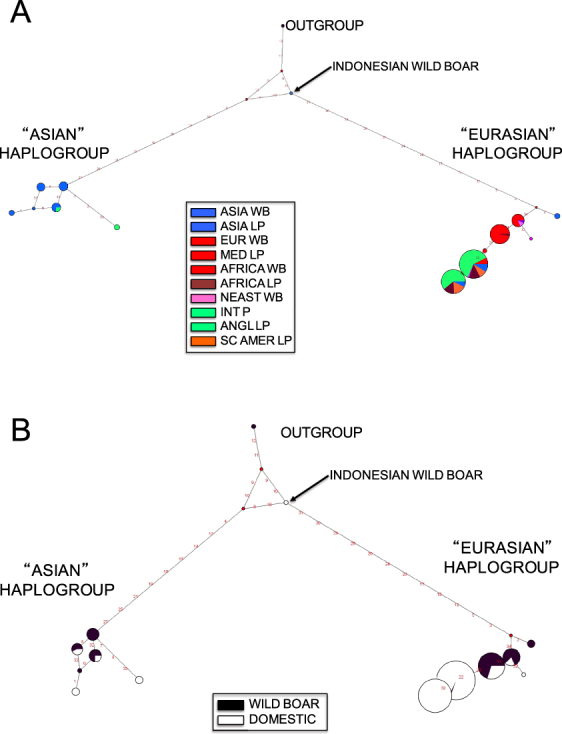
Median-joining network of Y-chromosome haplotypes in a ten pig and wild boar populations, and b domestic and wild pigs. The sizes of the circles are proportional to the haplotype frequencies of each population
The population differentiation between the Asian and non-Asian groups is quite high (Fst values >0.5) and statistically significant using either nucleotide or genotype data (Table S8). The pairwise Fst analysis using only genotype data (see below) revealed that the lowest population differentiation coefficients are those of populations harboring haplotypes belonging to both haplogroups at relatively high frequencies (i.e., ANGLP and ALP pigs vs. the remaining individuals; Table S9A, B). Note that when the Fst analysis is performed comparing each of the 10 groups of pigs among them, the EWB, MEDL, AWB and NEWB pigs show no differentiation among them as the ANGLP, INTP, AFP and SCAP do. The rejection of the null hypothesis of no differentiation mainly depends on the presence/absence of the Asian and the Non-Asian haplotypes (e.g., in the case of the comparison between MEDLP and ANGLP, we obtained a significant result because of the MEDLP population exhibits only the Non-Asian haplotypes whereas the ANGLP population exhibits both Asian haplotypes and non-Asian haplotypes) and the frequency (high or low) of the haplotypes 2, 2–3, 3–5 and 2–3–5 in these groups (e.g., EWB compared to SCAP). The Asian pigs (ALP and AWB) are the most differentiated ones, being the AWB the most differentiated among the rest of the pigs. Our Fst analysis was performed using SNP data because the sample size of sequence data was very small and the outcome of an Fst analysis based on them could lead to a type II error (i.e., lack of power), and thus, some discrepancies may arise due to a bias in the levels of variation due to the sampling process used to find the SNPs (i.e., Ascertainment bias) compared with an Fst analysis using sequence data. Of note, the presence of domesticated and wild animals carrying both Y-haplogroups strongly supports the hypothesis that domestication occurred independently in the Far East and Near East (Fig. 4b).
Estimates of nucleotide diversity and test statistics at Y-linked loci
The levels and patterns of silent nucleotide diversity at seven partially resequenced Y-linked loci are shown in Table 1 (see also the table of polymorphisms in Fig. S2). The level of silent nucleotide variation for each group is quite different, being generally low for non-Asian (except for African pigs) and quite high for Asian populations (wild and domesticated). As expected, the co-segregation of haplotypes belonging to the two highly divergent haplogroups increases the levels of estimated variability. Asian populations exhibit the highest variability, whereas the International, Anglosaxon and South and Central American pig breeds are the least variable. The lack of Y-chromosome nucleotide diversity in the International and Anglosaxon breeds could be a consequence of the small sample size; however, previous studies have shown that the autosomal nucleotide diversity of some non-Asian populations is generally low (Bosse et al. 2012).
Table 1.
Silent-nucleotide variability and patterns of variation for each defined group
| Group | nsam | Nucleotide variability | Patterns of variability | Mistmach distribution | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| S | Θ | Π | Tajima’s D | Fu&Li’s D | Fay&Wu’s H | s.d. | Skewness | Kurtosis | ||
| EWB | 2 | 1 | 0.00027 | 0.00027 | NA | NA | NA | NA | NA | NA |
| MEDLP | 7 | 2 | 0.00014 | 0.00013 | −0.710 | 1.441 | −2.729 | 1.025 | −1.079 | −2.339 |
| INTP | 14 | 0 | 0.00000 | 0.00000 | NA | NA | NA | 0.000 | NA | NA |
| ANGLP | 2 | 0 | 0.00000 | 0.00000 | NA | NA | NA | NA | NA | NA |
| AFWB | 5 | 4 | 0.00143 | 0.00143 | NA | NA | NA | 4.216 | −1.186 | −2.893 |
| AFP | 5 | 16 | 0.00115 | 0.00137 | 1.875 | 1.848 | 0.209 | 10.892 | −1.186 | −2.893 |
| NEWB | 5 | 2 | 0.00022 | 0.00022 | NA | 0.850 | −0.850 | 1.757 | −1.186 | −2.893 |
| SCAP | 2 | 0 | 0.00000 | 0.00000 | NA | NA | NA | NA | NA | NA |
| AWB | 3 | 18 | 0.00218 | 0.00218 | NA | 0.763 | −0.763 | 17.963 | −2.449 | NA |
| ALP | 6 | 21 | 0.00164 | 0.00179 | 0.628 | 0.752 | 0.006 | 14.008 | −1.115 | −2.513 |
| Total | 51 | 29 | 0.00098 | 0.00118 | 0.780 | 0.374 | −1.191 | 9.420 | −0.859 | −1.832 |
AFP African pig, AFWB African wild boar, ALP Asian local pig, ANGLP Anglo-Saxon local pig, AWB Asian wild boar, EWB European wild boar, INTP commercial pig, Kurtosis fourth moment of Tajima’s θ estimator, MEDLP Mediterranean local pig, NA non-available, NEWB Near-East wild boar, nsam number of samples, S number of polymorphic sites, SCAP South and Central American pig, s.d. standard deviation of Tajima’s θ estimator, Skewness third moment of Tajima’s θ estimator,Total all samples together as a single population, θ Watterson estimator, π nucleotide diversity
If we focus on non-commercial breeds (wild boars plus local pigs, excluding the ANGLP group; Table 2), the estimated nucleotide diversity at the Y-linked loci of the entire pig data set has the same order of magnitude as that estimated for autosomes (~0.0023; Bosse et al. 2012). Moreover, the estimated divergence (K = 0.023; Table 2) with the outgroup species is also similar at Y-linked and autosomal loci (K = 0.020; Ojeda et al. 2011). This similarity between the levels of variability observed at Y-chromosome and autosomal loci is surprising because it would be expected that the lack of recombination on the Y chromosome and its lower effective population size might result in a drastic reduction in its nucleotide diversity (Karafet et al. 2002; Pool and Nielsen 2007, 2008). We also observed that the level of silent nucleotide variation (π) was quite different between the Asian and non-Asian groups (Table 2), being low in non-Asian samples (0.29 variants per 1000 positions between two random individuals) and quite high in Asian samples (1.58 variants per 1000 positions between two random individuals).
Table 2.
Silent nucleotide variability for wild boar and local pigs in asia vs. derived populations (non-Asia)
| nsam | Nucleotide variability | Patterns of variability | Mismatch distribution | Divergenceb | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| S | θ | Π | Tajima’s D | Fu&Li’s D | Fay&Wu’s H | s.d. | Skewness | Kurtosis | K | ||
| Non-Asiaa | 19 | 6 | 0.00029 | 0.00030 | 0.228 | 0.781 | −1.198 | 2.29 | −1.009 | −2.036 | 0.023 |
| Asia | 9 | 24 | 0.00138 | 0.00158 | 0.875 | 0.864 | 0.163 | 12.15 | −1.044 | −2.184 | 0.023 |
a The Non-Asian sample contains European wild boars (EWB), Mediterranean local pigs (MEDLP), Near-East wild boars (NEWB), African wild boars (AFWB) and African pigs (AFP). The Asian sample contains Asian wild boars (AWB) and Asian local pigs (ALP). bThe divergence of S. scrofa populations is calculated regarding to B. Babyrussa. nsam number of samples, Kurtosis fourth moment of Tajima’s θ estimator, S number of polymorphic sites, s.d. standard deviation of Tajima’s θ estimator, Skewness third moment of Tajima’s θ estimator, θ Watterson estimator, π nucleotide diversity. The number of silent positions analyzed is 7561
The values of the statistics based on the frequency spectrum for non-commercial breeds of non-Asian population, although not significantly different from neutral expectations, may indicate an alternative non-stationary model in which the non-Asian population might have suffered a population decline (positive Tajima’s D and Fu and Li’s D values but negative Fay and Wu’s H; Table 2). In contrast, the Asian population might have undergone a strong migration event (positive Tajima’s D, Fu and Li’s D and Fay and Wu’s H values as well as a strong standard deviation of the mismatch distribution), as shown in Table 2.
The classification of the variants, depending on whether they are shared (S shared), exclusive to a group (S x), fixed (S f) or fixed in one group but polymorphic in the other (S fx), is shown in Fig. 5 (see Ramos-Onsins et al. 2004 for a description of the statistics). We found that there is no variation within the Asian haplogroup, whereas there is some diversity within the Eurasian haplogroup (S xASIA_E + S xDER + S shared = 9). We also found that the fixed differences between haplogroups (defined in Fig. 4 and indicated here by gray and black lines) are quite high (S f DERxASIA + S x ASIA_A = 17). Thus, there is high differentiation among haplogroups (π among = 0.0027 at silent positions) and higher variability in the Eurasian haplogroup (π = 0.00040) compared with the Asian one (π = 0).
Fig. 5.
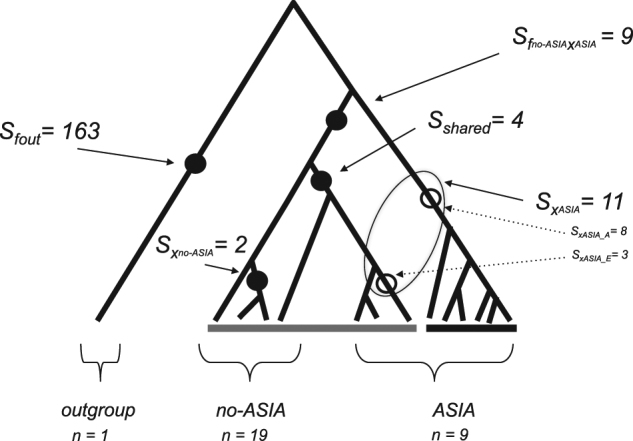
A description of Y-chromosome variation. Mutations are classified as fixed vs. the outgroup (S fout), exclusive to the Asian and non-Asian populations (S xASIA and S xDER), shared between the Asian and non-Asian populations (S shared) or fixed in the non-Asian population but polymorphic in the Asian population (S fDER×ASIA). Gray and black horizontal lines below the tree denote mutations belonging to the Eurasian (gray) or Asian (black) haplogroups
Comparison of demographic models through an ABC approach
It is known that some European and African domesticated breeds have been recently introgressed with Asian domestic breeds (Giuffra et al. 2000; Megens et al. 2008; Ramirez et al. 2009; Ai et al. 2013). On the contrary, wild boar populations (and traditional local breeds) are thought to be mostly unaffected by recent commercial introgression events (but see Goedbloed et al. 2013). Clearly, the history of the Y chromosome can be better discerned using wild and local domestic populations. The differential pattern of geographic distribution of the two haplogroups (two in Asian and one in non-Asian samples) could be explained by four different alternative hypotheses: (i) an ancestral population (Asian) that split very recently, creating a new, relatively small population (non-Asian) that might have inherited only a single haplogroup as a consequence of its small population size (model Irecent); (ii) a model assuming a relatively long isolation process between both groups (Asian and non-Asian) but large differences in their effective population sizes (model Iold); (iii) an isolation process followed by recent gene flow from the non-Asian to the Asian population (model IM); and (iv) an isolation event between the Asian and non-Asian groups with the additional introgression of individuals from a hidden population (i.e., an extinct population or other species) into the Asian population (model IME). We used an ABC approach to compare the first three models, and the fourth model is discussed below. We set the range of prior distributions of model parameters to encompass values that are compatible with biologically realistic data and with what is already known from autosomal and mitochondrial data. The Irecent isolation model, which assumes the recent divergence of the non-Asian subpopulation, yielded the best fit to our Y-chromosome data. However, this scenario becomes quite unrealistic when autosomal, mitochondrial and Y-linked data are considered (e.g., see estimated model parameters in Groenen et al. 2012; Ojeda et al. 2011; Giuffra et al. 2000). Figure S3 shows the expected ratio of variability between Y-chromosome and autosomal loci (Y/A ratio), data obtained by performing coalescent simulations under the Subdivision and Population Decline models. The expected Y/A ratio under a simple model (the stationary Standard Neutral Model, SNM) is 0.25 (i.e., there are four times more chromosomes in the autosomal population than in the Y one). Instead, we observed a much higher ratio (Y/A = 0.52; π Y = 0.0012; π A≃0.0023; Ojeda et al. 2011; Bosse et al. 2012) even when we normalized by the amount of divergence as a proxy for the mutation rate using B. babyrussa as an outgroup (Y/A = 0.46; π Y/K Y = 0.0012/0.023; π A/K A≃0.0023/0.020; CI 0.31–0.67). The observed Y/A ratio is not concordant with a recent split, but it is compatible with a moderately ancient split (approximately 0.6 × 4N generations; Fig. S3), which corresponds to approximately 50,000 generations or ~250,000 years (assuming N e = 20,000 and 5 years per generation, Groenen et al. 2012). In addition, when we included a reduction factor (e.g., 22×) of the levels of Y-chromosome variability as a proxy for the action of linked selection, we found that the observed values were compatible only with a model with a very ancient split time, i.e., approximately 0.9 × 4N generations (Fig. S3B), which corresponds to approximately 70,000 generations or ~360,000 years.
The IME and Irecent models suffer from similar incompatibilities with the empirical data. The main difference between the Irecent and IME models is that the high level of variation observed in the Asian population originates from different factors: in the Irecent model, the high level of variation in Asia originates from a large population size, whereas in the IME model it originates from the introgression of a hidden population into Asia. The introgression of a hidden population would introduce a divergent haplotype that would resemble the Y-chromosome variability patterns. Nevertheless, it is necessary to assume a very low divergence time between the European and Asian populations to explain the high similarity among the haplotypes belonging to the Eurasian haplogroup. Moreover, and as argued above, a recent split between these two populations is incompatible with inference analyses using autosomal and mitochondrial data performed to date, and it is also incompatible with simulations using the observed Y/A ratio of variability. Therefore, we discarded the Irecent and the IME model.
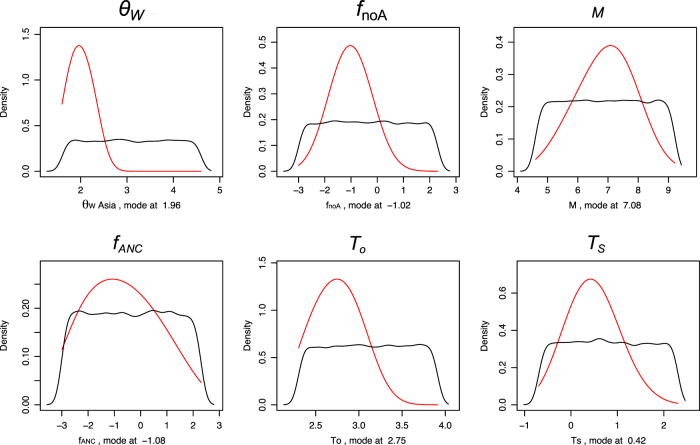
The posterior probabilities of models Iold and IM and the fraction of the retained simulations with smaller or equal likelihoods than our observed data (P-value of the model) are shown in Table S10. The cross-validation analysis using PODS clearly validates the comparison of both models in the ABC framework. Indeed, the confusion matrix confirms that the true model was correctly identified by our ABC model choice procedure in more than 96% of cases (96.1% and 97.8% for models Iold and IM, respectively; Fig. S4A). Moreover, the empirical model probabilities obtained from these PODS are larger than the ABC posterior probabilities; therefore, the model choice is conservative (Fig. S4B). The Y-chromosome data strongly support the asymmetric migration model (IM) over the Iold one (PP IM > 0.999). In addition, the high likelihood of the observed data (P-value = 0.95) demonstrates that our data are highly probable under this demographic scenario. Assuming that the divergence time between S. scrofa and B. babyrussa is at least 10 MYA (Theimer and Keim 1998; Gongora et al. 2010) and assuming a generation time of 5 years (Groenen et al. 2012), the posterior estimates of model parameters would suggest that the split of the current non-Asian and Asian Y lineages occurred not before than 0.97 MYA (95% interval of 0.36–2.97 MYA using Ts 95% HPD; Fig. 6; Table 3) from an ancestral population of approximately 28,000 male individuals (using the estimated mutation rate and the level of variability θ for calculating N e, note that the number of males is half of N e). We also estimated an increase in population size in the Asian lineages (~80,000 male individuals) and a recent introgression of European sequences into Asia (~0.7% of immigrants per generation). The estimated mutation rate is 1.15E-9 mutations/bp × year. This is a lower rate than that used for autosomes (2.5E-8 mutations/bp × year; Groenen et al. 2012), which suggests a reduction in the number of neutral positions in the Y-chromosome by the effect of selection (Wilson Sayres et al. 2014). Posterior predictive simulations (Fig. S5) corroborate model IM as a plausible demographic scenario for the Y-chromosome data. All the estimated summary statistics values were frequently obtained when simulations were performed using the posterior densities of this model as prior distributions, which are generally not biased (Fig. S6).
Fig. 6.
Priors and posterior densities of parameter estimates obtained in the ABC analysis (IM model). The x-axis is plotted on a log scale (except for the T O parameter). Prior densities are plotted in black, and posterior densities are shown in red
Table 3.
Estimates of the demographic parameters of models
| Model | Parameter | Mode | HPD 95 | ||
|---|---|---|---|---|---|
| Model Iold | θ W Asia | 3.00E-04 | 1.52E-04 | – | 3.42E-04 |
| f noA | 6.70E-02 | 3.48E-03 | – | 1.14 | |
| T s | 5.73E-01 | 5.00E-01 | – | 1.29 | |
| f ANC | 4.35E + 00 | 2.97E-01 | – | 10 | |
| T 0 | 4.47E + 01 | 22.09 | – | 50 | |
| Model IM | θ W Asia | 9.00E-04 | 3.81E-04 | – | 9.23E-04 |
| f noA | 3.59E-01 | 7.89E-02 | – | 1.63 | |
| Μ | 1.19E + 03 | 154.47 | – | 6002.91 | |
| T s | 1.52E + 00 | 5.54E-01 | – | 4.64 | |
| f ANC | 3.40E-01 | 5.00E-02 | – | 4.85 | |
| T 0 | 1.56E + 01 | 9.97 | – | 25.03 | |
θW Asia, Asian current population mutation parameter per nucleotide. f noA, a fraction of the non-Asian current population size. M, unidirectional population migration from the non-Asian to the Asian population. T s, time of split between the Asian and the non-Asian population. f ANC, fraction of the ancestral population size. T 0, time of split between the ancestral population of these populations and the outgroup. T M, time of the onset of migration is fixed to 1E-3. Times and population migration parameter are given in N units
A consequence of the migration IM scenario would be intense linkage disequilibrium produced by the segregation of highly differentiated haplotypes. It is expected that the disequilibrium among positions may decrease in autosomal regions of high recombination as a function of the time elapsed since the migration event. On the other hand, the variability of the Asian subpopulation should increase after the migration event. Interestingly, when we modeled the LD and nucleotide variability, we observed that the values for variability of the Y/A ratio (~0.44) and the A noAsian /A Asia (~0.18) as well as the LD values of the ratio A noAsian /A Asia (>1) were compatible with a model of recent migration (Fig. S7B).
Discussion
As expected, Y-chromosome variability was lower in the European wild and local domestic lines, which exhibited only one haplogroup, than in the Asian wild boars and local pig populations (which exhibited two). The high frequency of Asian mitochondrial haplotypes in commercial European breeds (Fang and Andersson 2006) combined with the lack of segregation of one of the Y-chromosome haplogroups in most of these breeds suggests that the introgression with Asian blood during the eighteenth and nineteenth centuries was exclusively maternal (Ramirez et al. 2009). The low levels of variability within haplogroups suggest the existence of population structure in the data set. In addition, the observed data can be explained using a simple non-recombining tree (Fig. 5), which indicates that the non-Asian samples are only a subset of the total variability observed in Asia. One possible scenario is that the Asian samples were, as a matter of fact, geographically divided into two populations. Indeed, although some level of population structure has been observed between North and South Chinese pigs in analyses of X-linked and autosomal data (Ai et al. 2014; Frantz et al. 2013), none of these populations seems to be closely related to the non-Asian population.
A puzzling observation made by us and highlighted in previous studies (Ramirez et al. 2009; Cliffe et al. 2010) is the extensive sharing of one Y-chromosome haplogroup among Asian and European wild and domestic local pigs. Genetic divergence is very low and, as shown in Fig. 4, Asian and European individuals cluster together despite having diverged 0.8–1 MYA. This finding contrasts with the reported results from taurine and zebuine cattle, two subspecies that diverged 250,000 years ago and that do not share Y-chromosome haplotypes (Pérez-Pardal et al. 2010).
We have discussed four models, model Irecent (recent split), model Iold (ancient split), model IM (migration) and model IME (migration into Asia from a hidden population) to explain these findings. Notice that henceforth, for model-based inferences, we refer to Asian and non-Asian populations as those only including wild boars and local domestic pigs. Models Irecent and IME are not in agreement with autosomal and mitochondrial data, which support an ancient split between European and Asian populations 0.2 and 1.6 MYA (Giuffra et al. 2000; Ojeda et al. 2011; Groenen et al. 2012; Frantz et al. 2015). However, the IM model is more probable than the Iold one, and it is in agreement with the autosomal and mitochondrial data. The proposed scenario (Fig. 7) assumes that an ancestral population originating in Southeast Asia split into an Asian and a non-Asian subpopulation and that the latter expanded across the Eurasian continent. Subsequently, a strong migration event would have caused the colonization of the Asian population with males from the non-Asian population. If so, we should observe marked differences in the Y/A ratio between the non-Asian and Asian populations because an increase in autosomal variability levels in the Asian population is expected, albeit at a slower rate compared with the Y chromosome. In consequence, the Y/A ratio should be markedly higher in Asian than in non-Asian populations. In fact, we observed significantly higher Y/A ratios (π Y/K Y)/(π A/K A) in Asia (0.46; CI 0.31–0.70) than in non-Asian populations (0.23; CI 0.06–0.45) (Fig. S1, P-value = 0.035). The autosomal variability estimates were obtained from Bosse et al. (2012; Table 2 and Fig. 1a), and the autosomal divergence value was obtained from Ojeda et al. (2011). This increased Y/A ratio in the Asian population is compatible with the IM model of the introduction of the non-Asian Y-chromosome into the Asian population (Fig. S7). Hence, these results could be explained by the combined effect of the high differentiation between Asia and non-Asia populations and the sex-biased migration process. Although it has not been tested explicitly here (since we do not have autosomal data from the same samples), indirect observations from genome data (i.e., the presence of highly divergent Y-chromosome haplotypes and the lack of mitochondrial DNA of European origin in Asian samples) point out to this hypothesis. Indeed, Ramirez et al. (2009) demonstrated that there is an extensive sharing of one of the two main Y-chromosome haplogroups by Asian and non-Asian pigs, while according to the results presented by Larson et al. (2005) and many others, the sharing of mitochondrial haplogroups between Asian and non-Asian pigs has not been observed (Giuffra et al. 2000; Larson et al. 2005; Table S2). Other demographic events, such as population decline (Groenen et al. 2012; Li et al. 2013), have been proposed to explain the evolution of S. scrofa genetic diversity. Nevertheless, there is no reason to expect that a strong effect of population reduction affected the Y/A ratio (Fig. S3C). Additionally, selection on the Y chromosome under a population decline scenario combined with its non-recombinant nature should decrease even more this ratio, as shown in Fig. S3D. The results obtained when we modeled LD and patterns of variation for Y-linked and autosomal data (Fig. S7) by means of coalescent simulations are also in agreement with the IM demographic model. A recent study by Frantz et al. (2015), also based on the ABC methodology, reported that Asian and European populations split from an ancestral population with the same order of magnitude as their current population sizes. These authors used a method to model the migration parameter that differed from ours; i.e., migration was defined along the entire period of isolation and thus is not directly comparable with our estimate. Note that in our model we cannot estimate the specific magnitude of the migration parameter, because migration is inversely related to the time since migration started. In any case, migration is decisive to fit the model to the empirical data.
Fig. 7.
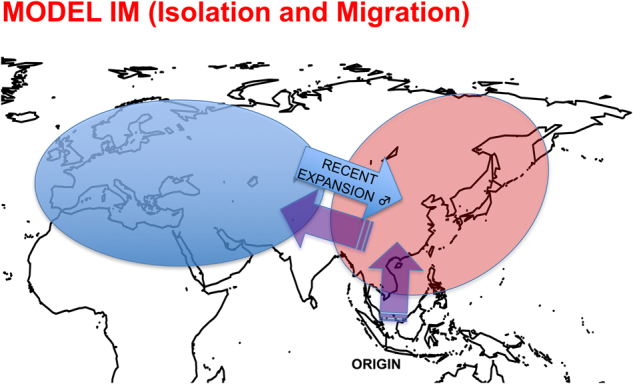
Proposed model of the evolution of pig Y-chromosome variation. Pigs emerged as a species in Southeast Asia and spread to south-central China and subsequently to Europe. Recently, a migration event from non-Asian to Asian populations occurred. Note that the figure is a simple representation of the model IM and do not indicate the real distribution of the populations
Our results are compatible with a differential migration process between males and females. The introduction of a large number of non-Asian haplotypes into Asian population can be explained by (i) a massive introduction of male individuals or by (ii) a moderate introduction of a number of males followed by a selective process that increased their frequency in a relative short time. The first hypothesis seems, in our opinion, less credible. Note that although an isolation with continuous and bidirectional migration model cannot be completely discarded, the absence of intermediate haplotypes in both populations, Asian and non-Asian, the presence of two highly differentiated Y-chromosome haplogroups only in non-Asian population and the significantly lower levels of variability in non-Asian populations compared with their Asian counterparts strongly suggest that two populations were isolated for a long time. Thus, the bidirectional migration model has not been considered in our analysis since there is no presence of two haplotypes in the non-Asian sampled population, and consequently the migration parameter from Asia to non-Asia population will be compatible with a value of zero. Frantz et al. (2015) showed that, at autosomal loci, a model of bidirectional migration (that is, including non-zero migration between population pairs) was more likely than a model with no migration. Nevertheless, none of their proposed models considered unidirectional migration from non-Asian to Asian wild boars, and hence there is no clear evidence of such bidirectional migration between these two populations.
In contrast to Y-chromosome data, population structure (i.e., the presence of two main haplotypes) has not been observed when autosomal data were analysed in Asian wild boar populations (Frantz et al. 2015). Given that the most probable model in our ABC analysis was model IM, we hypothesize that the high levels of recombination at autosomal loci might have produced a large number of shared polymorphisms, although signs of high divergence between the groups are still detectable. The presence of a large number of shared polymorphisms at autosomal loci in all of the sampled individuals implies that the effect of the migration was intense.
Two main different interpretations are compatible with the IM model: (i) a unique and relatively recent event of migration from non-Asian to Asian population that spread across all the Asian geographical distribution or (ii) a number of independent introgression events from non-Asian wild population that occurred at many different locations on the Asian continent, which may have taken place very recently (in the last three centuries). In the first case, the introduction and maintenance of a reduced number of non-Asian individuals harboring the non-Asian haplotype (only males contributed to this introgression event) into the Asian pig population might be favored by the existence of some kind of natural selection. Also, it is expected that linkage disequilibrium at autosomal regions would be relatively reduced given that both haplogroups could have enough time to recombine. In the second case, an alternative explanation would be that both, Asian wild boars and domestic pigs have been introgressed with European germplasm given that we observed some wild boars (e.g., three out of the six Japanese wild boars) and some Asian local pigs exhibiting the Non-Asian haplotypes (Fig. S2 and Table S7). We found that the distribution of Japanese pigs exhibiting the non-Asian and the Asian haplotypes are geographically structured, with pigs from the Ryukyu Islands exhibiting the Asian haplotype whereas pigs from the main Island exhibit the Non-Asian haplotype (Fig. S8). Although some studies (Watanobe et al. 1999; Cho et al. 2009) showed that some of these populations, which are genetically differentiated (e.g., Japanese wild boars from the main island and the Ryukyu islands belong to two different subspecies of wild boar), are descendants of distinct geographical populations, all of them were found to belong to the Asian wild boar cluster when they were analyzed jointly with a worldwide boars sample. It is worth to mention that all these studies were performed using mitochondrial DNA and different results might be obtained with other kind of markers. If Asian pigs were introgressed with European germplasm, one would expect that, given that some wild boars and domestic pigs exhibit the Non-Asian haplotype, multiple events of introgression, due to a secondary contact, should have occurred since pigs harboring the non-Asian haplogroup are distributed in multiple areas geographically distant. Moreover, if that was the case (e.g., in Japan but also in Korea and in some other regions of China), we should also observe a signal in the autosomes, with long haplotype regions well differentiated between Asian and non-Asian haplogroups and this has not been observed so far (Ramirez et al. 2009). Thus, it seems unlikely that our observations were due to such introgression events although we cannot formally discard it here.
In summary, the analysis of porcine Y-chromosome diversity performed by us indicates that the most plausible explanation for the extensive sharing of one Y-chromosome haplotype by Asian and non-Asian pig populations and the restricted distribution of the second haplogroup (only found in Asia) involves the occurrence of paternal gene flow from non-Asian to Asian wild populations. Further studies will be needed to ascertain the causal factors that triggered this male-biased migration event as well as the subsequent expansion of the non-Asian haplogroup in Asia.
Electronic supplementary material
Acknowledgements
We would like to thank Miguel Pérez-Enciso for his intellectual and data contributions to the project. Greger Larson also provided porcine samples. We acknowledge Erica Bianco for insightful discussions about models combining Y-chromosome and autosomal data sets. S.G-R. is supported by a Beautriu de Pinós postdoctoral fellowship (AGAUR; 2014 BP-B 00027). This work was supported by grants CGL2009-09346 (MICINN, Spain) and AGL2016-78709-R (MEC, Spain) to S.E.R.-O. We also acknowledge the financial support of the Spanish Ministry of Economy and Competitivity for the Center of Excellence Severo Ochoa 2016–2019 (SEV-2015-0533) grant awarded to the Center for Research in Agricultural Genomics and by the CERCA Programme/Generalitat de Catalunya.
Author contributions
M.A. contributed to the experimental design of the project and coordinated the sample collection; O.R. and A.O. performed the molecular analyses; S.G.-R. and S.E.R.-O. performed and interpreted the population genetics analyses; and S.G.-R. and S.E.R.-O. led the writing of the manuscript in collaboration with M.A.
Compliance with ethical standards
Conflict of interest
The authors declare no conflict of interest.
Data archiving
The sequences reported in this article have been submitted to GeneBank under accession numbers MF541816-MF542252. The genotype sequences reported in this article have been deposited in Figshare under the accession number doi: 10.6084/m9.figshare.5203897.
Footnotes
Ana Ojeda is deceased. This paper is dedicated to her memory.
Electronic supplementary material
The online version of this article (10.1038/s41437-017-0002-9) contains supplementary material, which is available to authorized users.
Contributor Information
Marcel Amills, Email: marcel.amills@uab.cat.
Sebastian E. Ramos-Onsins, Phone: +34 93 563 6600, Email: sebastian.ramos@cragenomica.es
References
- Ai H, Huang L, Ren J. Genetic diversity, linkage disequilibrium and selection signatures in Chinese and Western pigs revealed by genome-wide SNP markers. PLoS ONE. 2013;8:e56001. doi: 10.1371/journal.pone.0056001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ai H, Yang B, Li J, Xie X, Chen H, Ren J. Population history and genomic signatures for high-altitude adaptation in Tibetan pigs. BMC Genomics. 2014;15:834. doi: 10.1186/1471-2164-15-834. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bandelt HJ, Forster P, Röhl A. Median-joining networks for inferring intraspecific phylogenies. Mol Biol Evol. 1999;16:37–48. doi: 10.1093/oxfordjournals.molbev.a026036. [DOI] [PubMed] [Google Scholar]
- Beaumont MA, Zhang W, Balding DJ. Approximate Bayesian computation in population genetics. Genetics. 2002;162:2025–2035. doi: 10.1093/genetics/162.4.2025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bosse M, Megens HJ, Madsen O, Paudel Y, Frantz LA, Schook LB, et al. Regions of homozygosity in the porcine genome: consequence of demography and the recombination landscape. PLoS Genet. 2012;8:e1003100. doi: 10.1371/journal.pgen.1003100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cho IC, Han SH, Fang M, Lee SS, Ko MS, Lee H, et al. The robust phylogeny of Korean wild boar (Sus scrofa coreanus) using partial D-loop sequence of mtDNA. Mol Cells. 2009;28:423–430. doi: 10.1007/s10059-009-0139-3. [DOI] [PubMed] [Google Scholar]
- Chu J, Wegmann D, Yeh C, Lin R, Yang X. Inferring the geographic mode of speciation by contrasting autosomal and sex-linked genetic diversity. Mol Biol Evol. 2013;30:2519–2530. doi: 10.1093/molbev/mst140. [DOI] [PubMed] [Google Scholar]
- Cliffe KM, Day AE, Bagga M, Siggens K, Quilter CR, Lowden S, Finlayson HA, Palgrave CJ, Li N, Huang L, Blott SC, Sargent CA. Analysis of the non-recombining Y chromosome defines polymorphisms in domestic pig breeds: ancestral bases identified by comparative sequencing. Anim Genet. 2010;41:619–629. doi: 10.1111/j.1365-2052.2010.02070.x. [DOI] [PubMed] [Google Scholar]
- Fang M, Andersson L. Mitochondrial diversity in European and Chinese pigs is consistent with population expansions that occurred prior to domestication. Proc R Soc B. 2006;273:1803–1810. doi: 10.1098/rspb.2006.3514. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fay JC, Wu CI. A human population bottleneck can account for the discordance between patterns of mitochondrial a versus nuclear DNA variation. Mol Biol Evol. 1999;16:1003–1005. doi: 10.1093/oxfordjournals.molbev.a026175. [DOI] [PubMed] [Google Scholar]
- Fay JC, Wu CI. Hitchhiking under positive darwinian selection. Genetics. 2000;155:1405–1413. doi: 10.1093/genetics/155.3.1405. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ferretti L, Raineri E, Ramos-Onsins S. Neutrality tests for sequences with missing data. Genetics. 2012;191:1397–1401. doi: 10.1534/genetics.112.139949. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frantz LA, Schraiber JG, Madsen O, Megens HJ, Bosse M, Paudel Y, et al. Genome sequencing reveals fine scale diversification and reticulation history during speciation in Sus. Genome Biol. 2013;14:R107. doi: 10.1186/gb-2013-14-9-r107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frantz L, Schraiber JG, Madsen O, Megens HJ, Cagan A, Bosse M, et al. Evidence of long-term gene flow and selection during domestication from analyses of Eurasian wild and domestic pig genomes. Nat Genet. 2015;47:1141–1148. doi: 10.1038/ng.3394. [DOI] [PubMed] [Google Scholar]
- Frantz L, Meijaard E, Gongora J, Haile J, Groenen MA, Larson G. The evolution of Suidae. Annu Rev Anim Biosci. 2016;4:61–85. doi: 10.1146/annurev-animal-021815-111155. [DOI] [PubMed] [Google Scholar]
- Fu YX, Li WH. Statistical tests of neutrality of mutations. Genetics. 1993;133:693–709. doi: 10.1093/genetics/133.3.693. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gelman A, Carlin JB, Stern HS, Rubin DB. Bayesian data analysis. London/New York/Cleveland/Boca Raton, FL: Chapman & Hall/CRC Press; 2003. [Google Scholar]
- Giuffra E, Kijas JM, Amarger V, Carlborg O, Jeon JT, Andersson L. The origin of the domestic pig: independent domestication and subsequent introgression. Genetics. 2000;154:1785–1791. doi: 10.1093/genetics/154.4.1785. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goedbloed DJ, van Hooft P, Megens HJ, Langenbeck K, Lutz W, Crooijmans RP, van Wieren SE, Ydenberg RC, Prins HH. Reintroductions and genetic introgression from domestic pigs have shaped the genetic population structure of Northwest European wild boar. BMC Genet. 2013;14:43. doi: 10.1186/1471-2156-14-43. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Groenen MA, Archibald AL, Uenishi H, Tuggle CK, Takeuchi Y, Rothschild MF, et al. Analyses of pig genomes provide insight into porcine demography and evolution. Nature. 2012;491:393–398. doi: 10.1038/nature11622. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Groenen MA. A decade of pig genome sequencing: a window on pig domestication and evolution. Genet Sel Evol. 2016;48:23. doi: 10.1186/s12711-016-0204-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gongora J, Cuddahee RE, Do Nascimento FF, Palgrave CJ, Lowden S, Ho SYW, Simond D, Damayanti CS, White DJ, Tay WT, Randi E, Klingel H, Rodrigues-Zarate CJ, Allen K, Moran C, Larson G. Rethinking the evolution of extant sub-Saharan African suids (Suidae, Artiodactyla) Zool Scripta. 2010;40:327–335. doi: 10.1111/j.1463-6409.2011.00480.x. [DOI] [Google Scholar]
- Hudson RR, Boos DD, Kaplan NL. A statistical test for detecting geographic subdivision. Mol Biol Evol. 1992;9:138–151. doi: 10.1093/oxfordjournals.molbev.a040703. [DOI] [PubMed] [Google Scholar]
- Hudson RR, Slatkin M, Maddison WP. Estimation of levels of gene flow from DNA sequence data. Genetics. 1992;132:583–589. doi: 10.1093/genetics/132.2.583. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hudson RR. Generating samples under a Wright-Fisher neutral model of genetic variation. Bioinformatics. 2002;18:337–338. doi: 10.1093/bioinformatics/18.2.337. [DOI] [PubMed] [Google Scholar]
- Ingvarsson PK. Multilocus patterns of nucleotide polymorphism and the demographic history of Populus tremula. Genetics. 2008;180:329–340. doi: 10.1534/genetics.108.090431. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Karafet TM, Osipova LP, Gubina MA, Posukh OL, Zegura SL, Hammer MF, et al. High levels of Y-chromosome differentiation among native Siberian populations and the genetic signature of a boreal hunter-gatherer way of life. Hum Biol. 2002;74:761–789. doi: 10.1353/hub.2003.0006. [DOI] [PubMed] [Google Scholar]
- Kelly JK. A test of neutrality based on interlocus associations. Genetics. 1997;146:1197–1206. doi: 10.1093/genetics/146.3.1197. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Larson G, Dobney K, Albarella U, Fang M, Matisoo-Smith E, Robins J, et al. Worldwide phylogeography of wild boar reveals multiple centers of pig domestication. Science. 2005;307:1618–1621. doi: 10.1126/science.1106927. [DOI] [PubMed] [Google Scholar]
- Li SJ, Yang SL, Zhao SH, Fan B, Yu M, Wang HS, et al. Genetic diversity analyses of 10 indigenous Chinese pig populations based on 20 microsatellites. J Anim Sci. 2004;82:368–374. doi: 10.2527/2004.822368x. [DOI] [PubMed] [Google Scholar]
- Li M, Tian S, Jin L, Zhou G, Li Y, Zhang Y, et al. Genomic analyses identify distinct patterns of selection in domesticated pigs and Tibetan wild boars. Nat Genet. 2013;45:1431–1438. doi: 10.1038/ng.2811. [DOI] [PubMed] [Google Scholar]
- Megens HJ, Crooijmans RP, San Cristobal M, Hui X, Li N, Groenen MA. Biodiversity of pig breeds from China and Europe estimated from pooled DNA samples: differences in microsatellite variation between two areas of domestication. Genet Sel Evol. 2008;40:103–128. doi: 10.1186/1297-9686-40-1-103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nei M. Molecular evolutionary genetics. New York, NY, USA: Columbia University Press; 1987. [Google Scholar]
- Ojeda A, Ramos-Onsins SE, Marletta D, Huang LS, Folch JM, Pérez-Enciso M. Evolutionary study of a potential selection target region in the pig. Heredity. 2011;106:330–338. doi: 10.1038/hdy.2010.61. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pérez-Pardal L, Royo LJ, Beja-Pereira A, Curik I, Traoré A, Fernández I, Sölkner J, Alonso J, Alvarez I, Bozzi R, Chen S, Ponce de León FA, Goyache F. Y-specific microsatellites reveal an African subfamily in taurine (Bos taurus) cattle. Anim Genet. 2010;41:232–241. doi: 10.1111/j.1365-2052.2009.01988.x. [DOI] [PubMed] [Google Scholar]
- Pool JE, Nielsen R. Population size changes reshape genomic patterns of diversity. Evolution. 2007;61:3001–3006. doi: 10.1111/j.1558-5646.2007.00238.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pool JE, Nielsen R. The impact of founder events on chromosomal variability in multiply mating species. Mol Biol Evol. 2008;25:1728–1736. doi: 10.1093/molbev/msn124. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ramírez O, Ojeda A, Tomàs A, Gallardo D, Huang LS, Folch JM, et al. Integrating Y-chromosome, mitochondrial, and autosomal data to analyze the origin of pig breeds. Mol Biol Evol. 2009;26:2061–2072. doi: 10.1093/molbev/msp118. [DOI] [PubMed] [Google Scholar]
- Ramos AM, Crooijmans RP, Affara NA, Amaral AJ, Archibald AL, Beever JE, et al. Design of a high density SNP genotyping assay in the pig using SNPs identified and characterized by next generation sequencing technology. PLoS ONE. 2009;4:e6524. doi: 10.1371/journal.pone.0006524. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ramos-Onsins SE, Stranger BE, Mitchell-Olds T, Aguadé M. Multilocus analysis of variation and speciation in the closely related species Arabidopsis halleri and A. lyrata. Genetics. 2004;166:373–388. doi: 10.1534/genetics.166.1.373. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rogers A, Harpending H. Population growth makes waves in the distribution of pairwise differences. Mol Biol Evol. 1992;9:552–569. doi: 10.1093/oxfordjournals.molbev.a040727. [DOI] [PubMed] [Google Scholar]
- Tajima F. Evolutionary relationship of DNA sequences in finite populations. Genetics. 1983;105:437–460. doi: 10.1093/genetics/105.2.437. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tajima F. Statistical method for testing the neutral mutation hypothesis by DNA polymorphism. Genetics. 1989;123:585–595. doi: 10.1093/genetics/123.3.585. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Theimer TC, Keim P. Phylogenetic relationships of peccaries based on mitochondrial cytochrome B DNA sequences. J Mammal. 1998;79:566–572. doi: 10.2307/1382987. [DOI] [Google Scholar]
- Thornton K, Andolfatto P. Approximate Bayesian inference reveals evidence for a recent, severe bottleneck in a Netherlands population of Drosophila melanogaster. Genetics. 2006;172:1607–1619. doi: 10.1534/genetics.105.048223. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wakeley J, Hey J. Estimating ancestral population parameters. Genetics. 1997;145:847–855. doi: 10.1093/genetics/145.3.847. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Watanobe T, Okumura N, Ishiguro N, Nakano M, Matsui A, Sahara M, et al. Genetic relationship and distribution of the Japanese wild boar (Sus scrofa leucomystax) and Ryukyu wild boar (Sus scrofa riukiuanus) analysed by mitochondrial DNA. Mol Ecol. 1999;8:1509–1512. doi: 10.1046/j.1365-294x.1999.00729.x. [DOI] [PubMed] [Google Scholar]
- Watterson GA. On the number of segregating sites in genetical models without recombination. Theor Pop Biol. 1975;7:256–276. doi: 10.1016/0040-5809(75)90020-9. [DOI] [PubMed] [Google Scholar]
- Wegmann D, Leuenberger C, Neuenschwander S, Excoffier L. ABCtoolbox: a versatile toolkit for approximate Bayesian computations. BMC Bioinformatics. 2010;11:116. doi: 10.1186/1471-2105-11-116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weir BS, Cockerham CC. Estimating F-statistics for the analysis of population structure. Evolution. 1984;38:1358–1370. doi: 10.1111/j.1558-5646.1984.tb05657.x. [DOI] [PubMed] [Google Scholar]
- Wilson Sayres MA, Lohmueller KE, Nielsen R. Natural selection reduced diversity on human Y chromosomes. PLoS Genet. 2014;10:e1004064. doi: 10.1371/journal.pgen.1004064. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.