Abstract
Recent work in estimating species relationships from gene trees has included inferring networks assuming that past hybridization has occurred between species. Probabilistic models using the multispecies coalescent can be used in this framework for likelihood-based inference of both network topologies and parameters, including branch lengths and hybridization parameters. A difficulty for such methods is that it is not always clear whether, or to what extent, networks are identifiable—that is whether there could be two distinct networks that lead to the same distribution of gene trees. For cases in which incomplete lineage sorting occurs in addition to hybridization, we demonstrate a new representation of the species network likelihood that expresses the probability distribution of the gene tree topologies as a linear combination of gene tree distributions given a set of species trees. This representation makes it clear that in some cases in which two distinct networks give the same distribution of gene trees when sampling one allele per species, the two networks can be distinguished theoretically when multiple individuals are sampled per species. This result means that network identifiability is not only a function of the trees displayed by the networks but also depends on allele sampling within species. We additionally give an example in which two networks that display exactly the same trees can be distinguished from their gene trees even when there is only one lineage sampled per species.
Keywords: gene tree, hybridization, identifiability, maximum likelihood, species tree, phylogeny
Hybridization between distinct species or populations is often represented using a rooted phylogenetic network rather than a tree (Huson et al. 2010; Bapteste et al. 2013; Nakhleh 2013). In much of the literature on networks representing hybridization, there has been interest in which trees are displayed by a network, where a network displays a particular tree if removing some subset of hybridization edges results in the given tree (Huson and Scornavacca 2011; Morrison 2011). For example, several papers investigate finding a network with the minimum number of hybridization events that displays two conflicting input trees (Albrecht et al. 2012; Baroni et al. 2006; Bordewich and Semple 2007; Chen and Wang 2010; van Iersel et al. 2014). These input trees are often described as gene trees, and could arise, for example, from estimating trees from sequences from two different loci (e.g., one mitochondrial and one nuclear gene). However, it is not always clear in the literature if a displayed tree in a network refers to a gene tree or a species tree (representing species history rather than ancestry for a specific locus).
A number of methods have recently been developed to infer species networks that explicitly represent species relationships using a network while relationships at the gene level are modeled as gene trees within the network (Jones et al. 2013; Kubatko 2009; Meng and Kubatko 2009; Yu et al. 2011, 2012, 2014; Yu and Nakhleh 2015; Solís-Lemus and Ané 2016). These models are motivated by cases in which hybridization and incomplete lineage sorting are likely to occur simultaneously. In probabilistic versions of these models, gene trees are assumed to be strictly tree-like, and although they are embedded within the network, they do not have to be displayed by the network. In particular, by modeling species networks under the multispecies coalescent, all gene trees have positive probability whether or not they are displayed by the network. We refer to the multispecies coalescent model applied to networks as the Network Multispecies Coalescent (NMSC), and this model is the focus of this article.
The NMSC is intended to represent the case of two populations merging so that the hybrid population is expected to have many individuals with ancestry from both parental populations. Hybrid speciation due to changes in ploidy can result in all descendants of the hybrid having one ancestor, in which case incomplete lineage sorting would not occur. Our model is therefore restricted to homoploid hybridizations; see (Jones et al. 2013) for models applicable to polyploid hybridization. The NMSC is also not intended to model horizontal gene transfer, which causes much of the reticulation in bacterial networks, or recombination, two other processes that motivate network representations, including in likelihood frameworks (Strimmer and Moulton 2000; Jin et al. 2006; Abbott et al. 2010; Nguyen and Roos 2015).
An early study concerning the multispecies coalescent approach to networks assumed that a hybrid species occurred sometime in the past, and that a single allele is sampled from a population descended from this hybrid species (Meng and Kubatko 2009). Under this assumption, an allele from the hybrid species could have descended from one of two possible ancestral populations. This results in the probability of a gene tree being a linear combination of the gene tree probabilities from two parent species trees, where the parent species trees are obtained by removing one of the two hybridization edges. This reduces the network into a set of two species trees, and takes advantage of the fact that probabilities of gene trees given species trees under the multispecies coalescent can be computed. This approach is useful in cases where only one allele is sampled per locus from any species that is the result of hybridization. However, this approach does not generalize easily to cases where an ancient hybrid subsequently speciates or in which more than one allele is sampled from a hybrid species.
To compute more general likelihoods than the approach of Meng and Kubatko (2009), Yu et al. (2012) developed an algorithm that represented a species network as a multilabeled tree (MUL-tree) where species descended from hybrids are represented more than once in the tips of the MUL-tree. The likelihood is computed by summing over possible assignments of alleles to these nonuniquely labeled tips. This approach allows multiple alleles to be sampled within populations as well as hybrids to occur anciently in the network so that populations descended from hybrids can subsequently speciate.
A problem for inferring phylogenetic networks, however, is that they are not always identifiable. That is, examples can be found where two networks that correspond to distinct biological hypotheses about speciation and hybridization events can give rise to the same distribution of gene trees. Two networks that give the same probabilities on all gene tree topologies can be said to be mathematically indistinguishable. We might also differentiate between mathematical distinguishability, by which we mean that two models lead to distinct probability distributions, and practical distinguishability, which would mean that one can perform reasonably accurate model selection from finite data. In this article, we are primarily interested in mathematical distinguishability; however, we also do simulations to address the more practical sense of distinguishability.
Mathematical indistinguishability means that there are some sets of networks for which no amount of data could determine which of the networks gave rise to the data. Although several positive results have been found for identifying species trees from gene trees and sequences evolving on gene trees (DeGiorgio and Degnan 2010; Allman et al. 2011a,b; Chifman and Kubatko 2015), the identifiability of networks is a more challenging problem theoretically. One reason for this is that the space of phylogenetic networks is much larger than that of phylogenetic trees, and is infinite if the number of hybridization events is not bounded. Networks can also have “ghost” lineages (lineages that once existed but that went extinct) that can also make identifiability more difficult for networks than for trees (Marcussen et al. 2015).
One factor that affects network identifiability is whether or not gene trees have branch lengths (Pardi and Scornavacca 2015). If only gene tree topologies are used, then many distinct networks will give equivalent gene tree topology probabilities if speciation times and hybridization parameters are allowed to vary. In some cases, the distribution of the coalescence times in the gene trees (which are functions of the gene tree branch lengths) will depend on hybridization events, thus allowing it to be possible to distinguish two networks that could not be distinguished using only topologies.
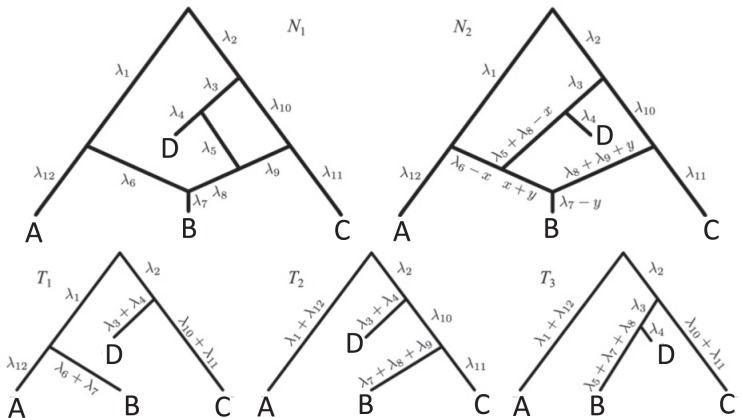
If only gene tree topologies are used, then the number of hybridization events that it is possible to infer may also be limited. An example is given in Yu et al. (2012) in which a network has three species and two hybridization events (Fig. 1). In that example, there are three times corresponding to either speciation or hybridization events, and there are two hybridization parameters. With only three observed gene tree topologies and five parameters, even if the network topology is known, this results in a system of three (estimated) equations and five unknowns (one equation for each gene tree topology). It is therefore not surprising that it is not possible to determine the five parameters using the gene tree topologies alone.
Figure 1.
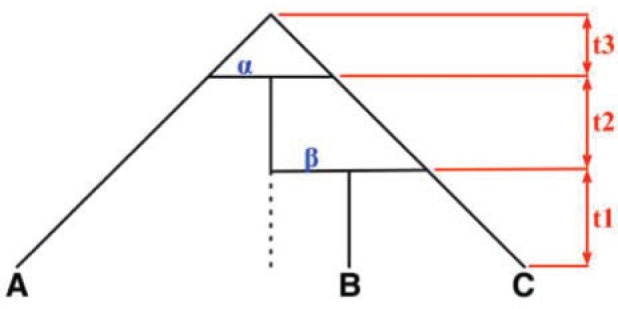
Example of three-taxon network in which parameters are not identifiable from gene tree topologies. The example is taken from Yu et al. (2012), Figure 4, doi:10.1371/journal.pgen.1002660.g004.
Yu et al. (2012) show that for the three-taxon example, identifiability is improved by allele sampling. If two alleles are sampled from species B, then there are 15 possible gene tree topologies (since we now have gene trees with four leaves). The 15 gene tree probabilities can then be used to estimate the five parameters.
A more difficult case of identifiability might appear to be that given by Pardi and Scornavacca (2015) (Fig. 2). In this example, when there is one allele sampled per species, the distribution of the gene trees, including their branch lengths, is identical for two different networks. The authors point out that there are three species trees displayed by the networks and that the three species trees can have identical branch lengths given certain choices of parameters in the two networks. The authors claim that “no method based on this definition of likelihood will be able to discriminate between” the two networks.
Figure 2.
Networks  and
and 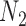 from Pardi and Scornavacca (2015), doi:10.1371/journal.pcbi.1004135.g003. The two networks both display exactly the same three trees,
from Pardi and Scornavacca (2015), doi:10.1371/journal.pcbi.1004135.g003. The two networks both display exactly the same three trees, 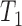 ,
, 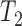 , and
, and 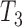 .
.
While we agree that the likelihood used in Yu et al. (2012) cannot distinguish the two networks if one allele per species is used (whether or not branch lengths are used for this case), we disagree if the data can have multiple alleles per species and if incomplete lineage sorting is possible. Some likelihood approaches assume that sequence alignments evolve on gene trees displayed by the network (Jin et al. 2006; Park and Nakhleh 2012; Pardi and Scornavacca 2015), leading to the likelihood:
| (1) |
where 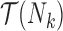 is the set of trees displayed by network
is the set of trees displayed by network 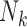 and
and 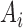 is the sequence alignment for the
is the sequence alignment for the 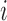 th locus. This likelihood sums over the trees displayed by the network, and is motivated by cases such as horizontal gene transfer in bacteria and hybrid speciation, in which gene trees are expected to be trees displayed by the network.
th locus. This likelihood sums over the trees displayed by the network, and is motivated by cases such as horizontal gene transfer in bacteria and hybrid speciation, in which gene trees are expected to be trees displayed by the network.
The likelihood used in Meng and Kubatko (2009) and Yu et al. (2012) treats gene trees as data, and can be written instead as
| (2) |
where 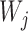 are species trees called parental trees in Meng and Kubatko (2009), and the
are species trees called parental trees in Meng and Kubatko (2009), and the 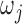 are weights based on the probability that lineages take certain paths through the network. In Meng and Kubatko (2009), in which there is only one descendant from any hybrid node, the trees
are weights based on the probability that lineages take certain paths through the network. In Meng and Kubatko (2009), in which there is only one descendant from any hybrid node, the trees 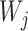 are indeed displayed by the network, whereas in Yu et al. (2012), the trees
are indeed displayed by the network, whereas in Yu et al. (2012), the trees 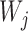 are generally MUL-trees which are not always displayed the network. The approach in this article can also be written using equation (2), where the
are generally MUL-trees which are not always displayed the network. The approach in this article can also be written using equation (2), where the 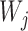 terms are uniquely labeled trees (not MUL-trees), and can be interpreted as parental trees, similarly to Meng and Kubatko (2009), but are not necessarily displayed by the network.
terms are uniquely labeled trees (not MUL-trees), and can be interpreted as parental trees, similarly to Meng and Kubatko (2009), but are not necessarily displayed by the network.
The description of the likelihood in Pardi and Scornavacca applies to cases where gene trees are considered known and can only arise as displayed trees within the network. This assumption might be reasonable for a number of biological processes such as hybrid speciation, in which an individual hybrid can be ancestral to a new species (Abbott et al. 2010), recombination among viruses, and horizontal gene transfer. Under the NMSC, gene trees are not necessarily displayed by the network. In the parental species tree approach of Meng and Kubatko (2009), parental species trees are displayed by the network if there is only one individual descended from each hybrid, or if all lineages are constrained to coalesce more recently than a hybridization event (such as for hybrid speciation). However, for cases where there are several lineages in a hybrid population, such as is allowed in Yu et al. (2012), parental species trees under the NMSC are also not necessarily displayed by the network.
The likelihood used in Yu et al. (2012) is calculated over a sum of probabilities based on MUL trees, with the summation being over allele assignments. Some allele assignments will correspond to displayed trees, but some may not, particularly when two lineages (whether or not they are from the same species) follow different paths up the network at a hybridization node. In these cases, the probability cannot be written in terms of a displayed tree obtained by dropping one of the hybridization edges. Consequently, equation (1) is not in general an accurate representation of the likelihood used in Yu et al. (2012).
In the next section, we describe an alternative method for representing gene tree probabilities that does not use MUL trees, and describes the probabilities of gene trees as linear combinations as in Equation (1), except that the sum is not necessarily over trees displayed by the network. This helps to explain why equivalence of displayed trees is not sufficient for determining that two networks are indistinguishable.
Gene Tree Probabilities as Linear Combinations Under Different Species Trees
An alternative way of deriving the likelihood of the network given the gene trees can be obtained by conditioning on events at hybridization nodes and branches descended from them and using recursion. This results in an alternative algorithm to that of Yu et al. (2012) for computing the likelihood of a gene tree and results in an expression more similar to the strategy of Meng and Kubatko (2009) of reducing the probability given a network to a linear combination of probabilities given species trees. Following Meng and Kubatko, we refer to these species trees as parental trees or parental species trees. For networks with more than one lineage descended from a hybridization node, the recursion results in a linear combination including some species trees that are not displayed by the network. An example is shown in Figure 3, which gives an intuitive picture of the procedure. The example generalizes the three-taxon example in Figure 1 by splitting taxon 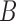 into two species and making hybridization edges to not be horizontal.
into two species and making hybridization edges to not be horizontal.
Figure 3.
Decomposition of network into parental species trees. Wiggly arrows indicate conditioning on a coalescence event. Solid arrows indicate conditioning on paths taken at a hybridization node. When a taxon is labeled 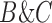 , this can be interpreted as a leaf where
, this can be interpreted as a leaf where 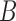 and
and 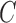 have been merged, or as a two-taxon tree where there is an infinite branch for the ancestor of
have been merged, or as a two-taxon tree where there is an infinite branch for the ancestor of 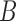 and
and 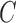 , guaranteeing that lineages sampled from
, guaranteeing that lineages sampled from 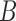 and
and 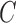 coalesce with each other more recently than with any other taxa.
coalesce with each other more recently than with any other taxa.
At each step in the recursive approach, we condition on whether lineages either coalesce or do not coalesce, or we condition on whether lineages go left versus right at a hybridization node. Each step reduces the network into a larger number of smaller networks until the process ends with a collection of species trees. Details of the algorithm are given in the Appendix.
Distinguishability of Networks with the Same Displayed Trees
Decomposition of Networks 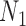 and
and 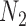
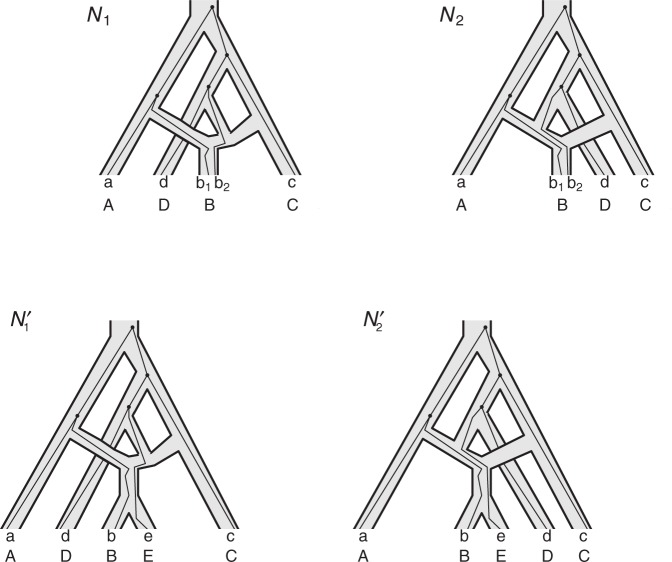
We use the networks 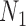 and
and 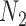 described as indistinguishable (Pardi and Scornavacca 2015) (Fig. 2).
described as indistinguishable (Pardi and Scornavacca 2015) (Fig. 2).
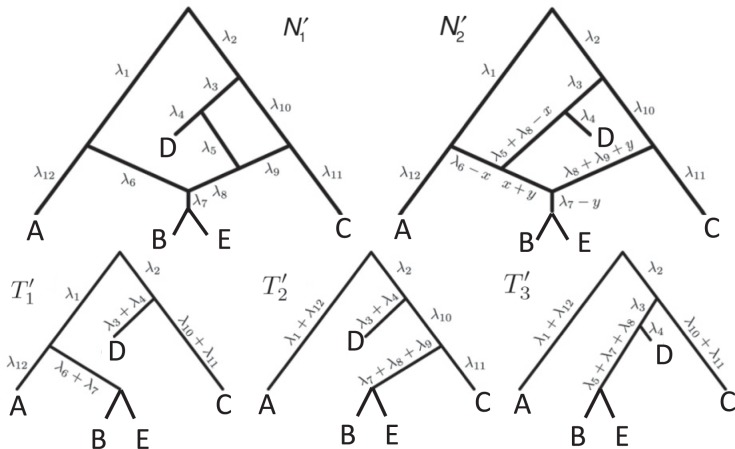
These networks are slightly modified from Pardi and Scornavacca (2015) with species written with capital letters. We then consider a modified version in which the population descended from both hybrid nodes undergoes speciation, resulting in species 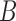 and
and 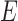 (networks
(networks 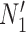 and
and  in Fig. 4). The networks
in Fig. 4). The networks 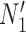 and
and 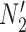 are similar to
are similar to 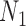 and
and 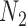 , respectively, when there are two lineages sampled from
, respectively, when there are two lineages sampled from  (Fig. 2). The number of lineages sampled per species affects the decomposition of the networks into parental species trees.
(Fig. 2). The number of lineages sampled per species affects the decomposition of the networks into parental species trees.
Figure 4.
Extension of networks  and
and  to allow two species descended from the most recent hybridization node. The figure is modified from doi:10.1371/journal.pcbi.1004135.g003.
to allow two species descended from the most recent hybridization node. The figure is modified from doi:10.1371/journal.pcbi.1004135.g003.
When there are two lineages sampled from species  in
in  , we denote the lineages by
, we denote the lineages by 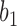 and
and 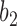 . They fail to coalesce in this branch with probability
. They fail to coalesce in this branch with probability 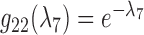 . Assuming no coalescence, the lineages from species
. Assuming no coalescence, the lineages from species  either both go to the left, one goes leftward and one rightward, or both go to the right at the lower hybridization node. The cases are listed in Supplementary Table 1 (available on Dryad). An example corresponding to case
either both go to the left, one goes leftward and one rightward, or both go to the right at the lower hybridization node. The cases are listed in Supplementary Table 1 (available on Dryad). An example corresponding to case 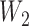 in Supplementary Table 1 (available on Dryad) is shown in Figure 5. We use
in Supplementary Table 1 (available on Dryad) is shown in Figure 5. We use 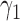 and
and 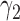 for the probability that a lineage goes left at the more recent and less recent hybridization nodes, respectively, in network
for the probability that a lineage goes left at the more recent and less recent hybridization nodes, respectively, in network 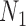 . Similarly,
. Similarly, 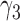 and
and 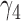 are the probabilities that a lineage goes left at the more recent and less recent hybridization nodes, respectively, in
are the probabilities that a lineage goes left at the more recent and less recent hybridization nodes, respectively, in  . These hybridization parameters are also called inheritance probabilities (Pardi and Scornavacca 2015). The parental species trees
. These hybridization parameters are also called inheritance probabilities (Pardi and Scornavacca 2015). The parental species trees 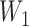 –
–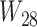 referred to in Supplementary Table 1 (available on Dryad) are given in newick format in Supplementary Tables 2 and 3 (available on Dryad).
referred to in Supplementary Table 1 (available on Dryad) are given in newick format in Supplementary Tables 2 and 3 (available on Dryad).
Figure 5.
Gene trees in networks that display the same trees. Here 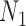 and
and 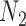 display the same trees with the same branch lengths given suitable choices of parameters. Similarly,
display the same trees with the same branch lengths given suitable choices of parameters. Similarly, 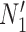 and
and 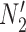 display the same trees. Two gene trees are shown with coalescence times that are compatible with both
display the same trees. Two gene trees are shown with coalescence times that are compatible with both 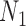 and
and 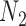 , and another two gene trees are shown with coalescence times compatible with both
, and another two gene trees are shown with coalescence times compatible with both 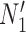 and
and 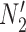 so that knowing the coalescence times in the gene tree does not determine which network it evolved in. The gene trees in this figure cannot be represented as having evolved in a species tree displayed by the networks. The gene tree in
so that knowing the coalescence times in the gene tree does not determine which network it evolved in. The gene trees in this figure cannot be represented as having evolved in a species tree displayed by the networks. The gene tree in 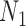 corresponds to case
corresponds to case 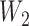 where
where 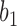 goes left,
goes left, 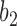 goes right, then left. The gene tree in
goes right, then left. The gene tree in 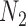 corresponds to case
corresponds to case 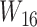 , where both go left, then
, where both go left, then 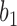 goes left,
goes left, 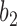 goes right.
goes right.
We wish to show that there is at least one gene tree topology with different probabilities under the two networks. The calculations are simplest for a gene tree that is very unlikely, in which case calculations can be done “by hand.” For example, consider the gene tree 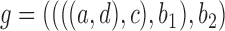 . The probability of this gene tree topology conditional on the above parental species trees is given in Supplementary Table 1 (available on Dryad).
. The probability of this gene tree topology conditional on the above parental species trees is given in Supplementary Table 1 (available on Dryad).
The probabilty of the gene tree 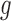 under the two networks can be written as
under the two networks can be written as
where 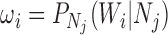 . To illustrate using Supplementary Table 1 (available on Dryad), the probability of
. To illustrate using Supplementary Table 1 (available on Dryad), the probability of  under
under 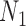 is
is
Here 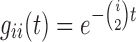 from equation (A.2).
from equation (A.2).
The probabilities do not depend on 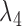 ,
, 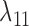 , or
, or 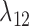 due to there only being one lineage on each of these pendant edges and therefore no probability of coalescence on these edges. The terms
due to there only being one lineage on each of these pendant edges and therefore no probability of coalescence on these edges. The terms 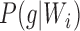 are equal to 0 for five choices of
are equal to 0 for five choices of 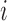 under both networks. These cases correspond to parental species trees that have conditioned on the event that lineages
under both networks. These cases correspond to parental species trees that have conditioned on the event that lineages 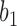 and
and 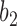 have coalesced more recently than one of the hybridization nodes, which is impossible for gene tree
have coalesced more recently than one of the hybridization nodes, which is impossible for gene tree 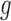 . This reduces the number of parental species trees needed in the sums from 14 to 9.
. This reduces the number of parental species trees needed in the sums from 14 to 9.
In addition, the gene tree forces all coalescences to occur more anciently than the root of the network for both networks. This means that only one coalescent history needs to be computed (instead of enumerating over several coalescent histories for each parental species tree). Because of the asymmetry in the gene tree, only one sequence of coalescences, out of 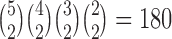 , produces the gene tree, which leads to the denominators in the probabilities.
, produces the gene tree, which leads to the denominators in the probabilities.
When there is only one lineage sampled per species, 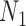 and
and 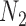 are indistinguishable under the following conditions (Pardi and Scornavacca 2015):
are indistinguishable under the following conditions (Pardi and Scornavacca 2015):
-
1.
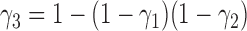
-
2.
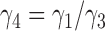
-
3.
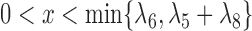
-
4.
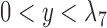
We pick a particular set of parameters to show that the networks are distinguishable when two lineages are sampled in species  . For the choice of parameters
. For the choice of parameters
the conditions for indistinguishability specified by Pardi and Scornavacca (2015) are met, and the probability of gene tree topology 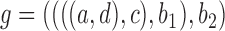 under the two networks is
under the two networks is
Thus, the gene tree probability is approximately 1.4% higher under  than
than 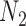 . Both probabilities are small because this gene tree is quite unlikely for both networks, requiring no coalescences to occur except more anciently than the root. Nevertheless, it shows that the two networks have different gene tree distributions.
. Both probabilities are small because this gene tree is quite unlikely for both networks, requiring no coalescences to occur except more anciently than the root. Nevertheless, it shows that the two networks have different gene tree distributions.
Rather than using gene tree probabilities, clade probabilities could also be used to distinguish the two networks for many parameter values. Let 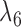 and
and 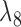 both be very large and let
both be very large and let 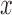 be very small, so that any two lineages on branches with these lengths will almost certainly coalesce. Similarly, let
be very small, so that any two lineages on branches with these lengths will almost certainly coalesce. Similarly, let 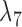 be very small, so that
be very small, so that 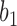 and
and 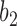 are very unlikely to coalesce. For these parameters, with high probability,
are very unlikely to coalesce. For these parameters, with high probability, 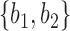 is a clade on the gene tree when, and only when, both lineages both go to the left or both go to the right at the more recent hybridization node. Then using the above values of
is a clade on the gene tree when, and only when, both lineages both go to the left or both go to the right at the more recent hybridization node. Then using the above values of 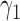 and
and 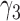 , the probability that a gene tree has clade
, the probability that a gene tree has clade 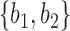 is approximately
is approximately 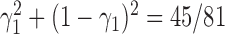 under
under 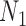 and is approximately
and is approximately 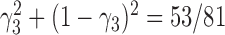 under
under 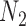 . The clade probability will therefore distinguish the two networks.
. The clade probability will therefore distinguish the two networks.
We emphasize that if there is only one lineage sampled per species, then there is at most one lineage present at each hybrid node for 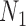 and
and 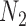 . In this case, the methods of Meng and Kubatko (2009) can be applied to calculate gene tree probabilities, but we agree with Pardi and Scornavacca (2015) that
. In this case, the methods of Meng and Kubatko (2009) can be applied to calculate gene tree probabilities, but we agree with Pardi and Scornavacca (2015) that 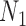 and
and 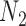 are indistinguishable in this situation.
are indistinguishable in this situation.
Rooted triples and quartets have also been used to reconstruct or infer networks under the NMSC (Yu and Nakhleh 2015) and Solís-Lemus and Ané (2016). Yu and Nakhleh (2015) give an example of networks that are not distinguishable using probabilities of triples in the gene trees that have evolved in the network (Fig. 6). They give an explanation that the networks display the same sets of triples. We agree that for this particular example, triples cannot be used to distinguish their networks 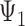 and
and 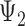 ,. However, for the case of
,. However, for the case of 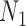 and
and 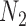 , triples can be used to distinguish the networks when there are two lineages sampled from
, triples can be used to distinguish the networks when there are two lineages sampled from 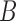 , even though
, even though 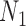 and
and 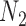 display the same set of rooted triples. For example, using the previous parameters, the probability of triple
display the same set of rooted triples. For example, using the previous parameters, the probability of triple 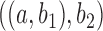 is approximately 0.081 under
is approximately 0.081 under 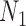 and approximately 0.089 under
and approximately 0.089 under 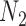 .
.
Figure 6.
Two networks taken from Figure 2 of Yu and Nakhleh (2015) that display the same trees and triplets. The networks are distinguishable using gene tree probabilities but not using rooted triple probabilities.
As an alternative explanation for why triples cannot be used to distinguish  and
and  , it is noticed that equating triple probabilities for the two networks, such as
, it is noticed that equating triple probabilities for the two networks, such as  results in a system of 12 equations. Removing linear dependencies, such as
results in a system of 12 equations. Removing linear dependencies, such as 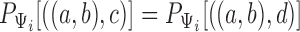 and that for any three taxa, the sum of the three rooted triple probabilities sums to 1. Removing such linearly dependencies from the system results in five linearly independent equations for a system with nine parameters, making the system underdetermined. This makes it possible to find parameters for
and that for any three taxa, the sum of the three rooted triple probabilities sums to 1. Removing such linearly dependencies from the system results in five linearly independent equations for a system with nine parameters, making the system underdetermined. This makes it possible to find parameters for 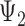 that will make the rooted triple probabilities match those for
that will make the rooted triple probabilities match those for 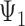 .
.
Probabilities of unrooted quartets can also be calculated, and again, these distinguish the networks 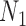 and
and 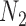 when there are two lineages sampled from species
when there are two lineages sampled from species 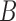 . For the same parameters as above, with
. For the same parameters as above, with 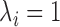 ,
, 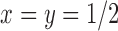 ,
, 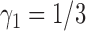 , and
, and 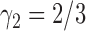 , the probability that a rooted gene tree displays the quartet
, the probability that a rooted gene tree displays the quartet 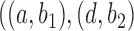 is approximately 0.10 and 0.14 for networks
is approximately 0.10 and 0.14 for networks 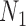 and
and 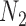 , respectively. We note this example in particular because the recently introduced method for inferring networks from quartets (Solís-Lemus and Ané 2016) cited the results in Pardi and Scornavacca (2015) as a reason to not apply the method to level-
, respectively. We note this example in particular because the recently introduced method for inferring networks from quartets (Solís-Lemus and Ané 2016) cited the results in Pardi and Scornavacca (2015) as a reason to not apply the method to level-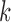 networks for
networks for 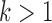 (networks in which an edge can appear in more than one cycle of the graph, such as
(networks in which an edge can appear in more than one cycle of the graph, such as 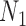 and
and 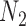 ).
).
The example from Yu and Nakhleh (2015) suggests that caution is indeed needed, since there are cases where trees but not summary statistics such as rooted triples can distinguish the networks. The example of 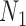 and
and 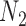 with multiple lineages per species, however, suggests that even more complicated networks are potentially distinguishable from rooted triples or quartets. In the Yu and Nakhleh (2015) example, we suspect that distinguishability would be achieved by sampling additional lineages. Their example is somewhat different from that of
with multiple lineages per species, however, suggests that even more complicated networks are potentially distinguishable from rooted triples or quartets. In the Yu and Nakhleh (2015) example, we suspect that distinguishability would be achieved by sampling additional lineages. Their example is somewhat different from that of 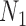 and
and 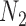 in that the different networks do not have the same species descended from the hybrid, and the number of descendants of the hybrid is not the same for the two networks. The networks are also level 1, with only one hybridization event, and distinguishability is a problem not because of the complexity of the networks but rather because of the small number of taxa and resulting small set of linearly independent rooted triple probabilities for the number of parameters.
in that the different networks do not have the same species descended from the hybrid, and the number of descendants of the hybrid is not the same for the two networks. The networks are also level 1, with only one hybridization event, and distinguishability is a problem not because of the complexity of the networks but rather because of the small number of taxa and resulting small set of linearly independent rooted triple probabilities for the number of parameters.
It is also possible to have distinguishability between two networks that each display the same set of trees when there is only one lineage sampled per species. In particular, the networks 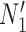 and
and 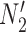 are essentially identical to
are essentially identical to 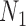 and
and 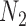 , respectively, when the pendant branches leading to species
, respectively, when the pendant branches leading to species  and
and 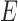 have length 0. In this case, the most recent ancestral population to
have length 0. In this case, the most recent ancestral population to 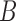 and
and 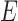 is a single population, and the lineages
is a single population, and the lineages 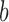 and
and 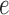 are two lineages from the same population. As a result, the distributions of gene tree topologies under
are two lineages from the same population. As a result, the distributions of gene tree topologies under 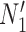 and
and 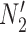 are identical with those of
are identical with those of 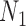 and
and 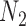 when lineage
when lineage 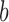 is replaced by
is replaced by 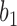 and lineage
and lineage 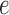 is replaced by
is replaced by 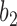 . Similarly, the networks
. Similarly, the networks 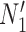 and
and  both display the trees
both display the trees 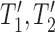 , and
, and 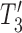 (Fig. 4), which are equivalent to
(Fig. 4), which are equivalent to 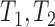 , and
, and 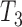 (Fig. 2), respectively, when
(Fig. 2), respectively, when 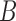 is replaced by
is replaced by 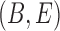 . The length of the pendant edges does not affect gene tree probabilities when one lineage is sampled per species. Consequently, gene tree
. The length of the pendant edges does not affect gene tree probabilities when one lineage is sampled per species. Consequently, gene tree 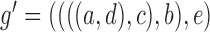 has the same probabilities under
has the same probabilities under 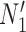 and
and 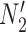
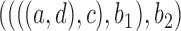 has under
has under  and
and  , respectively:
, respectively: 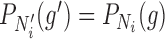 for
for 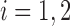 .
.
The important point is that there exist pairs of networks that display the same trees but can be distinguished under the NMSC model, even when there is only one lineage sampled per species. This example demonstrates that showing that two networks display the same trees (including branch lengths and inheritance probabilities) is not sufficient for showing that the networks are indistinguishable. In this particular case, the networks 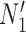 and
and 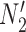 are also distinguishable using rooted triplets, quartets, or clades, in spite of the two networks displaying exactly the same rooted triplets, quartets, and clades. A crucial reason for the ability to distinguish networks is the following: if there is more than one lineage descended from a hybrid node (either due to the hybrid population speciating or due to sampling more than one lineage from a population descended from a hybrid), there can exist gene trees that are not embedded in a tree displayed by the network.
are also distinguishable using rooted triplets, quartets, or clades, in spite of the two networks displaying exactly the same rooted triplets, quartets, and clades. A crucial reason for the ability to distinguish networks is the following: if there is more than one lineage descended from a hybrid node (either due to the hybrid population speciating or due to sampling more than one lineage from a population descended from a hybrid), there can exist gene trees that are not embedded in a tree displayed by the network.
Simulation
Distinguishability of 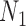 and
and  Using Model Selection
Using Model Selection
To illustrate the ability of network methods to distinguish two networks that display the same trees, we simulated gene trees from 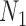 with two and three alleles sampled from species
with two and three alleles sampled from species 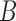 and one allele sampled from each of the other species. We used phylonet (Than et al. 2008) to compute likelihood scores by optimizing branch lengths and hybridization parameters assuming the fixed network topologies
and one allele sampled from each of the other species. We used phylonet (Than et al. 2008) to compute likelihood scores by optimizing branch lengths and hybridization parameters assuming the fixed network topologies 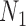 and
and 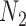 . The network branch lengths were based on using the network
. The network branch lengths were based on using the network 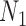 (Fig. 5) with the height of the network being 10 coalescent units. The networks used for simulation in hybrid-Lambda (Zhu et al. 2015) are, in coalescent units:
(Fig. 5) with the height of the network being 10 coalescent units. The networks used for simulation in hybrid-Lambda (Zhu et al. 2015) are, in coalescent units:
where species 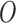 is an out-group. In this notation, all internal nodes (both hybridization and speciation nodes) are labeled. After the hybridization nodes,
is an out-group. In this notation, all internal nodes (both hybridization and speciation nodes) are labeled. After the hybridization nodes, 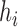 , the first number represents the probability of going “left,” and the second number represents the branch length from the hybridization node to the next node (either left or right). Thus, for both networks used in the simulation, the probability of going left for
, the first number represents the probability of going “left,” and the second number represents the branch length from the hybridization node to the next node (either left or right). Thus, for both networks used in the simulation, the probability of going left for 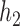 is
is 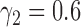 . In the extended newick string, the branch length after the first (second) instance (reading from the left) of
. In the extended newick string, the branch length after the first (second) instance (reading from the left) of 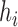 is the length of the branch leading from
is the length of the branch leading from 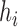 to the left (right) parent of
to the left (right) parent of 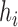 .
.
The networks have identical topologies, inheritance probabilities, and branch lengths, except that  for the first network and
for the first network and  for the second network. The second network has a higher probability that the lineages sampled from
for the second network. The second network has a higher probability that the lineages sampled from 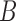 will fail to coalesce more recently than the most recent hybridization node, and therefore has a higher level of incomplete lineage sorting. We therefore refer to this as the “high ILS” network. Gene trees on this network are much less likely to have monophyly of lineages sampled from
will fail to coalesce more recently than the most recent hybridization node, and therefore has a higher level of incomplete lineage sorting. We therefore refer to this as the “high ILS” network. Gene trees on this network are much less likely to have monophyly of lineages sampled from 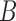 . The other network is referred to as the “low ILS” network.
. The other network is referred to as the “low ILS” network.
For each set of gene trees, the likelihood under the estimated parameters was compared with the two networks and the proportion of times that 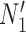 had a higher likelihood than
had a higher likelihood than 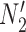 was reported. The simulation was performed with
was reported. The simulation was performed with 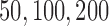 and 400 independent loci. For each gene tree, alignments with 500 sites were simulated using seq-gen (Rambaut and Grassly 1997) under the
and 400 independent loci. For each gene tree, alignments with 500 sites were simulated using seq-gen (Rambaut and Grassly 1997) under the 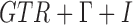 model with base frequencies of
model with base frequencies of 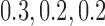 , and
, and 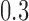 for
for 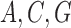 , and
, and 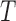 , respectively, with four rate categories and 10% invariable sites. As is typical with multilocus simulations, gene trees were independent with no recombination within loci. An out-group was added to the network with the MRCA of the out-group and in-group taxa being 10 coalescent units deeper than the root of the in-group taxa. This ensures extremely high probabilities that the in-group taxa are monophyletic in the gene trees. Gene trees were estimated using phyml (Guindon et al. 2010) under the
, respectively, with four rate categories and 10% invariable sites. As is typical with multilocus simulations, gene trees were independent with no recombination within loci. An out-group was added to the network with the MRCA of the out-group and in-group taxa being 10 coalescent units deeper than the root of the in-group taxa. This ensures extremely high probabilities that the in-group taxa are monophyletic in the gene trees. Gene trees were estimated using phyml (Guindon et al. 2010) under the  model assuming four rate categories and estimating all other parameters, and using default tree searches. Unrooted gene trees estimated by phyml were rooted using the out-group, and the out-group was then removed before inputting the estimated rooted gene trees into phyml.
model assuming four rate categories and estimating all other parameters, and using default tree searches. Unrooted gene trees estimated by phyml were rooted using the out-group, and the out-group was then removed before inputting the estimated rooted gene trees into phyml.
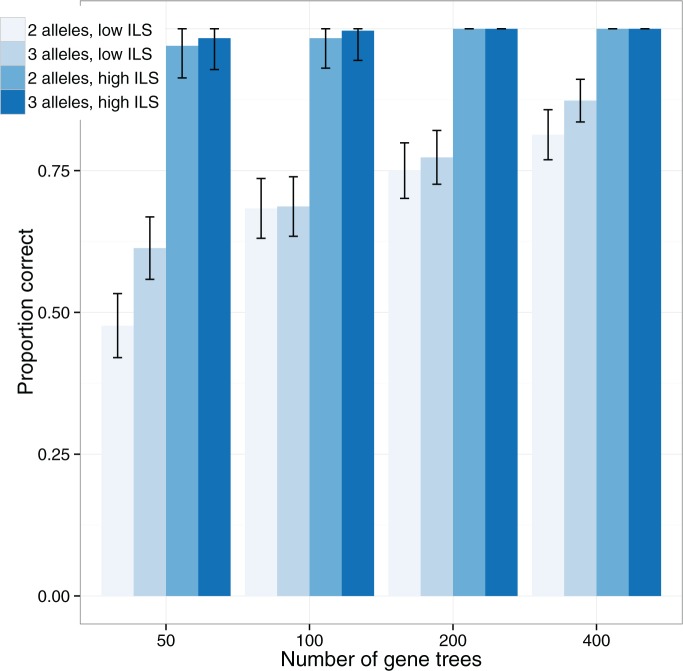
Not surprisingly, increasing the number of loci increased the ability to distinguish the two networks (Fig. 7). Increasing the number of alleles (from 2 to 3) increased the ability of maximum likelihood to distinguish the networks. An intuitive explanation is that with more alleles, it is more likely that lineages cannot be embedded in a tree displayed by the network. Having the higher level of ILS lineages (obtained by having a smaller value for 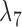 ) greatly increases the ability of phylonet to distinguish the two networks, and this also has the explanation that since
) greatly increases the ability of phylonet to distinguish the two networks, and this also has the explanation that since 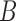 lineages are less likely to have coalesced more recently than the first hybridization node, gene trees in the high ILS case are less likely to be embedded in a tree displayed by the network than gene trees in the low ILS case. The fact that increasing allele sampling can improve inference of species relationships has been emphasized in the species tree literature as well (Maddison and Knowles 2006; DeGiorgio and Degnan 2014; Heled and Drummond 2010; Huang et al. 2010). In this case, however, sampling multiple alleles not only improves inference, but is also crucial for being able to distinguish the networks at all.
lineages are less likely to have coalesced more recently than the first hybridization node, gene trees in the high ILS case are less likely to be embedded in a tree displayed by the network than gene trees in the low ILS case. The fact that increasing allele sampling can improve inference of species relationships has been emphasized in the species tree literature as well (Maddison and Knowles 2006; DeGiorgio and Degnan 2014; Heled and Drummond 2010; Huang et al. 2010). In this case, however, sampling multiple alleles not only improves inference, but is also crucial for being able to distinguish the networks at all.
Figure 7.
Performance of phylonet for distinguishing networks 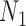 and
and 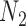 when data was simulated from
when data was simulated from 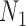 , with the indicated number of alleles sampled from species
, with the indicated number of alleles sampled from species  and all other species having one allele sampled. The fraction of times out of 300 iterations that the
and all other species having one allele sampled. The fraction of times out of 300 iterations that the  had a higher likelihood than
had a higher likelihood than  is reported when both networks were fixed and phylonet optimized branch lengths and inheritance probabilities. “High ILS” refers to
is reported when both networks were fixed and phylonet optimized branch lengths and inheritance probabilities. “High ILS” refers to 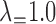 , and “Low ILS” refers to
, and “Low ILS” refers to  , with all other parameters kept the same.
, with all other parameters kept the same.
The “high ILS” case, with a branch length of 1.0 coalescent units, is typical for cases known to have significant amounts of ILS For example, the level of gene tree incongruence, for which approximately 60–80% of trees have humans and chimpanzees being the most closely related among humans, chimpanzees, and gorillas (Ebersberger et al. 2007) suggests an internal branch length of between 0.5 and 1.2 coalescent units (Ané 2010; Degnan 2010). The probability that two lineages coalesce within 1.0 coalescent units is 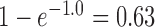 , whereas the probability that two lineages coalesce within 3.0 units (the low ILS case in our simulations) is 0.95. Thus, for the low ILS case with two alleles from
, whereas the probability that two lineages coalesce within 3.0 units (the low ILS case in our simulations) is 0.95. Thus, for the low ILS case with two alleles from  , more than 19 in 20 gene trees evolve on a tree displayed by the network, making it difficult to distinguish the two networks; for the high ILS case, using
, more than 19 in 20 gene trees evolve on a tree displayed by the network, making it difficult to distinguish the two networks; for the high ILS case, using 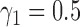 , the proportion of gene trees evolving on a tree not displayed by the network is close to
, the proportion of gene trees evolving on a tree not displayed by the network is close to 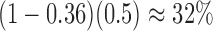 .
.
Comparison of Phylonet and Hybrid-Coal
Both phylonet and hybrid-coal compute probabilities of gene tree topologies given species networks, but the two programs use different algorithms. The program hybrid-coal uses a recursion that allows representing the gene tree topology probability as a linear combination of probabilities given species trees. In contrast, phylonet initially represented probabilities as a sum over probabilities of coalescent histories given MUL-tree representations of networks, and more recently also implemented the ancestral configuration approach (Wu 2012), which tends to run more quickly than the coalescent history approach for larger trees (roughly more than 10 taxa, depending on tree shape). There are also many features in phylonet not implemented in hybrid-coal, such as algorithms to infer the network from a set of gene trees, searching over network topologies, branch lengths, and inheritance probabilities, and using branch lengths in the gene trees.
The main idea of hybrid-coal is compatible with both the coalescent history and ancestral configuration approaches, since once the parental species trees have been enumerated, either coalescent histories or ancestral configurations could be used to compute the probability of the gene tree given the parental species tree. Currently, only the coalescent history approach is implemented in hybrid-coal, but the ancestral configuration method could be added in the future. In comparison with phylonet, hybrid-coal breaks down the network into a larger number of smaller problems, with the parental species trees tending to be smaller trees than the MUL-tree representation of the network, which can have more leaves than there are taxa. This could potentially be an advantage in future parallel programming implementations of the algorithm.
The main advantage for having the new algorithm in hybrid-coal is perhaps the theoretical insight it gives in terms of representing gene tree probabilities in terms of parental species trees. This appears to be a fairly intuitive way to think about the relationship between gene trees and species networks (Holland et al. 2008; Meng and Kubatko 2009), although we have shown that perhaps counterintuitively, the parental species trees are often not displayed by the network. We hope that future theoretical work will make use of the representation of gene tree probabilities as mixtures arising from different species trees. In other contexts, mixtures of trees have proved identifiable (Allman et al. 2012; Rhodes and Sullivant 2012), and this might be a useful approach for thinking about identifiability of networks.
Discussion
The Effect of Branch Lengths
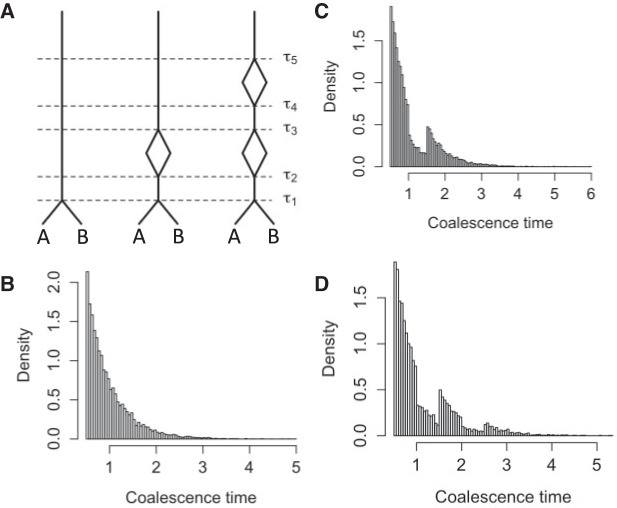
Consideration of branch lengths in the gene trees can lead to the ability to distinguish networks which could not be distinguished using only topologies. For example, if a species history has multi-edges—cases where two nodes are directly connected by two distinct edges—it can still be possible to estimate parameters of this model and to distinguish it from a model in which multi-edges are collapsed. An example of networks with multi-edges is shown in Figure 8. Biologically, a multi-edge could depict a population temporarily splitting into two populations with no gene flow followed by the populations merging at a later time before either population splits. This type of history would be desirable to be able to estimate since it could occur, for example, due to glaciation or other episodic events that temporarily divide populations (Comes and Kadereit 1998; Marshall et al. 2009).
Figure 8.
Coalescence times for networks with multi-edges. a) The leftmost species history is a two-taxon species tree. The middle and right species histories have one or two sets of multi-edges, reflecting species diverging and subsequently hybridizing without any other speciation. Histograms of 100,000 coalescence times for single genes sampled from species 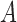 and
and 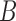 are depicted in (b)–(d). (c) and (d) correspond to the middle and rightmost species histories, respectively. Simulations are based on
are depicted in (b)–(d). (c) and (d) correspond to the middle and rightmost species histories, respectively. Simulations are based on 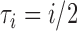 coalescent units and were done in the program ms (Hudson 2002).
coalescent units and were done in the program ms (Hudson 2002).
Coalescence times are potentially useful in these cases because multi-edges affect the distribution of coalescence times. Theoretically, a multi-edge will result in a bimodal distribution of coalescence times. In practice, estimated coalescence times are highly variable and subject to estimation error, so that a bimodal signature might be difficult to detect. However, this does not affect the point that multi-edges are potentially inferable given ideal data.
The example from Figure 8 essentially arises from the three-taxon network in Figure 1 when taxon 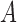 is dropped and
is dropped and 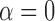 . The example illustrates that this network has potentially identifiable parameters when using branch lengths in the gene trees even when topologies cannot identify the parameters in the network.
. The example illustrates that this network has potentially identifiable parameters when using branch lengths in the gene trees even when topologies cannot identify the parameters in the network.
A deeper difficulty with identifiability is that it is not clear that hybridization can be distinguished from other population genetic processes that can result in gene tree incongruence and complicated distributions of coalescence times. For example, alternating bottlenecks and population expansions can result in similar multimodal distributions of coalescence times as that found in Fig. 8 (DeGiorgio et al. 2011). Bottlenecks can also be a problem in practice for distinguishing two networks since a smaller population size makes incomplete lineage sorting less likely, thereby making gene trees more likely to be displayed by the network. The extreme case is a bottleneck of size one, which can occur in hybrid speciation, and guarantees that all gene trees are displayed by the network.
As another example, it is well known that the multispecies coalescent on a three-taxon tree with no ancestral population structure predicts that one triplet is most frequent while the other two triplets are tied in probability, and that these tied probabilities are less frequent (Nei 1987). Consequently, a test of equality of proportions is sometimes used for the less frequent triplets as a goodness of fit test for the multispecies coalescent (Degnan and Rosenberg 2009; White et al. 2009; Ané 2010; Cranston 2010; Song et al. 2012). Asymmetry in the less frequent triplet can be explained by hybridization, but could also be explained by ancient population structure (Slatkin and Pollack 2008). Distinguishing hybridization from processes such as ancient population structure and changing population sizes might be at least as challenging as distinguishing one hybridization network from another assuming that population structure and population sizes that do not fluctuate.
Summary
To summarize our results, we find that
Two networks that display the same trees, including branch lengths and inheritance probabilities, might or might not be distinguishable under the NMSC in the sense of leading to the same probability distribution of gene tree topologies. In particular, there are examples where two networks display exactly the same trees, clades, triples, and quartets, yet are distinguishable from the probabilities of trees, clades, triples, and quartets.
Network distinguishability can be improved in some cases by using branch length information and/or by sampling more than one individual per species descended from a hybrid population.
Higher levels of incomplete lineage sorting can make inference of hybridization events easier in some cases.
A desirable property of a network inference method is to be able to distinguish networks that are in fact distinguishable, even when they display the same trees. We have shown that maximum likelihood can do this in at least some cases.
We agree with Pardi and Scornavacca (2015) that identifiability is an important topic when trying to infer networks. Much of the effort in the literature on hybridization networks has focused on constructing networks that display a set of input trees, which are treated as data (Bordewich and Semple 2007; Holland et al. 2008; van Iersel and Linz 2013). From this point of view, it is crucial to understand when two networks might display the same set of trees.
Much less work has been done on what we are calling the NMSC, which has only recently become an active area of research. We have shown that identifiability results from the combinatorial point of view do not necessarily immediately transfer to the NMSC framework, and that many cases thought to be indistinguishable turn out to be distinguishable using this probabilistic modeling approach. An analogy is that in the case of trees (rather than networks), unrooted trees might not be expected to have any information about the root of the trees from which they came. However, under a probabilistic model, unrooted trees can have information about the root (Steel 2012), and in particular, under the multispecies coalescent, the distribution of unrooted trees determines the rooted species tree when there are five or more taxa (but not for four taxa) (Allman et al. 2011b).
We hope that there will be more of an intersection in future phylogenetic network research between combinatorial approaches and the NMSC framework. A particular problem in need of more theoretical work is that of distances between networks. In particular, standard definitions of distance between networks, such as cluster-based definitions which extend Robinson–Foulds distances (Robinson and Foulds 1981) to networks (Cardona et al. 2009), return a distance of 0 between 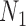 and
and 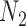 and between
and between 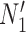 and
and 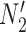 . This makes it difficult to determine whether an inferred network is closer to
. This makes it difficult to determine whether an inferred network is closer to 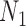 versus
versus 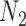 (or
(or 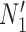 vs.
vs. 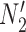 ), even for methods capable of distinguishing these networks.
), even for methods capable of distinguishing these networks.
The increased ability to distinguish networks using probabilistic models is good news for biologists interested in being able to infer biologically meaningful networks. However, much is still not understood about the space of networks in which we are interested in making inferences, and more theory is needed to determine what is and what is not distinguishable or identifiable under the NMSC. We showed that the particular example given by Pardi and Scornavacca (2015) turned out to be distinguishable if there is more than one lineage sampled from species 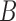 , and that generally there are cases of two networks that display exactly the same species trees (including branch lengths) that are nevertheless distinguishable under the NMSC, even with one lineage sampled per species.
, and that generally there are cases of two networks that display exactly the same species trees (including branch lengths) that are nevertheless distinguishable under the NMSC, even with one lineage sampled per species.
However, we did not establish that 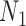 and
and 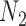 are distinguishable from all networks on four taxa, even if the number of hybridization nodes is capped. Nor did we establish that if, say, the topology of
are distinguishable from all networks on four taxa, even if the number of hybridization nodes is capped. Nor did we establish that if, say, the topology of 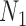 is known, then the parameters of the network would be identifiable. Here lack of identifiability would mean that two distinct sets of branch lengths and/or hybridization parameters (
is known, then the parameters of the network would be identifiable. Here lack of identifiability would mean that two distinct sets of branch lengths and/or hybridization parameters (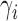 ), lead to the same distribution of gene trees. Since networks of any complexity can be conceived, we can construct networks on
), lead to the same distribution of gene trees. Since networks of any complexity can be conceived, we can construct networks on 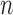 taxa with more parameters than there are gene tree topologies (assuming a fixed number of alleles sampled per species), and this will certainly result in lack of identifiability of the parameters from gene tree topologies even if the network topology is known. The challenge remains to determine what is and what is not identifiable for networks under the NMSC.
taxa with more parameters than there are gene tree topologies (assuming a fixed number of alleles sampled per species), and this will certainly result in lack of identifiability of the parameters from gene tree topologies even if the network topology is known. The challenge remains to determine what is and what is not identifiable for networks under the NMSC.
Supplemental Material
Data available from the Dryad Digital Repository: http://dx.doi.org/10.5061/dryad.t2d38.
Software Availability
The software hybrid-coal, which computes gene tree probabilities recursively, and hybrid-Lambda, which simulates gene trees in phylogenetic networks, are both available at Github at https://github.com/hybridLambda/ and can be freely used under GNU GPL Version 3 or later. Both have been tested in Mac OS X 10.9.5 and Ubuntu.
Funding
Much of this work was completed while SZ was a PhD student at University of Canterbury, supervised by JD and Mike Steel, [SZ and JD were funded by the New Zealand Marsden fund during 2010–2013]. JD was additionally supported by National Institutes of Health [grant R01 GM117590].
Acknowledgments
We are grateful to David Bryant and Mike Steel for comments on the description of the algorithm. We thank Bengt Oxelman and two anonymous reviewers for additional helpful comments.
Appendix
Recursive Method to Compute Gene Tree Probabilities Given Species Networks
In this section, we introduce a novel method to compute gene tree probabilities of a given species network. Nodes of the network are visited in a modified post-order traversal so that the algorithm works on the deepest nodes descended from hybrid nodes first and works from this node toward the root until all hybrid nodes are eliminated. We introduce two operations to decompose a network into reduced networks that have a smaller number of edges or nodes. The post-order traversal ensures that we perform the simplification operations in a correct order—a node is never operated on before removing its descendant internal nodes.
Decomposition Operations
In this section, we propose two operations to simplify a complex phylogeny structure into simpler structures with fewer hybridization events. To demonstrate this procedure, we first consider simple cases where one individual is sampled from each population at the present. We first make several restrictions and assumptions for the gene tree 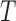 and the network
and the network  in this section:
in this section:
The gene tree
 and the network
and the network  are rooted.
are rooted.Gene tree
 and network
and network  have the same number of external edges.
have the same number of external edges.Gene tree
 is binary.
is binary.An interior node of
 can only have at most two parent nodes; a hybrid node refers to an internal node of
can only have at most two parent nodes; a hybrid node refers to an internal node of  which has two parent nodes.
which has two parent nodes.We do not consider the case that a hybrid node is also a leaf node.
The network 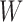 is initially reduced to a set of simpler networks (
is initially reduced to a set of simpler networks (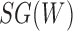 ) in a single step in the reduction process. Let
) in a single step in the reduction process. Let 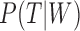 be the probability of gene tree
be the probability of gene tree 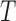 given a species network
given a species network 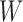 , by the law of total probability, we have the following:
, by the law of total probability, we have the following:
| (A.1) |
where  is a random variable that depends on
is a random variable that depends on 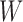 .
.
For any 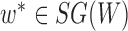 ,
, 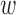 * implies either a particular parental branch that some lineages have followed at a hybrid node or some specific coalescences that have occurred beneath a hybridization node.
* implies either a particular parental branch that some lineages have followed at a hybrid node or some specific coalescences that have occurred beneath a hybridization node.
Prior to decomposing a network, nodes are ranked from the leaves of the network to the top: tip nodes have rank one; an interior node’s rank is one plus the highest rank of its child nodes.
The key to simplifying a network is to remove the interior nodes of the network in a specific order, along with the branches that are connected to the node. Here we define several functions to assist us identifying which nodes should be removed first. Let  be the set of nodes in the network; for
be the set of nodes in the network; for 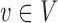 , let
, let 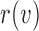 be the rank of
be the rank of 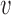 (the number of edges from
(the number of edges from 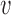 to the root), and
to the root), and 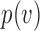 be the number parent node of
be the number parent node of 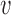 . We use indicator function
. We use indicator function 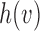 to identify if a node
to identify if a node 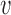 is a hybrid node:
is a hybrid node:
Let 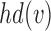 and
and 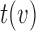 be the indicator functions that take values
be the indicator functions that take values
and
respectively.
Thus, we can apply Algorithm 1 to find which node should be removed from the network: If the algorithm returns value  , it means that
, it means that  is already tree-like, and does not need to be simplified; otherwise, it returns the index of the node that we need to perform the following operations.
is already tree-like, and does not need to be simplified; otherwise, it returns the index of the node that we need to perform the following operations.

Decomposition operation 1.—
If the chosen node is an interior descendant node 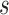 of a hybrid node, then this implies that
of a hybrid node, then this implies that 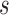 has a single parent node (otherwise
has a single parent node (otherwise 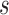 is a hybrid node), and child nodes of
is a hybrid node), and child nodes of 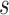 are the leaf nodes of
are the leaf nodes of 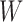 (since
(since 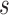 has the lowest rank beside the tips). The first step of operation 1 is to remove
has the lowest rank beside the tips). The first step of operation 1 is to remove 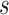 from
from 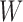 , along with all of the edges that are connected to
, along with all of the edges that are connected to 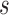 .
.
Let 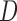 denote all of the leaf nodes descended from
denote all of the leaf nodes descended from 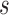 . We now enumerate all possible ways to partition
. We now enumerate all possible ways to partition 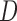 . For example, if
. For example, if 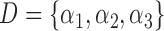 , let
, let 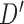 be one of the possible partitions of
be one of the possible partitions of 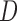 .
. 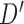 could be
could be 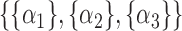 ,
, 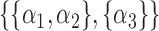 ,
, 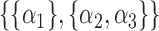 ,
, 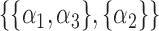 or
or 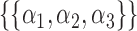 . We treat every element of any
. We treat every element of any 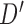 as a new leaf node. In the second part of operation 1, we create a new graph
as a new leaf node. In the second part of operation 1, we create a new graph 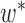 , by connecting the elements of
, by connecting the elements of 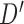 to the parent node of
to the parent node of 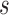 . Notice, if the element of
. Notice, if the element of 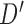 contains more than one leaf node, this implies that by changing from graph
contains more than one leaf node, this implies that by changing from graph 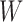 to
to 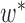 , we need to coalesce these leaves on the branch that connects
, we need to coalesce these leaves on the branch that connects 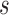 and its parent node.
and its parent node.
To calculate the probability of these events, we let 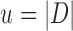 , and
, and 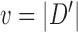 and
and 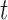 be the branch length from
be the branch length from 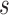 to its parent node. Then the probability of
to its parent node. Then the probability of  lineages coalesce into
lineages coalesce into 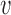 lineages within time
lineages within time 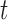 is (Tajima 1983; Saunders et al. 1984; Takahata and Nei 1985; Rosenberg 2002; Degnan and Salter 2005):
is (Tajima 1983; Saunders et al. 1984; Takahata and Nei 1985; Rosenberg 2002; Degnan and Salter 2005):
| (A.2) |
Therefore, we have:
| (A.3) |
where  is the number of ways for
is the number of ways for 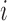 lineages to coalesce into
lineages to coalesce into 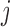 lineages, which is equal to
lineages, which is equal to 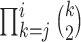 , and
, and 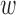 is the number of sequences of coalescences resulting in the same topology with
is the number of sequences of coalescences resulting in the same topology with 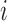 lineages coalescing into
lineages coalescing into  lineages. This is equal to
lineages. This is equal to 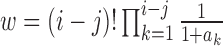 , where
, where 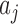 is the number of interior nodes that are descended from the coalesced nodes (Degnan and Salter 2005), and
is the number of interior nodes that are descended from the coalesced nodes (Degnan and Salter 2005), and 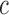 is the number of ways for
is the number of ways for 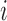 lineages to coalesce into
lineages to coalesce into 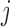 lineages, which is equal to
lineages, which is equal to 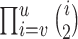 . The indicator function is defined as
. The indicator function is defined as
For instance, if the gene tree is 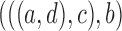 and
and 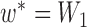 in Fig. 3, then
in Fig. 3, then 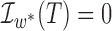 .
.
Operation 1 removes an internal node of network  . Therefore, any reduced network
. Therefore, any reduced network  ,
, 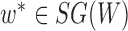 , has fewer interior nodes than network
, has fewer interior nodes than network  .
.
Decomposition operation 2.—
Before applying operation 2 on a hybrid node  of
of  , we need to make sure that operation 1 has been applied to all of the interior nodes descended from
, we need to make sure that operation 1 has been applied to all of the interior nodes descended from  . This implies that all of the child nodes of
. This implies that all of the child nodes of 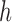 are the leaf nodes of
are the leaf nodes of 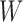 . Let
. Let 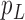 and
and 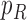 be the two parent nodes of
be the two parent nodes of  . We use
. We use  to denote the set of child nodes of
to denote the set of child nodes of  and
and  to denote the collection of all of the subsets of
to denote the collection of all of the subsets of  . The first step of operation 2, is to remove
. The first step of operation 2, is to remove  from
from  , and all of the edges connected to
, and all of the edges connected to  .
.
We then introduce two new nodes, 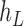 and
and 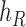 . For any
. For any 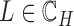 , we have a new graph
, we have a new graph 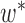 , connect
, connect 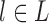 to
to 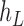 , then connect
, then connect 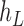 to
to 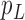 , and connect
, and connect 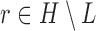 to
to 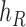 , then connect
, then connect 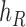 to
to 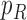 . Let
. Let 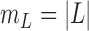 ,
, 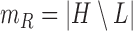 , and
, and 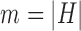 . The parameter
. The parameter 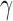 is the probability that one lineage is attached to
is the probability that one lineage is attached to 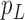 . Thus, we obtain the set of simpler networks
. Thus, we obtain the set of simpler networks 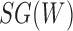 and the probabilities
and the probabilities 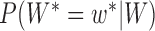 for any
for any 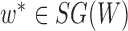 :
:
| (A.4) |
Operation 2 removes an internal node of network  . The newly added nodes
. The newly added nodes 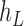 and
and 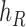 are effectively external nodes: as all of the nodes descended from
are effectively external nodes: as all of the nodes descended from 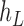 and
and 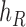 are leaf nodes, we can treat
are leaf nodes, we can treat 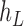 and
and 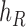 as leaf nodes, but sampling multiple lineages from each of them. Therefore, any reduced network
as leaf nodes, but sampling multiple lineages from each of them. Therefore, any reduced network 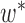 ,
, 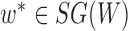 , has fewer interior nodes than network
, has fewer interior nodes than network 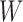 .
.
Simplifying a Network Recursively
Operations 1 and 2 are applied recursively on any networks in 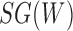 until all of the simplified network structures are tree-like. Gene tree probabilities can be computed using either coalescent histories (Degnan and Salter 2005) or ancestral configurations (Wu 2012). The approach outlined in this article will therefore reduce the probability of a gene tree, given a species network, to a linear combination of gene tree probabilities of given species trees.
until all of the simplified network structures are tree-like. Gene tree probabilities can be computed using either coalescent histories (Degnan and Salter 2005) or ancestral configurations (Wu 2012). The approach outlined in this article will therefore reduce the probability of a gene tree, given a species network, to a linear combination of gene tree probabilities of given species trees.
Let 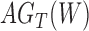 be an ordered list of directed graphs (trees or networks). Then
be an ordered list of directed graphs (trees or networks). Then 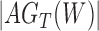 is the number of elements in the list. Here we borrow the concepts of set operations “
is the number of elements in the list. Here we borrow the concepts of set operations “ ” and “
” and “ ” for our use. Let
” for our use. Let 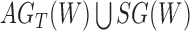 denote gradually appending the elements of
denote gradually appending the elements of 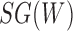 to the end of the list
to the end of the list 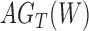 , then indexing the new elements of
, then indexing the new elements of 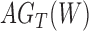 from
from 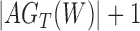 to
to 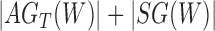 . For an element
. For an element 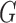 of
of 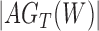 , we define operation
, we define operation 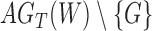 , as removing the element
, as removing the element  from
from 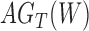 , the index of any element behind
, the index of any element behind  is now one less.
is now one less.
Then we apply Algorithm 2 to simplify a network  , and then compute the probability for gene tree
, and then compute the probability for gene tree  .
.

During the decomposition process, different sequences of removing the hybrid nodes may lead to the same subspecies trees  . For
. For 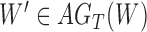 , we use
, we use 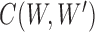 to denote the collection of ways to decompose
to denote the collection of ways to decompose 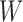 into
into 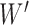 . Each sequence of decomposition corresponds to a unique weight
. Each sequence of decomposition corresponds to a unique weight 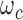 . Thus by simplifying Equation (A.1), we have:
. Thus by simplifying Equation (A.1), we have:
| (A.5) |
Figure 3 illustrates the decomposition of a species network on four taxa with two hybridization nodes.
Notice that even though 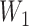 and
and 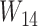 have the same topology, the branch lengths of these two trees differ. We consider them to be different species trees. For different gene trees, according to coalescent events,
have the same topology, the branch lengths of these two trees differ. We consider them to be different species trees. For different gene trees, according to coalescent events, 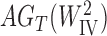 may differ. For example, if the gene tree is
may differ. For example, if the gene tree is 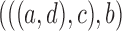 ,
,  , but when the gene tree is
, but when the gene tree is 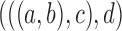 ,
, 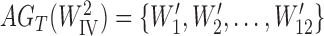 .
.
References
- Abbott R.J., Hegarty M.J., Hiscock S.J., Brennan A.C. 2010. Homoploid hybrid speciation in action. Taxon 59:1375–1386. [Google Scholar]
- Albrecht B., Scornavacca C., Cenci A., Huson D.H. 2012. Fast computation of minimum hybridization networks. Bioinformatics 28:191–197. [DOI] [PubMed] [Google Scholar]
- Allman E.S., Degnan J.H., Rhodes J.A. 2011a. Determining species tree topologies from clade probabilities under the coalescent. J. Theor. Biol. 289:96–106. [DOI] [PubMed] [Google Scholar]
- Allman E.S., Degnan J.H., Rhodes J.A. 2011b. Identifying the rooted species tree from the distribution of unrooted gene trees under the coalescent. J. Math. Biol. 62:833–862. [DOI] [PubMed] [Google Scholar]
- Allman E.S., Rhodes J.A., Sullivant S. 2012. When do phylogenetic mixture models mimic other phylogenetic models? Syst. Biol. 61:1049–1059. [DOI] [PubMed] [Google Scholar]
- Ané C. 2010. Reconstructing concordance trees and testing the coalescent model from genome-wide data sets. In: Knowles L. L., Kubatko L. S. editors. Estimating species trees: theoretical and practical aspects.Hoboken, (NJ): Wiley-Blackwell; p. 35–52. [Google Scholar]
- Bapteste E., van Iersel L., Janke A., Kelchner S., Kelk S., McInerney J.O., Morrison D.A., Nakhleh L., Steel M., Stougie L., Whitfield J. 2013. Networks: expanding evolutionary thinking. Trends Genet. 29:439–441. [DOI] [PubMed] [Google Scholar]
- Baroni M., Semple C., Steel M. 2006. Hybrids in real time. Syst. Biol. 55:46–56. [DOI] [PubMed] [Google Scholar]
- Bordewich M., Semple C. 2007. Computing the hybridization number of two phylogenetic trees is fixed-parameter tractable. IEEE/ACM Trans. Comp. Biol. Bioinform. 4:458–466. [DOI] [PubMed] [Google Scholar]
- Cardona G., Llabrés M., Rosselló F., Valiente G. 2009. Metrics for phylogenetic networks I: Generalizations of the Robinson-Foulds metric. IEEE/ACM Trans. Comp. Biol. Bioinform. 6:46–61. [DOI] [PubMed] [Google Scholar]
- Chen Z.-Z., Wang L. 2010. Hybridnet: a tool for constructing hybridization networks. Bioinformatics 26:2912–2913. [DOI] [PubMed] [Google Scholar]
- Chifman J., Kubatko L. 2015. Identifiability of the unrooted species tree topology under the coalescent model with time-reversible substitution processes, site-specific rate variation, and invariable sites. J. Theor. Biol. 374:35–47. [DOI] [PubMed] [Google Scholar]
- Comes H.P., Kadereit J.W. 1998. The effect of quaternary climatic changes on plant distribution and evolution. Trends Plant Sci. 3:432–438. [Google Scholar]
- Cranston K.A. 2010. Summarizing gene tree incongruence at multiple phylogenetic depths. In: Knowles L.L., Kubatko L.S. editors. Estimating species trees: practical and theoretical aspectsHoboken (NJ): Wiley-Blackwell; p. 129–143. [Google Scholar]
- DeGiorgio M., Degnan J.H., Rosenberg N.A. 2011. Coalescence-time distributions in a serial founder model of human evolutionary history. Genetics 189:579–593. [DOI] [PMC free article] [PubMed] [Google Scholar]
- DeGiorgio M., Degnan J.H. 2010. Fast and consistent estimation of species trees using supermatrix rooted triples. Mol. Biol. Evol. 27:552–569. [DOI] [PMC free article] [PubMed] [Google Scholar]
- DeGiorgio M., Degnan J.H. 2014. Robustness to divergence time underestimation when inferring species trees from estimated gene trees. Syst. Biol. 63:66–82. [DOI] [PubMed] [Google Scholar]
- Degnan J.H., Rosenberg N.A. 2009. Gene tree discordance, phylogenetic inference and the multispecies coalescent. Trends Ecol. Evol. 24:332–340. [DOI] [PubMed] [Google Scholar]
- Degnan J.H., Salter L.A. 2005. Gene tree distributions under the coalescent process. Evolution 59:24–37. [PubMed] [Google Scholar]
- Degnan J.H. 2010. Probabilities of gene trees with intraspecific sampling given a species tree. In: Knowles L.L., Kubatko L.S. editors. Estimating Species Trees: Practical and Theoretical AspectsWiley-Blackwell; p. 53–78. [Google Scholar]
- Ebersberger I., Galgoczy P., Taudien S., Taenzer S., Platzer M., von Haeseler A. 2007. Mapping human genetic ancestry. Mol. Biol. Evol. 24:2266–2277. [DOI] [PubMed] [Google Scholar]
- Guindon S., Dufayard J.-F., Lefort V., Anisimova M., Hordijk W., Gascuel O. 2010. New algorithms and methods to estimate maximum-likelihood phylogenies: assessing the performance of phyml 3.0. Syst. Biol. 59:307–321. [DOI] [PubMed] [Google Scholar]
- Heled J., Drummond A.J. 2010. Bayesian inference of species trees from multilocus data. Mol. Biol. Evol. 27:570–580. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holland B.R., Benthin S., Lockhart P.J., Moulton V., Huber K.T. 2008. Using supernetworks to distinguish hybridization from lineage-sorting. BMC Evol. Biol. 8:1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang H., He Q., Kubatko L.S., Knowles L.L. 2010. Sources of error inherent in species-tree estimation: impact of mutational and coalescent effects on accuracy and implications for choosing among different methods. Syst. Biol. 59:573–583. [DOI] [PubMed] [Google Scholar]
- Hudson R. 2002. Generating samples under a wright-fisher neutral model of genetic variation. Bioinformatics 18:337–338. [DOI] [PubMed] [Google Scholar]
- Huson D.H., Scornavacca C. 2011. A survey of combinatorial methods for phylogenetic networks. Genome Biol. Evol. 3:23–35. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huson D., Rupp R., Scornavacca C. 2010. Phylogenetic networks: concepts, algorithms and applications. New York: Cambridge University Press. [Google Scholar]
- Jin G., Nakhleh L., Snir S., Tuller T. 2006. Maximum likelihood of phylogenetic networks. Bioinformatics 22:2604–2611. [DOI] [PubMed] [Google Scholar]
- Jones G., Sagitov S., Oxelman B. 2013. Statistical inference of allopolyploid species networks in the presence of incomplete lineage sorting. Syst. Biol. 62:467–478. [DOI] [PubMed] [Google Scholar]
- Kubatko L.S. 2009. Identifying hybridization events in the presence of coalescence via model selection. Syst. Biol. 58:478–488. [DOI] [PubMed] [Google Scholar]
- Maddison W.P., Knowles L.L. 2006. Inferring phylogeny despite incomplete lineage sorting. Syst. Biol. 55:21–30. [DOI] [PubMed] [Google Scholar]
- Marcussen T., Heier L., Brysting A.K., Oxelman B., Jakobsen K.S. 2015. From gene trees to a dated allopolyploid network: Insights from the angiosperm genus Viola (Violaceae). Syst. Biol. 64:84–101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marshall D.C., Hill K.B., Fontaine K.M., Buckley T.R., Simon C. 2009. Glacial refugia in a maritime temperate climate: Cicada (kikihia subalpina) MTDNA phylogeography in New Zealand. Mol. Ecol. 18:1995–2009. [DOI] [PubMed] [Google Scholar]
- Meng C., Kubatko L.S. 2009. Detecting hybrid speciation in the presence of incomplete lineage sorting using gene tree incongruence: a model. Theor. Popul. Biol. 75:35–45. [DOI] [PubMed] [Google Scholar]
- Morrison D.A. 2011. Introduction to phylogenetic networks. Uppsala: RJR Productions. [Google Scholar]
- Nakhleh L. 2013. Computational approaches to species phylogeny inference and gene tree reconciliation. Trends Ecol. Evol. 28:719–728. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nei M. 1987. Molecular evolutionary genetics. New York: Columbia University Press. [Google Scholar]
- Nguyen Q., Roos T. 2015. Likelihood-based inference of phylogenetic networks from sequence data by phylodag. In: Algorithms for computational biology. Springer; p. 126–140. [Google Scholar]
- Pardi F., Scornavacca C. 2015. Reconstructible phylogenetic networks: do not distinguish the indistinguishable. PLoS Comput. Biol. e1004135. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Park H.J., Nakhleh L. 2012. Inference of reticulate evolutionary histories by maximum likelihood: the performance of information criteria. BMC Bioinform. 13:S12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rambaut A., Grassly N.C. 1997. Seq-gen: an application for the Monte Carlo simulation of DNA sequence evolution along phylogenetic trees. Comp. Appl. Biosci. 13:235–238. [DOI] [PubMed] [Google Scholar]
- Rhodes J.A., Sullivant S. 2012. Identifiability of large phylogenetic mixture models. Bull. Math. Biol. 74:212–231. [DOI] [PubMed] [Google Scholar]
- Robinson D., Foulds L. 1981. Comparison of phylogenetic trees. Math. Biosci. 53:131–147. [Google Scholar]
- Rosenberg N.A. 2002. The probability of topological concordance of gene trees and species trees. Theor. Pop. Biol. 61:225–247. [DOI] [PubMed] [Google Scholar]
- Saunders I.W., Tavaré S., Watterson G.A. 1984. On the genealogy of nested subsamples from a haploid population. Adv. Appl. Prob. 16:471–491. [Google Scholar]
- Slatkin M., Pollack J.L. 2008. Subdivision in an ancestral species creates asymmetry in gene trees. Mol. Biol. Evol. 25:2241–2246. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Solís-Lemus C., Ané C. 2016. Inferring phylogenetic networks with maximum pseudolikelihood under incomplete lineage sorting. PLoS Genet. 12:e1005896. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Song S., Liu L., Edwards S.V., Wu S. 2012. Resolving conflict in eutherian mammal phylogeny using phylogenomics and the multispecies coalescent model. Proc. Natl. Acad. Sci. USA: 109:14942–14947. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Steel M. 2012. Root location in random trees: a polarity property of all sampling consistent phylogenetic models except one. Mol. Phylogenet. Evol. 65:345–348. [DOI] [PubMed] [Google Scholar]
- Strimmer K., Moulton V. 2000. Likelihood analysis of phylogenetic networks using directed graphical models. Mol. Biol. Evol. 17:875–881. [DOI] [PubMed] [Google Scholar]
- Tajima F. 1983. Evolutionary relationship of DNA sequences in finite populations. Genetics 105:437–460. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Takahata N., Nei M. 1985. Gene genealogy and variance of interpopulational nucleotide differences. Genetics 110:325–344. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Than C., Ruths D., Nakhleh L. 2008. PhyloNet: a software package for analyzing and reconstructing reticulate evolutionary relationships. BMC Bioinformatics 9:322. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Iersel L., Kelk S., Lekić N., Scornavacca C. 2014. A practical approximation algorithm for solving massive instances of hybridization number for binary and nonbinary trees. BMC Bioinformat. 15:1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Iersel L., Linz S. 2013. A quadratic kernel for computing the hybridization number of multiple trees. Inform. Process. Lett. 113:318–323. [Google Scholar]
- White M.A., Ané C., Dewey C.N., Larget B.R., Payseur B.A. 2009. Fine-scale phylogenetic discordance across the house mouse genome. PLoS Genet. 5:e1000729. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu Y. 2012. Coalescent-based species tree inference from gene tree topologies under incomplete lineage sorting by maximum likelihood. Evolution 66:763–775. [DOI] [PubMed] [Google Scholar]
- Yu Y., Degnan J.H., Nakhleh L. 2012. The probability of a gene tree topology within a phylogenetic network with applications to hybridization detection. PLoS Genet. 8:e1002660–e1002660. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu Y., Dong J., Liu K.J., Nakhleh L. 2014. Maximum likelihood inference of reticulate evolutionary histories. Proc. Natl. Acad. Sci. USA: 111:16448–16453. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu Y., Nakhleh L. 2015. A maximum pseudo-likelihood approach for phylogenetic networks. BMC Genom. 16:S10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu Y., Than C., Degnan J.H., Nakhleh L. 2011. Coalescent histories on phylogenetic networks and detection of hybridization despite incomplete lineage sorting. Syst. Biol. 60:138–149. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu S., Degnan J.H., Goldstien S.J., Eldon B. 2015. Hybrid-lambda: simulation of multiple merger and kingman gene genealogies in species networks and species trees. BMC Bioinform. 16:292. [DOI] [PMC free article] [PubMed] [Google Scholar]