Development of a Translational Physiologically Based Pharmacokinetic Model for Antibody-Drug Conjugates: a Case Study with T-DM1

Abstract

Systems pharmacokinetic (PK) models that can characterize and predict whole body disposition of antibody-drug conjugates (ADCs) are needed to support (i) development of reliable exposure-response relationships for ADCs and (ii) selection of ADC targets with optimal tumor and tissue expression profiles. Towards this goal, we have developed a translational physiologically based PK (PBPK) model for ADCs, using T-DM1 as a tool compound. The preclinical PBPK model was developed using rat data. Biodistribution of DM1 in rats was used to develop the small molecule PBPK model, and the PK of conjugated trastuzumab (i.e., T-DM1) in rats was characterized using platform PBPK model for antibody. Both the PBPK models were combined via degradation and deconjugation processes. The degradation of conjugated antibody was assumed to be similar to a normal antibody, and the deconjugation of DM1 from T-DM1 in rats was estimated using plasma PK data. The rat PBPK model was translated to humans to predict clinical PK of T-DM1. The translation involved the use of human antibody PBPK model to characterize the PK of conjugated trastuzumab, use of allometric scaling to predict human clearance of DM1 catabolites, and use of monkey PK data to predict deconjugation of DM1 in the clinic. PBPK model-predicted clinical PK profiles were compared with clinically observed data. The PK of total trastuzumab and T-DM1 were predicted reasonably well, and slight systemic deviations were observed for the PK of DM1-containing catabolites. The ADC PBPK model presented here can serve as a platform to develop models for other ADCs.

INTRODUCTION

Antibody-drug conjugates (ADCs) are targeted therapeutic conjugates that employ antibodies for its specificity and long half-life and small molecules for their cytotoxic effect. Even though ADCs have been investigated for decades, the discovery and development of ADCs remain empirical. For example, the process of selection of an ADC target is very subjective, as the optimum difference in the expression of target required between the tumor and normal tissues for a better therapeutic index of an ADC is unknown. This optimum differential for the expression of the target will be different for each target and will depend on properties like abundance of the target on different cell types, turnover rate, internalization in the presence of ADC, and affinity for the ADC. Consequently, a quantitative tool that can integrate all these processes involved in the disposition of ADC in normal and tumor tissues can provide a better framework for making objective decisions regarding selection of ADC targets. Similarly, development of exposure-response relationships for ADCs remains empirical. All the relationships are developed using plasma exposure of different ADC analytes, and sometimes results in counterintuitive conclusions like decreased probability of clinical grade 3/4/5 hepatotoxicity for T-DM1 with increasing concentrations of ADC in plasma (1). These counterintuitive findings stem from the use of wrong analytes to correlate with the pharmacological effect of the ADC and/or the use of concentrations in the plasma that may not accurately reflect the concentrations at the site-of-action. Consequently, measurement of the concentrations of different ADC-related analytes (e.g., conjugated antibody, total antibody, conjugated drug, and unconjugated drug) at the site-of-action is essential for establishing reliable exposure-response relationships for ADCs. However, measurement of these analytes in tissues and tumor is not easy and not even feasible in the clinical setting. Therefore, there is a need to develop a quantitative tool that can characterize and predict the concentrations of different ADC-related analytes in various target expressing and non-target expressing tissues. As such, system pharmacokinetic (PK) models that can integrate the physiological processes to predict whole body disposition of ADCs are essential for rationale discovery and development of ADCs (2,3).

Physiologically based PK (PBPK) models are one such system of PK models that can not only be used to characterize the whole body PK of drugs but can also be used to accomplish successful preclinical-to-clinical translation of drug PK (4,5). However, development of a PBPK model for ADCs is challenging as one needs to not only characterize the whole body disposition of the conjugate but also need to simultaneously characterize the whole body disposition of the unconjugated drug and unconjugated antibody along with in vivo stability of the ADC. Thus, one needs to develop separate PBPK models for the antibody and the drug and needs to induce interaction between these PBPK models to develop the PBPK model for ADCs. Previously, we have developed a similar PBPK model that can simultaneously characterize the whole body disposition of an antitopotecan antibody and topotecan using two separate PBPK models and can also characterize the binding interaction between these two molecules by combining the two PBPK models. This work provides the base for the proposed ADC PBPK model and serves as the proof-of-concept for the combined PBPK model envisioned for ADCs (6).

In this manuscript, we have first described the development of the ADC PBPK model using biodistribution data of DM1 and T-DM1 in rats. The preclinical PBPK model for T-DM1 was scaled to humans, and a priori predictions made by the PBPK model for the PK of various analytes were compared with the clinically observed PK data to assess the quality of model predictions. The rat PBPK model was also used to perform a global sensitivity analysis and pathway analysis on the model.

METHODS

Datasets

All datasets were digitized from literature and mean data were used for model development and validation. The data on whole body disposition of DM1 in rats following intravenous administration of 200 μg/kg radiolabeled [³H]-DM1 was used to develop the small molecule PBPK model (7). The whole body disposition data generated by Shen et al. (8) following intravenous administration of 13 mg/kg radiolabeled T-[³H]DM1 in rats was used to validate the preclinical PBPK model for ADC. To estimate the average deconjugation rate of DM1 from T-DM1 in rats, plasma PK of total trastuzumab and T-DM1 obtained following administration of 13 mg/kg T-DM1 in rats was used (9). In order to support clinical translation of the PBPK model, the deconjugation rate of DM1 from T-DM1 in monkeys was estimated using plasma PK of total trastuzumab and T-DM1 obtained following an intravenous dose of 30 mg/kg T-DM1 in monkeys (10). To evaluate the quality of clinical PK predictions made by the translated T-DM1 PBPK model, total trastuzumab, T-DM1, and unconjugated DM1 PK profiles in patients were obtained from four different phase I and II clinical studies (11–14).

Model Development

PBPK Model for Unconjugated Drug (UD)

The PBPK model developed for unconjugated drug contained 14 tissue compartments: lung, heart, kidney, muscle, skin, liver, brain, adipose, thymus, bone, small intestine, large intestine, spleen, and pancreas (Fig. 1a). All the tissue compartments and a plasma/blood cell compartment were connected via plasma flow and arranged in an anatomical order. Each tissue compartment was further subdivided into vascular (plasma and blood cells), endothelial, interstitial, and cellular subcompartments (Fig. 1b). A rapid distribution of drug between the blood cell, plasma, endothelial, and interstitial compartments was assumed (i.e., 100 times the value of blood flow to the tissue, based on reference (6)). Distribution of drug between interstitial and cellular compartments was assumed to be either rapid or permeability limited depending on the accumulation profile for the drug in a specific tissue. Partitioning of the unconjugated drug to tissue cell spaces and blood cells was characterized using the partition coefficient (Kp) values, which were calculated using the observed ratio of tissue and plasma AUCs (area under the concentration-time profile curves). The calculated Kp values for each tissue were adjusted for fraction of unbound drug in the plasma and the fraction of tissue volume accounted by the cellular space, by dividing Kp values with them. Shen et al. (7) have reported that radioactive DM1 in rats was mainly cleared in feces and only 5% was eliminated in urine. Accordingly, here we assumed that unconjugated DM1 was eliminated only via the hepatic pathway. The model was fitted to the observed plasma and tissue PK data of DM1 to estimate the permeability surface area values for the select tissues and the hepatic clearance value. The equations for the unconjugated DM1 PBPK model are provided as the following:

Fig. 1.

a Structure of the whole body platform PBPK model for ADC disposition. It consists of two separate PBPK models for ADC and unconjugated drug. All organs are represented by a rectangular compartment (except tumor) and connected in an anatomical manner with blood/plasma flow (solid arrows) and lymphatic flow (dashed arrows). Arrows represent the direction of the flow. b Structure of the tissue level PBPK model for ADC disposition. Each tissue compartment, except blood and lymph node, is further divided into vascular, endosomal, interstitial, and cellular subcompartments. The vascular subcompartment is further divided into plasma and blood cells. For a detailed description of the symbols and drug disposition processes, please refer to the model structure section. c Schematics of mechanistic tumor PK model. Upon administration of ADC into systemic circulation, ADC may distribute to tumor compartment. Once inside the tumor extracellular matrix, ADC is either allowed to interact with the cell surface antigen or allowed to diffuse back to systemic circulation. Antigen binding leads to internalization and degradation with subsequent release of unconjugated drug. Unconjugated drug may bind to the target inside the cell or diffuse out of the cell. Non-specific dissociation of unconjugated drug from ADC in extracellular matrix is also allowed in the model (15)

Plasma

$$\text{Vplasma}\times \frac{d{C}_{UD}^{\text{plasma}}}{dt}=Q_{\mathit{plasma}}^{\mathit{heart}}\times C_{\text{plasma\_}UD}^{\text{heart}}+Q_{\text{plasma}}^{\text{kidney}}\times C_{\text{plasma\_}UD}^{\text{kidney}}+Q_{\text{plasma}}^{\text{brain}}\times C_{\text{plasma\_}UD}^{\text{brain}}+Q_{\text{plasma}}^{\text{muscle}}\times C_{\text{plasma\_}UD}^{\text{muscle}}+Q_{\text{plasma}}^{\text{marrow}}\times C_{\text{plasma\_}UD}^{\text{marrow}}+Q_{\text{plasma}}^{\text{thymus}}\times C_{\text{plasma\_}UD}^{\text{thymus}}+Q_{\text{plasma}}^{\text{skin}}\times C_{\text{plasma\_}UD}^{\text{skin}}+Q_{\text{plasma}}^{\text{fat}}\times C_{\text{plasma\_}UD}^{\text{fat}}+\left(Q_{\text{plasma}}^{\text{liver}}+Q_{\text{plasma}}^{\text{SI}}+Q_{\mathit{plasma}}^{LI}+Q_{\text{plasma}}^{\text{spleen}}+Q_{\text{plasma}}^{\text{pancreas}}\right)\times C_{\text{plasma\_}UD}^{\text{liver}}+C_{\text{plasma\_}UD}^{\text{other}}\times C_{\text{plasma}}^{\text{other}}+P{S}_{bc}\times \left(C_{UD}^{\text{bloodcells}}/k{p}_{bc}\right)-f_{up}\times P{S}_{bc}\times C_{UD}^{\mathit{plasma}}-Q_{\text{plasma}}^{\text{lung}}\times C_{UD}^{\mathit{plasma}}-\left(\frac{2\times P_{UD}\times R_{\mathit{cap}}}{{\text{Rkrogh}}^2}\right)\times \left(C_{UD}^{\text{plasma}}-\frac{C_{{\text{freeUD}}_{\mathit{extra}}}^{\text{tumor}}}{{\epsilon }_{UD}}\right)\times V_{\text{total}\text{tumor}}-\left(\frac{6\times D_{UD}}{{\text{Rtumor}}^2}\right)\times \left(C_{UD}^{\text{plasma}}-\frac{C_{{\text{freeUD}}_{\text{extra}}}^{\text{tumor}}}{{\epsilon }_{UD}}\right)\times V_{\text{total}\text{tumor}}+K_{\mathit{dec}}\times C_{\mathit{ADC}}^{\text{plasma}}\times V_{\text{plasma}}\times \mathit{DAR}$$ (1)

Blood cells (bc)

$$V_{bc}\times \frac{d{C}_{UD}^{bc}}{dt}=f_{up}\times P{S}_{bc}\times C_{UD}^{\mathit{plasma}}-P{S}_{bc}\times \left(C_{UD}^{bc}/k{p}_{bc}\right)-Q_{bc}^{\mathit{lung}}\times C_{UD}^{bc}+Q_{bc}^{\mathit{heart}}\times C_{bc\text{\_}UD}^{\mathit{heart}}+Q_{bc}^{\mathit{kidney}}\times C_{bc\text{\_}UD}^{\mathit{kidney}}+Q_{bc}^{\mathit{brain}}\times C_{bc\text{\_}UD}^{\mathit{brain}}+Q_{bc}^{\mathit{muscle}}\times C_{bc\text{\_}UD}^{\mathit{muscle}}+Q_{bc}^{\mathit{marrow}}\times C_{bc\text{\_}UD}^{\mathit{marrow}}+Q_{bc}^{\mathit{thymus}}\times C_{bc\text{\_}UD}^{\mathit{thymus}}+Q_{bc}^{\mathit{skin}}\times C_{bc\text{\_}UD}^{\mathit{skin}}+Q_{bc}^{\mathit{fat}}\times C_{bc\text{\_}UD}^{\mathit{fat}}+\left(Q_{bc}^{\mathit{liver}}+Q_{bc}^{SI}+Q_{bc}^{LI}+Q_{bc}^{\mathit{spleen}}+Q_{bc}^{\mathit{pancreas}}\right)\times C_{bc\text{\_}UD}^{\mathit{liver}}+Q_{bc}^{\mathit{other}}\times C_{bc\text{\_}UD}^{\mathit{other}}$$ (2)

The Liver

Blood cell compartment

$$V_{bc}^{\mathit{liver}}\times \frac{d{C}_{bc\text{\_}UD}^{\mathit{liver}}}{dt}=f_{up}\times P{S}_{bc}\times C_{\mathit{plasma}\text{\_}UD}^{\mathit{liver}}-P{S}_{bc}\times \left(C_{bc\text{\_}UD}^{\mathit{liver}}/k{p}_{bc}\right)+Q_{bc}^{\mathit{liver}}\times C_{bc\text{\_}UD}^{\mathit{lung}}+Q_{bc}^{SI}\times C_{bc\text{\_}UD}^{SI}+Q_{bc}^{LI}\times C_{bc\text{\_}UD}^{LI}+Q_{bc}^{\mathit{spleen}}\times C_{bc\text{\_}UD}^{\mathit{spleen}}+Q_{bc\text{\_}UD}^{\mathit{pancreas}}\times C_{bc\text{\_}UD}^{\mathit{pancreas}}-\left(Q_{bc}^{\mathit{liver}}+Q_{bc}^{SI}+Q_{bc}^{LI}+Q_{bc}^{\mathit{spleen}}+Q_{bc}^{\mathit{pancreas}}\right)\times C_{bc\text{\_}UD}^{\mathit{liver}}$$ (3)

Plasma compartment

$$V_{\mathit{plasma}}^{\mathit{liver}}\times \frac{d{C}_{\mathit{plasma}\text{\_}UD}^{\mathit{liver}}}{dt}=Q_{\mathit{plasma}}^{\mathit{liver}}\times C_{\mathit{plasma}\text{\_}UD}^{\mathit{lung}}+Q_{\mathit{plasma}}^{SI}\times C_{\mathit{plasma}\text{\_}UD}^{SI}+Q_{\mathit{plasma}}^{LI}\times C_{\mathit{plasma}\text{\_}UD}^{LI}+Q_{\mathit{plasma}}^{\mathit{spleen}}\times C_{\mathit{plasma}\text{\_}UD}^{\mathit{spleen}}+Q_{\mathit{plasma}}^{\mathit{pancreas}}\times C_{\mathit{plasma}\text{\_}UD}^{\mathit{pancreas}}-\left(Q_{\mathit{plasma}}^{\mathit{liver}}+Q_{\mathit{plasma}}^{SI}+Q_{\mathit{plasma}}^{LI}+Q_{\mathit{plasma}}^{\mathit{spleen}}+Q_{\mathit{plasma}}^{\mathit{pancreas}}\right)\times C_{\mathit{plasma}\text{\_}UD}^{\mathit{liver}}-f_{up}\times P{S}_{bc}\times C_{\mathit{plasma}\text{\_}UD}^{\mathit{liver}}+P{S}_{bc}\left(C_{bc\text{\_}UD}^{\mathit{liver}}/k{p}_{bc}\right)-f_{up}\times Q_{\mathit{plasma}}^{\mathit{lung}}\times G\times C_{\mathit{plasma}\text{\_}UD}^{\mathit{liver}}+Q_{\mathit{plasma}}^{\mathit{lung}}\times G\times C_{\mathit{endosomal}\text{\_}UD}^{\mathit{liver}}+K_{\mathit{dec}}\times C_{\mathit{plasma}\text{\_}\mathit{ADC}}^{\mathit{liver}}\times V_{\mathit{plasma}}^{\mathit{liver}}\times \mathit{DAR}$$ (4)

Endosomal compartment

$$V_{\mathit{endosomal}}^{\mathit{liver}}\times \frac{d{C}_{\mathit{plasma}\text{\_}UD}^{\mathit{liver}}}{dt}=Q_{\mathit{plasma}}^{\mathit{liver}}\times G\times f_{up}\times C_{\mathit{plasma}\text{\_}UD}^{\mathit{liver}}-2\times Q_{\mathit{plasma}}^{\mathit{lung}}\times G\times C_{\mathit{endosomal}\text{\_}UD}^{\mathit{liver}}+Q_{\mathit{plasma}}^{\mathit{liver}}\times G\times C_{\mathit{interstitial}\text{\_}UD}^{\mathit{liver}}+\mathit{DAR}\times K_{\mathit{deg}}\times C_{\mathit{unbound}\mathit{endo}\text{\_}\mathit{ADC}}^{\mathit{liver}}\times V_{\mathit{endosomal}}^{\mathit{liver}}$$ (5)

Interstitial compartment

$$V_{\mathit{interstitial}}^{\mathit{liver}}\times \frac{d{c}_{\mathit{interstitial}\text{\_}UD}^{\mathit{liver}}}{dt}=Q_{\mathit{plasma}}^{\mathit{lung}}\times G\times C_{\mathit{endosomal}\text{\_}UD}^{\mathit{liver}}-Q_{\mathit{plasma}}^{\mathit{lung}}\times G\times C_{\mathit{interstitial}\text{\_}UD}^{\mathit{liver}}-P{S}_{\mathit{liver}}\times C_{\mathit{interstitial}\text{\_}UD}^{\mathit{liver}}+P{S}_{\mathit{liver}}\times \left(C_{\mathit{cellular}\text{\_}UD}^{\mathit{liver}}/k{p}_{\mathit{liver}}\right)-C_{\mathit{interstitial}\text{\_}UD}^{\mathit{liver}}\times C{L}_{\mathit{hepatic}}+K_{\mathit{dec}}\times C_{\mathit{interstitial}\text{\_}\mathit{ADC}}^{\mathit{liver}}\times V_{\mathit{interstitial}}^{\mathit{liver}}\times \mathit{DAR}$$ (6)

Cellular compartment

$$V_{\mathit{cellular}}^{\mathit{liver}}\times \frac{d{C}_{\mathit{cellular}\text{\_}UD}^{\mathit{liver}}}{dt}=P{S}_{\mathit{liver}}\times C_{\mathit{interstitial}\text{\_}UD}^{\mathit{liver}}-P{S}_{\mathit{liver}}\times \left(C_{\mathit{cellular}\text{\_}UD}^{\mathit{liver}}/k{p}_{\mathit{liver}}\right)$$ (7)

Blood cell compartment

$$V_{bc}^{\mathit{tissue}}\times \frac{d{C}_{bc\text{\_}UD}^{\mathit{tissue}}}{dt}=f_{up}\times P{S}_{bc}\times C_{\mathit{plasma}\text{\_}UD}^{\mathit{tissue}}-P{S}_{bc}\times \left(C_{bc\text{\_}UD}^{\mathit{tissue}}/k{p}_{bc}\right)+Q_{bc}^{\mathit{tissue}}\times C_{bc\text{\_}UD}^{\mathit{lung}}-Q_{bc}^{\mathit{tissue}}\times C_{bc\text{\_}UD}^{\mathit{tissue}}$$ (8)

All other tissues

Plasma compartment

$$V_{\mathit{plasma}}^{\mathit{tissue}}\times \frac{d{C}_{\mathit{plasma}\text{\_}UD}^{\mathit{tissue}}}{dt}=Q_{\mathit{plasma}}^{\mathit{tissue}}\times C_{\mathit{plasma}\text{\_}UD}^{\mathit{tissue}}-Q_{\mathit{plasma}}^{\mathit{tissue}}\times C_{\mathit{plasma}\text{\_}UD}^{\mathit{tissue}}-f_{up}\times Q_{\mathit{plasma}}^{\mathit{tissue}}\times G\times C_{\mathit{plasma}\text{\_}UD}^{\mathit{tissue}}+Q_{\mathit{plasma}}^{\mathit{tissue}}\times G\times C_{\mathit{endosomal}\text{\_}UD}^{\mathit{tissue}}-f_{up}\times P{S}_{bc}\times C_{\mathit{plasma}\text{\_}UD}^{\mathit{tissue}}+P{S}_{bc}\times \left(C_{bc\text{\_}\mathit{UD}}^{\mathit{tissue}}/k{p}_{bc}\right)+K_{\mathit{dec}}\times C_{\mathit{plasma}\text{\_}\mathit{ADC}}^{\mathit{tissue}}\times V_{\mathit{plasma}}^{\mathit{tissue}}\times \mathit{DAR}$$ (9)

Endosomal compartment

$$V_{\mathit{endosomal}}^{\mathit{tissue}}\times \frac{d{C}_{\mathit{endosomal}\text{\_}UD}^{\mathit{tissue}}}{dt}=f_{up}\times Q_{\mathit{plasma}\text{\_}UD}^{\mathit{tissue}}\times G\times C_{\mathit{plasma}\text{\_}UD}^{\mathit{tissue}}-2\times Q_{\mathit{plasma}}^{\mathit{tissue}}\times G\times C_{\mathit{endosomal}\text{\_}UD}^{\mathit{tissue}}+Q_{\mathit{plasma}}^{\mathit{tissue}}\times G\times C_{\mathit{interstitial}\text{\_}UD}^{\mathit{tissue}}+\mathit{DAR}\times K_{\mathit{deg}}\times C_{\mathit{unbound}\mathit{endo}\text{\_}\mathit{ADC}}^{\mathit{tissue}}\times V_{\mathit{endosomal}}^{\mathit{tissue}}$$ (10)

Interstitial compartment

$$V_{\mathit{interstitial}}^{\mathit{tissue}}\times \frac{d{C}_{\mathit{interstitial}}^{\mathit{tissue}}}{dt}=Q_{\mathit{plasma}}^{\mathit{tissue}}\times G\times C_{\mathit{endosomal}\text{\_}UD}^{\mathit{tissue}}-Q_{\mathit{plasma}}^{\mathit{tissue}}\times G\times C_{\mathit{interstitial}\text{\_}UD}^{\mathit{tissue}}-P{S}_{\mathit{tissue}}\times C_{\mathit{interstitial}\text{\_}UD}^{\mathit{tissue}}+P{S}_{\mathit{tissue}}\times \left(C_{\mathit{cellular}\text{\_}UD}^{\mathit{tissue}}/k{p}_{\mathit{tissue}}\right)+K_{\mathit{dec}}\times C_{\mathit{interstitial}\text{\_}\mathit{ADC}}^{\mathit{tissue}}\times C_{\mathit{interstitial}}^{\mathit{tissue}}\times \mathit{DAR}$$ (11)

Cellular compartment

$$V_{\mathit{cellular}}^{\mathit{tissue}}\times \frac{d{C}_{\mathit{cellular}\text{\_}UD}^{\mathit{tissue}}}{dt}=P{S}_{\mathit{tissue}}\times C_{\mathit{interstitial}\text{\_}UD}^{\mathit{tissue}}-P{S}_{\mathit{tissue}}\times \left(C_{\mathit{cellular}\text{\_}UD}^{\mathit{tissue}}/k{p}_{\mathit{tissue}}\right)$$ (12)

The definition of each symbol used in the previous equations is provided in Table I. The terms associated with deconjugation and degradation of ADC and average drug:total-antibody ratio (DAR) of ADC are only active when the whole ADC PBPK model is considered. The tumor disposition of drug was only considered in the human PBPK model.

Table I.

Glossary and literature-derived values of model parameters used in the PBPK model

Parameter	Definition	Value	Source
Qp, Qtissues, plasma, Qlymph, Vtissue-plasma, Vtissue-blood cells, Vtissue-interstitial, Vtissue-endosomal, Vtissue-cellular	Physiological volumes and flow rates for rat and human		(4)
Human CLh	Hepatic clearance (L/h)	104.7	Allometric scaling
CLup	Clearance uptake by pinocytosis and exocytosis (L/h)	0.0366	(4)
Kdeg	Degradation rate constant (1/h)	42.9	(4)
FcRn	FcRn concentration in the endosomal space (nM)	49,800	(4)
C_LNLF	Rate of transfer from lymph to plasma	9.1	(4)
kon, koff	Binding parameters of humanized antibody and rat/human FcRn (kon = 1/nM h, koff = 1/h)	Rat: kon = 0.8, koff = 28 Human : kon = 0.5 6, koff = 54.8	(16)
Rcap	Radius of tumor blood capillary, m	8 × 10−6	(17)
Rkrogh	Average distance between two capillaries, m	75 × 10−6	(17)
PADC	Permeability rate of ADC across and around the tumor blood vessels, m/h	13.9 × 10−6	(17)
DADC	Diffusion rate of ADC across and around the tumor blood vessels, m2/h	0.92 × 10−7	(17)
εADC	Tumor void volume for ADC	0.25	(17)
Agtotal	Total antigen, nM	5200	(18)
konADC-antigen	Association rate constant between ADC and antigen, 1/nM hr	0.37	(17)
koffADC-antigen	Dissociation rate constant between ADC and antigen, 1/h	0.014	(18)
kintantigen	Internalization rate of antigen, 1/h	0.1	(18)
Rtumor	Tumor radius, m	1 × 10−2
PUD	Permeability rate of unconjugated drug (UD) across and around the tumor blood vessels, m/h	0.087 × 10−2	(17)
DUD	Diffusion rate of UD across and around the tumor blood vessels, m2/h	1.04	(17)
εUD	Tumor void volume for UD	0.44	(17)
kinUD	Non-specific uptake rate of UD in cells, 1/h	0.403	(17)
koutUD	Efflux of UD from the cell, 1/h	0.046	(17)
konUD-tubulin	Association rate constant between UD and tubulin, 1/nM h	0.03	Assumed
koffUD-tubulin	Dissociation rate constant between UD and tubulin, 1/h	27.9	Based on Kd = 930 nM (19)
Tubulintotal	Total concentration of tubulin, nM	65	(17)
DAR	Drug:total-antibody ratio at time = 0	3.5	FDA review document
fup	Fraction unbound in plasma	0.03 rat, 0.08 human	FDA review document
Kdec	Dissociation rate constant of UD from ADC, 1/h	Rat = 0.0049, human = 0.0079	Estimated using compartment model
G	A gain factor that is multiplied by tissue blood flow to make the unconjugated drug distribution instantaneous	100	(6)

PBPK Model for ADC

The ADC PBPK model was developed by integrating the unconjugated drug PBPK model and the platform PBPK model for antibodies (4) via ADC degradation and deconjugation processes as shown in Fig. 1a. In the figure, the right-hand side PBPK model characterizes conjugated antibody (i.e., ADC) disposition in each tissue, and the left-hand side model is the unconjugated drug PBPK model described previously. In the conjugated antibody model, each tissue compartment is subdivided into vascular (plasma and blood cells), endosomal, interstitial, and cellular subcompartments (Fig. 1b). ADC is assumed to enter the vascular compartment and taken up by the endosomal layer via pinocytosis. ADC is assumed to interact with neonatal Fc receptor (FcRn) in the endosomal compartment and the bound ADC is allowed to recycle back to either the plasma or interstitial fluid compartment via pinocytosis. ADC molecules in the endosomal space that are not bound to FcRn are assumed to degrade. ADC molecules are also assumed to enter the interstitial compartment directly from the vascular compartment via lymph flow, and also exit the interstitial space to the lymph node compartment via lymph flow. Distribution of ADC via lymph flow also depends on the reflection coefficients of the ADC (i.e., ${\sigma }_{\mathit{tissue}}^{IS}$ —interstitial reflection coefficient; and ${\sigma }_{\mathit{tissue}}^V$ —vascular reflection coefficient). It was also assumed that the ADC molecules do enter the cellular compartment.

It was assumed that, upon degradation, each ADC molecule releases all the attached drug molecules (equivalent to DAR at the time of degradation) to the respective tissue compartment in the unconjugated drug PBPK model. The constant degradation rate for the ADC was assumed to be the same as that of the typical antibody (20) and fixed to a value embedded within the platform PBPK model for antibodies. We also assumed that, during the entire time course of ADC in the plasma and tissues, drug molecules are shed by the deconjugation process within the vascular and interstitial compartments. All the shed molecules were assumed to enter the respective compartment of the unconjugated drug PBPK model. The non-specific deconjugation rate of the drug from ADC was estimated by fitting a modified two-compartment PK model (Supplementary Figure 1) developed for ADC to total antibody and ADC plasma PK data simultaneously (as detailed in (17)). This model assumes that total antibody and conjugated antibody eliminate from the central compartment at the same rate, and the additional clearance of conjugated antibody is due to deconjugation of drug from the ADC. The average DAR for the ADC was assumed to decrease over time according to the estimated ADC deconjugation rate.

Our previously published tumor disposition model for ADCs (Fig. 1c) (15,17) was also incorporated in the ADC PBPK model. In this model, the ADC and unconjugated drug molecules are allowed to travel between the plasma and tumor extracellular spaces via surface and vascular exchange processes, which depend on permeability and diffusion coefficients of the molecules and the tumor size. Once ADC is in the tumor extracellular environment, it is allowed to bind to the target antigen on the cell surface and internalize in the cells. Inside the tumor cells, ADC undergoes degradation and releases the conjugated drug molecules (equivalent to DAR), which are allowed to bind to the intracellular target (e.g., tubulin) or efflux out of the cell. Unconjugated drug molecules outside the tumor cells are also allowed to diffuse into the cells. It is also assumed that ADC can undergo nonspecific deconjugation in the tumor extracellular space to generate unconjugated drug molecules.

All the equations used to develop the conjugated antibody PBPK model are provided as the following:

Plasma

$$V_{\mathit{plasma}}\times \frac{d{C}_{\mathit{ADC}}^{\mathit{plasma}}}{dt}=-\left(Q_{\mathit{plasma}}^{\mathit{lung}}+Q_{\mathit{lymph flow}}^{\mathit{lung}}\right)\times C_{\mathit{ADC}}^{\mathit{plasma}}+\left(Q_{\mathit{plasma}}^{\mathit{heart}}-Q_{\mathit{lymph flow}}^{\mathit{heart}}\right)\times C_{\mathit{plasmaADC}}^{\mathit{heart}}+\left(Q_{\mathit{plasma}}^{\mathit{kidney}}-Q_{\mathit{lymph flow}}^{\mathit{kidney}}\right)\times C_{\mathit{plasmaADC}}^{\mathit{kidney}}+\left(Q_{\mathit{plasma}}^{\mathit{brain}}-Q_{\mathit{lymph flow}}^{\mathit{brain}}\right)\times C_{\mathit{plasmaADC}}^{\mathit{brain}}+\left(Q_{\mathit{plasma}}^{\mathit{muscle}}-Q_{\mathit{lymph flow}}^{\mathit{muscle}}\right)\times C_{\mathit{plasmaADC}}^{\mathit{muscle}}+\left(Q_{\mathit{plasma}}^{\mathit{marrow}}-Q_{\mathit{lymph flow}}^{\mathit{marrow}}\right)\times C_{\mathit{plasmaADC}}^{\mathit{marrow}}+\left(Q_{\mathit{plasma}}^{\mathit{thymus}}-Q_{\mathit{lymph flow}}^{\mathit{thymus}}\right)\times C_{\mathit{plasmaADC}}^{\mathit{thymus}}+\left(Q_{\mathit{plasma}}^{\mathit{skin}}-Q_{\mathit{lymph flow}}^{\mathit{skin}}\right)\times C_{\mathit{plasmaADC}}^{\mathit{skin}}+\left(Q_{\mathit{plasma}}^{\mathit{fat}}-Q_{\mathit{lymph flow}}^{\mathit{fat}}\right)\times C_{\mathit{plasmaADC}}^{\mathit{fat}}+\left(\left(Q_{\mathit{plasma}}^{SI}-Q_{\mathit{lymph flow}}^{SI}\right)+\left(Q_{\mathit{plasma}}^{LI}-Q_{\mathit{lymph flow}}^{LI}\right)+\left(Q_{\mathit{plasma}}^{\mathit{spleen}}-Q_{\mathit{lymph flow}}^{\mathit{spleen}}\right)+\left(Q_{\mathit{plasma}}^{\mathit{pancreas}}-Q_{\mathit{lymph flow}}^{\mathit{pancreas}}\right)+\left(Q_{\mathit{plasma}}^{\mathit{liver}}-Q_{\mathit{lymph flow}}^{\mathit{liver}}\right)\right)\times C_{\mathit{plasmaADC}}^{\mathit{liver}}+\left(Q_{\mathit{plasma}}^{\mathit{other}}-Q_{\mathit{lymph flow}}^{\mathit{other}}\right)\times C_{\mathit{plasmaADC}}^{\mathit{other}}+Q_{\mathit{lymph flow}}^{\mathit{lymph}\mathit{node}}\times C_{\mathit{ADC}}^{\mathit{lymph}\mathit{node}}-\left(\frac{2\times P_{\mathit{ADC}}\times \mathit{Rcap}}{{\mathit{Rkrogh}}^2}\right)\times \left(C_{\mathit{ADC}}^{\mathit{plasma}}-\frac{C_{\mathit{ADC free}}^{\mathit{tumor}}}{{\epsilon }_{\mathit{ADC}}}\right)\times V_{\mathit{total}\mathit{tumor}}-\left(\frac{6\times D_{\mathit{ADC}}}{{\mathit{Rtumor}}^2}\right)\times \left(C_{\mathit{ADC}}^{\mathit{plasma}}-\frac{C_{\mathit{ADC free}}^{\mathit{tumor}}}{{\epsilon }_{\mathit{ADC}}}\right)\times V_{\mathit{total}\mathit{tumor}}-K_{\mathit{dec}}\times C_{\mathit{ADC}}^{\mathit{plasma}}\times V_{\mathit{plasma}}$$ (13)

Blood cells

$$V_{bc}\times \frac{d{C}_{\mathit{ADC}}^{bc}}{dt}=-Q_{bc}^{\mathit{lung}}\times C_{\mathit{ADC}}^{bc}+Q_{bc}^{\mathit{heart}}\times C_{bc\text{\_}\mathit{ADC}}^{\mathit{heart}}+Q_{bc}^{\mathit{kidney}}\times C_{bc\text{\_}\mathit{ADC}}^{\mathit{kidney}}+Q_{bc}^{\mathit{brain}}\times C_{bc\text{\_}\mathit{ADC}}^{\mathit{brain}}+Q_{bc}^{\mathit{muscle}}\times C_{bc\text{\_}\mathit{ADC}}^{\mathit{muscle}}+Q_{bc}^{\mathit{marrow}}\times C_{bc\text{\_}\mathit{ADC}}^{\mathit{marrow}}+Q_{bc}^{\mathit{thymus}}\times C_{bc\text{\_}\mathit{ADC}}^{\mathit{thymus}}+Q_{bc}^{\mathit{skin}}\times C_{bc\text{\_}\mathit{ADC}}^{\mathit{skin}}+Q_{bc}^{\mathit{fat}}\times C_{bc\text{\_}\mathit{ADC}}^{\mathit{fat}}+\left(Q_{bc}^{SI}+Q_{bc}^{LI}+Q_{bc}^{\mathit{spleen}}+Q_{bc}^{\mathit{pancreas}}+Q_{bc}^{\mathit{liver}}\right)\times C_{bc\text{\_}\mathit{ADC}}^{\mathit{liver}}+Q_{bc}^{\mathit{other}}\times C_{bc\text{\_}\mathit{ADC}}^{\mathit{other}}$$ (14)

Lymph node

$$V_{\text{lymphnode}}\times \frac{d{C}_{\mathit{ADC}}^{\text{lymphnode}}}{dt}=\left(1-{\sigma }_{\text{lung}}^{\text{IS}}\right)\times Q_{\text{lymph flow}}^{\text{lung}}\times C_{\text{interstitial}\mathit{ADC}}^{\text{lung}}+\left(1-{\sigma }_{\text{heart}}^{\text{IS}}\right)\times Q_{\text{lymph flow}}^{\text{heart}}\times C_{\text{interstitial}\mathit{ADC}}^{\text{heart}}+\left(1-{\sigma }_{\text{kidney}}^{\text{IS}}\right)\times Q_{\text{lymph flow}}^{\text{kidney}}\times C_{\text{interstitial}\mathit{ADC}}^{\text{kidney}}+\left(1-{\sigma }_{\text{brain}}^{\text{IS}}\right)\times Q_{\text{lymph flow}}^{\text{brain}}\times C_{\text{interstitial}\mathit{ADC}}^{\text{brain}}+\left(1-{\sigma }_{\text{muscle}}^{\text{IS}}\right)\times Q_{\text{lymph flow}}^{\text{muscle}}\times C_{\text{interstitial}\mathit{ADC}}^{\text{muscle}}+\left(1-{\sigma }_{\text{marrow}}^{\text{IS}}\right)\times Q_{\text{lymph flow}}^{\text{marrow}}\times C_{\text{interstitial}\mathit{ADC}}^{\text{marrow}}+\left(1-{\sigma }_{\text{thymus}}^{\text{IS}}\right)\times Q_{\text{lymph flow}}^{\text{thymus}}\times C_{\text{interstitial}\mathit{ADC}}^{\text{thymus}}+\left(1-{\sigma }_{\text{skin}}^{\text{IS}}\right)\times Q_{\text{lymph flow}}^{\text{skin}}\times C_{\text{interstitial}\mathit{ADC}}^{\text{skin}}+\left(1-{\sigma }_{\mathit{fat}}^{\text{IS}}\right)\times Q_{\text{lymph flow}}^{\mathit{fat}}\times C_{\text{interstitial}\mathit{ADC}}^{\mathit{fat}}+\left(1-{\sigma }_{\mathit{SI}}^{\text{IS}}\right)\times Q_{\text{lymph flow}}^{\mathit{SI}}\times C_{\text{interstitial}\mathit{ADC}}^{\mathit{SI}}+\left(1-{\sigma }_{\mathit{LI}}^{\text{IS}}\right)\times Q_{\text{lymph flow}}^{\mathit{LI}}\times C_{\text{interstitial}\mathit{ADC}}^{\mathit{LI}}+\left(1-{\sigma }_{\text{spleen}}^{\text{IS}}\right)\times Q_{\text{lymph flow}}^{\text{spleen}}\times C_{\text{interstitial}\mathit{ADC}}^{\text{spleen}}+\left(1-{\sigma }_{\text{pancreas}}^{\text{IS}}\right)\times Q_{\text{lymph flow}}^{\text{pancreas}}\times C_{\text{interstitial}\mathit{ADC}}^{\text{pancreas}}+\left(1-{\sigma }_{\text{liver}}^{\text{IS}}\right)Q_{\text{lymph}\text{flow}}^{\text{liver}}\times C_{\text{interstitial}\mathit{ADC}}^{\text{liver}}+\left(1-{\sigma }_{\text{other}}^{\text{IS}}\right)\times Q_{\text{lymph}\text{flow}}^{\text{other}}\times C_{\text{interstitial}\mathit{ADC}}^{\text{other}}-Q_{\text{lymph}\text{flow}}^{\text{lymphnode}}\times C_{\mathit{ADC}}^{\text{lymphnode}}$$ (15)

Liver

Blood cell compartment

$$V_{bc}^{\mathit{liver}}\times \frac{d{C}_{bc\text{\_}\mathit{ADC}}^{\mathit{liver}}}{dt}=Q_{bc}^{\mathit{liver}}\times Q_{bc\text{\_}\mathit{ADC}}^{\mathit{lung}}+Q_{bc}^{SI}\times C_{bc\text{\_}\mathit{ADC}}^{SI}+Q_{bc}^{LI}\times C_{bc\text{\_}\mathit{ADC}}^{LI}+Q_{bc}^{\mathit{spleen}}\times C_{bc\text{\_}\mathit{ADC}}^{\mathit{spleen}}+Q_{bc}^{\mathit{pancreas}}\times C_{bc\text{\_}\mathit{ADC}}^{\mathit{pancreas}}-\left(Q_{bc}^{\mathit{liver}}+Q_{bc}^{SI}+Q_{bc}^{LI}+Q_{bc}^{\mathit{spleen}}+Q_{bc}^{\mathit{pancreas}}\right)\times C_{bc\text{\_}\mathit{ADC}}^{\mathit{liver}}$$ (16)

Plasma compartment

$$V_{\mathit{plasma}}^{\mathit{liver}}\times \frac{d{C}_{\mathit{plasma}\text{\_}\mathit{ADC}}^{\mathit{liver}}}{dt}=Q_{\mathit{plasma}}^{\mathit{liver}}\times C_{\mathit{plasma}\text{\_}\mathit{ADC}}^{\mathit{lung}}+\left(Q_{\mathit{plasma}}^{SI}-Q_{\mathit{lymphflow}}^{SI}\right)\times C_{\mathit{plasma}\text{\_}\mathit{ADC}}^{SI}+\left(Q_{\mathit{plasma}}^{LI}-Q_{\mathit{lymphflow}}^{LI}\right)\times C_{\mathit{plasma}\text{\_}\mathit{ADC}}^{LI}+\left(Q_{\mathit{plasma}}^{\mathit{spleen}}-Q_{\mathit{lymphflow}}^{\mathit{spleen}}\right)\times C_{\mathit{plasma}\text{\_}\mathit{ADC}}^{\mathit{spleen}}\left(Q_{\mathit{plasma}}^{\mathit{pancreas}}-Q_{\mathit{lymphflow}}^{\mathit{pancreas}}\right)\times C_{\mathit{plasma}\text{\_}\mathit{ADC}}^{\mathit{pancreas}}-\left(\left(Q_{\mathit{plasma}}^{\mathit{liver}}-Q_{\mathit{lymphflow}}^{\mathit{liver}}\right)+\left(Q_{\mathit{plasma}}^{SI}-Q_{\mathit{lymphflow}}^{SI}\right)+\left(Q_{\mathit{lymphflow}}^{LI}-Q_{\mathit{lymphflow}}^{LI}\right)+\left(Q_{\mathit{plasma}}^{\mathit{spleen}}-Q_{\mathit{lymphflow}}^{\mathit{spleen}}\right)+\left(Q_{\mathit{plasma}}^{\mathit{pancreas}}-Q_{\mathit{lymphflow}}^{\mathit{pancreas}}\right)\right)\times C_{\mathit{plasma}\text{\_}\mathit{ADC}}^{\mathit{liver}}-\left(\left(1-{\sigma }_{\mathit{lymphflow}}^V\right)\times Q_{\mathit{lymphflow}}^{\mathit{liver}}\times C_{\mathit{plasma}\text{\_}\mathit{ADC}}^{\mathit{liver}}\right)-C{L}_{up}^{\mathit{liver}}\times C_{\mathit{plasma}\text{\_}\mathit{ADC}}^{\mathit{liver}}+C{L}_{up}^{\mathit{liver}}\times FR\times C_{\mathit{endosomal}\text{\_}\mathit{ADCbound}}^{\mathit{liver}}-K_{\text{dec}}{\times }^{\mathit{dec}}{C}_{\mathit{plasma}\text{\_}\mathit{ADC}}^{\mathit{liver}}\times V_{\mathit{plasma}}^{\mathit{liver}}$$ (17)

Unbound ADC in endosomal compartment

$$V_{\mathit{endosomal}}^{\mathit{liver}}\times \frac{d{C}_{\mathit{unbound}\mathit{endo}\text{\_}\mathit{ADC}}^{\mathit{liver}}}{dt}=C{L}_{up}^{\mathit{liver}}\times C_{\mathit{plasma}\text{\_}\mathit{ADC}}^{\mathit{liver}}+C{L}_{up}^{\mathit{liver}}\times C_{\mathit{interstitial}\text{\_}\mathit{ADC}}^{\mathit{liver}}-V_{\mathit{endosomal}}^{\mathit{liver}}\times k_{on}\times C_{\mathit{unbound}\mathit{endo}\text{\_}\mathit{ADC}}^{\mathit{liver}}\times C_{\mathit{FCRN}}^{\mathit{liver}}+V_{\mathit{endosomal}}^{\mathit{liver}}\times k_{\mathit{off}}\times C_{\mathit{bound}\mathit{endo}\text{\_}\mathit{ADC}}^{\mathit{liver}}-K_{\mathit{deg}}\times C_{\mathit{unbound}\mathit{endo}\text{\_}\mathit{ADC}}^{\mathit{liver}}\times V_{\mathit{endosomal}}^{\mathit{liver}}$$ (18)

Bound ADC in endosomal compartment

$$V_{\mathit{endosomal}}^{\mathit{liver}}\times \frac{d{C}_{\mathit{bound}\mathit{endo}\text{\_}\mathit{ADC}}^{\mathit{liver}}}{dt}=V_{\mathit{endosomal}}^{\mathit{liver}}\times k_{on}\times C_{\mathit{unbound}\mathit{endo}\text{\_}\mathit{ADC}}^{\mathit{liver}}\times C_{\mathit{FCRN}}^{\mathit{liver}}-V_{\mathit{endosomal}}^{\mathit{liver}}\times k_{\mathit{off}}\times C_{\mathit{bound}\mathit{endo}\text{\_}\mathit{ADC}}^{\mathit{liver}}-C{L}_{up}^{\mathit{liver}}\times C_{\mathit{bound}\mathit{endo}\text{\_}\mathit{ADC}}^{\mathit{liver}}$$ (19)

Interstitial compartment

$$V_{\mathit{interstitial}}^{\mathit{liver}}\times \frac{d{C}_{\mathit{interstitial}\text{\_}\mathit{ADC}}^{\mathit{liver}}}{dt}=\left(\left(1-{\sigma }_{\mathit{liver}}^V\right)\times Q_{\mathit{lymphflow}}^{\mathit{liver}}\times C_{\mathit{plasma}\text{\_}\mathit{ADC}}^{\mathit{liver}}\right)-\left(\left(1-{\sigma }_{\mathit{liver}}^{IS}\right)\times Q_{\mathit{lymphflow}}^{\mathit{liver}}\times C_{\mathit{interstitial}\text{\_}\mathit{ADC}}^{\mathit{liver}}\right)+C{L}_{up}^{\mathit{liver}}\times \left(1-FR\right)\times C_{\mathit{bound}\mathit{endo}\text{\_}\mathit{ADC}}^{\mathit{liver}}-C{L}_{up}^{\mathit{liver}}\times C_{\mathit{interstitial}\text{\_}\mathit{ADC}}^{\mathit{liver}}-K_{\mathit{dec}}\times C_{\mathit{bound}\mathit{endo}\text{\_}\mathit{ADC}}^{\mathit{liver}}\times V_{\mathit{interstitial}}^{\mathit{liver}}$$ (20)

All other tissues

Blood cell compartment

$$V_{bc}^{\mathit{tissue}}\times \frac{d{C}_{bc\text{\_}\mathit{ADC}}^{\mathit{tissue}}}{dt}=Q_{bc}^{\mathit{tissue}}\times C_{bc\text{\_}\mathit{ADC}}^{\mathit{lung}}-Q_{bc}^{\mathit{tissue}}\times C_{bc\text{\_}\mathit{ADC}}^{\mathit{tissue}}$$ (21)

Plasma compartment

$$V_{\mathit{plasma}}^{\mathit{tissue}}\times \frac{d{C}_{\mathit{plasma}\text{\_}\mathit{ADC}}^{\mathit{tissue}}}{dt}=Q_{\mathit{plasma}}^{\mathit{tissue}}\times C_{\mathit{plasma}\text{\_}\mathit{ADC}}^{\mathit{lung}}-\left(Q_{\mathit{plasma}}^{\mathit{tissue}}-Q_{\mathit{lymphflow}}^{\mathit{tissue}}\right)\times C_{\mathit{plasma}\text{\_}\mathit{ADC}}^{\mathit{tissue}}-\left(1-{\sigma }_{\mathit{tissue}}^V\right)\times Q_{\mathit{lymphflow}}^{\mathit{tissue}}\times C_{\mathit{plasma}\text{\_}\mathit{ADC}}^{\mathit{tissue}}-C{L}_{up}^{\mathit{tissue}}\times C_{\mathit{plasma}\text{\_}\mathit{ADC}}^{\mathit{tissue}}+C{L}_{up}^{\mathit{tissue}}\times FR\times C_{\mathit{bound}\mathit{endo}\text{\_}\mathit{ADC}}^{\mathit{tissue}}-K_{\mathit{dec}}\times C_{\mathit{plasma}\text{\_}\mathit{ADC}}^{\mathit{tissue}}\times V_{\mathit{plasma}}^{\mathit{tissue}}$$ (22)

Unbound ADC in endosomal compartment

$$V_{\mathit{endosomal}}^{\mathit{tissue}}\times \frac{d{C}_{\mathit{unbound}\mathit{endo}\text{\_}\mathit{ADC}}^{\mathit{tissue}}}{dt}=C{L}_{up}^{\mathit{tissue}}\times C_{\mathit{plasma}\text{\_}\mathit{ADC}}^{\mathit{tissue}}+C{L}_{up}^{\mathit{tissue}}\times C_{\mathit{interstitial}\text{\_}\mathit{ADC}}^{\mathit{tissue}}-V_{\mathit{endosomal}}^{\mathit{tissue}}\times k_{on}\times C_{\mathit{unbound}\mathit{endo}\text{\_}\mathit{ADC}}^{\mathit{tissue}}\times C_{\mathit{FCRN}}^{\mathit{tissue}}\times V_{\mathit{endosomal}}^{\mathit{tissue}}\times k_{\mathit{off}}\times C_{\mathit{bound}\mathit{endo}\text{\_}\mathit{ADC}}^{\mathit{tissue}}-K_{\mathit{dec}}\times C_{\mathit{unbound}\mathit{endo}\text{\_}\mathit{ADC}}^{\mathit{tissue}}\times V_{\mathit{endosomal}}^{\mathit{tissue}}$$ (23)

Bound ADC in endosomal compartment

$$V_{\mathit{endosomal}}^{\mathit{tissue}}\times \frac{d{C}_{\mathit{bound}\mathit{endo}\text{\_}\mathit{ADC}}^{\mathit{tissue}}}{dt}=V_{\mathit{endosomal}}^{\mathit{tissue}}\times k_{on}\times C_{\mathit{unbound}\mathit{endo}\text{\_}\mathit{ADC}}^{\mathit{tissue}}\times C_{\mathit{FCRN}}^{\mathit{tissue}}-V_{\mathit{endosomal}}^{\mathit{tissue}}\times k_{\mathit{off}}\times C_{\mathit{bound}\mathit{endo}\text{\_}\mathit{ADC}}^{\mathit{tissue}}-C{L}_{up}^{\mathit{tissue}}\times C_{\mathit{bound}\mathit{endo}\text{\_}\mathit{ADC}}^{\mathit{tissue}}$$ (24)

Interstitial compartment

$$V_{\mathit{interstitial}}^{\mathit{tissue}}\times \frac{d{C}_{\mathit{interstitial}\text{\_}\mathit{ADC}}^{\mathit{tissue}}}{dt}=\left(1-{\sigma }_{\mathit{tissue}}^V\right)\times Q_{\mathit{lymphflow}}^{\mathit{tissue}}\times C_{\mathit{plasma}\text{\_}\mathit{ADC}}^{\mathit{tissue}}-\left(1-{\sigma }_{\mathit{tissue}}^{IS}\right)\times Q_{\mathit{lymphflow}}^{\mathit{tissue}}\times C_{\mathit{interstitial}\text{\_}\mathit{ADC}}^{\mathit{tissue}}+C{L}_{up}^{\mathit{tissue}}\times \left(1-FR\right)\times C_{\mathit{bound}\mathit{endo}\text{\_}\mathit{ADC}}^{\mathit{tissue}}-C{L}_{up}^{\mathit{tissue}}\times C_{\mathit{interstitial}\text{\_}\mathit{ADC}}^{\mathit{tissue}}-K_{\mathit{dec}}\times C_{\mathit{interstitial}\text{\_}\mathit{ADC}}^{\mathit{tissue}}\times V_{\mathit{interstitial}}^{\mathit{tissue}}$$ (25)

FcRn binding equation for all tissues

$$V_{\mathit{endosomal}}^{\mathit{tissue}}\times \frac{d{C}_{\mathit{FCRN}}^{\mathit{tissue}}}{dt}=k_{\mathit{off}}\times C_{\mathit{bound}\mathit{endo}\text{\_}\mathit{ADC}}^{\mathit{tissue}}\times V_{\mathit{endosomal}}^{\mathit{tissue}}-k_{on}\times C_{\mathit{unbound}\mathit{endo}\text{\_}\mathit{ADC}}^{\mathit{tissue}}\times C_{\mathit{FCRN}}^{\mathit{tissue}}\times V_{\mathit{endosomal}}^{\mathit{tissue}}+C{L}_{up}^{\mathit{tissue}}\times C_{\mathit{bound}\mathit{endo}\text{\_}\mathit{ADC}}^{\mathit{tissue}}$$ (26)

Tumor compartment equations for Both ADC and unconjugated drug

Free ADC in extracellular matrix

$$\frac{d{C}_{\mathit{ADCfree}}^{\mathit{tumor}}}{dt}=\left(\frac{2\times P\mathit{ADC}\times \mathit{Rcap}}{{\mathit{Rkrogh}}^2}\right)\times \left(C_{\mathit{ADC}}^{\mathit{plasma}}-\frac{C_{\mathit{ADCfree}}^{\mathit{tumor}}}{{\epsilon }_{\mathit{ADC}}}\right)+\left(\frac{6\times D\mathit{ADC}}{{\mathit{Rtumor}}^2}\right)\times \left(C_{\mathit{ADC}}^{\mathit{plasma}}-\frac{C_{\mathit{ADCfree}}^{\mathit{tumor}}}{{\epsilon }_{\mathit{ADC}}}\right)-k_{on-ag}\times C_{\mathit{ADCfree}}^{\mathit{tumor}}\times \left({\mathit{Antigen}}_{\mathit{total}}-C_{\mathit{ADCbound}}^{\mathit{tumor}}\right)+k_{\mathit{off}-ag}\times C_{\mathit{ADCbound}}^{\mathit{tumor}}-K_{\mathit{dec}}\times C_{\mathit{ADCfree}}^{\mathit{tumor}}$$ (27)

Bound ADC in extracellular matrix

$$\frac{d{C}_{\mathit{ADCbound}}^{\mathit{tumor}}}{dt}=k_{on-ag}\times \frac{C_{\mathit{ADCfree}}^{\mathit{tumor}}}{{\epsilon }_{\mathit{ADC}}}\times \left({\mathit{Antigen}}_{\mathit{total}}-C_{\mathit{ADCbound}}^{\mathit{tumor}}\right)-k_{\mathit{off}-ag}\times C_{\mathit{ADCbound}}^{\mathit{tumor}}-k_{\mathit{int}}\times C_{\mathit{ADCbound}}^{\mathit{tumor}}-K_{\mathit{dec}}\times C_{\mathit{ADCbound}}^{\mathit{tumor}}$$ (28)

Unconjugated drug in extracellular matrix

$$\frac{d{C}_{\mathit{FreeUD}\text{\_}\mathit{extra}}^{\mathit{tumor}}}{dt}=\left(\frac{2\times P_{UD}\times \mathit{Rcap}}{{\mathit{Rkrogh}}^2}\right)\times \left(C_{UD}^{\mathit{plasma}}-\frac{C_{{\mathit{freeUD}}_{\mathit{extra}}}^{\mathit{tumor}}}{{\epsilon }_{UD}}\right)+\left(\frac{6\times D_{UD}}{{\mathit{Rtumor}}^2}\right)\times \left(C_{UD}^{\mathit{plasma}}-\frac{C_{{\mathit{freeUD}}_{\mathit{extra}}}^{\mathit{tumor}}}{{\epsilon }_{UD}}\right)-k_{in}\times C_{\mathit{freeUD}\text{\_}\mathit{extra}}^{\mathit{tumor}}+k_{\mathit{out}}\times C_{\mathit{freeUD}\text{\_}\mathit{cell}}^{\mathit{tumor}}+\mathit{DAR}\times K_{\mathit{dec}}\times \left(C_{\mathit{ADCfree}}^{\mathit{tumor}}+C_{\mathit{ADCbound}}^{\mathit{tumor}}\right)$$ (29)

Unconjugated drug in cellular compartment

$$\frac{d{C}_{\mathit{FreeUD}\text{\_}\mathit{cell}}^{\mathit{tumor}}}{dt}=k_{\mathit{int}}\times \mathit{DAR}\times C_{\mathit{ADCbound}}^{\mathit{tumor}}-k_{\mathit{out}}\times C_{\mathit{freeUD}\text{\_}\mathit{cell}}^{\mathit{tumor}}+k_{in}\times C_{\mathit{freeUD}\text{\_}\mathit{extra}}^{\mathit{tumor}}-k_{on-tn}\times C_{\mathit{freeUD}\text{\_}\mathit{cell}}^{\mathit{tumor}}\times ({\mathit{Tubulin}}_{\mathit{total}}-C_{\mathit{boundUD}\text{\_}\mathit{tubulin}}^{\mathit{tumor}})+k_{\mathit{off}-tn}\times C_{\mathit{boundUD}\text{\_}\mathit{tubulin}}^{\mathit{tumor}}$$ (30)

Unconjugated drug bound to tubulin in the cellular compartment

$$\frac{d{C}_{\mathit{boundUD}\text{\_}\mathit{tubulin}}^{\mathit{tumor}}}{dt}=k_{on-tn}\times C_{\mathit{freeUD}\text{\_}\mathit{cell}}^{\mathit{tumor}}\times ({\mathit{Tubulin}}_{\mathit{total}}-C_{\mathit{boundUD}\text{\_}\mathit{tubulin}}^{\mathit{tumor}})-k_{\mathit{off}-tn}\times C_{\mathit{boundUD}\text{\_}\mathit{tubulin}}^{\mathit{tumor}}$$ (31)

Change in DAR

$$\frac{d\mathit{DAR}}{ }dt=-K_{\mathit{dec}}\times \mathit{DAR}$$ (32)

The definition of each symbol used in the previous equations is provided in Table I. The tumor disposition of ADC was only considered in the human PBPK model.

Model Parameters for the Rat PBPK Model

Sources and values of all the model parameters have been summarized in Tables I and II. All the physiological values for the PBPK model were taken from the literature (4). Partition coefficient values for the unconjugated drug (i.e., DM1) were calculated using the observed plasma and tissue PK data in rats. Permeability surface area value for select tissues and clearance of unconjugated drug from the liver were estimated by fitting the unconjugated drug PBPK model to DM1 disposition data. The ADC degradation rate was assumed to be the same as that of the typical antibody and obtained from (4). The average deconjugation rate of DM1 from T-DM1 was estimated from plasma PK of total trastuzumab and T-DM1 using the procedure mentioned earlier and model shown in Supplementary Figure 1.

Table II.

Partition coefficients derived from observed concentrations and model-estimated permeability surface values for rat

Tissues	Partition coefficient for rat*	Partition coefficient for human*	Rat PS (CV%) (L/h)
Blood cells	106.9	40.1	294.5 (Qplasma × 100)
Lung	1043.7	333.6	0.52 (10.7)
Heart	368.9	138.8	0.14 (9.8)
Kidney	2550.9	955.0	0.63 (7.4)
Brain	20.9	7.8	0.003 (11.9)
Muscle	544.5	202.9	1.6 (4.9)
Marrow	2.1	0.77	0.015 (39.9)
Thymus	630.5	236.3	0.0007 (7.5)
Skin	279.3	104.7	0.19 (8.5)
Fat	219.0	82.3	0.11 (7.3)
Small intestine	782.6	293.2	0.33 (7.2)
Large intestine	723.9	272.3	0.18 (7.2)
Spleen	1330.4	498.3	0.26 (8.6)
Liver	1889.2	754.7	12.4 (48.3)
Other	479.8	184.2	0.10 (8.2)
Pancreas	1 (no data)	1 (no data)	Qpancreasplasma
CLhepatic			1.53 (5.5)

^*Adjusted for fraction unbound in plasma (fup) and cellular volume (cellular volume/total volume)

Translation of the Rat ADC PBPK Model to Humans

The rat PBPK model developed for T-DM1 (Fig. 1a and b) was scaled to humans to evaluate the translational capabilities of the model. The rat conjugated antibody PBPK model was simply replaced with the human platform PBPK model developed for antibodies (4). The rat unconjugated drug (i.e., DM1) PBPK model was scaled to humans using the principles of allometric scaling, where the hepatic clearance and permeability surface area values were scaled using the following equations:

$$C{L}_{\mathit{human}}=C{L}_{\mathit{rat}}\times {(B{W}_{\mathit{human}}/B{W}_{\mathit{rat}})}^{0.75}$$

$$P{S}_{\mathit{human}}=P{S}_{\mathit{rat}}\times {(B{W}_{\mathit{human}}/B{W}_{\mathit{rat}})}^{0.75}$$

Partition coefficient (Kp) values for the human model were assumed to be the same as those for the rat model. The fraction bound in plasma for the unconjugated drug was changed to a literature-reported value for humans (1). It was assumed that the non-specific deconjugation rate of DM1 from T-DM1 in humans was similar to that in monkeys, and this value was estimated from the plasma PK of total trastuzumab and T-DM1 reported in monkeys using the procedure mentioned earlier and the model shown in Supplementary Figure 1.

Evaluation of the PBPK Model Performance

The plasma and tissue PK predictions made by the ADC PBPK model were quantitatively evaluated by comparing the observed and predicted PK profiles. The percent predictive error (%PE) for each predicted PK profile was calculated using the following equation: %PE = |AUC_pred−AUC_obs| × 100/AUC_obs, where AUC_pred is the AUC of the model-predicted PK profile and AUC_obs is the AUC of the observed PK profile.

Pathway Analysis of the Rat PBPK Model

Pathway analysis was performed in Berkeley Madonna (University of California at Berkeley, CA) for quantifying contribution of various tissues and deconjugation process in the appearance of unconjugated drug in plasma.

Equation for estimating the percent contribution of tissues:

$$\text{Percent}\text{contribution}=100\times Q_{\mathit{plasma}}^{\mathit{tissue}}\times C_{{\mathit{plasma}}_{\mathit{UD}}}^{\mathit{tissue}}/(Q_{\mathit{plasma}}^{\mathit{heart}}\times C_{{\mathit{plasma}}_{\mathit{UD}}}^{\mathit{heart}}+Q_{\mathit{plasma}}^{\mathit{kidney}}\times C_{{\mathit{plasma}}_{\mathit{UD}}}^{\mathit{kidney}}+Q_{\mathit{plasma}}^{\mathit{brain}}\times C_{{\mathit{plasma}}_{\mathit{UD}}}^{\mathit{brain}}+Q_{\mathit{plasma}}^{\mathit{muscle}}\times C_{{\mathit{plasma}}_{\mathit{UD}}}^{\mathit{muscle}}+Q_{\mathit{plasma}}^{\mathit{marrow}}\times C_{{\mathit{plasma}}_{\mathit{UD}}}^{\mathit{marrow}}+Q_{\mathit{plasma}}^{\mathit{thymus}}\times C_{{\mathit{plasma}}_{\mathit{UD}}}^{\mathit{thymus}}+Q_{\mathit{plasma}}^{\mathit{skin}}\times C_{{\mathit{plasma}}_{\mathit{UD}}}^{\mathit{skin}}+Q_{\mathit{plasma}}^{\mathit{fat}}\times C_{{\mathit{plasma}}_{\mathit{UD}}}^{\mathit{fat}}+\left(Q_{\mathit{plasma}}^{\mathit{liver}}+Q_{\mathit{plasma}}^{SI}+Q_{\mathit{plasma}}^{LI}+Q_{\mathit{plasma}}^{\mathit{spleen}}+Q_{\mathit{plasma}}^{\mathit{pancreas}}\right)\times C_{{\mathit{plasma}}_{\mathit{UD}}}^{\mathit{liver}}+C_{{\mathit{plasma}}_{\mathit{UD}}}^{\mathit{other}}\times Q_{\mathit{plasma}}^{\mathit{other}}+K_{\mathit{dec}}\times C_{\mathit{ADC}}^{\mathit{plasma}}\times V_{\mathit{plasma}}\times \mathit{DAR})$$ (33)

Equation for estimating the percent contribution of the deconjugation process:

$$\text{Percent}\text{contribution}=100\times K_{\mathit{dec}}\times C_{\mathit{ADC}}^{\mathit{plasma}}\times V_{\mathit{plasma}}\times \mathit{DAR}/(Q_{\mathit{plasma}}^{\mathit{heat}}\times C_{{\mathit{plasma}}_{\mathit{UD}}}^{\mathit{heart}}+Q_{\mathit{plasma}}^{\mathit{kidney}}\times C_{{\mathit{plasma}}_{\mathit{UD}}}^{\mathit{kidney}}+Q_{\mathit{plasma}}^{\mathit{brain}}\times C_{{\mathit{plasma}}_{\mathit{UD}}}^{\mathit{brain}}+Q_{\mathit{plasma}}^{\mathit{muscle}}\times C_{{\mathit{plasma}}_{\mathit{UD}}}^{\mathit{muscle}}+Q_{\mathit{plasma}}^{\mathit{marrow}}+C_{{\mathit{plasma}}_{\mathit{UD}}}^{\mathit{marrow}}+Q_{\mathit{plasma}}^{\mathit{thymus}}\times C_{{\mathit{plasma}}_{\mathit{UD}}}^{\mathit{thymus}}+Q_{\mathit{plasma}}^{\mathit{skin}}\times C_{\mathit{plasma}\text{\_}UD}^{\mathit{skin}}+Q_{\mathit{plasma}}^{\mathit{fat}}\times C_{\mathit{plasma}\text{\_}UD}^{\mathit{fat}}+\left(Q_{\mathit{plasma}}^{\mathit{liver}}+Q_{\mathit{plasma}}^{SI}+Q_{\mathit{plasma}}^{LI}+Q_{\mathit{plasma}}^{\mathit{spleen}}+Q_{\mathit{plasma}}^{\mathit{pancreas}}\right)\times C_{\mathit{plasma}\text{\_}UD}^{\mathit{liver}}+C_{\mathit{plasma}\text{\_}UD}^{\mathit{other}}\times Q_{\mathit{plasma}}^{\mathit{other}}+K_{\mathit{dec}}\times C_{\mathit{ADC}}^{\mathit{plasma}}\times V_{\mathit{plasma}}\times \mathit{DAR})$$ (34)

Global Sensitivity Analysis (GSA) of the Rat PBPK Model

Total sensitivity index was estimated using the SOBOL method (21) for variance-based sensitivity analysis. Using the IQM toolbox, the ADC PBPK model developed for rats was simulated over a range of parameter values generated by Latin hypercube sampling. An integrated SOBOL method algorithm was applied to estimate the total effect of parameters on the output by adding the first and higher order interaction effects. Parameter sensitivity was analyzed for plasma AUC of the T-DM1 and unconjugated drug.

Software

Plot Digitizer (Sourceforge) was used to digitize all datasets. Non-compartmental analysis of DM1 plasma and tissue PK profiles was performed using Phoenix WinNonlin (Certara) software. The unconjugated DM1 PBPK model was fitted to DM1 biodistribution data using the maximum likelihood estimation method in ADAPT V software (BMSR, CA) with the combined variance model. DM1 deconjugation rates from T-DM1 in rats and monkeys were estimated by fitting the two-compartment model (Supplementary Figure 1) to total trastuzumab and T-DM1 plasma PK data using the ADAPT V software. Simulations using the translated human PBPK model for ADC, and pathway analysis of the rat PBPK model, were performed using Berkeley Madonna software (University of California at Berkeley, CA). Global sensitivity analysis of the rat ADC PBPK model was conducted using the SOBOL method of the IQMTools software (MATLAB based).

RESULTS

Rat PBPK Model for Unconjugated Drug

Figure 2 provides observed and PBPK model-fitted DM1 PK profiles superimposed over each other for plasma and tissues. The model was able to characterize the sparse PK data reasonably well. Table II summarizes all the calculated Kp values for DM1 and estimated PS values for the different tissues in rats. PS values were estimated with good precision and most of the CV% (except the liver) were less than 50%. The hepatic clearance of DM1 in rats was estimated to be 1.48 L/h (CV% = 5.6), which was slightly higher than the reported systemic clearance value of 0.5–0.8 L/h (10). Since the Kp values were calculated based on sparse plasma PK data that was missing the last time point, it is important to note that any error in calculating plasma AUC may have led to propagated error in estimation of Kp and other model parameters. Nonetheless, it was observed that the Kp values for DM1 were relatively high (even without adjustment for f_up), suggesting strong binding of the drug molecule to tissue components (e.g., tubulin).

Fig. 2.

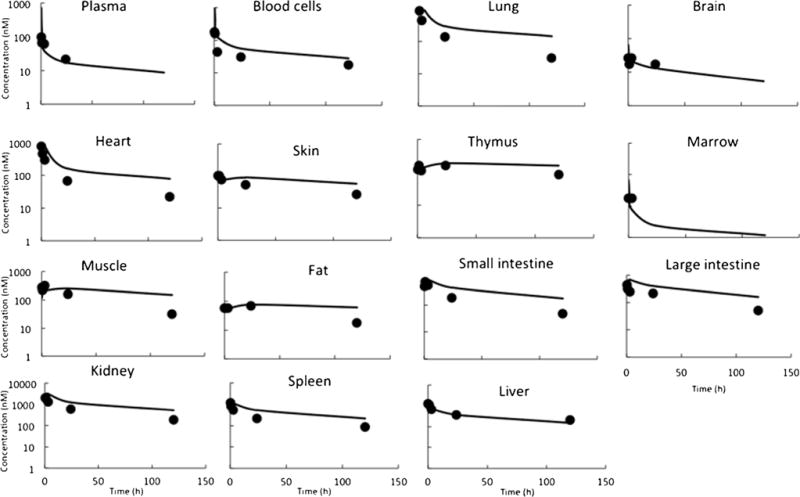
Plasma and tissue PK of DM1: observed (solid symbols) and PBPK model-fitted (lines) DM1 concentration vs. time profile, in various tissues, upon administration of 200 μg/mg radiolabeled [³H]-DM1 in rats

Rat PBPK Model for ADC

In order to integrate the unconjugated drug PBPK model with the antibody PBPK model, the non-specific deconjugation rate of DM1 from T-DM1 was estimated. Supplementary Figure 1 shows the two-compartment model used to estimate this rate was constant along with the model fittings for total trastuzumab and T-DM1 plasma PK data. The average DM1 deconjugation rate constant was found to be 0.0049 h⁻¹, resulting in deconjugation half-life of ~ 6 days. The integrated ADC PBPK model was used to a priori predict the plasma and tissue concentrations of conjugated antibody (i.e., T-DM1) and unconjugated drug (i.e., DM1- and DM1-containing catabolites combined) in rats following intravenous administration of 13 mg/kg T-DM1. Figure 3 provides superimposition of the observed PK data and PBPK model-predicted PK profiles in plasma and tissues. It was observed that for most tissues the model-predicted total DM1 concentration profiles superimposed well with the observed ADC concentration data, and not the model-predicted conjugated antibody concentration profiles. While counterintuitive at first, this observation is expected since the ADC concentrations reported by the authors (8) actually represent radioactivity observed in the tissues following systemic administration of labeled T-[H³]DM1. Thus, authors have in fact reported the sum of the concentration of conjugated and unconjugated drugs, which matches well with PBPK model-simulated total DM1 concentrations. Percent predictive error (%PE) values calculated for model-predicted total DM1 concentrations and observed concentrations are provided in Table III. Most of the PE values suggested the model predictions were within twofold of the observed concentrations (i.e., %PE value of 100 or less), except those for tissues like brain and thymus. We believe this discrepancy stems from the antibody model misspecifications for these tissues, as this model has not been validated for these two tissues (4). The PBPK model-predicted unconjugated DM1 concentration profiles in plasma and tissue are provided in Fig. 4. To date, there is no published data on the tissue PK of unconjugated DM1 (and DM1-containing catabolites) in rats following T-DM1 administration to compare with the model predictions. Nonetheless, model simulations suggest that unconjugated DM1 concentrations in some tissues (e.g., liver, spleen, and kidney) can be 10- to 100-fold higher than plasma concentrations.

Fig. 3.

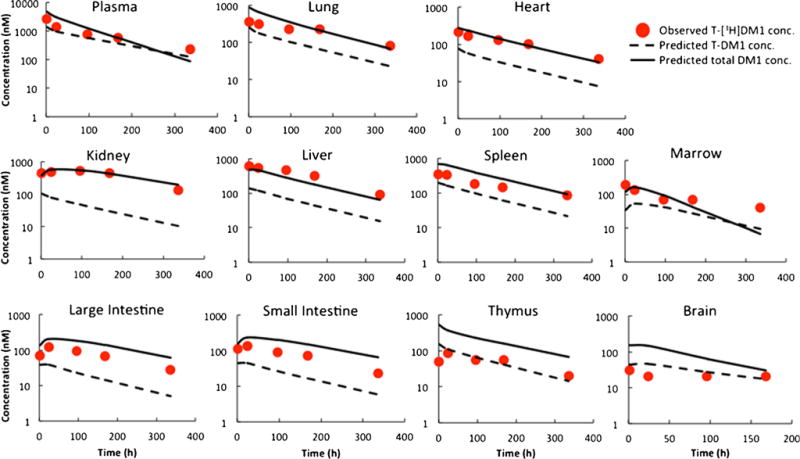
Predicted plasma and tissue PK of T-DM1 and total DM1 in rats: red circles represent observed T-[³H]DM1 concentration in rats, dash lines represent predicted T-DM1 concentrations, and solid lines represent total DM1 (conjugated and free) concentrations predicted by the platform PBPK model for ADCs

Table III.

Percent predictive error for quantitative comparison of observed and model-generated rat data

	%PE T-DM1 AUC till T	%PE total DM1 AUC till T
Plasma	34.7	46.6
Lung	58.6	40.4
Heart	73.8	8.4
Kidney	89.9	10.0
Brain	99.9	371
Marrow	61.8	19.8
Thymus	5.4	286
SI	71.6	110
LI	74.7	96.9
Spleen	54.9	79.5
Liver	83.0	33.0

Fig. 4.

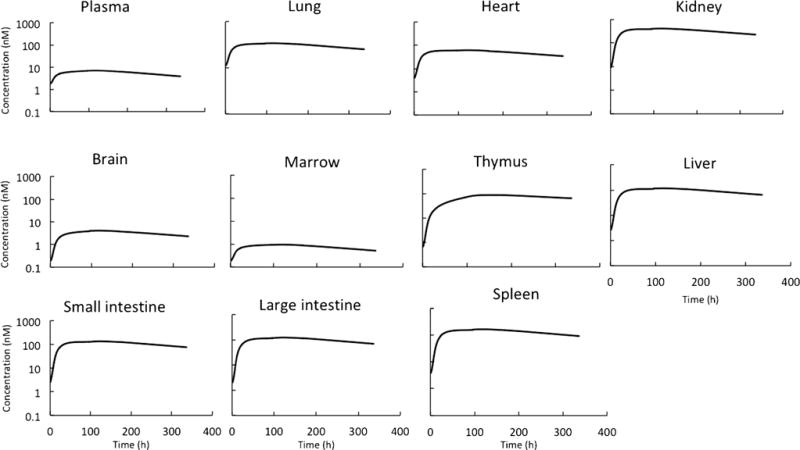
Predicted plasma and tissue PK of unconjugated DM1 in rats after administration of T-DM1

Translation of ADC PBPK Model to Humans

The non-specific deconjugation rate of DM1 from T-DM1 in humans was assumed to be similar to that of monkeys and was estimated using total trastuzumab and T-DM1 plasma PK data in monkeys. Supplementary Figure 1 shows the two-compartment model used to estimate this constant rate along with the model fittings for the plasma PK data. The average DM1 deconjugation constant rate in monkeys was found to be 0.0079 h⁻¹, resulting in deconjugation half-life of ~ 4 days. The clearance of unconjugated DM1 (and DM1-containing catabolites) in humans was allometrically scaled from rat, and this value was found to be 101.3 L/h. The translated human PBPK model for T-DM1 also included a tumor compartment with a 1-cm diameter, which does not significantly affect plasma PK predictions made by the model but was incorporated for the sake of completeness. Figure 5a provides the human PBPK model-predicted plasma PK profiles of total trastuzumab, T-DM1, and DM1 superimposed over the observed clinical data from several clinical trials. The model was able to predict clinical PK of total trastuzumab and T-DM1 reasonably well; however, systemic deviation was observed between model-predicted and clinically measured DM1 PK profiles. %PE values for T-DM1, DM1, and total trastuzumab were found to be 45.5, 4.1, and 34.2%. All three analytes had %PE values less than 100%, suggesting model predictions were within twofold of the observed PK data. The human PBPK model-predicted plasma, tissue, and tumor PK of T-DM1, unconjugated DM1, and total DM1 are provided in Supplementary Figure 2.

Fig. 5.

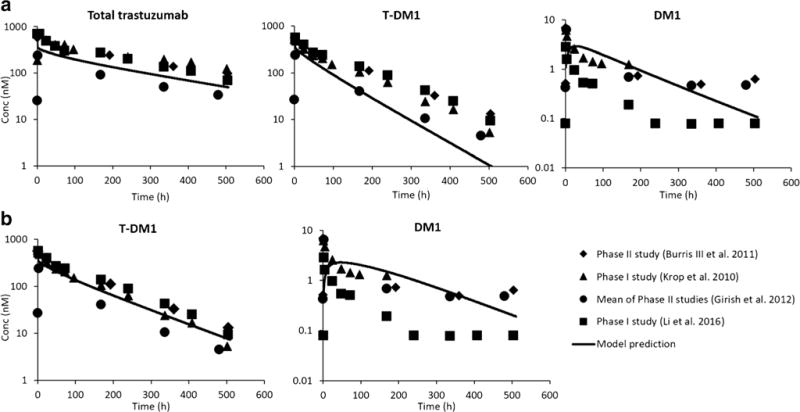
Predicted plasma PK of total trastuzumab, T-DM1, and unconjugated DM1 in humans: solid symbols represent observed clinical data from three different studies (P1: phase 1, P2: phase 2, and Avg: average of three phase 2 studies; Hepatic P1: patients with normal liver function in phase 1 study) and solid lines represent a priori predicted clinical concentrations using platform PBPK model. a Using dissociation constant determined by monkey data (0.0079 h⁻¹); b using dissociation constant (0.0039 h⁻¹) reported by Bender et al. (22)

Pathway Analysis

Pathway analysis was performed for plasma unconjugated DM1 exposure using the rat ADC PBPK model to quantify the relative contribution of various tissues and deconjugation process in generating unconjugated drug from ADC in plasma (Fig. 6). Analysis indicated that while drug deconjugation from ADC contributed significantly towards generation of unconjugated drug in plasma initially, the delivery of drug from tissues took over quickly as the major route for sustained exposure of unconjugated drug in plasma. Metabolically active tissues like liver and anatomically bigger tissues like muscle were found to be the major contributors.

Fig. 6.

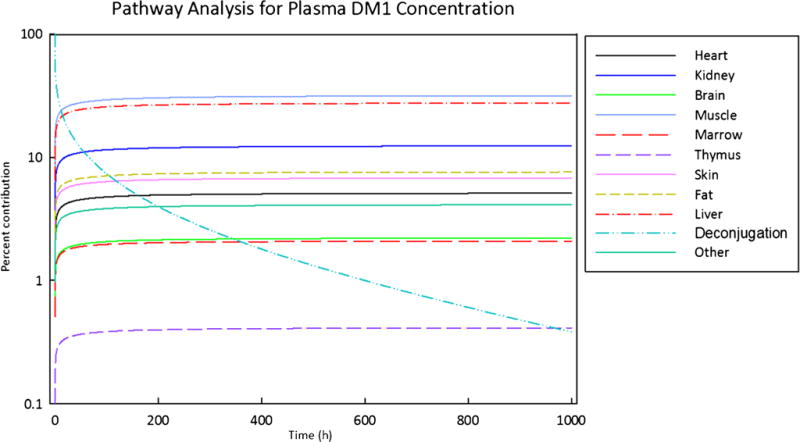
Pathway analysis for assessing relative importance of the contribution of different tissues and dissociation process towards the disposition of DM1 in plasma

Global Sensitivity Analysis

Global sensitivity analysis (GSA) of the rat PBPK model was performed to identify parameters which could have significant impact on the plasma exposure of ADC and the unconjugated drug (Fig. 7). The results show that plasma exposure of conjugated antibody was mainly affected by the parameters that influence the PK of monoclonal antibody (e.g., FcRn concentration, intracellular degradation rate of FcRn unbound antibody, and fraction of FcRn-bound antibody that recycles to the vascular compartment), and the parameter related to the stability of the ADC (i.e., deconjugation rate of the drug from the ADC). Plasma exposure of the unconjugated drug was mainly affected by the fraction unbound of the drug in the plasma, hepatic clearance of the drug, partition coefficient of the drug in tissues like muscle and liver, deconjugation rate of the drug from the ADC, and parameters associated with the degradation of the conjugated antibody (i.e., FcRn and K_deg).

Fig. 7.

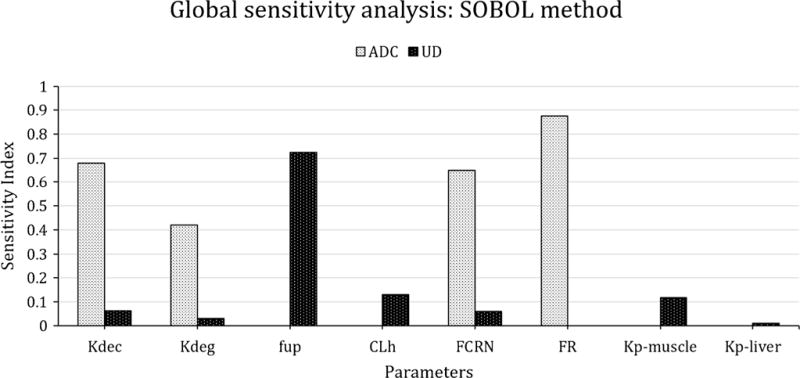
Result of global sensitivity analysis, using SOBOL method, highlighting the sensitive parameters of platform PBPK model for ADC (T-DM1) and UD (unconjugated DM1) PK. K_deg: degradation rate constant, K_dec: dissociation rate constant, CL_h: hepatic clearance of DM1, FCRN: FcRn concentration estimated from mAb PBPK model, fup: fraction of DM1 unbound in plasma, FR: fraction of ADC recycled by FCRN, kp-tissue: partition coefficient for a tissue

DISCUSSION

There are several benefits of using a PBPK model for the discovery and development of ADCs. At the discovery stage, the model can help assess the therapeutic potential of an ADC target by evaluating if the differential in the expression of the target between the normal and cancerous tissues is optimal to achieve the desired therapeutic index. In the preclinical setting, the PBPK model can help in establishing a quantitative relationship between the ADC dose and PK of different analytes in plasma, tumor, and other tissues. This preclinical dose-exposure relationship can be used to predict human PK of ADC and other analytes. In addition, the preclinical PBPK model of ADCs can also be used to establish reliable exposure-response relationships for ADCs, which can be further translated to humans to predict clinical efficacy and toxicity of ADCs. In the clinical setting, ADC PBPK models can help in examining and predicting drug interaction between ADC and other coadministered treatments. Lastly, PBPK models can also help in designing and evaluation of different hypotheses to improve the therapeutic outcome of ADCs at various stages of drug discovery and development.

There are only a few published reports so far that describe the development of a PBPK model for ADCs. One of the first report was published in a poster format by Zhao et al. (23), who developed a PBPK model to characterize plasma, tissue, and tumor PK of an anti-CD70 ADC SGN-75 in tumor-bearing mice. While this model was able to characterize the PK of ADC reasonably well, the PK of released drug was not captured accurately. In addition, the authors estimated many system parameters of the antibody PBPK model (e.g., vascular and lymph reflection coefficients, tissue clearance rate, and antigen expression levels in tumor) along with other parameters related to unconjugated drug disposition to accomplish the model fitting, which made extrapolation of the model challenging. Later, Chen et al. (24) developed a minimal PBPK model for vc-MMAE containing ADCs using SimCyp simulator to predict drug-drug interaction of the ADC in the human population. While this model was able to characterize the systemic disposition of the ADC and conjugated drug reasonably well, it employed empirical model components (i.e., single adjusting compartment) to characterize the data. In addition, being a minimal PBPK model, the model was not able to characterize or predict the concentration of ADC and its components at the site-of-action in tumor and other tissues. Very recently, in this special issue on system PK of ADCs, Cilliers et al. (25) have presented a multi-scale PBPK model to track the systemic distribution of the ADC and antibody. The model couples systemic and organ-level PBPK model of the antibody with a tissue-level distributed parameter model for the tumor to characterize biodistribution of fluorescently labeled T-DM1. While the model is very elegant and helpful in hypothesizing novel strategies to improve the efficacy of ADC (e.g., coadministration of antibody to overcome the binding-site barrier), it was only used to track the antibody component of the ADC and not the unconjugated drug. Also, the model was validated using single time-point tissue concentration data generated using fluorescently labeled ADC. Thus, all the PBPK models for ADCs reported so far have certain shortcomings that make them unfit for characterizing and predicting whole body PK of ADC and its components simultaneously, prompting us to develop a translational platform PBPK model for ADCs.

The inspiration for the ADC PBPK model proposed here comes from our recently published work (6,26), where we combined an antibody PBPK model with a small molecule PBPK model to predict the effect of antitopotecan antibody on the whole body disposition and toxicity of topotecan in mice. Accordingly, here we have combined our platform PBPK model for monoclonal antibody (4) with a typical PBPK model for small molecule to characterize the whole body disposition of ADC/antibody and unconjugated drug (Fig. 1a). Based on the prior knowledge that unconjugated drug enters the system from ADC via non-specific deconjugation or proteolytic degradation, the antibody PBPK model was connected to small molecule PBPK model via deconjugation and degradation processes at the tissue level (Fig. 1b). It was assumed that antibody and ADC demonstrate similar tissue distribution properties based on previously observed similarity in their biodistribution coefficient values (27). It was also assumed that conjugated antibody and unconjugated antibody have similar FcRn-binding properties and intracellular degradation rate. To make the model parsimonious, only the average DAR value was considered, which was changed with time based on the average rate of drug deconjugation from ADC. While it is known that sometimes the unconjugated drug molecules are an array of diverse molecules with different disposition properties (7,28), for the sake of simplicity here, we have assumed that all the unconjugated drug molecules possess a similar PK profile. For completeness, we have also added our previously published multi-scale mechanistic model of ADC disposition to the tumor into the final PBPK model (Fig. 1c) (15). As such, the ADC PBPK model presented here is developed to simultaneously characterize/predict whole body disposition of conjugated antibody (i.e., ADC), antibody conjugated drug, total antibody, total drug, and unconjugated drug.

The model was built using clinically approved ADC T-DM1, which is used to treat HER2-positive breast cancer patients. T-DM1 consists of clinically approved anti-HER2 antibody trastuzumab that is conjugated to cytotoxic drug DM1 using non-cleavable linker SMCC via the lysine residues. This ADC was chosen as a tool compound because of the availability of both preclinical biodistribution data and clinical PK data, which could allow us to validate clinical translation of the PBPK model. First, the small molecule PBPK model for unconjugated DM1 was developed using the biodistribution data generated in rats following systemic administration of radiolabeled DM1 alone. While this dataset is not ideal because it just covers one dose and the analytical technique employed cannot distinguish between different chemical metabolites of DM1, it was still used because it is the only reported dataset that provides biodistribution of unconjugated DM1. Following estimation of hepatic clearance and parameters related to cellular distribution of the drug, the small molecule PBPK model was able to capture the plasma and tissue PK of DM1 reasonably well (Fig. 2). While for several tissues the model fittings did not superimpose over all the observed data points, it is hard to judge the magnitude of this misfit as there are no error bars around the observed data. In addition, one should be careful before interpreting the parameter estimates obtained using this data, as it is generated from sparse data. Next, the platform PBPK model developed to characterize antibody disposition in rats (4) was used as such to drive the PK of total and conjugated trastuzumab in rats following T-DM1 administration. The PBPK models of conjugated trastuzumab and unconjugated DM1 were connected via antibody degradation rate, which was fixed to a value embedded in the antibody platform PBPK model (4). Both the PBPK models were also connected via an average DM1 deconjugation rate, which was estimated based on reported plasma PK of total trastuzumab and T-DM1 in rats following T-DM1 administration (Supplementary Figure 1). While this strategy is not ideal, unfortunately, there is no other reliable in vitro or ex vivo method that allows one to estimate this parameter for an ADC. In addition, we have shown in the past that the strategy employed by us provides a reasonable approximation of the actual deconjugation rate of drug from an ADC (17). In fact, the deconjugation rate of DM1 from T-DM1 in rats estimated by us was similar to the one reported by Bender et al. for DAR₁ to trastuzumab transformation (22). The final integrated ADC PBPK model was used to predict plasma and tissue PK of T-DM1 and other analytes following T-DM1 administration in rats, and the simulations were compared with the observed data.

The biodistribution data used to validate the PK predictions made by the rat PBPK model of T-DM1 were generated following systemic administration of T-DM1, where the DM1 was labeled using tritium, and radioactivity was measured to infer T-DM1 concentrations. As shown in Fig. 3, PBPK model-predicted T-DM1 concentrations in plasma and tissues were in general lower than the reported ADC concentrations, and predicted total DM1 concentrations were close to reported ADC concentrations for most tissues (Table III). These results point to an important fact that since the DM1 component of T-DM1 was labeled and tracked throughout the biodistribution study, the authors have actually measured conjugated as well as unconjugated DM1 concentrations. Thus, the model predictions are realistic and suggest that caution should be applied when interpreting ADC biodistribution data generated using labeled studies. When comparing PBPK model predictions made for all the tissues, it was found that tissues like brain and thymus were outliers. We believe this is mainly related to the performance of antibody PBPK model for these tissues, as the platform model was never validated for these tissues (4). It is also important to note that some of the discrepancies observed between the model-predicted and measured PK profiles can stem from the assumption that all the DM1-containing catabolites of T-DM1 follow the same PK profile as DM1. It is well known that apart from DM1, lysine-MCC-DM1 and MCC-DM1 are also observed in the biological system, and these analytes follow different and complex PK than pure DM1 (7,28). Thus, the simplifying assumption that all the analytes behave in a similar manner is bound to induce some error; however, this assumption is necessary to prevent the PBPK model from becoming very complex. This assumption can also affect the predicted PK of unconjugated DM1 shown in Fig. 4; however, in the absence of any observed data to compare with the predictions, the direction and extent of any error are hard to judge. Nonetheless, simulated PK of unconjugated DM1 provides an interesting insight into the PK behavior of ADCs. It suggests that the exposure of the unconjugated drug in tissues can be 10–100 times higher than the plasma exposure, and the PK of unconjugated drug in tissues may be a better analyte to correlate with tissue-specific pharmacological effects (e.g., toxicity). However, it is important to note that while the predictions of unusually high concentrations of unconjugated drug in several tissues are interesting, further investigation on this matter is needed to verify this finding. It is also important to note that while the simulated PK profiles of unconjugated drug in plasma and most tissues were parallel (Fig. 4), this may not always be true, especially for tissues that express the target antigen (which was not the case for T-DM1 in rats).

Considering the rat PBPK model for T-DM1 was able to characterize whole body disposition of ADC and unconjugated drug reasonably well, the model was further used to predict the clinical PK of T-DM1. In order to translate the rat PBPK model of ADC to that of humans, the antibody PBPK model component was simply replaced with the platform PBPK model of antibody developed for human, without any change. The small molecule PBPK model developed for unconjugated DM1 was kept the same; however, the hepatic clearance and permeability surface area values were scaled according to allometric principles and fraction unbound in plasma for DM1 was changed to a clinically reported value (1). The deconjugation rate of DM1 from T-DM1 in humans was assumed to be similar to that in monkeys, and this value was estimated from plasma PK data of total trastuzumab and T-DM1 obtained following T-DM1 administration in monkeys. The deconjugation rate estimated from monkey data was found to be 0.0079 h⁻¹, which is similar to DAR₁ to trastuzumab transformation rate in the clinic estimated by Chudasama et al. (29) (0.0073 h⁻¹) and two times higher than the value estimated by Bender et al. (22) (0.0039 h⁻¹). The translated human PBPK model for T-DM1 was also enhanced by the addition of a tumor compartment with a 1-cm diameter. The presence of this compartment did not alter the plasma PK of T-DM1 (data not shown), but it was included to allow hypothesis testing of different therapeutic scenarios using the platform PBPK model going forward. As shown in Fig. 5, the translated human PBPK model was able to capture the plasma PK of total trastuzumab reasonably well, providing confidence in the usage of platform PBPK model for antibody. The plasma exposure of conjugated antibody (i.e., T-DM1) was also captured reasonably well (%PE = 45.5), but there was a trend towards faster elimination in the predicted PK profile compared to the observed data. This suggests that the DM1 deconjugation rate estimated from monkey data was slightly overestimated. In fact, when the deconjugation rate was reduced by half to match the value reported by Bender et al. (22), the T-DM1 plasma PK profile predicted by the model superimposed over the observed data very well (Fig. 5b) (%PE = 22.4). The plasma exposure of unconjugated DM1 was also captured reasonably well by the ADC PBPK model (%PE = 4.1); however, there was a systemic deviation between the predicted and observed PK profiles (Fig. 5). The alpha phase of the predicted PK profile was shallower than the observed PK profile, suggesting the unconjugated drug is distributing to tissues faster than predicted by the model. In addition, the terminal phase of the predicted PK profile was steeper than that of the observed PK profile, suggesting the unconjugated drug is distributing from tissues to the plasma slower than predicted by the model. This discrepancy can stem from the assumption that the distribution characteristics of DM1 (e.g., Kp) in humans is similar to those in rats, and going forward, this issue can be resolved by estimating human Kp values of the unconjugated drug using established methods like Poulin and Theil’s method (30). In addition, assuming that all DM1-containing catabolites follow the same PK as DM1, the rate of DM1 deconjugation in humans is similar to that in monkeys, and clearance of unconjugated drug in human can be allometrically scaled from rats and can also lead to the observed discrepancy between the PBPK model-predicted and measured plasma PK of unconjugated DM1 in the clinic. It is also important to note that many reports have suggested that theoretically the generation of DM1 from T-DM1 in a biological system is highly unlikely (31–34), and the observed concentrations of DM1 in patient plasma may stem from formulation or analytical method-related issues. Therefore, extreme caution may be warranted before comparing the model-simulated DM1 concentrations with the observed data. The translated human PBPK model for T-DM1 was also able to predict plasma, tissue, and tumor PK of T-DM1, unconjugated DM1, and total DM1 in the clinic (Supplementary Figure 2); however, there is no way to verify the accuracy of this data.

In order to obtain better insight into the proposed PBPK model for ADCs, the rat model was subjected to pathway analysis and GSA (SOBOL). The pathway analysis was conducted to identify which are the major routes for unconjugated drug entry into systemic circulation following ADC administration. As shown in Fig. 6, it was found that deconjugation of DM1 from T-DM1 contributed significantly towards plasma DM1 concentration only in the initial time frame after ADC administration. As the time progressed, the return of DM1 from tissue space took over as the main pathway responsible for plasma exposure of DM1. Tissues with relatively large endosomal volumes (e.g., muscle) and blood flow (e.g., liver) were found to be the major contributor of unconjugated DM1 concentration in plasma. These results highlight the fact that, irrespective of the stability of the drug linker, the unconjugated drug will always be present in the systemic circulation, because it returns back from tissues following its generation and/or retention in the tissue space. The pathway analysis also stresses on the fact that understanding the disposition kinetic of the unconjugated drug (e.g., tissue binding) is essential for fully comprehending the PK behavior of an ADC. Figure 7 presents the data from GSA, which was conducted for both plasma T-DM1 and plasma DM1 exposure. Consistent with the pathway analysis results, it was found that unconjugated DM1 exposure in plasma is slightly sensitive to the drug deconjugation rate, but more sensitive to DM1 PK parameters like Kp values, hepatic clearance, and fraction unbound in plasma. In addition, parameters related to antibody degradation (e.g., K_deg and FcRn) were found to also influence plasma exposure of the unconjugated drug, emphasizing the fact that the PK of the ADC and unconjugated drug is intertwined. The plasma exposure of ADC was mainly affected by parameters related to antibody degradation (e.g., FcRn, FR, K_deg) and ADC stability (i.e., K_dec). Thus, a detailed analysis of the ADC PBPK model suggests that degradation and deconjugation rates of the ADCs, along with the PK parameters related to the unconjugated drug, are the main determinants for the whole body disposition of ADC.

Since the proposed model is envisioned as a platform PBPK model for ADCs, there are several issues that need to be addressed going forward. Here, we have assumed that the conjugated antibody follows similar disposition characteristics as the unconjugated antibody, except the faster clearance observed due to deconjugation. While this is true for some ADCs, especially for ADCs with low DAR values and hydrophilic linker-drug component, it is known that conjugation of drug can notably alter the PK of the antibody (35). However, there is no way to a priori find out if this is going to occur. Thus, we need to either find novel methodologies that can predict the effect of drug conjugation on antibody PK (e.g., hydrophobicity or charge-based methods) or to estimate the altered antibody clearance value from preclinical data, so that it can be used to update the antibody PBPK model component. Another important information that is hard to predict is the average deconjugation rate of drug from ADC. While deconjugation of drug in plasma can be estimated in vitro, there are no biological matrices that can provide an accurate indication of drug deconjugation in tissue microenvironment. As such, one needs to resort to an animal species that behaves similar to humans to estimate this parameter, as we have done here using monkeys. In addition, because most ADCs are a combination of different DAR species with different deconjugation rates, in reality there is no single value that can accurately characterize deconjugation of drug from each ADC molecule. Consequently, the proposed model is bound to possess only an approximation of the actual drug deconjugation rate, and a more complex PBPK model that accounts for the disposition of each DAR species may be more accurate. Lastly, our understanding of the distribution and elimination of unconjugated drug in humans needs to be improved significantly. Since these drugs are too toxic to be given by themselves to humans, going forward we should employ in vitro methods (e.g., sandwich culture assay (36)) to figure out the in vivo elimination rate of these drugs. Rather than relying on animals to give an estimation of partition coefficient values for the unconjugated drug, use of in silico methods (37) may be more appropriate to find out the realistic partition coefficient values for the unconjugated drug in various human tissues.

In summary, here we have presented development of a translational and platform PBPK model for ADCs, using T-DM1 as a tool compound. The trastuzumab component of the ADC was characterized using a previously published platform PBPK model for antibody (4), and the unconjugated drug component was characterized using a small molecule PBPK model that was developed using DM1 disposition data in rats (7). The PBPK model was able to predict total DM1 concentrations in rat tissues reasonably well, while highlighting the fact that one should be cautious during interpretation of ADC disposition data generated using labeled ADC molecules. The rat PBPK model for T-DM1 was translated to humans, and the human model was able to predict plasma PK of T-DM1 and total trastuzumab reasonably well, while a slight prediction bias was observed for DM1 PK profile in human plasma. The results of our investigation, and a detailed analysis of the PBPK model using pathway analysis and global sensitivity analysis, suggest that parameters related to antibody degradation, ADC deconjugation, and unconjugated drug PK are most important for understanding and characterizing whole body disposition of ADCs.