Abstract
Objective
The development of artificial pancreas (AP) technology for deployment in low-energy, embedded devices is contingent upon selecting an efficient control algorithm for regulating glucose in people with type 1 diabetes mellitus (T1DM). In this paper, we aim to lower the energy consumption of the AP by reducing controller updates, that is, the number of times the decision-making algorithm is invoked to compute an appropriate insulin dose.
Methods
Physiological insights into glucose management are leveraged to design an event-triggered model predictive controller (MPC) that operates efficiently, without compromising patient safety. The proposed event-triggered MPC is deployed on a wearable platform. Its robustness to latent hypoglycemia, model mismatch and meal misinformation is tested, with and without meal announcement, on the full version of the US-FDA accepted UVA/Padova metabolic simulator.
Results
The event-based controller remains on for 18h of 41h in closed-loop with unannounced meals, while maintaining glucose in 70–180 mg/dL for 25h, compared to 27h for a standard MPC controller. With meal announcement, the time in 70–180 mg/dL is almost identical, with the controller operating a mere 25.88% of the time in comparison with a standard MPC.
Conclusions
A novel control architecture for AP systems enables safe glycemic regulation with reduced processor computations.
Significance
Our proposed framework integrated seamlessly with a wide variety of popular MPC variants reported in AP research, customizes trade-off between glycemic regulation and efficacy according to prior design specifications, and eliminates judicious prior selection of controller sampling times.
Index Terms: Event-triggering, model predictive control, artificial pancreas, type 1 diabetes, embedded systems
I. Introduction
Although the effectiveness of an automated artificial pancreas (AP) in the regulation of blood glucose in people with Type 1 Diabetes Mellitus (T1DM) is widely recognized, there is an imminent need to design wearable or implantable AP systems operating with low energy costs.
Multiple effective approaches have been reported for implementing the AP on dedicated mobile platforms. For example, a control algorithm for bi-hormonal therapy that was clinically evaluated in an outpatient study of pre-adolescent children with T1DM [1] is implemented on an iPhone 4S. A model predictive control (MPC) algorithm implemented on a smartphone was evaluated in a hybrid-closed-loop clinical trial of adolescents with T1DM under free-living conditions [2]. Another smartphone implementation of a hybrid-closed-loop insulin delivery system was evaluated in a supervised outpatient study [3]. A pilot ‘at-home’ clinical study was conducted to evaluate the performance of a wearable device that integrates a Continuous Glucose Monitor (CGM), a Continuous Subcutaneous Insulin Infusion (CSII), a glucagon pump, the control algorithm and the wireless transmitters [4]. An AP system implemented on a miniature silicon microchip within a portable hand-held device is evaluated in [5]. The Medtronic hybrid closed-loop (HCL) system leverages a PID with insulin feedback (IFB) algorithm to automate basal insulin delivery while no meal is consumed. It is the first system to incorporate the control algorithm into the insulin pump and to operate as a fully integrated system with the continuous glucose sensor. The safety and efficacy of this system was evaluated in several clinical studies [6]–[8].
In the next-generation of AP technology, we envision further miniaturization and eventual implantation within the body. To this end, it is imperative to consider the factors involved in increasing the life expectancy of the device, since frequent alteration of hardware components such as the battery is undesirable, unsafe, and expensive. We have identified three main power drains on an embedded AP. First, there is the communication power for receiving CGM data and communicating with the pump and a display interface for user interaction, both of which are done via Bluetooth Low Energy in modern CGMs/pumps, thereby consumes low energy. Second is the idle power of the device as it is in sleep mode over most of the sampling time τ minutes. This can be minimized by optimized design of application-specific integrated circuits for the AP problem: that is, a prioritized design constraint could be to minimize idle current loss. Thirdly, and most importantly from this paper’s viewpoint, is the energy consumed by the processor. Although all three of these power ratings are extremely system dependent, a universal fact is that the MPC algorithm requires iterative solutions, and curtailing the number of iterations required implies that the time the processor on is lower and thus, energy is saved.
Multiple control algorithms have been computationally and clinically evaluated for current AP systems, including: Proportional-Integral-Derivative (PID) [6], Fuzzy-Logic [9] and MPC [10]–[12] with a hardware-in-the-loop implementation in [13]. Of these strategies, MPC generates a high computational burden in spite of demonstrating excellent closed-loop clinical performance [14]. Low-complexity MPC algorithms such as explicit, multi-parametric, and embeddable variants of MPC are well-established; see [15]–[18]. A common feature that is revealed in MPC-based control in T1DM is that the number of controller updates can be reduced by observing, predicting, and exploiting future insulin-glucose dynamics.
In this paper, we offer an efficacious event-triggered MPC [19] as an alternative to the standard MPC that computes optimal insulin doses at each time step (referred to as ‘time-triggered’ MPC). In event-triggered MPC, the sampling-period of the controller actions and the model used for predicting future glucose variations are rendered independent. That is, the optimal MPC action is computed only when specific events are triggered (or not triggered). A multitude of event-based strategies have been reported in the literature for various applications. Event-triggering mechanisms include: the difference between the estimated state and the system state exceeding a specified threshold [20]–[22], violation of a Lyapunov function decay rate [23], and migrating between critical regions in linear MPC [24].
For our application, we propose an event-triggering method that exploits physiological phenomena in conjunction with control-theoretic constructs to significantly lower the number of controller updates and processor runtime, while respecting constraints arising from a clinical safety perspective. The proposed method is tested with rigorous hardware-in-the-loop simulation studies that constitute a pre-clinical assessment of the algorithm’s safety and efficacy to be further evaluated in a clinical study setting. The contributions of this paper are:
the proposal of a novel T1DM-specific efficient event-triggering strategy that can be seamlessly integrated with any variant of the MPC for decision-making in the AP;
demonstration of significantly reduced processor runtime and energy consumption with good glycemic regulation performance in spite of large announced and unannounced meals;
investigating systematic design of trade-off parameters in the event-triggering algorithm; and
collection of preliminary power and controller update numbers using a hardware-in-the-loop simulation.
The rest of the paper is organized as follows. In Section II, we discuss a general MPC framework used in typical artificial pancreas systems. In Section III, we propose an event-triggering strategy amenable to any general MPC formalism, tractable on low-complexity devices. A case study of event-triggering with the periodic zone MPC described in [25] is presented in Section IV, and the efficacy of our method is demonstrated via hardware-in-the-loop simulations in Section V. We draw conclusions and discuss future work in Section VI.
II. Model Predictive Control Framework for the Artificial Pancreas
In this section, we provide a brief overview of general MPC strategies used in the artificial pancreas, along with constraints enforced for clinical safety.
A. Using predictive models to compute insulin doses
A CGM sensor provides an estimate of the subject’s blood glucose (BG) concentration. To regulate the BG, predictive control strategies employ models of the form
| (1a) |
| (1b) |
Here k denotes the time index, xk ∈ ℝn denotes the patient state, and the scalar yk denotes an estimate of computed via a measurement model. Let τ denote the sampling-period of the system; then the scalar denotes the actual insulin infusion rate in units (U) per τ minutes. This actual insulin infusion rate has two components: , where uk is the control action (deviation from basal), and denotes the time-varying, subject-specific, basal insulin infusion rate. General nonlinear functions f and h are presented in the predictive model formulation (1); these subsume widely used insulin-glucose models such as linear discrete-time models [26], nonlinear models [27], [28], and input-output autoregressive models [29].
The standard implementation of an MPC is via state-feedback. Therefore, it is necessary to design an estimator to procure the state xk of the system (1) based on the current CGM value , or other available information at time k (for example: previous control actions, CGM measurements, estimated glucose values). Popular estimation algorithms in the AP literature include: linear observers [30], moving horizon estimators [31], [32], or Kalman filters [33], [34]. Let Ny and Nu be the prediction and control horizon of the MPC, respectively. Let
denote a sequence of control actions from time step k + 1 to k +Nu. For any pair of integers a, b satisfying a < b, suppose . Then the optimal MPC control sequence is computed by solving
| (2) |
where is a cost function designed for glycemic regulation, and , are artificial variables used to denote open-loop states and control actions (deviations from basal), respectively. The framework in (2) captures commonly used MPC methods such as set-point MPC [36], adaptive set-point MPC [37], zone MPC [38], periodic zone MPC [30], and other MPC variants such as those reported in [33], [39], [40].
In addition to a positivity constraint (the drug infusion rate cannot be negative), the control action must also satisfy a time-varying upper bound umax,k. Widely used umax,k include mechanical constraints such as the maximum infusion rate of the pump, physiological constraints such as the insulin-on-board constraint, and safety constraints such as limitations on insulin infusion post-exercise, limits on glucose and insulin velocity; see [35], [41], [42].
An additional constraint on the insulin output is the insulin-on-board (IOB) upper bound, denoted . The IOB, described in [35], accounts for the administered insulin history and computes the remaining active insulin in the body based on clearance rates in the human endocrine system. Therefore, the quantity indicates how much insulin above the basal insulin rate can be administered safely (from a clinical perspective) at the current time step k.
It is standard practice in time-triggered MPC to implement only the first element of the sequence , and discard the tail . However, we will demonstrate in the following section that the information contained in the tail of the control sequence, if implemented carefully, provides an avenue for reducing the number of controller updates required, and therefore enhancing the efficacy of the design.
III. Event-Triggered MPC for an embeddable AP
In this section, we develop physiological conditions for event-triggering. Note that these event-triggers can be integrated with any MPC variant, or any control algorithm that leverages design models characterized in the form (1) for predicting future system behavior.
A. Predictive pump suspension
The highest priority in terms of clinical safety is to prevent sustained hypoglycemia (BG < 70 mg/dL). To this end, pump suspension algorithms such as low-glucose predictors have been devised in, for example, [43]. In this paper, we employ a linear predictor to estimate the BG level r ∈ ℕ samples into the future, that is,
When the predicted BG level ŷk+r is dangerously low, we suspend the pump until the BG levels return to the clinically safe region of 70–180 mg/dL. This event can be written as
where ξk ∈ ℝ is a design variable that enables the clinician or user to customize the predicted BG level below which they wish to suspend the pump; the dependence on the time step k implies that this variable can be altered when necessary. For example, users fearing nocturnal hypoglycemia can raise the value of ξk to enforce early pump suspension.
Remark 1
If a pump suspension is required, the control module need not be switched on, since the appropriate control action is . ■
Remark 2
We suggest using a linear predictor to predict future BG values instead of the design model (1). This is primarily to reduce computational effort, since this conditional statement is checked each time a new CGM value is available. To prevent frequent pump suspension due to inaccuracies inherent to linear extrapolation, the design parameter r is selected to be a small integer. ■
B. Exploiting insulin-on-board constraints
If the predicted CGM value does not warrant suspension, we choose our event-triggering variable to be , the IOB upper bound. From a physiological perspective, when = 0, the optimal MPC action lies in the set [ , 0]. Additionally, taking into account insulin pump quantizations, the cardinality of the set of allowable infusions in the range [ , 0] is very limited. Instead of invoking the optimal MPC action within this limited range, we infuse basal insulin if the predicted glucose trajectory is not low (in which case E1 will trigger, and the pump will suspend). We exploit this insight to formulate the condition
If the previous two events (pump suspension and saturation) are not triggered, we use the following event-triggered variant of the MPC.
C. Using the tail of the control sequence
Recall that the control horizon of the MPC is denoted by Nu, and that τ signifies the sample-period of the system. We define the output estimation error as
| (3) |
This is the difference between the CGM value and the estimated BG value at time step k. Suppose we solve (2) to derive an optimal MPC sequence at time k. Instead of implementing only the first control action , in this event-triggering step, we apply the control actions in the tail of the control sequence until either:
events E1 or E2 are triggered;
the output estimation error norm |Δyk| exceeds a pre-specified threshold εobs; or,
the first ℓmax control actions in are implemented.
Note that the exploitation of the tail of the control based on output estimation errors is adapted from [20]. The tail of the control sequence is applied only if the estimated BG and actual CGM values are in close proximity. If this happens, we expect the open-loop BG predictions to be sufficiently accurate estimates of the actual BG. This condition is written as: where denotes a counter initialized at one.
where ℓ denotes a counter initialized at one.
The selection of εobs is inextricably linked to the regulatory performance of the controller. If εobs is large, solving for the optimal MPC trajectory is not required until the estimation error Δyk is large, which may result in larger variability of BG values during glycemic regulation. The advantage of larger εobs is that the microprocessor is operated less often, as the system can rely on the stored tail of the control sequence to administer future insulin doses. Conversely, a small εobs results in tighter control but more frequent controller updates. Note that choosing εobs = 0 generalizes to the standard time-triggered approach with pump suspension.
The design parameter ℓmax signifies at most how many control actions in the tail could be actuated before recomputing an optimal MPC action trajectory (assuming that E1 and E2 have not triggered). The relation between ℓmax and the regulatory performance of the MPC is similar to εobs: namely, if ℓmax is small, the energy drain is large, but the control performance is tighter. Without a highly accurate model of the insulin-glucose dynamics, a large ℓmax (at most Nu) is expected to result in controller performance degradation.
If none of the conditions E1, E2 and E3 are satisfied, the control module is switched on and the optimization problem (2) is solved. That is,
Remark 3
This protocol requires problem (2) is solved. The tail of the control sequence can therefore be subsequently withdrawn from the memory, rather than resolving the optimization problem at each time-step. ■
Remark 4
From an embedded implementation perspective, a concern is that packets are dropped during CGM or pump transmissions. Therefore, it is critical to build robustness around the control algorithm. In case of multiple missing CGM measurements or if communication with the pump or CGM is not established within a predefined time, we switch the AP to open-loop mode or infuse basal insulin for safety. ■
A flowchart representation of the safety constrained event-triggered AP is presented in Fig. 1.
Fig. 1.
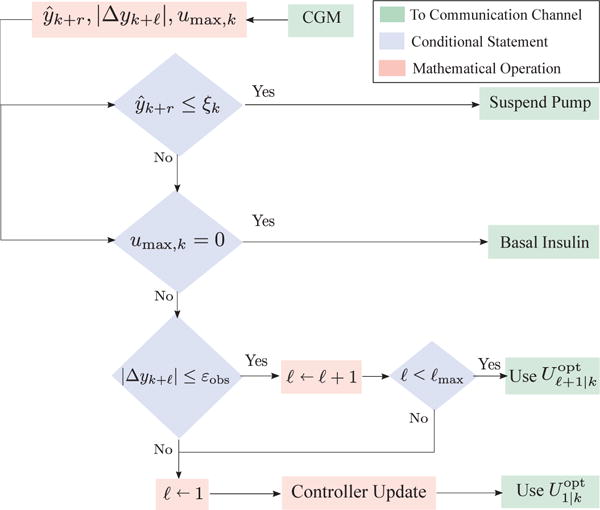
Flowchart for event-triggered MPC-based AP.
D. Prioritization for safe glycemic regulation
We will now address why it is important to prioritize the events in the afore-mentioned order through some illustrative scenarios.
Suppose the event-triggered MPC has higher priority than the pump suspension. Then, at low estimated BG levels it tends to be unlikely that control action other than suspension is useful, and thus it is generally wasteful to invoke expensive computations. Furthermore, even in cases where a non-suspension would be useful, for example, when BG is low and rising quickly, a suspension that is continued a short time longer than had MPC been invoked is not significantly deleterious to subjects’ health. Thus, this rule is computationally cost effective and safe.
Event E1 has higher priority than E2 for the following reasons. Recall that uk denotes the insulin infusion recommended above the basal rate. Hence, uk = 0 implies that the actual infusion is the basal, u⋆. When , event E2 will be triggered and basal insulin will be supplied instead of computing optimal MPC actions. If E1 has lower priority than E2, then one could be supplying basal insulin even if the optimal MPC action uk < 0, which would result in controller-induced hypoglycemia. To avoid this, we predictively suspend the pump, making E1 higher priority.
IV. Case Study: Event-Triggered Periodic Zone Model Predictive Control
In this section, we begin with an overview of the zone MPC (ZMPC) formulation proposed in [38], and the improved periodic zone MPC framework reported in [30]. The objective of this section is to illustrate how our event-triggering methodology integrates seamlessly with the periodic ZMPC.
A. Insulin-Glucose Model
A 3-dimensional linear discrete-time model, proposed in [26], is used as a design model. The model has a sampling time τ = 5 min. It is important to note that the model is linearized around a steady-state glucose value of y⋆ = 110 mg/dL with a time-varying basal insulin rate . The model is personalized with respect to each subject with T1DM via the insulin to carbohydrate ratio, total daily insulin amount, and basal insulin profile, and has been clinically validated in [30], [44] for demonstrating accurate predictive behavior.
The transfer function representation of the measurement output y and the control input u is given by
| (4) |
where z−1 is the backward shift operator, p1 = 0.98 and p2 = 0.95 are the poles, F = 1.5 is a safety factor determined by clinicians, uTDI denotes an admissible subject-specific total daily insulin amount, and c ≔ −60(1 − p1)(1 − p2)2 is a constant required for unit conversion, whose units depends on the units used in data for the design of the poles of the model. The state-space representation of the discrete-time transfer function model (4) has the form
| (5) |
where k is denotes the discrete time index, xk is the subject state at the kth time instant, uk is the control action, and yk is the output of the design model, with matrices
and Clearly, this model conforms to the representation (1) with f ≔ Ax + Bu and h ≔ Cx.
The state xk of the system (5) is computed based on the current CGM value using a linear observer of the form
| (6) |
where L is the observer gain matrix, and is an estimate of the current state based on the previously estimated state xk−1 and the (known) previous control action uk−1.
B. Constraints for safe glucose variation
The control objective is to regulate the subject’s glucose level to within a time-dependent periodic zone of safe glucose values. As hypothesized in [25] and clinically validated in [30], [44], employing a periodic zone as a glucose target rather than a fixed set point offers various clinical advantages such as reduction of nocturnal hypoglycemic events. Furthermore, the ZMPC leads to reduced actuation; our proposed event-triggering algorithm further reduces the actuation via prioritized, event-based conditional constructs.
A periodic zone is represented mathematically as
| (7) |
where the lower and upper bounds are given by
| (8a) |
and
respectively. For a, b ∈ ℝ, the map ψ(a, b) denotes a smooth transition between a and b; in this work, we choose ψ to be a cosine function. The positive scalars , , , and are design parameters which are determined after discussion with endocrinologists.
Remark 5
If the designer wishes to implement a fixed target glucose level (commonly referred to as a set-point MPC), this can be modeled as a zone with identical upper and lower bounds, that is, when . ■
C. Constraints for safe insulin delivery
As discussed before, the active insulin content in the body is formulated as the IOB constraint, which restricts the allowable magnitude of insulin infused. Empirical clinically-validated insulin action curves are used to compute the current IOB value. These discretized curves are sampled every τ min and represent the fraction of insulin that remains active after 2, 4, 6 and 8 hours. We denote these curves by Θℓhr ∈ ℝ8/(τ/60), where ℓ ∈ {2, 4, 6, 8}. In order to estimate the current IOB value, we first select the correct IOB curve based on the current CGM value and the following heuristic:
| (9) |
Let Uk−95:k ∈ ℝ96 and denote the vector of insulin infusions and meal-induced manual insulin boluses administered over the past 8 hours, respectively. Then the estimated current IOB value is given by
With an estimate of the current IOB, we compute the IOB upper bound as:
| (10) |
where Cf [(mg/dL)/U] is a patient-specific clinical parameter, called the ‘correction factor’. With the above constraints, we are now ready to formulate the optimization problem that yields appropriate insulin doses for safe glycemic regulation.
D. Computing insulin doses
An important ingredient required for the optimization formulation is the so-called ‘zone-excursion function’
where and have been previously defined in (8).
Let Ny and Nu denote the prediction and control horizon of the ZMPC, and let U1:Nu|k denote a sequence of control actions from time step k + 1 to k + Nu. Then the optimal control sequence is computed by solving
| (11) |
subject to:
Although we compute the optimal ZMPC control sequence , we only apply the first action of the sequence.
Remark 6
Since this optimized control action is derived with respect to the linearized model, the actual insulin dose administered is given by . ■
E. Event-triggered ZMPC parameters for simulation
Parameters for the ZMPC have been clinically validated in [30], [44]. We select a predictive horizon of Ny = 9 (45 min), and control horizon Nu = 5 (25 min) for the ZMPC. The periodic zone is parameterized by , , and . The weights are selected as Q = 1, and .
For the event E1, the linear predictor horizon is chosen to be r = 5 samples (25 min), and the pump suspend threshold ξk is selected to be 80 mg/dL in the morning (7 AM–11 PM), and raised to 100 mg/dL at night (11 PM–7 AM) to prevent nocturnal hypoglycemia. For event E2, we compute as in (10). For E3, we have a choice of 1 ≤ ℓmax ≤ Nu. We ℓmax = 3 because the linear model (5) typically stabilizes to the zone within three samples, and the rest of the control trajectory degrades to the basal insulin rate
Another design parameter for E3 is εobs: this scalar is strongly correlated with the trade-off between regulatory performance and controller update frequency. Thus, in the following section, we investigate the efficiency and regulatory performance trade-off with multiple εobs. To choose a viable range of εobs, we construct a histogram of absolute glucose deviations |Δyk| from a previous clinical study [14] using data from N = 17 subjects. This histogram is provided in Fig. 3, along with the median and interquartile ranges. Since the median is found to be 3 mg/dL, we restrict εobs = 1, 2, 3 mg/dL.
Fig. 3.
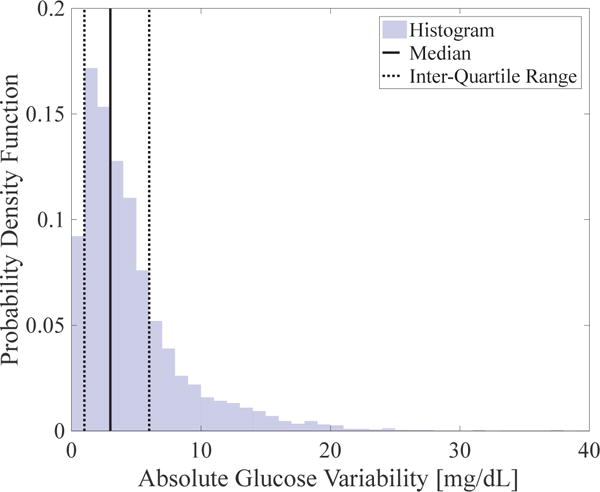
Histogram of absolute glucose deviations obtained from clinical CGM data [14] with 3 mg/dL median (continuous vertical line) and 1–6 mg/dL interquartile range (dashed vertical lines).
V. Simulated Hardware-in-the-Loop Experiments
We report the clinical scenario, hardware platform, and results of the simulation study on 111 subjects: 100 from the full version of the FDA-accepted UVA/Padova simulator [45], 10 from the freely available version of the simulator, and a subject constructed by averaging the parameters of the 110 other subjects. We begin by testing the performance of the event-triggered ZMPC (ET-ZMPC) with multiple εobs both with and without meal announcement to determine a satisfactory value. Fixing this value of εobs, we verify the robustness of the ET-ZMPC with respect to incorrect basal infusion rates and erroneously estimated carbohydrate levels in announced meals.
A. Clinical Scenario and Challenges
The clinical scenario used to test the proposed controller is presented in Fig. 2. Five meals in total are consumed within 41 simulated hours of closed-loop control. A 70 g meal of carbohydrates is consumed at 6 PM, after 2 hours of closed-loop initiation, followed by a snack of 40 g of carbohydrates at 9 PM. The system is challenged at 2 AM with an undetected insulin bolus to represent a sudden, nocturnal hypoglycemic episode that is a major concern for patients with T1DM. The following morning, a 70 g breakfast is provided at 8 AM, a 70 g lunch at 1 PM, and a dinner of 70 g of carbohydrates at 9 PM. Two cases are considered to evaluate the performance of the ET-ZMPC algorithm;
all meals are unannounced and the controller is responsible for computing appropriate insulin doses in a completely automated manner; and,
all meals are announced and a manual insulin bolus is administered based on a patient-specific carbohydrate/insulin ratio; the controller is expected to regulate the basal insulin satisfactorily in the pre- and postprandial time ranges.
Fig. 2.
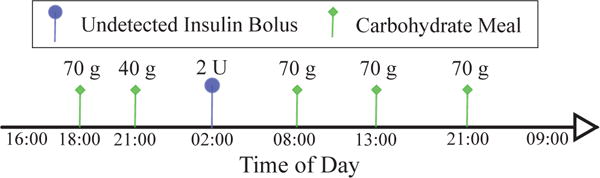
Scenario for testing the performance of the proposed event-triggered AP. The closed-loop starts at 4 PM the first day. Two meals are consumed the first day followed by a simulated secret insulin bolus to force a nocturnal hypoglycemic event. The second day includes a meal plan of three meals with long intervals between meals. The closed-loop ends the next day at 9 AM.
The challenge for the event-based controller is to perform comparably to the time-triggered ZMPC (TT-ZMPC), in a safe manner, with fewer controller updates. The safety of the event-triggering mechanism is tested by assessing its ability to prevent severe nocturnal hypoglycemia induced by an undetected insulin bolus (representing manual overbolusing, latent exercise effects, or heightened insulin sensitivity due to collateral illness) of 2 U magnitude at 2 AM on the first night.
B. Hardware-in-the-Loop-Simulation Studies
The periodic ZMPC control action sequences, observer, IOB computation, and the event-triggering mechanism are deployed on a single-board computer known as Raspberry Pi 3 Model B (https://www.raspberrypi.org/). A 32GB microSD card is used as the flash memory of the entire system. The board contains a 64-bit quad-core ARMv8 central processing unit (CPU) that operates on up to 1.2GHz clock speed. The Raspberry Pi emulates an embedded AP: it communicates with MATLAB via Ethernet to receive virtual CGM data from the Simulator and wirelessly transmits the computed control action back to the Simulator. All code for the Raspberry Pi is written in Python 2.7 and the quadratic programming problem inherent to the MPC is solved using the CVXOPT toolbox [46]. The rationale behind deploying the AP as an embedded system is to collect realistic power numbers and demonstrate the feasibility of implementing the event-based ZMPC algorithm on a miniaturized device. An overview of the hardware-in-the-loop (HIL) simulation protocol and the components used therein is provided in Fig. 4.
Fig. 4.
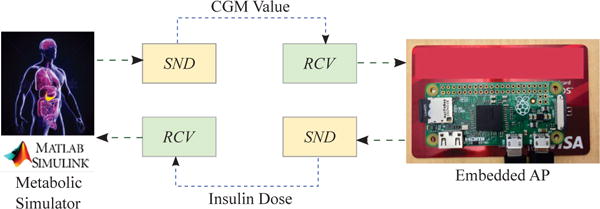
Hardware-in-the-loop implementation. Note that the Raspberry Pi Zero is smaller than the credit card beneath. SND and RCV denote sending and receiving data, respectively, via Bluetooth LE or WiFi.
C. Results and Discussion
The following results are obtained by testing the TT-ZMPC and ET-ZMPC on 111 in-silico subjects, obtained as follows: 100 subjects from the full version of the UVA/Padova simulator, 10 subjects from the short version of the UVA/Padova testbed, and 1 subject whose dynamics are generated by averaging the model parameters of the afore-mentioned 110 subjects.
1) Comparing TT-ZMPC and ET-ZMPC
We test the performance of the ET-ZMPC with εobs = 1, 2, 3 mg/dL and compare with the standard TT-ZMPC for both announced and unannounced meals. For this comparative study, we report BG performance metrics (as recommended in [47]) in Table I for the overall study and overnight periods (12 AM to 8 AM; depicted with gray rows). To determine the efficacy of the proposed control strategy, we provide the percentage of controller updates required for each variant of the ET-ZMPC, along with power consumed in mAh over the simulation time. A DROK USB 2.0 digital multimeter is used to measure the current (in mA) flowing into the Raspberry Pi during the simulation time period. The average current value is then multiplied by the total time (in hour) required by the control module to solve the quadratic program (11) to yield a first-order estimate of the total energy consumed. An implicit assumption is made in this estimation of the energy consumption: that the Raspberry Pi can be switched on/off instantaneously upon concluding communications with Simulink, and the idle current is negligible. Although this is not strictly true for the Raspberry Pi, we envision that future embedded AP technology would employ application-specific hardware, the operation of which can be tightly tailored to the task of being energy-efficient, thereby minimizing idle current loss.
TABLE I.
Controller performance comparison with announced and unannounced meals (Mean ± One Standard Deviation) for 111 subjects. The grey shading is used to depict overnight metrics. The ‘*’ implies a p-value< 0.05 and ‘**’ indicates a p-value< 0.001.
| Performance Metrics | Standard TT-ZMPC | Proposed ET-ZMPC | ||
|---|---|---|---|---|
|
| ||||
| εobs = 1 | εobs = 2 | εobs = 3 | ||
|
| ||||
| [A] Unannounced Meals
| ||||
| Overall BG < 70 mg/dL [%] | 1.64 ± 2.85 | 1.27 ± 2.09 | 1.15 ± 1.99 | 1.07 ± 1.84 |
| Overall BG in 70–180 mg/dL [%] | 66.00 ± 8.63 | 63.72 ± 8.81 (*) | 61.09 ± 8.87 (*) | 58.73 ± 8.85 (*) |
| Overall BG > 180 mg/dL [%] | 31.90 ± 8.64 | 34.51 ± 9.08 (*) | 37.27 ± 9.37 (*) | 39.80 ± 9.45 (*) |
| Overall BGmedian [mg/dL] | 141.95 ± 13.47 | 146.94 ± 15.99 (*) | 152.52 ± 18.92 (*) | 157.81 ± 21.40 (*) |
| Overall Percent Controller Updates [%] | 100.00 ± 0.00 | 59.34 ± 6.86 (**) | 47.58 ± 5.73 (**) | 38.83 ± 4.58 (**) |
| Overall Energy Consumed [mAh] | 4.79 ± 0.32 | 2.86 ± 0.33 (**) | 2.28 ± 0.29 (**) | 1.87 ± 0.23 (**) |
|
| ||||
| Overnight BG < 70 mg/dL [%] | 3.24 ± 5.29 | 2.71 ± 4.35 | 2.46 ± 4.24 | 2.45 ± 4.23 |
| Overnight BG in 70–180 mg/dL [%] | 88.24 ± 8.51 | 86.56 ± 8.86 | 84.37 ± 9.50 (*) | 81.93 ± 9.94 (*) |
| Overnight BG > 180 mg/dL [%] | 8.16 ± 6.55 | 10.36 ± 8.03 (*) | 12.75 ± 9.42 (*) | 15.22 ± 10.25 (*) |
| Overnight BGmedian [mg/dL] | 121.61 ± 8.53 | 123.93 ± 8.96 (*) | 126.39 ± 10.41 (*) | 129.12 ± 11.85 (*) |
| Overnight Percent Controller Updates [%] | 100.00 ± 0.00 | 48.02 ± 11.05 (**) | 37.48 ± 9.11 (**) | 30.17 ± 7.13 (**) |
| Overnight Energy Consumed [mAh] | 5.07 ± 0.43 | 2.43 ± 0.56 (**) | 1.88 ± 0.45 (**) | 1.53 ± 0.37 (**) |
|
[B] Announced Meals | ||||
| Overall BG < 70 mg/dL [%] | 0.76 ± 1.46 | 0.96 ± 1.66 | 0.85 ± 1.52 | 0.80 ± 1.49 |
| Overall BG in 70–180 mg/dL [%] | 86.65 ± 9.73 | 86.75 ± 10.26 | 86.38 ± 10.35 | 86.07 ± 10.79 |
| Overall BG > 180 mg/dL [%] | 12.60 ± 9.08 | 12.29 ± 9.71 | 12.77 ± 10.01 | 13.14 ± 10.49 |
| Overall BGmedian [mg/dL] | 130.40 ± 7.43 | 129.99 ± 9.10 | 130.89 ± 10.01 | 131.30 ± 10.97 |
| Overall Percent Controller Updates [%] | 100.00 ± 0.00 | 33.04 ± 10.16 (**) | 25.88 ± 8.26 (**) | 20.68 ± 6.92 (**) |
| Overall Energy Consumed [mAh] | 5.09 ± 0.30 | 1.70 ± 0.49 (**) | 1.34 ± 0.40 (**) | 1.07 ± 0.33 (**) |
|
| ||||
| Overnight BG < 70 mg/dL [%] | 1.67 ± 3.17 | 1.79 ± 3.23 | 1.54 ± 2.94 | 1.50 ± 3.05 |
| Overnight BG in 70–180 mg/dL [%] | 96.63 ± 5.43 | 96.22 ± 5.86 | 96.29 ± 5.68 | 96.22 ± 5.76 |
| Overnight BG > 180 mg/dL [%] | 1.50 ± 3.01 | 1.77 ± 3.77 | 1.89 ± 3.93 | 2.03 ± 4.13 |
| Overnight BGmedian [mg/dL] | 119.88 ± 7.75 | 119.41 ± 8.75 | 119.81 ± 9.37 | 120.10 ± 10.02 |
| Overnight Percent Controller Updates [%] | 100.00 ± 0.00 | 41.87 ± 13.16 (**) | 32.22 ± 10.67 (**) | 25.52 ± 8.59 (**) |
| Overnight Energy Consumed [mAh] | 5.27 ± 0.36 | 2.21 ± 0.70 (**) | 1.71 ± 0.55 (**) | 1.36 ± 0.44 (**) |
For unannounced meals, we note from Table I[A] that increasing εobs results in a decrease of time spent with BG less than 70 mg/dL both overall and overnight. This is primarily due to anticipatory pump suspension: as expected, this results in (statistically significant) increased time spent above 180 mg/dL. The time spent in the euglycemic range, along with the median BG concentration, decreases with increasing εobs. This can be explained by recalling the condition for event E3: as εobs increases, previously optimal, but currently suboptimal, control actions are employed with higher discrepancy between the CGM value and the estimated BG level. This suboptimality of controller decisions, coupled with the discrepancy in BG estimates, results in less tighter regulation of BG. However, this slight compromise (≈ 10% decrease of time in euglycemic range) in regulatory performance comes at an excellent trade-off: a 40–60% reduction in controller updates with less than half the energy consumed for overnight simulations (in comparison with the standard time-triggered controller), without a significant alteration of time in with BG <70 mg/dL.
The energy-saving capabilities of the proposed ET-ZMPC is more pronounced with meal announcement. We deduce from Table I[B] that the time in the BG ranges vary less than 2% for the ET-ZMPC versus the TT-ZMPC, while the controller updates are reduced by 67–80% and the energy consumed is less than half. At night, the ET-ZMPC maintains the subjects’ BG in the euglycemic range more than 96% of the time in spite of the undetected 2U insulin bolus with the controller in sleep mode for over 4 hours each night in spite of a sizable undetected insulin bolus (emulating a sudden, nocturnal hypoglycemic event).
A crucial question that remains unanswered is how to select a specific value of εobs utilizing the above data collected for εobs = {1, 2, 3}. This is the topic of the next subsection.
2) Selection of εobs
We propose the following systematic method of exploiting trade-off curves to select a particular value of εobs within the range εobs = {1, 2, 3}. Note that a fully automated AP should be capable of handling the case when meals are unannounced. Thus, from a safety perspective, it is important to leverage the controller performance data for unannounced meals to select εobs. We begin, therefore, by choosing trade-off metrics based on Table I[A]. Specifically, we select time in the 70–180 mg/dL range as the metric for glucose regulation performance, and the average controller update frequency for each εobs as the efficacy performance. Of course, the designer could choose other metrics (e.g. time in 80–140 mg/dL) of performance as prioritized by their specific investigation. Next, we construct the trade-off curves by polynomial regression for the chosen metrics; this is illustrated in Fig. 5. The Pareto-optimal nature of the metrics are evident from the trade-off curve (black dash-dot line). The next step involves formulating an admissible design space: for example, we specify that for overall performance, we require at least a 40% reduction in controller update frequency, and at least 60% time in the euglycemic range. Additionally, we require that, overnight, we require at least 60% of sleep time for the controller, and maintenance at least 80% of the time in the euglycemic region in spite of the onset of latent nocturnal hypoglycemia. Leveraging our regression-based trade-off curve and these controller specifications, we construct the admissible design space shown by shaded yellow boxes in Fig. 5. Noting that the TT-ZMPC is equivalent to an ET-ZMPC with εobs = 0 having predictive pump suspension, we assume a linear variation of εobs from 0 to 3 along the trade-off curve, as depicted by the thick black line at the bottom of Fig. 5. Then the intersection of the admissible design spaces are projected onto the range of εobs line (shown using red dashed arrows) to obtain an admissible range of εobs in [1.53, 2.47]. For low-complexity/embedded implementation, the value εobs = 2 is chosen as it offers a specific engineering advantage. Namely, it is represented using two-bits and therefore can be compared easily rather than using single precision and complicated multiplexers or combination of multiplexers. Comparing against εobs = 2 can be done more efficiently by shifting right |Δyk| bitwise to the right (division by 2) and comparing with a single bit: that is, checking whether |Δyk|/2 ≤ 1 instead of |Δyk|≤ 2. This indicates that simple hardware components can be used to implement a swift comparison if εobs = 2, as chosen for this exemplar design.
Fig. 5.
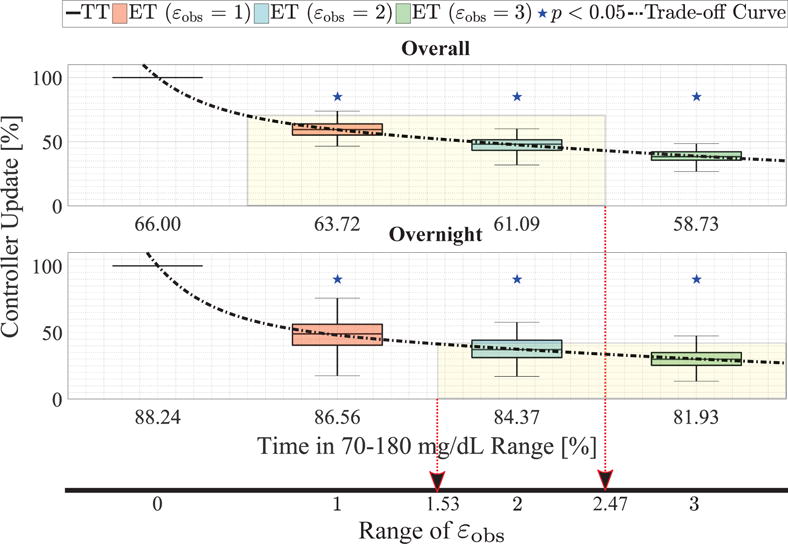
Box-and-whisker plots to compare the TT-ZMPC and ET-ZMPC strategies in terms of trade-off between glucose regulation (median time in the 70–180 mg/dL range) and percentage of controller updates required in closed-loop over the entire simulation and during the night-time with and without meal announcement. Statistical significance is shown with blue stars and regression-based trade-off curves are depicted using gray dashed lines. Note that the x-axis is reversed.
3) Resilience against model mismatch/misinformation
To verify the controller performance and controller update reduction with εobs = 2 mg/dL in a challenging simulated setting, we test the TT-ZMPC and ET-ZMPC with the following (sizable) model mismatch: (i) a random perturbation of ±20% on the TDI value, (ii) ±50% additive uncertainty on the basal insulin infusion rate, and (iii) for announced meals, incorrect estimation up to ±25% of the carbohydrate ratio. The objective of introducing these uncertainties is to estimate the controller performance in spite of temporal variations in these parameters, and to take into account inaccuracy in model fitting. The user also misinforms the controller by ±25% of the estimated carbohydrate content in the meal: this is a very common occurrence, although we selected a high misinformation magnitude of 25% to challenge the controller and ensure operational safety in clinically adverse scenarios.
The results of this robustness analysis are presented in Fig. 6 for unannounced meals (subplots [A]–[C]), and meal announcement (subplots [D]–[F]). Fig. 6[A] and [D] depicts the median of the event that was triggered at each time step. Both subplots show similar trends. The pump suspension E1 (black shade) closely follows the nocturnal injection of 2U of undetected insulin when the subjects enter the hypoglycemic range or when (in case of the announced meals) the meal size is incorrectly estimated leading to overbolusing of insulin. As expected, the event E2 (dark green shade) triggers postprandially, when the infused insulin drives the IOB upper bound to zero; this is more pronounced in the case of meal announcements since a large impulsive bolus is applied, so the duration for which is longer. Since the subplots [A] and [D] depict the median of the events, the white regions (illustrating controller updates) is mostly limited in case of announced meals, since the critical decision making during a meal is handled via manual bolusing, and thus, the MPC does not need to be invoked often. This is in contrast to the plentiful presence of controller updates in the case of unannounced meals, since the controller is solely responsible for decision making at the onset of a meal. We also draw attention to the fact that in the second night, when there is no latent hypoglycemia, and the IOB constraint is non-zero, the subplots [A] and [D] show that E3 is triggered. This can be explained from subplots [B] and [E], respectively. We observe that the BG levels are in the euglycemic zone without sharp variations between the estimated BG and CGM values; even with model mismatch, the controller does not require updating for more than half of the night. Subplots [B]–[F] testify that in spite of non-trivial mismatch and misinformation, the event-triggering strategies are robust and perform safely without frequent controller updates, and the time in the euglycemic range are quite similar.
Fig. 6.
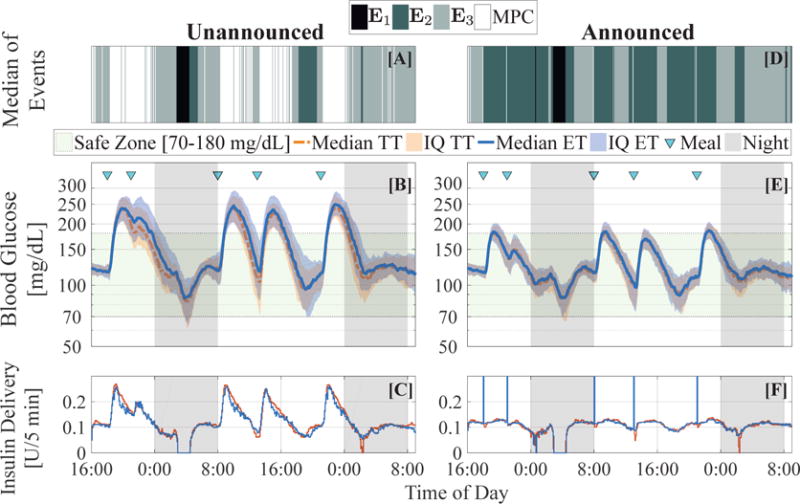
Robustness analysis of the controller with mismatched basal insulin rate, carbohydrate ratio and total daily insulin intake. (Left column) Controller performance with unannounced meals. [A] Median of events over the closed-loop simulation. [B] Median and interquartile (IQ) ranges of blood glucose concentration for ET-ZMPC (blue) and TT-ZMPC (red). [C] Median insulin profiles for ET-ZMPC (blue) and TT-ZMPC (red). (Right column) Controller performance with meal announcements. [D] Median of events over the closed-loop simulation. [E] Median and interquartile ranges of blood glucose concentration for ET-ZMPC (blue) and TT-ZMPC (red). [F] Median insulin profiles for ET-ZMPC (blue) and TT-ZMPC (red). The spikes (truncated at 0.3U) denote the manual insulin boluses
We provide a detailed illustration of controller update frequency in the presence of mismatch/misinformation in Fig. 7. We verify that our design specifications during the selection of εobs = 2 are satisfied: indeed, the controller is idle 55% of the time (median) overall, and around 65% of the time at night when meals are unannounced: the time no controller updates are required improves to 71% and 77%, respectively, when meals are announced. Furthermore, the time in the euglycemic range is 62% overall, and 80% overnight for unannounced meals. For announced meals, these numbers are 86% and 92%, respectively.
Fig. 7.
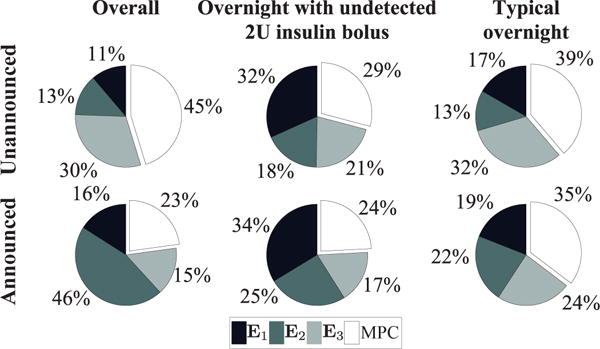
Pie charts of the distribution of events of the ET-ZMPC (εobs = 2 mg/dL) reported for the overall simulation time, the night-time with an undetected 2U insulin bolus, and a night-time without meals or latent hypoglycemia. (Top) Scenario of unannounced meal disturbances. (Bottom) Scenario of announced meal disturbances.
D. Testing on clinical data
To estimate the performance of our proposed algorithm with sensor noise and glucose variability, we test the algorithm with εobs = 1, 2, 3 mg/dL on clinical data* obtained in a randomized, crossover trial with 17 people with T1D in closed loop with MPC [14]. We evaluate our proposed algorithm on the CGM trace and compute the percentage time the processor implementing the ET-ZMPC can remain idle. We use the same MPC parameters as in the previous section, which differs from those used in the clinical study. In Fig. 8, the mean insulin traces over 17 patients are compared with the actual MPC control obtained in the clinical study.
Fig. 8.
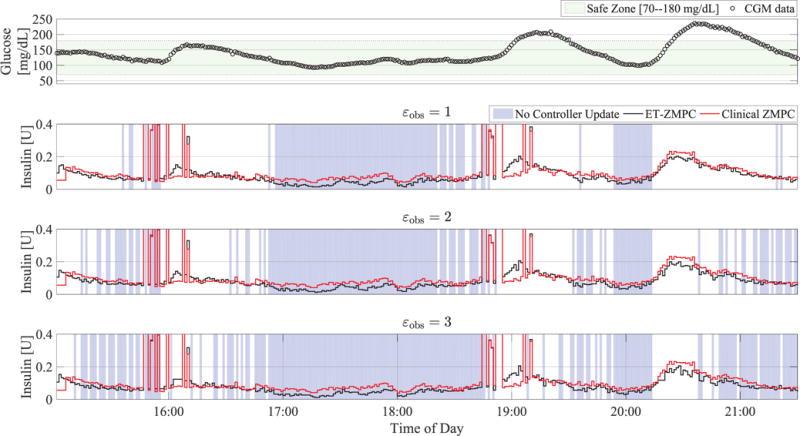
Clinical evaluation of ET-ZMPC using advisory mode with varying εobs on clinical data. The lower three plots compare mean insulin profiles of the ET-ZMPC (black) and the clinical controller (red) for 17 patients, where the background blue shading denotes times when the control module processor can be switched off.
Based on clinical data from a closed loop study that used the Dexcom G4 with the 505 algorithm (Dexcom, San Diego, CA), the percentage savings in controller updates for our proposed controller is statistically significant in all three cases (p < 0.001) based on a Wilcoxon rank sum test, and the percent updates required decrease consistently with increasing εobs. Specifically, the median percent updates required are 48.60, 40.36 and 34.64 for the ET-ZMPC tested on this data for εobs = 1, 2, 3 mg/dL, respectively. This can be deduced from the increasing density of the blue shades in Fig. 8. Albeit with limited updates, the control actions of the ET-ZMPC and the clinical ZMPC exhibit statistically similar trends, with total insulin infused being slightly lower: specifically, clinical: 39.64 ± 12.14 U, εobs = 1 mg/dL: 36.79 ± 8.83 U (p = 0.58), εobs = 2 mg/dL: 35.97 ± 8.65 U (p = 0.39), εobs = 3 mg/dL: 35.33 ± 8.56 U (p = 0.27).
Although the total insulin used is lower the mean insulin delivered (shown in Fig. 8) exhibits a dispersion of announced meal boluses around 16:00 and 19:00, and a slight rise of insulin following a meal. These phenomena can be explained as follows. In the clinical study, announced meals were provided shortly before/after 16:00 and 19:00 but not exactly at those times: this is why we see a dispersion in the announced bolus timings. The slight rise of the ET-ZMPC control action versus the clinical ZMPC is due to event E2. This event is triggered due to higher levels of glucose due to the meal, in conjunction with a sharp decay of to zero following a meal bolus. This infusion of basal following the meal bolus raises the average insulin in the ET-ZMPC above the clinical controller (which computes infusions lower than basal).
VI. Conclusions
For next generation AP systems, we envision miniaturization and low-power technology to ensure wearability, implantability and increased life expectancy of the medical device. A step in this direction is provided in this paper. Specifically, we present an event-triggering methodology that increases the idle time of the control module via reduction of controller updates. The proposed methodology utilizes the richness of MPC design features to enable skipping of control actions and using the tail of the control sequence to save energy. We also inject personalized design specifications into our event-based formalism through user-defined parameters such as ξk, ℓmax, and εobs. The simulation results indicate that the proposed method can achieve comparable performance to standard MPC, but with >50% reduction in controller updates, signifying its suitability for an embedded, power-saving AP.
We appreciate that although the microprocessor implementing the control algorithm is a significant energy drain, optimal power management is dependent on the efficient use of multiple components such as communication modules, safety alarms, end-user displays. Thus, our future work will be dedicated to extending the event-triggering mechanism to self-triggering methods to enable the CGM to be the ‘driver’ instead of the controller: that is, to design a smart CGM that decides when (and if) the controller needs a BG value, based on physiological trends. Other modes of investigation include the search for a low-energy communication module for secure and fast transferral of BG, constraints, and insulin information.
Acknowledgments
The authors thank Ravi Gondhalekar and Sunil Deshpande at Harvard University for their keen insights and helpful discussions. Access to the full version of the UVA/Padova metabolic simulator was provided by an agreement with Prof. C. Cobelli (University of Padova) and Prof. B. P. Kovatchev (UVA) for research purposes. This study was supported by the National Institutes of Health (grants DP3DK104057, DP3DK101068).
Footnotes
Specific details of the study can be found at clinicaltrials.gov ID: NCT02438670 and NCT01987206.
References
- 1.Russell SJ, Hillard MA, et al. Day and night glycemic control with a bionic pancreas versus conventional insulin pump therapy in preadolescent children with Type 1 Diabetes: a randomised crossover trial. Lancet Diabetes Endocrinol. 2016;4(3):233–243. doi: 10.1016/S2213-8587(15)00489-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Tauschmann M, Allen JM, et al. Day-and-Night Hybrid Closed-Loop Insulin Delivery in Adolescents With Type 1 Diabetes: A Free-Living, Randomized Clinical Trial. Diabetes Care. 2016;39(7):1168–1174. doi: 10.2337/dc15-2078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Grosman B, Ilany J, et al. Hybrid Closed-Loop Insulin Delivery in Type 1 Diabetes During Supervised Outpatient Conditions. Journal of Diabetes Science and Technology. 2016;10(3):708–713. doi: 10.1177/1932296816631568. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Blauw H, van Bon A, Koops R, DeVries J, on behalf of the PCDIAB Consortium Performance and safety of an integrated bihormonal artificial pancreas for fully automated glucose control at home. Diabetes, Obesity and Metabolism. 2016;18(7):671–677. doi: 10.1111/dom.12663. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Reddy M, Herrero P, et al. Metabolic Control With the Bio-inspired Artificial Pancreas in Adults With Type 1 Diabetes: A 24-Hour Randomized Controlled Crossover Study. Journal of Diabetes Science and Technology. 2015;17(10):405–413. doi: 10.1177/1932296815616134. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Ly TT, Roy A, et al. Day and Night Closed-Loop Control Using the Integrated Medtronic Hybrid Closed-Loop System in Type 1 Diabetes at Diabetes Camp. Diabetes Care. 2015;38(7):1205–1211. doi: 10.2337/dc14-3073. [DOI] [PubMed] [Google Scholar]
- 7.Ly TT, Weinzimer SA, Maahs DM, Sherr JL, Roy A, Grosman B, Cantwell M, Kurtz N, Carria L, Messer L, Eyben R von, Buckingham BA. Automated hybrid closed-loop control with a proportional-integral-derivative based system in adolescents and adults with type 1 diabetes: individualizing settings for optimal performance. Pediatric Diabetes. 2016 Apr;:1–8. doi: 10.1111/pedi.12399. [DOI] [PubMed] [Google Scholar]
- 8.Garg SK, Weinzimer SA, Tamborlane WV, Buckingham BA, Bode BW, Bailey TS, Brazg RL, Ilany J, Slover RH, Anderson SM, et al. Glucose outcomes with the in-home use of a hybrid closed-loop insulin delivery system in adolescents and adults with type 1 diabetes. Diabetes Technology & Therapeutics. 2017;19(3):155–163. doi: 10.1089/dia.2016.0421. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Nimri R, Muller I, et al. MD-logic overnight control for 6 weeks of home use in patients with type 1 diabetes: randomized crossover trial. Diabetes Care. 2014;37(11):3025–3032. doi: 10.2337/dc14-0835. [DOI] [PubMed] [Google Scholar]
- 10.Harvey RA, Dassau E, Bevier WC, Seborg DE, Jovanovič L, Doyle FJ, III, Zisser HC. Clinical evaluation of an automated artificial pancreas using zone-model predictive control and health monitoring system. Diabetes Technology and Therapeutics. 2014;16(6):348–357. doi: 10.1089/dia.2013.0231. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Kovatchev BP, Renard E, et al. Safety of outpatient closed-loop control: first randomized crossover trials of a wearable artificial pancreas. Diabetes Care. 2014;37(7):1789–1796. doi: 10.2337/dc13-2076. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Parker RS, Gatzke EP, Doyle FJ., III Advanced Model Predictive Control (MPC) for Type I Diabetic Patient Blood Glucose Control. Proc 2000 Amer Cont Conf (ACC) 2000 Jun;:3483–3487. [Google Scholar]
- 13.Dassau E, Palerm CC, Zisser H, Buckingham BA, Jovanovič L, Doyle FJ., III In Silico Evaluation Platform for Artificial Pancreatic β-cell Development — A Dynamic Simulator for Closed-Loop Control with Hardware-in-the-Loop. Diabetes Technology and Therapeutics. 2009;11(3):187–194. doi: 10.1089/dia.2008.0055. [DOI] [PubMed] [Google Scholar]
- 14.Pinsker JE, Lee JB, et al. Randomized crossover comparison of personalized MPC and PID control algorithms for the artificial pancreas. Diabetes Care. 2016;39(7):1135–1142. doi: 10.2337/dc15-2344. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Bemporad A, Morari M, Dua V, Pistikopoulos EN. The explicit linear quadratic regulator for constrained systems. Automatica. 2002;38:3–20. [Google Scholar]
- 16.Szücs A, Kvasnica M, Fikar M. A memory-efficient representation of explicit MPC solutions. Proc 50th IEEE Conf on Dec and Contr and Europ Cont Conf (CDC-ECC) 2011:1916–1921. [Google Scholar]
- 17.Chakrabarty A, Dinh V, Corless MJ, Rundell AE, Zak SH, Buzzard GT. Support vector machine informed explicit nonlinear model predictive control using low-discrepancy sequences. IEEE Transactions on Automatic Control. 2017;62(1):135–148. [Google Scholar]
- 18.Richter S, Jones CN, Morari M. Computational complexity certification for real-time MPC with input constraints based on the fast gradient method. IEEE Transactions on Automatic Control. 2012;57(6):1391–1403. [Google Scholar]
- 19.Heemels WPMH, Johansson KH, Tabuada P. An introduction to event-triggered and self-triggered control. Proc 51st IEEE Conf on Dec and Cont (CDC) 2012:3270–3285. [Google Scholar]
- 20.Lehmann D, Henriksson E, Johansson KH. Event-triggered model predictive control of discrete-time linear systems subject to disturbances. Proc Europ Cont Conf (ECC) 2013:1156–1161. [Google Scholar]
- 21.Bernardini D, Bemporad A. Energy-aware robust model predictive control based on noisy wireless sensors. Automatica. 2012;48(1):36–44. [Google Scholar]
- 22.Eqtami A, Dimarogonas DV, Kyriakopoulos KJ. Novel event-triggered strategies for model predictive controllers. Proc 50th IEEE Dec and Contr and Europ Cont Conf (CDC-ECC) 2011:3392–3397. [Google Scholar]
- 23.Eqtami A, Dimarogonas DV, Kyriakopoulos KJ. Event-triggered control for discrete-time systems. Proc 2010 Amer Cont Conf (ACC) 2010:4719–4724. [Google Scholar]
- 24.Jost M, Darup MS, Mönnigmann M. Optimal and suboptimal event-triggering in linear model predictive control. Proc Europ Cont Conf (ECC) 2015:1153–1158. [Google Scholar]
- 25.Gondhalekar R, Dassau E, Zisser HC, Doyle FJ., III Periodic-Zone Model Predictive Control for Diurnal Closed-Loop Operation of an Artificial Pancreas. Journal of Diabetes Science and Technology. 2013;7(6):1446–1460. doi: 10.1177/193229681300700605. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Heusden K van, Dassau E, Zisser HC, Seborg DE, Doyle FJ., III Control-relevant models for glucose control using a priori patient characteristics. IEEE Transactions on Biomedical Engineering. 2012;59(7):1839–1849. doi: 10.1109/TBME.2011.2176939. [DOI] [PubMed] [Google Scholar]
- 27.Hovorka R, Canonico V, et al. Nonlinear model predictive control of glucose concentration in subjects with Type 1 Diabetes. Physiological Measurement. 2004;25(4):905–920. doi: 10.1088/0967-3334/25/4/010. [DOI] [PubMed] [Google Scholar]
- 28.Man C Dalla, Rizza RA, Cobelli C. Meal simulation model of the glucose-insulin system. IEEE Transactions on Biomedical Engineering. 2007;54(10):1740–1749. doi: 10.1109/TBME.2007.893506. [DOI] [PubMed] [Google Scholar]
- 29.Eren-Oruklu M, Cinar A, Quinn L, Smith D. Estimation of future glucose concentrations with subject-specific recursive linear models. Diabetes Technology and Therapeutics. 2009;11(4):243–253. doi: 10.1089/dia.2008.0065. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Gondhalekar R, Dassau E, Doyle FJ., III Periodic zone- MPC with asymmetric costs for outpatient-ready safety of an artificial pancreas to treat type 1 diabetes. Automatica. 2016;71:237–246. doi: 10.1016/j.automatica.2016.04.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Gondhalekar R, Dassau E, Doyle FJ., III Moving-horizon-like state estimation via continuous glucose monitor feedback in MPC of an artificial pancreas for Type 1 Diabetes. Proc 53rd IEEE Conf on Dec and Cont, (CDC) 2014:310–315. doi: 10.1109/CDC.2014.7039399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Knab TD, Clermont G, Parker RS. Zone model predictive control and moving horizon estimation for the regulation of blood glucose in critical care patients. 9th IFAC Symposium on Adv Control of Chem Processes ADCHEM 2015. 2015;48(8):1002–1007. [Google Scholar]
- 33.Gillis R, Palerm CC, Zisser H, Jovanovic L, Seborg DE, Doyle FJ., III Glucose estimation and prediction through meal responses using ambulatory subject data for advisory mode model predictive control. Journal of Diabetes Science and Technology. 2007;1(6):825–833. doi: 10.1177/193229680700100605. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Maahs DM, Calhoun P, et al. A randomized trial of a home system to reduce nocturnal hypoglycemia in Type 1 Diabetes. Diabetes Care. 2014;37(7):1885–1891. doi: 10.2337/dc13-2159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Ellingsen C, Dassau E, Zisser H, Grosman B, Percival MW, Jovanovič L, Doyle FJ., III Safety Constraints in an Artificial Pancreatic β-cell: an implementation of model predictive control with insulin on board. Journal of Diabetes Science and Technology. 2009;3(3):536–544. doi: 10.1177/193229680900300319. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Magni L, Raimondo DM, Dalla Man C, De Nicolao G, Kovatchev B, Cobelli C. Model predictive control of glucose concentration in Type 1 Diabetic patients: An in silico trial. Biomedical Signal Processing and Control. 2009;4(4):338–346. [Google Scholar]
- 37.Wang Y, Dassau E, Zisser H, Jovanovič L, Doyle FJ., III Automatic bolus and adaptive basal algorithm for the artificial pancreatic β-cell. Diabetes Technology and Therapeutics. 2010;12(11):879–887. doi: 10.1089/dia.2010.0029. [DOI] [PubMed] [Google Scholar]
- 38.Grosman B, Dassau E, Zisser HC, Jovanovič L, Doyle FJ., III Zone model predictive control: a strategy to minimize hyper- and hypoglycemic events. Journal of Diabetes Science and Technology. 2010;4(4):961–975. doi: 10.1177/193229681000400428. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Breton M, Farret A, et al. Fully integrated artificial pancreas in Type 1 Diabetes: Modular closed-loop glucose control maintains near normoglycemia. Diabetes. 2012;61(9):2230–2237. doi: 10.2337/db11-1445. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Lee JB, Dassau E, Gondhalekar R, Seborg DE, Pinsker JE, Doyle FJ., III An Enhanced MPC (eMPC) Strategy for Automated Glucose Control. Industrial & Engineering Chemistry Research. 2016;55(46):11 857–11 868. doi: 10.1021/acs.iecr.6b02718. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Toffanin C, Messori M, Di Palma F, De Nicolao G, Cobelli C, Magni L. Artificial pancreas: model predictive control design from clinical experience. Journal of Diabetes Science and Technology. 2013;7(6):1470–1483. doi: 10.1177/193229681300700607. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Patek SD, Magni L, et al. Modular Closed-Loop Control of Diabetes. IEEE Transactions on Biomedical Engineering. 2012;59(11):2986–2999. doi: 10.1109/TBME.2012.2192930. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Dassau E, Cameron F, Lee H, et al. Real-time hypoglycemia prediction suite using continuous glucose monitoring a safety net for the artificial pancreas. Diabetes Care. 2010;33(6):1249–1254. doi: 10.2337/dc09-1487. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Dassau E, Brown SA, et al. Adjustment of open-loop settings to improve closed-loop results in Type 1 Diabetes: A multicenter randomized trial. Journal of Clinical Endocrinology and Metabolism. 2015;100(10):3878–3886. doi: 10.1210/jc.2015-2081. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Kovatchev BP, Breton M, Dalla Man C, Cobelli C. In Silico Preclinical Trials: A Proof of Concept in Closed-Loop Control of Type 1 Diabetes. Journal of Diabetes Science and Technology. 2009;3(1):44–55. doi: 10.1177/193229680900300106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Andersen M, Dahl J, Liu Z, Vandenberghe L. Interior-point methods for large-scale cone programming. Optimization for Machine Learning. 2011:55–83. [Google Scholar]
- 47.Maahs DM, Buckingham BA, et al. Outcome Measures for Artificial Pancreas Clinical Trials: A Consensus Report. Diabetes Care. 2016;39:1175–1179. doi: 10.2337/dc15-2716. [DOI] [PMC free article] [PubMed] [Google Scholar]


