A Semiparametric Single-Index Risk Score Across Populations

Abstract

We consider a problem motivated by issues in nutritional epidemiology, across diseases and populations. In this area, it is becoming increasingly common for diseases to be modeled by a single diet score, such as the Healthy Eating Index, the Mediterranean Diet Score, etc. For each disease and for each population, a partially linear single-index model is fit. The partially linear aspect of the problem is allowed to differ in each population and disease. However, and crucially, the single-index itself, having to do with the diet score, is common to all diseases and populations, and the nonparametrically estimated functions of the single-index are the same up to a scale parameter. Using B-splines with an increasing number of knots, we develop a method to solve the problem, and display its asymptotic theory. An application to the NIH-AARP Study of Diet and Health is described, where we show the advantages of using multiple diseases and populations simultaneously rather than one at a time in understanding the effect of increased Milk consumption. Simulations illustrate the properties of the methods.

1 Introduction

We describe a novel partially linear logistic single index model in which there are multiple populations, and multiple diseases within each population, but where the single index part of the model is shared across the populations and diseases. In the case of a single disease across independent populations, we derive B-spline based semiparametric efficient methodology. In other cases, such as multiple populations with multiple diseases, our B-spline based methods are consistent and we derive their asymptotic theory.

The problem arises from common practice in nutritional epidemiology, where the goal is to relate nutritional intakes to disease. In this area, it is increasingly common to relate the patterns of multiple dietary components, rather than an individual dietary component, to a disease. One popular way to summarize dietary intake patterns is through a dietary pattern score. While there are many avors of dietary pattern scores, in our example we use the U.S. Department of Agriculture’s (USDA’s) Healthy Eating Index-2005 (HEI-2005, http://www.cnpp.usda.gov/HealthyEatingIndex.htm). It is based on the key recommendations of the 2005 Dietary Guidelines for Americans available at http://www.health.gov/dietaryguidelines/dga2005/document/default.htm. The HEI-2005 comprises 12 distinct component scores. Intakes of each food or nutrient, represented by one of the 12 components, are expressed as a ratio to energy (caloric) intake, assessed, and given a score. See Table 1 for a list of these components and the standards for scoring, and see Guenther et al. (2008) and Guenther et al. (2008) for details. The 12 different component scores are then summed to get a total score, ranging from 0 for a terrible diet to 100 for the best possible diet.

Table 1.

Description of the HEI-2005 scoring system. Except for saturated fat and SoFAAS, density is obtained by multiplying intake by 1000 and dividing by intake of kilo-calories. For saturated fat, density is 9 × 100 saturated fat (grams) divided by calories, i.e., the percentage of calories coming from saturated fat intake. For SoFAAS, the density is the percentage of intake that comes from intake of calories, i.e., the division of intake of SoFAAS by intake of calories. Here, “DOL” is dark green and orange vegetables and legumes. Also, “SoFAAS” is calories from solid fats, alcoholic beverages and added sugars. The total HEI-2005 score is the sum of the individual component scores.

Component	Units	HEI-2005 score calculation
Total Fruit	cups	min {5, 5 × (density/.8)}
Whole Fruit	cups	min {5, 5 × (density/.4)}
Total Vegetables	cups	min {5, 5 × (density/1.1)}
DOL	cups	min {5, 5 × (density/.4)}
Total Grains	ounces	min {5, 5 × (density/3)}
Whole Grains	ounces	min {5, 5 × (density/1.5)}
Milk	cups	min {10, 10 × (density/1.3)}
Meat and Beans	ounces	min {10, 10 × (density/2.5)}
Oil	grams	min {10, 10 × (density/12)}
Saturated Fat	% of	if density ≥ 15 score = 0
	energy	else if density ≤ 7 score = 10
		else if density > 10 score = 8 − {8 × (density − 10)/5}
		else, score = 10 − {2 × (density − 7)/3}
Sodium	milligrams	if density ≥ 2000 score=0
		else if density ≤ 700 score=10
		else if density ≥ 1100 score = 8 − {8 × (density − 1100)/(2000 − 1100)}
		else score = 10 − {2 × (density − 700)/(1100 − 700)}
SoFAAS	% of	if density ≥ 50 score = 0
	energy	else if density ≤ 20 score=20
		else score = 20 − {20 × (density − 20)/(50 − 20)}

The key concept here is that the total score is developed before any health outcome data are considered. Once a total score is developed, it is then used, across multiple populations, in risk models to relate any disease to the total score. As an example, Panagiotakos et al. (2006) show that for colorectal cancer in the NIH-AARP Study of Diet and Health (Schatzkin et al., 2001), with diet assessed by a food frequency questionnaire, higher HEI-2005 total scores are statistically significantly associated with lower disease risks. They also consider three other dietary pattern scores. George et al. (2010) show that among breast cancer survivors, higher HEI-2005 total scores are associated with lower levels of chronic inflammation. Chiuve et al. (2012) show that the HEI-2005 total score and the Alternative Healthy Eating Index (AHEI) (McCullough et al., 2002) are significant predictors of chronic diseases such as coronary heart disease, diabetes, stroke and cancer, and that closer adherence to the 2005 Dietary Guidelines may lower the risk of major chronic diseases. The AHEI is also associated with all cause mortality (Akbaraly et al., 2011).

In its most general form, there are k = 1, …, K populations. Within population k, there are ℓ = 1, …, L_k diseases. As in the HEI-2005, there are j = 0, …, J dietary components. Let the J + 1 individual component scores in population k be (X_0k, …, X_Jk): in our case, J + 1 = 12. Then the current practice in nutritional epidemiology would be to form a total score ${\sum }_{j=0}^J{X}_{\mathit{\text{jk}}}$ for population k and use it as the risk predictor for all populations/diseases. Thus, for example, in a logistic regression with a binary outcome Y_kℓ, and with H(·) being the logistic distribution function, the model for population k and disease ℓ is

$$\text{pr}(Y_{k\ell }=1|X_{0k},\dots ,X_{\mathit{\text{Jk}}})=H({\beta }_{0k\ell }+{\beta }_{1k\ell }{\sum }_{j=0}^J{X}_{\mathit{\text{jk}}}).$$ (1)

This is important and convenient from a public health perspective, because it enables nutritional epidemiologists to use the same predictor, namely ${\sum }_{j=0}^J{X}_{\mathit{\text{jk}}}$, for all diseases, and to describe the effect of that predictor through a single quantity, β_1kℓ.

Crucially, it is undesirable to try to fit different parameters for each component score. That is, instead of fitting (1), one might fit

$$\text{pr}(Y_{k\ell }=1|X_{0k},\dots ,X_{\mathit{\text{Jk}}})=H({\beta }_{0k\ell }+{\sum }_{j=0}^J{\beta }_{\mathit{\text{jk}}\ell }{X}_{\mathit{\text{jk}}}).$$ (2)

The reason why (1) is preferred to (2) for public health purposes is that it is much more interpretable. Model (1) describes how a single, interpretable score, ${\sum }_{j=0}^J{X}_{\mathit{\text{jk}}}$, affects disease risk. Model (2) is chaotic because it requires policy makers to say things such as “if you are in population k = 1 and are worried about disease ℓ = 1 then your diet improves your risk if you eat this kind of food more and that kind of food less, but for disease ℓ = 2 you need to consider your dietary composition in another way”. Interpretability is even more complicated because the component scores have a reasonably complex pattern of correlations, see Table S.1 of the Supplementary Material. Since there are so many diseases and populations, this is not helpful practically and would not be used. Indeed, as seen above, the single HEI-2005 score is associated with colon cancer (Reedy et al., 2008), chronic inflammation, (George et al., 2010) and many chronic diseases (Chiuve et al., 2012), and its ease of interpretation is apparent.

Our goal is to develop a single interpretable score that, unlike the HEI-2005 score or other scores, is calibrated to different populations or diseases. We do this not by summing the component scores, but by weighting them and allowing a more flexible shape. Thus, for an unknown function m(·) and weights (α₀, …, α_J), we propose the single-index score $m({\sum }_{j=0}^J{X}_{\mathit{\text{jk}}}{\alpha }_j)$, and model the risk as

$$\text{pr}(Y_{k\ell }=1|X_{0k},\dots ,X_{\mathit{\text{Jk}}})=H\{{\beta }_{0k\ell }+{\beta }_{1k\ell }m({\sum }_{j=0}^J{X}_{\mathit{\text{jk}}}{\alpha }_j)\}.$$ (3)

Model (3), like model (1), is based upon a single interpretable score, $m({\sum }_{j=0}^J{X}_{\mathit{\text{jk}}}{\alpha }_j)$, that can be used across populations and/or diseases.

In Section 2, we present our model more formally. Section 3 describes how to fit the model for a single disease across independent populations, and we show that our method is semiparametric efficient in this case. In Section 4 we describe generalizations. Section 4.1 considers a single population with multiple diseases, while Section 4.2 describes the real goal of our data analysis, where there are multiple populations and multiple diseases. Section 5 gives results of the data example, while Section 6 describes simulation results. Computational and technical details are in an Appendix and in Supplementary Material.

2 Multiple Population Single-Index Model

2.1 Model and Splines

In this section, we consider a single disease across multiple different populations. There are k = 1, …, K populations. For the k^th population, there are i = 1, …, n_k individuals with binary responses Y_ik. Define X_ik = (X_ik1, …, X_ikJ)^T. In addition to the responses, for individual i in population k we observe (G_ik, X_ik0, X_ik, Z_ik, G_ikW_ik), defined as follows. The J + 1 dietary component scores are ${(X_{\mathit{\text{ik}}0},X_{\mathit{\text{ik}}}^{\mathrm{T}})}^{\mathrm{T}}$. Covariates that are observed for all individuals are Z_ik = (Z_ik1, …, Z_ikd)^T. Further, we allow for a subset of individuals to have additional covariates W_ik = (W_ik1, …, W_ika)^T, and define G_ik to be the binary indicator that these individuals have such additional covariates. For example, Reedy et al. (2008) fit models to men and women with many common covariates such as age and levels of educational status, but for women they in addition include indicators of types of hormone replacement therapy.

For the i^th individual and the k^th outcome, we posit the marginal model

$$\text{pr}(Y_{\mathit{\text{ik}}}=1|G_{\mathit{\text{ik}}},X_{\mathit{\text{ik}}0},X_{\mathit{\text{ik}}},Z_{\mathit{\text{ik}}},G_{\mathit{\text{ik}}}{W}_{\mathit{\text{ik}}})=H_{\mathit{\text{ik}}}=H\{({\beta }_{k1}+{\beta }_{k2}{G}_{\mathit{\text{ik}}})m(X_{\mathit{\text{ik}}0}+X_{\mathit{\text{ik}}}^{\mathrm{T}}\alpha )+Z_{\mathit{\text{ik}}}^{\mathrm{T}}({\theta }_{k1}+{\theta }_{k2}{G}_{\mathit{\text{ik}}})+G_{\mathit{\text{ik}}}{W}_{\mathit{\text{ik}}}^{\mathrm{T}}{\theta }_{k3}\}.$$ (4)

Here α ∈ ℝ^J, θ_k1 ∈ ℝ^d, θ_k2 ∈ ℝ^d, θ_k3 ∈ ℝ^a, β_k1 ∈ ℝ and β_k2 ∈ ℝ. Crucially, for use in practice, the function m(·) and the parameter α do not depend on k.

Remark 1

In model (4), the most general form of the single-index is $m(X_{\mathit{\text{ik}}0}{\alpha }_0+X_{\mathit{\text{ik}}}^{\mathrm{T}}\alpha )$. However, because m(·) is modeled nonparametrically, such a formulation is not identifiable. There are three equivalent ways to obtain identifiability. The first common method, what we have done, is to select one variable that is known to be related to the response, which we label as X_ik0, and to set its parameter α₀ = 1. A second common method is to make the restriction that ${\alpha }_0^2+{\alpha }^{\mathrm{T}}\alpha =1$. In the context of our problem, there is a third way. Since common nutritional epidemiology practice is to weight each variable the same, namely = 1, the sum of the weights = J + 1. For comparison purposes, we can achieve identifiability via the restriction α₀ + (1, …, 1)α = J + 1. We use the first method in our computations, but report results for the third.

Model (4) generalizes the now-classical generalized partially linear single-index model (Carroll et al., 1997), with the novelty being both the context and that the same single-index $m(X_{\mathit{\text{ik}}0}+X_{\mathit{\text{ik}}}^{\mathrm{T}}\alpha )$ is used across multiple outcomes.

Single-index models have been widely used as a popular tool in multivariate nonparametric regression to alleviate the “curse of dimensionality” (Bellman, 1961). For example, recently Yu and Ruppert (2002) used penalized spline least squares estimation for single-index models with independent and identically distributed observations: their number of knots was fixed, unlike in our development. Wang and Yang (2009a) proposed polynomial spline estimation and extended the results to weakly dependent response variables. Cui et al. (2011) developed a kernel estimating function method for generalized single-index models, while Ma and Zhu (2013) constructed robust and efficient estimation with high dimensional covariates. These papers are restricted to the case of one population, K = 1, and one outcome, L = 1. Here we consider multiple populations and multiple outcomes. We propose a regression spline based profile estimation procedure and establish the asymptotic properties of the estimators in model (4).

To set the main ideas clearly, it is convenient to first assume that the Y_ik are independent, see Section 4 for the more general cases of interest in the HEI-2005 problem. To ensure identifiability, we set β₁₁ = −1, and we set the first component of θ₁₁ = (θ₁₁₁, …, θ_11d) equal to zero, i.e., θ₁₁₁ = 0. Hence, our parameters are (ν, m), where m is an unspecified function that is sufficiently smooth, while

$$\nu ={({\alpha }^{\mathrm{T}},{\beta }_{12},{\beta }_{21},{\beta }_{22},\dots ,{\beta }_{K1},{\beta }_{K2},{\theta }_{112},\dots ,{\theta }_{11d},{\theta }_{12}^{\mathrm{T}},{\theta }_{13}^{\mathrm{T}},{\theta }_{21}^{\mathrm{T}},{\theta }_{22}^{\mathrm{T}},{\theta }_{23}^{\mathrm{T}},\dots ,{\theta }_{K1}^{\mathrm{T}},{\theta }_{K2}^{\mathrm{T}},{\theta }_{K3}^{\mathrm{T}})}^{\mathrm{T}}.$$

Thus, ν has total dimension d_ν = J + 2K + 2Kd + Ka − 2.

Let $U_{\mathit{\text{ik}}}(\alpha )=X_{\mathit{\text{ik}}0}+X_{\mathit{\text{ik}}}^{\mathrm{T}}\alpha$ be the realizations of $U_k(\alpha )=X_{k0}+X_k^{\mathrm{T}}\alpha$. The unknown function m(·) is estimated by polynomial splines described as follows. Without loss of generality, assume u ∈ [a, b]. Let N = N_n be the number of interior knots. Divide [a, b] into (N + 1) subintervals I_p = {(ξ_p, ξ_p+1), p = r, r + 1, …, N + r − 1}, I_N = (ξ_N+r, 1), where ${({\xi }_p)}_{p=r+1}^{N+r}$ is a sequence of interior knots, given as

$${\xi }_1=\cdots =a={\xi }_r<{\xi }_{(r+1)}<\cdots {\xi }_{(r+N)}<b={\xi }_{N+r+1}=\cdots ={\xi }_{N+2r}.$$

Define the distance between neighboring knots as h_p = ξ_p+1 − ξ_p, r ≤ p ≤ N + r, and h = max_r≤p≤N+r h_p. Let G_n be the space of B-splines of order r, so that P_n = N + r is the number of functions in G_n. For u ∈ [a, b], let G_n be the linear space spanned by the B-spline functions B_r(u) = {B_r,p(u), 1 ≤ p ≤ P_n}^T. Then m(u) can be approximated by $\stackrel{\sim }{m}(u)={\sum }_{p=1}^{P_n}{B}_{r,p}(u){\lambda }_p=B_r^{\mathrm{T}}(u)\lambda$, where λ = (λ₁, …, λ_Pn)^T. B-splines have been used frequently to estimate the nonparametric functions in nonparametric and semiparametric models because they are easy to compute with derivable asymptotic theory. See Huang (2003) and Wang and Yang (2009b) for their utility in nonparametric models, Stone (1985) and Huang and Yang (2004) in additive models, and Huang et al. (2002), Liu et al. (2011) and Wang et al. (2011) in semiparametric models.

3 Profile Estimating Procedure

Our estimation is performed through a conceptually simple profiling procedure, as described below.

Step 1

Define

$${\stackrel{\sim }{H}}_{\mathit{\text{ik}}}=H[({\beta }_{k1}+{\beta }_{k2}{G}_{\mathit{\text{ik}}})B_r^{\mathrm{T}}\{U_{\mathit{\text{ik}}}(\alpha )\}\lambda +Z_{\mathit{\text{ik}}}^{\mathrm{T}}({\theta }_{k1}+{\theta }_{k2}{G}_{\mathit{\text{ik}}})+G_{\mathit{\text{ik}}}{W}_{\mathit{\text{ik}}}^{\mathrm{T}}{\theta }_{k3}].$$

Treating ν as a fixed parameter, estimate m(u) by spline functions $\hat{m}(u,\nu )={\sum }_{p=1}^{P_n}{B}_{r,p}(u){\hat{\lambda }}_p(\nu )$ with λ̂(ν) = {λ̂₁(ν), ⋯, λ̂_Pn(ν)}^T through maximizing

$$L_n(\lambda ,\nu )={\sum }_{k=1}^K{\sum }_{i=1}^{n_k}\{Y_{\mathit{\text{ik}}}\text{log}({\stackrel{\sim }{H}}_{\mathit{\text{ik}}})+(1-Y_{\mathit{\text{ik}}})\text{log}(1-{\stackrel{\sim }{H}}_{\mathit{\text{ik}}})\}.$$ (5)

To prepare for the second step, we perform the following additional calculations. Let B_r−1(u) = {B_r−1,p(u) : 2 ≤ p ≤ P_n}^T be the B-spline functions of order r − 1. We estimate m′(u, ν), the first derivative of m, through $\hat{m}\prime (u,\nu )={\sum }_{p=2}^{P_n}{B}_{r-1,p}(u){\hat{\lambda }}_p^{(1)}(\nu )$, where ${\hat{\lambda }}_p^{(1)}(\nu )=(r-1)\{{\hat{\lambda }}_p(\nu )-{\hat{\lambda }}_{p-1}(\nu )\}/({\xi }_{p+r-1}-{\xi }_p)$, for 2 ≤ p ≤ P_n. This is because the first derivative of a spline function can be expressed in terms of a spline of one order lower see page 116 of de Boor (2001). Let D = (d_jj′)_{1≤j,j′≤Pn−1} be a (P_n − 1) × (P_n − 1) diagonal matrix with d_jj = 1/(ξ_j+r − ξ_j+1) and d_jj′ = 0 for j ≠ j′, and let D₁₁ = (−D, 0_Pn−1)_(Pn−1)×Pn and D₁₂ = (0_Pn−1, D)_(Pn−1)×Pn, where 0_Pn−1 is the (P_n − 1)-dimensional vector with 0’s as its elements. Then $\hat{m}\prime (u,\nu )=B_{r-1}^{\mathrm{T}}(u)D_1\hat{\lambda }(\nu )$, where D₁ = (r − 1) (D₁₁ + D₁₂). For u ∈ [a, b], define

$${\hat{\sigma }}^2(u,\nu )=B_r^{\mathrm{T}}(u){[{\sum }_{k=1}^K{\sum }_{i=1}^{n_k}{V}_{\mathit{\text{ik}}}(\nu ){({\beta }_{k1}+{\beta }_{k2}{G}_{\mathit{\text{ik}}})}^2{B}_r\{U_{\mathit{\text{ik}}}(\alpha )\}{B}_r{\{U_{\mathit{\text{ik}}}(\alpha )\}}^{\mathrm{T}}]}^{-1}{B}_r(u),$$ (6)

where V_ik(ν) = H_ik(ν)(1 − H_ik(ν)), and

$$H_{\mathit{\text{ik}}}(\nu )=H\{({\beta }_{k1}+{\beta }_{k2}{G}_{\mathit{\text{ik}}})m(X_{\mathit{\text{ik}}0}+X_{\mathit{\text{ik}}}^{\mathrm{T}}\alpha )+Z_{\mathit{\text{ik}}}^{\mathrm{T}}({\theta }_{k1}+{\theta }_{k2}{G}_{\mathit{\text{ik}}})+G_{\mathit{\text{ik}}}{W}_{\mathit{\text{ik}}}^{\mathrm{T}}{\theta }_{k3}\}.$$

Step 2

Define

$${\hat{H}}_{\mathit{\text{ik}}}(\nu )=H\{({\beta }_{k1}+{\beta }_{k2}{G}_{\mathit{\text{ik}}})B_r^{\mathrm{T}}(U_{\mathit{\text{ik}}}(\alpha ))\hat{\lambda }(\nu )+Z_{\mathit{\text{ik}}}^{\mathrm{T}}({\theta }_{k1}+{\theta }_{k2}{G}_{\mathit{\text{ik}}})+G_{\mathit{\text{ik}}}{W}_{\mathit{\text{ik}}}^{\mathrm{T}}{\theta }_{k3}\}.$$ (7)

Estimate ν by ν̂ through maximizing

$$L_n(\nu )={\sum }_{k=1}^K{\sum }_{i=1}^{n_k}[Y_{\mathit{\text{ik}}}\text{log}\{{\hat{H}}_{\mathit{\text{ik}}}(\nu )\}+(1-Y_{\mathit{\text{ik}}})\text{log}\{1-{\hat{H}}_{\mathit{\text{ik}}}(\nu )\}].$$

Once we obtain ν̂, we can plug it into m̂ to obtain ν̂, m̂(u, ν̂) as the final estimator. To prepare the description of the asymptotic properties of our procedure, we define

$$Q_{i1}(\nu )=\{{(-1+{\beta }_{12}{G}_{i1})m\prime (X_{i10}+X_{i1}^{\mathrm{T}}\alpha )X_{i1}^{\mathrm{T}},G_{i1}m(X_{i10}+X_{i1}^{\mathrm{T}}\alpha ),0_{1,2K-2},Z_{1i2},\cdots ,Z_{i1d},G_{i1}{Z}_{i1}^{\mathrm{T}},G_{i1}{W}_{i1}^{\mathrm{T}},0_{1,(K-1)(2d+a)}\}}^{\mathrm{T}},$$

and for k = 2, …, K define

$$Q_{\mathit{\text{ik}}}(\nu )={\{({\beta }_{k1}+{\beta }_{k2}{G}_{\mathit{\text{ik}}})m\prime (X_{\mathit{\text{ik}}0}+X_{\mathit{\text{ik}}}^{\mathrm{T}}\alpha )X_{\mathit{\text{ik}}}^{\mathrm{T}},0_{1,2k-3},m(X_{\mathit{\text{ik}}0}+X_{\mathit{\text{ik}}}^{\mathrm{T}}\alpha ),G_{\mathit{\text{ik}}}m(X_{\mathit{\text{ik}}0}+X_{\mathit{\text{ik}}}^{\mathrm{T}}\alpha ),0_{1,2K-2k+(k-1)(2d+a)-1},Z_{\mathit{\text{ik}}}^{\mathrm{T}},G_{\mathit{\text{ik}}}{Z}_{\mathit{\text{ik}}}^{\mathrm{T}},G_{\mathit{\text{ik}}}{W}_{\mathit{\text{ik}}}^{\mathrm{T}},0_{1,(K-k)(2d+a)}\}}^{\mathrm{T}}.$$

Denote the elements of $Q_{\mathit{\text{ik}}}(\nu )={(Q_{\mathit{\text{ik}},\ell }(\nu ))}_{l=1}^{d_{\nu }}$. Let

$${\nu }^0={({\alpha }^{0\mathrm{T}},{\beta }_{12}^0,{\beta }_{21}^0,{\beta }_{22}^0,\dots ,{\beta }_{K1}^0,{\beta }_{K2}^0,{\theta }_{112}^0,\dots ,{\theta }_{11d}^0,{\theta }_{12}^{0\mathrm{T}},{\theta }_{13}^{0\mathrm{T}},{\theta }_{21}^{0\mathrm{T}},{\theta }_{22}^{0\mathrm{T}},{\theta }_{23}^{0\mathrm{T}},\dots ,{\theta }_{K1}^{0\mathrm{T}},{\theta }_{K2}^{0\mathrm{T}},{\theta }_{K3}^{0\mathrm{T}})}^{\mathrm{T}}$$

be the collection of the true parameters. Let [a₀, b₀] be the support of $X_{k0}+X_k^{\mathrm{T}}{\alpha }^0$, where α⁰ is the true population parameter. Denote ‖·‖ as the L₂ norm of any square integrable function on [a₀, b₀]. For 1 ≤ ℓ ≤ d_ν, let ${\eta }_{\ell }^0(·)$ be the function η_ℓ(·) ∈L₂([a₀, b₀]) that minimizes $E[{\sum }_{k=1}^K{n}_k{\{Q_{\mathit{\text{ik}},\ell }({\nu }^0)-({\beta }_{k1}^0+{\beta }_{k2}^0{G}_{\mathit{\text{ik}}}){\eta }_{\ell }(U_{\mathit{\text{ik}}}({\alpha }^0))\}}^2{V}_{\mathit{\text{ik}}}]$. Also, define ${\eta }^0\{U_{\mathit{\text{ik}}}(\alpha )\}={\{{\eta }_1^0\{U_{\mathit{\text{ik}}}(\alpha )\},\dots ,{\eta }_{d_{\nu }}^0\{U_{\mathit{\text{ik}}}(\alpha )\}]}^{\mathrm{T}}$. For simplicity of notations, we let V_ik = V_ik(ν⁰), Q_ik = Q_ik(ν⁰) and U_ik = U_ik(α⁰). Let $n={\sum }_{k=1}^K{n}_k$.

In the following three theorems, we establish the consistency, asymptotic normality and efficiency of our procedure.

Theorem 1

Under the conditions in Appendix A.2, when ν is the collection of the true parameters or a $\sqrt{n}$-consistent estimator of ν⁰, (a) |m̂(u, ν) − m(u)| = O_p{(nh)^−1/2 + h^q} uniformly in u ∈ [a₀, b₀]; (b) |m̂′(u, ν) − m′(u)| = O_p(n^−1/2h^−3/2 + h^q−1) uniformly in u ∈ [a₀, b₀]; and (c) as n → ∞, σ̂⁻¹(u, ν⁰) {m̂(u, ν) − m(u)} → Normal(0, 1).

Theorem 2

Define n = n₁ and for k = 2, …, K, define n_k = nc_kn, where there are constants c_* > 0 and c_** < ∞ such that c_* ≤ c_k = lim_n→1 c_kn ≤ c_**. Under the conditions in Appendix A.2, ‖ν̂ − ν⁰‖₂ = O_p (n^−1/2), and

$$n^{1/2}(\hat{\nu }-{\nu }^0)={[n^{-1}{\sum }_{k=1}^K{\sum }_{i=1}^{n_k}{H}_{\mathit{\text{ik}}}(1-H_{\mathit{\text{ik}}}){(Q_{\mathit{\text{ik}}}-({\beta }_{k1}^0+{\beta }_{k2}^0{G}_{\mathit{\text{ik}}}){\eta }^0(U_{\mathit{\text{ik}}}))}^{\otimes 2}]}^{-1}\times [n^{-1/2}{\sum }_{k=1}^K{\sum }_{i=1}^{n_k}(Y_{\mathit{\text{ik}}}-H_{\mathit{\text{ik}}})\{Q_{\mathit{\text{ik}}}-({\beta }_{k1}^0+{\beta }_{k2}^0{G}_{\mathit{\text{ik}}}){\eta }^0(U_{\mathit{\text{ik}}})\}]+o_p(1),$$ (8)

for ν̂ in a neighborhood of ν⁰. Then as n → ∞, n^1/2(ν̂ − ν⁰) → Normal(0_dν, Σ), where

$$\mathbf{\sum }={({\sum }_{k=1}^K{c}_{k}E[V_{\mathit{\text{ik}}}{\{Q_{\mathit{\text{ik}}}-({\beta }_{k1}^0+{\beta }_{k2}^0{G}_{\mathit{\text{ik}}}){\eta }^0(U_{\mathit{\text{ik}}})\}}^{\otimes 2}])}^{-1},$$

and 0_dν is a d_ν-dimensional vector with “0” as its elements. Here and throughout the text, a^⊗2 ≡ aa^T for any matrix or vector a.

In practice, Σ is estimated by

$$\hat{\mathbf{\sum }}=n{({\sum }_{k=1}^K{\sum }_{i=1}^{n_k}[{\hat{V}}_{\mathit{\text{ik}}}{(Q_{\mathit{\text{ik}}}(\hat{\nu })-{\hat{\mathrm{\Pi }}}_n{Q}_{\mathit{\text{ik}}}(\hat{\nu }))}^{\otimes 2}])}^{-1},$$

where V̂_ik = Ĥ_ik(ν̂)(1 − Ĥ_ik(ν̂)), Π̂_nQ_ik(ν̂) = (Π̂_nQ_ik,ℓ(ν̂), 1 ≤ ℓ ≤ d_ν)^T, and for 1 ≤ l ≤ d_ν, ${\hat{\mathrm{\Pi }}}_n{Q}_{\mathit{\text{ik}},\ell }(\hat{\nu })=({\hat{\beta }}_{k1}+{\hat{\beta }}_{k2}{G}_{\mathit{\text{ik}}})B_r^{\mathrm{T}}(U_{\mathit{\text{ik}}}(\hat{\alpha })){\hat{\delta }}_{\ell }$, where

$${\hat{\delta }}_{\ell }=\text{arg }\underset{{\delta }_{\ell }\in R^{P_n}}{\text{min}}{\sum }_{k=1}^K{\sum }_{i=1}^{n_k}{\{Q_{\mathit{\text{ik}},\ell }(\hat{\nu })-(({\hat{\beta }}_{k1}+{\hat{\beta }}_{k2}{G}_i)B_r^{\mathrm{T}}(U_{\mathit{\text{ik}}}(\hat{\alpha }))\delta \}}^2{\hat{V}}_{\mathit{\text{ik}}}.$$

In addition, under the assumption of independence, or conditional independence of the Y_ik given the covariates, our estimation method is semiparametric efficient. We state this as

Theorem 3

Under the conditions in Appendix A.2, profile likelihood estimation of the parameter ν reaches the semiparametric efficiency bound. The minimum variance bound for estimating ν can be further simplified to

$${\mathit{\text{cov}}}_{\text{opt}}\{n^{1/2}(\hat{\nu }-{\nu }^0)\}={\left\{E\right({\sum }_{k=1}^K{c}_k{V}_{\mathit{\text{ik}}}[Q_{\mathit{\text{ik}}}{Q}_{\mathit{\text{ik}}}^{\mathrm{T}}-{({\beta }_{k1}^0+{\beta }_{k2}^0{G}_{\mathit{\text{ik}}})}^2{\{{\eta }^0(U_{\mathit{\text{ik}}})\}}^{\otimes 2}]\left)\right\}}^{-1}.$$

The proofs of the theorems are given in the Appendix.

4 Generalizations

4.1 Single Population, Multiple Diseases

In this section, we relax the assumption of independence of the Y_ik given the covariates, and consider the case of a single population with K outcomes, with a common sample size n. The response indicators remain as (Y_i1, …, Y_iK), but now the covariates are the same for each response, and are written as ℂ_i = (G_i, X_i0, X_i, Z_i, G_iW_i), and now we use $U_i(\alpha )=X_{i0}+X_i^{\mathrm{T}}\alpha$. Ignoring this correlation and invoking a “working independence” principle, the profile likelihood procedure described in Section 3 will still provide consistent estimation. However, more efficient estimation can be generally obtained through taking into account the correlation structure.

Specifically, the derivative of Y_iklog(H̃_ik) + (1 − Y_ik)log(1 − H̃_ik) with respect to λ is (Y_ik − H̃_ik)(β_k1 + β_k2G_i)B_r(U_i(α)). Translated to the setting of this section, Step 1 in Section 3 is equivalent to solving

$${\sum }_{k=1}^K{\sum }_{i=1}^{n_k}(Y_{\mathit{\text{ik}}}-{\stackrel{\sim }{H}}_{\mathit{\text{ik}}})({\beta }_{k1}+{\beta }_{k2}{G}_i)B_r(U_i(\alpha ))=0.$$

Here, we modify this step to

Step 1d

Let ${\mathrm{\Omega }}_i={({\mathrm{\Omega }}_{i,k,k\prime })}_{k,k\prime =1}^K$ represent a working covariance matrix of (Y_i1, …, Y_iK) conditional on ℂ_i. Let B_i(ν) be a K × K matrix with the (k, k′) entry B_i,k,k′ (ν) = Ω_i,k,k′ (β_k1 + β_k2G_i)(β_k′1 + β_k′2G_i). Obtain λ̂_w(ν) by solving ${\sum }_{i=1}^n{B}_r\{U_i(\alpha )\}{\stackrel{\sim }{\mathbf{A}}}_i(\nu ){\mathbf{B}}_i{(\nu )}^{-1}{\mathbf{\Phi }}_i(\nu )=0$ where

$${\mathbf{\Phi }}_i(\nu )={\{(Y_{i1}-{\stackrel{\sim }{H}}_{i1})({\beta }_{11}+{\beta }_{12}{G}_i),\dots ,(Y_{\mathit{\text{iK}}}-{\stackrel{\sim }{H}}_{\mathit{\text{iK}}})({\beta }_{K1}+{\beta }_{K2}{G}_i)\}}^{\mathrm{T}},$$

$${\stackrel{\sim }{\mathbf{A}}}_i(\nu )=\{{\stackrel{\sim }{V}}_{i1}{({\beta }_{11}+{\beta }_{12}{G}_i)}^2,\dots ,{\stackrel{\sim }{V}}_{\mathit{\text{ik}}}{({\beta }_{K1}+{\beta }_{K2}{G}_i)}^2\},$$

whereṼ_ik = H̃_ik(1 − H̃_ik).

Using λ̂_w(ν), we form the corresponding estimators of m(u) and m′(u), which are ${\hat{m}}_w(u,\nu )=B_r^{\mathrm{T}}(u){\hat{\lambda }}_w(\nu )$ and ${\hat{m}}_w^{\prime }(u,\nu )={\{B_r^{\prime }(u)\}}^{\mathrm{T}}{\hat{\lambda }}_w(\nu )$. Define A_i(ν) = {V_i1(β₁₁ + β₁₂G_i)², …, V_ik(β_K1 + β_K2G_i)²}. Let A_i = A_i(ν⁰) and B_i = B_i(ν⁰). For u ∈ [a, b], define ${\hat{\sigma }}_w^2(u,\nu )=B_r^{\mathrm{T}}(u){\mathrm{\Pi }}_n^{-1}{\mathrm{\Xi }}_n{\mathrm{\Pi }}_n^{-1}{B}_r(u)$, where

$${\mathrm{\Pi }}_n={\sum }_{i=1}^n{B}_r(U_i){\mathbf{A}}_i{\mathbf{B}}_i^{-1}{\mathbf{A}}_i^{\mathrm{T}}{B}_r{(U_i)}^{\mathrm{T}},$$

$${\mathrm{\Xi }}_n={\sum }_{i=1}^n{B}_r(U_i){\mathbf{A}}_i{\mathbf{B}}_i^{-1}{\mathbf{Q}}_i{\mathbf{B}}_i^{-1}{\mathbf{A}}_i^{\mathrm{T}}{B}_r{(U_i)}^{\mathrm{T}},$$

and where Q_i is a K × K matrix with the (k, k′) entry

$${\mathbf{Q}}_{i,k,k\prime }(\nu )=\{E(Y_{\mathit{\text{ik}}}{Y}_{\mathit{\text{ik}}\prime }|{ℂ}_i)-H_{\mathit{\text{ik}}}{H}_{\mathit{\text{ik}}\prime }\}({\beta }_{k1}^0+{\beta }_{k2}^0{G}_i)({\beta }_{k\prime 1}^0+{\beta }_{k\prime 2}^0{G}_i).$$

In the description above, Ω_i is a generic working covariance matrix. Here is how we implemented it. Let Ω_i be the conditional covariance matrix of Y_i = (Y_i1, …, Y_iK)^T given ℂ_i. Then the (k, k′) entry of Ω_i is Ω_i,k,k′ = E(Y_ikY_ik′ | ℂ_i) − H_ikH_ik′. In practice, we estimate Ω_i by ${\hat{\mathbf{\Omega }}}_i={\hat{\mathbf{V}}}_i^{1/2}\hat{\mathbf{R}}{\hat{\mathbf{V}}}_i^{1/2}$, where V̂_i is a K × K diagonal matrix with the k^th diagonal as Ĥ_ik(1 − Ĥ_ik) and $\hat{\mathbf{R}}=n^{-1}{\sum }_{i=1}^n{\hat{\mathbf{V}}}_i^{-1/2}({\mathbf{Y}}_i-{\hat{\mathbf{H}}}_i){({\mathbf{Y}}_i-{\hat{\mathbf{H}}}_i)}^{\mathrm{T}}{\hat{\mathbf{V}}}_i^{-1/2}$, where Ĥ_i = (Ĥ_i1, …, Ĥ_iK)^T and Ĥ_ik = Ĥ_ik(ν̂).

Similarly, the derivative of the (i, k) term in (7) with respect to ν is

$$(Y_{\mathit{\text{ik}}}-{\hat{H}}_{\mathit{\text{ik}}}(\nu ))\{{\hat{Q}}_{\mathit{\text{ik}}}(\nu )+({\beta }_{k1}+{\beta }_{k2}{G}_i){\{{\hat{\lambda }}_w^{\prime }(\nu )\}}^{\mathrm{T}}{B}_r(X_{i0}+X_i^{\mathrm{T}}\alpha )\},$$

where Ĥ_ik(ν) is the same as H̃_ik except that λ in H̃_ik is replaced by λ̂_w(ν) in Ĥ_ik(ν), and Q̂_ik(ν) is the same as Q_ik(ν) except that m(·), m′(·) in Q_ik(ν) are replaced by m̂_w(·, ν), ${\hat{m}}_w^{\prime }(·,\nu )$ in Q̂_ik, and ${\hat{\lambda }}_w^{\prime }(\nu )=\partial {\hat{\lambda }}_w(\nu )/\partial {\nu }^{\mathrm{T}}$ is the P_n × d_ν derivative matrix of λ̂_w(ν) with respect to ν. We thus modify Step 2 to

Step 2d

Let Ψ_i(ν) be the d_νK × 1 vector formed by K vectors, each of length d_ν, with the k^th, k = 1, …, K, vector being $(Y_{\mathit{\text{ik}}}-{\hat{H}}_{\mathit{\text{ik}}}(\nu ))\{{\hat{Q}}_{\mathit{\text{ik}}}(\nu )+({\beta }_{k1}+{\beta }_{k2}{G}_i){\{{\hat{\lambda }}_w^{\prime }(\nu )\}}^{\mathrm{T}}{B}_r(X_{i0}+X_i^{\mathrm{T}}\alpha )\}$. Obtain ν̂_w from solving ${\sum }_{i=1}^n{\hat{\mathbf{C}}}_i(\nu ){\hat{\mathbf{D}}}_i{(\nu )}^{-1}{\mathbf{\Psi }}_i(\nu )=0$, where Ĉ_i(ν) is a d_ν × d_νK matrix, with k^th block

$${\hat{\mathbf{C}}}_{i,k}(\nu )={\hat{V}}_{\mathit{\text{ik}}}(\nu ){\{{\hat{Q}}_{\mathit{\text{ik}}}(\nu )+({\beta }_{k1}+{\beta }_{k2}{G}_i){\hat{\lambda }}_w^{\prime }{(\nu )}^{\mathrm{T}}{B}_r(X_{i0}+X_i^{\mathrm{T}}\alpha )\}}^{\otimes 2},$$

where V̂_ik(ν) = Ĥ_ik(ν)(1 − Ĥ_ik(ν)) and D̂_i(ν) is a d_νK × d_νK matrix, with (k, k′) block

$${\hat{\mathbf{D}}}_{i,k,k\prime }(\nu )={\mathrm{\Omega }}_{i,k,k\prime }\{{\hat{Q}}_{\mathit{\text{ik}}}(\nu )+({\beta }_{k1}+{\beta }_{k2}{G}_i){\hat{\lambda }}_w^{\prime }{(\nu )}^{\mathrm{T}}{B}_r(X_{i0}+X_i^{\mathrm{T}}\alpha )\},\times {\{{\hat{Q}}_{ik\prime }(\nu )+({\beta }_{k\prime 1}+{\beta }_{k\prime 2}{G}_i){\hat{\lambda }}_w^{\prime }{(\nu )}^{\mathrm{T}}{B}_r(X_{i0}+X_i^{\mathrm{T}}\alpha )\}}^{\mathrm{T}},$$

and ${\hat{\lambda }}_w^{\prime }(\nu )$ can be obtained via numerical differentiation. Let β₁+β₂G_i = {(β_k1 + β_k2G_i), 1 ≤ k ≤ K}^T, and ${\mathrm{\Theta }}_i(\nu )=\text{diag}({\{V_{\mathit{\text{ik}}}(\nu )({\beta }_{k1}+{\beta }_k{G}_i)\}}_{k=1}^K$. Then A_i(ν) = (β₁ + β₂G_i)^TΘ_i(ν). Denote 1_dν as the d_ν-dimensional vector with 1’s as its elements. Let Θ_i = Θ_i(ν⁰). Let Q_i = (Q_i1, …, Q_iK)^T and let η be a vector of functions η(u) = {η₁(u), …, η_dν (u)}^T with η_ℓ(·) ∈L₂([a, b]) that minimizes

$${\mathbf{1}}_{d_{\nu }}^{\mathrm{T}}E[{\{Q_i-({\beta }_1^0+{\beta }_2^0{G}_i){\eta }^{\mathrm{T}}(U_i)\}}^{\mathrm{T}}{\mathrm{\Theta }}_i{\mathbf{B}}_i^{-1}{\mathrm{\Theta }}_i\{Q_i-({\beta }_1^0+{\beta }_2^0{G}_i){\eta }^{\mathrm{T}}(U_i)\}]{\mathbf{1}}_{d_{\nu }}.$$

Define C_i as a d_ν × d_ν K matrix, with k^th block ${\mathbf{C}}_{i,k}=V_{\mathit{\text{ik}}}{\{Q_{\mathit{\text{ik}}}-({\beta }_{k1}^0+{\beta }_{k2}^0{G}_i)\eta (U_i)\}}^{\otimes 2}$. Define D_i as a d_νK × d_νK matrix, with (k, k′) block

$${\mathbf{D}}_{i,k,k\prime }={\mathrm{\Omega }}_{i,k,k\prime }\{Q_{\mathit{\text{ik}}}-({\beta }_{k1}^0+{\beta }_{k2}^0{G}_i)\eta (U_i)\}{\{Q_{\mathit{\text{ik}}\prime }-({\beta }_{k\prime 1}^0+{\beta }_{k\prime 2}^0{G}_i)\eta (U_i)\}}^{\mathrm{T}},$$

and define ${\mathbf{D}}_i^{\ast }$ as a d_ν K × d_νK matrix, with (k, k′) block

$${\mathbf{D}}_{i,k,k\prime }^{\ast }=\{E(Y_{\mathit{\text{ik}}}{Y}_{\mathit{\text{ik}}\prime }|{ℂ}_i)-H_{\mathit{\text{ik}}}{H}_{\mathit{\text{ik}}\prime }\}\{Q_{\mathit{\text{ik}}}-({\beta }_{k1}^0+{\beta }_{k2}^0{G}_i)\eta (U_i)\}\times {\{Q_{\mathit{\text{ik}}\prime }-({\beta }_{k\prime 1}^0+{\beta }_{k\prime 2}^0{G}_i)\eta (U_i)\}}^{\mathrm{T}}.$$

In the following two theorems, we establish the consistency and asymptotic normality of our procedure. Different from the independent disease case, without a correct specification of the correlation structure of the occurrences of different diseases, we can no longer achieve semiparametric efficiency.

Theorem 4

Under the conditions in Appendix A.2, when ν is the collection of the true parameters or a $\sqrt{n}$-consistent estimator of ν, (a) ${\hat{\sigma }}_w^{-1}(u,{\nu }^0)\{{\hat{m}}_w(u,\nu )-m(u)\}\to \mathit{\text{Normal}}(0,1)$; (b) |m̂_w(u, ν) − m(u)| = O_p (nh)^−1/2 + h^q} uniformly in u ∈ [a₀, b₀]; and (c) $|{\hat{m}}_w^{\prime }(u,\nu )-m\prime (u)|=O_p(n^{-1/2}{h}^{-3/2}+h^{q-1})$ uniformly in u ∈ [a₀, b₀].

Let ${\hat{\mathbf{D}}}_i^{\ast }$ be a d_νK × d_νK matrix, with (k, k′) block

$${\hat{\mathbf{D}}}_{i,k,k\prime }^{\ast }={\hat{\mathrm{\Omega }}}_{i,k,k\prime }\{Q_{\mathit{\text{ik}}}(\hat{\nu })-({\hat{\beta }}_{k1}+{\hat{\beta }}_{k2}{G}_i)\hat{\eta }(U_i(\hat{\nu }))\}{\{Q_{\mathit{\text{ik}}\prime }(\hat{\nu })-({\hat{\beta }}_{k\prime 1}+{\hat{\beta }}_{k\prime 2}{G}_i)\hat{\eta }(U_i(\hat{\nu }))\}}^{\mathrm{T}},$$

where η̂(U_i(ν̂)) = {η̂₁(U_i(ν̂)), …, η̂_dν (U_i(ν̂))}^T and ${\hat{\eta }}_{\ell }(U_i(\hat{\nu }))=B_r^{\mathrm{T}}(U_{\mathit{\text{ik}}}(\hat{\nu })){\hat{\tau }}_{\ell }$ with {τ̂_ℓ} minimizing

$${\mathbf{1}}_{d_{\nu }}^{\mathrm{T}}{\sum }_{i=1}^n[{\{Q_i(\hat{\nu })-({\hat{\beta }}_1+{\hat{\beta }}_2{G}_i){\hat{\eta }}^{\mathrm{T}}(U_i(\hat{\nu }))\}}^{\mathrm{T}}{\mathrm{\Theta }}_i(\hat{\nu }){\mathbf{B}}_i{(\hat{\nu })}^{-1}{\mathrm{\Theta }}_i(\hat{\nu })\times \{Q_i(\hat{\nu })-({\hat{\beta }}_1+{\hat{\beta }}_2{G}_i){\hat{\eta }}^{\mathrm{T}}(U_i(\hat{\nu }))\left\}\right]{\mathbf{1}}_{d_{\nu }}.$$

Theorem 5

Let (C, D, D*) be generic notation for random variables with the same distribution as (C_i, D_i, ${\mathbf{D}}_i^{\ast }$). Under the conditions in Appendix A.2, $\sqrt{n}(\hat{\nu }-{\nu }^0)\to \mathit{\text{Normal}}(0_{d_{\nu }},\mathbf{\sum })$ for ν̂ in a neighborhood of ν⁰, where

$$\mathbf{\sum }={\{E({\mathbf{\text{CD}}}^{-1}{\mathbf{C}}^{\mathrm{T}})\}}^{-1}E({\mathbf{\text{CD}}}^{-1}{\mathbf{D}}^{\ast }{\mathbf{D}}^{-1}{\mathbf{C}}^{\mathrm{T}}){\{E({\mathbf{\text{CD}}}^{-1}{\mathbf{C}}^{\mathrm{T}})\}}^{-1}.$$

Here, Σ is consistently estimated by the sandwich estimator

$$\hat{\mathbf{\sum }}={(n^{-1}{\sum }_{i=1}^n{\hat{\mathbf{C}}}_i{\hat{\mathbf{D}}}_i^{-1}{\hat{\mathbf{C}}}_i^{\mathrm{T}})}^{-1}(n^{-1}{\sum }_{i=1}^n{\hat{\mathbf{C}}}_i{\hat{\mathbf{D}}}_i^{-1}{\hat{\mathbf{D}}}_i^{\ast }{\hat{\mathbf{D}}}_i^{-1}{\hat{\mathbf{C}}}_i^{\mathrm{T}}){(n^{-1}{\sum }_{i=1}^n{\hat{\mathbf{C}}}_i{\hat{\mathbf{D}}}_i^{-1}{\hat{\mathbf{C}}}_i^{\mathrm{T}})}^{-1}.$$ (9)

4.2 Multiple Populations and Multiple Diseases

Finally, we consider the general case that there are k = 1, …, K independent populations, and within the k^th population, there are ℓ = 1, …, L_k diseases and i = 1, …, n_k observations. The outcomes are Y_ikℓ and the covariates are ℂ_ik = (G_ik, X_ik0, X_ik, Z_ik, G_ik W_ik). The model is

$$\text{pr}(Y_{\mathit{\text{ik}}\ell }=1|{ℂ}_{\mathit{\text{ik}}})=H_{\mathit{\text{ik}}\ell }=H\{({\beta }_{k\ell 1}+{\beta }_{k\ell 2}{G}_{\mathit{\text{ik}}})m(X_{\mathit{\text{ik}}0}+X_{\mathit{\text{ik}}}^{\mathrm{T}}\alpha )+Z_{\mathit{\text{ik}}}^{\mathrm{T}}({\theta }_{k\ell 1}+{\theta }_{k\ell 2}{G}_{\mathit{\text{ik}}})+G_{\mathit{\text{ik}}}{W}_{\mathit{\text{ik}}}^{\mathrm{T}}{\theta }_{k\ell 3}\}.$$ (10)

We make the same assumptions as in Section A.2. As in Theorem 2, we write n = n₁ and for k = 2, ‥, K, define n_k = nc_kn, where there are constants c_* > 0 and c_** < ∞ such that c_* ≤ c_k = lim_n→∞ c_kn ≤ c_**.

Make the definitions of the terms in Section 4.1 appropriate to population k = 1, ‥, K, e.g., Ã_ik(ν), B_ik(ν), Φ_ik(ν), Ĉ_ik(ν), D̂_ik(ν), Ψ_ik(ν), C_ik, D_ik, Π_nk, Ξ_nk, etc. Obtain λ̂_w(ν) by solving ${\sum }_{k=1}^K{\sum }_{i=1}^{n_k}{B}_r\{U_{\mathit{\text{ik}}}(\alpha )\}{\stackrel{\sim }{\mathbf{A}}}_{\mathit{\text{ik}}}(\nu ){\mathbf{B}}_{\mathit{\text{ik}}}{(\nu )}^{-1}{\mathbf{\Phi }}_{\mathit{\text{ik}}}(\nu )=0$, and obtain ν̂_w by solving ${\sum }_{k=1}^K{\sum }_{i=1}^{n_k}{\hat{\mathbf{C}}}_{\mathit{\text{ik}}}(\nu ){\hat{\mathbf{D}}}_{\mathit{\text{ik}}}{(\nu )}^{-1}{\mathbf{\Psi }}_{\mathit{\text{ik}}}(\nu )=0$. Define

$${\hat{\sigma }}_w^2(u,\nu )=B_r^{\mathrm{T}}(u){\{{\sum }_{k=1}^K(n_k/n){\mathrm{\Pi }}_{\mathit{\text{nk}}}\}}^{-1}\{{\sum }_{k=1}^K(n_k/n){\mathrm{\Xi }}_{\mathit{\text{nk}}}\}{\{{\sum }_{k=1}^K(n_k/n){\mathrm{\Pi }}_{\mathit{\text{nk}}}\}}^{-1}{B}_r(u);$$

$$\mathbf{\sum }={\{{\sum }_{k=1}^K{c}_{k}E({\mathbf{C}}_{\mathit{\text{ik}}}{\mathbf{D}}_{\mathit{\text{ik}}}^{-1}{\mathbf{C}}_{\mathit{\text{ik}}}^{\mathrm{T}})\}}^{-1}\{{\sum }_{k=1}^K{c}_{k}E({\mathbf{C}}_{\mathit{\text{ik}}}{\mathbf{D}}_{\mathit{\text{ik}}}^{-1}{\mathbf{D}}_{\mathit{\text{ik}}}^{\ast }{\mathbf{C}}_{\mathit{\text{ik}}}^{\mathrm{T}})\}\times {\{{\sum }_{k=1}^K{c}_{k}E({\mathbf{C}}_{\mathit{\text{ik}}}{\mathbf{D}}_{\mathit{\text{ik}}}^{-1}{\mathbf{C}}_{\mathit{\text{ik}}}^{\mathrm{T}})\}}^{-1};$$

$$\hat{\mathbf{\sum }}={(n^{-1}{\sum }_{k=1}^K{\sum }_{i=1}^{n_k}{\hat{\mathbf{C}}}_{\mathit{\text{ik}}}{\hat{\mathbf{D}}}_{\mathit{\text{ik}}}^{-1}{\hat{\mathbf{C}}}_{\mathit{\text{ik}}}^{\mathrm{T}})}^{-1}(n^{-1}{\sum }_{k=1}^K{\sum }_{i=1}^{n_k}{\hat{\mathbf{C}}}_{\mathit{\text{ik}}}{\hat{\mathbf{D}}}_{\mathit{\text{ik}}}^{-1}{\hat{\mathbf{D}}}_{\mathit{\text{ik}}}^{\ast }{\hat{\mathbf{D}}}_{\mathit{\text{ik}}}^{-1}{\hat{\mathbf{C}}}_{\mathit{\text{ik}}}^{\mathrm{T}})\times {(n^{-1}{\sum }_{k=1}^K{\sum }_{i=1}^{n_k}{\hat{\mathbf{C}}}_{\mathit{\text{ik}}}{\hat{\mathbf{D}}}_{\mathit{\text{ik}}}^{-1}{\hat{\mathbf{C}}}_{\mathit{\text{ik}}}^{\mathrm{T}})}^{-1}.$$

Then Theorems 4–5 hold with these definitions, see Appendix A.8, and Σ̂ remains a sandwich estimator.

As in other problems involving correlated binary data and generalized estimating equations, the semiparametric efficiency established in Theorem 3 does not hold for the multiple populations and multiple diseases case, mainly due to the fact that the responses are correlated among different diseases and the correlation structure is unknown. Discussion of the working correlation matrix in parametric generalized estimating equation problems can be found in many papers, see for example Chaganty and Joe (2004).

Instead of embedding the problem in the generalized estimating equation framework, as we have done, there is some literature on developing a likelihood function that allows correlation among the binary responses while having the marginal probabilities be of logistic form, see for example Zhao and Prentice (1990) and Le Cessie and Van Houwelingen (1994). Our methods can be extended to this approach, but the ease of computation associated with a generalized estimating equation approach is a considerable advantage. This computational advantage is one of the reasons that generalized estimating equation methods are so widely employed in practice.

5 Data Analysis

5.1 Spline Setup

In all our implementations, we used cubic splines (r = 4) with equally spaced knots to approximate the nonparametric function m(·). We selected the number of interior knots N by minimizing a BIC criterion, where BIC(N) = −2L_n(λ̂, ν̂) + (N + p)log(n). See Xue and Yang (2006) and Ma and Yang (2011) for the properties of the BIC criterion.

5.2 Dietary Score Example

We applied our methods to the NIH-AARP Study of Diet and Health (Schatzkin et al., 2001). The method used for assessing dietary component intakes is the National Cancer Institute’s Dietary History Questionnaire (DHQ) (Subar et al., 2001). There were 294,673 men and 199,285 women in the data set. There were also dummy variables for various groups of age, body mass index, education, ethnicity, physical activity and smoking, making up the variables Z. In addition, for women, there were two dummy variables for hormone replacement therapy, making up the variables W. The HEI-2005 score for whole grains were taken as X_ik0 and X_ik. The sum of the weights was normalized to equal J + 1 = 12 for ease of comparison with the HEI-2005 total score, all of whose weights = 1: the standard errors of these weights were obtained by the delta-method after fitting the data as described in Sections 3 and 4.

For women, the data set contains four diseases, breast cancer, ovarian cancer, colorectal cancer and lung cancer, while for men there are prostate cancer, colorectal cancer and lung cancer. See Table 2 for the numbers and percentages of cancer cases. The minimum HEI-2005 total score in the data set was x_min = 19.67, while the maximum was x_max = 96.61.

Table 2.

Summary of the NIH-AARP data.

	Men		Women
Description	# Cases	Percentages	# Cases	Percentages
Sample size	294,673		199,285
Breast cancer			7,736	3.88%
Ovarian cancer			759	0.38%
Prostate cancer	23,477	7.97%
Colorectal cancer	4,693	1.59%	2,291	1.15%
Lung cancer	6,135	2.08%	3,630	1.82%

We used $F\{U(\hat{\alpha })\}=\mathrm{\Phi }([U(\hat{\alpha })-E\{U(\hat{\alpha })\}]/\sqrt{\text{Var }\{U(\hat{\alpha })\}})$ to construct B-spline functions, where Φ(·) is the distribution function of the standard normal distribution and U (α̂) = X₀ + X^Tα̂. Thus the nonparametric function m is estimated by $\hat{m}\{u(\hat{\alpha }),\nu \}={\sum }_{p=1}^{P_n}{B}_{r,p}[F\{u(\hat{\alpha })\}]{\hat{\lambda }}_p(\nu )$.

We performed two analyses. In the first, we took a single disease and the two independent populations of men and women, using the method in Section 3, and applied to colorectal cancer and lung cancer separately. In the second, we analyzed all the cancer outcomes, using the method in Section 4.2. The point of doing the former is to illustrate that analyzing single diseases at a time can lead to very different results than those from analyzing multiple diseases simultaneously, a point we made in Section 1.

5.3 Independent Populations, Single Disease

Our first analysis uses the setup in Section 3, where there are K = 2 independent populations, men and women, and L = 1 disease. We performed analyses separately for colorectal cancer and lung cancer, and display here the results for both. Because hormone replacement therapy occurs only for women, the right had side of model (4) is identifiable when the parameter subscripts do not involve k, e.g., β₁ + β₂G_ik.

Table 3 shows the estimates of the weights of the component scores, their standard errors and their p-values for testing whether the weights = 1, i.e., whether the weight equals the HEI-2005 weight.

Table 3.

Results for the analysis of Section 5.3, where lung cancer and colorectal cancer were analyzed separately, thus each analysis has one disease and 2 independent populations. The weights of the component scores were normalized so that their sum = 12, thus placing the weights on the same scale as the HEI-2005 total score, whose weights all = 1. The p-values for the test that the individuals components = 1 are also displayed.

	Colorectal Cancer			Lung Cancer
	Estimate	se	p-value	Estimate	se	p-value
Total Fruit	0.27	0.87	0.40	2.18	0.34	0.00
Total Grains	2.58	0.85	0.06	2.96	0.33	0.00
Whole Grains	2.44	0.85	0.09	0.53	0.27	0.08
Total Vegetables	0.01	1.02	0.33	0.99	0.36	0.98
DOL Vegetables	1.33	0.72	0.65	0.99	0.26	0.96
Dairy	2.44	0.42	0.00	0.42	0.10	0.00
Meat and Beans	0.00	0.53	0.06	0.00	0.18	0.00
Oils	0.58	0.32	0.20	0.33	0.11	0.00
Sodium	0.80	0.45	0.65	1.12	0.16	0.45
Saturated Fat	0.53	0.31	0.13	0.94	0.13	0.65
Empty Calories	0.49	0.21	0.02	0.21	0.08	0.00

The main conclusion of Table 3 is that the weights for the HEI-2005 component scores are strikingly different for total fruit, whole grains and dairy, depending on whether one is interested in colorectal cancer or lung cancer. This is a point we made in the discussion after equation (2) about having a single score and not one for every disease. Table 3 suggests that if one is worried about colorectal cancer, one should increase consumption of whole grains and dairy products, but if one is worried about lung cancer, such consumption would have only a minor effect, but total fruit intake should be increased.

One can see in Table 3 that the weights of many of the individual component scores differ from HEI-2005’s weight of 1.0. We also tested whether the HEI-2005 weights fit the data as well, by testing H₀ : α₁ = α₂ = ⋯ = α_J = 1. To this end, we constructed the Wald chi-square statistic ${\chi }_W^2={(\hat{\alpha }-{\mathbf{1}}_J)}^{\mathrm{T}}{\{\hat{\mathrm{V}}(\hat{\alpha })\}}^{-1}(\hat{\alpha }-{\mathbf{1}}_J)$, which has an asymptotic chi-square distribution with J degrees of freedom under H₀. Here, V̂ (α̂) is the estimated asymptotic variance-covariance matrix of α̂, and is calculated following Theorem 5. The p-value for this hypothesis is < 0.0001.

5.4 Multiple Populations and Multiple Diseases Analysis

Our second analysis uses the setup in Section 4.2, with all the cancers available in our data set: lung, colorectal, breast and ovarian cancers for women, and lung, colorectal and prostate cancers for men. We found that the working correlations among men and women were all < 0.03 in absolute value, so we report results for the working independence estimate.

Table 4 shows the estimated weights of the component scores and their standard errors. Because we are using multiple diseases and populations, and not just colorectal or lung cancer separately, but all the cancers simultaneously, we can expect differences between Table 4 and either analysis in Table 3. One of the striking difference is the vast down-weighting of increased Milk consumption compared to the results for colorectal cancer only. In the HEI-2005 score, increase of Milk consumption results in a monotonically increasing score for Milk. In the colorectal cancer case, a person who gets the top score of 10 on Milk contributes 24.4 to the single index. After accounting for the other diseases, however, the contribution is 0.61, a vast decrease. To us, this makes perfect sense, because the value of increased Milk consumption in adults is hardly universally accepted. For example, The Alternative Healthy Eating Index (McCullough et al., 2002) does not even include dairy as part of its index, i.e., increased Milk consumption gets zero weight. The Modified Mediterranean Diet Score (Trichopoulou et al., 2005) and the MedDietScore (Panagiotakos et al., 2006), have been shown to be related to overall survival and coronary heart disease respectively, but for these scores, increases in Milk consumption lead to decreases in the score for Milk, i.e., negative weight.

Table 4.

Results for estimated weights α̂ in the analysis of Section 5.4, with two populations (men and women), three diseases for men (lung, colorectal and prostate cancer) and four diseases for women (lung, colorectal, breast and ovarian cancer). The weights of the component scores were normalized so that their sum = 12, thus placing the weights on the same scale as the HEI-2005 total score, whose weights all = 1. The p-values for the test that the individuals components = 1 are also displayed. The actual estimated weights for Meat and Beans was actually negative, but we have set it = 0 for nutritional purposes.

	Estimate	se	p-value
Total Fruit	1.89	0.31	0.00
Whole Fruit	1.32	0.30	0.27
Total Grains	2.94	0.30	0.00
Whole Grains	0.70	0.26	0.32
Total Vegetables	0.97	0.34	0.93
DOL Vegetables	0.93	0.24	0.81
Dairy	0.61	0.09	0.00
Meat and Beans	0.00	0.17	0.00
Oils	0.39	0.11	0.00
Sodium	1.13	0.15	0.36
Saturated Fat	0.89	0.12	0.40
Empty Calories	0.23	0.07	0.00

Table 5 shows the estimates, standard errors (se) and p-values for the coefficients β. The β coefficient for men associated with lung cancer was = −1 for identifiability. However, when we instead set the coefficient for lung cancer for women to be = −1, the estimated coefficient for lung cancer for men was −1.06, and the p-value was very small. It is clear from the table that the real practical impact of diet here is its contribution to decreases in risk for lung and colorectal cancers, and for both men and women, and that the impact is greater for lung cancers. See below for a discussion of the relative risks, displayed in Figure 2, which supports our conclusion. The estimated values for all other groups are also negative except for the two groups: (a) men and prostate cancer; and (b) women and ovarian cancer, where the coefficients are very small: they have both been set = 0 under the constraint that a better diet is not a risk factor for either cancer. In the figures that we discuss, the index (x-axis) plotted is from the 3^rd to the 97^th percentiles of the actual index.

Table 5.

Results for β̂ for the analysis of Section 5.4, with two populations (men and women), three diseases for men (lung, colorectal and prostate cancer) and four diseases for women (lung, colorectal, breast and ovarian cancer). The weights of the component scores were normalized so that their sum = 12, thus placing the weights on the same scale as the HEI-2005 total score, whose weights all = 1. The p-values for the test that the individual β̂ terms = 0 are also displayed. The actual estimated coefficients for Prostate and Ovarian cancers were positive, but we have set them = 0 for nutritional purposes, with the constraint that a better diet is not a risk factor for either disease.

	Estimate	se	p-value
Men, Lung	−1.00	NA	NA
Men, Colorectal	−0.39	0.06	0.00
Men, Prostate	0.00	0.06	0.07
Women, Lung	−0.91	0.07	0.00
Women, Colorectal	−0.28	0.08	0.00
Women, Breast	−0.07	0.04	0.11
Women, Ovarian	0.00	0.14	0.90

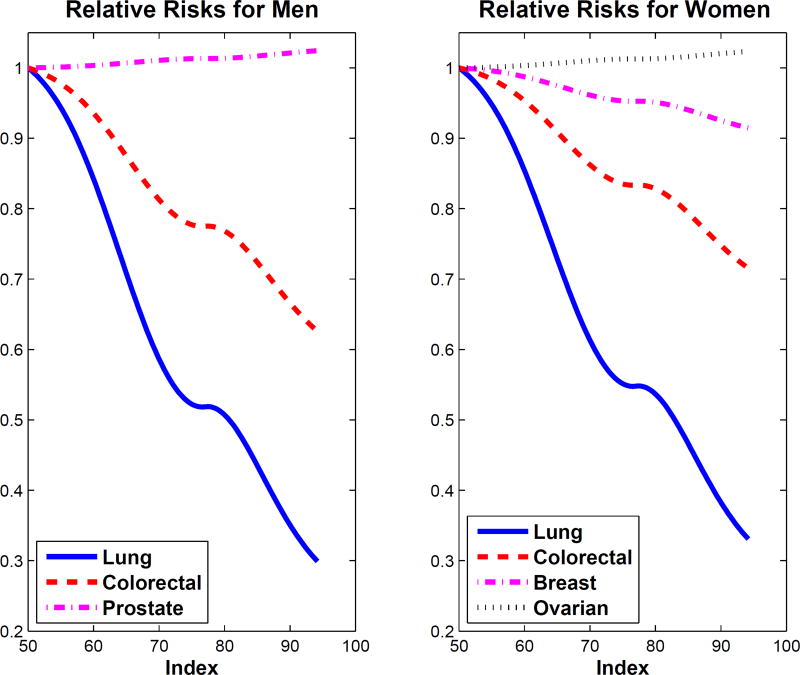
Figure 2.

Analysis of multiple diseases as in Section 5.4. Relative risks for men and women on a grid between the 3rd and 97^th percentile of the index. Left panel is for men: solid blue line is the relative risk for lung cancer, while the dashed red line is for colorectal cancer. The right is for women: solid blue line is the relative risk for lung cancer, dashed red line is for colorectal cancer and the dot-dashed magenta line is for breast cancer.

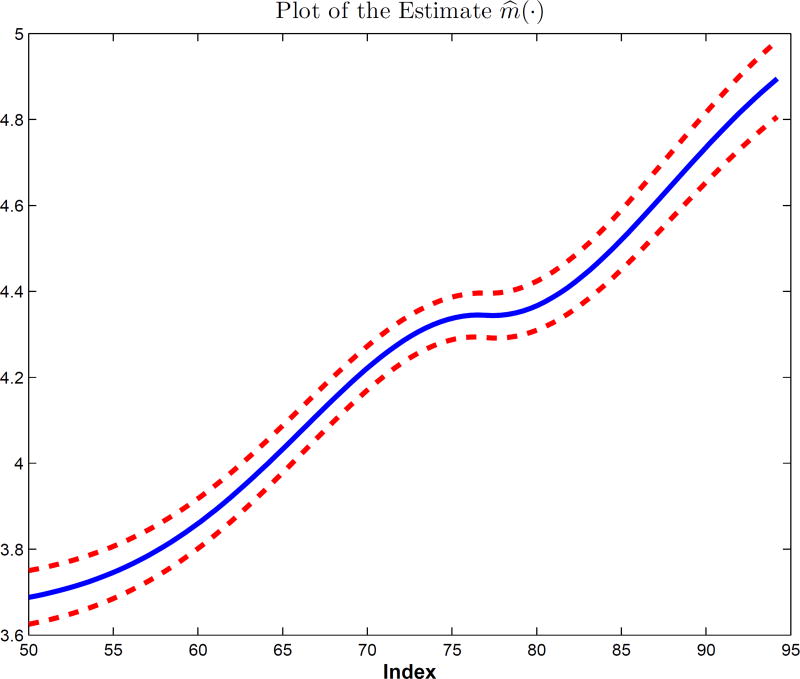
Figure 1 shows the plot of the estimates of m(·) against the index u (α̂) along with pointwise 95% confidence intervals, without any additional monotonicity constraints on m(·). The estimated function itself is monotone as expected. Observe that the estimated function is not an exact linear function, especially when considering the pointwise confidence intervals. Indeed, from the index value of 50 to 72, the estimated function has an increasing acceleration, then it becomes at, and it increases quickly again when the index value is greater than 82. When we refit the data with a linear link, the results, while different, are in good agreement, both in the estimated functions, the tables, and the analyses that are described next.

Figure 1.

Analysis of multiple diseases as in Section 5.4. The function m̂(X^Tα̂) along with its pointwise 95% confidence interval.

Figure 2 displays the estimated relative risks of the various cancers and separately for men and women. Clearly, we see that the index predicts stronger decreases for lung cancer relative risks for better diet index score as compared to the other diseases. In Figure 2, the effect of better diet on prostate cancer in men and ovarian cancer in women are is nearly null, and the effect of better diet is quite modest on breast cancer. When analyzing the HEI-2005 total score, the p-values for prostate cancer, breast cancer and ovarian cancer were 0.15, 0.09, and 0.44, respectively, roughly what is seen in Figure 2.

Figure S.1 of the Supplementary Material shows how the estimated relative risks differ between men and women for lung and colorectal cancer. In both cases, women have the lower risk in general, with the largest difference being in colorectal cancer, but even there, the differences are not great. This agrees with the marginal rate of lung cancer for men and women being 2.08% and 1.82%, respectively, while the marginal rate of colorectal cancer for men and women 1.59% and 1.15%, respectively, see Table 2.

The hypothesis for testing that the weights all equal 1.0 is rejected with a p-value numerically very close to 0, as expected.

6 Simulation

In this section, we describe a simulation study to assess the finite-sample performance of our method in the case of two populations and multiple diseases. Section S.1 of the Supplementary Material has results for two independent populations and one disease. Here simulated data from the logistic model with multiple populations and diseases, so that

$$\text{pr}(Y_{\mathit{\text{ik}}\ell }=1|{ℂ}_{\mathit{\text{ik}}})=H\{{\beta }_{k\ell }m(X_{\mathit{\text{ik}}}^{\mathrm{T}}\alpha )+Z_{\mathit{\text{ik}}}^{\mathrm{T}}{\theta }_{k\ell 1}+G_{\mathit{\text{ik}}}{W}_{\mathit{\text{ik}}}^{\mathrm{T}}{\theta }_{k\ell 3}\},$$

for i = 1, …, n and k = 1, 2. We consider two independent populations, and within the k^th population, there are ℓ = 1, …, L_k diseases and i = 1, …, n observations. We let L₁ = 3 and L₂ = 4, so that, as in the example of Section 5, the first and second populations have four and three diseases, respectively. There were 1, 000 simulated data sets.

For each simulated data set, we let n = 3, 000, and set the covariates to be randomly selected, without replacement, from the real data in Section 5. We set each component of α = 1, and made the convention that the estimates should sum to 12. The true values of β_kℓ are listed in Table 7. We simulated the components in θ_kℓ1 and θ_kℓ3 from the Uniform[−0.5, 0.5] distribution, except that, for identifiability, the first component in θ_k1 is taken to be zero. The true function is m(u) = exp(u/3).

Table 7.

Simulation results for β when n = 3000 and the binary responses have correlation 0.05. Estimate is the mean, Estimated se is the mean of the estimated standard errors, Actual se is the actual standard deviation of the estimates, and Coverage is the actual coverage of a nominal 95% confidence interval. The average total number of cases across the simulation = 7,975.

	Mean # Cases	True β	Mean β̂	Estimated se	Actual se	Coverage
Population 1, Disease 1	826	−1.00	−1.00	NA	NA	NA
Population 1, Disease 2	1052	−0.60	−0.61	0.12	0.11	97.00
Population 1, Disease 3	1347	−0.20	−0.21	0.10	0.09	97.70
Population 2, Disease 1	957	−0.80	−0.80	0.14	0.14	94.40
Population 2, Disease 2	1104	−0.57	−0.57	0.12	0.13	94.50
Population 2, Disease 3	1265	−0.33	−0.34	0.11	0.11	94.00
Population 2, Disease 4	1422	−0.10	−0.11	0.10	0.09	98.40

To generate the correlated binary data, we use the following algorithm. Suppose we want to generate M binary variables with probabilities (π₁, …, π_M). Let (U₁, …, U_M) be equicorrelated standard normal random variables with correlation ρ, and for m = 1, …, M, define T_m = log{π_m/(1 − π_m)} + log[Φ(U_m)/{1 − Φ(U_m)}]. Then setting Y_m = I(T_m > 0) creates correlated binary random variables with the desired probabilities. In our setting, the correlations of the binary variables were approximately ρ/2, so for the simulation in this section we set ρ = 0.10. This resulted in correlations somewhat higher than in the real data in Section 5.

We also conducted simulation experiments for independent binary outcomes and the sample size but with correlation nearly 0.10, (ρ = 0.20), and both correlations with n = 2000. These results similar to the results in this section, are in Section S.2 of the Supplementary Material.

To give some idea of how this simulation compares with the real data, Table 7 also lists the mean number of cases by disease and by population: the mean across both is 7, 975. These are many fewer than the number of cases seen in the actual data, see Table 2. Hence, since the effective sample size might be thought of as the number of cases, the simulation approximates a smaller study than the NIH-AARP data analyzed in Section 5.

Table 6 gives the results for the estimates of α, while Table 7 gives the results for the estimates of the β_kℓ. In both cases, the estimates are very nearly unbiased, the estimated standard errors very nearly equal the actual standard errors, and the coverage probabilities are close the nominal 95%.

Table 6.

Results of the simulation study when n = 3000, the binary responses have correlation 0.05 and where the actual values of α all = 1:00. Here Estimate is the mean of the estimates, Estimated se is the mean of the estimated standard errors, Actual se is the actual standard deviation of the estimates, and Coverage is the actual coverage of a nominal 95% confidence interval. The actual estimates α̂ were normalized to sum to 12.

	Mean	Estimated se	Actual se	Coverage
Total Fruit	1.03	0.32	0.34	93.00
Whole Fruit	1.04	0.55	0.59	95.40
Total Grains	1.00	0.55	0.58	95.00
Whole Grains	0.99	0.37	0.38	94.10
Total Vegetables	1.01	0.44	0.45	94.20
DOL Vegetables	0.99	0.38	0.38	94.90
Dairy	1.01	0.27	0.28	95.10
Meat and Beans	1.01	0.29	0.31	94.00
Oils	1.00	0.28	0.29	94.10
Sodium	0.98	0.35	0.37	94.30
Saturated Fat	0.98	0.40	0.42	94.20
Empty Calories	0.96	0.46	0.47	94.40

Figure S.2 of the Supplementary Material shows that the mean estimated function across the simulated data sets is also very nearly unbiased. Overall, the simulation suggests that our methodology leads to nearly unbiased estimates and inferences that achieve their nominal levels.

7 Discussion

Based on motivation from the current practice in nutritional epidemiology, we have developed generalized partially linear logistic single index models in the case that there are several populations and/or diseases. The novelty of the modeling is that the single-index function itself is the same across populations and diseases. In the case that the populations/diseases are independent given covariates, we developed a computable B-spline based semiparametric efficient methodology. In the case that the populations/diseases are correlated given the covariates, our method makes no assumptions about how the diseases are related.

The importance of developing a score that is constructed for health risk prediction across multiple diseases and populations, versus a different score for each population and disease, were illustrated in our work. When we analyzed men for colorectal cancer solely, increasing Milk consumption was given a very high weight in the single index. However, when we fit the model simultaneously for multiple diseases, the weight for increasing Milk consumption became much smaller. The importance of Milk consumption is a source of controversy in the nutrition literature, and our results agree with the Alternative Healthy Eating Index (AHEI), which assigns zero weight to increased Milk consumption, and the Mediterranean diets scores assigns negative weight to increased Milk consumption.

Our results are focused on logistic regression, so that they are readily transparent, but they are easily adapted to apply to any generalized linear model, by replacing H and its related quantities with a more general link function and its corresponding related quantities in the derivation.

We have strived to use a single overall score, which we have argued (a) avoids different diet for different disease; and (b) is important for interpretability. It is important to use as many diseases and populations as possible, and to draw inferences and projections only to those populations and diseases. One can think of what we have done as to come up with a framework for a type of “average” version of the individual model fits across multiple diseases and populations. We do not average directly, instead, we average across the estimating functions.

Appendix

A.1 Some Simplifications and Definitions

For simplicity of notation, we work through the asymptotics in the case that there is one population with a common sample size n, and thus the covariates are the same across the populations/diseases. The statements of Theorems 1–3 are readily verified when the responses are independent with different sample sizes and different covariates across k = 1, …, K.

For any vector ζ = (ζ₁, …, ζ_s)^T ∈ R^s, denote the norm ‖ζ‖_r = (|ζ₁|^r +⋯+|ζ_s|^r)^1/r, 1 ≤ r ≤ ∞. For positive numbers a_n and b_n, n > 1, let a_n ≍ b_n denote that lim_n→∞ a_n/b_n = c, where c is some nonzero constant. Denote the space of the q^th order smooth functions as C^(q)([a, b]) = {ϕ|ϕ^(q) ∈ C [a, b]}. For any s × s symmetric matrix A, denote its L_r norm as ${\Vert \mathbf{A}\Vert }_q={\text{max}}_{\varsigma \in R^s,\varsigma \ne 0}{\Vert A\varsigma \Vert }_q{\Vert \varsigma \Vert }_q^{-1}$. Let ${\Vert \mathbf{A}\Vert }_{\infty }={\text{max}}_{1\le i\le s}{\sum }_{j=1}^s|a_{\mathit{\text{ij}}}|$. For a vector a, let ‖a‖_∞ = max_1≤i≤s |a_i|.

A.2 Regularity Conditions

• (C1)The density function f_{X0+X^T α} (x₀ + x^T α) of random variable X₀ + X^T α is bounded away from 0 on S_α and satisfies the Lipschitz condition of order 1 on S_α, where S_α = {X₀ + X^T α,(X₀, X^T)^T∈S} and S is a compact support set of (X₀, X^T)^T, for α in a neighborhood of its true values α⁰.
• (C2)m(·) ∈ C^(q)([a₀, b₀]) for q ≥ 2, ${\eta }_{\ell }^0\in C^{(1)}([a_0,b_0)]$, 1 ≤ l ≤ d_ν, and the spline order satisfies r ≥ q.
• (C3)
  There exists 0 < c < ∞, such that the distances between neighboring knots satisfies

  $$\underset{r\le p\le N+r}{\text{max}}|h_{p+1}-h_p|=o(N^{-1})\text{ and }h/\underset{r\le p\le N+r}{\text{min}}{h}_J\le c.$$

  Furthermore, the number of knots satisfies N → ∞, as n → ∞, N⁻⁴n → ∞ and Nn^−1/(2q+2) → ∞.

• (C4)sup_i,k |G_ik| ≤ M < ∞. The eigenvalues of ${\sum }_{k=1}^K{c}_{k}E[V_{\mathit{\text{ik}}}{\{Q_{\mathit{\text{ik}}}-({\beta }_{k1}^0+{\beta }_{k2}^0{G}_{\mathit{\text{ik}}}){\eta }^0(U_{ik})\}}^{\otimes 2}]$ are bounded below from zero. The eigenvalues of E(CD⁻¹C^T) given in Theorem 5 are bounded below from zero.

Conditions (C1)–(C3) are commonly used in the nonparametric smoothing literature; see, for example, Zhou et al. (1998) and Cui et al. (2011). Condition (C4) is needed for asymptotic normality of the parametric estimator.

A.3 Proof of Theorem 1

We first introduce two lemmas which will be used in the following proofs.

Lemma 1

For any a = (a_p : 1 ≤ p ≤ P_n), there exist constants 0 < c_B ≤ C_B < ∞, such that for n large enough,

$$c_B{a}^{\mathrm{T}}\mathit{\text{ah}}\le a^{\mathrm{T}}E\{B_r(U_{\mathit{\text{ik}}}({\alpha }^0))B_r^{\mathrm{T}}(U_{\mathit{\text{ik}}}({\alpha }^0))\}a\le C_B{a}^{\mathrm{T}}\mathit{\text{ah}}.$$ (A.1)

$$\underset{1\le p,p\prime \le P_n}{\text{max}}|n^{-1}{\sum }_{k=1}^K{\sum }_{i=1}^{n_k}[B_{r,p}(U_{\mathit{\text{ik}}}({\alpha }^0))B_{r,p\prime }(U_{\mathit{\text{ik}}}({\alpha }^0))-E\{B_{r,p}(U_{\mathit{\text{ik}}}({\alpha }^0))B_{r,p\prime }(U_{\mathit{\text{ik}}}({\alpha }^0))\}]|=O_p\{\sqrt{h{n}^{-1}\mathit{\text{log}}(n)}\}.$$ (A.2)

Proof of Lemma 1

Result (A.1) follows from Theorem 5.4.2 of DeVore and Lorentz (1993), and (A.2) can be proved by Bernstein’s inequality in Bosq (1961).

Define

$${\mathbf{V}}_n^0(\nu )=n^{-1}{\sum }_{k=1}^K{\sum }_{i=1}^{n_k}E\{V_{\mathit{\text{ik}}}{({\beta }_{k1}+{\beta }_{k2}{G}_i)}^2{B}_r(U_{\mathit{\text{ik}}}(\alpha ))B_r^{\mathrm{T}}(U_{\mathit{\text{ik}}}(\alpha ))\}.$$ (A.3)

Lemma 2

There are constants 0 < c_υ < C_υ < ∞, and 0 < C_S < ∞, such that for n large enough,

$${\Vert {\mathbf{V}}_n^0{({\nu }^0)}^{-1}\Vert }_{\infty }\le C_S{h}^{-1}.$$ (A.4)

and

$$c_{\upsilon }h\le {\Vert {\mathbf{V}}_n^0({\nu }^0)\Vert }_2\le C_{\upsilon }h,C_{\upsilon }^{-1}{h}^{-1}\le {\Vert {\mathbf{V}}_n^0{({\nu }^0)}^{-1}\Vert }_2\le c_{\upsilon }^{-1}{h}^{-1},$$ (A.5)

Proof of Lemma 2

Result (A.5) follows from (A.1). The result that ${\Vert {\mathbf{V}}_n^0{({\nu }^0)}^{-1}\Vert }_{\infty }\le C_S{h}^{-1}$ follows from (A.5) and Theorem 13.4.3 in DeVore and Lorentz (1993).

If m ∈ C^q [a₀, b₀], there exists λ⁰ ∈ R^P_n, such that

$$\underset{u\in [a_0,b_0]}{\text{sup}}|m(u)-\stackrel{\sim }{m}(u)|=O(h^q),$$ (A.6)

where $\stackrel{\sim }{m}(u)=B_r^{\mathrm{T}}(u){\lambda }^0$ (de Boor, 2001). In the following, we prove the results for the nonparametric estimator m̂(u, ν) in Theorem 1 when ν = ν⁰. Then the results also hold when ν is a $\sqrt{n}$ consistent estimator of ν⁰, since the nonparametric convergence rate in Theorem 1 is slower than n^−1/2. Let ${\alpha }_n=n^{1/2}{P}_n+P_n^{-q+1/2}$. We will show that for any given ε > 0, for n sufficiently large, there exists a large constant C > 0 such that

$$\text{pr}\{\underset{{\Vert \tau \Vert }_2=C}{\text{sup}}{L}_n({\lambda }^0+{\alpha }_n\tau ,{\nu }^0)<L_n({\lambda }^0,{\nu }^0)\}\ge 1-\epsilon .$$ (A.7)

This implies that for n sufficiently large, with probability at least 1 − ε, there exists a local maximum for (5) in the ball {λ⁰ + α_nτ :‖τ‖₂ ≤ C}. Hence, there exists a local maximizer such that ‖λ̂(ν⁰) − λ⁰‖₂ = O_p(α_n). Since L_n(λ, ν⁰) is a concave function of λ, the local maximizer is the global maximizer of (5).

Define

$${\stackrel{\sim }{H}}_{\mathit{\text{ik}}}(\lambda ,\nu )=H[({\beta }_{k1}+{\beta }_{k2}{G}_{\mathit{\text{ik}}})B_r^{\mathrm{T}}\{U_{\mathit{\text{ik}}}(\alpha )\}\lambda +Z_{\mathit{\text{ik}}}^{\mathrm{T}}({\theta }_{k1}+{\theta }_{k2}{G}_{\mathit{\text{ik}}})+G_{\mathit{\text{ik}}}{W}_{\mathit{\text{ik}}}^{\mathrm{T}}{\theta }_{k3}],$$

then

$$\partial L_n(\lambda ,\nu )/\partial \lambda ={\sum }_{k=1}^K{\sum }_{i=1}^{n_k}\{Y_{\mathit{\text{ik}}}-{\stackrel{\sim }{H}}_{\mathit{\text{ik}}}(\lambda ,\nu )\}({\beta }_{k1}+{\beta }_{k2}{G}_{\mathit{\text{ik}}})B_r\{U_{\mathit{\text{ik}}}(\alpha )\},$$

$${\partial }^2{L}_n(\lambda ,\nu )/\partial \lambda \partial {\lambda }^{\mathrm{T}}=-{\sum }_{k=1}^K{\sum }_{i=1}^{n_k}{\stackrel{\sim }{H}}_{\mathit{\text{ik}}}(\lambda ,\nu )\{1-{\stackrel{\sim }{H}}_{\mathit{\text{ik}}}(\lambda ,\nu )\}{({\beta }_{k1}+{\beta }_{k2}{G}_i)}^2{B}_r\{U_{\mathit{\text{ik}}}(\alpha )\}{B}_r^{\mathrm{T}}\{U_{\mathit{\text{ik}}}(\alpha )\}.$$

By Taylor’s expansion, we have

$$L_n({\lambda }^0+{\alpha }_n\tau ,{\nu }^0)-L_n({\lambda }^0,{\nu }^0)={\{\partial L_n({\lambda }^0,{\nu }^0)/\partial \lambda \}}^{\mathrm{T}}{\alpha }_n\tau -[-2^{-1}{({\alpha }_n\tau )}^{\mathrm{T}}\{{\partial }^2{L}_n({\lambda }^{\ast },{\nu }^0)/\partial \lambda \partial {\lambda }^{\mathrm{T}}\}{\alpha }_n\tau ],$$ (A.8)

where λ* = ϱλ + (1 − ϱ)λ⁰ for some ϱ ∈ (0, 1). Moreover,

$$|{\{\partial L_n({\lambda }^0,{\nu }^0)/\partial \lambda \}}^{\mathrm{T}}{\alpha }_n\tau |\le {\alpha }_n{\Vert \partial L_n({\lambda }^0,{\nu }^0)/\partial \lambda \Vert }_2{\Vert \tau \Vert }_2=C{\alpha }_n{\Vert \partial L_n({\lambda }^0,{\nu }^0)/\partial \lambda \Vert }_2,$$

and ∂L_n(λ⁰, ν⁰)/∂λ = Δ_n1 + Δ_n2, where

$${\mathrm{\Delta }}_{n1}={\sum }_{k=1}^K{\sum }_{i=1}^{n_k}(Y_{\mathit{\text{ik}}}-H_{\mathit{\text{ik}}}({\nu }^0))({\beta }_{k1}^0+{\beta }_{k2}^0{G}_{\mathit{\text{ik}}})B_r(U_{\mathit{\text{ik}}}({\alpha }^0)),$$

$${\mathrm{\Delta }}_{n2}={\sum }_{k=1}^K{\sum }_{i=1}^{n_k}(H_{\mathit{\text{ik}}}({\nu }^0)-{\stackrel{\sim }{H}}_{\mathit{\text{ik}}}({\lambda }^0,{\nu }^0))({\beta }_{k1}^0+{\beta }_{k2}^0{G}_{\mathit{\text{ik}}})B_r(U_{\mathit{\text{ik}}}({\alpha }^0)).$$

Since E(Δ_n1) = 0, and $E{[\{Y_{\mathit{\text{ik}}}-H_{\mathit{\text{ik}}}({\nu }^0)\}({\beta }_{k1}^0+{\beta }_{k2}^0{G}_{\mathit{\text{ik}}})B_{r,p}\{U_{\mathit{\text{ik}}}({\alpha }^0)\}]}^2\le C_{1}h$ for some constant 0 < C₁ < ∞, then $E({\Vert n^{-1}{\mathrm{\Delta }}_{n1}\Vert }_2^2)\le P_n{\mathit{\text{Kn}}}^{-1}{C}_{1}h$. By Condition (C3), we have $h\le {\mathit{\text{cP}}}_n^{-1}$. Then $E({\Vert n^{-1}{\mathrm{\Delta }}_{n1}\Vert }_2^2)\le P_n{\mathit{\text{Kn}}}^{-1}{C}_1{\mathit{\text{cP}}}_n^{-1}={\mathit{\text{KC}}}_1{\mathit{\text{cn}}}^{-1}$. Then for any ε > 0, by Chebyshev’s inequality, we have $\text{pr}({\Vert n^{-1}{\mathrm{\Delta }}_{n1}\Vert }_2\ge \sqrt{n^{-1}{\mathit{\text{KC}}}_{1}c{\epsilon }^{-1}})\le \epsilon$. Hence, there exists an event A_n1 with $\text{pr}(A_{n1}^C)\le \epsilon$, such that on A_n1 we have ${\Vert {\mathrm{\Delta }}_{n1}\Vert }_2<\sqrt{{\mathit{\text{KC}}}_{1}c{\epsilon }^{-1}}{n}^{1/2}$. Moreover, by (A.6), we have sup_i,k |H_ik(ν⁰) − H̃_ik(λ⁰, ν⁰)| = O(h^q). Denote

$${\mathrm{\Delta }}_{\mathit{\text{ikp}}}=(H_{\mathit{\text{ik}}}({\nu }^0)-{\stackrel{\sim }{H}}_{\mathit{\text{ik}}}({\lambda }^0,{\nu }^0))({\beta }_{k1}^0+{\beta }_{k2}^0{G}_{\mathit{\text{ik}}})B_{r,p}(U_{\mathit{\text{ik}}}({\alpha }^0)).$$

Then, there exist constants 0 < C₂, $C_2^{\prime }<\infty$ such that

$$\begin{gathered} E({\Vert {\mathrm{\Delta }}_{n2}\Vert }_2) \\ \le P_n^{1/2}{\{\underset{1\le p\le P_n}{\text{sup}}E{({\sum }_{k=1}^K{\sum }_{i=1}^{n_k}{\mathrm{\Delta }}_{\mathit{\text{ikp}}})}^2\}}^{1/2} \\ \le P_n^{1/2}[{\{\underset{1\le p\le P_n}{\text{sup}}{\sum }_{k=1}^K{\sum }_{i=1}^{n_k}E({\mathrm{\Delta }}_{\mathit{\text{ikp}}}^2)\}}^{1/2}+{\{\underset{1\le p\le P_n}{\text{sup}}{\sum }_{(k,i)\ne (k\prime ,i\prime )}E({\mathrm{\Delta }}_{\mathit{\text{ikp}}}{\mathrm{\Delta }}_{i\prime k\prime p})\}}^{1/2}] \\ \le P_n^{1/2}\{{(C_2{\mathit{\text{nh}}}^{2q}h)}^{1/2}+{(C_2^{\prime }{n}^2{h}^{2q}{h}^2)}^{1/2}\} \\ \le P_n^{1/2}(\sqrt{C_2}+\sqrt{C_2^{\prime }}){\mathit{\text{nh}}}^{q+1}\le P_n^{1/2}{C}_3{\mathit{\text{nc}}}^{q+1}{P}_n^{-(q+1)}=C_3{c}^{q+1}{\mathit{\text{nP}}}_n^{-q-1/2}, \end{gathered}$$

where $C_3=(\sqrt{C_2}+\sqrt{C_2^{\prime }})$, for n sufficiently large given that nh → ∞. Again by Chebyshev’s inequality, for any ε > 0, we have $\text{pr}({\Vert {\mathrm{\Delta }}_{n2}\Vert }_2\ge {\epsilon }^{-1/2}{C}_3{c}^{q+1}{\mathit{\text{nP}}}_n^{-q-1/2})\le \epsilon$. Hence, there exists an event A_n2 with $\text{pr}(A_{n2}^C)\le \epsilon$, such that on A_n2 we have ${\Vert {\mathrm{\Delta }}_{n2}\Vert }_2<{\epsilon }^{-1/2}{C}_3{c}^{q+1}{\mathit{\text{nP}}}_n^{-q-1/2}$. Therefore, by the above results, we have for n sufficiently large, on the event A_n1 ∩ A_n2 with pr(A_n1 ∩ A_n2) ≥ 1 − 2ε, such that

$$|{\{\partial L_n({\lambda }^0,{\nu }^0)/\partial \lambda \}}^{\mathrm{T}}{\alpha }_n\tau |\le C{\alpha }_n{\Vert \partial L_n({\lambda }^0,{\nu }^0)/\partial \lambda \Vert }_2\le C{\alpha }_n({\Vert {\mathrm{\Delta }}_{n1}\Vert }_2+{\Vert {\mathrm{\Delta }}_{n2}\Vert }_2)\le C{\alpha }_n(\sqrt{{\mathit{\text{KC}}}_{1}c{\epsilon }^{-1}}{n}^{1/2}+{\epsilon }^{-1/2}{C}_3{c}^{q+1}{\mathit{\text{nP}}}_n^{-q-1/2}).$$ (A.9)

Moreover, by (A.1) and (A.2), we have for n sufficiently large, with probability approaching 1,

$$-2^{-1}{\tau }^{\mathrm{T}}\{{\partial }^2{L}_n({\lambda }^{\ast },{\nu }^0)/\partial \lambda \partial {\lambda }^{\mathrm{T}}\}\tau \ge {\mathit{\text{nC}}}_3{\tau }^{\mathrm{T}}\tau h\ge C_4{C}^2{\mathit{\text{nP}}}_n^{-1}.$$

Thus, there exists an event A_n3 with $\text{pr}(A_{n3}^C)\le \epsilon$ for any ε > 0, such that on A_n3,

$$-2^{-1}{({\alpha }_n\tau )}^{\mathrm{T}}\{{\partial }^2{L}_n({\lambda }^{\ast },{\nu }^0)/\partial \lambda \partial {\lambda }^{\mathrm{T}}\}({\alpha }_n\tau )\ge {\alpha }_n^2{C}_4{C}^2{\mathit{\text{nP}}}_n^{-1}.$$ (A.10)

Therefore, by (A.8), (A.9) and (A.10), for n sufficiently large, on the event A_n1 ∩ A_n2 ∩ A_n3 with pr(A_n1 ∩ A_n2 ∩ A_n3) ≥ 1 − 3ε, we have

$$L_n({\lambda }^0+{\alpha }_n\tau ,{\nu }^0)-L_n({\lambda }^0,{\nu }^0)\le C{\alpha }_n(\sqrt{{\mathit{\text{KC}}}_{1}c{\epsilon }^{-1}}{n}^{1/2}+{\epsilon }^{-1/2}{C}_3{c}^{q+1}{\mathit{\text{nP}}}_n^{-q-1/2})-{\alpha }_n^2{C}_4{C}^2{\mathit{\text{nP}}}_n^{-1}=C{\alpha }_n{P}_n^{-1}\{\sqrt{{\mathit{\text{KC}}}_{1}c{\epsilon }^{-1}}{n}^{1/2}{P}_n+{\epsilon }^{-1/2}{C}_3{c}^{q+1}{\mathit{\text{nP}}}_n^{-q+1/2}-{\mathit{\text{CC}}}_{4}n{\alpha }_n\}=C{\alpha }_n{P}_n^{-1}\{\sqrt{{\mathit{\text{KC}}}_{1}c{\epsilon }^{-1}}{n}^{1/2}{P}_n+{\epsilon }^{-1/2}{C}_3{c}^{q+1}{\mathit{\text{nP}}}_n^{-q+1/2}-{\mathit{\text{CC}}}_4{n}^{1/2}{P}_n-{\mathit{\text{CC}}}_4{\mathit{\text{nP}}}_n^{-q+1/2}\}<0,$$

when $C>\text{max}(C_4^{-1}\sqrt{{\mathit{\text{KC}}}_{1}c{\epsilon }^{-1}},{\epsilon }^{-1/2}{C}_4^{-1}{C}_3{c}^{q+1})$. This shows (A.7). Hence, we have ${\Vert \hat{\lambda }({\nu }^0)-{\lambda }^0\Vert }_2=O_p({\alpha }_n)=O_p(n^{-1/2}{P}_n+P_n^{-q+1/2})$. A similar strategy for proving consistency has been used in the literature when the dimension of the parameter is diverging, see for example the proof of Theorem 3 in Fan and Lv (2011).

Next, let

$$V_{\mathit{\text{ik}}}=\text{var}(Y_{\mathit{\text{ik}}}|G_{\mathit{\text{ik}}},X_{\mathit{\text{ik}}0},X_{\mathit{\text{ik}}},Z_{\mathit{\text{ik}}},G_{\mathit{\text{ik}}}{W}_{\mathit{\text{ik}}})=H_{\mathit{\text{ik}}}(1-H_{\mathit{\text{ik}}}),$$

and

$${\mathbf{V}}_n(\nu )=n^{-1}{\sum }_{k=1}^K{\sum }_{i=1}^{n_k}{V}_{\mathit{\text{ik}}}{({\beta }_{k1}+{\beta }_{k2}{G}_{\mathit{\text{ik}}})}^2{B}_r(U_{\mathit{\text{ik}}}(\alpha ))B_r^{\mathrm{T}}(U_{\mathit{\text{ik}}}(\alpha )).$$ (A.11)

By (A.2), (A.6) and the assumption that $P_n^4{n}^{-1}=o(1)$,

$${\Vert -n^{-1}{\partial }^2{L}_n({\lambda }^0,{\nu }^0)/\partial \lambda \partial {\lambda }^{\mathrm{T}}-{\mathbf{V}}_n({\nu }^0)\Vert }_{\infty }=O(h^q){\Vert n^{-1}{\sum }_{k=1}^K{\sum }_{i=1}^{n_k}{B}_r(U_{\mathit{\text{ik}}}({\alpha }^0))B_r^{\mathrm{T}}(U_{\mathit{\text{ik}}}({\alpha }^0))\Vert }_{\infty }=O(h^q){\Vert E\{B_r(U_{\mathit{\text{ik}}}({\alpha }^0))B_r^{\mathrm{T}}(U_{\mathit{\text{ik}}}({\alpha }^0))\}\Vert }_{\infty }+O(h^q)P_n{O}_p\{\sqrt{{\mathit{\text{hn}}}^{-1}\text{log}(n)}\}=O(h^q)O(h)+O(h^q)P_n{O}_p\{\sqrt{{\mathit{\text{hn}}}^{-1}\text{log}(n)}\}=O_p(h^{q+1}).$$

By (A.2) and (A.4), we have ‖V_n(ν⁰)⁻¹‖_∞ = O_p(h⁻¹). Thus by the above results, one has

$${\Vert {\{-n^{-1}{\partial }^2{L}_n({\lambda }^0,{\nu }^0)/\partial \lambda \partial {\lambda }^{\mathrm{T}}\}}^{-1}-{\mathbf{V}}_n{({\nu }^0)}^{-1}\Vert }_{\infty }=O_p(h^{q-1}).$$

Let

$${\mathbf{D}}_n(\nu )=n^{-1}{\sum }_{k=1}^K{\sum }_{i=1}^{n_k}(Y_{\mathit{\text{ik}}}-H_{\mathit{\text{ik}}})({\beta }_{k1}+{\beta }_{k2}{G}_{\mathit{\text{ik}}})B_r(U_{\mathit{\text{ik}}}(\alpha )).$$

Since $E\{({\beta }_{k1}^0+{\beta }_{k2}^0{G}_{ik})B_{r,p}(U_{ik}({\alpha }^0))\}=O(h)$, by Bernstein’s inequality, we have

$${\Vert n^{-1}{\sum }_{i=1}^n{\sum }_{k=1}^K({\beta }_{k1}^0+{\beta }_{k2}^0{G}_{\mathit{\text{ik}}})B_r(U_{\mathit{\text{ik}}}({\alpha }^0))\Vert }_{\infty }=O_p(h).$$

By the above result and (A.6),

$${\Vert n^{-1}\partial L_n({\lambda }^0,{\nu }^0)/\partial \lambda -{\mathbf{D}}_n({\nu }^0)\Vert }_{\infty }=O(h^q){\Vert n^{-1}{\sum }_{i=1}^n{\sum }_{k=1}^K({\beta }_{k1}^0+{\beta }_{k2}^0{G}_{\mathit{\text{ik}}})B_r(U_{\mathit{\text{ik}}}({\alpha }^0))\Vert }_{\infty }=O_p(h^{q+1}).$$

Let ${ℂ}_{\mathit{\text{ik}}}={(G_i,X_{\mathit{\text{ik}}0},X_{\mathit{\text{ik}}}^{\mathrm{T}},Z_{\mathit{\text{ik}}}^{\mathrm{T}},G_i{W}_{\mathit{\text{ik}}}^{\mathrm{T}})}^{\mathrm{T}},{ℂ}_i={({ℂ}_{\mathit{\text{ik}}}^{\mathrm{T}},1\le k\le K)}^{\mathrm{T}}$, and ℂ = (ℂ₁, …, ℂ_n)^T. It can be proved by Bernstein’s inequality in Bosq (1961) that ${\Vert {\mathbf{D}}_n({\nu }^0)\Vert }_{\infty }=O_p\left(\sqrt{{\mathit{\text{hn}}}^{-1}\text{log}(n)}\right)$. Also, by (A.4), ‖{−n⁻¹∂²L_n(λ⁰, ν⁰)/∂λ∂λ^T}⁻¹‖_∞ = O_p (h⁻¹). Thus for a ∈ R^P_n with ‖a‖₂ = 1,

$$a^{\mathrm{T}}[{\{-n^{-1}{\partial }^2{L}_n({\lambda }^0,{\nu }^0)/\partial \lambda \partial {\lambda }^{\mathrm{T}}\}}^{-1}\{n^{-1}\partial L_n({\lambda }^0,{\nu }^0)/\partial \lambda \}-{\mathbf{V}}_n{({\nu }^0)}^{-1}{\mathbf{D}}_n({\nu }^0)]\le {\Vert a\Vert }_{\infty }{\Vert {\{-n^{-1}{\partial }^2{L}_n({\lambda }^0,{\nu }^0)/\partial \lambda \partial {\lambda }^{\mathrm{T}}\}}^{-1}\Vert }_{\infty }{\Vert n^{-1}\partial L_n({\lambda }^0,{\nu }^0)/\partial \lambda -{\mathbf{D}}_n({\nu }^0)\Vert }_{\infty }+{\Vert a\Vert }_{\infty }{\Vert {\{-n^{-1}{\partial }^2{L}_n({\lambda }^0,{\nu }^0)/\partial \lambda \partial {\lambda }^{\mathrm{T}}\}}^{-1}-{\mathbf{V}}_n{({\nu }^0)}^{-1}\Vert }_{\infty }{\Vert {\mathbf{D}}_n({\nu }^0)\Vert }_{\infty }=O_p(h^q)+O_p(h^{q-1})O_p\left(\sqrt{{\mathit{\text{hn}}}^{-1}\text{log}(n)}\right).$$ (A.12)

Let ê = V_n(ν⁰)⁻¹D_n(ν⁰). By Central Limit Theorem, ${[B_r^{\mathrm{T}}(u)\text{var }(\hat{e}|ℂ)B_r(u)]}^{-1/2}{B}_r^{\mathrm{T}}(u)\hat{e}\to \text{Normal}(0,1)$, where var(ê|ℂ) = {nV_n(ν⁰)}⁻¹ and $B_r^{\mathrm{T}}(u)\text{var}(\hat{e}|ℂ)B_r(u)={\hat{\sigma }}^2(u,{\nu }^0)$. By Lemma 2 and (A.2), there are constants $0<c_{\upsilon }^{\prime }<C_{\upsilon }^{\prime }<\infty$, such that with probability approaching 1, $c_{\upsilon }^{\prime }{h}^{-1}\le {\Vert {\mathbf{V}}_n{({\nu }^0)}^{-1}\Vert }_2\le C_{\upsilon }^{\prime }{h}^{-1}$, and

$${\Vert {\mathbf{V}}_n{({\nu }^0)}^{-1}-{\mathbf{V}}_n^0{({\nu }^0)}^{-1}\Vert }_2=O_p(h^{-2}\sqrt{{\mathit{\text{hn}}}^{-1}\text{log}(n)}).$$ (A.13)

Therefore, there exist constants 0 < c_σ ≤ C_σ < ∞ such that with probability approaching 1 and for large enough n,

$$c_{\sigma }{(\mathit{\text{nh}})}^{-1/2}\le \underset{u\in [a_0,b_0]}{\text{inf}}\hat{\sigma }(u,{\nu }^0)\le \underset{u\in [a_0,b_0]}{\text{sup}}\hat{\sigma }(u,{\nu }^0)\le C_{\sigma }{(\mathit{\text{nh}})}^{-1/2}.$$ (A.14)

Thus $B_r^{\mathrm{T}}(u)\hat{e}=O_p\{{(\mathit{\text{nh}})}^{-1/2}\}$ uniformly in u ∈ [a₀, b₀], and

$$B_r^{\mathrm{T}}(u){\{-{\partial }^2{L}_n({\lambda }^0,{\nu }^0)/\partial \lambda \partial {\lambda }^{\mathrm{T}}\}}^{-1}\{\partial L_n({\lambda }^0,{\nu }^0)/\partial \lambda \}=O_p\{{(\mathit{\text{nh}})}^{-1/2}+h^q\}$$

uniformly in u ∈ [a₀, b₀]. By Taylor’s expansion,

$$\hat{\lambda }({\nu }^0)-{\lambda }^0={\{-{\partial }^2{L}_n({\lambda }^0,{\nu }^0)/\partial \lambda \partial {\lambda }^{\mathrm{T}}\}}^{-1}\{\partial L_n({\lambda }^0,{\nu }^0)/\partial \lambda \}\{1+o_p(1)\}.$$ (A.15)

Thus by (A.12), (A.14), and Condition (C3),

$$\underset{u\in [a_0,b_0]}{\text{sup}}\left|\hat{\sigma }{(u,{\nu }^0)}^{-1}\right[B_r^{\mathrm{T}}(u)\{\hat{\lambda }({\mathrm{\nu }}^0)-\lambda \}-B_r^{\mathrm{T}}(u)\hat{e}\left]\right|=O_p\{{(\mathit{\text{nh}})}^{1/2}\}{O}_p\{(h^q)+O_{a.s.}(h^{q-1})O_{a.s.}(\sqrt{{\mathit{\text{hn}}}^{-1}\text{log}(n)}\left)\right\}+O_p\{{(\mathit{\text{nh}})}^{1/2}\}{o}_p\{{(\mathit{\text{nh}})}^{-1/2}+h^q\}=o_p(1).$$

Therefore by Slutsky’s theorem σ̂⁻¹(u, ν⁰) {m̂(u, ν⁰) − m̃(u)} → Normal(0, 1) and m̂(u, ν⁰) − m̃(u) = Op {(nh)^−1/2} uniformly in u ∈ [a₀, b₀]. By sup_u∈[a0,b0] |m(u) − m̃(u)| = o(h^q), we have |m̂(u, ν⁰) − m(u)| = O_p{(nh)^−1/2 + h^q} uniformly in u ∈ [a₀, b₀]. By Slutsky’s theorem, we have

$${\hat{\sigma }}^{-1}(u,{\mathrm{\nu }}^0)\{\hat{m}(u,{\mathrm{\nu }}^0)-m(u)\}\to \text{Normal}(0,1).$$

Since $\hat{m}\prime (u,\nu )=B_{r-1}^{\mathrm{T}}(u)D_1\hat{\lambda }(\nu )$ and B_r−1(u) are B-spline basis functions with one order lower than B_r(u), by the same argument as in Zhou and Wolfe (2000) and the proof for m̂(u, ν⁰), we have the result (b) in Theorem 1. Then the proof is complete.

A.4 Proof of Theorem 2

Define $L_{\mathit{\text{ik}}}(\nu )=({\beta }_{k1}+{\beta }_{k2}{G}_{\mathit{\text{ik}}})m(X_{\mathit{\text{ik}}0}+X_{\mathit{\text{ik}}}^{\mathrm{T}}\alpha )+Z_{\mathit{\text{ik}}}^T({\theta }_{k1}+{\theta }_{k2}{G}_{\mathit{\text{ik}}})+G_{\mathit{\text{ik}}}{W}_{\mathit{\text{ik}}}^{\mathrm{T}}{\theta }_{k3}$. It is straight-forward to prove that ∂L_i1(ν)/∂ν = Q_i1(ν), and for k = 2, …, K, ∂L_ik(ν)/∂ν = Q_ik(ν). Then by (A.15) and Condition (C3) and by the same arguments as the proof for proposition 4.1 in Ai and Chen (2003), we have

$$\partial L_n({\nu }^0)/\nu ={\sum }_{k=1}^K{\sum }_{i=1}^{n_k}[(Y_{\mathit{\text{ik}}}-H_{\mathit{\text{ik}}}({\nu }^0))\times \{\partial L_{\mathit{\text{ik}}}({\nu }^0)/\partial \nu -({\beta }_{k1}^0+{\beta }_{k2}^0{G}_{\mathit{\text{ik}}}){\eta }^0(U_{\mathit{\text{ik}}}({\alpha }^0))\}]\{1+o_p(1)\}={\sum }_{k=1}^K{\sum }_{i=1}^{n_k}[(Y_{\mathit{\text{ik}}}-H_{\mathit{\text{ik}}}({\nu }^0))\times \{Q_{\mathit{\text{ik}}}({\nu }^0)-({\beta }_{k1}^0+{\beta }_{k2}^0{G}_{\mathit{\text{ik}}}){\eta }^0(U_{\mathit{\text{ik}}}({\alpha }^0))\}]\{1+o_p(1)\},$$

$${\partial }^2{L}_n({\nu }^0)/\partial \nu \partial {\nu }^{\mathrm{T}}=-{\sum }_{k=1}^K{\sum }_{i=1}^{n_k}[H_{\mathit{\text{ik}}}({\nu }^0)(1-H_{\mathit{\text{ik}}}({\nu }^0))\times {\{\partial L_{\mathit{\text{ik}}}({\nu }^0)/\partial \nu -({\beta }_{k1}^0+{\beta }_{k2}^0{G}_{\mathit{\text{ik}}}){\eta }^0(U_{\mathit{\text{ik}}}({\alpha }^0))\}}^{\otimes 2}]\{1+o_p(1)\}=-{\sum }_{k=1}^K{\sum }_{i=1}^{n_k}[V_{\mathit{\text{ik}}}({\nu }^0){\{Q_{\mathit{\text{ik}}}({\nu }^0)-({\beta }_{k1}^0+{\beta }_{k2}^0{G}_{\mathit{\text{ik}}}){\eta }^0(U_{\mathit{\text{ik}}}({\alpha }^0))\}}^{\otimes 2}]\{1+o_p(1)\}.$$

By Taylor’s expansion, we have

$$\nu -{\nu }^0=-{\{{\partial }^2{L}_n({\nu }^0)/\partial \nu \partial {\nu }^{\mathrm{T}}\}}^{-1}\{\partial L_n({\nu }^0)/\nu \}\{1+o_p(1)\}.$$

By the above result, we have (8). Then the asymptotic normality in Theorem 2 follows from the Central Limit Theorem and (8).

A.5 Proof of Theorem 3

Here we show that our method for estimating ν is semiparametric efficient when (Y_i1, …, Y_iK) are independent given ℂ_i. We have that

$$\text{log}\{\text{pr}(Y_i=y_i|{ℂ}_i)\}={\sum }_{k=1}^K\{y_{\mathit{\text{ik}}}\text{log}(H_{\mathit{\text{ik}}})+(1-y_{\mathit{\text{ik}}})\text{log}(1-H_{\mathit{\text{ik}}})\}.$$

The i^th score with respect to ν is $S_{\nu i}={\sum }_{k=1}^K(Y_{\mathit{\text{ik}}}-H_{\mathit{\text{ik}}})Q_{\mathit{\text{ik}}}$. The nuisance tangent space is

$$\mathrm{\Lambda }=\{{\sum }_{k=1}^K(Y_{\mathit{\text{ik}}}-H_{\mathit{\text{ik}}})({\beta }_{k1}^0+{\beta }_{k2}^0{G}_{\mathit{\text{ik}}})\eta (X_{\mathit{\text{ik}}0}+X_{\mathit{\text{ik}}}^{\mathrm{T}}{\alpha }^0):\eta (·)\in {ℝ}^{J+2K+2Kd+Ka-2}\}.$$

We decompose S_νi as S_νi = S_eff,i + S_1i, where

$$S_{\text{eff},i}={\sum }_{k=1}^K(Y_{\mathit{\text{ik}}}-H_{\mathit{\text{ik}}})\{Q_{\mathit{\text{ik}}}-({\beta }_{k1}^0+{\beta }_{k2}^0{G}_{\mathit{\text{ik}}}){\eta }_{0i}\},$$

$$S_{1i}={\sum }_{k=1}^K(Y_{\mathit{\text{ik}}}-H_{\mathit{\text{ik}}})({\beta }_{k1}^0+{\beta }_{k2}^0{G}_{\mathit{\text{ik}}}){\eta }_{0i},$$

$${\eta }_{0i}=\frac{E\{{\sum }_{k=1}^K{V}_{\mathit{\text{ik}}}{Q}_{\mathit{\text{ik}}}({\beta }_{k1}^0+{\beta }_{k2}^0{G}_{\mathit{\text{ik}}})|X_{\mathit{\text{ik}}0}+X_{\mathit{\text{ik}}}^{\mathrm{T}}{\alpha }^0\}}{E\{{\sum }_{k=1}^K{V}_{\mathit{\text{ik}}}{({\beta }_{k1}^0+{\beta }_{k2}^0{G}_{\mathit{\text{ik}}})}^2|X_{\mathit{\text{ik}}0}+X_{\mathit{\text{ik}}}^{\mathrm{T}}{\alpha }^0\}}.$$

Obviously, S_1i ∈ Λ. For any element S_i ∈ Λ, say $S_i={\sum }_{k=1}^K(Y_{\mathit{\text{ik}}}-H_{\mathit{\text{ik}}})({\beta }_{k1}^0+{\beta }_{k2}^0{G}_{\mathit{\text{ik}}})\eta (X_{\mathit{\text{ik}}0}+X_{\mathit{\text{ik}}}^{\mathrm{T}}{\alpha }^0)$, we can easily verify that $E(S_{\text{eff},i}^{\mathrm{T}}{S}_i)=0$.

Thus, S_eff,i is the residual of the orthogonal projection of S_νi onto Λ, hence it is the efficient score. The minimum variance bound for estimating ν is therefore

$${\text{cov}}_{\mathit{\text{opt}}}\{n^{1/2}(\hat{\nu }-\nu )\}={\{E(S_{\text{eff},i}{S}_{\text{eff},i}^{\mathrm{T}})\}}^{-1}={[E{\sum }_{k=1}^K{V}_{\mathit{\text{ik}}}{\{Q_{\mathit{\text{ik}}}-({\beta }_{k1}^0+{\beta }_{k2}^0{G}_{\mathit{\text{ik}}}){\eta }_{0i}\}}^{\otimes 2}]}^{-1}.$$

Since S_1i is the orthogonal projection of S_νi onto Λ, it minimizes the covariance matrix of S_νi − S_i among all the functions S_i ∈ Λ, i.e., η_0i minimizes

$$\text{cov}[{\sum }_{k=1}^K(Y_{\mathit{\text{ik}}}-H_{\mathit{\text{ik}}})\{Q_{\mathit{\text{ik}}}-({\beta }_{k1}^0+{\beta }_{k2}^0{G}_i)\eta (X_{\mathit{\text{ik}}0}+X_{\mathit{\text{ik}}}^{\mathrm{T}}{\alpha }^0)\}]=[E{\sum }_{k=1}^K{V}_{\mathit{\text{ik}}}{\{Q_{\mathit{\text{ik}}}-({\beta }_{k1}^0+{\beta }_{k2}^0{G}_i)\eta (X_{\mathit{\text{ik}}0}+X_{\mathit{\text{ik}}}^{\mathrm{T}}{\alpha }^0)\}}^{\otimes 2}]$$

among all possible $\eta (X_{\mathit{\text{ik}}0}+X_{\mathit{\text{ik}}}^{\mathrm{T}}{\alpha }^0)\in {ℝ}^{J+2K+2Kd+Ka-2}$. This shows that Σ in Theorem 2 reaches the semiparametric efficiency bound, as claimed.

A.6 Proof of Theorem 4

Let ${\epsilon }_{\mathit{\text{ik}}}=({\beta }_{k1}^0+{\beta }_{k2}^0{G}_i)(Y_{\mathit{\text{ik}}}-H_{\mathit{\text{ik}}})$ and ε_i = (ε_i1, …, ε_iK)^T. Following the same procedure as the proof of Theorem 1, we have that ${\Vert {\hat{\lambda }}_w({\nu }^0)-{\lambda }^0\Vert }_2=O_p(n^{-1/2}{P}_n+P_n^{-q+1/2})$. By this result and Taylor’s expansion, we have

$$0={\sum }_{i=1}^n{B}_r(U_i){\mathbf{A}}_i{\mathbf{B}}_i^{-1}{\mathbf{A}}_i^{\mathrm{T}}{B}_r^{\mathrm{T}}(U_i)\{{\lambda }^0-{\hat{\lambda }}_w({\nu }^0)\}+{\sum }_{i=1}^n{B}_r(U_i){\mathbf{A}}_i{\mathbf{B}}_i^{-1}{\epsilon }_i+o_p(n^{1/2}).$$

Thus

$${\hat{\lambda }}_w({\nu }^0)-{\lambda }^0={\{n^{-1}{\sum }_{i=1}^n{B}_r(U_i){\mathbf{A}}_i{\mathbf{B}}_i^{-1}{\mathbf{A}}_i^{\mathrm{T}}{B}_r^{\mathrm{T}}(U_i)\}}^{-1}\times \{n^{-1}{\sum }_{i=1}^n{B}_r(U_i){\mathbf{A}}_i{\mathbf{B}}_i^{-1}{\epsilon }_i\}\{1+o_p(1)\}.$$ (A.16)

Then with probability approaching 1, var{λ̂_w(ν⁰) − λ⁰|ℂ_i} approaches ${\prod }_n^{-1}{\Xi }_n{\prod }_n^{-1}$. Theorem 4 can be proved following the same methods as in the proof of Theorem 1.

A.7 Proof of Theorem 5

Let ζ_i be the d_νK × 1 vector formed by K length d_ν vectors. The kth, k = 1, …, K vector component is $(Y_{\mathit{\text{ik}}}-H_{\mathit{\text{ik}}}(\nu ))\{{\hat{Q}}_{\mathit{\text{ik}}}(\nu )+({\beta }_{k1}+{\beta }_{k2}{G}_i){\{{\hat{\lambda }}_w^{\prime }(\nu )\}}^{\mathrm{T}}{B}_r(X_{i0}+X_i^{\mathrm{T}}\alpha )\}$. Following the same outline as the proof of Theorem 2, it can be proved that

$$\sqrt{n}({\hat{\nu }}_w-{\nu }^0)=\sqrt{n}{({\sum }_{i=1}^n{\mathbf{C}}_i{\mathbf{D}}_i^{-1}{\mathbf{C}}_i^{\mathrm{T}})}^{-1}({\sum }_{i=1}^n{\mathbf{C}}_i{\mathbf{D}}_i^{-1}{\zeta }_i)+o_p(1).$$

Therefore,

$$\text{var}(\sqrt{n}({\hat{\nu }}_w-{\nu }^0)|{ℂ}_i)=n{({\sum }_{i=1}^n{\mathbf{C}}_i{\mathbf{D}}_i^{-1}{\mathbf{C}}_i^{\mathrm{T}})}^{-1}({\sum }_{i=1}^n{\mathbf{C}}_i{\mathbf{D}}_i^{-1}{\mathbf{D}}_i^{\ast }{\mathbf{D}}_i^{-1}{\mathbf{C}}_i^{\mathrm{T}})\times {({\sum }_{i=1}^n{\mathbf{C}}_i{\mathbf{D}}_i^{-1}{\mathbf{C}}_i^{\mathrm{T}})}^{-1}+o_p(1),$$

and the asymptotic normality of $\sqrt{n}({\hat{\nu }}_w-{\nu }^0)$ given in Theorem 5 follows from the Central Limit Theorem.

A.8 Extending to Multiple Study Centers

Here we indicate briefly the necessary changes needed if there are multiple study centers, and multiple dependent disease outcomes within each study center. Suppose that there are k = 1, …, K study centers, with ℓ = 1, …, L_k binary disease outcomes in each center, and with i = 1, …, n_k observations at the k^th center. Write the outcomes at Y_ik = (Y_ik1, …, Y_ikLk), and write the covariates as ℂ_ik = (G_ik, X_ik0, X_ik, Z_ik, G_ikW_ik). The model is

$$\text{pr}(Y_{\mathit{\text{ik}}\ell }=1|{ℂ}_{\mathit{\text{ik}}})=H_{\mathit{\text{ik}}\ell }=H_{\mathit{\text{ik}}\ell }=H\{({\beta }_{k\ell 1}+{\beta }_{k\ell 2}{G}_{\mathit{\text{ik}}})m(X_{\mathit{\text{ik}}0}+X_{\mathit{\text{ik}}}^{\mathrm{T}}\alpha )+Z_{\mathit{\text{ik}}}^{\mathrm{T}}({\theta }_{k\ell 1}+{\theta }_{k\ell 2}{G}_{\mathit{\text{ik}}})+G_{\mathit{\text{ik}}}{W}_{\mathit{\text{ik}}}^{\mathrm{T}}{\theta }_{k\ell 3}\}.$$ (A.17)

We make the same assumptions as in Section A.2, but in addition we assume that lim_{n1, …, nK→∞}(max n_k/ min n_k) = c with 0 < c < ∞.

From the above model, we can see that in different centers, because different physical populations are studied, the same disease occurrence is modeled with different parameters. Thus, we can simply view the L_k diseases in k = 1, …, K centers as ${\sum }_{k=1}^K{L}_k$ different diseases from a single center, and all our analyses formulated for data from one center applies.