Inverse Probability Weighted Cox Regression for Doubly Truncated Data

Summary

Doubly truncated data arise when event times are observed only if they fall within subject-specific, possibly random, intervals. While non-parametric methods for survivor function estimation using doubly truncated data have been intensively studied, only a few methods for fitting regression models have been suggested, and only for a limited number of covariates. In this paper, we present a method to fit the Cox regression model to doubly truncated data with multiple discrete and continuous covariates, and describe how to implement it using existing software. The approach is used to study the association between candidate single nucleotide polymorphisms and age of onset of Parkinson’s disease.

1. Introduction

Truncated data are often encountered in survival problems. Left or right truncation occurs when lifetimes are observed only if they are larger or smaller than a random truncation variable, respectively. Familiar examples from the literature are the left-truncated Channing House data (Hyde, 1977) and the right-truncated HIV incubation data (Kalbfleisch and Lawless, 1989). Here we study random variables that are both left and right truncated to a random interval; these are termed doubly truncated data. Our motivating example is a study of the association of candidate single nucleotide polymorphisms (SNP’s) and age of onset of Parkinson’s disease (Clark et al, 2011, Austin, Simon and Betensky 2014). To limit selection biases related to survival, the patients were required to have had their DNA sample taken within eight years of their onset of Parkinson’s disease, and additionally, their onset age was required to be prior to their DNA sample. Thus, the age of onset is right truncated by the age at blood sampling for genetic analysis and left truncated by age at sampling minus eight years.

Let h_T(t) ≔ lim_Δ↘0 P(t ≤ T ≤ t + Δ | T ≥ t) be the hazard function of the time variable T. The data are left truncated when T is observed only if T ≥ L, for some random variable L. Since {T ≥ L} ⊃ {T ≥ t} on t ≥ L, the hazard for a left truncated lifetime satisfies h_T|L(t | l) ≔ lim_Δ↘0 P(t ≤ T ≤ t + Δ | T ≥ t, T ≥ L, L = l) = h_T (t)I(t ≥ l), where I(·) is the indicator function. This unique relation shows that the standard risk-set approaches, applied by the non-parametric product-limit estimator and the Cox’s regression maximum partial likelihood estimator, can be readily modified to left truncated data by including a subject in risk sets only from his truncation time on. However, this equivalence relation between the conditional hazard and the marginal hazard does not hold for right or doubly truncated observations for which sampling is restricted to observations satisfying T ≤ U or L ≤ T ≤ U, where U is the right truncation random variable. Therefore, specialized methods are required for analysis of such data.

Non-parametric approaches for estimating the survivor function of doubly truncated data use the self-consistency algorithm of Turnbull (1976) or similar iterative algorithms (see Efron and Petrosian 1999, Shen 2010). These methods are implemented in the R package DTDA (Moreira, de Uña-Álvarez and Crujeiras 2010). Austin et al. (2014) study doubly truncated data under independence of the left and right truncation variables and under parametric models for the truncation distribution (see also Moreira and de Uña-Álvarez 2010).

To date, only few papers deal with regression methods for doubly truncated data. Alioum and Commenges (1996) extend Turnbull’s (1976) non-parametric approach to the proportional hazards model. They jointly maximize the regression coefficients and the baseline survival curve using an EM or a Newton-Raphson type algorithm. As the number of parameters grows with sample size (for the non-parametric part of the baseline survival function), maximization is quite challenging and problems with inverting the second-derivative may occur. Shen (2013) studies a family of regression models for doubly truncated and doubly censored data, which includes as a special case the proportional hazards model. His method requires consistent non-parametric estimators for the survivor function for each covariate value, and therefore is applicable only for discrete covariates having few categories. Moreira, de Uña-Álvarez and Meira-Machado (2016) study non-parametric regression in the framework of doubly truncated data. They observe that the density of sampled lifetimes is weighted by the bivariate distribution of the truncation variables, which motivates their use of inverse probability weights. The latter probabilities are estimated non-parametrically using the approach of Shen (2010). Being non-parametric, their method is best suited to one continuous covariate. Shen (2016) and Shen and Liu (2017) suggest methods that can handle continuous and discrete covariates; the first is based on estimating equations similar to those used by Shen (2013) and the second is based on the EM algorithm.

In this paper, we propose a new approach for Cox regression analysis of doubly truncated data. As in Moreira et al. (2016), we view the truncated lifetimes as having a weighted or biased distribution, and modify the approach of Qin and Shen (2010) for length biased observations to handle data with more general biased sampling mechanisms. Unlike the length-bias case that assumes a uniform distribution for the truncation variable, the weight function here depends on the unknown bivariate distribution of the truncation variables, which we propose to estimate non-parametrically.

Section 2 describes the new estimation approach and discusses its large sample properties, with technical details deferred to the Web Appendix. Section 3 examines the estimator’s performance using simulations, and Section 4 applies it to Parkinson’s disease data. A brief discussion completes the paper.

2. Estimation

2.1 Estimation of Regression Parameters

Consider a lifetime variable T and a covariate vector Z satisfying, in the general population, the Cox model

$$h(t|z;\beta )=h_0(t)\text{ exp}({\beta }^{t}z),$$ (1)

where h(· | z; β) is the hazard function of T conditional on the covariate realization z, h₀(·) is a baseline hazard function, and β is the vector of coefficients. For simplicity of presentation, we consider only a single covariate, but the extension to multiple covariates is straightforward.

In the context of double truncation, the sample is not randomly selected from the population, but instead is truncated to the region L ≤ T ≤ U, where (L, U) is a random truncation interval that follows a bivariate law G. In many examples, (L, U) is independent of (T, Z), which greatly simplifies estimation and inference. We assume such an independence throughout the paper, and consider inference based on independent realizations (T₁, Z₁, L₁, U₁), …, (T_n, Z_n, L_n, U_n) of (T, Z, L, U) conditionally on the double-truncation event D = {L ≤ T ≤ U}. Denote by W(t) = P(L ≤ t ≤ U) the probability of observing a lifetime of length t, and assume that W(t) > 0 on the support of T. The joint density of sampled observations is

$$f_{L,U,T,Z|D}(l,u,t,z)=\frac{W(t)h(t|z;\beta )\text{ exp}(-{\int }_0^{t}h(y|z;\beta )\mathit{\text{dy}})f_Z(z)}{E\{W(T)\}}\times \frac{G(\mathit{\text{dl}},\mathit{\text{du}})I(l<t<u)}{W(t)},$$ (2)

where f_V denotes the density of a random variable V. The right-hand side of (2) involves multiplication by W (t) in the first factor, followed by division by W(t) in the second factor, to facilitate representation of the joint density as the product of the marginal density of (T, Z) | D (first term) and the conditional density of (L, U) | {(T = t, Z = z), D}. The rightmost term in (2) does not involve β, so estimation of β can be carried out based on the first term

$$f_{T,Z|D}(t,z)=\frac{W(t)h(t|z;\beta )\text{ exp}(-{\int }_0^{t}h(y|z;\beta )\mathit{\text{dy}})f_Z(z)}{E\{W(T)\}},$$ (3)

which is the joint density of the lifetime and the covariates weighted by W(t). The weighted density of lifetimes conditional on the covariate is therefore

$$f_{T|Z,D}(t|z)=\frac{W(t)h(t|z;\beta )\text{ exp}(-{\int }_0^{t}h(y|z;\beta )\mathit{\text{dy}})}{E\{W(T)|z\}}.$$ (4)

Note that E{W(T) | z} = P(L ≤ T ≤ U | z) depends on β, and thus this biased sampling must be accounted for in the estimation of β.

In the framework of length-biased data, Qin and Shen (2010) consider inference on proportional hazards models with likelihood terms similar to (4) and W(t) = t. Here W(t) is more general, and moreover, it is unknown. We propose estimation of W, which is a functional of the bivariate distribution G, using the triplets (T, L, U) sampled under the double truncation rule, followed by use of (4) for estimation of β. This approach is closely related to that taken by Qin and Shen (2010) to deal with censoring.

Since the weight in (3) is a function of t alone, it follows that f_Z|T,D = f_Z|T, and we can therefore use the following standard probabilistic result for the Cox model:

$$E(Z|T=t,D)=E(Z|T=t)=\frac{E\{{\mathit{\text{Ze}}}^{\beta Z}{\overline{F}}_{T|Z}(t|Z)\}}{E\{e^{\beta Z}{\overline{F}}_{T|Z}(t|Z)\}},$$

where F̄ = 1−F denotes a survivor function. Letting f_Z|D(z) = E{W(T) | z}f_Z(z)/E{W(T)} denote the marginal weighted density of the covariate, we have

$$E(Z|T=t,D)=\frac{E[{\mathit{\text{Ze}}}^{\beta Z}{\overline{F}}_{T|Z}(t|Z)/E\{W(T)|Z\}|D]}{E[e^{\beta Z}{\overline{F}}_{T|Z}(t|Z)/E\{W(T)|Z\}|D]},$$ (5)

which represents the expectation in terms of the observable truncated variables. However, (5) contains the term F̄_T|Z(t | Z)/E{W(T) | Z}, which involves functionals of the variables Z and T unconditionally on D. To represent the expectation as a function of observed variables, we see from (4) and the assumption that W(t) > 0 on the support of T that

$$E[{\{W(T)\}}^{-1}I\{T\ge t\}|Z=z,D]={\overline{F}}_{T|Z}(t|z)/E\{W(T)|Z=z\},$$ (6)

and after plugging (6) into (5) we obtain

$$E(Z|T=t,D)=\frac{E[{\mathit{\text{Ze}}}^{\beta Z}{\{W(T)\}}^{-1}I\{T\ge t\}|D]}{E[e^{\beta Z}{\{W(T)\}}^{-1}I\{T\ge t\}|D]}.$$ (7)

Thus, if (Z₁, T₁) and (Z₂, T₂) are independent pairs in the sample, then

$$E(Z_1|D)=\mathit{\text{EE}}(Z_1|T_1,D)=E\left(\frac{E[Z_2{e}^{\beta Z_2}{\{W(T_2)\}}^{-1}I\{T_2\ge T_1\}|T_1,D]}{E[e^{\beta Z_2}{\{W(T_2)\}}^{-1}I\{T_2\ge T_1\}|T_1,D]}\right|D).$$

The last identity suggests the estimating equation

$$U(\beta )=\sum _{i=1}^n\left[Z_i\frac{{\sum }_{j=1}^n{Z}_j{e}^{\beta Z_j}{\{W(T_j)\}}^{-1}I\{T_j\ge T_i\}}{{\sum }_{j=1}^n{e}^{\beta Z_j}{\{W(T_j)\}}^{-1}I\{T_j\ge T_i\}}\right]=0.$$ (8)

As W is unknown, we propose the following estimation algorithm:

1. Calculate the non-parametric maximum likelihood estimate of G and then calculate W(T_i) = P(L ≤ T ≤ U | T = T_i) = G(T_i, ∞) − G(T_i, T_i−) for i = 1, …, n. Estimation of G is discussed in Section 2.2.

2. Plug W into (8) and solve for β. This can be accomplished by calling the function coxph in the survival package of R (Therneau 2015), introducing − log{W(T_j)} as an offset with coefficient 1 (e.g., coxph(srv.object ~ covariates + offset(−log(W))).

The method can easily handle multiple discrete or continuous covariates and is implementable using existing R functions. However, the standard errors produced by R are not valid as they do not account for the additional variability induced by estimation of the weights. For estimation of standard errors and construction of confidence intervals, we suggest use of the bootstrap.

2.2 Estimation of G

Joint non-parametric estimation of the lifetime distribution, F, of T and the bivariate distribution, G, of (L, U) are discussed by Shen (2010) and are implemented in the function shen in the DTDA package of R (Moreira et al. 2010). Here we suggest a faster way to calculate Shen’s estimator of G using its relation to the estimate of F suggested by Efron and Petrosian (1999), which is based on the likelihood of T conditional on the event {T ∈ [L, U]}.

As in many non-parametric problems, the estimators assign mass only to observed points, that is, F̂ assigns positive mass only to observed lifetimes, t₁, …, t_n, and Ĝ assigns positive mass only to the observed truncation pairs, (l₁, u₁), …, (l_n, u_n). For simplicity we assume no ties, and denote by f_i the mass assigned to the value t_i, and by g_i the mass assigned to the pair (l_i, u_i). Let ${\mathrm{P}}_i=P(l_i\le T\le u_i)={\sum }_{j=1}^n{f}_{j}I(l_i\le t_j\le u_i)$ be the probability that a lifetime, not subject to truncation, falls in the interval [l_i, u_i]. The likelihood of the doubly truncated data, (t_i, l_i, u_i) i = 1, …, n, is given by (see Equation (2) of Moreira et al. 2010):

$$\prod _{i=1}^n\frac{f_i}{{\mathrm{P}}_i}\times \prod _{i=1}^n\frac{{\mathrm{P}}_i{g}_i}{{\sum }_{j=1}^n{\mathrm{P}}_j{g}_j}.$$ (9)

While Shen (2010) maximizes (9) for ${\{f_i\}}_1^n$ and ${\{g_j\}}_1^n$ simultaneously, Efron and Petrosian (1999) maximize the first term in (9) with respect only to ${\{f_j\}}_1^n$. Inspecting the likelihood, it is seen that the second term is a weighted density of G, with g_i weighted by P_i. This term is maximized by assigning mass proportional to 1/P_i to the ith observation (e.g., Vardi 1985). Thus, profiling out g_i by replacing it with 1/P_i in the likelihood above, clarifies that the conditional approach of Efron and Petrosian (1999) yields the NPMLE of F also for the problem of maximizing F and G simultaneously.

The discussion above reveals that ĝ_i ∝ 1/P̂_i is the maximum likelihood estimate of g_i, where P̂_i is the Efron and Petrosian’s estimate of P_i. The latter is implemented by the efron.petrosian function in the DTDA package of R (Moreira et al. 2010).

Our proposed estimator is based on the unconstrained model for G, which is also the estimator for the setting L = U −d₀ for some constant d₀ used for the Parkinson’s disease data analyzed in Section 4. See Austin et al. (2014) for estimation of G under the independence assumption between L and U, and Moreira and de Uña-Álvarez (2010) for estimation of a parametric model for G.

2.3 Large Sample Properties

The estimating equation (8) involves the weight function W, which is known only in very special circumstances. In practice, the estimator β̂ is the solution of (8) with Ŵ substituted for W. This complicates the analysis considerably as the estimator Ŵ in the most general double truncation case does not have a closed form, see Section 2.2. We conjecture that the following two conditions hold for Ŵ under the assumptions and regularity conditions listed in Web Appendix A:

• Conjecture 1 (Uniform convergence): max_1≤i≤n{Ŵ(T_i) − W(T_i)} → 0 in probability.

• Conjecture 2 (IID representation): $\sqrt{n}\{\hat{W}(t)-W(t)\}=n^{-1/2}{\sum }_{i=1}^n{\zeta }_n({𝒟}_i,t)+o_p(1)$ uniformly on t ∈ [t_min, t_max], where 𝒟_i = (T_i, L_i, U_i) is the data for subject i, and ζ_n(𝒟_i, t) are independent and identically distributed zero mean random variables having finite variance.

It is shown in the Web Appendix that if these two strong conditions hold, then under certain standard regularity conditions the solution of (8) with Ŵ plugged-in is consistent and asymptotically normal. In fact, the result in the Web Appendix is not limited to the double truncation model and applies to observations (T_i, Z_i) that follow model (3) with a certain weighting function W and with h(t|z) given by model (1).

Uniform consistency and asymptotic normality of the estimator of W are established by Woodroofe (1985) for the right and left truncation models, which are special cases of the double truncation model with L ≡ −∞ and U ≡ ∞, respectively. Many authors have studies the double truncation model, see Section 2.2 for several references, but large sample properties have not been established. The main difficulty is that Ŵ is obtained in an iterative algorithm and lacking a representation as a functional of an empirical process, so standard techniques do not apply. Recently, Shen (2016) gives conditions under which Conjectures 1 and 2 are claimed to hold, but the technical proofs are incomplete, and more investigation is needed. This is beyond to scope of the current paper.

The variance of the estimator is quite complicated and we consider instead a simple bootstrap approach that generates samples of n observations with replacement from the data and estimates W and then β in each. This approach is recommended by Shen (2016) and Shen and Liu (2017) who use the variance of the bootstrap estimates to generate normal based confidence intervals. As we could not formally prove asymptotic normality for the truncation mechanism of our data, L = U − 8, we explore in the simulation study also the performance of qunatile bootstrap intervals having the form $(2\hat{\beta }-{\beta }_{1-\alpha /2}^{\ast },2\hat{\beta }-{\beta }_{\alpha /2}^{\ast })$, where ${\beta }_{\alpha }^{\ast }$ is the α percentile of the bootstrap sample (Davison and Hinkley 1997).

3. Simulations

Truncation may affect the sample size and the Fisher information carried by the observed data (Iyengar, Kvam, and Singh 1999), and our first set of simulations explores the effect of double truncation on inference. We generated T from the linear baseline hazard model h₀(t) = 2t. The explanatory variable Z was either a continuous covariate having a standard normal distribution or a binary covariate with probability P(Z = 1) ≈ 0.38; for both, we set β = 1. The truncation limits L and U were generated independently from the Gamma(1,2) and Gamma(2,1) distributions. We first sampled 1000 covariate realizations, Z₁, …, Z₁₀₀₀, and conditional on the Z’s, we generated 1000 triplets (L, U, T); these comprise the complete unbiased sample. We then generated the truncated sample by retaining only those observations that satisfied L ≤ T ≤ U (about 500–550 on average). Finally, we estimated β using the following three approaches:

1. Standard Cox model, using the complete data (1000 observations) before truncation.

2. Standard Cox model, using the truncated data but not accounting for truncation.

3. Weighted Cox model, using the truncated data and accounting for truncation.

Although we generated (L, U) as independent random variables, we did not exploit that in our estimation of the weights for approach III. Table 1 presents the average bias of β̂, the standard deviation of the estimates and the average of the naive analytical standard errors provided by the R coxph function, based on 1000 simulations.

Table 1.

Bias and variance of β̂ (β = 1) using the complete data (I), the truncated data with no adjustment for truncation (II) and the truncated data using the proposed weighted method (III).

		Estimation approach
Z		I	II	III
binary	mean bias	−0.003	0.050	−0.003
	simulation SD	0.073	0.095	0.100
	mean estimated SE	0.070	0.095	0.095
continuous	mean bias	−0.001	0.113	0.001
	simulation SD	0.043	0.059	0.070
	mean estimated SE	0.042	0.061	0.059

Clearly, accounting for truncation is important and ignoring it (approach II) may lead to a substantial bias. The magnitude of the bias depends on the nature of the truncation, and in this simulation is worse for a continuous covariate than for the binary covariate. It is also seen that our approach for estimation of β is quite efficient, with empirical standard deviations that are 37% and 63% larger than those from the complete sample, which is in the range of what would be expected for a 50–55% decrease in sample size due to truncation. Finally, while our weighting approach provides valid estimates for β, it underestimates the variances, as seen by comparing the average analytical standard errors with the empirical standard deviations of the estimates. Thus, an alternative procedure, such as the bootstrap, should be used for variance estimation and confidence interval construction.

The second set of simulations compares the inverse weighting approach to the EM method recently suggested by Shen and Liu (2017). Data were sampled from the following model: h(t | z₁, z₂; β) = exp(t − 2z₁ − 3z₂), z₁ a binary covariate with probability 0.5, and z₂ uniformly distributed on {1,2,3,4}. The left limit of the truncation interval, L, was generated independently of lifetimes and covariates from the Exponential distribution with mean 4, and U = L + d₀ for d₀ = 6,9,12, which corresponded to P(L ≤ T ≤ U) ≈ 0.42, 0.62 and 0.75, respectively. The parameters β₁, β₂ were estimated using our proposed inverse weighting method and were compared to the results of Shen and Liu (2017). Each of the settings was repeated 400 times with 1000 bootstrap samples. As in Shen and Liu (2017), bootstrap confidence intervals were calculated using the normal approximation β̂±z_1−α/2SE_boot, where z_α is the α normal quantile and SE_boot is the bootstrap estimate of the standard error.

Table 2 compares the performance of the inverse weighting estimator to the EM approach suggested by Shen and Liu (2017). Both the bias (Bias) and empirical standard error (ESE) decrease with sample size, with the bias becomes 3–6 times smaller than the standard error for the settings with n = 400. The average of the bootstrap estimates of the standard error (ASE_boot) is quite close to the empirical standard error. The confidence intervals look somewhat conservative, though still perform quite well. We explore also the performance of 95% quantile based bootstrap intervals (cover2) described at the end of Section 2.3. These intervals perform well, though for two settings they were anti-conservative. Comparing the inverse weighting method to that recently suggested by Shen and Liu (2017), it is seen that the inverse weighting estimators have smaller variances (and smaller MSEs) and the bootstrap estimator of the standard errors performs better. The method of Shen and Liu (2017) has smaller bias (but larger variance) when the probability of truncation is small (d₀ = 12, P(L ≤ T ≤ U) ≈ 0.75).

Table 2.

Bias, empirical standard error (ESE), average of the bootstrap estimate of standard error (ASE_boot), and coverage of 95% normal confidence intervals (cover) and quantile based intervals (cover2).

			Shen and Liu Approach				Inverse Weighting Approach
β	d0	n	Bias	ESE	ASEboot	cover	Bias	ESE	ASEboot	cover	cover2
β1	6	100	0.229	0.400	0.365	0.936	−0.130	0.319	0.339	0.959	0.949
	6	200	0.153	0.301	0.282	0.940	−0.071	0.205	0.215	0.958	0.958
	6	400	0.105	0.166	0.159	0.944	−0.024	0.144	0.146	0.955	0.935
	9	100	0.117	0.382	0.348	0.937	−0.124	0.299	0.328	0.975	0.963
	9	200	0.096	0.263	0.252	0.941	−0.069	0.197	0.207	0.965	0.960
	9	400	0.072	0.137	0.132	0.945	−0.033	0.140	0.141	0.950	0.970
	12	100	0.070	0.323	0.297	0.939	−0.136	0.291	0.324	0.975	0.960
	12	200	0.038	0.256	0.241	0.942	−0.069	0.185	0.205	0.982	0.970
	12	400	0.015	0.132	0.126	0.947	−0.031	0.135	0.138	0.950	0.953
β2	6	100	0.384	0.520	0.482	0.937	−0.204	0.324	0.358	0.962	0.964
	6	200	0.235	0.393	0.365	0.941	−0.102	0.206	0.222	0.955	0.950
	6	400	0.186	0.192	0.184	0.944	−0.050	0.162	0.148	0.935	0.918
	9	100	0.197	0.454	0.420	0.938	−0.188	0.309	0.330	0.975	0.943
	9	200	0.138	0.298	0.280	0.942	−0.088	0.193	0.207	0.972	0.943
	9	400	0.085	0.143	0.137	0.945	−0.045	0.135	0.140	0.965	0.945
	12	100	0.069	0.447	0.422	0.940	−0.181	0.292	0.333	0.988	0.953
	12	200	0.027	0.286	0.269	0.943	−0.097	0.189	0.209	0.968	0.945
	12	400	0.010	0.150	0.144	0.946	−0.049	0.144	0.140	0.952	0.923

A third simulation study was conducted in order to compare the performance of the inverse weighting estimator to that of the standard delayed entry approach for left truncated data. We use the settings of Shen and Liu (2017) described above, but set U = ∞. The delayed entry approach maximizes the partial likelihood Π_i exp(βZ_i)/Σ_j∈Ri exp(βZ_j), where R_i = {j | L_j ≤ T_i ≤ T_j}. Table 1 in the Web Appendix compares the bias and the mean squared errors (MSEs) of the two approaches based on 400 replications. Both the bias and the MSE of the two approaches are comparable, showing no advantage of either method. It will be interesting to further explore the differences of the two approaches in other settings and under right censoring. This is beyond the scope of the current paper.

4. Parkinson’s Age of Onset Study

Several studies have implicated mitochondrial dysfunction and oxidative stress in the pathogenesis of Parkinsons disease (PD)(e.g., Shapira, 2008, Sherer et al, 2002, Thomas and Beal, 2007). Deficiency of PGC-1a, which regulates mitochondrial biogenesis and antioxidant defenses, also has been implicated in PD (Clark and Simon, 2009, Shin et al, 2011). A previous study (Clark et al, 2011) hypothesized that the rs8192678 PGC-1a single nucleotide polymorphism (SNP) and the A10398G mitochondrial SNP may influence risk or age of onset of PD. To test these hypotheses, genomic DNA samples from human blood samples were obtained from the National Institute of Neurological Disorders and Stroke (NINDS) Human Genetics DNA and Cell Line Repository at the Coriell Institute for Medical Research (Camden, New Jersey). The samples consisted of DNA from 199 Caucasian PD patients with either earlier onset PD (age 35–55 years) or later onset PD (age 63–87 years). The separate samples of early and late onset cases were undertaken in recognition of the possibility that there may be different genetic mechanisms that vary by age. Thus, the regression model fitted to the data assumes

$$h(t|z,T\le 55)=h_0(t)\text{ exp}({\beta }_{\mathit{\text{Early}}}^{t}z)$$

$$h(t|z,T\ge 63)={\stackrel{\sim }{h}}_0(t)\text{ exp}({\beta }_{\mathit{\text{Late}}}^{t}z).$$ (10)

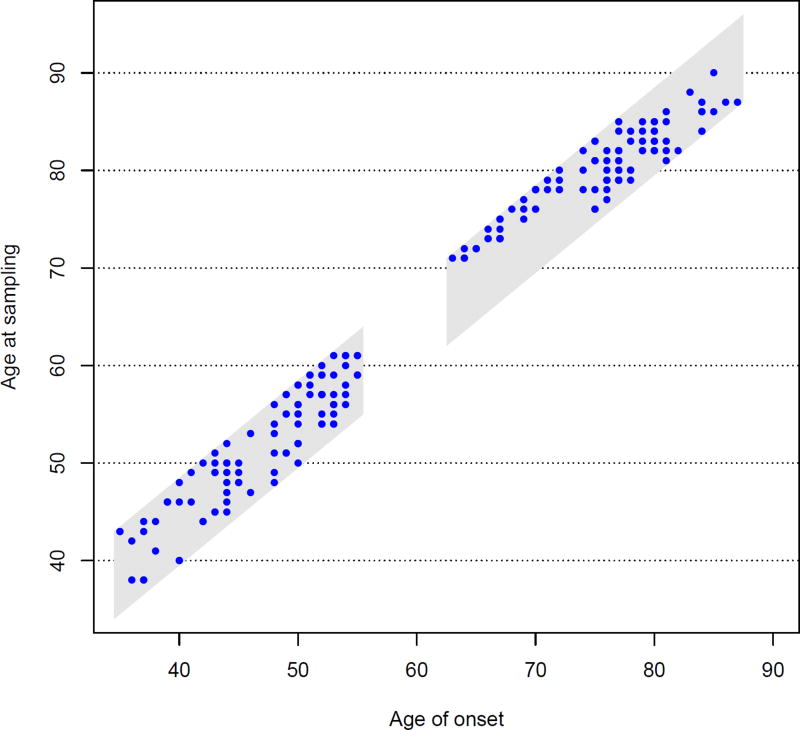
As described in Section 1, the sampling mechanism translates into double truncation for age of onset by the interval [L, U], where U =age at sampling and L=age at sampling-8 years. Note, by (10), that the right truncation time for the early onset group is min(U, 55) and the left truncation time for the late onset group is max(L, 63). However, these additional truncations have no effect on the non-parametric estimate of W. The ages of onset and associated truncation regions are shown in Figure 1.

Figure 1.

The truncation region (grey) and the survival data. Patients were sampled independently in the early and late onset groups.

The earlier publication on these data (Clark et al, 2011) treated only the right truncation of age of onset by age at DNA sampling. Several modeling approaches undertaken in that paper, which all adjusted in some way for the right truncation, did not find a significant association between either the rs8192678 PGC-1a SNP or the A10398G SNP and risk of PD or age of onset of PD. Here we fit separate Cox models to the early and late onset groups as described in (10). The SNP frequencies are given in Table 3. Two patients from the early-onset group have missing data on A10398G SNP and on age of sampling and therefore are excluded from the analysis.

Table 3.

SNP distributions in the two age groups

		Early Onset			Late Onset
		PGC-1a			PGC-1a
		A	AG	G	A	AG	G
SNP10398	A	6	40	30	7	30	36
	G	2	10	9	3	7	17

In order to estimate the effect of the SNPs on the age of onset, proportional hazards models were fit, one to each gene separately (univariate model) and one with the two genes assuming additive effects. Interaction terms are not included due to small samples (see Table 3). The main results are presented in Table 4; data and R code for the multivariate analysis are provided in the Web Appendix. Confidence intervals were calculated based on 2000 bootstrap samples using the quantile approach described in Section 3.

Table 4.

Results of univariate and multivariate models. β̂ - coefficient, 95% CI - bootstrap confidence interval, β̂_naive - estimate without correction for double truncation.

		Early Onset			Late Onset
SNP	Allele	β̂	95% CI	β̂naive	β̂	95% CI	β̂naive
SNP10398	G	−0.126	[−0.62,0.32]	−0.137	0.623	[−0.31,1.26]	0.157
PGC-1a	AG	0.150	[−0.23,0.54]	0.238	−1.161	[−2.00,0.21]	−0.637
	G	0.196	[−0.28,0.64]	0.340	−0.560	[−1.06,0.19]	−0.273
SNP10398	G	−0.140	[−0.68,0.34]	−0.169	0.598	[−0.04,1.18]	0.145
PGC-1a	AG	0.144	[−0.26,0.55]	0.288	−1.193	[−2.03,0.01]	−0.648
PGC-1a	G	0.210	[−0.28,0.63]	0.360	−0.639	[−1.13,0.00]	−0.295

The univariate and multivariate analyses agree well; neither detects any association between the two SNPs and PD age of onset among those with early onset. The effect of the SNPs on age of onset among those with later onset is less clear, as the confidence intervals for SNP PGC-1a barely include 0. We also note that blood sampling was conducted very close to onset for subjects who had onset between ages 63–75 (see Figure 1), which suggests that there may have been an additional formal or informal selection mechanism for this group, about which we are unaware. Fitting the Cox model only to patients with age of onset 75+ (n = 65), the coefficients of the PGC-1a SNP become marginally significant (not shown). However, this latter analysis is data driven and therefore more data must be collected for this group in order to evaluate the association between the PGC-1a SNP and age of onset. Our null findings are consistent with those of Clark et al (2011), although our results account for both the left and right truncation of age of onset in these data rather than solely for right truncation.

Table 4 also compares the estimates based on inverse weighting to the naive approach that does not account for double truncation. The differences are substantial, emphasizing the importance of correcting for selection bias. Figure 1 in the Web Appendix presents box-plots of the weights for the different genotype groups; the difference in the distributions of weights, especially between the PCG-1a genotypes, may explain the difference in the results.

5. Discussion

The popularity of the semi-parametric proportional hazards regression model is attributed to the fact that likelihood-based estimation and inference can be conducted based on the parametric portion of the model via the partial likelihood. Left truncated data are easily accommodated through redefintion of the risk sets. However, when data are subject to right or double truncation, the risk-sets cannot be easily corrected and the partial likelihood approach breaks down. A solution developed in this article is to view truncation as a selection mechanism that produces biased or weighted data. This suggests inference using inverse weighting of the standard estimating equations, where the weights may be estimated using the data at hand. This idea, that was demonstrated here for double truncation, can be applied to many other problems; one of special interest is right truncated data.

Moreover, several authors have studied various semi-parametric models for length-bias or more general selection bias. See, for example, Tsai (2009), Shen (2009), Shen, Ning, and Qin (2009), Huang, Qin, and Follmann (2012), and Kim et al. (2013). The inverse weighting approach suggested here for the proportional hazards model may be adopted also to other models. This is a topic for further research.

The method studied here assumes that the lifetime variables, (Z, T), are independent of the truncation variables, (L, U). Austin et al. (2014) develop a test for quasi-independence of truncated data when the left truncation variable functionally depends on the right truncation variable (e.g., L = U−d₀, for some constant d₀). They applied the test to Parkinson data and found that independence is indeed plausible (p value = 0.186). In case of dependence between (Z, T) and (L, U), the weight function becomes W(t, z) = P(L ≤ t ≤ U | T = t, Z = z) and it is no longer a function of G alone. A possible direction, not studied here, is to model W as a function of t and z and to implement the inverse weighting approach.