Hydrodynamics in Cell Studies

Abstract

Hydrodynamic phenomena are ubiquitous in living organisms and can be used to manipulate cells or emulate physiological microenvironments experienced in vivo. Hydrodynamic effects influence multiple cellular properties and processes, including cell morphology, intracellular processes, cell–cell signaling cascades and reaction kinetics, and play an important role at the single-cell, multicellular, and organ level. Selected hydrodynamic effects can also be leveraged to control mechanical stresses, analyte transport, as well as local temperature within cellular microenvironments. With a better understanding of fluid mechanics at the micrometer-length scale and the advent of microfluidic technologies, a new generation of experimental tools that provide control over cellular microenvironments and emulate physiological conditions with exquisite accuracy is now emerging. Accordingly, we believe that it is timely to assess the concepts underlying hydrodynamic control of cellular microenvironments and their applications and provide some perspective on the future of such tools in in vitro cell-culture models. Generally, we describe the interplay between living cells, hydrodynamic stressors, and fluid flow-induced effects imposed on the cells. This interplay results in a broad range of chemical, biological, and physical phenomena in and around cells. More specifically, we describe and formulate the underlying physics of hydrodynamic phenomena affecting both adhered and suspended cells. Moreover, we provide an overview of representative studies that leverage hydrodynamic effects in the context of single-cell studies within microfluidic systems.

1. Introduction

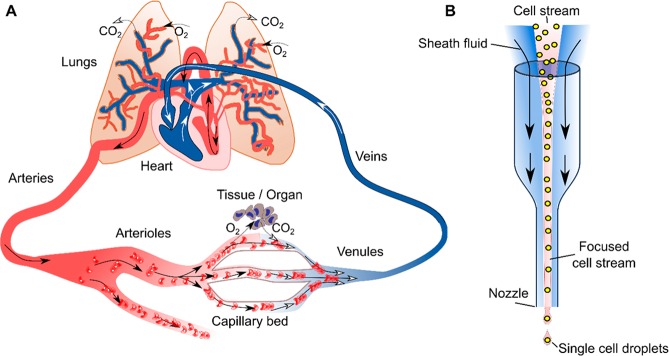
Hydrodynamic phenomena are critical in almost all physiological functions and bodily systems. A prominent example is the cardiovascular system, wherein the heart, a mechanical pump, maintains blood flow throughout an intricate network of blood vessels. Blood, containing red and white cells, flowing through the body ensures sustained cell metabolism and, among other functions, defends the body against pathogens (Figure 1A). Both the flow of blood and the kinematics of blood cells are ultimately governed by the laws of fluid mechanics. The flow of blood and other bodily fluids within the body exerts mechanical stimuli on adherent and nonadherent cells within the endothelium and epithelium, and triggers cell response to mechanical stimulation.^1,2 For instance, endothelial cells representing the walls of blood vessels and capillaries respond to an increase in shear stress due to increased blood pressure by secreting nitric oxide, which in turn results in vasodilation and alleviation of blood pressure.^3,4 Another prominent example for the central role of hydrodynamics within the body is the interaction of leukocytes with blood flow and their sequestration by the walls of blood vessels in immune response and inflammation.^5,6

Figure 1.

Contrasting blood circulation inside the body with artificially created structures used to realize hydrodynamic focusing in single-cell analysis. (A) The heart pumps oxygen-rich blood from its left chamber into the circulatory system. Blood flows through arteries and arterioles before it reaches capillaries supplying target organs and cells with nutrients and oxygen. Subsequently, oxygen-poor blood continues through venules and veins back into the right chamber of the heart. From there, it is pumped to the lungs, where red blood cells are replenished with oxygen. The blood finally flows back into the left heart chamber, from where it can re-enter the circulatory system. (B) Hydrodynamic focusing in flow cytometry. A sheath fluid flow within a capillary engulfs a central cell-laden stream. Control of the velocities and/or densities of the two liquid streams allows formation of a stable two-layer flow, with cells moving in single file toward a detector and outlet nozzle.

The application of hydrodynamic effects on living cells in laboratory environments dates back to the 1960’s, with the first demonstrations of Coulter counters and flow cytometers.^7,8 In most flow cytometers, a sheath flow is used to focus the cells into a narrow stream, whereby they move in single file and can be probed and counted in a sequential fashion (Figure 1B). During the past 20 years, the development and maturation of microfluidic technologies enabled manipulation and control of minute volumes of fluids geometrically constrained within environments with characteristic dimensions on a scale of microns, thereby spawning a new generation of cell manipulation tools that leverage the physics of flows on micron length-scales. These microfluidic technologies in conjunction with novel materials and microfabrication techniques are now routinely providing experimentalists with novel capabilities for cell manipulations and studies. Put simply, microfluidic systems afford precise control and engineering of cell microenvironments down to the single-cell level. This level of control has allowed researchers to begin to emulate physiological microenvironments or functional organs using a range of microengineered cell or tissue culture platforms. For wall-adherent cells hydrodynamic control of the microenvironment affects not only the rate of nutrient delivery and replenishment but also defines the dispersion rate (and dilution) of extracellular molecules as well as mechanical stress, such as the shear stress on wall-adherent cells. For suspended cells (“nonadherent”) in a microscale flow, hydrodynamic forces control cellular trajectories and have long been used in cell studies. In this review, we term cells “adhered”, if they are attached to the channel wall during the microfluidic study. Depending of the experimental settings, a certain cell type appears in the adhered or suspended state: leukocytes are adhered in cell migration experiments (section 2.2.3) and suspended in cell sorting experiments (section 3.3).

Indeed, hydrodynamics has been exploited to sort, focus, manipulate, and isolate cells in a passive fashion and has the potential to replace relatively more intrusive methods for cell manipulation that include external forces, such as dielectrophoresis,⁹⁻¹⁴ magnetophoresis,¹⁵⁻¹⁸ acoustophoresis,¹⁹⁻²² and immunomagnetic cell sorting.²³⁻²⁶

Hydrodynamic control of cellular microenvironments represents a toolbox comprising hydrodynamic control of mechanical stresses, hydrodynamic control of analyte transport (and convection/diffusion of molecules), as well as hydrodynamic control of local temperature. These tools can be exploited to create local or universal conditions that can support a certain line of biological investigations. Mechanical stresses not only can alter cell morphology and intracellular processes but also can affect reaction kinetics and association/dissociation rates (for instance, in scenarios where cell–cell or cell–surface binding reactions are of interest).²⁷ Moreover, flow-induced concentration gradients and dispersion of ligands can significantly alter cell fate, for instance, in the context of stem-cell differentiation. Indeed, flow-induced concentration gradients may be used to precisely control and vary the amount of a chemical to which each cell or population of cells is exposed.

Herein, we comprehensively review the role of hydrodynamics in studies of single mammalian cells and describe, in simple mathematical terms, the basic hydrodynamic phenomena present in cellular microenvironments. We hope that such a review will provide readers (of varied backgrounds) with the necessary information and theoretical guidelines to both understand and apply hydrodynamics in the context of cell studies. Furthermore, we believe that such a review is especially timely as new in vitro cell culture and organ-on-chip models are becoming increasingly popular in drug screening and personalized medicine. We aim to describe relevant theoretical concepts from a simplified and understandable point of view but without sacrificing critical details. In this respect, we strive to find a balance between theory and application, with a view to engaging a more general audience and adopting a language that is free of application-specific jargon (and with only a minimum use of fluid mechanics terminology). In addition, we identify discrepancies and inconsistencies in certain application areas, particularly those pertaining to suspended cells in flow and attempt to reconcile such disparities.

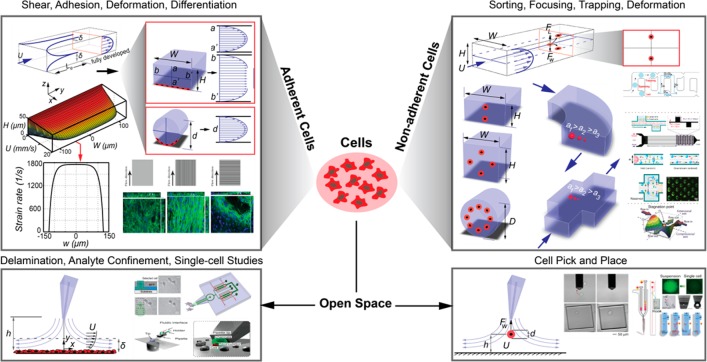
First we present key hydrodynamic principles and their relevance to cell studies. We introduce basic aspects of fluid flow in microchannels and design parameters that are critical to achieving certain hydrodynamic and transport characteristics. Because of different flow physics for adherent and nonadherent cells, we provide separate treatments for each. A snapshot of the content of key sections in this review is provided in Figure 2. As indicated, we divide the review into five main sections. Sections 2 and 3, which constitute the bulk of the review, are devoted to wall-adhered and suspended cells subjected to fluid flow and their corresponding hydrodynamic effects. For adherent cells, we discuss flow-induced shear and molecular transport and their effects on cell adhesion, cellular structure and shape, as well as on cell differentiation and fate. For nonadherent cells, hydrodynamic cell manipulation techniques for sorting, counting, focusing and trapping cells are discussed in detail. In section 4, we address hydrodynamic effects on cells cultured on open substrates (such as culture well plates) and manipulated using various “open-space” probes and tools. Finally, section 5 provides a summary and some perspective on future cell studies.

Figure 2.

Graphical summary. This article contains three main sections: hydrodynamics in adherent and nonadherent cell studies and in cell studies on open surfaces and substrates. Each section begins with hydrodynamic theory and design rules and then discusses key parameters that engender novel applications. (Top left) Adapted with permission from ref (28). Copyright 2013 the Royal Society of Chemistry. (Top right) Adapted with permission from ref (29). Copyright 2011 the American Institute of Physics. Adapted with permission from ref (30). Copyright 2015 the American Institute of Physics. Adapted with permission from ref (31). Copyright 2010 the American Institute of Physics. (Bottom left) Adapted with permission from ref (32). Copyright 2005 MacMillan Publishers. Adapted with permission from ref (33). Copyright 2014 MacMillan Publishers. Adapted from ref (34). Copyright 2010 the American Chemical Society. (Bottom right) Adapted with permission from ref (35). Copyright 2014 the Royal Society of Chemistry. Adapted from ref (36). Copyright 2014 the American Chemical Society.

2. Adhered Cells in Microchannels

In the human body, fluid flow in the lymphatic or circulatory systems modulates not only cell morphology but also gene expression patterns, properties of the extracellular matrix, protein secretion, and cell–cell and cell–matrix interactions.³⁷ The spatial and temporal distribution of fluid flow varies throughout the body owing to differences in vessel dimensions, properties of the surrounding tissue, driving pressure, as well as the mechanical properties of bodily fluids. These variations result in distinct flow patterns and shear stress levels, which in turn induce or repress certain signaling cascades within the cells that regulate single-cell and multicellular processes, such as angiogenesis,³⁸ lymph transport and function,³⁹ and stem cell differentiation.⁴⁰ Hydrodynamic delivery of nutrients, signaling molecules, antibodies, hormones, and enzymes also influences the cell behavior significantly,^41,42 resulting, for instance, in cell remodeling,⁴³ signaling,⁴⁴ and pathogenesis.⁴⁵

Existing in vitro cell culture models are commonly developed in macroscale well plates or Petri dishes that are severely limited in terms of accurate recapitulation of the physiological microenvironment. The disadvantages of such existing in vitro cell culture models have triggered new efforts that adopt engineering techniques, including microfabrication to engineer specific physical and biochemical cellular microenvironments that enable cell culture and study under physiologically more accurate conditions. For instance, in recent years, a tremendous body of work has been devoted to wall-adherent cell culture in microfluidic channels. Because of their high degree of hydrodynamic control, microfluidic culture devices can generate well-defined microenvironments with various patterns of fluid flow (pulsatile, steady, or oscillatory) and, as a result, emulate distinct features of native tissue. It has been demonstrated that cell viability can be sustained successfully in microfluidic culture platforms.⁴⁶ With appropriate choice of protein surface coatings, culture medium and flow conditions, cultured human cells have been shown to express tissue-specific differentiated functions.⁴⁷ Typical cell types that have been successfully cultured in microfluidic devices include endothelial cells, stem cells, fibroblasts, osteoblasts, smooth muscle cells, hepatocytes, cancer cells, and neuronal cells.⁴⁷ In the following section, we provide an overview of the fundamentals of fluid flow on the microscale that are most relevant to the study of cells, particularly to wall-adhered cells.

2.1. Hydrodynamic Effects in Microchannels

Fluid flow is commonly characterized by dimensionless numbers, such as the Reynolds number, Re, which reports the ratio of inertial forces to viscous forces, or in mathematical terms

1

where ρ is the density of the fluid, U is the characteristic velocity of the flow, d_H is the hydraulic diameter of the channel, μ is the dynamic viscosity of the fluid, and A and P are the cross-sectional area and wetted perimeter of the channel, respectively. Fluid flow in microfluidic channels is described by small characteristic dimensions (d_H) and velocities (U) and therefore, in most cases, is characterized by low Reynolds numbers, where flow is laminar and fluid elements move along orderly parallel streamlines. Low Reynolds numbers also indicate that the viscous forces dominate the inertial forces on the microscale. Put simply, viscous forces arise when fluid elements slow down because of friction, for instance, in the vicinity of a channel wall.

2.1.1. Momentum and Mass Transfer Boundary Layers

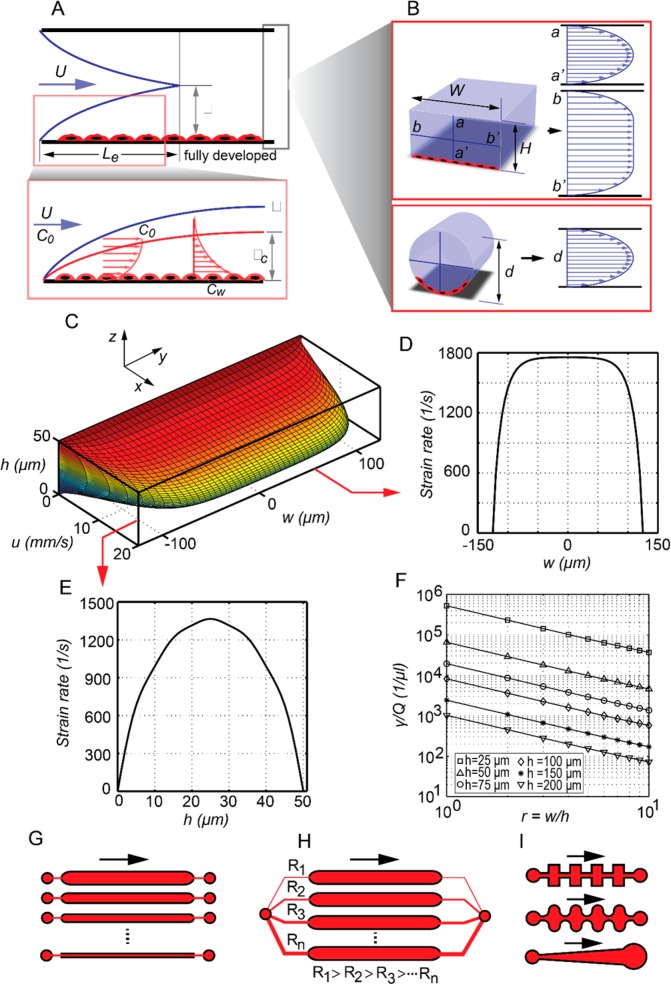
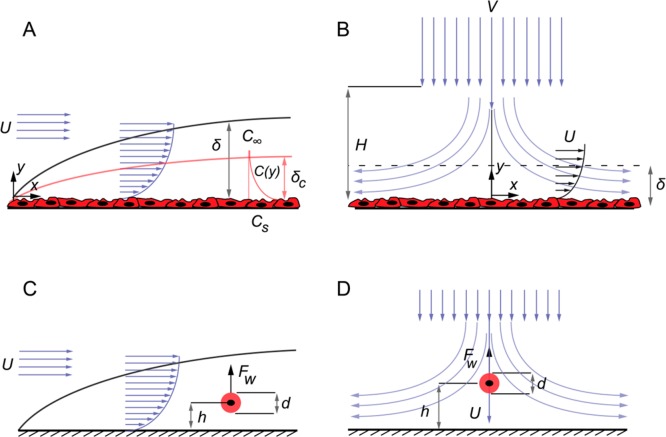
When a fluid enters a fluidic channel, the walls of the channel slow down adjacent fluid elements and as a result form a momentum boundary layer in which the flow moves relatively slowly compared with the far-field flow (fluid flowing at a distance far away from the wall). In a confined channel, such as a capillary, the boundary layer begins to grow at the entrance of the channel until the growing boundary layers meet at the center of the channel, as shown in Figure 3A.

Figure 3.

Hydrodynamic effects on adhered cells. (A) Channel flow and entrance length in a microfluidic channel. (B) Schematic velocity profiles for a rectangular and a circular cross-section microchannel. (C) Velocity profile for a rectangular cross-section channel with w = 250 μm, h = 50 μm, and Q = 10 μL min^–1. (D and E) Associated wall shear rate distributions. (F) Shear rate per unit flow rate plotted for various channel heights and aspect ratios. (G) A multishear cell culture device with channels of various sizes and independent inlets and outlets. (H) A multishear device with channels of various hydraulic resistance and cell culture chambers of equal dimension all connected to a common inlet and outlet. The varying flow rate in each culture chamber will result in a different level of shear experienced by the wall-adhered cells. (I) Periodic and variable shear-culture channels for exposing a population of cells to variable levels of shear.

The momentum boundary layer grows on a flat wall according to the relationship obtained from the Blasius solution for a laminar boundary layer,^48,49 i.e.

2

where δ is the thickness of the boundary layer and x is the distance from the edge of the wall. The channel position (i.e., x) at which the boundary layers meet determines the entrance length, and the fluid flow beyond this point is described as being “fully developed”.⁵⁰ Beyond the entrance length (L_e), the velocity distribution across the channel cross section will no longer evolve but remains steady along the channel length. The entrance length for a channel with an arbitrary cross section and hydraulic diameter, d_h, and low Re number flow is given by⁴⁸

3

From eq 3, it is notable that for low Reynolds number microchannel flows (Re ∼ 1), the entrance length is only a fraction of the hydraulic diameter and is therefore negligible in most microfluidic applications. In microfluidic application for cell studies in general, it is safe to assume that fluid flow in microchannels is fully developed at all times.

The concentration of analytes within the oncoming flow is also affected by the momentum (velocity) distribution. As an analyte is consumed or produced by the cells attached to the wall, it will be transported across the channel cross section by a combination of mass diffusion and convection, resulting in a mass transfer boundary layer. The mass transfer boundary-layer thickness (δ_c) is related to the momentum boundary layer (δ) according to⁵¹

4

where Sc is the Schmidt number (that defines the ratio of momentum diffusion in the fluid to analyte diffusion within the fluid), D is the analyte diffusion coefficient and v the kinematic viscosity. Figure 3A illustrates the mass transfer boundary layer plotted schematically versus the momentum boundary layer. The momentum boundary layer is often thicker than the mass transfer boundary layer because the momentum diffusion coefficient (also known as the kinematic viscosity) is often several orders of magnitude larger than the analyte diffusion coefficient.

Similar to the characterization of flow and momentum transport through the Reynolds number, mass transport in channels and capillaries is characterized by the dimensionless Péclet number (Pe = Ud_h/D). The Péclet number defines the ratio of convective mass transport (i.e., transport due to flow) to diffusive mass transport, and as such, the larger the velocity in a capillary, the larger the Péclet number and the associated convective transport. An additional and important mass transport characteristic of fluid flow in microfluidic environments is the Taylor dispersion, which describes enhanced axial propagation of analytes due to the wall-induced velocity distribution across the channel cross section. The enhanced or “effective” diffusion coefficient (D_e) can be determined from the following relationship:⁵²

5

Equation 5 suggests that for low Pe numbers, the effective diffusion coefficient is essentially equal to the molecular diffusion coefficient, and that as the flow velocity increases, effective diffusion is enhanced, smearing the analyte in flow and resulting in more effective axial dispersion of the analyte. Analytical solutions for the concentration distribution along a capillary are described in detail elsewhere.^53,54

2.1.2. Velocity Profile and Shear

The fully developed velocity profile across the cross section of a microfluidic channel can be determined from the solution of the governing equations of fluid motion, namely, the Navier–Stokes and conservation of mass (or continuity) equations. We will not discuss the derivation in detail herein, as detailed derivations are available elsewhere.^50,55 However, for a circular cross-section channel of diameter d, the velocity profile is given by the following relationship in cylindrical coordinates (r,θ,z):

6

where Q is the volumetric flow rate and r is the radial distance from the centerline of the channel. Equation 6 describes a parabolic function in the radial direction, and therefore, the velocity profile inside a circular channel or pipe is referred to as being “parabolic”, with a maximum velocity occurring at the channel centerline (Figure 3B). The velocity distribution in a square or rectangular channel, however, is more complex. For example, the velocity profile for a rectangular channel of height h and width w, with no-slip boundary condition at the walls, is an infinite series function of both z and y, indicating that the channel velocity has different distributions along the z and ydirections (Figure 3C). The equation for the velocity distribution in a rectangular channel is provided in Section S1 for the interested reader. The qualitative velocity distribution along the width and height of a rectangular channel is also illustrated in Figure 3B. The velocity distribution along the smaller dimension (in this case, the height) exhibits a parabolic distribution, whereas across the larger dimension (in this case, the width), the velocity initially increases and then remains essentially constant in the central part of the channel. This particular velocity profile (in a rectangular channel) is the product of boundary layer interactions between the side walls and the top and bottom walls and the difference in their dimensions. By introducing dimensional symmetry, for instance, by adopting a channel with identical height and width, the velocity profiles along the width and the height of the channel become identical.

Wall shear stress in a microchannel is critical in the context of microfluidic cell cultures, as shear forces can alter the cellular behavior or even damage the cytoskeletal structure if excessively large.⁵⁶ To obtain the shear distribution on the channel wall, the velocity gradient (i.e., the strain rate) at the wall must be determined. For a circular channel, this is done by differentiating eq 6 with respect to r, which yields

7

Equation 7 indicates that wall shear in a circular tube or channel is constant across the channel walls and is a function of the flow rate, the fluid viscosity, and the channel diameter. The higher the flow rate and the smaller the channel diameter, the higher the wall shear stress is at constant viscosity. Conversely, wall shear in a rectangular channel is not constant and varies across the top, bottom, and side walls of the channel. The velocity gradient (strain rate) at the wall is obtained by differentiating the velocity profile with respect to y or z (Figure 3C), depending on the wall on which the shear is being calculated, i.e.,

8

Detailed expressions for the wall strain rate and shear stress for a rectangular channel are given in the Section S1. To showcase a typical velocity and shear variations in a rectangular microchannel, the velocity profile and shear stress are plotted in Figure 3 (panels C, D, and E) for a situation in which the channel width and height are 250 and 50 μm, respectively, and the flow rate is 10 μL min^–1. It can be seen that the wall shear is not constant and varies across the width and the height of the bottom and side walls of the channel, with maximum shear occurring at the center of the channel.

The wall strain rate in a rectangular channel can also be expressed in terms of the aspect ratio, r (= w/h), and the height of the channel. The strain rate per unit flow rate for various channel heights and aspect ratios is shown in Figure 3F. This analysis shows that an increase in the wall strain rate occurs with decreasing channel height and decreasing aspect ratio. Importantly, the information in Figure 3F can be used as a guide when designing rectangular cross-section channels having specific values of wall shear. For instance, at a given flow rate, the smaller the channel height, h, and the smaller the aspect ratio (i.e., smaller w), the higher the wall strain rate.

2.1.3. Hydraulic Resistance

The concept of hydraulic resistance is often introduced through a hydraulic–electric circuit analogy in which the flow rate (Q) of a fluid in a channel or pipe is equivalent to the electrical current passing through a circuit, and the hydraulic pressure (ΔP) required to deliver this flow rate is equivalent to the electric potential required to generate the current. The flow rate and the pressure difference across the flow conduit are proportional, with a proportionality coefficient that defines the hydraulic resistance (R),⁵⁰

9

Conceptually, hydraulic resistance can be thought of as the resistance to fluid flow at a given driving pressure. The higher the resistance, the lower the resulting flow rate.

Fully developed incompressible (constant density) laminar flow in conduits with the characteristic flow profiles shown in Figure 3 (panels B and C) can be described using the Hagen–Poiseuille equation,⁵⁰ i.e.,

10

where μ is the dynamic viscosity, L is the length, and d_h the hydraulic diameter of the conduit. As indicated in eq 10, the hydraulic resistance is proportional to the length of the conduit and inversely proportional to its hydraulic diameter. Simply put, eq 10 implies that the longer and the narrower the flow channel, the higher the hydraulic resistance and the lower fluid flow through the channel will be. Hydraulic resistance in rectangular conduits is of special interest in microfluidic applications as they are the most common channel geometry in microfluidic devices. The Hydraulic resistance in a rectangular microchannel with a width of W, a height of H, and a length of L can be calculated from the following relationship:⁵⁷

11

2.2. Cell Adhesion and Shear Stress Studies

As physical entities, living cells possess structural and physical properties that enable them to withstand the physiological environment⁵⁸ as well as mechanical forces from inside and outside of the body.^1,56,59,60 The most ancient and universal mechanical force is the osmotic force, which is crucial to all life forms.⁶⁰ Interestingly, bacteria have developed a mechanism to sense the osmotic turgor through mechanosensitive channels and protect themselves from cell lysis. Such mechanogated ion channels are also present in mammalian cells⁶¹ and are important for mechanotransduction.² In addition to mechanogated channels, mammalian cells can sense their mechanical environments via lamellipodia, cilia, glycoproteins in the glycocalyx,⁶² transmembrane receptors,⁶³ extracellular matrix molecules, or cytoskeletal structures among others that have been recently identified in the emerging field of mechanobiology.¹ Mechanical stressors around a mammalian cell arise from complex interactions of gravitational forces, shear flows,⁶⁴ or intra- and intercellular tensions from the cytoskeleton.⁶⁵ Once a cell is stimulated by a mechanical stressor, downstream signaling cascades are initiated and leading to a wide range of altered gene expression profiles.^58,66

As discussed in section 2.1, a straight microchannel allows for the control of the shear on adhered cells. Adhered cells grow on the microchannel walls and mostly at the bottom due to sedimentation and adhesion. A change in the flow rate within any microchannel will lead to a change in the shear stress on adhered cells, with the resulting effects being easily monitored. Indeed, at a given flow rate at the channel inlet, a cell inside a small channel will experience higher shear forces than an identical cell in a larger channel (eq 7 and Figure 3F). Accordingly, the behavior of adhered cells in a small channel is inherently different from the behavior of those grown in larger channels. Implementing different channel dimensions within a microfluidic device allows for the study of different cell populations under identical conditions but at different shear stress levels. A common design for such experiments contains parallel channels of varying hydrodynamic resistance connected to independent perfusion inlets and outlets (Figure 3G). Alternatively, multiple identical culture chambers connected to a common inlet and outlet via channels of varying hydraulic resistance (Figure 3H and 4D) can be used for the same purpose. Such multishear devices enable parallelized analysis by capturing the effects of varying shear on cells simultaneously.

Figure 4.

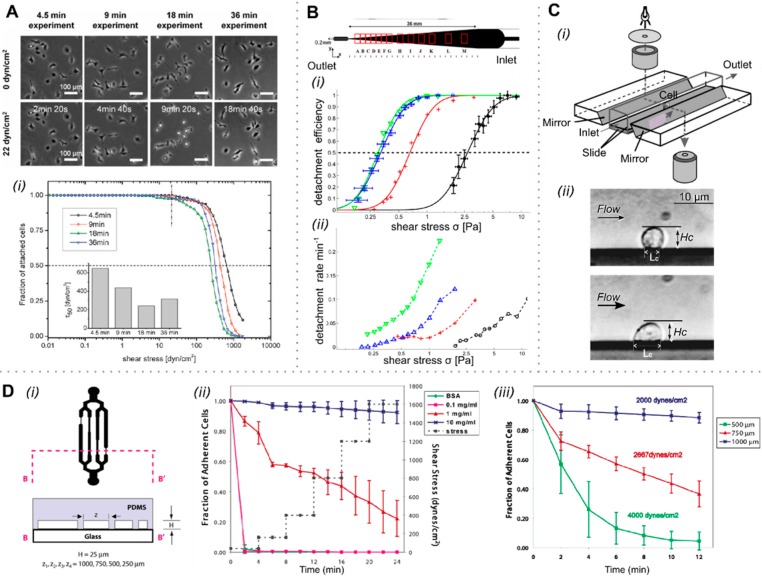
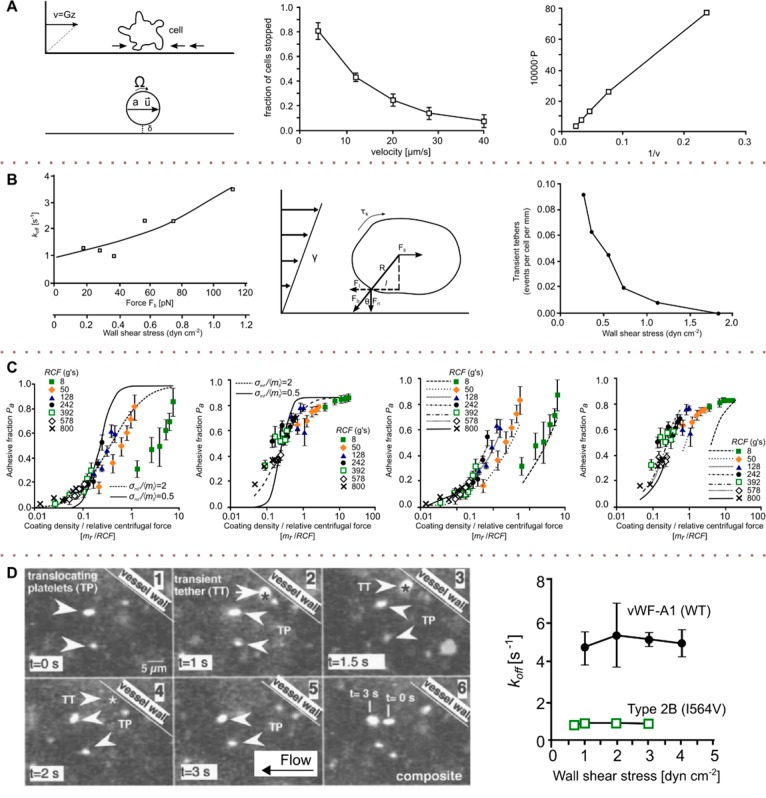
Global cell adhesion studies in shear flow. (A) REF52 cells were exposed to a stepwise shear gradient, with the adhesion strength being analyzed at a shear stress of 22 dyn cm^–2 (2.2 Pa). (i) Cells are able to adapt to the shear stress at longer exposure times (>9 min), with the cell adhesion strength being higher than at shorter exposure times. At low exposure times, cell adhesion is not affected by shear. (B) A tapered channel microfluidic device for comprehensive cell adhesion analysis allows the measurement of detachment kinetics and shear-induced motion. The detachment efficiencies of MDA-MB-231 and D. discoideum (i) were calculated from the detachment kinetics measured (ii). The critical shear level at which 50% of the cells are detached was assessed for four data sets: D. discoideum on a glass substrate in highly conditioned medium (green ▼) and in fresh medium (blue, ▲) and in fresh medium on APTES-coated substrate (red +), as well as MDA-MB-231 on a collagen-coated substrate (black, ●). (C) Biomechanics of cell rolling: shear flow, cell surface adhesion, and cell deformability were examined by monitoring cells via an installed mirror (i). The cell substrate contact length, L_c, as well as the cell height, H_c, were measured for different shear levels (ii) using finite element analysis. (D) Substrate-dependent adhesion of cells in channels having different hydrodynamic resistances (i). At high shear, appropriate fibronectin coating leads to enhanced cell adhesion (ii). At a shear of 2000 dyn cm^–2 (200 Pa) applied for 12 min, only 10% of the cells detached, but at twice that shear stress, more than 90% of the cells came off the surface in the same time period (iii). (A) Adapted with permission from ref (77). Copyright 2010 the Royal Society of Chemistry. (B) Adapted with permission from ref (78). Copyright 2012 the American Institute of Physics. (C) Adapted with permission from ref (79). Copyright 2000 Elsevier. (D) Adapted from ref (80). Copyright 2004 the American Chemical Society.

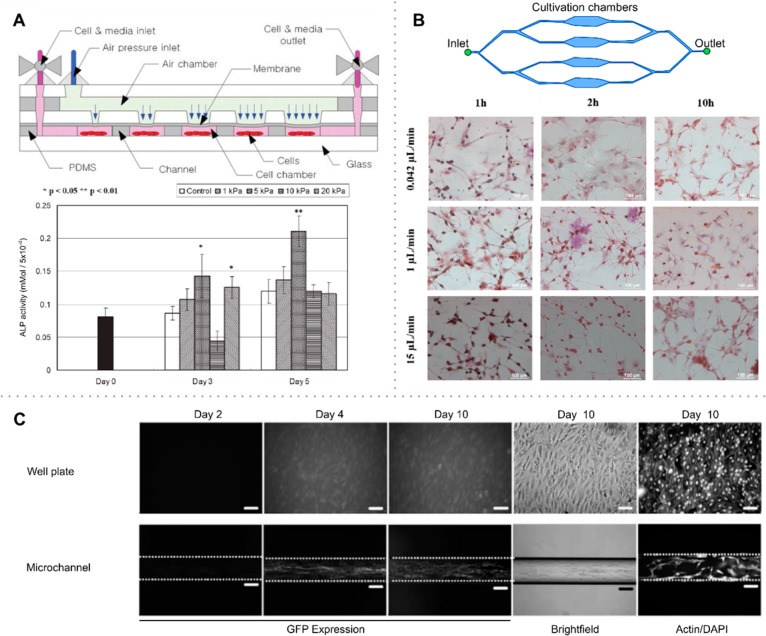
In certain studies, it may be important to exert varying or periodic levels of shear on a single population of cells.⁶⁷ Periodic shear levels can be induced through the use of tapered or periodic microchannel geometries, as shown in Figure 3I. An alternative method for producing variable shear is to vary the pressure on a deformable membrane that seals the culture chamber. As the membrane is deformed, it induces a flow within the culture chamber, and as a result, contained cells are exposed to a level of shear that is proportional to the deformation in the membrane (Figure 7A). Importantly, all the designs discussed above have been used in various studies of cell response to shear stress.

Figure 7.

Hydrodynamic effects on cell differentiation. (A) Microfluidic device to present mechanical stimuli to cells. Mechanical stimuli are modulated by changing the pressure on the membrane. At selected times (1, 3, and 7 days), cells were assessed by monitoring ALP, a differentiation marker. The stimulated groups with 5 and 20 kPa stimulus at day 3 compared with the control group. (B) Shear-stress stimulation on a multiplexed microfluidic device for rat bone-marrow stromal cell differentiation enhancement. Chambers with different flow resistances enable a multiplexed analysis. Cells were exposed to shear forces of 0.0009, 0.022, and 0.33 dyn cm^–2 for 10 min in different chambers. The cell differentiation ratio was visualized by immunohistochemistry for the differentiation markers. Increased flow shear leads to an enhancement of the differentiation ratio. (C) Osteoblast-based continuous perfusion microfluidic system for drug screening. Cells were cultured either in a microchannel under hydrodynamic shear or cultured on a static well plate for a period of 10 days. In the microchannel culture, the shear stress of 0.07 dyn cm^–2 (7 × 10^–3 Pa) induced enhanced GFP compared with the static culture, suggesting that shear induces differentiation. ALP, an enzyme marker of osteoblasts, supported the results of GFP expression. (A) Adapted with permission from ref (104). Copyright 2007 Royal Society of Chemistry. (B) Adapted with permission from ref (105). Copyright 2015 MDPI AG. (C) Adapted with permission from ref (106). Copyright 2008 Springer.

2.2.1. Cell Adhesion

When cells are first introduced to a microfluidic culture channel, the rounded cells settle, attach to the surface of the channel via electrostatic attraction, or bind to proteins on the channel surface through the integrin receptor-protein binding.⁶⁸ Once the cells have adhered, they flatten, secrete extracellular matrix (ECM) proteins, and begin to proliferate. Cell adhesion is also important in triggering signals that regulate cell differentiation, the cell cycle, cell migration, and cell survival.⁶⁹ Fluid flow in a cell culture channel exerts a shear force on the cells, which competes with the adhesion forces between the cells and their substrate.^58,70 At high shear (>1 Pa) such as in hemodynamic flows, the shear force induces a stress response in adhered cells, which can lead to altered adhesion properties of cells, such as rounding, detachment, and change in the expression of adhesion proteins. Stress-induced cytoskeletal rearrangements may even lead to apoptosis of the cell in certain scenarios.⁷¹ In contrast, at low shear (<1 Pa) such as in interstitial, extravascular flow in the body, the hydrodynamic forces constitute a mechanotactic signal that can drive the motion (section 2.2.3) of a cell and affect cell differentiation (section 2.3).^59,72−74 These shear-induced cell alterations have been studied using microfluidic shear devices.^{37,59,72,73,75,76}

There is mounting evidence that cells adapt to stress over time and reinforce cell adhesion by overexpressing adhesion-related molecules. For example, Christophis et al.⁷⁷ exposed rat embryonic fibroblast cells to different shear flows and investigated the adaptation of a cell to reinforce cell adhesion in shear flow. The authors established a shear gradient ranging from 0 to ∼1000 dyn cm^–2 (0 to 100 Pa) by increasing the flow velocities in a stepwise manner and characterized the cell adhesion strength by varying the exposure time to shear stress at each shear level (with exposure times of 5, 10, 20, and 40 s per shear stress level). This yielded total experimental times and shear exposure times of 4.5, 9, 18, and 36 min. Finally, they compared adhesion strengths for an applied shear magnitude of 22 dyn cm^–2 (2.2 Pa) for various exposure times (2, 4, 9, and 18 min) and observed that the cells were best able to adapt to the applied shear stress at longer exposure times. Conversely, at extremely low exposure times, cell adhesion was unaffected, with the adhesion strength increasing with exposure to shear as the cells respond and adapt to the shear stimulus (Figure 4A).

Unsurprisingly, adhered cells tend to detach from surfaces in shear flow when the shear rate reaches a certain threshold. Cell detachment under shear and shear-induced cell movement have been studied in a microfluidic device containing parallel tapered channels by Rupprecht et al.⁷⁸ (Figure 4B). Along tapered channels, effective shear forces vary owing to the expanding channel dimensions, and therefore, using a single input flow rate, the cellular response to a 25-fold variation in shear stress could be studied simultaneously. MDA-MB-231 breast-cancer cells and a unicellular organism (D. discoideum) were used as model systems, with cell adhesion being quantitatively examined by the analysis of kinetics, adhesive strength, and migration behavior or cell shape (Figure 4B). The authors experimentally determined the critical shear level at which 50% of cells become detached and analyzed the detachment kinetics. They found that the data for the detachment efficiency (the percentage of the cells detached) versus shear followed a log-normal distribution as shown in Figure 4B(i) and that the cell detachment process follows first-order kinetics [see Figure 4B(ii)].

Dong et al.⁷⁹ investigated leukocyte rolling on P-selectin-coated surfaces (artificial vascular epithelium) in relation to cell movement and deformation in response to shear stress. The degree of cell deformation, the cell–substrate contact length, as well as the rolling velocity of the cells were assessed using a side view flow chamber in different shear flows using the device shown in Figure 4C(ii). On the basis of the measured cell height, H_c, and cell substrate contact area, L_c, in different shear flows, they calculated the adhesion energy using finite element analysis. Such an analysis suggested that the cell substrate contact area under high wall shear (20 dyn cm^–2, 2 Pa) was nearly twice as large as the contact area under low shear levels (0.5 dyn cm^–2, 0.05 Pa). This increased contact area was attributed to shear-induced cell deformation, with an increase in contact area resulting in more energy dissipation to both adhesion bonds and viscous cytoplasm. Furthermore, the authors proposed that a more flattened cell geometry leads to a decreased hydrodynamic drag force on the cell.

To study cell surface detachment and adhesion in fibroblast cultures, Lu et al.⁸⁰ used a multishear device consisting of different shear chambers connected to a common inlet and outlet as shown in Figure 4D(i). The device consisted of 500, 750, and 1000 μm wide microchannels, yielding shear stress magnitudes of 4000, 2700, and 2000 dyn cm^–2 (400, 270, and 200 Pa) for the flow rates adopted. The fraction of adherent WT NR6 cells after 0 and 12 min of shear exposure was measured. At a shear stress level of 2000 dyn cm^–2 for 12 min, only 10% of the cells detached, whereas a shear stress of 4000 dyn cm^–2 caused more than 90% of the cells to detach from the surface within 12 min [Figure 4D(iii)]. The authors also assessed the adhesion of the cells to fibronectin-coated substrates as a function of the shear stress and fibronectin concentration, observing that adhesion under flow strongly depends on the fibronectin coating [Figure 4D(ii)].

2.2.2. Shear-Induced Stress

The cellular response to mechanical stimuli has been the subject of numerous studies. Many of these use techniques that incorporate a probe, such as an atomic force microscope (AFM) tip, as a vehicle for inducing a mechanical stimulus. However, cells are fragile, and therefore contact-based studies^81,82 are undesirable as they might disrupt the cell membrane during investigation or even permanently destroy the cell. In contrast, microfluidic-based culture platforms, with their ability to deliver controlled shear and mechanical stimuli, are an attractive tool for investigating the mechanosensitivity of cells.

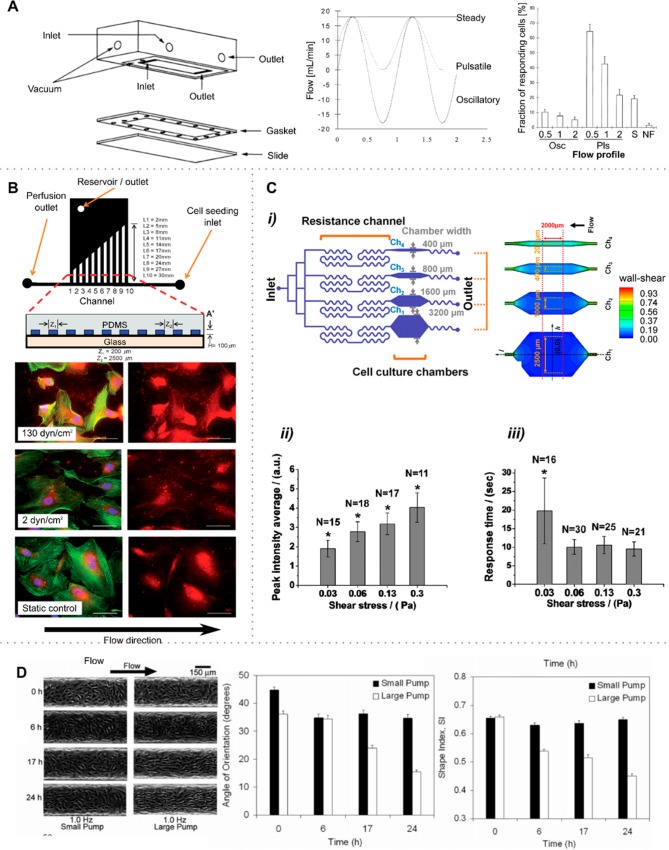
Jacobs et al.⁸³ investigated the effect of alternating flow on osteoblast-like immortalized human fetal osteoblasts. They subjected the cells to various flow patterns, including a steady flow (resulting in a wall shear stress of 2 N m^–2), an oscillating flow (shear between ±2 N m^–2), and a pulsatile flow (shear from 0 to 2 N m^–2). Alternating flow patterns were applied using a sinusoidal waveform at frequencies of 0.5, 1.0, and 2.0 Hz, and the intracellular calcium concentration was monitored with a fluorescent dye. The results indicated that oscillatory flow was a significantly weaker stimulator of bone cells than both steady and pulsatile flows and resulted in a decrease in cell responsiveness as the frequency increased. For both oscillating and pulsatile flow patterns, the reduction in responsiveness coincided with a reduction in the net fluid transport, which suggested that the response of bone cells to fluid flow is a function of chemotransport effects (Figure 5A).

Figure 5.

Using hydrodynamics to modulate the shear stress on cells. (A) Flow stimulation of bone cells with steady flow resulting in a wall shear stress of 2 N m^–2, oscillating flow (−2 to 2 N m^–2) and pulsatile flow (0 to 2 N m^–2). Dynamic flows were applied with sinusoidal profiles of 0.5, 1.0, and 2.0 Hz. The stimulation of cells with pulsatile and steady flow (Pls, S) was significantly stronger than with oscillating (Osc) flow. (B) Multishear device containing ten channels of varying lengths (top). HUVECs were immunostained for intracellular and extracellular vWF factor (red), rhodamine phalloidon (green), and Hoechst (blue) after 20 h of perfusion under different shear flows. For shear stresses above 5 dyn cm^–2 (0.5 Pa), cells exhibited significantly higher vWF secretion and were at least 30% smaller in size. (Scale bar: 50 μm). (C) A multishear microfluidic device for quantitative analysis of calcium dynamics in osteoblasts. (i) Four different shear levels (0.3, 0.6, 1.2, and 3 dyn cm^–2) were exerted on osteoblasts to study the cytosolic calcium concentration Ca2+ dynamics. (ii and iii) The cytosolic calcium concentration increased with shear stress from 0.3 to 3 dyn cm^–2 (0.03 to 0.30 Pa); the response to shear was delayed with an activation threshold between 0.3 and 0.6 dyn cm^–2 (0.03 and 0.06 Pa). (D) Effect of flow rate and shear level on the shape and orientation of endothelial cells in a straight microfluidic channel. At high flow rates (large pump, high shear) and flow exposure times, the HDMECs tend to align and elongate significantly (decreasing Supporting Information) in the direction of flow (decreased angle of alignment). In contrast, at low flow rates (small pump, low shear), the flow and flow exposure time do not affect the cell shape and orientation. (A) Adapted with permission from ref (83). Copyright 1998 Elsevier. (B) Adapted with permission from ref (85). Copyright 2009 the Royal Society of Chemistry. (C) Adapted with permission from ref (87). Copyright 2011 Elsevier. (D) Adapted from ref (88). Copyright 2005 the American Chemical Society.

Shear stress affects the morphology and fate of many cell types, including endothelial, smooth muscle, and osteoblast cells.^43,84 Chau et al.⁸⁵ used a multishear device for the simultaneous evaluation of 10 different shear levels over 2 orders of magnitude (between 0.07 and 13 Pa, Figure 5B). Human umbilical vein endothelial cells (HUVECs) were exposed to these shear stress levels over a 20 h period, and the secretion level of the von Willebrand factor (vWF) was investigated. Increasing shear resulted in increased vWF secretion. HUVECs under a shear level between 1 and 3 dyn cm^–2 (0.1 to 0.3 Pa) exhibited a similar vWF content, size, and perimeter as cells in static culture. In contrast, cells that underwent shear stresses above 5 dyn cm^–2 (0.5 Pa) showed significantly higher vWF secretion and were at least 30% smaller in size. Interestingly, Chau et al. also found that cells exposed to a shear stress of 0.7 dyn cm^–2 (0.07 Pa) showed significantly lower levels of vWF and were 35% smaller in size than those under static conditions.

Fluid shear stress also affects calcium dynamics, resulting in variation in bone cell function and remodelling.⁸⁶ For example, Kou et al.⁸⁷ developed a microfluidic device with four culture channels, each providing a different shear level. This multichannel device was used to study cytosolic calcium-concentration [Ca²⁺] variations of osteoblasts. The device contains four cell culture chambers of different widths, with resistance correction channels being used to homogenize the hydrodynamic resistance across the four lines and to ensure equal flow rates in all four chambers (Figure 5C). The authors computed the local shear distribution to assess the preferred section in the cell chamber for measuring calcium dynamics. The cytosolic calcium concentration was observed to increase proportionally with the magnitude of the shear stress from 0.3 to 3 dyn cm^–2 (0.03 to 0.30 Pa), and the response to shear was delayed with an activation threshold between 0.3 and 0.6 dyn cm^–2.

Endothelial cells (ECs) lining the inner lumen of blood vessels are continuously subjected to hemodynamic shear stress, which is known to modify EC morphology and biological activity.⁸⁸ Song et al.⁸⁸ developed a self-contained microcirculatory endothelial cell culture system to study the effect of hemodynamic shear on EC alignment and elongation. Specifically, they investigated human dermal microvascular endothelial cells (HDMECs), which they exposed to pulsatile flows. Within a microfluidic device, they integrated two pumps, a large one and a small one. By pumping at a frequency of 1.0 Hz, cells were exposed to <1 dyn cm^–2 (<0.1 Pa) with the small pump and ∼9 dyn cm^–2 (∼0.9 Pa) with the large pump. Such flows caused ECs to align and elongate significantly in the direction of the flow according to the level of shear stress (Figure 5D). Furthermore, the authors defined a dimensionless shape index (SI), quantifying cell elongation in the direction of flow as 4πAP^–2. If SI = 0, the cell shape is a line, and if SI = 1 the cell is circular. The SI of cells exposed to low shear remained constant at ∼0.65 over 24 h (right graph, Figure 5D), whereas the SI of cells exposed to high shear decreased from 0.65 to 0.45 over 24 h of exposure to a flow.

2.2.3. Shear and Cell Migration

As mentioned in section 2.2.1, low shear flows affect the motility of cells.^73,74,89 Mammalian cells use amoeboid motility as a fast mode of cellular movement to enter and translocate through various tissues and organs.⁷⁰D. discoideum is a simple lower eukaryote and is a genetically and biochemically tractable model organism. It shares many migration characteristics with leukocytes⁹⁰ and has therefore been used extensively to study cytoskeleton organization, chemotaxis, cell differentiation, and development.⁹¹

The actin cytoskeleton is able to sense and to adapt to mechanical changes in the environment.⁶⁵ Décave et al. subjected D. discoideum to low shear in a transparent lateral flow chamber and showed that the cells started migrating (Figure 6E).⁷³ Addition of CIPC (drug inhibiting actin polymerization) resulted in reduced formation of cell–substrate contact area and reduced the motility, implicating that actin cytoskeleton remodeling is indeed a crucial player in cell migration.

Figure 6.

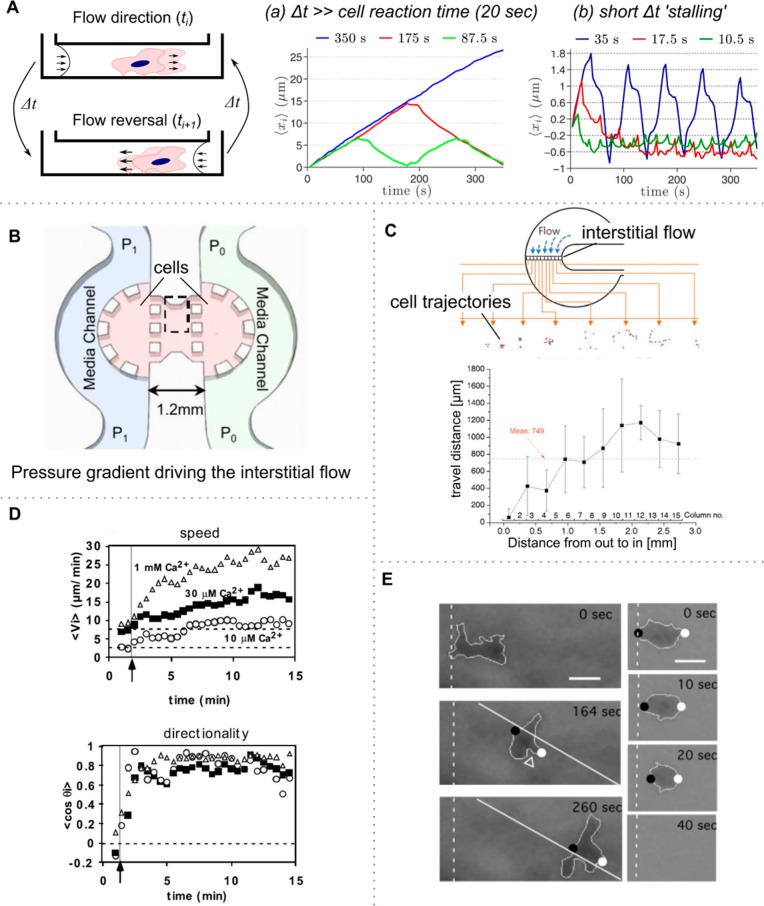
Shearotaxis and artificial interstitial fluid flows. (A) Dependence of migration directionality on the reversal of the flow direction in a straight channel. At low frequencies, (a) the cells migrate steadily along the streamline. At high reversing frequency (b), the cells are trapped. (B) A pressure gradient between P₁ and P₀ establishes an artificial interstitial flow microenvironment for studying (e.g., cancer cell progression). (C) Fibroblasts in the center of the device were subjected to a minimal osmosis driven flow mimicking the interstitial fluid. (D) Motility of D. discoideum depends on mechanical and chemical stimuli. Shear induced migration along the streamlines. Calcium concentration affected the speed but had no influence on the directionality of cell migration. (A) Adapted with permission from ref (74). Copyright 2014 Public Library of Science. (B) Adapted with permission from ref (72). Copyright 2011 National Academy of Sciences. (C) Adapted with permission from ref (103). Copyright 2009 Royal Society of Chemistry. (D) Adapted with permission from ref (92). Copyright 2005 Company of Biologists Ltd. (E) Adapted with permission from ref (73). Copyright 2003 Company of Biologists Ltd.

In a related study, Fache et al. investigated the dependence of shearotaxis with respect to mechanical and chemical stimuli.⁹² They found that with increasing calcium concentration, the cell migration speed was increasing and that shear alone was affecting the directionality but not the speed of cell migration of D. discoideum. Thus, for an efficient mechanotactic response, external calcium is required (Figure 6D).

Chemotaxis is one means of cellular migration where cells tend to migrate toward the high concentration of chemoattractant. Meier et al.⁹³ exposed D. discoideum to alternating chemoattractant fields and were able to stall the cells at one position by switching the chemoattractant gradient at 0.1 Hz. Similarly, Zhu et al. performed exposed D. discoideum to alternating shear by switching the flow direction (e.g., reversing the direction of the mechanotactic stimulus at various frequencies).⁷⁴ Interestingly, at frequencies of 0.06–0.1 Hz, they achieved cellular trapping (Figure 6A). Surprisingly the stalling frequencies for mechanotaxis and chemotaxis were comparable, leading to a hypothesis that the limiting factor is the chemical-based internal apparatus in the cell.⁷⁴

While in the vascular system, the wall shear stress can reach levels up to 7 Pa,⁹⁴ interstitial fluid flow is characterized as an extremely slow flow through the ECM. This extravascular flow results in low shear stress (≤0.01 Pa) because of the high flow resistance of the ECM.⁹⁵ Interstitial fluid flow is expected to have an impact on cell morphogenesis and pathogenesis, drug transport in cancer patients,⁹⁶⁻⁹⁸ and cancer cell proliferation and invasion.⁹⁹⁻¹⁰² The challenge in the microfluidics community is to flow fluids at extremely low flow rates in order to build a system, which can emulate interstitial fluid flow of less than a few μm sec^–1.¹⁰³

Park et al. proposed an osmotic pump: the osmosis-driven flow is generated across the cellulose membrane between a water and a polyethylene glycol solution (Figure 6C). Subsequently, they subjected mouse fibroblasts to this interstitial flow. Interstitial flow below 10 μm sec^–1 was sufficient for fibroblast attachment, and above this value cell mobility increased significantly.

To examine the effects of interstitial flow on breast cancer cell morphology and migration Polacheck et al. designed a chip emulating interstitial flows across a pressure gradient. They seeded MDA-MB-231 at different densities onto a gel in the center region of the device (Figure 6B). They were able to create a flow field across the gel and studied cell migration at fluid flow of 0.3 and 3 μm sec^–1. In the presence of the interstitial flow, they observed cell migration along streamlines;⁷² however, when blocking CCR7, the cells started migrating from downstream to upstream and was independent of cell density.

2.3. Effects of Hydrodynamic Forces on Cell Differentiation and Phenotyping

In nature, mechanical stimuli not only trigger stress responses inside organisms but also affect events such as cell differentiation. As an example, flow-induced shear stress stimulates human osteoblast proliferation and differentiation by triggering multiple signal transduction pathways⁸⁴ (Figure 7B). Accordingly, it is important to take note of hydrodynamic effects on cells, especially when working with nondifferentiated cells that are exposed to fluid flow.

For instance, it has been shown that mechanical stimulation results in the differentiation of human mesenchymal stem cells (hMSCs) into osteoblast-like cells.¹⁰⁴ Sim et al. used a micro cell stimulator to expose cells to compressive pressure and induce osteogenesis. Their stimulator was based on the pneumatic actuation of a flexible diaphragm placed between an air chamber and the cell chambers. All membranes were connected to the same pressure source on one side and to culture chambers on the other side, in which human mesenchymal stem cells were cultivated with an intermittent mechanical stimulus over 7 days. An experimental group was mechanically stimulated twice a day for 10 min with a cyclic compressive stimulus of 5 kPa. For comparison, an unstimulated group was cultured in the same chambers. At selected times (1, 3, and 7 days), cells were assessed by monitoring cluster of differentiation 90 (CD90), actin, alkaline phosphatase (ALP), and alizarin expression. Cells stimulated at 5 and 20 kPa presented a statistically significant variation on day 3 compared with the control group. The authors noted that the average ALP activity shows the highest level (0.211 ± 0.023 mMol per 5 0 × 10⁴ cells) in the 5 kPa stimulation group on day 5 (Figure 7A). Their work demonstrated that cyclic pressure stimulation enhances osteogenesis of hMSCs.

The combination of mechanical (shear) and chemical effects on rat bone marrow stromal cells (rBMSCs) has also been investigated by Tsao et al.¹⁰⁵ using a four-channel microfluidic cell culture bioreactor. The authors used 1-methyl-3-isobutylxanthine (IBMX) in combination with hydrodynamic shear to trigger rBMSC differentiation into neurons. The four culture chambers (Figure 7B), having a height of 100 μm and a width of 1000 μm, were subjected to flow rates of 0.042, 1, and 15 μL min^–1, corresponding to wall shear magnitudes of 9 × 10^–4, 2.2 × 10^–3, and 0.33 dyn cm^–2 (9 × 10^–5, 2.2 × 10^–4, and 0.033 Pa). The cells were exposed to the different shear levels for 10 min and the cell differentiation ratio compared with static culture after 1 and 10 h of cultivation. To monitor the differentiation ratio, cells were stained by immunohistochemistry using neuron-specific enolase antibody, demonstrating that increased flow shear leads to an enhancement of the differentiation ratio (Figure 7B).

To gain further insight into the differentiation of cells under static and dynamic (in flow) culture conditions, Jang et al.¹⁰⁶ compared the differentiation of cells in a microfluidic channel under hydrodynamic shear with that of cells in a static well plate over a period of 10 days. The authors used mouse Col1a1GFP MC-3T3 E1 osteoblastic cells possessing a marker gene system expressing green fluorescent protein (GFP) under the control of osteoblast-specific promoters. Cells were cultured in dexamethasone (DEX) standard medium with and without bone morphogenetic protein-2(BMP-2). In the dynamic microchannel culture, cells were subjected to a shear stress of 0.07 dyn cm^–2 (7 × 10^–3 Pa) at a flow rate of 0.2 μL min^–1, which led to enhanced GFP expression and osteoblast differentiation. Moreover, analysis of alkaline phosphatase, an enzyme marker of osteoblasts, supported GFP expression results (Figure 7C).

2.4. Effect of Hydrodynamic Transport of Molecules on Cell Fate

Cells do not function as single independent entities, and it is known that cells continuously secrete molecules that bind to the receptors of the same cell (autocrine signaling) or of neighboring cells (paracrine and endocrine signaling) to mediate processes such as cell–cell communication,¹⁰⁷ cell morphogenesis,¹⁰⁸ and cell migration.¹⁰⁹

Perfusion cell culture systems, in which the cells are exposed to a steady flow of fluid, are a powerful tool for studying the effect of signaling molecules and their gradients on cellular function and fate. Microfluidic perfusion culture platforms, in particular, are useful as they allow precise spatiotemporal control of the gradients of such molecules in cellular microenvironments. Secreted molecules are transported with the flow of the oncoming perfusion liquid, forming a species transport boundary layer (Figure 3A), and are dispersed throughout the culture chamber (or channel) by diffusion and convection. The mode of the axial dispersion and the channel length required to achieve a certain gradient can be defined by the Péclet number (Pe = UR/D). At very low Péclet numbers, the molecules will be transferred predominantly by molecular diffusion, whereas at higher Péclet numbers, the effect of convection becomes more pronounced, resulting in a “trail” of various molecular concentrations along the flow direction. Exact solutions for the axial dispersion of analytes in long capillaries with uniform cross section can be found elsewhere.⁵⁴

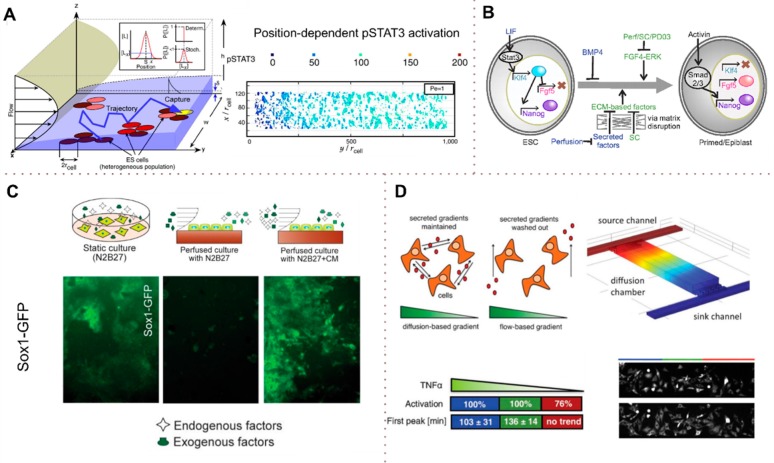
The flow-dependent modulation of the diffusion of signaling molecules has been studied using microfluidic perfusion culture systems. For instance, Moledina et al.⁶⁷ used a microfluidic perfusion culture approach coupled with numerical models for Brownian motion of signaling ligands under flow to study the effects of flow on the heterogeneity of cell signaling and fate. They studied the local impact of endogenously secreted glycoprotein 130 (gp130)-activating ligands and their activation of the signal transducer and activator of transcription3 (STAT3) in mouse embryonic stem cells (mESC). Both their model and perfusion experiments showed a gradient of STAT3 activation along the channel axis, with STAT3 activation increasing in the direction of the flow (Figure 8A). Moreover, the authors showed both experimentally and numerically that STAT3 activation levels decrease with increasing flow rate (i.e., with the Péclet number), resulting in an increased differentiation of mESCs. In addition, the cell density was found to be inversely proportional to the phosphorylated STAT3 (pSTAT3) levels, suggesting that in the regions of high cell density, the contribution of each cell to the pluripotency of the colony is lower than in less dense regions.

Figure 8.

Spatiotemporal concentration profiles of autocrine and paracrine factors and their effect on the cell phenotype. (A) LIF activates STAT3 and induces self-renewal. In this study, the effects of the flow rate, the position of the flow field and the local field organization on STAT3 activation and the fate of mESC were analyzed, mathematically described, and compared with the static culture. (B and C) Effect of endogenous autocrine and paracrine factors on stem cell differentiation of mESC. (B) In a flow chamber, Nanog, Klf4, and Rex1 were washed off from stem cells, which induces differentiation. (C) Adding endogenous factors to the medium (complex medium, CM) allows the impact of each of these factors on stem cell self-renewal and maintenance of the undifferentiated stage to be studied. (D) Stable TNFα gradient across a rectangular diffusion chamber. Across the chamber, there is a minimal flow that does not disturb the spatiotemporal gradients of secreted molecules from the cells. Sink and drain channels perpendicular to the chamber maintain the gradient constant, which allows global effects of TNFα on cells to be studied without disrupting the local cell–cell pattern. (A and B) Adapted with permission from refs (67 and 110). Copyright 2012 Proceedings of the National Academy of Sciences. (C) Adapted with permission from ref (111). Copyright 2011 Public Library of Science. (D) Adapted with permission from ref (112). Copyright 2013 Royal Society of Chemistry.

In a related work,¹¹⁰ the effect of flow on the removal of endogenous molecules and their effect on autocrine and paracrine signaling was investigated. Przybyla et al.¹¹⁰ studied mESC in microfluidic perfusion chambers under both static and flow conditions. Figure 8B (top) shows the role of selected autocrine factors for the maintenance of mESC. Under static conditions, the cells remained in the embryonic state. In flow, however, secreted autocrine factors responsible for stem cell maintenance [Nanog, Reduced expression 1 (Rex1), Kruppel Like Factor (Klf4)] were washed out, and cells began to differentiate. Effective removal of secreted factors prior to the initiation of any reaction was ensured by maintaining the ratio of the Péclet number (a measure of convective mass transport) to the Damköhler number (a measure of the reaction rate) at 1.5. These findings confirmed that previously discovered exogenous factors for maintaining stem cell self-renewal, such as Leukemia inhibitory factor (LIF) and Bone morphogenetic protein 4 (BMP4), are insufficient to maintain self-renewal in the absence of cell-secreted factors.

In an earlier study, Blagovic et al.¹¹¹ had examined the sufficiency of fibroblast growth factor 4 (FGF4) for producing neuroectodermal precursors. Using a microfluidic perfusion culture, they were able to remove cell-secreted molecules, resulting in an inhibition of growth. To elucidate the reason behind the low growth, the system was perfused with medium-containing cell-secreted factors obtained from the static differentiating cells on day 3 (Figure 8C).

Frank et al.¹¹² generated concentration gradients of tumor necrosis factor alpha (TNFα) across a rectangular diffusion chamber, demonstrating differential activation of the NFkB pathway of fibroblasts and macrophages. TNFα is a factor secreted by cells and involved in the activation of the nuclear factor kappa-light-chain-enhancer of activated B cells (NFkB) pathway, leading to programmed cell death.¹¹³ The diffusion chamber, which is automated and programmable, is connected to two perpendicular channels at its two ends, a source channel and a sink channel (Figure 8D). Concentration gradients are achieved through modulation of the flow rates in the source and the sink as well as through temporal switching between the sink and the chamber and the source and the chamber, allowing a static “diffusion only” chamber with desirable gradients. With this chamber, the authors studied the global effect of different concentrations of TNFα on the cultured cells without disturbing the spatiotemporal gradient of the molecules secreted by the cells.

2.5. Mechanical Microenvironments

The ability of a eukaryotic cell to resist deformation,¹¹⁴ to transport an intracellular cargo by membrane trafficking, and to change shape during movement depends on its cytoskeleton, a network of filamentous polymers and regulatory proteins.⁶⁵ Mechanical stimuli induce cytoskeletal rearrangement¹¹⁵ via a process called mechanotransduction, which in turn influences cell spreading, growth, and stress.

Various parameters, such as shear, substrate morphology, and flow direction, all affect the mechanobiology of cells.^{59,116,117,2,118,119} Importantly shear stress (section 2.3), substrate topography, flexibility, and rigidity can be precisely controlled and engineered in microfluidic systems, and therefore, microengineered platforms have been used extensively in cell and are becoming more and more important especially in the field of organs-on-chip for drug long-term studies.^118,120

While the need to tailor the surface chemistry of biomimetic materials has been given significant attention for decades, the need to also consider their mechanical properties and its effects on cells has only been gaining momentum in recent years.¹²¹ For a recent review on biomimetic materials see ref (66). Stiffness is a measure of the ability of a material to resist deformation. In the body, tissue stiffness ranges over several orders of magnitude, from adipose tissue (Young’s Modulus E ∼ several kPa)¹²² to bone (E ∼ GPa).¹²³

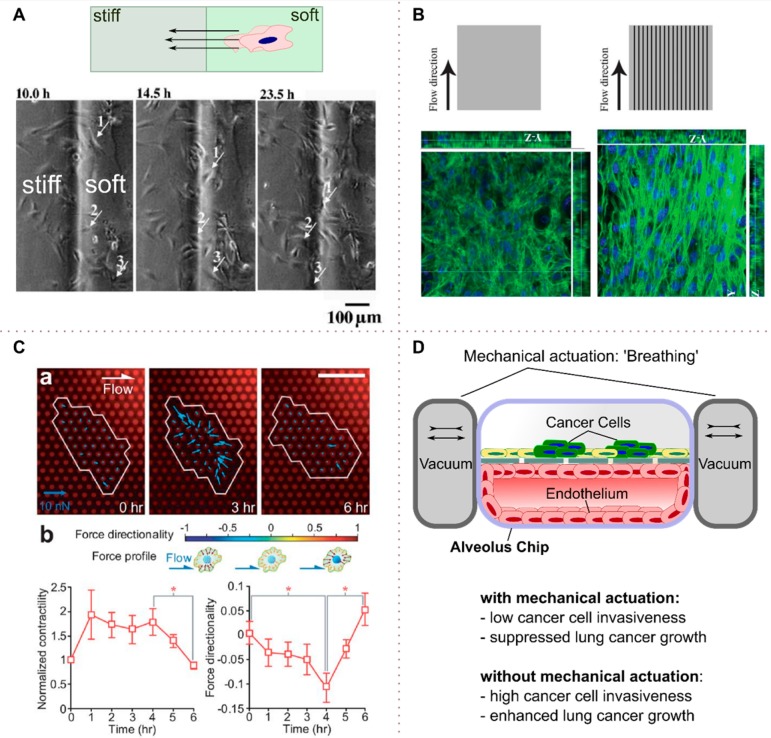
The preference for stiff over soft substrate is called “durotaxis” and was first described by Lo et al.⁵⁸ They found that stiff substrates lead to a strong mechanical input, which stimulates lamellipodia and substrate contact. Local protrusions therefore probe the mechanical properties and guide the cell toward more rigid substrates with strong mechanical feedback. Figure 9A is an example of such a study where 3T3 cells were seeded onto a collagen-coated polyacrylamide gel with different stiffness gradients, emulating an ECM with regions of varying stiffness. The cells were found to move from the soft to the stiff region.¹²⁴ For gels with a soft region of 10 kPa and a stiff region of 80 kPa, they observed the strongest induction of mechanotaxis. A mathematical model for Durotaxis from soft to stiff has recently been presented.¹²⁵

Figure 9.

Mechanical microenvironments. (A) Durotaxis of fibroblasts on a microelastic polyacrylamide gradient gel. Manipulation of the elasticity jumps affects cell migration speed and mechanotaxis efficiency. (B) Characteristic alignment of C2C12 cells on a grooved microfluidic channel substrate. Depending on the orientation of the flow and the geometry of the grooved substrate, cultured cells orient into characteristic 3D cellular constructs. Aligned C2C12 3D cellular constructs showed enhanced differentiation into skeletal muscles than randomly aligned cells. (C) Micropillar arrays allow for the monitoring of cell contraction forces as well as for the investigation of the force directionality of cells grown on the micropillar substrates. (D) Application of a vacuum allows for the mimicking of the breathing motions in the lung. Modulated strain on the artificial alveolus affects cancer cell proliferation and migration. (A) Adapted with permission from ref (124). Copyright 2008 Elsevier. (B) Adapted with permission from ref (28). Copyright 2013 Royal Society of Chemistry. (C) Adapted from ref (131). Copyright 2012 Royal Society of Chemistry.

Also the surface topography has a significant impact on the development of a cell. Peyrin et al. developed a chip with asymmetric channels allowing for the control of the directionality of cultivated neurons and were able to recreate functional synaptic connections.¹²⁶ Anene-Nzelu et al.²⁸ studied the effect of topographical features on the orientation of cells in flow. C2C12 mouse myoblasts were cultured in a microfluidic chip with incorporated microgrooves. The grooved substrate remodelled the cells into an aligned 3D cellular construct when the grooves were oriented in the direction of the flow, with the actin cytoskeleton and nuclei preferentially oriented along the microgrooves. Significantly, aligned C2C12 3D cellular constructs showed enhanced differentiation into skeletal muscles compared with randomly aligned cells (Figure 9B).

Biomechanical characterization of cells using elastomeric pillars has been widely used.^127−130

Lam et al. investigated flow-mediated endothelial mechanotransduction process using an ECM coated PDMS micropost array. The array could be used to modify the rigidity, adhesion pattern, and at the same time, the posts could be used as force sensors. (Figure 9C) They subjected HUVEC cells to a constant shear flow of 2 Pa and investigated the live-cell subcellular contractile forces as part of their study.¹³¹

In the context of cancer development and progression, it has been reported that mechanical properties of tissues are altered in many disease states, leading to cellular dysfunction and further disease progression.¹²¹ Malignancy for example has been associated with increased stiffness of the ECM by cross-linking ECM fibers.¹³² Lachowski et al.¹³³ cultured healthy pancreatic stellate cells (PSC) onto a polyacrylamide gel with a stiffness gradient. Healthy PSCs were activated and underwent durotaxis. Further, the cells shifted to a high matrix secreting cells, leading to even higher stiffness. This led to activation and recruitment of more PSC and could be the mechanisms of how fibrotic stroma in the human body is regulated.

With yearly ∼160000 deaths, lung and bronchus cancer is the leading cause of death of males in the United States.¹³⁴ Nonsmall-cell lung cancer (NSCLC) is one of many lung cancer subtypes and makes up about 40% of the deaths caused by lung cancer. Hassell et al.¹³⁵ investigated the growth of NSCLC on a human lung alveolus chip (Figure 9D). The chip design was presented earlier by Huh et al.¹³⁶ and allows for the mimicking of a breathing motion by applying differential pressure, which deforms the artificial “alveolus”. The NSCLC cells were seeded into the upper channel of the alveolar chip, where they integrated into the artificial epithelium. The authors were then able to study the effect of mechanical strain on tumor invasiveness. The breathing motion suppressed lung cancer growth and invasiveness significantly (by >50%; p < 0.001). The authors further speculated that the breathing motion might on the other hand promote development of cancer persister cells that become resistant to a third-generation tyrosine kinase inhibitor drug.

3. Suspended Cells in Microchannels

Historically, interest in the motion of particles and cells in flow was triggered by the observation that red blood cells flowing in capillaries tend to keep away from the capillary walls.^137−139 It has been shown that deformable particles^140,141 and particles of a certain shape¹⁴² undergo lateral forces while flowing in capillaries, even in very low velocity regimes. Segré and Silberberg^143,144 observed experimentally that particles flowing in a capillary tend to organize themselves at a radial equilibrium position that is 0.6 times the capillary radius away from the capillary center. These experimental findings have perhaps been the most prominent driving force behind a large number of theoretical and numerical works attempting to elucidate the lateral forces on particles and cells flowing in capillaries. In this section, we summarize the theory behind hydrodynamic forces and phenomena that affect the motion of particles and cells in flow. These phenomena have been widely used in the study of cells and exploited to perform various functions, such as counting, sorting, and trapping of cells and particles.^{141,145−150} Therefore, the phenomena discussed in this section hold a prominent position in the context of the hydrodynamic manipulation of cells. It is noteworthy that herein we focus predominantly on mammalian cells that are passive in flow. Hydrodynamics of swimming microorganisms such as bacteria are not discussed here but can be found elsewhere in the literature.^151,152

3.1. Nonlinear Effects

3.1.1. Cell Deformability

Cells and biological matter are almost always deformable. The cell membrane is a highly interesting feature of the cells. In contrast to a simple bilayer vesicle, the cells’ fluid lipid bilayer is structurally supported by the cortical cytoskeleton leading to shear rigidity. Recently it has also been shown that cells even have the ability to regulate the prestress of their membrane.^114,2 Therefore, the deformability of cells can result in nonlinear effects and induce hydrodynamic forces that are nonexistent in the case of rigid particles. Consequently, it is important to take these effects into account when studying cells in flow. Three primary methods for modeling cells exist: (1) The solid elastic model: in this model, cells are seen as solid particles that are elastic and will deform as a result of applied forces, such as flow-induced shear stress. (2) The deformable drop model: in this model, the cell is considered to be an immiscible drop of fluid that slips at the interface in response to an external flow. Here internal recirculation will form, and elasticity is given by the interfacial tension. (3) The fluid filled capsule or vesicle model: this model considers a cell as a deformable capsule of fluid with an elastic solid shell.^153,154

Regardless of the model chosen, in steady-state flow conditions, cells assume a constant shape coupled with a tank-treading motion in response to shear forces from the external flow.^{145,155−157} In line with common knowledge in the literature, we will assume a constant cell shape in our kinematic analysis of cells in flow.

3.1.2. Non-Newtonian Fluids

Fluids may be characterized as Newtonian or non-Newtonian based on their response to an applied strain. For a Newtonian fluid, the shear stress is linearly proportional to the strain rate or the velocity gradient in the flow. The proportionality constant is conventionally termed the fluid viscosity, μ (eq 7). In non-Newtonian fluids, in contrast, the relationship between the shear stress and the strain rate is nonlinear and variable, resulting in different flow patterns and behavior. Shear-thinning and shear-thickening fluids are the two most common groups of non-Newtonian fluids. In a shear-thinning fluid, the viscosity of the fluid decreases with the strain rate, whereas a shear-thickening fluid behaves in the opposite manner. Many biological fluids are non-Newtonian. Blood, for instance, is widely known to be shear-thinning.¹⁵⁸ Therefore, it is important that any nonlinearity in fluid behavior is taken into account when studying cells or particles in a flow.

3.2. Hydrodynamic Effects on Flowing Cells and Particles in Microchannels

To describe the flow of cells in a microchannel, the flow regime in the microchannel must be identified. The flow regime can be characterized using the particle (cell) Reynolds number defined as

12

where ρ is the fluid velocity, V_s is the shear velocity, a is the cell diameter, U_max is the centerline velocity, and D_h is the hydraulic diameter of the microchannel. When Re_p is smaller than unity, viscous forces dominate and a creeping flow regime prevails, whereas if Re_p is greater than unity, inertial forces become significant and their effect must be taken into account. In the next subsection, we discuss the two flow regimes and the forces on cells in each of these conditions.

3.2.1. Creeping Flow Regime (Re_p≪ 1)

In this regime, only viscous effects are present, and the Navier–Stokes equations of fluid motion are reduced to the linear Stokes equation.⁴⁰ It has been shown that, owing to linearity, spherical particles moving in this regime rotate and translate along the undisturbed streamlines without any lateral lift forces.^142,145,159 The only force present on the spherical particles is the drag force that can be described by Stokes law:¹⁶⁰

13

where a is the cell radius and U is the relative velocity of the cell and the flow. The mirror symmetry time reversal theorem proposed by Bretherton suggests that asymmetric particles may experience a lateral lift force even in the Stokes flow regime.¹⁴² The theorem states that if a particle can be rotated around its axis of rotation until it is perfectly superimposed on its mirror reflection (i.e., the particle must be mirror symmetric), it cannot experience a net lift force during one cycle of rotation in flow, whereas for mirror asymmetric particles the lateral lift force can exist even in Stokes flow.^142,145

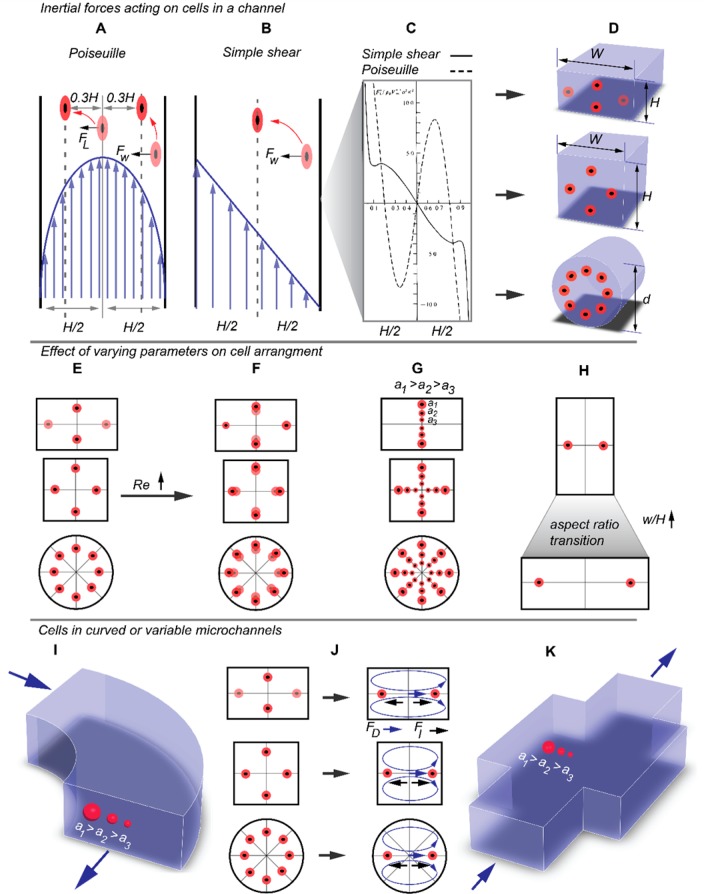
3.2.2. Inertial Flow Regime (1 < Re_p< 500)

At higher flow velocities, inertial effects become important and can result in lateral forces on particles or cells moving in such flow regimes. Unlike the Stokes regime, where mirror symmetrical particles experience no lateral force, in the inertial flow regime even spherical or symmetric particles can experience lateral forces when flowing along microchannels. For a neutrally buoyant particle with a density similar to that of the flow, the following forces will act on the particle.

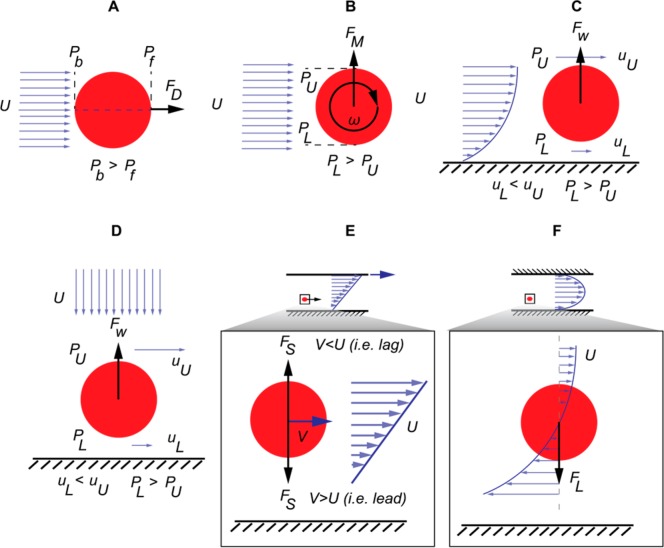
Drag Force

Cells and particles in channel flow often lag behind the flow as their velocity at the streamline going through the center of the particle or cell is lower than the oncoming flow velocity. As a result, there exists a drag force that acts on the cell in the direction of the flow (see Figure 10A).¹⁶¹ The drag force can be determined from

14

where C_D is the drag coefficient widely reported in the literature for particles of various shapes in a flow,^49,50 and U and A_c are the relative velocity and cross-sectional area, respectively, of the particle perpendicular to the direction of the flow. It is reasonable to assume that a cell in a flow is a spherical particle allowing the drag force acting on the cell to be extracted from eq 14.

Figure 10.

Various hydrodynamic forces acting on suspended cells in a flow. (A) Drag forces are exerted on a particle in the direction of the flow or in the opposite direction of the flow, depending on the direction of the relative velocity. Drag forces are present in both the creeping and the inertial flow regime. (B) Magnus forces on a rotating particle as a result of a rotation-induced pressure imbalance. Magnus forces are always directed toward the side having the higher relative velocity. (C and D) Wall forces for a particle or a cell moving parallel or perpendicular to a wall. The fluid between the particle and the wall has a lower velocity and higher pressure, forcing the particle away from the wall. (E) Saffman forces for a particle in a simple shear flow. The Saffman force is always directed toward the side having the higher relative velocity and as a result will have a different direction depending on the relative velocity of the particle. (F) Shear-induced lift force as a result of the parabolic velocity profile and the varying relative velocity on either side of the particle. This force is directed toward the side having the higher relative velocity. In a microchannel with a parabolic velocity distribution, a particle will be pushed toward the channel walls.

Magnus Force

The rotation of a particle in a flow results in a pressure imbalance in the direction perpendicular to the flow, which in turn results in a force toward the particle side with the higher relative velocity (lower pressure side), as shown in Figure 10B. For a sphere of diameter a in a flow with relative velocity of U and rotating with a constant angular velocity of ω, the Magnus force is given as¹⁵⁶

15

Wall Lift Force

The flow between a particle and an adjacent wall is slowed down as the presence of the wall results in a pressure build-up (Figure 10, panels C and D). This results in a force on the particle directed away from the wall. For 0.05 < a/H ≪ 0.2 (where H is the distance between the walls of the channel) and 20 < Re < 80,

16

Saffman Force

This is the lateral force on a particle that leads (V > U) or lags (V < U) in a simple shear flow (i.e., a flow with a linear velocity distribution and a constant velocity gradient) and is directed toward the direction of maximum relative velocity between the particle and the flow, as shown in Figure 10E. The Saffman force is solely the result of the velocity gradient in the flow and does not take into account the rotation of the particle. In purely hydrodynamic flows in microchannels, this is negligible compared with other governing effects. However, when other forces, such as gravitational, electrical, or magnetic effects are present (resulting in leading or lagging particles), the Saffman force must be taken into account. For the case of a particle in simple shear flow, Saffman¹⁶² calculated the lift force as

17

where U is the relative velocity, a is the particle radius, k is the velocity gradient, and μ and ν are the fluid dynamic and kinematic viscosity, respectively.

Shear Gradient Lift force

The channel walls in a microchannel or capillary result in a particle lagging behind the flow in the velocity field.¹⁶⁰ The lagging of a particle in a flow with a parabolic velocity distribution results in an increased force toward a larger relative velocity between the cell and the flow.⁸⁵ The larger relative velocity results in a pressure gradient across the particle, forcing the particle into the direction of lower pressure (toward the channel walls) as shown in Figure 10F. For a/H ≪ 1, Re > 1, and Re_p ≪ 1,

18

For 0.05 < a/H ≪ 0.2 and 20 < Re < 80,

19

For a neutrally buoyant particle flowing in a straight microchannel, all the aforementioned forces are present. However, the Saffman and Magnus forces are negligible compared with the other forces. As a result, the motion of a cell in a microchannel is governed predominantly by shear gradient lift forces that drive the cell toward the channel walls and the wall forces that drive the cell away from the walls and toward the channel center. The interplay between these forces and the resulting equilibrium defines the steady-state equilibrium position of the cell within the channel, as shown in Figure 11A. Ho and Leal¹⁶⁰ solved the governing equations for a particle moving in a flow for both Poiseuille and simple shear flows and determined the net force acting on the particle (F_t) across the channel. Figure 11C reports the lateral force (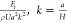) (from Ho and Leal) plotted against the lateral position. The data in Figure 11C indicate that for simple shear flows there is only one equilibrium position (F_t= 0) at the channel center, whereas for Poiseuille flow (with a parabolic velocity distribution) there are three points across the channel where the net force is zero: one unstable equilibrium point at the channel center and two stable equilibrium points 0.3 H away from the channel centerline. The distribution of these equilibrium points across the channel cross section depends on the shape of the channel cross section. As shown in Figure 11D, for a rectangular channel, the stable equilibrium points are located across the small channel dimension, whereas in square channels, there are two pairs of equilibrium points across both the height and the width of the channel. For a circular channel, the equilibrium points are evenly distributed along an annulus with a radius of 0.3H.¹⁵⁷

Figure 11.

Hydrodynamic effects on suspended cells in flow. (A) Cells in parabolic flow will be driven away from the center and the wall and find an equilibrium position at 0.3 H away from the center. (B) In simple shear flow, the only effect is the wall effect that drives the cells away from the wall until they find a stable position at the center. (C) Hydrodynamic forces acting on a particle in parabolic (dashed) and simple shear (solid) flow profiles. (D) Stable equilibrium positions for particles in an inertial Poiseuille flow in channels with different cross sections. (E and F) Effect of increasing Re on the stable positions for cells in channels with different cross sections. (G) Effect of the particle size on the inertial lift experienced by the particle. The larger the particle, the bigger the inertial lift forces, and as a result, the particle will find an equilibrium position closer to the walls. (H) Effect of varying the aspect ratio in the stable positions in a rectangular channel. (I) Curved microchannels result in cross-sectional, secondary flows around the bend, which affect the focusing of particles according to their size. (J) Secondary Dean flows occur as a result of mismatching fluid inertia along the curved channel and the resulting migration of the cells due to the interplay between the secondary flow drag force and the inertial lift forces. Two potential equilibrium positions in the vicinity of the inner and outer wall of the curve have been reported in the literature, with the inner wall position being the most frequently reported stable position for particles in curved channels. (K) Steps, converging-diverging channels, and wall irregularities will result in secondary Dean flow recirculation and, similarly to curved channels, induce a size-dependent separation of particles in the channel. (C) Reproduced with permission from ref (160). Copyright 1974 Cambridge University Press.

The channel length required for focusing cells at these equilibrium positions in a straight microchannel can be determined from the following relationship:^145,157

20

where U_m is the maximum channel velocity and f_L is the lift coefficient (with average values between 0.02 and 0.05). The flow rate required to achieve focusing at the length L_f of a straight channel can be obtained from the following equation:

21

In a curved channel, however, the flow behavior is quite different. Because of the curvature in the channel, centrifugal forces acting on fluid elements create a radial pressure gradient that drives the fluid radially, triggering a secondary recirculating flow across the channel cross section that consists of two symmetric vortices^163,164 (Figure 11J) and is referred to as a Dean flow.¹⁶¹ The strength of the secondary flow in a curved channel is a function of the Dean number, i.e.

22

As such, the Dean flow strength depends on the Reynolds number and the dimensions of the channel cross section and its curvature, R. The interplay between inertial lift and the drag forces resulting from the secondary Dean flow creates new and interesting possibilities for equilibrium points within curved channels. The drag forces and the inertial lift forces both depend on the particle size (a), which renders curved channels suitable for size-based separation of particles and cells. It has been suggested that the scaling ratio of the inertial lift force and the Dean flow drag force is a defining parameter for particle focusing in curved channels.^145,157,161 The force ratio, R_f, is defined as

23

where a is the particle diameter, R is the curvature of the channel, and H is the smallest dimension of the channel cross section. To achieve focusing, it has been suggested that R_f cannot be smaller than 0.04.^145,157 At very small ratios, the Dean flow effects would be so powerful that the particles would recirculate across the channel cross section without ever achieving a steady equilibrium position. In contrast, if the inertial forces are significantly larger than the Dean drag forces, the channel curvature will play no role in the focusing of the particles and thus the size-dependent features of curved channel focusing cannot be exploited. Accordingly, an appropriate balance between the inertial and Dean forces is required to achieve focusing of particles in curved channels. With the right balance, curved channels can enhance the focusing of particles when compared with straight channels, resulting in an increase in focusing speed by a factor between 0.2 and 1.¹⁴⁵ It has also been observed that larger particles tend to be focused near the inner wall of the channel, whereas smaller particles are focused further away from the inner channel wall, as shown in Figure 11I. This observation is attributed to the greater inertial forces experienced by larger particles than by smaller particles (which are influenced more strongly by the Dean drag). Generally speaking, based on the relative importance of the inertial and drag forces, it has been shown that the steady-state equilibrium positions in Figure 11D are reduced to two possible equilibrium positions close to either the inner or the outer wall of the curve^165,166 (Figure 11J). However, the interplay of all forces and parameters involved is complex, and the possible focusing outcomes cannot be simplified to just one or two scenarios.^145,157,161

Variable channel geometries as well as wall grooves and irregularities (Figure 11K) can induce secondary Dean flows across the channel cross section.^149,167 The underlying physical phenomena are similar to those in curved channels, with inertial and secondary Dean drag forces present in the microchannel defining the final focusing position of the particle or the lack thereof. As the final focusing position will strongly depend on both particle size and deformability, specific channel geometries can be used to sort and separate heterogeneous cell suspensions.

3.3. Separation and Sorting

Nonadherent cells in nature occur as heterogeneous cell suspensions, and thus isolation of cells is necessary prior to cell-specific studies. Blood, for example, is a mixture of red and white blood cells that have different physical properties, such as size and deformability. Cell separation using hydrodynamic flows in microchannels has been developed for and shown to be capable of exploiting the physical characteristics of cells to perform label-free separation and sorting. A common way to sort cells uses specific channel designs that include features or nonuniformities that exert hydrodynamic forces on cells of a specific size or elasticity and thus enable manipulation of the cell trajectory. In section 3.2, we discussed various channel cross sections and designs leading to specific arrangement of cells. On the basis of the function of interest, a combination of channel designs and features as shown in Figure 11 can be used to achieve a certain cell trajectory. Figure 12 summarizes the most common channel designs used for cell sorting, namely, spirals, serpentines, and channel expansions.

Figure 12.

Hydrodynamic effects for selective cell sorting. (A) Hydrodynamic-lift effects are induced by a viscous orthogonally flowing sheath fluid. Height of RBCs (z position in the channel) significantly increases, whereas platelets flow along the wall. (B) Expansion-contraction channels for separating rare cancer cells from blood cells. The combination of inertial lift and viscous drag forces acts on particles of various sizes. The contraction channel aligns the center of inertia of the rare cells (green) toward the channel center, while the other cells are still flowing along the channel walls. (C) Dual role of Dean forces for focusing larger particles (7.32 μm) in a single equilibrium position and transposing smaller (1.9 μm) particles from the inner half to the outer half of the microchannel cross section. (D) Dean flow and centrifugal forces induced by the serpentine channel design induce size-based differential equilibrium positions of the particles. Larger cells migrate toward the center, whereas smaller particles flow along the wall. (E) Obstacles translate cells based on their deformability and viscosity. In the channel, the cells experience a hydrodynamic force and an elastic force as they are being deformed by the ridges. The difference in the gradient of the free energy of soft and stiff cells leads to different transverse forces. These forces deflect the cell trajectories in the microchannel perpendicularly to the ridge, depending on cell stiffness. This method enabled the separation of K562 and Jurkat cells. (F) Randomly distributed particles experience an elastic force, proportional to the particle volume. Large particles migrate toward the centerline. Larger particles laterally migrate farther than smaller particles while flowing in the second stage. (G) Deterministic lateral displacement: particles that are smaller than the lane width follow the streamlines in lane 1, pass through lane 3 in the second row, then pass lane 2 in the third row, flow through lane 1, whereas particles with a radius larger than the width will be displaced repeatedly. (A) Adapted with permission from ref (168). Copyright 2012 the American Institute of Physics. (B) Adapted with permission from ref (169). Copyright 2011 Royal Society of Chemistry. (C) Adapted with permission from ref (165). Copyright 2008 Royal Society of Chemistry. (D) Adapted with permission from ref (172). Copyright 2015 Nature Publishing Group. (E) Adapted with permission from ref (173). Copyright 2013 Wang et al. (F) Adapted with permission from ref (174). Copyright 2015 the American Institute of Physics. (G) Adapted with permission from ref (175). Copyright 2004 the American Association for Advancement of Science.

Geislinger et al.¹⁶⁸ used size and deformability as intrinsic biomarkers to separate red blood cells (RBCs) from other blood components. To perform separations, they exploited the repulsive wall effect, which is a viscous lift at low Reynolds numbers and induces lateral migration of soft objects perpendicular to the streamlines of the fluid (section 3.2.2 and eq 16). The separation section of the device consisted of a straight channel with a square cross section. Cells entered this region through a small inlet and were hydrodynamically focused by a sheath flow. Separation of red blood cells and blood platelets was performed at a moderate flow rate of 200 μL h^–1, with red blood cells drifting away from the wall owing to wall effects along the length of the separation channel and platelets remaining on the same streamline adjacent to the walls (Figure 12A).

A combination of high aspect ratio microchannels and channel expansions has also been used to isolate low abundance cells from blood in the work of Bhagat et al.¹⁶⁹ Their separation device consisted of three sections (labeled X, Y, and Z in Figure 12B). In region X, all cells are guided toward the channel walls as they travel through a high aspect ratio rectangular channel. In region Y, the contracted channel width is comparable to the diameter of the rare cells (green), and thus the centers of inertia of the rare cells align with the channel centerline, whereas smaller blood cells flow along the sides adjacent to the channel walls. In section Z, rare cells flow through the center and are collected at the central outlet, whereas small cells are guided toward side outlets. Using their separation technique, Bhagat et al. isolated circulating tumor cells (CTCs) in blood based on differences in size between CTCs and hematologic cells. The authors spiked whole blood with MCF-7 cells and isolated these cells at a recovery rate of over 80% and with a more than 10⁴-fold enrichment over red and white blood cells.

Spirals and curved channels are common tools for size-based hydrodynamic separations as they introduce secondary flows across the channel cross section (Figure 11, panels I and J) and have been used for the separation of blood cells.^170,171 Bhagat et al.¹⁶⁵ used a spiral-channel microdevice for the separation of micrometer-sized particles (Figure 12C). A spiral microchannel geometry leverages the dual effects of Dean forces, which tend to focus larger particles in a single equilibrium position near the inner wall of the spiral, while transposing smaller particles from the inner half to the outer half of the microchannel (Figure 11, panels I and J). Using a five-loop spiral microchannel, with a width of 100 μm and a height of 50 μm, they separated 7.32 μm and 1.9 μm particles at a Dean number of 0.47.

As noted, serpentine microchannel networks can induce cross-sectional secondary flows and promote size-based separations of particles and cells in certain flow regimes. For example, Zhang et al.¹⁷² designed a serpentine microchannel (Figure 12D) to continuously separate particles and cells. They experimentally characterized the size-dependent equilibrium positions for 3 to 13 μm particles at different channel Reynolds numbers. At low channel Reynolds, separation relies on size-based differential equilibrium positions of species (i.e., larger cells are pushed toward the center, while smaller particles flow along the wall). Working at Re_c = 120, they were able to separate a mixture of 3 and 10 μm and 5 and 13 μm polystyrene beads with high purity >90% in all collection outlets. For a mixture of murine erythroleukemia cells (∼12.6 μm diameter) and 5 μm polystyrene beads in phosphate-buffered saline (PBS), they also achieved a high purity of 94.6%.

Microchannels with patterned walls have also been shown to be effective for performing cell separation based on cell stiffness. For example, Wang et al.¹⁷³ developed one such device. In this, ridges were added to the top walls of the microchannel, with the gap between the ridges and the bottom wall being smaller than the cell diameter. Cells flowing inside the channels were “squeezed” through the gap between the ridges and the bottom wall and, as a result, experienced both a hydrodynamic force and an elastic force (due to cell deformation by the ridge). The summation of these forces resulted in a transverse displacement that was strongly dependent on the cell stiffness. The authors demonstrated both experimentally and numerically that cells with higher stiffness experience a larger lateral displacement in the flow. Using this method, they were able to separate K562 cells (CCL-243) and Jurkat cells (CRL-1990), which are of similar size, but differ in stiffness (Figure 12E).

In addition, Nam et al.¹⁷⁴ developed a two-stage microfluidic device for separating MCF-7 cells and leukocytes using a viscoelastic fluid (5 wt % of polyvinylpyrrolidone (PVP) aqueous solution) (Figure 12F). They used a circular capillary as the first stage of their device, ensuring particle focusing prior to separation, and in doing so enhanced the separation efficiency in the second stage. In such a system, a circular capillary is superior to a square capillary as the former prevents trapping of particles. The authors suggested that by using a viscoelastic fluid in a circular capillary, a synergic interplay of fluid inertia and elasticity results in the focusing of particles at the center if the ratio of particle diameter to capillary diameter (blockage ratio) is higher than 0.1. In the second stage, the focused particles separate because of the forces acting on them, with larger particles experiencing a larger force and migrating toward the centerline faster than smaller particles. Exploiting such size-based differential migration and a bifurcating channel design, Nam et al. were able to separate 5 and 10 μm diameter polystyrene particles, collecting each particle size at a separate outlet (Figure 12F). They also used their platform to successfully separate MCF-7 cells from leukocytes, with >94% separation efficiency, a purity of >97%, and high cell viability (>90%).

Deterministic lateral displacement (DLD) is another elegant technique for size-based separation of cells. Figure 12G illustrates the implementation of DLD by Huang et al.¹⁷⁵ for particle separation. The separation process leverages a laminar flow through a periodic array of micron-scale obstacles, with the laminar flow bifurcating asymmetrically around the obstacles. For visualization, the gap between the obstacles is divided into three lanes (pink, 1; yellow, 2; and blue, 3) (Figure 12G). Particles that are smaller than the lane width will follow the streamlines. For example, the particle in lane 1 will pass through lane 3 in the second row, lane 2 in the third row, and back to lane 1 in the fourth row. In contrast, particles with a radius larger than the width of lane 1 behave differently because the particle cannot fit into lane 1 and therefore cannot travel along the first stream line. As a result, the particle will be “bumped” and its center will be displaced into lane 2, where it will move along the second streamline owing to a reduced resistance. The bumping is repeated each time a large particle approaches a row of obstacles, resulting in the size-based separation of particles with a resolution of ∼10 nm at the outlet of the pillar array. DLD-based separation of blood cells was first shown by Davis et al.,¹⁷⁶ and DLD has been also used to separate different microorganisms, such as rod-shaped bacteria E. coli.^177,178

3.4. Cell Trapping

Cell trapping is an important function for long-term on-chip manipulations and studies of suspended cells. The majority of cell-trapping strategies presented to date use microchannels decorated with obstacles that can capture the cells as they flow through the microchannel. Thereafter, trapped cells can be studied or manipulated. In addition to mammalian cell studies, trapping devices have also been used for long-term studies of yeast and the separation of mother and daughter cells.^179,180 Moreover, the use of hydrodynamic (rather than physical) cell traps has shown much promise for high-throughput size-selective trapping of cells and particles. To date, hydrodynamic trapping relies on the use of microvortices generated by geometrical modification of the microchannel profile.^29,181,182

Di Carlo et al.¹⁸³ developed the first hydrodynamic trapping device for high-throughput single-cell studies. The device contained U-shaped trapping structures designed to trap single cells, and they were able to capture and subsequently culture HeLa cells on these structures. An instructive adaptation of this type of physical trapping of cells was later presented by Dura et al.,¹⁸⁴ in which a flow-through microchannel decorated with an array of capture “cups” was used for high-throughput cell capture and pairing of T-cells and B-cells (Figure 13A). Using a combination of forward and backward capture cups and alternating the flow direction in the microchannel, the authors were able to successfully pair cells of interest (Figure 13A). They designed the traps such that each trap has a weir structure with forward and backward capture cups connected via an underpass, allowing flow of liquid through the trap. The pillar heights were made smaller than the cell diameter to ensure that cells can be trapped once they enter the capture cup. Once a cell has been trapped, the flow is redirected around the trap, and flowing cells may be trapped in subsequent rows of the trapping array (Figure 13A). Using such a trapping array, the authors were able to pair off lymphocytes for defined contact times. In addition, they characterized the early activation dynamics of cluster of differentiation 8 (CD8) T cells from OT-1 and TRP1 transnuclear mice by measuring the cytosolic [Ca²⁺] mobilization of CD8 T cells through different modes of stimulation.

Figure 13.

Physical and purely hydrodynamic trapping in microchannels. (A) Cells of a first type (green) are first trapped on the frontside of the traps. Then a backflow guides the cells into the single traps on the back-side of the double trap. Then cells of a second type (red) are flowed into the channel, and single cells of cell both types are trapped in the front two-cell trap. (B) Individual cells are transported into the trap sites, where they act as plugs. This increases the flow resistance of path 1 dramatically. Under this condition, the cell medium prefers to travel in the main channel (bypassing mode), the cell travels around the filled trap site, and is captured in the next empty trap site. (C) The resistance in the main channel is higher than the resistance across the 3 μm high gap, and thus the cells are trapped in the empty cavity. (D) The array of circular holes traps and funnels the cells into the cavities aligned below the holes. (E) In the high aspect ratio inlet channels, the wall lift force is the main force and aligns the particles near the channel wall. In the channel expansions, the shear gradient lift force lifts the larger particles, which are trapped by microvortices. (F) Hydrodynamic forces act on the particles in the flow field, and manipulation of the stagnation point along the extensional axis can be used to steer the particle. (A) Adapted with permission from refs (184 and 187). Copyright 2015 and 2009 Macmillan Publishers, respectively. (B) Adapted with permission from ref (30). Copyright 2015 American Institute of Physics. (C) Adapted with permission from ref (185). Copyright 2010 Royal Society of Chemistry. (D) Adapted with permission from ref (186). Copyright 2015 Royal Society of Chemistry. (E) Adapted with permission from ref (29). Copyright 2011 American Institute of Physics. (F) Adapted with permission from ref (31). Copyright 2010 American Institute of Physics.

Using a different strategy, Jin et al.³⁰ conceived a passive microfluidic cell-trapping device that operates on the principle of “least flow resistance paths”. The core trapping structure of their microdevice consists of a series of concatenated T- and inverse T-junction pairs, which function as trapping constrictions and bypass channels. As cells flow through the network of channels and constrictions, they always select the path of lowest resistance (i.e., the path with the shortest length and/or the largest width), resulting in entrapment at constrictions. Using this technique, the authors demonstrated the successful trapping of HeLa and HEK-293T cells. They were able to capture cells (with either 1 or more cells per trap) in 100% of the traps and obtained single cells in 90% of over 400 trap sites (Figure 13B). Using the same concept of least flow resistance, Kobel et al.¹⁸⁵ combined fluid dynamics simulations with particle image velocimetry to design and optimize the trap architectures. The device contains a long looped main channel with cavities and a 3-μm high gap connecting the cavity with the main channel (Figure 13C). As the resistance of the main channel is high, the flow passes mainly through the gap, and a flowing cell will be dragged into the cavity. Once the first cavity is occupied, the flow path will lead any subsequent cells along the loop until they are captured in a next empty cavity. Once trapped, the cells remain in place because of the pressure difference across the inlet and the outlet.

A vertically integrated array trap developed by Chanasakulniyom et al.¹⁸⁶ is another example of a microfluidic platform that allows physical trapping of single cells and can be used to explore quantitative functional assays, including single-cell attachment, proliferation, and migration studies (Figure 13D). The device consists of three layers: a polydimethylsiloxane (PDMS) chamber (top), an array of circular holes (middle), and 100 μm diameter circular cavities (bottom), all bonded to a glass substrate. Trapping regions are connected to two inlets and outlets for perfusion and cell loading. The researchers were able to trap cells in up to 85% of the traps after multiple rounds of cell loading (with a loading density of 3 × 10⁶ cells mL^–1 and a flow rate of 0.1 μL min^–1 for 30 s). The flow paths inside the device facilitated cell trapping and additionally protected cells from flow-induced mechanical stress. Specifically, the trapping device was used to study the attachment and detachment of MDA-MB-231 human breast cancer cells during the cell cycle and to explore the influence of the chemokine stromal cell-derived factor 1 (SDF-1).

As noted, hydrodynamic cell entrapment using microvortices has been demonstrated as a viable means of cell trapping. For instance, through a combination of inertial focusing and microscale laminar vortices, Hur and co-workers²⁹ succeeded in performing size-based cell trapping (Figure 13E) using a microfluidic device consisting of eight parallel, high aspect ratio straight channels with ten cell-trapping reservoirs per channel. Microvortices were induced by incorporating channel expansions and maintaining sufficiently high Reynolds numbers. In high aspect ratio channels, particles are focused at a uniform height near the channel wall (as discussed in section 3.2). As a particle flows past a channel expansion, the wall effect is suddenly removed, and the prominent force now acting on the particle is the shear gradient lift force (which scales with the cube of the particle diameter). Accordingly, larger particles experience a larger lift force, driving them into the trapping reservoirs, whereas smaller particles remain in the channel and flow downstream.

In another hydrodynamic trapping strategy, flow stagnation points have been exploited by Tanyeri et al.³¹ to trap both particles and E. coli. Their trapping device consists of a junction where four channels coincide. Two laminar inlet streams meet at the channel junction from opposing directions and are diverted through the two perpendicular outlet channels as shown in Figure 13F. Thereby, a stagnation point is created in the center of the junction. Through active control of outlet flow rates (extensional axis), the authors were able to maintain a trapped particle at the center of the junction. That said, in the absence of active flow control, trapped particles would ultimately escape owing to Brownian fluctuations coupled with fluid convection along the extensional axis.

3.5. Cell Focusing

Focusing is a critical process for high-throughput sorting and imaging of cells. For instance, in flow cytometry, a key motivation for replacing conventional flow chambers with their microscale counterparts is the ability to focus cells within a narrow space so that they can be imaged effectively despite the narrow field of view typical of conventional microscopes. Hydrodynamic focusing has been demonstrated using a variety of methods, such as sheath fluids, non-Newtonian fluids, channel geometry adaptations, or a combination of these approaches. Channel expansions induce Dean vortices, sheath fluids can facilitate the lateral positioning of cells, and non-Newtonian fluids¹⁸⁸ have recently been used to tailor cell migration. However, a challenge faced when using non-Newtonian fluids is that cell viability may be compromised and that biocompatible viscoelastic systems are needed to prevent cell harm. As such, the viscoelastic focusing methods presented here were predominantly used to focus particles, but the concepts could also be adapted for cell studies.

Several implementations for cell focusing using sheath fluids exist. Lee et al.¹⁸⁹ designed a single-layer microchannel incorporating contraction–expansion array structures that enables hydrodynamic focusing through the interaction of a sheath flow with secondary flow vortices (Figure 14A). In initial experiments, PBS sheath flow was used to engulf the sample stream. Owing to the Dean flow effects, the focused sample was gradually being shifted toward the sheath flow as shown in Figure 14A. Using this technique, the authors demonstrated the successful focusing of a red blood cell suspension. Similarly, Yuan et al.¹⁹⁰ demonstrated three-dimensional particle focusing using a straight microchannel with asymmetrical expansion-contraction cavity arrays, designed to induce secondary Dean flows across the channel and to facilitate focusing in combination with inertial and viscoelastic forces present within the system (Figure 14B). Using this platform, particle focusing with Newtonian (deionized water) and non-Newtonian fluids [aqueous solution of poly(ethylene oxide) 500 ppm] was achieved for three different particle sizes (3.2, 4.8, and 13 μm). Interestingly, particles were focused on the cavity side when flowing in a Newtonian fluid (because of inertial and Dean drag forces), whereas in a viscoelastic fluid, they were aligned to the opposite side of the cavity (owing to the viscoelastic forces). Sheath flows have also been combined with curved channels and shown to be effective in focusing particles and cells, as demonstrated by Tripathi et al.¹⁹¹ In that work, a sheath flow maintained particles (6 μm melamin resin-based particles) or blood cells (from diluted whole blood) near the inner wall of the curved channel, whereas Dean flow effects shifted the particles or cells toward the opposite wall, resulting in their focusing at the middle of the channel (Figure 14C).

Figure 14.

Asymmetric geometries leverage hydrodynamic focusing properties in microchannels. (A) The sheath fluid is exposed to the Dean flow at the contraction region and wraps the RBC suspension close to side 2 (s2). RBCs simultaneously begin to shift toward side 1 (s1). This leads to a three-dimensional focusing of the RBCs in a cross-sectional plane of the microchannel. (B) Asymmetric elements induce secondary flows and facilitate particle focusing with Newtonian and non-Newtonian fluids. (C) The sheath flow maintains the cells near the inner wall of the curved channel, and the Dean flow shifts the cells toward the opposite wall. (D) Particles undergo two opposing forces, the elastic force (F_E) and the Dean drag force (F_D). The Dean elasto-inertial focusing (DEF) band is created on the right-hand side of the confined spiral channel (red box). In the region of the DEF band, lateral migration is dictated by the competition of F_D and F_E. Single-line particle focusing has been achieved when using a viscoelastic medium but not in a Newtonian medium. (E) Three-dimensional hydrodynamic flow focusing of dye, particles, and cells in a microfluidic device by using two bends of opposite curvature. (A) Adapted with permission from ref (189). Copyright 2009 the Royal Society of Chemistry. (B) Adapted with permission from ref (190). Copyright 2015 the American Institute of Physics. (C) Adapted with permission from ref (191). Copyright 2016 Springer. (D) Adapted with permission from ref (192). Copyright 2013 Nature Publishing Group. (E) Adapted with permission from ref (146). Copyright 2007 Proceedings of the National Academy of Sciences.

Lee et al.¹⁹² also used a combination of viscoelastic forces and secondary flow Dean drag forces in a spiral microfluidic channel to perform particle focusing (Figure 14D). Through numerical modeling, it was demonstrated that particles in a viscoelastic Dean flow experience an elastic force as a result of the first normal stress difference within the fluid and a Dean flow drag due to the secondary Dean flow across the channel. The authors further explained that a balance between these two forces results in size-based focusing of particles, with larger particles experiencing a larger Dean force (attributed to their larger particle Dean number), which pushes them further toward the outer wall (than smaller particles). The viscoelastic fluid focusing strategy was used to successfully focus and separate 1.5 and 10 μm polystyrene particles.

Finally, Di Carlo and co-workers¹⁴⁶ performed particle focusing in both straight and curved channels using a variety of particle and carrier fluid densities. Their study indicated that regardless of the particle or fluid density a similar focusing behavior occurs (Figure 14E, right), an observation they rationalized by the fact that the inertial forces acting on a particle depend on the shear and viscosity rather than on the fluid or particle density. Further studies demonstrated the focusing of red blood cells (in diluted whole blood) in straight channels, with the red blood cells assuming four focusing positions in the vicinity of the channel sides (Figure 14E, left). Interestingly, experiments with blood cells, cultured cells, and particles yield very similar focusing behaviors, implying that the cells within inertial microscale flows behave as solid particles.

3.6. Cell Deformation and Mechanobiology

Cell viscosity is affected by a multitude of parameters, and therefore every cell has a specific viscosity and thus deformability. For example, the deformability of red blood cells decreases when they are infected with Plasmodium falciparum. In contrast, cancer cells tend to be more deformable than healthy cells in their environment.¹⁹³ Accordingly, cell deformation studies are of great potential in the development of novel methods to sort and isolate cells or even study biological processes. Traditionally, cell deformation studies are conducted with an AFM probe that is in direct contact with the cell.¹⁹⁴ Alternatively, the cell substrate (on which the cell is growing) can be stretched or deformed.⁸² Both methods, however, involve either direct contact for a mechanical manipulation of the cell, which may damage or alter its structure.

To avoid direct contact with a cell and prevent unwanted damage or alteration to the cellular structure, cell deformation studies have also been conducted using hydrodynamic manipulation in microfluidic systems. For instance, microchannel crossings have been used to immobilize cells at stagnation points created by two confluent streams, whereas stretching the trapped cell (hydrodynamically) may be achieved by adjusting the flow parameters. Using the microfluidic design shown in Figure 15A, Gossett et al.¹⁹⁵ were able to probe the deformability of single cells at a rate of approximately 2000 cells per second. Specifically, they incorporated inertial focusing to uniformly deliver MCF-7 cells to a T-junction at high speed, where cells were entrapped and deformed by hydrodynamic shear from the surrounding streams. Using this deformability probe, they assayed populations of leukocytes and malignant cells in pleural effusions and predicted the state of disease in patients with cancer and immune activation with a sensitivity of 91% and a specificity of 86% (Figure 15A). Similarly, Deng et al.¹⁹⁶ developed an inertial microfluidic cell stretcher to distinguish epithelial-mesenchymal transition from other cells in a heterogeneous cell suspension. In a high aspect ratio channel, with interspersed obstacles, cells are focused to a single equilibrium position before they reach a T-junction. At the T-junction, they are deformed and the deformability can be monitored on a microscope.

Figure 15.

Cell deformation in microchannels and blood cell studies. (A) Hydrodynamic cell stretching of MCF-7 cells. MCF-7 cells are delivered to a T-junction at high flow rates, where they are exposed to and deformed by the shear strain. Also, the deformability of native populations of leukocytes and malignant cells in pleural effusions was investigated and the disease state in patients with cancer and immune activation predicted with a sensitivity of 91% and a specificity of 86%. (B) Analysis of the shape recovery of Plasmodium falciparum-infected and healthy RBCs. Elastic RBCs cells of 8 μm diameter as well as infected cells in the early ring stages flowed through the cavities of 8, 6, 4, and 2 μm width. Trophozoite stages traversed 6 and 8 μm but failed to transverse 2 μm and partly also 4 μm. Schizont stages traversed only 8 μm. Uninfected RBCs easily passed through the 2 μm constriction. (C) Microfluidic biomechanical assay for RBCs parasitized by Plasmodium falciparum. Individual RBCs are deformed by flowing them through multiple funnel-shaped constrictions with openings ranging from 5 down to 1 μm. Parasitized cells from the ring through the Schizont stage were shown to be 1.5 to 200 times stiffer than uninfected cells. (D) The role of actin organization and myosin-II activity during the different stages of leukocyte trafficking through narrow capillaries using specific drugs (Lat-A, Jpk, and Blb). The channel was 20 μm wide, with constrictions of 4 μm. Case I: control and Jpk- and Lat-A-treated cells have a puck shape, with a diameter of 17 μm and height of W = 4 μm. Case II: Blb-treated cells have a roughly parallelepiped shape, with dimensions of 4, 16, and 29 μm. (A) Adapted with permission from ref (195). Copyright 2012 National Academy of Sciences. (B) Adapted with permission from ref (204). Copyright 2003 National Academy of Sciences. (C) Adapted with permission from ref (203). Copyright 2012 Royal Society of Chemistry. (D) Adapted with permission from ref (205). Copyright 2009 Elsevier.

Another prominent class of hydrodynamic tools for cell deformation studies involves microchannel constrictions, wherein a cell is forced through a narrow channel or nozzle having a size smaller than the diameter of the cell (Figure 15, panels B, C, and D). Cell deformability probes based on constricted microchannels¹⁹⁷ have been used in addition to DLD-based approaches¹⁹⁸ to detect Malaria-infected red blood cells in blood. Constrictions have also been used to study deformation of oocytes,¹⁹⁹ cancer cells,^200,201 and cell nuclei.²⁰²

Red blood cells parasitized by Plasmodium falciparum can be distinguished from uninfected cells and characterized on the basis of deformability variations.²⁰³ Using one such platform, Shelby and co-workers²⁰⁴ characterized the behavior of healthy and infected RBCs while the cells were flowing through narrow constrictions in elastomeric PDMS microchannels (Figure 15B). Normal and Plasmodium falciparum-infected erythrocytes in various stages of infection were perfused through constrictions of different widths (8, 6, 4, and 2 μm) and monitored for passage or blockage. Results demonstrated that uninfected RBCs, owing to their elastic properties, passed through all constriction sizes, including the 2 μm constriction. Ring-stage infected erythrocytes retained much of their original elasticity and were also able to pass through all four constrictions, whereas trophozoite-stage cells only passed through the 6 and 8 μm constrictions and clogged the 2 and 4 μm channels. Schizont-stage cells were only able to pass through the 8 μm channel. Moreover, the authors suggest that when using elastomeric channels with varying wall elasticity, their method could be used to study the cytoadherence and flexibility of healthy and infected RBCs or to perform antimalarial drug screening.

Using a similar, but more quantitative approach, Guo et al.²⁰³ developed a microfluidic platform to measure the deformability of healthy and malaria-infected RBCs using controlled flow pressure. By perfusing RBCs through funnel-shaped constrictions (ranging from 1 to 5 μm in size) and measuring the hydraulic pressure required to drive each cell through the constriction, the cortical tension of the cell membrane could be extracted and used to report the intrinsic deformability of the red blood cells. Using this methodology, they showed that infected cells in various infection stages (from the ring stage through Schizont) were between 1.5 and 200 times stiffer than uninfected cells (Figure 15C).

Another example where cell deformability measurements using constricted channels are useful is in the study of capillary leukocyte trafficking. Blockage of lung capillaries by circulating leukocytes is implicated in the pathophysiology of several conditions, such as the acute lung injury (ALI). Gabriele et al.²⁰⁵ investigated the roles of actin organization and myosin-II activity during the different stages of leukocyte trafficking through narrow capillaries (entry, transit, and shape relaxation) using specific drugs that affect actin and myosin-II activity (latrunculin A, jasplakinolide, and blebbistatin) (Figure 15D). Constrictions were approximately 16 μm deep and 4 μm wide and made to mimic the dimensions of pulmonary microvessels. Results confirmed that actin activity was the dominant factor during the entry stage, with actin disrupted cells showing entrance times (the time needed by the cell to enter the constriction) that were up to two times shorter than those of the control, whereas myosin-II activity did not alter the entrance times. Conversely, they also showed that myosin-II activity was critical during the transit stage, with myosin II-inhibited cells (Figure 15D, case II) exhibiting significant membrane unfolding and increased surface area compared with noninhibited cells (Figure 15D, case I).

3.7. Effect of Hydrodynamic Forces on the Receptor–Ligand Binding Kinetics

Cellular adhesion is often mediated by a small number of receptor–ligand bonds, sometimes even by only a single bond. As a result of these small bond numbers, cell binding events become stochastic. The presence of external forces (such as hydrodynamic dislodging forces) during the binding reaction further complicates binding (in terms of stochasticity). This multifaceted probabilistic nature of receptor–ligand binding has stimulated attempts to elucidate these stochastic effects through both mathematical modeling and experimentation.²⁰⁶

To account for the external forces acting against the association of the receptor–ligand pair, Bell²⁷ suggested a relationship between the dissociation rate of the binding reaction and the dislodging force, [K_d(f) = K_d⁰ exp[(af/K_BT)^b]], where K_d is the dissociation rate in the absence of an external force, a defines the bond state, f is the dislodging force, and K_B and T are the Boltzmann constant and temperature, respectively. Many experimental studies have been devoted to testing the validity of Bell’s model, and a range of mathematical and numerical investigations have implemented the model in their solutions. For example, Kaplanski et al.²⁰⁷ studied the kinetics of bond formation and dissociation of activated neutrophils and endothelial cells interacting with the surface of a flow chamber (Figure 16A). They used a low flow rate so that the exerted shear force was lower than the strength of a single bond. On the basis of the empirical binding parameter and the average leukocyte rolling velocity, the corresponding bond formation could be calculated. Cells stopped with a median of 2.43 s short-term arrest, and anti-E-selectin antibodies prevented the binding of leukocytes to E-selectin, leading to an inhibited stop frequency. Also, they defined the spontaneous dissociation rate of 0.5 s^–1. Free rolling cells with a mean velocity of >19 μm s^–1 exhibited a bond formation rate that was on the order of 0.04 s^–1.

Figure 16.

Shear effects on receptor–ligand binding kinetics. (A) Studies of the kinetics of bond formation and dissociation of activated neutrophils and endothelial cells on the surface on a flow chamber. A minimal shear drag force was exerted that was lower than the strength of a single molecular bond. The graph shows the observed relation of the probability of neutrophile adhesion to the bilayer and the flow velocity. x Axis: (flow velocity)⁻¹, y axis: probability of adhesion. (B) In a flow chamber, binding and unbinding events of neutrophils flowing over a bilayer containing P-selectin tethers were monitored to understand the biophysics of cell rolling. The k_off values shown in the graph were calculated by comparing the binding rates in shear stressed and nonstressed systems. x Axis: shear stress vs off-rate; y axis: k_off (s^–1). (C) Comparison of the abilities of the two models to account for the data. Predictions (curves) of model II (a and b) and model I (c and d) for the unsaturated (a and c) and saturated (b and d) bindings. (D) Dependence of k_off on the shear stress for WT and mutant substrates. On the basis of Goldman’s equations, the force acting on a platelet in shear flow was calculated. (A) Adapted with permission from ref (207). Copyright 1993 Elsevier. (B) Adapted with permission from ref (208). Copyright 1995 MacMillan Publisher (C) Adapted with permission from ref (209). Copyright 1998 Elsevier. (D) Adapted with permission from ref (210). Copyright 2002 Elsevier.

Alon et al.²⁰⁸ used a similar approach as Kaplanski et al., but instead of working with an endothelial cell layer, they flowed neutrophils over a lipid bilayer. The bilayer consisted of lipids and P-selectin tethers (at a density of 1 to 15 tethers per μm²). They validated the dissociation rates at various tensile forces to better understand the biophysics of cell rolling and investigated the detachment of neutrophils in shear flow (3.5 s^–1) and without tensile stress (1 s^–1) to define kinetic parameters (Figure 16B). Their experimental data matched the equation proposed by Bell’s model, and they were able to calculate a bond distance of 0.05 nm.

Piper et al.²⁰⁹ applied centrifugal forces to Colo205 tumor cells and measured their binding to E-selectin using a common centrifugation assay to quantify adhesion. Two stochastic models that couple the bond-applied force to the binding affinity were compared with experimental results (Figure 16C). Using this method, the authors were able to investigate parameters such as the adhesion strength, binding affinity, and binding range. They estimated a 2D dissociation constant of 5 × 10^–3 μm^–2 for E-selectin-carbohydrate binding with a sub-Ångström bonding range, with the results suggesting that five bonds mediate adhesion.

The ability of platelets to tether to and translocate on injured vascular endothelium depends on the interaction between the platelet glycoprotein receptor Ibα (GPIbα) and the A1 domain of the von Willebrand factor (vWF-A1).²¹⁰ Some bleeding disorders are caused by gain-of-function mutations in vWF, leading to binding of vWF to circulating platelets and subsequent clearance of both of these hemostatic elements from the blood. Doggett et al.²¹⁰ used a parallel plate flow chamber apparatus to assess the impact of hydrodynamic forces on platelet adhesion by analyzing the GPIbα-vWF-A1 tether bond in flow, working with purified platelets (5 × 10⁷ mL^–1) and perfusing them over absorbed vWF-A1 proteins (1 to 100 μg mL^–1 coating concentrations) or plasma vWF (25 μg mL^–1) at shear stresses ranging from 0.25 to 4 dyn cm^–2 (25 × 10^–3 to 0.4 Pa). Similarly to Alon et al., they determined the dissociation rate constants of platelets and tethers and analyzed transient adhesive events between platelets and vWF in flow (Figure 16D). Using Monte Carlo simulations, they determined the rate constants (k_on and k_off⁰) by fitting sets of simulated pause times to the sets of experimental pause times at each experimental condition. They found the cellular dissociation rate to be constant for this receptor–ligand pair, with a magnitude similar to the values reported for selectin-dependent interactions. Further, the tether bond lifetimes observed during an analysis of platelets in vivo at an injured vascular endothelium site corresponded to in vitro observations of rapid bond dissociation with k_off = 3.45 ± 0.37 s^–1.

4. Hydrodynamic Effects on Cells on Standard Open Substrates

In recent years, microfluidic technologies have been used to perform localized processing on biological samples, such as adhered cells or tissue samples, or to pattern proteins, cells, and other biomaterials on open substrates.²¹¹ This emerging field, often referred to as “open-space” microfluidics, opens up new opportunities for cell handling and manipulation using hydrodynamic effects that are markedly different from those encountered in channel microfluidics.

4.1. Review of Basic Hydrodynamics of Adhered Cells on Open Substrates

The most important characteristic of cell manipulation on common substrates (Petri dishes, well plates, chambers, or slides) is that the reagents or biomaterials of interest are dispensed on an open surface using a probe or dispenser tip. Accordingly, the fluid mechanics of open microfluidic systems is often a combination of boundary layer growth on a flat plate and stagnation flow on a flat plate as shown in Figure 17 (panels A and B).

Figure 17.

Hydrodynamic effects on adhered and suspended cells in open flows. (A) Open flow over adhered cells and corresponding momentum and mass transfer boundary layers. (B) Stagnation flow above a substrate covered with adhered cells and the corresponding boundary layer formation. (C) A suspended cell flowing over a flat surface in open flow and corresponding hydrodynamic forces on the cell. (D) A suspended cell in stagnation flow over a flat surface and corresponding hydrodynamic force on the cell.

Similar to our discussion of boundary layers inside a microfluidic channel, the laminar momentum boundary layer grows on an open flat surface according to the Blasius solution in eq 2, indicating that as the fluid flows (increasing x) on a flat surface, a thicker layer of the fluid is slowed down by the shear forces originating from the surface. As discussed, any mass transfer between the surface and the oncoming flow results in a mass transfer boundary layer as the concentration of the species transitions from the surface concentration, C_s, to the far-field concentration, C_∞. Equation 4 relates the thickness of the mass transfer boundary layer to the thickness of the momentum boundary layer.

An important parameter for adhered cells on surfaces subject to fluid flow is the wall shear on the surface. For a flow configuration on an open surface, such as the one shown schematically in Figure 17A, the wall shear can be found from the following relationship:^39,40

24

where τ_wall is the wall shear stress and c_f is the friction coefficient. Often when processing an open surface, the fluid flow is brought to the surface from the top rather than parallel to the surface. This flow pattern can be described by a stagnation flow pattern as shown in Figure 17B. Stagnation flow is a classical boundary layer problem, and its detailed mathematical description is available in Section S2. The most important features of stagnation flow are the boundary layer thickness and the wall shear stress. The boundary layer thickness is constant for stagnation flow and a function of the distance from the surface, H, and the oncoming flow velocity, V:

25

The wall shear stress for stagnation flow can be obtained as follows:

26

where U is the velocity in the x direction outside of the boundary layer. Equation 26 indicates that the shear stress in an axisymmetric stagnation flow increases as the velocity and viscosity of the fluid increase, whereas an increase in the distance between the jet and the surface will reduce the shear.

4.2. Review of Basic Hydrodynamics of Suspended Cells on an Open Surface

When a particle or cell is brought into the vicinity of a flat surface with a velocity parallel to the surface as shown in Figure 17C, the particle experiences a force away from the surface. This lateral force is in addition to any hydrodynamic drag forces that the particle experiences in flow. The dimensionless distance from the wall is defined as

27

where h is the particle distance from the surface and v_s is the sedimentation velocity of the particle in a quiescent fluid. It has been shown that for h* ≪ 1, the drift velocity (V_d) away from the wall for the particle can be obtained from the following relationship:

28

where a is the diameter of the spherical particle. At high distances from the surface, the drift velocity approaches zero because the wall effects become negligible.^156,212,213 In contrast, the drag force acting on a particle with diameter d moving perpendicular to a solid surface at an approach velocity U (as shown in Figure 17D) is given by

29

The coefficient, λ, is calculated from a series function that is provided in Section S3. It is proportional to the particle diameter and has an inverse relationship with the distance from the surface. This signifies that the wall drag force is greater for larger particles and increases as the distance between the particle and the surface decreases.¹⁵⁶

4.3. Hydrodynamic Cell Manipulation in the “Open Space”

Adhered cells are typically cultured on standard cytological substrates, such as Petri dishes, polystyrene culture flasks, and treated glass slides. In certain cases, it is of interest to analyze specific cells from a culture at a given time point, while leaving the other cells untouched and ready for analysis at a later point in time. Accordingly, researchers have developed microfluidic techniques that can be operated in “open space” and are compatible with standard cytological substrates. Application of these techniques allows treatment of selected cells from a culture locally and at the micron length-scale by leveraging hydrodynamic effects without dramatically changing the native environment of the untreated cells.

Guillaume-Gentil et al.³⁵ used a fluid force microscope (FluidFM), which combines AFM with microchannels, to pattern or isolate single cells in an immersion liquid. Specifically, a pressure controller is connected to cantilevers containing microchannels with apertures on a nanometre length-scale. Using this force-controlled nanoinjector, the authors isolated single HeLa cells from culture (Figure 18A). First, the target cell was detached by delivery of trypsin at the FM tip. The cell was trapped by gentle aspiration and transferred onto a new substrate or deposited into a microwell.

Figure 18.

Hydrodynamic manipulation of cells on immersed surfaces. (A) The fluidFM aspirates cells to the tip (negative pressure). A positive pressure pulse allows the cell to be placed at a selected location. (B) Trypsin is hydrodynamically confined to a selected adherent cell until the cell detaches. After detachment, the cell is aspirated into the MFP head. (C) Single cell analysis is leveraged by detaching a cell using hydrodynamic confinement of trypsin. The detached cell is then lysed and analyzed on-chip. (D) Hydrodynamics are leveraged to guide axons using a micropipette. (E) Single cell drug testing is performed by confining pharmacological agents on a selected cell. (F) The single-cell pipet is used to retrieve multiple cells from a suspension culture and trap a single cell from the aspirated cells. The method allows reinjection of the single cell. (A) Adapted with permission from ref (35). Copyright 2014 the Royal Society of Chemistry. (B) Adapted with permission from ref (32). Copyright 2005 MacMillan Publishers. (C) Adapted with permission from ref (33). Copyright 2014 MacMillan Publishers. (D) Adapted with permission from ref (216). Copyright 2015 Nature Publishing Group. (E) Adapted from ref (34). Copyright 2010 the American Chemical Society. (F) Adapted from ref (36). Copyright 2014 the American Chemical Society.

Another technology for the local treatment of cells with (bio)chemicals is the microfluidic probe (MFP). The MFP uses multiple apertures to establish a hydrodynamic flow confinement. A significant advantage of microfluidic probes over conventional micro- and nanopipettes is that flow confinement allows the localization of miscible liquids on the micrometer scale. Microfluidic probes have been used to stain, lyse, or detach adherent cells from the surface.^32,214,215 For instance, Juncker et al.³² used the microfluidic probe to trypsinize an adherent fibroblast cell. After detachment, the cell was aspirated into the aspiration channel of the probe (Figure 18B). Ainla et al.³⁴ used a microfluidic pipet to perform single-cell pharmacological tests. Using confined superfusion and cell stimulation, they activated human transient receptor potential vanilloid type 1(hTRPV1) receptors in single cells, measured the response by means of a patch-clamp pipet, and induced membrane bleb formation by exposing selected groups of cells to formaldehyde/dithiothreitol-containing solutions (Figure 18E). A demonstration of a microfluidic-probe-based total analysis system was presented by Sarkar et al.³³ Herein, a single cell was selectively exposed to lysis buffer using hydrodynamic flow confinements. Subsequently, the cell contents were aspirated into the probe and then mixed with assay reagents in integrated nanoliter-volume chambers for high-sensitivity single cell assays. Kinase and housekeeping protein activities from single hepatocellular carcinoma (HepG2) cells in an adherent tissue culture were then measured (Figure 18C).

Microfluidic probes have been further refined for diagnostic and research purposes for the life sciences. For example, open-space hydrodynamic devices have also been used to exert mechanical (shear) forces on selected cells in an open and immersed environment. Gu et al.²¹⁶ assessed the impact of fluid flow on axonal migration, producing turning angles of up to 90° by applying flows. Microfluidic flow simulations indicated that an axon may experience significant bending forces due to cross-flow, which are likely to contribute to the observed axonal bending. The flow rate was fixed at 2.5 μL min^–1 for the entire duration of the experiment (between 40 and 80 min). Of the actively growing axons (n = 23), 35% of the growth cones were found to respond to the microfluidic flow. Out of these flow-responsive growth cones (n = 8), 78% followed the fluid flow direction, whereas 22% grew against the flow (Figure 18D).

Finally, for single-cell analysis of nonadherent cells in suspension, isolation of a single cell must be performed prior to the chemical or biological assay. Zhang et al.³⁶ developed a hand-held single-cell pipet (hSCP) for isolation of single viable suspended SK-BR-3 cells directly from submicrolitre cell suspensions into nanolitre droplets without the assistance of any additional equipment (Figure 18F). The pipet is of the dual-channel type and contains both a positive and a negative pressure channel. Cells from a suspension are aspirated into the pipet through application of negative pressure. At the wall of the pipet, there is a hook in which a single cell is trapped. Next, the pipet is dipped into cell-free medium to wash off the free-flowing cells and ensure that the only cell in the pipet channel is the trapped cell. Thereafter, the trapped cell is reinjected by applying a positive pressure on the channel.

5. Summary and Outlook

We highlighted the importance of hydrodynamics in the study of both adhered and suspended cells and have emphasized the key physical forces that can be leveraged to influence and manipulate cells in microfluidic systems.

By analyzing the underlying physics and assessing selected applications (describing how hydrodynamic forces can be used to direct short- and long-term behavior), we hope that we have been successful in illustrating the remarkable role that hydrodynamics plays in cellular behavior. We have also introduced the concept of open microfluidics, where the advantages of microfluidic systems, in terms of precisely controlling microenvironments, can be leveraged in open substrates, which are the norm in the laboratory. Finally, we have presented the core hydrodynamic phenomena that underlie such surface probes and described their potential for analyte localization or single-cell studies through examples.

As noted, we believe that our analysis will be valuable for life-science researchers of varied backgrounds, in that it provides the necessary information and tools to understand and apply hydrodynamic effects and phenomena in the context of cell studies. However, each such analysis must be understood and assessed carefully before performing microfluidic cell manipulations. Indeed, parameters such as channel dimensions, volumetric flow rates, fluid viscosity, and substrate chemistry are recognized to significantly affect the development of a wide range of cells.

There are several highly exciting new areas of cell biology being explored with microfluidics primarily as a means of a bioanalytical tool set. In this article, we focused on literature detailing advances in two-dimensional microfluidic cell studies, which led to fundamental insights into molecular mechanisms inside and around single cells or allowed for the navigation of cells along or against the streamline. 2D Studies of cells are important to understand how single cells function, develop, or move and how cells interact with their microenvironments such as neighboring cells, chemical, or mechanical stimuli. Further, through advances in microscopy, major discoveries in the field of mechanobiology have been leading to a better understanding of the interplay between cells, cell populations, and their mechanical environment such as hemodynamic, interstitial flows, rigidity of cells, or the ECM. Efforts in the field of material science have also led to new biomimetic and biocompatible materials, which are nontoxic and can be used to tailor the mechanical properties such as Young’s modulus of the microfluidic chip walls as an example. Leveraging from the gained knowledge in various research fields, in the past years, researchers have started to make the transition from 2D to 3D studies. Many research groups have been developing highly promising approaches toward organs-on chip for drug-screening, studying tumor progression, invasion, infections, or the blood-brain barrier.

Emulating physiological environments requires a thorough knowledge of the biochemical and mechanical properties. Every cell type originates from a specific mechanical and chemical environment and will retain the proper functions only if the microfluidic environment is modeled appropriately. This said, studies may be easily misleading and inconsistencies in the literature may be found if not all factors are considered in a highly complex study such as an organ on chip. Therefore, multidisciplinary teams with not only a deep knowledge on biology, but also an understanding of the underlying physics and chemistry around cells, effected by the fluids and their associated properties, will help to achieve more rapidly the goal of the human body on-chip, which could, as we believe, eventually replace animal models.

Finally, we are of the opinion that the creative use of microfluidic tools in closed microchannels or on open surfaces will further grow significantly over the next decade and enable the rapid, precise, and efficient analysis of complex cellular populations. We hope that these developments will catalyze new scientific insights, discoveries, and even diagnostic devices and methodologies.

Glossary

Glossary

AFM

atomic force microscope

ALI

acute lung injury

ALP

alkaline phosphatase

APTES

(3-aminopropyl)triethoxysilane

Blb

blebbistatin

BMP-2

bone morphogenetic protein 2

BMP-4

bone morphogenetic protein 4

Ca²⁺

calcium

CCR7

C–C chemokine receptor type 7

CD8

cluster of differentiation 8

CD90

cluster of differentiation 90

CIPC

isopropyl N-(3-chlorophenyl-)carbamate

CTC

circulating tumor cell

DEF

dean elasto-inertial focusing

DEX

dexamethasone

DLD

deterministic lateral displacement

EC

endothelial cell

ECM

extracellular matrix

FGF4

fibroblast growth factor 4

FluidFM

fluid force microscope

GFP

green fluorescent protein

gp130

glycoprotein 130

GPIbα

glycoprotein receptor Ibα

HDMEC

human dermal microvascular endothelial cell

hMSC

human mesenchymal stem cell

hSCP

hand-held single-cell pipet

hTRPV1

human transient receptor potential vanilloid type 1

HUVEC

human umbilical-vein endothelial cell

IBMX

1-methyl-3-isobutylxanthine

Jpk

jasplakinolide

Klf4

Kruppel like factor 4

Lat-A

latrunculin A

LIF

leukemia inhibitory factor

mESC

mouse embryonic stem cells

MFP

microfluidic probe

NFkB

nuclear factor kappa-light-chain-enhancer of activated B cells

NSCLC

nonsmall-cell lung cancer

PBS

phosphate-buffered saline

PCP

polyvinylpyrrolidone

PDMS

polydimethylsiloxane

PSC

pancreatic stem cells

pSTAT3

phosphorylated signal transducer and activator of transcription3

RBC

red blood cell

rBMSC

rat bone-marrow stromal cells

REF52

rat embryonic fibroblast 52

Rex1

reduced expression 1

SDF-1

stromal cell-derived factor 1

SI

shape index

STAT3

signal transducer and activator of transcription3

TNFα

tumour necrosis factor alpha

TRP1

tyrosinase-related protein 1

vWF

von Willebrand factor

vWF-A1

A1 domain of the von Willebrand factor

Biographies

Deborah Huber is a researcher at IBM Research-Zurich and a Ph.D. candidate at the Department of Chemistry and Applied Biosciences at ETH Zurich. She received her B.Sc. and M.Sc. from the Department of Biosystems Science and Engineering department at ETH Zurich in 2012 and 2014, respectively. Her research interests include microfluidic cell assays and their use in cancer diagnostics and personalized medicine. Currently she is combining microfluidic technology with biochemical engineering for research and diagnostic applications.

Ali Oskooei is a researcher with IBM Research Zurich currently working on computational methods for cancer diagnostics. He completed his Ph.D. at the University of Toronto where he developed technologies related to lab-on-a-chip microdevices that have been patented or published in prestigious scientific journals. His research interests involve combining mathematical and computational modeling and experimentation to develop novel biomedical diagnostic devices and solutions.

Xavier Casadevall i Solvas obtained his Ph.D. in 2009 at the university of California, Irvine, working on BioMEMS. He then did postgraduate research at Imperial College London and at ETH Zurich, where he has been developing microfluidic technology for the screening of single cells and C. elegans nematodes. His research interests are in the application of microtechnology to tackle fundamental biological questions in small biological models and to enable new biotechnological applications.

Andrew deMello is Professor of Biochemical Engineering in the Department of Chemistry and Applied Biosciences at ETH Zurich. Prior to his arrival in Zurich, he was Professor of Chemical Nanosciences and Head of the Nanostructured Materials and Devices Section in the Chemistry Department at Imperial College London. He obtained a first Class Degree in Chemistry and Ph.D. in Molecular Photophysics from Imperial College London in 1995 and subsequently held a Postdoctoral Fellowship in the Department of Chemistry at the University of California, Berkeley, working with Professor Richard Mathies. His research interests cover a broad range of activities in the general area of microfluidics and nanoscale science.

Govind V. Kaigala is a Research Staff Member at IBM Research-Zurich and is currently leading activities on liquid-based noncontact scanning probe technologies, microfluidic probe, and is championing new concepts on “microfluidics in the open space” and “tissue microprocessing”. His broader research interests include leveraging micro- and nanosystems for microchip-based chemical and biomolecular analysis applied to medical applications. Prior to joining IBM, he was a postdoctoral fellow in the Mechanical Engineering and Urology faculty at Stanford University. He received his Ph.D. and M.Eng. from the University of Alberta, Canada. He has authored and coauthored 45 scientific publications in leading journals, 60 conference papers, about 30 patent families, and has edited a book. He received several IBM awards, including Research Division Accomplishment Awards in 2014 and 2017, the Horizon Alumni Award from the University of Alberta, and he is a Senior Member of IEEE.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.chemrev.7b00317.

• Derivation of the velocity distribution in a rectangular channel; analytical solution for stagnation flow; and mathematical description of coefficient, λ (PDF)

Author Contributions

^§ D.H. and A.O. contributed equally to this work.

The authors declare no competing financial interest.