Atomically thin gallium layers from solid-melt exfoliation

A unique way to synthesize innovative 2D gallenene.

Abstract

Among the large number of promising two-dimensional (2D) atomic layer crystals, true metallic layers are rare. Using combined theoretical and experimental approaches, we report on the stability and successful exfoliation of atomically thin “gallenene” sheets on a silicon substrate, which has two distinct atomic arrangements along crystallographic twin directions of the parent α-gallium. With a weak interface between solid and molten phases of gallium, a solid-melt interface exfoliation technique is developed to extract these layers. Phonon dispersion calculations show that gallenene can be stabilized with bulk gallium lattice parameters. The electronic band structure of gallenene shows a combination of partially filled Dirac cone and the nonlinear dispersive band near the Fermi level, suggesting that gallenene should behave as a metallic layer. Furthermore, it is observed that the strong interaction of gallenene with other 2D semiconductors induces semiconducting to metallic phase transitions in the latter, paving the way for using gallenene as promising metallic contacts in 2D devices.

INTRODUCTION

The isolation of graphene from graphite has fueled research in layered two-dimensional (2D) materials as building blocks of 2D nanoelectronics (1, 2). The development of top-down approaches of exfoliation (2–4) as well as the bottom-up approaches of chemical vapor deposition (5, 6) and epitaxial growth on specific lattice planes of substrates (7) have resulted in the isolation of monolayers of many layered materials such as the transition metal dichalcogenides (2, 3, 8–15) and other elemental analogs of graphene such as phosphorene (16), silicene (17–21), germanene (22–24), stanene (25), and borophene (26). These 2D materials exhibit a wide range of electronic, thermal, mechanical, and chemical properties, thus making them promising candidates for many applications (27–30). The hexagonal crystal structure of the many layered bulk materials, where the layers are held together by the weak van der Waals forces, aids in the easy extraction or growth of stable monolayers. On the other hand, silicene, germanene, borophene, and stanene do not have layered bulk counterparts, but yet have been extracted into atomically thin layers regardless of several issues such as stability and scalability. However, unlike graphene, the strong spin-orbit interaction and buckled structure in these materials make them even more interesting because they can have topological insulator phases, which can lead to dissipationless electrical conduction and support a quantum spin Hall state (25, 31–35). The recent development of epitaxial growth of single atomic layers of Pb and In on the Si(111) substrate has led to the demonstration of superconductivity in the extreme 2D limit (36–38). On a similar note, epitaxially grown ultrathin Fe films have important implications in the development of 2D nanomagnets (39). These “metallenes,” which are the metallic analogs of graphene, also form a relatively new class of 2D materials with interesting properties. In brief summary, 2D materials research began with the isolation of graphene, but it has expanded to include many other materials, all in an effort to develop new nanoplatforms for research and industrial applications that can outperform graphene.

Gallium, with its rich low-temperature phase diagram (40), is a liquid metal at room temperature and displays impressive potential for use as a 2D material. Its chemical stability has been used to demonstrate optical phase-change memories with low power consumption (41–45). Epitaxially grown Ga films on the GaN substrate display superconductivity with increased values of superconducting transition temperature and critical field as compared to bulk Ga (46). Thin Ga films undergo superconductor-to-insulator quantum phase transition driven by a magnetic field, which served as the first experimental evidence of the Griffiths singularity in a 2D superconducting system (47). Finally, very recently, there was a report of GaS and GaO with exciting functional properties (48). All these experimental results suggest that ultrathin gallium films can offer interesting physics and possible electronic applications.

The conventional deposition technique for Ga does not provide freedom to select the substrate, which is one of the major requirements for using atomically thin Ga for multiple applications. Here, we demonstrate, for the first time, a simple exfoliation technique of surface solid layers from the molten phase of Ga, which yields atomically thin 2D layers of gallium that we term as “gallenene” (the monolayer to few layers of Ga atoms). The exfoliation technique from solid-melt interfaces of low-melting metallic materials could be a generic technique to obtain atomically thin layers of many materials, not just Ga. In addition to the extraction of gallenene, we demonstrate that gallenene can be stabilized on a substrate in two distinct crystallographic orientations using the density functional theory (DFT), which is in agreement with our experimental observations. The electronic structure of the gallenene films is highly anisotropic with a combination of partially filled Dirac cones and nonlinear dispersive bands, which can lead to new fundamental phenomena and a wide range of applications for Ga-based 2D materials. Gallenene, unlike other 2D van der Waals solids, shows a strong interaction with substrates validated by mechanical indentation tests, and band structure and transport properties evaluated by the DFT calculations. The substrate-gallenene interaction has been explored in both heterostructures of layered 2D materials (MoS₂) and gallenene to demonstrate interesting phenomena such as structural phase change in MoS₂ and subsequent use of gallenene as electrical contacts.

RESULTS AND DISCUSSION

We first present the theoretical aspects of the gallenene structure. Using DFT calculations, we first explored the stability of layers oriented along specific crystallographic directions in bulk α-Ga, because α-Ga is the most stable among the different bulk Ga phases (49). α-Ga has an orthorhombic crystal structure with space group Cmca (a = 4.58 Å, b = 7.78 Å, c = 4.59 Å) and contains eight atoms in the conventional unit cell (see fig. S1) (49). The calculated electron localization function (ELF) on different planes indicates that the first nearest-neighbor Ga–Ga bonds are covalently bonded, whereas the second, third, and fourth nearest-neighbor Ga–Ga bonds are more metallic in character. The atoms between two layers of Ga along 100 (a₁₀₀) are bonded by a mixture of metallic and covalent bonds, whereas the atoms between two Ga layers along 010 (b₀₁₀) are bonded by covalent bonds (see fig. S2). To construct an atomically thin layer of gallenene, a monolayer of Ga along 100 (a₁₀₀) and another along 010 (b₀₁₀) from α-Ga were extracted and subsequently relaxed, as shown in Fig. 1 (A to C). The unit cells of the two types of gallenene have four atoms each. After complete relaxation, gallenene a₁₀₀ transforms to a honeycomb structure, whereas gallenene b₀₁₀ retains its original structure. The Ga–Ga bond lengths in gallenene a₁₀₀ are nearly equal because the two nearest neighbors of a Ga atom are both at 2.50 Å (δ₁) and the third one is at 2.51 Å (δ₂). However, these bond lengths are longer than that of 2D sheets of group IV B elements sheets (50), because of the relatively larger atomic radius of Ga. Moreover, one of the interior angles of gallenene a₁₀₀ is 122.56°, whereas the other two are 118.9°. This suggests that the hybridization in the gallenene a₁₀₀ layer is not completely sp² despite the planar structure. The relaxed gallenene b₀₁₀ structure is found to have lower symmetry and resembles a zigzag rhombic lattice. The bond lengths are 2.69 and 2.74 Å, and the angles are 122.24° and 117.59°. Unlike planar gallenene a₁₀₀, gallenene b₀₁₀ forms a quasi-2D multidecker structure, where the two Ga dimers are separated by 1.32 Å along the vertical direction (also defined as buckling height). This buckling is often found in other 2D materials including penta-graphene, phosphorene, silicene, germanene, and stanene (50–52). The formation energies (with respect to α-Ga) of gallenene b₀₁₀ (0.36 eV per atom) are lower than those of gallenene a₁₀₀ (0.64 eV per atom), indicating better stability. Here, we observe the possibility of having two distinct sheet structures exfoliated from the same parent material, as was similarly reported for penta-graphene (53).

Fig. 1. Crystal structure of gallenene polymorphs.

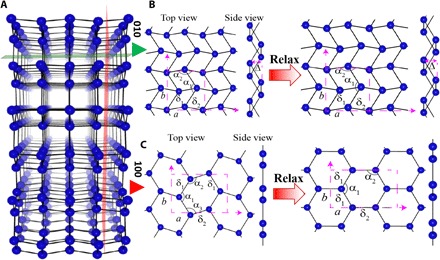
(A) Crystal structure of α-Ga. (B) Monolayer gallenene structure obtained after cleaving along the (010) direction from the bulk α-Ga as shown by the green plane. On relaxation, this forms a distorted rhombic lattice. (C) Monolayer gallenene structure obtained after cleaving along the (100) direction from the bulk α-Ga as shown by the red plane, which forms a honeycomb structure after relaxation. The unit cell of monolayer structures is represented by dashed rectangular magenta box. a and b are the cell parameters of the structure. The bond lengths and bond angles are shown by δ (in angstrom) and α, respectively. The symbol Δ (in angstrom) represents the buckling height of the monolayer gallenene structure. The cleaved a₁₀₀ structure (δ₁ = 2.72, δ₂ = 2.54; α₁ = 139.54°, α₂ = 105.43°, α₃ = 115.03°; Δ = 0) transformed to a graphene-like structure (δ₁ = 2.51, δ₂ = 2.50; α₁ = 122.56°, α₂ = α₃ = 118.9°; Δ = 0) after relaxation using DFT. The cleaved b₀₁₀ structure (δ₁ = 2.77, δ₂ = 2.72; α₁ = 111.64°, α₂ = 115.03°; Δ = 1.46) forms a quasi-2D multidecker structure (δ₁ = 2.77, δ₂ = 2.72; α₁ = 111.64°, α₂ = 115.03°; Δ = 1.32) upon relaxation. The blue balls and solid black line represents Ga atoms and Ga-Ga bonds.

To investigate the dynamic instability of gallenene sheets, we calculated the phonon dispersions of a₁₀₀ and b₀₁₀. The phonon dispersions of gallenene a₁₀₀ and b₀₁₀ display an imaginary frequency indicative of the dynamical instability (see fig. S3). However, the phonon dispersion of 6% uniformly strained gallenene a₁₀₀ does not display any imaginary frequencies, as shown in Fig. 2A. Eventually, the lattice parameter of strained gallenene a₁₀₀ is identical to the bulk lattice parameter. This indicates that the multilayers with a lattice parameter closer to the bulk value will have a better stability. The negative frequencies in the phonon dispersion of gallenene b₀₁₀ disappear after an application of only ~2% strain (Fig. 2B). This also results in lattice parameters that are closer to the bulk value, again leading to the conclusion that better stability arises when a lattice parameter approaches the bulk value. This also suggests another possibility of forming stabilized monolayers of gallenene (either a₁₀₀ or b₀₁₀) on substrates with lattice parameters closer to those of α-Ga. Further insight into the relative stability of these sheets can be obtained by analyzing the ELF of gallenene a₁₀₀ and b₀₁₀, as shown in Fig. 2C. As expected, the electron charge density of a₁₀₀ (Fig. 2C, iii) accumulates at the center between the bonds, which indicates the covalent nature between Ga–Ga. The Ga–Ga bonds in gallenene b₀₁₀ show some directionality, which is indicative of more toward covalent character along the y direction; at the same time, in other directions, it shows less directionality, which is indicative of metallic nature (as shown in Fig. 2C, i and ii). Because of the mixture of metallic and covalent nature in gallenene b₀₁₀, it shows better stability than gallenene a₁₀₀. Furthermore, the total energies of these strained gallenene sheets are only a few millielectron volts higher than those of the optimized structures, indicating shallow minima extending to a wide range of lattice parameters, as shown in Fig. 2D. Therefore, growing gallenene on substrates with different lattice parameters in the x and y directions would serve as a method to control the thickness. Overall, from the synthesis perspective, gallenene can offer one of the richest opportunities to tune the thickness and crystallographic type by engineering the strain or the substrates.

Fig. 2. DFT calculations of stability and bandstructure of gallenene polymorphs.

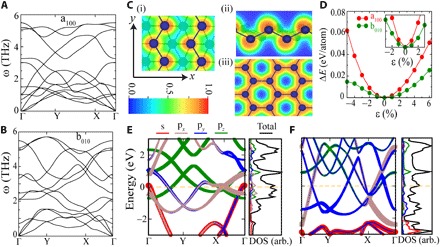
(A and B) Phonon dispersion of 6 and 2% uniformly strained monolayers of a₁₀₀ and b₀₁₀, respectively. (C) ELF of 2% strained structure of b₀₁₀ along (i) y direction and (ii) x direction and 6% strained structures of a₁₀₀ (iii) monolayers. The ELF is shown by the color bar, with red (blue) showing maxima (minima). (D) Total energy per atom with respect to the lowest-energy structure as a function of uniform strain. The inset shows ΔE for a smaller range of strain. (E and F) Orbital projected band structure, total density of states (DOS), and partial density of states of stabilized (strained) a₁₀₀ and b₀₁₀ monolayers with Fermi energy (E_F) set to 0 eV.

Next, we calculated the electronic properties of stabilized (strained) gallenene and the corresponding orbital projected band structure and density of states, which are shown in Fig. 2 (E and F). Gallenene a₁₀₀ and b₀₁₀ are metallic because of the finite density of states at the Fermi energy. Because of the planar structure of gallenene a₁₀₀, the p_z bands remain unhybridized and form Dirac cones, which lie above the Fermi level. This is expected because Ga has one less valence electron than graphene; therefore, it requires one extra electron to fill up the holes in the Dirac cone. Unlike graphene, the other sp² bands in gallenene are very close to the Fermi energy (some of them cross the Fermi energy), thus giving rise to anisotropy in the low-energy bands. The band structure of gallenene b₀₁₀ is very different. Because of buckling and nonhexagonal lattice, p_z orbitals hybridize strongly with the in-plane orbitals, providing extra stability to this sheet. Furthermore, the bands are highly dispersive with a large bandwidth, implying lighter charge carriers and higher mobilities. The binding energy increases with the number of layers for both gallenene sheets (see fig. S2E). A detailed study of the band structures as a function of layer number for both a₁₀₀ and b₀₁₀ gallenene sheets shows multiple Dirac cones emerging with the increasing number of layers, indicating the similar bonding nature to monolayer gallenene (see figs. S4 and S5). Considering these findings from the synthesis perspective, gallenene offers a rich opportunity to tune material thickness and crystallographic type by properly engineering the strain or the substrates.

To synthesize 2D sheets of lower-symmetry materials such as α-Ga (orthorhombic structure), conventional top-down techniques of exfoliation prove difficult. We now demonstrate a new and unique method of exfoliation of conducting anisotropic Ga ultrathin films. The strength of a metal decreases with the increase in temperature because of larger thermal vibrations, and strength becomes extremely low close to the melting temperature. During the cooling of a liquid metal droplet on a solid substrate, the temperature difference between the liquid and the substrate results in heterogeneous nucleation at the substrate-liquid metal interface. The free energy (G) of heterogeneous nucleation is related to the free energy of homogeneous nucleation (52) as

$${\mathit{G}}_{\text{hetero}}={\mathit{G}}_{\text{homo}}\times \mathit{f}(\mathrm{\theta })$$ (1)

where θ is the contact angle between the solid and liquid surface. For an interface with a larger contact angle (70° for Ga on SiO₂, as listed in table S1), heterogeneous nucleation is preferred over homogeneous nucleation, resulting in the growth of the surface solid crystalline layer above the liquid metal. Because of large differences in the strengths of metals in the solid and liquid states, the force required to separate the surface solid layer from the rest of the liquid melt is expected to be much lower. We call this new technique of exfoliation of the surface solid layer from the underlying liquid metal the “solid-melt exfoliation technique.” The gallium with a low melting point (T_m ~29.7°C) and good wettability with SiO₂ makes a good candidate for solid-melt exfoliation. High-temperature melting needs to be avoided during this new technique to avoid higher oxidation of Ga and oxide formation (48).

We demonstrate this new technique using an in situ nanomechanical testing system attached to a scanning electron microscope (SEM). The liquid Ga droplet on the Si/SiO₂ substrate was cooled down to room temperature (30°C) inside the SEM chamber under high vacuum (~10⁻⁸ mbar). The onset of solidification is checked by compressing the top surface using the indenter with controlled loading. A snapshot of the exfoliation process during the tensile test is shown in Fig. 3A. During compression, a large sink-in of the surface and good wetting with diamond indenter were observed, as shown in Fig. 3A (i). A tensile testing of Ga was conducted by pressing the indenter on the surface and applying strain in the displacement-controlled mode. We observed good contact between Ga and the diamond flat punch until some strain appeared, followed by the formation of a void at one corner of the interface (Fig. 3A, ii). The void grew with further loading (Fig. 3A, iii), and at the end of the procedure, a thin layer of Ga was separated out from the bulk Ga droplet (Fig. 3A, iv). An atomistic schematic of this process is shown along with the images. The surface was compressed to ~5 μm and then pulled out along the tensile direction of the indenter. The load required for the exfoliation was found to be ~30 μN for the 6-μm displacement, as shown in Fig. 3B, and requires a stress of 1.5 MPa to separate the thin Ga layer, which is much lower than the maximum tensile strength of solid α-Ga (40 MPa). The energy required for the exfoliation is given by the area under the load-displacement curve for exfoliation and was estimated to be 48 pJ.

Fig. 3. Solid-melt exfoliation of gallenene.

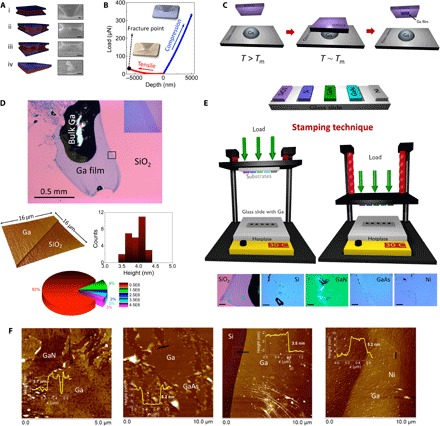
(A) Snapshots of real-time imaging of gallenene exfoliation using a flat punch indenter inside SEM. The corresponding atomistic schematic of the fracturing is also shown, where the red regions correspond to Ga and the blue region is the surface on which the Ga ultrathin layer is formed. Scale bar, 1 μm. (B) Load versus displacement curve obtained from the in situ compression and tension test on molten Ga inside SEM. The inset reveals SEM images during tensile and compression loading of the indenter. (C) Schematic of the proposed solid-melt exfoliation technique of gallenene onto Si/SiO₂ wafers. (D) Optical image of Ga sheet on SiO₂ wafer showing regions with uniform ultrathin layers. The AFM measurements on the films reveal the thickness of this film to be ~4 nm, as shown from the histogram of step height at the edge along different line scans. The pie chart shows the distribution of the percentage of the area (in μm²) of the exfoliated Ga films obtained from among 30 different flakes. (E) Schematic of the stamping technique developed for exfoliation on multiple substrates for a fixed load. Optical micrographs of gallenene flakes obtained on various types of substrates are shown at the bottom. Scale bar, 100 μm. (F) AFM images showing exfoliation of gallenene on various substrates like GaN, GaAs, Si, and Ni.

Following the above approach, we explored the gallenene exfoliation on large (millimeter-sized) Si/SiO₂ wafers. The schematic of this exfoliation process is shown in Fig. 3C. A Ga droplet is first heated to 50°C on a hot plate to achieve uniform melting of the entire droplet. The temperature is then reduced to 30°C, which is slightly above the T_m of Ga. At this point, a clean Si/SiO₂ wafer is brought into contact with the surface of the Ga droplet. The lower temperature at the SiO₂-Ga interface results in the solidification of the surface Ga layers, which are then exfoliated onto the SiO₂ substrate. As predicted in the theory, the free-standing Ga is difficult to exfoliate, but the substrate stabilizes gallenene. The optical image in Fig. 3D reveals a millimeter-sized thin layer of gallenene around a bulk Ga droplet. The continuous gallenene layer is free of any crack or aggregation. The height profile of this gallenene sheet measured using atomic force microscopy (AFM) reveals the thickness to be ~4 nm, indicating the film to be about four to six layers thick (see fig. S7). The formation of a-few-layer-thick gallenene films turns out to be an essential condition for stabilizing these sheets, as was also revealed from the phonon dispersion calculations. Furthermore, unlike van der Waals solids, the strong mixture of covalent and metallic bonding can be exploited for a multitude of applications.

To investigate the scalability and reproducibility of the solid-melt exfoliation technique, we developed a stamping method, as shown in Fig. 3A, to demonstrate simultaneous exfoliation on multiple wafers. We achieved a success rate varying between 80 and 90% for each batch (see fig. S6). The pie chart in Fig. 3D shows the distribution of the areal coverage of gallenene films obtained from a set of 30 different samples using this technique. Following this, we investigated the substrate effects on gallenene exfoliation by exfoliating these films on various other substrates such as Si(111), GaN(0001), GaAs(111), and polycrystalline Ni using this stamping technique. Their respective optical micrographs are shown in Fig. 3E. On the average, we find that the exfoliation on Si and GaN yielded flakes of lower thicknesses when compared to the ones exfoliated on GaAs and Ni. A closer microscopic investigation using AFM, as shown in Fig. 3F, reveals that the gallenene films on Ni were highly discontinuous when compared to the ones on other substrates despite similar average surface roughness for the Ni substrate. This also indicates that the solid layer exfoliation highly depends on the interaction between the substrate and Ga. The contact angle test performed using a liquid Ga droplet on different substrates (see fig. S9) reveals a much larger contact angle for Ni, which leads to discontinuous layers because of the low wettability of Ga on Ni. The calculated binding energies and ELF analysis explored the chemical interaction of gallenene with the substrate. The details of the change in the geometry of gallenene on different substrates were analyzed by DFT calculations and are discussed later. It is important to note that unlike other traditional growth techniques, such as molecular beam epitaxy, the novel technique of exfoliation allows the study of ultrathin Ga films on a wide variety of substrates.

The SEM image in Fig. 4A shows gallenene with mostly a darker appearance than SiO₂, but it also consists of some brighter regions. The energy-dispersive x-ray spectroscopy (EDS) spectrum acquired on the brighter regions (i) shows significant signal originating from the Ga L_α absorption edge. The EDS spectrum from the darker region (ii) also shows this peak for Ga L_α, but the signal is very weak because of the extreme thinness of this layer. From the elemental composition data obtained from the EDS, we confirmed that these films are Ga sheets. The crystalline nature of these gallenene films was further confirmed by electron diffraction studies in transmission electron microscopy (TEM). Gallenene sheets were transferred onto holey C–coated TEM grids using a poly(methyl methacrylate) (PMMA)–assisted transfer technique, as shown in the bottom panel of Fig. 4A. The composition map obtained using TEM (inset in Fig. 4B) shows uniform distribution of Ga with negligible oxygen, verifying the absence of oxidation of these Ga films. The chemical bonding states of Ga were further investigated using x-ray photoelectron spectroscopy (XPS) (Fig. 4B), which reveal two intense peaks at binding energies of 1117.0 and 1143.0 eV and correspond to 2p_3/2 and 2p_1/2 of Ga, respectively. This also reveals that Ga is in the zero-valence state, thereby confirming the absence of any oxide formation during exfoliation. The XPS is calibrated using a gold standard, and the energy values are matched with XPS standards (54).

Fig. 4. Characterization of gallenene films.

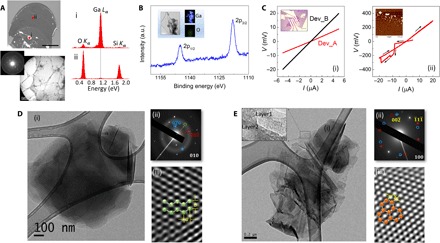
(A) Top: SEM image of the gallenene sheet on the SiO₂ substrate. Scale bar, 50 μm. The EDS spectrum collected from the bulk region (i) shows a strong Ga L peak, whereas the spectrum of the thinner region (ii) also shows this peak but with much reduced intensity. Bottom: The TEM image of this transferred film along with SAED showing that these Ga films are crystalline. Scale bar, 2 μm. (B) XPS data showing two intense peaks at binding energies of 1117.0 and 1143.0 eV, which correspond to 2p_3/2 and 2p_1/2 states, respectively, of metallic Ga. Inset: Composition mapping of Ga films in TEM showing the presence of Ga with negligible amount of O. Scale bar, 100 nm. a.u., arbitrary units. (C) (i) I-V characteristics of two gallenene devices. The inset shows the optical image of Dev_B. Scale bar, 15 μm. (ii) I-V curve showing breakdown of gallenene device at higher currents. The insets show the AFM image of the Ga film after breakdown. (D and E) Representative bright-field TEM images (i) along with SAED patterns (ii) and HRTEM image (iii) for the gallenene b₀₁₀ and a₁₀₀ sheets, respectively. The simulated crystal structure for these two orientations is superimposed on the HRTEM images. Scale bar, 200 nm.

The two-probe I-V curves, shown in Fig. 4C, obtained from two devices, Dev_A and Dev_B (shown in the inset), display linear characteristics with resistance values of 1.7 and 4 kilohms, respectively, indicating ohmic contacts to gallenene. Figure 4C (ii) shows the breakdown characteristics of ultrathin Ga films, revealing that a current flow higher than −10 μA breaks the film into small particles because of Joule heating, as shown in the AFM image in the inset. The long-time exposure of gallenene sheets in open air results in the formation of gallium oxide. The I-V characteristics of these sheets show an insulating behavior. The oxidation of these sheets can be prevented by encapsulation using the hBN sheet.

In an effort to obtain better insights into the crystal structure and various lattice orientations of these gallenene sheets, a detailed TEM analysis on several exfoliated samples was performed. The contamination originating in PMMA-assisted transfer was avoided by direct exfoliation of ultrathin Ga films onto TEM grids. From the statistical analysis of these sheets using selected area electron diffraction (SAED), we observe gallenene films of predominantly two different lattice orientations whose representative images are shown in Fig. 4 (D and E). The low-magnification bright-field TEM image in Fig. 4D (i) shows an atomically thin film of Ga. The SAED pattern obtained for this Ga sheet (Fig. 4D, ii) shows that it originates from the (010) lattice orientation of orthorhombic Ga, with a and b having values of 0.2 and 0.26 nm, respectively, and α = 90°. The ratio of a/b is ~0.8, which indicates possible strain in these sheets giving rise to lattice distortion. The high-resolution TEM (HRTEM) image in Fig. 4D (iii) shows the lattice arrangement on which the DFT b₀₁₀ structure of gallenene is superimposed. From the HRTEM image, we obtain the lattice spacings as a = 0.27 nm and b = 0.28 nm, which are in agreement with the lattice parameters of the equilibrium structure obtained from DFT. In Fig. 4E (i), we show the representative low-magnification bright-field TEM image from gallenene with a different lattice orientation. The inset shows regions with layer thicknesses in the few-layer to monolayer limit. The SAED pattern obtained for this gallenene sheet (Fig. 4E, ii) shows two hexagons that are rotated with respect to each other by an angle of 6°, which could arise due to slightly misoriented gallenene multilayers. This hexagonal symmetry of the diffraction pattern corresponds to the relaxed hexagonal lattice obtained from the (100) plane of the orthorhombic structure of gallenene. The HRTEM image in Fig. 4E (iii) shows this hexagonal structure of Ga with a lattice spacing of 0.2 nm and resembles the a₁₀₀ structure obtained from DFT, which is superimposed on this image. The above experimental findings using solid-melt exfoliation result in gallenene with two distinct structures with (100) and (010) crystallographic orientations, which are in agreement with the structures predicted using DFT calculation. The finite thickness observed in experiments further validates the removal of dynamic instability of a monolayer by stacking or straining. A single layer of gallenene can be potentially synthesized on suitable substrates with lattice parameters similar to those of α-Ga. The experimental verification of the electronic band structure changes as a function of varying thickness of Ga films would require detailed angle-resolved photoelectron spectroscopy (ARPES) measurements, which would be a subject of future studies.

We next explored the stability of gallenene on the various classes of substrates such as metals (Al, Ag, and Ni), Si, and ceramics (α-SiO₂ and GaN) (see the Supplementary Materials). We again find a strong correlation between the structure of gallenene and the orientation, topology, and type of the substrates. The calculated binding energy of gallenene on substrates is shown in Fig. 5A. The gallenene a₁₀₀ structure shows good structural stability on Al, Ag, Si, GaN, and α-SiO₂, whereas the gallenene b₀₁₀ structure shows good structural stability on α-SiO₂ and Ni. The calculated interaction energy per atom of Ga indicates a strong chemical interaction of gallenene with substrates, unlike the van der Waals solids (graphene, h-BN, MoS₂, etc.). The charge transfer analysis shows a charge transfer from gallenene to Si, SiO₂, and Ag substrates, whereas Al gives the charge to gallenene (see the Supplementary Materials). To gain a better insight into the nature of the chemical bonding, we carried out ELF analysis (see fig. S10). The electrons are localized along the Ga and substrate bonds for Si and SiO₂ substrates, suggesting a mixture of ionic and covalent character. On the other hand, Al and Ag substrates show a nearly uniform electron charge distribution indicating mostly a metallic character. These strong interactions lead to the enhancement of the stability of gallenene. Depending on the strength of the bonding of Ga with the substrate (more covalent in Si and less covalent on metals), it determines the thickness and stability of gallenene sheets, as observed in experiments. Furthermore, because of this strong interaction, the electronic properties become severely modified depending on the substrate (see fig. S18). Gallenene offers an entirely different approach to tune the fundamental electronic properties of the sheet itself by changing the underlying substrates. The unique behavior of gallenene’s interaction with the substrate is further verified using a scratch test with a diamond tip, as shown in Fig. 5B (inset). The measured force on different substrates (Si, SiO₂, GaAs, and Ag) shows different loads. The adhesive force for gallenene on Si is highest followed by GaN, SiO₂, and Ag (lowest). The adhesive force (energy) variation is consistent with the interaction energy of gallenene on different substrates.

Fig. 5. Substrate effects on gallenene.

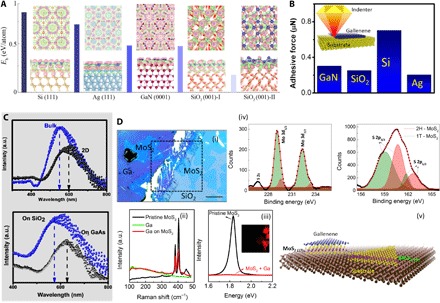
(A) Charge accumulation and depletion of gallenene a₁₀₀ on Si, Ag, GaN, and SiO₂ substrates. Charge accumulation and depletion of gallenene b₀₁₀ on the SiO₂ substrate are shown in the rightmost panel. The accumulation and depletion of charge are shown in pink and green. Top and bottom rows represent top and side views of the structures. The charge uniformly accumulates at the interface of gallenene and metallic substrates, whereas the charge accumulates at the Si (Ga) and Ga bond for Si (GaN) and SiO₂ substrates. This implies that the interaction between gallenene and the metallic substrate is nondirectional toward metallic bonding, whereas the interaction between gallenene and semiconductors (GaN, Si, and SiO₂) is toward covalent bonding. The bars represent the interlayer binding energy (E_b) per Ga atom between gallenene and the substrate. The larger value of binding energy indicates the greater interaction between gallenene and the substrate. Blue, yellow, cyan, brown, purple, and red spheres are Ga, Si, Ag, Ga (in GaN), N, and O atoms, respectively. Dotted purple line represents the unit cell of the structure. The iso-surface value is set to ~0.002 (e/ų). (B) Relative interaction (adhesive force) of gallenene with substrates (Si, Ag, SiO₂, and GaAs) as measured using indenter. (C) Top: Absorption spectra of bulk Ga and ultrathin gallenene sheets. Bottom: Absorption spectra of gallenene sheets on two different substrates, SiO₂ and GaAs. (D) (i) Optical micrograph of gallenene sheet on MoS₂. Scale bar, 20 μm. Raman (ii) and PL (iii) spectra of pristine MoS₂ and MoS₂ underneath gallenene are shown. The PL map of the region indicated by dashed lines in (i) is shown in the inset. (iv) The XPS spectra for the MoS₂ region underneath Ga are shown, indicating the evolution of 1T phase of MoS₂. (v) Schematic illustrating the idea.

Plasmonics with 2D materials has achieved considerable attention recently following the demonstration of surface plasmon resonance (SPR) in 2D layered materials like graphene (55), in addition to other conventional 2D electron gas systems such as perovskites (56–58) and semiconductor heterostructures (59). 2D materials have distinct optical properties as compared to bulk materials due to dimension-dependent plasmon dispersion that is observed in our gallenene sheets. The absorption spectrum in Fig. 5C (top) shows the SPR peak shift for gallenene sheets as compared to the bulk Ga. The ultrathin film nature of gallenene sheets enables light penetration through the Ga-substrate interface, which also enables tuning of the SPR by modifying the dielectric environment of the underlying substrate. This is demonstrated by comparing the SPR of gallenene that is exfoliated on two different substrates, SiO₂ (ε_s = 3.9) and GaAs (ε_s = 12.9), where ε_s is the static dielectric constant. The SPR peak on GaAs with a much larger ε_s is shifted to longer wavelengths, as shown in Fig. 5C (bottom), which is to be expected from the plasmon dispersion for thin films.

The strong substrate-gallenene interaction can also be explored in devices using artificially stacked heterostructure assemblies comprising various 2D layered materials. For instance, we have studied the interlayer interactions in a heterostructure of monolayer MoS₂ and gallenene. The optical micrograph in Fig. 5D (i) shows a large-area gallenene layer partially covering a region of MoS₂. The Raman spectra of MoS₂ under Ga (Fig. 5D, ii) show a difference in the relative intensities of the Raman modes of MoS₂ (E_2g¹ at 383 cm⁻¹ and A_1g at 404 cm⁻¹). The photoluminescence (PL) map for the area enclosed in Fig. 5D (i) and spectra are shown in Fig. 5D (iii), which indicate quenching of PL in the MoS₂ regions under Ga. These data suggest a semiconducting (2H) to metallic (1T) structural phase transition in the MoS₂ regions underneath gallenene. Further confirmation is obtained from the XPS spectra of the sample, which also shows the presence of a 1T binding state, as shown in Fig. 5D (iv). The Mo 3d_3/2 and 3d_5/2 peaks can be fitted using a two-peak fitting procedure, whereas the S 2p peak is fitted using four peaks corresponding to the 2H and 1T phases of MoS₂ (see the Supplementary Materials for more details) (60, 61). Although the XPS peaks of Mo 3d_3/2 and Mo 3d_5/2 have values consistent with the 1T and 2H phases of MoS₂, indicating a structural transformation to 1T phase, the S 2p peak has broadened and also shifted to lower binding energy values. This could be the result of the strong interaction between the top layer of S atoms in MoS₂ with Ga. DFT calculations also show that 2D gallenene can stabilize the 1T phase of MoS₂ (see fig. S20). This 2H (semiconductor) to 1T (metallic) transformation of MoS₂ is of high interest in the fields of catalysis, sensors, and 2D metallic contacts to semiconductors.

Last, we also explored the thermal and magnetic properties of 2D gallenene. The thermal conductivity (κ) of gallenene was found to be <1 W/mK, which is low compared to that of other 2D materials, such as graphene (2000 to 5000 W/mK at 300 K), silicene (5 to 50 W/mK at 300 K), and stanene (zigzag and armchair directions are 10.83 and 9.2 W/mK) (see figs. S21 and S22) (62–65). Having a very low thermal conductivity together with a very high electrical conductivity makes gallenene very unique among the 2D materials. Hence, gallenene can be used as a potential on-chip electrical connector or as a thermal barrier in devices. This is a promising avenue for the application of gallenene and requires further experimental exploration. The spin-polarized calculations of monovacancy gallenene show no magnetic ordering, nor do we find any signature of magnetic ordering on substrates (see figs. S23 and S24). We have also theoretically explored different polymorphs of gallenene, inspired by the recent findings of borophene (26, 66, 67), because Ga is located in the same group as boron, and boron shows potential for a variety of 2D structures. To explore the possibility of the formation of gallenene in a borophene-like 2D structure, we have calculated the energy per atom of gallenene by considering all the lowest-energy structures of borophenes (see fig. S25) (26, 66, 67). The borophene-like planar and buckling structures of Ga are 81 and 41 meV higher in energy compared to the gallenene b₀₁₀ structure, which indicates that the b₀₁₀ structure remains most stable. Because these structures are only a few millielectron volts lower in energy than gallenene b₀₁₀, their existence cannot be ruled out by the analysis carried out here. Like B, Ga can appear to offer a richer palette for the exploration of 2D structures with varying functionalities.

CONCLUSION

In summary, using a combined theoretical and experimental approach, we demonstrated the stability of gallenene sheets with distinct atomic arrangements oriented along two crystallographic (010) and (100) directions. The one-to-one correspondence between the gallenene structures as observed in TEM and the theoretically predicted structures revealed the formation of stable 2D gallenene sheets. The phonon dispersion calculations showed that gallenene sheets can be stabilized with bulk lattice parameters. Our new technique for the extraction of gallenene sheets using the solid-melt exfoliation technique could be further extended to exfoliate other metallenes of low-melting pure metals and alloys (fig. S26 demonstrates the possibility of generating ultrathin Sn 2D sheets). Our easily scalable and simple technique allowed us to exfoliate different substrates, which can be used for a variety of applications. Unlike other van der Waals solids, 2D gallenene strongly interacts with its substrate, which was observed in both our experiments and theoretical predictions. On the basis of this idea, we were able to use gallenene contacts to transform the MoS₂ from a semiconductor to metallic phase, resulting in better 2D contacts for devices. The electronic band structure of gallenene sheets showed a unique combination of unfilled Dirac cone and a highly dispersive band near the Fermi level. Our findings suggest that gallenene provides excellent opportunities to explore its applications as a 2D metal in plasmonics, sensors, and electrical contacts.

MATERIALS AND METHODS

We used the first-principles plane-wave method within DFT for structural optimization, total energy, and electronic structure calculations, as implemented in the Vienna ab initio simulation package (VASP) (68, 69). The valence-valence electron and core-valence electron interactions were represented by all-electron projector-augmented wave potentials (70, 71). We used a Ga norm-conserving pseudo-potential with valence configurations 4s² 4p¹. The exchange-correlation potentials were approximated by the generalized gradient approximation of the Perdew-Burke-Ernzerhof functional (72). The kinetic energy cutoff of the plane-wave basis set was considered to be 500 eV. The structures were optimized using the conjugate gradient scheme until the forces on every atom were ≤10⁻³ eV/Å, unless otherwise specified. The Brillouin zone of α-Ga was sampled by 19 × 19 × 19 Monkhorst-Pack (MP) k-mesh (73). To prevent artificial interaction among the neighboring layers, a sufficiently large ~20 Å vacuum region was used in the out-of-plane direction. For the 2D structure, the Brillouin zone was sampled by well-converged 2D MP k-mesh grids. The Fermi-level smearing was taken at 0.1 eV for all self-consistent calculations. The interatomic forces were calculated with strict energy convergence criteria of 10⁻⁸ and energy cutoff of 500 eV. These interatomic forces were used for phonon dispersion calculations using the Parlinski-Li-Kawazoe method as implemented in the PHONOPY package (74). The phonon dispersion of monolayer a₁₀₀ and b₀₁₀ structures was calculated with 96 and 196 atoms of supercell size 4 × 6 × 1 and 7 × 7 × 1, respectively. To investigate the lattice parameter effects of the dynamical stability of monolayer structures, we calculated the phonon dispersion of a₁₀₀ and b₀₁₀ monolayers by applying the uniform in-plane strain. The instantaneous in-plane lattice parameter (l) in each direction of the monolayer structure was given by l = l₀ + l₀ × ε, where ε and l₀ are the instantaneous uniform strain value and lowest-energy structure lattice parameters of the monolayer. The interlayer binding energy (E_b) was calculated using the following formula

$${\mathit{E}}_{\mathrm{b}}={\mathit{E}}_{\text{total}}-{\displaystyle {\sum }_{\mathit{i}}}{\mathit{E}}_{\text{total}}^{\mathit{i}}$$

where E_total and ${\mathit{E}}_{\text{total}}^{\mathit{i}}$ are the total energy of the system and the ith component of the system, respectively.

For example, the binding energy per atom of the three layers of gallenene is

$${\mathit{E}}_{\mathrm{b}}=({\mathit{E}}_{\text{total}}^{3-\text{layers}}-{\displaystyle {\sum }_{\mathit{i}=3}}{\mathit{E}}_{\text{total}}^{\mathit{i}(\text{Gallenene})})/(\mathit{j}\mathit{n})$$

where j and n are the number of layers of gallenene and the total number of Ga atoms in three layers of gallenene. The dipole correction was not considered in calculating the binding energy of gallenene on SiO₂ and GaN substrates.

The lattice thermal conductivity of free-standing gallenene was calculated by solving the phonon Boltzmann transport equation (PBTE) (75), by considering the three-phonon scattering processes. To solve the PBTE, harmonic and anharmonic interatomic force constants were calculated on supercell of 4 × 6 × 1 and 7 × 7 × 1, respectively. To obtain accurate forces, an MP k-mesh grid of 5 × 5 × 1 and an energy criterion of 10⁻⁸ eV were used. The lattice thermal conductivity (κ_ii) within the PBTE approximation at temperature T is given by

$${\mathrm{\kappa }}_{\text{ii}}=\frac{1}{{\mathit{N}}_{\mathit{q}}\mathit{V}}{\displaystyle \sum _{\mathit{q}}}\mathrm{\hslash }{\mathrm{\omega }}_{\mathit{q}}{\mathit{v}}_{\mathit{i},\mathit{q}}{\mathit{v}}_{\mathit{i},\mathit{q}}{\mathrm{\tau }}_{\mathit{q}}\left(\frac{\partial \mathit{f}}{\partial \mathit{T}}\right)$$

where N_q, V, f, and v_i,q are the number of q points in the Brillouin zone, the volume of the unit cell, the Bose-Einstein distribution function (which depends on the phonon frequency ω_q), and the velocity along the ith direction (i = x, y), respectively. The linearized PBTE was numerically solved by using the Sheng BTE code (76–78). The VESTA package was used to visualize crystal structures and to make graphics/images (79).

The gallium metal with 99.995% purity from Sigma-Aldrich was used for the experiments. A 5-μm flat punch indenter integrated with an in situ nanomechanical testing system, PI88 SEM PicoIndenter (Hysitron Inc.), in a field-emission SEM (FEI Company), was used for in situ mechanical testing. The height profile of the gallenene sheet was measured using the Bruker MultiMode 8 AFM system together with the NanoScope V controller. Device-grade Si, GaN, GaAs, and 99.99% purity polycrystalline Ni were used in the stamping technique. Elemental composition characterizations were performed using FEI Quanta 400 ESEM FEG (FEG-SEM) equipped with EDS. PHI Quantera XPS with 200-eV Al K_α x-rays was used for surface composition analysis. The XPS peaks were fitted using MultiPak software. The TEM analysis on several exfoliated samples was performed using a 200-kV JEOL 2011 cryo-TEM. To study the electrical transport in these films, we fabricated Ga devices on the Si/SiO₂ substrate with Ti/Au (10/100 nm) contacts using standard e-beam lithography. Renishaw inVia Raman microscopy setup using a 532-nm laser with 10 and 1% power was used for Raman spectroscopy and PL studies. The maps of Raman and PL were acquired with a setup step size of 0.5 μm.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/4/3/e1701373/DC1

section S1. Bulk gallium structural analysis

section S2. Stability of gallenene sheets

section S3. Effect of thickness on the band structure of gallenene

section S4. Stamping technique of solid-melt exfoliation

section S5. AFM analysis of Ga films

section S6. Contact angle measurements

section S7. Substrate effects on gallenene

section S8. Absorption measurements on gallenene

section S9. XPS measurements on Ga/MoS₂ heterostructures

section S10. Structural stability of Ga/MoS₂ heterostructures

section S11. Thermal conductivity of gallenene

section S12. Defects in gallenene

section S13. Polymorphism in gallenene

section S14. Exfoliation of ultrathin Sn sheets

fig. S1. Structure of gallium.

fig. S2. Bonding nature of gallium.

fig. S3. Phonon dispersion of gallenene.

fig. S4. Effect of number of layers of gallenene b₀₁₀.

fig. S5. Effect of number of layers of gallenene a₁₀₀.

fig. S6. Stamping technique used for simultaneous exfoliation of multiple samples.

fig. S7. AFM analysis.

fig. S8. Thickness for different substrates.

fig. S9. Contact angle measurements.

fig. S10. Gallenene on different substrates.

fig. S11. Gallenene on Si.

fig. S12. Gallenene on Si.

fig. S13. Gallenene on Ag.

fig. S14. Gallenene on Al.

fig. S15. Gallenene on Si.

fig. S16. Gallenene on Ni.

fig. S17. Gallenene on GaN.

fig. S18. Band structure of gallenene on different substrates.

fig. S19. XPS measurements of heterostructures.

fig. S20. Structure of heterostructure.

fig. S21. Thermal properties of gallenene.

fig. S22. Thermal conductivity variation as a function of temperature.

fig. S23. Defects in gallenene.

fig. S24. Defects in gallenene.

fig. S25. Polymorphism.

fig. S26. Thin film of tin.

table S1. Contact angle of Ga on different substrates.

table S2. Structural parameters of the substrate and gallenene.

References (80–84)