Deamidation of Protonated Asparagine–Valine Investigated by a Combined Spectroscopic, Guided Ion Beam, and Theoretical Study

Abstract

Peptide deamidation of asparaginyl residues is a spontaneous post-translational modification that is believed to play a role in aging and several diseases. It is also a well-known small-molecule loss channel in the MS/MS spectra of protonated peptides. Here we investigate the deamidation reaction, as well as other decomposition pathways, of the protonated dipeptide asparagine–valine ([AsnVal + H]⁺) upon low-energy activation in a mass spectrometer. Using a combination of infrared ion spectroscopy, guided ion beam tandem mass spectrometry, and theoretical calculations, we have been able to identify product ion structures and determine the energetics and mechanisms for decomposition. Deamidation proceeds via ammonia loss from the asparagine side chain, initiated by a nucleophilic attack of the peptide bond oxygen on the γ-carbon of the Asn side chain. This leads to the formation of a furanone ring containing product ion characterized by a threshold energy of 129 ± 5 kJ/mol (15 kJ/mol higher in energy than dehydration of [AsnVal + H]⁺, the lowest energy dissociation channel available to the system). Competing formation of a succinimide ring containing product, as has been observed for protonated asparagine–glycine ([AsnGly + H]⁺) and asparagine–alanine ([AsnAla + H]⁺), was not observed here. Quantum-chemical modeling of the reaction pathways confirms these subtle differences in dissociation behavior. Measured reaction thresholds are in agreement with predicted theoretical reaction energies computed at several levels of theory.

Introduction

Various mass spectrometry (MS) studies have focused on the loss of small neutral molecules from protonated peptides containing asparagine (Asn) and glutamine (Gln).¹⁻¹⁰ Deamidation reactions of Asn and Gln have been the focus of significant attention, inspired by the spontaneous post-translational deamidation processes in proteins. These processes are believed to play a role in several diseases such as Alzheimer’s and Parkinson’s but also in aging effects for which it acts as a molecular clock.¹¹⁻¹⁶ Furthermore, the deamidation rates of several peptides containing Asn have been investigated and vary over 3–4 orders of magnitude.¹⁷ The fastest deamidation rates were observed for peptides that contain smaller amino acid residues near Asn, presumably because they cause little to no steric hindrance to inhibit the deamidation process, although the detailed rationale for these variations has not yet been established.

The deamidation of Asn residues has been studied in condensed media, and it was shown that the reaction proceeds via a succinimide structure.^14,15 Subsequent hydration leads to the formation of an aspartic acid (Asp) or isoaspartic acid residue. More recently, the deamidation of [Asn + H]⁺ was studied in the gas phase using a combination of threshold collision-induced dissociation (TCID) and high-level computations of the potential energy surface.⁵ These results indicated that deamidation proceeds via a nucleophilic attack of the N-terminal nitrogen atom on the γ-carbon atom of Asn to form a succinic anhydride structure for [Asn + H – NH₃]⁺. This identification was later confirmed by infrared action spectroscopy.⁷

Earlier gas-phase studies have also examined the deamidation reactions of protonated dipeptides that contain Asn, involving glycine as the second residue (AsnGly), valine as the first residue (ValAsn), and alanine as the first and second residues, (AlaAsn) and (AsnAla). The deamidation of [AlaAsn + H]⁺ forms a succinic anhydride structure, initiated by a nucleophilic attack of the carbonyl oxygen on the Asn side chain.⁸ [AsnAla + H]⁺ follows a bifurcating mechanism leading to both a furanone (an imino-butyrolactone) and a succinimide structure. These reactions are initiated by the amide bond oxygen and the amide bond nitrogen, respectively. The deamidation of [AsnGly + H]⁺ leads to a succinimide structure at threshold energies, with contribution from the furanone product at higher energies.⁹ The deamidation reaction of [ValAsn + H]⁺ has been investigated by theoretical modeling at the density functional theory (DFT) level.⁶ According to this study, the nucleophilic attack occurs from the backbone amide oxygen onto the side-chain carbonyl carbon, leading to a six-membered lactone structure. Summarizing, ammonia loss takes place from the side chain in all cases considered thus far; however, differences in reaction rates and the mechanisms for deamidation as the adjacent residue varies remain incompletely understood.

In the present study, we investigate the deamidation of protonated asparagine–valine ([AsnVal + H]⁺) and its MS³ product ion. Valine contains an isopropyl side chain and is expected to have a larger steric hindrance in forming the deamidation product ion in comparison to alanine and glycine. The structures of the product ions were elucidated using a combination of infrared (IR) ion action spectroscopy, guided ion beam experiments, and quantum-chemical calculations.

Ion spectroscopy is a compelling technique for detailed structural characterization of small gas-phase ions in MS experiments. Using this technique, earlier studies showed it is possible to determine the structures of parent ions, as well as their reaction products after CID, on the basis of the ability to distinguish between isomers, protonation sites, and conformers.¹⁸⁻²² For an accurate determination of thermochemistry involved during the fragmentation of peptides, TCID carried out in a guided ion beam tandem mass spectrometer has been applied.⁹ Specifically, bond dissociation energies of metal–peptide interactions²³ as well as threshold energies for peptide fragmentation,^4,5,9,24,25 including deamidation reactions, have been established. Such information allows for the comparison of experimental and theoretical values such that likely decomposition mechanisms and product identities can be verified, a key aspect of TCID studies.

Separately, ion spectroscopy and guided ion beam experiments in combination with computational chemistry have already been proven as powerful techniques to establish the molecular structures of deamidated ions. The present study represents a novel combination of these techniques to assign the molecular structure of the product ions with high confidence. Additionally, complete quantum-chemical calculations were performed allowing for the identification of likely decomposition pathways. Such theoretical calculations were valuable in identifying key rate-limiting elementary steps of the possible reaction mechanisms for comparison with experimental TCID values. In all cases, the lowest energy pathways located for the observed fragmentation were in agreement with the experimental results.^4,5,9,24,25 Combining the structural and energetic information, the present study enables the identification of product ions and allows the differences in deamidation rates among different dipeptides to be explained.

Experimental and Computational Methods

Infrared Ion Spectroscopy

Infrared multiple photon dissociation (IRMPD) spectra of the protonated AsnVal precursor ion and the deamidated fragment ions are measured in a modified three-dimensional (3D) quadrupole ion trap mass spectrometer (Bruker, AmaZon Speed ETD, Bremen, Germany)^26,27 coupled to the beamline of the infrared free electron laser FELIX.²⁸ The AsnVal sample was purchased from Biomatik (Canada) and used for all experiments without further purification. For electrospray ionization (ESI), peptides were dissolved in 50:50 acetrontrile:water solution with addition of 0.1% formic acid. A concentration of 10^–6 M was used to generate the protonated precursor peptide. MSⁿ fragments were produced by low-energy collisional activation with helium for 40 ms with an amplitude parameter of approximately 0.3 V. The isolated peptide fragment ions were irradiated with two 6 μs long macropulses from FELIX at a repetition rate of 10 Hz, each pulse having an energy of 5–40 mJ and a bandwidth of about 0.5% of the center frequency. IRMPD spectra were generated from the relative dissociation yield at each FELIX wavelength via ∑I(fragment ions)/∑I(fragment ions + precursor ion), where I is the ion intensity.²⁹ The dissociation yield at each laser frequency was determined from five averaged mass spectra and was linearly corrected for the frequency dependent variation of the infrared laser pulse energy. All spectra were recorded over the 800–2000 cm^–1 range.

Guided Ion Beam Mass Spectrometry

Kinetic energy dependent cross sections for the decomposition of [AsnVal + H]⁺ with Xe were measured using a guided ion beam tandem mass spectrometer (GIBMS) that has been described in detail elsewhere.³⁰⁻³² Briefly, ions were generated using an ESI source³³ and 10^–4 M AsnVal in 50:50 MeOH/H₂O solution, acidified with an appropriate amount of acetic acid, and syringe-pumped at a rate of 0.35 μL/h into a 35 gauge stainless steel needle biased at 2200–2400 V relative to ground. Ions were directed through a heated capillary at 80 °C into a radio frequency (rf) ion funnel,³⁴ where they were focused into a tight beam. After exiting the ion funnel, the ions entered an rf trapping hexapole ion guide where the ions underwent on the order of 10⁴ thermalizing collisions with ambient gas. As demonstrated in earlier studies, ions produced in the source region have a Maxwell–Boltzmann distribution of rovibrational states at 300 K.^{23,33,35−38}

The precursor [AsnVal + H]⁺ ions were extracted from the source and mass selected using a magnetic momentum analyzer, decelerated to a well-defined and variable kinetic energy, and focused into an rf octopole ion guide that traps the ions radially,^39,40 which minimizes losses of product and reactant ions. The ions passed through a collision cell containing xenon^41,42 at a sufficiently low pressure (≤0.4 mTorr) such that the opportunity for multiple collisions to occur was minimal, although the number of ions undergoing single collisions was sufficient to produce product cross sections characterized by a high intensity. (In this respect, the collisional activation of the two techniques is slightly different, where TCID uses single, higher energy collisions to induce dissociation whereas multiple, low energy collisions are employed in the ion spectroscopy studies.) The product and residual reactant ions drift to the end of the octopole guide, where they were extracted and focused into a quadrupole mass filter for mass analysis. High resolution conditions were used such that characterization of cross sections for channels separated by 1 amu was possible. As discussed previously,⁹ high mass resolution conditions decrease the energy range suitable for TCID experiments, such that only high intensity channels were observed under these conditions.

Ions were detected with a high voltage dynode and scintillation detector,⁴³ and the signal was processed using standard pulse counting techniques. Ion intensities of reactants and products, measured as a function of collision energy, were converted to absolute cross sections as described previously.³⁰ Briefly, the calculation of the cross section from the ion intensities utilized a relationship that is directly analogous to the Beer–Lambert Law, specifically, I = I₀e^–ρσl, where I is the reactant ion intensity after passing through the collision cell, I₀ is the sum of the intensities of the reactant ion and all product ions, l is the length of the collision cell (8.3 cm), and ρ is the number density of the neutral reactant and equals P/k_BT, where P and T are the pressure and temperature of the gas and k_B is Boltzmann’s constant. The uncertainty in the relative cross sections is about ±5%, and that for the absolute cross sections is about ±20%. The ion kinetic energy distribution was measured using a retarding potential analysis and found to be Gaussian with a typical full width at half-maximum (fwhm) of 0.1–0.2 eV (lab). Uncertainties in the absolute energy scale are about ±0.05 eV (lab). Ion kinetic energies in the laboratory (lab) frame were converted to energies in the center-of-mass (CM) frame using E_CM = E_labm/(m + M), where M and m are the masses of the ionic and neutral reactants, respectively. All energies in this work are reported in the CM frame unless stated otherwise.

Cross-Section Modeling

Thresholds of the TCID cross sections were modeled using eq 1:

1

where σ_0,j is an energy-independent scaling factor for channel j, n is an adjustable, empirical representation of factors that describe the efficiency of the energy transfer during collision and varies with the complexity of the system being studied,³¹E is the relative kinetic energy of the reactants, E_0,j is the threshold for dissociation of the ground electronic and rovibrational state of the reactant ion at 0 K for channel j, τ is the experimental time for dissociation (∼5 × 10^–4 s, as measured by previous time-of-flight studies),³¹ ε is the energy transferred from kinetic to internal modes during the collision, and E* is the internal energy of the energized molecule (EM) after the collision, so that E* = ε + E_i. The summation is over the rovibrational states of the reactant ions, i, where E_i is the excitation energy of each state and g_i is the fractional population of those states (∑g_i = 1). The Beyer–Swinehart–Stein–Rabinovitch algorithm⁴⁴⁻⁴⁶ was used to evaluate the number and density of the rovibrational states and the relative populations g_i were calculated for a Maxwell–Boltzmann distribution at 300 K. The term k_j(E*) is the unimolecular rate constant for dissociation of the EM to channel j via its rate-limiting transition state (TS). The rate coefficients k_j(E*) and k_tot(E*) are defined in Rice–Ramsperger–Kassel–Marcus (RRKM) theory^47,48 as

2

where d_j is the reaction degeneracy of channel j, N_j^†(E* – E_0,j) is the sum of rovibrational states for the TS of channel j at an energy E* – E_0,j, and ρ(E*) is the density of states of the EM at the available energy E*. These rate coefficients allow both kinetic shifts (where the probability of dissociation is given by the term 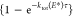in eq 1 and competition between multiple channels (which is controlled by the ratio of rate coefficients in eq 1, [k_j(E*)/k_tot(E*)]) to be modeled accurately.^49,50

To evaluate the rate coefficients in eqs 1 and 2, values for rovibrational energies for the EM and the rate-limiting TSs were determined from quantum-chemical calculations described below. Additionally, the entropy of activation at 1000 K for each dissociation channel was calculated as described in detail elsewhere.⁴⁹ The model cross sections of eq 1 were convoluted with the kinetic energy distributions of the reactants³⁰ and compared to the experimental data. A nonlinear least-squares analysis was used to provide optimized values for σ_0,j, n, and E_0,j. The uncertainty in E_0,j (reported as one standard deviation) was estimated from the range of threshold values determined from multiple sets of data, variations in the parameter n (±10% around the optimum value), variations in vibrational frequencies (±10%), changes in τ by factors of 2, and the uncertainty in the absolute energy scale (0.02 eV). Uncertainties associated with variations in the vibrational frequencies that control the internal energy and the kinetic shifts were assessed independently.

Computational Chemistry

For all product ion structures, a first computational exploration was performed using DFT at the B3LYP/6-311+G(d,p) level of theory using Gaussian 09, revision D.01.⁵¹ Different protonation sites were considered for each structure. First guess structures were optimized and their computed infrared spectra were compared with the experimental one. For the lowest energy structure and the spectroscopically best matching structure, potential energy surfaces were further explored to identify the lowest energy conformers using a molecular mechanics/molecular dynamics (MM/MD) approach employing AMBER 12.⁵² No MM/MD calculations were performed for the MS³ fragments, as their conformational flexibility was small enough that chemical intuition was sufficient to generate input structures for DFT optimization. Within AMBER, an initial MM geometry optimization was performed, followed by a simulated annealing procedure up to 500 K resulting in 500 structures. These structures were grouped on the basis of their structural similarity using appropriate root-mean-square (rms) atom position criteria and yielded 20–30 candidate structures. These candidate structures were then optimized using DFT and their predicted IR spectra were compared with the experimental spectra. All computed harmonic vibrational frequencies were scaled by 0.975 and convoluted with a 25 cm^–1 fwhm Gaussian line shape to facilitate comparison with experimental spectra. Finally, single-point 298 K Gibbs free energies were calculated from MP2(full)/6-311+G(2d,2p) electronic energies using the B3LYP/6-311+G(d,p) optimized structures and zero point vibrational energy (ZPE) corrections. The computational procedure is described in more detail elsewhere.^7,26,53

Independently, and to ensure that the ground structures (GS) of reactant and product species were correctly identified, structures analogous to those previously reported for [AsnGly + H]⁺⁹ were also used as starting structures. Here, optimizations of all unique low-energy structures were conducted at the B3LYP/6-311+G(d,p) level of theory. Starting structures for additional key reaction intermediates and all TSs were also initially taken from the resulting structures reported from the [AsnGly + H]⁺ study.⁹ Rotational constants and vibrational frequencies were calculated from optimized structures, and vibrational frequencies were scaled by a factor of 0.989⁵⁴ when used for the determination of internal energy, RRKM calculations, and ZPE corrections. Single point energies of all reaction species were calculated using the 6-311+G(2d,2p) basis set at the B3LYP, B3P86, and MP2(full) levels using B3LYP/6-311+G(d,p) geometries and ZPE corrections.

Results and Discussion

Precursor Ion [AsnVal + H]⁺

Figure 1 presents three low-energy conformers of the precursor ion [AsnVal + H]⁺, with their relative energies calculated at the B3LYP, B3P86, and MP2(full)/6-311+G(2d,2p) levels of theory using B3LYP/6-311+G(d,p) geometries. Conformers are named according to their protonation sites including additional hydrogen bonds by using the designation [X, Y, Z], where X = protonated atom and Y/Z are sites that hydrogen bond to the protonated site, in order of increasing hydrogen bond length. The protonation site is followed by the series of dihedral angles starting from the N-terminal side-chain amide-group nitrogen to the C-terminal carboxylic acid. Backbone nitrogen and oxygen atoms are numbered by residue along the backbone chain starting from the N-terminus. Side-chain nitrogen and oxygen atoms are designated by a superscript “s”. Dihedral angles are distinguished as cis (c, for angles between 0 and 45°), gauche (g, 45°–135°), or trans (t, 135°–180°).

Figure 1.

Experimental IRMPD spectrum (black) of the [AsnVal + H]⁺ precursor ion compared with the calculated spectra of the three lowest energy conformers (blue). All structures are protonated at the N-terminus. Relative 0 K single point energies (kJ/mol) at the B3LYP, B3P86, and MP2(full)/6-311+G(2d,2p)//B3LYP/6-311+G(d,p) levels of theory are given in square brackets.

The three lowest energy [AsnVal + H]⁺ conformers are all located within 10 kJ/mol of each other at all levels of theory and protonate at the amine nitrogen (N¹) of the backbone. As shown in Figure 1, the N¹ protonation site interacts via hydrogen bonds with the carbonyl oxygen of both the side-chain amide (CO^s) and backbone amide (CO¹), [N¹, CO^s, CO¹], in all three conformations. B3LYP predicts the [N¹, CO^s, CO¹]-ttgtgtt conformer to be lowest in energy, whereas B3P86 and MP2 predict [N¹, CO^s, CO¹]-gggtgtt to be lowest in energy. These two structures differ in the hydrogen bonding interaction of the carbonyl group of the Val residue, CO²: either with HN² in ttgtgtt or in a head-to-tail arrangement with HN^s in gggtgtt. The low-lying ttgtttt conformer lies only 2–3 kJ/mol above the similar ttgtgtt conformer, and they differ primarily in the orientation of the valine side chain.

To verify the conformation of the [AsnVal + H]⁺ precursor ion, its IRMPD spectrum was recorded as shown in Figure 1 together with computed spectra for the three low-energy conformers of Figure 1. The top panel shows the calculated spectrum for the lowest energy conformer at the B3LYP level of theory (ttgtgtt), the middle panel that for the lowest energy conformer at the MP2 and B3P86 levels of theory (gggtgtt), and the bottom panel that for the conformer with an alternative Val side chain arrangement (ttgtttt). Clearly, the agreement in the 1300–1800 cm^–1 range between experiment and the computation for the ttgtgtt conformer is convincing, although the computed spectrum for ttgtttt (bottom) is nearly as close. The peak at 1750 cm^–1 is assigned to the C-terminal C=O stretch, and shifts to 1730 cm^–1 for the gggtgtt conformer (middle). The band at 1710 cm^–1 in all three computed spectra is assigned to the C=O stretch of the peptide bond. The shoulder at 1680 cm^–1 in the middle spectrum results from the C=O stretch of the Asn side chain, which remains unresolved in the spectra of the other two conformers. The feature at 1610 cm^–1 is assigned to NH bending of the NH₃ group in the top and the bottom panels, and shifts to 1640 cm^–1 in the middle panel. The peaks around 1530 (top and middle spectra) and 1515 cm^–1 (bottom spectrum) are assigned to NH bending of the amide bond. The intense NH bending mode at 1470 cm^–1 predicted for the gggtgtt conformer (middle) is not reproduced in the experimental spectrum, and clearly disqualifies this conformer. This mode is shifted to 1410 cm^–1 in the other two conformers (top and bottom) in good agreement with observations. The main deviations between the computed spectra for ttgtgtt (top) and ttgtttt (bottom) is found between 1000 and 1200 cm^–1, where the sharper band in the bottom spectrum is assigned to OH bending at the C-terminus, while the weaker, broadened band in the top spectrum results from this OH bending mode in combination with several other nonlocalized bending modes. Clearly, none of the calculated spectra reproduce the intensity observed in the experimental spectrum at 1120 cm^–1 well, although the ttgtgtt conformer does have a band at this position, whereas the ttgtttt conformer does not. Arguably, perhaps, the top spectrum appears to be in better agreement with experiment, and we conclude the protonated precursor ion to be predominantly in the [N¹, CO^s, CO¹]-ttgtgtt conformation although minor contributions from other conformers cannot be eliminated. Importantly, these results suggest that an open chained structure is preferred under our experimental conditions, whereas protein/peptide folding is more prominent in solution.

Deamidated Asparagine–Valine, [AsnVal + H – NH₃]⁺

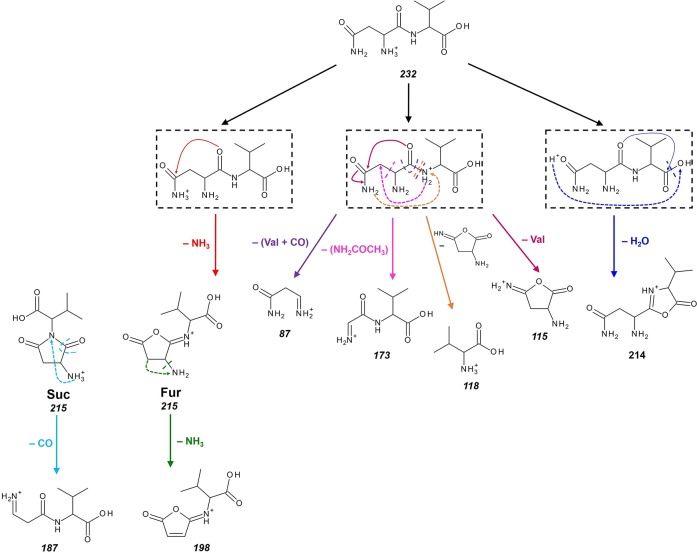
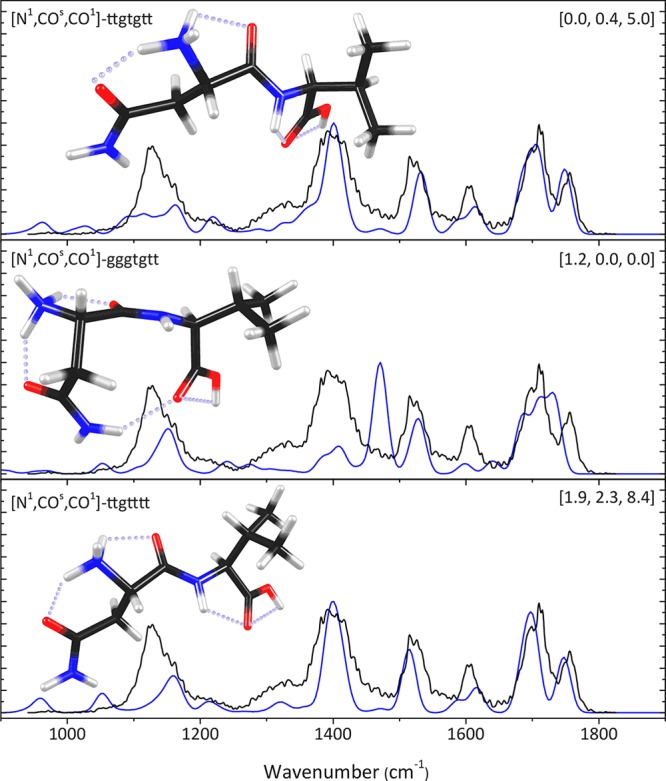
Loss of ammonia from [AsnVal + H]⁺ can reasonably occur through ammonia loss either from the Asn carboxamide side chain or from the N-terminus (technically a deamination), especially considering the mobile proton model, which suggests that the proton can migrate from the most basic site to a less favored protonation site after collisional activation.⁵⁵⁻⁵⁹ It is also not unreasonable to assume that ammonia loss is accompanied by a nucleophilic rearrangement involving the electrophilic carbon adjacent to the NH₃ leaving group. Scheme 1 shows possible rearrangements leading to the expulsion of ammonia from [AsnVal + H]⁺ with concomitant formation of a five- or six-membered-ring structure. The green arrow indicates a nucleophilic attack of the amide bond nitrogen onto the side chain, leading to a succinimide structure (1). The pink arrow indicates a nucleophilic attack of the amide bond oxygen onto the side chain leading to a furanone structure (2). The blue arrow indicates a nucleophilic attack of the C-terminal oxygen onto the N-terminus, leading to a diketo-morpholine structure (3). Possible protonation sites (1–5) for each of these three final structures are indicated in Scheme 1. The geometries of all these possible structures were optimized, their infrared spectra were calculated, and their relative energies are provided in Table 1. The overall lowest energy structure is the succinimide structure (1.1), where the proton resides on the amino group that was the N-terminus. The lowest energy furanone structure (2.3) is protonated at the nitrogen of the peptide bond and lies 15–40 kJ/mol above 1.1. The lowest energy diketo-morpholine lies 43–76 kJ/mol above 1.1 and is protonated on the side-chain carbonyl (3.2), partly because there is a strong hydrogen bond with a keto group of the ring structure (position 3).

Scheme 1. Possible Nucleophilic Attack Rearrangements Leading to the Deamidation of [AsnVal + H]⁺.

Loss of ammonia from the side chain (top and middle) and from the N-terminus (bottom) is considered. Numbered atoms are used to indicate different protonation sites in each of the product ion structures.

Table 1. Relative 298 K Gibbs Free Energies (kJ/mol) for Possible Deamidation Product Ion Structures of [AsnVal + H]^+a.

	succinimide (1)		furanone (2)		diketo-morpholine (3)
protonation site	B3LYP	MP2	B3LYP	MP2	B3LYP	MP2
1	0	0	91	109	57	86
2	46	57	82	102	43	76
3	117	112	15	40	54	83
4	37	47			118	143
5					87	125

^aCalculated at the B3LYP/6-311+G(d,p) and MP2(full)/6-311+G(2d,2p) levels using B3LYP/6-311+G(d,p) geometries. The numbers in the first column refer to the different protonation sites indicated in each structure in Scheme 1. Entries in boldface indicate the lowest energy species for each type of product structure.

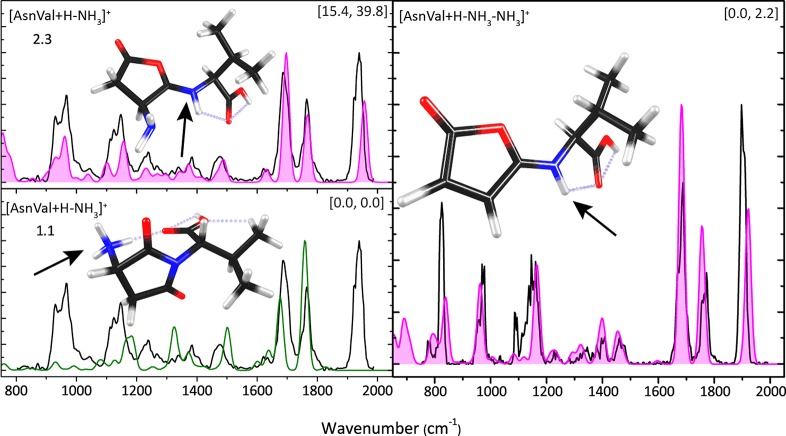
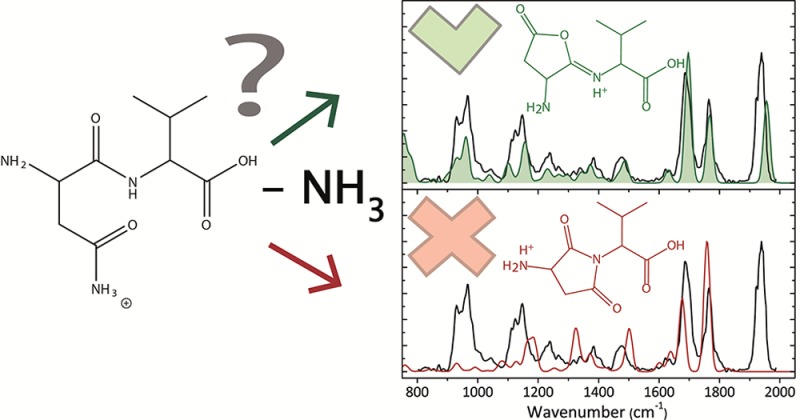
In Figure 2, the experimental IRMPD spectrum (black) for the deamidation product ion [AsnVal + H – NH₃]⁺ is displayed along with calculated spectra for the lowest-energy isomer 1.1 (bottom left panel) and for the furanone isomer 2.3 (top left panel). Figure S2 in the Supporting Information shows the spectral comparison with diketo-morpholine structure 3.2. It is immediately clear that the furanone structure provides an excellent match to the experimental spectrum throughout the experimental region studied, even though its energy is substantially higher than that for the succinimide structure 1.1. For the furanone structure, the diagnostic high-frequency band near 1950 cm^–1 is assigned to the CO stretch of the carbonyl group. The 1770 cm^–1 band is the C-terminal C=O stretch (red-shifted because of the hydrogen bond to the protonated imine), and the band at 1710 cm^–1 is the protonated imine CN stretch. The succinimide structure does not reproduce the high-frequency band nor bands below 1200 cm^–1. Here, the band predicted at 1760 cm^–1 results from succinimide CO stretching, while the band at 1680 cm^–1 is assigned to the C-terminal carbonyl stretch. Bands at 1640 and 1510 cm^–1 are NH bending modes. Figure S3 in the Supporting Information shows the calculated spectra of alternative conformers of structure 2.3 with higher energy. The main difference between the assigned structure and the higher energy conformers is the band around 900–1000 cm^–1, which is not reproduced well experimentally.

Figure 2.

IRMPD spectra (black) of [AsnVal + H – NH₃]⁺ (left panels) and [AsnVal + H – NH₃ – NH₃]⁺ (right panel). The top left panel shows the computed spectrum for the furanone ring structure 2.3, whereas the lower left panel shows that for the lowest-energy deamidated isomer, the succinimide structure 1.1. In the right panel, the experimental spectrum is compared with the computed spectrum for the NH₃-loss fragment ion from the furanone ring structure. Protonation sites are indicated with arrows. Hydrogen bonds <2.5 Å are indicated with gray dashed lines. Energies (kJ/mol, in square brackets) are calculated at the B3LYP/6-311+G(d,p) (first value) and MP2(full)/6-311+G(2d,2p) levels using B3LYP/6-311+G(d,p) geometries (second value).

The right panel of Figure 2 shows the IRMPD spectrum of the MS³ fragment ion (black) [AsnVal + H – NH₃ – NH₃]⁺ at m/z 198. Loss of an ammonia molecule from the furanone ring leads to the inlaid structure, for which the predicted spectrum is overlaid onto the experimental one. A reasonably good spectral match is found (especially above 1100 cm^–1), further supporting our assignment of the MS² fragment as the furanone structure. The spectrum computed for the furanone structure of [AsnVal + H – NH₃ – NH₃]⁺ exhibits main bands at 1910 cm^–1 (C=O stretch of the furanone ring), 1770 cm^–1 (C=O stretch of the C-terminal carboxyl group), and 1680 cm^–1 (CN stretch of protonated imine). Most features at the low-frequency end of the spectrum (750–1500 cm^–1) are reproduced reasonably well, namely the two sharp, intense bands at 825 and 960 cm^–1 in the experimental spectrum, which correspond primarily to furanone CH out-of-plane bending and amide NH out-of-plane bending (calculated at 837 cm^–1) and furanone COC stretching, CNH bending, and furanone ring distortion (calculated at 961 cm^–1). Figure S4 in the Supporting Information shows the comparison of the experimental spectrum of [AsnVal + H – NH₃ – NH₃]⁺ with other possible structures for additional loss of NH₃, none of which reproduce the experimental spectrum in its entirety (although the II-1 structures do match reasonably well in the high-frequency region, a result of similar CO and peptide bond CN stretching). Therefore, we assign the structure in the right panel of Figure 2 on the basis of the good match across the entire spectral range.

Cross Sections for Collision-Induced Dissociation of [AsnVal + H]⁺

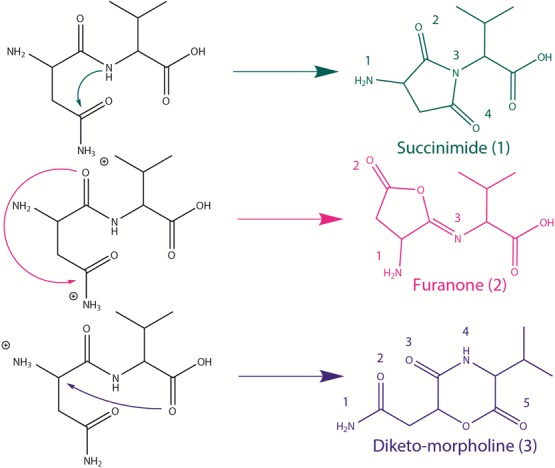
Figure 3 shows the cross sections for the interaction of [AsnVal + H]⁺ with Xe under high mass resolution conditions. Deamidation (m/z 215) and dehydration (m/z 214) are the dominant reaction channels, which is consistent with the dissociations observed previously for [AsnGly + H]⁺ and [AsnAla + H]⁺.^8,9 At thresholds of about 0.8 eV higher, the formation of m/z 118 and 187 occur competitively, with m/z 87 and 198 arising still 0.3 eV higher. At even higher energies, the formation of m/z 115 and 173 is observed. As shown in Scheme 2, six primary channels are observed in the decomposition of [AsnVal + H]⁺. Here, deamidation forms m/z 215, which is a protonated furanone species as identified in the ion spectroscopy experiment described above. Dehydration of [AsnVal + H]⁺ leads to the b₂-sequence ion, which is proposed to possess an oxazolone structure, similar to that observed in [AsnGly + H]⁺ and [AsnAla + H]⁺ studies.^8,9 Concomitant loss of (Val + CO) leads to the formation of m/z = 87, with analogous channels observed in the previous studies. Interestingly, parallel pathways are observed for the primary loss of Val (leading to m/z = 115) as well as the primary formation of [Val + H]⁺ (m/z = 118), which deviates from the behavior exhibited by [AsnGly + H]⁺ and [AsnAla + H]⁺. Specifically, no analogous parallel dissociation was observed in the [AsnGly + H]⁺ study,⁹ and in the analysis of [AsnAla + H]⁺, only the loss of Ala was observed. The difference in behavior is presumably a reflection of the increasing complexity of the second residue, which influences the resulting relative proton affinities (PA) (where Gly < Ala < Val). Here, [Val + H]⁺ formation is characterized by a lower threshold and greater intensity than the parallel loss of neutral Val across the entire energy range. Two secondary losses, m/z 198 and m/z 187, are assigned as sequential NH₃ and CO losses from the deamidation product, respectively. The structure of the m/z 198 product is as assigned from the ion spectroscopy experiment above. The m/z 173 product corresponds to the loss of the Asn side chain, leading to the product given in Scheme 2. An alternative cyclic structure (as presented in the [AsnGly + H]⁺ study⁹) was also explored there, but was found to be ∼10 kJ/mol higher in energy.

Figure 3.

Cross sections for the collision-induced dissociation of [AsnVal + H]⁺ with Xe as a function of kinetic energy in the center-of-mass frame (lower x-axis) and laboratory frame (upper x-axis). Numbers indicate the mass to charge ratio of the ionic reaction products. Cross sections were measured at a pressure of 0.2 mTorr of Xe.

Scheme 2. Major Decomposition Reaction Pathways for [AsnVal + H]⁺ Observed in the TCID Analysis under High Mass Resolution Conditions.

Numbers indicate mass to charge ratios. Short dashed lines indicate proton movement. Longer dashed lines indicate bond cleavages. Solid lines indicate bond formation. An alternative succinimide deamidation product is shown on the far left.

Theoretical Results for the Mechanism of [AsnVal + H]⁺ Deamidation

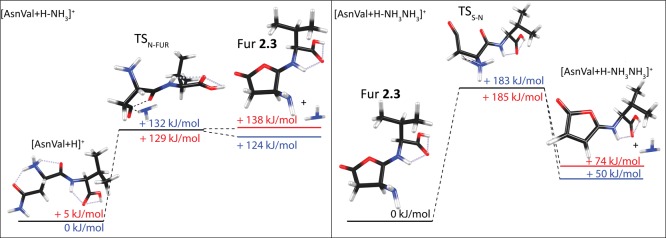
The pathway yielding the furanone product ion parallels those located in the [AsnGly + H]⁺ study.⁹ Specifically, proton transfer from the protonated N-terminus to the side-chain amide nitrogen allows for the formation of the NH₃ leaving group. Subsequent C–NH₃ bond rupture is facilitated by nucleophilic attack of the backbone carbonyl of the first residue and occurs via TS_N-FUR (132, 139, and 129 kJ/mol above the [AsnVal + H]⁺ ground structure at the B3LYP, B3P86, and MP2 levels of theory, respectively). This leads to formation of furanone 2.3 (Table 1) as shown in Figure 4. Here, TS_N-FUR is rate-limiting at the B3LYP and B3P86 levels of theory by 3–8 kJ/mol, whereas the MP2 level of theory instead predicts a product limited pathway where the furanone 2.3 + NH₃ product asymptote is 8.2 kJ/mol higher in energy than TS_N-FUR. Given this small energetic difference, the tight TS_N-FUR is still likely to control the rate of reaction at the MP2 level of theory.

Figure 4.

Overview of the transition states for the primary and secondary deamidation reactions of [AsnVal + H]⁺. Blue numbers indicate the 0 K B3LYP energies (kJ/mol); red numbers indicate 0 K MP2 energies (kJ/mol). Dotted lines indicate hydrogen bonds <2.5 Å, whereas dashed lines indicate bonds being formed or broken in the transition states.

An alternative pathway for deamidation of the complex was also explored. Here, the rate-limiting step for succinimide formation, TS_N-SUC (shown in Figure S1 and formed via a pathway parallel to that reported in a previous dipeptide analysis⁹), was found to be 40, 25, and 7 kJ/mol higher in energy than TS_N-FUR at the B3LYP, B3P86, and MP2 levels of theory, respectively (see the Supporting Information, Table S1). This explains why the furanone 2.3 structure is formed even though the final succinimide 1.1 product is much lower in energy (Table 1). In the GIBMS studies, the deamidation channel is likely dominated by furanone formation at threshold energies, although contribution of both dissociation pathways is possible at higher energies. Contributions of both furanone and succinimide formation at higher energies have been reported previously in the analysis of [AsnGly + H]⁺.⁹

Theoretical Results for the Mechanism of [AsnVal + H]⁺ Dehydration

Similar to deamidation, dehydration of [AsnVal + H]⁺ follows the mechanisms reported previously for [AsnGly + H]⁺.⁹ Namely, a proton transfer from the N-terminus to the carbonyl oxygen of the side-chain carboxamide (CO^s) is followed by dihedral angle rotations such that the complex arranges itself in a head-to-tail conformation. This orientation forms a hydrogen bond between the protonation site and carboxylic acid hydroxyl group (O³H); see Scheme 2. From here, a proton transfer from CO^s to O³H results in the formation of the H₂O leaving group, and nucleophilic attack of the CO¹ carbonyl initiates bond rupture of C–O³ and oxazolone ring formation. This process (via TS_O, 103–118 kJ/mol above the GS) is rate-limiting at all levels of theory, where the oxazolone product lies 18–30 kJ/mol lower in energy than TS_O. Dehydration of [AsnVal + H]⁺ is the lowest energy dissociation process observed, consistent with predicted reaction energies that are 16–35 kJ/mol lower in energy than the rate-limiting steps for the above-mentioned deamidation process.

Theoretical Results for the Formation of m/z 198 (−NH₃), m/z 197 (−H₂O), and m/z 187 (−CO) from the Deamidation Product

The deamidation product is observed to undergo sequential loss of another ammonia molecule (see Figures 2 and 3 and Scheme 2), and although not observed experimentally, sequential loss of H₂O is also conceivable. Both reaction pathways were explored theoretically. Secondary ammonia loss from the furanone (Fur) 2.3 product follows a straightforward mechanism that parallels that detailed in a forthcoming study on [AsnAla + H]⁺. Here, proton transfer from the furanone CH₂ group to N¹ via TS_S-N (where “S-N” stands for the sequential loss of an NH₃ group) results in the formation of the NH₃ leaving group. This process partially opens the furanone ring, where C–NH₃ bond rupture in the following step allows for ring closure. Notably, these motions are not concerted, such that C–NH₃ bond rupture via rate-limiting TS_S-N (307–323 kJ/mol above the reactant ground structure) is ∼50 kJ/mol higher in energy than ring closure, which occurs in the following step. These motions lead to the formation of [AsnVal + H – NH₃ – NH₃]⁺ as shown in Figure 2, characterized by a product asymptote of 174–212 kJ/mol.

At higher energies, a pathway for the sequential loss of water from Fur 2.3 was found in the computations. Here, proton transfer from N¹ to O³H occurs resulting in dehydration and N¹–CO² bond formation, stabilized by the formation of bicyclic m/z 197 as shown in Figure S1 of the Supporting Information. Similar to secondary ammonia loss, TS_S-O (360–367 kJ/mol above the ground state) is predicted to be rate-limiting, with the m/z 197 + H₂O product asymptote located 170–188 kJ/mol lower in energy than TS_S-O. Note that TS_S-O is >40 kJ/mol higher in energy than TS_S-N, plausibly explaining why subsequent loss of H₂O from Fur 2.3 is not observed in the IRMPD or TCID experiments.

The loss of neutral CO forming m/z 187 was also observed in the TCID experiments as a decomposition channel from the m/z 215 deamidation product with a threshold lower than loss of a second NH₃ group. Initially, a pathway exploring this decarbonylation of the furanone product was explored. Here, proton transfer to the NH₂ amino group (from the adjacent carbon) weakens the furanone ring, which can undergo ring opening in the following rate-limiting step, TS_S(FUR)-C (362–389 kJ/mol above the GS). Once past this TS, the system eliminates CO. Notably, this process is considerably higher in energy than predicted reaction energetics for secondary ammonia loss, in contrast to the relative thresholds observed in the TCID cross sections.

Thus, decarbonylation of the alternative succinimide 1.1 product (which may be present at higher energies as discussed above) was also explored. Here, proton transfer from the NH₃⁺ protonation site to the cyclic nitrogen weakens the succinimide ring. In the following step elongation of the N–C bond breaks the ring via TS_S(SUC)-C (266–293 kJ/mol above the GS). Importantly, this process is 92–119 kJ/mol lower in energy than decarbonylation of the furanone 2.3 product, and 33–57 kJ/mol below NH₃ loss from furanone 2.3. The latter is consistent with the cross-sectional behavior observed in the TCID studies at threshold energies.

TCID Data Analysis and Modeling

Equation 1 was used to analyze the thresholds for the primary competitive deamidation and dehydration channels in the decomposition of [AsnVal + H]⁺, where the simultaneous modeling of these primary channels accounts directly for competition. Using parameters given in Table 2, the data were reproduced over the full range of the energy and cross-section magnitude, as shown in Figure 5. The experimental deamidation channel shown includes the summation of the sequential dissociations forming m/z 187 and 197 (thus incorporating all relevant cross sections). For the reactions limited by a tight TS (deamidation via TS_N-FUR and dehydration via TS_O), the TS frequencies used for the cross-section modeling were taken from the theoretical results discussed above. Higher energy channels observed in Figure 3, including the sequential dissociations into channels m/z 187 and 197, could not be modeled accurately because their high energy thresholds lead to relatively low intensities.

Table 2. Fitting Parameters of Eq 1, Threshold Energies at 0 K, and Entropies of Activation at 1000 K for Cross Sections of the Reactions Indicated^a.

reaction	TS	freq scalingb	σ0	n	E0 (eV)	ΔS‡1000 (J/K mol)
dehydration, m/z 215	TSO	1.02	15.1 (1.3)	1.2 (0.2)	1.18 (0.05)	–39 (1)
deamidation,cm/z 214	TSN-FUR	1.00	15.1 (1.3)	1.2 (0.2)	1.34 (0.05)	–2 (1)

^aUncertainties in parentheses.

^bFrequency scaling factor applied to frequencies <900 cm^–1.

^cValues obtained using tight TS parameters; see text.

Figure 5.

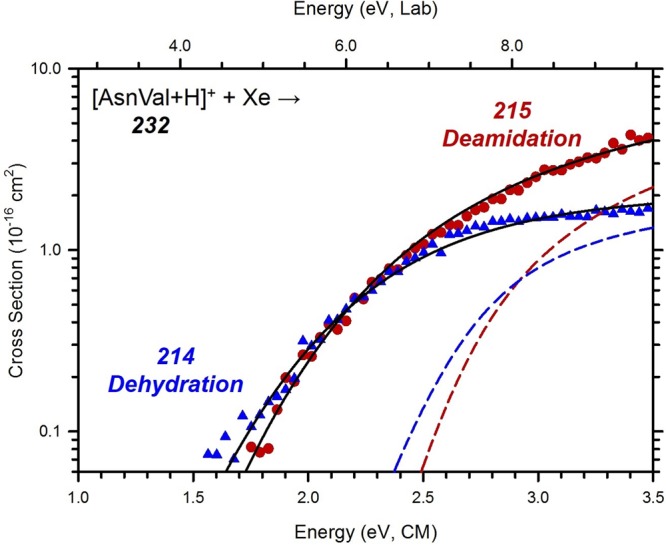
Cross-section models of the main decomposition products of [AsnVal + H]⁺ as a function of collision energy with Xe in the center-of-mass frame (lower x-axis) and the laboratory frame (upper x-axis). Solid lines show the best fit to the data extrapolated to zero pressure (solid symbols), using the model of eq 1 convoluted over the neutral and ion kinetic and internal energy distributions. Dashed lines show the model cross sections in the absence of experimental kinetic energy broadening for reactants with an internal energy of 0 K.

As shown in Figure S5 of the Supporting Information, zero pressure extrapolated deamidation and dehydration cross sections could be modeled over the full energy range fairly well using TS_N-FUR and TS_O molecular parameters, respectively. However, improved fits in the threshold regions of these respective cross sections could be obtained by scaling the low-frequency modes (<900 cm^–1) of either TS_N-FUR or TS_O (as shown in Figure 5). Here, low-frequency modes for TS_O were tightened by 2–5% while holding those for the tight TS_N-FUR constant. (Notably, a comparable fit can be achieved by loosening the low-frequency modes of TS_N-FUR by the same magnitude. In the current analysis, however, tightening of the TS_O modes is more appropriate because this approach does not alter the dominant dissociation pathway.) This analysis suggests that the calculated harmonic frequencies for TS_O provide a characterization of this channel that is slightly too loose relative to those for TS_N-FUR. Similar (and even larger) frequency scaling factors have been used in previous studies on comparable systems.^5,9,22 Notably, although the analysis with no scaling (as given in Figure S5) provides a similar global representation of the data that is not quite as good in the critical threshold region, it results in threshold energies within the stated uncertainties of the values provided in Table 2. Additionally, the deamidation channel was only modeled using tight TS parameters, even though the MP2 level predicts a product limited pathway by 8 kJ/mol. However, as noted above, this small energy difference means that the tight TS barrier is still likely to control the reaction. Previous modeling analyses of similarly characterized pathways confirm this behavior.⁹ It can be noted that the entropies of activation, ΔS^‡₁₀₀₀, for these two channels indicate that dehydration is entropically disfavored compared with deamidation, which explains why the former cross section is smaller at higher energies even though it is less endothermic.

For comparison of the thermodynamic information obtained experimentally to room temperature conditions, Table 3 provides the conversion from 0 K thresholds to 298 K enthalpies and Gibbs free energies. This conversion was accomplished using the rigid rotor/harmonic oscillator approximation with rotational constants and vibrational frequencies calculated at the B3LYP/6-311+G(d,p) level. Uncertainties listed were determined by scaling the vibrational frequencies by ±10%.

Table 3. Enthalpies and Gibbs Free Energies of Reaction at 0 and 298 K for Deamidation and Dehydration Reactions^a.

reaction	ΔH0b	ΔH298 – ΔH0c	ΔH298	TΔS298c	ΔG298
dehydration, TSO	114 (5)	0.4 (0.2)	114 (4)	–11.0 (0.1)	125 (4)
deamidation, TSN-FUR	129 (5)	3.7 (0.1)	133 (4)	–1.1 (0.2)	134 (5)

^aUncertainties in parentheses.

^bExperimental values.

^cCalculated using standard formulas and molecular constants at the B3LYP/6-311+G(d,p) level.

TCID Experimental versus Theoretical Results

Experimental threshold energies for the primary deamidation and dehydration reactions are compared with calculated theoretical reaction energies in Table 4 at several levels of theory. Such comparisons are important in ensuring that thermal ions were produced experimentally and can confirm the validity of the reaction mechanism. Here, “hot” ions would systematically result in threshold energies that are uncharacteristically low. For the deamidation pathway leading to furanone 2.3 formation, the experimentally determined threshold was found to be 129 ± 5 kJ/mol, in excellent agreement with B3LYP and MP2 theoretical values. B3P86 suggests a reaction threshold higher by about 10 kJ/mol. The competitive dehydration channel was found to have an experimental threshold of 114 ± 5 kJ/mol, which is within the uncertainty of the experimental value for the B3LYP and B3P86, whereas MP2 suggests a threshold lower by 11 kJ/mol (just outside two standard deviations).

Table 4. Experimental and Theoretical Reaction Energies (kJ/mol) for Decomposition Reactions of [AsnVal + H]⁺.

reaction	TS	expta	B3LYPb	B3P86b	MP2(full)b
dehydration, m/z 172	TSO	114 (5)	116	118	103
deamidation, m/z 173	TSN-FUR	129 (5)	132	139	129
MADsc			3 (1)	7 (4)	6 (8)

^aExperimental values from Table 3. Uncertainties in parentheses.

^bCalculations performed at the stated level of theory using a 6-311+G(2d,2p) basis set with geometries calculated at B3LYP/6-311+G(d,p) level, ZPE corrections included.

^cCalculated mean absolute deviations (MADs) from experiment for the deamidation and dehydration channels.

For both decomposition processes, there is good agreement between experiment and theory when modeled competitively using parameters for the tight TS limited pathways. Such agreement is quantified via mean absolute deviations (MADs) from the experimental results as shown in Table 4, where all MADs are lower than 10 kJ/mol. B3LYP exhibits the lowest MAD at 3 kJ/mol, whereas B3P86 overestimates the reaction thresholds such that this level resulted in the highest MAD, 7 kJ/mol. The consistent agreement between theory and experiment for both modeled channels verifies that the necessary experimental conditions to produce thermal ions were used and confirms that the mechanisms located for these reactions are reasonable pathways. Notably, the experimental threshold for deamidation is not consistent with predicted reaction energies found for succinimide formation, 145–172 kJ/mol (Table 5), consistent with the failure to observe this species in the ion spectroscopy experiments.

Table 5. Comparison of 0 K Reaction Energies for the Deamidation and Dehydration of Asparagine Dipeptides^a.

reaction	species	expt9,60	B3LYP	B3P86	MP2(full)
succinimide formation	[AsnGly + H]+	129 (6)	151	143	135
	[AsnAla + H]+		163	155	137
	[AsnVal + H]+		172	164	145
furanone formation	[AsnGly + H]+		132	139	142
	[AsnAla + H]+	126 (5)	132	139	134
	[AsnVal + H]+	129 (5)	132	139	138
dehydration	[AsnGly + H]+	117 (6)	127	130	112
	[AsnAla + H]+	105 (8)	119	122	98
	[AsnVal + H]+	114 (5)	116	118	103

^aCalculations performed using a 6-311+G(2d,2p) basis set with geometries calculated at the B3LYP/6-311+G(d,p) level. Energies are given relative to the ground structure of the reactant at each respective level of theory.

Comparison to Solution-Phase Reactivity

Notably, the behavior observed in the current analysis (specifically formation of furanone, rather than succinimide) differs from that in solution-phase studies.^14,15 On this basis, we explored solvated reaction pathways, both implicitly by optimizing reaction TSs and intermediates in a polarizable continuum model (PCM) cavity, and explicitly by the addition of one water molecule. Here, succinimide formation via a tetrahedral intermediate is favored over furanone formation in solution by 19 and 37 kJ/mol at the B3P86 and MP2 levels of theory, respectively, although B3LYP predicts succinimide is higher in energy than furanone formation by 18 kJ/mol. However, the better correlation between experiment and theory at the MP2 level of theory for the deamidation processes (as given in Table 5) suggests that this level of theory likely handles the reaction dynamics more accurately. Notably, the MP2 level predicts the TS is ∼60 kJ/mol lower in energy than the B3LYP level, an energy difference not likely to be water mediated to the degree that succinimide would be favored over furanone formation at the B3LYP level of theory. Thus, the differences between gas-phase and condensed-phase dynamics appear to be controlling the observed deamidation product in these respective studies.

Analysis of the TS motions involved in the solvated reactions for furanone and succinimide formation provides insight as to how the reaction dynamics are affected in gas-phase and condensed-phase media. Specifically, succinimide formation via tetrahedral intermediates proceeds through a rate-limiting TS characterized by several concerted proton tranfers.⁹ These motions can be facilitated by water mediation effects that lower the reaction barriers. However, furanone formation in solution proceeds through an analogous pathway as depicted in Figure 4, where concerted motions of bond rupture and bond formation are observed. Here, no water mediation effects are observed because the available water molecule does not facilitate the reaction, but rather stabilizes the NH₃ group throughout the reaction, leading to an increase of the reaction barrier. Thus, succinimide formation is most commonly reported, where subsequent hydrolysis yields a combination of isoaspartic acid and aspartic acid. Although furanone formation is not likely energetically competitive with succinimide formation in condensed media, hydrolysis of such furanone structures could similarly lead to ring opening in solution, forming an Asp residue, but not the alternative iso-Asp.

Comparison to [AsnGly + H]⁺ and [AsnAla + H]⁺

In previous studies, our groups have investigated the deamidation reactions of protonated AsnGly and AsnAla.^8,9 Interestingly, increasing the size of the C-terminal residue side chain influences the reaction energetics for succinimide and furanone formation upon deamidation; see Table 5. For succinimide formation, a larger C-terminal residue side chain correlates with an increase in the energy of the rate-limiting TS. Relative to [AsnGly + H]⁺, rate-limiting TSs of the Ala- and Val-containing species exhibit increases in energy of 12 and 21 kJ/mol at the B3LYP and B3P86 levels (4 and 12 kJ/mol at the MP2 level), respectively. Notably, succinimide formation occurs via parallel pathways in each of the complexes such that the difference in energy among these three systems appears to be a direct effect of increased steric hindrance. Conversely, for furanone formation, no clear correlation between C-terminal residue side chain size and TS energy is observed. At the B3LYP and B3P86 levels, specifically, reaction energies are within 1 kJ/mol of each other for the three dipeptide systems.

Experimentally, deamidation of [AsnGly + H]⁺ and [AsnAla + H]⁺ were observed to exhibit bifurcating reaction pathways, forming the succinimide and furanone product ions in parallel. For the [AsnVal + H]⁺ dipeptide studied here, this is not the case: only the furanone product is observed, in agreement with the trends in the computed reaction barriers.

Dehydration of all three systems was observed to compete with deamidation, in all cases being lower in energy but entropically disfavored. It can be seen that there is no systematic trend in the experimental dehydration energies as a function of side-chain complexity, but the experimental values match the trends predicted at the MP2 level nicely. Because the oxazolone formation occurs within the second residue containing the aliphatic side chains, one can imagine that a combination of inductive and steric effects could lead to the changes observed.

Conclusions

The decomposition, and in particular the deamidation, of protonated AsnVal has been studied using a combination of infrared ion spectroscopy, guided ion beam tandem mass spectrometry, and quantum-chemical calculations. Loss of water and ammonia are the main fragmentation channels, which is consistent with results found for [AsnGly + H]⁺ and [AsnAla + H]⁺.^8,9,60 Molecular structures for the ionic decomposition products as well as energy dependent dissociation cross sections and transition state energies have been determined. We suggest that deamidation occurs via a nucleophilic attack of the backbone amide oxygen onto the amide carbon of the asparagine side chain, leading to the formation of a reaction product incorporating a furanone moiety with a reaction energy of 129 ± 5 kJ/mol above the GS (within experimental uncertainty of predicted values at the B3LYP and MP2 levels). This furanone structure is in line with earlier studies on the deamidation of [AsnAla + H]⁺ and [AsnGly + H]⁺, although for those species a bifurcating mechanism was established, with the formation of a succinimide structure in parallel to the furanone product. Calculations of the rate-limiting TSs for each of these species predict an increasing barrier toward succinimide formation with increasing alkyl side chain of the C-terminal residue, Val (145–172 kJ/mol) > Ala (137–163 kJ/mol) > Gly (133–151 kJ/mol), whereas the barriers toward the furanone product are independent of the C-terminal residue, qualitatively explaining the subtle differences in decomposition behavior for the three dipeptides. For [AsnVal + H]⁺, the TS for succinimide formation is 7–40 kJ/mol higher than that for furanone formation.

Formation of furanone structures upon deamidation appears to be exclusive for gas-phase reactions. In condensed-phase media, only formation of succinimide as an intermediate on the way to (iso-)aspartic acid has been reported. We speculate that the amide carbonyl is more strongly involved in H-bonding interactions in condensed media, reducing its nucleophilicity and thus reducing the likeliness of forming furanone structures. Further, on the basis of our structural analysis above, the relative energetics controlling deamidation appear to be related to the proximity of TS motions to the bulky Val isopropyl group. Thus, furanone formation (where TS motions are localized to the Asn side chain) is energetically favorable compared to succinimide formation, where these motions are closer to the isopropyl group. Interestingly, for the succinimide reaction, the lowest energy TS orients the Val side-chain methyl groups toward either of the oxygens of the carboxylic acid (as observed in the TS_N-FUR), although one could imagine that such an orientation could sterically hinder the reaction as a result of the close proximity between the TS motions and the CH₃ group. However, rotation of the isopropyl group to other positions results in higher energy TSs. For instance, one TS was located where the isopropyl CH hydrogen was oriented toward the bond rupture/formation TS motions, although this TS was located ∼10 kJ/mol higher in energy than TS_N-SUC.

Given these subtleties governing the deamidation reaction pathways of protonated AsnXxx peptides, it remains difficult to speculate on the outcome of the reaction for other Xxx residues (i.e., whether succinimide or furanone formation is observed). However, our current results do suggest that succinimide formation, the dominant pathway in solution, is controlled (at least in part) by steric effects of the n + 1 residue. Thus, reaction barriers for larger n + 1 residues are expected to increase, although our studies to date have only involved aliphatic side chains. One can imagine that polar side chains having favorable or unfavorable inductive effects or that present more specific orientations resulting from hydrogen bonding may play a significant role in mediating the deamidation process. Investigations involving the n + 1 residues of Ser and Thr are currently underway in our laboratories.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jpca.7b12348.

• Relative energies at B3LYP, B3P86, and MP2(full) levels of theory for major reaction species and for alternate conformations of the furanone product; structures of major reaction species, calculated at B3LYP/6-311+G(d,p) level of theory; experimental versus theoretical spectral comparison for the lowest energy diketo-morpholine 3.2 structure; comparison of IRMPD spectra of [AsnVal + H – NH₃]⁺ and [AsnVal + H – NH₃ – NH₃]⁺with computed spectra; modeling of cross-section data with and without use of frequency scaling (PDF)

The authors declare no competing financial interest.