The biology and polymer physics underlying large‐scale chromosome organization

Abstract

Chromosome large‐scale organization is a beautiful example of the interplay between physics and biology. DNA molecules are polymers and thus belong to the class of molecules for which physicists have developed models and formulated testable hypotheses to understand their arrangement and dynamic properties in solution, based on the principles of polymer physics. Biologists documented and discovered the biochemical basis for the structure, function and dynamic spatial organization of chromosomes in cells. The underlying principles of chromosome organization have recently been revealed in unprecedented detail using high‐resolution chromosome capture technology that can simultaneously detect chromosome contact sites throughout the genome. These independent lines of investigation have now converged on a model in which DNA loops, generated by the loop extrusion mechanism, are the basic organizational and functional units of the chromosome.

1. INTRODUCTION

The physics of polymers has been the subject of intense research over many decades. The 1991 Nobel Prize in physics was awarded to Pierre‐Gilles de Gennes in part for his work on polymers,1 the general term for very long chains assembled from simpler links, of which DNA is a perfect example. One of the deep insights de Gennes and others contributed to this field is that polymers typically show universal behavior independent of their underlying chemical composition. This means that polyethylene, polystyrene and DNA should all follow the same mathematical laws. Particularly relevant to the topic of chromosome organization, de Gennes and others also formulated mathematical models to describe both the concentration‐dependent arrangement of polymers in solution, and the snake‐like motion of a polymer through a sea of surrounding polymer chains, called reptation. We have learned a great deal in the last decade about the reasons and extent to which DNA follows the well‐known polymer physics laws and gained insight into the reasons why they do not always obey these laws inside of the nucleus. In contrast to the focus of physicists on widely applicable mathematical laws, biologists historically did not focus on the universal properties that underlie DNA structure and function in all cells.

There are 3 fundamental organizational principles of the interphase nucleus in which biology and polymer physics significantly impact one another: the sequestration of chromosomes into nuclear territories; the partition of transcriptionally active and inactive regions of the genome; and the organization of chromosomes into loops.2, 3, 4 These topics are particularly timely in light of recent technological advances that resulted in high‐resolution maps of the genome‐wide physical contacts within and between chromosomes, based on data collected from large populations of human cells.5, 6, 7, 8, 9 The Hi‐C methodology5, 7 and the chromosome capture approach upon which it is based10 documented millions of chromosome contacts throughout the human genome that were unimaginable in the late 1800s and early 1900s when the structure and function of DNA was unknown and the nonrandom organization of interphase chromosomes was first documented.11, 12, 13

These Hi‐C data documented interchromosomal associations among active or inactive chromatin within nuclear compartments (originally named A and B, respectively, and subsequently subdivided into 6 compartments), intrachromosomal interactions consistent with the physical separation of individual chromosomes into territories within the nucleus and the organization of chromosomes into loops with previously characterized DNA sequence motifs and proteins at their bases.7 Emerging from this latter observation is the “loop extrusion model” that proposes a mechanism for loop formation, position and stabilization.6, 14, 15, 16 Taken together, these data made it possible to formulate, test and revise earlier biological and polymer physics models of chromosome organization from a new perspective.

Building on the conceptual advances resulting from the confluence of biology and physics poses challenges for scientists from different disciplines but with common interests and scientific goals. Nonspecialists may find it challenging to understand or appreciate the historical context, methodological details, analytical methods, principles or utility of unfamiliar experimental approaches, computer simulations or biophysical modeling.17, 18, 19, 20 To address the challenge of integrating this information within a broader context, we will review, evaluate and reassess the historical underpinnings, current data, and successive revisions of models describing chromosome conformation and organization.

2. EUKARYOTIC CHROMOSOMES AND POLYMERS

2.1. What is a eukaryotic chromosome?

The signature characteristic of a eukaryotic cell, which distinguishes it from archaea and eubacteria, is the double phospholipid membrane‐bound nucleus that encapsulates the cellular genome (reviewed in References 21 and 22; Figure 1). As detailed in excellent books by Alberts et al23 and Morgan,24 the nucleus and chromosomes undergo a precisely orchestrated series of dynamic organizational, structural and functional changes during the cell cycle (Figure 2), as each cell replicates its DNA, condenses, segregates and decondenses its chromosomes, then divides to produce 2 daughter cells (Figure 2B).

Figure 1.

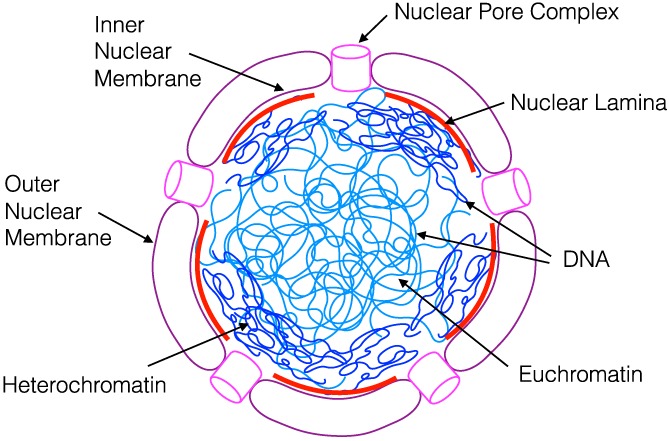
The human cell nucleus. The nucleus of all eukaryotic cells is bounded by a double phospholipid membrane (purple) composed of an inner and outer leaflet. The nuclear envelope forms a physical barrier between the chromosomes (blue) and the cytoplasm, a structural scaffold for the nucleus, and a permeability barrier between the nucleoplasm and the cytoplasm. It is perforated by nuclear pore complexes (pink) through which small molecules diffuse, and larger molecules are selectively transported. In human cells, the inner nuclear membrane is lined by the nuclear lamina (red) to which heterochromatin (dark blue) and specific chromosome domains are anchored, whereas euchromatin (light blue) is enriched in the nuclear interior21

Figure 2.

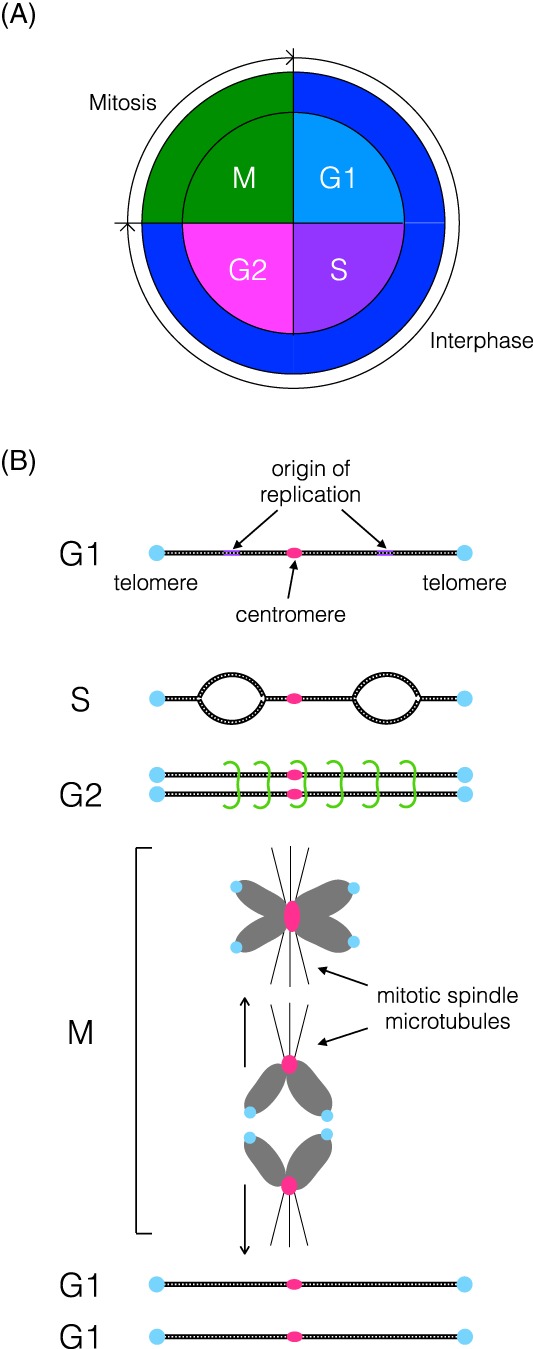
The eukaryotic cell and chromosome cycle: (A) The eukaryotic cell cycle is divided into mitosis and interphase, and interphase is further subdivided into G1, S and G2. DNA is duplicated in S phase, the chromosomes condense and segregate in M phase, and these phases are separated by Gap (growth) phases called G1 and G2. (B) Each chromosome has telomeres (blue) at its ends, a centromere (pink), to which spindle microtubules attach at M phase, and multiple origins of DNA replication (purple). In S and G2, the replicated chromosomes are held together by cohesin (green). At M, the chromosomes condense, align at the metaphase plate, individualize and are separated from one another by the mitotic spindle after cohesin release. The centromeres are at the leading edge of this mitotic chromosome movement, the telomeres trail behind, and some cell types retain this polarized positioning, called the Rabl orientation in G1, even after chromosome decondensation23, 24

The genetic material of eukaryotic cells is distributed among multiple linear chromosomes, the number of which varies widely between organisms (eg, 3 in the haploid fission yeast Schizosaccharomyces pombe vs 46 in diploid humans). Chromosomes are not naked DNA, although they have the same double‐helical DNA core in all cells. Their structure, conformation and function are determined and regulated by the large collection of proteins to which they are bound.

The most abundant class of chromosome‐associated proteins are histones that assemble into octameric complexes around which DNA winds to form nucleosomes (reviewed in Reference 25) resulting in a 10‐nm wide “string of beads” fiber that reduces chromosome length by ~10‐fold. The details and mechanism of the higher‐order chromosome folding that compacts the approximately 2‐m long human genome into a 10 to 20 μm wide nucleus, including the controversial 30 nm fiber, remain unclear (reviewed in Reference 26). However, it is well documented that chromosome structure and function are influenced by the assembly, positioning and spacing of nucleosomes and post‐translational modifications of their histone subunits.25, 27, 28, 29, 30 The complex pattern of histone modifications also influences whether a particular region of the chromosome is tightly packed into nontranscribed “inactive” heterochromatin or is loosely organized into the more open “active” euchromatin conformation that renders the DNA more accessible to a variety of DNA binding proteins, including those that activate transcription. Other characteristics that distinguish euchromatin from heterochromatin are the presence of DNA repeats, the density of genes and the timing of replication (reviewed in Reference 4). Although euchromatin and heterochromatin lie in distinct blocks along each human chromosome, a stretch of heterochromatin artificially inserted into a euchromatic domain can convert the adjacent regions into heterochromatin by propagating or “spreading” its characteristic set of histone modifications.31 These and other observations eventually led to the discovery that in its normal context euchromatin is physically and functionally insulated from heterochromatin (reviewed in Reference 31).

2.2. What is a polymer?

Polymers are huge molecules forming long one‐dimensional chains of small units called monomers. If these units are identical it is called a homopolymer, otherwise it is called a heteropolymer. DNA belongs, strictly speaking, to the latter class but its physical properties are essentially independent of the underlying nucleotide composition so that it is often treated as a member of the former. Being long and thin, all polymers behave like flexible chains (when looking at large enough length scales). They are thus characterized by a multitude of configurations that all have similar energies and that thus occur with similar probabilities. Typically, the behavior of polymers does not depend on their underlying chemical composition, that is, it does not matter whether we look at polyethylene, polystyrene or, in fact, DNA; they all follow the same polymer rules. This is far from trivial and has some deep roots in the fact that within the limits of infinitely long chains, such systems are at a so‐called critical point where the structure becomes self‐similar on all length scales, that is, statistically speaking the polymer looks the same on all length scales, except the very small scales (around the monomer size). This leads to universal behavior1 where a large class of polymers all obeys a small set of simple mathematical relations (eg, a relation between the typical size of a polymer coil and the number of its monomers) and where these relations do not depend on the underlying chemistry.

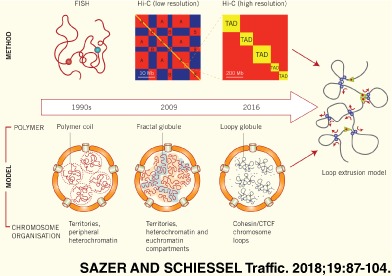
This means that there exist well‐defined “reference states” for polymers to which chromosome structures need to be compared. Whenever it is found that DNA conformations in cells deviate substantially from such states, it is important to understand the cause for such a deviation. During the last 25 years there have been at least 3 such moments where a comparison between polymer physics and experimental data on chromosomes revealed fundamental differences between the behavior of standard polymers and chromosomes. In each case, new experimental methods revealed those differences, and new theoretical approaches were developed to explain them (see Figure 3).

Figure 3.

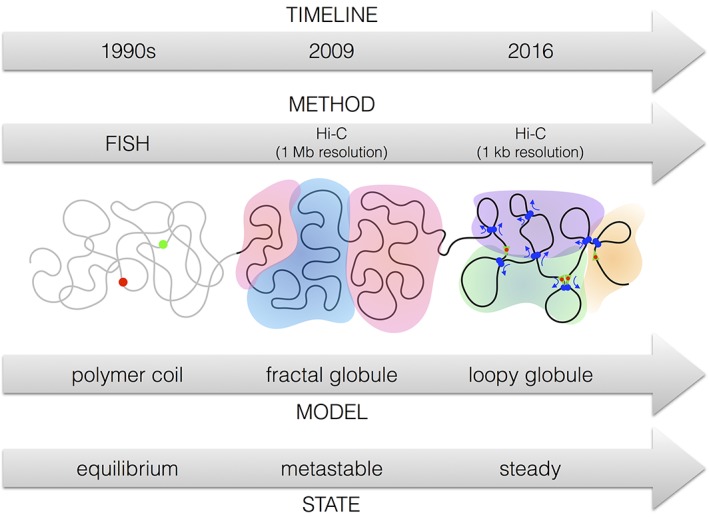
Paradigm shifts in chromatin organization. Fluorescent in situ hybridization experiments (Figure 6) on chromosomes in the 1990s suggested that DNA conformations in interphase chromosomes behave like random polymer coils at equilibrium. Chromosome conformation capture (specifically Hi‐C data at 1 Mb resolution) suggested in 2009 that the chromosomes are in a metastable polymer state, the fractal or crumbled globule. In addition, it mapped 2 sub‐compartments (indicated here by colors). More recently, Hi‐C experiments at 1 kb resolution point toward a loopy globule state, a steady state maintained by the continuous action of molecular motors called loop extrusion complexes. About 6 different sub‐compartments have been identified (3 of which are indicated here by colors, see main text for details)

In order to understand the relationship between the behavior of chromosomes and polymers, it is crucial at this point to outline the universal behavior of the simplest polymer analogue to a nucleus filled with interphase chromosomes. In the language of polymer physics this state would be that of a concentrated solution of polymers.

Let us begin with a single isolated polymer chain. Such a polymer has myriad different configurations which come about because of the random orientations of neighboring bonds along the chain. Specific polymer configurations are thus not of interest but statistical averages over many configurations are. A typical quantity to look at is the mean‐squared end‐to‐end distance (one looks at the squared distance because the end‐to‐end vector averages out to zero). This is straightforward to calculate as the polymer shows the configuration of a so‐called random walk. The effective step length depends on the stiffness of the molecule and is 100 nm for DNA.32 A random walk of N steps with step length a (called bond length in the polymer analogue) has a mean‐squared end‐to‐end distance of a random walk that scales like a ² N. Therefore, such polymer coils have a typical size R that scales like aN ^1/2 (see Figure 4A which also contains an explanation of polymer physics jargon such as “scales like aN ^1/2”), substantially shorter than the total contour length aN of the molecule. This is because the polymer typically has the shape of random coil.

Figure 4.

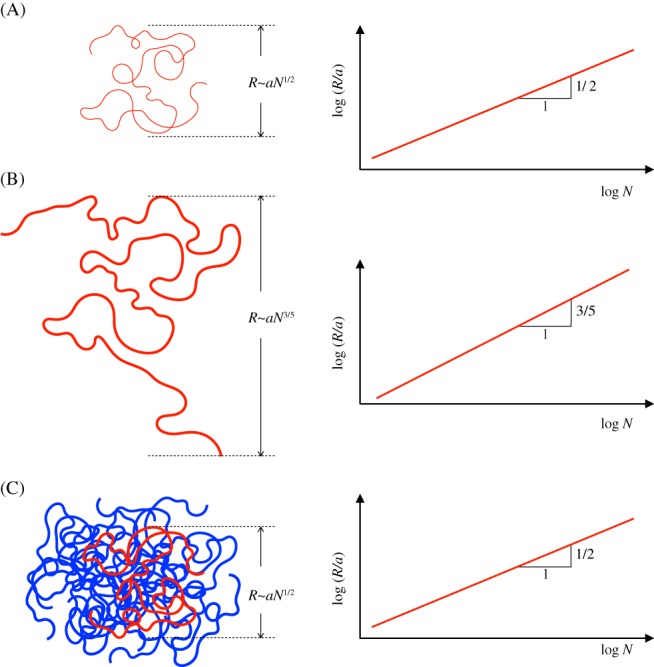
Ideal and swollen polymer coils follow different scaling laws. (A) An infinitely thin ideal polymer chain behaves like a random walk with an overall size that scales like aN ^1/2 (“size” here means a quantity with units of length like the end‐to‐end distance or other related quantities that capture the overall extension of the polymer; “scales like” means that when the logarithm of the dimensionless size R/a is plotted vs the logarithm of the monomer number, N, for polymers of different degrees of polymerization the data points would lie along a line of slope 1/2 (see the right plot); a numerical prefactor in front of aN ^1/2 does not affect this slope and is thus disregarded, that is, it does not matter whether R/a = N ^1/2 or R/a = 10N ^1/2, only that R/a ~ N ^1/2). (B) The monomers of a real polymer occupy space and this excluded volume leads to a swelling of the chain to a size that scales like aN ^3/5. (C) A real polymer in a dense solution of other polymers behaves like an ideal chain (compare (C) and (A)). The reason is that the outward pointing pressure produced by the monomers of the red chain is canceled by an inward pointing pressure of the other chains, shown in blue

So far, we neglected the argument that different parts of the chain cannot occupy the same region in space. Such “phantom” chains are called ideal chains. For real chains the excluded volume (ie, multiple monomers cannot occupy the same space) leads to a substantial swelling of the chain such that its end‐to‐end distance scales like N ^v, where v is now larger than 1/2, and close to 3/51, 32 (Figure 4B). Interestingly, however, when one considers a sufficiently dense solution of polymers, that is, many overlapping polymer chains in a container (our reference states for chromosomes in a nucleus) the excluded volume has no effect on the polymer configuration as the polymer tries as much to get out of its own way as out of the way of the other chains (Flory theorem1). In other words, individual polymers behave like ideal polymer chains whose end‐to‐end distance scales like N ^1/2 (Figure 4C). Because the polymer solution is dense but individual chains are spread out, different polymers overlap. In addition, as each polymer is self‐similar we find that the same laws hold for the spatial distance between a given pair of monomers as for the end‐to‐end distance of the whole chain. Specifically, for 2 monomers g steps of length a apart (ie, at a chemical distance ag along the chain, see Figure 5A) the root‐mean‐squared spatial distance is given by ag ^1/2, see Figure 5B. That polymer chains in a solution behave like ideal chains has been verified experimentally, for instance, by performing neutron scattering on a few labeled (deuterated) polystyrene chains in a melt of unlabeled (hydrogenated) chains.33 But does all this also apply to the behavior of interphase chromosomes?

Figure 5.

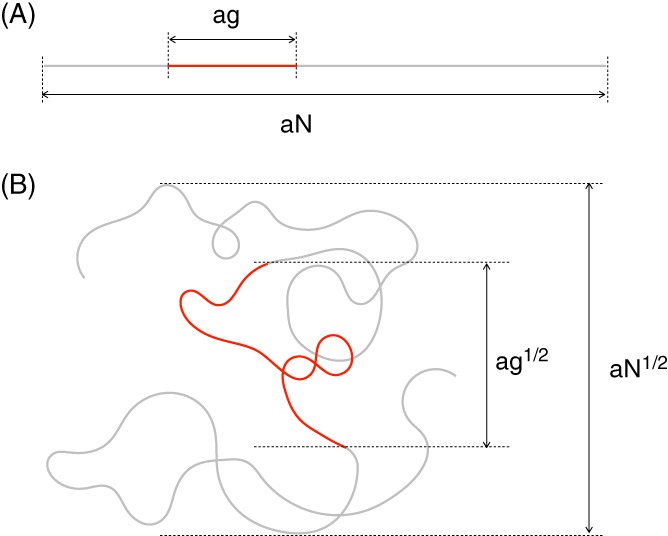
Polymer coils are self‐similar. (A) A polymer of length aN with a stretch of length ag marked in red. (B) For an ideal chain the overall coil size scales like aN ^1/2 and the size of the piece shown in red also shows the same scaling law, namely ag ^1/2. Note that the polymers in (A) and (B) are shown on a different scales ((B) is magnified about 5‐fold relative to (A))

3. CHROMOSOME TERRITORIES

3.1. What is a chromosome territory?

In the late 1800s, before anyone knew what chromosomes were, they were visualized in a sub‐population of proliferating cells using simple light microscopes and dyes that are now known to bind DNA (reviewed in References 34 and 35). These distinct condensed mitotic chromosomes (we now know that each is actually a pair of duplicated sister chromatids) transiently appeared in the nucleus, aligned with one another, split in half longitudinally, and then moved apart (Figure 2B). However, between 1 mitosis and the next, in the cell cycle stage called interphase (Figure 2A), discrete chromosomes could no longer be detected, and the DNA‐binding dye filled the nucleoplasm. At the time, these observations raised the possibility that chromosomes fragment in interphase only to be reassembled at the next mitosis. Although individual interphase chromosomes could not be resolved microscopically, we now know that these decondensed chromosomes do retain their integrity in interphase and that underlying their apparent interphase randomness is a well‐organized territorial configuration.

As far as 1888, while studying the eggs of the nematode worm Ascaris, Boveri and coworkers11, 36 confirmed the prediction of Rabl13 that each interphase chromosome occupies a separate nuclear position, subsequently named a chromosome territory.12 However, the prevailing model at the time was that interphase chromosomes are randomly organized, and it persisted for decades despite mounting, albeit indirect, evidence of territoriality (see comprehensive reviews 34, 35).

The ability to visualize the 3D position of chromosomal loci within the nucleus, and to compare their genomic and spatial distances was made possible when the FISH (fluorescent in situ hybridization) technique was developed35, 37 (Figure 6).

Figure 6.

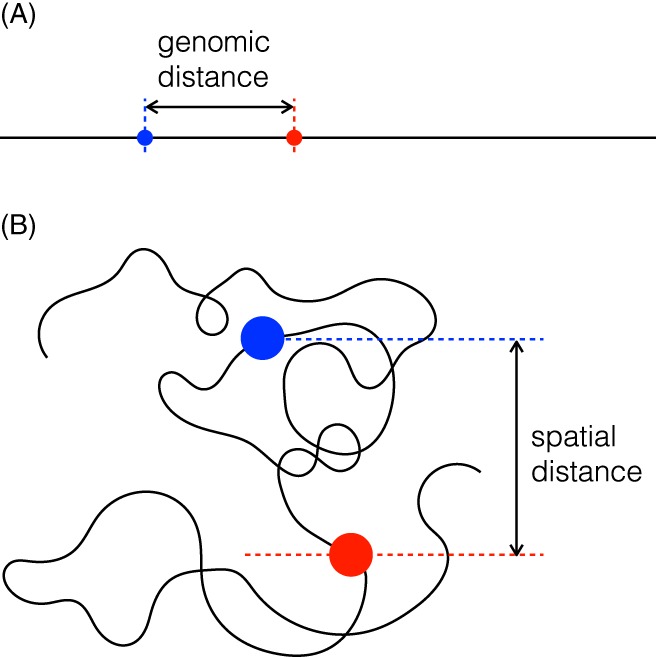
Fluorescent in situ hybridization (FISH) can be used to determine the positions of fluorescently labeled genomic loci within the nucleus. The principles of the Southern Blot in which a specific chromosomal locus is detected in vitro by hybridization to a complementary stretch of radioactively labeled DNA of known DNA sequence, were adapted for the detection of specific DNA motifs in intact cells. This in situ hybridization (ISH) technique was subsequently redesigned to use fluorescent reporters for FISH analysis. (A) A DNA polymer (chromosome) with a stretch whose ends are tagged with blue and red fluorochromes. The distance between the fluorochromes along the chain is called the chemical or genomic distance. (B) The DNA polymer (chromosome) diagrammed in (A) within a fixed cell in which the spatial distance of the 2 loci relative to nuclear landmarks or to one another can be measured. Note that the polymers in (A) and (B) are shown on different scales ((B) is magnified about 5‐fold relative to (A))

Plots of the mean‐squared spatial distance vs the genomic distance from a large number of such FISH measurements allowed a direct comparison to polymer models. As mentioned earlier, one expects by analogy to polymer solutions that individual DNA molecules show a random walk geometry, that is, on average the spatial distance between chromosomal loci should increase as the square root of the genomic distance. This was tested in a 1992 study37 which found that the data for short enough distances (namely distances up to about 1.8 Mb) are consistent with the random walk model. Beyond this, however, the spatial distance levels off. This observation points toward some kind of confinement or, as the authors of the paper put it, “some constraining higher‐order structure.” The leveling‐off, which reflects the territoriality of chromosomes, is the opposite of what one expects from ordinary polymers which show random walk statistics for all distances (beyond the effective step length).

Various approaches have since then been developed to account for the experimentally observed leveling‐off. One possibility is to model a chromosome as if it is confined inside a small volume.38, 39 This produces a reasonable agreement to experimental data but does not explain the origin of this confinement because it is put into the model “by hand.” Attempts to explain the leveling‐off on more physical grounds involve polymer models with loops.40, 41, 42 In fact, when plotting the mean‐squared distances determined from FISH measurements for longer genomic distances (up to 190 Mb) the data did not level off but lay on a straight line with a small slope.40 Data were then fitted by a fixed Mb giant loop model where the bases of the loops form a random walk on a larger scale.40 A loop model with excluded volume effects41 and with random loops42 (instead of loops of fixed sizes) also produced reasonable agreement with FISH data. However, strictly speaking, polymer models with loops do not really explain the leveling‐off observed in the data either. The problem is that such models are based on the artificial assumption that a given chromosome forms (temporary) crosslinks only to itself (thereby forming intrachromosomal loops). These contacts are assumed to occur over Mb distances. It is far from obvious how a given stretch of chromosome could distinguish between intra‐ and interchromosomal contacts, as chromosomes do not carry individual “markers” to distinguish them from each other. In that sense these early loop models also put in by hand what they want to find. A model that would allow for temporary crosslinking between all binding partners would behave effectively as a polymer solution where each polymer takes up a random walk conformation. There would be no leveling‐off or territory formation.

However, there is no doubt about the existence of interphase chromosome territories in mammals. In fact, beyond FISH data that show the juxtaposition of a handful of loci (Figure 6), whole individual chromosomes in interphase cells can be visualized.34 The development of a large collection of molecular tags that fluoresce in a rainbow of colors coupled with chromosome‐specific collections of DNA probes made it possible to visually identify individual condensed mitotic human chromosomes using fluorescence microscopy (Figure 7A). This technique, called chromosome painting, was also the technical breakthrough that led to the unambiguous visualization of individual chromosome territories in interphase nuclei (Figure 7C). The organization of chromosomes in territories greatly increases the likelihood of intrachromosomal contacts compared to interchromosomal contacts.

Figure 7.

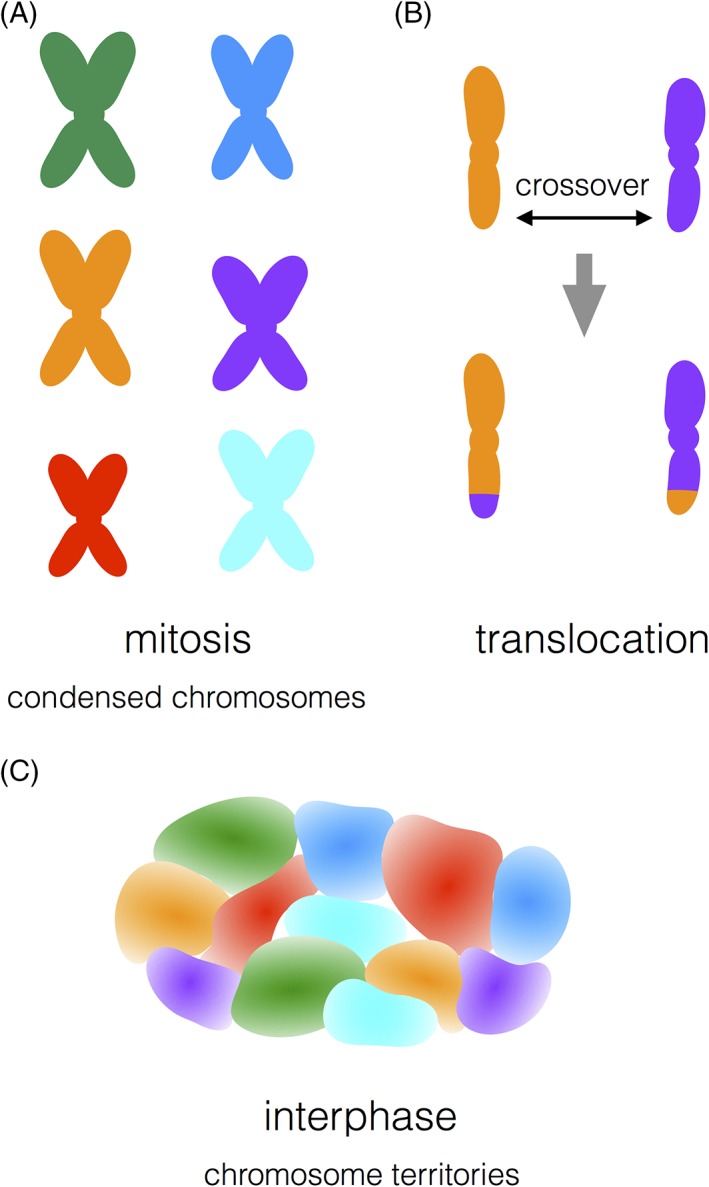
Chromosome painting identifies individual mitotic chromosomes, monitors chromosome translocations and maps chromosome territories. Chromosome painting is a technique in which chromosome‐specific fluorescently labeled DNA probes are hybridized to chromosomes and visualized using fluorescence microscopy. Chromosome painting identifies (A) individual mitotic chromosomes, (B) chromosome translocations that result from recombination crossovers between chromosomes and (C) decondensed interphase chromosome territories

3.2. How are chromosome territories established and maintained?

As explained earlier, the organization of chromosomes into territories is not consistent with standard polymer physics which predicts that polymers in dense solutions overlap. So what is the mechanism that causes the spatial segregation of chromosomes?

Consistent with Boveri's observation that the spatial position of each interphase chromosome territory corresponds to the site previously occupied by a single mitotic chromosome,12 chromosome territories may be the passive consequence of the decondensation of mitotic chromosomes at the positions they occupied in the nucleus at the end of the previous mitosis. Because each post‐mitotic human chromosome is highly compact and occupies a distinct position in the nucleus, as it begins to decondense in place, it occupies a discrete territory.

In fact, a mechanism of territory establishment based solely on the decondensation of mitotic chromosomes in place has been successfully modeled without invoking any interchromosomal DNA interactions.43 This computer simulation starts with dense, neatly folded polymers that mimic mitotic chromosomes and then lets them swell inside a container. The expanding chains eventually collide with each other and are then topologically hindered from further expansion. Remarkably, the configurations produced with this method resulted in plots for the spatial vs genomic distance that were strikingly similar to those from the FISH data presented in Reference 40 without having to assume any special architectural features like loops.

A crucial point made in this study relates to time scales: even though for very long times the collection of polymers will adopt the equilibrium state with strongly overlapping polymers, this is an extremely slow process. Each polymer is effectively trapped in a tube by surrounding chains (formed by other parts of the polymer itself and by other polymers) and can only explore new configurations by leaving its tube through a snake‐like motion at its two ends. This reptation process is extremely slow, roughly increasing with the cube of the chain length.1 In Reference 43 it was estimated that human chromosomes are so long that their equilibration would take about 500 years whereas yeast chromosomes are short enough to equilibrate within a few hours. Even though these are very rough estimates, they point toward the fact that for large chromosomes the system cannot reach equilibrium on any biologically relevant time scale. In fact, if there were an infinite amount of time available for them to reorganize, there would be no chromosome territories in interphase cells. Although there is not enough time for large chromosomes to mix, we discuss in the following section the extent to which chromosome territories are insulated from one another.

3.3. Are chromosome territories completely self‐contained?

Although chromosome painting revealed distinct chromosome territories in human cells (Figure 7C), its ability to visualize sharp territory edges is variable and sensitive to the parameters of image analysis (reviewed in Reference 44), leaving open the possibility of physical interactions between chromosomes at territory edges. In fact, there is now ample evidence of physical contact and mixing between territories45: the juxtaposition of chromosome stretches or specific gene pairs from different chromosomes can facilitate chromosomal translocations associated with inherited genetic defects (Figure 7B),46 regions from multiple chromosomes associate within separate heterochromatic and euchromatic compartments5 or in transcriptional hubs of co‐regulated genes,47, 48 reviewed in Reference 49; genes transiently relocalize out of their territory when transcriptionally activated44, 50; telomeres are localized near the nuclear periphery; and a recent single cell Hi‐C study estimates an approximately 15% mixing frequency between chromosomes.51 Taken together these data indicate that chromosome territories are not completely self‐contained.

4. Hi‐C, FRACTAL GLOBULES AND RING SOLUTIONS

4.1. Hi‐C at 1‐Mb resolution and the fractal globule

Hi‐C experiments give much more detailed information about the conformations of chromosomes than FISH data. Whereas FISH data provide, in a given experiment, the spatial distance between just a few loci, Hi‐C data give simultaneous information about millions of pairs of loci that happen to be close in space.5 The renowned polymer theorist Alexander Grosberg calls it “the type of information a polymer physicist could only dream of.”52 The trick in chromosome conformation capture experiments is to covalently link chromosomes in situ (with formaldehyde), cut the genome into small pieces (with a restriction enzyme), perform intramolecular ligation (to permanently link the crosslinked DNA fragments), remove the crosslinks, and finally determine which DNA stretches have been ligated (via massively parallel DNA sequencing). This allows the construction of a genome‐wide contact matrix (Figure 8).18 It is important to note that such contact maps do not indicate the position of a given DNA stretch in space, that is, its 3D location inside the nucleus. Instead it gives information about which parts of the genome are close in space to each other. This is captured by the contact probability between pairs of loci. This probability is simply proportional to the number of ligation products between a given pair of loci. Dependent on the resolution of the experiment loci can be relatively large, for example, in Reference 5 each locus corresponds to a 1‐Mb long region. Because the whole human genome sequence is known, the contact probability at each point along the heteropolymer of DNA can be determined. This is impossible in the case of a homopolymer. Hence it is the “polymer physicist's dream.”

Figure 8.

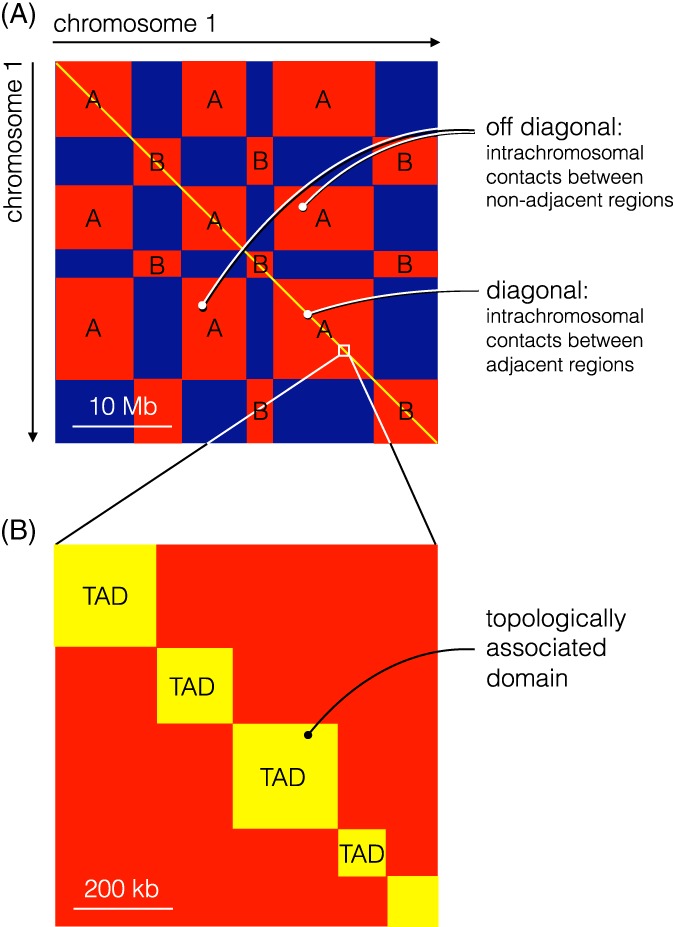
Schematic chromosome contact map of a chromosome (“chromosome 1”) at 2 levels of resolution. (A) Hi‐C data at low resolution (eg, 1 Mb resolution) display a checkerboard pattern with regions of higher probability of contact (red) and lower probability of contact (blue). This suggests the existence of 2 types of compartments, A and B, as indicated. (B) Hi‐C at higher resolution (eg, 1 kb) makes it possible to zoom in on the diagonal and reveal topologically associated domains (TADs; yellow squares) with a high probability of intradomain contact (yellow) that are physically insulated from the rest of the chromosome7

Hi‐C data taught us that the conformations of chromosomes are incompatible with what we know about equilibrium polymer statistics, that is, the set of conformations that one would expect a polymer to adopt given enough time for it to relax from any given initial configuration. On one hand, contact probabilities between loci on the same chromosome are always higher than between loci on different chromosomes, showing that chromosomes are segregated into chromosome territories, something that was already known from the FISH data and chromosome painting as discussed earlier (Figures 6 and 7C). New and surprising information was gained concerning the spatial organization of interphase chromosomes within a territory. Specifically, Hi‐C data allowed determination of the probability of spatial contact of 2 loci (on the same chromosome) as a function of their genomic distance g along the DNA molecule. It was observed that this probability decreases for human interphase chromosomes as 1/g in the range ~500 kb to ~7 Mb.5 As we explain now, this mathematical relation is not compatible with the random walk statistics that were claimed to be observed in the FISH experiments.37

Why is the 1/g‐law in the contact probability inconsistent with the earlier claims? We discussed earlier that the typical spatial distance inside an ideal polymer stretch of length g scales like g ^1/2, see Figure 5B. This means that this chain portion occupies a typical volume that scales like g ^3/2. This suggests that 2 loci at a genomic distance g apart will find themselves close in space with a chance 1/g ^3/2 and not 1/g as found by Hi‐C. Other known equilibrium polymer models also do not produce the 1/g‐law in the contact probability. How can this discrepancy be resolved? Since DNA molecules inside chromosomes are polymers but no known equilibrium polymer model accounts for their behavior we are led to conclude that chromosomal DNA is not in equilibrium.

Remarkably, this was proposed long ago by Grosberg et al.53, 54 They speculated that as a result of its extreme length a DNA molecule in equilibrium is so hopelessly entangled that it would be of no use as a carrier of genetic information. They proposed that DNA is somehow hierarchically folded to avoid this kind of topological trouble. In the lab, such a neat state could be achieved by starting with a swollen polymer and letting it collapse by switching on an attraction between its monomers (which can be achieved by a sudden change in temperature). Because the “open” polymer coil was not very entangled in the first place and the collapse was fast, it is still largely unentangled in the collapsed state. Moreover, the “topologically unentangled” state remains unentangled for a very long time because any internal polymer stretch is surrounded by other stretches of the same polymer (which are typically far from that stretch along the backbone), trapping it inside an effective tube out of which it can only slowly escape via reptation.

Note that the collapse described above is not necessarily meant to reflect an actual biological process but provides a way to think about how an unentangled compact polymer state might look. It was suggested that during its collapse a polymer crumples in a hierarchical fashion where smaller collapsed stretches combine sequentially with other smaller collapsed stretches nearby to form larger units and so on. This leads to a crumpled or fractal globule (see Figure 3), a space‐filling configuration that is self‐similar on all scales: meaning that small crumples close by along the chain form larger crumples which form yet larger crumples with their neighbors all of which have the same structure. As space is filled up progressively by crumples, the volume of a stretch of g monomers is proportional to g and the contact probability decays like 1/g, as suggested by the Hi‐C data.5 The authors of this paper were aware of Grosberg's idea and claimed accordingly that they had found the fractal globule state of chromosomes. Hi‐C data thus suggested that the conformations of DNA molecules are nonequilibrium conformations and, moreover, that these configurations are unentangled making them manageable for the cellular machinery.

However, even though the idea is very appealing because of its simplicity, things are not as straightforward. The authors of Reference 5 supplied computer simulations of collapsing polymers to support their idea and also looked at idealized mathematical space‐filling self‐similar curves. But neither computer simulations nor mathematical models easily render the 1/g relation in contact probability. The computer simulation had to be run under rather extreme (nonbiological) conditions and the mathematical models needed to assume strong interdigitation of the different crumples to obtain this value (a whole family of such highly artificial mathematical curves with various exponents has been presented in the meantime55). Other computer simulations could either not recapture the 1/g decrease in the contact probability56 or found it only for very long chains in very poor solvent conditions,57 suggesting that the crumpled globule does not quite capture the actual polymer state of chromosomes.

Also, it is not clear what the simulated polymer collapse has to do with any biological process. If anything, it has to be considered as a computational tool to obtain unentangled configurations. A different view that does not have to rely on such a rather arbitrary assumption has emerged recently from a consideration of the role that the chromosome ends play (or rather, as we shall see, do not play) in shaping the conformations of interphase chromosomes. We first discuss chain ends in their biological context and then turn to the surprising idea of how to consider them from the polymer physics perspective.

4.2. Interphase chromosome entangling

Two linear chromosomes can become entangled in the nucleus if a free chromosome end moves by reptation, as it is following the restricted path of a hollow tube through surrounding chromosome polymers. Possible sources of such ends in a cellular context are the natural telomeric end of a chromosome arm or the 2 broken ends generated by a DNA double‐strand break.

The telomeric ends of human chromosomes are not buried within chromosome territories. They are protected by end‐binding specific proteins and often tethered to the proteinaceous nuclear lamina that underlies the nuclear envelope in interphase human cells. Potentially lethal double strand breaks, which could cause partial or complete chromosome loss, are also rapidly recognized by end‐binding proteins that sense DNA damage, anchor the two ends to one another, and initiate repair.58, 59

However, even if free ends did exist, it is unlikely that they would cause chromosome intermingling or broadly impact chromosome territory organization because polymer physics tells us that it would take a nonphysiological amount of time for a chromosome end to become entangled with another chromosome.43 This led to the idea that chain ends do not need to be considered if one wants to understand their behavior from a theoretical point of view as we explain in the following section.

4.3. Solutions of nonconcatenated polymer rings

We discussed earlier, several polymer models for chromosomes assume that their configurations do not have enough time to reach equilibrium. These kinds of models have the disadvantage that these predicted configurations depend on the somewhat arbitrarily chosen starting configuration. It is not clear why one would start the simulations in Reference 5 from a swollen polymer coil or from a “generalized helix” (mimicking the dimension of mitotic chromosomes) in Reference 43. All this goes against the physicist's instinct to have a model that is of general validity.

A big step forward was the realization in Reference 43 that the configurations of a set of interphase chromosomes (or the configurations of the nonequilibrated polymer configurations in that very paper) should share strong similarities with an entirely different polymer system in equilibrium: a solution of nonconcatenated polymer rings. After a chromosome has expanded, it is essentially trapped in a tube‐like region following the chain contour and can only leave this particular topological state through reptation.1 As this process toward equilibrium is very slow, one might neglect the presence of the polymer ends altogether and close each polymer into a ring. As the chains were initially separated from each other (real mitotic chromosomes or the ones in simulations like Reference 43) these rings are nonconcatenated. Therefore, interphase chromosomes that are trapped in such topological states for a very long time (like human chromosomes) should show conformations similar to nonconcatenated rings in solution at equilibrium.

This stimulated research focused on understanding the behavior of polymer ring solutions via computer simulations60, 61, 62, 63, 64 and theoretical approaches.65, 66 This is still an ongoing field and the behavior of ring polymers is not yet fully understood. However, large‐scale computer simulations of solutions of nonconcatenated polymer rings show features that are substantially different from solutions of linear polymers.60 Notably, rings under these conditions show an overall compact structure, that is, an overall size that scales like N ^1/3. Importantly, the structure of these rings is self‐similar on all length scales, that is, a stretch of g monomers has a size that scales like g ^1/3. Again one has crumples within crumples akin to the crumpled globule mentioned above. Also the contact probability between monomers decreases with genomic distance as 1/g ^1.1 60 ^, 63 which is compatible with Hi‐C data.5 In addition, since rings are compact objects they segregate from one another, consistent with the existence of chromosomal territories and in sharp contrast to the behavior of linear polymers. However, the situation is not perfectly straightforward, for example, substantial interpenetration between rings leading to only partial segregation was observed in the simulations.

We conclude this section by stressing again the surprising idea that equilibrium polymer physics of ring polymers can teach us something about nonequilibrium polymer physics of linear polymers, the latter reflecting how chromosomes behave in the nucleus. Interestingly, this does not apply to budding yeast where the chromosomes are so short that they should have time to equilibrate. In fact, its chromosomes appear to mix.67

5. EUCHROMATIN AND HETEROCHROMATIN

5.1. Spatial distribution of euchromatin and heterochromatin in the nucleus

Chromosomes are heterogeneous consisting of blocks of euchromatin and heterochromatin that are interspersed among individual linear human chromosomes. This has important consequences for the spatial organization in which euchromatin and heterochromatin are enriched in separate compartments within each chromosome territory and within the volume of the nucleus5, 51, 68, 69 (Figure 1). We start with the overall organization of the nucleus where active euchromatin is typically enriched at the center and inactive heterochromatin is concentrated at the periphery of the nucleus.

Based in part on its unique physical and chemical properties, including its high refractive index, compact heterochromatin abutting the nuclear envelope was visualized many decades ago using electron and light microscopy and confirmed more recently using a variety of state‐of‐the‐art approaches.68 For example, specific DNA domains called LADs (lamin‐associated domains) that are tethered to the nuclear periphery have been identified.68

The organizational pattern at the nuclear envelope depends on a complex of proteins collectively called the nuclear lamina (Figure 1), that constitutes the nuclear skeleton underlying the inner nuclear envelope in humans and other metazoans.21 Among its many functions, the lamina is a docking site for heterochromatin at the nuclear periphery. The lamina (reviewed in Reference 69), consists of the intermediate filament lamin proteins Lamin A/C and Lamin B1 and B2, LAPs, the lamin B receptor (LBR), LEM (Lap2/Emerin/Man) family proteins and other nuclear envelope associated proteins. Independent disruption of the function of various lamina components results in altered gene transcription profiles, loss of peripheral heterochromatin and a variety of human diseases that are collectively called laminopathies.

The enrichment of heterochromatin at the nuclear periphery is evolutionarily conserved but not universal, and the exceptions shed light on the functional significance of this organizational plan70: strikingly, euchromatin is peripheral, and heterochromatin is central in the nuclei of rod retinal cells in adult nocturnal animals.4 This developmentally regulated nuclear reorganization occurs as embryonic stem cells differentiate into rod cells, and because heterochromatin has a higher refractive index than euchromatin, its central localization helps light to reach photoreceptors by acting as a collecting lens. This developmental switch is attributed to changes in the Lamin A/C and/or the LBR components of the nuclear lamina that are present in almost all differentiated mouse cell types except the rod cells, which lack one or both of these proteins.4, 70, 71 Consistent with these findings, several mammals that independently evolved from a nocturnal to a diurnal life style concomitantly regained high levels of Lamin A/C and/or LBR in their rod cells.71 The loss of the LBR protein in mouse olfactory neuron nuclei also correlates with a developmentally regulated cell‐type specific relocalization of transcriptionally inactive genes on several different chromosomes from the periphery to the interior of the nucleus.72

The spatial segregation of euchromatin and heterochromatin is also related to the positioning of whole chromosomes within the nucleus. Chromosome painting not only demonstrated that each chromosome occupies a distinct territory but also mapped their positions relative to other chromosomes and nuclear landmarks.44 Within a population of human cells, smaller chromosomes are consistently localized in the center of the nucleus, whereas larger chromosomes are peripheral. However, it is not yet clear whether chromosome size determines this radial positioning, since large chromosome size, low euchromatin content, low gene density and low transcriptional activity are all correlated with one another.44 The relationship between chromosome size and position is not universal (reviewed in Reference 73), and is most consistently observed in cells with flattened nuclei74 suggesting that territory organization can be influenced by nuclear shape.

There are several theoretical studies devoted to the question of what causes the preferences observed in the radial positioning of chromosomes within a nucleus. Computer simulations presented in Reference 75 support the idea that non‐specific entropic forces might be sufficient to explain these positional preferences. When 2 different types of polymers are enclosed in a compartment, they typically segregate from one another. For instance, in a mix of compact and swollen chains, the compact ones (“heterochromatin”) localize closer to the wall than the swollen ones (“euchromatin”). In Reference 73 another possible effect is suggested, namely the presence of active processes (see also References 76, 77, 78). Simulating a compartment in which different polymers have different temperatures, they found that the “hotter” polymers (“euchromatin”) move preferentially toward the center. So both simulations produce the most commonly observed in vivo positioning. However, as mentioned earlier, this nuclear architecture relies on docking of heterochromatin to the nuclear periphery. Models that predict this in vivo organizational pattern include a dynamic loop model,79 a pulsating container model with polymers of different mobility80 and an active chromatin brush model.81 It is, however, fair to say that these various explanations point toward the fact that the overall nuclear organization of heterochromatin and euchromatin might result from multiple effects, which are hard to disentangle from each other.

5.2. The organization of euchromatin and heterochromatin within chromosome territories

Hi‐C analysis5, 7, 51 detected 2 sets of genomic loci that have a higher probability of contact with other loci of the same type than with loci of the opposite type, leading to a “checkerboard” pattern in the contact matrix, see Figure 8A. Further characterization revealed that the A (active) compartment corresponds to euchromatin and the B (inactive) compartment has the characteristics of heterochromatin. The observation that the A and B compartments are comprised of DNA from more than 1 chromosome is consistent with the emergence of transcriptionally activated chromatin from the edges of chromosome territories.44, 50 Although chromatin polymers do not have the time to mix on the length scale of the full polymer,43 these high‐resolution data indicate that there is enough time for segments from multiple chromosomes to associate in separate compartments. The spatial segregation of euchromatin and heterochromatin into separate A and B compartments in the nucleus is consistent with the known positioning of these 2 chromatin types between the interior and periphery of the nucleus, respectively. However, the spatial position of the A and B compartments with respect to the nuclear envelope cannot be directly determined from the contact probability data upon which they were defined. Recently, however, a highly reproducible reconstruction of the spatial structure of the whole genome of individual cells has been demonstrated based on single‐cell Hi‐C,51 an innovative single‐cell non‐Hi‐C, nonligation‐based approach called GAM (genome architecture mapping),82 and a reconstruction based on a population average.83 These structures are consistent with the previous data documenting the distribution of A and B compartments.

The division of chromatin into A and B compartments has a well‐known analogue in standard polymer physics, namely the microphase separation of block copolymers.84 In a solution of polymers which are made of blocks of A and B monomers that do not mix, each type of monomer aggregates with other monomers of the same type. Unlike the demixing of small molecules (like oil and water) this type of demixing cannot occur on a macroscopic scale since A and B blocks are connected into polymers. In this case, only smaller domains enriched with one or the other type of monomer can form, resulting in what is termed microphase separation. This is highly consistent with what has been seen for chromosomes in the nucleus. In fact, it is possible to construct copolymers that mimic the contact maps of actual genomes, as demonstrated in Reference 85. However, the fact that chromosomes in the nucleus reside in their own territories is most likely the result of the system not having reached equilibrium, as explained earlier, and thus goes beyond what is usually considered when studying microphase separation of copolymers.

6. CHROMOSOME LOOPS

So far, we have mainly spoken of contacts between different sections of DNA molecules in general. Here we look more specifically at DNA loops which are structures that are “generated by a protein or complex of proteins that simultaneously binds to 2 different sites on a DNA molecule.”86 The human genome is organized into tens of thousands of such chromosome loops that impact a plethora of cellular functions (Figure 9). Loops reduce the spatial distance of DNA elements relative to their genomic distance, physically sequester and functionally insulate stretches of DNA from the rest of the genome, and bring into juxtaposition at the base of the loop DNA‐bound proteins whose physical proximity is essential for their function. The size, distribution and stability of individual or compressed arrays of loops influence higher‐order chromosome organization: interphase chromosome compaction, mitotic chromosome condensation, centromere organization, sister chromatid individualization and separation.9, 92, 93, 94

Figure 9.

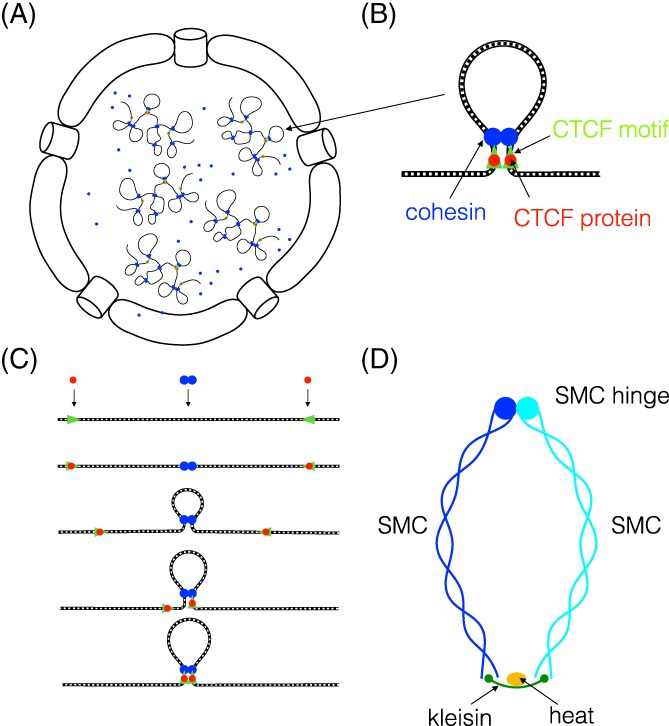
The loop extrusion model of interphase chromosome organization. (A) Decondensed interphase chromosomes territories within which the DNA is organized into loopy globules composed of topologically associated domain loops. (B) In humans and other bilaterians, cohesin (blue) and CTCF proteins (red) bound to convergent CTCF binding sites (green) localize at the base of TAD loops.87 (C) According to the loop extrusion model, 2 linked cohesins (or possibly a single cohesin) associate with DNA, form and enlarge a DNA loop until they encounter CTCF proteins bound to convergent CTCF binding motifs. Note that alternative models have been proposed and there is no known mechanism by which SMC family proteins form and enlarge chromosome loops.88, 89 Whether cohesin binds as a single complex or 2 linked complexes and the mechanism by which cohesin associates with and then dissociates from DNA are also unknown.90 (d) SMC protein complexes in eukaryotes (cohesin, condensin, SMC5/6) and prokaryotes are tripartite ring‐shaped ATPases, composed of 2 SMC proteins, (light blue, dark blue), and a Kleisin linker protein (green) that joins their head domains and assembles the nucleotide binding domain, and to which one of a family of HEAT protein regulators (yellow) bind.91 Although they share a common architecture, these complexes vary in composition (SMCs are heterodimers in eukaryotes but homodimers in prokaryotes) and biological function, which may be influenced by the Kleisin subunit and/or the Kleisin‐associated HEAT‐family regulatory component91

Although the mechanistic details of loop formation and organization are still emerging, it has been known for decades from electron micrographs that there are loops at the surface of mitotic human chromosomes.86, 95, 96, 97, 98 Chromosome looping rather than folding is also consistent with early FISH99 and more recent Hi‐C analysis9 showing that genes maintain their interphase linear order during chromosome condensation in mitosis, which is brought about by linear compaction of an array of chromosome loops.

Chromosome looping is also the basis of centromeric chromatin organization, the chromosome individualization process whereby the 2 condensed chromatids disentangle and partially disengage from one another and centromere separation that then allows the mitotic spindle to pull them apart.93

In fact, recent evidence suggests that it is the loop extrusion mechanism that is responsible for the compaction and individualization process leading to the mitotic chromosome state. This mechanism also seems to account for the TADs (topologically associated domains) that organize interphase chromosomes (Figure 8B). We first present an overview over TADs in the next section before discussing the role of the loop extrusion mechanism in organizing mitotic and interphase chromosomes.

6.1. Hi‐C at 1‐kb resolution: the discovery of TADs

Increasing the resolution of Hi‐C contact maps from 1 Mb to 1 kb led to a surprising finding.7 TADs (or contact domains) with a median length of 185 kb appeared in the data, see Figure 8B. These show up as squares of high contact probability along the diagonal of the contact map (whereas the A and B compartments of euchromatin and heterochromatin appear as a checkerboard pattern, Figure 8A), reflecting their physical insulation from the flanking DNA.

TADs are clearly related to looping: About 10 000 peak loci (anchor points at the base of chromatin loops that are seen as high contact probability peaks in the contact matrix off the diagonal) were observed; 98% correspond to loops between loci less than 2 Mb apart. Peaks are well conserved between different human cells and cell types and even across species. A vast majority of peak loci are bound by the insulator protein CTCF and cohesin subunits (Figure 9B). The consensus sequence for a CTCF binding site is 5′‐CCACNAGGTGGCAG‐5′ which is nonpalindromic. It is therefore possible to conclude that the 2 CTCF sites corresponding to peak loci are overwhelmingly found in the convergent orientation but raises the question of how the relative orientation of 2 CTCF sites a large distance apart along the DNA molecule is recognized.

6.2. The role of TADs in gene regulation: the physical pairing of gene promoters and regulators

Gene regulation depends on the spatial proximity of promoters and their regulatory elements that might be separated by thousands to tens of thousands of nucleotides in humans, and chromosome looping has long been predicted to play a critical role in this process.86, 100 Promoter elements direct transcription of the coding regions of adjacent genes by providing a binding site for transcription factors, RNA polymerase, and other regulatory proteins. Promoters can also physically interact with regulatory regions, such as enhancers, repressors and insulators, which modulate their activity,49 reviewed in References 94, 100, 101.

However, it was not clear how enhancers pair in the proper orientation with their target promoters, while avoiding incorrect intra‐ or interchromosomal interactions. Because of the high contact probability within chromosome territories, particularly within TADs, enhancers most often interact with nearby genes (reviewed in References 3, 19). However, the looping mechanism must also account for more complex situations in which 1 gene has multiple enhancers or multiple genes compete for the same enhancer.94

6.3. Loop extrusion: a proposed mechanism for precise formation and positioning of intrachromosomal loops

Chromosome loops may be formed and stabilized by a common loop extrusion mechanism4, 6, 14, 15, 102 (Figure 9C). The loop extrusion model for human cells has at its core two previously well‐characterized components, the cohesin complex, and the CTCF protein, and predicts how they contribute to the generation and stabilization of chromosome loops although many details are still unknown90, 103, 104, 105 (Figure 9). In its simplest form, the loop extrusion model proposes that the cohesin complex binds 2 sites on the chromosome, extrudes a loop of DNA between them and then translocates in opposite directions along the DNA while bridging these increasingly distant chromosomal sites, thereby increasing the size of the loop.16 According to the model, the spooling of DNA into the loop continues until cohesin encounters CTCF proteins bound to flanking, convergently arranged CTCF DNA motifs which block further extrusion.

Therefore, CTCF binding sites dictate loop size by blocking loop extrusion and anchoring and stabilizing the base of the loop at that position in the genome by means of its interaction with cohesin. Deleting, mutating or changing the relative orientation of the CTCF binding sites in the genome changes the DNA contact domains and thereby alters in a predictable manner loop size and organization in vivo.6, 106

6.4. The role of the cohesin complex in loop extrusion

Cohesin is a V‐shaped heteroduplex of 2 structural maintenance of chromosomes (SMC)‐family coiled‐coil proteins, joined at 1 end via their hinge domains and bridged at their other ends by the kleisin protein that stabilizes the closed ring structure and assembles 2 functional ATP‐binding domains90 (Figure 9D). Cohesin's architectural organization and subunit structures are closely related to those of the chromosome condensation complex named condensin and other SMC complexes91 (see Figure 9D), but they have no common subunits. Although the DNA loops formed by cohesin and condensin serve different cellular purposes, they are both predicted to be generated by the loop extrusion mechanism.14

Cohesin was discovered and is best characterized in the budding yeast S. cerevisiae, for its role in holding sister chromatids together during mitosis until they are properly aligned and captured by the mitotic spindle and only then releasing them to allow for their segregation,90 Figure 2B. This function of cohesin may have evolved more recently than its role in loop formation.91

Deciphering the details of cohesin function has been challenging90 and is likely to be more complex than early models in which a cohesin ring was proposed to hold 2 DNA strands together by encircling them.90

6.5. Loop extrusion: history and relation to polymer physics

The history behind loop extrusion and how this mechanism relates to polymer physics are closely related. It started with the realization that the spontaneous segregation of intertwined pairs of identical DNA molecules after duplication (to form the mitotic chromosome) is far from trivial. It is known that 2 overlapping polymers feel only a repulsion on the order of the thermal energy, no matter how long they are.107 This energy scale is too small to drive them apart. An active process involving molecular motors is needed. But how can such motors distinguish between 2 identical DNA molecules to pull them apart? This occurs only later when the 2 sister chromatids are separated by the spindle apparatus (Figure 2B) but then the 2 DNA copies are already separated into the 2 halves of the mitotic chromosome. But how did the system get to the point of 2 well‐separated sister chromatids in the first place?

In 2001, the yeast geneticist Kim Nasmyth came up with an elegant solution to this conundrum.108 He suggested that chromosome segregation could be achieved by condensins that act as processive motors that act locally: “One possibility is that condensin associates with the bases of small loops or coils of chromatin and enlarges these loops or coils in a processive manner, which ensures that all chromatin within the loop or coil must have been cleanly segregated from all other sequences in the genome.”

Independently, physicists invented “hypothetical DNA‐loop‐extruding enzyme machines” a few years later.102 This proposed mechanism also started with the realization that “random formation of polymer loops is not by itself likely to be the main mechanism underlying the spatial organization of chromosomes.” In this theoretical study, the role of protein processivity and dissociation was studied on a short DNA molecule, focusing on the distribution of machines along the chain (without studying the ensuing 3D structure), see also Reference 16 for simulations for a long DNA molecule.

Nasmyth's idea108 was finally tested in a large‐scale polymer simulation.15 Two intertwined polymers (held together at the middle) were simulated. The polymer segregated through loop extrusion if chain crossing was also allowed (mimicking the presence of topoisomerase II). Two well‐segregated compact but elongated chromosomal bodies were formed and held together at the middle, in striking resemblance to the X‐shaped configurations of mitotic chromosomes held together by centromeric cohesin. In addition, the loop extruders at the loop bases formed an elongated core in the middle of the chromosomes, in agreement with the pattern of condensin localization on mitotic chromosomes.109, 110

The driving force for the stiffening of the chromosomal bodies and, most importantly, the separation of the sister chromatids is the entropic repulsion between the nonconcatenated loops. This constitutes a remarkable connection between loop extrusion and chromosomal territories.111 Also the existence of chromosomal territories can be understood by its similarity to solutions of nonconcatenated polymer rings (as discussed earlier). In both cases the spatial separation is caused by the same topological effect.

Similarly for interphase chromosomes the formation of nonconcatenated loops by loop extrusion machines seems to hold the key to understand the surprising finding of TADs with 2 CTCF sites in convergent orientation at their base (Figure 9). In Reference 6, polymer simulations were presented with condensing polymers, extrusion complexes and orientated “anchor polymers” that stop the extrusion complex. That model fits well with both Hi‐C and FISH data. Loop anchors create “cliques” of loops. Systematically erasing loop anchors in the simulations changes the size and position of TADs as expected and confirmed in experiments in which genome editing was used to change the sequence and orientation of CTCF motifs. A systematic simulation study of the effect of the loop extrusion mechanism on contact matrices was performed in Reference 14. The best agreement with Hi‐C data was found for loop‐extruding factors separated on average by about 120 kb with similar processivity. This leads to the dynamical formation of loops of various sizes within a domain and an approximately 2‐fold increase in contact probability.

What kind of system represents a loopy globule? It is not a system at equilibrium, as energy is constantly pumped into it via the loop extrusion machinery. It is also not trapped in a metastable state as is the case for the crumpled or fractal globule. Instead it is, after a short initial time, in a stationary state, that is, in a state where all the quantities on average are constant. Details of the polymer physics of these loopy globules have yet to be studied in detail.

6.6. The loop extrusion model overview: unanswered questions

The loop extrusion model originally proposed by Nasmyth108 and elaborated by Alipour and Marko,102 Lieberman Aiden and coworkers6 and Mirny and coworkers14 is consistent with experimental findings.6, 7 The model ensures that cohesin acts on contiguous DNA segments, generates nonoverlapping and nonknitted loops, and avoids interchromosomal entanglement.

However, the properties of cohesin necessary to orchestrate loop extrusion and the mechanism by which CTCF dictates loop boundaries have not been determined.90, 103 Many questions remain about the conformation of DNA‐bound cohesin, how it holds sister chromatids together in mitosis and then releases them at a precise point in mitosis and how it dynamically associates with chromosomes to generate chromosome loops.90, 103 Other outstanding questions include whether DNA strands are encircled by the cohesin ring or are captured by a different conformation of the complex, whether 1 or multiple DNA strands are entrapped in a single cohesin complex, and whether the functional form of cohesin is a monomer, homoduplex or multimeric array.90, 103 Despite several recent studies87, 88, 112, 113 the mechanism by which cohesin and other SMC complexes translocate along DNA also remains relatively uncharacterized. The conformational dynamics by which cohesin binds and then releases the DNA and the mechanism or mechanisms by which it both holds sister chromatids together in mitosis and bridges chromosomal sites that are spatially distant in the genome are also unknown.

7. DO THE PRINCIPLES OF CHROMOSOME ORGANIZATION, SO WELL‐DOCUMENTED IN HUMAN CELLS, ALSO GOVERN NUCLEAR ORGANIZATION THROUGHOUT THE TREE OF LIFE?

Based on the currently available evidence, there is general agreement that chromosomes are organized into self‐interacting loops and compartments that are structurally, epigenetically and/or functionally distinct. It is also clear that the underlying mechanisms by which these topologies are formed and stabilized rely on both evolutionary conserved and organism‐specific proteins. However, it is challenging to address the broad question of whether the principles of human chromosome organization are universal in part because direct comparisons are complicated by organism‐specific differences in chromosome organization and information is lacking about some or all aspects of nuclear organization in most species. Given these caveats, we will use specific examples to address questions about the evolution and evolutionary conservation of the proteins that shape and organize genomes and the mechanisms by which they carry out these functions. For comprehensive reviews, readers are referred to several informative articles.3, 87, 90, 91, 114, 115

7.1. Chromosome territories

Chromosome territories are an evolutionarily conserved feature in metazoans but in other organisms whether they exist depends in part on how territories are defined.

As first described in interphase (nonmitotic) animal cells, each decondensed chromosome is organized into a territory that occupies a distinct portion of the nuclear volume (see Figure 7C). High‐resolution data from chromosome conformation capture and other methods made it possible to refine this definition to include a significantly increased likelihood of intrachromosomal vs interchromosomal contacts within individual whole chromosomes.

According to this definition, neither the fission yeast S. pombe nor the budding yeast S. cerevisiae has chromosome territories, although the term has been used to describe various aspects of their chromosomal structure. In many organisms, nuclear organization is constrained by the Rabl conformation in which centromeres and telomeres localize to opposite sides of the nucleus (Figure 2B). In yeast, this reflects the facts that all centromeres are clustered at the spindle pole body (centrosome equivalent) embedded in the nuclear envelope and telomere clusters are tethered at the membrane on the opposite side of the nucleus.116, 117, 118 This configuration results in an alignment of chromosome arms and increased intrachromosomal contacts that are more frequent near centromeres and to a lesser extent near telomeres, and on this basis have sometimes been referred to as territories.119, 120, 121, 122, 123, 124, 125

In addition, it is important to stress the fact that the yeast chromosomes are much smaller than human chromosomes. As mentioned earlier, unlike for yeast cells, the equilibration time of human chromosomes is many orders of magnitude longer than the cell cycle43 which does not allow for mixing of chromosomes. This suggests that chromosome territories might have occurred in organisms once their chromosomes had evolved to sizes too large for their equilibration on biologically relevant time scales.

7.2. Euchromatin and heterochromatin

Many eukaryotes have both heterochromatin and euchromatin that are separately partitioned into compartments (Figure 8A). Human and other metazoan genomes are composed of large blocks of interspersed transcriptionally active euchromatin and inactive heterochromatin, whereas the compact genome of the fission yeast S. pombe is 95% euchromatic with heterochromatin concentrated primarily at the centromeres, telomeres, rDNA and mating type loci.117 In both cases, euchromatin and heterochromatin self‐interact and physically segregate within the nucleus into peripheral heterochromatin and central euchromatin (Figure 1). This general organizational scheme has been observed in most eukaryotes, although these distinct intranuclear localizations are established and maintained by different mechanisms in different species.

In fission and budding yeast, the localization of heterochromatin at the nuclear periphery is due in large part to the Rabl orientation in which heterochromatic centromeres are anchored to the spindle pole body by microtubules, and heterochromatic telomeres are tethered at the nuclear envelope by telomere‐binding proteins and their interaction partners in the nuclear pore complex or the nuclear membrane.

Nuclear lamins anchor heterochromatin to the nuclear periphery in metazoan cells and were long thought to be absent from yeast, land plants, and several other organisms with peripheral heterochromatin, because clear sequence orthologs could not be identified in their genomes. However, we now know that lamins are ancient proteins that were present in the last eukaryotic common ancestor (LECA). Despite significant sequence divergence, lamin orthologs have now been identified in 12 eukaryotic lineages that include the land plant Arabidopsis and the amoeba Dictyostelium. Lamins were secondarily lost from the fungal lineage, however, in the budding yeast S. cerevisiae, a protein with structural but not clear sequence similarity to lamin plays an analogous role.126, 127

7.3. TADs and chromosome looping

Are TADs with CTCF and cohesin at their bases the basic organizational unit of chromosomes? Chromosome loops are a feature of all characterized organisms, but the answer to this specific question is no because although SMC‐protein complexes (see Figure 9), including cohesin, are ubiquitous, CTCF is not. This could mean that: in some organisms another protein plays the role of CTCF in cohesin localization and loop formation; cohesion is positioned by a different mechanism; or TAD loops do not play a role in transcriptional regulation.128, 129, 130

SMC protein complexes were present in LECA91, 115 and are universal key regulators of chromosome shape and topology.89, 91, 108 In contrast, the CTCF protein131 is present only in animals with bilateral symmetry (bilaterians) such as vertebrates, arthropods and mollusks.87 These organisms have a high proportion of promoters that are regulated by distant cis‐regulators brought into contact by cohesin and CTCF‐dependent TAD loop formation.132, 133

Changing CTCF binding sites influences the size and distribution of TADs which, like mutations in the cohesin protein, has been associated with a variety of human diseases including cancer.134 The TAD organization of transcriptional units has a profound influence on their evolution. The modular organization of transcriptional units in TADS and the ability of a single mutational event to change TAD borders and facilitate promoter pairing with newly evolved cis‐regulatory elements can drive the evolution of gene expression.114

Humans have a single CTCF insulator protein131 but Drosophila has CTCF plus 10 more recently derived DNA‐binding insulator proteins. However, there is no evidence that CTCF localizes to TAD loop anchors in this organism, suggesting that these loops may be formed by a mechanism that differs from that of other metazoans.3, 114, 135

Nematode worms provide an example of the relationship between the CTCF protein and the organization of transcriptional units.136 Basal organisms of the nematode lineage have cohesin, CTCF and promoters with distal cis‐regulators. CTCF was lost during evolution in the lineage of C. elegans and other derived nematodes. In these organisms there is no evidence of cohesin‐dependent TADs, and many genes are organized into operons in which a single promoter regulates the transcription of a group of adjacent genes.

In S. pombe, S. cerevisiae and other fungi that do not have CTCF, cis‐regulatory regions are adjacent to the promoters they regulate. In S. pombe, chromosomes are organized into “globules” or “crumples”137 and in S. cerevisiae into “self‐associating domains”138 that depend on the cohesin complex, but there is no evidence that either of these structures influence transcription. These structures are even sometimes referred to as TADs,117 although they are not loops.138

In stark contrast to eukaryotes, prokaryotes such as E. coli and B. subtilis have circular, supercoiled chromosomes packaged by histone‐like nucleoid proteins and genes organized into operons, such as the lac operon. These and most other bacteria have condensin‐like SMC complexes that form loops to facilitate the properly regulated expression of genes in operons and to regulate chromosome topology by orchestrating genome compaction, segregation and other functions.113, 133, 139, 140

8. FUTURE PERSPECTIVES

Our understanding of the organization of the nucleus has progressed rapidly over the past 10 years, in large part because of the innovative and impactful technological advances we have described in this study. Continued progress will depend on improved imaging, tools for nucleomics, and modeling, and their application to address a variety of outstanding issues.

8.1. Biological questions

Current techniques raise the possibility of addressing a wide variety of scientific questions that have been intractable in their absence. Outstanding challenges include monitoring chromosome position in three dimensions and in relation to nuclear landmarks such as the nuclear periphery or nuclear bodies and genome dynamics in living cells as they progress through the cell cycle, undergo development, and respond to external and internal perturbations. Comparative genome‐wide maps of chromosome organization in normal and abnormal cells will be informative with regard to the characterization, and perhaps the diagnosis, of a variety disease states, the regulation of gene expression and the rearrangement of chromosomes by recombination and translocation. These and many other topics are the focus of the ongoing National Institutes of Health 4D Nucleome Project141 (https://commonfund.nih.gov/4dnucleome), the International Nucleome Consortium142 and the proposed 4DNucleome Initiative in Europe (https://ec.europa.eu/futurium/en/content/4dnucleome-initiative-europe). It will also be interesting to directly compare imaging and Hi‐C data, for example, by mapping the 3D positioning of the A and B compartments defined by Hi‐C and comparing them to the localization of euchromatin and heterochromatin visualized microscopically.

8.2. Nucleome physical approaches

The explosion of chromosome capture techniques and their application to a range of cell types carries with it the challenges to comparing data from different sources that may use different strategies. Efforts to validate, standardize, improve and develop new technological, analytical and nucleomics tools and to establish a Data Analysis Center are currently underway as part of the NIH 4D Nucleome Project. Future research includes the development of high‐throughput experimental and computational approaches to achieve single‐cell 4D chromosome capture data, examine higher‐order genome structure and develop new methods for crosslinking DNA.

8.3. Genome imaging approaches

At the time when chromosome capture and Hi‐C techniques were being developed, FISH analysis was the state‐of‐the‐art for monitoring co‐localization of DNA loci at a resolution of several hundred nanometers (nm). Although the optical resolution is limited by the diffraction of light waves, 2 recent developments now make it possible to overcome this diffraction barrier. The first was the development of new optical instrumentation that increases image resolution to approximately 100 nm and is capable of 3D imaging using optical sectioning. The second was the development of a new class of fluorophores with novel properties that make it possible to resolve the overlapping emissions of neighboring single molecules and achieve sub‐diffraction limit resolution as low as 10 nm.143 These techniques have been widely used to study the 3D localization of a variety of proteins in their cellular context.143 More recently, they have been adapted to allow high‐resolution super‐resolution imaging of up to 30 genomic loci using short oligonucleotide probes144 or up to 6 loci using modified CRISPR‐based systems targeted to the genome by engineered guide RNAs.145, 146 Although both approaches have their drawbacks, they represent significant improvements over traditional FISH analysis yet can still detect only a tiny fraction of the genome‐wide contacts seen with Hi‐C.144, 147, 148, 149, 150 However, improvements and innovative new approaches are certainly on the horizon. Optical imaging can also capture chromosome dynamics and 3D positioning of loci in live cells, neither of which can be determined using static Hi‐C data from large heterogeneous populations of cells. However, recent Hi‐C analysis of single cells or populations of mouse and yeast cells with known positions in the cell cycle has documented stage‐specific differences in chromosome conformation.151, 152, 153, 154 The next challenge in this area is to describe the 4D changes in chromosome structure and dynamics in living cells progressing through an unperturbed cell cycle. All of these efforts will be advanced by the development of new imaging instrumentation and experimental tools that will achieve higher resolution and higher content imaging of live single cells.

8.4. Polymer physics approaches

We have pointed out repeatedly in this review that discoveries on the structure and dynamics of chromatin at large scales, made possible through new experimental methods, have inspired various new directions in polymer physics. The structure of melts of polymer rings60, 61, 62, 63, 64, 65, 66 or the segregation of polymers at different temperatures76, 77, 78 mentioned earlier are such examples. Some of these new polymer studies are performed specifically to understand experimental findings on chromatin whereas others attempt to come up with general laws that govern such systems and might eventually form new branches in polymer physics. As new experimental data pour in with more and more detailed insights on chromatin structure and dynamics and as information on single cells becomes available, the questions that polymer models need to address will continue to widen the scope of polymer physics in the future, both applied to chromatin and fundamental physics. In the immediate future, individual polymers or polymer solutions in the presence of energy consuming processes (eg, the loopy globule52 or activity‐based polymer segregation76, 77, 78) certainly provide a wide range of possible questions, as indicated by an increased frequency of publications in this field.

9. CONCLUSIONS

All organisms from E. coli to humans have some mechanism of segregating functionally similar units of the genome by tethering them to nuclear structures, partitioning them into loops of various sizes and/or forming territories. The universal properties of the 3D organization of all polymers, including DNA, are governed by the laws of polymer physics. However, as we have discussed, when DNA is assembled into chromatin within a living cell it does not always follow the well‐known standard laws. For example, the conformations of larger interphase chromosomes are clearly out‐of‐equilibrium. In these cases, identifying and understanding the basis of the incompatibilities between chromosome biology and standard polymer physics have been and will continue to be informative. In hopes of facilitating continued interdisciplinary efforts, we have focused on 3 basic organizational properties of chromosomes from both the cell biological and polymer physics perspectives and discussed the evolution of 3D chromosome organization in order to explore a range of chromosome topologies and the varied mechanisms cells use to arrive at common and species‐specific outcomes.

Supporting information

Editorial Process

Sazer S, Schiessel H. The biology and polymer physics underlying large‐scale chromosome organization. Traffic. 2018;19:87–101. https://doi.org/10.1111/tra.12539