Smooth-threshold multivariate genetic prediction with unbiased model selection

Abstract

We develop a new genetic prediction method, smooth-threshold multivariate genetic prediction, using single nucleotide polymorphisms (SNPs) data in genome-wide association studies (GWASs). Our method consists of two stages. At the first stage, unlike the usual discontinuous SNP screening as used in the gene score method, our method continuously screens SNPs based on the output from standard univariate analysis for marginal association of each SNP. At the second stage, the predictive model is built by a generalized ridge regression simultaneously using the screened SNPs with SNP weight determined by the strength of marginal association. Continuous SNP screening by the smooth-thresholding not only makes prediction stable but also leads to a closed form expression of generalized degrees of freedom (GDF). The GDF leads to the Stein’s unbiased risk estimation (SURE) which enables data-dependent choice of optimal SNP screening cutoff without using cross-validation. Our method is very rapid because computationally expensive genome-wide scan is required only once in contrast to the penalized regression methods including lasso and elastic net. Simulation studies which mimic real GWAS data with quantitative and binary traits demonstrate that the proposed method outperforms the gene score method and genomic best linear unbiased prediction (GBLUP), and also shows comparable or sometimes improved performance with the lasso and elastic net being known to have good predictive ability but with heavy computational cost. Application to whole-genome sequencing (WGS) data from the Alzheimer’s Disease Neuroimaging Initiative (ADNI) exhibits that the proposed method shows higher predictive power than the gene score and GBLUP methods.

1 Introduction

Genome-wide association study (GWAS) is a popular tool for discovering disease-susceptibility genes using large number of single nucleotide polymorphisms (SNPs) without prior knowledge [The Wellcome Trust Case Control Consortium 2007]. Apart from discovery of susceptibility genes, prediction of individual’s phenotype from high-dimensional genetic information, termed as a genetic prediction, is an important task for personalized medicine. Currently, researchers are exploring the most effective way of building genetic prediction models [Purcell et al. 2009, Evans et al. 2009]. In this paper, we develop a new statistical approach, smooth-threshold multivariate genetic prediction, for building genetic predictive models with input of large-scale genome-wide SNPs data.

We consider standard multiple regression model but with high-dimensional predictor variables. To be specific, y = (y₁, . . . , y_n)^T represent response variables of individual’s phenotype data modeled by a conditional distribution given predictor variables X = (X₁, . . . , X_p) observed for n individuals, in which X_j = (x_1,j, . . . , x_n,j)^T for j ∈ M = {1, . . . , p}. The conditional expectation of y_i given x_i = (x_i,1, . . . , x_i,n) is assumed to be a linear combination η{E(y_i|x_i)} = x_iβ, where η is some known monotone function and β is a vector of regression coefficients. In this paper, we consider linear regression with identity map η for quantitative trait such as clinical characteristics, and logistic regression with logit function η for binary trait such as affected/unaffected status. Each X_j is either genotype at a SNP site or other covariate such as sex, age, body mass index (BMI), smoking status, alcohol consumption and principal components for population stratification [Price et al. 2006]. Each SNP can take one of three possible genotypes, gg, gG and GG, where g and G denote minor and major alleles at the SNP site, respectively. If X_j represents the observed count of minor allele g at a SNP site, X_j takes a value from {0, 1, 2}. Under the Hardy–Weinberg equilibrium (HWE), the observed count of minor allele g at each SNP follows a binomial distribution with parameter f ∈ [0, 0.5] called a minor allele frequency (MAF), i.e. frequency of the minor allele g in general population. Quality controls (QCs) are often conducted to remove low-quality SNPs by checking HWE and missing rates as well as low MAF SNPs. Even after those QCs, large number of SNPs still remain. Since sample sizes are usually far less than the number of SNPs, the predictive modeling in GWAS faces the p ≫ n problem (e.g. Fan and Lv [2008]). The p ≫ n condition hampers multiple regression that fits simultaneously using p predictors X.

Standard GWAS analysis conducts marginal association scan between y and each X_j independently, i.e. a univariate analysis which tests the slope parameter in univariate regression model [The Wellcome Trust Case Control Consortium 2007, Yamagata University Genomic Cohort Consortium 2014], followed by multiple test using a Bonferroni correction with a stringent significance level (e.g. p-value less than 5 × 10⁻⁸) in order to control the rate of false positive findings. Meanwhile, suppose that X does not include covariates and consists of SNPs only. Let T_j(y, X) represent a non-negative test statistic for testing association between jth SNP X_j and y as a function of y and X, and the corresponding inclusion threshold be t > 0. For example, t is a chi-squared quantile at a given p-value cutoff for chi-squared test statistics T_j(y, X). The resulting SNP set from a marginal association screening at a threshold t is defined by A = {j ∈ M : T_j(y, X) > t}. Purcell et al. [2009] proposed a gene score method which simply averages each genotype data weighted by estimated effect size for each SNP in A. Warren et al. [2013] consider multiple regression for SNPs in A, called a multivariate gene score method.

In the purpose of prediction, the cutoff t can be chosen in terms of prediction ability. However, evaluating prediction ability is not straightforward unlike in traditional setting without screening. It is known that, the screening invalidates traditional statistical procedures, called an winner’s curse effect [Zollner and Pritchard 2007, Zhong and Prentice 2008, Ghosh et al. 2008]. Analogous problem arises in the context of prediction modeling. Actually, simulation studies as well as examination on real GWAS datasets reported that screening leads to overfitting [Kooperberg et al. 2010]. In Supplementary Material, we show that the screening can deflate the residual sum of squares (RSS) compared with the RSS without screening, so that the RSS becomes too optimistic. Since screening complicates the behavior of RSS, naive use of RSS is unwarranted in measuring prediction ability. Instead, we can use cross-validation (or sample splitting) which divides the training data into two parts, one of which is used for ranking SNPs and remaining is used to construct a predictive model [Purcell et al. 2009, Kooperberg et al. 2010, Wray et al. 2013, Wei et al. 2013]. Purcell et al. [2009] choose an optimal inclusion cutoff by cross-validation.

Although cross-validation takes into account of the screening, reduced sample sizes in training stage may lose predictive power [Dudbridge 2013], which is a severe concern when sample sizes are small. Five or ten-folds cross-validation is commonly used in model selection. For example, the SparSNP program [Abraham et al. 2012] implementing penalized regression methods, the lasso and elastic net, searches for entire genome-wide SNPs data without SNP screening. SparSNP selects the tuning parameter by k-fold cross-validation with default setting of k = 10. Repeated genome-wide scans needed at each candidate tuning parameter and multiple runs of model fit-ting in each fold increase computational cost. For large-scale data such as the whole-genome sequencing (WGS) data, heavy computational cost critically limits the applicability although penalized methods are known to give better predictive power than the simpler gene score method [Purcell et al. 2009].

In this paper, we develop a new predictive modeling approach, a smooth-threshold multivariate genetic prediction, which is really applicable to large-scale genome-wide data such as WGS data while preserving high prediction ability. Our method consists of two stages. At the first stage, our method continuously screens SNPs based on the output from standard univariate analysis for marginal association of each SNP. At the second stage, the predictive model is built by a generalized ridge regression simultaneously using the screened SNPs with SNP weight determined by the strength of marginal association reflecting the uncertainty of inclusion. Since the final predictive model is essentially built in multiple regression model as in the sure independence screening [Fan and Lv 2008], the correlations between predictor variables are accounted for (See also Warren et al. [2013]). Marginal association signal is used only for penalizing each regression coefficient. Our method is very rapid because computationally expensive genome-wide scan is required only once in contrast to the penalized methods which need genome-wide scan several times. Our proposal can be seen as a smoothed version of multiple regression after single SNP-GWAS screening of predictor variables at some p-value cutoff, in which the discontinuous process in screening is replaced by a continuous function. The resulting continuity makes the prediction stable in the sense of Breiman [1996]. The continuity in SNP screening also leads to a closed form expression of generalized degrees of freedom (GDF) [Ye 1998, Efron 2004], and allows an application of Stein’s unbiased risk estimation (SURE) [Stein 1981]. While the Mallows’ C_p [Mallows 1973] with the usual degrees of freedom is no longer unbiased model selection criterion due to the effect of screening, we can readily construct an unbiased C_p-type model selection criterion using the GDF [Ye 1998, Efron 2004]. It allows data-dependent choice of optimal SNP inclusion cutoff without relying on cross-validation. The effect of screening is properly accounted for by the SURE’s unbiasedness. Since no cross-validation is needed, computationally expensive genome-wide scan is required only once in ranking SNPs. We also extend to generalized linear models and propose a loglikelihood-based C_p-type model selection criterion. Simulation studies which mimic real SNP-GWAS data for both quantitative and binary traits show that the proposed method gives better performance than gene score and genomic best linear unbiased prediction (GBLUP) [Goddard et al. 2009, Yang et al. 2011, Lee et al. 2011, Makowsky et al. 2013, de Los Campos et al. 2013, Speed and Balding 2014] and attains a comparable or sometime improved prediction performance with the lasso and elastic net in SparSNP program. Application to large-scale WGS data from Alzheimer’s Disease Neuroimaging Initiative (ADNI) exhibits that the proposed method gives higher predictive performance than both the gene score and GBLUP methods.

2 Materials and Methods

Here we consider linear multiple regression model, y = μ + ε, where μ = E(y|X) = Xβ, ε ~ N(0, σ²I_n), X is a p-dimensional design matrix and β is the corresponding p regression coefficients. Since p is much larger than n in typical GWAS data, some dimensionality reduction is required. Sparsity assuming that many components of β are zero would be a realistic assumption. If susceptible SNPs show relatively large marginal signal, marginal association screening effectively reduces the dimensionality. The gene score method [Purcell et al. 2009] and its multivariate generalization [Warren et al. 2013] use upper-ranked SNPs in marginal association, A = {j ∈ M : T_j(y, X) > t}, for a given cutoff value t > 0. Although dimensionality is effectively reduced, discontinuity in y present in the screening process in A may incur instability of prediction, i.e. small change in data can make large changes in the prediction [Breiman 1996]. See also Fan and Li [2001]. To address the discontinuity issue, we use a smooth-thresholding proposed by Ueki [2009]. To be specific, we propose to estimate the regression coefficients by

$$\check{\beta }=\left(\begin{array}{c}{\check{\beta }}_A\\ {\check{\beta }}_{A^c}\end{array}\right)=\left(\begin{array}{c}{\check{G}}_A(I_{\mid A\mid }-{\check{D}}_A)X_A^{T}y\\ 0\end{array}\right),$$ (1)

where A^c indicates the complement set of A, Ǧ_A = {(I_|A|−Ď_A)(Σ_AA+λI_|A|)+τĎ_A}⁻¹, Σ = X^TX, Σ_AA = (Σ_jk)_j∈A,k∈A, γ and τ are non-negative tuning parameters and λ > 0 is a small constant to avoid singularity of Ǧ_A. The corresponding prediction of y_i is then ${\check{\mu }}_i(y)=X_i^T\check{\beta }$. Here Ď_j is an adaptive lasso smooth-thresholding function defined by

$${\check{D}}_j=min[1,{\{t/T_j(y,X)\}}^{\frac{1+\gamma }{2}}].$$ (2)

Since Ď_j = 1 if and only if T_j(y, X) ≤ t, the screened set A with Ď_j is the same as that with D̂_j = 1_{{Tj(y,X)≤t}}, where 1_{·} denotes the indicator function. It can be seen that Ď_j replaces the discontinuous screening process D̂_j by a continuous function. As a result, μ̌_i(y) turns out to be continuous in y.

The regression coefficient for the screened set in (1), β̌_A, can be seen as a solution to

$$X_A^T(X_A{\check{\beta }}_A-y)+W_A{\check{\beta }}_A=0,$$ (3)

with W_A = diag(W_j : j ∈ A) where W_j = λ + τ Ď_j/(1 − Ď_j), which is the minimizer of a generalized ridge regression loss, ${\Vert y-X_A{\beta }_A\Vert }^2+{\sum }_{j\in A}{\beta }_j^2{W}_j$, with respect to β_A. Ridge weight for each predictor variable, W_j, represents uncertainty of marginal association screening. If the marginal association is very weak, we have Ď_j ≈ 1 and large W_j, then the corresponding regression coefficient is strongly shrunken towards zero. If the marginal association is strong, we have Ď_j ≈ 0 and W_j ≈ λ, then the corresponding regression coefficient is less penalized. From the fact that the winner’s curse effect produces larger selection bias for small regression coefficient [Zhong and Prentice 2008], it is expected that the above penalization decreases the selection bias.

Predictive power largely depends on the choice of t. It may be done using cross-validation by dividing a dataset into test and training samples [Warren et al. 2013]. Cross-validation takes into account sampling variability due to the screening [Wray et al. 2013, Wei et al. 2013]. However, repeated genome-wide scans to obtain the screened set A needed in cross-validation incurs computational burden. It is also concerned that the reduction in training sample sizes decreases the predictive power of the model [Dudbridge 2013]. Instead of cross-validation, we propose a C_p-type criterion based on SURE using GDF. The continuity of μ̌_i(y) in y leads to a closed-form expression of GDF. In what follows, we consider p-value cutoff α instead of t by a one-toone transformation t = F⁻¹(1 − α), where F⁻¹ is a quantile function of the distribution of T_j(y, X) under the null hypothesis of no marginal association such as F or χ² distribution. An optimal α is determined by minimizing the C_p-type criterion within a range of α for search, [α_min, α_max]. The proposed procedure is outlined at the end of this section. It is noteworthy that the computational intensive genome-wide scan is required only once in the single-SNP association screening at Step 1. Subsequent Steps 2–4 are performed on the reduced set of SNPs whose single-SNP association p-value is less than α_max.

It is shown that in Supplementary Material that expectation of the C_p-type criterion equals to ${\sum }_{i=1}^n[E\{{({\mu }_i-{\widehat{\mu }}_i)}^2\}+{\sigma }^2]$. The selection bias in RSS due to screening mentioned above is accounted for by this unbiasedness property. Consequently, model selection with the C_p-type criterion is expected to work properly. In principle, the two tuning parameters (γ and τ) other than α may be selected by the C_p-type criterion. However, simulation studies and our experiences in real data applications suggested that better predictive power is attained with some fixed values of γ and τ, possibly, because the reduction of tuning parameters decreases sampling variability due to search of optimal prediction model. Specifically, we use fixed values of γ = 1 and $\tau =n/\sqrt{logn}$ throughout. Consequently, we consider single tuning parameter α to be optimized. The C_p-type criterion contains σ² which is often unknown. A surrogate estimate of σ² is given in Supplementary Material. More details of this section including formulas, derivations, extension to generalized linear models and additional descriptions are given in Supplementary Material.

Outline of algorithm

• Step 1. Perform single-SNP association analysis for p SNPs.

• Step 2. Screen SNPs whose single-SNP association p-value is less than α_max.

• Step 3. Fix γ and τ as suggested in main text, and select an optimal α from candidate values in [α_min, α_max] by minimizing the C_p-type criterion:

  $$C(\alpha )=\sum _{i=1}^n{\{y_i-{\check{\mu }}_i(\alpha )\}}^2+2{\sigma }^2\text{GDF}(\alpha ).$$

  Explicit formulas are given in Supplementary Material.

• Step 4. Compute β̌ by (1) using the selected α.

3 Results

3.1 Simulation results

To examine the performance of the proposed method, we conducted simulation studies with artificial data which mimic real SNP-GWAS data. Simulations were based on sampling individuals from general population where HAPGEN v2.2.0 [Su et al. 2011] was used with input of haplotype data consisting of 73,832 SNPs on chromosome 10 from HapMap3 east Asian population (JPT+CHB). In our experiments, we compared the proposed method, lasso, elastic net, GBLUP and gene score (GS) methods. For lasso and elastic net, we used SparSNP program, in which default parameters of 10 × 10 cross-validation were used for tuning. For elastic net, a fixed L₂ penalty of λ₂ = 1 was used throughout as in Abraham et al. [2013]. For GBLUP, we used GCTA v1.24.4 [Yang et al. 2011]. For GS, we used PRSice v1.23 [Euesden et al. 2015] with default setting with clumping, in which samples are randomly divided into two datasets with 1:9 proportion (1/10 for target data and 9/10 for training data) for selecting optimal p-value cutoff from {0.01, 0.02, , . . . , 0.5}.

Quantitative traits

Using HAPGEN v2.2.0, n individuals from general population were sampled. Then, a quantitative phenotype y_i for each individual i = 1, . . . , n was generated according to the linear regression model, y_i = μ_i + ε_i, where X_0,iβ₀, ε_i ~ N (0, σ²) is an independent Gaussian noise, X_0,i is a vector of p₀ causal SNPs, a subset from 73,832 SNPs coded 0, 1, 2 for minor allele counts in the generated genotype data and β₀ is the p₀ true regression coefficients for causal SNPs. In our simulations, p₀ was set in advance, then p₀ causal SNPs were randomly assigned from 73,832 SNPs.

We consider both oligogenic and polygenic architectures as follows. For oligogenic scenario, we set n = 1000, and each of p₀ elements of β₀, β_0,j, was randomly chosen from three values {0.2, 0.1, 0.05}. We repeated simulations 50 times and examined the following four models: Model O1, p₀ = 10, σ² = 1 (h² = 0.13); Model O2, p₀ = 10, σ² = 2 (h² = 0.07); Model O3, p₀ = 50, σ² = 1 (h² = 0.47); Model O4, p₀ = 50, σ² = 2 (h² = 0.31). Here h² denotes the narrow sense heritability averaged over 50 replicates. For each replicate, the narrow sense heritability is computated by ${\sigma }_A^2/({\sigma }_A^2+{\sigma }^2)$ where ${\sigma }_A^2={\sum }_{j=1}^{p_0}2q_j(1-q_j){\beta }_{0,j}^2$ and q_j is the MAF for each of p₀ causal SNPs. For polygenic scenario, we set n = 5000, and each of p₀ elements of β₀ was set as ${\beta }_{0,j}={\xi }_j/\sqrt{2q_j(1-q_j)}$ and ξ_j was independently and identically generated from a double exponential (or Laplace) distribution with zero median and $\sqrt{h^2/(2p_0)}$ scale parameter. We then set σ² = 1 − h² so that $var(y_i)={\sigma }_A^2+{\sigma }^2=1$. We repeated simulations 20 times and examined the following six models: Model P1, p₀ = 100, h² = 0.3; Model P2, p₀ = 100, h² = 0.1; Model P3, p₀ = 100, h² = 0.05; Model P4, p₀ = 200, h² = 0.3; Model P5, p₀ = 200, h² = 0.1; Model P6, p₀ = 200, h² = 0.05.

In all simulations, we randomly chose 100 subjects for test samples, say N_te, and set the remaining N_tr = {1, . . . , n} \ N_te as training samples. Predictive power was evaluated by whether the proposed method trained on the training samples predicts the phenotype of test samples. Using the proposed unbiased model selection criterion, an optimal p-value cutoff was chosen from 50 equally-spaced candidate values between α_max = 9n/(p log n) and α_min = 5 × 10⁻⁸ in −log₁₀ scale, i.e. α_max = α₍₁₎ > α₍₂₎ > ··· > α₍₅₀₎ = α_min We used PLINK --assoc option to compute marginal association p-values, and then screened SNPs whose p-value is less than α_max. Since the PLINK’s association p-value is based on Wald test, we recomputed F-test statistics (T_j(y, X) described in Supplementary Material) for the above screened SNPs. In practice, each p-value cutoff, α_k, was converted to a threshold for T_j(y, X)s to be optimized, t_(k) = F⁻¹(1 − α_(k)), where F⁻¹ denotes the quantile function of F (1, n − 1)-distribution. The optimal cutoff was determined from t₍₁₎ < t₍₂₎ <···< t₍₅₀₎ which minimizes the C_p-type criterion.

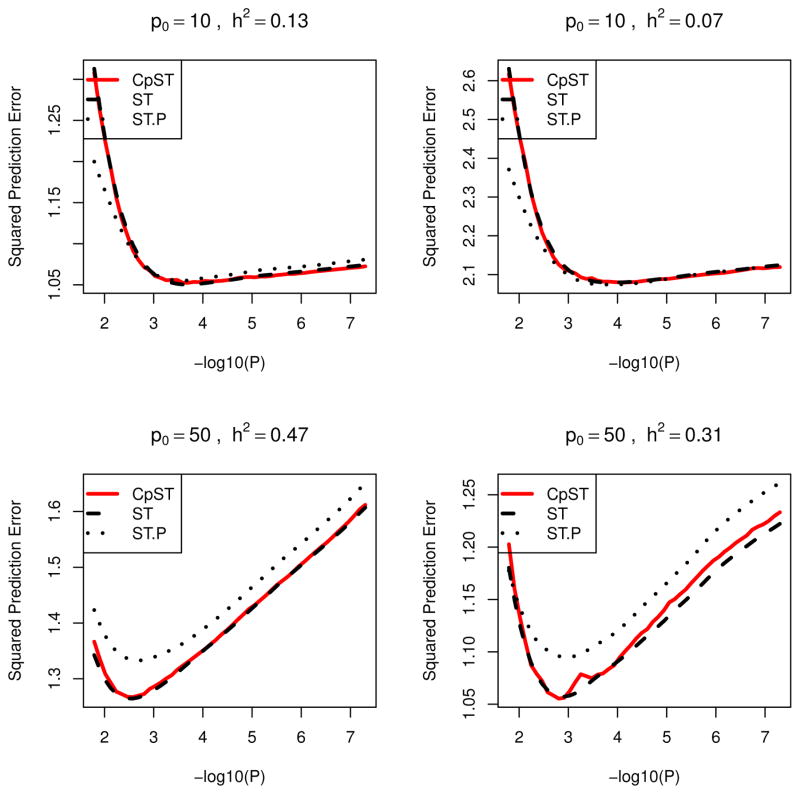
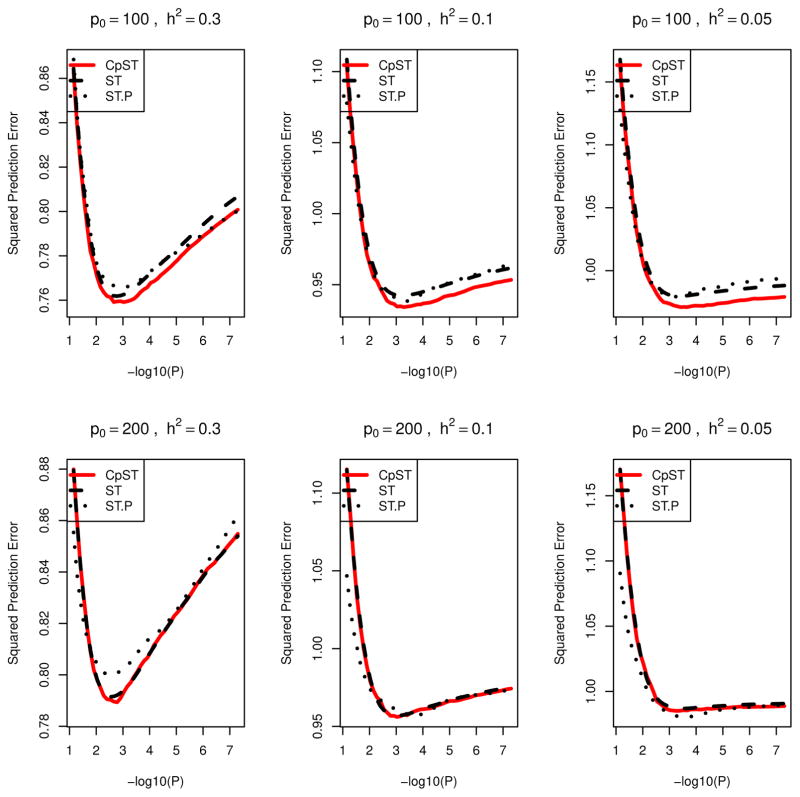
Resulting prediction errors, PSE_tr = |N_tr|⁻¹ Σ_i∈Ntr E{(y_0,i − μ̌_tr,i)²} = |N_tr|⁻¹Σ_i∈NtrE{(μ_i − μ̌_tr,i)²} + σ², and PSE_te =|N_te|⁻¹ Σ_i∈NteE{(y_i − μ̌_tr,i)²}, are plotted as a function of α in Figures 1 (oligogenic scenario) and 2 (polygenic scenario) averaged over replicates. Here, μ̌_tr,i = X_iβ̌_tr denotes the predicted value for ith sample using the regression coefficients β̌_tr by the proposed smooth-threshold multivariate genetic prediction based on training samples, while y_0,i is an independent future observation from the same distribution of y_i given X_i, i.e., μ_i + ε_0,i, with Gaussian noise ε_0,i ~ N (0, σ²) independent of ε_i and μ_i = X_0,iβ₀. It can be seen that the proposed C_p-type criterion indeed possesses the unbiasedness to the true mean squared prediction error for training samples, PSE_tr, across various p-value cutoff values. Each curve had a minimum at some optimal cutoff value and formed a convex function.

Figure 1.

Prediction errors averaged over 50 simulation replicates for quantitative traits in oligogenic scenarios (Models O1,...,O4). Black dashed line (ST), average of mean prediction squared error for training data (PSEtr) for predictive models from smooth-threshold multivariate genetic prediction at each p-value threshold in minus log10-scale (x-axis). Black dotted line (ST.P), average of prediction squared error for test data (PSEte) for predictive model from smooth-threshold multivariate genetic prediction trained on the training data. Red solid line (CpST), average of the proposed Cp-type criterion (an unbiased estimator of the black dashed line).

Figure 2.

Prediction errors averaged over 20 simulation replicates for quantitative traits in polygenic scenarios (Models P1,...,P6). Black dashed line (ST), average of mean prediction squared error for training data (PSEtr) for predictive models from smooth-threshold multivariate genetic prediction at each p-value threshold in minus log10-scale (x-axis). Black dotted line (ST.P), average of prediction squared error for test data (PSEte) for predictive model from smooth-threshold multivariate genetic prediction trained on the training data. Red solid line (CpST), average of the proposed Cp-type criterion (an unbiased estimator of the black dashed line).

The regression coefficients β̌_tr estimated on training samples were used for predicting phenotype value of test samples. In Table 1, the predictive power was evaluated by the predictive correlation coefficient (PCC) which is the Pearson’s correlation between the predicted value and the actual phenotype of test samples. For the proposed method, the predicted values for test samples were computed at an optimal p-value cutoff value selected by minimizing the proposed C_p-type criterion. From the PCCs given in Table 1, the prediction performance of lasso and elastic net was comparable with the proposed method. On the other hand, the GBLUP and GS showed much lower performance than the proposed method, lasso and elastic net in some oligogenic scenarios. In polygenic scenarios, the proposed method gave slightly lower performance than the lasso and elastic net. We also conducted additional polygenic simulations assuming low heritabilities. The results given in Supplementary Material show that all methods gave very low predictive performance, agreeing with the observation in Warren et al. [2013].

Table 1.

Quantitative traits simulations, average predictive correlation co-efficient (PCC) with standard deviation in parenthesis, average number of true/false positive (TP/FP) results for three methods in replicates. STMGP, smooth-threshold multivariate genetic prediction, Enet, elastic net; GS, gene score. The best performing method is emphasized in bold.

p0	h2		STMGP	Lasso	Enet	GCTA	GS
Oligogenic scenarios (n = 1000)
10	0.13	PCC	0.27 (0.11)	0.28 (0.11)	0.27 (0.11)	0.09 (0.1)	0.1 (0.09)
		TP/FP	3/115	2/46	3/194	-	4/3088
10	0.07	PCC	0.16 (0.12)	0.16 (0.12)	0.16 (0.12)	0.05 (0.1)	0.04 (0.11)
		TP/FP	2/78	1/32	2/133	-	4/7105
50	0.47	PCC	0.55 (0.1)	0.57 (0.09)	0.55 (0.09)	0.27 (0.09)	0.29 (0.1)
		TP/FP	16/509	11/151	19/816	-	20/3488
50	0.31	PCC	0.18 (0.21)	0.17 (0.21)	0.17 (0.2)	0.18 (0.09)	0.19 (0.11)
		TP/FP	5/133	3/50	6/264	-	18/4373
Polygenic scenarios (n = 5000)
100	0.3	PCC	0.46 (0.11)	0.48 (0.11)	0.47 (0.11)	0.28 (0.14)	0.31 (0.1)
		TP/FP	29/904	24/502	36/1073	-	36/2636
100	0.1	PCC	0.23 (0.1)	0.23 (0.11)	0.23 (0.11)	0.11 (0.13)	0.13 (0.14)
		TP/FP	12/257	10/215	17/570	-	30/6413
100	0.05	PCC	0.12 (0.11)	0.13 (0.09)	0.13 (0.11)	0.06 (0.12)	0.05 (0.12)
		TP/FP	6/125	5/129	9/406	-	23/7521
200	0.3	PCC	0.41 (0.09)	0.44 (0.1)	0.43 (0.1)	0.28 (0.09)	0.3 (0.09)
		TP/FP	40/1017	30/434	52/1395	-	54/2726
200	0.1	PCC	0.15 (0.12)	0.17 (0.13)	0.18 (0.12)	0.11 (0.1)	0.11 (0.1)
		TP/FP	13/263	8/140	19/600	-	37/4577
200	0.05	PCC	0.09 (0.1)	0.09 (0.12)	0.1 (0.11)	0.06 (0.11)	0.06 (0.06)
		TP/FP	5/117	4/109	7/300	-	37/7312

For the proposed method, lasso, elastic net and gene score, Table 1 gives the average number of true and false positives, respectively, defined by that non-zero coefficients from each method are truly and falsely causal SNPs. Overall, all methods yielded large number of false positives, which would result from that the assumed effect sizes were small relative to the noise.

Binary traits

For simulations of binary traits, case-control data were used for training samples to build a predictive model, and then the predictive model was tested through independent test samples from general population. We consider both oligogenic and polygenic architectures as follows. For oligogenic scenario, 1000 balanced case-control samples (500 cases and 500 controls) for training and 1000 samples for test were considered. Case-control samples were collected based on repeated sampling from general population as described below in detail. A binary phenotype y_i ∈ {0, 1} of each individual from general population was generated according to the logistic regression model μ_i = P (y_i = 1|X_i) = 1/{1 + exp(−θ_i)}, where X_i denotes a realization of the individual i’s SNPs vector with additive coding as in the quantitative trait simulation, θ_i = X_iβ₀ + b₀, b₀ is the baseline regression coefficient and β₀ denotes p₀ true regression coefficients. p₀ causal SNPs were randomly chosen from all 73,832 SNPs, and then, 0,1,2 coding was carried out according to the minor allele count in reference haplotype data. Then, p₀ regression coefficients β₀ were randomly assigned from three values {(m/2) log 1.1, (m/2) log 1.2, (m/2) log 1.5}, with a constant parameter m. The following four models were considered: Model O5, p₀ = 10, m = 2, b₀ = −4 (h² = 0.05); Model O6, p₀ = 10, m = 3, b₀ = −5 (h² = 0.11); Model O7, p₀ = 50, m = 0.8, b₀ = −4 (h² = 0.04); Model O8, p₀ = 50, m = 1.2, b₀ = −5 (h² = 0.09). Here h² denotes the narrow sense heritability averaged over 50 replicates just like the quantitative traits simulations using ${\sigma }_A^2/({\sigma }_A^2+{\sigma }^2)$ except that σ² = p²/3 which is the variance of logistic distribution with unit scale (i.e. liability follows logistic distribution rather than Gaussian). For polygenic scenario, 5000 balanced case-control samples (2500 cases and 2500 controls) for training and 1000 samples for test were considered. First we generated liability from Gaussian distribution as done in the polygenic quantitative traits simulations, in which mean of liability is adjusted to be zero. Then, we assigned y_i = 1 if the liability exceeds Φ⁻¹(1 − K₀) and 0 otherwise, where K₀ = 0.1 and Φ⁻¹ is the standard normal quantile function. We repeated simulations 20 times and examined the following six models: Model P7, p₀ = 100, h² = 0.3; Model P8, p₀ = 100, h² = 0.1; Model P9, p₀ = 100, h² = 0.05; Model P10, p₀ = 200, h² = 0.3; Model P11, p₀ = 200, h² = 0.1; Model P12, p₀ = 200, h² = 0.05, which correspond to the models with liability generated from Models P1,. . . ,P6.

n₀ cases and n₁ controls data were generated as follows. First, 1000 individuals were sampled from general population using HAPGEN as described in earlier of this subsection. In each sampling, case/control status was assigned for each individual according to the specified model. Since the number of cases was in general smaller than that of controls, a subset of controls with the same number of cases occurred was randomly chosen. As a result, cases and controls with equal numbers were stored. The above process was continued until total sample size reaches to the desired number. In addition, 1000 individuals were generated from general population using HAPGEN, and a case/control status was assigned from the specified regression model. The 1000 individuals were used for test samples.

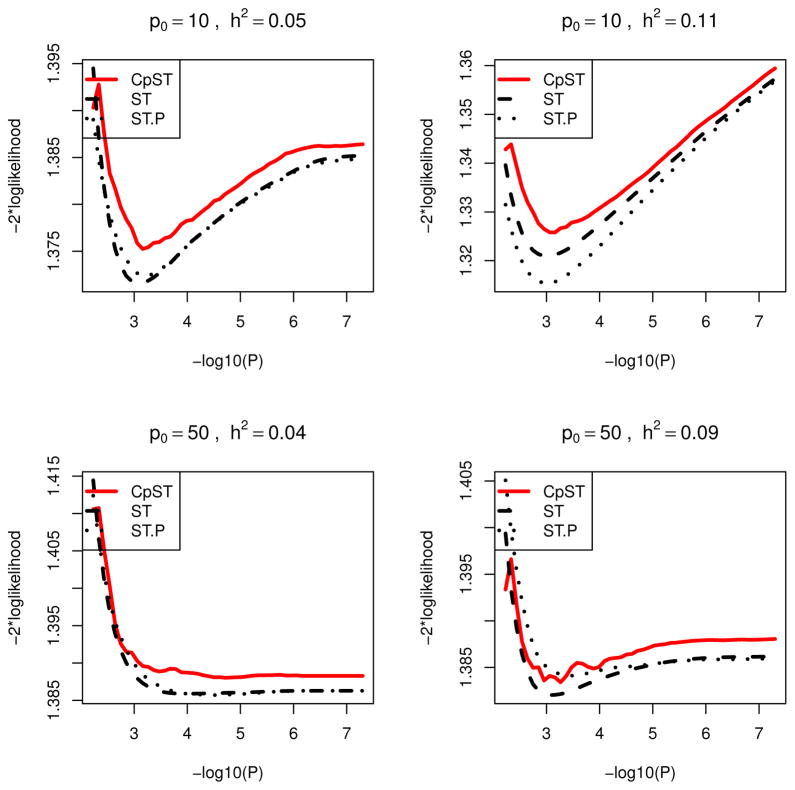
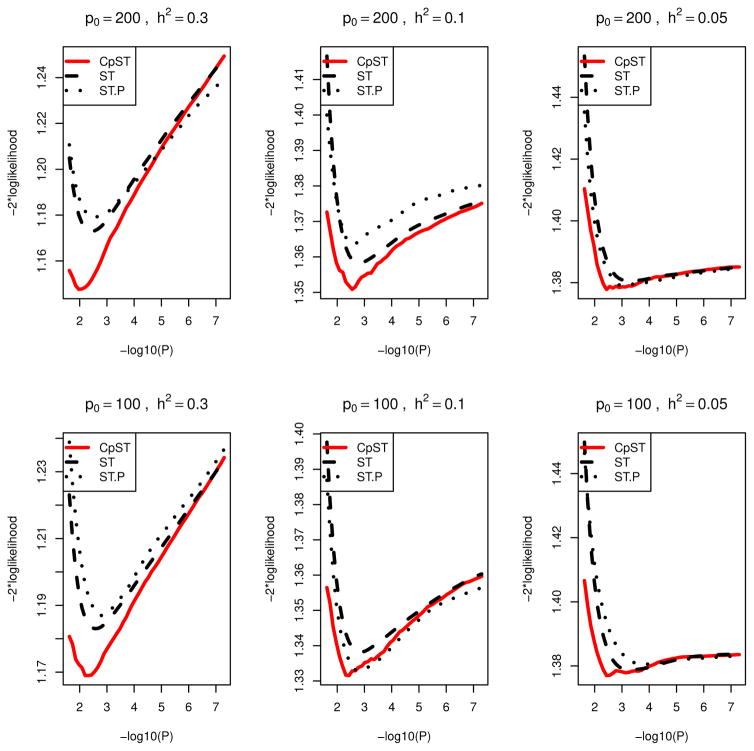
Using the proposed (approximate) unbiased model selection criterion, an optimal p-value cutoff was chosen from 50 equally-spaced candidate values between α_max = 3n/(p log n) and α_min = 5 × 10⁻⁸ in −log₁₀ scale. Marginal association screening was conducted as in the quantitative trait simulations except that the score test statistic was used for T_j(y, X) instead of the F-test statistic and that F ⁻¹ is the quantile function of χ² distribution with one degree of freedom. As in Figures 1 and 2, Figures 3 and 4 give prediction errors measured by −2× loglikelihood, PL_tr = |N_tr|⁻¹Σ_i∈Ntrq{(μ_i, θ̌_tr,i) and PL_te = |N_te|⁻¹Σ_i∈Nteq{(y_i, θ̌_tr,i), as a function of α. Here θ̌_tr,i = X_iβ̌_tr denotes the predicted value for ith sample using the regression coefficients β̌_tr by the proposed smooth-threshold multivariate genetic prediction learned on the training samples. From Figures 3 and 4, the proposed C_p-type criterion appeared to be close to the true mean prediction −2× loglikelihood. Each curve had a minimum at some optimal cutoff value and formed a convex function.

Figure 3.

Prediction −2 × loglikelihood averaged over 50 simulation replicates for binary traits in oligogenic scenarios (O5,...,O8). Black dashed line (ST), average of mean −2 × loglikelihood for training data (PSEtr) for predictive models from smooth-threshold multivariate genetic prediction at each p-value threshold in minus log10-scale (x-axis). Black dotted line (ST.P), average of prediction −2 × loglikelihood for test data (PSEte) for predictive model from smooth-threshold multivariate genetic prediction trained on the training data. Red solid line (CpST), average of the proposed Cp-type criterion (an approximate unbiased estimator of the black dashed line).

Figure 4.

Prediction −2 × loglikelihood averaged over 20 simulation replicates for binary traits in polygenic scenarios (P7,...,P12). Black dashed line (ST), average of mean −2 × loglikelihood for training data (PSEtr) for predictive models from smooth-threshold multivariate genetic prediction at each p-value threshold in minus log10-scale (x-axis). Black dotted line (ST.P), average of prediction −2 × loglikelihood for test data (PSEte) for predictive model from smooth-threshold multivariate genetic prediction trained on the training data. Red solid line (CpST), average of the proposed Cp-type criterion (an approximate unbiased estimator of the black dashed line).

The regression coefficients β̌_tr estimated on training samples were used to predict the phenotype of test samples. In Table 2, the predictive power was evaluated by the area under a receiver operating characteristic curve (AUC). For the proposed method, the mean prediction errors for test samples were computed using an optimal p-value cutoff value selected by minimizing the proposed C_p-type criterion. Resulting prediction performances were given in Table 2. The proposed method, lasso and elastic net, showed comparable predictive power. On the other hand, the GBLUP and GS showed much lower performance than the proposed method, lasso and elastic net in some oligogenic scenarios. In Supplementary Material, we also conducted additional polygenic simulations assuming low heritabilities. The results are similar to that in quantitative traits simulations. For the proposed method, lasso, elastic net and gene score, average number of true and false positives were compared in Table 2. As in quantitative traits simulations, large number of false positives resulted in all methods.

Table 2.

Binary traits simulations, average AUC with standard deviation in parenthesis, and average number of true/false positive (TP/FP) results for three methods in replicates. STMGP, smooth-threshold multivariate genetic prediction; Enet, elastic net; GS, gene score. The best performing method is emphasized in bold.

p0	h2		STMGP	Lasso	Enet	GCTA	GS
Oligogenic scenarios (n = 1000)
10	0.05	AUC	0.55 (0.06)	0.55 (0.06)	0.56 (0.05)	0.51 (0.06)	0.52 (0.06)
		TP/FP	2/99	1/238	2/451	-	4/5441
10	0.11	AUC	0.64 (0.06)	0.64 (0.08)	0.64 (0.07)	0.52 (0.07)	0.53 (0.06)
		TP/FP	3/115	2/31	3/64	-	5/6082
50	0.04	AUC	0.51 (0.05)	0.5 (0.05)	0.51 (0.05)	0.51 (0.06)	0.51 (0.05)
		TP/FP	1/47	1/360	2/688	-	9/8119
50	0.09	AUC	0.53 (0.05)	0.52 (0.05)	0.53 (0.05)	0.52 (0.05)	0.52 (0.04)
		TP/FP	2/111	2/273	3/407	-	13/9175
Polygenic scenarios (n = 5000)
100	0.3	AUC	0.74 (0.05)	0.74 (0.04)	0.74 (0.04)	0.64 (0.05)	0.66 (0.05)
		TP/FP	30/1150	21/142	29/435	-	36/2754
100	0.1	AUC	0.61 (0.05)	0.61 (0.05)	0.61 (0.05)	0.55 (0.04)	0.55 (0.04)
		TP/FP	15/432	8/60	13/178	-	21/1459
100	0.05	AUC	0.54 (0.03)	0.54 (0.03)	0.54 (0.04)	0.53 (0.04)	0.52 (0.03)
		TP/FP	7/285	4/248	7/680	-	17/3956
200	0.3	AUC	0.75 (0.05)	0.76 (0.05)	0.76 (0.04)	0.66 (0.05)	0.68 (0.07)
		TP/FP	53/1745	32/223	49/694	-	55/2341
200	0.1	AUC	0.58 (0.03)	0.59 (0.04)	0.59 (0.04)	0.55 (0.03)	0.55 (0.04)
		TP/FP	18/505	9/95	15/277	-	49/7276
200	0.05	AUC	0.54 (0.03)	0.53 (0.03)	0.54 (0.03)	0.52 (0.03)	0.53 (0.04)
		TP/FP	7/212	7/820	11/1178	-	39/7869

3.2 Application to ADNI-WGS data

We applied our proposed method to ADNI-WGS dataset obtained from the publicly available data of the Alzheimer’s Disease Neuroimage Initiative (ADNI) database (adni.loni.usc.edu). The ADNI was launched in 2003 as a public-private partnership, led by Principal Investigator Michael W. Weiner, MD. The primary goal of ADNI has been to test whether serial magnetic resonance imaging (MRI), positron emission tomography (PET), other biological markers, and clinical and neuropsychological assessment can be combined to measure the progression of mild cognitive impairment (MCI) and early Alzheimer’s disease (AD). For up-to-date information, see www.adni-info.org. ADNI is an ongoing longitudinal study with the primary purpose of exploring the genetic and neuroimaing information associated with late-onset Alzheimer’s disease (LOAD). The study recruited elderly subjects older than 65 years of age consisting about 400 subjects with mild cognitive impairment (MCI), about 200 subjects with Alzheimer’s disease (AD), and around 200 healthy controls (normal). Each subject was followed for at least 3 years. During the study period, the subjects were assessed with magnetic resonance imaging (MRI) measures and psychiatric evaluation to determine the diagnosis status at each time point.

We used high coverage WGS data called using Broad best practices (BWA & GATK HaplotypeCaller). From the ADNI-WGS data, we extracted 8,657,877 single nucleotide variant (SNV) sites. In our analysis, we used 713 non-Hispanic Caucasian samples excluding one of pairs showing cryptic relatedness implied by the PLINK’s pairwise π̂ statistic [Purcell et al. 2007] greater than 0.125. Consequently, the total numbers of subjects with the current status of normal, MCI and AD were 245, 426 and 42, respectively. We separately considered three different definitions of phenotypes: (i) normal (= 1), MCI (= 2) and AD (= 3) as quantitative traits, (ii) normal (= 1), MCI (= 2) and AD (= 2) as binary traits, (iii) normal (= 1), MCI (= 1) and AD (= 2) as binary traits. We also considered two kinds of adjustments for covariates: (a) sex and age, (b) sex, age, year of education (EDU) and family history (FH). For family history, we coded 1 if any of subject’s mother, father and siblings had affected AD, and 0 otherwise. We chose the above covariates because of the known influence on AD.

We used the proposed smooth-threshold multivariate genetic prediction, GBLUP and GP methods for building prediction model. In all three methods, covariates were adjusted. Since the ADNI-WGS data include large number of SNVs, we did not apply the lasso and elastic net in SparSNP due to prohibitive computational cost.

First, we randomly divided 718 samples into ten groups with roughly equal size. Then, one of ten groups was set as test samples and remaining was set as training samples. Consequently, we had ten combinations of test/training samples (i.e. 10-fold cross-validation). For each of ten combinations, we built a prediction model based on training samples, and predict phenotype data of test samples by the prediction model. For each training data, we used SNVs with MAF > 1% and with missing genotype rates < 10% in building prediction model. For the proposed smooth-threshold multivariate genetic prediction, we searched for an optimal p-value cutoff from 50 equally-spaced points between α_max = 3000/8657877 and α_min = 5 × 10⁻⁸ in −log₁₀ scale while we fixed γ = 1 and $\tau =n/\sqrt{logn}$.

In Table 3, predictive power for each three methods averaged over ten test/training datasets was given where standard deviation was given in parenthesis. In (i), phenotype data were treated as a quantitative trait, and the predictive power was evaluated by PCC. In (ii) and (iii), phenotype data were treated as binary traits, and the predictive power was evaluated by AUC. The proposed method showed the best predictive power among three competing methods as observed in simulation studies.

Table 3.

Predictive power for ADNI-WGS samples for three kinds of phenotype definitions and two covariate adjustments: (i) normal (=1), MCI (=2) and AD (=3) (measured by predictive correlation coefficient (SD)), (ii) normal (=1), MCI (=2) and AD (=2) (measured by AUC (SD)), (iii) normal (=1), MCI (=1) and AD (=2) (measured by AUC (SD)); (a) sex and age, (b) sex, age, year of education (EDU) and family history (FH). OptP, optimal p-value cutoff by STMGP (−log10 scale). NS, number of screened SNVs by STMGP.

(i)
Covariates	STMGP	GCTA	GS	OptP	NS
(a)	0.22 (0.11)	0.06 (0.14)	0.07 (0.11)	4.7 (0.5)	362 (350)
(b)	0.24 (0.12)	−0.06 (0.1)	0.05 (0.1)	4.9 (0.3)	247 (160)

(ii)
Covariates	STMGP	GCTA	GS	OptP	NS
(a)	0.61 (0.05)	0.54 (0.09)	0.51 (0.09)	4.8 (0.4)	143 (104)
(b)	0.63 (0.08)	0.44 (0.08)	0.51 (0.09)	4.8 (0.4)	113 (82)

(iii)
Covariates	STMGP	GCTA	GS	OptP	NS
(a)	0.60 (0.15)	0.51 (0.17)	0.52 (0.18)	3.5 (0)	3523 (309)
(b)	0.69 (0.15)	0.47 (0.15)	0.55 (0.21)	3.5 (0)	3601 (296)

In Table 3, we also provided selected optimal p-value cutoff values in −log₁₀ scale and number of screened SNVs by the proposed method averaged over 10 test/training datasets. We note that, in (iii), the proposed C_p-type criterion failed to identify the optimal p-value cutoff in the sense that the minimum value of the criterion was always at the boundary for search, 3000/8657877 (or 3.5 in −log₁₀ scale), as seen in the zero standard deviation in Table 3. It implies that the results for the proposal in Table 3 were suboptimal despite the higher predictive power than the competing methods. One reason of failing to select an optimal p-value cutoff in (iii) would be the small sample size in cases, which made the estimation of C_p-type criterion highly unstable. On the other hand, for (i) and (ii), the proposed C_p-type criterion could take an optimal p-value cutoff which was not at the boundary, i.e. the selection of optimal p-value cutoff was successful.

Our proposed method gave higher predictive power than the GBLUP and gene score as observed in our oligogenic simulations. In our analyses, we included SNVs on APOE (Apolipoprotein E) gene known to have large contribution to developing AD. For such disease, the genetic architecture may be approximated by sparse models considered in the oligogenic scenarios. We note that the predictive power is still insufficient for practical genetic prediction. Recent studies [Chatterjee et al. 2013, Dudbridge 2013] under infinitesimal models [Fisher 1918] state that more sample sizes are needed to construct accurate predictive models. It is expected that increasing sample sizes improve the predictive power. Our proposed approach is general and has a potential to apply to various high-dimensional problems based on multiple linear regression.

4 Conclusion

In this paper, we presented a new efficient predictive modeling using smooth-threshold multivariate genetic prediction. The method can be seen as a smoothed version of multiple regression after marginal association screening or multivariate gene score [Warren et al. 2013]. Advantages of continuity include (i) stabilizing prediction and (ii) applicability of C_p-type unbiased model selection criterion. For (i), through extensive simulation studies, the predictive power of the proposed method had a comparable performance with the contemporary shrinkage methods, lasso and elastic net, which has large computational cost. For (ii), the unbiasedness property of C_p-type criterion was confirmed by simulation studies. The use of C_p-type criterion allows to tune an optimal p-value cutoff without using cross-validation. We are unnecessarily to be concerned on training sample sizes.

The fact that the proposed method requires computationally intensive genome-wide scan only once makes computation more rapid. It is advantageous for WGS data which include large number of variants. An R code which implements the proposed method with input of PLINK-binary format data and summary statistics such as single-SNP association p-values is available from the authors upon request.