Abstract
The genetic changes responsible for evolutionary transitions from generalist to specialist phenotypes are poorly understood. Here we examine the genetic basis of craniofacial traits enabling novel trophic specialization in a sympatric radiation of Cyprinodon pupfishes endemic to San Salvador Island, Bahamas. This recent radiation consists of a generalist species and two novel specialists: a small-jawed “snail-eater” and a large-jawed “scale-eater.” We genotyped 12 million single nucleotide polymorphisms (SNPs) by whole-genome resequencing of 37 individuals of all three species from nine populations and integrated genome-wide divergence scans with association mapping to identify divergent regions containing putatively causal SNPs affecting jaw size—the most rapidly diversifying trait in this radiation. A mere 22 fixed variants accompanied extreme ecological divergence between generalist and scale-eater species. We identified 31 regions (20 kb) containing variants fixed between specialists that were significantly associated with variation in jaw size which contained 11 genes annotated for skeletal system effects and 18 novel candidate genes never previously associated with craniofacial phenotypes. Six of these 31 regions showed robust signs of hard selective sweeps after accounting for demographic history. Our data are consistent with predictions based on quantitative genetic models of adaptation, suggesting that the effect sizes of regions influencing jaw phenotypes are positively correlated with distance between fitness peaks on a complex adaptive landscape.
Keywords: candidate gene, trophic morphology, fitness landscape, adaptive radiation, de novo mutation, standing genetic variation, ecological speciation, selective sweep
Introduction
Identifying genetic changes underlying phenotypic diversity is necessary to understand how these changes drive adaptation and speciation (Coyne and Orr 2004; Moczek 2008; Byers et al. 2016; but see Rausher and Delph 2015). Adaptive radiations showcase the world’s most dramatic instances of rapid ecological divergence (Turner 1976; Schluter 2000; Seehausen 2006; Losos and Ricklefs 2009; Lamichhaney et al. 2016) making them ideal for investigating the genetic basis of traits influencing novel niche use. Characterizing divergent regions underlying adaptation will address several longstanding questions in evolutionary genomics, such as how many differentiated regions do we find between closely related species? Is novel trophic specialization driven by selective sweeps? Does the effect size of loci contributing to phenotypic divergence depend on the distance between fitness peaks across an adaptive landscape? (Hermisson and Pennings 2005; Orr 2005; Noor and Feder 2006, Barrett and Schluter 2008; Jensen 2014; Dittmar et al. 2016; Hoban et al. 2016). Genomic divergence scans measuring relative genetic differentiation and genome-wide association mapping are two strategies used to detect candidate gene regions responsible for species differences (Visscher et al. 2012; Gompert et al. 2012; Pallares et al. 2014; Comeault et al. 2014; Puzey et al. 2015; Irwin et al. 2016; Chaves et al. 2016). Together, these powerful tools can be used to discover genomic regions that are both highly diverged between species and associated with ecologically important traits (Li et al. 2011; Xia et al. 2013; Byers et al. 2016).
A number of recent genome-wide Fst scans comparing closely related species pairs have located small regions (typically < 200 kb) that are highly differentiated relative to the rest of the genome (Carneiro et al. 2014; Soria-Carrasco et al 2014; Poelstra et al. 2014; Malinsky et al. 2015; Lamichhaney et al. 2015), suggesting that these regions are responsible for species-specific phenotypes. Recent literature has emphasized the importance of estimating Fst alongside within-population nucleotide diversity (π) and between-population divergence (Dxy) in order to more accurately interpret the evolutionary significance of genetically differentiated regions (Nachman and Payseur 2012; Cruickshank and Hahn 2014; Irwin et al. 2016). Importantly, any reduction of within-population diversity will necessarily inflate estimates of Fst because it is a relative measure of differentiation (reviewed in Noor and Bennett 2009; Nachman and Payseur 2012; Cruickshank and Hahn 2014). Therefore, Fst interpretations are heavily dependent on the interplay of forces acting to reduce within-population diversity, including selective sweeps, purifying selection, background selection, and low recombination rates (Noor and Bennett 2009; Cruickshank and Hahn 2014). Estimating between-population divergence at loci with high Fst and low within-population diversity can help distinguish between these possibilities because nucleotide divergence between species increases at loci under different selective regimes (Nachman and Payseur 2012; Cruickshank and Hahn 2014; Irwin et al. 2016). However, between-population divergence can also be influenced by patterns of hitchhiking and background selection (Cruickshank and Hahn 2014). Selection statistics comparing the distribution of allele frequencies across segregating sites can also help determine if reduced diversity at a locus is due to selective sweeps, in which selection has increased the frequency of a single (hard sweep) or multiple haplotypes (soft sweep) (Maynard Smith and Haigh 1974; Tajima 1989; Hermisson and Pennings 2005; Pavlidis et al. 2013; Jensen 2014). Statistics that rely on the distribution of allele frequencies within and between populations should be interpreted in the context of their demographic history (Galtier et al. 2000; Andolfatto 2001; Nielsen 2005; Nielsen et al. 2005; Hoban et al. 2016). This can be achieved by inferring changes in ancestral population sizes and using these estimates to model a demography-corrected neutral distribution of allele frequencies (Pavlidis et al. 2013; Schiffels and Durbin 2014). Combining Fst, π, Dxy, and selective sweep statistics can reveal functionally diverged regions of the genome; however, these statistics alone are insufficient to determine how such regions might affect phenotypic differences between species.
Genome-wide association studies expand on divergence scans by identifying regions that are directly associated with phenotypic differences between species. The simplest approach involves estimating associations between single nucleotide polymorphisms (SNPs) and quantitative traits by fitting a linear regression of phenotype on allele frequency (Purcell et al. 2007; Visscher et al. 2012), whereas more advanced methods account for population structure and estimate the effect size of SNPs associated with traits (Price et al. 2006; Kang et al. 2010; Zhou and Stephens 2012; Zhou et al. 2013). Accounting for population structure can help filter out false-positive associations but may also filter out true associations (Marchini et al 2004; Zhao et al. 2011). Thus, we implemented both types of association models alongside genome divergence scans. We used this mixed strategy to identify candidate SNPs affecting novel ecological traits in an excellent system for examining rapid adaptive diversification.
Three sympatric Cyprinodon pupfish species inhabit the hypersaline lakes of San Salvador Island, Bahamas, and radiated within the past 10,000 years based on the most recent drying of these lakes (Mylroie and Hagey 1995; Turner et al. 2008). A generalist species, Cyprinodonvariegatus, feeds primarily on algae and detritus, a diet representative of all allopatric Cyprinodontidae (Martin and Wainwright 2011). The first of two specialist species, the “snail-eater” C. brontotheroides, expanded its diet to include more gastropods and ostracods (Martin and Wainwright 2013a). Snail-eater oral jaws are smaller with a larger in-lever to out-lever ratio compared with the generalist, increasing mechanical advantage for biting (Martin and Wainwright 2013a). The snail-eater is also defined by a prominent protruding nasal region that may be used for leverage while crushing hard-shelled prey (Martin and Wainwright 2013a, 2013b). The second sympatric specialist, the ‘scale-eater’ C. desquamator, expanded its diet to include scales removed from other species during quick strikes. Scale-eaters have greatly enlarged jaws with a smaller in-lever to out-lever ratio, larger adductor muscles, and an elongated body compared with the generalist and snail-eater species (Martin and Wainwright 2013a). Phylogenetic analyses of outgroup Cyprinodon species and surveys of pupfish populations on neighboring Bahamian islands confirm that scale-eating and snail-eating niches are entirely unique to C. desquamator and C. brontotheroides, respectively, and that each species is endemic to hypersaline lakes on San Salvador Island, providing strong support that these specialists diverged from a generalist common ancestor during recent adaptive radiation (Martin and Wainwright 2011; Martin 2016a).
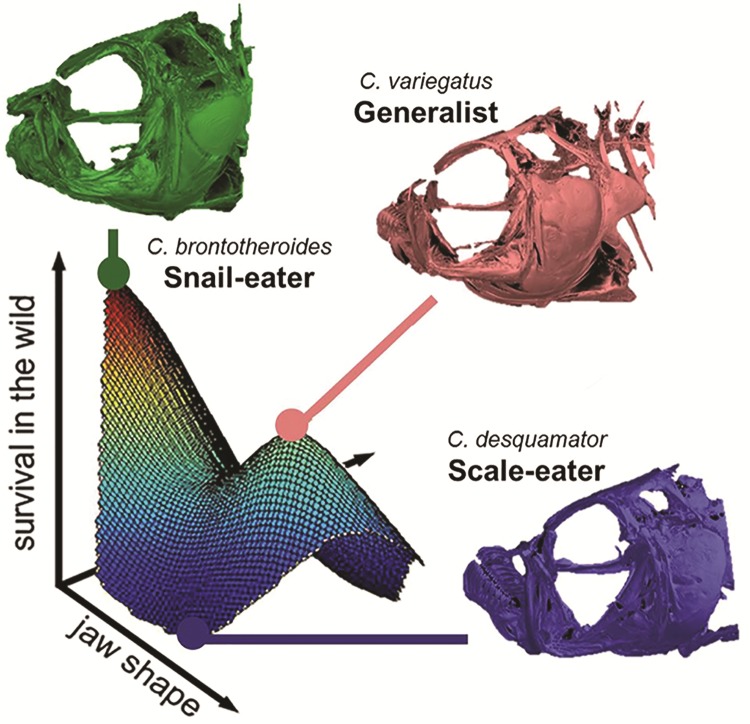
Adaptive landscapes describe the relative fitness of various trait (or allelic) combinations given a particular environment—where adaptive peaks represent optimal combinations and adaptive valleys represent unfit combinations (Wright 1932; Wright 1988; Schluter 2000). If the scale-eater and snail-eater specialists rapidly ascended to novel adaptive peaks within the past 10,000 years, then we should expect to see high rates of morphological diversification in traits associated with trophic specialization. Indeed, San Salvador Cyprinodon pupfishes exhibit morphological diversification rates up to 51 times faster than other Cyprinodontidae clades, with jaw size undergoing the most rapid diversification (Martin and Wainwright 2011; Martin 2016a). The San Salvador pupfish system is one of the few examples of a multipeak adaptive landscape measured for multiple species (Martin and Wainwright 2013c; Martin 2016b), presenting an excellent opportunity to test mathematical models of adaptation. This landscape was estimated using F2 hybrids generated from F1 hybrid intercrosses and backcrosses to all three species. This produced a continuum of phenotypes that were used to estimate relationships between fitness and phenotypic resemblance to parental types. The fitness optima for generalist and snail-eater phenotypes were separated by a small fitness valley, whereas the phenotypic optimum of the scale-eater presumably exists outside of the range of phenotypic variation tested in the F2 population (fig. 1) (Martin and Wainwright 2013c). Although this landscape did not indicate a scale-eater fitness optimum, it does show that the phenotypic distance is greater between the generalist fitness peak and the fitness valley surrounding hybrid phenotypes most resembling the scale-eaters than between the generalist and snail-eater fitness peaks (supplementary fig. S1A, Supplementary Material online). This greater phenotypic distance is primarily due to the large jaws of scale-eaters (supplementary fig. S1B, Supplementary Material online). Orr’s extension of Fisher’s geometric model predicts that de novo mutations with a large effect on phenotypic variation are more likely to be fixed during adaptation toward distant phenotypic optima than nearby optima (Orr 1998, 2005). Based on this model, we predict more large-effect variants mediated the transition from generalist to scale-eater due to the greater phenotypic distance across the fitness valley separating these species.
Fig. 1.
Survival fitness landscape for San Salvador Cyprinodon Pupfish. C. variegatus (red), C. desquamator (blue), and C. brontotheroides (green) from each lake population were intercrossed in every direction to produce F2 hybrids that were left for 3 months in an enclosure on San Salvador. Survival probability is plotted against the two axes of the discriminant morphospace, indicating a wide range of jaw phenotypes in the F2 hybrids (modified from Martin and Wainwright 2013a). Heat colors correspond to survival probability (with blue being low and red being high). µ CT scans of the cranial skeleton of each species modified from Hernandez et al. (in revision).
Here, we focus on identifying loci associated with variation in jaw morphology within this radiation due to the strikingly rapid divergence of this trait that has clear ecological fitness consequences. We identified 12 million SNPs from 37 genomes sequenced to 7× coverage across nine populations of all three species on San Salvador Island. We discovered novel candidate genes associated with jaw size along with evidence supporting the role of large-effect alleles in crossing between distant phenotypic optima.
Results
Estimating Phenotypic Distances
Orr’s extension of Fisher’s geometric model predicts that de novo mutations with a large effect on phenotypic variation are more likely to be fixed during adaptation toward distant phenotypic optima than nearby optima (Orr 1998, 2005). To test this prediction, we measured the phenotypic distance between hybrids used to estimate the multipeaked adaptive landscape for San Salvador pupfishes (dataset published in Dryad repository (data from Martin 2016b) and originally used for Martin and Wainwright 2013b). These hybrids were measured for 16 morphological traits. We visualized the distance between fitness peaks along the first two principal component axes of phenotypic variation and for the key trait of upper jaw length. We found that the distance between phenotypic optima is greater between the generalist fitness peak and the fitness valley surrounding hybrid phenotypes most resembling the scale-eaters than between the generalist fitness peak and the neighboring higher fitness peak corresponding to hybrids resembling the snail-eater (supplementary fig. S1, Supplementary Material online).
Population Structure and Genome Scans
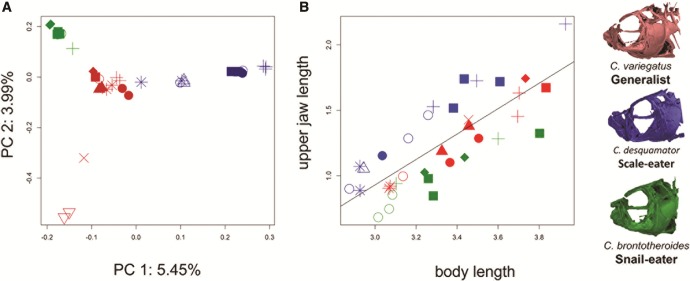
Principal component analysis revealed population structure at the level of species and individual lake population, with the top two principal components together explaining 9.44% of the genetic variation (fig. 2A). The axes show two distinct clusters of scale-eaters: smaller-jawed individuals from Osprey Lake, Great Lake, and Oyster Pond and larger-jawed individuals from Crescent Pond and Little Lake. Genome-wide mean estimates of within-species diversity (π: generalist = 0.00402, snail-eater = 0.00321, scale-eater = 0.00324) and mean between-population divergence (Dxy: generalist × snail-eater = 0.000166, generalist × scale-eater = 0.000169, scale-eater × snail-eater = .000167) were similar for all comparisons, revealing that most variants were shared among species. The similarity between Dxy among species suggests that divergence from a generalist ancestor likely occurred near the same time for both specialists.
Fig. 2.
Standardized jaw size and population structure. (A) Principal component analysis showing axes accounting for a combined 9.45% of the total genetic variation between samples from 12 million SNPs genotyped from 37 whole-genome sequences. (B) Log-transformed upper jaw length (mm) standardized by log-transformed body length for Cyprinodon variegatus (red), C. desquamator (blue), and C. brontotheroides (green). Symbols represent individual lake of origin. µ CT scans of the cranial skeleton of each species modified from Hernandez et al. (in revision). + = Crescent Pond, × = Lake Cunningham, ▴= Mermaid’s Pond, ▪ = Little Lake, ○ = Osprey Lake, • = Stout Lake, * = Great Lake, ♦ = Moon Rock, ▿ = Pigeon Creek, ▵ = Oyster Lake).
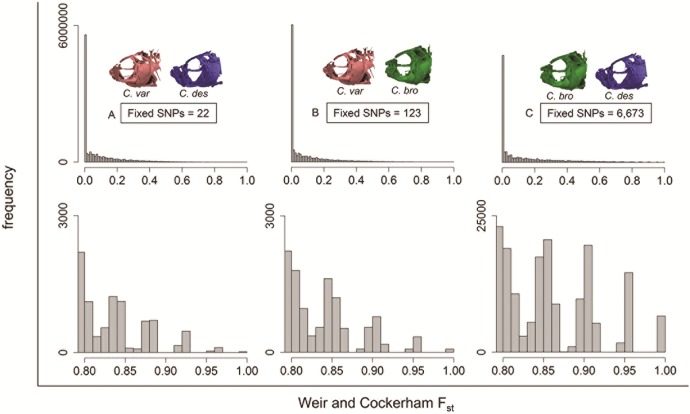
We used genome-wide Fst scans to identify fixed regions associated with each species across nine lake populations on San Salvador and one neighboring island. Very few fixed sites corresponded to the discrete species-specific phenotypes across populations. We found 6,673 sites fixed between specialists, 123 sites fixed between generalist and snail-eater species, and a mere 22 sites fixed between generalist and scale-eater species (fig. 3; supplementary table S1, Supplementary Material online). Eight of these 22 fixed SNPs were also fixed between specialists. Genome-wide mean Fst estimates for each comparison (scale-eater/snail-eater = 0.143, generalist/snail-eater = 0.080, generalist/scale-eater = 0.089) were comparable to previous estimates based on microsatellites (Turner et al. 2008) and RADseq-derived SNPs (Martin and Feinstein 2014).
Fig. 3.
Fst distribution across 9,259 scaffolds. Upper panels show the distribution of genome-wide per-site Fst estimates for 12,586,315 SNPs across all Cyprinodon scaffolds for (A) Cyprinodon variegatus vs. C. desquamator (28 individuals from 10 lake populations), (B) C. variegatus vs. C. brontotheroides (24 individuals from 9 lake populations), and (C) C. brontotheroides vs. C. desquamator (23 individuals from 6 lake populations). Lower panels show the distribution of SNPs with Fst estimates >0.80.
Association Mapping
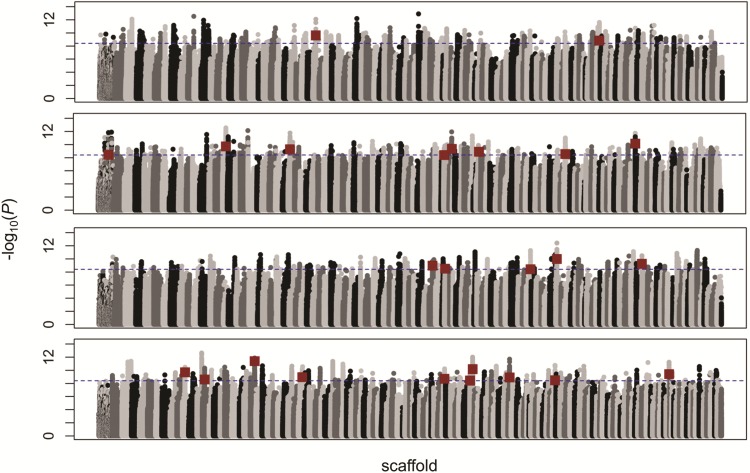
We initially used quantitative trait association mapping in PLINK to identify SNPs associated with jaw length variation among individuals without correcting for population structure, which would remove true positives in addition to false-positives. This uncorrected PLINK analysis identified 9,214 variants associated with jaw size variation between the generalist, scale-eater, and snail-eater species (P < 4.0 × 10−9; fig. 4). Of these variants, 556 were fixed in at least one pairwise species comparison. Five hundred fifty-five of these SNPs were fixed between the two specialists; nine were fixed between the generalist and scale-eater; zero were fixed between the generalist and snail-eater.
Fig. 4.
Quantitative trait association mapping. Log-transformed P values for 12,586,315 SNP associations with jaw size variation estimated by PLINK (n = 37 individuals). Dotted blue line shows Bonferroni-corrected level of significance (P < 4.0 × 10−9). Red squares show the 31 SNPs spread across 25 scaffolds most strongly associated with jaw size that are also fixed between specialists.
Out of the nine PLINK outlier SNPs significantly associated with jaw size and fixed between the generalist and scale-eater, six were located across four different gene regions (magi3, cabp2, lingo1, and pigr) and three unannotated regions (supplementary table S1, Supplementary Material online). Out of the top 20 outliers fixed between the snail-eater and scale-eater, 13 were located across five different gene regions (galr2, gmds, soga3, tmem30a, and plxna2) and seven were located across three unannotated regions (table 1). Combined, PLINK identified 14 divergent regions (nine genic and five unannotated) significantly associated with jaw size and fixed in scale-eaters.
Table 1.
Jaw size Association Statistics and Gene Annotations for SNPs Fixed Between C. desquamator (scale-eater) and C. brontotheroides (snail-eater).
| SNP | Scaffold | Median PIP | PIP Percentile | Median β | P Values | Gene Region |
|---|---|---|---|---|---|---|
| 1 | KL652649.1 | 0.01795 | 1.0000 | 7.764633 | 1.82e−10 | — |
| 2 | KL652649.1 | 0.0124 | 0.9999 | 4.10637 | 3.29e−10 | — |
| 3 | KL653712.1 | 0.00975 | 0.9999 | 1.036102 | 6.65e−11 | FAM49B/ZNF664 |
| 4 | KL653062.1 | 0.0076 | 0.9999 | −2.32365 | 3.82e−13 | GMDS |
| 5a,b | KL652786.1 | 0.0069 | 0.9998 | 2.207843 | 6.66e−12 | GALR2 |
| 6 | KL652758.1 | 0.0066 | 0.9998 | −1.15222 | 1.60e−11 | SOGA3 |
| 7a,b | KL652786.1 | 0.00625 | 0.9998 | 2.018056 | 1.41e−10 | GALR2 |
| 8 | KL652715.1 | 0.0058 | 0.9998 | −2.21671 | 1.62e−09 | PARD3 |
| 9 | KL652649.1 | 0.0052 | 0.9998 | 2.223139 | 1.05e−10 | — |
| 10a | KL653271.1 | 0.0052 | 0.9996 | 0.291561 | 2.05e−10 | ELN |
| 11a | KL652666.1 | 0.0043 | 0.9995 | −0.33468 | 5.30e−10 | DYNC2LI1/ABCG5 |
| 12a | KL654513.1 | 0.00405 | 0.9994 | −0.99172 | 1.24e−11 | PLAUR |
| 13a | KL653122.1 | 0.004 | 0.9994 | 1.029314 | 5.63e−10 | ATP8A1 |
| 14 | KL653046.1 | 0.0039 | 0.9993 | 1.189392 | 3.43e−09 | LRP1B |
| 15 | KL653805.1 | 0.0038 | 0.9991 | 0.473089 | 1.23e−09 | — |
| 16a | KL652666.1 | 0.0037 | 0.9986 | 0.368651 | 1.98e−09 | LYRM7/DYNC2LI1/HINT1 |
| 17 | KL652617.1 | 0.0035 | 0.9983 | 1.517635 | 1.48e−12 | PLXNA2 |
| 18 | KL652527.1 | 0.0034 | 0.9983 | 0.140283 | 8.12e−13 | TMEM30A/FILIP1L |
| 19a | KL652983.1 | 0.0034 | 0.9981 | −0.76248 | 1.06e−09 | SKI |
| 20 | KL653291.1 | 0.00335 | 0.9977 | −0.0425 | 4.74e−11 | — |
| 21 | KL652991.1 | 0.0032 | 0.9967 | −0.66796 | 3.12e−09 | DLGAP1 |
| 22 | KL653356.1 | 0.003 | 0.9961 | 0.979591 | 3.95e−12 | — |
| 23 | KL653356.1 | 0.00295 | 0.9952 | 1.580411 | 4.39e−10 | — |
| 24 | KL653706.1 | 0.00285 | 0.9947 | −0.80369 | 1.60e−09 | PLECKHG6 |
| 25 | KL653420.1 | 0.0028 | 0.9940 | −0.93815 | 7.16e−11 | — |
| 26 | KL652585.1 | 0.00275 | 0.9936 | 1.384922 | 8.98e−11 | FAM172A |
| 27 | KL654513.1 | 0.0027 | 0.9927 | −0.41968 | 5.95e−12 | — |
| 28a | KL653925.1 | 0.00265 | 0.9927 | −0.50498 | 1.15e−10 | B3BNT3/B3GNT2 |
| 29 | KL652727.1 | 0.00265 | 0.9927 | 0.075912 | 1.25e−09 | RABGAP1 |
| 30 | KL653654.1 | 0.00265 | 0.9919 | 0.056305 | 1.96e−09 | COL15A1 |
| 31a | KL652717.1 | 0.0026 | 0.9919 | −0.22127 | 4.65e−10 | ASH1L/DAP3/GBA |
Note.—Fixed SNPs fall within 20-kb windows showing significant association with jaw size after controlling for population structure (Median PIP > 99th percentile).
SNPs in gene regions (underlined) annotated for skeletal system effects.
Overlap with a scaffold within a QTL affecting jaw size (Martin et al. 2016).
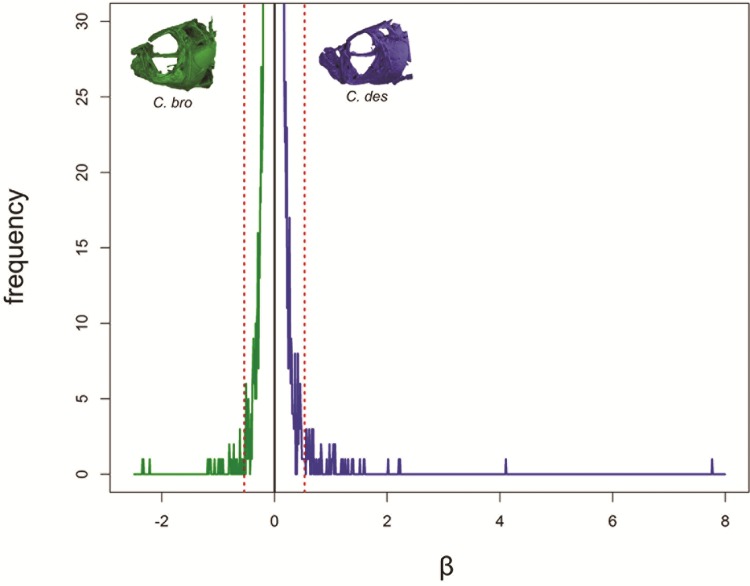
We further assessed the significance of jaw size associations for these top candidate regions containing fixed SNPs by correcting for population structure using two methods. First, we used PLINK to include the top two principal components as covariates in the model (Price et al. 2006; Hunter et al. 2007). This stringent analysis did not identify any SNPs associated with jaw size at our highly conservative Bonferroni-corrected significance threshold (supplementary table S2, Supplementary Material online). However, this likely reflects the fact that the first principal component is significantly correlated with jaw size (P = 0.0013; supplementary fig. S2, Supplementary Material online). Next, we performed independent association mapping with GEMMA, which corrects for population structure by incorporating a genetic relatedness matrix as a covariate in a Bayesian sparse linear mixed model (Zhou et al. 2013). This is a more reliable correction for population structure because the relatedness matrix accounts for pairwise relatedness between individuals; whereas principal components only capture broad linear axes of population structure (Novembre and Stephens 2008; Kang et al. 2010). Because the uncorrected PLINK analysis likely identified a subset of true associations in addition to false positives, we chose to combine uncorrected PLINK results with our corrected GEMMA results in order to evaluate the significance of regions associated with jaw size (following Zhao et al. 2011). We identified 31 regions (20 kb each) implicated by uncorrected PLINK analyses that also showed association with jaw size after correcting for population structure in GEMMA (fig. 4). We assessed the significance of associations based on PIP (posterior inclusion probability) parameters that report the proportion of iterations in which a SNP is estimated to have a non-zero effect on phenotypic variation (effect size β ≠ 0). These 31 regions showed robust association across 10 independent Markov chain Monte Carlo (MCMC) runs. We used β effect size parameters to assess whether regions contributed to larger jaw size (+β) or decreasing jaw size (−β) and found slightly more candidate regions increased (16) than decreased jaw size (13).
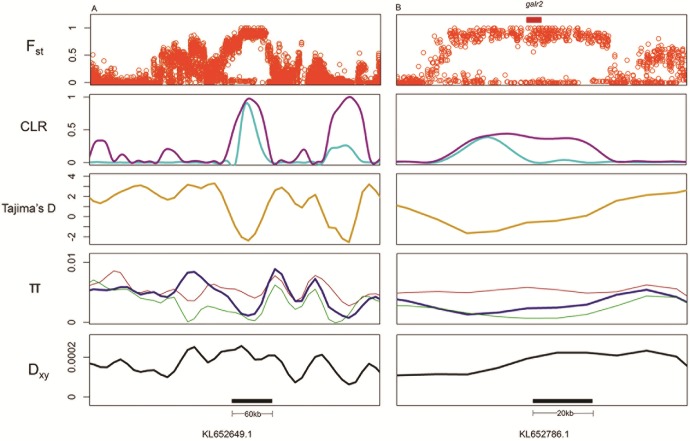
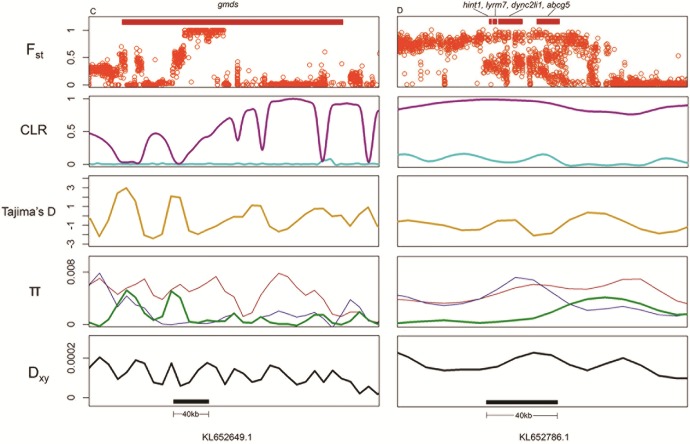
All 31 regions contained variants fixed between specialists and showed outlier median parameter values in the 99th percentile for PIP estimated across all SNPs included in the analysis (following Gompert et al. 2012), indicating an association with jaw size after accounting for population structure (table 1). These regions span 25 scaffolds and contain 29 genes, 11 of which are annotated for skeletal system functions (NCBI Cyprinodon release 100). The top 10 regions with the highest PIP implicated three of the same genes identified by PLINK (galr2, gmds, and soga3) along with three additional genes (fam49b, znf664, and pard3) and one large (60 kb) unannotated region. The unannotated region and galr2 showed the highest β values in the direction of large jaws, whereas the region containing gmds showed the highest β values in the direction of smaller jaws (figs. 5and 6). Encouragingly, galr2 is within a QTL explaining 15% of the variation in jaw size in an F2 intercross between specialist species (Martin et al. 2016).
Fig. 5.
Candidate regions associated with large jaw size. Row 1 shows individual SNP Fst values between Cyprinodon variegatus/C. desquamator. Row 2 shows CLRs estimated by SweeD using an analytical site frequency spectrum assuming a population bottleneck (magenta) and a frequency spectrum calculated without demographic assumptions (cyan) for C. desquamator. Row 3 shows Tajima’s D (dark yellow) for C. desquamator. Row 4 shows within-population diversity (π) (red: C. variegatus, green: C. brontotheroides, blue: C. desquamator). Row 5 shows between-population divergence (Dxy, black) for C. variegatus/C. desquamator. Black bars in row 4 show windows containing fixed SNPs that showed significant association with jaw size in both PLINK and GEMMA association mapping analyses. Red bars in row 1 show exonic and intronic gene regions within windows.
Fig. 6.
Candidate regions associated with small jaw size. Row 1 shows individual SNP Fst values between Cyprinodon variegatus/C. brontotheroides. Row 2 shows CLRs estimated by SweeD using an analytical site frequency spectrum assuming a population bottleneck (magenta) and a frequency spectrum calculated without demographic assumptions (cyan) for C. brontotheroides. Row 3 shows Tajima’s D (dark yellow) for C. brontotheroides. Row 4 shows within-population diversity (π) (red: C. variegatus, green: C. brontotheroides, blue: C. desquamator). Row 5 shows between-population divergence (Dxy, black) for C. variegatus/C. brontotheroides. Black bars in row 4 show windows containing fixed SNPs that showed significant association with jaw size in both PLINK and GEMMA association mapping analyses. Red bars in row 1 show exonic and intronic gene regions within windows.
History of Selection and Demography
To determine whether candidate regions were potentially subject to hard selective sweeps, we interrogated the site frequency spectrum using SweeD (Pavlidis et al. 2013) and Tajima’s D (Tajima 1989). Tajima’s D compares observed nucleotide diversity with diversity under a null model assuming genetic drift, where negative values indicate a reduction in diversity across segregating sites (Tajima 1989). SweeD scans across nonoverlapping windows to calculate a composite likelihood ratio (CLR), comparing a model assuming selection to a null model calibrated by the observed site frequency spectrum across the entire scaffold. Both of these statistics infer selection based on the shape of the site frequency spectrum, which can also be influenced by changes in effective population size over time (Galtier et al. 2000; Nielsen 2005; Nielsen et al. 2005). We therefore used the Multiple Sequentially Markovian Coalescent (MSMC) (Schiffels and Durbin 2014) to infer historical population sizes in all three species and applied these estimates to analytically calculate the expected neutral site frequency spectrum in SweeD. MSMC results suggest that that the population size of all three species has been decreasing across at least the last 10,000 years (∼20,000 generations) (supplementary fig. S3, Supplementary Material online). This model suggests a population decrease that is consistent with changes in sea level during the last glacial maximum when saline lakes on San Salvador Island first appeared (Mylroie and Hagey 1995; Turner et al. 2008). We first looked for signatures of hard sweeps in both specialist populations by analyzing the site frequency spectrum without demographic assumptions. Next, we calculated the expected neutral site frequency spectrum assuming a population decline as suggested by our demographic model. Windows that showed CLRs above the 95th percentile across their respective scaffolds in this second analysis were interpreted as regions that recently experienced a hard sweep.
Out of our 31 candidate regions affecting jaw size, six were consistent with hard selective sweeps. One candidate region was excluded from these analyses because it fell within a small scaffold that could not be used to sample an adequate background distribution of heterogeneity. All six regions also showed negative estimates of Tajima’s D (figs. 5and 6). The 60-kb unannotated region associated with large jaws showed the strongest signatures of selection, followed by a 40-kb region associated with small jaws. This smaller region contains four genes all annotated for skeletal system effects (hint1, lyrm7, dync2li1, and abcg5) (fig. 6). Five of the six regions that experienced strong selection also show reduced within-population diversity (π) in the specialist species and increased between-population divergence (Dxy) when compared with generalists (figs. 5and 6). This pattern may suggest that strong selection on a beneficial allele reduced diversity within specialists across candidate regions. Importantly, low diversity in these regions is not shared between specialists and generalists, possibly suggesting that selection unique to each specialist was responsible for reduced diversity. This combined evidence implicates divergent regions influencing jaw morphology that experienced strong selection within the specialist linages. Finally, we did not find evidence for hard sweeps in 25 of our 31 candidate regions, possibly suggesting that multiple haplotypes were swept to fixation (Hermisson and Pennings 2005; Jensen 2014).
More Large-Effect Alleles Were Associated with Large Jaws than Small Jaws
Based on differences in the phenotypic distance across fitness valleys separating each specialist species from its putative generalist ancestor (fig. 1), we predicted to find more large-effect SNPs associated with large jaws than with small jaws. There are two lines of evidence supporting this prediction. First, we directly compared positive and negative effect sizes for regions associated with small jaws (−β) and large jaws (+β). Our β outlier threshold included 83 of the regions most strongly associated with jaw size that had the largest effects on jaw size (β > 99.9th percentile). We found more than twice as many outlier SNPs with large effects on increasing jaw size (n = 56) compared with large-effects on decreasing jaw size (n = 27) (fig. 7). Second, we identified five times fewer SNPs fixed between the generalist and scale-eater (n = 22) than SNPs fixed between the generalist and snail-eater species (n = 123) (fig. 3), supporting the prediction that SNPs with larger effect sizes should fix faster than SNPs with smaller effects, especially given short divergence times (Griswold 2006; Yeaman and Whitlock 2011).
Fig. 7.
More large-effect regions control large jaw phenotypes. Distribution of effect size posterior parameters (β) estimated using GEMMA for 20-kb regions with a posterior inclusion probability (PIP) greater than zero. We report median β and PIP taken across 10 independent MCMC runs. Association mapping analysis shows twice as many outlier regions with large effects (β > 99th percentile [dotted red line]) on increasing jaw size (n = 56) compared with large-effects on decreasing jaw size (n = 27).
Discussion
Genome-wide divergence scans revealed that the evolution of trophic novelty in two ecological specialists involved surprisingly few genetic variants fixed between species. We determined which of these fixed variants influenced the most rapidly diversifying trait in this radiation—jaw size—using quantitative trait association mapping. We uncovered 31 candidate regions fixed between species and associated with jaw size after correcting for population structure, with six of these regions showing signs of hard selective sweeps. We used these data to test the prediction that more large-effect variants should affect large-jawed scale-eaters than small-jawed snail-eaters.
Genetic Basis of Jaw Size Divergence
We report 31 divergent candidate regions associated with jaw size among San Salvador Cyprinodon pupfish. We identified these regions using 37 genomes sequenced to 7× coverage across nine populations. This is significant because much work on the genetic basis of adaptation has relied on reduced representation strategies (i.e., RADseq, RNAseq) that likely overlook loci contributing to adaptation (Hoban et al. 2016). All 31 regions contained SNPs fixed between specialists that were significant in both association mapping approaches. We searched genes listed under the “skeletal system” ontology in the phenotype database Phenoscape (Mabee et al. 2012; Midford et al. 2013; Manda et al. 2015, Edmunds et al. 2016) finding matches for 11 genes within candidate regions (table 1). The most strongly associated gene annotated for skeletal effects, galr2, is interesting for several reasons. The protein product of galr2 is a transmembrane galanin receptor with a role in numerous physiological functions (Webling et al. 2012). Galanin, the binding substrate of GALR2, has been shown to facilitate bone formation by increasing the size and proliferation of osteoblasts (McDonald et al. 2007; McGowen et al. 2014). Additionally, the scaffold containing galr2 overlaps with a moderate effect QTL explaining 15% of the variation in jaw size in an independent F2 mapping cross between the two specialist pupfishes (Martin et al. 2016), increasing confidence in our association mapping strategy. The gene region most associated with smaller jaws was gmds, which is important for tagging cell surface proteins involved in many cellular processes such as cell growth, migration, and apoptosis (Moriwaki et al. 2009). This gene represents a novel candidate for craniofacial effects. We identified four genes annotated for skeletal effects spanning a 40-kb region that showed significant association with smaller jaws (hint1, lyrm7, dync2li1, and abcg5). Mutations in lyrm7 have been associated with mitochondrial complex III deficiency, a disorder characterized by skeletal muscle weakness and weak muscle tone (hypotonia) (Invernizzi et al. 2013). Mutations in dync2li1, a gene involved in skeletogenesis and expressed in the cartilage of growth plates, have been shown to cause short rib polydactyly skeletal disorders (Taylor et al. 2015). Thus, our candidate regions are associated with genes involved in bone and skeletal muscle development—the two tissues most differentiated in the external anatomy of San Salvador pupfishes. Finally, we identified eight SNPs fixed between the generalist and scale-eater that were also fixed between specialists, possibly indicating that these regions affect traits in both specialists. However, none of these overlapping SNPs showed significant association with jaw size after correcting for population structure.
Caveats to Our Association Mapping Approach
The significance of our association mapping results should be interpreted with caution. Our principal component analysis revealed significant population structure associated with four different clusters of jaw sizes across species and between two different clusters of large- and short-jawed scale-eaters among lake populations (fig. 2A), which likely created a bias toward false-positive associations implicated by PLINK. Furthermore, when we accounted for this structure by incorporating the first two principal components as covariates in the model, we did not find any SNPs reaching significance at our conservative Bonferroni-corrected level of significance. However, this analysis almost certainly filtered out true associations because the first principal component is highly correlated with the jaw size. We reassessed the significance of these associations by using GEMMA—a complementary mapping approach that corrects for population structure by incorporating a genetic relatedness matrix into a Bayesian sparse linear mixed model (BSLMM) (Zhao et al. 2013). We used the BSLMM to investigate the genetic architecture of jaw size—a complex polygenic trait (Helms and Schneider 2003; Albertson et al. 2003; Pallares et al. 2014; Porto et al. 2016; Martin et al. 2016). Our PIP estimates for regions associated with jaws size variation suggest that the jaw shape is controlled by many loci of relatively small effect (see Comeault et al. 2016 for an example of BSLMMs used for a simple Mendelian color locus; see Gompert et al. 2012, Chaves et al. 2013 for complex traits). Indeed, a linkage mapping analysis of phenotypic diversity in an F2 intercross between specialists identified QTL with only moderate effects explaining up to 15% of the variation in jaw size (Martin et al. 2016).
Although uncommonly implemented across species, association mapping techniques have proven successful at identifying associations across varieties, subspecies, and ecotypes with greater genetic differentiation (Fournier-Level et al. 2011; Zhao et al. 2011; Pallares et al. 2014) or minimal divergence similar to that of San Salvador pupfishes (Comeault et al. 2014). Association mapping within populations may result in spurious associations due to background population structure (Kang et al. 2010; Marchini et al. 2011), but our sampling of multiple, relatively isolated populations may have provided greater resolution of candidate regions due to sampling a diversity of genetic backgrounds. We do not expect false associations due to sequencing error biases because mean coverage across candidate SNPs mirrored coverage across individuals (range: 4.9×–6.6×). It is possible that our methods excluded significant SNPs as false-negatives. We examined the position of all 22 SNPs fixed between the generalist and scale-eater for gene annotations (supplementary table S1, Supplementary Material online), finding four within the gene col11a1. None of these four SNPs showed a significant association with jaw size in either mapping approach; however, col11a1 has been associated with jaw skeleton phenotypes in humans (Hufnagel et al. 2014). It is unclear whether col11a1 variants influence jaw divergence in pupfishes but escaped detection in both mapping analyses.
Variants with Relatively Large Effects Drive Divergence across a Large Fitness Valley
Orr’s extension of Fisher’s geometric model of adaptation predicts that de novo mutations with a large effect on phenotypic variation are more likely to be fixed during adaptation toward distant phenotypic optima than nearby optima (Orr 1998, 2005). This distribution of effect sizes for mutations fixed during adaptation has been supported by QTL mapping analyses in multiple systems (Baxter et al. 2009; Rogers et al. 2012; Conte et al. 2015; Martin et al. 2016). We show that the phenotypic distance across the fitness valley is larger between the generalist and large-jawed scale-eater species than between the generalist and small-jawed snail-eater species (fig. 1; supplementary fig. S1, Supplementary Material online) (Martin and Wainwright 2013c; Martin 2016b). Based on this adaptive landscape, we predicted more large-effect variants associated with large jaws than with small jaws. Adaptive landscapes are not static, and the distance between fitness optima may have fluctuated over the past 10,000 years of divergence in this system (Merrell 1994; Hansen et al. 2008). However, scale-eater prey has been available since the initial colonization of San Salvador by generalists. Furthermore, the availability of hard-shelled prey (ostracods, gastropods) is likely not substantially depleted in these lakes due to the rarity of snail-eater specialists (<5% of the total pupfish population) and high productivity of eutrophic saline lakes (Martin and Wainwright 2013a).
Although Orr’s model assumes a single population and ignores standing genetic variation (Orr, 1998; Dittmar et al. 2016) and thus may not apply here, we present two lines of evidence supporting the model in this system. First, we found twice as many outlier regions with the largest effect sizes associated with larger jaws than with smaller jaws (fig. 7). Second, there are more than five times as many fixed SNPs between the generalist and snail-eater than between the generalist and scale-eater (fig. 3). Divergent demographic histories could account for this pattern; however, similar changes in population size over 20,000 generations for each species (supplementary fig. S3, Supplementary Material online), combined with evidence for gene flow between species in sympatry (Martin and Feinstein 2014), suggest that this is not the case. Large-effect variants are predicted to become fixed between species more quickly than variants with smaller effects in the presence of gene flow, especially when divergence time is short (Griswold 2006; Yeaman and Whitlock 2011). This difference suggests that more large-effect alleles influencing jaw size were necessary to evolve the specialized scale-eating phenotype, whereas smaller jaw phenotypes may result from more alleles with small to moderate effect sizes. Further support for this prediction within the San Salvador pupfish system comes from a complementary linkage mapping study that found moderate effect QTL explaining up to 15% of variance in jaw size within an F2 intercross between both specialists but no significant QTL with effects on nasal protrusion—a trait unique to the snail-eater species (Martin et al. 2016). Overall, these data agree with Orr’s model, suggesting that large-effect loci are used to cross larger distances between fitness optima (Orr 1998, 2005).
Strong Selection on Candidate Regions
We reasoned that strong selection on variants within candidate genes would be necessary for extreme shifts in ecological specialization. This can result in a pattern of hard selective sweeps resulting from a single haplotype rising quickly to fixation in a population derived from de novo mutation or standing variation (Orr and Betancourt 2001; Jensen 2014). Alternatively, a soft sweep occurs when selection drives multiple adaptive haplotypes to fixation—a pattern that can only result from selection on standing variation (Hermisson and Pennings 2005; Jensen 2014). Currently, there are no theoretical predictions about the likelihood of adaptation from standing genetic variants versus de novo mutation for populations with small values of within-population divergence such as ours (Dittmar et al. 2016), and the relative importance of hard sweeps versus soft sweeps during adaptation is a subject of much debate (Hermisson and Pennings 2005; Pritchard et al. 2010; Jensen 2014; Garud et al. 2015; Schrider et al. 2015). In order to investigate whether regions associated with large jaws experienced hard sweeps, we examined the site frequency spectrum across candidate regions looking for signature shifts in variant frequencies across scaffolds.
Changes in ancestral population size can produce similar signals to hard selective sweeps. To account for this, we first estimated the effective population size changes of all three species over the past 20,000 generations and observed a 100-fold population decrease occurring within the same time as we predict ancestral populations colonized lakes on San Salvador Island (Mylroie and Hagey 1995; Turner et al. 2008; Martin and Wainwright 2013a). We next calculated a neutral site frequency spectrum under this bottleneck scenario and still detected hard sweeps in six of our candidate regions (three contributing to smaller jaws and three to larger jaws) (figs. 5and 6). Regions containing hint1, lyrm7, dync2li1, and abcg5 along with a large unannotated region showed the strongest signs of hard sweeps after accounting for demographic history (fig. 6). Low estimates of Tajima’s D, low nucleotide diversity in specialists, and high divergence between specialists and generalists lend further support for past selection at these loci (Tajima 1989; Nielsen 2005; Nielsen et al. 2005; Cruickshank and Hahn 2014). Alternatively, low recombination rates could account for low nucleotide diversity and high divergence at these loci (Nachman and Payseur 2012). A decrease in population size can also reduce genome-wide nucleotide diversity (Tajima 1989; Galtier et al. 2000). However, our demographic analysis indicates comparable decreases in population size for the generalist and specialist populations. Interestingly, 25 of our 31 strongest candidate regions do not show signs of hard selective sweeps. This may support a history of soft selective sweeps, where beneficial standing genetic variants were swept to fixation resulting in multiple haplotypes at candidate loci (Hermisson and Pennings 2005; Jensen 2014).
Conclusions
The San Salvador Cyprinodon pupfish radiation has proven itself as an excellent system for investigating the genetic basis of novel trophic specialization. The extensive phenotypic diversity among these species results from low levels of genetic divergence and very few fixed variants. Thirty-one regions with fixed variants showed significant associations with jaw size—the most rapidly diversifying trait in this system (Martin 2016a). Selection scans across regions associated with the jaw size revealed a history of novel adaptation driven in part by hard selective sweeps. Additionally, we identified more variants with larger effects used to adapt to a more distant phenotypic optimum—consistent with Orr’s model of adaptation. Our evidence for the evolution of larger jaw size raises an alluring question with broad implications for research on adaptation: why has trophic novelty evolved exclusively on San Salvador Island? It is surrounded by islands with comparable physiochemistry, lake areas, macroalgae communities, and generalist Cyprinodon pupfish populations that exhibit similar genetic, phenotypic, and dietary diversity to generalist populations on San Salvador Island. This is consistent with similar levels of ecological opportunity on neighboring islands without specialists (Martin 2016a). Nonetheless, scale-eating and snail-eating species appear to be endemic to a single island. Answering this question will require continued exploration of the ecological and genetic factors shaping this exceptional case of rapid ecological specialization.
Materials and Methods
Study System and Sample Collection
Individuals were caught from hypersaline lakes on San Salvador Island, Bahamas using a hand net or seine net. Fourteen scale-eaters were sampled from six populations; 10 snail-eaters were sampled from four populations; and 11 generalists were sampled from nine populations on San Salvador and a neighboring island. Samples were collected from nine isolated lakes on San Salvador (Great Lake, Stout’s Lake, Oyster Lake, Little Lake, Crescent Pond, Moon Rock, Mermaid’s Pond, Osprey Lake, Pigeon Creek, and one closely related outgroup C. variegatus population from Lake Cunningham, New Providence Island, Bahamas). Fish were euthanized in an overdose of buffered MS-222 (Finquel, Inc.) following approved protocols from the University of California, Davis Institutional Animal Care and Use Committee (#17455) and University of California, Berkeley Animal Care and Use Committee (AUP-2015-01-7053) and stored in 95–100% ethanol.
Morphometrics
Upper jaw length was measured using digital calipers from external landmarks on ethanol-preserved tissue specimens from the point of rotation on the quadroarticular joint (lower jaw joint), to the tip of the most anterior tooth on the dentigerous arm of the premaxilla. Body length was measured from the midline of the posterior margin of the caudal peduncle to the tip of the lower jaw (the nasal protrusion on some preserved C. brontotheroides samples obscured the upper jaw). In order to remove the effects of size variation, all measurements were log transformed and regressed against log-transformed body length. We fit a log-transformed trait by log-transformed body length linear regression and used the residuals for association mapping.
Genomic Sequencing and Bioinformatics
DNA was extracted from muscle tissue using DNeasy Blood and Tissue kits (Qiagen, Inc.) and quantified on a Qubit 3.0 fluorometer (Thermofisher Scientific, Inc.). PCR-free Truseq-type genomic libraries were prepared using the automated Apollo 324 system (WaferGen BioSystems, Inc.) at the Vincent J. Coates Genomic Sequencing Center (QB3). Samples were fragmented using Covaris sonication, barcoded with Illumina indices, and quality checked using a Fragment Analyzer (Advanced Analytical Technologies, Inc.). Nine to ten samples were pooled in four different libraries for sequencing on four lanes of Illumina 150PE Hiseq4000.
We mapped raw reads from 37 individuals to the Cyprinodon reference genome (NCBI, C.variegatus annotation release 100; total sequence length = 1,035,184,475; number of scaffolds = 9,259; scaffold N50 = 835,301; contig N50 = 20,803) with the Burrows-Wheeler Alignment Tool (Li and Durbin 2009 [v. 0.7.12]). The Picard software package (http://broadinstitute.github.io/picard/; last accessed December 15, 2016) was used to identify duplicate reads (MarkDuplicates) and create BAM indexes (BuildBamIndex). We followed the best practices guide recommended by the Genome Analysis Toolkit (DePristo et al. 2011; Van der Auwera et al. 2013 [v. 3.5]) in order to call and refine our SNP variant dataset using Haplotype Caller. Filtering SNP variants in GATK for model organisms conventionally requires high-quality known variants to act as a reference. Instead we called SNPs in our dataset using conservative hard-filtering parameters following GATK guidelines (DePristo et al. 2011; Marsden et al. 2014): Phred-scaled variant confidence divided by the depth of nonreference samples >2.0, Phred-scaled P-value using Fisher's exact test to detect strand bias > 60, Mann–Whitney rank-sum test for mapping qualities (z > 12.5), Mann–Whitney rank-sum test for distance from the end of a read for those with the alternate allele (z > 8.0). Further filtering was performed using VCFtools (Danecek et al. 2011 [v. 0.1.14]) to only include individuals with a genotyping rate above 90% (no individuals were excluded by this filter) and SNPs with minor allele frequencies higher than 5%. Our final filtered dataset included 12,586,315 variant sites across 37 individuals with a mean aligned read sequencing depth of 7.19 per individual (range: 5.15–9.28).
Population Genetic Analyses
Our filtered dataset was converted from Variant Call Format to PED and MAP files using VCFtools. In order to visualize population structure in our samples (McVean 2009), we performed principal component analyses using eigenvectors output by PLINK’s “pca” function (Purcell et al. 2007 [v. 1.9]). We plotted the first two principal components in R (R Core Team 2016 [v. 3.2.4]).
Genome-wide Fst for pairwise species comparisons was calculated for each variant site using VCFtools’ weir-fst-pop function. Within-population nucleotide diversity (π) was estimated across 10-kb windows using VCFtools’ window-pi function. We used a custom python script to extract allele frequencies from the VCF files that were then used to estimate between-population divergence (Dxy) with a separate R script (provided by A. Comeault). We calculated Dxy across 10-kb windows for ten scaffolds (totaling 9.7-Mb) containing candidate SNPs for jaw size variation.
Association Mapping
We first estimated SNP × trait associations for jaw size variation using the PLINK assoc function that fits a standard linear regression of phenotype on allele frequency and subsequently estimates P values for each SNP with an asymptotic Wald test. We set a genome-wide level of significance using Bonferroni correction (0.05/12,586,315 = 4.0 × 10−9). Although this correction is highly conservative (Johnson et al. 2010), we are concerned here with only the most significant outliers. We then used the first two principal components explaining 9.44% of the variance in our dataset to correct for population structure by incorporating them into the model as covariates. We also performed an alternative method of mapping using a BSLMM implemented in the GEMMA software package (Zhou et al. 2013 [version 0.94.1]). GEMMA’s BSLMM combines linear mixed models, which assume every genetic variant has an effect on phenotype, and sparse regression models, which assume few variants will affect the phenotype. Importantly, GEMMA controls for background population structure by estimating and incorporating a kinship relatedness matrix as a covariate in the regression model. The BSLMM uses MCMC to estimate the proportion of phenotypic variation explained by every SNP included in the analysis (PVE), the proportion of phenotypic variation explained by SNPs of large effect (PGE), which are defined as SNPs with a non-zero effect on the phenotype, and the number of large-effect SNPs needed to explain PGE (nSNPs). GEMMA calculates an effect size coefficient (β) and a posterior inclusion probability (PIP) for each SNP. Markers with non-zero values of β are inferred to affect phenotypic variation in one iteration of the MCMC sampler. β can be a positive or negative integer based on the direction of association, so we present estimates of this parameter in terms of its absolute value. PIP reports the proportion of iterations in which a SNP is estimated to have a non-zero effect on phenotypic variation (β ≠ 0). This estimate might be difficult to interpret for SNPs in high linkage disequilibrium (LD) because tightly linked neutral and causal SNPs could each have a high probability of inclusion in separate iterations. We estimated pairwise LD (r2) between SNPs on the largest scaffold (4.5 Mb) and found that linkage dropped to background levels between SNPs separated by >20 kb (r2 < 0.1) (supplementary fig. S4, Supplementary Material online). Thus, we summed β and PIP parameters across 20-kb windows to account for any unwanted dispersion of these values across SNPs in LD.
We performed 10 independent runs of the BSLMM for all 37 individuals (following Comeault et al. 2016) using a step size of 100 million with a burn-in of 50 million steps. We used GEMMA to assess the significance of regions associated with jaw size variation and report the median β and PIP summed across windows for the 10 independent MCMC runs. Independent runs were consistent in reporting the strongest associations for the same 20-kb windows. In order to compare the abundance and effect size of candidate loci between specialist species, we plotted the frequency of β estimates for regions with effects on smaller jaws (negative β) and larger jaws (positive β).
Identification of Candidate Genes
We restricted our search to those regions both fixed between species and associated with the jaw size. Accordingly, candidate regions met two rigorous criteria: 1) they must contain one or more SNPs that are fixed in at least one pairwise species comparison and 2) they show significant association with the jaw size in both association mapping analyses (P < 4.0 × 10−9 and outlier PIP estimates above the 99th percentile). We also took advantage of a recent linkage mapping analysis of phenotypic diversity in San Salvador Cyprinodon pupfish by comparing our candidate regions for overlap with the four scaffolds containing QTL with moderate effects on jaw size in an F2 intercross between specialists (Martin et al. 2016).
In addition to our candidate regions, we also report association mapping statistics and gene annotations for all 22 SNPs fixed between the generalist and scale-eater species. We used the Phenoscape Knowledgebase (phenoscape.org; Mabee et al. 2012; Midford et al. 2013; Manda et al. 2015, Edmunds et al. 2016) to determine whether any of the annotated genes within fixed SNP regions were associated with skeletal system phenotypes across model taxa.
Detecting Selection and Demographic History
We first calculated Tajima’s D for each species in 10-kb genomic windows using VCFtools’ TajimaD function. This statistic compares observed nucleotide diversity to diversity under a null model assuming genetic drift, where negative values indicate a reduction in diversity across segregating sites that may be due to positive selection (Tajima 1989). Second, we used the SweepFinder method first developed by Nielsen et al. (2005) and implemented in the software package SweeD (Pavlidis et al. 2013). SweeD scans across nonoverlapping windows to calculate a CLR using a comparison between two contrasting models. The first assumes a window has undergone a recent selective sweep, whereas the second assumes a null model where the site frequency spectrum of the window does not differ from that of the entire scaffold. Windows with high CLR suggest a history of selective sweeps because the site frequency spectrum is shifted toward low-frequency– and high-frequency–derived variants (Pavlidis et al. 2013; Nielsen et al. 2005).
Various demographic histories can shift the distribution of low-frequency– and high-frequency–derived variants to falsely resemble signatures of hard selection (Galtier et al. 2000; Nielsen 2005; Nielsen et al. 2005). In order to account for demography, we used the MSMC (Schiffels and Durbin 2014) to infer historical effective population sizes (Ne) in all three species. MSMC is an extension of the Pairwise Sequentially Markovian Coalescent (PSMC) (Li and Durbin 2011), which uses a hidden Markov model to scan genomes analyzing patterns of heterozygosity where long DNA segments with low heterozygosity reflect recent coalescent events. The rate of coalescent events is then used to estimate Ne at a given time. We ran MSMC on unphased GATK-called genotypes from the 100 largest scaffolds for each individual separately, thus using only two haplotypes as in PSMC (the analysis of multiple individuals simultaneously would inform on more recent timescales, but requires phasing). As recommended in the MSMC documentation, we masked out sites with less than half or more than double the mean coverage for that individual, or with a genotype quality below 20. We also excluded sites with <10 reads as recommended by Nadachowska-brzyska et al. (2016). Nadachowska-brzyska et al. (2016) also recommend to only use individuals with a mean coverage of at least 18×. However, all our individuals were sequenced at a lower coverage, and we included only the seven individuals with a coverage of at least 7.5×. This means that our MSMC results should be interpreted with caution; however, the consistency among individuals of the same species (see supplementary fig. S3, Supplementary Material online) suggests that the general patterns of the analysis are likely to be robust.
To scale the output of MSMC to real time and population sizes, we assumed a 6-month generation time (Martin et al. 2016c) and a mutation rate measured for cichlids (6.6 × 10−8 mutations per site per year, Recknagel et al. 2013), one of the most closely related fish groups with an available estimate of spontaneous mutation rates.
We used ancestral population sizes determined by MSMC to analytically calculate the expected neutral site frequency spectrum with SweeD. We used the “-eN” flag to model a 100-fold population decrease around 10,000 years ago (20,000 generations). We used a grid size of 1 kb across our folded SNP dataset, which defined sites as ancestral or derived variants based on the major and minor allele frequencies. We also ran SweeD without demographic assumptions for comparison. Because the significance of the CLR depends on the background site frequency spectrum of each scaffold, we compared the percentile of each likelihood estimate across unique scaffolds for candidate regions. Windows that showed CLRs above the 95th percentile across their respective scaffolds under the assumptions of a population decrease determined by MSMC were interpreted as regions that recently experienced a hard sweep.
The size of the scaffolds containing jaw size candidate loci should be large enough to discover regions under strong selection. Out of our 31 candidate regions, we excluded one because it fell within a small scaffold that could not be used to sample an adequate background distribution of heterogeneity. Of the 25 scaffolds containing the 31 regions that we analyzed with SweeD, the mean scaffold length was 863,416 bp. Furthermore, we set a conservative threshold (>95th percentile) to define regions that have experienced hard sweeps. We plot π, Dxy, and Tajima’s D across 10-kb windows using a cubic smoothing spline in R.
Supplementary Material
Supplementary data are available at Molecular Biology and Evolution online.
Author Contributions
J.A.M. wrote the manuscript, measured trait data, and conducted all bioinformatic and population genetic analyses. Both authors contributed to the conception and development of the ideas and revision of the manuscript.
Supplementary Material
Acknowledgments
This study was funded by the University of North Carolina at Chapel Hill, the Center for Population Biology, and ARCS Foundation awards to CHM. We thank Daniel Matute for helpful comments during the preparation of this article; Jelmer Poelstra for help with PSMC analyses; Aaron Comeault, David Turissini, and Sara Suzuki for valuable discussions and computational assistance; Katelyn Gould for performing the DNA extractions; the Vincent J. Coates Genomic Sequencing Center and Functional Genomics Laboratory at UC Berkeley, supported by NIH S10 OD018174 Instrumentation Grant, for whole-genome resequencing; the Gerace Research Centre for accommodation; and the Bahamian government for permission to conduct this research.
References
- Albertson RC, Streelman JT, Kocher TD.. 2003. Directional selection has shaped the oral jaws of Lake Malawi cichlid fishes. Proc Natl Acad Sci U S A. 100:5252–5257. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Andolfatto P. 2001. Adaptive hitchhiking effects on genome variability. Curr Opin Genet Dev. 11:635–641. [DOI] [PubMed] [Google Scholar]
- Barrett RDH, Schluter D.. 2008. Adaptation from standing genetic variation. Trends Ecol Evol. 23:38–44. [DOI] [PubMed] [Google Scholar]
- Baxter SW, Johnston SE, Jiggins CD.. 2009. Butterfly speciation and the distribution of gene effect sizes fixed during adaptation. Heredity 102:57–65. [DOI] [PubMed] [Google Scholar]
- Byers KJRP, Xu S, Schlüter PM.. 2016. Molecular mechanisms of adaptation and speciation: why do we need an integrative approach? Mol Ecol. Advance Access published May 27, 2016, doi:10.1111/mec.13678. [DOI] [PubMed] [Google Scholar]
- Carneiro M, Albert FW, Afonso S, Pereira RJ, Burbano H, Campos R, Melo-Ferreira J, Blanco-Aguiar JA, Villafuerte R, Nachman MW, et al. 2014. The genomic architecture of population divergence between subspecies of the European Rabbit. PLoS Genet. 10(8):e1003519. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chaves JA, Cooper EA, Hendry AP, Podos J, Albert J, Uy C.. 2016. Genomic variation at the tips of the adaptive radiation of Darwin’s finches. Mol Ecol. 25:5282–5295. [DOI] [PubMed] [Google Scholar]
- Comeault AA, Soria-Carrasco V, Gompert Z, Farkas TE, Buerkle CA, Parchman TL, Nosil P.. 2014. Genome-wide association mapping of phenotypic traits subject to a range of intensities of natural selection in Timema cristinae. Am Nat. 183:711–727. [DOI] [PubMed] [Google Scholar]
- Comeault AA, Carvalho CF, Dennis S, Nosil P.. 2016. Color phenotypes are under similar genetic control in two distantly related species of Timema stick insect. Evolution 70(6):1283–1296. [DOI] [PubMed] [Google Scholar]
- Conte GL, Arnegard ME, Best J, et al. 2015. Extent of QTL reuse during repeated phenotypic. Genetics 201:1189–1200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Coyne J, Orr HA.. 2004. Speciation. Sunderland, ( MA: ): Sinauer Associates. [Google Scholar]
- Cruickshank TE, Hahn MW.. 2014. Reanalysis suggests that genomic islands of speciation are due to reduced diversity, not reduced gene flow. Mol Ecol. 23:3133–3157. [DOI] [PubMed] [Google Scholar]
- Edmunds RC, Su B, Balhoff JP, et al. 2016. Phenoscape: identifying candidate genes for evolutionary phenotypes. Mol Biol Evol. 33:13–24. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Danecek P, Auton A, Abecasis G, Albers CA, Banks E, DePristo MA, Handsaker RE, Lunter G, Marth GT, Sherry ST, et al. 2011. The variant call format and VCFtools. Bioinformatics 27:2156–2158. [DOI] [PMC free article] [PubMed] [Google Scholar]
- DePristo MA, Banks E, Poplin R, Garimella KV, Maguire JR, Hartl C, Philippakis AA, del Angel G, Rivas MA, Hanna M, et al. 2011. A framework for variation discovery and genotyping using next-generation DNA sequencing data. Nat Genet. 43:491–498. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dittmar EL, Oakley CG, Conner JK, Gould BA, Schemske DW.. 2016. Factors influencing the effect size distribution of adaptive substitutions. Proc Biol Sci. 283:20153065.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fournier-Level A, Korte A, Cooper MD, Nordborg M, Schmitt J, Wilczek AM.. 2011. A map of local adaptation in Arabidopsis thaliana. Science 334:86–89. [DOI] [PubMed] [Google Scholar]
- Galtier N, Depaulis F, Barton NH.. 2000. Detecting bottlenecks and selective sweeps from DNA sequence polymorphism. Genetics 155:981–987. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Garud NR, Messer PW, Buzbas EO, Petrov DA.. 2015. Recent selective sweeps in North American Drosophila melanogaster show signatures of soft sweeps. PLoS Genet 11:1–32. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gompert Z, Lucas LK, Nice CC, Buerkle CA.. 2012. Genome divergence and the genetic architecture of barriers to gene flow between Lycaeides idas and L. melissa. Evolution 67-9:2498–2514. [DOI] [PubMed] [Google Scholar]
- Griswold CK. 2006. Gene flow’s effect on the genetic architecture of a local adaptation and its consequences for QTL analyses. Heredity (Edinb) 96:445–453. [DOI] [PubMed] [Google Scholar]
- Hansen TF, Pienaar J, Orzack SH.. 2008. A comparative method for studying adaptation to a randomly evolving environment. Evolution 62(8): 1965–1977. [DOI] [PubMed] [Google Scholar]
- Helms JA, Schneider RA.. 2003. Cranial skeletal biology. Nature 423:326–331. [DOI] [PubMed] [Google Scholar]
- Hoban S, Kelley JL, Lotterhos KE, Antolin MF, et al. 2016. Finding the genomic basis of local adaptation: pitfalls, practical solutions, and future directions. Am Nat. 188:379–397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hermisson J, Pennings PS.. 2005. Soft sweeps: molecular population genetics of adaptation from standing genetic variation. Genetics 169:2335–2352. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hufnagel SB, Weaver KN, Hufnagel RB, Bader PI, Schorry EK, Hopkin RJ.. 2014. A novel dominant COL11A1 mutation resulting in a severe skeletal dysplasia. Am J Med Genet Part A 164:2607–2612. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hunter DJ, Kraft P, Jacobs KB, et al. 2007. A genome-wide association study identifies alleles in FGFR2 associated with risk of sporadic postmenopausal breast cancer. Nat Gen 39:870–874. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Invernizzi F, Tigano M, Dallabona C, et al. 2013. A Homozygous Mutation in LYRM7/MZM1L Associated with Early Onset Encephalopathy, Lactic Acidosis, and Severe Reduction of Mitochondrial Complex III Activity. Hum Mutat.: 1–4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Irwin DE, Alcaide M, Delmore KE, Irwin JH, Owens GL.. 2016. Recurrent selection explains genomic regions of high relative but low absolute differentiation in the greenish warbler ring species. bioRxiv Available from: biorxiv.org/content/early/2016/02/26/041467.abstract [DOI] [PubMed]
- Jensen JD. 2014. On the unfounded enthusiasm for soft selective sweeps. Nat Commun. 5:5281.. [DOI] [PubMed] [Google Scholar]
- Johnson RC, Nelson GW, Troyer JL, Lautenberger JA, Kessing BD, Winkler CA, O’Brien SJ.. 2010. Accounting for multiple comparisons in a genome-wide association study (GWAS). BMC Genomics 11:724.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kang HM, Sul JH, Service SK, Zaitlen NA, Kong SY, Freimer NB, Sabatti C, Eskin E.. 2010. Variance component model to account for sample structure in genome-wide association studies. Nat. Genet 42:348–354. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lamichhaney S, Han F, Berglund J, Wang C, Almen MS, Webster MT, Grant BR, Grant PR, Andersson L.. 2016. A beak size locus in Darwins finches facilitated character displacement during a drought. Science 352:470–474. [DOI] [PubMed] [Google Scholar]
- Lamichhaney S, Berglund J, Almén MS, Maqbool K, Grabherr M, Martinez-Barrio A, Promerová M, Rubin C-J, Wang C, Zamani N, et al. 2015. Evolution of Darwin’s finches and their beaks revealed by genome sequencing. Nature 518:371–375. [DOI] [PubMed] [Google Scholar]
- Li GHY, Cheung CL, Xiao SM, Lau KS, Gao Y, Bow CH, Huang QY, Sham PC, Kung AWC.. 2011. Identification of QTL genes for BMD variation using both linkage and gene-based association approaches. Hum. Genet 130:539–546. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li H, Durbin R.. 2009. Fast and accurate short read alignment with Burrows-Wheeler transform. Bioinformatics 25:1754–1760. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Losos JB, Ricklefs RE.. 2009. Adaptation and diversification on islands. Nature 457:830–836. [DOI] [PubMed] [Google Scholar]
- Mabee P, Balhoff JP, Dahdul WM, Lapp H, Midford PE, Vision TJ, Westerfield M.. 2012. 500,000 fish phenotypes: the new informatics landscape for evolutionary and developmental biology of the vertebrate skeleton. J Appl Ichthyol. 28:300–305. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Manda P, Balhoff JP, Lapp H, Mabee P, Vision TJ.. 2015. Using the Phenoscape knowledgebase to relate genetic perturbations to phenotypic evolution. Genesis 561–571. 571. [DOI] [PubMed] [Google Scholar]
- Marchini J, Cardon LR, Phillips MS, Donnelly P.. 2004. The effects of human population structure on large genetic association studies. Nat Genet. 36:512–517. [DOI] [PubMed] [Google Scholar]
- Marsden CD, Lee Y, Kreppel K, Weakley A, Cornel A, Ferguson HM, Eskin E, Lanzaro GC.. 2014. Diversity, differentiation, and linkage disequilibrium: prospects for association mapping in the malaria vector Anopheles arabiensis. G3 4:121–131. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martin CH, Wainwright PC.. 2011. Trophic novelty is linked to exceptional rates of morphological diversification in two adaptive radiations of Cyprinodon pupfish. Evolution 65:2197–2212. [DOI] [PubMed] [Google Scholar]
- Martin CH, Wainwright PC.. 2013a. A remarkable species flock of Cyprinodon pupfishes endemic to San Salvador Island, Bahamas. Bull Peabody Museum Nat Hist. 54:231–241. [Google Scholar]
- Martin CH, Wainwright PC.. 2013b. On the measurement of ecological novelty: scale-eating pupfish are separated by 168 my from other scale-eating fishes. PLoS One 8:e71164.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martin CH, Wainwright PC.. 2013c. Multiple fitness peaks on the adaptive landscape drive adaptive radiation in the wild. Science 339:208–211. [DOI] [PubMed] [Google Scholar]
- Martin CH, Feinstein LC.. 2014. Novel trophic niches drive variable progress towards ecological speciation within an adaptive radiation of pupfishes. Mol Ecol. 23:1846–1862. [DOI] [PubMed] [Google Scholar]
- Martin Christopher H, Priscilla A Erickson, Miller CT.. 2016. The genetic architecture of novel trophic specialists: higher effect sizes are associated with exceptional oral jaw diversification in a pupfish adaptive radiation. Mol Ecol. Advance Access published December 26, 2016, doi: 10.1101/031575. [DOI] [PubMed]
- Martin CH. 2016a. Context-dependence in complex adaptive landscapes: frequency and trait-dependent selection surfaces within an adaptive radiation of Caribbean pupfishes. Evolution 70-6:1265–1282. [DOI] [PubMed] [Google Scholar]
- Martin CH. 2016b. Data from: Context dependence in complex adaptive landscapes: frequency and trait-dependent selection surfaces within an adaptive radiation of Caribbean pupfishes. Dryad Digital Repository. Advance Access Published: April 18, 2016, http://dx.doi.org/10.5061/dryad.n3mj3. [DOI] [PubMed] [Google Scholar]
- Martin CH, Crawford JE, Turner BJ, Simons LH.. 2016c. Diabolical survival in Death Valley: recent pupfish colonization, gene flow, and genetic assimilation in the smallest species range on earth. Proc R Soc B 283:23–34. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Merrell DJ. 1994. The adaptive seascape: the mechanism of evolution. Minneapolis (MT): University of Minnesota Press. [Google Scholar]
- McDonald AC, Schuijers JA, Gundlach AL, Grills BL.. 2007. Galanin treatment offsets the inhibition of bone formation and downregulates the increase in mouse calvarial expression of TNF and GalR2 mRNA induced by chronic daily injections of an injurious vehicle. Bone 40:895–903. [DOI] [PubMed] [Google Scholar]
- McGowan HW, Schuijers JA, Grills BL, McDonald SJ, McDonald AC.. 2014. Galnon, a galanin receptor agonist, improves intrinsic cortical bone tissue properties but exacerbates bone loss in an ovariectomised rat model. J. Musculoskelet Neuronal Interact. 14:162–172. [PubMed] [Google Scholar]
- McVean G. 2009. A genealogical interpretation of principal components analysis. PLoS Genet. 5:e1000686.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Midford PE, Dececchi TA, Balhoff JP, Dahdul WM, Ibrahim N, Lapp H, Lundberg JG, Mabee PM, Sereno PC, Westerfield M, et al. 2013. The vertebrate taxonomy ontology: a framework for reasoning across model organism and species phenotypes. J Biomed Semantics 4:34.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Malinsky M, Challis RJ, Tyers AM, et al. 2015. Genomic islands of speciation separate cichlid ecomorphs in an East African crater lake. Science 350:1493–1498. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moczek AP. 2008. On the origins of novelty in development and evolution. BioEssays 30:432–447. [DOI] [PubMed] [Google Scholar]
- Moriwaki K, Noda K, Furukawa Y, Ohshima K, Uchiyama A, Nakagawa T, Taniguchi N, Daigo Y, Nakamura Y, Hayashi N, et al. 2009. Deficiency of GMDS leads to escape from NK cell-mediated tumor surveillance through modulation of TRAIL signaling. Gastroenterology 137:188–198. [DOI] [PubMed] [Google Scholar]
- Mylroie JE, Hagey FM.. 1995. Pleistocene lake and lagoon deposits, San Salvador Island, Bahamas In: Curran HA, White B, editors. Terrestrial and shallow marine geology of the Bahamas and Bermuda. Boulder (CO: ): Geological Society of America; p. 77–90. [Google Scholar]
- Nadachowska-brzyska K, Burri R, Linn E.. 2016. PSMC analysis of effective population sizes in molecular ecology and its application to black-and-white Ficedula flycatchers. Mol Ecol. 25:1058–1072. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nachman MW, Payseur BA.. 2012. Recombination rate variation and speciation: theoretical predictions and empirical results from rabbits and mice. Philos Trans R Soc B Biol Sci. 367:409–421. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nielsen R. 2005. Molecular signatures of natural selection. Annu Rev Genet. 39:197–218. [DOI] [PubMed] [Google Scholar]
- Nielsen R, Williamson S, Kim Y, Nielsen R, Williamson S, Kim Y, Hubisz MJ, Clark AG, Bustamante C.. 2005. Genomic scans for selective sweeps using SNP data Genomic scans for selective sweeps using SNP data. 1566–1575. [DOI] [PMC free article] [PubMed]
- Noor MAF, Bennett SM.. 2009. Islands of speciation or mirages in the desert? Examining the role of restricted recombination in maintaining species. Heredity (Edinb) 103:439–444. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Noor MAF, Feder JL.. 2006. Speciation genetics: evolving approaches. Nat. Rev. Genet 7:851–861. [DOI] [PubMed] [Google Scholar]
- Novembre J, Stephens M.. 2008. Interpreting principal component analyses of spatial population genetic variation. Nat. Genet 40:646–649. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Orr HA. 2005. The genetic theory of adaptation: a brief history. Nat Rev Genet. 6:119–127. [DOI] [PubMed] [Google Scholar]
- Orr HA, Betancourt AJ.. 2001. Haldane’s sieve and adaptation from the standing genetic variation. Genetics 157:875–884. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Orr HA. 1998. The population genetics of adaptation: the distribution of factors fixed during adaptive evolution. Evolution (N. Y) 52:935–949. [DOI] [PubMed] [Google Scholar]
- Pallares LF, Harr B, Turner LM, Tautz D.. 2014. Use of a natural hybrid zone for genomewide association mapping of craniofacial traits in the house mouse. Mol Ecol. 23:5756–5770. [DOI] [PubMed] [Google Scholar]
- Pavlidis P, Živković D, Stamatakis A, Alachiotis N.. 2013. SweeD: Likelihood-based detection of selective sweeps in thousands of genomes. Mol. Biol. Evol 30:2224–2234. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Price AL, Patterson NJ, Plenge RM, Weinblatt ME, Shadick NA, Reich D.. 2006. Principal components analysis corrects for stratification in genome-wide association studies. Nat Genet 38:904–909. [DOI] [PubMed] [Google Scholar]
- Poelstra JW, Vijay N, Bossu CM, Lantz H, Ryll B, Müller I, Baglione V, Unneberg P, Wikelski M, Grabherr MG, et al. 2014. The genomic landscape underlying phenotypic integrity in the face of gene flow in crows. Science 344:1410–1414. [DOI] [PubMed] [Google Scholar]
- Porto A, Schmelter R, VandeBerg JL, Marroig G, Cheverud JM.. 2016. Evolution of the genotype-to-phenotype map and the cost of pleiotropy in mammals. Genet 10:1534/genetics.116.189431 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pritchard JK, Pickrell JK, Coop G.. 2010. The genetics of human adaptation: hard sweeps, soft sweeps, and polygenic adaptation. Curr Biol. 20:R208–R215. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Purcell S, Neale B, Todd-Brown K, Thomas L, Ferreira MAR, Bender D, Maller J, Sklar P, de Bakker PIW, Daly MJ, et al. 2007. PLINK: a tool set for whole-genome association and population-based linkage analyses. Am J Hum Genet. 81:559–575. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Puzey JR, Willis JH, Kelly JK.. 2015. Whole genome sequencing of 56 Mimulus individuals illustrates population structure and local selection. bioRxiv. doi: http://dx.doi.org/10.1101/031575.
- Rausher MD, Delph LF.. 2015. Commentary: when does understanding phenotypic evolution require identification of the underlying genes? Evolution 69:1655–1664. [DOI] [PubMed] [Google Scholar]
- Rogers SM, Tamkee P, Summers B, Balabahadra S, Marks M, Kingsley DM, Schluter D.. 2012. Genetic signature of adaptive peak shift in three spine stickleback. Evolution 66(8): 2439–2450. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Recknagel H, Elmer KR, Meyer A.. 2013. A hybrid genetic linkage map of two ecologically and morphologically divergent midas cichlid fishes (Amphilophus spp.) obtained by massively parallel DNA sequencing (ddRADSeq). G3 3:65–74. [DOI] [PMC free article] [PubMed]
- Schiffels S, Durbin R.. 2014. Inferring human population size and separation history from multiple genome sequences. Nat Publ Gr 46:919–925. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schluter D. 2000. The ecology of adaptive radiation. New York: Oxford University Press. [Google Scholar]
- Schrider DR, Mendes FK, Hahn MW, Kern AD.. 2015. Soft shoulders ahead: spurious signatures of soft and partial selective sweeps result from linked hard sweeps. Genetics 200:267–284. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seehausen O. 2006. African cichlid fish: a model system in adaptive radiation research. Proc R Soc B 273:1987–1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Soria-Carrasco V, Gompert Z, Comeault AA, Farkas TE, Parchman TL, Johnston JS, Buerkle CA, Feder JL, Bast J, Schwander T, et al. 2014. Stick insect genomes reveal natural selection’s role in parallel speciation. Science 344:738–742. [DOI] [PubMed] [Google Scholar]
- Tajima F. 1989. Statistical method for testing the neutral mutation hypothesis by DNA polymorphism. Genetics 123:585–595. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taylor SP, Dantas TJ, Duran I, Wu S, et al. 2015. Mutations in DYNC2LI1 disrupt cilia function and cause short rib polydactyly syndrome. Nat Commun. 6:1–11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Turner BJ, Duvernell DD, Bunt TM, Barton MG.. 2008. Reproductive isolation among endemic pupfishes (Cyprinodon) on San Salvador Island, Bahamas: microsatellite evidence. Biol J Linn Soc. 95:566–582. [Google Scholar]
- Turner JRG. 1976. Adaptive radiation and convergence in subdivisions of the butterfly genus Heliconius (Lepidoptera: Nymphalidae). Zool J Linn Soc. 58:297–308. [Google Scholar]
- Van der Auwera GA, Carneiro MO, Hartl C, Poplin R, Del Angel G, Levy-Moonshine A, Jordan T, Shakir K, Roazen D, Thibault J, et al. 2002. Current protocols in bioinformatics. In: Bateman A, Pearson WR, Stein LD, Stormo GD, Yates JR, editors. Hoboken (NJ: ): John Wiley & Sons, Inc. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Visscher PM, Brown MA, McCarthy MI, Yang J.. 2012. Five years of GWAS discovery. Am J Hum Genet. 90:7–24. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Webling KEB, Runesson J, Bartfai T, Langel Ü.. 2012. Galanin receptors and ligands. Front. Endocrinol (Lausanne). 3:1–14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wright S. 1932. The roles of mutation, inbreeding, crossbreeding and selection in evolution. In: Proceedings of the sixth international congress of genetics, Brooklyn (NY): Brooklyn Botanic Garden. p. 356–366.
- Wright S. 1988. Surfaces of selective value revisited. Am Nat. 131(1): 115–123. [Google Scholar]
- Xia JH, Lin G, He X, Liu P, Liu F, Sun F, Tu R, Yue GH.. 2013. Whole genome scanning and association mapping identified a significant association between growth and a SNP in the IFABP-a gene of the Asian seabass. BMC Genomics 14:295.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yeaman S, Whitlock MC.. 2011. The genetic architecture of adaptation under migration-selection balance. Evolution (N. Y) 65:1897–1911. [DOI] [PubMed] [Google Scholar]
- Zhao K, Tung C-W, Eizenga GC, Wright MH, Ali ML, Price AH, Norton GJ, Islam MR, Reynolds A, Mezey J, et al. 2011. Genome-wide association mapping reveals a rich genetic architecture of complex traits in Oryza sativa. Nat Commun. 2:467.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou X, Carbonetto P, Stephens M.. 2013. Polygenic modeling with bayesian sparse linear mixed models. PLoS Genet 9:e1003264.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou X, Stephens M.. 2012. Genome-wide efficient mixed-model analysis for association studies. Nat. Genet 44:821–824. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.