A Surrogate Function for One-Dimensional Phylogenetic Likelihoods

Abstract

Phylogenetics has seen a steady increase in data set size and substitution model complexity, which require increasing amounts of computational power to compute likelihoods. This motivates strategies to approximate the likelihood functions for branch length optimization and Bayesian sampling. In this article, we develop an approximation to the 1D likelihood function as parametrized by a single branch length. Our method uses a four-parameter surrogate function abstracted from the simplest phylogenetic likelihood function, the binary symmetric model. We show that it offers a surrogate that can be fit over a variety of branch lengths, that it is applicable to a wide variety of models and trees, and that it can be used effectively as a proposal mechanism for Bayesian sampling. The method is implemented as a stand-alone open-source C library for calling from phylogenetics algorithms; it has proven essential for good performance of our online phylogenetic algorithm sts.

Introduction

With improved technology, molecular sequence data sets are becoming larger. At the same time, phylogenetic substitution models are becoming more realistic and consequently, more complex (Lartillot and Philippe 2004; Zoller and Schneider 2012; Groussin et al. 2013; Wang et al. 2014). This combination motivates research into useful approximations to the phylogenetic likelihood function.

One simple opportunity for efficiency improvement is in optimization of, or sampling from, the likelihood function as parametrized by a single branch length while fixing other parameters. In this case the likelihood function is simply a function that takes a nonnegative real input and gives out another real number. One common approach for numerical maximization of such functions ℓ is to sample an ℓ at a number of points, fit a simple curve to those points, and then use the fit as an approximation to ℓ. We will call ℓ the original function and the fitted function the surrogate function. Such an approach is useful if the original function is expensive to evaluate, but the surrogate function can be quickly fit to the sample points and evaluated. It is already being used implicitly in phylogenetics by inference programs that use Brent’s method (Brent 1973) for likelihood maximization, a method which effectively uses linear interpolation via the secant method. Recent work by (Aberer et al. 2016) shows that proposals built using common probability distribution functions (PDFs) as surrogates, in particular the Γ distribution, can have high acceptance rates. Bayesian statistics in general has benefited from the use of likelihood function approximations, such as for variational analysis (Wainwright and Jordan 2008).

Although existing functions can provide useful surrogates in phylogenetics, one might desire a class of surrogate functions that is specialized to the task. Indeed, phylogenetic likelihood functions parameterized by a single branch length have special characteristics: they asymptote at a nonzero value as the branch length becomes long, and sometimes achieve infinite slope as the branch length becomes short. Neither of these features can be true for any polynomial, and the first characteristic is not true for any PDF.

In this article, we show that a slight generalization of the likelihood function for the binary symmetric model (BSM) on a two-taxon tree can serve as a useful surrogate function for likelihood functions parameterized by branch lengths. We call this surrogate the lcfit function, short for “likelihood curve fit.” With only four parameters, it can be easily and efficiently fit in a least-squares sense with standard algorithms; even more robust fitting can be achieved using the ML branch length and corresponding second derivative. We show via experiments with simulated and real data that it is readily fit and does a good job of approximating even complex models, making it a useful tool when those models are expensive to evaluate. Our code to use lcfit is available as an open-source C library.

Results

Surrogate Formula and Fitting

The lcfit surrogate function f(c, m, r, b; t) evaluated at branch length t ≥ 0 is

$$c\hspace{0.17em}\text{log}\hspace{0.17em}[(1+e^{-r(t+b)})/2]+m\hspace{0.17em}\text{log}\hspace{0.17em}[(1-e^{-r(t+b)})/2]$$ (1)

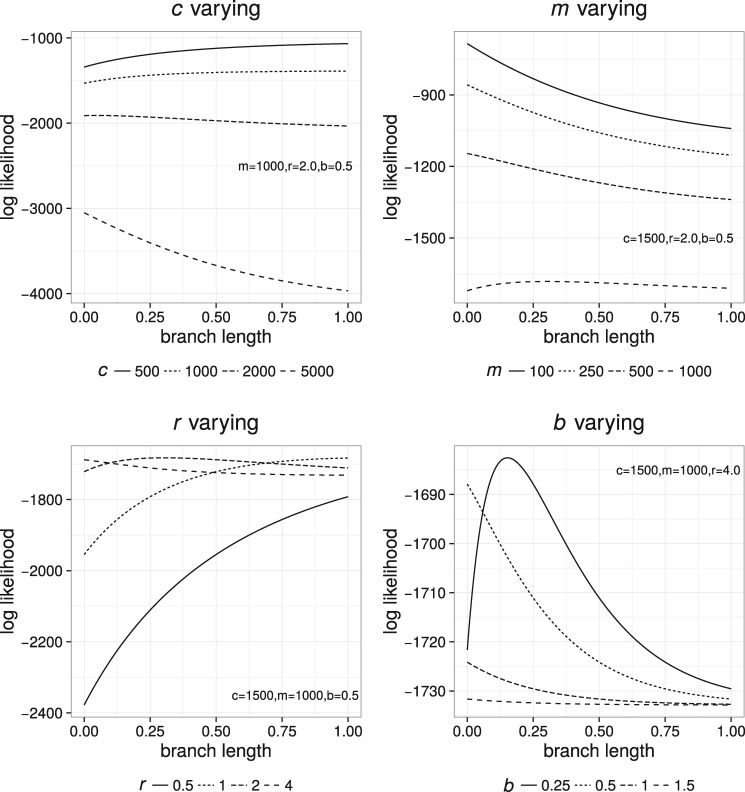
for any positive values of the lcfit coefficients c, m, r, and nonnegative b. It can be considered as an abstract surrogate function that takes a set of shapes resembling those of phylogenetic likelihood curves (fig. 1). However, when b is zero this function is the log likelihood function for the BSM (see, e.g., Semple and Steel 2003) where c is the number of constant sites, m is the number of substituted sites, and r is the substitution rate. The inclusion of the b term simply serves to truncate the likelihood function on the left, which is helpful in fitting likelihood functions for trees with more than two taxa. Indeed, without truncation the limit of f as branch lengths go to 0 is always negative infinity; this does not typically make for a good fit to likelihood functions parameterized by branches of nontrivial phylogenetic trees. As the branch length becomes long, f approaches an asymptote of $-(c+m)\hspace{0.17em}\text{log}\hspace{0.17em}(2)$.

Fig. 1.

How each of the four parameters changes the shape of our surrogate function f defined in equation (1).

We will assume that r > 0 and b ≥ 0, so that e^−r(t+b) as a function of nonnegative t goes from some positive value down to zero. The maximum of the log likelihood function for this setting is

$$t_0=-b+\hspace{0.17em}\text{log}\hspace{0.17em}[(c+m)/(c-m)]/r.$$ (2)

This has a finite real solution exactly when c > m. In the BSM interpretation this means that the number of constant sites strictly exceeds the number of substituted sites. Other characteristics of the lcfit function f are easily derived, such as the second derivative at the maximum, and the inflection point when it exists (see Supplementary Material online). Using such formulas we have found it useful in some cases to reparameterize f in terms of the original c, m, f’s maximum t₀, and the second derivative at this maximum value $f″(t_0)$.

Briefly, our fitting methods combine two strategies to fit the parameters of the lcfit function. Both use least-squares fitting of sampled branch lengths and their likelihoods. The first strategy (lcfit2) applies when the maximum likelihood branch length is positive, and uses the second derivative at this branch length to eliminate two parameters so that only two parameters need to be fit. The second strategy (lcfit4) simply fits the lcfit parameters using least-squares directly.

We can simply multiply an lcfit curve by a branch length prior to get an approximate (unnormalized) PDF. For sampling from this PDF we have used a simple rejection sampling strategy with an exponential proposal distribution. Although this may require many proposals for an acceptance for certain lcfit shapes, individual lcfit evaluations are computationally cheap so we have not found this to be a significant burden in practice. Adaptive rejection sampling (Gilks and Wild 1992) would provide a more efficient alternative.

Our C library with unit tests, continuous testing, simulation framework, and manual is at https://github.com/matsengrp/lcfit, last accessed October 1, 2017.

Performance

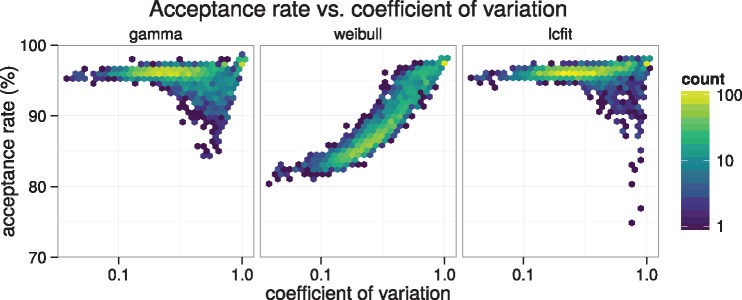
We obtain slightly better results than Aberer et al. (2016) in terms of acceptance rate for branch length proposals using their benchmarking strategy (fig. 2). Briefly, we reused their acceptance rate results for their Γ and Weibull proposals and used the same trees and likelihoods to compute the lcfit surrogate function (see Supplementary Methods, Supplementary Material online). In terms of computational time, both our method and the method of Aberer et al. (2016) require the maximum of the likelihood function to be found, along with the second derivative. This computational effort dominates the required effort, and thus they require approximately equal amounts of computation.

Fig. 2.

Expected acceptance rate for maximum-likelihood fits of gamma, Weibull, and lcfit distributions versus coefficient of variation of sampled single-branch-length posterior distributions for 12 data sets tested by (Aberer et al. 2016). Fit parameters for the gamma and Weibull distributions were obtained directly from data provided by (Aberer et al. 2016); those results reproduced here for comparison to lcfit.

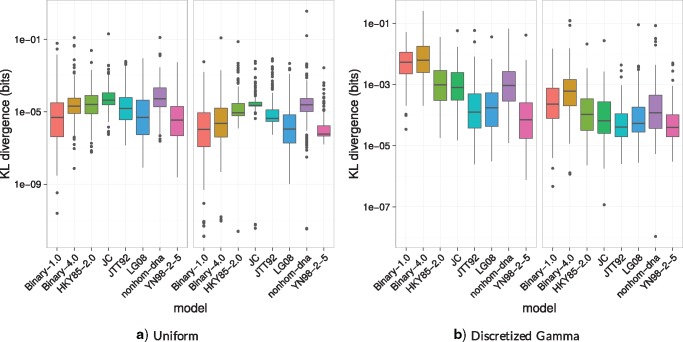
We then performed simulation to explore how well the lcfit surrogate fits a broader range of models. To do so, we simulated data under a variety of models, and fit lcfit to the resulting likelihood curves under the same models. We quantified the difference between the two curves using the Kullback–Leibler (KL) divergence from the surrogate function to the likelihood, specifically by computing each for a dense collection of points in a range enclosing the maximum of the likelihood function then normalizing to get a probability distribution for each (details in Supplementary Methods, Supplementary Material online). We found that KL divergence for complex models is similar to KL divergence for data simulated under binary model (fig. 3). We were surprised that lcfit performance by this metric was worse for variants of the binary model (e.g., the nonsymmetric binary model or a mixture of rates) than for some complex models.

Fig. 3.

Estimated Kullback–Leibler divergence from the original likelihood function to the surrogate function. Simulations done using (a) uniform rates across sites and (b) discretized Gamma distributed rates across sites (4 categories, α = 0.2). Branch lengths are either drawn from an exponential with mean either μ = 0.1 or μ = 0.01. See supplementary table S1 in Supplementary Material online for a list of model name abbreviations.

Discussion

In this article, we present lcfit, the first surrogate function specialized to the case of 1D phylogenetic likelihood functions. Our work shares goals with those of (Aberer et al. 2016), however there are several aspects of our framework that make it appealing. This previous work uses several standard probability distributions as surrogate functions for posteriors. In particular, they fit normal, lognormal, Weibull, and Γ distributions to approximate per-branch posterior distributions in order to obtain efficient proposals. With the best performing of these distributions (typically Γ) they obtain high acceptance rates. However, there are inherent limitations to using standard distributions for this application. For example, the Γ and Weibull have two different shapes, depending on if their shape parameter is greater and less than one; when the shape parameter is greater than one, the value at zero is zero, and when it is less than one then the first derivative at zero is negative. Neither of these need hold for phylogenetic likelihood curves or posteriors. Indeed, likelihood curves for internal branches are typically nonzero at zero and have a nonzero modes, for example, see fig. 1c of Aberer et al. (2016). The truncated normal can take this shape, but its symmetry makes it a bad choice in this setting (supplementary fig. S2a, Supplementary Material online). In addition, lcfit matches real per-branch likelihoods by enabling a nonzero asymptote, whereas the (Aberer et al. 2016) surrogates are all zero at infinity.

In addition to theoretical advantages of the lcfit framework, there are several practical advantages. (Aberer et al. 2016) develop a fitting procedure using a linear relationship between the second derivative of the likelihood function and the standard deviation of the posterior density of the branch length. However, to use this relationship the parameters of this linear relationship must be inferred. Because it is inefficient to infer these parameters on the fly, (Aberer et al. 2016) use consensus values and a somewhat complex tuning procedure; here in most cases we simply fit two coefficients using standard least-squares methods. In addition, lcfit is implemented as a stand-alone library for incorporation into other software, whereas the independence sampler of (Aberer et al. 2016) is baked into ExaBayes (Aberer et al. 2014).

We have found lcfit to be essential for an efficient implementation (Fourment et al. 2017) of Online Phylogenetic Sequential Monte Carlo (Dinh et al. 2016). This Sequential Monte Carlo sampling procedure updates a Bayesian phylogenetic posterior given an additional sequence to include. To do so, it must propose attachment branch lengths for the new sequence onto the backbone of a tree from the original posterior. We have observed that the effective sample size (ESS) of the particle ensemble generated using lcfit is on an average 7 times higher than a naïve proposal that simply draws from the prior (supplementary fig. S3, Supplementary Material online). Although lcfit requires additional computation to approximate the posterior distribution of branches, this proposal has significantly higher ESS per unit of time relative to the naïve proposal (supplementary fig. S4, Supplementary Material online).

This work on online phylogenetics also points the way to needed extensions. Here, we have focused on approximating phylogenetic likelihood as a function of a single branch length at a time, but one could similarly concoct surrogate functions for other low-dimensional settings. For example, one could develop a surrogate function for three branch lengths around an internal node using the BSM likelihood function for a three taxon tree, or consider branch length changes and nearest-neighbor interchange moves simultaneously by using a surrogate function based on the BSM likelihood function for a four taxon tree.

Supplementary Material

Supplementary methods and data are available at Molecular Biology and Evolution online.