Effects of Demographic History on the Detection of Recombination Hotspots from Linkage Disequilibrium

Abstract

In some species, meiotic recombination is concentrated in small genomic regions. These “recombination hotspots” leave signatures in fine-scale patterns of linkage disequilibrium, raising the prospect that the genomic landscape of hotspots can be characterized from sequence variation. This approach has led to the inference that hotspots evolve rapidly in some species, but are conserved in others. Historic demographic events, such as population bottlenecks, are known to affect patterns of linkage disequilibrium across the genome, violating population genetic assumptions of this approach. Although such events are prevalent, demographic history is generally ignored when making inferences about the evolution of recombination hotspots. To determine the effect of demography on the detection of recombination hotspots, we use the coalescent to simulate haplotypes with a known recombination landscape. We measure the ability of popular linkage disequilibrium-based programs to detect hotspots across a range of demographic histories, including population bottlenecks, hidden population structure, population expansions, and population contractions. We find that demographic events have the potential to greatly reduce the power and increase the false positive rate of hotspot discovery. Neither the power nor the false positive rate of hotspot detection can be predicted without also knowing the demographic history of the sample. Our results suggest that ignoring demographic history likely overestimates the power to detect hotspots and therefore underestimates the degree of hotspot sharing between species. We suggest strategies for incorporating demographic history into population genetic inferences about recombination hotspots.

Introduction

The rate of meiotic recombination shapes major features of the genomic landscape and influences the efficacy of selection (Hill and Robertson 1966; Felsenstein 1974; Begun and Aquadro 1992; Charlesworth et al. 1993, 1994; Comeron et al. 1999; Duret and Arndt 2008). Recombination rate varies between species (Burt and Bell 1987; Dumont and Payseur 2011; Smukowski and Noor 2011), between populations (Koehler et al. 2002; Kong et al. 2010; Comeron et al. 2012), within populations (Broman et al. 1998; Cullen et al. 2002; Jeffreys and Neumann 2005), and between the sexes (Burt et al. 1991; Ma et al. 2015; Johnston et al. 2016). The recombination rate also varies along the genome (Kong et al. 2002; Cox et al. 2009; Rockman and Kruglyak 2009; Comeron et al. 2012; Kawakami et al. 2014). In some species, crossovers are finely localized into short stretches of sequence (1–2 kb) with highly elevated recombination rates termed “hotspots” (Steinmetz et al. 1982; Chakravarti et al. 1984; Lichten and Goldman 1995; Petes 2001; Kelmenson et al. 2005; Myers et al. 2005; Auton et al. 2012; Singhal et al. 2015; Stevison et al. 2016). For example, an estimated 80% of all recombination events in humans are concentrated in <15% of the genome (The International HapMap Consortium 2005; Myers et al. 2006). In contrast, other species, including the model genetic organisms Drosophila melanogaster and Caenorhabditis elegans, show heterogeneity in recombination rate across chromosomes, but lack punctate hotspots (Chan et al. 2012; Kaur and Rockman 2014; Smukowski-Heil et al. 2015).

The characterization of fine-scale heterogeneity in recombination rate—including the detection of hotspots—requires that a reasonable number of crossovers be mapped to the genome with high precision. Because crossovers are rare, large sample sizes are needed. The most direct method converts haplotype frequencies estimated in large numbers of sperm into recombination rates for short genomic intervals (Li et al. 1988; Cui et al. 1989; Hubert et al. 1994; Jeffreys et al. 2000; Tiemann-Boege et al. 2006; Clark et al. 2007). This approach currently does not scale up with high enough precision to identify hotspots on the genomic level, and it ignores recombination occurring in females. Transmission patterns in crosses or pedigrees can locate hotspots (Coop et al. 2008; Kong et al. 2010; Ma et al. 2015), but only with very large sample sizes that are impractical in most species. Although double-strand break (DSB) hotspots can be detected using chromatin immunoprecipitation–sequencing (ChIP-Seq) (Pan et al. 2011; Smagulova et al. 2011; Brick et al. 2012; Pratto et al. 2014; Lam and Keeney 2015), only a fraction of DSBs are resolved as crossover events and as a result, the relationship between these genomic locations and recombination hotspots remain poorly understood. These challenges motivate the use of an indirect, population genetics approach to characterizing recombination hotspots.

Historical recombination occurring at high levels in hotspots erodes associations among nearby polymorphisms, leading to localized decays in linkage disequilibrium (LD) in samples of unrelated individuals. Building on the demonstration that the population recombination rate can be estimated from the composite likelihood of pairwise combinations of polymorphic sites (Hudson 2001), this signature formed the foundation for statistical methods that detect hotspots and measure their recombination rates (Fearnhead and Donnelly 2001; McVean et al. 2002, 2004; Li and Stephens 2003; Stumpf and McVean 2003; Fearnhead and Smith 2005; Fearnhead 2006; Auton and McVean 2007, 2012; Wang and Rannala 2009; Auton et al. 2014). These approaches easily scale to the whole genome and take advantage of the increasing availability of population genomic data sets. As a result, current knowledge about the genomic distribution of hotspots comes disproportionately from the LD-based strategy, which has been applied to a variety of species (Myers et al. 2005; 1000 Genomes Project Consortium 2010; Auton et al. 2012, 2013; Axelsson et al. 2012; Brunschwig et al. 2012; Chan et al. 2012; Horton et al. 2012; Paape et al. 2012; Singhal et al. 2015; Wallberg et al. 2015; Stevison et al. 2016).

Genomic maps of recombination hotspots inferred from LD in different populations and species can be compared to understand how hotspots evolve. LD-based hotspot locations show little overlap between closely related species of primates (Ptak et al. 2005; Winckler et al. 2005; Auton et al. 2012; Stevison et al. 2016), with an estimated 10% shared between humans and chimpanzees, suggesting rapid evolution of hotspot location (Auton et al. 2012). Interestingly, the rate of hotspot turnover itself appears to evolve. For example, hotspot turnover in chimpanzees has been estimated to be 2–3 times faster than hotspot turnover within populations of hominids (1–2 My vs. ∼3 My, respectively) (Lesecque et al. 2014; Stevison et al. 2016). In contrast, the majority of LD-based hotspot locations appear to be conserved across species of canids and across species of birds over long times scales (up to 10–20 My) (Axelsson et al. 2012; Singhal et al. 2015). Two finch species with a similar divergence time to humans and chimpanzees share >70% of their LD-based hotspots (Singhal et al. 2015). Experimentally inferred double-strand break hotspots are also conserved between highly diverged species of yeast (Lam and Keeney 2015). These variable evolutionary patterns motivate the application of LD-based approaches to compare genomic hotspot maps across a range of species groups.

Conclusions about the abundance and intensity of recombination hotspots drawn from patterns of LD must be tempered by the challenges inherent in this indirect strategy. LD-based methods estimate a historical recombination rate that is averaged over time and over individuals in a population. Hence, these estimates ignore changes in recombination rate during the history of the sample as well as rate variation among individuals, including often-observed differences between females and males (Burt et al. 1991; Kong et al. 2010). Furthermore, recombination hotspots first detected as local maxima in LD-based recombination maps must be statistically validated. The performance of these statistical methods is largely unknown and is likely sensitive to variation in its implementation, such as the size of the genomic window used to estimate the background recombination rate (Wall and Stevison 2016). As a result, it has been suggested that previous applications to empirical data may have been underpowered (Wall and Stevison 2016).

A major assumption of LD-based approaches is that patterns of variation reflect neutral, equilibrium conditions (Hudson 2001; McVean et al. 2002). Positive selection creates local distortions in LD that resemble hotspot signatures, increasing the false positive (FP) rate associated with hotspot inference (Reed and Tishkoff 2006). Common demographic events, including population size change and migration, are also expected to shape genomic patterns of linkage disequilibrium in complex ways (Zavattari et al. 2000; McVean 2002; Rogers 2014), raising the prospect that unmet assumptions about demographic history could mislead inferences about recombination hotspots. Although it is possible to reduce the effect of selection by avoiding genes and other functional elements, the imprint of demography should extend across the genome. Broadly, demography has been demonstrated to bias estimates of the population recombination rate ($\rho$) (Fearnhead and Donnelly 2001; McVean et al. 2002; Smith and Fearnhead 2005). Yet, it is unclear how such biases affect hotspot identification, which focuses on relative differences in $\rho$ within the genome. Early simulation-based analyses suggested that LD-based identification of hotspots is likely robust to demographic perturbations and that population bottlenecks may actually increase the ability to identify hotspots (McVean et al. 2004). In contrast, Li and Stephens (2003) reported that population growth can reduce the power of hotspot detection and lead to overestimation of hotspot magnitude. Similarly, Chan et al. (2012) observed moderate to strong decreases in the power of hotspot detection following population growth and population bottlenecks, respectively. A more recent simulation-based analysis suggested that complex demographic history can also create the appearance of hotspots in the absence of variation in recombination rate (Johnston and Cutler 2012). Some LD-defined recombination hotspots may simply be regions of the genome with relatively deep genealogies, and thus, more historical recombination events (Johnston and Cutler 2012). The broader implications of these results are unclear because a limited range of demographic scenarios were explored and performance of current statistical methods for hotspot identification was measured only in the context of a constant background recombination rate. Collectively, these studies and ideas motivate a wider examination of how deviations from demographic equilibrium affect the performance of LD-based methods for identifying hotspots. In this article, we use coalescent simulations to evaluate the ability of LD-based methods to detect hotspots across a wide range of common, demographic perturbations.

Results

To determine the effects of demographic events on the power and accuracy of LD-based methods of recombination hotspot detection, we used coalescent-based programs to simulate chromosomes with a known recombination map and demographic history (Hudson 2001; Hellenthal and Stephens 2007; McVean and Auton 2007). We then used LDhat to measure recombination rate along the simulated chromosomes and LDhot to identify all statistically significant recombination hotspots in the simulated samples (McVean and Auton 2007; Auton et al. 2014). With perfect knowledge of the true underlying recombination map, we determined whether significant hotspots were either true positives or FPs, allowing us to compute two metrics of performance: power and the frequency of FPs. For each condition, we simulated 1,000 data sets. Each data set contained 32 chromosomes (equivalent to sampling 16 diploid individuals, assuming random mating), a modest sample size intended to mimic genome sequencing studies of natural populations, especially in non-model organisms. We considered four common demographic events that affect patterns of linkage disequilibrium: population bottlenecks, hidden population structure, exponential population growth, and exponential population contraction. Except where explicitly noted, we hold the frequency of recombination events, r/kb, constant within and between simulations. Accordingly, the population recombination rate, $\rho$/kb (4Nr/kb), changes within and between simulations due to changes in population size, N.

We identified pervasive and complex effects of demographic history on the ability of a popular program—LDhot—to detect recombination hotspots (Auton et al. 2014). Both measures of performance, power and FP rate, were highly sensitive to the parameters of the simulated demographic scenarios. Reductions in the power to identify hotspots were observed following all four types of demographic events simulated. The most severe reductions in power occurred following recent, strong population bottlenecks and old, hidden population subdivision. Furthermore, we observed increases in the frequency of FPs following all types of demographic events, apart from hidden population subdivision. Most strikingly, we observed a very strong effect of background recombination rate on the frequency of FPs, which interacted with demographic history to produce up to 6-fold increases relative to control simulations. We also found that certain demographic scenarios, particularly older or gradual population expansions, reduced the frequency of FPs.

Control Simulations

It is likely that differences in population size (N) and by extension the population mutation rate ($\theta$ = 4N$\mu$, where $\mu$ is the mutation rate per base pair) may impact performance even in equilibrium populations. To account for these effects, we compared performance following demographic events to control simulations featuring a constant population size that were otherwise equivalent. Both the mutation rate, $\mu$, and the recombination rate, r, were held constant, with reductions in the population mutation rate, $\theta$, and the population recombination rate, $\rho$, reflecting changes in population size, N. Where applicable, we performed multiple control simulations across the range of population sizes experienced by populations undergoing changes in population size and structure (minimum, maximum, and intermediate population sizes). By comparing between control simulations, we noted effects on performance that arose due to the length of the simulated scaffold, the number of hotspots simulated, and the population mutation rate. The largest effects on power arose from differences in equilibrium values of the population mutation rate, resulting in a positive relationship. The reduction in power when decreasing the population mutation rate from 0.0005 (N = 5,000) to 0.0001 (N = 1,000) was much greater (loss of ∼45% of total hotspots) than the reduction in power when decreasing the population mutation rate from 0.001 (N = 10,000) to 0.0005 (N = 5,000) (loss of ∼6–10% of total hotspots) (supplementary table S1, Supplementary Material online). In comparison, the effects of scaffold size on performance were minimal (<3% difference in performance) (supplementary table S1, Supplementary Material online).

Similar patterns were observed for the frequency of FPs among control simulations. There was a strong, positive, nonlinear relationship between the population mutation rate and the frequency of FPs (supplementary table S2, Supplementary Material online). There was also a noticeable, but smaller effect of scaffold size. Both power and FP frequency in the 500-kb control simulation were lower than expected, given the other control simulations with the same population mutation rate ($\theta$ = 0.001) (supplementary tables S1 and S2, Supplementary Material online). This simulation differed from the other control simulations in two ways that may contribute to this deviation: (1) eight hotspots (instead of one) were simulated on each scaffold and (2) a different coalescent simulator was used to simulate the sequence data (fin: McVean and Auton 2007 vs. msHOT: Hellenthal and Stephens 2007). Strikingly, we found that the background recombination rate substantially affected performance among the control simulations, and in some cases, even reversed the relationship between the population mutation rate and performance.

Instantaneous Bottleneck

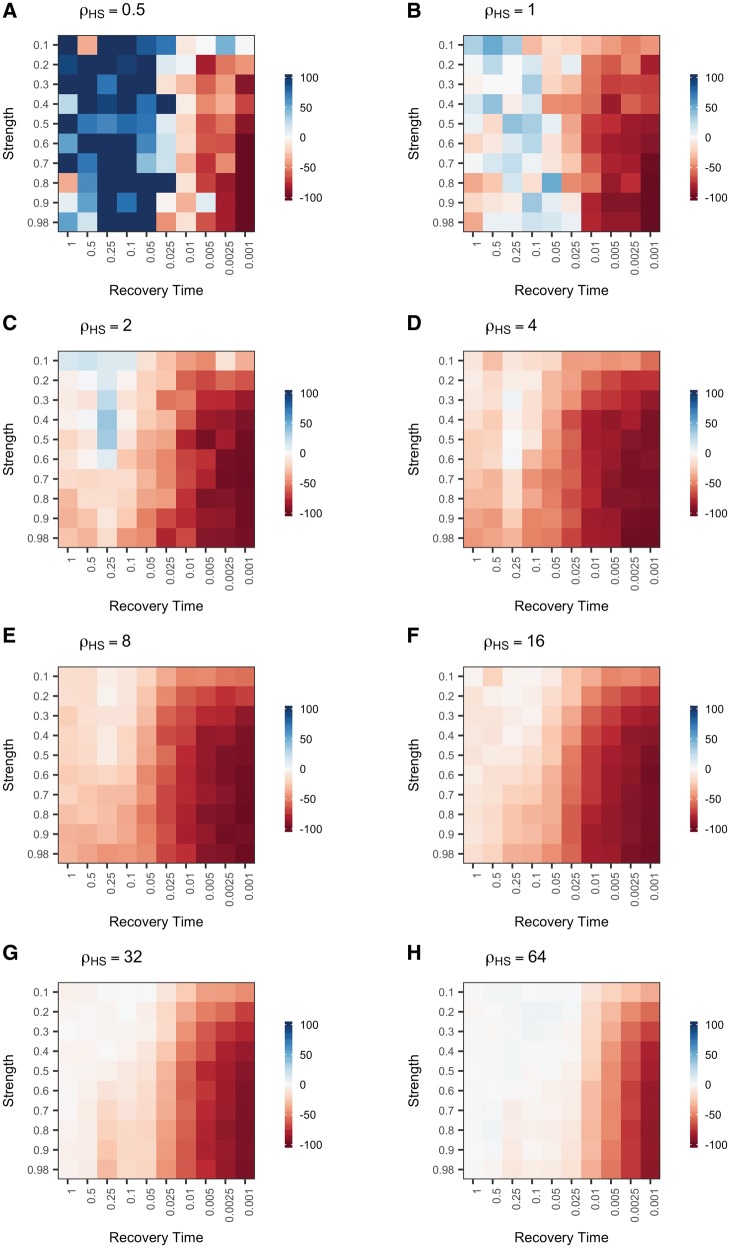
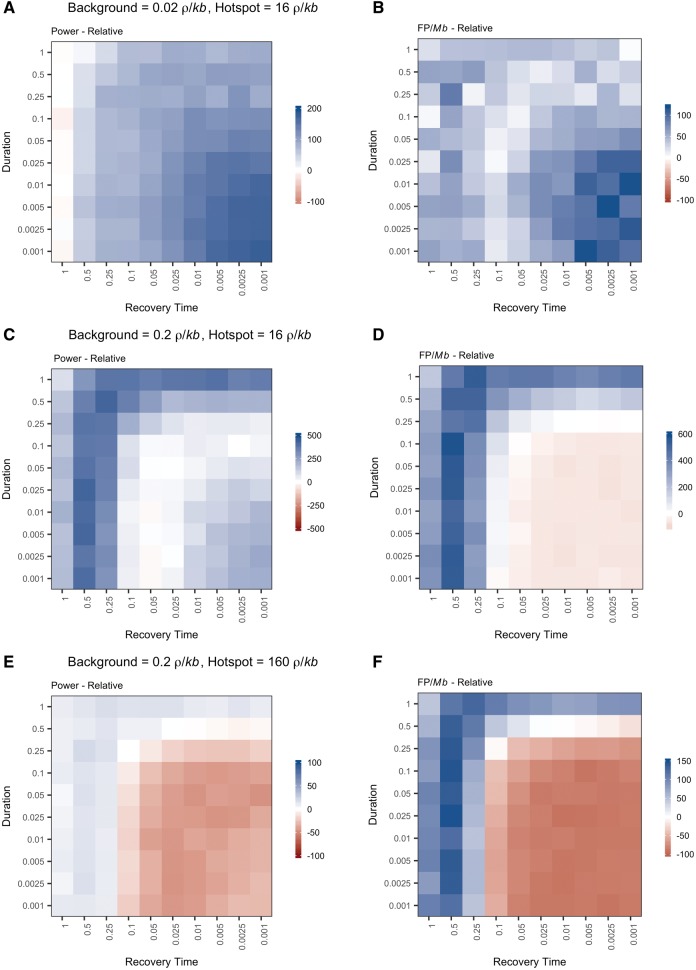
To simulate the effects of an instantaneous bottleneck, we modeled single 500-kb chromosomes with eight recombination hotspots, each 2-kb in length, evenly spaced 50-kb apart using the coalescent simulator (fin) within the LDhat package (McVean and Auton 2007). The intensity of each recombination hotspot is double the intensity of the preceding hotspot, spanning a range from 0.5 to 64 $\rho$/kb ($\rho$/kb = 4Nr, where r is the rate of recombination per kb). The background recombination rate (rate of recombination events outside of recombination hotspots), is 0.02 $\rho$/kb. The values of $\rho$/kb are given for the ending population size of 10,000 individuals. We designed the scaffold to be identical to that used to test the performance of LDhot by the authors of the program (Auton et al. 2014). Among the demographic scenarios we examined, population bottlenecks induced the greatest and most pervasive reductions in power (fig. 1 and supplementary table S3, Supplementary Material online). Power depended upon both the strength and the timing of the bottleneck, as well as the magnitude of the recombination hotspot (fig. 2). In the most extreme cases, we observed virtually no power to detect hotpots of any magnitude following a strong, recent bottleneck (fig. 2), resulting in a close to 100% decrease in power relative to the control population (fig. 1). However, weak, recent bottlenecks and strong, older bottlenecks also produced substantial reductions in power (30–50%) in comparison to the control simulations (fig. 1). The largest relative decreases in power were seen for hotspots of intermediate magnitude ($\rho$/kb = 4–16) (fig. 1D–F). Although relative increases in power to identify weak hotspots ($\rho$/kb = 0.5–2) were observed following old and weak population bottlenecks (fig. 1A–C), the absolute effect on performance was limited by the very low power to statistically detect these hotspots even under ideal conditions (fig. 2A–C).

Fig. 1.

Population bottlenecks decrease power to detect recombination hotspots. Each square in the plot represents the percent difference in power to detect a hotspot for a population with a bottleneck of a given strength (y-axis) and recovery time (x-axis) relative to a control equilibrium population of the same size (N₀ = 10,000). Power was calculated as the percent of measurable simulations for each condition in which the true recombination hotspot was significantly identified by LDhot. Panels display power for hotspots with different intensities (${\rho }_{HS})$.

Fig. 2.

The power to detect a hotspot is strongly affected by its intensity. Each square in the plot represents the power to detect a hotspot for a population with a bottleneck of a given strength (y-axis) and recovery time (x-axis). Power was calculated as the percent of measurable simulations for each condition in which the true recombination hotspot was significantly identified by LDhot. Panels display power for hotspots with different intensities (${\rho }_{HS})$.

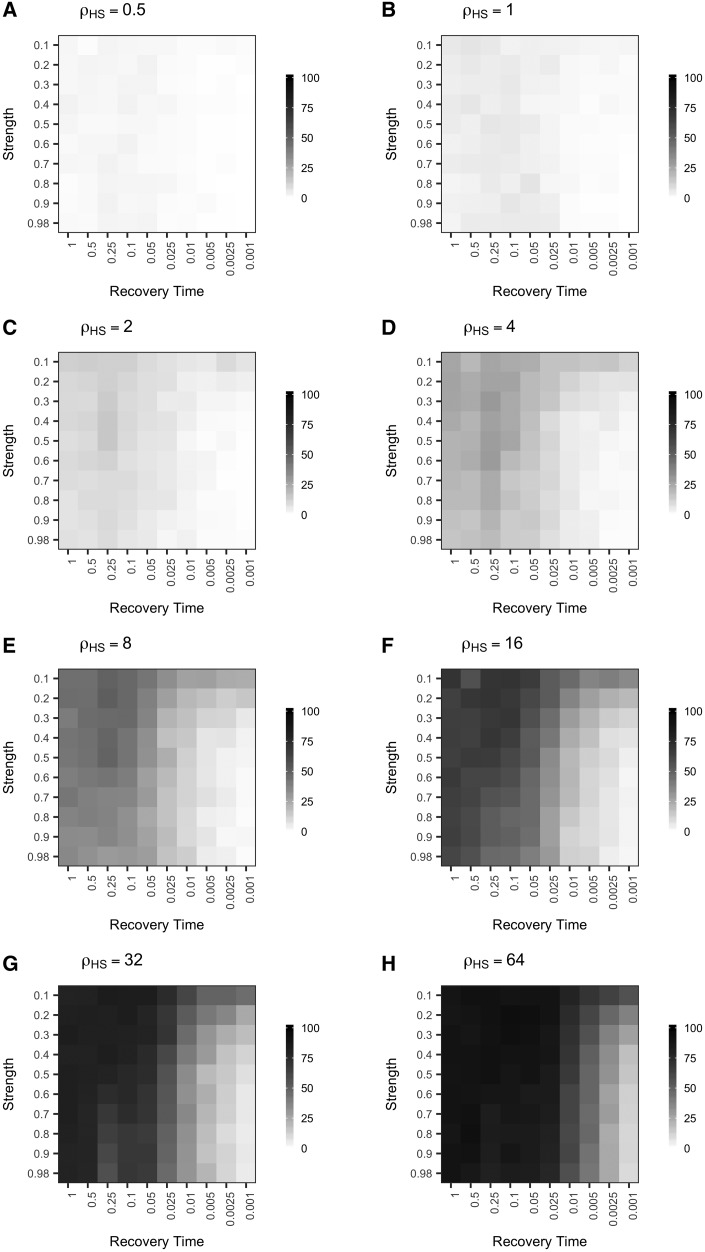
We also identified transient increases in the frequency of FPs per Mb (FP/Mb) following an instantaneous bottleneck (fig. 3 and supplementary table S3, Supplementary Material online). The frequency of FPs slightly decreased immediately following a population bottleneck relative to the control population (fig. 3B). However, as populations began to return to equilibrium, the frequency of FPs increased, peaking between 2,000–4,000 generations after the bottleneck occurred (t = 0.05–0.1, t is given in coalescent units [4N₀], where N₀ is the current population size; N₀ = 10,000) (fig. 3A and supplementary table S3, Supplementary Material online). Strong bottlenecks produced greater transient increases in the FP rate. In the control simulations, FPs occurred at a frequency of 0.16 FP/Mb (∼1 FP per 6.25 Mb) (supplementary table S2, Supplementary Material online). The maximum frequency of FPs observed following a bottleneck was 0.53 FP/Mb (1 FP per 1.89 Mb), a >3-fold increase compared with a population of constant size (supplementary table S3, Supplementary Material online). This maximum was reached 2,000 generations (t = 0.05, N₀ = 10,000) after a strong bottleneck in which the probability of coalescence was 80%.

Fig. 3.

Population bottlenecks transiently increase the frequency of false positives per Mb. (A) Each square represents the frequency of false positives observed per Mb following a bottleneck of a given strength (y-axis) and recovery time (x-axis). The false positive frequency was calculated as the total number of false positives identified per condition divided by the sum of the measurable length per condition. (B) Each square represents the percent difference in frequency of false positives observed per Mb following a population bottleneck relative to a control, equilibrium population of the same size (N₀ = 10,000). The color of each square represents increased (blue) or decreased (red) false positive frequency following a population bottleneck relative to a control population with a constant historical population size.

Exponential Population Growth

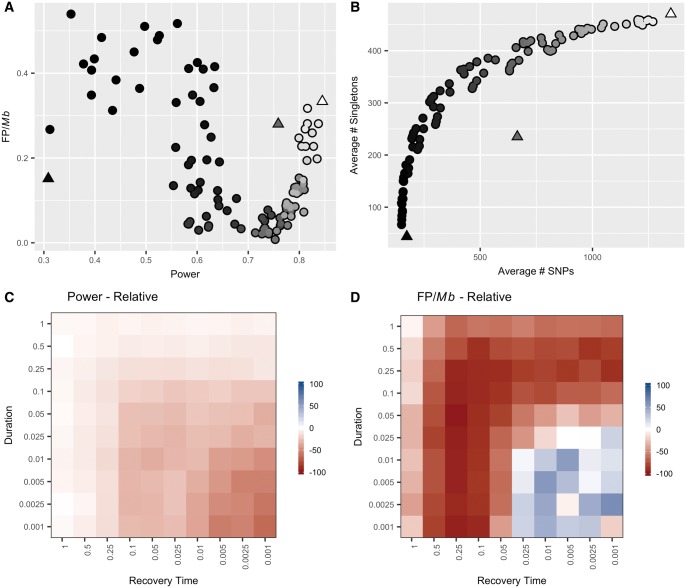
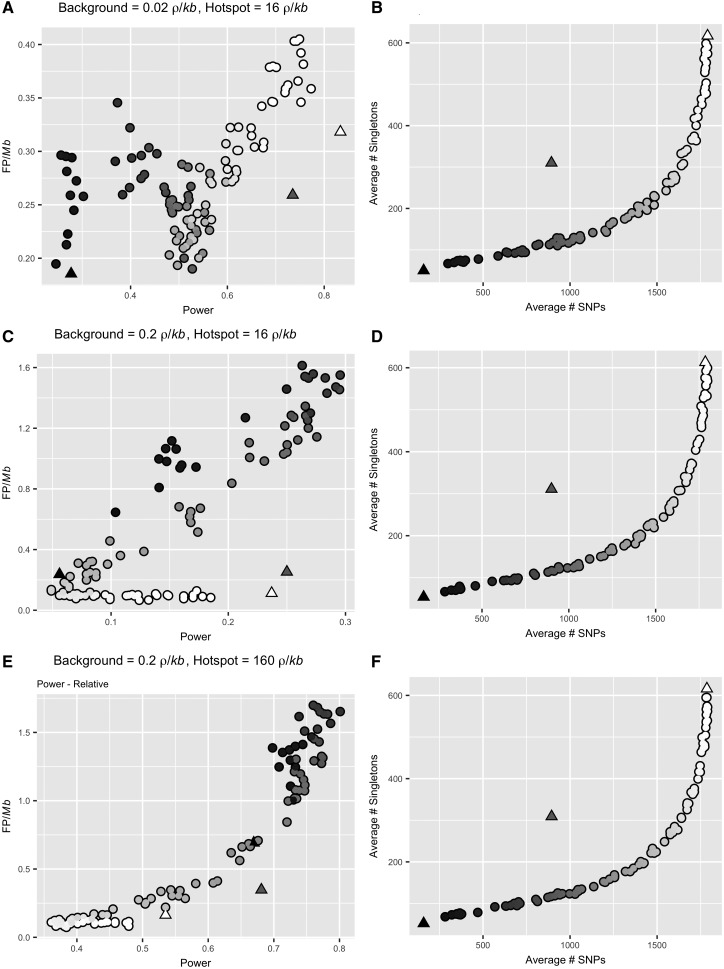
To model the consequences of exponential population growth, we used msHOT to simulate a 450-kb scaffold with a single, central 2-kb recombination hotspot of magnitude 16 $\rho$/kb with a background recombination rate of 0.02 $\rho$/kb (when N = 10,000, the current population size) (Hellenthal and Stephens 2007). We simulated populations that experienced a 10-fold exponential increase in population size from an ancestral size of 1,000 individuals to a current population size of 10,000 individuals ($\theta$ = 0.001). The values of $\rho$/kb are given for the ending population size of 10,000 individuals, but change during the simulations in accordance with population size. Changes in the FP frequency and power following a population expansion were complex and depended upon both timing and duration of the expansion (fig. 4 and supplementary table S4, Supplementary Material online). We observed a large decrease in power (up to 50%) following recent, rapid population expansions in comparison to control populations that maintained a constant population size of 10,000 individuals (84.5% of hotspots detected; $\theta$ = 0.001), the current population size of the expanded populations (fig. 4C andsupplementary tables S1 and S4, Supplementary Material online). However, power to detect recombination hotspots in control populations that maintained a constant population size of 1,000 individuals, the ancestral population size of the expanded populations, was very low (30.9% of hotspots detected, $\theta$ = 0.0001) (supplementary table S1, Supplementary Material online). The reduction in power following population expansions did not exceed this lower bound in any of the expansion scenarios we simulated (fig. 4A).

Fig. 4.

The relationship between power and false positive frequency following a population expansion is complex and depends upon both timing and duration. (A) Each point (circles) on the plot indicates the power (x-axis) and false positive frequency (y-axis) following a population expansion that varies in duration and recovery time. The power, but not the false positive frequency, fell within the range observed among the equilibrium, control populations (triangles). The shading of the points represents the average number of SNPs per simulation, which directly corresponds to the values on the x-axis of (B). (B) Following an equilibrium demographic history, there is a constant linear expectation for the relationship between the number of SNPs and the number of singletons (triangles). Population expansions result in the observation of more singletons than expected given the number of SNPs (circles). The shading of the points corresponds to the average number of SNPs per simulation plotted on the x-axis. (C) Each square in the plot represents the relative power to detect a hotspot for a population with a population expansion of a given duration (y-axis) and recovery time (x-axis) compared with a control equilibrium population of the same ending size (N₀= 10,000). Power was calculated as the percent of measurable simulations for each condition in which the true recombination hotspot was significantly identified by LDhot. (D) Each square represents the percent difference in frequency of false positives observed per Mb following a population expansion relative to a control, equilibrium population of the same ending size (N₀= 10,000). The false positive frequency was calculated as the total number of false positives identified per condition divided by the sum of the measurable length per condition.

Unlike power, the range of FP frequencies following population expansions (0.008–0.57 FP/Mb) exceeded the range among control populations of equivalent, constant population size (0.15–0.33 FP/Mb) (fig. 4A and supplementary table S2, Supplementary Material online). The direction and magnitude of the change in the frequency of FPs was highly variable, depending on both the duration and timing of the population expansion (fig. 4D). In most simulated expansion scenarios, the FP frequency was lower than that seen in equilibrium control populations (fig. 4D). In particular, we observed a large relative decrease in the frequency of FPs, as low as 0.01 FP/Mb or 1 FP per 100 Mb, coupled with only moderated reductions in power following older and more gradual population expansions (fig. 4C and D;supplementary table S4, Supplementary Material online). For example, following an expansion that occurred over 2,000 generations (t = 0.05, N₀ = 10,000) and ended 10,000 generations in the past (t = 0.25, N₀ = 10,000), there was only a minimal decrease in power (75.3% of hotspots discovered) and a large decrease in the frequency of FPs (0.008 FP/Mb) (supplementary table S4, Supplementary Material online). In contrast, large increases in the frequency of FPs relative to the controls occurred following intense, recent population expansions (fig. 4D). For example, following expansions that occurred over 100 generations (t = 0.0025, N₀ = 10,000) and ended only 40 generations in the past (t = 0.001, N₀ = 10,000), we detected 1 FP per 1.75 Mb (0.57 FP/Mb) (supplementary table S4, Supplementary Material online).

Exponential Population Contraction

To model the consequences of an exponential population contraction, we used msHOT to simulate a 600-kb scaffold with a single, central 2-kb recombination hotspot of magnitude 16 $\rho$/kb with a background recombination rate of 0.02 $\rho$/kb (Hellenthal and Stephens 2007). We simulated populations that experienced a 10-fold exponential decrease in population size from an ancestral size of 10,000 individuals to a current population size of 1,000 individuals ($\theta$ = 0.0001). The values of $\rho$/kb are given for the starting population size of 10,000 individuals, but change during the simulations in accordance with decreasing population size. As observed following population expansions, changes in the FP frequency and power following a population contraction were complex and depended upon both the timing and duration of the event (fig. 5A and supplementary table S5, Supplementary Material online). Although power varied greatly among contraction scenarios, this variation did not exceed the range of power observed among the equilibrium, control populations (27.7–83.4%) (supplementary table S1, Supplementary Material online). In contrast with the observation that power was the highest following older, gradual population expansions, for population contractions power was the highest following recent, rapid events (figs. 4A and 5A).

Fig. 5.

The relationship between power and false positive frequency following a population contraction is complex and depends on timing, duration, and background recombination rate. (A, C, E) Each point (circles) on the plot indicates the power (x-axis) and false positive frequency (y-axis) following a population contraction that varies in duration and recovery time. Performance for three control, equilibrium populations (N = 1,000, 5,000, 10,000) are also shown (triangles). The second two rows of plots show the change in performance with the background recombination rate is increased (10×) and the absolute (C) or relative (E) magnitude of the hotspot is held constant. The shading of the points represents the average number of SNPs per simulation, which directly corresponds to the values on the x-axis of (B, D, F). (B, D, F) Following an equilibrium demographic history, there is a constant linear expectation for the relationship between the number of SNPs and the number of singletons (triangles). Population contractions result in the observation of less singletons than expected given the number of SNPs (circles). The relationship between the average number of SNPs and singletons remains constant, as expected, when only the recombination rate is modified (D, F). The shading of the points represents the average number of SNPs per simulation plotted on the x-axis.

Population contractions resulted in pervasive, but moderate increases in the frequency of FPs (fig. 6B). The frequency of FPs was highest following the oldest, intense contractions and most recent, intense contractions, exceeding the upper range observed in the control simulations (0.19–0.32 FP/Mb) (fig. 5A and supplementary table S5, Supplementary Material online). The maximum frequency of FPs, 1 FP per 2.44 Mb (0.41 FP/Mb), was seen following a contraction that occurred over 20 generations (t = 0.005, N₀ = 1,000) and ended 10 generations before the end of the simulation (t = 0.0025, N₀ = 1,000) (supplementary table S5, Supplementary Material online).

Fig. 6.

The relationship between demographic history and performance is sensitive to the background recombination rate (A, C, E). Each square in the plot represents the relative power to detect a hotspot for a population with a population expansion of a given duration (y-axis) and recovery time (x-axis) compared with a control equilibrium population of the same ending size (N₀ = 1,000). Power was calculated as the percent of measurable simulations for each condition in which the true recombination hotspot was significantly identified by LDhot. The relationship between demographic history and performance changes when the background recombination rate is increased (10×) and the absolute (C) or relative (E) magnitude of the hotspot is held constant. (B, D, F) Each square represents the percent difference in frequency of false positives observed per Mb following a population contraction relative to a control, equilibrium population of the same ending size (N₀ = 1,000). The false positive frequency was calculated as the total number of false positives identified per condition divided by the sum of the measurable length per condition. The frequency of false positives following certain demographic histories increased dramatically when the background recombination rate was increased (10×) and the absolute (D) or relative (F) magnitude of the hotspot was held constant.

Background Recombination Rate

Hotspots are detected as local decays in LD compared with the surrounding sequence, raising the prospect that assumptions about the background recombination rate could influence the effects of demography on method performance. To further investigate interactions between the background recombination rate and hotspot detection, we ran additional sets of simulations, focusing on population contractions. Using the same set of demographic scenarios, we increased the background recombination rate 10-fold (0.02$–$0.2 $\rho$/kb). We then measured performance under this higher background rate when either the absolute (80×, 16 $\rho$/kb) or relative magnitude (800×, 160 $\rho$/kb) of the hotspot was maintained. The values of $\rho$/kb are given for the starting population size of 10,000 individuals, but change during the simulations in accordance with decreasing population size. This allowed us to parse the effects of raising the background recombination rate and increasing the intensity of the recombination hotspot.

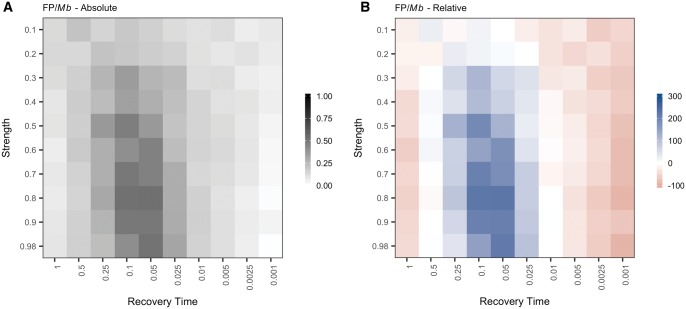
We observed complex interactions between demographic history, background recombination rate, and hotspot magnitude related to performance (fig. 5C and E). Surprisingly, when the background recombination rate was increased, the correlation between the population mutation rate ($\theta$) and power reversed, even in the control simulations (fig. 5C and E). The power to detect hotspots was highest in historically smaller populations and lowest in historically larger populations. When the absolute magnitude of the hotspot was held constant (16 $\rho$/kb), the relative magnitude of the hotspot in comparison to the background recombination rate decreased (80×). As expected, there was a large corresponding reduction in power (fig. 5C). We ascribe this reduction in power to changes in the magnitude of the recombination hotspot relative to the background recombination rate. The power to detect the hotspot remained largely within the range of the equilibrium, control populations (fig. 6C). When the relative magnitude of the hotspot was held constant (800×), the absolute magnitude of the hotspot was necessarily increased (160 $\rho$/kb). The overall range of power observed was not reduced compared with our original simulations (hotspot = 16 $\rho$/kb, background = 0.02 $\rho$/kb). However, the range of power greatly exceeded the range observed in the equivalent equilibrium, control populations (fig. 5E). Following recent, rapid population contractions, power decreased by ∼20% in comparison to control, equilibrium populations that maintained a constant, historical population size of 10,000 individuals (∼55%) (figs. 5E and 6E). On the other hand, following old, gradual contractions power increased by ∼10% in comparison to control, equilibrium populations that maintained a constant, historical population size of 1,000 individuals (∼68%) (figs. 5E and 6E).

Most strikingly, under certain contraction scenarios, the frequency of FPs increased many-fold relative to both the simulations run with a lower background recombination rate, and to the relevant control simulations (figs. 5C–E and 6C–E). Following older, intense population contractions, the FP frequency exceeded 1.6 FP/Mb (1 FP per 0.625 Mb) (fig. 5C and E). The magnitude of the increase in FP frequency was observed independently of the magnitude of the hotpot (16 $\rho$/kb vs. 160 $\rho$/kb) (fig. 5C and E). Thus, we can attribute the rise in the frequency of FPs to the increase in background recombination rate.

Hidden Population Structure

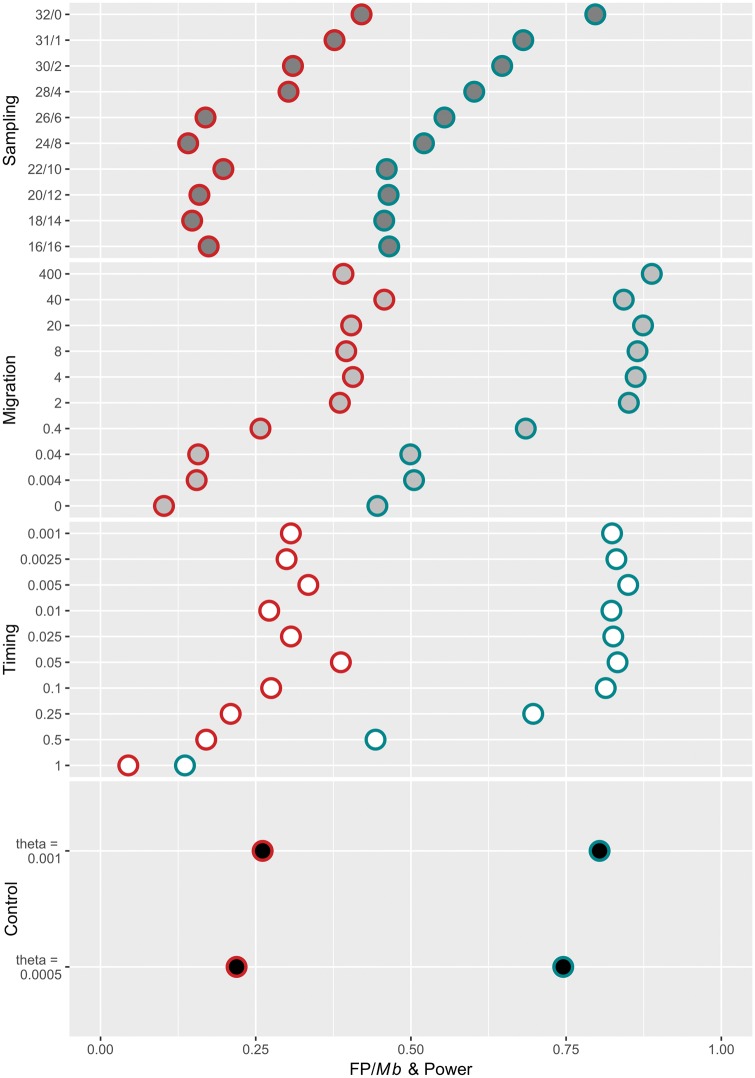
To replicate the consequences of sampling with hidden population structure, we modeled demographic histories in which a population of 10,000 individuals ($\theta$ = 0.001) split at time t into two subpopulations of equal size ($\theta$ = 0.0005). Hidden population structure greatly reduced power to detect recombination hotspots in certain scenarios. Reductions in power were sensitive to the split time between the two sampled populations (fig. 7). Recent population splits that occurred between 20–2,000 generations in the past (t = 0.001–0.1, N₀ = 5,000) had little to no effect on power (fig. 7). In each of these cases, power ranged between 80% and 85%—similar to that observed in an equivalent control, panmictic population (80.4%) (supplementary table S6, Supplementary Material online). However, a precipitous drop-off in power was observed as the timing of the split increased past 2,000 generations (t = 0.1, N₀ = 5,000) (fig. 7 and supplementary table S6, Supplementary Material online). In the case of the oldest split simulated (t = 1, N₀ = 5,000), the power dropped from ∼80% to only 13.6% (supplementary table S6, Supplementary Material online).

Fig. 7.

Hidden population structure decreases power to detect hotspots and the frequency of false positives relative to control, equilibrium populations. Each horizontal line indicates the power (blue) and the frequency of false positives per Mb (red) for each demographic scenario: (A) Population subdivision with unequal sampling and no migration (t_split = 0.5). (B) Population subdivision with equal sampling and migration (t_split = 0.5). Migration (y-axis) is measured in units 4N₀m, where m is the proportion of migrants per generation. (C) Population subdivision with equal sampling and no migration (t_split = 0.001–1, y-axis), and (D) Control, equilibrium populations ($\theta$ = 0.001, total population size; and $\theta$ = 0.0005, subpopulation size).

Hidden population structure did not increase the frequency of FPs. As observed with power, recent population splits that occurred between 20–2,000 generations in the past (t = 0.001–0.1, N₀ = 5,000) had little to no effect on the frequency of FPs (fig. 7C and D). The frequency of FPs ranged between 0.27–0.37 per Mb among these cases, which was again consistent with a FP rate of 0.26 FP/Mb observed in the control population (fig. 7C and D). However, the frequency of FPs decreased, as power did, when the split occurred >2,000 generations in the past, to as low as 0.044 FP/Mb. Thus, old, hidden population subdivision resulted in the detection of many fewer recombination hotspots, both true and false.

To identify the effect of migration between the two hidden subpopulations, we focused upon the case of a population split occurring 10,000 generations in the past (t = 0.5, N₀ = 5,000) for which we observed intermediate power (44.3%) and FP frequency (0.17 FP/Mb) (supplementary table S6, Supplementary Material online). As the migration rate between the two populations increased, power and the FP frequency rapidly increased (fig. 7 and supplementary table S6, Supplementary Material online). One migrant every other generation (m = 2, m is given in units of 4N₀M, where M is the fraction of the population made up of migrants each generation) between subpopulations was enough to recover the power observed in the control population (fig. 7). To gauge the effect of unequally sampling individuals from two hidden subpopulations, we again focused upon simulations of a population split occurring 10,000 generations in the past (t = 0.5, N₀ = 5,000). As the sampling became less equal, with >75% of the individuals sampled arising from one of the two subpopulations, the power and FP frequency rapidly increased (fig. 7). As expected, when all individuals were sampled from a single subpopulation, the power and FP frequency were not distinguishable from performance in the control simulations.

Singletons

Even though singletons are non-informative for measurement of linkage disequilibrium and were excluded prior to calculating linkage disequilibrium in our reported analyses, we found that their inclusion does not generally affect the ability to identify recombination hotspots (supplementary figs. S1–S4, Supplementary Material online). One important exception involved population expansions, which increase the proportion of singletons (Tajima 1989a,b; Slatkin and Hudson 1991). In this case, the inclusion of singletons reduced power by up to 20% (supplementary fig. S2, Supplementary Material online).

Other Measures of Sequence Variation

Non-equilibrium demographic histories alter patterns of sequence variation beyond linkage disequilibrium. To address the possibility that patterns of sequence variation could be used to account for the effects of demographic history on hotspot detection, we analyzed the relationship between performance and four summary statistics of sequence variation known to be affected by demography: the number of segregating sites (S), the average number of pairwise differences ($\pi$) (Nei and Li 1979), Tajima’s D (Tajima 1989a), and the number of singletons.

None of the summary statistics exhibited a consistent relationship with performance across the entire range of demographic conditions simulated. The relationship between sequence variation and performance varied within and across demographic conditions (supplementary figs. S6–S9, Supplementary Material online). For example, the average number of segregating sites (S) was a decent predictor of power within the expansion or contraction scenarios simulated, when the background recombination rate was 0.02 $\rho$/kb (supplementary fig. S6A, Supplementary Material online). However, S was a relatively poor predictor of power within bottleneck scenarios simulated, as well as across all conditions (supplementary fig. S6A, Supplementary Material online). Interestingly, one of the best predictors of power within and across demographic conditions was the average number of singletons (supplementary fig. S6D, Supplementary Material online). However, this relationship did not extend to hidden population subdivisions and was inconsistent across population contractions that varied in background recombination rate (supplementary figs. S6A and S8A, Supplementary Material online). It is important to note that all singletons were removed prior to analysis in LDhat/LDhot. Thus, this correlation arises due to features of the demographic history captures by the number of singletons in the sample, not the effect of singletons themselves on the performance of these programs. None of the summary statistics were correlated with the frequency of FPs, indicating that FPs may be a much more difficult problem to address (fig. 7).

Correlations between sequence variation and performance appeared to be highly sensitive to the background recombination rate (supplementary fig. S8A–D, Supplementary Material online). As expected, the magnitude of the recombination hotspot relative to the background recombination rate strongly influences power (yellow vs. teal, supplementary fig. S8A–D, Supplementary Material online). However, unexpectedly, the background recombination rate has a strong effect on the direction of the relationship between sequence variation and performance. For example, among simulations with the same relative magnitude of recombination hotspots, correlations between the performance and the number of segregating sites, the average number of pairwise differences, and the number of singletons were almost completely reversed (yellow vs. red, supplementary fig. S8A–D, Supplementary Material online).

Window Size

LDhot statistically validates potential hotspots by comparing localized maxima to the surrounding genomic region (Auton et al. 2014). By default, LDhot (2014) compares each local maxima to a 100-kb background window. However, the size of the background window specified has been shown to alter performace of LD-based programs (Wall and Stevison 2016). To determine how background window size may affect performace of LDhot in cases of non-equilibrium demographic histories, we chose a subset of demographic conditions and re-ran LDhot analyses with two additional background window sizes (50 and 200 kb). Specifically, we chose to further analyze two conditions with low power: (1) instantaneous bottlenecks (hotspot = 16 $\rho$/kb, background = 0.02 $\rho$/kb) and (2) population contractions with elevated background recombination rates (hotspot = 16 $\rho$/kb, background = 0.2 $\rho$/kb). The population contraction simulations also exhibited elevated frequencies of FPs. Consistent with previous results (Wall and Stevison 2016), we observed higher power using a smaller background window size (supplementary figs. S10–S13, Supplementary Material online). Following population contractions, this increase in power was also associated with an increase in FPs with smaller background window sizes. We observed minor attenuation or exaggeration of the effects of window size across the nonequilibrium demographic histories examined (supplementary figs. S10–S13, Supplementary Material online).

Discussion

We observed widespread and complex effects of demographic history on the performance of LD-based methods for detecting recombination hotspots. Depending on the demographic scenario, these effects included both loss of power and increase in the frequency of FPs.

Demographic processes can reduce the power to identify hotspots by decoupling measures of linkage disequilibrium from recombination rate heterogeneity. Large reductions in power in populations that have experienced a historical bottleneck may provide an additional explanation as to why some recombination hotspots discovered via sperm-typing in humans were not identified using LD-based approaches (figs. 1 and 2) (Jeffreys et al. 2005). Among the demographic events we simulated, two distinct processes resulted in elevated measures of linkage disequilibrium and reduced power to observe recombination hotspots. First, population subsampling that occurs in certain demographic events can erase the historical record of recombination rate. This phenomenon is most extreme following a population bottleneck in which a small sample of haplotypes disproportionately contributes to subsequent generations. In this scenario, linkage disequilibrium is elevated because ancestrally recombined haplotypes were lost and the current population has yet to return to equilibrium. Conversely, it is also possible that demographically reduced linkage disequilibrium could decrease statistical power by reducing the difference between estimates of the background recombination rate and the hotspot recombination rate (Zavattari et al. 2000; McVean 2002; Rogers 2014). Second, hidden population subdivision can inflate linkage disequilibrium due to sampling artifacts. When haplotypes are fixed in separate subpopulations, but are assumed to be drawn from a panmictic population, the result is an elevated estimate of linkage disequilibrium and a loss of power to detect recombination events.

Demographic processes also affect the power to detect hotspots by changing the density of informative SNPs (supplementary tables S3–S6, Supplementary Material online). For example, population samples with fewer common SNPs contain less information about fine-scale heterogeneity in linkage disequilibrium. Nevertheless, two lines of evidence suggest that the distortions in performance we found do not simply reflect changes in SNP number. First, reductions in power in non-equilibrium populations often exceeded those observed in control populations that featured similar SNP densities (e.g., see, figs. 4A and 5A, C, and E). Second, we did not observe consistent relationships between the number of segregating sites or the average number of pairwise differences and power (supplementary figs. S6A and B and S8A and B, Supplementary Material online). In the most extreme case, the direction of the relationship was reversed when the background recombination rate was elevated (supplementary fig. S8A and B, Supplementary Material online). However, even when the direction of the relationship between power and SNP density was the same, it was not possible to predict performance based upon SNP density without also incorporating information about the demographic history of the population (supplementary figs. S6 and S8, Supplementary Material online). These results suggest that there is not an easy way to predict performance of LD-based methods for hotspot detection without estimating both the demographic history and the background recombination rate.

All four types of demographic processes we simulated proved capable of elevating the frequency of FPs beyond the range seen in relevant control simulations (e.g., see, figs. 4A and 5A, C, and E). It has been proposed that demographic events that expand the interlocus variance in the time to the most recent common ancestor (TMRCA)—thereby elevating interlocus heterogeneity in linkage disequilibrium—can lead to FP inference of hotspots when equilibrium conditions are assumed (Johnston and Cutler 2012). Our results are consistent with this explanation: we discovered the highest frequency of FPs following older population contractions with high background recombination rate, conditions that increase fine-scale variance in the TMRCA (fig. 5C and E). The same effect would be predicted for recent population bottlenecks and contractions; reductions in SNP density might have obscured its signal.

We measured the frequency of FPs in units of physical genomic distance (FP/Mb). In practice, the measurement of interest is the false discovery rate, which indicates the likelihood that an inferred hotspot is false. To compare the rate of true and FPs directly, one must know the length of the genome in question and have an estimate of the true number of hotspots identified in the genome. For example, if we assume a genome is 3,200 Mb in size and contains 30,000 hotspots, similar to the human genome (McVean et al. 2004; The International HapMap Consortium 2005; Myers et al. 2005; Winckler et al. 2005), a FP rate of 0.53 FP/Mb translates to 1,696 FPs, resulting in a ratio of 1 FP per 16.69 true positives or a false discovery rate of 5.7%. Thus, in the human genome, FP rates below roughly 0.50 FP/Mb would likely be deemed acceptable because >95% of hotspots identified would be true positives. Most (though not all) FP rates observed under non-equilibrium scenarios fell below this threshold. Alternatively, considering a genome of the same size that contained only 5,000 hotspots, similar to the chimpanzee genome (Auton et al. 2012; Stevison et al. 2016), a FP rate of 0.16 FP/Mb would result in a false discovery rate of 10.2% and a FP rate of 0.53 FP/Mb would result in a false discovery rate of 33.9%. The importance of the frequency of FPs under different demographic scenarios therefore depends on the genome in question.

The frequency of FPs was also shaped by the background recombination rate (figs. 5 and 6). When this parameter was increased by 10-fold, the frequency of FPs under certain contraction scenarios rose to as high as 1.6 FP/Mb. Notably, this elevation in FPs was only observed in the context of population contractions and not in the control simulations, suggesting an interaction between background recombination rate and demographic history. For the human genome, a FP frequency of 1.6 FP/Mb could translate to 5,120 FPs, resulting in a ratio of 1 FP per 4.9 true positives or a false discovery rate of 17%. Because the background rate of recombination shows considerable within-genome variation in many species (Kong et al. 2002; Cox et al. 2009; Rockman and Kruglyak 2009; Comeron et al. 2012; Kawakami et al. 2014), our findings suggest that the frequency of FP hotspots will vary among genomic regions.

As observed in other demographic simulation-based analyses (Li and Stephens 2003; McVean et al. 2004), LD-based methods actually performed better under certain non-equilibrium conditions than in control populations of constant size. Of note, older and more gradual population expansions resulted in a highly reduced frequency of FPs and only minor reductions in power (fig. 4). Thus, considering both the type and the intensity of the demographic scenario is vital to understanding its effects on the inference of hotspots.

Natural populations often undergo population size changes and exhibit hidden population structure, making our results relevant to empirical attempts to characterize hotspots from linkage disequilibrium. Three limitations of our study should be considered when applying our findings to empirical studies. First, we assumed an intermediate sample size of 16 diploid individuals (n = 32 phased haploid genomes), with the motivation that this number is practical for individual labs to achieve through whole genome sequencing or SNP genotyping. However, LD-based methods have been used to identify recombination hotspots with much larger sample sizes, especially in humans (The International HapMap Consortium 2005, 2010). Previous analyses indicate that the performance of LD-based methods improves with increasing sample size (Wall and Stevison 2016). Including more individuals could partially ameliorate some of the challenges we observed. Second, we focused on the most popular LD-based approach for identifying hotspots (LDhot), but other methods exist and there is evidence that they vary in performance (Li and Stephens 2003; Fearnhead 2006; Chan et al. 2012; Yang et al. 2014). Third, the demographic history of a real population is likely to be more complicated than the scenarios we examined.

Overall, our results demonstrate that non-equilibrium demographic histories frequently interfere with the ability to detect hotspots from LD-based methods, suggesting that inferences about the genomic landscape of hotspots that assume equilibrium could be misleading. If we assume that the effects of demography on patterns of linkage disequilibrium are independent among species, reduced performance is expected to artificially decrease the proportion of hotspots inferred to be shared. Further investigation of this bias will be needed to accurately quantify the rapid rate of hotspot evolution in primates and mice (Ptak et al. 2005; Winckler et al. 2005; Auton and McVean 2012; Brunschwig et al. 2012; Stevison et al. 2016).

Additionally, while our study focuses specifically on the identification of recombination hotspots, the underlying mechanism is that demography alters linkage disequilibrium. LDhot statistically validates local maxima in recombination rate to identify recombination hotspots (Auton et al. 2014). However, these local maxima must first be estimated from linkage disequilibrium data using programs such as LDhat (McVean and Auton 2007). Non-equilibrium history likely contributes to error in both the estimation of fine-scale recombination rate, via over- or underestimation of the true recombination rate (Zavattari et al. 2000; McVean 2002; Rogers 2014), and the identification of recombination hotspots, via increases in the variance in estimated recombination rate (Johnston and Cutler 2012). Thus, our results reinforce the notion that attempts to estimate recombination rate throughout the genome are also susceptible to the effects of demographic history (Stumpf and McVean 2003; Clark et al. 2010).

More generally, our findings emphasize the need to explicitly account for demographic history when using linkage disequilibrium to locate and characterize hotspots. We recommend the following strategy for empirical studies. First, major aspects of demographic history that are expected to interfere with hotspot inference can be reconstructed using population genomic approaches (Beaumont et al. 2002; Gutenkunst et al. 2009; Excoffier et al. 2013; Terhorst et al. 2017). For most studies of the hotspot landscape—which sample variation across large fractions of the genome—the data to infer demographic history will already be in hand. Second, the ability of LD-based methods to detect hotspots can be measured by simulating under the estimated history. Finally, the effects of demographic history should be incorporated into the inference of hotspots. One promising approach along these lines is to compute look-up tables of two-locus likelihoods under the reconstructed history of population size change (Kamm et al. 2016) and use these tables in LDhot or a related program. We expect this strategy will improve our understanding of hotspot landscapes in natural populations. When building knowledge of demographic history into the inference procedure is not feasible, investigators could either avoid populations that show signs of departing from demographic equilibrium, such as a skew in the genome-wide site frequency spectrum, or use an alternative approach, such as one that directly measures recombination rate.

Methods

Simulations

We used two coalescent-based programs to simulate chromosomes with a known recombination map and demographic history: (1) fin, included in LDhat2.1 (McVean and Auton 2007) to simulate instanteous bottlenecks and (2) msHOT (Hellenthal and Stephens 2007), an extension of ms (Hudson 2001) to simulate all other demographic histories. We then used LDhat (McVean and Auton 2007) to measure recombination rate along the simulated chromosomes and LDhot (Auton et al. 2014) to identify all statistically significant recombination hotspots in the simulated samples. With perfect knowledge of the true underlying recombination map, we determined whether significant hotspots were either true positives or FPs, allowing us to compute two metrics of performance: power and the frequency of FPs. For each condition, we simulated 1,000 data sets. Each data set contained 32 chromosomes (equivalent to sampling 16 diploid individuals, assuming random mating), a modest sample size intended to mimic genome sequencing studies of natural populations, especially in non-model organisms. We considered four common demographic events that affect patterns of linkage disequilibrium: population bottlenecks, hidden population structure, exponential population growth, and exponential population contraction. Except where explicitly noted, we hold the frequency of recombination events, r/kb, constant within and between simulations. Accordingly, the population recombination rate, $\rho$/kb (4Nr/kb), changes within and between simulations due to changes in population size, N.

Instantaneous Bottlenecks

To simulate the effects of an instantaneous bottleneck, we modeled single 500-kb chromosomes with eight recombination hotspots, each 2-kb in length, evenly spaced 50-kb apart using fin, the coalescent simulator within the LDhat2.1 package (McVean and Auton 2007). We included an additional 75 kb between the distal hotspots and the ends of the scaffold to reduce edge effects. We assumed a current effective population size of 10,000 and a mutation rate of 2.5×10⁻⁸, such that the population mutation rate ($\theta$) is equal to 0.001. The background recombination rate between the hotspots was 0.02 $\rho$/kb, which is equivalent to 0.05 cM/Mb and consistent with the background recombination rate observed via sperm typing in humans (Jeffreys et al. 2005; Auton et al. 2014). The hotspots doubled in magnitude from a minimum 0.5 $\rho$/kb (25× the background rate) to a maximum of 64 $\rho$/kb (3,200× the background rate) ($\rho$/kb = 0.5, 1, 2, 4, 8, 16, 32, and 64). We designed the scaffold to be identical to that used to test the performance of LDhot by the authors of the program (Auton et al. 2014) and used the default program parameters except where specifically indicated. The timing of the single instantaneous bottleneck spanned from 40 (0.001 4N₀) to 40,000 (4N₀) generations in the past (t = 0.001, 0.0025, 0.005, 0.01, 0.025, 0.05, 0.1, 0.25, 0.5, 1). We varied the strength of a bottleneck by changing the probability that a given lineage coalesces during the bottleneck from 10% to 98% (s = 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 0.98). We simulated every pairwise combination of strength and time of bottleneck for a total 100 different bottlenecks varying from very recent and very strong (98% of lineages coalesce 40 generations in the past: t = 0.001, s = 0.98) to very old, and very weak (10% of lineages coalesce 40,000 generations in the past: t = 1, s = 0.1). We compared performance to a population that maintained a constant population size of 10,000 ($\theta$ = 0.001).

Hidden Population Structure

To simulate more complicated demographic histories, we used the coalescent simulator msHOT, shifting attention to a single hotspot (Hudson 2001; Hellenthal and Stephens 2007). This change was a pragmatic decision based upon the increased time required to simulate complex recombination landscapes in msHOT. We simulated 300-kb chromosomes with one 2-kb hotspot directly in the center with the magnitude of 16 $\rho$/kb, equivalent to 40 cM/Mb. This value was chosen because it is similar to the observed average magnitude of recombination hotspots in humans (17.2 $\rho$/kb or 43 cM/Mb) (The International HapMap Consortium 2007). We again assumed a current total effective population size of 10,000 and a mutation rate of 2.5×10⁻⁸, such that the population mutation rate ($\theta$) is equal to 0.001. Likewise, the values of $\rho$/kb are given for the total population size of 10,000 individuals. To replicate the consequences of sampling with hidden population structure, we modeled demographic histories in which the population split at time t (units 4N₀, where N₀ is the present population size of the subpopulations) into two subpopulations of equal size (N₀ = 5,000). We assumed no migration between the two demes following the split. Additionally, we assumed each “hidden” population was sampled equally (16 chromosome/pop.) and that there was no change in population growth before or after the split. We varied the timing of the split using the same ten time points as above (t = 0.001, 0.0025, 0.005, 0.01, 0.025, 0.05, 0.1, 0.25, 0.5, 1). We compared performance to two control conditions: (1) a population that maintained a constant population size of 10,000 ($\theta$ = 0.001), the combined size of the two subpopulations and (2) a population that maintained a constant population size of 5,000 ($\theta$ = 0.0005), the size of a single subpopulation.

We also explored the consequences of two assumptions: (1) no migration between subpopulations and (2) equal sampling of the two subpopulations. Migration between demes is expected to reduce the effects of hidden population structure on patterns of linkage disequilibrium. To determine the effects of migration between the subpopulations on performance of LD-based programs, we introduced migration between the two populations after the split. We varied the migration rate from one individual every 1,000 generations (4N₀m = 0.004, where m is the fraction of the population made up of migrants each generation) to 100 individuals every generation (4N₀m = 400) between two subpopulations that split 20,000 generations ago (t = 0.5; 4N₀m = 0, 0.004, 0.04, 0.4, 2, 4, 8, 20, 40, 400). Additionally, we examined the effect of unequal sampling between subpopulations by varying the proportion of individuals sampled from each population, from equal sampling of each subpopulation (n1/n2 = 16/16) to all of the samples originating in one of the two populations (n1/n2 = 32/0) (t = 0.5; n1/n2 = 16/16, 18/14, 20/12, 22/10, 24/8, 26/6, 28/4, 30/2, 31/1, 32/0).

Exponential Population Growth

To model the consequences of exponential population growth, we used msHOT to simulate a 450-kb scaffold with a single, central 2-kb recombination hotspot with the magnitude of 16 $\rho$/kb. We simulated populations that experienced a 10-fold exponential increase in population size from an ancestral size of 1,000 individuals to a current population size of 10,000 individuals ($\theta$ = 0.001) and varied the timing and duration of the increase. The values of $\rho$/kb are given for the ending population size of 10,000 individuals, but change during the simulations in accordance with population size. We varied how long ago the population returned to equilibrium conditions to simulate recent exponential increases, as well as old exponential increases, in population size (t_recovery = 0.001, 0.0025, 0.005, 0.01, 0.025, 0.05, 0.1, 0.25, 0.5, 1). We also varied the duration of the exponential increase to simulate both gradual and sharp increases in population size (t_duration = 0.001, 0.0025, 0.005, 0.01, 0.025, 0.05, 0.1, 0.25, 0.5, 1). We simulated every pairwise combination of timing and duration of population expansions for a total of 100 different demographic histories varying from a very recent and very sharp increase in population size (10-fold increase in population size over 40 generations that ended 40 generations in the past; t_recovery = 0.001, t_duration = 0.001) to very old, and very gradual population expansions (10-fold increase in population size over 40,000 generations that ended 40,000 generations in the past; t_recovery = 1, t_duration = 1). We compared performance to three control conditions: (1) a population that maintained a constant population size of 10,000 (θ = 0.001), the current size of the population, (2) a population that maintained a constant population size of 1,000 (θ = 0.0001), the ancestral size of the population, and (3) a population that maintained a constant population size of 5,000 (θ = 0.0005), an intermediate population size.

Exponential Population Contraction

To model the consequences of exponential population contraction, we used msHOT to simulate a 600-kb scaffold with a single, central 2-kb recombination hotspot with the magnitude of 16 $\rho$/kb (Hudson 2001; Hellenthal and Stephens 2007). The increase in the number of SNPs we encountered modeling an equivalent population contraction of 100,000 to 10,000 individuals caused significant deviations from the infinite alleles model assumed by msHOT (Hudson 2001; Hellenthal and Stephens 2007). Therefore, to conduct our simulations in a suitable parameter space, we decreased the population mutation rate by an order of magnitude (θ = 0.0001) and modeled contractions from 10,000 to 1,000 individuals. The values of $\rho$/kb are given for the starting population size of 10,000 individuals, but change during the simulations in accordance with decreasing population size. The scaffold length was concomitantly increased to reduce the number of simulated samples that did not meet the threshold of 100 SNPs. We varied the timing and duration of the population contraction. To determine the effect of timing, we varied how long in the past the contraction ended and the population returned to equilibrium conditions (t_recovery = 0.001, 0.0025, 0.005, 0.01, 0.025, 0.05, 0.1, 0.25, 0.5, 1). To determine the effect of the duration of the exponential contraction, we varied the length of time over which the contraction occurred (t_duration = 0.001, 0.0025, 0.005, 0.01, 0.025, 0.05, 0.1, 0.25, 0.5, 1) and thus the intensity of the population contraction. We simulated every pairwise combination of timing and duration for a total of 100 different contractions varying from very recent and intense (t_recovery = 0.001, t_duration = 0.001) to very old and gradual (t_recovery = 1, t_duration = 1).

We also investigated the effect of background recombination rate on the incidence of FPs following population contractions. To accomplish this, we varied the background recombination rate and hotspot intensity and measured performance following the same set of population contractions. We increased the background rate 10-fold from 0.02 $\rho$/kb to 0.2 $\rho$/kb. In the first set of simulations we kept the absolute intensity of the hotspot the same (16$\rho$/kb), which decreased its relative intensity (80× background rate). In the second set of simulations we kept the relative intensity of the hotspot constant (800× background rate), which increased the absolute intensity of the hotspot (160 $\rho$/kb). Again, we compared performance to three control conditions: (1) a population that maintained a constant population size of 10,000 (θ = 0.001), the ancestral size of the population, (2) a population that maintained a constant population size of 1,000 (θ = 0.0001), the current size of the population, and (3) a population that maintained a constant population size of 5,000 (θ = 0.0005), an intermediate population size.

Identification of Recombination Hotspots

We used LDhat2.1 (McVean and Auton 2007) to measure recombination rate along the simulated chromosomes and LDhot (Auton et al. 2014) to identify all statistically significant recombination hotspots in the simulated samples. LDhat determines the likelihood of recombination between pairwise combinations of SNPs to estimate variable $\rho$/kb across a chromosome (McVean and Auton 2007). LDhot determines whether local maxima in the recombination rate estimates represent significant recombination hotspots (Auton et al. 2014). To accomplish this, LDhot identifies 3-kb windows that overlap with local maxima and asks whether they are significantly different from a 100-kb background window (Auton et al. 2014). If consecutive 3-kb windows are significant they are combined into a single hotspot (Auton et al. 2014). In all cases, mutations observed once in the sample (“singletons”) were removed prior to data analysis. These sites were removed because they produce inherently uninformative measurements of LD. We also separately analyzed versions of the simulated data before the removal of singletons, allowing us to determine how the inclusion/exclusion of these sites influenced performance of LD-based methods of hotspot detection. The coalescent simulator msHOT assumes an infinite alleles model when assigning positions to SNPs (Hudson 2001). As such, given a finite chromosome size, it was unavoidable, but infrequent, that two SNPs would fall within a single base pair position. When this occurred, both SNPs were removed prior to data analysis. Additionally, we did not include simulated samples in measures of performance in cases without at least 50 SNPs on either side of the true recombination hotspot. Except where explicitly stated, we used the default parameters (Auton et al. 2014). The exact parameterization and command line usage for each simulation can be found on the Open Science Framework (DOI 10.17605/OSF.IO/JNXPV |, ARK c7605/osf.io/jnxpv).

Measures of Performance

As we have perfect knowledge of the true underlying recombination map, we can determine if significant hotspots are either true positives or FPs. We used permissive criteria to define true positives. A significant hotspot was considered a true positive if the local maxima in recombination rate measured in LDhat overlapped with the boundaries of the true hotspot location. The power to discover hotspots was calculated as the proportion of the total number of measurable true hotspots that were identified as statistically significant. A hotspot was considered measurable if it was flanked by 50 or more SNPs on either side. We calculated the FP frequency as the number of significant hotspots identified that did not overlap with the location of true hotspots per Mb. We divided the total number of FPs identified in each condition by the sum total measurable length of the simulated chromosomes in each condition to determine the frequency of FPs per Mb. We examined the power and FP rate under three different significance thresholds, p < 0.05, p < 0.005, and the recommended threshold of p < 0.001 (Auton et al. 2014). We used the recommended threshold of p < 0.001 for all data reported in the results section, as well as the figures.

Supplementary Material

Supplementary data are available at Molecular Biology and Evolution online. Data files are available on the Open Science Framework (DOI 10.17605/OSF.IO/JNXPV; ARK c7605/osf.io/jnxpv).