The Structured Coalescent and Its Approximations

Abstract

Phylogeographic methods can help reveal the movement of genes between populations of organisms. This has been widely done to quantify pathogen movement between different host populations, the migration history of humans, and the geographic spread of languages or gene flow between species using the location or state of samples alongside sequence data. Phylogenies therefore offer insights into migration processes not available from classic epidemiological or occurrence data alone. Phylogeographic methods have however several known shortcomings. In particular, one of the most widely used methods treats migration the same as mutation, and therefore does not incorporate information about population demography. This may lead to severe biases in estimated migration rates for data sets where sampling is biased across populations. The structured coalescent on the other hand allows us to coherently model the migration and coalescent process, but current implementations struggle with complex data sets due to the need to infer ancestral migration histories. Thus, approximations to the structured coalescent, which integrate over all ancestral migration histories, have been developed. However, the validity and robustness of these approximations remain unclear. We present an exact numerical solution to the structured coalescent that does not require the inference of migration histories. Although this solution is computationally unfeasible for large data sets, it clarifies the assumptions of previously developed approximate methods and allows us to provide an improved approximation to the structured coalescent. We have implemented these methods in BEAST2, and we show how these methods compare under different scenarios.

Introduction

The relatedness of samples of homologous genetic sequences are the result of a past branching process. The same applies to other sources of data, such as languages or phenotypic markers. This past branching process contains information about ancestral population histories and can be inferred from data using phylogenetic trees. In particular, phylogenies encode information about the structure of a population and the movement of information (e.g., genes or words) between subpopulations. Phylogeographic methods allow us to elucidate such movements given the state or location of samples. Phylogeographic methods have been used to analyze the global spread of influenza viruses (Bedford et al. 2010; Bahl et al. 2011; Lemey et al. 2014; Bedford et al. 2015), the origins of HIV-1 (Faria et al. 2014) and various other diseases (Bourhy et al. 2008; Raghwani et al. 2011). Analogously to the analysis of epidemics, such methods have been used to study the geographic origin of species such as brown and polar bears (Edwards et al. 2011). Related methods have been used to study the demographic history of species, including their divergence from related species of humans (Gronau et al. 2011) and great apes (Mailund et al. 2012). Similar methods have also been applied to study the origin of the Indo-European language family (Bouckaert et al. 2012).

A range of phylogeographic methods for inferring population structure from phylogenies have been proposed. The mugration method (Lemey et al. 2009) treats migration as a continuous time Markov chain, such as used to model mutation, and assumes the migration process to be independent of the tree generating process. In other words, it is assumed that the shape of a phylogeny is not in any way influenced by the migration process. This assumption can lead to biases in estimates of migration rates when sampling is biased (De Maio et al. 2015). Other methods, such as those based on the structured coalescent (Takahata 1988; Hudson 1990; Notohara 1990) and the related isolation-with-migration models (Wakeley 2000; Nielsen and Wakeley 2001; Hey 2010), do not make this independence assumption. In contrast to the mugration-based methods, they require the state (or location) of any ancestral lineage in the phylogeny at any time to be inferred (Beerli and Felsenstein 2001; Ewing et al. 2004; Vaughan et al. 2014). Inferring lineage states is computationally expensive, as it normally requires Markov chain Monte Carlo (MCMC) based sampling, and limits the complexity of scenarios that can be analyzed.

Other approaches (Volz 2012; Palczewski and Beerli 2013) seek to marginalize over all possible migration histories by treating lineage states probabilistically instead of using MCMC based sampling. Rather than assigning lineages to particular states, the probability of each lineage being in each state is calculated at all times using a set of previously described differential equations (Volz 2012). Such a marginalization approach (rather than explicit sampling of states) allows for the analysis of larger data sets (De Maio et al. 2015). Although this approach appears to only make the assumption of lineage independence, that is, that the state or location of one lineage does not depend on any other lineage (De Maio et al. 2015), it remains unclear if there are additional assumptions not being accounted for.

In this paper, we derive an exact numerical solution of the structured coalescent with discrete states for neutrally evolving homologous non-recombinant sequences. This solution is based on the joint probabilities of lineages being in any possible configuration. However, it quickly becomes computationally unfeasible for more than a few lineages and states. It allows us however to clarify the assumptions used in previous approaches (Volz 2012; De Maio et al. 2015) and to develop a more refined approximation to the structured coalescent. We then show how the different approximations compare in terms of tree, parameter and root state inference under both biased and unbiased sampling conditions. Simulations reveal that our new approximation outperforms previous approximations at comparable computational cost. We then apply these different approximations to a previously described avian influenza virus data set (Lu et al. 2014) sampled from different regions of North America to show that the choice of method influences the interpretation of data in practice.

New Approaches

The structured coalescent describes a coalescent process in subpopulations between which individuals can migrate (see Methods). The state of a lineage in a phylogenetic tree now denotes the subpopulation to which the lineage belongs. Approaches that calculate the probability density of a phylogeny under the structured coalescent given a set of coalescent and migration rates typically use MCMC to integrate over possible migration histories, that is, to integrate over ancestral lineage states. Using this Monte Carlo integration however strongly limits the size of data sets that can be analyzed. Already at a small number of different states, efficiently exploring the space of all possible migration histories becomes unfeasible. Methods that are able to integrate over these migration histories but avoid MCMC sampling hold great promise in their ability to analyze larger data sets. We therefore derive an exact solution to the structured coalescent process with discrete states for neutrally evolving populations that integrates over all possible migration histories using ordinary differential equations. We refer to this approach as ESCO, the exact structured coalescent.

Although ESCO is exact, it requires solving a number of differential equations that is proportional to the “number of different states” to the power of the “number of coexisting lineages”. This originates from the need to calculate the probability of every possible configuration of a set of coexisting lineages and states using migration and coalescent rates. We therefore develop a lower-dimensional approximation that is based on keeping track of the marginal lineage state probabilities instead. We call this approach the marginal lineage states approximation of the structured coalescent (MASCO). This approach allows us to reduce the number of differential equations that have to be solved between events to the “number of states” times “number of lineages”, but ignores any correlations between lineages. Using this approach, the state of a lineage is calculated backwards through time, integrating over potential migration events and incorporating the probability of no coalescent events between branching events in the phylogeny. This means that the state or location of a lineage is directly dependent on the coalescent process. In particular, the observation that two lineages that do not coalesce for a longer time are unlikely to be in the same state is incorporated in this approach.

In comparison to MASCO, we show that the approach of (Volz 2012) requires the additional assumption that the state of a lineage evolves independently of the coalescent process between events. This means that changes in the probabilities of lineages being in a certain state are only dependent on the migration rates, and are completely independent of other lineages in the phylogeny. We refer to this approach as SISCO, the state independence approximation of the structured coalescent. The differential equations describing how lineages evolve between events for ESCO and MASCO are both derived in the Materials and Methods section and the differential equations for SISCO have been derived previously (Volz 2012).

Results

Tree Height Distributions under the Structured Coalescent and Its Approximations

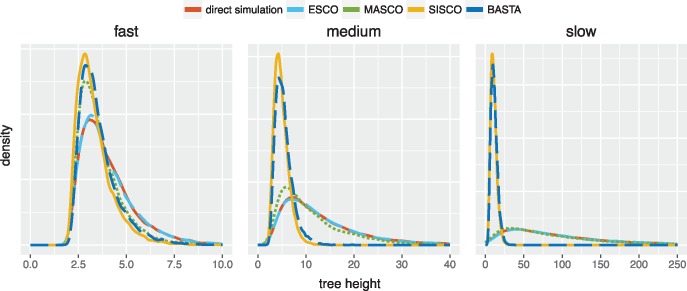
The structured coalescent and its approximations describe different probability distributions over trees. To see how these distributions compare, we performed direct backwards-in-time simulations under the structured coalescent using MASTER (Vaughan and Drummond 2013), analogously to Vaughan et al. (2014). These trees were compared with trees sampled under ESCO, MASCO, SISCO, as well as BASTA (De Maio et al. 2015), a numerical approximation of SISCO. Under these latter four models, trees were sampled from their respective probability distributions using MCMC in BEAST2 (Bouckaert et al. 2014). Since it is difficult to directly compare distributions of trees, we instead compared the distribution of tree heights.

For each of the five scenarios (direct, ESCO, MASCO, SISCO, BASTA) and three different overall migration rates, we obtained 8,000 trees. We used a model with three different states, sampling three, two and one individuals from each state, respectively. Coalescent rates were different in each state (${\lambda }_1=1,{\lambda }_2=2,{\lambda }_3=4$) and migration rates were different between states ($m_{1,2}=1,m_{1,3}=2,m_{2,1}=0.1,m_{2,3}=0.3,m_{3,1}=1,m_{3,2}=1$). To show how the different methods perform under different overall migration rates, the rates between states were scaled by factors of 1 (fast migration), 0.1 (medium migration), and 0.01 (slow migration). All rates are given in arbitrary units of time.

Figure 1 shows the distribution of tree heights sampled using MCMC and compares them to the distribution of tree heights obtained by directly simulating trees under the structured coalescent. Of the different methods, only the distribution of ESCO is consistent with direct simulation. Only keeping track of the marginal lineage states (MASCO) leads to slightly shorter tree heights. Further assuming lineage states to be independent of the coalescent process (SISCO) results in much shorter trees. BASTA (De Maio et al. 2015), being an approximation of SISCO, performs very similar to SISCO. The shorter tree heights under SISCO compared with MASCO can be explained in the following way. Not taking into account how the coalescent process influences lineage states leads to an overestimation of the probability of two lineages being in the same state if no coalescent event is observed by SISCO compared with MASCO. Overestimating the probability of two lineages being in the same state then also leads to a higher probability of them coalescing. This in turn results in shorter trees since lineages are expected to coalesce at a faster rate. SISCO and BASTA in general perform worse at slower migration rates than at rates in the same order of magnitude as the rates of coalescence.

Fig. 1.

Comparison of MCMC sampled to simulated tree heights using the different structured coalescent approaches. Sampled tree heights in arbitrary units of time when the rates of migration are fast, that is, in the same order of magnitude as coalescence, when the rates of migration are medium, that is, one order of magnitude lower than coalescence and slow, that is, two orders of magnitude lower than coalescence. The trees were sampled using MCMC for one million iterations, storing every thousandth step, after a burn-in of 20%.

Root State Probabilities

The ancestral state or location of lineages back in time is often of interest for biological questions. For example, in a pathogen phylogeny the root location is informative of the geographic origin of an epidemic. Here, we show on one fixed tree how the exact structured coalescent compares in the inference of the root state to its approximations. We additionally inferred the root state using MultiTypeTree (Vaughan et al. 2014), which uses MCMC to sample lineage states and does not rely on approximations, to obtain a reference root state probability (Vaughan et al. 2014). We inferred the probability of the root being in either state for different migration rates in one direction while holding the rate in the other direction constant.

The exact structured coalescent and only keeping track of the marginal lineage states (MASCO) agree well with the inferred posterior mean using MultiTypeTree (fig. 2). The inferred state probabilities using SISCO on the other hand do not, showing that the assumption of independence between the lineage states and the coalescent process does not only describe a misspecified probability distribution over trees but can also lead to biased inference of ancestral states.

Fig. 2.

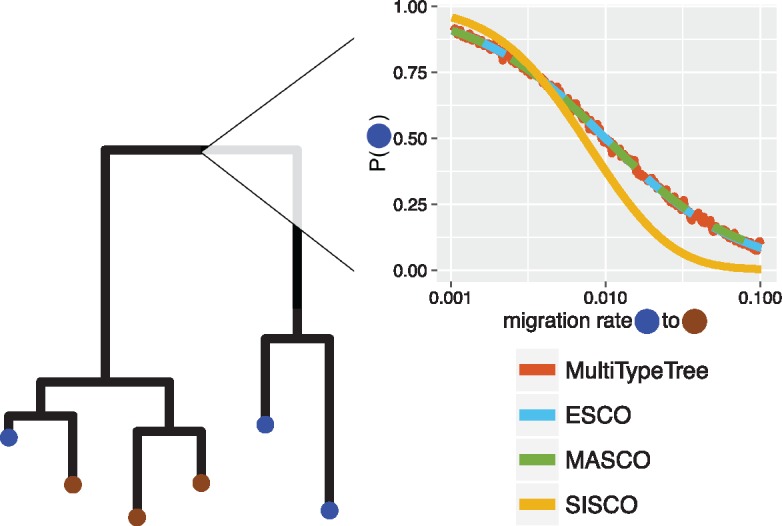
Inferred location of the root for different migration rates and structured coalescent approaches. The plot shows the probability of the root being in the blue state (y-axis) depending on the migration rate from blue to brown (x-axis), for the given tree and sampling states. The migration rate from brown to blue was held constant at 0.01. The height of the tree was ∼42 arbitrary units of time and the coalescent rates were 2 (in blue) and 4 (in red).

Estimation of Migration Rates

Coalescent methods are often used to infer population and migration parameters from trees. To show how the inference of the migration rates compares to the true rate, we simulated 1,000 trees under the structured coalescent with symmetric migration rates from 10^–5 to 1 and pairwise coalescent rates of 2 using MASTER. Hence, we consider a range of cases from very strong to very weak population structure, where the probability of migration is on the same order as coalescence. Each tree consisted of four contemporaneously sampled leafs from each of the two states. We fixed the coalescent rates to the truth, assumed symmetric migration rates and then inferred the maximum likelihood estimate of the migration rate using the exact structured coalescent (ESCO) and its approximations MASCO and SISCO.

The results are summarized in figure 3. When only keeping track of the marginal lineage states (MASCO), the migration rates are estimated well. Making the further assumption of independence of the lineage states and the coalescent process (SISCO) leads to strong biases in estimates of the migration rates. The lower the migration rates are compared with the coalescent rates, the greater the underestimation of the migration rates becomes.

Fig. 3.

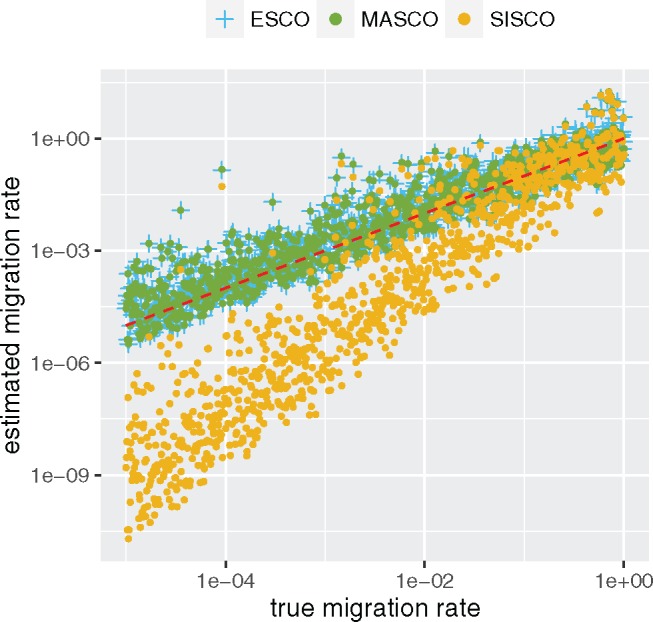
Maximum likelihood estimates of migration rates using the exact structured coalescent and its approximations. Here, we compare simulated migration rates (x-axis) to the maximum likelihood estimates of the migration rate (y-axis), estimated using the exact structured coalescent ESCO and its approximations MASCO and SISCO. The coalescent rates are fixed to the truth, and the migration rates are assumed to be symmetric. The red line indicates where the true values should lie.

Estimation of Rate Asymmetries

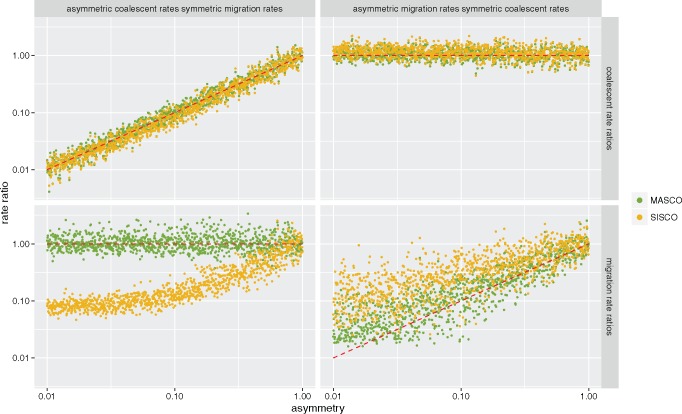
In the previous section, we inferred the rate of migration given (or conditional on) the true coalescent rate and the information that the migration rates were the same in both directions. In reality, these rates can greatly vary across states or locations. It is therefore important for methods to be able to perform well in situations where rates are asymmetric. Previous work showed that the ability to infer migration rate asymmetries greatly depends on the method used (De Maio et al. 2015). Here, we compare inferences of rate asymmetries under MASCO and SISCO. Applying ESCO to the same trees would not be computationally feasible, due to the larger number of lineages existing in parallel.

Figure 4 shows the median ratios of inferred coalescent and migration rates using MASCO and SISCO. The estimates of coalescent rate ratios (fig. 4, top row) are accurate under both simulation scenarios and methods. Estimates of the migration rate ratios are biased in the presence of asymmetric coalescent rates (fig. 4, bottom left) using SISCO, but not MASCO. SISCO overestimates the backwards in time migration rate out of the state with a faster coalescent rate and into the state with a slower coalescent rate. An underestimation of the rate in the other direction was observed as well. When the coalescent rates are symmetric, both methods are unable to capture very strong asymmetries in the migration rate ratios (fig. 4, bottom right). However, when taking into account the highest posterior density (HPD) intervals of the estimates, most estimates contain the true rate ratio (see supplementary figs. S1 and S2, Supplementary Material online). MASCO is overall better at inferring those migration rate asymmetries than SISCO.

Fig. 4.

Inferred asymmetry of migration and coalescent rates. Here we show the inferred median coalescent (upper row) and migration (lower row) rate ratios under different conditions. In the first column, the coalescent rate ratios (x-axis) are varied while the migration rates ratios are kept constant. In the second column, the migration rate ratios (x-axis) are varied, whereas the coalescent rate ratios are kept constant. We simulated a total of 2,000 trees using MASTER with 100 tips from each of the two different states sampled uniformly between times t = 0 and t = 10. Of these trees, 1,000 were simulated with pairwise coalescent rate ratios λ₁/λ₂ from 0.01 to 1, λ₁ + λ₂ = 4 and migration rates in both directions equal to 1. The other 1,000 trees were simulated with migration rate ratios from m₁₂/m₂₁ from 0.01 to 1, m₁₂ + m₂₁ = 2 and pairwise coalescent rates in both states equal to 2, using exponential priors with mean 2 for the coalescent rates and mean 1 for the migration rates. Both coalescent rates and both migration rates are estimated. The red line indicates where the estimates should lie.

Sampling Bias

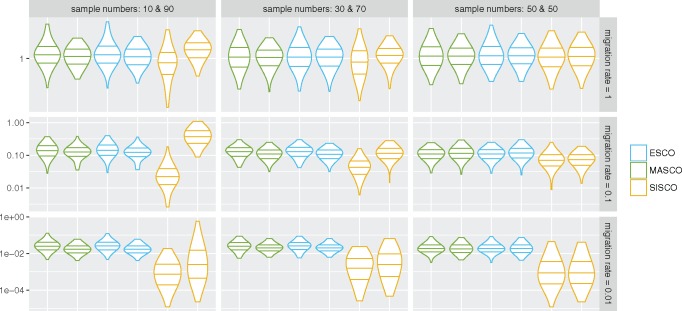
Previous work showed that the approximate structured coalescent is able to accurately infer migration rates even when sampling fractions are biased, given samples are taken contemporaneously (De Maio et al. 2015). Here, we explore the effect of biased sampling fractions in the presence of serial sampling. We compare the exact structured coalescent ESCO to its approximations MASCO and SISCO.

Figure 5 reveals that ESCO is able to unbiasedly infer the migration rates in both directions, independent of sampling biases or migration rates. The same applies to MASCO. For SISCO however, biased sampling leads to an underestimation of the backwards migration rate into the oversampled state and an overestimation of the rates into the undersampled state for intermediate and high migration rates. At low migration rates, both rates are underestimated.

Fig. 5.

Inferred migration rates under different sampling conditions. The plot shows the distribution of mean inferred migration rates using ESCO, MASCO, and SISCO. From the left, the first distribution of a color (indicating the different methods) always shows the distribution of mean inferred migration rates from state 1 to state 2. The second distribution from the same color shows the rates from state 2 to 1. From left to right the number of samples from state 1 and state 2 are changed, whereas from top to bottom the true symmetric migration rates are going from 1 to 0.01. The lines within the violin plots indicate the first, second, and third quantiles. The coalescent rates were 2 in both states and the migration rates ranged from 0.01 to 1. The migration rates were always symmetric, that is, the same in both directions. The leaves were sampled uniformly between t = 0 and t = 25. Each simulation was repeated 100 times and each inference was run with 3 parallel MCMC chains, each with different initial values. An exponential prior distribution with the mean $=1$ was used on the migration and coalescent rates.

Application to Avian Influenza Virus

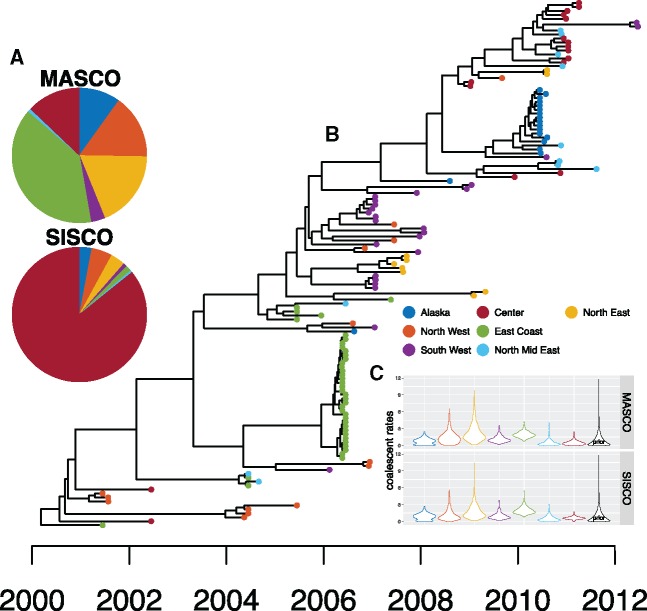
To show how the inference of the origin of an epidemic varies with the method used, we applied the two approximations of the structured coalescent (MASCO and SISCO) to a previously described avian influenza data set (Lu et al. 2014; De Maio et al. 2015) to infer the geographic location of the root.

In figure 6, we show the inferred region of the root using MASCO and SISCO. Despite the fact that almost all samples from the central US were collected after 2009 and that samples from the East Coast and the North West fall closer to the root, SISCO places the root with over 80% probability in the central US. MASCO on the other hand places the root to be most likely at the East Coast, one of the least likely root locations according to SISCO. Also, in contrast to SISCO it does not exclude most regions from being the location of the root based on the phylogenetic data available. We provide a possible explanation to why we observe differences in the inferred root state in the Discussion below.

Fig. 6.

Inference of the root regions of AIV sampled from different places in North America. (A) Maximum clade credibility tree inferred from AIV sequences sampled in different regions of the USA, Canada, and Mexico using MASCO as a population prior. The node heights represent the mean node heights. The tip colors indicate the different sampling regions shown in the legend. (B) Inferred root regions using MASCO (top) and SISCO (bottom). The pie charts show the inferred probability of the root being in either of the different states/regions by MASCO and SISCO. (C) Violin plots of the inferred coalescent rates for the different regions. The black plot distribution is the exponential prior with mean 1. We used this prior for both coalescent and migration rates.

Discussion

We provide an exact way to calculate the probability density of a phylogenetic tree under the structured coalescent (Takahata 1988; Hudson 1990; Notohara 1990) without the need to sample migration histories, as in previously described approaches (Beerli and Felsenstein 2001; Ewing et al. 2004; Vaughan et al. 2014), by solving a set of ordinary differential equations.

Additionally, we introduce a new approximation that is more accurate than a previously described approximation (Volz 2012). This new approximation facilitates a trade-off between speed and accuracy. The increased speed compared with the exact solution originates from ignoring any correlations between lineages. This assumption leads to better scaling of the computational complexity with the number of states and lineages. We show that this assumption allows us to infer migration, coalescent rates and root states in all scenarios tested within this simulation study.

Additionally assuming independence of the lineages states from the coalescent process, as introduced in (Volz 2012), leads however to major biases in parameter and root state inference. These biases are especially pronounced in our simulations when migration is slow compared with the coalescent rate. This observation can be explained in the following way: The lower the migration rates are compared with coalescent rates, the stronger the influence of the coalescent process on the configuration of lineages across states becomes. The assumption of independence of the lineage states from the coalescent process does not allow for the incorporation of this information into the calculation of lineage state probabilities though.

Next, we showed how the approximations of the structured coalescent perform in inferring asymmetric coalescent and migration rates. Although coalescent rates are inferred accurately for both approximations, inference of migration rate ratios is biased when coalescent rates are asymmetric under SISCO. We also showed that under biased sampling, inferences of migration rates are strongly biased under SISCO, but not under MASCO.

Both biases can be understood in the following way. A lineage may have a higher probability of coalescing in one state than another either because the pairwise coalescent rate in one state is higher (e.g., due to a smaller effective population size) or because more lineages reside in one state than another (e.g., because of biased sampling). Taking the influence of the coalescent process on lineage states into account, as done under MASCO, reduces the probability of a lineage occupying a state with a high coalescent rate if no coalescent events occur.

In other words, MASCO redistributes the probability mass assigned to each state to reflect the observed coalescent history, including the observation that a lineage may have not yet coalesced (see eq. 3). SISCO does not redistribute probability mass to reflect the observation that a lineage has not yet coalesced. In order to reduce the probability of lineages coalescing in a state with high rates of coalescence, it overestimates the migration rate out of such states. This overestimation of migration rates out of a state is observable when having asymmetric coalescent rates due to either a higher pairwise coalescent rate within a state or having more lineages in a given state due to biased sampling. Either way, the migration rate out of the state with a higher coalescent rate is overestimated and underestimated in the other direction. While revising this manuscript, it was brought to our attention that updates to the R package rcolgem (Volz 2016; based on Volz [2012]), uses a related approach to redistribute probability mass between states.

Although MASCO does redistribute probability mass via the coalescent process, it ignores the correlations between lineages encoded in the joint probabilities when only considering marginal lineage state probabilities. These correlations, induced by the coalescent process, are expected to be especially strong in parts of the tree where there are only a few coexisting lineages present. The rate at which lineages coalesce is highly dependent on the number of lineages in a state. Having one or two lineages in the same state is the difference between having a zero or nonzero rate of coalescence, whereas having a 1,000 or a 1,001 lineages in the same state doesn’t impact the rate of coalescence as much. In turn, this means that at lower number of lineages, the state of a single lineage has a much larger impact on the rate at which coalescent events are expected. In the case of two lineages, two states and high coalescent rates, the two lineages are highly unlikely to occupy the same state and not coalesce. Therefore, their states would be highly correlated. We however did not find a scenario under which MASCO would be considerably biased compared with the exact description of the structured coalescent.

We applied the different approximations of the structured coalescent to avian influenza virus HA sequences sampled from different orders of birds in North America. We found that the inferred region of the root varies with the method used. SISCO places high confidence in the center of the USA being the root state. MASCO on the other hand infers the East coast to be the most likely location of the root, while also placing a considerable amount of probability mass on other locations such as the North East or North West, reflecting greater uncertainty in the root location.

Asymmetric coalescent rates may offer one explanation why SISCO places more probability on the center being the root location than MASCO and why it excludes all other states from being possible root states. We have shown that asymmetric coalescent rates can bias the inference of migration rates. Under SISCO, asymmetric coalescent rates lead to an overestimation of the migration rate from a state with a fast coalescent rate into a state with a slow coalescent rate and an underestimation of the migration rates in the other direction (recall that we consider backwards in time rates). Because the coalescent rate in the center is inferred to be low, SISCO puts much more weight on it being the source than MASCO. The opposite appears to occur for the East Coast, which is inferred to have a very high rate of coalescence. MASCO infers the East Coast to be the most likely source region while it is almost excluded using SISCO. We expect seeing such differences in cases where coalescent rates differ significantly across different states.

Although we used the AIV analysis to illustrate how inferences obtained from MASCO and SISCO can differ, the results presented here should be interpreted with caution with regards to any biological implications as we ignored population structure arising between different avian host species. We additionally assumed coalescent and migration rates to be constant over time, potentially further biasing the inference of the root state.

Although population dynamics such as changing transmission (i.e., coalescent) and migration rates through time can greatly influence the shape of a phylogeny, we ignored such dynamics in this study. However, compared with mugration type methods (Lemey et al. 2009), the structured coalescent approximation introduced here can be extended in a conceptually straightforward way to allow for dynamic populations (Volz et al. 2009; Volz 2012). The improved approximation to the structured coalescent introduced here should therefore allow for more accurate quantification of movement in structured populations with complex population dynamics while still being computationally efficient enough to be applied to large data sets.

Materials and Methods

Principle of the Structured Coalescent Process

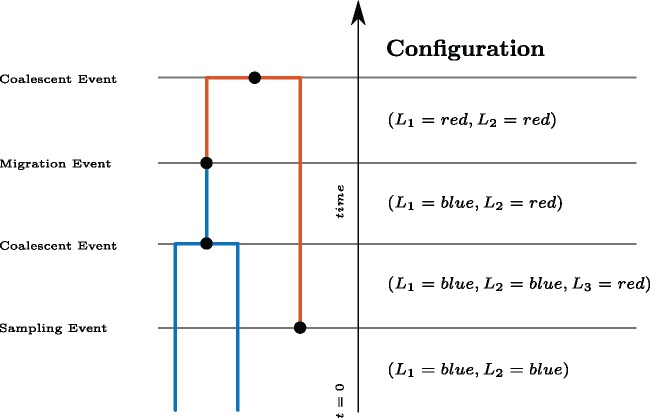
The structured coalescent (Takahata 1988; Hudson 1990; Notohara 1990) extends the standard coalescent by allowing lineages (branches in a phylogeny) to occupy different states and to migrate between these states, which constitute different subpopulations. Given n coexisting lineages, we label them randomly by $\{1,\dots ,n\}$. If we consider L_i to be a random variable that denotes the state of lineage i, $i\in \{1,\dots ,n\}$, with state space $\{1,\mathrm{\dots },m\}$, there are mⁿ different possible configurations $\mathcal{K}$ of how n lineages can be arranged ($\mathcal{K}=(L_1=l_1,\mathrm{\dots },L_i=l_i,\mathrm{\dots },L_n=l_n),l_i\in \{1,\mathrm{\dots },m\})$. These configurations can change over time by adding and removing lineages or by lineages changing state. Throughout this paper, we consider time going backwards from present to past, as typically done under the coalescent.

A migration event along one lineage i from state a to state b changes the configuration of lineages as follows:

$$\begin{array}{c}(L_1=l_1,\mathrm{\dots },L_{i-1}=l_{i-1},L_i=a,L_{i+1}=l_{i+1},\mathrm{\dots },L_n=l_n)\\ \stackrel{migration\hspace{0.17em}event\hspace{0.17em}from\hspace{0.17em}a\hspace{0.17em}to\hspace{0.17em}b}{\to }\\ (L_1=l_1,\mathrm{\dots },L_{i-1}=l_{i-1},L_i=b,L_{i+1}=l_{i+1},\mathrm{\dots },L_n=l_n)\end{array}$$

In figure 7, this corresponds to lineage 1 in blue changing to red.

Fig. 7.

Events and configurations on an example tree. Here, we illustrate the possible events and the configurations before and after each event on a simple tree, with time going backwards from present to past. The first two lineages, are both in state blue, that is, the configuration is $(L_1=blue,L_2=blue)$, with lineage 1 being the parent lineage of 1 and 2 after relabeling. After a lineage in state red is sampled, the configuration changes, as given in the figure. A coalescent event in state blue then reduces the number of lineages in state blue to 1. A migration event then causes lineage L₁ to change state from blue to red.

Configurations can additionally change due to sampling. Sampling events simply add lineages, such as $L_3=red$ is added in figure 7. Typically, we condition on the sampling events, but one can also introduce a rate for samples being obtained.

A coalescent event between lineage i and j with i < j changes the configuration as follows:

$$\begin{array}{c}(L_1=l_1,\mathrm{\dots },L_{i-1}=l_{i-1},L_i=a,L_{i+1}=l_{i+1},\mathrm{\dots },\\ L_{j-1}=l_{j-1},L_j=a,L_{j+1}=l_{j+1},\mathrm{\dots },L_n=l_n)\\ \stackrel{coalescent\hspace{0.17em}event}{\to }\\ (L_1=l_1,\mathrm{\dots },L_{i-1}=l_{i-1},L_i=a,L_{i+1}=l_{i+1},\mathrm{\dots },\\ L_{j-1}=l_{j-1},L_j=l_{j+1},\mathrm{\dots },L_{n-1}=l_n)\end{array}$$

Lineages $j+1,\mathrm{..},n$ are relabeled to $j,\mathrm{\dots },n-1$ and lineage i denotes the parent lineage of i and j after a coalescent event. The most recent coalescent event in figure 7 for example changes the configuration from $(L_1=blue,L_2=blue,L_3=red)$ to $(L_1=blue,L_2=red)$.

The rate at which coalescent events in state a happen can be calculated from the pairwise coalescent rate λ_a in state a and the number of lineages $k_a(\mathcal{K})$ in state a for a given configuration $\mathcal{K}$. The pairwise coalescent rate denotes the rate at which any two lineages in a state coalesce. For a given configuration $\mathcal{K}$, the total rate $\mathcal{C}$ at which coalescent events between any two lineages in the same state happen is:

$$\mathcal{C}=\sum _{a=1}^m{\lambda }_a\left(\begin{array}{c}{k}_a(\mathcal{K})\\ 2\end{array}\right)$$ (1)

where $\left(\begin{array}{c}{k}_a(\mathcal{K})\\ 2\end{array}\right)$ is the number of pairs of lineages in state a given configuration $\mathcal{K}$. Under the standard Wright–Fisher model and haploid organisms, the pairwise coalescent rates, λ_a, are the inverse of the effective population sizes $N_{e_a}$. Throughout this paper, we consider the coalescent and migration rates to be in the same time unit as the phylogeny. In the simulations, these are arbitrary units and in the case of the AIV example, these are per year rates.

Calculating the Likelihood for a Tree under the Structured Coalescent

Structured coalescent methods typically use MCMC to integrate over possible lineage state configurations along a tree (Beerli and Felsenstein 2001; Ewing et al. 2004; Vaughan et al. 2014). This is sometimes referred to as sampling migration histories. Given a migration history, the likelihood for a tree can be calculated under the structured coalescent with given migration and coalescent rates. Here, we want to calculate the marginal likelihood for a tree without sampling those migration histories, but by integrating over all possible migration histories H. Formally, we seek to calculate the following probability:

$$P(T|S,M,\Lambda )={\int }_{H}P(T,H|S,M,\Lambda )dH$$

with T being the tree, S the sampling states of the tips, M the set of migration rates and Λ the set of coalescent rates.

Let $P_t(L_1=l_1,\mathrm{\dots },L_i=l_i,\mathrm{\dots },L_n=l_n,T)$ be the probability density that the samples more recent than time t evolved according to the coalescent history, that is, the branching pattern, given by our tree T between the present time 0 and time t and that the n lineages at time t, $L_1,\dots ,L_n$, are in states $l_1,\dots ,l_n$. Furthermore, this probability is conditional on S, M, and Λ. For convenience, we do not explicitly write this. In figure 7, this probability is the joint probability of a configuration at time t with the lineages being either in red or blue, and the probability of the branching pattern and tip states being as observed between time t and 0 (ignoring the particular configurations in that time interval).

We aim to calculate P_t for t = t_mrca, with t_mrca being the time of the root of the tree T. At the root of the tree, summing over the probability of the remaining lineage being in any state will yield the likelihood for the tree, $P(T|S,M,\Lambda )=\sum _{a=1}^m{P}_{t_{mrca}}(L_1=a,T).$

In order to evaluate P_t at t = t_mrca, we start at the time of the most recent sample, at t = 0, and iteratively calculate P_t+Δt based on P_t. To calculate P_t, we split the calculation into three parts: time intervals in the tree where no coalescent or sampling events happen, sampling events, and coalescent events.

Interval Contribution

For the interval part, we calculate P_t+Δt based on P_t allowing for no event in time step $\Delta t$ (second line below), observing a migration event leading to the configuration at $t+\Delta t$ (third line below), or seeing more than one event (i.e., higher order terms which are of order $O({(\Delta t)}^2)$ leading to the configuration at $t+\Delta t$ (forth line below):

$$\begin{array}{c}{P}_{t+\Delta t}(L_1=l_1,\mathrm{\dots },L_i=l_i,\mathrm{\dots },L_n=l_n,T)\\ =P_t(L_1=l_1,\mathrm{\dots },L_i=l_i,\mathrm{\dots },L_n=l_n,T)(1-\mathcal{M}\Delta t-\mathcal{C}\Delta t)\\ +\sum _{i=1}^n\sum _{a=1}^m({\mu }_{a{l}_i}\Delta t{P}_t(L_1=l_1,\mathrm{\dots },L_i=a,\mathrm{\dots },L_n=l_n,T))\\ +O({(\Delta t)}^2)\end{array}$$

Here, $\mathcal{M}$ is the sum of migration rates and $\mathcal{C}$ the sum of coalescent rates for configuration $(L_1=l_1,\mathrm{\dots },L_i=l_i,\mathrm{\dots },L_n=l_n)$. The rate ${\mu }_{a{l}_i}$ denotes the rate at which migration events from a to l_i happen. Now, when rearranging and letting $\Delta t\to 0$, we obtain the differential equation,

$$\begin{array}{c}\frac{d{P}_t(L_1=l_1,\mathrm{\dots },L_i=l_i,\mathrm{\dots },L_n=l_n,T)}{dt}\\ =-(\mathcal{M}+\mathcal{C})P_t(L_1=l_1,\mathrm{\dots },L_i=l_i,\mathrm{\dots },L_n=l_n,T)\\ +\sum _{i=1}^n\sum _{a=1}^m({\mu }_{a{l}_i}{P}_t(L_1=l_1,\mathrm{\dots },L_i=a,\mathrm{\dots },L_n=l_n,T)).\end{array}$$

With explicitly writing $\mathcal{M}$ and $\mathcal{C}$ (using eq. 1 for $\mathcal{C}$), we obtain,

$$\begin{array}{c}\frac{d{P}_t(L_1=l_1,\mathrm{\dots },L_i=l_i,\mathrm{\dots },L_n=l_n,T)}{dt}\\ =\sum _{i=1}^n\sum _{a=1}^m({\mu }_{a{l}_i}{P}_t(L_1=l_1,\mathrm{\dots },L_i=a,\mathrm{\dots },L_n=l_n,T)\\ -{\mu }_{l_{i}a}{P}_t(L_1=l_1,\mathrm{\dots },L_i=l_i,\mathrm{\dots },L_n=l_n,T))\\ -\sum _{a=1}^m{\lambda }_a\left(\begin{array}{c}{k}_a(\mathcal{K})\\ 2\end{array}\right)P_t(L_1=l_1,\mathrm{\dots },L_i=l_i,\mathrm{\dots },L_n=l_n,T)\\ (interval\hspace{0.17em}contribution)\end{array}$$ (2)

with the double summation on the right hand side considering the contribution of migration and the fourth line considering the contribution of coalescence. Note that in the case of $l_i=a$, the two terms in the migration part cancel each other out and the net migration is 0. This interval contribution equation allows us to calculate P_t within intervals by solving the differential equation.

It is important to note that this differential equation shows a direct link between the coalescent process and the probability of a set of lineages being in a configuration. For example, configurations that would favor high coalescent rates among lineages would become less probable over intervals during which no coalescent events occur in the tree.

Sampling Event Contribution

At every sampling event the state of the sampled lineage is independent of all other lineages in the tree. We can therefore calculate the probability of any configuration at a sampling event at time t as follows:

$$\begin{array}{c}{P}_t^{\hspace{0.17em}after}(L_1=l_1,\mathrm{\dots },L_i=l_i,\mathrm{\dots },L_{n+1}=l_{n+1},T)\\ =P_t(L_1=l_1,\mathrm{\dots },L_i=l_i,\mathrm{\dots },L_n=l_n,T)P_t(L_{n+1}=l_{n+1}|T)\\ (sampling\hspace{0.17em}event)\end{array}$$

with after indicating the probability density after the event at time t (going backwards in time) and the other expressions indicating the probability density before the event. In scenarios where the sampling state is known to be say a, as assumed throughout this paper, we have $P_t(L_{n+1}=a|T)=1$ and $P_t(L_{n+1}=b|T)=0$ for $b\ne a$. One can allow for uncertainty in the sampling states by allowing this value to be between 0 and 1, such that $\sum _{a=1}^m{P}_t(L_{n+1}=a|T)=1$.

Coalescent Event Contribution

Next, we have to calculate the probability of the new configuration resulting from a coalescent event between lineages i and j in state a at time t. This probability can be expressed by the following equation:

$$\begin{array}{c}{P}_t^{\hspace{0.17em}after}(L_1=l_1,\mathrm{\dots },L_i=a,\mathrm{\dots .},L_{n-1}=l_n,T)\\ =P_t(L_1=l_1,\mathrm{\dots },L_i=a,\mathrm{\dots },L_j=a,\mathrm{\dots .},L_n=l_n,T){\lambda }_a\\ (coalescent\hspace{0.17em}event)\end{array}$$

Likelihood for a Tree

Based on the three equations, (interval contribution), (sampling event), (coalescent event), we can calculate the likelihood for a tree, $P(T|S,M,\Lambda )$. We refer to this approach as the exact structured coalescent (ESCO).

Approximations of the Exact Structured Coalescent

Between events (sampling and coalescent), the exact structured coalescent requires mⁿ differential equations to be solved, with m being the number of different states and n the number of coexisting lineages at a point in time. To be able to analyze data sets with more than a few states and lineages, approximations have to be deployed.

In the exact structured coalescent, the state of a lineage i is always associated with a configuration $\mathcal{K}$ and the coalescent history described by the tree T. Keeping track of these configurations automatically keeps track of all correlations between lineages. We will now assume that lineages i, j, and k and their states l_i, l_j, and l_k are uncorrelated, that is:

$$\begin{array}{c}{P}_t(L_j=l_j,L_k=l_k,L_i=l_i|T)\\ \stackrel{MASCO}{=}\\ P_t(L_i=l_i|T)P_t(L_j=l_j|T)P_t(L_k=l_k|T)\end{array}$$

Using this approximation, we will write down an expression for:

$$P_t(L_i=l_i,T)=\sum _{\mathcal{K}\backslash i}{P}_t(\mathcal{K},T),$$

with ${\sum }_{\mathcal{K}\backslash i}$ being the summation over all configurations while fixing the state of lineage i.

The interval contribution, that is, the change in marginal lineage state probability over time, $\frac{d}{dt}{P}_t(L_i=l_i,T)$, can be derived from equation (2), employing the MASCO assumption. This derivation is explained step by step in the Supplementary Material online, and results in the following differential equation:

$$\begin{array}{c}\frac{d}{dt}P(L_i=l_i,T)=\sum _{a=1}^m({\mu }_{a{l}_i}{P}_t(L_i=a,T)-{\mu }_{l_{i}a}{P}_t(L_i=l_i,T))\\ -P_t(L_i=l_i,T)({\lambda }_{l_i}\sum _{\stackrel{k=1}{k\ne i}}^n{P}_t(L_k=l_i|T)\\ +\sum _{a=1}^m\frac{{\lambda }_a}{2}\sum _{\stackrel{j\ne i}{j=1}}^n\sum _{\stackrel{k\ne j,i}{k=1}}^n{P}_t(L_j=a|T)P_t(L_k=a|T)).\end{array}$$ (3)

The second line denotes the change in marginal lineage state probability due to migration. The third line denotes the reduction in $P(L_i=l_i,T)$ due to the rate of coalescent events directly involving lineage i. The fourth line denotes the reduction in probability due to rate at which coalescent events that do not involve lineage i are expected to occur. Integrating equation (3) over time is equivalent to calculating the probability that the lineage i is in state l_i and that all lineages evolved up to time t as given by the coalescent history T. The above equation ensures that $\sum _{a=1}^m{P}_t(L_i=a,T)=P_t(T)$ for every lineage i.

For the coalescent event contribution, we calculate the probability of lineage i coalescing with lineage j in state a as,

$$P_t^{\hspace{0.17em}after}(L_i=a,T)=P_t(L_i=a|T)P_t(L_j=a|T)P_t(T){\lambda }_a$$

with $\sum _{a=1}^m{P}_t(L_i=a,T)=P_t(T)$ being the probability of having observed the coalescent history T up to time t, and $P_t(L_i=a|T)=P_t(L_i=a,T)/P_t(T)$ where $P_t(L_i=a,T)$ is obtained through equation (3). As with ESCO, we relabel the indices of all lineages after each coalescent event such that the labels of n coexisting lineages are always $i\in \{1,\mathrm{..},n\}$. Note that since we keep track of the joint probabilities of lineages being in any state and the coalescent history T, the probabilities of all lineages k not involved in the coalescent event have to be updated as well. For all lineages k not involved in the coalescent event, the probability after the event can be written as $P_t^{\hspace{0.17em}after}(L_k=a,T)=P_t(L_k=a|T)\sum _{a=1}^m{P}_t^{\hspace{0.17em}after}(L_i=a,T)$.

For the sampling event contribution, we can simply add a lineage n + 1 with associated probability $P_t^{\hspace{0.17em}after}(L_{n+1}=l_{n+1},T)=P_t(L_{n+1}=l_{n+1}|T)P_t(T)$.

The likelihood for a given tree under the MASCO approximation now is, $P(T|S,M,\Lambda )=\sum _{a=1}^m{P}_{t_{mrca}}(L_1=a,T)=P_{t_{mrca}}(T).$

A further approximation to the interval contribution can be obtained by ignoring the two coalescent terms in equation (3), that is, additionally assuming independence of the lineage states from the coalescent process between events. Thus, we assume that lineages move independently of the coalescent process between events:

$$P_t(L_i=l_i|T)\stackrel{SISCO}{=}{P}_t(L_i=l_i).$$

This allows to simplify equation (3) to:

$$\frac{d{P}_t(L_i=l_i)}{dt}=\sum _{a=1}^m({\mu }_{a{l}_i}{P}_t(L_i=a)-{\mu }_{l_{i}a}{P}_t(L_i=l_i))$$ (4)

and:

$$\frac{d{P}_t(T)}{dt}=-P_t(T)\sum _{a=1}^m\frac{{\lambda }_a}{2}\sum _{i=1}^n{P}_t(L_i=a)\sum _{\stackrel{j\ne i}{j=1}}^n{P}_t(L_j=a).$$

The derivation of the two equations above is explained step by step in the Supplementary Material online.

At a coalescent event between lineage i and j, the probability of $P_t(T)$ is updated as follows:

$$P_t^{\hspace{0.17em}after}(T)=P_t(T)\sum _{a=1}^m{\lambda }_a{P}_t(L_i=a)P_t(L_j=a).$$

Similarly, we can calculate the probability of the parent lineage being in state a as:

$$P_t^{\hspace{0.17em}after}(L_i=a)=\frac{{\lambda }_a{P}_t(L_i=a)P_t(L_j=a)}{\sum _{b=1}^m{\lambda }_b{P}_t(L_i=b)P_t(L_j=b)}.$$

That is the probability of observing a coalescent event in state a over the probability of observing a coalescent event in any state. The sampling event contribution can be written as $P_t^{\hspace{0.17em}after}(L_{n+1}=l_{n+1})=P_t(L_{n+1}=l_{n+1})$.

The likelihood for a given tree under the structured coalescent under the SISCO approximation now is, $P(T|S,M,\Lambda )=P_{t_{mrca}}(T)\sum _{a=1}^m{P}_{t_{mrca}}(L_1=a)=P_{t_{mrca}}(T).$

We refer to this as the state independence approximation of the structured coalescent (SISCO). The equations used by SISCO to calculate the state of a lineage over time have been described previously in Volz (2012). Although these lineage state probabilities evolve independently of the coalescent history T between events, they do depend on T at sampling and coalescent events.

Application to Avian Influenza Virus

We applied the different approximations of the structured coalescent to a previously described data set of Avian Influenza Virus H7 hemagglutinin (HA) sequences (Lu et al. 2014), sampled from the bird orders Anseriformes, Charadriiformes, Galliformes, and Passeriforms in Canada, Mexico and the USA. We used previously aligned sequences from De Maio et al. (2015). The sequences were analyzed in BEAST2 (Bouckaert et al. 2014) using an $\text{HKY}+{\Gamma }_4$ site model. A strict molecular clock model was assumed and the first two and the third codon positions were allowed to have different mutation rates. MASCO and SISCO were used as structured coalescent population priors. The data set was split into seven different states according to geographic regions in North America (see supplementary table S1, Supplementary Material online). Three parallel MCMC chains were run for $1*{10}^7$(MASCO) and $2*{10}^7$(SISCO) iterations with different initial migration and coalescent rates. After a burn-in of 10%, the chains were combined and the probability of the root being in each state was assessed. The combined chain had ESS values above 100 for any inferred probability density or parameter.

Implementation

We implemented all three approximations in one common package for BEAST2. ESCO and MASCO use a forth order Runge–Kutta solver with fixed step size implemented in the Apache Commons Math library (version 3.1.1, http://commons.apache.org; last accessed March 27, 2017) to solve equations (2) and (3). SISCO uses matrix exponentiation to solve the lineage state probabilities over time (eq. 4). All three structured coalescent methods use pairwise coalescent rates and backwards in time migration rates as described above. In the Results section, we present simulation analyses highlighting the quality of the different structured coalescent approximations.

Software

Simulations were performed using a backwards in time stochastic simulation algorithm of the structured coalescent process using MASTER 5.0.2 (Vaughan and Drummond 2013) and BEAST 2.4.2 (Bouckaert et al. 2014). We then used these simulated trees to infer parameters and root states. Script generation and postprocessing were performed in Matlab R2015b. Plotting was done in R 3.2.3 using ggplot2 (Wickham 2009). Tree plotting and tree height analyses were done using ape 3.4 (Paradis et al. 2004) and phytools 0.5–10 (Revell 2012). Effective sample sizes for MCMC runs were calculated using coda 0.18–1 (Plummer et al. 2006).

Data Availability

All scripts for performing the simulations and analyses presented in this paper as well as the Java source code for the structured coalescent methods are available at https://github.com/nicfel/The-Structured-Coalescent.git (last accessed March 27, 2017). Output files from these analyses, which are not on the GitHub folder, are available upon request from the authors.

Supplementary Material

Supplementary data are available at Molecular Biology and Evolution online.