Abstract
The authors of this work present a real-time measurement of heart rate across different lighting conditions and motion categories. This is an advancement over existing remote Photo Plethysmography (rPPG) methods that require a static, controlled environment for heart rate detection, making them impractical for real-world scenarios wherein a patient may be in motion, or remotely connected to a healthcare provider through telehealth technologies. The algorithm aims to minimize motion artifacts such as blurring and noise due to head movements (uniform, random) by employing i) a blur identification and denoising algorithm for each frame and ii) a bounded Kalman filter technique for motion estimation and feature tracking. A case study is presented that demonstrates the feasibility of the algorithm in non-contact estimation of the pulse rate of subjects performing everyday head and body movements. The method in this paper outperforms state of the art rPPG methods in heart rate detection, as revealed by the benchmarked results.
OCIS codes: (170.1470) Blood or tissue constituent monitoring, (170.3880) Medical and biological imaging, (280.4788) Optical sensing and sensors
1. Introduction
Rhythmic pulsating action of the heart causes blood volume changes all over the body [1]. This pulsating action results in the generation of cardiac pulse, which can be tracked/observed in the skin, wrist, and fingertips [1]. Photo- plethysmography (PPG) is an optic based plethysmography method, based on the principle that blood absorbs more light than surrounding tissue and hence, variations in blood volume affect transmission or reflectance correspondingly [2]. Several papers have been published that capture the cardiac pulse caused by skin color changes with the help of cameras [3–16]. However, measuring heart rate (HR) still remains a challenge, as the changes caused by the cardiac pulse are small in comparison to the numerous other factors that affect skin appearance over time, such as motion (rigid and non-rigid) and changes in lighting conditions [11].
A major limitation of current methods is their inability to accurately predict heart rate when a subject performs non-stationary actions such as head rotation, talking and walking in varying lighting conditions, though studies have tried implementing new methods and improving prior ones [5,8,12,13,17,18] and [19]. Light incident on a person is subject to scattering and absorption by the blood flowing in the skin [20]. It is this combination of light distortion that leads to detection of pulsation in synchronism with the cardiac cycle; which is typically (1-2)% of the total light detected [20]. Reflected light is found to decrease with an increase in blood flow [21]. This requires methods to have accurate capture of light intensities from the points being tracked.
However, focus on the problem of motion during HR prediction reveals that facial landmark predictors and frontal face detectors cease to detect faces subject to motion artifacts like blurring [22,23]. Motion blur causes the edges of the face to be distorted, resulting in swaying of landmark detection algorithms or an inability to detect the face [22,23]. Most commercially-available cameras have an increased exposure time of the shutter under low lighting conditions and hence, the motion of an object or a person gets embedded in the captured frame [24]. People tend to usually move their faces in a common workplace. This movement when captured by a camera, is subject to having most of its frames blurred (noisy), depending on a person’s speed of head movement and the shutter speed of the camera.
If features in the region of interest (ROI) do not get tracked either because of motion blur or occlusion, it causes discontinued pixel intensity measurements to be made, affecting the accuracy of heart rate measurement. Thus, motion robust feature tracking algorithms are required to enable motion estimation, motion compensation or deblurring of motion artifacts.
In this paper, a HR measurement method is presented that utilizes facial key-point data to overcome the challenges presented in real world settings as described earlier. In summary, our contributions are:
-
1.
The ability to identify motion blur and to dynamically (algorithmically) denoise blurred frames to enable frame to frame face capture
-
2.
The ability to enable motion estimation of feature points with higher accuracy in terms of range and speed as compared to Optical Flow based methods
-
3.
The ability to accurately capture heart rate at distances up to 4ft
This work will foster the development of research in other domains such as affective computing and gamification, where the real-time quantification of individuals’ response states, is paramount to measuring performance [25,26]. The following sections will explain the work in detail. The rest of the paper is organized as follows. This section provides an introduction and motivation of this work. Section 2 summarizes work done in related research areas. Section 3 presents the method designed to effectively measure HR while subjects are performing various motion scenarios under varying lighting conditions. Section 4 discusses the experimental setup and performance evaluation criteria. Section 5 elucidates the results while Section 6 presents a discussion on the case study, its advantages and limitations. Section 7 draws conclusion to the study and recommends possible future work.
2. Related work
The following section reviews related work corresponding to the topic and the proposed method. Careful observation of related research papers makes clear the fact that each method differs based on its architecture and not the flow, which is coherent with chronological improvements.
2.1 Static HR detection methods
The underlying source signal of interest in the image-guided and motion-guided techniques is cardiovascular blood volume pulse (BVP). The feature point trajectories in the case of head motion based technique is influenced by movement due to BVP as well as by sources like respiration, vestibular activity and changes in facial expression [27–29]. In PPG based techniques, this result is due to a mixture of light fluctuations and plethysmographic signals reflected off of the skin [1,2,6,8,9,11,12,18].
Poh et al. [9,30] made use of the Viola-Jones face detection algorithm [31] and computed the mean intensity values of the red (R), green (G) and blue (B) color channels from each frame. The authors employed Independent Component Analysis (ICA), a blind source separation (BSS) technique, in order to separate the PPG signal from the three-color traces. Results from Verkruysse et al. and Poh et al. reveal that ICA separated sources were able to achieve a higher accuracy, compared to BVP extracted from green channel trace [9,30]. However, their claim of the rPPG signal of a subject being the second component of an ICA, may not always be true, given the nonlinear nature of motion and optical properties of light.
Lewandowska et al. ran a comparative study using Principal Component Analysis (PCA) and ICA and found the processing time of finding HR using PCA to be multi folds faster for both a whole face ROI and forehead ROI, without compromising on accuracy [7]. Lewandowska et al. also found that a decrease in ROI size increases the level of noise in the BVP. However, their method requires the subject to be motionless and does not account for variations in illumination.
Lam and Kuno extend the use of BSS for HR detection with the help of a nonlinear skin appearance model [11]. Their skin model assumes the reflected light to contain information on the short time varying BPV and long term varying melanin formation. Assuming melanin formation to be constant, FASTICA [32] was implemented to extract information corresponding to BPV, using Welch’s PSD [33].
The algorithm of Li et al. enables remote HR measurement under realistic conditions such as when subject performs rigid movements like head tilt, and non-rigid movements like eye blinking and smiling. They employ a Normalized Least Mean Square (NLMS) adaptive filtering method to counter the effects of illumination variation using background illumination rectification [10]. They model an illumination rectification step, which uses the green channel intensity variation of the background to correlate an equivalent non BVP reflected light intensity from the ROI using NLMS. However, the authors fail to recognize the difference in spectral reflectance of the background and the skin, resulting in lower accuracies where such rectification is not possible
Our model improves processing speed and reduces latency by avoiding BSS based methods and extracting HR signals using alternative color spaces, thus concurring with results as reported in [8]. This enables real time HR detection in settings (subject performing normal (voluntary) head movements) requiring the subject to be remotely diagnosed by a medical practitioner.
2.2 Motion tracking and motion-based HR detection
The primary focus of the previous section was in illumination rectification and blind source separation of raw signals. The following section features methods which are robust not only to illumination changes, but also to motion changes. Wang et al. proposed one of the first motion robust algorithms [5] using the CHROM [12] method to create and optimize pixel-based remote PPG (rPPG) sensors in the spatial and temporal domain for robust pulse measurement. They use Farneback’s dense optical flow algorithm to track the translational displacement of each image pixel between two frames [34]. However, Farneback’s algorithm is a dense optical flow method, which is computationally heavier than Lucas and Kanade’s optical flow algorithm (i.e., the KLT algorithm) as used by [3,13]. The KLT algorithm utilizes Shi and Tomasi’s good features to track algorithm [35,36]. Features such as corners are tracked by using the concept of flow vectors to detect motion in two subsequent frames of a video. However, it has been reported that both optical flow methods are computationally heavy and prone to error magnification, not performing well in scenarios featuring large motions [37]. Optical flow equations rely on first-order Taylor- expansion, which breaks down when the input motion is large, causing ghosting artifacts [4]. Additionally, white Gaussian noise with variance gets summed with intensity value of the pixels being tracked [4], adding process noise.
Kumar et al. [13] have employed KLT based region of interests tracking from frame to frame to compute motion vectors. Additionally, Kumar et al. have developed a goodness metric for determining the weights of regions of interest, based only on the video recording of the subject. Although their method was developed to estimate the dynamic heart rate using a computationally efficient approach when compared to existing methods, it requires parameters to be set for static and motion based video analysis based on heuristic alone.
The existing optical flow based methods have a time complexity rate dependent on the quadratic power of the number of warp parameters used to compute the Hessian [38]. However, optical flow methods can effectively be utilized to track small displacements with high accuracy [4]. On the other hand, computational time complexity of feature tracking (as enabled in the algorithm being proposed) varies linearly with n (number of pixels being tracked in every frame). Additionally, motion noise due to a subject’s head movements is handled by ROI regions having high rPPG SNR (Signal to Noise Ratio) strength [39]. The time complexity of the optical flow algorithm is significantly greater than appearance based feature tracking except when warp parameters are absent. Since the primary objective of the proposed algorithm is to foster remote/tele PPG based health care monitoring which is immune to large/random motion errors, the proposed method mitigates the limitations by reducing drift errors and increasing the range of motion tracking. In addition to detecting motion when seated, our algorithm is able to estimate HR at a range of up to four feet, with accuracies greater than state of the art rPPG methods.
2.3 Alternative color spaces and skin segmentation
Though illumination robust algorithms were discussed in section 2.1, alternative color space exploration is gaining momentum in the research community and offers tangible results. Shifting color spaces help alleviate motion artifacts and accounts for better illumination variation, while being computationally efficient with less or limited latency in BVP estimation [8]. The primary reason for a shift in color space is due to the fact that the Red Green Blue (RGB) color system requires additional filtering and the use of PCA and ICA techniques. Both PCA and ICA are linear dimension reduction methods with significant estimation latencies [8,12].
The use of alternative color space for HR measurement has also been studied by [8]. Their result reveals that reflection of light intensity changes from the skin due to BPV, was enhanced and stronger in the H and Y channel of the Hue Saturation Lightness (HSL) and Luma and Chrominance (YUV) color spaces, thus accounting for high illumination variation. Hue is a representation of the dominant wavelength in a mixture of light waves. Additionally [40], tests the hypothesis of pulsatile components being independent of wavelength and lying in the range of (660-805) nanometers. Nevertheless taking a closer look at the absorption spectrum of oxy-hemoglobin reveals that absorption of light is greatest in the (500-600) nanometers wavelength, which coincidently, is green channel’s dominant wavelength, supporting the hypothesis of numerous research on finding an accurate HR measurement in the green channel of the image [41]. Kramer et al. conducted an experiment using oxygenated blood, measuring the transmittance of light through blood and found that it does not obey the simple Beer-Lambert law, and that the optical density of blood is a non-linear function of hemoglobin [42]. Enson et al. discovered that a variation in light reflected from blood occurs with pulsating flow and that the variation could be higher than 20% with reflectance PPG [43]. Thus, the theories show that it is important to detect the dominant wavelength of light being reflected from the skin of a subject to detect the BVP.
The algorithm presented employs hue, saturation and value color space for HR signal extraction and automatic skin segmentation for face detection for every frame. Following face detection and ROI selection, the feature points in the regions of interest are tracked. Table 1 summarizes the related work section, highlighting the contributions of other methods and the novelty of the method presented in this work.
Table 1. Related Works Table (Black Shading Indicates Contributions Made by Corresponding Papers).
| Authors | Year of Publication | Stationary Subjects | Moving Subjects | Dynamic Feature Selection |
Manual ROI
Selection |
Head motion- based HR
detection |
Change of Color space/ Spectrum | Non-linear signal extraction method |
BSS
Method of signal extraction |
Different Skin Tones | Illumination Variance | Motion Robustness with Uniform Movements/Mi nor movements | Motion Robustnes s against walking | Motion Denoising |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
Verkruysse et al. [ 2 ] |
2008 | |||||||||||||
| Poh et al. [ 9 , 30 ] | 2010, 2011 | |||||||||||||
| Lewandowska et al. [ 7 ] | 2011 | |||||||||||||
|
De Haan et al. [ 12 ] |
2013 | |||||||||||||
| Balakrishnan et al. [ 27 ] | 2013 | |||||||||||||
| McDuff et al. [ 6 ] | 2014 | |||||||||||||
| Li et al. [ 10 ] | 2014 | |||||||||||||
|
W. Wang et al. [ 5 ] |
2015 | |||||||||||||
| Lam and Kuno [ 11 ] | 2015 | |||||||||||||
| Tsouri and Li [ 8 ] | 2015 | |||||||||||||
|
Kumar et al. [ 13 ] |
2015 | |||||||||||||
|
Amelard et al. [ 15 ] |
2016 | |||||||||||||
| This Paper | 2018 |
3. Method
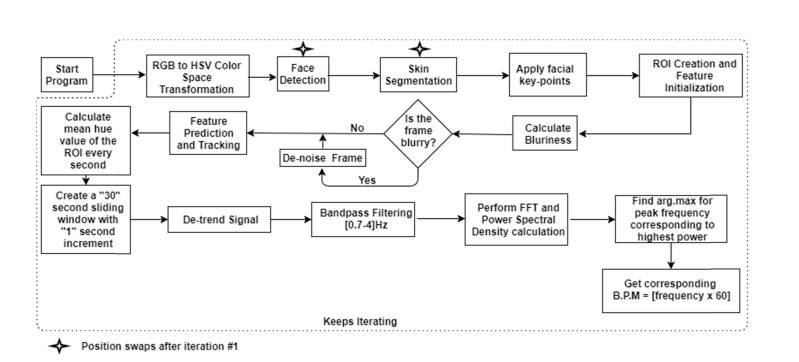
The objective of the method is to enable a real-time measurement of HR across different lighting and motion conditions. Figure 1 is an outline of the method, with the following sections providing a detailed explanation of the various processes involved in achieving the objective.
Fig. 1.
Outline of the proposed algorithm [The stars indicate that Face Detection and Skin Segmentation sub-blocks swap positions after iteration #1].
3.1 Face detection and skin segmentation
Face detection is performed using the Viola-Jones algorithm [44] which employs the Haar Classifier from OpenCV [31,45]. This gives a coarse detection of non-face regions and fails when a subject makes a rotational motion. The Haar classifier searches the entire frame each time to detect a face. To avoid performing a face search for each frame, the face detection algorithm is employed only for the first frame when the camera turns on. After which, the automatic skin segmentation step is performed. Following the color space transformation, skin segmentation is performed using the Back Projection function from the OpenCV library [46], once it computes the model histogram of the skin using the detected face from the first frame. Since skin color changes as a result of sudden changes in lighting/angle of face, a model template is utilized prior to face detection on the next frame. This step enables robust face detection without substantial loss of processing time during each subsequent frame.
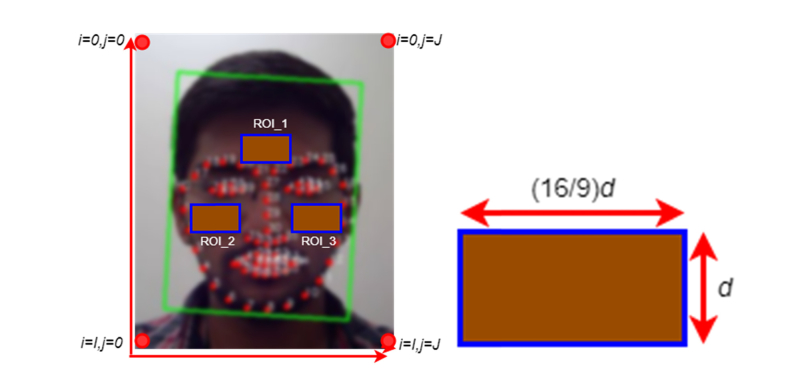
Following face detection, facial landmarks are laid on the face of a person as shown in Fig. 2. Regions of interest are created based on the facial key-points on the detected face, using an ensemble of regression trees method proposed by [47]. This method is used to regress the location of facial landmarks from a sparse subset of intensity values extracted from the input frame containing the detected face.
Fig. 2.
Left: Frame (). ROI detection and tracking. The green colored box represents a detected face, while, the three blue (outlined) boxes represent the ROIs (with the shading to represent all pixels within the ROI boundary as feature points being tracked for raw rPPG signal extraction). The red points indicate the 68 landmarks being tracked in the face. Right: Dimensions of the ROI, where d is being adapted as it is from the study [7].
Regions of interest identification is a crucial step in HR measurement. Facial hair growth is a commonly observed feature and causes partial occlusion when detecting the face and region of interest [24]. Detecting such regions or an inability to detect the face will not yield accurate HR measurements [10]. Also, detecting only the forehead region is not an effective approach, as smaller the area of the ROI(s), the higher the probability of inaccurate measurements [1,7]. The ROIs have been modelled as per the process highlighted by Lewandowska et al. [7], while changing the aspect ratio of the ROIs to 16:9 (ratio of frame dimensions used to record subjects performing movements) to avoid expansion or contraction of ROIs when they are multi-scaled as a function of the distance from the camera. A constraint on aspect ratio helps keep the proportion of increase or decrease of ROI uniform, maintaining consistency in mean rPPG signal quality [48]. The described constraint can be established provided the ROIs are scaling-factor-constrained when a subject either moves toward the camera or away from it. The size of all the ROIs are the same and are scaled between minimum and maximum sizes of the ROI used in the training of the Haar Classifier [31,45] (a part of the OpenCV [46] library). Down scaling of the ROI has been found to reduce the noise sensitivity of camera-based rPPG devices [5]. Up sampling on the other hand would add extra feature points while reducing camera or motion noise, until face detection fails. However, the algorithm and tracking of at least one ROI fails when face detection fails. Thus, the algorithm is dependent on the detection of a subject’s face at all times. A small ROI (16 pixel neighborhood) from cheeks and forehead region have been found to contain good rPPG SNR signal quality [39,48] and hence, have been chosen as the 3 ROIs. The ROIs are positioned with reference to the facial landmarks for additional rigidity against rotational motion. In each ROI, the pixels are spatially averaged to yield ROI level raw hue traces and ) represented as , where r ϵ {1,2,3} is used to index the ROIs as identified in Fig. 2, while (t) represents time period over which is calculated. As HR measurement involves comparing the light intensity changes over the frames, it is important to normalize the raw hue traces.
This processing step is performed over a 30 second sliding window with 1 second increments, consistent with the literature [9,10,49]. 30 seconds of PPG signal has been found to contain a pulse rate resolution of 2 b.p.m. (60 seconds/length of sliding window (30 seconds) period in seconds) [50]. Additionally, over longer periods of time, the temporal information in the PPG spectrum tends to get obscured because of the slight variability of HR [49]. The raw hue traces are normalized as for each 30 second sliding window individually using Eq. (1) as given below.
| (1) |
where, and denote the mean and standard deviation of respectively. Normalization of , transforms the signal to which has zero-mean and unit variance
3.2 Blur detection and denoising
Blurring happens as a result of convolving an image frame with the point spread function (PSF) (also called a blur kernel) [51] as shown in Eq. (2). Blurring is caused by a slower shutter speed, causing the motion of the moving object to be embedded in the image. However, blurriness of an image depends upon the presence of movement, speed and direction.
The blur kernel’s (H) dimensions are represented as . For (H), let n ϵ {1,2,…,N} represent the index of the blur kernel element. The frame () is represented as a matrix of dimensions , as shown in Fig. 2. For any frame (F), let i ϵ {1,2,…,I} and j ϵ {1,2,…,J} be used to index every pixel in a frame along the horizontal and vertical direction respectively as shown in Fig. 2. Convolution of a frame as shown in Fig. 2 with an unknown blur kernel (primarily caused by motion artifacts/unknown elements) , creates a blurred frame having the same size as frame . Frame can mathematically be represented using Eq. (2), where “*” represents the convolution operation.
| (2) |
Equation (2) represents an element by element convolution of frame , starting with the pixel location i = 0, j = 0 and ending with i = I and j = J. However, blur kernel determination and deblurring by blur kernel estimation is a topic out of scope from this paper and the problem aiming to be solved. However, given the nuisance of a blurred frame, blur detection and denoising is chosen as an alternative technique to minimize blur effects caused by motion artifacts. By convolving the detected face region with a 3x3 (used in the experiment) edge detecting Laplacian kernel [52], the 2nd derivatives of the image are approximated [52] using Eq. (3). The reason for using the specified kernel size (3x3) is to exploit spatial coherence of neighboring pixels, thereby averaging noise associated with motion artifacts. Calculating the 2nd derivative of an image frame provides responses in the form of edge magnitudes. Edge magnitudes depends on the amount of moving subject blending with the stationary background. Greater blending with the background causes the subject of interest to be severely motion blurred (subject appearance gets distorted), rendering the frame invalid for continued face detection, causing a break in pixel intensity estimation from the regions of interest. Hence, to avoid said problem, the magnitude of blurriness is determined by measuring its variance spread as given by Eq. (4). Greater the variance response, greater the number of edges being detected and sharper the image in the frame becomes. Hence, a bigger sized kernel can be preferred with loss in information from edge magnitudes. Based on the assumption that a subject starts off any motion scenario from a static position with the background being static (camera position fixed), the first 30 frames (if 30 frames per second (fps) camera is used) are motion and blur free. The variance of each of the first 30 frames is calculated using Eq. (4). The average of the calculated variances over the first 30 frames is taken as the threshold for blurriness detection. Using the threshold, the current frame is either labelled blurry or normal. :
| (3) |
| (4) |
where is the mean of absolute values as given by,
| (5) |
If the blurriness of a motion induced frame falls below the threshold, the frame is deemed blurred and is subject to de-noising (as illustrated in Fig. 1), followed by further processing for HR estimation.
3.3 Feature point tracking using bounded Kalman filter technique
The goal of feature tracking is to consistently track feature points of the 3 ROIs in every frame, thereby capturing the pulsatile information using the reflected hue values from the tracked features. The dynamic tracking of color intensity change per pixel is handled by HSV color space transformation. As color is not sensitive to rotation, shift and scale, the selected color space (HSV) though device dependent, has been found to show better or equal results in comparison with CIE XYZ (a device independent color space) color space [8].
Tracking feature points between frames is a challenging task. The points are stochastic and may cause observations to become missing due to poor video quality, noisy observations due to changes in illumination, occlusions, features that are moving in close proximity to each other, etc.
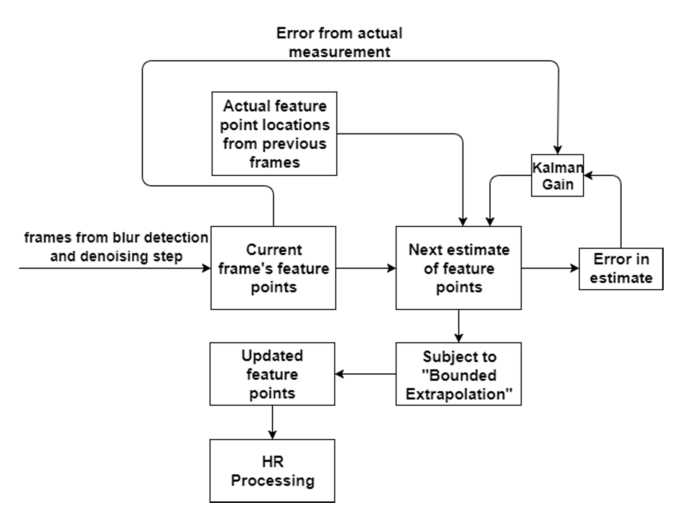
The proposed Bounded Kalman Filter (BKF) approach is a motion estimation model that is employed to track the regions of interest from frame to frame. It serves as a mathematical extension to the existing Kalman filter [53]. An assumption that the predicted frame’s (i.e., frame F) feature point locations depend on the velocity of the feature points from previous frames is being made. Thus, by modelling a function whose input is the actual (frame (F-2) and frame (F-3)) and predicted (frame (F-1)/ current frame) feature point locations, the errors due to drift and instantaneous movements can be minimized. After substitution of the predicted feature point position in the modelled function, the new feature point location is calculated with minimum error. The model as shown in Fig. 3 aims to achieve frame to frame feature tracking with negligible drift error in various illumination conditions by modelling the trajectory of the previous state of the feature points as a function. The original Kalman filter predicts the feature locations by estimating the uncertainty of the predicted value and computing a weighted average of the predicted and measured value, with drift errors of feature points associated with sensitivity caused by sudden and fast movements of a subject. However, BKF eliminates drift errors/ errors caused by sudden/instantaneous subject head movements using the modelled historical (trajectory) function of the feature points.
Fig. 3.
Cubic Spline Bounded Kalman Filter Method.
The BKF makes use of the cubic spline interpolated function modelled using historic feature point predictions to extrapolate the next possible feature point locations. The 5 x 5 neighborhood (based on heuristic) of the extrapolated feature point, will serve as the boundary kernel for the Kalman filter prediction. The boundary kernel, in combination with BKF, is found to eliminate drift errors associated with motion estimation.
3.3.1 Prediction state calculation
The BKF consists of three primary phases, predict phase as given by Eq. (6), Eq. (7), Eq. (8) and Eq. (9), update phase as given by Eq. (11) and Eq. (12) and boundary comparison phase as given by Eq. (13) and Eq. (14).
Let frame F (predicted) be as shown in Fig. 2. and frame (F-1). The feature points in the three ROIs is subject to the following processes. Let K feature points be tracked for every frame from all the three ROIs put together.
| (6) |
where,
: Predicted feature point matrix at frame F (predicted frame)
: Predicted feature point (kth feature point) location =
xk: Predicted horizontal coordinate from the ith coordinate of the current frame’s feature point
yk: Predicted vertical coordinate from the jth coordinate of the current frame’s feature point
K: Total number of feature points being tracked from all ROIs, where, k ϵ {1,2, 3,…,K}is used to index each of the feature point being tracked
The location () of a feature point (kth feature point) in frame (F) can be predicted with the help of acceleration and velocity of the same feature point from the current frame (F-1) using Eq. (7) (kinematic equation). The feature point matrix () stores all the predicted locations of feature points being tracked. For each predicted frame F, The Kalman filter function helps in the calculation of acceleration () for each tracking feature point and associated process noise () or uncertainty due to unmodeled influences (like a sudden change in the position of a subject’s head because they wanted to) for frame F. While frame F is a matrix, its subscript representation in Eqs. (7) - (14) denote a reference to that frame.
| (7) |
where,
F: Predicted frame
F-1: Current frame
: Predicted feature point location = in frame F
: Feature point location for frame F-1 (current frame)
: time between two frames (see A and B matrix below)
: acceleration of kth feature point in frame F
: process noise of kth feature point in frame F (is the process noise which is assumed to be drawn from a zero-mean multivariate normal distribution with variance (), where ~N(0, )
Feature point locations vary between frames in terms of changes in velocity and acceleration. Hence, it can be assumed that the feature points can be represented in terms of the fundamental matrix for Newtonian systems [54]. The matrix A (4x4 matrix represents a change in horizontal and vertical directions) depicts a change in time () between frame F and frame (F-1) as a result of the kth feature point’s velocity in frame (F-1). Since there is a change in velocity of the feature point between frames, there is also a change in acceleration. The prediction ()is further fine-tuned by summing the velocity component () with the acceleration component by multiplying acceleration of the kth feature point in frame (F-1) and matrix B (4x2 matrix, where the first column represents coefficients for change in position (), and coefficients for change in velocity () along horizontal direction, while the second column represents the same for change in vertical direction). This section provides detail on predicting the locations of all the feature points being tracked for the predicted frame F and its parameters.
3.3.2 Predicted process covariance matrix
The covariance matrix and is the uncertainty in the predicted feature point location and its associated noise respectively as given by Eq. (9) and Eq. (10). Process covariance matrix captures the correlation of the feature point’s position and velocity. The process covariance vector () stores the process covariance matrix of each feature point being tracked.
| (8) |
where,
: Process covariance matrix of the feature points being tracked in frame F
: Process covariance matrix of feature point in frame F
| (9) |
where,
: Process covariance matrix of kth feature point in frame F
Process noise covariance matrix of kth feature point in frame F
: Process covariance matrix of kth feature point in frame (F-1)
| (10) |
Process covariance matrix for kth feature point assumes that the highest order term (acceleration of feature point) is constant for the duration of each time period [53,54]. However, not only does the acceleration of a feature point differ between time periods (), but is also uncorrelated between time periods [53,54]. Hence covariance of the process noise can be defined by Eq. (10). The described equation has significant ramifications for the behavior of the Kalman filter. If the value of is too small (change in time period () between frames and variance () due to acceleration values are small), then the filter will be overconfident in predicting the location and will diverge from the actual measurement. If the value of is too large, then the filter will be influenced by the noise in the measurements and may not perform optimally. This section provides the uncertainty prevalent in predicting locations of all the feature points being tracked for the predicted frame F.
3.3.3 Kalman gain
The Kalman gain () of the kth feature point being tracked in frame F is inversely proportional to measurement error (). Since Kalman gain is a minimum mean square error estimator, as measurement error decreases, the accuracy of feature point tracking improves, while keeping the Kalman gain low.
| (11) |
where,
: Kalman gain for the kth feature point in frame F
: Observation/measurement errors
: Dimension-preserving matrix
When making an actual measurement of the true position of feature points being tracked, measurement noise is assumed to be summed with the actual measurement, making it noisy. So, measurement noise is also assumed to be normally distributed, with mean 0 and standard deviation (). Hence R (measurement error) can be calculated as the variance of the measurement noise (). The calculation of R is straight forward because the variance associated with measurement noise can be calculated from the actual measurement of the feature point from the previously predicted frame. This section provides information on Kalman gain and its parameter values for each feature point being tracked in frame F.
3.3.4 Current state calculation
The current state of the kth feature point is calculated using the predicted feature point (), Kalman gain () and the measured position of the tracking feature point () as given by Eq. (12). The current state helps improve the accuracy of the next prediction with the help of the current observation
| (12) |
where,
: Updated predicted feature point after an actual observation has been made
: A new observation (measurement) of the feature point in frame F when the current frame of prediction is (F + 1)
The current state of all the feature points being tracked helps reduce the uncertainty associated with extreme motions (roll, pitch and yaw of head) and improves accuracy of prediction over time.
3.3.5 Extrapolated bound
The Cubic spline interpolation function takes as its input, the actual (frame (F-2) and frame (F-3)) and predicted (frame (F-1)/ current frame) feature point locations of the kth feature point. The function is modelled as given by Eq. (13).
| (13) |
where,
and the coefficients of the spline functions , , and are derived by solving Eq. (14) for each of the previous frames as presented below.
| (14) |
where,
[frame F]
[frame F-1]
[frame F-2]
[frame F-3]
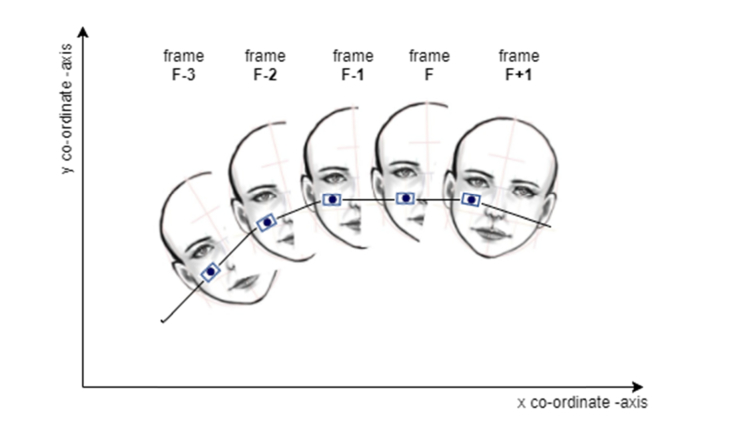
Equation (13) (modelled trajectory function) is the extrapolator created using Eq. (14), and is a function of the Fth frame and takes as its input, the x coordinate of kth feature point as computed by Kalman filter, to find the corresponding location of the kth feature point in the same frame based on the trajectory of the previous 3 frames. This step is illustrated in Fig. 4 for a single feature point for the Fth frame using the feature point’s location in F-3 th, F-2 th and F-1 th frame. Once found, the Kalman filter predicted point is confined to the 5x5 neighborhood (based on heuristic) of the extrapolated feature point. If the Kalman filter point is within the neighborhood, no change in location is instituted, else, it is made to assume the nearest neighbor within the 5x5 neighborhood of the extrapolated feature point.
Fig. 4.
Illustration of extrapolated bound using interpolated spline function for predicted feature point k (Face image from Ref [55]).
Once extrapolated, the new location will become the current state of Kalman filter, for which the process covariance matrix gets calculated, which then determines the uncertainty in the predicted value, providing it as feedback for the next iteration.
3.4 HR estimation
The normalized hue value of all the feature points being tracked using the BKF within the 3 ROIs are calculated for each second and appended to a 30 second sliding window [9] for Stationary, Mixed and Rotation motion types as explained later. Fast Fourier Transform [FFT] is effective when the sliding window length is 30 seconds or less [49]. For the walk based motion type, the average hue values are appended to a 4 second sliding window because of the short duration (13-15 seconds) of the videos. The signal is detrended to remove slow and stationary trends of the signal to avoid errors due to motion artifacts. A finite impulse response (FIR) Butterworth bandpass filter with a band-pass of [0.75, 4] Hz corresponding to a pulse range of [45, 240] beats per minute (bpm) is computed [10]. The power spectrum of the signal is then computed every second to yield a pulse rate. Pulse rate estimation is performed by finding the peak frequency from the power spectrum within the range of 0.75 to 4 Hz corresponding to a pulse rate range of 45 to 240 bpm [10,30]. The HR estimation step is described concisely as shown in the Algorithm box below.
Algorithm: HR Estimation.
Input: Frames from previous section
|
|
Output: Heart rate of the subject in beats per minute [B.P.M.] |
4. Experiment
This section presents the experimental setup for evaluating the proposed algorithm along with three other state of the art methods. We evaluate the proposed method using the following experiment. The methods are implemented in Python using OpenCV 2.4 library [46] and ran on a laptop with an Intel Core i7 2.7Ghz. processor and 8 GB RAM. The source code for the proposed algorithm has been publicly made available [56].
4.1 Benchmark data set
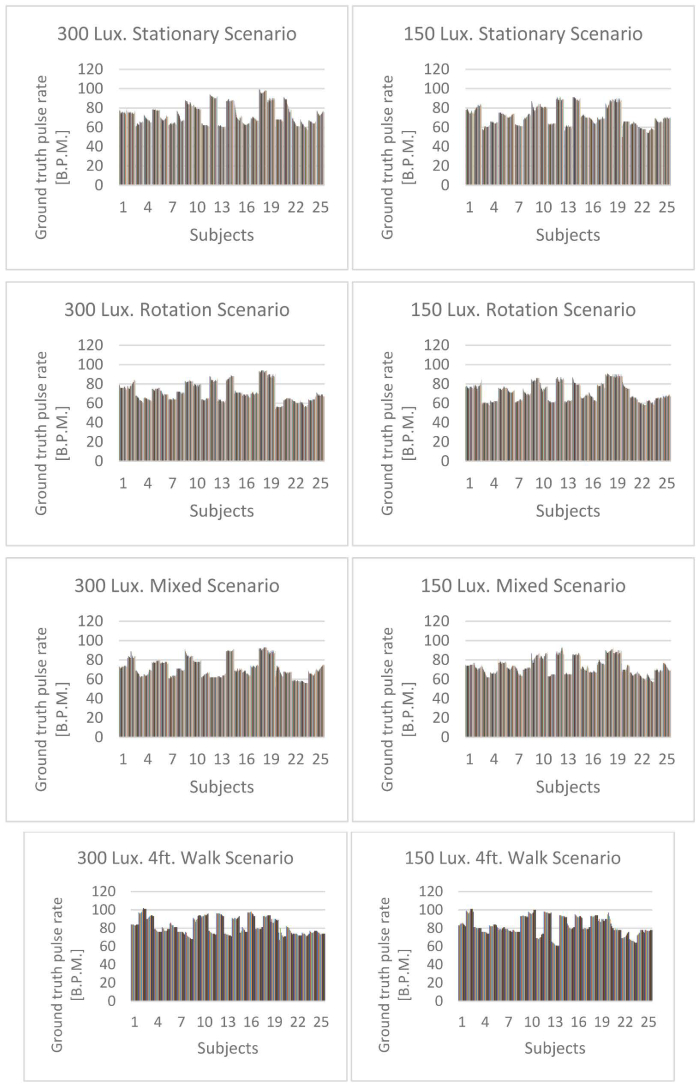
For this study, we created our own data set containing 200 video sequences (each video lasting 60 seconds) using the front HD camera which is a CMOS type sensor of a Surface 4 tablet. All videos are recorded in a 24-bit RGB color format having a resolution of 1920 x 1080, recorded at 29.97 frames/second (NTSC video standard) and stored as uncompressed data. The videos were debayered and recorded using the default applications set by the manufacturer in the H264–MPEG–4 AVC (part 10) (avc1) codec using the (.mp4) video format. The Polar H7 HR Bluetooth monitoring system is an FDA approved device that has been used for pulse rate monitoring to record the ground truth HR. The Polar H7 monitor is a wireless chest electrode worn by the subjects around their chest and has been used in prior studies [57–61]. The studies have proven Polar H7 monitor measurements to be significantly reliable in comparison with ECG and fingertip pulse oximeter readings. Additionally, HR monitoring devices have grown to be worn as common monitoring devices in the recent years and Polar H7 monitor has been proven to be used in comparison with the gold standard ECG device, while the growing hand worn HR monitoring devices have not yet been. Thus, in order to obtain accurate ECG grade pulse rate readings and to enable the proposed algorithm to be used reliably for remote HR monitoring, a case study using Polar H7 monitor has been made. A total of 25 subjects (eighteen male and seven female subjects; mean = 22.8, sd. = 2.31) aged from 20 to 28 years were enrolled for the experiment. The age distribution of the subjects recruited for the experiment is further illustrated as shown in Fig. 5. As the experiment involves human subjects, Institutional Review Board (IRB) approval was sought and attained. Each subject was recorded (one minute) performing four types of activities (termed motion), namely Stationary action, Rotation (Roll) action as shown in Fig. 6 (first row), Mixed action (yaw, pitch, scaling and translation) as shown in Fig. 6 (second row) and a 4ft. walk towards the camera as shown in Fig. 7 in two different lighting scenarios, 300 Lux and 150 Lux. The heart rate distributions of all the 25 participants for each motion scenario is depicted as shown in Fig. 8. Additionally, Table 2 describes the mean and standard deviation of all the ground truth HR for 25 subjects as measured via Polar H7 monitor as they perform the various motion scenarios. Each motion recording starts with the subject remaining stationary for the first five seconds to allow face detection, following which, the subject performs the motion activity until the end of the recording. The subjects were instructed to perform the motion with a fast pace and changing head orientations to better replicate the various real-world scenarios. An iPhone application (Light meter), calibrated with high-precision illuminometer, along with the rear-view camera of iPhone SE (CMOS_Exmor RS sensor, 12 Megapixel resolution) has been used to continuously measure the lighting conditions throughout the course of the experiment for all video sequences. A D65 standard illuminant has been utilized as the illuminant source for the experiment. From literature review, it was discovered that research studies [5,12] describe the type of lighting used in a general manner with no quantification, which does not help in scientific comparison. Since the goal of the study is in formulating a motion robust algorithm, motion and varied illumination is considered as the key variables/factors.
Fig. 5.
Histogram depicts the age distribution of the subjects recruited for the experiment.
Fig. 6.
Subject (first row) performing rotation motion; subject (second row) performing mixed (yaw and pitch) motion; ROI tracking enabled
Fig. 7.
Subject walking a distance of 4ft. towards the camera.
Fig. 8.
Histograms representing the distribution of ground truth HR as captured from the Polar H7 monitor across 25 subjects in 8 motion scenarios.
Table 2. Mean and standard deviation of the ground truth HR as captured from the Polar H7 monitor across 25 subjects in 8 motion scenarios.
| Motion Scenario | Mean (B.P.M.) | Standard Deviation (B.P.M.) |
|---|---|---|
| 300 Lux Stationary Scenario | 73.39 | 10.42 |
| 150 Lux Stationary Scenario | 71.32 | 10.02 |
| 300 Lux Rotation Scenario | 71.42 | 9.82 |
| 150 Lux Rotation Scenario | 71.62 | 9.37 |
| 300 Lux Mixed Scenario | 71.83 | 9.74 |
| 150 Lux Mixed Scenario | 73.21 | 8.69 |
| 300 Lux 4ft. Walk Scenario | 82.34 | 9.05 |
| 150 Lux 4ft. Walk Scenario | 82.40 | 9.96 |
4.2 Evaluation metrics
For evaluating the accuracies of HR measurement methods, different kinds of statistics have been used in previous papers. For a comprehensive comparison of the algorithms, three kinds of primary statistics used in previous research works are employed [5,9–11]. The first one is the mean error (HRerror), where HRerror = HRgt – HRmethod, and HRmethod denotes HR measured from video using the various methods, and HRgt is the ground truth HR obtained from the Polar system. The second metric is the standard deviation of Me denoted as SDerror. The third metric is the root mean squared error denoted as RMSE.
Finally, the Analysis of Variance (ANOVA) is performed on the mean B.P.M. values obtained from three factors, Luminance, Motion and rPPG method, having two levels for luminance, and four levels for motion and rPPG methods to analyze the significance of difference in the means, i.e., to show if the main variation in mean B.P.M. is due to variation in method, motion or luminance. Tukey honestly significant criterion (HSC) is used for post-hoc comparison to further evaluate the posteriori pairwise comparison in order to determine which method is significantly better than the other in terms of accuracy and agreement of predicted HR values with respect to the ground truth values.
4.3 Compared methods
The proposed algorithm is compared against the following state-of-the-art rPPG methods, namely, CHROM [12], DistancePPG [13] and Lam et al. [11]. All three methods claim motion robustness and hence help in effective comparison against the proposed method. The CHROM method assumes specular reflection (illuminant information only) and intensity variations as being primary barriers for accurate heart rate measurement and effectively removes the specular reflection by color difference. The DistancePPG method is chosen for comparison to illustrate the advantage of the proposed method over optical flow based techniques. Though [27] employs a similar optical flow estimation technique, we were not able to obtain worthy results against any motion condition and hence choose to report our results using a latter DistancePPG method. In addition, some components of related work include proprietary data [5] and when its implementation was tried, better results were obtainable from [12] as mentioned in [62]. For the sake of uniformity, the comparing algorithms were tested using the created data set. All parameters remain identical when processing different videos.
5. Results
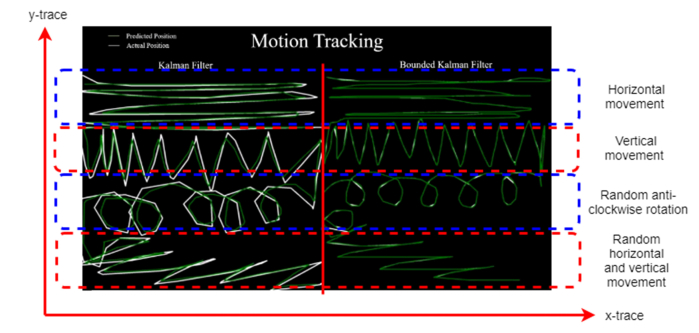
The x and y trace of a sample feature point from the ROIs as shown in Fig. 2 is subject to different motion scenarios (except for walk (as the traces primarily change with respect to the distance from the camera) and stationary scenario) in a 150 Lux lighting condition as illustrated with the help of Fig. 9. Figure 9 describes the motion tracking of a sample feature point while a subject was performing various head movements. The bounded Kalman filter technique and Kalman filter are compared. With reference to Fig. 9, the accuracy of the Kalman filter method is significantly diminished during rapid direction changes or continuous direction changes, in comparison with the bounded Kalman filter technique being proposed in the paper.
Fig. 9.
Figure explaining the x and y trace of a sample feature point from the ROIs during the specified movements (from top: Horizontal movement, Vertical movement, Random anti-clockwise rotation and Random horizontal and vertical movement). The actual and predicted position of the sample feature point is represented using a white and green colored line respectively.
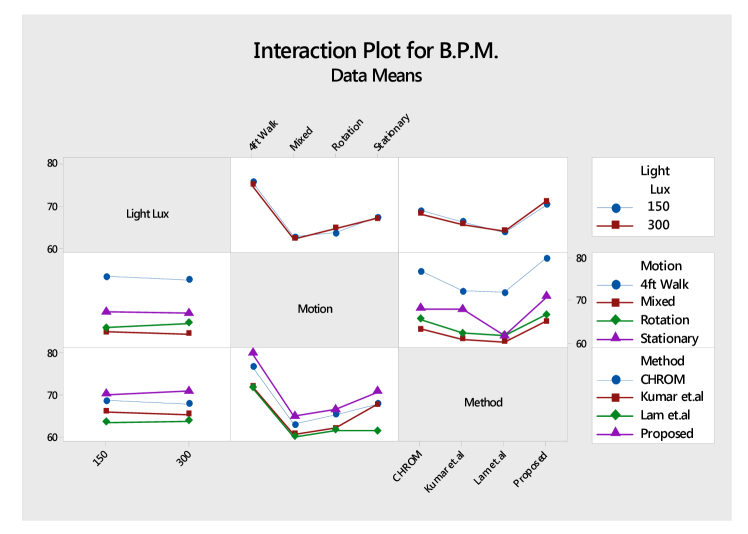
The result from the ANOVA analysis is shown in Table 3. For each comparison, a common significance threshold (p-value < 0.05) is used. Illumination variation was found to not be statistically significant, with a high p value of 0.879. Since p>0.05, the result reveal that the variation of illumination is limited against the comparing methods and various motion conditions. Thus, using results from Table 3 and by observing the flat responses as shown in Fig. 10 and Fig. 11, we can conclude that illumination variation does not have a significant role to play in the experiment. A study by [13] reveals that ambient light ranges from (400-500) Lux. However, this work conducted the experiment in a typical real-world work environment (i.e., office space) having a maximum luminance of 300 Lux with all lights turned on. Thus, the experiment was conducted with lighting luminance below the ambient condition. This might be one of the reasons for lighting to not play a significant role. At the same time, the proposed and comparing methods as proven by their respective papers are illumination invariant.
Table 3. Output of ANOVA for a 2x4x4 factorial design.
| Source | DF | Adj SS | Adj MS | F-Value | P-Value |
|---|---|---|---|---|---|
| Light Lux | 1 | 1.6 | 1.62 | 0.02 | 0.879 |
| Motion | 3 | 19798.3 | 6599.42 | 94.52 | 0.000 |
| Method | 3 | 5248.6 | 1749.55 | 25.06 | 0.000 |
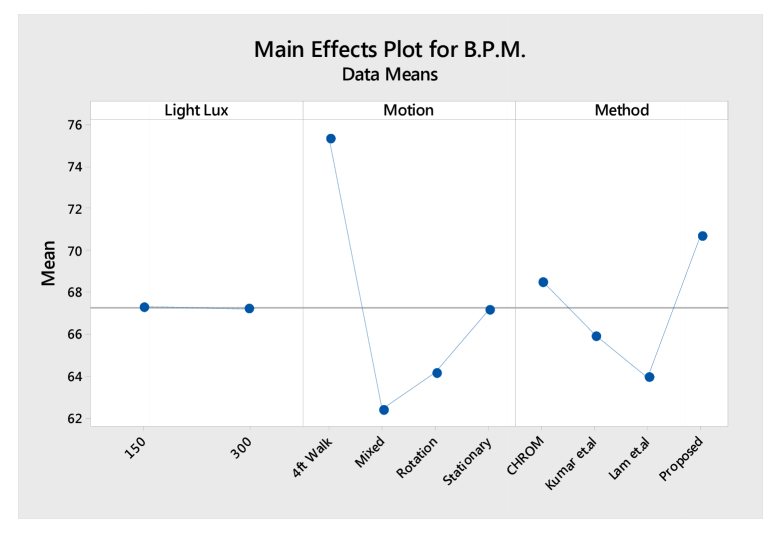
Fig. 10.
Main Effects Plot for the 2x4x4 Factorial Design.
Fig. 11.
Interaction Plot for the 2x4x4 Factorial Design.
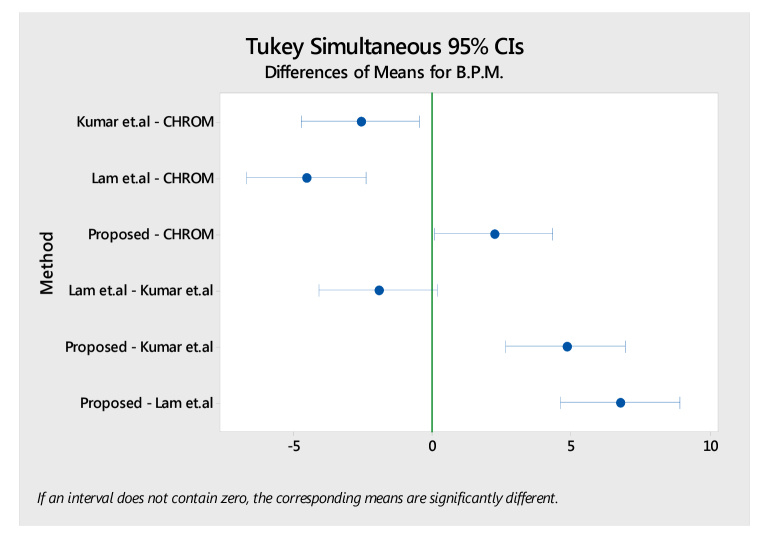
However, the other two factors, motion and rPPG method reveal a statistically significant difference in mean B.P.M. measurements. This statement is supported by the results in Table 3 for both the lighting conditions. The main effects plot and the interaction effects plot as shown in Fig. 10 and Fig. 11 reveals the proposed method to have a significantly stronger main effect in comparison to Lam et al. and DistancePPG method. However, the difference in effects of the proposed method with CHROM seems visually minimal and hence post-hoc analysis is sought to numerically verify significance. Since the ANOVA results only show a significance in mean B.P.M., a sensitivity analysis using Tukey’s Honestly Significant Criterion is conducted to analyze which rPPG method exhibits significance. The two rPPG methods, namely the proposed and CHROM methods show statistical significance using Tukey’s post-hoc analysis as shown in Fig. 12 and Table 4, meaning that the difference in mean B.P.M. caused by these methods is not due to chance or sampling. The significance of the proposed method against the comparing methods, with p value < 0.05 has been shaded for identification purposes as shown in Table 4.
Fig. 12.
Tukey Simultaneous Tests for Differences of Means in rPPG Methods.
Table 4. Tukey's Honestly Significant Criterion results for significance in rPPG methods.
| Difference of Method Levels | Difference of Means | SE of Difference | Simultaneous 95% CI | T-Value | Adjusted P-Value |
|---|---|---|---|---|---|
| Kumar et al. - CHROM | −2.600 | 0.836 | (−4.745, −0.455) | −3.11 | 0.010 |
| Lam et al. - CHROM | −4.560 | 0.836 | (−6.705, −2.415) | −5.46 | 0.000 |
| Proposed - CHROM | 2.200 | 0.836 | (0.055, 4.345) | 2.63 | 0.042 |
| Lam et al. - Kumar et al. | −1.960 | 0.836 | (−4.105, 0.185) | −2.35 | 0.088 |
| Proposed - Kumar et al. | 4.800 | 0.836 | (2.655, 6.945) | 5.74 | 0.000 |
| Proposed - Lam et al. | 6.760 | 0.836 | (4.615, 8.905) | 8.09 | 0.000 |
Additionally, Table 5 shows RMSE (the average of the measures which amplifies and penalizes large errors, describing the reliability of the methods against the ground truth HR values) values for the proposed method to be significantly low (illustrated through the grey shading) in comparison with CHROM and the other comparing methods, making the proposed method a reliable option in predicting HR with robustness. The standard deviation of mean error and the values for bias as shown in Table 5 reveal that the proposed method and CHROM method underestimate HR measurements. The mixed motion conditions seem to have the most underestimation in comparison to other conditions. Another result worth highlighting is the higher RMSE values associated with the rPPG methods being compared. This however is at the cost of computation and latency costs while using ICA based method as highlighted by [7,8] in their respective papers. The error associated with motion tracking is significantly low in comparison to the optical flow based DistancePPG method.
Table 5. Summary of Evaluation Metrics (Shaded cells illustrate lowest errors).
| Mean Error | SD Error | RMSE | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Illumination | Motion Type | Proposed | CHROM [ 12 ] | Kumar et al. [ 13 ] | Lam et al. [ 11 ] | Proposed | CHROM [ 12 ] | Kumar et al. [ 13 ] | Lam et al. [ 11 ] | Proposed | CHROM [ 12 ] | Kumar et al. [ 13 ] | Lam et al. [ 11 ] |
| 300 Lux | Stationary | -2.24 | -6.51 | -6.52 | -11.13 | 2.71 | 3.41 | 5.02 | 4.14 | 5.58 | 9.00 | 12.35 | 12.87 |
| Rotation | -4.14 | -5.59 | -9.15 | -9.86 | 2.68 | 3.83 | 2.95 | 3.59 | 7.36 | 12.34 | 14.23 | 12.46 | |
| Mixed | -7.81 | -9.64 | -10.57 | -10.72 | 2.47 | 2.85 | 3.47 | 3.24 | 9.88 | 14.67 | 13.22 | 12.80 | |
| 4ft. Walk | -2.22 | -3.72 | -10.88 | -11.69 | 3.42 | 5.63 | 5.69 | 4.36 | 7.72 | 11.99 | 14.18 | 15.29 | |
| 150 Lux | Stationary | -1.66 | -1.76 | -2.28 | -11.10 | 2.60 | 3.52 | 4.40 | 3.66 | 5.56 | 10.29 | 9.66 | 13.52 |
| Rotation | -5.73 | -5.28 | -9.46 | -9.55 | 2.67 | 3.54 | 3.62 | 3.76 | 8.09 | 13.58 | 12.83 | 13.73 | |
| Mixed | -7.27 | -8.44 | -12.69 | -14.09 | 2.70 | 3.66 | 2.69 | 3.52 | 9.96 | 13.40 | 14.94 | 15.12 | |
| 4ft. Walk | -2.60 | -3.98 | -8.18 | -8.35 | 3.76 | 6.24 | 4.38 | 3.97 | 8.60 | 12.75 | 13.15 | 12.97 | |
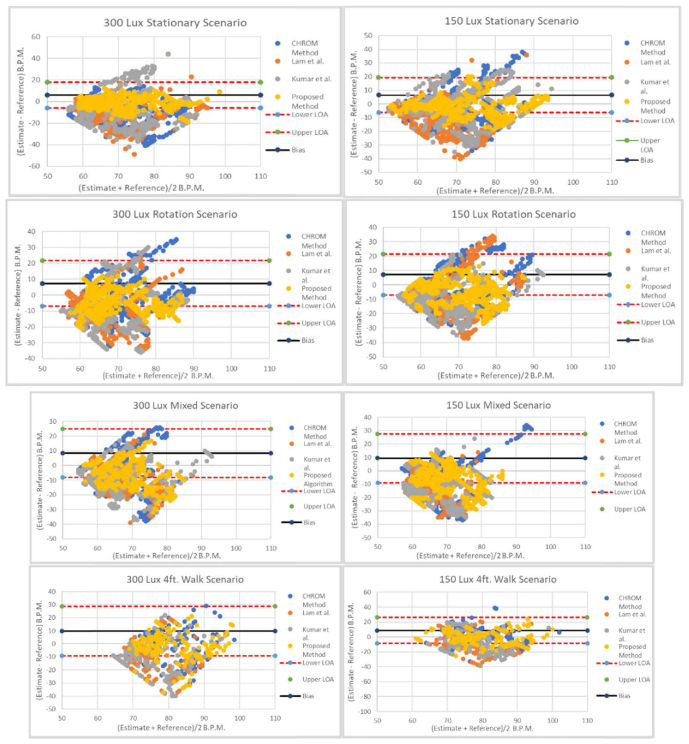
Bland-Altman plots for each motion and light scenario are shown in Fig. 13. Table 6 shows the agreements of the HR measurements between the rPPG and ground truth sensor in correspondence to the plots in Fig. 13. The lower and upper level of agreements are calculated as ± 1.96σ, where σ is obtained between the HR values of the proposed method and the ground truth sensor to denote the variance range. The proposed method has a consistent performance with the 95% agreements ranging from 52%-81%, surpassing the benchmarked methods.
Fig. 13.
Bland-Altman plots for four motion-scenarios in two illumination conditions. The Bland-Altman agreements are calculated between rPPG-signals and HRgt values.
Table 6. Bland-Altman Agreements.
| Bland-Altman Agreements | Proposed | CHROM | Kumar | Lam |
|---|---|---|---|---|
| 300 Lux Stationary | 80% | 65% | 59% | 44% |
| 150 Lux Stationary | 81% | 61% | 68% | 41% |
| 300 Lux Rotation | 64% | 55% | 44% | 43% |
| 150 Lux Rotation | 56% | 41% | 41% | 37% |
| 300 Lux Mixed | 52% | 43% | 46% | 35% |
| 150 Lux Mixed | 60% | 52% | 40% | 39% |
| 300 Lux Walk | 80% | 67% | 47% | 40% |
| 150 Lux Walk | 71% | 60% | 48% | 44% |
6. Discussion
The proposed method has been evaluated on subjects while they performed natural head (Roll, yaw, pitch) and body (walk from a distance of 4 ft.) movements under various lighting conditions (150 Lux and 300 Lux). Pulse-rate prediction during a walk however is found to be limited to a distance of 4ft (as observed across all benchmarked algorithms during the study). To enable continuous face detection from frame to frame, skin segmentation backed facial detection is employed to predict a human face. The face detector and feature tracker are both appearance dependent (visibility and clarity of human face in frame). This constraint makes sure that anything which matches the skin histogram template and contains facial features is only detected as a face (non-facial objects having similar skin color tone or any random objects do not get detected). This functionality also aids in detecting subjects from a distance (4ft. walk motion) as shown in the paper.
The ROIs of feature points are selected such that they represent high SNR quality and correlation with respect to the rPPG signal. The ROIs in the forehead and cheeks dynamically resizes depending on the distance of the camera from the subject whose face is being detected. Though a dynamic ROI is noisy, the ROI sizes modelled for the proposed method are constrained by a fixed aspect ratio. A fixed aspect ratio helps reduce disproportionate expansion or contraction of the ROIs, helping maintain consistency in the mean quality of the rPPG signal. However, the work can be expanded to find the optimal number of feature points to be tracked, as the distance from the camera varies. This expansion might assist in an increase in the accuracy of rPPG signals as the distance of the subject from the camera varies.
Feature point and ROI tracking is enabled by a bounded Kalman filter approach as designed in the paper. The bounded Kalman filter uses a cubic spline extrapolation mechanism to effectively control drift and sensitivity of feature point motion detection to improve accuracy of tracking against random head movements/motion artifacts. However, illumination variation has been consistently found to be a limitation found in the literature. The proposed algorithm addresses the illumination variation limitation. By utilizing the rotation, size and shift invariance property of the dynamically changing pixel intensity values, feature tracking is further made illumination invariant by utilizing the HSV color space [8]. The hue parameter of the HSV color space represents the dominant wavelength of light either being reflected from or absorbed by the ROIs. HSV color space, though device-dependent, after being found to be successful in capturing noise-free rPPG signal [8], has been made use of in extracting the dominant wavelength from the detected face, making the method illumination invariant. The experimental results reveal that the proposed algorithm is prone to illumination variation. However, the proposed algorithm has not been utilized for rPPG signal detection in scenarios featuring colored illumination or multi-colored illumination. That being said, incorporating a white-balancing step to the existing algorithm might possibly enable the proposed algorithm to process a video recorded in a different colored lighting.
Table. 5 draws upon an interesting observation. The mean error of the proposed and comparing algorithms seems to all be negative. This means that the proposed and comparing algorithms are under predicting the heart rate of the subjects. Taking a closer look at each person’s mean error for each motion scenario reveals the magnitude of underestimation to have a dominant effect over the entire HR estimation process. However, the reason for such an occurrence of this magnitude can be reasoned from Table 2. Table 2 illustrates each motion scenario (Except for 4ft. walk) to approximately have the same mean and standard deviation. The ground truth heart rate of most of the subjects seems to lie in the range of 60-80 b.p.m. Taking a closer look at the data of each motion scenario against a subject reveals that whenever a prediction of e.g. (60 – 65) b.p.m (say ground truth data) is to be made, the predictions by the algorithms (primarily the comparing algorithms) seem to find difficulty identifying the right peaks in the HR spectrum. The reason for such a problem to arise has rightly been explained by [63]; where the authors find uncorrelated motion artifact as a result of some activity by the subject and a correlated mechanical motion artifact signal by the name of ballistocardiogram to get summed up to provide the PPG signal, causing low frequency oscillations to get multiplied by the same factor with which motion gets scaled. The proposed algorithm, based on Table 5 and the discovered problem, is found to be relatively motion robust in comparison with the other algorithms, even in the presence of low frequency PPG signal with motion artifacts.
Though the study has presented significant results, the ability of a rPPG algorithm has to be enhanced to monitor pulse rate in scenarios featuring extensive motion activity (head movements during walk etc.). Feasibility and accuracy of an rPPG system can be improved with additional scenarios and advanced noiseless motion tracking algorithms. Currently, the Polar H7 monitor does not possess the functionality to output PPG signals. Therefore, the variation between camera-based PPG signals and the Polar device has not been illustrated. Future work will explore the use of devices capable of also measuring PPG signals.
7. Conclusion
Prior rPPG methods of pulse-rate measurement from face videos attain high accuracies under well controlled uniformly illuminated and motion-free situations, however, their performance degrades when illumination variations and subjects’ motions are involved. The proposed method has been found to be more accurate in comparison with the compared publicly available state of the art rPPG methods. From the results of the study, it can be inferred that variation in light illumination is not found to impact HR detection. The proposed method was applied in an environment featuring subjects walking towards the camera from a distance of 4ft. as shown in Fig. 7, attaining a mean error of ≈ ± 3 B.P.M., thus opening up a new paradigm in rPPG research domain. This advancement will enable the detection of heart rate while a person performs an exercise in the gym (though this was discussed in [12], it featured a stationary stepping device) without intimidating the subject by keeping a close distance.
The presented work can be combined with affective computing research in determining the heart rate of a person without having the subject wear a heart rate monitor. It also has the potential of being employed in hospitals to predict the heart rate as patients walk in, without the constraint of having to be in a stationary position. Moreover, it can be combined with Microsoft Kinect to be used as a real time ergonomic system as done by [64] or predicting designers’ comfort with engineering equipment [65]. Future research expansions could be devoted to predicting pulse-rate in environments where subjects are made to walk longer distances, gender difference is considered an experimental design factor and activities other than motions performed before the subject’s laptops/desktop computers are devised as part of the experimental design.
Funding
National Center for Advancing Translational Sciences, National Institutes of Health (NIH), through Grant UL1 TR000127 and TR002014. National Science Foundation (NSF) NRI award #1527148 and NSF I/UCRC Center for Healthcare Organization Transformation (CHOT), NSF I/UCRC award #1624727. The content is solely the responsibility of the authors and does not necessarily represent the official views of the NSF or NIH.
Disclosures
The authors declare that there are no conflicts of interest related to this article.
References and links
- 1.Sikdar A., Behera S. K., Dogra D. P., “Computer-vision-guided human pulse rate estimation: a review,” IEEE Rev. Biomed. Eng. 9, 91–105 (2016). 10.1109/RBME.2016.2551778 [DOI] [PubMed] [Google Scholar]
- 2.Verkruysse W., Svaasand L. O., Nelson J. S., “Remote plethysmographic imaging using ambient light,” Opt. Express 16(26), 21434–21445 (2008). 10.1364/OE.16.021434 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Lomaliza J.-P., Park H., “Detecting Pulse from Head Motions Using Smartphone Camera,” in International Conference on Advanced Engineering Theory and Applications (Springer, 2016), pp. 243–251. [Google Scholar]
- 4.Wadhwa N., Wu H.-Y., Davis A., Rubinstein M., Shih E., Mysore G. J., Chen J. G., Buyukozturk O., Guttag J. V., Freeman W. T., “Eulerian video magnification and analysis,” Commun. ACM 60(1), 87–95 (2016). 10.1145/3015573 [DOI] [Google Scholar]
- 5.Wang W., Stuijk S., de Haan G., “Exploiting spatial redundancy of image sensor for motion robust rPPG,” IEEE Trans. Biomed. Eng. 62(2), 415–425 (2015). 10.1109/TBME.2014.2356291 [DOI] [PubMed] [Google Scholar]
- 6.McDuff D., Gontarek S., Picard R. W., “Improvements in remote cardiopulmonary measurement using a five band digital camera,” IEEE Trans. Biomed. Eng. 61(10), 2593–2601 (2014). 10.1109/TBME.2014.2323695 [DOI] [PubMed] [Google Scholar]
- 7. Lewandowska M., Rumiński J., Kocejko T., Nowak J., “Measuring pulse rate with a webcam—a non-contact method for evaluating cardiac activity,” in Computer Science and Information Systems (FedCSIS), 2011 Federated Conference on (IEEE, 2011), pp. 405–410. [Google Scholar]
- 8.Tsouri G. R., Li Z., “On the benefits of alternative color spaces for noncontact heart rate measurements using standard red-green-blue cameras,” J. Biomed. Opt. 20(4), 048002 (2015). 10.1117/1.JBO.20.4.048002 [DOI] [PubMed] [Google Scholar]
- 9.Poh M.-Z., McDuff D. J., Picard R. W., “Non-contact, automated cardiac pulse measurements using video imaging and blind source separation,” Opt. Express 18(10), 10762–10774 (2010). 10.1364/OE.18.010762 [DOI] [PubMed] [Google Scholar]
- 10.Li X., Chen J., Zhao G., Pietikainen M., “Remote heart rate measurement from face videos under realistic situations,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (2014), pp. 4264–4271. 10.1109/CVPR.2014.543 [DOI] [Google Scholar]
- 11.Lam A., Kuno Y., “Robust heart rate measurement from video using select random patches,” in Proceedings of the IEEE International Conference on Computer Vision (2015), pp. 3640–3648. 10.1109/ICCV.2015.415 [DOI] [Google Scholar]
- 12.de Haan G., Jeanne V., “Robust pulse rate from chrominance-based rPPG,” IEEE Trans. Biomed. Eng. 60(10), 2878–2886 (2013). 10.1109/TBME.2013.2266196 [DOI] [PubMed] [Google Scholar]
- 13.Kumar M., Veeraraghavan A., Sabharwal A., “DistancePPG: Robust non-contact vital signs monitoring using a camera,” Biomed. Opt. Express 6(5), 1565–1588 (2015). 10.1364/BOE.6.001565 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Yu Y.-P., Raveendran P., Lim C.-L., Kwan B.-H., “Dynamic heart rate estimation using principal component analysis,” Biomed. Opt. Express 6(11), 4610–4618 (2015). 10.1364/BOE.6.004610 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Amelard R., Clausi D. A., Wong A., “Spectral-spatial fusion model for robust blood pulse waveform extraction in photoplethysmographic imaging,” Biomed. Opt. Express 7(12), 4874–4885 (2016). 10.1364/BOE.7.004874 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Wang W., den Brinker A. C., Stuijk S., de Haan G., “Amplitude-selective filtering for remote-PPG,” Biomed. Opt. Express 8(3), 1965–1980 (2017). 10.1364/BOE.8.001965 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Wang W., Stuijk S., de Haan G., “A novel algorithm for remote photoplethysmography: spatial subspace rotation,” IEEE Trans. Biomed. Eng. 63(9), 1974–1984 (2016). 10.1109/TBME.2015.2508602 [DOI] [PubMed] [Google Scholar]
- 18.Chen D.-Y., Wang J.-J., Lin K.-Y., Chang H.-H., Wu H.-K., Chen Y.-S., Lee S.-Y., “Image sensor-based heart rate evaluation from face reflectance using Hilbert–Huang transform,” IEEE Sens. J. 15(1), 618–627 (2015). 10.1109/JSEN.2014.2347397 [DOI] [Google Scholar]
- 19. Cheng J., Chen X., Xu L., Wang Z. J., “Illumination variation-resistant video-based heart rate measurement using joint blind source separation and ensemble empirical mode decomposition,” IEEE J. Biomed. Heal. informatics (2017). 10.1109/JBHI.2016.2615472 [DOI] [PubMed]
- 20.Roberts V. C., “Photoplethysmography-fundamental aspects of the optical properties of blood in motion,” Trans. Inst. Meas. Contr. 4(2), 101–106 (1982). 10.1177/014233128200400205 [DOI] [Google Scholar]
- 21.Nijboer J. A., Dorlas J. C., Mahieu H. F., “Photoelectric plethysmography-some fundamental aspects of the reflection and transmission method,” Clin. Phys. Physiol. Meas. 2(3), 205–215 (1981). 10.1088/0143-0815/2/3/004 [DOI] [PubMed] [Google Scholar]
- 22. Wolf L., Hassner T., Maoz I., “Face recognition in unconstrained videos with matched background similarity,” in Computer Vision and Pattern Recognition (CVPR), 2011 IEEE Conference on (IEEE, 2011), pp. 529–534. 10.1109/CVPR.2011.5995566 [DOI] [Google Scholar]
- 23.Chan C. H., Tahir M. A., Kittler J., Pietikäinen M., “Multiscale local phase quantization for robust component-based face recognition using kernel fusion of multiple descriptors,” IEEE Trans. Pattern Anal. Mach. Intell. 35(5), 1164–1177 (2013). 10.1109/TPAMI.2012.199 [DOI] [PubMed] [Google Scholar]
- 24. He X. C., Luo T., Yuk S. C., Chow K. P., Wong K.-Y., Chung R. H. Y., “Motion estimation method for blurred videos and application of deblurring with spatially varying blur kernels,” in Computer Sciences and Convergence Information Technology (ICCIT), 2010 5th International Conference on (IEEE, 2010), pp. 355–359. 10.1109/ICCIT.2010.5711083 [DOI] [Google Scholar]
- 25.Lopez C. E., Tucker C., “Board# 91: When to Provide Feedback? Exploring Human-Co-Robot Interactions in Engineering Environments,” in 2017 ASEE Annual Conference & Exposition (2017). [Google Scholar]
- 26.Lopez C. E., Tucker C. S., “A quantitative method for evaluating the complexity of implementing and performing game features in physically-interactive gamified applications,” Comput. Human Behav. 71, 42–58 (2017). 10.1016/j.chb.2017.01.036 [DOI] [Google Scholar]
- 27.Balakrishnan G., Durand F., Guttag J., “Detecting pulse from head motions in video,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (2013), pp. 3430–3437. 10.1109/CVPR.2013.440 [DOI] [Google Scholar]
- 28. Shan L., Yu M., “Video-based heart rate measurement using head motion tracking and ICA,” in Image and Signal Processing (CISP), 2013 6th International Congress on (IEEE, 2013), Vol. 1, pp. 160–164. 10.1109/CISP.2013.6743978 [DOI] [Google Scholar]
- 29. Irani R., Nasrollahi K., Moeslund T. B., “Improved pulse detection from head motions using DCT,” in Computer Vision Theory and Applications (VISAPP), 2014 International Conference on (IEEE, 2014), Vol. 3, pp. 118–124. [Google Scholar]
- 30.Poh M.-Z., McDuff D. J., Picard R. W., “Advancements in noncontact, multiparameter physiological measurements using a webcam,” IEEE Trans. Biomed. Eng. 58(1), 7–11 (2011). 10.1109/TBME.2010.2086456 [DOI] [PubMed] [Google Scholar]
- 31. Viola P., Jones M., “Rapid object detection using a boosted cascade of simple features,” in Computer Vision and Pattern Recognition, 2001. CVPR 2001. Proceedings of the 2001 IEEE Computer Society Conference on (IEEE, 2001), Vol. 1, pp. I. 10.1109/CVPR.2001.990517 [DOI] [Google Scholar]
- 32.Hyvärinen A., Oja E., “Independent component analysis: algorithms and applications,” Neural Netw. 13(4-5), 411–430 (2000). 10.1016/S0893-6080(00)00026-5 [DOI] [PubMed] [Google Scholar]
- 33.Welch P., “The use of fast Fourier transform for the estimation of power spectra: a method based on time averaging over short, modified periodograms,” IEEE Trans. Audio Electroacoust. 15(2), 70–73 (1967). 10.1109/TAU.1967.1161901 [DOI] [Google Scholar]
- 34.Farnebäck G., “Two-frame motion estimation based on polynomial expansion,” Image Anal. 2749, 363–370 (2003). [Google Scholar]
- 35.Lucas B. D., Kanade T., “An iterative image registration technique with an application to stereo vision,” Proc. DARPA (1981).
- 36. Shi J., “Good features to track,” in Computer Vision and Pattern Recognition, 1994. Proceedings CVPR’94., 1994 IEEE Computer Society Conference on (IEEE, 1994), pp. 593–600. [Google Scholar]
- 37.Wu H.-Y., Rubinstein M., Shih E., Guttag J., Durand F., Freeman W., “Eulerian video magnification for revealing subtle changes in the world,” ACM Tans. Graphics 31, 1–8 (2012). [Google Scholar]
- 38. Mathis A., Nothwang W., Donavanik D., Conroy J., Shamwell J., Robinson R., Making Optic Flow Robust to Dynamic Lighting Conditions for Real-Time Operation (US Army Research Laboratory Adelphi United States, 2016). [Google Scholar]
- 39. Kwon S., Kim J., Lee D., Park K., “ROI analysis for remote photoplethysmography on facial video,” in Engineering in Medicine and Biology Society (EMBC), 2015 37th Annual International Conference of the IEEE (IEEE, 2015), pp. 4938–4941. [DOI] [PubMed] [Google Scholar]
- 40.Challoner A. V. J., “Photoelectric plethysmography for estimating cutaneous blood flow,” Non-invasive Physiol. Meas. 1, 125–151 (1979). [Google Scholar]
- 41.Van Kampen E. J., Zijlstra W. G., “Determination of hemoglobin and its derivatives,” Adv. Clin. Chem. 8, 141–187 (1966). 10.1016/S0065-2423(08)60414-X [DOI] [PubMed] [Google Scholar]
- 42.Kramer K., Elam J. O., Saxton G. A., Elam W. N., Jr., “Influence of oxygen saturation, erythrocyte concentration and optical depth upon the red and near-infrared light transmittance of whole blood,” Am. J. Physiol. 165(1), 229–246 (1951). 10.1152/ajplegacy.1951.165.1.229 [DOI] [PubMed] [Google Scholar]
- 43.Enson Y., Briscoe W. A., Polanyi M. L., Cournand A., “In vivo studies with an intravascular and intracardiac reflection oximeter,” J. Appl. Physiol. 17(3), 552–558 (1962). 10.1152/jappl.1962.17.3.552 [DOI] [PubMed] [Google Scholar]
- 44.Viola P., Jones M. J., “Robust real-time face detection,” Int. J. Comput. Vis. 57(2), 137–154 (2004). 10.1023/B:VISI.0000013087.49260.fb [DOI] [Google Scholar]
- 45. Lienhart R., Maydt J., “An extended set of haar-like features for rapid object detection,” in Image Processing. 2002. Proceedings. 2002 International Conference on (IEEE, 2002), Vol. 1, pp. I–I. 10.1109/ICIP.2002.1038171 [DOI] [Google Scholar]
- 46.Bradski G., “The OpenCV Library,” Dr. Dobbs J. Softw. Tools Prof. Program. 25, 120–123 (2000). [Google Scholar]
- 47.Kazemi V., Sullivan J., “One millisecond face alignment with an ensemble of regression trees,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (2014), pp. 1867–1874. 10.1109/CVPR.2014.241 [DOI] [Google Scholar]
- 48. Lempe G., Zaunseder S., Wirthgen T., Zipser S., Malberg H., “ROI Selection for Remote Photoplethysmography.,” in Bildverarbeitung Für Die Medizin (Springer, 2013), pp. 99–103. [Google Scholar]
- 49. Daly J., “Video camera monitoring to detect changes in haemodynamics,” PhD dissertation University of Oxford; (2016). [Google Scholar]
- 50.Uggla Lingvall K., “Remote heart rate estimation by evaluating measurements from multiple signals,” (2017).
- 51.Zhong L., Cho S., Metaxas D., Paris S., Wang J., “Handling noise in single image deblurring using directional filters,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (2013), pp. 612–619. 10.1109/CVPR.2013.85 [DOI] [Google Scholar]
- 52. Pech-Pacheco J. L., Cristóbal G., Chamorro-Martinez J., Fernández-Valdivia J., “Diatom autofocusing in brightfield microscopy: a comparative study,” in Pattern Recognition, 2000. Proceedings. 15th International Conference on (IEEE, 2000), Vol. 3, pp. 314–317. 10.1109/ICPR.2000.903548 [DOI] [Google Scholar]
- 53.Kalman R. E., “A new approach to linear filtering and prediction problems,” J. Basic Eng. 82(1), 35–45 (1960). 10.1115/1.3662552 [DOI] [Google Scholar]
- 54.Eom K. H., Lee S. J., Kyung Y. S., Lee C. W., Kim M. C., Jung K. K., “Improved kalman filter method for measurement noise reduction in multi sensor rfid systems,” Sensors (Basel) 11(12), 10266–10282 (2011). 10.3390/s111110266 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Lai, “How to Draw a Human Face,” https://www.dragoart.com/tuts/6736/1/1/how-to-draw-a-human-face.htm.
- 56.C. Arul Prakash, S. Kumar; Tucker, “A Bounded Kalman Filter Method for Motion-Robust, Non-Contact Heart Rate Estimation,” https://github.com/DataLabPSU/A-Bounded-Kalman-Filter-Method-for-Motion-Robust-Non-Contact-Heart-Rate-Estimation-. [DOI] [PMC free article] [PubMed]
- 57.Giles D., Draper N., Neil W., “Validity of the Polar V800 heart rate monitor to measure RR intervals at rest,” Eur. J. Appl. Physiol. 116(3), 563–571 (2016). 10.1007/s00421-015-3303-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Achten J., Jeukendrup A. E., “Heart rate monitoring,” Sports Med. 33(7), 517–538 (2003). 10.2165/00007256-200333070-00004 [DOI] [PubMed] [Google Scholar]
- 59.Goodie J. L., Larkin K. T., Schauss S., “Validation of Polar heart rate monitor for assessing heart rate during physical and mental stress,” J. Psychophysiol. 14(3), 159–164 (2000). 10.1027//0269-8803.14.3.159 [DOI] [Google Scholar]
- 60.Mateu-Mateus M., Guede-Fernández F., García-González M. A., “RR time series comparison obtained by H7 polar sensors or by photoplethysmography using smartphones: breathing and devices influences,” in 6th European Conference of the International Federation for Medical and Biological Engineering (Springer, 2015), pp. 264–267. 10.1007/978-3-319-11128-5_66 [DOI] [Google Scholar]
- 61.Plews D. J., Scott B., Altini M., Wood M., Kilding A. E., Laursen P. B., “Comparison of Heart Rate Variability Recording With Smart Phone Photoplethysmographic, Polar H7 Chest Strap and Electrocardiogram Methods,” Int. J. Sports Physiol. Perform. 12, 1–17 (2017). 10.1123/ijspp.2017-0343 [DOI] [PubMed] [Google Scholar]
- 62.Tulyakov S., Alameda-Pineda X., Ricci E., Yin L., Cohn J. F., Sebe N., “Self-adaptive matrix completion for heart rate estimation from face videos under realistic conditions,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (2016), pp. 2396–2404. 10.1109/CVPR.2016.263 [DOI] [Google Scholar]
- 63.Butler M. J., Crowe J. A., Hayes-Gill B. R., Rodmell P. I., “Motion limitations of non-contact photoplethysmography due to the optical and topological properties of skin,” Physiol. Meas. 37(5), N27–N37 (2016). 10.1088/0967-3334/37/5/N27 [DOI] [PubMed] [Google Scholar]
- 64.Dering M., Tucker C., Kumara S., “An Unsupervised Machine Learning Approach To Assessing Designer Performance During Physical Prototyping,” J. Comput. Inf. Sci. Eng. 18(1), 011002 (2017). 10.1115/1.4037434 [DOI] [Google Scholar]
- 65.Bezawada S., Hu Q., Gray A., Brick T., Tucker C., “Automatic Facial Feature Extraction for Predicting Designers’ Comfort With Engineering Equipment During Prototype Creation,” J. Mech. Des. 139(2), 021102 (2017). 10.1115/1.4035428 [DOI] [Google Scholar]