Confidence intervals for heritability via Haseman-Elston regression

Abstract

Heritability is the proportion of phenotypic variance in a population that is attributable to individual genotypes. Heritability is considered an important measure in both evolutionary biology and in medicine, and is routinely estimated and reported in genetic epidemiology studies. In population-based genome-wide association studies (GWAS), mixed models are used to estimate variance components, from which a heritability estimate is obtained. The estimated heritability is the proportion of the model’s total variance that is due to the genetic relatedness matrix (kinship measured from genotypes). Current practice is to use bootstrapping, which is slow, or normal asymptotic approximation to estimate the precision of the heritability estimate; however, this approximation fails to hold near the boundaries of the parameter space or when the sample size is small. In this paper we propose to estimate variance components via a Haseman-Elston regression, find the asymptotic distribution of the variance components and proportions of variance, and use them to construct confidence intervals (CIs). Our method is further developed to estimate unbiased variance components and construct CIs by meta-analyzing information from multiple studies. We demonstrate our approach on data from the Hispanic Community Health Study/Study of Latinos (HCHS/SOL).

1 Introduction

Heritability is the proportion of phenotypic variance that is due to genetic variation among individuals in a population. Heritability is often estimated using mixed models (Zaitlen and Kraft, 2012), where the genetic relatedness between any two individuals in a given study population is estimated (e.g. kinship coefficients may be calculated from GWAS data, or inferred from pedigrees) and then taken as fixed. Then, a variance component due to genetic variation is estimated, and the estimated heritability is the ratio between this variance component and the total variance in the model.

Inference about heritability when estimated from mixed models, and more generally, about other proportions of variance, usually relies on asymptotic normal approximation to the distribution of the estimators. However, multiple studies showed (e.g., Burch (2011), Kruijer et al. (2015)) that such confidence intervals are inaccurate, and may yield values that are not permissible (e.g. negative values). Recently, Schweiger et al. (2016) proposed a bootstrap approach that does not rely on asymptotic normality for estimating confidence intervals for heritability, and a numerical approximation that does not require bootstrapping under a specific way of calculating the genetic relatedness matrix. While they show that their confidence intervals are accurate, their method is limited by computation time, by requiring a single modeled variance parameter, and by requiring a specific form for the genetic relatedness matrix when using the numerical approximation. In addition, current meta-analysis approaches for heritability estimates rely on the inaccurate normal asymptotic approximation.

In this work we proposes to use Haseman-Elston regression for estimating variance components. This approach entails regressing multiplied residuals against entries of covariance matrices. We find the distribution of the variance component estimators as well as the distributions of the proportions of variance, in a general model that allows for multiple sources of variation. We provide an algorithm to estimate the confidence intervals, and to obtain an unbiased meta-analytic estimator of heritability that accurately combines information from multiple studies. In the case where genetic relatedness (or kinship) is the only sources of variation, our algorithm is very quick, with the computationally demanding step being the calculation of eigenvalues from a sub-matrix of the kinship matrix. We demonstrate our method by estimating heritability and proportion of variance attributed to house-hold and community sharing for 47 health outcomes in the Hispanics Community Health Study/Study of Latinos.

2 Materials and methods

2.1 Haseman-Elston regression

Suppose that a quantitative trait Y, measured on n individuals, follows the regression model

$$y_i=w_i^T\beta +b_{i,a}+\dots +b_{i,k}+e_i=w_i^T\beta +{\epsilon }_i,i=1,\dots ,n$$

with β a vector of fixed effects of a covariates vector w, b_i,l, l = a, …, k, i = 1, …, n are mean-zero random effects with b_l = (b_i,1, …, b_n,l) and $\text{cov}(b_l)={\sigma }_l^{2}L$, so that ${\sigma }_a^2,\dots ,{\sigma }_k^2$ are variances corresponding to a, …, k independent sources of variation, and A, …, K are n × n matrices with i, j entries a_i,j, …, k_i,j modeling the correlation between the individuals’ random effects. Also e_i, i = 1, …, n are independent errors with variance ${\sigma }_e^2$. In genetic association studies one of these matrices, say K, is a kinship, or genetic relatedness, matrix. Then

$$E[y_i-w_i\beta ]=E[\epsilon ]=\mathbf{0}\text{var}[\epsilon ]={\sigma }_e^2{\mathbf{I}}_{n\times n}+{\sigma }_a^2\mathbf{A}+\dots +{\sigma }_k^2\mathbf{K}=\sum ,\text{ and}E[{\epsilon }_i{\epsilon }_j]=\text{cov}({\epsilon }_i,{\epsilon }_j)={\sigma }_e^2{1}_{(i=j)}+{\sigma }_a^2{a}_{i,j}+\dots +{\sigma }_k^2{k}_{i,j},$$

where here ${\sigma }_k^2/({\sigma }_a^2+\dots +{\sigma }_k^2+{\sigma }_e^2)\equiv {\sigma }_k^2/{\sigma }_T^2$ is the heritability.

Let β̂ be an unbiased estimator of β, and let ${\hat{\epsilon }}_i=y_i-w_i^T\hat{\beta }$ be an estimator ε_i, i = 1, …, n. We estimate the variance components in a residual regression, i.e. by taking the vector of all unique pairs of residuals ε̂_i ε̂_j, i ≤ j (we can do it by taking the upper diagonal sub-matrix of ε̂ ε̂^T that includes the diagonal), denoted by ε̃^d and regressing it according to the above model. The regression design matrix is given by:

$$\mathbf{X}=\left(\begin{array}{cccc}\hfill 1\hfill & \hfill a_{1,1}\hfill & \hfill \dots \hfill & \hfill k_{1,1}\hfill \\ \hfill 0\hfill & \hfill a_{1,2}\hfill & \hfill \dots \hfill & \hfill k_{1,2}\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill \\ \hfill 0\hfill & \hfill a_{1,n}\hfill & \hfill \dots \hfill & \hfill k_{1,n}\hfill \\ \hfill 1\hfill & \hfill a_{2,2}\hfill & \hfill \dots \hfill & \hfill k_{2,2}\hfill \\ \hfill 0\hfill & \hfill a_{2,3}\hfill & \hfill \dots \hfill & \hfill k_{2,3}\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill \\ \hfill 0\hfill & \hfill a_{2,n}\hfill & \hfill \dots \hfill & \hfill k_{2,n}\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill \\ \hfill 1\hfill & \hfill a_{n-1,n-1}\hfill & \hfill \dots \hfill & \hfill k_{n-1,n-1}\hfill \\ \hfill 0\hfill & \hfill a_{n-1,n}\hfill & \hfill \dots \hfill & \hfill k_{n-1,n}\hfill \\ \hfill 1\hfill & \hfill a_{n,n}\hfill & \hfill \dots \hfill & \hfill k_{n,n}\hfill \end{array}\right)=\left(\begin{array}{cccc}\hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill \\ \hfill 0\hfill & \hfill a_{1,2}\hfill & \hfill \dots \hfill & \hfill k_{1,2}\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill \\ \hfill 0\hfill & \hfill a_{1,n}\hfill & \hfill \dots \hfill & \hfill k_{1,n}\hfill \\ \hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill \\ \hfill 0\hfill & \hfill a_{2,3}\hfill & \hfill \dots \hfill & \hfill k_{2,3}\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill \\ \hfill 0\hfill & \hfill a_{2,n}\hfill & \hfill \dots \hfill & \hfill k_{2,n}\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill \\ \hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill \\ \hfill 0\hfill & \hfill a_{n-1,n}\hfill & \hfill \dots \hfill & \hfill k_{n-1,n}\hfill \\ \hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill \end{array}\right)$$

where the second equality is because a_i,i, …, k_i,i = 1 for all i. Denote the vector of variance components estimated from the Haseman-Elston regression by ${\hat{\sigma }}^2={({\hat{\sigma }}_e^2,{\hat{\sigma }}_a^2,\dots ,{\hat{\sigma }}_k^2)}^T$.

2.2 Properties of the variance components and proportions of variance estimators

Complete mathematical derivations are provided in the Supplementary Information. Below are statements of some of the results to provide intuition to the findings and methods.

Lemma 2

Variance component estimators corresponding to the matrices A, …, K depend only on the between-observation multiplied residuals of the form ε̂_i ε̂_j for i ≠ j.

Lemma 3

Denote by ${\sigma }_T^2={\sigma }_e^2+{\sigma }_a^2+\dots +{\sigma }_k^2$. Then ${\hat{\sigma }}_T^2=\frac{1}{n}{\sum }_{i=1}^n{\hat{\epsilon }}_i^2$.

Theorem

We say that two matrices C₁ and C₂ are orthogonal in the trace inner product, or “trace orthogonal” if tr (C₁C₂) = 0. Let the matrix L⁻ be the matrix L with all diagonal values set to 0. If a matrix L⁻ is trace orthogonal to all other matrices in the set {A⁻, …, K⁻} \ L⁻, then

$${\hat{\sigma }}_l^2=\frac{1}{{\sum }_{j>i}{l}_{i,j}^2}\sum _{j>i}{l}_{i,j}{\hat{\epsilon }}_i{\hat{\epsilon }}_j=\frac{{\hat{\epsilon }}^T{L}^{-}\hat{\epsilon }}{\mathit{\text{tr}}(L^{-}{L}^{-})},$$

and the estimator of the proportion of variance modeled in L is the ratio between two quadratic forms given by:

$$\frac{{\hat{\sigma }}_l^2}{{\hat{\sigma }}_T^2}=\frac{{\hat{\epsilon }}^T{L}^{-}\hat{\epsilon }}{\frac{1}{n}\mathit{\text{tr}}(L^{-}{L}^{-}){\hat{\epsilon }}^T\hat{\epsilon }}.$$

The above theorem provides a closed form estimator for a variance component and the proportion of variance corresponding to a correlation matrix L when it represents either the only modeled source of variation in the model, or when it is orthogonal to all other modeled sources of variation. The formula in the theorem explicitly shows that in Haseman-Elston regression the estimator of the total variance of an observation equals the “natural” estimator, the mean sum of squares of the marginal regression residuals, and that variance estimators corresponding to correlation matrices depend only on between-sample correlations (and not within-sample variances). Lemma 2 in the supplementary material shows that the same holds when the various correlation matrices are not trace orthogonal (after setting the diagonal values to zero).

In general, the estimators of variance components are quadratic forms. It is possible to obtain closed form expressions in the more complicated case of multiple modeled sources of variation that are not orthogonal, but the form of the estimator is not as nice as in the case of orthogonality. We here provide intuition to these estimators. Suppose that the correlation between two matrices is the Pearson correlation between the vectorized matrices. Consider the symmetric matrix (X^TX) with the l, m = 1, …, k entry being equal to tr(L⁻ M⁻). This is the design matrix of the Haseman-Elston regression. It describes relationships between the matrices in our model (e.g. if L⁻ and M⁻ are trace orthogonal, the l, m entry will be zero). Moreover, its inverse matrix (X^TX)⁻¹ could be referred to as the “precision matrix” (Li and Gui, 2006), a term we adopt from the gaussian graphical models literature. Here it means that the l, m, l ≠ m entry of (X^TX)⁻¹ represents the partial correlation between the matrices L⁻ and M⁻ given all other matrices in the model, so that if L⁻ and M⁻ are uncorrelated given other correlation matrices, the corresponding entry of (X^TX)⁻¹ would be equal to zero. The quadratic form used for obtaining the estimator of the variance component corresponding to the matrix L = 1, …, K is of the form Q = (w_aA⁻ + … + w_kK⁻), with w_m, m = 1, …, k being equal to the the l, m entry of (X^TX)⁻¹, or the partial correlation between L⁻ and M⁻ given all other matrices in the model.

2.3 Computation

2.3.1 Variance component estimators

While any unbiased estimator of β̂ suffices to generate residuals ε̂ and use them to obtain variance component estimators as (X^TX)⁻¹ X^T ε̃^d, a more efficient estimator iterates between estimating β and σ² as follows:

1. Initialization step: set β̂⁽⁰⁾ = (W^T W)⁻¹W^T y.

2. Iteration step:

   1. Given the kth estimator of β, β̂^(k), set ε̂ = y − Wβ^(k). Let ε̃ denote the vector of upper diagonal matrix (including the diagonal) of ε̂ ε̂^T. Set ${\hat{\sigma }}^{2,(k)}=({\hat{\sigma }}_e^{2,(k)},{\hat{\sigma }}_a^{2,(k)},\dots ,{\hat{\sigma }}_k^{2,(k)})={({\mathbf{X}}^T\mathbf{X})}^{-1}{\mathbf{X}}^T\stackrel{\sim }{\epsilon }$.
   2. Given the kth estimator of σ², σ̂^2,(k), let ${\hat{\sum }}^{(k)}={\hat{\sigma }}_e^{2,(k)}{\mathbf{I}}_{n\times n}+{\hat{\sigma }}_a^{2,(k)}\mathbf{A}+\dots +{\hat{\sigma }}_k^{2,(k)}\mathbf{K}$ with inverse Σ̂^−1,(k). Set β̂^(k+1) = (W^T Σ̂^−1,(k) W)⁻¹ W^TΣ̂^−1,(k)y

The iteration step repeats until convergence.

2.3.2 Confidence intervals for the variance components

From Lemma 4 in the Supplementary Information, any variance component (or sum of variance components) is given as a quadratic form. Let Q be the quadratic form corresponding to a variance component estimate ${\hat{\sigma }}_l^2$, such that ${\hat{\sigma }}_l^2={\hat{\epsilon }}^T\mathbf{Q}\hat{\epsilon }$. This ${\hat{\sigma }}_l^2$ is distributed as the sum of independent ${\chi }_{(1)}^2$ variables in ${\sum }_{i=1}^n{\lambda }_i{\chi }_{(1)}^2$, where λ₁, …, λ_n are the eigenvalues of cov(ε̂)^1/2 Qcov(ε̂)^1/2. In practice, for cov(ε̂) we use the estimated $\hat{\sum }=\hat{\sum }({\hat{\sigma }}_e^2,\dots ,{\hat{\sigma }}_k^2)$. Functions in the R package CompQuadForm (Duchesne and de Micheaux, 2010) calculate the probability function (or survival function) of this quadratic form based on λ₁, …, λ_n. While it takes times to compute the eigenvalues, once they are computed, calculating the probabilities associated with the quadratic form is quick. We can test the hypothesis $H_0:{\sigma }_l^2=0$ by calculating the probability

$$\text{Pr }({\epsilon }^T\mathbf{Q}\epsilon =0)=1-\text{Pr }({\epsilon }^T\mathbf{Q}\epsilon >0),$$

and calculate two-sided confidence intervals for ${\hat{\sigma }}_l^2$ by calculating the appropriate quantiles of the survival probability. For example, for a 95% confidence interval we take the values (c₁, c₂) for which

$$c_1=u:\text{Pr }({\epsilon }^T\mathbf{Q}\epsilon >u)=0.025$$

$$c_2=u:\text{Pr }({\epsilon }^T\mathbf{Q}\epsilon >u)=0.975.$$

We find these values using a binary search on the interval [0, ${\hat{\sigma }}_T^2$].

We comment here that cov(ε̂) is in fact given by V̂ = Σ̂ − W (W^T Σ̂⁻¹ W)⁻¹ W^T because ε̂ = y − W β̂. In practice, we compared the coverage of confidence intervals when using V̂ and when using Σ̂ and the results were essentially the same.

2.3.3 Computing heritability estimates and their confidence intervals

Suppose that the variance component corresponding to the kinship matrix is ${\sigma }_k^2$, with quadratic form denoted by Q_k. We estimate heritability as ${\hat{h}}_k={\hat{\sigma }}_k^2/{\hat{\sigma }}_T^2$. However, we cannot use the confidence intervals for ${\sigma }_k^2$ to construct confidence intervals for h_k. Instead, we note that the point estimate ĥ_k is given by:

$${\hat{h}}_k=\frac{{\hat{\epsilon }}^T{\mathbf{Q}}_k\hat{\epsilon }}{\frac{1}{n}{\hat{\epsilon }}^T\mathbf{I}\hat{\epsilon }}~\frac{x^T{\hat{\sum }}^{1/2}{\mathbf{Q}}_k{\hat{\sum }}^{1/2}x}{\frac{1}{n}{x}^T\hat{\sum }x}=\frac{x^T\mathbf{F}x}{x^T\mathit{\text{Gx}}}$$

where x ~ 𝒩 (0, I), for F = Σ̂^1/2 Q_kΣ̂^1/2 and G = Σ̂ /n. Thus, it is a ratio between two quadratic forms in (what we assume are) normal variables. For the squared root Σ̂^1/2, we use the Cholesky decomposition of Σ̂.

We use the saddlepoint approximation for the distribution of a ratio of quadratic forms in normal variables, proposed by Lieberman (1994). Complete detailed are provided in the Supplementary Information. In brief, for each potential value of h_k, say $h_k^{\ast }$, we can calculate the survival probability $\mathit{\text{Pr }}(h_k\ge h_k^{\ast })$ using the saddlepoint approximation. Each such calculation requires as input $d_1^{\ast },\dots ,d_n^{\ast }$, the eigenvalues of the matrix ${\mathbf{D}}^{\ast }=\mathbf{F}-h_k^{\ast }G$. We apply a binary search on the potential values $h_k^{\ast }\in [0,1]$ to find end points c₁ and c₂ for the confidence intervals, as was done for calculating a confidence intervals for ${\sigma }_k^2$.

2.3.4 Fast computation when genetic relatedness is the only modeled source of correlation

If we have only have a single kinship matrix K modeling the phenotypic variance, we can compute the eigenvalues λ₁, …, λ_n of the matrix K⁻ once, and then transform these eigenvalues to obtain the eigenvalues $d_1^{\ast }(h_k^{\ast }),\dots ,d_n^{\ast }(h_k^{\ast })$ for each value $h_k^{\ast }$, and save computation time. To see this, suppose that u is an eigenvector of K⁻ with an eigenvalue λ. Then, by definition, K⁻u = λu. Since $\sum ={\sigma }_k^2({\mathbf{K}}^{-}+\mathbf{I})+{\sigma }_e^2\mathbf{I}$, it is straightforward to see that u is also an eigenvector of Σ:

$$\sum u=[{\sigma }_k^2({\mathbf{K}}^{-}+\mathbf{I})+{\sigma }_e^2\mathbf{I}]u=({\sigma }_k^2\lambda +{\sigma }_k^2+{\sigma }_e^2)u.$$

Similarly, u is an eigenvector of Σ^1/2 with an eigenvalue $\sqrt{{\sigma }_k^2\lambda +{\sigma }_k^2+{\sigma }_e^2}$, which finally leads to the transformation between an eigenvalue λ_i of K⁻ to an eigenvalue of ${\mathbf{D}}^{\ast }(h_k^{\ast })$:

$$d_i^{\ast }(h_k^{\ast },{\lambda }_i)=\frac{1}{2{\sum }_{i<j}{v}_{\mathit{\text{ij}}}^2}{\lambda }_i({\lambda }_i{\sigma }_k^2+{\sigma }_k^2+{\sigma }_e^2)-h_k^{\ast }({\lambda }_i{\sigma }_k^2+{\sigma }_k^2+{\sigma }_e^2)/n.$$

As before, we use the estimated ${\hat{\sigma }}_k^2,{\hat{\sigma }}_e^2$ instead of the true unknown values.

2.3.5 Meta-analysis across studies when kinship is the only source of correlation

Suppose that there are S studies that we wanted to combine in meta-analysis. We assume that kinship is the only source of correlation. Each study has a vector of residuals ε̂_s = (ε̂_s,1, …, ε̂_s,ns)^T, s = 1, …, S. Consider the Haseman-Elston regression, but incomplete, so that only the pairs of multiplied residuals within study ε̂_s,i ε̂_{s, j} are regressed against entries of the kinship covariance matrix, but not ε̂_s,i ε̂_{t, j} for s ≠ t. For this, we do not need to assume that a participant in one study is genetically unrelated of a participant in another study. The meta-analytic estimator of ${\sigma }_T^2$ is given by ${\hat{\sigma }}_T^2={\sum }_{s=1}^S{\sum }_{i=1}^{n_s}{\hat{\epsilon }}_{s,i}^2/{\sum }_{s=1}^S{n}_s$. Let $\hat{\epsilon }={({\hat{\epsilon }}_1^T,\dots ,{\hat{\epsilon }}_S)}^T$. The meta-analytic kinship variance component estimator is given by

$${\hat{\sigma }}_k^2=\frac{1}{\text{tr }({\mathbf{K}}_S^{-}{\mathbf{K}}_S^{-})}{\hat{\epsilon }}^T{\mathbf{K}}_S^{-}\hat{\epsilon }$$

where ${\mathbf{K}}_S^{-}$ is the block diagonal matrix that have all the study-specific kinship matrix (without their diagonal values) arranged diagonally, as

$${\mathbf{K}}_S^{-}=\left(\begin{array}{ccccc}\hfill {\mathbf{K}}_1^{-}\hfill & \hfill \mathbf{0}\hfill & \hfill \dots \hfill & \hfill \dots \hfill & \hfill \hfill \\ \hfill \mathbf{0}\hfill & \hfill {\mathbf{K}}_2^{-}\hfill & \hfill \hfill & \hfill \hfill & \hfill \mathbf{0}\hfill \\ \hfill ⋮\hfill & \hfill \hfill & \hfill \ddots \hfill & \hfill \hfill & \hfill \hfill \\ \hfill ⋮\hfill & \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill & \hfill \hfill & \hfill {\mathbf{K}}_s^{-}\hfill \end{array}\right)$$

To see that this meta-analytic estimator of ${\sigma }_k^2$ is unbiased, note first that $\text{cov}(\hat{\epsilon })=({\sigma }_e^2+{\sigma }_k^2)\mathbf{I}+{\sigma }_k^2{\mathbf{K}}^{-}$, where now K⁻ has kinship coefficients for individuals across studies (and diagonals set to zero). From characteristics of quadratic forms:

$$E[{\hat{\sigma }}_k^2]=E\left[\frac{1}{\text{tr }({\mathbf{K}}_S^{-}{\mathbf{K}}_S^{-})}{\hat{\epsilon }}^T{\mathbf{K}}_S^{-}\hat{\epsilon }\right]=\frac{1}{\text{tr }({\mathbf{K}}_S^{-}{\mathbf{K}}_S^{-})}\text{tr }({\mathbf{K}}_S^{-}\text{cov}(\hat{\epsilon }))=\frac{1}{\text{tr }({\mathbf{K}}_S^{-}{\mathbf{K}}_S^{-})}\text{tr }\{{\mathbf{K}}_S^{-}[({\sigma }_e^2+{\sigma }_k^2)\mathbf{I}+{\sigma }_k^2{\mathbf{K}}^{-}]\}=\frac{1}{\text{tr }({\mathbf{K}}_S^{-}{\mathbf{K}}_S^{-})}\text{tr }({\mathbf{K}}_S^{-}{\sigma }_k^2{\mathbf{K}}^{-})=\frac{1}{\text{tr }({\mathbf{K}}_S^{-}{\mathbf{K}}_S^{-})}\text{tr }({\mathbf{K}}_S^{-}{\sigma }_k^2{\mathbf{K}}_S^{-})={\sigma }_k^2.$$

Let ${\mathbf{K}}^{-}={\mathbf{K}}_S^{-}+{\mathbf{K}}_C^{-}$, where ${\mathbf{K}}_C^{-}$ is the matrix of cross-study relatedness. Although the variance components estimates and their ratios depend only on ${\mathbf{K}}_S^{-}$, their distribution depend on ${\mathbf{K}}_C^{-}$ as well.

Computing the meta-analytic heritability estimator and confidence intervals

Suppose that each of S independent studies calculated the residuals from a “null model” (a regression model without genetic fixed effects other than PCs). Each study s reports:

1. ${𝒦}^s=2{\sum }_{i<j}{k}_{\mathit{\text{ij}}}^2$,

2. ${\hat{\sigma }}_{k,s}^2$,

3. ${\hat{\sigma }}_{T,s}^2$,

4. The number of participants in the study n_s,

5. The eigenvalues ${\lambda }_1^s,\dots ,{\lambda }_{n_s}^s$ of its matrix ${\mathbf{K}}_s^{-}$.

The meta-analysis estimates of the kinship variance components and the total variance are:

$${\hat{\sigma }}_k^2=\frac{{\sum }_{s=1}^S{𝒦}^s{\hat{\sigma }}_{k,s}^2}{{\sum }_{s=1}^S{𝒦}^s}$$

$${\hat{\sigma }}_T^2=\frac{{\sum }_{s=1}^S{n}_s{\hat{\sigma }}_{T,s}^2}{{\sum }_{s=1}^S{n}_s}.$$

The error variance component is taken to be the difference ${\hat{\sigma }}_e^2={\hat{\sigma }}_T^2-{\hat{\sigma }}_k^2$, and the eigenvalues of the across-studies matrix K⁻ (= ${\mathbf{K}}_S^{-}$ under independence between studies) are taken to be ${\lambda }_1^1,\dots ,{\lambda }_{n_1}^1,\dots ,{\lambda }_1^S,\dots ,{\lambda }_{n_S}^S$. Using these, the central location calculates heritability estimates and confidence intervals. These estimators are the estimators that one would have obtained if all regression residuals and kinship values were available at the central location and individuals were unrelated between studies. Interestingly, the estimator of the kinship variance is the weighted average of the kinship variance estimators from the various studies, weighted by the sum of squared entries of the study-specific kinship matrices with diagonal values set to zero. Therefore, a study with larger values of relatedness overall will make a stronger contribution to the kinship variance estimator. The estimator of the total variance is simply weighted by the sample sizes. Thus, as when estimating variance components from a single study, all residuals have equal contribution to the estimator of the total variance, while multiplied residual pairs with greater corresponding kinship coefficients have large influence on the kinship variance estimator.

2.4 The Hispanic Community Health Study/Study of Latinos

The HCHS/SOL (LaVange et al., 2010, Sorlie et al., 2010)) is a community based cohort study, following self-identified Hispanic individuals from four field centers (Chicago, IL; Miami, FL; Bronx, NY; and San Diego, CA). Individuals were sampled via a two-stage sampling scheme, in which households were randomly sampled from sampled community block units. Almost 13,000 study participants consented for genotyping. Correlation matrices to model environmental variance due to households and community block units were generated so that the i, j entry of a given matrix was set to 1 if the i and j individuals live in the same household (or community block unit), and 0 otherwise.

HCHS/SOL individuals were classified into ‘genetic analysis groups’: Central American, Cuban, Dominican, Mexican, Puerto Rican, and South American. These groups are based on self reported ethnicities and genetic similarity (Conomos et al., 2016a). This study was approved by the institutional review boards at each field center, where all participants gave written informed consent. The HCHS/SOL genotype and phenotype data are available on dbGaP under accession numbers phs000880.v1.p1 and phs000810.v1.p1.

2.4.1 Genotyping, imputation and quality control

Blood samples from HCHS/SOL individuals were genotyped on a custom array consisting of Illumina Omni 2.5M content plus ~150,000 custom markers selected to include ancestry-informative markers, variants characteristic of Amerindian populations, known GWAS hits and other candidate gene polymorphisms. Quality control was similar to the procedure described in Laurie et al. (2010) and included checks for sample identity, batch effects, missing call rate, chromosomal anomalies (Laurie et al., 2012), deviation from Hardy-Weinberg equilibrium, Mendelian errors, and duplicate sample discordance. 12,784 samples passed quality control, and 2,232,944 SNPs passed quality filters. Pairwise kinship coefficients and principal components reflecting ancestry were estimated in an iterative procedure which accounts for admixture (Conomos et al., 2016a). All common variants were used to estimate kinship coefficients. Finally, we removed some individuals at random to generate a set of 10,255 individuals without any pair having kinship coefficient higher than 2⁻¹¹.

2.4.2 Heritability and proportion of variance estimation in the HCHS/SOL

Due to the sampling structure of the HCHS/SOL, the correlation between individuals is modeled via a kinship matrix, and two matrices modeling environmental effects: household and community block unit matrices. For each investigated trait we estimated variance components corresponding to the three correlation matrices via the Haseman-Elston regression. We estimated 95% confidence intervals for heritability, and for the proportion of variance explained by both modeled environmental effects together.

We first consider 47 traits for which previous GWAS was performed (though not necessarily published) in the HCHS/SOL. The traits were, by groups, white and red blood cells counts and indices: eosinophils (EOS), hemoglobin (HB), lymphocytes (LYMPH), neutrophils (NEUT), total white blood cell count (WBC), monocytes (MONO), total red blood cells count (RBC), hematocrit (HCT), mean corpuscular hemoglobin (MCH), mean corpuscular volume (MCV), mean corpuscular hemoglobin concentration (MCHC), red cell distribution width (RDW), and platelet count (PLT), anthropometric measures: BMI, waist circumference adjusted for BMI (WCadjBMI), waist-to-hip ratio adjusted to BMI (WHRadjBMI), hip circumference adjusted for BMI (HIPadjBMI), height, ECG measures: heart rate and its variability (HR, HRV_SD and HRV_RMS), QT and PR intervals (QT, PR), lipid measures: LDL and HDL cholesterol (HDL, LDL), total cholesterol (TC) and triglycerides (TG), measures of lung function: forced vital capacity (FVC), forced expiratory volume in one second (FVC1), and their ration (FEV1_FVC_ratio), blood pressure measures: systolic and diastolic blood pressure (SBP, DBP), mean arterial pressure (MAP) and pulse pressure (PP), iron measures: ferritin, total iron binding capacity (TIBC), transferring and its saturation (iron, Saturation), glycemic control, kidney and other metabolic traits: fasting insulin, ankle-brachial index (ABI), estimated glomerular filtration rate (eGFR), urine albumin to creatinine ratio (ACR), glycated hemoglobin (HbA1c), dental traits: periodontitis (PERIO) approximated by the cube root of the mean attachment loss interproximal teeth areas, and measures of dental caries (counts of cavities) on teeth surface (TS) and teeth (TT), and a depression score (known as CESD10, a sum of ten questionnaire items related to depression in the week prior to the clinic visit). All regression models were adjusted (via the design matrix W) to the 5 first principal components, study center, age, sex, and genetic analysis group. For some traits we used additional covariates.

We also studied the use of our method for meta-analysis when there are some related individuals across studies on a subset of five traits. We first generated a restricted data set of 7,848 individuals that none of them lived in the same house-hold. We then treated each of the genetic analysis groups as a separate study, and used the proposed procedure for calculating heritability in each of the genetic analysis groups and in meta-analysis. We also compared these analyses to the pooled analysis that modeled all 7,848 individuals together. Note that for this exercise we neglected block unit correlation, i.e. assumed that it does not contribute to the phenotypic variance.

2.5 Simulation studies

We study the accuracy of the proposed method for calculating confidence intervals in simulations, and compare it to other methods for obtaining estimates and confidence intervals. All methods under investigations are those that use pre-defined between-individuals correlation matrices. We used correlation matrices from the HCHS/SOL corresponding to kinship, household, and community block unit, to generate quantitative outcomes with realistic correlation structures. In the Supplementary Information we provide additional simulation studies with correlation matrices that are not directly based on the HCHS/SOL. In any given simulation, data were sampled by first generating an error vector e^ind from a standard normal distribution. We simulated the covariance structure

$$\text{cov}(e)={\sigma }_e^2\mathbf{I}+{\sigma }_k^2\mathbf{K}+{\sigma }_h^2\mathbf{H}+{\sigma }_c^2\mathbf{C}=\sum$$

by taking e = Σ^1/2e^ind. The matrices K, H, and C were the kinship, household, and community matrices in the HCHS/SOL. The outcomes were simulated by

$$y=2+3{\text{PC}}_1+e,$$

where PC₁ is the first principal component of the HCHS/SOL data. All simulations were performed 1,000 times.

In the first simulation study we set $\sigma =({\sigma }_e^2,{\sigma }_k^2,{\sigma }_h^2,{\sigma }_c^2)=(100,40,15,2)$, and studied our method in settings of small sample size (n = 1,500) and large sample size (n = 12, 784). We compared the Haseman-Elston approach to a REML approach, with confidence intervals that rely on normal approximation. For this we used the GENESIS R package (Conomos et al., 2016b) that can estimate multiple variance components. In a second simulation study we set $\sigma =({\sigma }_e^2,{\sigma }_k^2,{\sigma }_h^2,{\sigma }_c^2)=(100,{\sigma }_k^2,0,0)$, with ${\sigma }_k^2\in \{0,40\}$, so that kinship is the only source of correlation. In these settings we are able to compare additional methods: a combination of REML with the GENESIS R package and the ALBI package (Schweiger et al., 2016) for estimating bootstrap confidence intervals, the REML implementation in the heritability R package (Kruijer et al., 2016) with confidence intervals based on asymptotic normal approximation of either the variance component themselves, or their log. Here we also considered small and large sample sizes, and in addition, we randomly divided the large dataset into 5 subgroups, to generate data mimicking five different studies with possible genetic relatedness between participants of different studies, and studied our meta-analysis approach in this scenario. We randomly partitioned the data to subgroups four times, to make sure that results did not depend on a specific partition.

3 Results

3.1 Simulation studies

Table 1 provides simulation results in terms of root-mean-squared-error (RMSE) of the variance proportion estimator, where RMSE is given by

$$\sqrt{\frac{1}{n_{\text{sim}}}\sum _{i=1}^{n_{\text{sim}}}{(\frac{{\hat{\sigma }}_l^2}{{\hat{\sigma }}_T^2}-\frac{{\sigma }_l^2}{{\sigma }_T^2})}^2}$$

and n_sim = 1,000 is the number of simulations; coverage, which is the proportion of simulations in which the true variance proportion is within the confidence interval; and width, which is the average width of the 95% confidence interval. Table 1 is divided to two parts. On the left side, it provides results from simulation settings that included three different correlation matrices, mimicking the HCHS/SOL, for large and small sample sizes. This part only provides results computed using the proposed Haseman-Elston (HE) procedure and using the asymptotic normal approximation based on REML as implemented in the GENESIS R package. The right side of the table provides results from simulation settings in which only a single kinship matrix was used, again in large and small sample sizes. For these, results from all compared methods are provided.

Table 1.

Simulation results comparing the various methods for estimating proportions of variance and 95% confidence intervals. HE is the Haseman-Elston regression with the proposed procedure for obtaining confidence intervals. HE-meta is the implementation of the meta-analysis procedure when the data set is randomly divided into multiple studies. In this case there are correlation individuals between the studies, while the meta-analysis procedures ignores these correlations. GENESIS is an R package that implements an average-information REML procedure. GENESIS-asymp provides confidence intervals (CIs) based on asymptotic normality. When these CIs contained inadmissible values, they were truncated to include only admissible values. The size of the confidence intervals for GENESIS-asypm was calculated using only simulations that had non-zero estimate of the variance component. GENESIS-ALBI provides confidence intervals calculated in a parametric bootstrap procedure implemented in the ALBI package. ‘P heritability’ is the R package ‘heritability’ implementation of the REML procedure. CIs are based on asymptotic normality. When ‘log’ is specified, the asymptotic normality is calculated on the log transformed variance components, and 0 value is assumed when an estimate is smaller than 0.001. Note that the ‘P heritability’ had convergence problems in the large sample size, null scenario, so that a small number of simulations was used to calculate parameters.

	3 correlation matrices						Only kinship matrix
	Large sample			Small sample			Large sample		Smalle sample
	Community (2/157)	HH (15/157)	kinship (40/157)	Community (2/157)	HH (15/157)	kinship (40/157)	kinship (0/140)	kinship (40/140)	kinship (0/140)	kinship (40/140)
					RMSE
HE	0.004	0.016	0.030	0.016	0.092	0.180	0.015	0.028	0.132	0.182
HE - meta							0.054	0.153
GENESIS	0.004	0.014	0.026	0.016	0.089	0.180	0.015	0.025	0.134	0.181
P heritability							0.026	0.025	0.140	0.177
					Coverage
HE	0.92	0.96	0.95	0.98	0.98	0.99	0.98	0.94	0.97	1.00
HE - meta							0.95	0.96
GENESIS asymp	0.94	0.96	0.95	0.72	0.78	0.86	0.98	0.95	0.98	0.91
GENESIS - ALBI							0.95	0.96	1.00	0.96
P heritability							0.92	0.96	0.98	0.97
P heritability - log							0.79	0.96	0.79	0.99
					Width
HE	0.02	0.06	0.12	0.06	0.32	0.63	0.05	0.11	0.46	0.68
HE - meta							0.14	0.21
GENESIS asymp	0.01	0.06	0.10	0.06	0.32	0.64	0.06	0.10	0.52	0.64
GENESIS - ALBI							0.05	0.10	0.55	0.57
P heritability							0.06	0.10	0.48	0.63
P heritability - log							0.42	0.10	0.90	0.73

The HE estimates of proportion of variance are very similar to those obtain using REML procedures, though often slightly less efficient (usually slightly larger RMSE when compared to the GENESIS estimates). The confidence intervals obtained from the HE regression are better than the REML normal distribution based confidence intervals when the sample size is small, but are similar otherwise. Additional simulation results in the Supplementary Information demonstrate that the normal approximation based confidence intervals perform poorly also when the actual values in the correlation matrix are small, and when multiple correlation matrix are somewhat correlated. Asymptotic REML-based confidence intervals that use the log-transform do not perform well. The bootstrap confidence intervals (GENESIS-ALBI) perform well and tend to be slightly narrower than other confidence interval.

The meta-analysis procedure that ignores between-study relatedness had proper coverage of the proportion of variance, but had less efficient estimates, as seen by the large RMSE and wide confidence intervals. This is expected because we discarded some information compared to the procedure that used the entire data.

3.2 Heritability estimation in the HCHS/SOL

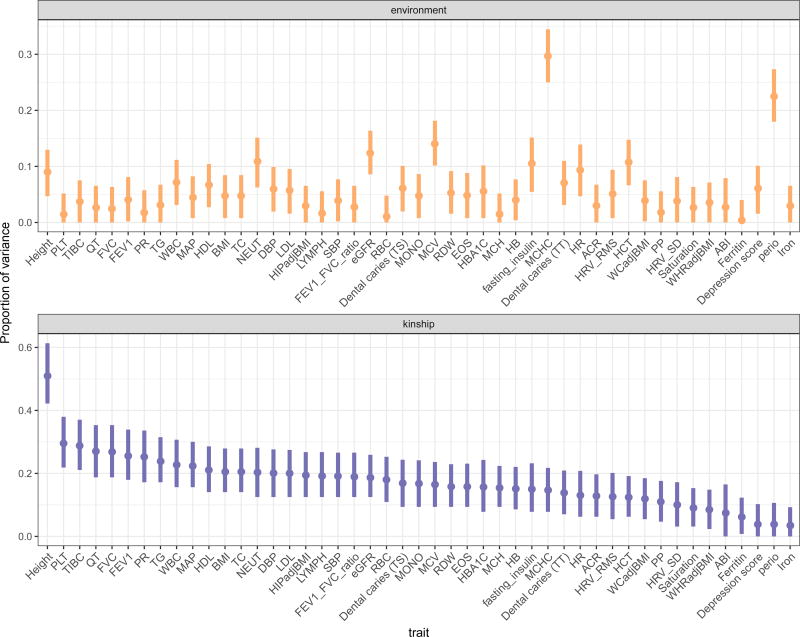
Figure 1 provides the estimated heritability and proportion of variance due to modeled environmental factors (household and community) for the 47 traits examined in the HCHS/SOL, together with 95% confidence intervals. The results are ordered by the estimated heritability. Height has the largest estimated heritability (almost 60%, consistent with other estimates from GWAS), while the heritability of iron (transferrin), periodontitis and the depression score are close to 0, with confidence interval containing zero. Interestingly, the proportion of variance of periodontitis explained by household and community sharing was very high, larger then 20%, and that of CESD10 was also statistically significant at the 0.05 level. The trait with the largest proportion of variance attributable to modeled environmental factors was MCHC (a measure of hemoglobin concentration in red blood cells). Perhaps this is due to environmental exposure that varies among households. For instance, it is known that smoking is associated with MCHC levels (Asif et al., 2013). While smoking status (never, past, current) was used as a covariate in the MCHC model, this variable may not have capture passive smoking that may vary by households.

Figure 1.

Estimated proportion of variance due to kinship (i.e., heritability) and due to modeled environmental factors (household and community sharing) for 47 traits in the HCHS/SOL data of 10,255 individuals. The investigated traits are related to blood cell count and indices (EOS, HB, LYMPH, NEUT, WBC, MONO, RBC, HCT, MCH, MVC, MCHC, RDW, PLT), anthropometric measures (BMI, height, WCadjBMI, HIPadjBMI, WHRadjBMI), ECG traits (HR, HRV_SD, HRV_RMS, QT and PR), lipid measures (LDL, HDL, TC, TG), measures of lung function (FVC, FEV1, FEV1_FVC_ratio), blood pressure measures (SBP, DBP, MAP, PP), dental traits (perio, Dental caries (TS, TT)), iron (iron, ferritin, TIBC, saturation), depression score, and other metabolic, glycemic and kidney traits (fasting_insulin, ABI, eGFR, ACR, HBA1C).

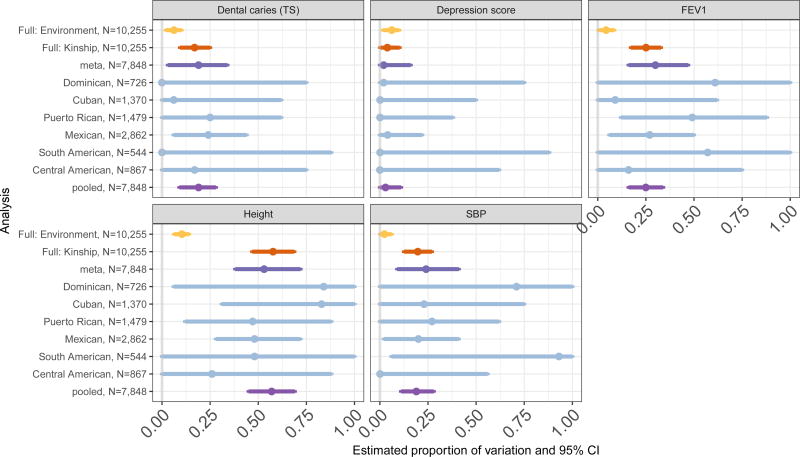
Figure 2 provides results from studying the meta-analysis procedure. For the five investigated traits, it provides estimated proportion of variance (heritability and environmental variance) and 95% confidence intervals from the Full data set, that included environmentally correlated individuals (and was used for Figure 1), and from the restricted data set that did not include environmentally correlated individuals. We used the restricted data set to compare a pooled analysis, genetic analysis group specific analyses, and meta-analysis that ignores the correlation between individuals from different genetic analysis groups, to mimic meta-analysis across different studies. Considering the restricted data set, the analyses of specific genetic analysis groups yielded wide confidence intervals, which often included zero. This is expected due to low power. In addition, the meta-analyses that did not account for the correlations between the genetic analysis groups had wider confidence intervals than the corresponding pooled analyses.

Figure 2.

Estimated proportions of variance from the various subsets of the HCHS/SOL data. The Full dataset included 10,255 individuals with mutual kinship coefficient smaller than 2^−11/2. Using Full, we estimated both heritability and the proportion of variance that is due to modeled environmental effects: the sum of the variance components corresponding to household and community block unit sharing. A restricted data set included 7,848 individuals from separate households and was used to compare meta and pooled analysis heritability estimates, where the meta-analysis used information from each of the genetic analysis groups. Dental caries (TS) is a measure of teeth damage on teeth surfaces. Depression score is a summation of responses to questions related to depressive behavior or feelings in the week prior to a participant’s clinic visit. FEV1 is a measure of lung function. SBP is systolic blood pressure.

4 Discussion

In this manuscript we investigate the properties of Haseman-Elston regression estimators of variance components. We get a closed-form expression for the variance estimators, and use them to characterize the distribution of the estimated variance components and ratios of variance, and to compute confidence intervals. Our confidence intervals require normality of the residuals from the trait regression model after adjusting for covariates. We further show how to obtain unbiased estimates of the variance components and proportions of variance by meta-analyzing information from multiple studies. In this case, the heritability estimates are unbiased even if individuals are related between studies, but the asymptotic distribution of the estimators depends on the unknown (and non-estimated) kinship coefficients of cross-study individuals.

The Haseman-Elston regression does not naturally constrain the variance component estimators to be non-negative. In practice, if an estimator of a variance component parameter becomes negative during the algorithm iteration process, it is set to zero, as is also done in REML estimation. However, unlike REML with asymptotic confidence intervals, where there is no uncertainty associated with the parameter that was set to zero, here we can obtain a confidence interval for the variance component estimator, because we can still estimate quantiles of the distribution of the quadratic form. The solution is still somewhat ad-hoc, as we constrain the confidence interval to have 0 as its low end point, and the high end point is that of estimated 97.5% probability. Still, in simulations with null heritability values and values close to 0, the confidence intervals had good coverage.

In the simulation studies, we compared our proposed approach to the approach that calculates confidence intervals based on the asymptotic normal approximation to the distribution of the variance components obtained by maximizing the REML. Using the latter method to obtain confidence intervals is attractive, because it is straightforward to implement and has almost no computational cost. However, the normal approximation does not hold close to the boundary of the parameter space, and when the information is low, e.g. when the values of the kinship matrix are small, as is shown in simulations in the Supplementary Information. In contrast, the proposed Haseman-Elston based confidence intervals perform well, and are almost as efficient (have similar width) as the normal approximation based ones when the sample size is large. The computational cost of calculating the proposed confidence intervals is large when using multiple matrices to model the covariance structure of the outcomes. However, this can be substantially reduced using recent developments in algorithms for fast calculations of the largest eigenvalues of matrices (e.g. Lumley et al. (2016)).

Our approach for heritability estimation and for obtaining confidence intervals relies on having a pre-defined kinship matrix that models the relatedness between individuals. The same is true for other mixed-models based approaches that use individual-level data. Other, relatively new approaches such as the LD-score regression (Bulik-Sullivan et al., 2015) and MQS (Zhou (2016), unpublished manuscript) use summary statistics from GWAS and a reference panel (for calculating confidence intervals, MQS also proposes a combination of the two approaches). Therefore, these methods use actual estimated effect sizes and LD between variants, instead of genetic correlation between individuals. It is a topic of future research to study the relative advantages (e.g. power under various settings) of these manners for estimating heritability: using genetic relatedness between individuals without estimating variants’ effect sizes, versus estimating effect sizes and using correlation between the variants.

We show in simulations based on the HCHS/SOL correlation structure that the coverage of our confidence intervals is good both in pooled analysis, and in meta-analysis (even when individuals are related between studies) while being quite conservative when the sample size is small. More work is needed to study the analytic properties of the confidence intervals in meta-analysis when individuals are related between studies and when some individuals belong to multiple studies. We expect such a scenario to cause a larger deviation between the estimated and the actual distribution of the kinship variance component and heritability, potentially leading to worse coverage of the estimated confidence intervals, depending on the how many such overlaps in study participants exists.

5 Software

An R code for estimating heritability (or proportion of variances due to other modeled factors), and their confidence intervals, together with an example script and with sample code and instructions for running simulation studies can be found at https://github.com/tamartsi/Heritability_CIs.