Abstract
Motivation
The identification of heterogeneities in cell populations by utilizing single-cell technologies such as single-cell RNA-Seq, enables inference of cellular development and lineage trees. Several methods have been proposed for such inference from high-dimensional single-cell data. They typically assign each cell to a branch in a differentiation trajectory. However, they commonly assume specific geometries such as tree-like developmental hierarchies and lack statistically sound methods to decide on the number of branching events.
Results
We present K-Branches, a solution to the above problem by locally fitting half-lines to single-cell data, introducing a clustering algorithm similar to K-Means. These halflines are proxies for branches in the differentiation trajectory of cells. We propose a modified version of the GAP statistic for model selection, in order to decide on the number of lines that best describe the data locally. In this manner, we identify the location and number of subgroups of cells that are associated with branching events and full differentiation, respectively. We evaluate the performance of our method on single-cell RNA-Seq data describing the differentiation of myeloid progenitors during hematopoiesis, single-cell qPCR data of mouse blastocyst development, single-cell qPCR data of human myeloid monocytic leukemia and artificial data.
Availability and implementation
An R implementation of K-Branches is freely available at https://github.com/theislab/kbranches.
Supplementary information
Supplementary data are available at Bioinformatics online.
1 Introduction
Recent advances in single-cell technologies have led to the discovery and characterization of novel cell types in multicellular organisms. Studying diverse cell populations that differ in morphology and function can pinpoint distinct cell types in different stages of regulatory processes, such as cellular development. For example, single-cell methods have led to new discoveries related to hematopoietic stem cells (Moignard et al., 2015; Paul et al., 2015), as well as the immune system (Jaitin et al., 2014; Mahata et al., 2014; Proserpio et al., 2016).
The development of novel computational techniques for the analysis of single-cell data is an active research topic in the field of bioinformatics (de Vargas Roditi and Claassen, 2015; Grün and van Oudenaarden, 2015; Stegle et al., 2015). The key idea of the Waddington epigenetic landscape (Waddington, 1942, 1957) is that individual cells can be mapped from a high-dimensional space to a low-dimensional manifold of trajectories that reflect the continuous regulatory processes. As a result, a number of methods have been proposed that can reconstruct differentiation trajectories, given snapshot data of individual cells in different stages of the differentiation process, such as Monocle (Trapnell et al., 2014), Wishbone (Setty et al., 2016), Diffusion Pseudotime (DPT) (Haghverdi et al., 2016), SLICER (Welch et al., 2016) and TSCAN (Ji and Ji, 2016). Given a ‘root’ cell as a starting point, most of these methods can also calculate an ordering of the cells (pseudotime) based on the stage each cell is in the differentiation process. However, with the exception of DPT, while these methods are successful in assigning cells to discrete differentiation trajectories (branches) they do not tackle the problem of identifying the local dimensionality around each cell. That is, identifying branching regions of cells not yet strongly associated to any branch, intermediate regions along a branch and tip regions of fully differentiated cells. Moreover, all the above methods lack a sound statistical model to identify the existence and number of cell subgroups associated to branching events. Finally, while TSCAN employs model selection to decide on the number of cell-clusters, it does not aim to identify branching and tip regions.
In this study, we propose a data driven, model-based clustering method that identifies the exact number of ‘branching regions’, as well as the exact number of fully differentiated ‘tip regions’ in the lineage tree. The method then proceeds to assign each cell to a branching, intermediate or tip region. The proposed methodology does not aim to infer a pseudotemporal ordering of the cells and as such no ‘root’ cell needs to be defined. Moreover, since characterization of each cell is based on local information in the differentiation trajectory, the method can successfully identify cells belonging to the aforementioned regions of interest in trajectories of arbitrary geometry.
2 Materials and methods
2.1 Problem formulation
Given a center c and direction v, a halfline L is defined as the set of points satisfying . We aim to find K halflines with a common center c and K distinct direction vectors . In this case, each halfline Lk corresponds one cluster Ck. As a prerequisite to defining a cost function, note that the Euclidean distance of a given point x to a halfline Lk reads:
| (1) |
Additionally, one may also use other distance metrics (Kiselev et al., 2017).
The clustering method aims to assign each of the given data points (cells) into its closest halfline, while minimizing the total cost. In other words, the goal is to identify the center c, as well as the direction vectors of unit length that minimize the overall clustering cost. To this end, we define the cost function J to describe the total dispersion, which corresponds to the sum of dispersions over the K clusters and reads:
| (2) |
where corresponds to all elements in cluster k and correspond to the sets of elements in cluster k with negative and positive dot product to all vectors in the direction of Lk, respectively.
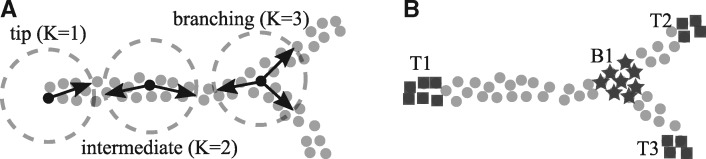
The main idea of the proposed methodology is to perform local clustering in single-cell trajectories, by fitting K halflines (branches) that share a common center. Then, model selection is applied to identify the number of K branches best fitting the local neighborhood around each cell. Thus, the local structure of single-cell trajectories is identified and each cell is assigned to a tip, intermediate or branching region, as illustrated in Figure 1.
Fig. 1.
Local application of K-Branches clustering reveals tip, intermediate and branching regions in single-cell trajectories. (A) Each cell is used as the center of the branches (halflines) and local clustering is performed in its neighborhood. Then, by using model selection the center cell is either characterized as a tip cell, a cell belonging to an intermediate region or a cell belonging to a branching region depending on which of the three models ( branches) best describes the structure of the neighborhood. (B) After local clustering is performed on the dataset, cells belonging to three tips (T1, T2, T3) and one branching region (B1) have been identified, while the rest of the cells are considered to belong to intermediate regions. The exact number of tip and branching regions is inferred from the data and does not need to be specified by the user
2.1.1 The K-Branches clustering method
In order to calculate the model parameters, after random initialization we follow an EM-like iterative optimization procedure similar to that of K-Means (Hastie et al., 2009). Namely, we iteratively (i) assign data points to their closest cluster and (ii) update the estimates of c and while minimizing J in each step, until convergence. Since the method might converge to a local optimum of the cost function, multiple executions using different initializations have to be carried out. The method is randomly initialized by assigning one random data point as the center c and K other random data points as the direction vectors . In the following subsections we present the update equations for the center and directions, respectively.
2.1.2 Estimating the center of the halflines
First, we optimize the cost function J with respect to the center of the halflines c. Therefore, we have to calculate the gradient , as follows:
| (3) |
where the matrix is defined as:
| (4) |
with .
The equation can be solved in closed form, and the optimal c reads:
| (5) |
where refers to the size of the set . In the case K = 1 the right part of Equation (5) simplifies to , which is not full rank and therefore not invertible when . Although the method for local clustering introduced in a subsequent section is also performed with K = 1, it uses a fixed center c, rendering the above limitation irrelevant.
2.1.3 Estimating the directions of the halflines
To optimize the cost function J with respect to the direction vector of unit length , we have to calculate the gradient , as follows:
| (6) |
Assuming that is as matrix whose ith row corresponds to , then setting to zero is equivalent to computing the first eigenvector of .
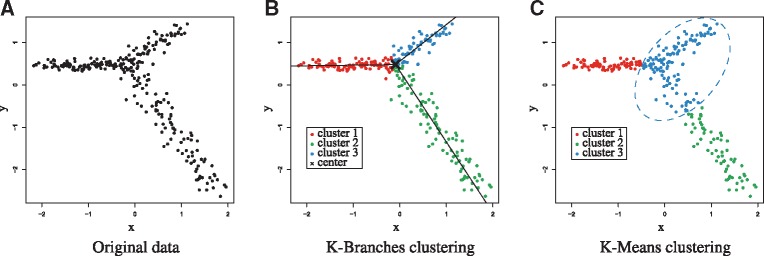
The pseudocode for the K-Branches algorithm is presented in Algorithm 1, while a comparison between K-Branches and K-Means is illustrated in Figure 2.
Algorithm 1 .
K-Branches clustering
1: Inputs: K: number of clusters, : data points
2: Random initialization of
3: forn in 1:N do ▹ N: number of all data points
4: assign to nearest Lk, according to Equation (1)
5: end for
6: repeat
7: update the center c ▹ according to Equation (5)
8: update the direction vectors
9: for n in 1:N do
10: assign to nearest Lk, according to Equation (1)
11: end for
12: until no change in cluster assignments
Algorithm 2 .
K-Branches clustering, medoid version
1: Inputs: K: number of clusters, : data points
2: Define: ▹ medoid indices
3: Random initialization of ▹ to random indices
4: for n in 1:N do ▹ N: number of all data points
5: assign to nearest Lk, according to Equation (1)
6: end for
7: while total cost J decreases do ▹ Repeat until convergence
8: ▹ update the center
9: for k in 1:K do ▹ iterate over K directions
10: ▹ update the directions
11: end for
12: forn in 1:N do
13: assign to nearest Lk, according to Equation (1)
14: end for
15: end while
Fig. 2.
Illustration of K-Branches clustering on artificial data and comparison to K-Means. (A) Original data (B) In the case artificial data, K-Branches successfully clusters the three halflines. The center of the halflines as well as the lines corresponding to the direction of each cluster are plotted on top of the data points. The medoids version yields almost identical results for the same data. (C) Unlike K-Branches, K-Means (also with K = 3) merges part of the bottom halfline into the middle cluster. Since K-Means clusters points in spherical clusters, it is clearly not suitable for clustering data points which belong to distinct differentiation trajectories
2.1.4 Medoid version of K-Branches
As in K-Means, the K-Branches method described above determines a ‘centroid’ per cluster, which depends on arbitrary vectors . We can easily modify this to use data points, as in K-Medoids (Hastie et al., 2009; Theodoridis and Koutroumbas, 2008). The goal of the Medoid version of K-Branches is to identify one data point as the center medoid and K data points as the direction medoids. That is, the model parameters now correspond to K + 1 data points, instead of K + 1 points in , where P the number of dimensions. Similar to K-Medoids, the proposed algorithm searches over all data points during each iteration in a greedy manner and identifies the data points that minimize the cost function J given by Equation (2). All medoids are reassigned during each iteration of the algorithm, until a local minimum for J is reached and the total clustering cost cannot be further decreased. At this point, the algorithm converges to a solution where one of the data points is the center medoid of the halflines and K data points correspond to the direction medoids . The relationship between the original and the medoid version is similar to that of K-Means and K-Medoids. That is, the medoid version is more robust in selecting the center of the halflines with respect to non-global optima and usually even only one random initialization is sufficient in practice. In the original algorithm, calculating the parameters requires time proportional to the number of data points O(N). A speedup of the medoid version is possible by computing the distance matrix D only once, where . Then, the distance of a data point to a halfline can be computed in O(1) time from Equation (8). However, for every one of the candidate medoids, the distance to every other data point is taken into consideration to calculate the overall clustering cost. As a result, time is required to update the medoids during every iteration.
| (8) |
To summarize, in cases where robustness in the identification of the center of the halflines is crucial, the medoid version might be preferable. In applications where robust identification of the center of the halflines is not as crucial, especially in larger datasets, the original version of the algorithm could be preferable. Last, in cases where the center of the halflines is known (or held fixed), such as the case of local clustering presented later in the methods section, there is no advantage to using the medoid over the original version, since both are equally robust in identifying the directions of the halflines.
2.2 Identifying branching and tip regions through local clustering
2.2.1 Local clustering
In this section we derive a method for the identification of” regions of interest” in single-cell data, in particular, the identification of branching regions and tips of branches in lineage trees of differentiating single cells. The main idea is to center the previous model on each data point and adopt a local perspective by examining only the neighborhood of S nearest neighbors to the center. We will show that by fixing the center of the halflines on a given data point and fitting the previous model of K halflines using a neighborhood size of S data points, one can infer whether the center data point itself belongs to branching, intermediate or tip region, through appropriate model selection.
2.2.2 Selection of the neighborhood size S
The proposed method utilizes a number of S nearest neighbors to extract the neighborhood of the center data point that is being examined. The size of the neighborhood must be sufficiently large to reflect the local structure of the data, without capturing irrelevant global information. The proposed method is able to automatically suggest a value for S using a threshold on , which ensures that the average cumulative squared distance δ of each data point to all other data points in the dataset is kept at a constant value. Moreover, the accompanying software package provides the option of visualization and manual fine tuning of S through a graphical user interface. Supplementary Figure S1 demonstrates the effect of neighborhood size in the overall performance of the method on a toy model of differentiation (Haghverdi et al., 2015).
2.2.3 Neighborhood scaling
Another challenging aspect is related to datasets showing strong variation in the density of data points along the differentiation trajectories. For example, in the dataset of Guo et al., 2010), there are sparse and dense regions. Variability of data point density might reflect an artifact of the data acquisition process, or could be a result of the underlying biological system. In the datasets examined so far, regions of very low density do not pose a threat to the performance of the method, since efficient selection of S will expand the neighborhood size accordingly. On the other hand, the fixed number of S neighbors may drastically shrink the size of the neighborhood in regions of very high density. To compensate for this effect, an appropriate heuristic rule was implemented. To be precise, for a given number of S neighbors, we calculate the median neighborhood radius over all neighborhoods of size S. The neighborhood scaling scheme is as follows: prior to performing local clustering for the ith data point, its neighborhood radius ρi (which corresponds to its distance to the furthest point in the neighborhood) is calculated and the condition is assessed. If it is true, clustering is performed as usual. Otherwise, the neighborhood size (S) of the ith data point is increased until holds.
2.2.4 Local model selection
The goal is to infer whether each data point belongs to a tip, intermediate or branching region of a differentiation trajectory, based on local clustering. That is, using a given data point as the fixed center c of the halflines, three different models are fit using K = 1, 2 and 3 halflines. The aim of the model selection step in the problem at hand is to identify the clustering model, i.e. the value of K, that best fits the data of the local neighborhood centred around the data point in question. If one halfline best fits the neighborhood, then the central data point belongs to a branch tip. If two halflines provide the best fit, then the central data point belongs to an intermediate region. If three halflines best fit the local neighborhood, then the central data point belongs to a branching region. Although values of K > 3 could in theory be considered for local clustering and model selection, we have observed that K = 3 is sufficient in practice for the identification of branching regions. Therefore, the computational overhead of assessing additional values of K can be safely avoided.
The GAP statistic (Tibshirani et al., 2001) is a popular method for identifying the number of clusters that best fit some given data. It depends on the sum of pairwise distances of points in each cluster. If the Euclidean distance is used as the distance measure, it corresponds to the dispersion around the cluster means (clustering cost). The GAP statistic compares the decrease in the clustering cost of the original data with the decrease in clustering cost of data drawn from a null distribution where no natural cluster structure exists. In theory, the dispersion in the data sampled from the null distribution decreases monotonically as K increases, while the dispersion in the original data drops rapidly for the value of K that best fits the dataset. Thus, the GAP statistic is maximized when the best value of K is used for clustering. Assuming that the Euclidean distance is used as the distance measure, the total within-cluster-dispersion WK (Tibshirani et al., 2001) is:
| (9) |
where denotes the mean cluster of k. Then, the equation for the GAP statistic for a given number of clusters K reads:
| (10) |
where and the dispersions are calculated by applying Equation (9) after performing clustering on each of the bootstrap datasets (of the same size as the original dataset) drawn from the null reference distribution.
In the case of local K-Branches clustering, we introduce a modification of the GAP statistic that calculates the dispersion around halflines, as follows:
| (11) |
where is given by Equation (1). Moreover, in contrast to the original GAP we do not take the logarithm of the dispersion, since it has been reported to overestimate the number of clusters in some cases (Mohajer et al., 2010). Finally, the modified GAP statistic is given by:
| (12) |
The dispersions are calculated by applying Equation (11) after performing clustering on each of the bootstrap datasets (of the same size as the original dataset) drawn from the null reference distribution.
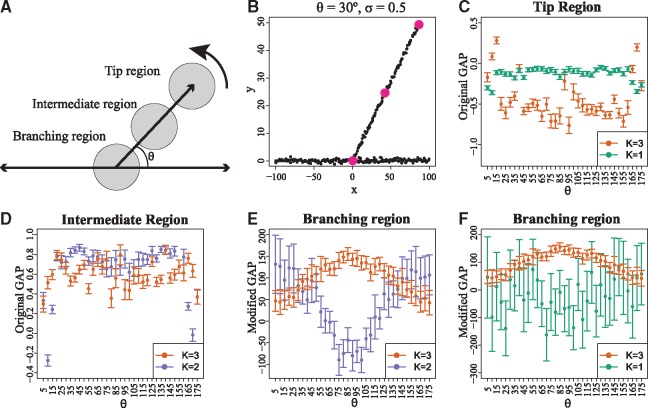
To summarize, given a data point as the center of the halflines, local clustering is performed. Then, if , it belongs to a branch tip. Otherwise, if the data point does not belong to a tip and holds, it belongs to an intermediate region. Finally, if the data point does not belong to a tip and , it belongs to a branching region. Both the original and modified versions of the GAP statistic are necessary for model selection and are complementary to each other. That is, GAP can identify tip cells (Fig. 3C) but is not suitable for separating intermediate from branching cells (Fig. 3D). On the other hand, can separate intermediate and branching cells (Fig. 3E), but it not suitable for identifying tip cells, since it would falsely identify a large number of branching cells as tip cells (Fig. 3F). The performance comparison of the different GAP statistics is illustrated in Figure 3. Moreover, the behavior of the GAP statistic when additional noise is added is illustrated in the Supplementary Figure S2. After all data points have been assigned to tip, intermediate and branching regions, an optional filtering of each cell’s label (tip, branching, or intermediate) based of the values of a few (e.g. 5) nearest neighbors can be performed to aid in smoothing out any random false positives caused by the inherent stochasticity of the GAP statistic. As a final step, K-Means clustering is performed on the subset of the data belonging to tips, using the original GAP statistic for model selection. In this manner, the exact number of tips is identified and each data point that has been characterized as belonging to a tip region is uniquely assigned to a specific tip. The same process is applied to cells belonging in branching regions in order to identify the exact number of branching events and assign branching region cells to their corresponding branching event.
Fig. 3.
The original, as well as the modified versions of the GAP statistic are necessary for the identification of regions of interest in single-cell differentiation trajectories. (A) Toy data were generated by uniform sampling of data-points along three line segments. Two of the segments are held fixed and one of them is positioned at an angle θ. A new dataset is sampled for each value of θ and zero-mean Gaussian noise of standard deviation σ is added. Then, local clustering is performed on centred on three cells, each being in a distinct region: Tip, Intermediate and Branching. The S = 31 (as selected by the proposed heuristic) nearest neighbors of each center-cell define the region used for local clustering. (B) Example of toy data generated for and . The centers of the three regions are highlighted. (C) The original GAP successfully identifies the tip region cell, since holds for a wide variety of angles. (D)GAP cannot be used to identify branching region cells, since in many cases holds in the intermediate region. As a result, a large number of intermediate region cells would be false positive branching region cells. (E) successfully identifies the branching region cell, since holds for a wide variety of angles. (F) cannot be used to identify tip cells. In many cases there is strong overlap between the confidence intervals for and , which in practice would lead to a large number of branching cells being falsely identified as tip cells. All error bars in the plot correspond to 95% CIs generated using 500 bootstrap datasets
2.2.5 Dimension reduction precedes model selection
In this section we focus on the selection of the null reference distribution. Uniform sampling of features over a box aligned with the principal components of the data is suggested in (Tibshirani et al., 2001). Alternatively, uniform sampling over the range of every feature in the original dimensions of the data is suggested for simplicity. Although the K-Branches clustering method performs well in the original space, model selection does not. This follows from the ‘curse of dimensionality’ (Hastie et al., 2009), since it becomes exponentially hard to estimate the null distribution in high dimensions. As a result, dimensionality reduction is a necessity if model selection is to be performed. Diffusion maps (Coifman et al., 2005) are a non-linear dimensionality reduction method which are known to successfully identify differentiation trajectories (Haghverdi et al., 2015), outperforming traditional dimensionality reduction methods such as principal component analysis (PCA) (Hastie et al., 2009) and Locally Linear Embedding (LLE) (Roweis and Saul, 2000). As a result, the dataset is first processed by diffusion maps and the first few diffusion components (DCs) are selected. Then, local clustering is performed for each data point in the space of the selected DCs. Finally, the reference distribution is calculated by uniform sampling over a box aligned with the same DCs, resulting in the computation of the GAP and statistics used for model selection.
3 Results
3.1 Datasets
The performance of local K-Branches is evaluated using three publicly available datasets, as well as one synthetic dataset. The first dataset corresponds to single-cell RNA-seq data describing the differentiation of myeloid progenitors during hematopoiesis (Paul et al., 2015); Accession Number GSE72857) and consists of measurements of 2730 cells and 8716 genes. The second dataset consists of single-cell qPCR data related to mouse blastocyst development (Guo et al., 2010); Accession Number J:140465) and includes measurements of 428 cells and 48 genes. The third dataset corresponds to a single-cell qPCR dataset of multiple time points where THP-1 human myeloid monocytic leukemia cells undergo differentiation into macrophages (Kouno et al., 2013); Data available in the supplement of the original publication) and include measurements of 960 cells and 45 genes. The last dataset corresponds to an artificial dataset used as proof of concept and includes measurements of 2 synthetic genes and 244 cells that differentiate into three branches but the differentiation process includes a loop. Such a dataset could for example correspond to cellular reprogramming, or cells exiting the cell cycle, as also suggested by (Welch et al., 2016).
3.2 Comparison to other methods
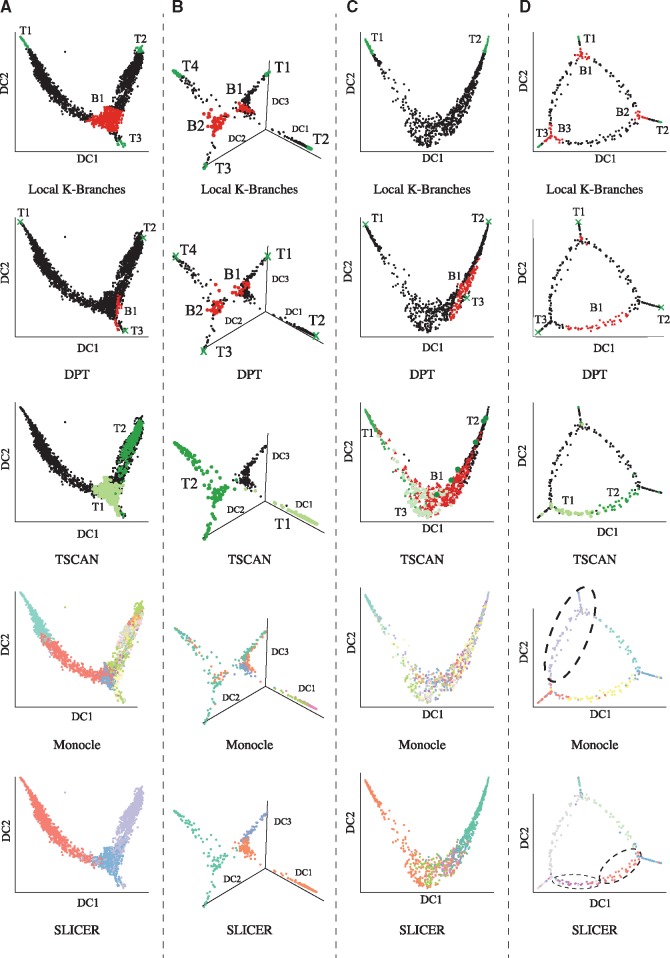
The purpose of local K-Branches is to identify branching and tip regions, while current popular methods assign cells to distinct branches. Local K-Branches is compared with DPT (Haghverdi et al., 2016) which in addition to assigning cells to distinct branches, also identifies tip cells and undecided cells in branching regions. One difference between DPT and the proposed method is that DPT only identifies one cell of each branch as the tip, while the proposed method typically identifies a region of tip cells. Although TSCAN does not directly identify branching and tip regions, it does construct a minimum spanning tree that connects the cluster centers. As a result, one could consider as tip, intermediate and branching clusters those clusters that are connected to one, two and more than two clusters in the minimum spanning tree. Monocle is similar to TSCAN. However, it connects single cells instead of cell-clusters on the minimum spanning tree. Consequently, extending monocle to identify tip and branching regions in a similar manner is not straightforward or statistically motivated. As such, Monocle (Trapnell et al., 2014) and SLICER (Welch et al., 2016) are only indirectly compared with the proposed method, in terms of estimating correct branching in the data. The results of applying the above methods on all datasets are presented in Figure 4. The proposed method was either performed on the first two or three DCs, depending on the morphology of the dataset. On the other hand, DPT always takes all available DCs into account. All other methods perform dimensionality reduction as part of their pre-processing and they are only visualized using diffusion maps. Additionally, the performance of local K-Branches when LLE (Roweis and Saul, 2000) is used for dimensionality reduction is presented in the Supplementary Figure S3. Finally, in the datasets where ground truth for the identification of tip cells is available, quantitative comparison of local K-Branches, DPT and TSCAN was performed, assessing their capability to identify tips cells in terms of precision and recall. Precision calculates the fraction of cells identified as tip-cells that actually correspond to true tip-cells. Recall calculates the fraction of true tip-cells selected by the method, over the total number of true tip-cells present in the dataset. Both scores range from zero to one, with one corresponding to a perfect score. Another quantitative comparison is performed on the basis of correct identification of the number of branching events present in the dataset. Quantitative results are summarized in Table 1.
Fig. 4.
Results local K-Branches, DPT, TSCAN, Monocle and SLICER on all datasets. (A) Single-cell RNA-Seq data of myeloid progenitors (Paul et al., 2015). Common myeloid progenitor (CMP) cells branch into MEPs and GMPs. (B) Single-cell qPCR data of mouse blastocyst development (Guo et al., 2010), where the initial population of 2-cell blastocyst differentiates into three different groups of 64-cell blastocysts, undergoing two distinct branching events. (C) Single-cell qPCR data of human monocytic leukemia (Kouno et al., 2013). In this dataset, THP-1 human myeloid monocytic leukemia cells differentate into macrophages and no branching event is present. (D) Artificial data of arbitrary geometry where three distinct tips are connected by a loop
Table 1.
Quantitative comparison of methods
| Dataset | Score | Local K-Branches | DPT | TSCAN |
|---|---|---|---|---|
| Paul et al.a | precision | 0.77 | 0.67 | 0.61 |
| recall | 0.04 | 0.001 | 0.24 | |
| correct branchingb | Yes | Yes | No | |
| Guo et al. | precision | 0.96 | 1.0 | 0.6 |
| recall | 0.36 | 0.02 | 0.89 | |
| correct branchingb | Yes | Yes | No | |
| Kouno et al. | precision | 0.77 | 1.0 | 0.47 |
| recall | 0.4 | 0.012 | 0.43 | |
| correct branchingb | Yes | No | No |
Quantifying tip recall is problematic since ground truth is based on thresholding of FACS markers and hence recalls too many cells.
The number of branching events was identified correctly.
3.2.1 Single-cell RNA-seq data of myeloid progenitors
When applied to the first two DCs of the single-cell RNA-Seq dataset of (Paul et al., 2015), the proposed method identifies three branch tips of fully differentiated cells, as well as one branching region. The regions identified by K-Branches are illustrated with respect to Fluorescence Activated Cell Sorting (FACS) labels in Figure 5. In order to perform a quantitative comparison, true tip-cells were considered cells belonging in the granulocyte/macrophage progenitor (GMP) and megakaryocyte/erythrocyte progenitor (MEP) gates of Figure 5. However, selecting tip cells in this manner is only approximately accurate. The results of DPT on the same data agree with the findings of local K-Branches. Two of the three tips identified by DPT are in the tip regions of local K-Branches, while the third tip of DPT is not inside but in the vicinity of the local K-Branches tip region. When comparing the branching region, the undecided cells of DPT are either inside or in close proximity to the branching region identified by local K-Branches. However, considerably fewer cells are considered as undecided by DPT. Additionally, TSCAN finds no branching and identifies two tip regions. Finally, Monocle overestimates, while SLICER underestimates the overall branching. According to the results in Table 1, local K-Branches is the most precise method, while TSCAN achieves better recall but fails to identify the branching event.
Fig. 5.
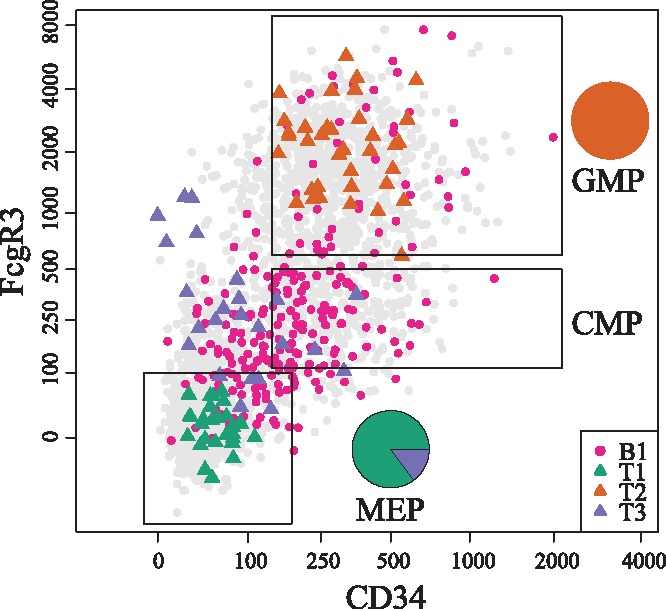
Cells plotted according to FACS-measured FcgR3 and CD34 protein expression values (Paul et al., 2015). The cells corresponding to regions B1, T1, T2, T3, as identified by local K-Branches, are highlighted. The MEP, granulocyte/macrophage progenitors and CMPs gates are also plotted. Pie-charts correspond to the distribution of T1, T2 and T3 cells in the MEP and GMP gates. The cells of branching region B1 are enriched only in the CMP gate (Fisher’s exact test P-value < ). The cells of tip T1 correspond to MEP, while the cells of tip T2 correspond to GMP. The cells of tip T3 correspond to outlier groups of dendritic cells and natural killer cells (lymphocytes)
3.2.2 Single-cell qPCR data of mouse blastocyst development
The proposed method was applied to the first three DCs of the single-cell qPCR data which contains two distinct branching events (Guo et al., 2010). Once more there is close agreement between the results of local K-Branches and DPT. Both methods identify four branch tips and the tip cells of DPT are in the tip regions of the proposed method. One key difference is that the proposed method automatically identified four branch tips and two branching regions, while DPT had to be manually executed twice on the data: First, three branches were identified, then DPT was performed on one of the branches, identifying the second branching region and new branch tips. On the other hand, TSCAN identifies two tips, one of which corresponds to a tip in the diffusion map trajectory, while it identifies no branching regions in the data. In order to perform quantitative comparisons, cells belonging to the 2- and 64-cell blastocysts were considered tip-cells. DPT is the most precise method achieving precision of 1, with local K-Branches being a close second with 0.96 precision. On the other hand, TSCAN achieves only 0.6 precision and fails to identify the branching events. However, it performs better in terms of recall, even though it does not identify any cells of the 2-cell stage tip (T1 of local K-Branches and DPT). Finally, Monocle identifes 5, while SLICER finds 3 clusters in the data.
3.2.3 Single-cell qPCR data of human monocytic leukemia cells
The third dataset contains measurements of 960 THP-1 human myeloid monocytic leukemia cells which undergo differentiation into macrophages and includes measurements along eight distinct timepoints (Kouno et al., 2013). In order to perform a quantitative comparison, we considered the cells belonging to the first and last timepoints as the two tip populations. In terms of pre-processing, one of the genes (KLF10) was removed, since it was only strongly expressed during the second timepoint and hindered the average performance of all methods as shown in the Supplementary Figure S4. Local K-Branches was performed on the first two DCs and identified two tips and no branching event. On the other hand, DPT and TSCAN identified three tips and a branching event. As such, local K-Branches is the only method that successfully does not identify branching in the data. On the other hand, all three tip-cells of DPT lie in tip regions and it achieves the highest precision of 1, followed by local K-Branches with 0.77 and TSCAN with 0.47. Finally, TSCAN achieves the greatest recall score of 0.43, followed closely by local K-Branches with 0.4 while DPT only achieves recall of 0.012. Monocle finds 23, while TSCAN identifies 5 clusters in the data.
3.2.4 Artificial data of arbitrary geometry
The final dataset highlights an important advantage of the proposed methodology. Namely, the identification branch tips and branching regions in datasets of arbitrary geometry. In this case, the dataset was manually generated to consist of three branches with a loop among them and the first two DCs retain the same geometry as the original dataset. Even though it could be directly applied to the original two-dimensional data, the proposed method was performed on the first two DCs. This was done for two reasons: First, for real data of high dimensions clustering and model selection will be performed on the DCs and we assume that dimensionality reduction through diffusion maps will also retain the loop structure of real data. Second, by using the DCs there are direct comparison to the performance of DPT. Despite the challenging geometry of the dataset, the proposed method correctly identifies the three regions corresponding to the branch tips, as well as the three branching regions. On the other hand, DPT correctly identifies the three tip cells but fails in identifying the branching regions. To be precise, it identifies one branching region correctly, but then it fails to find the other two and considers one irrelevant part of the loop as a branching region. Monocle underestimates the number of branching events, probably since it always assumes that the differentiation trajectory corresponds to a tree-like structure. Finally, SLICER overestimates the overall branching in the data, while TSCAN identifies two tips mostly lying in an intermediate region. An illustration of the performance of K-Branches on the same dataset for different levels of added noise is presented in the Supplementary Figure S5.
4 Conclusion and discussion
In this study, a model based clustering approach was introduced for the identification of regions of interest in single-cell data. First, a novel clustering method called K-Branches was introduced, which clusters data points into a set of K halflines with a common center. Subsequently, this clustering method was applied locally to the neighborhood of each cell and a modified version of the GAP statistic was developed to perform model selection. The goal of model selection is to identify the local dimensionality of the data. That is, identify fully differentiated tip cells and cells belonging to branching regions. In this manner, all branching events, as well as all end-points (tips) in differentiation trajectories can be identified. As demonstrated, this local view of the data allows the method to be successfully applied to challenging datasets that include sparsity and complex geometries.
The main idea of the proposed methodology is different from that of commonly used methods such as DPT, Monocle, Wishbone, SLICER or TSCAN. To be precise, these methods aim to assign each cell to a distinct branch in the differentiation process and also calculate pseudotime: an ordering of the cells, relevant to their distance from a starting root cell, which reflects how far they have progressed in the differentiation process. As such, K-Branches cannot be directly compared with most of these methods, perhaps with the exceptions of DPT and TSCAN. To be precise, DPT also identifies tip cells and branching regions of undecided cells, while TSCAN can be extended to search for tip, intermediate and branching clusters. The performance of the proposed method was compared with that of DPT and TSCAN in three single-cell datasets, as well as an artificial dataset. Local K-Branches achieved high precision and correctly identified the number (or absence) of branching events in all three single-cell datasets, while performing better than DPT in terms of recall. DPT was very precise and found the correct number of branching events in two of the three datasets, but since it only selects one cell per tip, it is poor in terms of recall. TSCAN was the least precise of all methods and did not identify the correct number of branching events in any dataset. However, it performed better than all other methods in terms of recall, in part since it selects a large number of cells. Moreover, in the dataset which consists of three branches with a loop in between, the local approach of the proposed methodology successfully identifies all tip and branching regions, while DPT only identifies the branch tips and TSCAN finds two tips in an intermediate region. Although this difference was observed on a synthetic dataset, real datasets containing loops could in theory correspond to cells exiting cell cycle, cells resulting in the same state through different differentiation trajectories, or cellular reprogramming (Bendall et al., 2014). One advantage of DPT is faster execution time since the entire dataset is typically processed in a few minutes. On the other hand, local K-Branches requires a few seconds per data point. However, in the case of local K-Branches each data point can be processed completely in parallel. TSCAN is also faster than local K-Branches but was less precise in the identification of tip-cells. To be fair, it was designed to solve a different problem and uses PCA for dimensionality reduction. PCA can be sufficient when the goal is to identify distinct cell-clusters, but has limited capabilities when it comes to learning continuous manifolds of differentiation trajectories which appear to be a necessity for the accurate identification of branching and tip regions. Finally, TSCAN utilizes a model-based approach to decide on the global number of clusters. In contrast, local K-Branches utilizes model selection to identify the dimensionality of the data in a local context.
In terms of future work, it would be interesting to extend the method to support explicit identification of the branches that lie between the branching and tip regions, which are currently only characterized as intermediate regions. Although clustering works in the original dimensions, model selection using the GAP statistic does not. As such, the proposed method utilizes diffusion maps for dimensionality reduction. Although LLE achieved similar results, it required tedious fine-tuning to produce satisfactory trajectories. Moreover, developing a different model selection method, other than the GAP statistic, that would allow the methodology to be directly applied in the original dimensions could be an additional topic of future work.
Supplementary Material
Acknowledgements
We would like to acknowledge L. Haghverdi for her helpful advice. We would like to thank M. Büttner for her comments and support on drawing biological conclusions. Finally, we would like to thank P. Angerer and D. S. Fischer for their comments on the R package and article, respectively.
Funding
N.K.C. is supported by a DFG Fellowship through the Graduate School of Quantitative Biosciences Munich (QBM). F.A.W. acknowledges support by the ‘Helmholtz Postdoc Programme’, Initiative and Networking Fund of the Helmholtz Association. F.J.T. acknowledges financial support by the German Science Foundation (SFB 1243 and Graduate School QBM) as well as by the Bavarian government (BioSysNet).
Conflict of Interest: none declared.
References
- Bendall S. et al. (2014) Single-cell trajectory detection uncovers progression and regulatory coordination in human b cell development. Cell, 157, 714–725. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Coifman R.R. et al. (2005) Geometric diffusions as a tool for harmonic analysis and structure definition of data: diffusion maps. Proc. Natl. Acad. Sci. USA, 102, 7426–7431. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Vargas Roditi L., Claassen M. (2015) Computational and experimental single cell biology techniques for the definition of cell type heterogeneity, interplay and intracellular dynamics. Curr. Opin. Biotechnol., 34, 9–15. Systems biology Nanobiotechnology. [DOI] [PubMed] [Google Scholar]
- Grün D., van Oudenaarden A. (2015) Design and analysis of single-cell sequencing experiments. Cell, 163, 799–810. [DOI] [PubMed] [Google Scholar]
- Guo G. et al. (2010) Resolution of cell fate decisions revealed by single-cell gene expression analysis from zygote to blastocyst. Develop. Cell, 18, 675–685. [DOI] [PubMed] [Google Scholar]
- Haghverdi L. et al. (2015) Diffusion maps for high-dimensional single-cell analysis of differentiation data. Bioinformatics, 31, 2989–2998. [DOI] [PubMed] [Google Scholar]
- Haghverdi L. et al. (2016) Diffusion pseudotime robustly reconstructs lineage branching. Nat. Methods, 13, 845–848. [DOI] [PubMed] [Google Scholar]
- Hastie T.J. et al. (2009) The Elements of Statistical Learning: data Mining, Inference, and Prediction. Springer series in statistics, Springer, New York. Autres impressions: 2011 (corr), 2013 (7e corr). [Google Scholar]
- Jaitin D.A. et al. (2014) Massively parallel single-cell rna-seq for marker-free decomposition of tissues into cell types. Science, 343, 776–779. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ji Z., Ji H. (2016) Tscan: pseudo-time reconstruction and evaluation in single-cell rna-seq analysis. Nucleic Acids Res., 44, e117.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kiselev V.Y. et al. (2017) Sc3 - consensus clustering of single-cell rna-seq data. Nat. Meth., 14, 483–486. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kouno T. et al. (2013) Temporal dynamics and transcriptional control using single-cell gene expression analysis. Genome Biol., 14, R118.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mahata B. et al. (2014) Single-cell rna sequencing reveals t helper cells synthesizing steroids de novo to contribute to immune homeostasis. Cell Rep., 7, 1130–1142. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mohajer M. et al. (2010) A comparison of gap statistic definitions with and without logarithm function. https://epub.ub.uni-muenchen.de/11920/.
- Moignard V. et al. (2015) Decoding the regulatory network of early blood development from single-cell gene expression measurements. Nat. Biotech., 33, 269–276. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paul F. et al. (2015) Transcriptional heterogeneity and lineage commitment in myeloid progenitors. Cell, 163, 1663–1677. [DOI] [PubMed] [Google Scholar]
- Proserpio V. et al. (2016) Single-cell analysis of cd4+ t-cell differentiation reveals three major cell states and progressive acceleration of proliferation. Genome Biol., 17, 1–15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roweis S.T., Saul L.K. (2000) Nonlinear dimensionality reduction by locally linear embedding. Science, 290, 2323–2326. [DOI] [PubMed] [Google Scholar]
- Setty M. et al. (2016) Wishbone identifies bifurcating developmental trajectories from single-cell data. Nat. Biotech., 34, 637–645. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stegle O. et al. (2015) Computational and analytical challenges in single-cell transcriptomics. Nat. Rev. Genet., 16, 133–145. [DOI] [PubMed] [Google Scholar]
- Theodoridis S., Koutroumbas K. (2008) Pattern Recognition, 4th edn., Academic Press, Burlington, MA. [Google Scholar]
- Tibshirani R. et al. (2001) Estimating the number of clusters in a data set via the gap statistic. J. R Stat. Soc. Ser. B (Stat. Methodol.), 63, 411–423. [Google Scholar]
- Trapnell C. et al. (2014) The dynamics and regulators of cell fate decisions are revealed by pseudotemporal ordering of single cells. Nat. Biotech., 32, 381–386. Research. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Waddington C.H. (1942) Canalization of development and the inheritance of acquired characters. Nature, 150, 563–565. [DOI] [PubMed] [Google Scholar]
- Waddington C.H. (1957) The Strategy of the Genes. A Discussion of Some Aspects of Theoretical Biology. With an appendix by Kacser H. Allen & Unwin, London. [Google Scholar]
- Welch J.D. et al. (2016) Slicer: inferring branched, nonlinear cellular trajectories from single cell rna-seq data. Genome Biol., 17, 106.. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.