GPU-powered model analysis with PySB/cupSODA

Abstract

Summary

A major barrier to the practical utilization of large, complex models of biochemical systems is the lack of open-source computational tools to evaluate model behaviors over high-dimensional parameter spaces. This is due to the high computational expense of performing thousands to millions of model simulations required for statistical analysis. To address this need, we have implemented a user-friendly interface between cupSODA, a GPU-powered kinetic simulator, and PySB, a Python-based modeling and simulation framework. For three example models of varying size, we show that for large numbers of simulations PySB/cupSODA achieves order-of-magnitude speedups relative to a CPU-based ordinary differential equation integrator.

Availability and implementation

The PySB/cupSODA interface has been integrated into the PySB modeling framework (version 1.4.0), which can be installed from the Python Package Index (PyPI) using a Python package manager such as pip. cupSODA source code and precompiled binaries (Linux, Mac OS/X, Windows) are available at github.com/aresio/cupSODA (requires an Nvidia GPU; developer.nvidia.com/cuda-gpus). Additional information about PySB is available at pysb.org.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

Kinetic modeling of complex biochemical systems is central to the emerging field of systems biology (Kitano, 2002; Le Novère, 2015). Kinetic models require definition of numerous free parameters, usually obtained by calibration to experimental data, that specify initial species concentrations and kinetic rate constants. Once calibrated, a model should be analyzed for its sensitivity and predictive power over ranges of parameter values (Fisher and Henzinger, 2007). Both model calibration and analysis can require thousands to millions of model simulations for statistical convergence and significance (Eydgahi et al., 2013; Gutenkunst et al., 2007). In many cases, the computational expense of simulation at this scale makes detailed model analysis infeasible.

Recently, efforts have been made to leverage the highly parallel structure of graphics processing units (GPUs) to accelerate scientific computations (Dematté and Prandi, 2010; Nobile et al., 2016). GPUs are well suited for applications in which the same arithmetic operations are applied to many independent data elements, e.g. solving independently parameterized systems of ordinary differential equations (ODEs). GPU-based kinetic simulators thus hold great promise for accelerating tasks such as model calibration and analysis, but are challenging for non-experts to use because they require specialized settings and inputs.

To address this problem, we have created a user-friendly interface between the GPU-based kinetic simulator cupSODA (Nobile et al., 2013, 2014) and PySB, a Python-based modeling and simulation platform (Lopez et al., 2013). cupSODA is built around the well-known adaptive stiff/non-stiff ODE integrator LSODA (Petzold, 1983). It is designed to perform thousands of parallel simulations, each independently parameterized, of mass-action kinetic models by leveraging the high-performance memories on the GPU, specifically the cached and non-mutable constant memory and the low-latency on-chip shared memory. PySB is a rule-based modeling (Chylek et al., 2014, 2015) platform for constructing and analyzing complex models of biochemical systems. Models can be constructed in native Python code or imported from various formats, including the Systems Biology Markup Language (SBML) (Hucka et al., 2003). PySB leverages powerful libraries within the Python ecosystem, such as NumPy, SymPy and SciPy (Perez et al., 2011), and provides user-friendly interfaces to numerous third-party simulation and analysis tools, including BioNetGen (Faeder et al., 2009; Harris et al., 2016), KaSim (Suderman and Deeds, 2013) and StochKit (Sanft et al., 2011).

Below, we briefly describe the main features of the PySB/cupSODA interface and showcase its utility by performing run time and sensitivity analyses for three model systems of varying size (Table 1).

Table 1.

Models used for PySB/cupSODA performance testing

Model	Species	Reactions	End time	Output steps
Cell cyclea	5	7	100	100
Ras/cAMP/PKAb	33	39	1500	100
EARMc	77	105	20 000	100

^aTyson (1991).

^bBesozzi et al. (2012).

^cLopez et al. (2013).

2 Features and implementation

cupSODA is designed to exploit the massive parallelism of the CUDA architecture (Nickolls et al., 2008). To run simulations with cupSODA, one must construct multiple input files containing, e.g. the reaction stoichiometries and the initial species concentrations and rate parameter values for each specified simulation. Numerous simulator-specific parameters must also be defined, such as the number of CUDA ‘blocks’ to use and the desired cupSODA memory configuration (see Supplementary Information). The number of simulations that cupSODA can run in parallel is limited by the number of CUDA ‘cores’ on the GPU (usually a few thousand; see Supplementary Table S1), but the number of simulations that can be loaded onto the GPU at one time is usually many more than this, limited by the available memory (Nobile et al., 2013, 2014).

The PySB/cupSODA interface simplifies and streamlines the use of cupSODA via a CupSodaSimulator class, available within the PySB package. The class constructor accepts the following arguments:

• model: A PySB model object (required)

• tspan: A list of output time points (default: None)

• initials: A list or dictionary of initial species concentrations for each simulation (default: None)

• param_values: A list or dictionary of rate parameter values for each simulation (default: None)

• verbose: Verbose output (default: False)

The CupSodaSimulator constructor also recognizes numerous keyword arguments (kwargs), such as n_blocks, the number of CUDA blocks and memory_usage, the desired memory configuration. Importantly, default values are defined for each kwarg, removing the need for user input. For example, if a user-defined value is not provided, the number of CUDA blocks is automatically calculated by querying the specifications of the GPU in use.

The CupSodaSimulator.run() method performs the simulations by constructing the cupSODA input files and invoking cupSODA as a subprocess (the method takes tspan, initials and param_values as optional arguments). Additionally, the method reads into a three-dimensional array the results of the simulations (species time courses), which cupSODA outputs to (typically thousands of) separate text files. The user then has the ability to analyze and/or visualize the results using tools available within the Python ecosystem, e.g. plotting the time courses using the Matplotlib library (Perez et al., 2011). For convenience, a run_cupSODA wrapper function has also been implemented that combines invocations of the CupSodaSimulator constructor and run method into a single step. A workflow diagram and example Python script using the run_cupSODA function are provided in Supplementary Figures S1 and S2, respectively.

3 Results

In Figure 1A–C and Supplementary Figure S3, we compare the run time efficiency of PySB/cupSODA to the CPU-bound ODE integrator LSODA, available in the Python package SciPy (Oliphant, 2007), for three example models listed in Table 1 (see Supplementary Information for descriptions). These include models of the eukaryotic cell cycle (Tyson, 1991), the Ras/cAMP/PKA signaling pathway in Saccharomyces cerevisiae (Besozzi et al., 2012), and extrinsically induced apoptosis in mammalian cells (EARM: extrinsic apoptosis reaction model) (Lopez et al., 2013). Run time comparisons show that in all cases SciPy/LSODA is faster for small numbers of simulations but PySB/cupSODA overtakes it for large numbers of simulations, achieving a maximum speedup of approximately one order of magnitude. Comparable speedups are achieved for other memory settings and GPUs (Supplementary Information and Supplementary Figs S4 and S5).

Fig. 1.

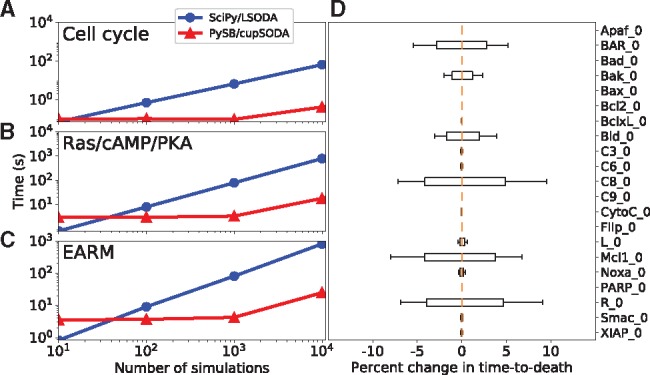
(A–C) Run time comparisons between PySB/cupSODA and SciPy/LSODA for the example models in Table 1 (all simulations performed with the same initial protein concentrations and rate parameters). (D) Sensitivity in time-to-death in EARM to variations (±20%; 25 410 total simulations) in the initial protein concentrations (gold lines are medians; boxes range from the first to third quartile; whiskers extend to the minimum and maximum values). PySB/cupSODA simulations were run using cupSODA 1.0.0 on a GeForce GTX 980 Ti GPU (2816 cores, 16 threads/block); SciPy/LSODA simulations were run on an Intel Xeon E5-2667 v3 @ 3.20 GHz CPU (see Supplementary Table S1)

For each model in Table 1, we also performed sensitivity analyses (Fig. 1D and Supplementary Figs S6–S12) by quantifying changes in defined model outputs to variations (±20%) in initial protein concentrations around a set of reference values (Supplementary Tables S2–S4; see Supplementary Information for further details). The ability to efficiently perform such analyses is critical since non-genetic variability within isogenic cell populations has been attributed to significant variations in protein concentrations across cells (Spencer et al., 2009). In Figure 1D and Supplementary Figure S11, we analyze the sensitivity in ‘time-to-death’ in EARM (defined as the time at which Smac reaches 50% cleavage; see Supplementary Information and Supplementary Fig. S10) for a specific set of rate parameters. Our results show that time-to-death is sensitive to the initial levels of six of the 21 proteins considered. Of particular interest is the sensitivity to Bak. The same analysis performed for a different set of rate parameters (Supplementary Fig. S12) shows insensitivity to Bak but sensitivity to Bax. This indicates that the model harbors at least two alternative pathways to apoptosis induction. The analysis comprised 25 410 total simulations and took ∼11 min with PySB/cupSODA and ∼35 min with SciPy/LSODA (for both parameter sets). Similar accelerations were seen for the cell cycle and Ras/cAMP/PKA models (Supplementary Information).

4 Conclusion

The PySB/cupSODA interface provides the modeling community with a high-performance GPU-based kinetic simulator, that can run thousands of parallel simulations on a common desktop workstation, within the easy-to-use framework of a full-fledged, open-source programming and analysis environment in Python. This will greatly accelerate and streamline the process of analyzing complex biochemical models for systems biology applications.