IntegratedMRF: random forest-based framework for integrating prediction from different data types

Abstract

Summary

IntegratedMRF is an open-source R implementation for integrating drug response predictions from various genomic characterizations using univariate or multivariate random forests that includes various options for error estimation techniques. The integrated framework was developed following superior performance of random forest based methods in NCI-DREAM drug sensitivity prediction challenge. The computational framework can be applied to estimate mean and confidence interval of drug response prediction errors based on ensemble approaches with various combinations of genetic and epigenetic characterizations as inputs. The multivariate random forest implementation included in the package incorporates the correlations between output responses in the modeling and has been shown to perform better than existing approaches when the drug responses are correlated. Detailed analysis of the provided features is included in the Supplementary Material.

Availability and Implementation

The framework has been implemented as a R package IntegratedMRF, which can be downloaded from https://cran.r-project.org/web/packages/IntegratedMRF/index.html, where further explanation of the package is available.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

A primary objective of precision medicine for cancer is the selection of an anti-cancer drug or drug combination that is most effective for the individual patient (Garnett and et al., 2012). A diverse set of regression models such as linear regression with regularization, non-linear regression, kernel based techniques and ensemble based approaches have been applied to the problem of drug response prediction from genetic characterizations for enabling personalized cancer therapy. The NCI-DREAM drug sensitivity prediction challenge was a crowd sourced initiative to apply a diverse set of prediction models on the same set of heterogeneous genetic characterization training data to evaluate model performance on holdout datasets (Costello and et al., 2014). The current computational framework development was motivated by the second best performance of random forest based approach in the NCI-DREAM challenge among more than 40 different submissions (Wan and Pal, 2014). Individual predictions from each genetic or epigenetic characterization dataset such as RNAseq, Protein expression or methylation based on Random Forests were combined using a linear regression model to arrive at combined predictions. We have considered further enhancements to the framework by (i) considering Multivariate Random Forests (Segal and Xiao, 2011) that improves prediction accuracy by incorporating the correlation between output responses, (ii) analyzing different error estimation techniques as the estimated error can be significantly different from the true or validation error for small sample scenarios. This application note describes the IntegratedMRF package that has been implemented in R and C ++. The package provides various functionalities to implement an integrated prediction from different data subtypes using either univariate or multivariate Random Forests along with options for different error estimation techniques to select the weights for generating the integrated model from individual predictions.

2 Methods and results

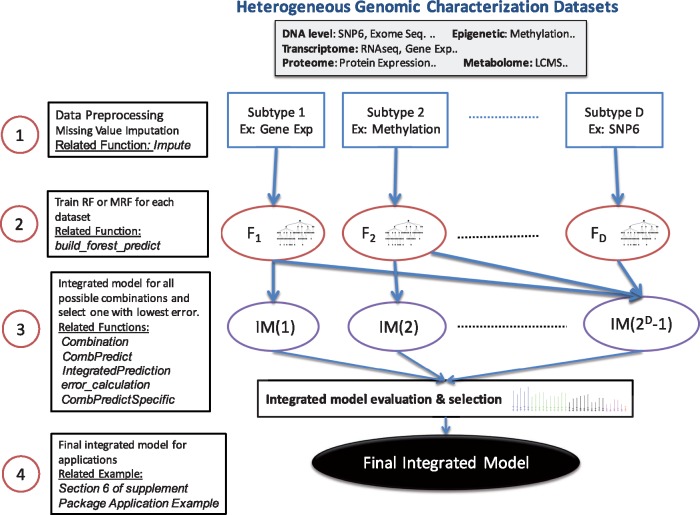
A conceptual overview of the computational framework is illustrated in Figure 1. For each individual genomic characterization (such as Gene Expression, Methylation, Exome Sequence, RPPA or SNP6 (CNV) denoted by Subtypes 1 to D in Fig. 1), a Random Forest (RF) or Multivariate Random Forest (MRF) model is estimated using the training samples. For generating integrated model predictions for all possible data subtype combinations, a specific error estimation method (such as Leave-one-out, N-fold Cross Validation, Bootstrap or 0.632+ Bootstrap) is applied to generate weights for individual predictions using least square regression. The integrated model that provides the minimum mean absolute prediction error is selected for predicting the testing samples.

Fig. 1.

Overview of Integrated Prediction Methodology

Algorithms: The IntegratedMRF package provides various options for design of integrated ensemble predictive models, each with the following significant features:

Model Inference: The package provides options for estimation of regular RF or MRF as the predictive modeling approach. If the number of output responses is greater than 1, the default selection is MRF whereas for a single output response, a RF model is generated. The suitability of MRF for prediction as compared to RF is discussed in next section. We have observed that MRF provides higher accuracy than RF when the output responses are correlated as observed through common targets in the drugs.

Error Estimation techniques: We provide options for Leave-one-out, n-fold cross validation, Bootstrap and 0.632+ Bootstrap (Bradley Efron, 1997) error estimation approaches to estimate the true error of a designed model. Bootstrap error estimates can sometimes be upward biased (estimate higher than true error) and 0.632+ Bootstrap attempts to correct that bias by linearly combining the high biased Bootstrap estimate with low biased training error estimate. The detailed descriptions of the error estimation techniques are included in the Supplementary Section 2. Among the considered error estimation approaches, leave-one-out appears closer to validation error for smaller samples based on DREAM challenge results described in next section. For larger sample sizes, it is preferable to use n-fold CV or Bootstrap (details included in the Supplementary Section 5.3). We recommend the use of Leave-one-out error estimation for small sample scenarios (such as DREAM challenge dataset with 35 samples; Costello and et al., 2014) and the application of n-fold CV or Bootstrap for larger datasets (such as 400 sample dataset of CCLE; Barretina and et al., 2012).

Integrated Model: IntegratedMRF provides an option for applying linear least square regression on predictions from models trained on different data types to estimate the weights for combining the model predictions. Based on the selected error estimation approach, the training and testing datasets are created. The training samples are used to estimate the individual model parameters along with the integrated model regression coefficients. The testing samples are used to evaluate the performance of each integrated model in terms of mean absolute prediction error. Note that for D different genetic or epigenetic characterizations, there will be $2^D-1$ integrated model combinations. The alternative possibilities of concatenating all features before generating a single RF or MRF model or applying feature selection before model generation is compared to our current approach in the Supplementary Section 5.2. Results indicate that it is better to generate individual predictive models for each dataset and then combine them to form an integrated model rather than designing a single model from a concatenated dataset.

2.1 Performance

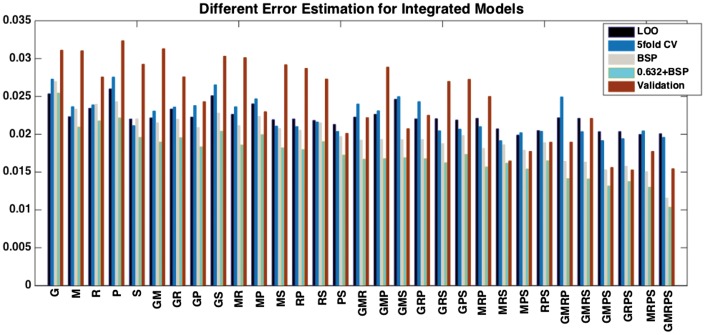
Error estimation and integrated model performance: The computational framework presented here has been utilized to analyze drug response prediction from NCI-DREAM drug sensitivity prediction challenge (Costello and et al., 2014) and Cancer Cell Line Encyclopedia (CCLE) (Barretina and et al., 2012) datasets. The model training and error estimates are based on 35 samples of the DREAM challenge dataset whereas the validation or true error of an inferred model is estimated based on a separate set of 18 hold-out samples. Figure 2 displays the different error estimates (Leave One Out, 5-fold CV, Bootstrap, 0.632 + Bootstrap) and validation error in terms of Mean Absolute Error for drug 3 from NCI Dream Challenge Dataset for 31 ($2^5-1$) different Integrated Models. Figure 2 shows that different error estimates can have variations but the overall trend of the error estimates along with validation error shows a reduction in prediction error with addition of more datasets. We also observe that LOO followed by 5fold CV and BSP provides the closest estimate of the true error. Similar behavior is observed for another scenario (drug 1) as reported in the Supplementary Section 5.1.

Fig. 2.

Multiple Mean Absolute Error estimates (LOO: Leave one out, 5foldCV: 5 fold cross validation, BSP: Bootstrap, 0.632 + BSP: 0.632 + Bootstrap) and mean absolute validation error for drug 3 from NCI Dream Challenge Dataset for 31 ($2^5-1$) different data subtype Integrated Models. The datasets are denoted by: G: Gene Expression, M: Methylation, R: RNASeq, P: RPPA and S: SNP6

We have also compared the various error estimation techniques to validation error for CCLE dataset where 100 random samples out of around 500 samples were used for model generation and error estimations. The remaining hold-out set of around 400 samples were used to estimate the true error or validation error. The results reported in the Supplementary Section 5.3 support the earlier hypothesis of LOO followed by 5-fold CV and BSP provides the closest estimate of the true error. Comparing Figure 2 and Supplementary Figure S6, we observe that the difference between validation error and the error estimates reduces when the initial set of training samples is increased from 35 to 100.

Comparison of MRF with other approaches: In this section, we compare the prediction performance of Multivariate Random Forest (MRF) to Random Forest (RF) (Wan and Pal, 2014), Elastic Net (EN) (Barretina and et al., 2012) and Kernelized Bayesian Multi Task Learning (KBMTL) (Gonen and Margolin, 2014) approaches using Genomics of Drug Sensitivity in Cancer (GDSC) gene expression dataset (Yang, 2013). Table 1 shows the 5-fold cross validation performance in terms of correlation coefficient between predicted and actual responses on GDSC dataset for MRF, RF, EN and KBMTL approaches for four sets of drugs (S₁, S₂ and S₃ are the pairs with the highest correlations among training responses while S₄ is the pair with the lowest correlation). Table 1 shows that MRF outperforms RF, EN and KBMTL for S1, S2 & S3 drug sets whereas RF outperforms MRF for S4 drug set.

Table 1.

Fivefold Cross validation results for GDSC dataset response prediction for four drug sets (S₁, S₂ and S₃ sets consists of highly correlated responses whereas the set of S₄ has low correlated responses)

			Correlation coefficients
Drug set	Correlation	Drug name	EN	KBMTL	RF	MRF
	among responses
S1	0.8439	RDEA119	0.62	0.57	0.63	0.66
		PD-0325901	0.48	0.47	0.61	0.63
S2	0.8410	BI-2536	0.23	0.23	0.26	0.28
		GW843682X	0.30	0.28	0.31	0.33
S3	0.8366	CI-1040	0.46	0.51	0.59	0.60
		PD-0325901	0.50	0.52	0.62	0.65
S4	6.59e-7	Axitinib	0.31	0.33	0.36	0.32
		Mitomycin C	0.28	0.25	0.37	0.38

Correlation coefficients between actual and predicted drug responses using Elastic Net (EN), Kernelized Bayesian multitask learning (KBMTL), Random Forest (RF) and Multivariate Random Forest (MRF) are reported. The parameters for EN and KBMTL were same as the parameters used by earlier drug sensitivity prediction studies of Barretina and et al. (2012) and Gonen and Margolin (2014) respectively.

We have also compared MRF to RF approach using other drug pairs of GDSC, DREAM challenge and CCLE datasets that are reported in the Supplementary Tables S2 and S4–S7. Similar to GDSC scenario, we observed MRF outperforms RF when the drug responses are correlated (Supplementary Tables S2, S5 and S6) and RF outperforms MRF when drug responses are not correlated (Supplementary Tables S4 and S7). Note that, we expect that drug responses will be correlated when they share common primary targets and the use of MRF will likely be advantageous in such scenarios.

3 Conclusions

The presented computational framework provides the following enhanced features of: (i) generation of multivariate random forests that incorporates dependencies in output responses which has been shown to outperform existing approaches for correlated drug responses, (ii) application of multiple error estimation approaches and (iii) integration of predictions from different genetic characterizations that results in a decrease in average error estimates and validation error with additional datasets.