IGESS: a statistical approach to integrating individual-level genotype data and summary statistics in genome-wide association studies

Abstract

Motivation: Results from genome-wide association studies (GWAS) suggest that a complex phenotype is often affected by many variants with small effects, known as ‘polygenicity’. Tens of thousands of samples are often required to ensure statistical power of identifying these variants with small effects. However, it is often the case that a research group can only get approval for the access to individual-level genotype data with a limited sample size (e.g. a few hundreds or thousands). Meanwhile, summary statistics generated using single-variant-based analysis are becoming publicly available. The sample sizes associated with the summary statistics datasets are usually quite large. How to make the most efficient use of existing abundant data resources largely remains an open question.

Results: In this study, we propose a statistical approach, IGESS, to increasing statistical power of identifying risk variants and improving accuracy of risk prediction by integrating individual level genotype data and summary statistics. An efficient algorithm based on variational inference is developed to handle the genome-wide analysis. Through comprehensive simulation studies, we demonstrated the advantages of IGESS over the methods which take either individual-level data or summary statistics data as input. We applied IGESS to perform integrative analysis of Crohns Disease from WTCCC and summary statistics from other studies. IGESS was able to significantly increase the statistical power of identifying risk variants and improve the risk prediction accuracy from 63.2% ($\pm 0.4\%$) to 69.4% ($\pm 0.1\%$) using about 240 000 variants.

Availability and implementation: The IGESS software is available at https://github.com/daviddaigithub/IGESS.

Contact: zbxu@xjtu.edu.cn or xwan@comp.hkbu.edu.hk or eeyang@hkbu.edu.hk

Supplementary information: Supplementary data are available at Bioinformatics online.

1 Introduction

As of October 2016, more than 29 000 single-nucleotide polymorphisms (SNPs) have been reported to be significantly (P-value $\le 5.0\times {10}^{-8}$) associated with complex human phenotypes (including quantitative traits and complex diseases) in about 2600 GWAS (see the GWAS Catalog database https://www.ebi.ac.uk/gwas/) (Welter et al., 2014). However, these genome-wide significant hits can only explain a small proportion of genetic contribution to complex human phenotypes. For example, 70–80% of variance of human height can be attributed to genetic variations (i.e. heritability of human height is about 70–80%) (Visscher et al., 2008) while the GWAS hits of human height can only explain about 10% of the variance (Allen et al., 2010, Wood et al., 2014). This is the so-called ‘missing heritability’ problem (Manolio et al., 2009). Recent progresses suggested that most of the heritability is not missing but can be explained by many common SNPs with individually weak effects (Visscher et al., 2012; Yang et al., 2010). However, due to limited sample sizes, genetic variants with small effects do not achieve the genome-wide statistical significance and thus the majority of them remain undiscovered yet. Recently, world-wide researchers are forming large genomic consortia, such as the Genetic Investigation of ANthropometric Traits (GIANT) Consortium and the Wellcome Trust Case Control Consortium (WTCCC), to collect samples and analyze data.

Numerous GWAS data analysis methods (e.g. PLINK (Purcell et al., 2007), BOOST (Wan et al., 2010) and GCTA (Yang et al., 2011)) have recently been proposed. A detailed survey of these tools can be found in Stephens and Balding (2009), Cantor et al. (2010) and Pasaniuc and Price (2016). These methods could be roughly divided into two categories: (i) individual-level data analysis and (ii) summary data (mostly P-values or z-scores) analysis. Some popular methods in the first category include penalized regression methods (Liu et al., 2013; Wu et al., 2009) and Bayesian regression methods (Carbonetto et al., 2012; Zhou et al., 2013). It is noteworthy that linear mixed models (LMM) are gaining increasing interest in genomic data analysis. Some popular LMM-based approaches include GEMMA (Zhou and Stephens, 2012) and SKAT (Ionita-Laza et al., 2013). In the absence of individual-level data, methods in the second category play the major role. GSEA (Zhang et al., 2010) and VEGAS (Liu et al., 2010) are the two well-known methods in this category. Some recent approaches including CPASSOC (Zhu et al., 2015), GPA (Chung et al., 2014), EPS (Liu et al., 2016) and LD-score regression (Bulik-Sullivan et al., 2015), are able to incorporate functional data, such as DNase I hypersensitive site (DHS) data and expression quantitative trait loci (eQTL) data. Compared with the methods in the first category, the methods in the second category often have computational advantages but may be statistically less efficient because only summary statistics are used.

It may be more preferable for researchers to work with the individual-level data as it retains more information than summary statistics data. However, it is often hard for a research group to get fully access to the individual-level data of large sample sizes. For instance, a core research group from the GIANT consortium reported that they could only access genotype data from about 44 000 individuals (Yang et al., 2015) while the total sample size is more than 250 000 for the consortium (Wood et al., 2014). In reality, access to individual-level data is often quite restricted due to practical issues, such as privacy protection issue and logistics in data transportation and storage. On the contrary, summary statistics from GWAS are widely available through many public gateways. Therefore, it is very typical for a research group to get access to summary statistics from hundreds of GWAS with a large sample size freely, but only have limited sample size of individual-level data (usually a few hundreds or thousands of samples at hand). A simple strategy in this situation is to first obtain summary statistics from individual-level data and then conduct some meta-analyses with the collected summary data. But this strategy does not fully make use of the individual-level data, leading to inefficient use of data at hand. How to make the most efficient use of existing data resources to pinpoint disease-associated genetic variants with small effects is of great interest.

In this study, we propose a statistical approach, IGESS, to integrating individual level genotype data and summary statistics for exploration of genetic architechture of complex phenotypes. An efficient algorithm based on variational inference has been developed such that it is scale up to genome-wide analysis. Not only does IGESS provide the posterior probability of association status between each SNP and the given phenotype, but also offer the effect size of each SNP for risk prediction. We conducted comprehensive simulation studies to evaluate the performance of IGESS and then applied it to Crohn’s disease (CD). The results demonstrate that IGESS is able to integrate different types of data, gaining increased power in identification of risk variants and improved accuracy of risk prediction.

2 IGESS

2.1 Model

Given a phenotype, suppose we have an individual-level GWAS dataset $\{\mathbf{y},\mathbf{X}\}$ of N samples, where $\mathbf{y}\in {ℝ}^N$ is the vector of phenotypic values and $\mathbf{X}\in {ℝ}^{N\times M}$ is the genotype matrix of M SNPs from these samples. Without loss of generality, we assume both $\mathbf{X}$ and $\mathbf{y}$ have been centered. In addition, we collect summary statistics, i.e. P-values for this phenotype from K independent GWAS in matrix $\mathbf{P}=[p_{jk}]\in {ℝ}^{M\times K}$, where p_jk corresponds to the P-value of the jth SNP in the kth GWAS. First, we consider the following linear model that links $\mathbf{y}$ to $\mathbf{X}$,

$$\mathbf{y}=\mathbf{X}\mathit{\beta }+\mathbf{e},$$ (1)

where $\mathit{\beta }={[{\beta }_1,\dots ,{\beta }_M]}^T$ is a vector of effect sizes, and $\mathbf{e}\sim N(0,{\sigma }_e^2\mathbf{I})$ is an independent noise term due to non-genetic factors. Under this model, identification of risk variants is equivalent to identifying nonzero entries in $\mathit{\beta }$. For this purpose, we introduce a binary variable γ_j to indicate whether β_j is zero or not. Assuming the spike and slab prior (Mitchell and Beauchamp, 1988) for β_j, we have

$$\begin{array}{c}{\beta }_j|{\gamma }_j;{\sigma }_{\beta }^2\sim \{\begin{array}{cccc}\hfill & N\left({\beta }_j\right|0,{\sigma }_{\beta }^2)\hfill & \hfill & \text{if} {\gamma }_j=1,\hfill \\ \hfill & {\delta }_0\left({\beta }_j\right)\hfill & \hfill & \text{if} {\gamma }_j=0,\hfill \end{array}\hfill \end{array}$$ (2)

where $N\left({\beta }_j\right|0,{\sigma }_{\beta }^2)$ denotes the Gaussian distribution with mean 0 and variance ${\sigma }_{\beta }^2$ and ${\delta }_0\left({\beta }_j\right)$ is the Dirac function centered at zero, and γ_j is assumed to be drawn from the Bernoulli distribution $\text{Bern}\left({\gamma }_j\right|\pi )$,

$${\gamma }_j|\pi \sim {\pi }^{{\gamma }_j}{(1-\pi )}^{1-{\gamma }_j}.$$ (3)

To incorporate information from summary statistics, we also consider a two-groups model, i.e. the P-values of each study are assumed to come from the mixture of null and non-null groups. Since we are considering the same phenotype across multiple studies, it is reasonable to assume the vector of association status $\mathit{\gamma }$ is the same in these studies. This gives us the following model: The obtained P-values from the kth GWAS are assumed to come from a mixture distribution

$$\begin{array}{c}{p}_{jk}|{\gamma }_j;{\alpha }_k\sim \{\begin{array}{cccc}\hfill & \mathrm{U}(0,1)\hfill & \hfill & \text{if} {\gamma }_j=0,\hfill \\ \hfill & \text{Beta}\left(p_{jk}\right|{\alpha }_k,1)\hfill & \hfill & \text{if} {\gamma }_j=1,\hfill \end{array}\hfill \end{array}$$ (4)

where P-values from the null group follow the uniform distribution $\mathrm{U}(0,1)$, and P-values of the kth study from the non-null group follow a beta distribution with parameter $({\alpha }_k,1)$, which captures the pattern that P-values from the non-null group is closer to zero. Comprehensive experiment results provided in the Supplementary Document demonstrate that the beta distribution is a good approximation of the P-value distribution under the alternative. Given γ_j, we assume $p_{j1},\dots ,p_{jK}$ are independent. Thus, we have

$$\text{Pr}\left(\mathbf{P}\right|\mathit{\gamma })=\prod _{j=1}^M{\left(\prod _{k=1}^K{\alpha }_k{p}_{jk}^{{\alpha }_k-1}\right)}^{{\gamma }_j}.$$ (5)

Let $\mathit{\theta }=\{\pi ,{\sigma }_{\beta }^2,{\sigma }_e^2,{\alpha }_k,k=1\dots K\}$ be the collection of model parameters. The probabilistic model can be written as

$$\text{Pr}(\mathbf{y},\mathbf{P},\mathit{\beta },\mathit{\gamma }|\mathbf{X};\mathit{\theta })=\text{Pr}(\mathbf{y}|\mathbf{X},\mathit{\beta };\mathit{\theta })\text{Pr}\left(\mathit{\beta }\right|\mathit{\gamma };\mathit{\theta }\left)\text{Pr}\right(\mathit{\gamma }\left|\mathit{\theta }\right)\text{Pr}\left(\mathbf{P}\right|\mathit{\gamma };\mathit{\theta }).$$ (6)

Our goal is to first obtain $\widehat{\mathit{\theta }}$ (the estimate of $\mathit{\theta }$) by maximizing the marginal likelihood (known as type II maximum likelihood estimate or Empirical Bayes estimate)

$$\text{Pr}(\mathbf{y},\mathbf{P}|\mathbf{X};\mathit{\theta })=\sum _{\gamma }{\int }_{\mathit{\beta }}\text{Pr}(\mathbf{y},\mathbf{P},\mathit{\beta },\mathit{\gamma }|\mathbf{X};\mathit{\theta })d\mathit{\beta },$$ (7)

and then compute the posterior

$$\text{Pr}(\mathit{\beta },\mathit{\gamma }|\mathbf{y},\mathbf{X},\mathbf{P};\widehat{\mathit{\theta }})=\frac{\text{Pr}(\mathbf{y},\mathbf{P},\mathit{\beta },\mathit{\gamma }|\mathbf{X};\widehat{\mathit{\theta }})}{\text{Pr}(\mathbf{y},\mathbf{P}|\mathbf{X};\widehat{\mathit{\theta }})}.$$ (8)

The above IGESS model was developed with quantitative traits following a Gaussian distribution. Although it can be extended to handle case-control studies using the logit or probit link function, the performance has very minor difference from the Gaussian assumption as long as the sample size is moderate (e.g. a few hundreds) but the computational cost is much more expensive. In fact, direct application of linear models to the analysis of case-control GWAS datasets has been justified in Kang et al. (2010). Therefore, we focus on the Gaussian assumption in this paper. Results from both simulation study and real data analysis suggest that linear models (Gaussian assumption) can often provide satisfactory performance on risk variant identification and risk prediction in case-control studies when the population structure is not very complex (see comprehensive results in the Supplementary Document).

2.2 Algorithm

The challenge is that the exact evaluation of (7) is intractable. To overcome this difficulty, we derive an efficient algorithm based on variational inference (Bishop, 2006). Before we describe the algorithm, we first reparameterize our model to get rid of the Dirac function such that we can have an easier derivation. Let ${\tilde{\beta }}_j$ be a Gaussian variable with $N\left({\tilde{\beta }}_j\right|0,{\sigma }_{\beta }^2)$, and γ_j be a Bernoulli variable with $\text{Bern}\left({\gamma }_j\right|\pi )$, respectively. Their product ${\tilde{\beta }}_j{\gamma }_j$ has the exact the same distribution as β_j in (2). With this reparameterization, the joint model (6) becomes

$$\text{Pr}(\mathbf{y},\mathbf{P},\tilde{\mathit{\beta }},\mathit{\gamma }|\mathbf{X};\mathit{\theta })=\text{Pr}(\mathbf{y}|\mathbf{X},\tilde{\mathit{\beta }},\mathit{\gamma };\mathit{\theta })\text{Pr}(\tilde{\mathit{\beta }};\mathit{\theta })\text{Pr}\left(\mathit{\gamma }\right|\mathit{\theta }\left)\text{Pr}\right(\mathbf{P}|\mathit{\gamma };\mathit{\theta }),$$ (9)

where

$$\begin{array}{l}\text{Pr}\left(\mathbf{y}\right|\mathbf{X},\tilde{\mathit{\beta }},\mathit{\gamma };\mathit{\theta })=N(\mathbf{y}|\sum _j{\mathbf{x}}_j{\tilde{\beta }}_j{\gamma }_j,{\sigma }_e^2\mathbf{I}),\hfill \\ \text{Pr}(\tilde{\mathit{\beta }};\mathit{\theta })=\prod _j^{M}N\left({\tilde{\beta }}_j\right|0,{\sigma }_{\beta }^2),\hfill \\ \text{Pr}\left(\mathit{\gamma }\right|\mathit{\theta })=\prod _j^M{\pi }^{{\gamma }_j}{(1-\pi )}^{1-{\gamma }_j},\hfill \\ \text{Pr}\left(\mathbf{P}\right|\mathit{\gamma };\mathit{\theta })=\prod _j^M(\prod _k^K{\alpha }_k{p}_{jk}^{{\alpha }_k-1}{)}^{{\gamma }_j}.\hfill \end{array}$$ (10)

Clearly, the Dirac function is not involved and the prior of ${\tilde{\beta }}_j$ does not depend on γ_j anymore. Next, we apply variational approximation to $\text{Pr}(\mathbf{y},\mathbf{P},\tilde{\mathit{\beta }},\mathit{\gamma }|\mathbf{X};\mathit{\theta })$. Let $q(\tilde{\mathit{\beta }},\mathit{\gamma })$ be an approximated distribution of the posterior $\text{Pr}(\tilde{\mathit{\beta }},\mathit{\gamma }|\mathbf{y},\mathbf{X},\mathbf{P};\mathit{\theta })$. Then we have a lower bound of the logarithm of the marginal likelihood

$$\begin{array}{c}\hspace{0.17em}\text{log}\hspace{0.17em}\text{Pr}(\mathbf{y},\mathbf{P}|\mathbf{X};\mathit{\theta })\hfill \\ =\hspace{0.17em}\text{log}\hspace{0.17em}\sum _{\mathit{\gamma }}{\int }_{\tilde{\mathit{\beta }}}\text{Pr}(\mathbf{y},\mathbf{P},\tilde{\mathit{\beta }},\mathit{\gamma }|\mathit{\theta })d\tilde{\mathit{\beta }}\hfill \\ \ge \sum _{\mathit{\gamma }}{\int }_{\tilde{\mathit{\beta }}}q(\tilde{\mathit{\beta }},\mathit{\gamma })\hspace{0.17em}\text{log}\hspace{0.17em}\frac{\text{Pr}(\mathbf{y},\mathbf{P},\tilde{\mathit{\beta }},\mathit{\gamma }|\mathbf{X};\mathit{\theta })}{q(\tilde{\mathit{\beta }},\mathit{\gamma })}d\tilde{\mathit{\beta }}\hfill \\ ={\mathbb{E}}_q[\text{log}\hspace{0.17em}\text{Pr}(\mathbf{y},\mathbf{P},\tilde{\mathit{\beta }},\mathit{\gamma }|\mathbf{X};\mathit{\theta })-\text{log}\hspace{0.17em}q(\tilde{\mathit{\beta }},\mathit{\gamma })]\hfill \\ :=\ell \left(q\right),\hfill \end{array}$$ (11)

where the inequality follows Jensen’s inequality and the equality holds if and only if $q(\tilde{\mathit{\beta }},\mathit{\gamma })$ is the true posterior $\text{Pr}(\tilde{\mathit{\beta }},\mathit{\gamma }|\mathbf{y},\mathbf{P},\mathbf{X};\mathit{\theta })$. Instead of working with the marginal likelihood, we can iteratively maximize $\ell \left(q\right)$. To make it feasible to evaluate this lower bound, we use mean-field method (Bishop, 2006), assuming that $q(\tilde{\mathit{\beta }},\mathit{\gamma })$ can be factorized as

$$q(\tilde{\mathit{\beta }},\mathit{\gamma })=\prod _{j=1}^M{q}_j({\tilde{\beta }}_j,{\gamma }_j).$$ (12)

This is the only assumption we made in variational approximation. According to the nice property of factorized distributions in variational inference (Bishop, 2006), we can obtain the best approximation as

$$\text{log}\hspace{0.17em}{q}_j({\tilde{\beta }}_j,{\gamma }_j)={\mathbb{E}}_{i\ne j}[\text{log}\hspace{0.17em}\text{Pr}(\mathbf{y},\mathbf{P},\tilde{\mathit{\beta }},\mathit{\gamma }|\mathbf{X};\mathit{\theta })]+\text{const}\hspace{0.17em},$$ (13)

where the expectation is taken with respect to all of the other factors $\left\{q_i\right({\tilde{\beta }}_i,{\gamma }_i\left)\right\}$ for $i\ne j$. After some derivations (refer to Section 1.1 of the Supplementary Document), we have

$$\begin{array}{c}{q}_j({\tilde{\beta }}_j,{\gamma }_j)={\left[{\pi }_{j}N\right({\tilde{\beta }}_j|{\mu }_j,s_j^2)]}^{{\gamma }_j}{\left[\right(1-{\pi }_j\left)N\right({\tilde{\beta }}_j|0,{\sigma }_{\beta }^2)]}^{1-{\gamma }_j},\hfill \end{array}$$ (14)

where

$$s_j^2=\frac{{\sigma }_e^2}{{\mathbf{x}}_j^T{\mathbf{x}}_j+\frac{{\sigma }_e^2}{{\sigma }_{\beta }^2}},$$

$${\mu }_j=\frac{{\mathbf{x}}_j^T\mathbf{y}-\sum _{i\ne j}\mathbb{E}\left[{\gamma }_i{\tilde{\beta }}_i\right]{\mathbf{x}}_j^T{\mathbf{x}}_i}{{\mathbf{x}}_j^T{\mathbf{x}}_j+\frac{{\sigma }_e^2}{{\sigma }_{\beta }^2}},$$ (15)

and

$${\pi }_j=\frac{1}{1+\text{exp}\hspace{0.17em}(-w_j)},$$

$$w_j=\text{log}\hspace{0.17em}\frac{\pi }{1-\pi }+\frac{1}{2}\text{log}\hspace{0.17em}\frac{s_j^2}{{\sigma }_{\beta }^2}+\frac{{\mu }_j^2}{2s_j^2}+\sum _{k=1}^K\hspace{0.17em}\text{log}\hspace{0.17em}\left({\alpha }_k{p}_{jk}^{{\alpha }_k-1}\right).$$ (16)

Since $q(\tilde{\mathit{\beta }},\mathit{\gamma })$ is an approximation to the true posterior, the above result (14) can be interpreted as follows. Here π_j can be viewed as an approximation of $\text{Pr}({\gamma }_j=1|\mathbf{y},\mathbf{X},\mathbf{P};\mathit{\theta })$. As we can see, the posterior of ${\gamma }_j=1$ is affected by its prior and the evidence from both individual-level data and P-values. When SNP j is irrelevant to the phenotype (${\gamma }_j=0$), the approximated posterior of ${\tilde{\beta }}_j$ remains the same as its prior, i.e. ${\tilde{\beta }}_j\sim N\left({\tilde{\beta }}_j\right|0,{\sigma }_{\beta }^2)$. When SNP j is relevant, its posterior changes accordingly as ${\tilde{\beta }}_j\sim N\left({\tilde{\beta }}_j\right|{\mu }_j,s_j^2)$.

With $q_j({\tilde{\beta }}_j,{\gamma }_j)$ given in (14), we can evaluate the lower bound analytically

$$\begin{array}{cc}L\left(q\right)\hfill & ={\mathbb{E}}_q[\text{log}\hspace{0.17em}\text{Pr}(\mathbf{y},\tilde{\mathit{\beta }},\mathit{\gamma },\mathbf{P}|\mathbf{X},\mathit{\theta })]-{\mathbb{E}}_q[\text{log}\hspace{0.17em}q(\tilde{\beta },\gamma )]\hfill \\ \hfill & =-\frac{N}{2}\text{log}\hspace{0.17em}{\sigma }_e^2-\frac{\left|\right|\mathbf{y}-{\sum }_{j=1}^M{\pi }_j{\mu }_j{\mathbf{x}}_j|{|}^2}{2{\sigma }_e^2}\hfill \\ \hfill & -\frac{1}{2{\sigma }_e^2}\sum _{j=1}^M \left[{\pi }_j\right(s_j^2+{\mu }_j^2)-{\left({\pi }_j{\mu }_j\right)}^2]{\mathbf{x}}_j^T{\mathbf{x}}_j\hfill \\ \hfill & -\frac{1}{2{\sigma }_{\beta }^2}\sum _{j=1}^M \left[{\pi }_j\right({\mu }_j^2+s_j^2)+(1-{\pi }_j\left){\sigma }_{\beta }^2\right]\hfill \\ \hfill & +\sum _{j=1}^M{\pi }_j\hspace{0.17em}\text{log}\hspace{0.17em}\left(\frac{\pi }{{\pi }_j}\right)+\sum _{j=1}^M(1-{\pi }_j)\hspace{0.17em}\text{log}\hspace{0.17em}\left(\frac{1-\pi }{1-{\pi }_j}\right)\hfill \\ \hfill & +\sum _{j=1}^M{\pi }_j\sum _{k=1}^K\hspace{0.17em}\text{log}\hspace{0.17em}\left({\alpha }_k{p}_{jk}^{{\alpha }_k-1}\right)+\sum _{j=1}^M\frac{1}{2}{\pi }_j\hspace{0.17em}\text{log}\hspace{0.17em}\frac{s_j^2}{{\sigma }_{\beta }^2}+\text{Const}\hspace{0.17em}.\hfill \end{array}$$

Therefore, model parameters in $\mathit{\theta }$ can be updated by solving $\frac{\partial \ell }{\partial \mathit{\theta }}=0$ as

$$\pi =\frac{\sum _j{\pi }_j}{M},{\sigma }_{\beta }^2=\frac{\sum _j{\pi }_j({\mu }_j^2+s_j^2)}{\sum _j{\pi }_j},{\alpha }_k=\frac{{\sum }_{j=1}^M{\pi }_j}{{\sum }_{j=1}^M{\pi }_j(-\text{log}\hspace{0.17em}{p}_{jk})},$$

$${\sigma }_e^2=\frac{\left|\right|\mathbf{y}-{\sum }_{j=1}^M{\pi }_j{\mu }_j{\mathbf{x}}_j|{|}^2+{\sum }_{j=1}^M\left({\pi }_j\right(s_j^2+{\mu }_j^2)-{\left({\pi }_j{\mu }_j\right)}^2){\mathbf{x}}_j^T{\mathbf{x}}_j}{N}.$$

In summary, our algorithm can be viewed as a variational expectation-maximization (EM) algorithm. In the expectation step, we evaluate the expectation w.r.t. the distribution q to obtain the lower bound $\ell \left(q\right)$ given in (11). In the maximization step, we maximize current $\ell \left(q\right)$ w.r.t. model parameters in $\mathit{\theta }$. Hence, the lower bound increases in each EM iteration and the convergence of the proposed algorithm is guaranteed. Alternatively, the variational EM algorithm can be considered as a deterministic approximation to a Monte-Carlo EM algorithm which is a golden standard for statistical inference. We have provided detailed discussions about their connection in the Supplementary Document.

2.3 Identification of risk variants and risk prediction

After the convergence of the algorithm, we extract information from our model for identification of risk variants and risk prediction. Since π_j given in (16) is an approximation to the true posterior $\text{Pr}({\gamma }_j=1|\mathbf{y},\mathbf{P},\mathbf{X};\mathit{\theta })$ of SNP j, we use $fd{r}_j=1-{\pi }_j$ as an approximation of the local false discovery rate (FDR) of SNP j (Efron, 2010) and thus SNP j will be considered as a risk variant if fdr_j is close to 0, e.g. $fd{r}_j\le 0.05$.

Besides identification of risk variants, we are also interested in risk prediction. Based on the reparameterized model, the effect size of SNP j is given as $\mathbb{E}\left({\gamma }_j{\tilde{\beta }}_j\right)={\pi }_j{\mu }_j$. Given a genotype vector $\tilde{\mathbf{x}}={[{\tilde{x}}_1,\dots ,{\tilde{x}}_M]}^T$ of an individual, the predicted phenotypic value will be $\widehat{y}=c_0+\sum _j({\tilde{x}}_j-c_j){\pi }_j{\mu }_j$, where c₀ and $c_1,\dots ,c_p$ are the mean of the phenotype and each SNP before centering, respectively. For case-control study, $\widehat{y}$ should only be interpreted as the relative risk score rather than the absolute risk score (Chatterjee et al., 2016).

2.4 Selection of informative studies from summary statistics data

As given in Equations (2–4), we assume variant j has the same association status (denoted as γ_j) across all studies. This assumption is reasonable when all the studies are conducted for the same phenotype in the same population. However, this assumption may be violated if GWAS are conducted in different populations. Here we propose a forward stepwise procedure to select informative studies from summary statistics data. We use prediction accuracy by cross-validation as the criterion to select summary statistics from relevant study. Precisely, the prediction accuracy is measured by correlation between predicted values and observed values in quantitative trait studies or the area under the receiver operating characteristic (ROC) curve (AUC) in case-control studies. In forward stepwise selection, IGESS tries to add one summary-statistic data at a time and picks the summary-statistic dataset which maximizes prediction accuracy. If prediction accuracy gets worse when a summary-statistic data is incorporated, IGESS will automatically exclude this study in the following steps. More specifically, we start with individual level data $\{\mathbf{X},\mathbf{y}\}$ to have a baseline model. Then we try to add each column of $\mathbf{P}$ to the baseline model to check the model performance and select the best one into the model. We keep adding the columns of $\mathbf{P}$ in such a way until all relevant columns have been included in the model. The cross-validation is used to determine the right model.

2.5 Computational cost of the variational EM algorithm

Regarding the computational time of IGESS, here we report the CPU time for 100 iterations with different sample size N and different number of SNPs M in Figure 1. All the timings were carried out on a notebook with a configuration of 2.6 GHz Intel Core i7 and 16G memory. The computational time is nearly linear with respect to N and M. In real data analysis, the total number of iterations depends on the strength of the GWAS signal. The stronger the GWAS signal, the faster the algorithm converges. IGESS often takes less than twenty minutes to handle a GWAS dataset with thousands of samples and hundreds of thousands of SNPs. The R package of IGESS is available at https://github.com/daviddaigithub/IGESS.

Fig. 1.

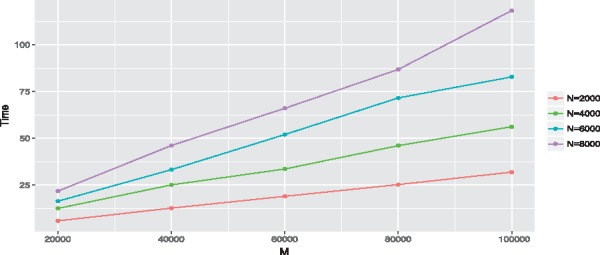
Timing (CPU seconds) with respect to different sample size N and different number of SNPs M (Color version of this figure is available at Bioinformatics online.)

3 Results

3.1 Simulation

In this section, we describe how to evaluate the performance of IGESS in simulation studies. We first evaluated its performance on identification of risk variants, in comparison with Lasso (Tibshirani, 1996) and BVSR (Carbonetto et al., 2012) which only take individual-level data as input, as well as P-value-based ranking and CPASSOC (Zhu et al., 2015) which only use summary statistics (specifically, z-scores). After that, we evaluated its accuracy on risk prediction, where the performance of BVSR (Carbonetto et al., 2012) and Lasso (Friedman et al., 2010; Tibshirani, 1996) served as a reference because they only use individual-level data.

3.1.1 Simulation settings

The simulation datasets were generated as follows. For the individual-level dataset, the genotype matrix $\mathbf{X}$ was first simulated from normal distribution, where autoregressive correlation ${\rho }^{|j-j\prime |}$ was set to mimic the linkage disequilibrium between variants j and $j\prime$. Next, the entries in $\mathbf{X}$ were discretized to genotype codes {0, 1, 2} according to the Hardy-Weinberg principle based on the minor allele frequencies drawn from $\mathcal{U}[0.05,0.5]$. The number of samples and the number of variants were set to be N = 2000 and M = 10 000, respectively. To simulate the vector of effect sizes $\mathit{\beta }$, we randomly chose 500 nonzero entries and simulated their values from N(0, 1). Accordingly, the association status was recorded in $\mathit{\gamma }$. Since heritability is defined as $h=\frac{\text{Var}\left(\mathbf{X}\mathit{\beta }\right)}{\text{Var}\left(\mathbf{X}\mathit{\beta }\right)+{\sigma }_e^2}$, the noise level was specified according to the pre-specified heritability at $\{0.3,0.5,0.8\}$.

To simulate summary statistics, we did not adopt the generative model (4) but obtain them from the individual-level data. This helps us to evaluate whether the Beta distribution can model the P-values from the non-null group. We considered two scenarios to simulate the positions of nonzero entries. In the first scenario, the vector of association status ${\mathit{\gamma }}^{\left(k\right)}$ of the kth study was set to be the same as $\mathit{\gamma }$, for $k=1,\dots ,K$. Clearly, this setting is favorable to our model as all studies share the same sets of associated risk variants. In the second scenario, ${\mathit{\gamma }}^{\left(k\right)}$ was allowed to be different from $\mathit{\gamma }$. To do so, we varied the conditional probability $u_k=\text{Pr}({\mathit{\gamma }}_j^{\left(k\right)}=1|{\mathit{\gamma }}_j=1)$ at $\{0.05,0.1,0.3,0.5,0.7,0.9,1\}$. In such a way, ${\mathit{\gamma }}^{\left(k\right)}$ was simulated and the corresponding nonzero entries of ${\mathit{\beta }}^{\left(k\right)}$ were simulated from N(0, 1). The assumption of IGESS is violated in this scenario. For each study k, we first used the above steps to generate genotype matrix ${\mathbf{X}}^{\left(k\right)}$ and phenotype data ${\mathbf{y}}^{\left(k\right)}$, then we conducted univariate linear regression to get summary statistics (z-score and P-value) for each SNP across K studies.

For IGESS, both the individual-level data $\{\mathbf{X},\mathbf{y}\}$ and the P-value matrix $\mathbf{P}$ were used, where $\{{\mathbf{X}}^{\left(k\right)},{\mathbf{y}}^{\left(k\right)}\}$ were pretended to be unavailable. For BVSR and the Lasso, only the individual level dataset $\{\mathbf{X},\mathbf{y}\}$ was used and their performance could serve as a reference. For CPASSOC, an $M\times (1+K)$ matrix $\mathbf{Z}$ containing the z-scores from $\{\mathbf{X},\mathbf{y}\}$ and the z-scores from K studies was used as its input.

3.1.2 Results

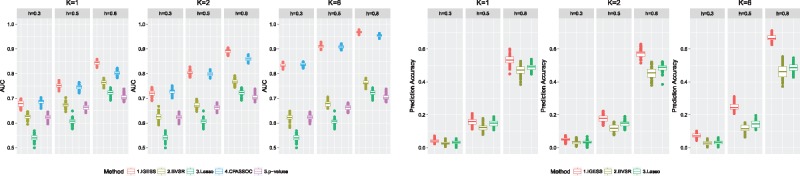
To evaluate the performance of risk variant identification, we adopted the area under the receiver operating characteristic (ROC) curve (AUC). We started with the results evaluated in the first scenario where ${\mathit{\gamma }}^{\left(k\right)}=\mathit{\gamma }$ for $k=1,2,\dots ,K$. Figure 2 shows the comparison results of IGESS, BVSR, CPASSOC, Lasso and P-value-based ranking for autoregressive correlation $\rho =0.6$ and K = 1, 2, 6. The results for other parameter settings, e.g. $\rho =0,0.3$, are given in the Supplementary Document. Here the results of BVSR, Lasso and P-value-based ranking only serve as a reference since they only used $\{\mathbf{X},\mathbf{y}\}$ as input. In the left panel, the AUC of both IGESS and CPASSOC steadily increases as the number of summary statistics datasets K increases. IGESS has similar performance with CPASSOC when heritability is moderate (h = 0.5) and outperforms CPASSOC when the heritability is high (h = 0.8). We have observed that CPASSOC is slightly better than IGESS in terms of AUC when heritability is very small (e.g. h = 0.3). A closer examination reveals that both methods have nearly zero power with the nominal FDR controlled at 0.1. This implies that the slightly better AUC of CPASSOC is due to the ranking results of risk variants with a larger false positive rate which is not of interest in practice (see more results in the Supplementary Document). Because the top findings with small false positive rate (FPR) are of more interest, the ROC curves of the three methods with FPR < 0.1 are provided in the Supplementary Document. To see the benefits of integrating individual-level data with summary statistics in risk predication, we evaluated prediction accuracy of IGESS, where the performance of BVSR and Lasso can serve as a reference. The right panel of Figure 2 shows the performance of the three methods, indicating that prediction accuracy can be steadily improved by incorporating summary statistics.

Fig. 2.

Comparison of IGESS, BVSR, CPASSOC, Lasso and P-value-based ranking with different heritability h, and different number of GWAS studies K. Left panel: Performance of risk variant identification measured by AUC. Right panel: Performance of risk prediction measured by correlation between the observed phenotype values and the predicted values. The autoregressive correlation $\rho =0.6$ and the number of summary statistics datasets k = 1, 2 and 6. All the results are summarized based on 50 replications (Color version of this figure is available at Bioinformatics online.)

Next, we investigated the performance of IGESS in the second scenario. We simulated P-values from K = 7 studies, where $u_k=\text{Pr}({\gamma }_j^{\left(k\right)}=1|{\gamma }_j=1)\in \{0.05,0.1,0.3,0.5,0.7,0.9,1\}$. Note that u_k also indicates the proportion of nonzero effect sizes shared between the study with individual-level data and each study with summary statistics. The stepwise strategy (Section 2.4) was used to select relevant studies. Figure 3 shows performance of risk variant identification (measured by AUC in the left panel) and prediction accuracy (measured by the correlation between the observed values and predicted values in the right panel) during the stepwise process. At the first step, the stepwise strategy attempted to combine individual-level data $\{\mathbf{X},\mathbf{y}\}$ with P-values from each study. The first subplot of the left panel shows that the performance of risk variant identification degrades when the P-values from studies with $u_k\in \{0.05,0.1,0.3\}$ are incorporated and the performance starts to be improved from $u_k=0.5$. Since IGESS adopts the forward stepwise strategy, it will select the study which offers the best improvement of the prediction performance at each step and keep adding P-values from remaining studies, as indicated by $s=1,\dots ,7$. As we can see clearly, the performance of IGESS improves steadily until irrelevant or nearly irrelevant studies included (s = 5). The similar pattern has been observed for the performance of prediction accuracy, as shown in the right panel of Figure 3. In summary, it is clear that the performance improvement of IGESS does not require u_k = 1, suggesting that IGESS is robust to the noise in the P-value dataset.

Fig. 3.

Performance evaluation in presence of irrelevant studies. Left panels: Performance of risk variant identification measured by AUC. Right panels: Performance of risk prediction measured by correlation between the observed phenotype values and the predicted values. In all panels, $\{\mathbf{X},\mathbf{y}\}$ in the x-axis indicates the performance of individual-level data only, q corresponds to the performance of integrating the individual-level data with P-values from a study simulated using parameter $u_k=\text{Pr}({\gamma }_j^{(k)}=1|{\gamma }_j=1)\in \{0.05,0.1,0.3,0.5,0.7,0.9,1\}$, and s indicates the stepwise performance achieved at the s-step

3.2 Real data analysis

We applied IGESS to analyze GWAS data of Crohn’s disease (CD). The individual-level data is from the Welcome Trust Case Control Consortium (WTCCC) (Burton et al., 2007). There are 5009 samples, of which 2005 are cases and 3004 are controls. The summary data of Crohn’s Disease is from Franke et al. (2010), comprised of the P-values of six GWAS in total.

3.2.1 Quality control on the individual-level data

We performed strict quality control on the individual-level data from WTCCC using PLINK(Purcell et al., 2007) and GCTA (Yang et al., 2011). First, we removed individuals with $>2\%$ missing genotypes. For the case of CD and the two control datasets, we removed SNPs with minor allele frequencies $<0.05$ and SNPs with missing rate $>1\%$. Then we combined the case sets of CD and the two control sets into case/control studies. SNPs with P-value <0.001 in Hardy-Weinberg equilibrium test were removed. Pairs of subjects with estimated relatedness $>0.025\%$ were identified and one member of these pairs was removed at random by GCTA (Yang et al., 2011). After quality control, we had a dataset including 1656 cases and 2880 controls, each with 308 950 SNPs.

3.2.2 Summary-statistic data for CD

Besides the WTCCC data, Franke et al. (2010) provided summary statistics of CD. The samples were from Germany, Cedars-Sinai Medical Center (Los Angeles, California, USA), the Children’s Hospital of Philadelphia, Scotland, Toronto and Italy Crohn’s and Colitis in Childhood Study consortium (of early onset cases), and the National Institute of Diabetes and Digestive and Kidney Disease (NIDDK) and Belgian-French Studies. According to Franke et al. (2010), the samples from the Cedars-Sinai Medical Center were divided into two studies (Cedar1 and Cedar2) and the samples from NIDDK were divided into the Jewish study (NiddkJ) and the non-Jewish study (NiddkNJ). After extracting overlapped SNPs of individual-level data (after quality control) and summary statistics, we had the individual-level data ${\left\{\mathbf{X}\right\}}_{N\times M},{\mathbf{y}}_{N\times 1}$ and $\mathbf{P}\in {ℝ}^{M\times K}$ for the analysis, where N = 4536, M = 248 409 and K = 7.

3.2.3 Analysis result of Crohn’s disease

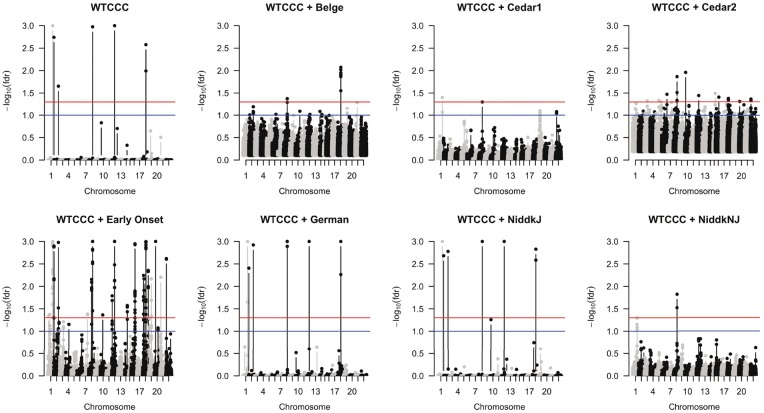
We first applied IGESS to analyze the WTCCC data only and then incorporated P-values from each of the seven studies. The results are summarized in Table 1, where the number of GWAS hits is reported based on $fdr\le 0.05$. The locations of those GWAS hits in the genome are shown in the Manhattan plots in Figure 4. As a reference, the analysis result of Lasso is also reported in Table 1. Clearly, the P-values from the Early Onset dataset offers most relevant information, improving prediction accuracy (measured by AUC) from 63.28% (± 0.37%) to 68.62% (± 0.36%). Meanwhile, we also observe that the incorporation of P-values from the Belge and Cedar2 studies degraded the performance. This is because the P-values from these two studies are inflated, as pointed out in Franke et al. (2010). Therefore, IGESS would not consider the P-values from the Belge and Cedar2 studies in the selection process. As the P-values from the remaining studies been selected in the stepwise manner, the prediction accuracy of IGESS keeps increasing until 69.4% ($\pm 0.1\%$), as shown in Figure 5. The complete list of GWAS hits ($fdr\le 0.05$) and their corresponding genes are provided in the Supplementary Document.

Table 1.

Summary of IGESS analysis result on Crohn’s disease

Data	No. of hitsa	Prediction accuracy (AUC)
WTCCC only (BVSR)	7	63.2% ± 0.4%
WTCCC only (Lasso)	227b	63.5% ± 0.5%
WTCCC+Belge	10	62.1% ± 0.6%
WTCCC+Cedar1	2	64.3% ± 0.5%
WTCCC+Cedar2	17	61.9% ± 0.7%
WTCCC+Early Onset	120	68.6% ± 0.3%
WTCCC+German	10	65.4% ± 0.3%
WTCCC+NiddkJ	7	64.1% ± 0.4%
WTCCC+NiddkNJ	3	64.3% ± 0.5%

^aThe number of GWAS hits is reported based on estimated $fdr\le 0.05$.

^bFor Lasso, we reported the number of nonzero coefficients with regularization parameter selected by cross-validation using R package ‘glmnet’ (Friedman et al., 2010).

Fig. 4.

Manhattan plots of the analysis results of Crohn’s Disease using IGESS. The red lines and blue lines are corresponding to fdr = 0.05, and fdr = 0.1, respectively (Color version of this figure is available at Bioinformatics online.)

Fig. 5.

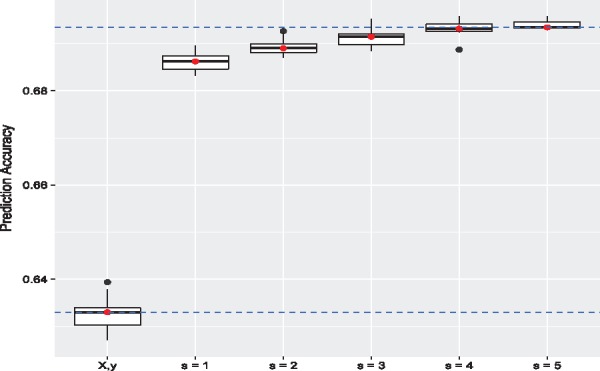
Prediction accuracy measured by AUC during forward stepwise selection

At last, we demonstrated the benefit of using IGESS with different sample sizes of the individual-level data. To do so, we randomly partitioned the WTCCC data (N = 4536) into five folds of nearly equal sample size. We used IGESS to integrate the P-values from the Early Onset study with individual-level data of different sample sizes. Specifically, we used the first $k=1,2,3,4$ folds of the WTCCC data as the training data (with sample size N = 908, N = 1815, N = 2722 and N = 3629, respectively) and the fifth fold as the testing data. The prediction accuracies of different sample sizes are shown in Figure 6. As we can see here, a more noticeable improvement in prediction can be achieved when the sample size of the individual-level data is smaller. For example, when N = 908, the prediction accuracy is improved by 8.7% from $55.6\%\hspace{0.17em}(\pm 2.8\%)$ to $64.3\%\hspace{0.17em}(\pm 1.9\%)$. This result suggests that more benefits can be gained by integrating summary statistics when the sample size of individual level data is small.

Fig. 6.

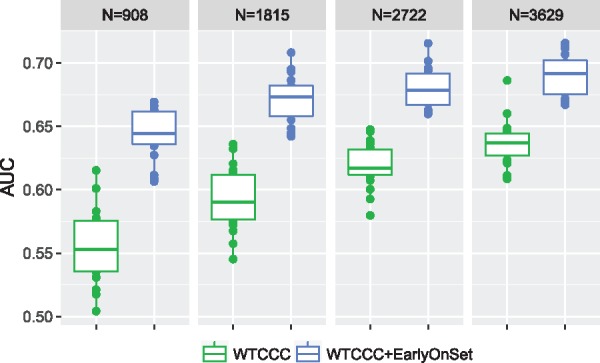
Improvement of prediction accuracy with different sample sizes after incorporating P-values from the Early Onset study (Color version of this figure is available at Bioinformatics online.)

4 Conclusion

It is often difficult to get approval of accessing individual-level data of a large sample size. In contrast, the summary statistics of many GWAS have been widely available via public gateway. The integration of individual-level data and summary statistics is a promising direction to address the challenges raised by the polygenicity of complex phenotypes. There is a great demanding of the methods and tools that can help researchers to mine scientific evidence hidden in the rich data resources. In this paper, we propose a statistical approach, IGESS, to integrating data from both the individual-level and the summary level. The variational EM algorithm is shown to be scalable to handle genome-wide data in minutes. The results from comprehensive simulations suggest the advantages of IGESS and the real data analysis of Crohn’s disease indicates the applicability of IGESS in practice. We believe that IGESS can serve as an effective tool in integrating individual-level data and summary statistics for more powerful genetic analysis.