Novel probabilistic models of spatial genetic ancestry with applications to stratification correction in genome-wide association studies

Abstract

Motivation: Genetic variation in human populations is influenced by geographic ancestry due to spatial locality in historical mating and migration patterns. Spatial population structure in genetic datasets has been traditionally analyzed using either model-free algorithms, such as principal components analysis (PCA) and multidimensional scaling, or using explicit spatial probabilistic models of allele frequency evolution. We develop a general probabilistic model and an associated inference algorithm that unify the model-based and data-driven approaches to visualizing and inferring population structure. Our spatial inference algorithm can also be effectively applied to the problem of population stratification in genome-wide association studies (GWAS), where hidden population structure can create fictitious associations when population ancestry is correlated with both the genotype and the trait.

Results: Our algorithm Geographic Ancestry Positioning (GAP) relates local genetic distances between samples to their spatial distances, and can be used for visually discerning population structure as well as accurately inferring the spatial origin of individuals on a two-dimensional continuum. On both simulated and several real datasets from diverse human populations, GAP exhibits substantially lower error in reconstructing spatial ancestry coordinates compared to PCA. We also develop an association test that uses the ancestry coordinates inferred by GAP to accurately account for ancestry-induced correlations in GWAS. Based on simulations and analysis of a dataset of 10 metabolic traits measured in a Northern Finland cohort, which is known to exhibit significant population structure, we find that our method has superior power to current approaches.

Availability and Implementation: Our software is available at https://github.com/anand-bhaskar/gap.

Contacts: abhaskar@stanford.edu or ajavanma@usc.edu

Supplementary information: Supplementary data are available at Bioinformatics online.

1 Introduction

Modern human genomic datasets routinely contain samples from geographically diverse populations (1000 Genomes Project Consortium et al., 2010; Nelson et al., 2008), and analyses of these datasets has shown that the patterns of genetic variation across human populations encodes substantial information about their geographic ancestry (Cavalli-Sforza et al., 1994; Novembre et al., 2008; Ramachandran et al., 2005). Inferring such spatial population structure from genetic data is of fundamental importance to many problems in population genetics — identifying genomic regions under selective pressure (Coop et al., 2009; Lewontin and Krakauer, 1973; Yang et al., 2012), correcting for population structure in genome-wide association studies (Price et al., 2006), and shedding light on ancient human history (Jakobsson et al., 2008), to name a few.

A fundamental technique for studying spatial demography is the visualization and inference of population structure through low-dimensional representations of genomic data. Methods like principal components analysis (PCA) (Lao et al., 2008; Novembre et al., 2008) and multidimensional scaling (MDS) (Jakobsson et al., 2008) were among the first approaches that demonstrated that genotype data could be used to accurately recapitulate geographic ancestry. Moreover, their performance and interpretation has been backed by theoretical work (McVean, 2009; Novembre and Stephens, 2008; Paschou et al., 2007; Patterson et al., 2006). There is also a wide spectrum of spatial genetic models and methods (Baran and Halperin, 2015; Bradburd et al., 2016; Rañola et al., 2014; Wasser et al., 2004; Yang et al., 2012) which have been developed for inferring geographic ancestry coordinates. The SPA model Yang et al. (2012) uses a logistic function over space to parameterize the allele frequency at each SNP, while methods like SCAT (Wasser et al., 2004) and SpaceMix (Bradburd et al., 2016) consider allele frequency covariance functions which decay exponentially with geographic distance. The OriGen algorithm of Rañola et al. (2014), while not positing a specific functional form for the allele frequency function, performs an optimization which encourages smoothness in allele frequency over space. In all these spatial models, the inference of ancestry coordinates is performed using maximum likelihood or expectation-maximization algorithms that are tailored to the details of the model.

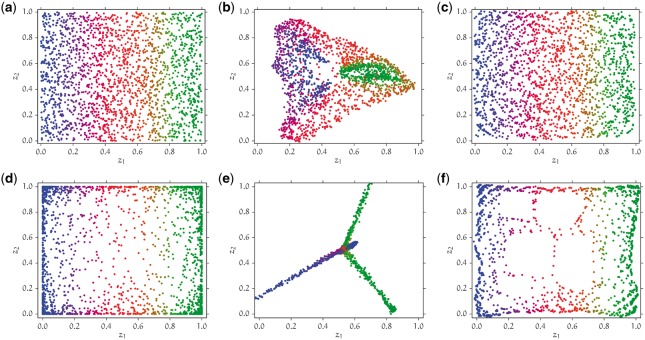
In this work, we marry the previously mentioned model-free and model-based approaches to geographic ancestry localization by developing a flexible spatial stochastic process model that subsumes previously developed parametric allele frequency models such as SPA, SCAT and SpaceMix as special cases. Furthermore, we develop a data-driven spatial reconstruction algorithm Geographic Ancestry Positioning (GAP), that exploits the structural properties of our stochastic process while being agnostic to its minutiae. Our localization algorithm is inspired by principles from manifold learning, and can be viewed as a generalization of PCA. The idea behind our approach is to infer the local spatial distances between sampled individuals using their genotypes, and to then create a global spatial embedding that is faithful to the local geometry information. Our probabilistic process and associated inference algorithm bridge the long threads of work in data-driven and model-based ancestry localization from genotypic data. Through extensive simulations, we demonstrate that GAP often performs substantially better than PCA at both visually discerning spatially structured populations (Fig. 1) as well as inferring the spatial coordinates of individuals (Table 1). We also prove theoretically that, under our probabilistic model, GAP performs at least as well as PCA in reconstructing the spatial coordinates of genetic samples. We apply GAP to three public genotype datasets from the Human Origins (Lazaridis et al., 2014), GLOBETROTTER (Hellenthal et al., 2014) and POPRES (Nelson et al., 2008) projects. Compared to PCA, GAP exhibits 31% lower error in spatial reconstruction of the subpopulations in the Human Origins dataset, 10% lower error on the GLOBETROTTER dataset, and 56% lower error on the POPRES dataset (If we use only a subset of SNPs with minor allele frequency $\ge 10\%$, GAP and PCA perform similarly. See Supplementary Information §1.7 for details.).

Fig. 1.

Simulated datasets with the PCA and GAP reconstructions. The genotype data were simulated using the isotropic covariance decay model, where the z₁ and z₂ coordinates of each individual were sampled independently and (a) uniformly, (d) according to a Beta(0.25, 0.25) distribution from the unit square. The covariance decay parameters for the simulation are ${\alpha }_0={\alpha }_2=1$ and ${\alpha }_1=16$. (a) and (d) True locations of sampled individuals; (b) and (e) Reconstructed locations using PCA (RMSE 0.2554 and 0.4390, respectively), (c) and (f) Reconstructed locations using GAP (RMSE 0.0245 and 0.0293, respectively) (Color version of this figure is available at Bioinformatics online.)

Table 1.

Isotropic covariance decay model

α2	α1	$\frac{\text{RMSE}\hspace{0.17em}\mathrm{GAP}}{\text{RMSE} \text{PCA}}$	RMSE PCA	RMSE GAP
0.5	1	1.010	0.0879	0.0888
	2	0.978	0.1030	0.1008
	4	0.699	0.1001	0.0700
	8	0.414	0.1151	0.0477
	16	0.307	0.1372	0.0421
1	1	1.018	0.0716	0.0729
	2	0.880	0.0929	0.0818
	4	0.359	0.1285	0.0461
	8	0.094	0.1733	0.0163
	16	0.096	0.2554	0.0245
1.5	1	1.028	0.0555	0.0570
	2	0.857	0.0983	0.0843
	4	0.212	0.1647	0.0349
	8	0.100	0.2842	0.0285
	16	0.100	0.3114	0.0311

Comparison of the localization accuracy of GAP and PCA in the isotropic model simulation setup described in Simulations, with parameters $\beta ={\alpha }_0=1$. Bold entries indicate those parameter combinations where GAP outperforms PCA.

Population structure also has serious implications for genome-wide association studies (GWAS). In the GWAS setting, one is interested in finding loci that are causal for the trait, while being resilient to false associations arising from hidden population structure and environmental confounders. Spurious associations can arise due to ancestry-induced correlations between causal and non-causal loci, or when ancestry is correlated with both the genotype and the trait (Campbell et al., 2005). PCA (Price et al., 2006) and linear mixed models (LMM) (Kang et al., 2010) are two popular classes of methods for correcting ancestry confounding in human genetics studies. Both of these methods test genetic associations in prospective models describing the distribution of the trait conditional on the genotype. On the other hand, retrospective models describing the distribution of genotypes conditional on the trait are more natural in the setting of case–control studies and have been shown to be equivalent to prospective models under suitable assumptions (Prentice and Pyke, 1979; Song et al., 2015). Based on this, Song et al. (2015) developed a testing procedure, GCAT, that controls for ancestral confounding by using a latent factor model (Hao et al., 2016) to estimate the allele frequencies at each SNP across the sample. We propose an alternative allele frequency estimation procedure and association test, Stratification Correction via GAP (SCGAP), that can effectively correct for ancestry confounding by using the spatial coordinates inferred by GAP. SCGAP employs an allele frequency smoothing procedure using the inferred coordinates from GAP in order to estimate the allele frequency at each SNP across the sample. Our association testing procedure uses these estimates of the allele frequency to test each SNP in an inverse regression of the genotype against the trait, conditional on the estimated allele frequency. Through simulations, we show that our allele frequency estimation procedure when used with the ancestry coordinates from our localization algorithm GAP has almost as high power as if the true ancestry coordinates were known, and has considerably higher power than if the ancestry coordinates were inferred using PCA. We applied SCGAP to a birth cohort from Northern Finland containing several quantitative metabolic traits and observe that it compares favorably to state-of-the-art computationally intensive approaches such as LMMs. For instance, SCGAP and GCAT are the only methods to identify a SNP (rs2814982) associated with height in this dataset.

2 Methods

2.1 Model

Suppose that we are given genotype or sequence data from n individuals at p SNPs. We will use X to denote the n × p genotype matrix, where entry $x_{i\ell }\in \{0,1,2\}$ is the number of alleles at SNP $\ell$ in individual i. We let ${\mathbf{z}}_i\in {ℝ}^2$ denote the unknown ancestral origin of individual i. In our spatial probabilistic model, the allele frequencies for different SNPs are assumed to be drawn from independent stochastic processes defined over the two-dimensional geographical space. Specifically, letting $q_{\ell }(\mathbf{z})$ be the allele frequency of SNP $\ell$ at location $\mathbf{z}$, we let ${\mu }_{\ell }:=\mathbb{E}[q_{\ell }(\mathbf{z})]$ denote the mean allele frequency of SNP $\ell$ in the population. The covariance $\text{Cov}(q_{\ell }(\mathbf{z}),q_{\ell }(\mathbf{z}\prime ))$ in allele frequencies between pairs of locations $\mathbf{z}$ and $\mathbf{z}\prime$ is captured by a covariance decay function η as follows,

$$\text{Cov}(q_{\ell }(\mathbf{z}),q_{\ell }(\mathbf{z}\prime ))=\mathbb{E}[(q_{\ell }(\mathbf{z})-{\mu }_{\ell })(q_{\ell }(\mathbf{z}\prime )-{\mu }_{\ell })]=:\eta (\mathbf{z}-\mathbf{z}\prime ).$$ (1)

This assumption allows us to model the phenomenon of isolation by distance, where the covariance in allele frequencies decays with geographic separation, while also allowing for different rates of covariance decay in different spatial directions. Such observations of anisotropic isolation by distance have been reported by previous studies of African, Asian and European populations (Jay et al., 2013). Moreover, several previous spatial genetic models (Bradburd et al., 2016; Wasser et al., 2004; Yang et al., 2012) can be recast as specific parametrizations of the autocovariance function η of our model (Supplementary Information §1.4). However, in contrast to these models, we do not impose any explicit parametric form on the autocovariance function η. Supplementary Figure S2 shows example allele frequency surfaces from two such previously proposed spatial processes (Wasser et al., 2004; Yang et al., 2012) that are captured by our model formulation.

2.2 Algorithm

Our localization algorithm GAP takes a data-driven approach while exploiting the structure of the autocovariance function in (1). The idea behind our algorithm is to define a genetic squared-distance d² between each pair of sampled individuals as follows,

$$d_{ij}^2=\eta (0)-\eta ({\mathbf{z}}_i-{\mathbf{z}}_j).$$ (2)

We can exploit the structure of our model in (1) to relate the genetic squared-distances $d_{ij}^2$ between genetically similar pairs of individuals to their spatial squared-distances ${\Vert {\mathbf{z}}_i-{\mathbf{z}}_j\Vert }^2$. More precisely, we show that,

$$d_{ij}^2\approx {\Vert J({\mathbf{z}}_i-{\mathbf{z}}_j)\Vert }^2\hspace{0.17em},\hspace{0.17em}\text{for}\hspace{0.17em}i,j\text{where}\hspace{0.17em}{d}_{ij}\hspace{0.17em}\text{is}\hspace{0.17em}\text{small}\hspace{0.17em}\text{enough}.$$ (3)

In (3), J is a 2 × 2 invertible matrix that is determined by the underlying stochastic process. We use (3) only for those pairs of individuals i and j where d_ij is smaller than some threshold parameter τ.

Our localization algorithm consists of three main steps, which we describe below, leaving some of the involved details to §1.2 of the Supplementary Information:

• (1) Using the genotype matrix X, we construct provably consistent estimators ${\widehat{\eta }}_0$ and ${\widehat{\eta }}_{ij}$ for $\eta (0)$ and $\eta ({\mathbf{z}}_i-{\mathbf{z}}_j)$ respectively. These estimators are given in Theorem 1 in the Supplementary Information.

• (2) We estimate the genetic squared-distances ${\widehat{d}}_{ij}^2$ according to (2) using the estimates for $\eta (0)$ and $\eta ({\mathbf{z}}_i-{\mathbf{z}}_j)$ computed in the previous step. Applying relation (3), local genetic distances are good proxies for the spatial distances. We therefore keep estimates ${\widehat{d}}_{ij}$ only for those pairs of individuals where ${\widehat{d}}_{ij}\le \tau$.

• (3) We find a global embedding of individuals in the geographic space from their estimated local pairwise distances. To this end, we borrow tools from the area of manifold learning. In this work, we have used the ISOMAP algorithm (Tenenbaum et al., 2000) for this step. However, other algorithms developed for manifold learning can be applied in this step too, some of which are discussed in the Supplementary Information.

The spatial reconstruction accuracy of our procedure will depend on the threshold τ that is chosen in step (2) above. The optimal choice of the threshold τ will depend on the dataset and the validity of the second-ordinary stationarity assumption of our model. One can pick τ in a similar manner to how parameter tuning is done in machine learning. Specifically, we will use a small subset (20%) of the samples as a training set with known spatial coordinates, and perform cross-validation over a grid of τ (see Supplementary Information §1.2 and §1.3).

3 Results

3.1 Simulations

We considered two simulation scenarios to model isotropic and direction-dependent allele frequency covariance decay. For both simulation scenarios, we simulated $n=2000$ individuals at $p=50\hspace{0.17em}000$ SNPs. The true geographic origin ${\mathbf{z}}_i$ of individual i was simulated by sampling each coordinate according to a Beta($\beta ,\beta$) distribution from the unit square. This distribution lets us smoothly interpolate between dense sampling of individuals in the interior of the space to dense sampling at the boundaries (Fig. 1(a) and (d)), with the setting β = 1 representing uniform sampling. The spatial allele frequencies at each SNP were generated by applying the logistic function to sample paths from a spatial Gaussian process. Assuming Hardy-Weinberg equilibrium, the genotypes of each individual i were drawn according to a binomial distribution from the allele frequencies at their geographic origin ${\mathbf{z}}_i$.

• Isotropic covariance decay: The allele frequency $q_{\ell }(\mathbf{z})$ of SNP $\ell$ at location $\mathbf{z}$ is given by $q_{\ell }(\mathbf{z})=1/(1+\text{exp}\hspace{0.17em}(G_{\ell }(\mathbf{z})))$, where $G_{\ell }(\mathbf{z})$ is a sample path of a two dimensional stationary Gaussian process with mean zero and covariance kernel $K(\mathbf{z},\mathbf{z}\prime )=\text{exp}\hspace{0.17em}(-{({\alpha }_1\Vert \mathbf{z}-\mathbf{z}\text{'}\Vert )}^{{\alpha }_2})/{\alpha }_0$. Such models have been previously considered by the SCAT (Wasser et al., 2004) and SpaceMix (Bradburd et al., 2016) methods. In order for $K(\mathbf{z},\mathbf{z}\prime )$ to be a valid covariance kernel, $0\le {\alpha }_2\le 2$.

• Directional covariance decay: The allele frequency $q_{\ell }(\mathbf{z})$ of SNP $\ell$ at location $\mathbf{z}$ is given by $q_{\ell }(\mathbf{z})=1/(1+\text{exp}\hspace{0.17em}(G_{\ell }(\mathbf{z})))$, where $G_{\ell }(\mathbf{z})$ is a sample path of a two dimensional stationary Gaussian process with mean zero and covariance kernel $K(\mathbf{z},\mathbf{z}\prime )=\text{exp}\hspace{0.17em}(-{({\alpha }_1|<\mathbf{u},\mathbf{z}-\mathbf{z}\text{'}>|)}^{{\alpha }_2})/{\alpha }_0$, and $\mathbf{u}$ is a unit-length direction vector in ${ℝ}^2$. The resulting allele frequencies are equal along directions perpendicular to $\mathbf{u}$, and this model can thus be viewed as a generalization of the SPA model (Yang et al., 2012) (Supplementary Information §1.4). In the simulations, we drew 100 different direction vectors ${\mathbf{u}}_k$ from a von Mises distribution (a circular analogue of the Normal distribution), and simulated 500 SNPs using each of these direction vectors.

Supplementary Figure S2 shows example allele frequency surfaces from these two covariance decay models. For each parameter combination in the above models, we simulated 10 random datasets, and used PCA and our algorithm GAP to infer the spatial coordinates ${\mathbf{z}}_i$. PCA infers the locations up to an orthogonal transformation, while GAP infers these locations up to an invertible linear transformation which is related to the curvature of the allele frequency variance $\eta (0)$. We use the true geographic locations of a random subset of 20% of the simulated individuals to rescale the coordinates inferred by PCA and GAP. As a measure of spatial reconstruction accuracy, we use the root mean squared error (RMSE) between the inferred locations ${\widehat{\mathbf{z}}}_i$ and the true locations ${\mathbf{z}}_i$ measured as $\sqrt{1/n\sum _{i=1}^n{\Vert {\mathbf{z}}_i-{\widehat{\mathbf{z}}}_i\Vert }^2}$.

For most parameter combinations in both the covariance decay models, the RMSE of GAP is substantially lower than that of PCA (Table 1 and Supplementary Table S6). In fact, we prove that under our spatial probabilistic model, GAP performs at least as well as PCA in the asymptotic regime where the sample size n goes to infinity (Supplementary Information §1.4). For some simulation parameter combinations, the RMSE of PCA is slightly better than the RMSE of GAP by a few percent (Table 1 and Supplementary Table S6), which is due to the sample size being finite. Figure 1 illustrates the conceptual difference between GAP and PCA. PCA tries to embed individuals into a two dimensional space which preserves the pairwise genetic distance between all pairs of individuals as estimated from their genotype data. On the other hand, GAP takes a more local approach by using the genotype data from only genetically similar pairs of individuals to estimate their spatial distance. This leads to a qualitatively better low-dimensional embedding. Simulation results for other parameter settings for these isotropic and directional covariance decay models bear out this intuition (Supplementary Tables S1–S10).

3.2 Analysis of diverse human population datasets

We applied GAP to three public genotype datasets that have been previously analyzed in studies of population structure—(i) the Human Origins dataset containing 198 diverse populations that has been used to analyze ancient admixture (Lazaridis et al., 2014), (ii) the GLOBETROTTER dataset of 95 populations (Hellenthal et al., 2014) and (iii) the Population Reference Sample (POPRES) dataset (Nelson et al., 2008) (Supplementary Information §1.6).

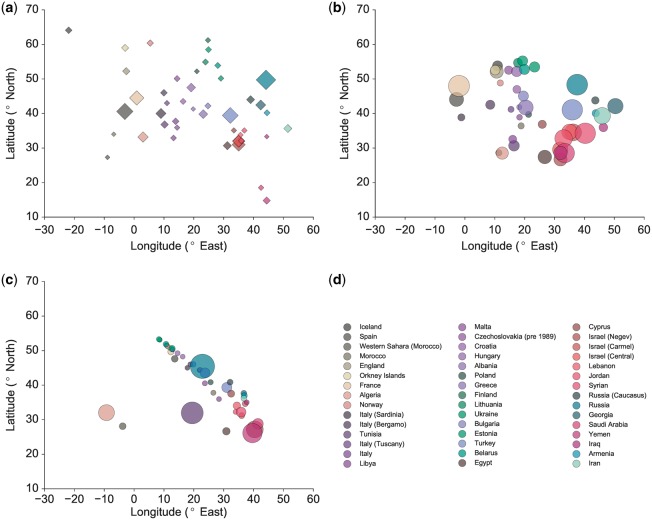
$•$ Human Origins: The publicly available release (Lazaridis et al., 2014) contains 1945 individuals genotyped at 600 841 SNPs. We used a subset of 863 individuals from 91 diverse populations from North Africa and Western Eurasia in order to have fairly uniform sampling over the relevant geographic region. We considered autosomal SNPs which were filtered using plink for deviation from Hardy-Weinberg equilibrium, and also excluded SNPs in linkage disequilibrium by pruning SNP pairs which had a pairwise genotypic linkage disequilibrium r² of greater than 10% within sliding windows of 50 SNPs (with a 5-SNP increment between windows). This left us with a set of 127 922 SNPs. PCA applied to this dataset produced a visually poor separation of the populations in Eastern Europe and Western Asia (Fig. 2(c)). However, population structure is better discerned using our localization algorithm GAP, which also shows a strong correlation between the true sampling locations and the inferred population locations (Fig. 2(b)). This pulling together of individuals from geographically disparate regions by PCA is consistent with our observations in simulated data (Fig. 1), where we see that the genetic correlation between distant samples is not as informative about spatial ancestry as that between spatially proximate samples. On the other hand, our approach of using local genetic distances alleviates this issue and better preserves the separation between geographically dispersed populations.

Fig. 2.

PCA and GAP visualization of the North African and West Eurasian samples in the Human Origins dataset. Each data point corresponds to the sampling location of a population. (a) True sampling locations, (b) GAP reconstructed locations, (c) PCA reconstructed locations and (d) population legends. The areas of the circles are proportional to the estimated variance in the reconstructed locations of the samples in each subpopulation, while the areas of the diamonds are proportional to the number of sampled individuals from the population (Color version of this figure is available at Bioinformatics online.)

$•$ GLOBETROTTER: This dataset contains 486 669 SNPs from 1 530 individuals from 95 diverse human populations. We considered the subset of individuals sampled from Europe, the Middle East, North and East Africa and Western, Central and South Asia in order to have a fairly uniform sampling across geography. We filtered SNPs in linkage disequilibrium and violating Hardy-Weinberg equilibrium in the same manner as for the Human Origins dataset, resulting in a final dataset of 71 736 SNPs from 1046 individuals from 59 subpopulations. Applying PCA and our localization algorithm GAP to this dataset (Supplementary Fig. S3), we noticed a similar pattern as in the Human Origins dataset, where PCA pulls together individuals from Southern Europe, North Africa and the Middle East into a cluster, much more so than GAP.

3.3 Spatial reconstruction accuracy

The spatial coordinates assigned by GAP are effective at visually discerning population structure (Fig. 2, Supplementary Figs S3 and S4), even where PCA has difficulty distinguishing them. We also evaluated the performance of GAP in assigning spatial coordinates to new samples given access to the sampling locations of a subset of individuals. We used a random subset of 20% of the subpopulations in each dataset to transform the PC coordinates from PCA and the coordinates inferred by GAP into latitude-longitude coordinates (Supplementary Information §1.6). Since there is substantial variability in the reconstruction error depending on the subset that is used for rescaling coordinates, we used 100 random training data subsets and computed the reconstruction RMSE on each of them. We find that GAP exhibits 31% lower error for the Human Origins dataset than PCA, and 10% lower error for the GLOBETROTTER dataset (Supplementary Table S11).

3.4 Application to correcting ancestry confounding in GWAS

Consider the following prospective model for a quantitative phenotype y,

$$y_i=\alpha +\sum _{\ell =1}^p{\beta }_{\ell }{x}_{i\ell }+{\lambda }_i+{\epsilon }_i,$$ (4)

where α is an intercept term, ${\beta }_{\ell }$ is the effect size of SNP $\ell$ and λ_i and ${\epsilon }_i$ are the environmental and noise contributions respectively. The linear model in (4) can also be adapted to binary phenotypes using the following generalized linear model,

$$y_i\sim \mathrm{Binomial}\hspace{0.17em}(2,{\text{logit}}^{-1}(\alpha +\sum _{\ell =1}^p{\beta }_{\ell }{x}_{i\ell }+{\lambda }_i\left)\right).$$ (5)

Population structure can induce correlations between the genotypes at different SNPs $\ell$ and $\ell \prime$, and also between the genotypes and environmental contribution λ. Unaccounted structure can thus lead to spurious genotype-phenotype associations (Campbell et al., 2005).

PCA-correction (Price et al., 2006) and linear mixed models (LMM) (Kang et al., 2010) are popular approaches for dealing with ancestral confounding which use the above prospective models for testing if ${\beta }_{\ell }=0$. Song et al. (Song et al., 2015) showed that testing ${\beta }_{\ell }=0$ in (4) or (5) is equivalent to testing $R_{\ell }=1$ in the following inverse regression model,

$$\begin{array}{cc}\hfill & x_{i\ell }|y_i,{\mathbf{z}}_i\sim \mathrm{Binomial}\hspace{0.17em}(2,{\theta }_{i\ell })\hfill \\ \hfill & {\theta }_{i\ell }=\frac{{\kappa }_{\ell }{R}_{\ell }^{y_i}{q}_{\ell }({\mathbf{z}}_i)}{1-q_{\ell }({\mathbf{z}}_i)+{\kappa }_{\ell }{R}_{\ell }^{y_i}{q}_{\ell }({\mathbf{z}}_i)}.\hfill \end{array}$$ (6)

In (6), $R_{\ell }$ is the genetic risk factor of the alternate allele at SNP $\ell$ and ${\kappa }_{\ell }$ is an intercept term that absorbs the effects of the other SNPs. The retrospective model in (6) accounts for population structure by testing the distribution of the genotype conditional on the ancestry-dependent allele frequency function $q_{\ell }(\mathbf{z})$. Our association testing procedure, Stratification Correction via GAP (SCGAP), also operates in the retrospective model of (6). We first estimate the ancestry coordinates ${\widehat{\mathbf{z}}}_i$ for each individual i in the sample using our localization algorithm GAP. We then estimate ${\kappa }_{\ell }$ under the null hypothesis (while setting $R_{\ell }=1$), and estimate $R_{\ell }$ and ${\kappa }_{\ell }$ under the alternate hypothesis for each SNP as follows:

(1) Estimate the spatial allele frequency function $q_{\ell }(\mathbf{z})$ for each SNP $\ell$ by assuming that the allele frequencies vary smoothly over space. To this end, we use the squared exponential kernel,

$${\widehat{q}}_{\ell }({\widehat{\mathbf{z}}}_i)\propto \sum _{j=1}^n\frac{x_{j\ell }}{2}\hspace{0.17em}\text{exp}\hspace{0.17em}\left(-\frac{1}{2}{\Vert H^{-1}({\widehat{\mathbf{z}}}_i-{\widehat{\mathbf{z}}}_j)\Vert }^2\right)\hspace{0.17em}.$$ (7)

The two-dimensional kernel bandwidth matrix H in (7) is chosen using Scott’s rule (Scott, 1979).

(2) Estimate the genetic risk factor $R_{\ell }$ and intercept term ${\kappa }_{\ell }$ using Newton’s method (Supplementary Information §2).

In principle, one could perform the above two steps using the coordinates ${\widehat{\mathbf{z}}}_i$ inferred from some other algorithm, and we thus also compare performance using the (unknown) true ancestry coordinates ${\mathbf{z}}_i$ and using the coordinates inferred by PCA. We refer to the work of Song et al. (2015) for a comparison of the retrospective model association test common to their method GCAT and our work, with the prospective model association tests performed by the PCA-correction and LMM approaches.

3.4.1 Simulations

We simulated genotype data for $n=2000$ individuals at $p=50\hspace{0.17em}000$ SNPs using the isotropic and directional allele frequency covariance decay models described earlier. We generated phenotype data using a linear model with genotypic, ancestry-dependent and random environmental effects, with 20%, 10% and 70% contributions respectively to the phenotypic variance, and with 10 SNPs randomly chosen to have non-zero effects drawn from a standard Normal distribution. In our simulations, we inferred the two-dimensional ancestral coordinates using GAP and PCA, and also compared them against an oracle which has access to the true ancestry coordinates. Since our hypothesis test conditional on estimated allele frequencies operates in the same retrospective model as the GCAT method (Song et al., 2015), we also compare our results using GCAT with 2 and 6 latent factors. For most parameter combinations, SCGAP has higher power than PCA or GCAT (Fig. 3 and Supplementary Figs S5–S10 and Supplementary Tables S12–S13), and has similar power as the oracle procedure that uses the true ancestry coordinates in our association test.

Fig. 3.

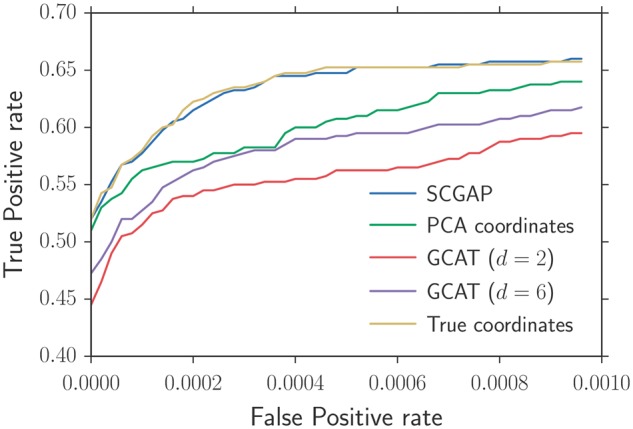
ROC curves for our stratification correction procedure with ancestral coordinates inferred using GAP (SCGAP), PCA, or using the true coordinates. We also compared our results with the GCAT method, which uses a latent factor model (indexed by d) to estimate the allele frequencies for each individual at each locus. Genotypes were drawn according to the isotropic covariance decay model with ${\alpha }_0={\alpha }_2=1$ and ${\alpha }_1=16$ (same simulation parameters as Figure 1(a)) (Color version of this figure is available at Bioinformatics online.)

3.4.2 Analysis of Northern Finland Birth Cohorts dataset

We analyzed a dataset of 10 quantitative metabolic traits from 364 590 SNPs of 5,402 individuals of a birth cohort from Northern Finland (NFBC) (Sabatti et al., 2009). We filtered individuals and SNPs using the same criteria described by Song et al. (2015), and were left with 335 143 SNPs and 5246 individuals. We added features for known confounders such as sex, oral contraceptive use, pregnancy status and fasting status according to the same procedure described in the first analysis of this dataset by Sabatti et al. (2009), and performed a Box-Cox transform on the median 95% of trait values to make the distribution of traits as close to a normal distribution as possible (We also performed the association test on the untransformed values for the C-reactive protein and Triglyceride level traits, since these traits appear exponentially distributed and the equivalence of the retrospective and prospective models that we rely on also holds for exponentially distributed traits (Song et al., 2015).). After applying genomic control (Devlin and Roeder, 1999) to correct for inflation of the log-likelihood ratios from our association test (Supplementary Fig. S11), we identified 17 significant loci (Supplementary Tables S14 and S15), 16 of which were also reported by GCAT, at a significance threshold of $p<7.2\times {10}^{-8}$ that has been used in previous works on this data. Other association tests that operate in the prospective model identify between 11 and 14 loci (Kang et al., 2010). Out of these 17 loci identified by SCGAP, 15 have been identified in independent association studies on different samples (Supplementary Table S16).

4 Discussion

In this paper, we developed a novel spatial probabilistic model of allele frequency evolution that avoids imposing any explicit parametric form for the dependence of allele frequencies on geographic location. The flexibility of our model allows us to generalize several popular parametric models of allele frequency evolution. Based on our model, we develop an ancestry localization algorithm GAP that generalizes parameter-free dimensionality reduction approaches such as PCA, and that we prove performs at least as well as PCA for large sample sizes. Our algorithm, which can be viewed as a form of manifold learning, also adds to the rich literature on theoretical population genetic models (McVean, 2009; Paschou et al., 2007; Patterson et al., 2006) that can motivate the application of PCA for detecting population structure from genotype data. Our algorithm is also very efficient: for any candidate distance threshold used for estimating local spatial distances from local genetic distances, our algorithm has computational complexity $O(n^{2}p)$ (assuming $p\gg n$), which is the cost of computing the inner product matrix from a genotype matrix with n individuals and p SNPs. This is also the same computational complexity required by dimension-reduction methods such as PCA.

Our spatial probabilistic model can also be extended to incorporate other demographic and evolutionary forces, and we leave these for future work. One can potentially infer the spatial origin of the ancestors of admixed samples by applying our method to the output of local-ancestry inference algorithms (Price et al., 2009). Admixture might also be directly incorporated into our spatial probabilistic model by jointly inferring admixture proportions along with the spatial covariance function, similar in approach to the SpaceMix (Bradburd et al., 2016) and SPA (Yang et al., 2012) models.

Our probabilistic model assumes that the decay in allele frequency covariance around a given spatial location does not depend on the location itself. This is an idealized model of isolation by distance where there are no sharp geographic or genetic barriers to random mating between spatially proximate populations. We leave the extension of our model to handle such spatial heterogeneity for future work.

We also developed an association testing procedure, SCGAP, for genotype-trait association that uses the ancestral coordinates inferred by GAP and an exponential kernel to estimate smooth allele frequency functions for every SNP. Our association test is based on a retrospective model that tests the distribution of the genotype conditional on the phenotype and the estimated allele frequency function (Song et al., 2015). We find that using the ancestry coordinates inferred by GAP in our association test performs almost as well as knowing the true spatial ancestry coordinates. Moreover, for simulated datasets, our association test exhibits slightly better performance than the GCAT test that uses a different allele frequency estimation procedure (Hao et al., 2016). On the NFBC dataset, our method recovers the same set of associations as GCAT. However, our procedure can control for ancestry confounding using just two ancestry components, as opposed to GCAT which was used with six latent factors and an intercept, in both the simulations and for the NFBC dataset. Our maximum likelihood estimation for the hypothesis test at each SNP is also very efficient, employing the quadratically converging Newton method to estimate the intercept and genetic risk factors at each SNP.

Data: The POPRES and NFBC datasets were obtained from dbGaP (Study Accession phs000145.v4.p2 and phs000276.v2.p1, respectively). The Human Origins dataset was obtained from https://genetics.med.harvard.edu/reich/Reich_Lab/Datasets_files/EuropeFullyPublic.tar.gz, and the GLOBETROTTER dataset was made available by George Busby.

Software: The source code for our software is available at https://github.com/anand-bhaskar/gap.