Abstract
Motivation
Protein complexes are one of the keys to studying the behavior of a cell system. Many biological functions are carried out by protein complexes. During the past decade, the main strategy used to identify protein complexes from high-throughput network data has been to extract near-cliques or highly dense subgraphs from a single protein–protein interaction (PPI) network. Although experimental PPI data have increased significantly over recent years, most PPI networks still have many false positive interactions and false negative edge loss due to the limitations of high-throughput experiments. In particular, the false negative errors restrict the search space of such conventional protein complex identification approaches. Thus, it has become one of the most challenging tasks in systems biology to automatically identify protein complexes.
Results
In this study, we propose a new algorithm, NEOComplex (NECC- and Ortholog-based Complex identification by multiple network alignment), which integrates functional orthology information that can be obtained from different types of multiple network alignment (MNA) approaches to expand the search space of protein complex detection. As part of our approach, we also define a new edge clustering coefficient (NECC) to assign weights to interaction edges in PPI networks so that protein complexes can be identified more accurately. The NECC is based on the intuition that there is functional information captured in the common neighbors of the common neighbors as well. Our results show that our algorithm outperforms well-known protein complex identification tools in a balance between precision and recall on three eukaryotic species: human, yeast, and fly. As a result of MNAs of the species, the proposed approach can tolerate edge loss in PPI networks and even discover sparse protein complexes which have traditionally been a challenge to predict.
Availability and Implementation
Supplementary information
Supplementary data are available at Bioinformatics online.
1 Introduction
Understanding mechanisms underlying protein complexes is one of the keys to revealing the behavior of a cell system. Protein complexes are important functional units to biological processes within a living cell. Most proteins cooperate with their protein interaction partners and form a complex to perform their biological function.
To detect protein complexes, several experimental methods have been proposed. The Tandem Affinity Purification with mass spectrometry (TAP-MS) (Rigaut et al., 1999) is one of the most preferred experimental methods to detect protein complexes. In brief, TAP-MS adds a designed TAP tag on the C-terminal of a target protein and uses beads coated with antibodies or other proteins which can bind with the tag to catch the target protein and all other proteins which are binding with the target protein. Note that these experimental approaches produce high-throughput protein–protein interaction (PPI) data, but they actually result in false positives and false negatives in protein complex detection (Berger et al., 2013) due to the designed TAP tags (Xu et al., 2010) and multiple washing in the purification steps (Li et al., 2010). Luminescence-based mammalian interactome mapping is another popular method to detect interaction between proteins (Blasche and Koegl, 2013), but it has a similar disadvantage that proteins are linked to Renilla luciferase and affinity tags. The cell lysis step also causes the disruption of weak and transient PPIs (Sahni et al., 2015; Snider et al., 2015; Taipale et al., 2014).
On the other hand, genome-scale PPI data are currently available through high-throughput methods such as yeast-two-hybrid. With the increasing amount of PPI data, automatically identifying protein complexes from PPI networks has become an efficient way to achieve the objectives of this study during the past decade. Many approaches have been developed to discover protein complexes, such as MCL (van Dongen, 2000), MCODE (Bader and Hogue, 2003), RNSC (King et al., 2004), DPClus (Altaf-UI-Amin et al., 2006), CFinder (Adamcsek et al., 2006), PCP (Chua et al., 2008), CMC (Liu et al., 2009), COACH (Wu et al., 2009), ClusterONE (Nepusz et al., 2012) and WPNCA (Peng et al., 2014). All in all, these tools aim to extract from a single PPI network near-cliques or highly connected clusters, which may have the potential to be considered protein complexes. However, as mentioned earlier, most existing PPI networks have errors and missing interactions.
Therefore, other methodologies have provided different kinds of information, such as gene expression data (Maraziotis et al., 2007; Ulitsky and Shamir, 2007), structural interface data of protein domains (Jung et al., 2010; Singh et al., 2010) and functional annotation (Cho et al., 2007, 2015; Li et al., 2007; Zhang et al., 2006). The extra information might help search for protein complexes, but they require wet lab experiments. Also, the functional annotations of proteins may be unverified or outdated. In addition, machine learning techniques have been proposed based on topological properties of protein complexes to solve this problem (Qi et al., 2008), but they require training data. Readers may refer to Li et al.’s (2010) survey for further details of these proposed approaches.
As more and more PPI data from different species have been obtained, a few studies have begun to use cross-species comparison to reveal conserved protein complexes (Davis et al., 2015; Dost et al., 2007; Hirsh and Sharan, 2006; Sharan et al., 2004). Sharan et al. defined a complete node- and edge-weighted (pairwise) orthology graph, in which each node contains two proteins from different species, and it is weighted by the sequence similarity between these two proteins. Each edge is weighted by the weights of the two interactions within every PPI network of the two species. Then they used a probabilistic model to define the likelihood ratio score of each subgraph in the orthology graph and utilized a bottom-up seed-and-extension approach to search for potential conserved protein complexes (Hirsh and Sharan, 2006; Sharan et al., 2004). Later, Dost et al. (2007) developed a tool for querying similar subgraphs between PPI networks, called QNet. They considered both node and edge similarity as well as the penalty score for node insertion and deletion to define the similarity between two subgraphs. Then, QNet employed a color coding algorithm to perform tree queries in a bounded-treewidth graph. In their computational experiments, they obtained conserved complexes by querying known yeast protein complexes against the PPI network of fly. Dutkowski and Tiuryn (2007) exploited evolution-based PPI network alignment techniques to detect conserved functional modules across multiple species. They first clustered all the proteins from different species based on pairwise sequence similarity such that the proteins in each cluster are assumed to have an evolutionary relationship. Then, the conserved protein complexes were identified based on edge weights in a conserved PPI network, in which edge weights are defined under the duplication model and speciation mode of the PPI network. Recently, Davis et al. (2015) utilized canonical correlation analysis to analyze the relationships between topological features and biological function in PPI networks, and clustered functionally conserved proteins between different species.
In summary, these previous studies used network alignment or orthology information between different species to detect conserved complexes only. However, they found only functionally similar components between PPI networks of different species (Cho et al., 2016). Moreover, network alignment approaches typically focus on clustering similar proteins across species, whereas solving the protein complex identification problem requires clustering proteins with high connectivity in the same species.
On the other hand, there are three significant challenges in protein complex identification. First, as mentioned, PPI networks may have many false positive interactions and false negative edge loss due to the limitations of high-throughput experiments, which result in the restricted search space of topology-based approaches because edge connectivity information is critical to such methods. Second, PPI networks could have gene duplication and interaction rewiring in the evolution process. More precisely, once gene duplication has occurred, the duplicated genes could have functional divergence due to sequence mutations, which may change the structure of the interface between interacting proteins (Zhao et al., 2014). Moreover, interaction rewiring could also cause corresponding proteins to lose original interactions or make new interactions with other proteins (Arabidopsis Interactome Mapping Consortium, 2011; Berg et al., 2004; Wagner, 2001). These evolutionary events may lead to distinct topology and a different number of constituent proteins in two functionally similar protein complexes from different species. To accurately determine protein complexes from topology-based PPI network alignment techniques is thus difficult.
Another problem which needs to be addressed is that the subunits of a heteromultimeric complex may not have similar sequences and functions. Therefore, sequence-only-based approaches have difficulty detecting such protein complexes.
Nevertheless, the aforementioned previous work shows that cross-species orthology information can enhance protein complex identification. For this reason, the aim of this study is to better address this challenging problem in a more principled and comprehensive way by utilizing functional orthology information across multiple species to expand the search space of protein complex identification and compensate for the false negative edge loss in PPI networks.
Unlike most of the previous protein complex identification approaches which searched for protein complexes in a single PPI network or aligned only conserved protein complexes across species, our algorithm, NEOComplex, provides a seed-and-extension approach for identifying protein complexes by appending MNAs. More importantly, the proposed algorithm discovers some biological examples that cannot be found by conventional complex identification tools. Precisely, this evidence, such as the Mob1p–Dbf2p kinase complex of human, the chaperonin containing TCP-1:oligomeric protein prefoldin (CCT:PFD) complex of yeast, and the tubulin complex of fly, derived from our computational experiment across the three species, have very low density. Furthermore, the proposed algorithm identifies the protein complexes even if the sequence similarity between the subunits in these complexes is non-obvious. Finally, we show that NEOComplex outperforms five popular complex identification tools on three species: human, yeast and fly. It is expected that approaches such as ours, which employ sequence and local topology through seed-and-extension, will expand protein complex identification as network data continues to grow.
2 Methods
We first find local clusters through seed-and-extension in a single PPI network and then pursue the intuition that by combing orthology information of each protein in these clusters across multiple species, the algorithm can compensate for missing PPIs and be tolerant to the effects of noise in PPI data. To achieve this goal, we also designed a new edge clustering coefficient (NECC) and apply this measure to orthology relationships which are incorporated into MNA.
2.1 New edge clustering coefficient
In order to better quantify the connectivity between two nodes, we present a new edge clustering coefficient (NECC) in this study. As the clustering coefficient of a node cannot indicate how its neighbors are interconnected (Soffer and Vázquez, 2005), Wang et al. (2012) and Peng et al. (2014) introduced the ECC to predict essential proteins and protein complexes. For each edge, they attempted to measure the closeness between its two end nodes as well as the entire neighborhood of the nodes.
| (1) |
where a PPI network is represented by an undirected graph , and each node represents a protein and each edge represents an interaction between nodes u and v. is defined to be the set of all common neighbors of u and v. The degree of node u is denoted by d(u).
To characterize in-depth connectivity among the neighborhoods of the common neighbors of two adjacent nodes u and v, we introduce the following NECC. The main idea is to estimate the neighborhood connectivity of u and v in a more hierarchical way. Precisely, we further look at the common neighbors of the common neighbors of the two adjacent nodes. The NECC is defined as follows:
| (2) |
where
| (3) |
Obviously, NECC considers more widely the connectivity of the entire neighborhood of two adjacent nodes and may better determine whether a protein belongs to a complex. Based on such an NECC measure, we identify protein complexes in a given center species by using a seed-and-extension approach and combine this with the functional orthology clusters derived by MNA across other species.
We remark that there have been several other mechanisms for describing local connectivity. For example, the edge-GDV (Graphlet Degree Vector) centrality (Solava et al., 2012) clusters edges based on the similarity of edge-GDV, where edge-GDV illustrates the topological feature of the involving neighborhood of an edge (Milenković and Przulj, 2008; Milenković et al., 2010). Solava et al. (2012) showed that edge-GDV is a sensitive measure of the topological similarity of edges, and the proteins clustered through edge-GDV centrality have more closely related functions. In this study, we alternatively used NECC to cluster proteins due to its emphasis on the connectivity between their neighborhoods.
2.2 Weighted edge density
To ensure the high quality of our candidate complexes, we extend the definition of edge density defined by Coleman and More (1983) and redefined weighted edge density. We use weighted edge density to remove the proteins that have a weak connection with the other proteins in a candidate complex. Given a graph , the weighted edge density is defined as follows:
| (4) |
where w(e) is the NECC weight of edge e.
2.3 Functional orthologs
Any kind of orthology relationship between different species can be used in NEOComplex. However, a series of studies used network alignment to construct the orthology relationship and find conserved patterns or pathways between PPI networks of different species (Kelly et al., 2003; Sharan et al., 2004). In this study, we employed one of the popular MNA methods, IsoRankN (Liao et al., 2009), to construct the functional orthology relationship between proteins of multiple species. IsoRankN builds up an MNA by using the Personalized PageRank algorithm to do the local partitioning of the functional similarity graph constructed by the IsoRank algorithm (Singh et al., 2008); it has been demonstrated that IsoRankN outperforms other existing global network alignment algorithms in coverage and consistency on multiple species. Also, IsoRankN is error tolerant, computationally efficient and can provide many-to-many functional similarity relationships between proteins in different species. In the Supplementary Material, we compare IsoRankN with several recent MNA tools and show the advantages of IsoRankN over them. Here, we note that the MNA tools cannot successfully derive protein complexes on their own because they consider functionally conserved clusters only as opposed to protein complex identification approaches.
2.4 Redundant complex filtering
We use the overlapping score OS(A, B) to measure the similarity of two protein complexes A, B and remove redundant predicted complexes. If the OS score of two protein complexes is larger than a given threshold, the complex with the lower weight edge density is eliminated. The definition of OS(A, B) is as follows:
| (5) |
where and are the protein numbers of a predicted complex A and a known complex B, respectively, and is the number of common proteins between complex A and complex B. Notably, the OS score has been used in many previous studies (Bader and Hogue, 2003; Jung et al., 2010; Li et al., 2008; Peng et al., 2014; Wu et al., 2009) to determine whether a predicted complex matches a known complex. Typically, if the , A and B are considered to be matched. We count only those proteins that belong to at least one known complex in each output cluster.
2.5 Main algorithm
Our algorithm, NEOComplex, proceeds in the following steps:
For every protein v in a chosen species, order the neighbors of v by the NECC weight of the edge between v and its neighbors.
Let each protein be a seed. Insert one neighbor of the seed protein at a time into a set from the neighborhood with the highest NECC weight. Then, repeat to add neighbors of the neighbor, if needed, with the currently highest NECC, until the weighted edge density of the complex is lower than the threshold (i.e.
After the extension step, such a complex is considered a candidate complex (called a NECC complex).
Collect all candidate complexes and filter out the highly overlapping candidate complexes and the candidate complexes with less than three member proteins.
For each of the target NECC complexes, include the previously-determined functional orthologs of all the proteins in the complex from the other species as a cluster. Consider those proteins which are included by a functional orthology relationship from the other species to be orthology complexes. For each orthology complex, calculate NECC pairwisely for those protein pairs which do not have an edge in their PPI network and add an edge between a protein pair if the NECC weight between them is non-zero. Finally, remove the proteins that do not have any edge in the orthology complexes.
Output complex clusters, where each cluster contains one NECC complex and several orthology complexes (as shown in Fig. 1).
Fig. 1.
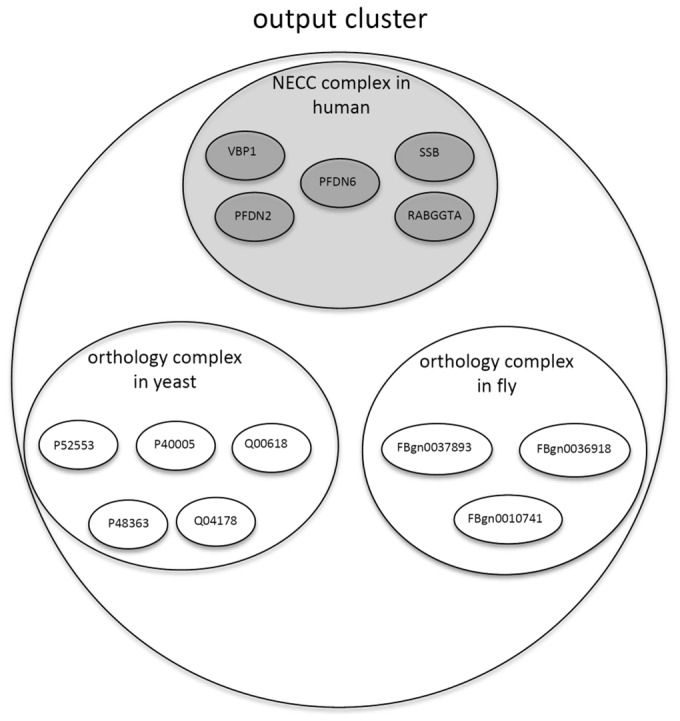
An example illustrating one of the output clusters derived by NEOComplex: each output cluster contains one NECC complex extracted from a single PPI network (e.g. the PPI network of human) based on NECC and may derive additional orthology complexes across other species (e.g. from yeast and fly) based on the orthology information of the proteins in the NECC complex
2.6 Performance comparison
We compared the performance of NEOComplex against five protein complex identification approaches: MCL (van Dongen, 2000), MCODE (Bader and Hogue, 2003), CMC (Liu et al., 2009), COACH (Wu et al., 2009) and ClusterONE (Nepusz et al., 2012).
Prior work: Basically, these approaches can be divided into two categories: local clustering of a single PPI network: MCL, MCODE and ClusterONE, and searching for clique-based complexes in a single PPI network: CMC and COACH. MCL (Markov Clustering) is a classic graph clustering algorithm which applied two operators, expansion and inflation, on an adjacency matrix to simulate random walks within the graph. The expansion operator was in charge of extending the distance of random walks. The inflation operator then changed the probabilities for all the walks in the graph, which increased the probabilities of intra-cluster walks and reduced the probabilities of inter-cluster walks. Finally, iterative expansion and inflation separated the graph into many different segments. MCODE is a seed-and-extension approach, which initially assigned every node a weight, based on their local neighborhood densities. Then, it chose the nodes with high weights as seed nodes to form initial clusters and expanded these clusters by outward traversing from the seeds. Finally, MCODE filtered out the non-dense subgraphs and outputted overlapping complexes. On the other hand, CMC, a maximal-clique-based algorithm proposed by Liu et al. (2009) identified protein complexes from a single PPI network. First, CMC applied a maximal clique mining algorithm (Tomita et al., 2006) to obtain all maximal cliques. CMC then weighed all the interactions based on a reliability measure (Liu et al., 2008) and ranked each clique with its weighted density. In the last step, for any two highly overlapping cliques, CMC either merged the two cliques into one or removed the one that had lower weighted density depending on its inter-connectivity. COACH (Wu et al., 2009) also detected protein complexes based on finding cliques or highly dense subgraphs. Moreover, it considered the core–attachment structure of protein complexes to provide insights into the inherent organization of protein complexes. Recently, ClusterOne (Nepusz et al., 2012), which is most similar to local clustering, is one of the state-of-the-art protein complex identification algorithms. Nepusz et al. (2012) defined a cohesiveness score for a group of proteins based on two properties of a subgraph representing a protein complex: (1) the subgraph should have many reliable interactions between its subunits, and (2) it should be well separated from the rest of the graph. Also, a penalty term was defined to model the uncertainty in the data by assuming the existence of undiscovered interactions in the PPI network. Finally, they used a greedy seed-and-extension procedure to generate predicted protein complexes.
We refer to the previous studies (Brohee and van Helden, 2006; Liu et al., 2009; Nepusz et al., 2012; Wu et al., 2009) and follow their recommended settings. A list of the parameter settings used in our experiments is as follows. For MCL, we set inflation to 3.0. For MCODE, we set node score percentage to 0, depth to 100 and percentage for complex fluffing to 0.3 (Brohee and van Helden, 2006). For CMC, we set the number of iterations to 1, filter method to Adjusted CD-distance, filter min score to 0, add method to Adjusted CD-distance, add min score to 0, min size to 3, overlap threshold to 0.5 and merge threshold to 0.15 (Liu et al., 2009). For COACH, we used the recommended setting. For ClusterONE, we used the recommended parameter setting and set density threshold to 0.6, merging threshold to 0.8, and penalty value of each node to 2 (Nepusz et al., 2012).
3 Results
Here, we introduce the evaluation method and compare NEOComplex against the five well-known complex identification approaches. We demonstrate that our predicted complexes match with the reference set and the algorithm achieves the best balance in precision and sensitivity. Moreover, we show that MNA is capable of tolerating the edge loss of PPI networks and discovering very sparse complexes that have missing interactions in PPI networks. Note that we did not compare NEOComplex against the previous approaches for cross-species comparison because these studies focused on finding only conserved protein complexes between species rather than all possible protein complexes. Our goal is to use network similarity to expand the list of complexes.
3.1 Datasets
We carried out all the experiments on three eukaryotic PPI networks: Homo sapiens (human), Saccharomyces cerevisiae (yeast) and Drosophila melanogaster (fly). For human, the PPI network was constructed by combining the data from HPRD (Human Protein Reference Database, 7/2010) (Keshava Prasad et al., 2009) and BioGRID (version 3.2.109) (Chatr-aryamontri et al., 2013). For yeast and fly, both of the PPI networks were retrieved from BioGRID. The numbers of nodes and edges are 15459 and 144895, 6194 and 74852, and 7970 and 36047 in the three PPI networks of human, yeast, and fly, respectively.
3.2 Reference sets
For the purpose of evaluating the predicted protein complexes, we used the protein complexes catalog compiled by Vinayagam et al. (2013). The catalog was divided into two parts: one was extracted from the literature and the other was predicted by their approach. Here, we used only the former to compile our reference set due to the high confidence interactions. In particular, for human, they used the data collected from the Comprehensive Resource of Mammalian protein complexes (CORUM) (Ruepp et al., 2008), and protein complexes were annotated by GO (Ashburner et al., 2000), Proteins Interacting in the Nucleus database (PINdb) (Luc and Tempst, 2004) and KEGG modules (Kanehisa et al., 2012). For yeast, the data source came from the Wodak database (CYC2008) (Pu et al., 2009), PINdb and GO complexes. For fly, they used GO complexes and 556 protein complexes identified by the affinity purification mass spectrometry pull-down study (AP-MS) in Guruharsha et al. (2011). There were 3638, 2173 and 3077 protein complexes for human, yeast and fly, respectively. We further eliminated those proteins that are not in our PPI networks. Moreover, complexes that contained at most two proteins were ignored. Consequently, there were a total of 2351, 1278 and 1637 protein complexes in the reference sets of human, yeast and fly, respectively.
3.3 Quality of complex identification
To formally evaluate the quality of our predicted results, we calculated two statistic measures which are widely used in the literature: precision and recall. Precision is the fraction of the number of the predicted complexes that match at least one known complex over the total number of all predicted complexes. On the other hand, recall is the fraction of the known complexes that match at least one predicted complex among all known complexes. The F-measure is the harmonic mean of precision and recall and shows the overall performance of a predicted result. The definition of F-measure is as follows:
| (6) |
As mentioned in Section 2, we used the overlapping score (OS) to determine the correctness of our predicted complexes. Note that a predicted complex is defined to be matched with a known complex if the OS score between them is not <0.2. Moreover, for each predicted complex, we only count its best match with the highest OS score in our experimental results.
3.4 Performance comparison result
We compared the performance of NEOComplex against the five protein complex identification approaches (see Section 2.6). For our algorithm, we found that the best value for the threshold of weighted edge density through experimental observation was 0.009. Similar to many previous studies, we set the OS threshold to 0.2 to determine whether two complexes are matched or not. For IsoRankN, since the topology of protein complex could be rewired between species, we set alpha to 0.2 to reduce the effect of topology, and set K to 3.
Table 1 shows the comparison results in the PPI networks of the three species. The results demonstrate that NEOComplex outperforms the other approaches in F-measure in all cases. In particular, the performance of NEOComplex is stable in the PPI network of each species. This demonstrates that our algorithm has the best balance between precision and recall. More precisely, as shown in Table 1, MCODE and MCL have good precision in yeast (and MCODE also has good precision in fly); however, their recall is very low due to the fact that the number of their total output complexes is small. The number of our output complexes is at least 42 and 5 times larger than that of MCODE’s complexes in yeast and fly, respectively (777 versus 18 for yeast, and 483 versus 90 for fly). The number of our output complexes for yeast is 16 times as large as MCL’s (777 versus 46). Moreover, although ClusterONE has better precision than NEOComplex for the three species, its recall is relatively smaller (0.26 versus 0.47 for human, 0.28 versus 0.41 for yeast and 0.19 versus 0.29 for fly). The number of our output complexes is at least twice as large as that of ClusterONE’s complexes for every species (1154 versus 495 for human, 777 versus 259 for yeast and 483 versus 224 for fly). On the other hand, CMC and COACH generated a large set of predicted complexes, and thus have better results in #Matched complexes, i.e. more predicted complexes that match a known complex. However, NEOComplex actually has similar performance in the number of matched known complexes (see Column 4 in Table 1), though it generally has higher F-measure than that of CMC and COACH.
Table 1.
Performance comparison result
| Tools | #Matched complexes | #Total complexes | #Matched known complexes | Precision | Recall | F-measure |
|---|---|---|---|---|---|---|
|
Human | ||||||
| NEOComplex | 538 | 1154 | 1100 | 0.47 | 0.47 | 0.47 |
| MCL | 153 | 389 | 391 | 0.39 | 0.17 | 0.23 |
| MCODE | 33 | 63 | 115 | 0.52 | 0.05 | 0.09 |
| CMC | 1402 | 5417 | 1673 | 0.26 | 0.71 | 0.38 |
| COACH | 1024 | 4274 | 1150 | 0.24 | 0.49 | 0.32 |
| ClusterONE | 271 | 495 | 609 | 0.55 | 0.26 | 0.35 |
|
Yeast | ||||||
| NEOComplex | 334 | 777 | 519 | 0.43 | 0.41 | 0.42 |
| MCL | 27 | 46 | 72 | 0.59 | 0.06 | 0.10 |
| MCODE | 17 | 18 | 41 | 0.94 | 0.03 | 0.06 |
| CMC | 367 | 2316 | 520 | 0.16 | 0.41 | 0.23 |
| COACH | 341 | 1517 | 333 | 0.22 | 0.26 | 0.24 |
| ClusterONE | 184 | 259 | 359 | 0.71 | 0.28 | 0.40 |
|
Fly | ||||||
| NEOComplex | 191 | 483 | 468 | 0.40 | 0.29 | 0.33 |
| MCL | 113 | 324 | 292 | 0.35 | 0.18 | 0.23 |
| MCODE | 45 | 90 | 97 | 0.5 | 0.06 | 0.11 |
| CMC | 167 | 445 | 453 | 0.38 | 0.28 | 0.32 |
| COACH | 274 | 701 | 484 | 0.39 | 0.30 | 0.33 |
| ClusterONE | 131 | 224 | 317 | 0.58 | 0.19 | 0.29 |
Note:#Matched complexes is the number of predicted complexes that match at least a known complex. #Total complexes is the total number of predicted complexes generated by each approach. #Matched known complexes is the number of known complexes in a reference set matched with the complexes derived by each approach. Note that the number of the known complexes in human, yeast and fly are 2351, 1278 and 1637, respectively.
As shown in Table 1, ClusterONE has good precision in the three species. Note that, like our algorithm, ClusterONE performed a greedy seed-and-extension approach to generating predicted protein complexes. The difference between these two seed-and-extension algorithms is how to quantify the within-connectivity of a protein complex. ClusterONE used a cohesiveness score to describe how likely a cluster of proteins is a complex (Nepusz et al., 2012). In contrast, in this study, we developed NECC to measure the closeness between two proteins, i.e. the weight of their PPI edge. Moreover, we incorporated orthology information into protein complex identification by appending network alignments across multiple species. We have further compared with ClusterONE in the Supplementary Material.
3.5 Robustness and error-tolerance
Due to many false negatives in most PPI networks, we further verify the error tolerance of NEOComplex to PPI edge loss. For this purpose, we randomly removed the PPI edges from our test yeast network (with 6194 nodes and 74 852 edges) to create four simulated yeast networks, and evaluated the performance of NEOComplex on them (Liu et al., 2009). The current edge density of the test yeast network is 0.0039. We reduced the edge number from 74 852 to 65 211, 55 621, 46 031 and 38 400 to uniformly decrease the edge density of the yeast network from 0.0039 to 0.0034, 0.0029, 0.0024 and 0.002, respectively. Note that the value of the lowest edge density, 0.002, is the same as the edge density of the yeast PPI network in highly reliable Krogan dataset (Krogan et al., 2006). Another highly confident PPI datasets such as Gavin et al. (2006) and Collins (2007) have larger edge density though.
Figure 2 shows that the performance of NEOComplex remains stable in F-measure for the four simulated yeast networks. Specifically, in comparison with the performance of the other approaches conducted in the simulated yeast network with the lowest edge density, the F-measure of NEOComplex is 0.31, while MCL, CMC, COACH and ClusterONE derived relatively lower F-measure: 0.03, 0.18, 0.19 and 0.24, respectively. Note that MCODE output only eight complexes in this experiment. These tools cannot perform as they did because the edge connectivity information is critical to them. NEOComplex utilized functional orthology information and can tolerate the effects of missing interactions in PPI data. More precisely, for the simulated yeast network with edge density equal to 0.002, 22% (143/641) of total output complexes, 25% (58/233) of matched complexes and 35% (119/343) of matched known complexes are contributed by orthology complexes in our result. We will discuss more benefits derived by the orthology complexes in the next section.
Fig. 2.
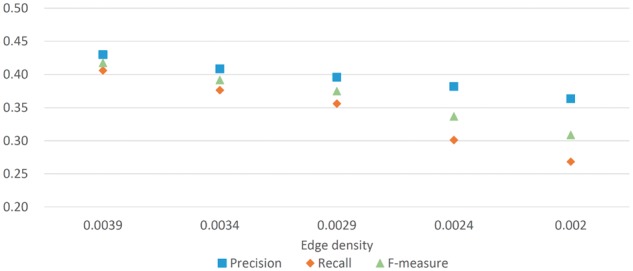
Simulation experiments for the robustness of NEOComplex
3.6 Orthology complexes
Our other contribution is that we demonstrate that there are some predicted complexes that cannot be revealed by other conventional approaches due to false negative edge loss in PPI networks. We call these complexes sparse complexes. These are in fact not sparse in real biological systems, but they are sparse in PPI networks due to experimental false negatives. Note that each cluster derived by NEOComplex contains one NECC complex and several orthology complexes, as illustrated in Figure 1. In Figure 3, the proteins colored in gray belong to the NECC complex in each cluster. Here, in particular, we consider the sparse orthology complexes and show the benefit of utilizing MNA. The number of such complexes is 17, 49 and 43 in human, yeast and fly, respectively. These complexes actually contain few PPI edges so that they are neither near-cliques nor highly dense clusters. Precisely, these complexes have very low density no matter what kind of edge weight is used to define density. The reason why such sparse protein complexes can be discovered by NEOComplex is that, MNA across different species can compensate for missing PPI edges in one species from the other species.
Fig. 3.
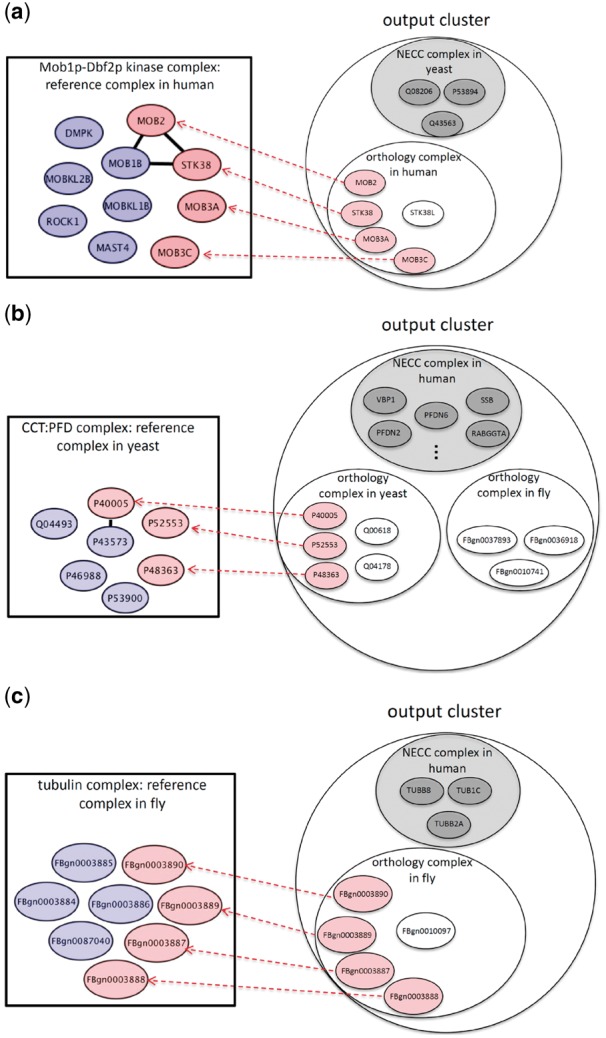
The protein complexes that can only be discovered by NEOComplex with functional orthology information: the pink nodes represent the matched proteins in the reference complexes by NEOComplex in (a) human, (b) yeast and (c) fly
Figure 3a–c shows three examples of these predicted complexes. The first example is the Mob1p–Dbf2p kinase complex of human cells (see Fig. 3a). There are only three edges between the member proteins in this complex, but our algorithm can correctly predict the Mob1p–Dbf2p kinase complex in the PPI network of human and match four proteins (in pink color) in the complex. For the other two examples, the CCT:PFD complex of yeast (see Fig. 3b) and the tubulin complex of fly (see Fig. 3c), they have few interactions between member proteins in their corresponding PPI networks (i.e. only one edge in the CCT:PFD complex and no edge in the tubulin complex), which results in restricted search space. Similarly, NEOComplex reveals these two complexes through network alignment across species. We specifically consider the performance of the orthology complexes derived by our algorithm. As mentioned, NEOComplex can extract sparse complexes, because they are actually derived from orthology complexes. Table 2 presents the detailed performance of the orthology complexes, which emphasizes the benefit of the multiple alignment process. The numbers of the total predicted orthology complexes are only 247, 195 and 147 for human, yeast and fly, respectively (i.e. only 21.4, 25.0 and 30.4% of the total output complexes obtained for human, yeast and fly, respectively). Note that the average precision of our orthology complexes can achieve over 32%, which guarantees the quality of such network-alignment-based complexes. Moreover, we filtered out those orthology complexes that can be identified by other approaches and derived the so-called sparse complexes (as shown in Fig. 3). Most of the sparse complexes have too few interaction edges in their PPI networks to be detected. Our algorithm, surprisingly, can discover such complexes with the assistance of MNA across the three species. The ratios of the sparse complexes derived to the total output orthology complexes are 6.8% for human, 25.1% for yeast and 29.2% for fly.
Table 2.
Performance of orthology complexes identification
| Species | #Matched orthology complexes | #Total orthology complexes | Precision | #Sparse complexes |
|---|---|---|---|---|
| Human | 71 | 247 | 0.29 | 17 |
| Yeast | 68 | 195 | 0.35 | 49 |
| Fly | 51 | 147 | 0.35 | 43 |
Note:#Matched orthology complexes is the number of identified orthology complexes that match at least one known complex. #Sparse complexes represents the number of complexes that can only be found by NEOComplex.
4 Conclusion
This study has demonstrated the benefit of combing orthology relationships across species with the proposed seed-and-extension approach to identify protein complexes. Our algorithm, NEOComplex, can include the result of an arbitrary MNA algorithm as an input to provide orthology information. Moreover, in the Supplementary Material, we further analyzed the effect of weighted edge density threshold used in NEOComplex and ClusterONE. Also, we investigated the performance of using different functional orthology relationships obtained by different network alignment algorithms. The further comparison has showed the usefulness of our algorithm by incorporating orthology information. We hope that our algorithm fills the gap in network data to enable better identification of particularly sparse protein complexes, which may reveal novel biological findings.
Funding
This work was supported by the National Science Council (Taiwan) (NSC102-2221-E007-075-MY3 and NSC105-2628-E007-010-MY3 to C.-S.L. and C.-Y.M.) and Australian Research Council Grant (ARC DP130104770 to Y.-P.P.C.). This work was also supported by the National Institutes of Health (United States) (NIH R01GM081871 to B.B.).
Conflict of Interest: none declared.
Supplementary Material
References
- Adamcsek B. et al. (2006) Cfinder:locating cliques and overlapping modules in biological networks. Bioinformatics, 22, 1021–1023. [DOI] [PubMed] [Google Scholar]
- Altaf-Ul-Amin M. et al. (2006) Development and implementation of an algorithm for detection of protein complexes in large interaction networks. BMC Bioinformatics, 7, 207.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arabidopsis Interactome Mapping Consortium. (2011) Evidence for network evolution in an Arabidopsis interactome map. Science, 333, 601–607. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ashburner M. et al. (2000) Gene Ontology: tool for the unification of biology. Nat. Genet., 25, 25–29. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bader G.D., Hogue C.W.V. (2003) An automated method for finding molecular complexes in large protein interaction networks. BMC Bioinformatics, 4, 2.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berg J. et al. (2004) Structure and evolution of protein interaction networks: a statistical model for link dynamics and gene duplications. BMC Evol. Biol., 4, 51.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berger B. et al. (2013) Computational solutions for omics data. Nat. Rev. Genet, 14, 333–346. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blasche S., Koegl M. (2013) Analysis of protein-protein interactions using LUMIER assays. Methods Mol. Biol., 1064, 17–27. [DOI] [PubMed] [Google Scholar]
- Brohee S., van Helden J. (2006) Evaluation of clustering algorithms for protein-protein interaction networks. BMC Bioinformatics, 7, 488.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chatr-Aryamontri A. et al. (2013) The BioGRID interaction database: 2013 update. Nucleic Acids Res., 41, D816–D823. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cho H. et al. (2016) Compact integration of multi-network topology for functional analysis of genes. Cell Systems, 3, 540–548. Also appeared in RECOMB (2015), LNCS, vol. 9029, 62–64. [DOI] [PMC free article] [PubMed]
- Cho Y.R. et al. (2007) Semantic integration to identify overlapping functional modules in protein interaction networks. BMC Bioinformatics, 8, 265.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chua H.N. et al. (2008) Using indirect protein-protein interactions for protein complex prediction. J. Bioinform. Comput. Biol., 6, 435–466. [DOI] [PubMed] [Google Scholar]
- Coleman T.F., More J.J. (1983) Estimation of sparse Jacobian matrices and graph coloring problems. SIAM J. Numer. Anal., 20, 187–209. [Google Scholar]
- Collins S.R. et al. (2007) Toward a comprehensive atlas of the physical interactome of Saccharomyces cerevisiae. Mol. Cell. Proteomics, 6, 439–450. [DOI] [PubMed] [Google Scholar]
- Davis D. et al. (2015) Topology-function conservation in protein-protein interaction networks. Bioinformatics, 31, 1632–1639. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dost B. et al. (2007) QNet: a tool for querying protein interaction networks. In: Proceedings of the Of the 11th Research in Computational Molecular Biology (RECOMB), LNCS, 4453, 1–15. [DOI] [PubMed]
- Dutkowski J., Tiuryn J. (2007) Identification of functional modules from conserved ancestral protein-protein interactions. Bioinformatics, 23, 149–158. [DOI] [PubMed] [Google Scholar]
- Gavin A. et al. (2006) Proteome survey reveals modularity of the yeast cell machinery. Cell, 440, 631–636. [DOI] [PubMed] [Google Scholar]
- Guruharsha K.G. et al. (2011) A protein complex network of Drosophila melanogaster. Cell, 147, 690–703. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hirsh E., Sharan R. (2006) Identification of conserved protein complexes based on a model of protein network evolution. Bioinformatics, 23, e170–e176. [DOI] [PubMed] [Google Scholar]
- Jung S.H. et al. (2010) Protein complex prediction based on simultaneous protein interaction network. Bioinformatics, 26, 385–391. [DOI] [PubMed] [Google Scholar]
- Kanehisa M. et al. (2012) KEGG for integration and interpretation of large-scale molecular data sets. Nucleic Acids Res., 40, D109–D114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kelly R.M. et al. (2003) Conserved pathways within bacteria and yeast as revealed by global protein network alignment. PNAS, 100, 11394–11399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keshava Prasad T.S. et al. (2009) Human protein reference database!X2009 update. Nucleic Acids Res., 37, D767–D772. [DOI] [PMC free article] [PubMed] [Google Scholar]
- King A.D. et al. (2004) Protein complex prediction via cost-based clustering. Bioinformatics, 20, 3013–3020. [DOI] [PubMed] [Google Scholar]
- Krogan N.J. et al. (2006) Global landscape of protein complexes in the yeast Saccharomyces cerevisiae. Nature, 440, 637–643. [DOI] [PubMed] [Google Scholar]
- Li X.L. et al. (2007) Discovering protein complexes in dense reliable neighborhoods of protein interaction networks. IN: Proceedings of the Computational Systems Bioinformatics (CSB), pp. 157–168. [PubMed]
- Li X.L. et al. (2010) Computational approaches for detecting protein complexes from protein interaction networks: a survey. BMC Genomics, 11(Suppl. 1), S3.,. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li M. et al. (2008) Modifying the DPClus algorithm for identifying protein complexes based on new topology structures. BMC Bioinformatics, 9, 398.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liao C.S. et al. (2009) IsoRankN: spectral methods for global alignment of multiple protein networks. Bioinformatics, 25, i253–i258. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu G. et al. (2008) Assessing and predicting protein interactions using both local and global network topological metrics. In: Proceedings of the 19th International Conference on Genome Informatics. Gold Coast, Australia, pp. 138–149. [PubMed]
- Liu G. et al. (2009) Complex discovery from weighted PPI networks. Bioinformatics, 25, 1891–1897. [DOI] [PubMed] [Google Scholar]
- Luc P.V., Tempst P. (2004) PINdb: a database of nuclear protein complexes from human and yeast. Bioinformatics, 20, 1413–1415. [DOI] [PubMed] [Google Scholar]
- Maraziotis I.A. et al. (2007) Growing functional modules form a seed protein via integration of protein interaction and gene expression data. BMC Bioinformatics, 8, 408.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Milenković T., Przulj N. (2008) Uncovering biological network function via graphlet degree signatures. Cancer Inf., 6, 257–273. [PMC free article] [PubMed] [Google Scholar]
- Milenković T. et al. (2010) Uncovering biological network function via graphlet degree signatures. Cancer Informatics, 9, 121–137. [PMC free article] [PubMed] [Google Scholar]
- Nepusz T. et al. (2012) Detecting overlapping protein complexes in protein-protein interaction networks. Nat. Methods, 9, 471–472. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peng W. et al. (2014) Identification of protein complexes using weighted Pagerank-nibble algorithm and core-attachment structure. IEEE/ACM Trans. Comput. Biol. Bioinformatics, 12, 179–192. [DOI] [PubMed] [Google Scholar]
- Pu S. et al. (2009) Up-to-date catalogue of yeast protein complexes. Nucleic Acids Res., 37, 825–831. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Qi Y. et al. (2008) Protein complex identification by supervised graph local clustering. Bioinformatics, 24, i250–i268. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rigaut G. et al. (1999) A generic protein purification method for protein complex characterization and proteome exploration. Nat. Biotech., 17, 1030–1032. [DOI] [PubMed] [Google Scholar]
- Ruepp A. et al. (2008) CORUM: the comprehensive resource of mammalian protein complexes. Nucleic Acids Res., 36, D646–D650. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sahni N. et al. (2015) Widespread macromolecular interaction perturbations in human genetic disorders. Cell, 161, 647–660. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sharan R. et al. (2005) Identification of protein complexes by comparative analysis of yeast and bacterial protein interaction data. J. Comp. Biol., 12, 835–846. [DOI] [PubMed]
- Singh R. et al. (2008) Global alignment of multiple protein interaction networks with application to functional orthology detection. Proc. Natl Acad. Sci. USA, 105, 12763–12768. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Singh R. et al. (2010) Struct2Net: a web service to predict protein-protein interactions using a structure-based approach. Nucleic Acids Res., 38, W508–W515. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Snider J. et al. (2015) Fundamentals of protein interaction network mapping. Mol. Syst. Biol., 11, 848.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Soffer S.N., Vázquez A. (2005) Network clustering coefficient without degree-correlation biases. Phys. Rev. E, 71, 057101.. [DOI] [PubMed] [Google Scholar]
- Solava R.W. et al. (2012) Graphlet-based edge clustering reveals pathogen-interacting proteins. Bioinformatics, 28, i480–i486. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taipale M. et al. (2014) A quantitative chaperone interaction network reveals the architecture of cellular protein homeostasis pathways. Cell, 158, 434–448. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tomita E. et al. (2006) The worst-case time complexity for generating all maximal cliques and computational experiments. Theor. Comput. Sci, 363, 28–42. [Google Scholar]
- Ulitsky I., Shamir R. (2007) Identification of functional modules using network topology and high-throughput data. BMC Syst. Biol., 1, 8.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Dongen S. (2000) Graphclusteringbyflowsimulation.PhD thesis, University of Utrecht, Utrecht, The Netherlands.
- Vinayagam A. et al. (2013) Protein complex-based analysis framework for high-throughput data sets. Sci. Signal, 6, rs5.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang J. et al. (2012) Identification of essential proteins based on edge clustering coefficient. IEEE/ACM Trans Comput Biol a Bioin, 9, 1070–1080. [DOI] [PubMed] [Google Scholar]
- Wagner A. (2001) The yeast protein interaction network evolves rapidly and contains few redundant duplicate genes. Mol. Biol. Evol., 18, 1283–1292. [DOI] [PubMed] [Google Scholar]
- Wu M. et al. (2009) A core-attachment based method to detect protein complexes in PPI networks. BMC Bioinformatics, 10, 169.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu X. et al. (2010) The tandem affinity purification method: an efficient system for protein complex purification and protein interaction identification. Protein Express. Purif., 72, 149–156. [DOI] [PubMed] [Google Scholar]
- Zhang S.H. et al. (2006) Prediction of protein complexes based on protein interaction data and functional annotation data using kernel methods. Lnbi, 4115, 514–524. [Google Scholar]
- Zhao N. et al. (2014) Determining effects of non-synonymous SNPs on protein-protein interactions using supervised and semi-supervised learning. PLoS Comput. Biol., 10, e1003592.. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


