Identification of Homophily and Preferential Recruitment in Respondent-Driven Sampling

Abstract

Respondent-driven sampling (RDS) is a link-tracing procedure used in epidemiologic research on hidden or hard-to-reach populations in which subjects recruit others via their social networks. Estimates from RDS studies may have poor statistical properties due to statistical dependence in sampled subjects’ traits. Two distinct mechanisms account for dependence in an RDS study: homophily, the tendency for individuals to share social ties with others exhibiting similar characteristics, and preferential recruitment, in which recruiters do not recruit uniformly at random from their network alters. The different effects of network homophily and preferential recruitment in RDS studies have been a source of confusion and controversy in methodological and empirical research in epidemiology. In this work, we gave formal definitions of homophily and preferential recruitment and showed that neither is identified in typical RDS studies. We derived nonparametric identification regions for homophily and preferential recruitment and showed that these parameters were not identified unless the network took a degenerate form. The results indicated that claims of homophily or recruitment bias measured from empirical RDS studies may not be credible. We applied our identification results to a study involving both a network census and RDS on a population of injection drug users in Hartford, Connecticut (2012–2013).

Epidemiologic studies of stigmatized or criminalized populations—such as drug users, men who have sex with men, or sex workers—can be challenging because potential subjects may be unwilling to participate if they fear exposure or persecution. Respondent-driven sampling (RDS) is a widely used procedure for recruiting members of hidden or hard-to-reach populations (1, 2). Starting with a set of initial participants called “seeds,” subjects are interviewed and given a small number of coupons they use to recruit other members of the study population. Participants recruit others by giving them a coupon bearing a unique code and information about how to participate in the study. Each subject receives a reward for being interviewed and another for every new subject they recruit. Most methodological research on RDS assumes the existence of a social network connecting members of the target population, where recruitments take place across edges in that network (3–5). Subjects in an RDS study typically do not provide identifying information about their network alters; instead, researchers measure respondents’ social network degree (also sometimes called their “egocentric network size”) in the target population. Because RDS only reveals recruitment links, many links in the network of respondents remain unobserved.

Because the RDS recruitment process is network-based, the traits of recruiter and recruitee may not be independent (6, 7). Two mechanisms account for this dependence. First, homophily is the tendency for people to exhibit social ties with others who share their traits. Second, recruiters in RDS choose new recruits from among their network neighbors. Preferential recruitment of subjects with certain traits, conditional on existing social ties, can make RDS recruitment chains appear more homogeneous, even in the absence of network homophily. While homophily is a property of the target population social network, preferential recruitment is a property of the RDS recruitment process, conditional on that network.

Epidemiologists and public health researchers focus on homophily and preferential recruitment in RDS studies for 2 primary reasons. First, empirical and simulation results have repeatedly shown that these distinct forms of dependence can bias estimates of population-level quantities in different ways (6–13). Gile et al. (14, Table 1) stated that 2 assumptions “required” by the most popular estimator of the population mean (4) are “homophily sufficiently weak” and “random referral” by recruiters (see (15) for more general identification conditions for the population mean). Lunagomez and Airoldi (16) showed that RDS is a nonignorable sampling design because the distribution of observed data depends on unobserved parts of the network; when the network exhibits homophily with respect to the trait of interest, estimates may be biased. Second, many studies of infectious disease outcomes explicitly seek characteristics of an epidemiologic contact network connecting members of the target population (e.g., 17). The topology of the contact network may govern the dynamics of infectious disease spread (18, 19); because RDS is a network-based recruitment method, it may reveal features of this contact network. Stein et al. (20, 21) treated RDS recruitments as epidemiologic contacts to estimate homophily (also called assortative mixing) in the close-contact network relevant for transmission of pathogens. Stein et al. (20, p. 18) suggested that from RDS data “correlations between linked individuals can be used to improve parameterization of mathematical models used to design optimal control” for epidemic management.

While epidemiologists generally recognize the importance of preferential recruitment and homophily in determining the statistical properties of estimators of population-level quantities (e.g., human immunodeficiency virus prevalence) from RDS data, they do not agree on the definitions of these sources of dependence. White et al. (11) observed that the term homophily has “inconsistent usage in the RDS community. Sometimes it is used to refer to the tendency for sample recruitments to occur between participants in the same social category and sometimes to refer to the tendency for relationships in the target population to occur between participants in the same social category.” Often homophily is defined as a characteristic of recruiters’ behavior during the study. Ramirez-Valles et al. (22, p. 388) defined homophily as “a tendency toward in-group recruitment.” Uusküla et al. (23, p. 307) defined homophily as “the extent to which recruiters are likely to recruit individuals similar to themselves.” Léon et al. (24, p. 3) defined homophily as a property of recruitment, while making reference to the variety of other definitions: “[w]hen an individual tends to recruit persons who resemble him or her, especially with regard to the variable of interest, this is classically defined as homophily, even if several definitions coexist.” Likewise, many researchers have described preferential recruitment behavior during the study as a network property. Abramovitz et al. (25, p. 751) wrote that “[d]ifferential recruitment patterns are usually the result of individuals’ tendencies to associate with other individuals who are similar to them, also known as homophily.” Rudolph et al. (26, p. 2326) wrote that “[d]ifferential recruitment based on the outcome of interest may occur when 1) the outcome clusters by network or 2) network members cluster in space and the outcome is spatially clustered.”

Even when homophily and preferential recruitment are well-defined, there are serious problems with traditional approaches for measuring these features and interpretation of their role in statistical properties of estimators. Several authors have recognized the observational ambiguity between preferential recruitment and homophily: Tomas and Gile (7, p. 911) pointed out that “it is not always possible to distinguish from the sample if differential recruitment exists, because its effect on the resulting sampling chain is similar to that of homophily.” Fisher and Merli (27) introduced the term “stickiness,” the tendency of recruitments to become stuck within a group of subjects with similar traits. In response to the difficulty of simultaneously estimating these features from RDS recruitment data alone, several authors have proposed alternative methods of data collection to elicit additional features of the network proximal to recruited subjects (13, 28–30). This extra information, along with suitable assumptions, may reveal topological information (e.g., nonrecruitment links between recruited subjects) that permits tighter inferences about homophily and preferential recruitment.

Nevertheless, many authors have claimed to measure homophily in the target population social network, or preferential recruitment in the recruitment chain, directly from traditional RDS data; there is widespread confusion about the difference between the RDS recruitment path and the underlying network (2, 26, 31–36). Some researchers have employed regression to estimate factors associated with “productive recruiting” of network alters (37) or “network risk factors” for outcomes (17). Two software tools for analysis of RDS data produce estimates of homophily or preferential recruitment—RDSAT (38) and RDS Analyst (39)—but the estimators used by these programs are not documented.

In this work, we show that homophily and preferential recruitment are generally not identified in RDS studies. We adapt ideas from partial identification (40) and confounding in social network studies (41) to show that these sample functionals are not point identified unless the recruitment tree is identical to the underlying subgraph. Fortunately, researchers can still make credible claims about homophily and preferential recruitment in empirical RDS studies: We describe nonparametric graph-theoretical bounds under minimal assumptions about the underlying network and recruitment process. To illustrate the nonparametric bounds and their implications for an important epidemiologic risk population, we analyzed data from an RDS survey of people who inject drugs (PWID) in Hartford, Connecticut, in which the subgraph of respondents and their network alters is known with near certainty. We compare the true values of homophily and preferential recruitment obtained by using the full network with the identification intervals computed using RDS data alone. Web Appendix 1 (available at https://academic.oup.com/aje) briefly describes an algorithm for finding the bounds.

RDS DATA

We first state some basic assumptions about the target population and RDS procedure (2–6). We assume that the social network connecting members of the target population exists and is an undirected graph $G=(V,E)$ with no parallel edges or self-loops. Members of the target population are vertices in V, and edges in E represent social ties between individuals. A seed is a vertex that is not recruited by a network peer but is chosen by some other mechanism. A recruiter is a vertex known to the study that has at least 1 coupon. A susceptible vertex is not yet known to the study but has at least 1 neighbor in G that is a recruiter. Every vertex $i\in V$ has a binary attribute $Z_i$ that is observed when i is recruited. RDS recruitments happen across edges in G, and no subject can be recruited more than once.

We now define the network data collected by typical RDS studies (42). The directed recruitment graph is $G_R=(V_R,E_R)$, where $V_R$ is the set of n sampled vertices (including seeds), and a directed edge from i to j indicates that i recruited j. The recruitment-induced subgraph is an undirected graph $G_S=(V_S,E_S)$, where $V_S=V_R$ and $\{i,j\}\in E_S$ if and only if $i\in V_S$, $j\in V_S$, and $\{i,j\}\in E$. Subjects also report their network degree $d_i$ for $i\in V_R$, the number of edges incident to i in G. Let ${\mathbf{d}}_R$ and ${\mathbf{t}}_R$ be the $n\times 1$ vectors of recruited vertices’ degrees and times of recruitment in the order they entered the study, and let M be the set of seeds. Label the vertices in $V_R$ by the time-order of their recruitment: $i<j$ if $t_i<t_j$. Furthermore, we observe a vector ${\mathbf{Z}}_R=(Z_1,\dots ,Z_n)$ of subjects’ binary trait values. Researchers conducting an RDS study observe only $G_R$, ${\mathbf{d}}_R$, ${\mathbf{t}}_R$, and ${\mathbf{Z}}_R$.

Finally, let U be the set of unsampled vertices connected by at least 1 edge to a sampled vertex in $V_R$ at the end of the study. Let $E_U$ be the set of edges connecting vertices in U to sampled vertices in $V_R$. The augmented recruitment-induced subgraph is an undirected graph $G_{SU}=(V_{SU},E_{SU})$, where $V_{SU}=V_S\cup U$ and $E_{SU}=E_S\cup E_U$. Note that $G_{SU}$ does not contain edges between vertices in U. For each vertex $u\in U$, let $d_u$ be its degree in $G_{SU}$.

HOMOPHILY AND PREFERENTIAL RECRUITMENT

Consider an RDS sample of size n with recruitment graph $G_R=(V_R,E_R)$, degrees ${\mathbf{d}}_R$, and univariate binary traits ${\mathbf{Z}}_R$. Let $G_{SU}=(V_{SU},E_{SU})$ be the augmented subgraph for this sample, with traits ${\mathbf{Z}}_{SU}$. The observed traits ${\mathbf{Z}}_R$ are a subset of ${\mathbf{Z}}_{SU}$. Let $\mathbf{A}=\left\{A_{ij}\right\}$ be the adjacency matrix of $G_{SU}$. A standard definition of network homophily is the correlation between edges and trait values, known as the assortativity coefficient (43–45).

Definition 1 —

Homophily is the correlation between trait values of vertices connected by an edge,

$$h(G_{SU},{\mathbf{Z}}_{SU})=\frac{{\sum }_{i,j\in V_{SU}}(A_{ij}-d_i{d}_j\mathrm{/2|}{E}_{SU}|)Z_i{Z}_j}{{\sum }_{i,j\in V_{SU}}(d_i{\delta }_{ij}-d_i{d}_j\mathrm{/2|}{E}_{SU}|)Z_i{Z}_j},$$ (1)

where ${\delta }_{ij}\mathrm{=1}$ when $i=j$ and 0 otherwise, and for $i\in U$, $d_i=\left|\right\{j\in V_S:\{i,j\}\in E_{SU}\left\}\right|$.

Let $S_i(t)$ be the set of susceptible neighbors of $i\in V_R$ just before time t (the set-valued function $S_i(t)$ is left-continuous). Let $r_j$ be the recruiter of the sampled vertex $j\in V_S$. Under proportional (unbiased) recruitment, the probability of a recruiter recruiting a susceptible neighbor with the same trait value is proportional to the number of its susceptible neighbors with the same trait, $\left|\right\{k\in S_{r_j}(t_j):Z_{r_j}=Z_k\left\}\right|$. In other words, recruitment is uniformly at random among susceptible neighbors.

Definition 2 —

Preferential recruitment is the average deviation from proportional recruitment, given knowledge of $G_{SU}$, $G_R$, ${\mathbf{t}}_R$, and ${\mathbf{Z}}_{SU}$,

$$\begin{array}{c}p(G_{SU},G_R,{\mathbf{t}}_R,{\mathbf{Z}}_{SU})=\frac{1}{n-\left|M\right|}\sum _{j\notin M}(\mathrm{1\{}{Z}_j=Z_{r_j}\}\hfill \\ -\frac{\left|\right\{k\in S_{r_j}(t_j):Z_{r_j}=Z_k\left\}\right|}{\left|S_{r_j}(t_j)\right|}),\hfill \end{array}$$ (2)

where M is the set of seeds.

To ease notation, we will often use h and p to refer to $h(G_{SU},\mathbf{Z})$ and $p(G_{SU},G_R,{\mathbf{t}}_R,{\mathbf{Z}}_{SU})$ respectively.

IDENTIFICATION

The quantities h and p are features of the network proximal to the sampled vertices, and the observed recruitment process. The observed recruitment subgraph $G_R$ and reported degrees ${\mathbf{d}}_R$ place strong topological restrictions on the structure of $G_{SU}$ and hence imply restrictions on h and p.

Definition 3 —

Compatibility: The pair $(G_{SU},{\mathbf{Z}}_{SU})$ is compatible with the observed data $G_R$, ${\mathbf{d}}_R$, and${\mathbf{Z}}_R$ if 1) the recruitment graph is preserved ($G_R\subseteq G_{SU}$); 2) the set of recruited subjects’ trait values is preserved (${\mathbf{Z}}_R\subseteq {\mathbf{Z}}_{SU}$); 3) all unsampled vertices are connected to a recruited vertex (every $u\in V_{SU}$ with $u\notin V_S$ has an edge $\{v,u\}$ such that $v\in V_S$); and 4) total degree is preserved (for every $i\in V_R$, $d_i={\sum }_{j\in V_{SU}}\mathrm{1\{\{}i,j\}\in E_{SU}\}$).

Let $\mathcal{C}(G_R,{\mathbf{d}}_R,{\mathbf{Z}}_R)$ be the set of pairs $(G_{SU},{\mathbf{Z}}_{SU})$ compatible with the observed data in the sense of definition 3 (this is a finite set).

First, we examine whether $G_S$ and $G_{SU}$ are revealed by the observed data in RDS. Let $d_i^r$ be the degree of subject $i$ in the recruitment subgraph $G_R$.

Result 1 —

Suppose there exist $i,j\in V_R$ with $i<j$, $(i,j)\notin E_R$, $d_i^r<d_i$, and $d_j^r<d_j$. Then neither $G_S$ nor $G_{SU}$ are identified.

Proof is given in the Appendix. This result establishes the conditions under which statements about the population graph proximal to the sample can be made precise. Next, we define the information about h and p that is revealed by the observed data.

Definition 4 —

Identification region: The identification regions for h and p are given by the smallest intervals that contain $h(G_{SU},{\mathbf{Z}}_{SU})$ and $p(G_{SU},G_R,{\mathbf{t}}_R,{\mathbf{Z}}_{SU})$ for every $(G_{SU},{\mathbf{Z}}_{SU})\in \mathcal{C}(G_R,{\mathbf{d}}_R,{\mathbf{Z}}_R)$.

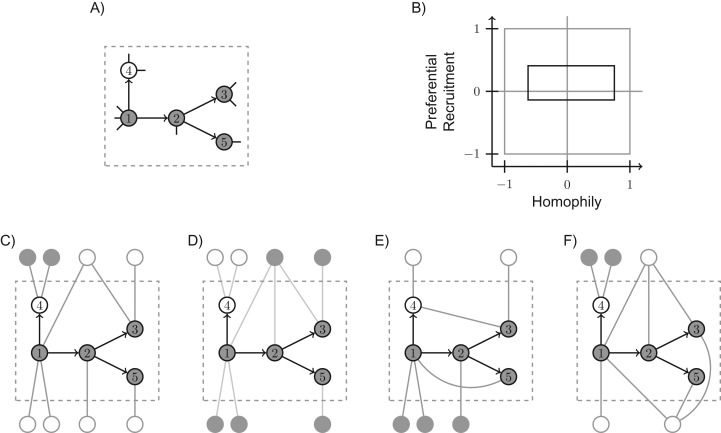
When the identification region for h or p contains only a single point, that parameter is point identified. Figure 1 shows an example of the identification regions.

Result 2 —

Suppose there exist 2 vertices $i\in V_R$ and $j\in V_R$ such that $d_i>d_i^r$, $d_j>d_j^r$, and $Z_i\ne Z_j$. Then h is not point identified.

Result 3 —

Suppose there exists a vertex $i\in V_R$ that recruited at least 1 other vertex $j\in V_R$, $j\ne i$, and $d_i>d_i^r$. Then p is not point identified.

Figure 1.

Example illustration of extrema for h and p with corresponding augmented subgraphs $G_{SU}$ and ${\mathbf{Z}}_{SU}$. Vertices are shaded according to their binary type. A) $G_R$ is shown with arrows indicating recruitments, and pendant edges implied by vertex degrees; B) the joint homophily/preferential recruitment space $[-\mathrm{1,1]}\times [-\mathrm{1,1]}$ (gray square), with the identification rectangle (shown in black) containing all values of (h, p) compatible with the observed data; C) a subgraph that achieves the minimum value of homophily, h = −0.625; D) maximum value of homophily, h = 0.752; E) minimum value of preferential recruitment, p = −0.138; and F) maximum value of preferential recruitment, p = 0.408. Some extremal subgraphs are not unique.

Proof is given in the Appendix. In practice, point identification of both homophily and preferential recruitment can be achieved only if the recruitment graph $G_R$ is nearly identical to the augmented recruitment-induced subgraph $G_{SU}$. Because RDS recruitment is without replacement, the recruitment subgraph $G_R$ is acyclic, so $G_R=G_{SU}$ means that the population network proximal to recruited vertices is a tree, a situation that seems unlikely to occur in a real-world social network. Furthermore, results 1, 2, and 3 apply directly to the case where all vertices in the population have been sampled, and we have $V_R=V$: If pendant edges remain, then h and p may not be point identified.

APPLICATION: INJECTION DRUG USERS IN HARTFORD, CONNECTICUT

We now apply the ideas developed above to an RDS data set in which the augmented subgraph $G_{SU}$ of an RDS sample $G_R$ is known with near certainty. In the RDS-net study, researchers conducted an RDS survey of $n=|V_R\mathrm{|\; =\; 527}$ injection drug users from $|M\mathrm{|\; =\; 6}$ seeds in Hartford, Connecticut. Researchers simultaneously performed a census of the augmented recruitment-induced subgraph, consisting of $|V_{SU}\mathrm{|\; =\; 2,626}$ unique injection drug users (46). Subjects were given $25 for being interviewed and $10 for recruiting another eligible subject (up to a maximum of 3). Subjects were required to be at least 18 years old, reside in the Hartford area, and report injecting illicit drugs in the last 30 days. The study was approved by the institutional review board for the Institute for Community Research, and informed consent was obtained from all subjects.

This study differs from typical RDS surveys because in addition to reporting their network degree, respondents also enumerated (nominated) their network alters—other people eligible for the study whom they knew by name and could possibly recruit. Unsampled injection drug users nominated by more than 1 participant were matched using identifying characteristics, including name (including aliases), photograph, multiple addresses, phone numbers, locations frequented, and social network links (47, 48). The resulting “nomination” network is the augmented subgraph $G_{SU}$. Figure 2 shows the nomination network $G_{SU}$ with the recruitment graph $G_R$ overlaid.

Figure 2.

The nomination network and recruitment graph for injection drug users in the RDS-net study conducted in Hartford, Connecticut, 2012–2013. Recruited subjects are shown in dark gray, and recruitment edges are shown as a directed edge (arrow) from the recruiter to the recruitee. Nonrecruitment edges (linking recruited subjects to unrecruited subjects, or recruited to recruited subjects) are shown as light gray lines.

The RDS-net study included $|V_{SU}\mathrm{|\; =\; 2,626}$ people, of whom $n=|V_R\mathrm{|\; =\; 527}$ were either seeds or recruited subjects, and 2,099 were nominated but never-recruited subjects. There are $|E_{SU}\mathrm{|\; =\; 3,307}$ edges in $G_{SU}$, of which $|E_S\mathrm{|\; =\; 1,180}$ link recruited subjects to recruited subjects, and 2,127 link recruited subjects to unrecruited subjects. Demographic and trait data relevant to drug use were collected about each recruited subject. Each recruited subject also reported the traits of their nominees. Nominees who were never personally interviewed were assigned trait information as follows: If their nominating alters agreed on their trait value, that value was assigned to them. If there was disagreement, the modal value was assigned. When trait information for a recruited subject or an unrecruited alter was absent or contradictory, it was treated as missing. We selected 3 traits with the least missing data for analysis: sex, “crack” cocaine use, and homelessness. This information was fully observed for every recruited subject, but some values were missing for nominated but unrecruited subjects.

First we computed h and p using the full data $(G_{SU},G_R,{\mathbf{t}}_R,{\mathbf{Z}}_{SU}),$where we omitted vertices in $V_{SU}$ whose trait was missing (all recruited subjects’ trait values were fully observed), any edges incident to these vertices, and the corresponding elements of ${\mathbf{Z}}_{SU}$. Second, we computed bounds for h and p using only the data observed in the RDS portion of the study, $(G_R,{\mathbf{d}}_R,{\mathbf{t}}_R,{\mathbf{Z}}_R)$, using a procedure described in Web Appendixes 1 and 2. Table 1 shows values of h and p calculated using the full data. The intervals I_h and I_p give the identification bounds obtained using the observed RDS data alone. Point values (where unrecruited vertices with missing traits were excluded) always lay within the identification intervals. Values of homophily with respect to sex and crack use were positive, and they were negative for homelessness, while p was smaller in magnitude and positive for sex and homelessness but negative for crack use. The identification regions for each trait covered h = 0 and p = 0.

Table 1.

Homophily and Preferential Recruitment in the RDS-Net Study for the Traits of Sex, Crack Cocaine Use, and Homelessness Among Injection Drug Users in Hartford, Connecticut, During 2012–2013.

Trait	Homophily		Preferential Recruitment
	h	Ih	p	Ip
Sex	0.2638	−0.7027, 0.8292	0.00397	−0.190, 0.534
Crack cocaine use	0.2711	−0.6918, 0.8231	−0.00051	−0.272, 0.453
Homelessness	−0.2154	−0.7179, 0.8242	0.04527	−0.221, 0.504

Abbreviations: h, homophily; p, preferential recruitment; RDS, respondent-driven sampling.

^a Point values are given first, followed by identification intervals I_h and I_p, for h and p, respectively, obtained by using only the information observed in the recruitment portion of the study.

DISCUSSION

Statisticians, epidemiologists, and sociologists have conducted a wide variety of rigorous empirical and simulation studies devoted to understanding the influence of homophily and preferential recruitment on population-level estimates from RDS studies (6–10, 13, 49). Several researchers have correctly pointed out the definitional (11, 24) and observational ambiguity between these quantities (7, 27).

But to our knowledge, none have explained formally why these quantities are difficult to measure: In most empirical RDS studies, neither homophily nor preferential recruitment is identified from the observed data alone because the underlying network remains only partially observed. There is reason to be skeptical of claims that the social network of a particular target population surveyed by RDS exhibits homophily (26, 32–35) or that a particular RDS study suffers from selection bias due to preferential recruitment with respect to particular traits (36). The identification results described in this paper establish a formal basis for the skepticism expressed by Tomas and Gile (7) as well as others about estimates of homophily and preferential recruitment from RDS. Fortunately, researchers can still make credible claims about homophily and preferential recruitment without invoking additional assumptions, using the identification bounds introduced here.

The identification results depend on 3 assumptions: The network exists, subjects are recruited across its edges, and nobody can be recruited more than once. When these assumptions are met, the structure of data from RDS studies allows computation of credible bounds for h and p. However, the observed data impose strict limits on the precision of these estimates, and in practice bounds are often wide. Stronger assumptions about the topology of the network and dynamics of the recruitment process may yield narrower bounds, or point identification, at the cost of decreased credibility (40). Our identification results pertain to definitions of homophily and preferential recruitment for a univariate binary trait. Generalizations to multiple traits are possible, and similar identification results may continue to hold.

Alternative survey designs may reveal much more about homophily and recruitment behavior than RDS. Many researchers have traced social links of participants, sometimes alongside a traditional RDS study, to reveal the induced subgraph of respondents (50–53). Surveying respondents’ egocentric networks can also reveal enough of the network to reliably estimate homophily (28, 30). Better estimates of preferential recruitment in RDS studies have been obtained by administering a follow-up questionnaire to subjects about their recruitment behavior (13, 14, 29, 54). Given auxiliary information and suitable assumptions, these data-collection procedures may yield tighter identification or even point identification. These approaches may also permit researchers to engage with generalizations of the definitions that we have considered here (e.g., proportional recruitment conditional on shared covariates). We believe that further methodological and empirical study of these approaches is of scientific interest.

Although it may be disappointing that homophily and preferential recruitment are not point identified in traditional RDS studies, researchers can still draw credible inferences about these parameters. The identification regions for sex, crack use, and homelessness in the RDS-net study were considerably smaller than the outcome space $[-\mathrm{1,1]}$. Under some circumstances, it may be possible to deduce that homophily or preferential recruitment is strictly positive or negative in the augmented subgraph, even without exact knowledge of that subgraph. Informally, the more $G_{SU}$ resembles $G_R$, the narrower the identification regions for (h, p) will be. Researchers who find the identification regions too wide for their scientific purposes may wish to consider alternative study designs that are more likely to reveal the quantities of interest.

Abbreviations

RDS

respondent-driven sampling

Appendix

Proof of Result 1 —

Call a recruitment-induced subgraph $G_S=(V_S,E_S)$ compatible with the observed data if $V_S=V_R$, $\{i,j\}\in E_R$ implies $\{i,j\}\in E_S$, and ${\sum }_{j\ne i}\mathrm{1\{\{}i,j\}\in E_S\}\le d_i$ for each $i\in V_R$. Call an augmented recruitment-induced subgraph $G_{SU}=(V_{SU},E_{SU})$ compatible with the observed data if conditions 1, 3, and 4 of definition 3 hold. Suppose $i\in V_R$ has $d_i^r<d_i$ and $j\in V_R$ has $d_j^r<d_j$, with $i<j$ and $(i,j)\notin E_R$. Let $G_{SU}^1=(V_{SU}^1,E_{SU}^1)$ be any compatible subgraph with $\{i,u\}\in E_{SU}^1$, $\{j,u\}\in E_{SU}^1$, where $u\notin V_R$ is an unsampled vertex. Let $G_{SU}^2=(V_{SU}^2,E_{SU}^2)$ be identical to $G_{SU}^1$ except that $\{i,j\}\in E_{SU}^2$, so neither i nor j is connected to u. If in the resulting subgraph u has no neighbors in $V_R$ (i.e., there does not exist $k\in V_R$ such that $\{k,u\}\in E_{SU}^2$), then remove u from $V_{SU}^2$. Because there exist at least 2 augmented recruitment-induced subgraphs compatible with the observed data, $G_{SU}$ is not identified. Let $G_S^1$ be the recruitment-induced subgraph obtained by removing any unsampled vertices (and edges connected to them) from $G_{SU}^1$. Define $G_S^2$ in the same way. Clearly both $G_S^1$ and $G_S^2$ are compatible with the observed data under the conditions of definition 3, but $\{i,j\}\notin G_S^1$ and $\{i,j\}\in G_S^2$. Because there exist at least 2 recruitment-induced subgraphs compatible with the observed data, $G_S$ is not identified.

Proof of Result 2 —

Suppose the observed RDS data are $G_R$, ${\mathbf{Z}}_R$, ${\mathbf{t}}_R$, ${\mathbf{d}}_R$, and there exist distinct $i\in V_R$ and $j\in V_R$ with $d_i^r<d_i$, $d_j^r<d_j$, and $Z_i\ne Z_j$. Without loss of generality, suppose $Z_i\mathrm{=\; 0}$ and $Z_j\mathrm{=\; 1}$. We will exhibit $(G_{SU}^1,{\mathbf{Z}}_{SU}^1)\in \mathcal{C}(G_R,{\mathbf{d}}_R,{\mathbf{Z}}_R)$ and $(G_{SU}^2,{\mathbf{Z}}_{SU}^2)\in \mathcal{C}(G_R,{\mathbf{d}}_R,{\mathbf{Z}}_R)$ such that $h(G_{SU}^1,G_R,{\mathbf{Z}}_{SU}^1)\ne h(G_{SU}^2,G_R,{\mathbf{Z}}_{SU}^2)$. Let $(G_{SU}^1,{\mathbf{Z}}_{SU}^1)$ be any compatible subgraph and trait set with the property that $\{i,u_1\}\in E_{SU}^1$ and $\{j,u_2\}\in E_{SU}^1$, where $u_1$ and $u_2$ are unsampled vertices with $Z_{u_1}^1\mathrm{=\; 0}$ and $Z_{u_2}^1\mathrm{=\; 1}$. Let $(G_{SU}^2,{\mathbf{Z}}_{SU}^2)$ be identical to $(G_{SU}^1,{\mathbf{Z}}_{SU}^1)$ except that the edges connecting i and j to $u_1$ and $u_2$ are swapped: $\{i,u_1\}\notin E_{SU}^2$,$\{j,u_2\}\notin E_{SU}^2$, and $\{i,u_2\}\in E_{SU}^2$ and $\{j,u_1\}\in E_{SU}^2$. Clearly $(G_{SU}^2,{\mathbf{Z}}_{SU}^2)\in \mathcal{C}(G_R,{\mathbf{d}}_R,{\mathbf{Z}}_R)$. Let $h_1=h(G_{SU}^1,G_R,{\mathbf{Z}}_{SU}^1)$ and $h_2=h(G_{SU}^2,G_R,{\mathbf{Z}}_{SU}^2)$ be the calculated values of homophily. The difference is

$$\begin{array}{ll}{h}_1-h_2\hfill & =\frac{2\left(1-\frac{d_j{d}_{u_2}}{\mathrm{2|}{E}_{SU}|}\right)-2\left(0-\frac{d_j{d}_{u_2}}{\mathrm{2|}{E}_{SU}|}\right)}{{\sum }_{k,l\in V_{SU}}(d_k{\delta }_{kl}-d_k{d}_l\mathrm{/2|}{E}_{SU}|)Z_k{Z}_l}\hfill \\ \hfill & =\frac{2}{{\sum }_{k,l\in V_{SU}}(d_k{\delta }_{kl}-d_k{d}_l\mathrm{/2|}{E}_{SU}|)Z_k{Z}_l}\ne 0.\hfill \end{array}$$ (A1)

Therefore homophily is not point identified.

Proof of Result 3 —

Again suppose there exists $i\in V_R$ such that $d_i^r<d_i$ and $i$ recruited $j\in V_R$, $j\ne i$. Without loss of generality, suppose $Z_i\mathrm{=\; 1}$. Let $(G_{SU}^1,{\mathbf{Z}}_{SU}^1)$ be any compatible subgraph and trait set such that 1 edge connects i to an unsampled vertex u, where u has no other neighbors in $V_R$, and $Z_u\mathrm{=\; 1}$. Let $K^1=\left|\right\{k\in S_i(t_j):Z_i=Z_k\left\}\right|$ under the trait values given by ${\mathbf{Z}}_{SU}^1$. Let $(G_{SU}^2,{\mathbf{Z}}_{SU}^2)$ be identical to $(G_{SU}^1,{\mathbf{Z}}_{SU}^1)$ except that $Z_u\mathrm{=\; 0}$. Let $p_1=p(G_{SU}^1,G_R,{\mathbf{t}}_R,{\mathbf{Z}}_{SU}^1)$ and $p_2=p(G_{SU}^2,G_R,{\mathbf{t}}_R,{\mathbf{Z}}_{SU}^2)$. The difference is

$$\begin{array}{ll}{p}_1-p_2\hfill & =\frac{1}{n-\left|M\right|}\left[\left(\mathrm{1\{}{Z}_i=Z_j\}-\frac{K^1}{\left|S_i(t_j)\right|}\right)-\left(\mathrm{1\{}{Z}_i=Z_j\}-\frac{K^1-1}{\left|S_i(t_j)\right|}\right)\right]\hfill \\ \hfill & =\frac{-1}{(n-|M|)\left|S_i(t_j)\right|}\ne 0.\hfill \end{array}$$ (A2)

Therefore preferential recruitment is not point identified.