SUMMARY
Evaluating and understanding the risk and safety of using medications for autoimmune disease in a woman during her pregnancy will help both clinicians and pregnant women to make better treatment decisions. However, utilizing spontaneous abortion (SAB) data collected in observational studies of pregnancy to derive valid inference poses two major challenges. First, the data from the observational cohort are not random samples of the target population due to the sampling mechanism. Pregnant women with early SAB are more likely to be excluded from the cohort, and there may be substantial differences between the observed SAB time and those in the target population. Second, the observed data are heterogeneous and contain a “cured” proportion. In this article, we consider semiparametric models to simultaneously estimate the probability of being cured and the distribution of time to SAB for the uncured subgroup. To derive the maximum likelihood estimators, we appropriately adjust the sampling bias in the likelihood function and develop an expectation-maximization algorithm to overcome the computational challenge. We apply the empirical process theory to prove the consistency and asymptotic normality of the estimators. We examine the finite sample performance of the proposed estimators in simulation studies and illustrate the proposed method through an application to SAB data from pregnant women.
Keywords: Biased sampling, Cure rate model, Left truncation, EM algorithm
1. Introduction
During pregnancy, women have consistently low rates of compliance with treatment recommendations for medical conditions not related to their pregnancy. Major barriers to compliance among pregnant women have repeatedly been shown to include fear of the safety of the treatments for themselves and for their developing fetus. Some medications used to treat autoimmune disease have been associated with spontaneous abortion (SAB) during pregnancy (Visser and others, 2009; Skorpen and others, 2016). Hence, it is essential to evaluate and understand the safety and risk of treatments given to pregnant women in order to help both clinicians and pregnant women make better treatment decisions. This work was motivated by studies conducted by the Organization of Teratology Information Specialists (OTIS), which is a North American network of university or hospital-based teratology services that counsel between 70 000 and 100 000 pregnant women every year. The OTIS autoimmune disease in pregnancy database included 964 pregnant women between 2005 and 2012. During the studies, the pregnant women participated in phone interviews and recorded information in a diary throughout their pregnancy. A final outcome phone interview was conducted shortly after the pregnancy ended. While SAB as an outcome of interest is, at first sight, and perhaps ultimately, a binary endpoint, our recruitment of pregnant women leads to biased sampling. Following the research interest to assess the effects of medication exposure on SAB (Xu and Chambers, 2011; Chambers and others, 2011), we evaluate the relationship between the use of medications for autoimmune disease during pregnancy and the probability of experiencing SAB, as well as the time to SAB. Specifically, besides the effect of medications for autoimmune disease on the risk of experiencing SAB, we are interested in evaluating whether the use of the medications will significantly affect the distribution of time to SAB for pregnant women who experience SAB (the uncured group).
In the medical literature, SAB is defined as the natural death of an embryo or fetus before 20 weeks of gestation; any pregnancy loss after 20 weeks is called still birth (Medical Encyclopedia, National Institutes of Health website: https://www.nlm.nih.gov/medlineplus/ency/article/001488.htm). Using this definition of SAB, the pregnant women who do not experience SAB are considered to be “cured.” Hence, the population is a mixture of two subgroups: those who are non-susceptible (cured) and those who are susceptible (uncured) to SAB. Note that we are able to observe the SAB status (membership of the two subgroups) for uncensored subjects, which is different from the classical cured data. Cure rate models that consider such population heterogeneity have been well studied in the literature for time-to-event data. Most survival cure rate models have been developed on the basis of mixture models (Peng and Dear, 2000; Sy andTaylor, 2000). Various survival regression models have been considered including Cox proportional hazards models (Sy and Taylor, 2000; Kuk and Chen, 1992) and accelerated failure time models (Zhang and Peng, 2009; Li and Taylor, 2002). Also, several cure rate models have been developed along the lines of non-mixture models (Chen and others, 1999; Zeng and others, 2006).
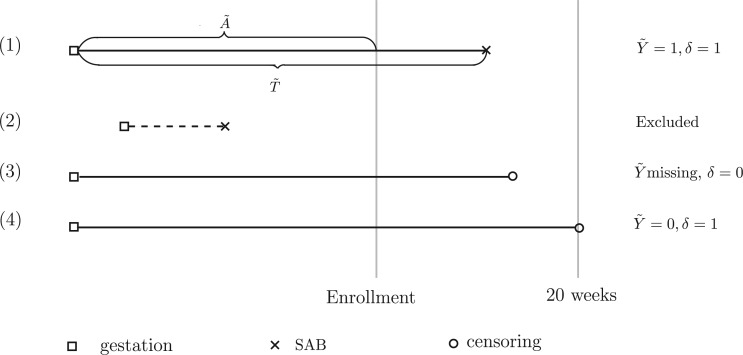
However, the existing methods to handle survival data with a cured proportion cannot be directly applied to our motivating data because of the unique data structure of biased sampling. The data consist only of pregnant women who have not experienced the failure event, SAB, at the time of enrollment. In other words, pregnant women who have early SAB events are less likely to be included in the study and thus tend to represent left-truncated data, as indicated in Figure 1. Such a sampling bias due to left truncation is also confirmed by exploratory analysis in which the empirical SAB rate is only 7%, which is much lower than the known incidence rate (around 12%) in the general population (Wilcox and others, 1988). Determining the best way to adjust for sampling bias has been a longstanding statistical problem. Statistical methods for analyzing survival data subject to biased sampling have been actively studied by Wang and others (1986), Shen and others (2009), Tsai (2009), Qin and others (2011), Kim and others (2013), Ning and others (2014) and more. However, most of the methods used in the aforementioned publications have two limitations. First, they focus on a special type of left-truncated data in which the incidence of the initial event (e.g., pregnancy) is constant over time. In our motivating study, the p-value from the test of the stationarity assumption is 0.0001 (Addona and Wolfson, 2006), indicating that such a stationarity assumption is not satisfied. Second, to the best of our knowledge, the existing methods for adjusting sampling bias have not considered the data that include a cured proportion. Our goal is to provide models and estimating procedures to simultaneously account for sampling bias and population heterogeneity.
Fig. 1.
Survival data from a cure model that is subject to biased sampling. Patients with IDs (1), (3), and (4) are sampled, whereas Patient (2) is excluded.
The remainder of the article is organized as follows. In Section 2, we introduce the notations and mixture models in which the SAB status is modeled by logistic regression and the time to SAB for the uncured subgroup is characterized by a semiparametric proportional hazards model. In Section 3, we derive the full likelihood function with appropriate adjustment for biased sampling and the cured proportion, and then derive an expectation-maximization (EM) algorithm to solve the computational challenge. In Section 4, we establish the asymptotic properties of the proposed estimators. In Section 5, we report the results of simulation studies to assess the finite sample performance of the proposed method. We apply our method to the SAB data in Section 6 and provide concluding remarks in Section 7. We provide details for the proofs of the asymptotic properties in the supplementary materials available at Biostatistics online.
2. Notations and model
By the definition of SAB, the loss of a pregnancy prior to 20 weeks of gestation, some pregnant women appear to be free of the risk of SAB, which we consider to be the cured population. Considering that the observed data are subject to biased sampling, we introduce notations first for the target population and then for the observed biased population. Let  be the status indicating whether a subject experiences the SAB event (
be the status indicating whether a subject experiences the SAB event ( ) or does not experience the SAB event (
) or does not experience the SAB event ( ). For subjects with
). For subjects with 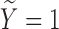 (uncured population), let
(uncured population), let 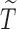 be the unbiased duration from the first day of the last menstrual period to the SAB, with a density function
be the unbiased duration from the first day of the last menstrual period to the SAB, with a density function 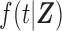 and survival function
and survival function 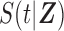 , where
, where 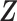 is a
is a 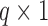 vector of the covariates. Define
vector of the covariates. Define 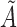 to be the duration from the beginning of the pregnancy to study entry. Under biased sampling, only pregnant women who did not experience SAB prior to their enrollment were enrolled, and those who experienced SAB were excluded from the study. In other words, we have a sampling constraint of
to be the duration from the beginning of the pregnancy to study entry. Under biased sampling, only pregnant women who did not experience SAB prior to their enrollment were enrolled, and those who experienced SAB were excluded from the study. In other words, we have a sampling constraint of 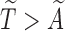 . Let
. Let 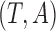 be the observed biased counterparts of unbiased
be the observed biased counterparts of unbiased 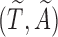 . Define the censoring time from the study enrollment and censoring indicator to be
. Define the censoring time from the study enrollment and censoring indicator to be 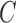 and
and 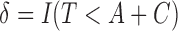 , respectively. With potential right censoring, the observed time is denoted as
, respectively. With potential right censoring, the observed time is denoted as 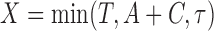 , where
, where 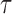 is the time after which an individual is no longer considered to be susceptible to the event (i.e.,
is the time after which an individual is no longer considered to be susceptible to the event (i.e., 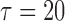 in the SAB data). Note that the indicator
in the SAB data). Note that the indicator 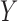 is not available for subjects with
is not available for subjects with 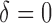 . For the cured population (
. For the cured population (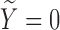 ), we define
), we define 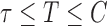 for notational consistency. Throughout this article, we assume that (i)
for notational consistency. Throughout this article, we assume that (i) 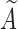 and
and 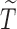 are conditionally independent given covariates
are conditionally independent given covariates 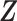 and
and 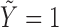 , and (ii)
, and (ii) 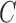 is conditionally independent of
is conditionally independent of 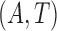 given covariates
given covariates 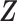 . Figure 1 illustrates the sampling mechanism of the data that has a cured proportion and is subject to biased sampling.
. Figure 1 illustrates the sampling mechanism of the data that has a cured proportion and is subject to biased sampling.
We impose a logistic regression for the risk of SAB (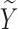 ) and a proportional hazards model for the time to SAB (
) and a proportional hazards model for the time to SAB (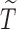 ) for subjects with
) for subjects with  :
:
| (2.1) |
| (2.2) |
where 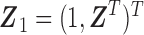 and
and 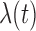 is an unspecified baseline hazard function. For simplicity of notation, we use the same covariates in both models; however, it is easy to accommodate different sets of covariates for the two models. As discussed by Sy and Taylor (2000) and Taylor (1995), one essential assumption for model identifiability given survival data with a cured proportion is the zero-tail constraint, which refers to the conditional survival function as zero for a value of time greater than the longest time to the event of interest. In our SAB data, the constraint assumption is naturally satisfied by the definition of SAB, the natural death of an embryo or fetus before 20 weeks of gestation.
is an unspecified baseline hazard function. For simplicity of notation, we use the same covariates in both models; however, it is easy to accommodate different sets of covariates for the two models. As discussed by Sy and Taylor (2000) and Taylor (1995), one essential assumption for model identifiability given survival data with a cured proportion is the zero-tail constraint, which refers to the conditional survival function as zero for a value of time greater than the longest time to the event of interest. In our SAB data, the constraint assumption is naturally satisfied by the definition of SAB, the natural death of an embryo or fetus before 20 weeks of gestation.
3. Likelihood and estimation procedure
Recall that the unbiased time-to-SAB data are not directly observed. Instead, the biased samples and their corresponding covariates are observed. We first consider the length-biased data, and then extend the likelihood and estimating procedure to the general left-truncated data. Length-biased data are a special case of left-truncated data in which the truncation times are uniformly distributed on a defined interval 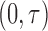 .
.
Given covariates 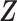 , the probability of a subject being selected from the target population is
, the probability of a subject being selected from the target population is 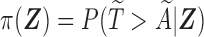 , which equals
, which equals 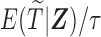 for the length-biased data. Given that the population is a mixture of cured and uncured components, the marginal survival function of the observed time
for the length-biased data. Given that the population is a mixture of cured and uncured components, the marginal survival function of the observed time 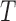 is
is
where 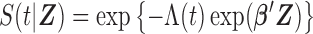 .
.
Consider a study with a sample of 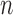 subjects, with observed data of
subjects, with observed data of 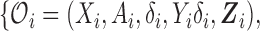
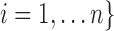 . Let
. Let 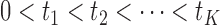 denote the ordered distinct observed time points including censored and uncensored time, which is different from the hazard estimator in the traditional survival analysis (Qin and others, 2011). The true baseline hazard function
denote the ordered distinct observed time points including censored and uncensored time, which is different from the hazard estimator in the traditional survival analysis (Qin and others, 2011). The true baseline hazard function 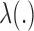 is unspecified under the Cox model and is an infinite-dimensional parameter. In our estimation procedure, following the nonparametric maximum likelihood principle (Vardi, 1989; Qin and others, 2011), we assume that the estimated
is unspecified under the Cox model and is an infinite-dimensional parameter. In our estimation procedure, following the nonparametric maximum likelihood principle (Vardi, 1989; Qin and others, 2011), we assume that the estimated 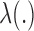 has positive masses only at distinct observed time points
has positive masses only at distinct observed time points 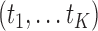 , where the value of
, where the value of 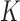 depends on the observed data and can reach infinity as
depends on the observed data and can reach infinity as 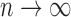 . Given the conditional independence assumptions, the full likelihood function of the observed data conditional on the covariates is proportional to
. Given the conditional independence assumptions, the full likelihood function of the observed data conditional on the covariates is proportional to
| (3.1) |
where the parameter vector of interest is denoted as 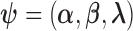 and the density function
and the density function 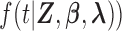 is denoted as
is denoted as 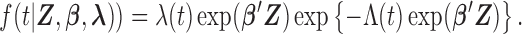 Note that the sampling probability
Note that the sampling probability 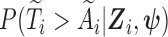 involves the parameter
involves the parameter 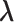 ;C hence, directly maximizing the observed likelihood or the profile likelihood method is computationally prohibitive due to a lack of an analytical expression for the optimal value of parameter
;C hence, directly maximizing the observed likelihood or the profile likelihood method is computationally prohibitive due to a lack of an analytical expression for the optimal value of parameter  . To overcome this computational challenge, we derive an EM algorithm that naturally incorporates the bias sampling mechanism into a missing data framework.
. To overcome this computational challenge, we derive an EM algorithm that naturally incorporates the bias sampling mechanism into a missing data framework.
3.1 EM algorithm under length-biased sampling
There are two missing components in the observed data. First, the SAB status is not observable for any subject with censored survival time (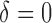 ). Conditional on the observed data, we can derive the expectation of
). Conditional on the observed data, we can derive the expectation of 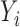 as
as
| (3.2) |
Next, we treat the truncated observations as missing data. For any subject 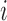 in the observed data, the data generating mechanism can be considered as sampling the unbiased time
in the observed data, the data generating mechanism can be considered as sampling the unbiased time 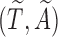 for a random
for a random 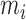 times until
times until 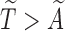 . This random integer
. This random integer 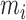 then follows a geometric distribution with parameter
then follows a geometric distribution with parameter 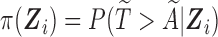 . We denote the truncated (unobserved) data corresponding to subject
. We denote the truncated (unobserved) data corresponding to subject 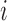 by
by 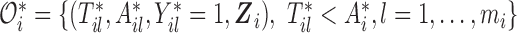 . Then the complete data for the
. Then the complete data for the 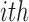 subject include the observed data
subject include the observed data 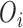 , and unobserved data
, and unobserved data 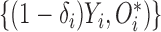 . Accordingly, the log-likelihood function of the complete data is
. Accordingly, the log-likelihood function of the complete data is
| (3.3) |
where 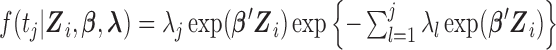 and
and 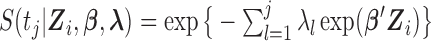 . We first select initial values
. We first select initial values 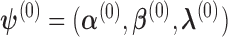 , and let
, and let 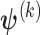 denote the estimates of the parameters in the
denote the estimates of the parameters in the 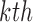 iteration. Following the principle of the EM algorithm, in the E-step of the
iteration. Following the principle of the EM algorithm, in the E-step of the 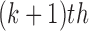 iteration, we calculate the conditional expectation of the log-likelihood function of the complete data based on the observed data and the estimated parameters from the last iteration,
iteration, we calculate the conditional expectation of the log-likelihood function of the complete data based on the observed data and the estimated parameters from the last iteration,
| (3.4) |
where 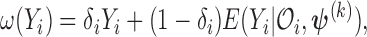 the expected number of truncated latent subjects who would experience the failure event at
the expected number of truncated latent subjects who would experience the failure event at 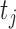 is
is
and 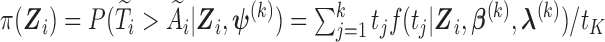 .
.
In the M-step, we maximize the expected complete log-likelihood function (3.4) to update the parameter estimates. The estimates can be updated by solving the corresponding score equation, defined as the first derivative of the expected complete log-likelihood. The score equation of 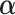 is
is
| (3.5) |
By solving the score equation of 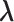 , the maximizer for the baseline hazard can be written as a function of
, the maximizer for the baseline hazard can be written as a function of 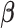 ,
,
| (3.6) |
After plugging equation (3.6) into the score equation of 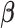 , we have the following estimating equation set
, we have the following estimating equation set
| (3.7) |
Hence, the updated estimate of 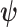 can be obtained by cycles. Specifically, given
can be obtained by cycles. Specifically, given 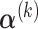 and
and 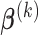 ,
, 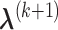 can be obtained by equation (3.6); given
can be obtained by equation (3.6); given 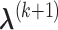 and
and 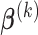 ,
, 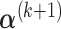 can be calculated by equation (3.5); and given
can be calculated by equation (3.5); and given 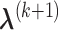 and
and 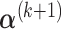 ,
, 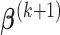 can be derived by equation (3.7).
can be derived by equation (3.7).
We iterate between the E- and M-steps until the difference between the likelihoods and estimates at two successive iterations is less than a prespecified value. The proposed EM algorithm has several desirable features. First, the conditional expectations in the E-step only involve at most 1D integration. Second, in the M-step, the high-dimensional parameters 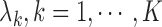 are calculated explicitly (3.6), while the low-dimensional parameters can be updated through the novel use of existing software. Specifically, to solve equation (3.5) for updating parameter
are calculated explicitly (3.6), while the low-dimensional parameters can be updated through the novel use of existing software. Specifically, to solve equation (3.5) for updating parameter 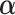 , we can use the existing logistic regression program by creating a new data set. We first generate a data set for the unobserved and truncated subjects in which the binary outcomes are all set to be 1. The covariates are repeated
, we can use the existing logistic regression program by creating a new data set. We first generate a data set for the unobserved and truncated subjects in which the binary outcomes are all set to be 1. The covariates are repeated 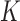 times with
times with 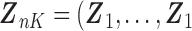 ,
,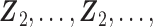
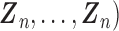 . We next combine the generated data for the truncated subjects with the observed data. By using the combined data set,
. We next combine the generated data for the truncated subjects with the observed data. By using the combined data set, 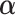 can be estimated by the function glm() with the “weights” option in R,
can be estimated by the function glm() with the “weights” option in R,
where 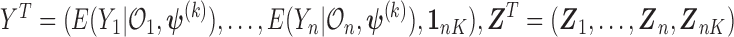 and the weights equals
and the weights equals 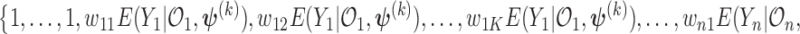
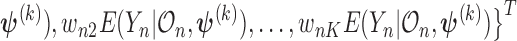 .
.
Similarly, equation (3.7) can be solved by the existing program for right-censored data under the Cox model. First, we generate a data set for the unobserved and truncated subjects in which the failure times are constructed by repeating the observed unique survival time 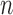 times, i.e.,
times, i.e., 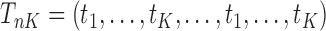 . The corresponding death indicator is a vector of 1, denoted as
. The corresponding death indicator is a vector of 1, denoted as 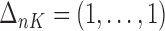 . The covariates are matched with the failure times, with
. The covariates are matched with the failure times, with 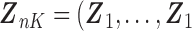 ,
,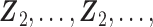
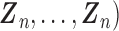 . After combining the generated data with the observed data, we can estimate
. After combining the generated data with the observed data, we can estimate 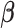 by the function coxph() with the “weight” option in R,
by the function coxph() with the “weight” option in R,
where 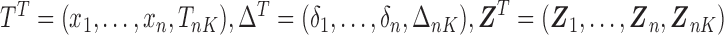 and the weight equals
and the weight equals 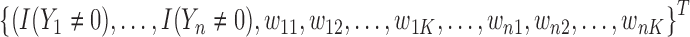 . Note that the first
. Note that the first 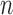 elements have a weight of
elements have a weight of 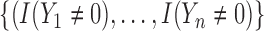 since we need to exclude the cured population and have a weight of 1 for the others.
since we need to exclude the cured population and have a weight of 1 for the others.
3.2. Extension to general left-truncated data
The stationarity assumption is required for applying the model and methods described in Section 3.1; however, that assumption can be easily violated in application. For example, in the event of an infectious disease outbreak, the number of people infected usually grows exponentially rather than linearly over time. Hence, the truncation times are unlikely to be uniformly distributed. In this section, we consider a flexible class of semiparametric models and the associated full maximum likelihood estimation for general left-truncated data. For the purpose of model identifiability, we assume a parametric model for the distribution of the truncation variable, with cumulative density function 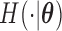 and density function
and density function 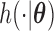 . The joint model of the truncation time and the time to the event of interest is not identifiable if both distributions have nonparametric components Wang, 1989. Here, we choose the semiparametric model for the time to the event of interest (e.g., time to SAB event) and the parametric model for the truncation time. Under these assumptions, the full likelihood function of the observed data is proportional to
. The joint model of the truncation time and the time to the event of interest is not identifiable if both distributions have nonparametric components Wang, 1989. Here, we choose the semiparametric model for the time to the event of interest (e.g., time to SAB event) and the parametric model for the truncation time. Under these assumptions, the full likelihood function of the observed data is proportional to
| (3.8) |
where 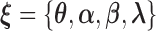 .
.
As mentioned previously, directly maximizing the likelihood function is computationally prohibitive due to the lack of an analytical expression for the optimal value of parameter 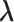 . In the following equations, we extend the EM algorithm introduced in Section 3.1 to maximize (3.8). Similarly, we treat the SAB status for censored subjects and those truncated due to the sampling mechanism as missing data and denote
. In the following equations, we extend the EM algorithm introduced in Section 3.1 to maximize (3.8). Similarly, we treat the SAB status for censored subjects and those truncated due to the sampling mechanism as missing data and denote 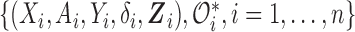 as the “complete data.” Accordingly, the log-likelihood of the complete data is
as the “complete data.” Accordingly, the log-likelihood of the complete data is
| (3.9) |
We denote the parameter estimator from the 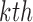 iteration by
iteration by 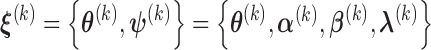 . Then given
. Then given 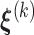 and the observed data, we have
and the observed data, we have 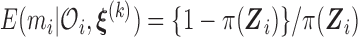 and
and
The expected number of truncated latent subjects who would have the event at time 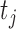 is
is
The expectation of 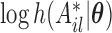 given the observed data
given the observed data 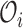 under the constraint
under the constraint 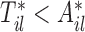 is
is
where 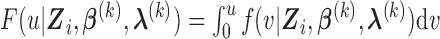 . It follows that the expected log-likelihood function for the complete data conditional on the observed data and
. It follows that the expected log-likelihood function for the complete data conditional on the observed data and 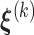 is
is
| (3.10) |
where 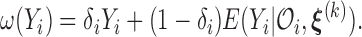 The M-step maximizes (3.10) to update the parameter estimates. Specifically, the updates can be obtained through cycles of
The M-step maximizes (3.10) to update the parameter estimates. Specifically, the updates can be obtained through cycles of 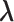 ,
, 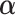 ,
, 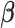 and
and 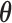 . The parameters
. The parameters 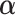 ,
, 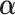 and
and 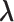 can be estimated in a manner similar to that described in Section 3.1. The estimate of
can be estimated in a manner similar to that described in Section 3.1. The estimate of 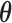 can be derived by solving the following score equation
can be derived by solving the following score equation
| (3.11) |
where 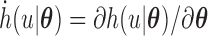 . For the implementation of the M-step, we can easily use the existing program for logistic regression and traditional right-censored data under the Cox model as described in Section 3.1.
. For the implementation of the M-step, we can easily use the existing program for logistic regression and traditional right-censored data under the Cox model as described in Section 3.1.
4. Asymptotic properties
We establish the asymptotic properties of the estimators, denoted as 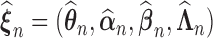 , under general left-truncation sampling. Here, the subscript
, under general left-truncation sampling. Here, the subscript 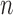 indicates the sample size. The true values of the parameters are denoted as
indicates the sample size. The true values of the parameters are denoted as 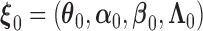 . By the counting process formulation, the observed log-likelihood function can be rewritten as
. By the counting process formulation, the observed log-likelihood function can be rewritten as
where 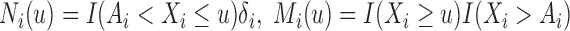 and
and 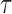 is the upper bound for the support of
is the upper bound for the support of 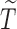 . Under the regularity conditions provided in the supplementary materials available at Biostatistics online, we establish strong consistency by the classical Kullback–Leibler information approach, and prove the weak convergence of the estimators by the Z-theorem for infinite-dimensional estimating equations (Van Der Vaart and Wellner, 1996).
. Under the regularity conditions provided in the supplementary materials available at Biostatistics online, we establish strong consistency by the classical Kullback–Leibler information approach, and prove the weak convergence of the estimators by the Z-theorem for infinite-dimensional estimating equations (Van Der Vaart and Wellner, 1996).
Theorem 1: Under the regularity conditions listed in the supplementary materials available at Biostatistics online, the estimators 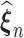 are consistent: (
are consistent: (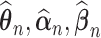 ) converge almost surely to (
) converge almost surely to (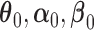 ),
), 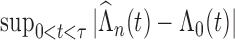 converges almost surely to 0 as
converges almost surely to 0 as 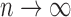 .
.
As 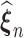 maximizes the likelihood function, the empirical Kullback–Leibler information
maximizes the likelihood function, the empirical Kullback–Leibler information 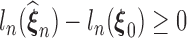 must always be negative. If
must always be negative. If 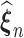 converges, say, to
converges, say, to 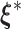 , then following the uniform law of large numbers, we can show that
, then following the uniform law of large numbers, we can show that 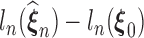 must converge to the negative Kullback–Leibler distance between
must converge to the negative Kullback–Leibler distance between 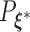 and
and 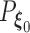 , where
, where 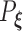 is the probability measure under the parameter
is the probability measure under the parameter 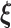 . As the Kullback–Leibler information is always non-negative, it implies that
. As the Kullback–Leibler information is always non-negative, it implies that 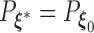 almost surely. Under the regularity conditions provided in the supplementary materials available at Biostatistics online, model
almost surely. Under the regularity conditions provided in the supplementary materials available at Biostatistics online, model 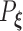 is identifiable, implying that
is identifiable, implying that 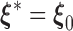 .
.
Theorem 2: Under the regularity conditions listed in the supplementary materials available at Biostatistics online, 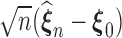 converges weakly to a tight, mean zero Gaussian process
converges weakly to a tight, mean zero Gaussian process 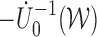 , where
, where 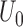 is defined as the expectation of score function
is defined as the expectation of score function 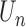 under true parameter values
under true parameter values 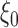 .
.
By the von Mises method for semiparametric maximum likelihood estimators (Gill and others, 1989), the score functions are derived by taking the derivative of 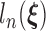 with respect to
with respect to 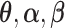 , and a submodel
, and a submodel 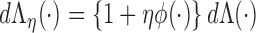 . Here,
. Here, 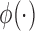 is a bounded and integrable function, and
is a bounded and integrable function, and 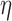 is a positive constant. We denote the infinite-dimensional score functions by
is a positive constant. We denote the infinite-dimensional score functions by 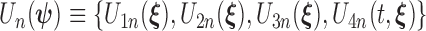 , and its expectation under true values
, and its expectation under true values 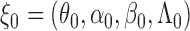 by
by
Both the score function 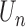 and its expectation
and its expectation 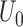 are defined on the parameter set
are defined on the parameter set 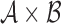 , where set
, where set 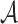 is assumed to be compact in
is assumed to be compact in 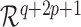 , and the set
, and the set 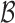 consists of nondecreasing functions in the space of functions with bounded variation. The true value
consists of nondecreasing functions in the space of functions with bounded variation. The true value 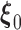 satisfies the population score function
satisfies the population score function 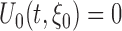 . The estimating functions evaluated at the true value
. The estimating functions evaluated at the true value 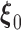 can be written as an empirical process
can be written as an empirical process 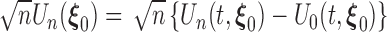 . By the uniform central limit theorem, it can be shown that
. By the uniform central limit theorem, it can be shown that 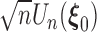 converges weakly to
converges weakly to 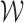 .
. 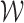 is defined as
is defined as 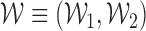 , where
, where 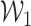 is a Gaussian random vector with covariance matrix
is a Gaussian random vector with covariance matrix 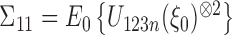 and
and 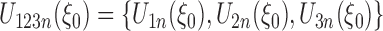 , and
, and 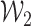 is a tight Gaussian process with covariance matrix
is a tight Gaussian process with covariance matrix 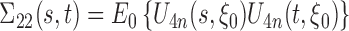 . Denote the Fréchet derivative of
. Denote the Fréchet derivative of 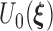 evaluated at
evaluated at 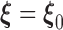 by
by  . In the supplementary materials available at Biostatistics online, we outline the proof for the three main conditions for using the Z-theorem: Fréchet differentiability and invertibility, weak convergence of
. In the supplementary materials available at Biostatistics online, we outline the proof for the three main conditions for using the Z-theorem: Fréchet differentiability and invertibility, weak convergence of 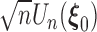 and a stochastic approximation condition of the estimating equations. Note that we show the proof under the general left-truncated sampling, which includes length-biased sampling as a special case.
and a stochastic approximation condition of the estimating equations. Note that we show the proof under the general left-truncated sampling, which includes length-biased sampling as a special case.
4.1. Variance estimation
We use an EM-aided computational differentiation approach with the profile likelihood to estimate the variances of the finite dimensional estimators 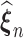 (Chen and Little, 1999; Murphy and Van Der Vaart, 2000). By the perturbation around the obtained estimators, the information matrix can be estimated as shown below:
(Chen and Little, 1999; Murphy and Van Der Vaart, 2000). By the perturbation around the obtained estimators, the information matrix can be estimated as shown below:
(1) Perturb the
 th entry of
th entry of 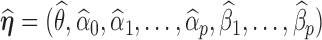 by a small value
by a small value 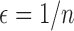 in the neighborhood in one direction or both directions, denoted as
in the neighborhood in one direction or both directions, denoted as 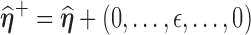 and
and 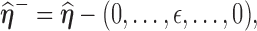 respectively.
respectively.(2) Use the EM algorithm to obtain
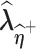 and
and 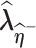 given
given 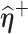 and
and 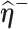 , respectively.
, respectively.- (3) Approximate the
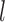 th row of the information matrix of
th row of the information matrix of 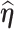 by
by
5. Simulation study
We conducted simulations studies to evaluate the finite sample performance of the proposed method. The SAB status indicator 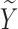 was generated from a logistic regression model with two covariates
was generated from a logistic regression model with two covariates 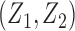 , where
, where 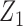 followed a Bernoulli distribution with probability 0.5, and
followed a Bernoulli distribution with probability 0.5, and 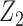 followed a uniform distribution,
followed a uniform distribution, 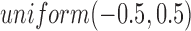 . We set
. We set 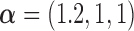 , such that the uncured proportion was around 75%. For the uncured subjects (i.e.,
, such that the uncured proportion was around 75%. For the uncured subjects (i.e., 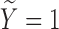 ), we generated unbiased survival times
), we generated unbiased survival times 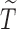 from a Cox proportional hazards model with covariates
from a Cox proportional hazards model with covariates 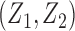 and
and 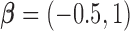 . For model identifiability, the baseline hazard function was chosen such that all events occurred before
. For model identifiability, the baseline hazard function was chosen such that all events occurred before 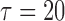 . Specifically, we used
. Specifically, we used  . The truncation time
. The truncation time 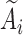 was generated from a uniform distribution
was generated from a uniform distribution 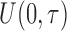 for the length-biased data and from a truncated Weibull distribution with the density function
for the length-biased data and from a truncated Weibull distribution with the density function 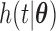 for the general left-truncated data, where
for the general left-truncated data, where 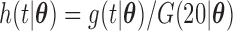 with
with
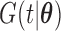 is the cumulative density function and
is the cumulative density function and 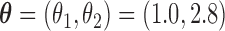 . Following the sampling mechanism, we only kept subjects with
. Following the sampling mechanism, we only kept subjects with 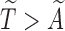 in the observed data sets. The residue censoring time was generated from a uniform distribution with varying boundaries to have different censoring rates. For a subject with censored observations, the value of the SAB status
in the observed data sets. The residue censoring time was generated from a uniform distribution with varying boundaries to have different censoring rates. For a subject with censored observations, the value of the SAB status 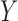 was set to be missing. We set
was set to be missing. We set 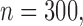 or
or  and used 1000 replicates for each sample size.
and used 1000 replicates for each sample size.
We first assessed the validity of our proposed estimation and inference procedures in finite samples. Tables 1 and 2 summarize the average estimates, empirical standard errors and average EM-aided standard errors for the length-biased data and general truncated data, respectively. As shown in the tables, all point estimates had negligible bias for both length-biased data and general left-truncated data. The standard errors estimated by the EM-aided procedure approximated the empirical standard errors well. Generally, the empirical biases did not change much when varying the percentage of censoring, while the standard errors consistently increased with an increasing percentage of censoring. Also, as the sample size increased from 300 to 600, the standard errors of all estimates decreased.
Table 1.
Summary of simulation studies with length-biased data. EST: empirical mean; SD: empirical standard deviation; ESE: average of asymptotic standard error estimates
| Proposed method | Naive method | |||||||
|---|---|---|---|---|---|---|---|---|
| N | CENSOR | PARA | TRUE | EST | SD | ESE | EST | SD |
| 300 | 0% |
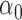
|
1.2 | 1.16 | 0.14 | 0.12 | 0.49 | 0.13 |
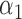
|
1.0 | 1.05 | 0.27 | 0.23 | 1.27 | 0.26 | ||
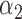
|
1.0 | 0.94 | 0.45 | 0.39 | 0.49 | 0.43 | ||
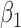
|
-0.5 | -0.50 | 0.14 | 0.14 | -0.50 | 0.16 | ||
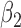
|
1.0 | 1.01 | 0.27 | 0.25 | 1.01 | 0.29 | ||
| 10% |
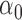
|
1.2 | 1.16 | 0.15 | 0.12 | 0.69 | 0.15 | |
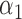
|
1.0 | 1.06 | 0.28 | 0.25 | 1.22 | 0.29 | ||
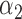
|
1.0 | 0.94 | 0.47 | 0.41 | 0.59 | 0.48 | ||
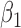
|
-0.5 | -0.50 | 0.16 | 0.15 | -0.43 | 0.16 | ||

|
1.0 | 1.01 | 0.29 | 0.27 | 0.89 | 0.29 | ||
| 30% |
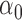
|
1.2 | 1.18 | 0.18 | 0.14 | 0.79 | 0.18 | |
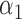
|
1.0 | 1.07 | 0.32 | 0.28 | 1.20 | 0.34 | ||
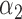
|
1.0 | 0.95 | 0.54 | 0.47 | 0.68 | 0.57 | ||
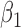
|
-0.5 | -0.49 | 0.17 | 0.17 | -0.40 | 0.19 | ||
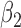
|
1.0 | 1.01 | 0.32 | 0.30 | 0.83 | 0.34 | ||
| 600 | 0% |

|
1.2 | 1.16 | 0.10 | 0.08 | 0.49 | 0.09 |
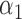
|
1.0 | 1.03 | 0.19 | 0.16 | 1.25 | 0.18 | ||
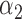
|
1.0 | 0.94 | 0.32 | 0.27 | 0.49 | 0.31 | ||
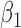
|
-0.5 | -0.50 | 0.10 | 0.10 | -0.50 | 0.12 | ||
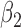
|
1.0 | 1.00 | 0.17 | 0.17 | 1.00 | 0.19 | ||
| 10% |
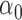
|
1.2 | 1.17 | 0.11 | 0.09 | 0.69 | 0.10 | |
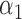
|
1.0 | 1.04 | 0.20 | 0.17 | 1.21 | 0.20 | ||
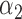
|
1.0 | 0.95 | 0.33 | 0.29 | 0.58 | 0.34 | ||
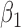
|
-0.5 | -0.50 | 0.11 | 0.11 | -0.43 | 0.12 | ||
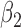
|
1.0 | 1.00 | 0.19 | 0.19 | 0.88 | 0.20 | ||
| 30% |
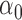
|
1.2 | 1.17 | 0.12 | 0.10 | 0.78 | 0.12 | |
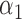
|
1.0 | 1.04 | 0.22 | 0.20 | 1.18 | 0.23 | ||
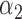
|
1.0 | 0.95 | 0.37 | 0.33 | 0.66 | 0.39 | ||
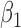
|
-0.5 | -0.49 | 0.12 | 0.12 | -0.39 | 0.13 | ||
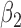
|
1.0 | 1.00 | 0.21 | 0.21 | 0.82 | 0.23 | ||
Table 2.
Summary of simulation studies with general left-truncated data. EST: empirical mean; SD: empirical standard deviation; ESE: average of asymptotic standard error estimates
| Proposed method | Naive method | |||||||
|---|---|---|---|---|---|---|---|---|
| N | CENSOR | PARA | TRUE | EST | SD | ESE | EST | SD |
| 300 | 0% |
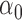
|
1.2 | 1.20 | 0.14 | 0.15 | 1.05 | 0.14 |
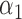
|
1.0 | 1.03 | 0.29 | 0.27 | 1.09 | 0.29 | ||
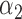
|
1.0 | 0.98 | 0.46 | 0.49 | 0.85 | 0.47 | ||
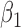
|
-0.5 | -0.50 | 0.15 | 0.14 | -0.50 | 0.15 | ||
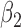
|
1.0 | 1.01 | 0.25 | 0.25 | 1.00 | 0.26 | ||
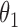
|
1.0 | 1.01 | 0.06 | 0.06 | 1.02 | 0.05 | ||
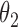
|
2.8 | 2.78 | 0.24 | 0.24 | 2.46 | 0.15 | ||
| 10% |
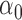
|
1.2 | 1.22 | 0.17 | 0.18 | 1.88 | 0.21 | |
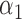
|
1.0 | 1.05 | 0.34 | 0.31 | 1.02 | 0.42 | ||
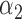
|
1.0 | 0.98 | 0.52 | 0.56 | 1.02 | 0.68 | ||
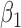
|
-0.5 | -0.50 | 0.17 | 0.17 | -0.41 | 0.15 | ||
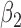
|
1.0 | 1.00 | 0.29 | 0.29 | 0.82 | 0.26 | ||
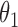
|
1.0 | 1.01 | 0.06 | 0.06 | 1.02 | 0.05 | ||
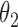
|
2.8 | 2.78 | 0.24 | 0.24 | 2.46 | 0.15 | ||
| 30% |
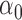
|
1.2 | 1.27 | 0.24 | 0.26 | 2.50 | 0.52 | |
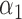
|
1.0 | 1.10 | 0.49 | 0.46 | 1.02 | 0.99 | ||
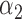
|
1.0 | 0.97 | 0.75 | 0.76 | 1.22 | 1.09 | ||
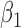
|
-0.5 | -0.50 | 0.21 | 0.21 | -0.34 | 0.17 | ||
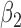
|
1.0 | 1.01 | 0.35 | 0.36 | 0.69 | 0.28 | ||
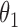
|
1.0 | 1.00 | 0.06 | 0.06 | 1.02 | 0.05 | ||
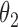
|
2.8 | 2.79 | 0.23 | 0.24 | 2.46 | 0.15 | ||
| 600 | 0% |
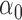
|
1.2 | 1.20 | 0.10 | 0.11 | 1.05 | 0.10 |
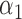
|
1.0 | 1.01 | 0.21 | 0.18 | 1.07 | 0.20 | ||
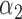
|
1.0 | 0.98 | 0.33 | 0.35 | 0.85 | 0.33 | ||
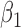
|
-0.5 | -0.50 | 0.10 | 0.10 | -0.50 | 0.10 | ||
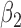
|
1.0 | 1.01 | 0.17 | 0.17 | 1.01 | 0.17 | ||
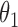
|
1.0 | 1.00 | 0.04 | 0.04 | 1.01 | 0.03 | ||
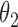
|
2.8 | 2.79 | 0.17 | 0.17 | 2.47 | 0.10 | ||
| 10% |
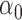
|
1.2 | 1.21 | 0.12 | 0.13 | 1.86 | 0.15 | |
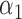
|
1.0 | 1.02 | 0.24 | 0.21 | 1.00 | 0.29 | ||
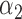
|
1.0 | 0.97 | 0.37 | 0.41 | 0.99 | 0.49 | ||
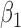
|
-0.5 | -0.50 | 0.12 | 0.12 | -0.40 | 0.10 | ||
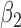
|
1.0 | 1.01 | 0.20 | 0.20 | 0.83 | 0.17 | ||
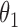
|
1.0 | 1.00 | 0.04 | 0.04 | 1.01 | 0.03 | ||
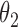
|
2.8 | 2.78 | 0.16 | 0.18 | 2.47 | 0.10 | ||
| 30% |
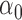
|
1.2 | 1.23 | 0.17 | 0.17 | 2.41 | 0.23 | |
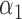
|
1.0 | 1.04 | 0.33 | 0.28 | 0.95 | 0.44 | ||
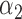
|
1.0 | 0.98 | 0.50 | 0.54 | 1.19 | 0.72 | ||
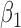
|
-0.5 | -0.50 | 0.15 | 0.15 | -0.34 | 0.11 | ||
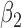
|
1.0 | 1.01 | 0.25 | 0.25 | 0.70 | 0.20 | ||
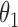
|
1.0 | 1.00 | 0.04 | 0.04 | 1.01 | 0.03 | ||
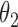
|
2.8 | 2.79 | 0.16 | 0.18 | 2.47 | 0.10 | ||
For comparison, we also performed a naive analysis by ignoring the unique data structure. Specifically, we first fitted a logistic regression model by excluding subjects with unknown values of 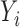 , and then performed Cox proportional hazards modeling for left-truncated data by using subjects with
, and then performed Cox proportional hazards modeling for left-truncated data by using subjects with 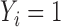 . As shown in the right-sided columns of Tables 1 and 2, this naive method resulted in biased estimates for all parameters in both the logistic regression model and Cox proportional hazards model, since the missing mechanism was not random in our setting.
. As shown in the right-sided columns of Tables 1 and 2, this naive method resulted in biased estimates for all parameters in both the logistic regression model and Cox proportional hazards model, since the missing mechanism was not random in our setting.
6. Data application
To evaluate the entire effects of treatments for autoimmune disease on the risk of experiencing SAB and time to SAB among pregnant women, we analyzed the data from the OTIS autoimmune disease in pregnancy database that we introduced in Section 1. The data set included a total of 930 pregnant women with complete records who entered the studies before week 20 of their gestation during the years between 2005 and 2012. Among these pregnant women, 483 (51.9%) had autoimmune diseases and were treated with the medications under investigation (this group comprises the exposure group); 264 (28.4%) also had autoimmune diseases but were not treated with the medications under investigation (this group comprises the diseased control group); 183 (19.70%) were healthy pregnant women without any autoimmune diseases who were also not treated with the medications under study (this group comprises the healthy control group). There were 66 SAB events and 2 censoring events observed during the study. Biased sampling occurred because the women who had experienced SAB early in the course of their pregnancy had been excluded from the study. As a result, the observed time to the SAB event tended to be longer than that in the general population, as illustrated in Figure 1.
We extracted the baseline covariates for the subjects, including maternal age (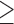 35 or
35 or 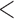 35), smoking status, alcohol status, prior SAB status, and prior therapeutic abortion status, from the database. We performed univariate analysis to select the covariate set to use in the joint model of the risk of experiencing SAB and the time to SAB. The purpose of the univariate screening is to identify the potential confounders when evaluating the risk of using autoimmune disease medications in pregnant women, which is a common practice. The univariate analysis was performed to account for the sampling bias by using the proposed method. Specifically, for each covariate, except for the treatment indicators, we have jointly modeled the cure probability and survival distribution, and used the proposed method for model fitting. Covariates with p-values smaller than 0.2 in either the logistic regression or Cox regression model were included in the final multivariate model. Our final models included maternal age (
35), smoking status, alcohol status, prior SAB status, and prior therapeutic abortion status, from the database. We performed univariate analysis to select the covariate set to use in the joint model of the risk of experiencing SAB and the time to SAB. The purpose of the univariate screening is to identify the potential confounders when evaluating the risk of using autoimmune disease medications in pregnant women, which is a common practice. The univariate analysis was performed to account for the sampling bias by using the proposed method. Specifically, for each covariate, except for the treatment indicators, we have jointly modeled the cure probability and survival distribution, and used the proposed method for model fitting. Covariates with p-values smaller than 0.2 in either the logistic regression or Cox regression model were included in the final multivariate model. Our final models included maternal age (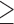 35 or
35 or 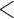 35) and treatment group indicators (exposure group, healthy control or disease control groups).
35) and treatment group indicators (exposure group, healthy control or disease control groups).
We first examined the stationarity assumption using the observed time-to-SAB data. The formal test of stationarity assumption given by Addona and Wolfson (2006) yielded a two-sided p-value of 0.0001, which indicated that the stationarity assumption did not hold and the observed time-to-SAB data were not length-biased data. We then used the Weibull distribution to model the truncation time. Both the estimated values of shape and scale parameters were very large compared with their standard errors, also suggesting the stationarity assumption did not hold in the study. Table 3 lists the estimated coefficients along with standard errors and p-values from the proposed method and the naive analyses. The model fitting of the logistic regression by the proposed method indicated that the healthy controls had significantly lower risk (p-value 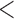 0.01) of experiencing SAB compared with the other two groups after controlling for the age effect. Interestingly, our comparison of the exposure group and the disease control group suggested that the use of the medications under investigation for pregnant women with autoimmune diseases did not change their risk of experiencing SAB. Consistent with previous reports (Andersen and others, 2000), we found that older maternal age (
0.01) of experiencing SAB compared with the other two groups after controlling for the age effect. Interestingly, our comparison of the exposure group and the disease control group suggested that the use of the medications under investigation for pregnant women with autoimmune diseases did not change their risk of experiencing SAB. Consistent with previous reports (Andersen and others, 2000), we found that older maternal age (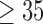 ) significantly increases the risk of SAB (p-value
) significantly increases the risk of SAB (p-value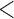 0.01). The Cox regression part of the joint model suggested that autoimmune disease status, use of the newer medications and maternal age did not significantly affect the distribution of time to SAB for the uncured group, although the healthy control group tended to have a lower hazard function indicating later timing of SAB events, compared with that of the other two groups after controlling for the maternal age (
0.01). The Cox regression part of the joint model suggested that autoimmune disease status, use of the newer medications and maternal age did not significantly affect the distribution of time to SAB for the uncured group, although the healthy control group tended to have a lower hazard function indicating later timing of SAB events, compared with that of the other two groups after controlling for the maternal age (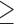 35 or
35 or 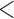 35). The naive analysis that ignored the data structure had similar results for the parameters in the survival model, but had misleading results for the risk model. Specifically, the naive analysis greatly underestimated the overall risk of experiencing SAB, which is similar to our previous simulation findings when the censoring rate is low. Note that the conclusion is conditional on
35). The naive analysis that ignored the data structure had similar results for the parameters in the survival model, but had misleading results for the risk model. Specifically, the naive analysis greatly underestimated the overall risk of experiencing SAB, which is similar to our previous simulation findings when the censoring rate is low. Note that the conclusion is conditional on 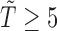 weeks, due to a lack of instantaneous detection of pregnancy in the early stage.
weeks, due to a lack of instantaneous detection of pregnancy in the early stage.
Table 3.
Estimated coefficients with standard errors (SE) and p-values for SAB data
| Proposed method | Naive method | ||||||
|---|---|---|---|---|---|---|---|
| Coefficient | SE | P-value | Coefficient | SE | P-value | ||
| Logistic model | |||||||
| Treatment | |||||||
| Exposed | |||||||
| Healthy control |
 1.04 1.04 |
0.34 |
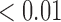
|
 0.91 0.91 |
0.45 | 0.04 | |
| Disease control | 0.05 | 0.21 | 0.82 | 0.03 | 0.28 | 0.93 | |
| Age | |||||||
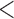 35 35 |
|||||||
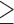 35 35 |
0.67 | 0.19 |
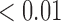
|
0.55 | 0.26 | 0.04 | |
| Intercept |
 2.01 2.01 |
0.14 |
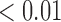
|
 2.64 2.64 |
0.20 |
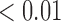
|
|
| Cox proportional hazard model | |||||||
| Treatment | |||||||
| Exposed | |||||||
| Healthy control |
 0.31 0.31 |
0.43 | 0.47 |
 0.33 0.33 |
0.49 | 0.51 | |
| Disease control | 0.06 | 0.23 | 0.81 | 0.26 | 0.28 | 0.36 | |
| Age | |||||||
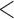 35 35 |
|||||||
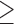 35 35 |
0.27 | 0.22 | 0.20 | 0.10 | 0.26 | 0.68 | |
| Shape parameter | 3.13 | 0.30 | 2.77 | 0.07 | |||
| Scale parameter | 10.59 | 0.60 | 12.66 | 0.16 | |||
7. Discussion
We have proposed new EM algorithms for biased sampling survival data with a cured proportion to obtain full likelihood maximum estimators. We first considered length-biased data and then generalized the estimation and inference procedure to general left-truncated data. As pointed out by Wang (1989), the joint model is not identifiable if distributions of the truncation time and event time of interest both have nonparametric components. Here, we choose the semiparametric model for the event time of interest (e.g., time to SAB event) and adopt a parametric model for the truncation time. One way to relax the parametric assumptions is to use a flexible parametric model, such as a truncated generalized Gamma distribution with three parameters (Stacy, 1962) for the truncation time. Specifically, the density function of a truncated generalized Gamma distribution is 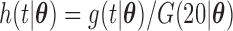 with
with 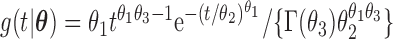 , and
, and 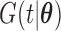 is the cumulative density function, where
is the cumulative density function, where 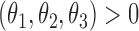 . The generalized Gamma distribution degenerates to the Weibull distribution if
. The generalized Gamma distribution degenerates to the Weibull distribution if 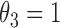 , and degenerates to the Gamma distribution if
, and degenerates to the Gamma distribution if 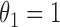 . In the supplementary materials available at Biostatistics online, we have conducted additional simulation studies to investigate the effects of model misspecification of the truncation time on the estimation of the parameters of interest, i.e., regression coefficients under the logistic regression model and Cox model. In summary, the estimators of interest have robust performance with violations of the parametric model assumptions on the truncation time. As discussed in Section 2, the zero tail constraint for survival data with a cure portion is naturally satisfied. Different from the usual cure rate data where the long-term survivors are always right-censored, in our pregnancy studies we observe majority of the “cured” women. This greatly improves the practical identifiability of the cured portion (Farewell, 1986; Lu and Ying, 2004), as well as substantially increase the amount of information available for estimating the model parameters.
. In the supplementary materials available at Biostatistics online, we have conducted additional simulation studies to investigate the effects of model misspecification of the truncation time on the estimation of the parameters of interest, i.e., regression coefficients under the logistic regression model and Cox model. In summary, the estimators of interest have robust performance with violations of the parametric model assumptions on the truncation time. As discussed in Section 2, the zero tail constraint for survival data with a cure portion is naturally satisfied. Different from the usual cure rate data where the long-term survivors are always right-censored, in our pregnancy studies we observe majority of the “cured” women. This greatly improves the practical identifiability of the cured portion (Farewell, 1986; Lu and Ying, 2004), as well as substantially increase the amount of information available for estimating the model parameters.
Even though the proposed point and variance estimation involves iterations, the computation is fast and efficient. The conditional expectations in the E-step of both the point and variance estimations involve at most one-dimensional integration and can be easily estimated. In the M-step, the non-specified baseline hazard function can be calculated explicitly, while the low-dimensional parameters can be updated quickly using available statistical software. For example, in a 100-run simulation for the general left-truncated data using a 3.30GHz desktop CPU under the scenario with 600 samples and 10% censoring rate, the CPU time was 3.16 hours and 0.34 hours for the point estimation and variance estimation, respectively. The average number of iterations to achieve convergence was 14, with convergence criterion defined as 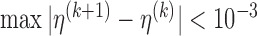 . For the SAB data, the CPU time for fitting the final model was 0.18 hours, including the point and variance estimation.
. For the SAB data, the CPU time for fitting the final model was 0.18 hours, including the point and variance estimation.
Although this work focused on the logistic regression model for the cured proportion and the proportional hazards model for the time to the event of interest, the proposed estimation and inference method can be extended to other types of models such as the probit model for the cured proportion and the proportional odds model for the event time. In applications, one challenge when applying the proposed method is model checking. Due to the biased sampling issue, the distribution of the observed data is not representative of that of the target population. Accordingly, standard diagnostic tools, such as model checking tests of proportionality for traditional survival data, cannot be directly applied here. Developing rigorous statistical tools for model checking is beyond the scope of this article, and is a worthy objective for future research.
8. Software
Software in the form of R code and documentation is online at https://github.com/JPiao7u089/Cured-Proportion-and-Biased-Sampling.git.
Supplementary Material
Acknowledgments
We gratefully acknowledge support from the National Cancer Institute at the National Institutes of Health (CA016672 and CA193878). Conflict of Interest: None declared.
Supplementary Material
Supplementary material is available online at http://biostatistics.oxfordjournals.org.
References
- Addona V. and Wolfson D.B. (2006). A formal test for the stationarity of the incidence rate using data from a prevalent cohort study with follow-up. Lifetime data analysis 12, 267–284. [DOI] [PubMed] [Google Scholar]
- Andersen A. M. N., Wohlfahrt J., Christens P., Olsen J. and Melbye M. (2000). Maternal age and fetal loss: population based register linkage study. BMJ 320, 1708–1712. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chambers C. D., Johnson D. L., Xu R., Taylor S., Rosillon D., Wolleswinkel J. H. and Baril L. (2011). Challenges and design of a prospective, observational cohort study to assess the risk of spontaneous abortion following administration of human papillomavirus (hpv) bivalent (types 16 and 18) recombinant vaccine. In:Strom Brian L. (editor), Pharmacoepidemiology and Drug Safety, Volume 20 Malden, MA USA: Wiley.S358–S358. [Google Scholar]
- Chen H. Y. and Little R. J. A. (1999). Proportional hazards regression with missing covariates. Journal of the American Statistical Association 94, 896–908. [Google Scholar]
- Chen M. H., Ibrahim J. G. and Sinha D. (1999). A new bayesian model for survival data with a surviving fraction. Journal of the American Statistical Association 94, 909–919. [Google Scholar]
- Farewell V. T. (1986). Mixture models in survival analysis: Are they worth the risk? Canadian Journal of Statistics 14, 257–262. [Google Scholar]
- Gill R. D, Wellner J. A and PrÆstgaard J. (1989). Non-and semi-parametric maximum likelihood estimators and the von Mises method (part 1)[with discussion and reply]. Scandinavian Journal of Statistics 16, 97–128. [Google Scholar]
- Kim J. P., Lu W., Sit T. and Ying Z. (2013). A unified approach to semiparametric transformation models under general biased sampling schemes. Journal of the American Statistical Association 108, 217–227. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuk A. Y. C. and Chen C. H. (1992). A mixture model combining logistic regression with proportional hazards regression. Biometrika 79, 531–541. [Google Scholar]
- Li C. S. and Taylor J. M. G. (2002). A semi-parametric accelerated failure time cure model. Statistics in Medicine 21, 3235–3247. [DOI] [PubMed] [Google Scholar]
- L u W. and Ying Z. (2004). On semiparametric transformation cure models. Biometrika 91, 331–343. [Google Scholar]
- Murphy S. A. and Van der Vaart A. W. (2000). On profile likelihood. Journal of the American Statistical Association 95, 449–465. [Google Scholar]
- Ning J., Qin J. and Shen Y. (2014). Score estimating equations from embedded likelihood functions under accelerated failure time model. Journal of the American Statistical Association 109, 1625–1635. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peng Y. and Dear K. B. G. (2000). A nonparametric mixture model for cure rate estimation. Biometrics 56, 237–243. [DOI] [PubMed] [Google Scholar]
- Qin J., Ning J., Liu H. and Shen Y. (2011). Maximum likelihood estimations and em algorithms with length-biased data. Journal of the American Statistical Association 106, 1434–1449. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shen Y., Ning J. and Qin J. (2009). Analyzing length-biased data with semiparametric transformation and accelerated failure time models. Journal of the American Statistical Association 104, 1192–1202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Skorpen C. G., Hoeltzenbein M., Tincani A., Fischer-Betz R., Elefant E., Chambers C., Da Silva J., Nelson-Piercy C., Cetin I., Costedoat-Chalumeau N.. and others (2016). The eular points to consider for use of antirheumatic drugs before pregnancy, and during pregnancy and lactation. Annals of the Rheumatic Diseases 75, 795–810. [DOI] [PubMed] [Google Scholar]
- Stacy E. W. (1962). A generalization of the gamma distribution. The Annals of mathematical statistics 33, 1187–1192. [Google Scholar]
- S y J. P. and Taylor J. M. G. (2000). Estimation in a cox proportional hazards cure model. Biometrics 56, 227–236. [DOI] [PubMed] [Google Scholar]
- Taylor J. M. G. (1995). Semi-parametric estimation in failure time mixture models. Biometrics 51, 899–907. [PubMed] [Google Scholar]
- Tsai W. Y. (2009). Pseudo-partial likelihood for proportional hazards models with biased-sampling data. Biometrika 96, 601–615. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Der Vaart A. W. and Wellner J. A. (1996). Weak Convergence and Empirical Processes. New York: Springer. [Google Scholar]
- Vardi Y. (1989). Multiplicative censoring, renewal processes, deconvolution and decreasing density: nonparametric estimation. Biometrika 76, 751–761. [Google Scholar]
- Visser K., Katchamart W., Loza E., Martinez-Lopez J.A., Salliot C., Trudeau J., Bombardier C., Carmona L., Van der Heijde D., Bijlsma J.W.J.. and others (2009). Multinational evidence-based recommendations for the use of methotrexate in rheumatic disorders with a focus on rheumatoid arthritis: integrating systematic literature research and expert opinion of a broad international panel of rheumatologists in the 3e initiative. Annals of the Rheumatic Diseases 68, 1086–1093. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang M. C. (1989). A semiparametric model for randomly truncated data. Journal of the American Statistical Association 84, 742–748. [Google Scholar]
- Wang M. C., Jewell N. P. and Tsai W. Y. (1986). Asymptotic properties of the product limit estimate under random truncation. The Annals of Statistics 14, 1597–1605. [Google Scholar]
- Wilcox A. J., Weinberg C. R., O’Connor J. F., Baird D. D., Schlatterer J. P., Canfield R. E., Armstrong E. G. and Nisula B. C. (1988). Incidence of early loss of pregnancy. New England Journal of Medicine 319, 189–194. [DOI] [PubMed] [Google Scholar]
- X u R. and Chambers C. (2011). A sample size calculation for spontaneous abortion in observational studies. Reproductive Toxicology 32, 490–493. [DOI] [PubMed] [Google Scholar]
- Zeng D., Yin G. and Ibrahim J. G. (2006). Semiparametric transformation models for survival data with a cure fraction. Journal of the American Statistical Association 101, 670–684. [Google Scholar]
- Zhang J. and Peng Y. (2009). Accelerated hazards mixture cure model. Lifetime Data Analysis 15, 455–467. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.