Summary
In comparative effectiveness research, we are often interested in the estimation of an average causal effect from large observational data (the main study). Often this data does not measure all the necessary confounders. In many occasions, an extensive set of additional covariates is measured for a smaller and non-representative population (the validation study). In this setting, standard approaches for missing data imputation might not be adequate due to the large number of missing covariates in the main data relative to the smaller sample size of the validation data. We propose a Bayesian approach to estimate the average causal effect in the main study that borrows information from the validation study to improve confounding adjustment. Our approach combines ideas of Bayesian model averaging, confounder selection, and missing data imputation into a single framework. It allows for different treatment effects in the main study and in the validation study, and propagates the uncertainty due to the missing data imputation and confounder selection when estimating the average causal effect (ACE) in the main study. We compare our method to several existing approaches via simulation. We apply our method to a study examining the effect of surgical resection on survival among 10 396 Medicare beneficiaries with a brain tumor when additional covariate information is available on 2220 patients in SEER-Medicare. We find that the estimated ACE decreases by 30% when incorporating additional information from SEER-Medicare.
Keywords: Bayesian data augmentation, Model averaging, Missing data, Bayesian adjustment for confounding, Confounder selection
1. Introduction
In this new era of big data, it is becoming standard practice to address questions of comparative effectiveness research and estimation of causal effects from analyses of large observational data (e.g. Medicare claims data). A key feature of these data sources (which we will refer to as the main study) is that they include very large and often nationally representative populations. For example, approximately 85% of the US population of people older than 65-years-old is enrolled in the Medicare Fee For Service Plans. However, a potential limitation of these data is that they measure a limited number of potential confounders, that is, basic demographics, and some information on co-morbidities from previous claims. When the goal is to estimate the average causal effect (ACE) of a particular treatment on an outcome, failure to measure and therefore to adjust for even one key confounder will lead to biased estimates of causal effects.
In many settings, additional data on potential confounders (e.g. behavioral risk factors, biological samples, tumor characteristics, electronic medical records etc.) is collected in a smaller subpopulation compared to the main study. Sometimes this subpopulation is part of the main study, that is an internal validation study. Examples of such studies include SEER-Medicare (Cooper and others, 2002), which collects additional information regarding tumor characteristics on cancer patients in Medicare, or larger cohorts such as the Nurses Health Study, which measure genetic information on a subset of the population (Hiraki and others, 2014). Alternatively, additional data may be available from external validation studies that collect outcome, treatment and more extensive covariate information on separate populations. In both cases, the internal or external validation study might not be representative of the main study population and the ACEs might be different than the ACE in the main study. In this context, we are challenged by the need to efficiently augment the main study with covariate information from the validation study to reliably estimate causal effects in the larger, more representative population. Although this could be cast as a missing covariate problem, the smaller size of the validation data and the large number of missing covariates in the main study make a standard application of multiple imputation highly variable and sensitive to model assumptions.
More generally, this setting is met with the following challenges: (i) the need to reduce the dimension of a possibly high-dimensional set of potential confounders; (ii) missing data imputation; (iii) propagation of the uncertainty in the model selection and missing data imputation when estimating the ACE in the main study; and (iv) potentially different treatment effects in the main and the validation studies. There exist several approaches that address a subset of the aforementioned issues. Some of these approaches have the inferential goal of predicting the outcome and not of estimation of causal effects. As discussed in Crainiceanu and others (2008); Wang and others (2012); Wilson and Reich (2014); Vansteelandt and others (2012), methods for covariate selection in the context of prediction are inadequate when the goal is confounding adjustment for effect estimation.
1.1. Review of existing methods
Perhaps the most popular framework in causal inference to reduce the dimension of the confounders relies on propensity score methods (Rosenbaum and Rubin, 1983). These approaches are attractive because they avoid specifying a model for missing data imputation of a large vector of unobserved potential confounders in the main study. In the context of propensity score methods, two approaches have been proposed to deal with the setting of a main and validation study. The first is called propensity score calibration (Stürmer and others, 2005) which estimates: (i) an error prone propensity score from the main study; and (ii) a “gold standard” propensity score that relies on the additional covariates from the validation study. Then, it uses regression calibration to impute the “gold standard” propensity score in the main study. This approach is useful when no outcome information is available in the validation sample. However, it relies on a surrogacy assumption that requires the outcome to be independent of the error prone propensity score conditional on the gold standard propensity score (Stürmer and others, 2007).
The second approach, called conditional propensity scores (CPSs), was proposed in McCandless and others (2012). The idea is to first estimate a propensity score in the validation study, and then define the CPS as the linear component of the propensity score model that depends upon the covariates that are observed in the validation study only. The treatment effect in the main study is then estimated by integrating over the distribution of the missing CPS. This approach, however, relies on an assumption that the CPS is independent from the treatment or outcome. A limitation common to both of these propensity score based approaches is that they are only applicable to binary treatments.
An alternative to propensity score methods in the context of missing potential confounders is to treat the data from the main and validation studies as a combined data set and apply methods for multiple imputation of the missing covariates in the main study. There exists a vast literature on multiple imputation (Little and Rubin, 2014). One of the most common challenges is how to specify a correct imputation model, and in our setting, this can be challenging as the number of missing covariates can be large. Nonparametric Bayesian models such as those in Murray and Reiter (2016) flexibly specify the joint distribution of the missing covariates, which alleviates problems that stem from the misspecification of the missing data model. Several approaches have been developed to combine data sets and build a regression model, when certain covariates are missing in some of the data sources. For example, Gelman and others (1998) addressed the problem of multiple imputation across multiple surveys under the assumption of multivariate normality. Jackson and others (2009) extended these ideas to more complicated structures in a graphical modeling framework. All of these approaches, however, ignore a crucial challenge commonly faced in our setting: the sample size of the validation data is small relative to the number of covariates being imputed, which can limit the usefulness of existing approaches due to high estimation uncertainty. Thus our setting necessitates introducing variable selection or dimension reduction to decrease the variability induced from the imputation of a large number of missing covariates.
Approaches have been developed to perform simultaneous variable selection and missing data imputation when the goal is prediction of an outcome. Yang and others (2005) implemented variable selection within multiple imputation under multivariate Normality. Mitra & Dunson (2010) extended this approach to binary covariates and implemented a second layer of variable selection on the imputation models. However, as mentioned earlier, variable selection methods based on prediction can omit important confounders and therefore a model selection tool that aims at dimension reduction when the goal is confounding adjustment is required.
1.2. Proposed approach
In this article, we develop a new approach, which we will refer to as Guided Bayesian Adjustment for Confounding (GBAC), that addresses the four challenges introduced above (dimension reduction on the selection of confounders; missing data imputation; propagation of uncertainty; and treatment effect heterogeneity) under a unified framework. We build upon the work by Wang and others (2012) called Bayesian Adjustment for Confounding (BAC) and generalize it in the context of missing data in the main study by adopting a proper Bayesian approach to modeling the missing data. Our proposed approach will treat the main study and validation study as one combined data set while allowing for different treatment effects in the two studies. By reducing the dimension of the covariate space to only the necessary confounders we will improve the efficiency in estimating the ACE.
The remainder of the article is structured as follows: In section 2, we will introduce the modeling approach including details on posterior simulation. In section 3, we will detail our modelling assumptions. Here we will also demonstrate that that our proposed approach does not rely on the surrogacy assumption nor the conditional independence assumption that are necessary in the propensity score calibration and in the CPS approaches. In section 4, we will introduce a simulation that will compare our proposed method to CPSs and standard multiple imputation. In section 5, we will analyze the effect of surgical resection on cancer patients in Medicare, and we will conclude in section 6 with further discussion.
2. Methods
2.1. Estimation of the ACE
Let 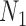 and
and 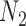 be the sample sizes of the main study and of the validation study, respectively where
be the sample sizes of the main study and of the validation study, respectively where 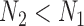 . Let
. Let 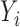 be the outcome,
be the outcome, 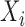 be the treatment, and
be the treatment, and 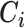 be the full vector of
be the full vector of 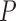 pre-treatment covariates for subject
pre-treatment covariates for subject 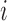 . Assume that
. Assume that 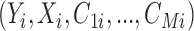 are observed in both the main and the validation study and that the
are observed in both the main and the validation study and that the 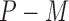 covariates
covariates 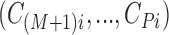 are observed for the
are observed for the 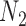 subjects of the validation study but missing for the
subjects of the validation study but missing for the 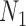 subjects in the main study. We also assume that
subjects in the main study. We also assume that 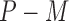 , the number of missing covariates, can be large relative to
, the number of missing covariates, can be large relative to  , though not greater than
, though not greater than 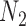 .
.
Our goal is to borrow information from the validation study to estimate the ACE in the main study. We define the AEC 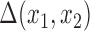 as follows
as follows
| (2.1) |
where the expectations are taken with respect to the population represented in the main data. We forego potential outcomes notation, but note that (2.1) is interpretable as the ACE of assignment to 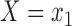 versus
versus 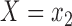 under the assumption of strongly ignorable treatment assignment, which states that potential outcomes under different levels of
under the assumption of strongly ignorable treatment assignment, which states that potential outcomes under different levels of 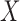 are independent of assignment to
are independent of assignment to 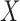 , conditional on
, conditional on 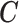 , and that every observation has a positive probability of receiving any level of
, and that every observation has a positive probability of receiving any level of 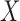 . We will also assume that all the necessary confounders required for the strong ignorability assumption to hold are an unknown subset of
. We will also assume that all the necessary confounders required for the strong ignorability assumption to hold are an unknown subset of 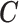 .
.
Letting 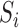 be the indicator of whether or not individual
be the indicator of whether or not individual 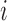 is in the validation study, we introduce the following outcome model for estimating (2.1)
is in the validation study, we introduce the following outcome model for estimating (2.1)
| (2.2) |
for 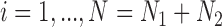 , where
, where 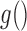 is an arbitrary link function that falls within the Generalized linear model (GLM) framework. We introduce the unknown parameter
is an arbitrary link function that falls within the Generalized linear model (GLM) framework. We introduce the unknown parameter 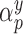 , such that if
, such that if 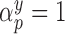 then covariate
then covariate 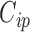 is included into the outcome model. Note that by including the interaction terms between
is included into the outcome model. Note that by including the interaction terms between 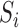 and
and 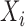 as well as between
as well as between 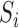 and
and 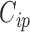 for
for 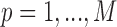 , we allow the treatment effect and adjustment of the fully observed covariates to differ between the main and validation study, respectively. The parameters
, we allow the treatment effect and adjustment of the fully observed covariates to differ between the main and validation study, respectively. The parameters 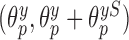 denote the regression parameters for the potential confounders in the outcome model, and
denote the regression parameters for the potential confounders in the outcome model, and 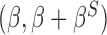 are parameters representing the effect of
are parameters representing the effect of 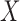 on
on 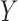 conditionally on
conditionally on 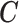 in the two populations, respectively. Estimation of the ACE comes with two major methodological challenges in this setting: (i) selection of confounders in the outcome model that are necessary for the strong ignorability assumption to hold; (ii) some of these confounders may be missing in the main study. We will address both of these challenges in the following sections.
in the two populations, respectively. Estimation of the ACE comes with two major methodological challenges in this setting: (i) selection of confounders in the outcome model that are necessary for the strong ignorability assumption to hold; (ii) some of these confounders may be missing in the main study. We will address both of these challenges in the following sections.
2.2. Prior distribution for confounder selection
Following the ideas of Wang and others (2012); Lefebvre and others (2014b); Wang and others (2015) we introduce a treatment model as
| (2.3) |
where 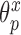 ,
, 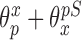 , and
, and 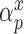 have analogous interpretations as in the outcome model. We then define a prior distribution on
have analogous interpretations as in the outcome model. We then define a prior distribution on 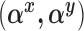 as
as
| (2.4) |
| (2.5) |
The goal of this prior is to assign high posterior probabilities to outcome models that include covariates that are associated with both 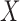 and
and 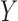 . Details of this prior distribution can be found in Wang and others (2012), though we will briefly summarize them here. We assume that if a given covariate is included into the treatment model, that is
. Details of this prior distribution can be found in Wang and others (2012), though we will briefly summarize them here. We assume that if a given covariate is included into the treatment model, that is 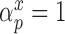 , then the prior odds of including the same covariate into the outcome model is equal to
, then the prior odds of including the same covariate into the outcome model is equal to  . If
. If 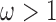 , we assume that covariates that are associated with the treatment have higher prior probabilities to be included into the outcome model. We also assume that if a covariate does not enter into the treatment model, then the prior odds for this same covariate to be included into the outcome model is 1. Wang and others (2012) showed that this prior distribution with a large
, we assume that covariates that are associated with the treatment have higher prior probabilities to be included into the outcome model. We also assume that if a covariate does not enter into the treatment model, then the prior odds for this same covariate to be included into the outcome model is 1. Wang and others (2012) showed that this prior distribution with a large 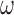 assigns most of the posterior mass,
assigns most of the posterior mass, 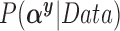 , to models that include all the necessary confounders.
, to models that include all the necessary confounders.
The remaining prior distributions are intended to reflect no prior information. We use non-informative, Normal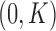 prior distributions on all regression coefficients with
prior distributions on all regression coefficients with 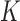 large and assign Inv-Gamma
large and assign Inv-Gamma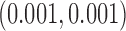 prior distributions on all variance parameters in the model.
prior distributions on all variance parameters in the model.
2.3. Modeling the missing data
A second major challenge is the fact that a large number of covariates are missing in the main data, and some of these may be important confounders. We will be imputing them within a fully Bayesian framework. Specifically, building upon ideas from Raghunathan and others (2001), we define the following sequence of regression models for the missing covariates
| (2.6) |
where 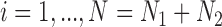 . For the remainder of this article, we will assume the missing covariates are binary or continuous, and therefore
. For the remainder of this article, we will assume the missing covariates are binary or continuous, and therefore 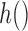 is the identity or probit link functions to facilitate posterior sampling using the latent variable approach of Albert & Chib (1993). An extension of the latent variable approach to ordered categorical covariates is straightforward and is described in Mitra & Dunson (2010). Here we have introduced a set of unknown parameters
is the identity or probit link functions to facilitate posterior sampling using the latent variable approach of Albert & Chib (1993). An extension of the latent variable approach to ordered categorical covariates is straightforward and is described in Mitra & Dunson (2010). Here we have introduced a set of unknown parameters 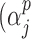 ) to indicate whether a given covariate enters into the missing data models. That is
) to indicate whether a given covariate enters into the missing data models. That is 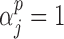 denotes that covariate
denotes that covariate 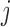 enters into the imputation model for covariate
enters into the imputation model for covariate 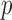 . We implement a non-informative prior on
. We implement a non-informative prior on 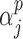 for
for 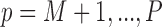 that assigns equal weight to all models as done in standard Bayesian model averaging (BMA).
that assigns equal weight to all models as done in standard Bayesian model averaging (BMA).
2.4. Implementation
Full details of the posterior derivations and Markov Chain Monte Carlo (MCMC) sampling can be found in Appendix A of the Supplementary Material available at Biostatistics online. A brief description of how we obtain posterior samples of the ACE using MCMC is as follows:
Sample from the posterior distribution of
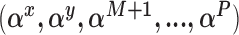 using the complete data set defined by the observed data and the current state of the missing data imputations. Here we will make repeated use of the BIC approximation to the Bayes factor between two models (Raftery, 1995).
using the complete data set defined by the observed data and the current state of the missing data imputations. Here we will make repeated use of the BIC approximation to the Bayes factor between two models (Raftery, 1995).For models defined by the current values of
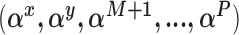 update all regression parameters. Specifically, for all covariates with
update all regression parameters. Specifically, for all covariates with 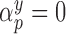 , we force
, we force 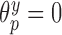 , and then update the remaining regression parameters from their full conditional distributions. Analogous operations are performed for the treatment and missing data models.
, and then update the remaining regression parameters from their full conditional distributions. Analogous operations are performed for the treatment and missing data models.Conditional on a chosen model identified by
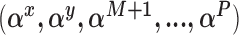 and current state of the regression coefficients, the missing data are imputed from their full conditional distribution.
and current state of the regression coefficients, the missing data are imputed from their full conditional distribution.
Once we obtain 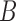 draws of all the parameters and missing data we can obtain an estimate of the ACE as follows:
draws of all the parameters and missing data we can obtain an estimate of the ACE as follows:
| (2.7) |
where the superscript 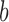 denotes the
denotes the 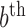 draw from our posterior. Note that we sum over the
draw from our posterior. Note that we sum over the 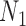 subjects in the main study to approximate the distribution of
subjects in the main study to approximate the distribution of 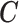 in the main study. This quantity is averaging over the space of all models governed by
in the main study. This quantity is averaging over the space of all models governed by 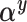 as well as the missing data imputations,
as well as the missing data imputations, 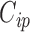 for
for 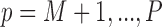 . Therefore, our final estimates of the ACE obtained from this procedure will account for the uncertainty associated with model selection as well as variable imputations.
. Therefore, our final estimates of the ACE obtained from this procedure will account for the uncertainty associated with model selection as well as variable imputations.
It is important to note that at each stage of the MCMC, the whole set of missing covariates is imputed, however, only the covariates for which 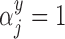 enter into the outcome model and therefore directly impact the estimate,
enter into the outcome model and therefore directly impact the estimate, 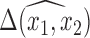 . Other imputed covariates indirectly affect
. Other imputed covariates indirectly affect 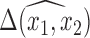 if they are used to impute another covariate that is included in the outcome model. Another important point is that the posterior distribution of
if they are used to impute another covariate that is included in the outcome model. Another important point is that the posterior distribution of 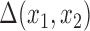 obtained from posterior samples of
obtained from posterior samples of 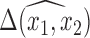 is an approximation since there is a nonzero probability that we will average over models that exclude a necessary confounder. Conditional on having imputed the full data, Wang and others (2012, 2015) showed that the posterior of
is an approximation since there is a nonzero probability that we will average over models that exclude a necessary confounder. Conditional on having imputed the full data, Wang and others (2012, 2015) showed that the posterior of 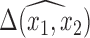 primarily uses outcome models that include the necessary confounders, thereby improving the approximation.
primarily uses outcome models that include the necessary confounders, thereby improving the approximation.
3. Assumed commonalities between the main and validation studies
Beyond the typical assumptions required to infer causal effects from observational studies, we further require certain quantities to be shared between the main and validation studies. Specifically, the distribution of the missing covariates conditional on the observed data must be the same in the main and validation study. Letting superscript 1 denote quantities in the main study and superscript 2 denote quantities in the validation study, this assumption can be written as
| (3.1) |
We rely on Assumption 3.1 to impute the missing covariates in the main study. This assumption is commonly made in the data fusion literature, which solves a different, though very related problem, where certain variables are never jointly observed in the two data sets Reiter (2012); Rässler (2004). It is also related to the assumption of transportability in the measurement error literature (Carroll and others, 2006; Spiegelman and others, 2000), in which a model relating variables measured with noise to their true counterparts is assumed to be shared between the main and validation studies. Assumption 3.1 is also implicitly made in any implementation of multiple imputation, typically framed in terms of a missing data mechanism that is missing at random (MAR). There is no empirical way of verifying that this assumption holds, because 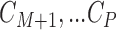 are completely missing in the main study, so careful consideration must be given to whether the main and validation studies are similar enough for this assumption to be reasonable.
are completely missing in the main study, so careful consideration must be given to whether the main and validation studies are similar enough for this assumption to be reasonable.
While the model for the missing covariates in (2.6) is specified only in terms of 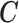 , the missing covariates are imputed from their full conditional distribution conditional on observed values of
, the missing covariates are imputed from their full conditional distribution conditional on observed values of 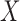 and
and 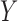 as well. This is an important distinction with McCandless and others (2012), which adopts the more restrictive assumption that the missing CPS depends only on the observed
as well. This is an important distinction with McCandless and others (2012), which adopts the more restrictive assumption that the missing CPS depends only on the observed 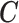 . This approach is also significantly less restrictive than the methods in Stürmer and others (2005) that rely on the aforementioned surrogacy assumption.
. This approach is also significantly less restrictive than the methods in Stürmer and others (2005) that rely on the aforementioned surrogacy assumption.
4. Simulation study
We focus on a continuous outcome and a binary treatment to facilitate comparison between our approach and propensity score based methods, though our approach can handle any treatment or outcome that falls in the GLM framework. In all scenarios 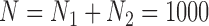 , while we vary the validation sample size,
, while we vary the validation sample size, 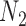 from 100 to 500. We set
from 100 to 500. We set 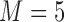 and
and 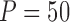 , which means that 45 of the 50 covariates are missing in the main data. All of the covariates are independent of each other. We let 1 of the
, which means that 45 of the 50 covariates are missing in the main data. All of the covariates are independent of each other. We let 1 of the 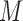 fully observed variables to be a confounder (
fully observed variables to be a confounder (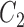 ), 2 of the partially observed variables to be confounders (
), 2 of the partially observed variables to be confounders (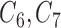 ), and the remaining variables are not associated with either the treatment or outcome. To specify different treatment effects in the two populations we set
), and the remaining variables are not associated with either the treatment or outcome. To specify different treatment effects in the two populations we set 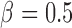 and
and 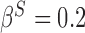 . Specifically, we generate 1000 data sets from the following models:
. Specifically, we generate 1000 data sets from the following models:
| (4.1) |
| (4.2) |
where 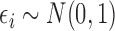 . In this setting,
. In this setting, 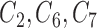 are the minimal set of confounders required for valid estimation. Since we are analyzing a continuous outcome, the ACE can be defined as
are the minimal set of confounders required for valid estimation. Since we are analyzing a continuous outcome, the ACE can be defined as 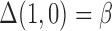 , where
, where 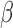 is the coefficient for the effect of
is the coefficient for the effect of 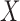 on
on 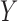 in the outcome model. This implies that
in the outcome model. This implies that 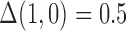 in the main study and
in the main study and 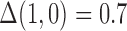 in the validation study. We implemented a variety of approaches aimed at obtaining an unbiased estimate of the ACE in the main study:
in the validation study. We implemented a variety of approaches aimed at obtaining an unbiased estimate of the ACE in the main study:
Gold standard approach which fits the correct regression model to the main study that includes
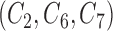 as if they were fully observed in both studies.
as if they were fully observed in both studies.CPS approach of McCandless and others (2012) with an interaction term between treatment and study included in the outcome model to allow for differing treatment effects. We refer to this as CPS.
GBAC with
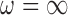 . We will refer to this as GBAC(
. We will refer to this as GBAC(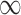 )
)GBAC with
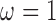 . This is very similar to the approach in Mitra & Dunson (2010) as it performs variable selection on the imputation model and outcome model, but ignores treatment information when selecting variables for the outcome model and selects variables based on their ability to predict
. This is very similar to the approach in Mitra & Dunson (2010) as it performs variable selection on the imputation model and outcome model, but ignores treatment information when selecting variables for the outcome model and selects variables based on their ability to predict 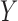 . We will refer to this as GBAC(1)
. We will refer to this as GBAC(1)Fully Bayesian Multiple imputation. This is the proposed GBAC approach fixing
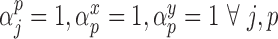 . We will refer to this as MI.
. We will refer to this as MI.
To examine the performance of the various methods in estimating the ACE we look at three operating characteristics: bias and mean squared error (MSE) of posterior mean estimates, and 95% credible interval coverage, where credible intervals are taken to be the 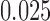 and
and 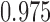 quantiles of the posterior distribution.
quantiles of the posterior distribution.
4.1. Results of the simulation study
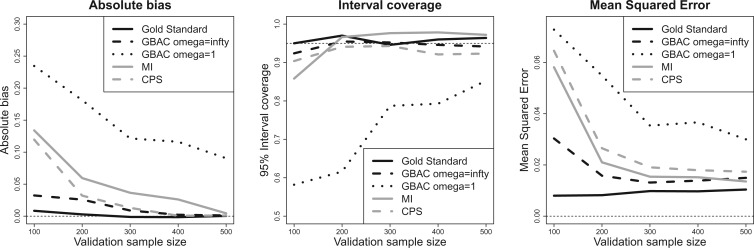
Figure 1 shows the bias, MSE, and interval coverage of the five methods. As expected the gold standard method is unbiased, has the lowest MSE, and obtains the desired interval coverage. This is the scenario in which we know the true values of the missing data and minimal confounder set, which will never be the case in practice. The performance of the imputation based approaches is substantially different. For any validation sample size, GBAC(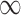 ) performs comparatively or better than GBAC(1) and the MI approaches. This is evident particularly for smaller
) performs comparatively or better than GBAC(1) and the MI approaches. This is evident particularly for smaller 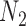 . For
. For 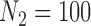 , The MSE for GBAC(
, The MSE for GBAC(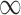 ) is 48% and 59% lower than MI and GBAC(1), respectively. These differences decrease as the sample size increases, however, GBAC(
) is 48% and 59% lower than MI and GBAC(1), respectively. These differences decrease as the sample size increases, however, GBAC(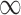 ) achieves the smallest MSE with the exception of
) achieves the smallest MSE with the exception of 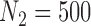 where the MI approach has a slightly smaller MSE. The CPS approach also fares poorly when
where the MI approach has a slightly smaller MSE. The CPS approach also fares poorly when 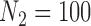 as the MSE is twice that of GBAC
as the MSE is twice that of GBAC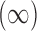 , but improves as the validation sample size increases.
, but improves as the validation sample size increases.
Fig. 1.
Bias, MSE, and interval coverage of the various estimators across 1000 simulations. 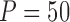 ,
, 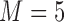 .
.
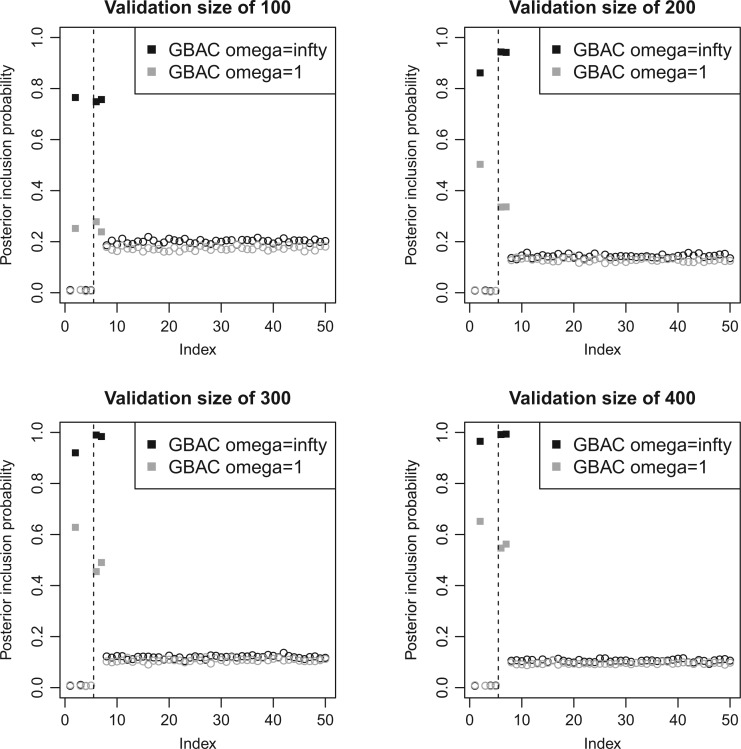
4.2. Posterior inclusion probabilities
It is also of interest to examine whether our model selects the correct covariates to enter in the outcome regression model, which is used to estimate the ACE. Figure 2 shows the posterior inclusion probabilities under GBAC(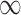 ) and GBAC(1) for a variety of sample sizes. Specifically, we are interested in examining the posterior inclusion probabilities of the true confounders (
) and GBAC(1) for a variety of sample sizes. Specifically, we are interested in examining the posterior inclusion probabilities of the true confounders (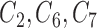 ), where
), where 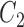 is observed in the main study and (
is observed in the main study and (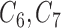 ) are missing in the main study. When
) are missing in the main study. When 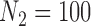 , we estimate
, we estimate 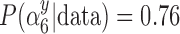 for the GBAC(
for the GBAC(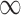 ) approach, and
) approach, and 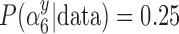 for GBAC(1), therefore GBAC(
for GBAC(1), therefore GBAC(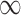 ) selects
) selects 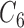 most of the time, whereas GBAC(1) does not. This explains the bias seen for GBAC(1) as it is averaging over a set of models that usually does not contain all the necessary confounders. As the sample size increases, both approaches estimate posterior inclusion probabilities closer to 1 for the true confounders. For any sample size, setting
most of the time, whereas GBAC(1) does not. This explains the bias seen for GBAC(1) as it is averaging over a set of models that usually does not contain all the necessary confounders. As the sample size increases, both approaches estimate posterior inclusion probabilities closer to 1 for the true confounders. For any sample size, setting 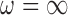 dramatically increases posterior inclusion probabilities of true confounders. The MI approach, by definition sets
dramatically increases posterior inclusion probabilities of true confounders. The MI approach, by definition sets 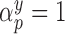 a priori for all
a priori for all 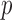 , which means that it always includes all covariates into the outcome model. This comes at a cost, particularly at small sample sizes, because using imputations from 45 covariates induces substantial amounts of variation. The posterior inclusion probabilities show that our approach is a nice balance between balancing our desire to remove unnecessary covariates and our desire to include all important confounders.
, which means that it always includes all covariates into the outcome model. This comes at a cost, particularly at small sample sizes, because using imputations from 45 covariates induces substantial amounts of variation. The posterior inclusion probabilities show that our approach is a nice balance between balancing our desire to remove unnecessary covariates and our desire to include all important confounders.
Fig. 2.
Estimated 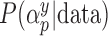 for each of the 50 covariates that can potentially enter into the outcome model, for GBAC(
for each of the 50 covariates that can potentially enter into the outcome model, for GBAC(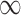 ) and GBAC(1). The points in black correspond to GBAC(
) and GBAC(1). The points in black correspond to GBAC(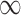 ), while those in grey correspond to GBAC(1). Squares represent the true confounders (
), while those in grey correspond to GBAC(1). Squares represent the true confounders (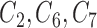 ), while circles represent covariates that are noise. Points to the left of the dotted line (indices 1–5) are covariates that are fully observed, while those to the right (indices 6–50) are only observed in the validation study).
), while circles represent covariates that are noise. Points to the left of the dotted line (indices 1–5) are covariates that are fully observed, while those to the right (indices 6–50) are only observed in the validation study).
4.3. Sensitivity to assumptions and data generating mechanisms
Appendix B of the Supplementary Material available at Biostatistics online presents a variety of simulations under a large number of data generating mechanisms, and when the assumptions for validity of our approach are not met. We first tested our approach against different treatment and confounding effects. This included null treatment effects, correlated confounders, larger confounding bias, smaller confounding bias, and different directions of confounding. We found similar results as the proposed approach was again superior, particularly at small validation sample sizes, regardless of the data generating mechanism. We also assessed the proposed approach’s ability to adjust for confounding when the missing data came from a skewed distribution, different from the assumed model. If the true confounders are skewed, then our method still correctly includes them into the model, though some bias is induced in estimation of the ACE. This bias is not substantial, however, as the MSE of the proposed approach is only slightly increased relative to the scenario with normal confounders. If the variables that aren’t confounders are skewed, then our approach remains unbiased and still correctly excludes them from the outcome model a large percentage of the time. Finally, we assessed our approach when either Assumption 3.1 fails or when the true exposure and outcome models are highly nonlinear. These are the worst case scenarios for our approach, which relies heavily on these assumptions, and because of this we see more substantial bias and MSE. Notably, our approach still performs the best in these scenarios in terms of MSE or bias, as the CPS approach also relies on some of these assumptions.
5. Analysis of Seer-Medicare
We apply the methods proposed in this paper to estimate the ACE of resection versus biopsy on 30 day survival for Medicare beneficiaries ages 65 and older, diagnosed with malignant neoplasm of the brain between 2000 and 2007. We use the Medicare dataset as our main study, and the SEER-Medicare dataset as our validation study. We focus on the subset of the Medicare population with no previous history of cancer that underwent surgical resection or biopsy. The SEER-Medicare data can not be linked to the Medicare data, therefore it is possible that some subjects could appear in both the main and validation data. To avoid this problem, we subset the SEER-Medicare data to patients who underwent surgery in even years (2000,2002,2004,2006), while we subset the Medicare data to patients from odd years (2001,2003,2005,2007). After these restrictions, the sample size of the SEER-Medicare is 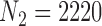 and the sample size of the Medicare sample is
and the sample size of the Medicare sample is 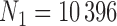 . For GBAC to provide an unbiased estimate of the ACE, we require assumption 3.1 to hold. Warren and others (2002) studied the differences between the SEER population and the general Medicare population and found that there were some differences in terms of the race, poverty, and mortality rates, however, they suggest that the SEER-Medicare data is a useful tool for studying cancer among the general elderly population. For this reason, we feel that using the SEER-Medicare as validation data in this context is justified.
. For GBAC to provide an unbiased estimate of the ACE, we require assumption 3.1 to hold. Warren and others (2002) studied the differences between the SEER population and the general Medicare population and found that there were some differences in terms of the race, poverty, and mortality rates, however, they suggest that the SEER-Medicare data is a useful tool for studying cancer among the general elderly population. For this reason, we feel that using the SEER-Medicare as validation data in this context is justified.
Table 1 shows descriptive statistics of all the covariates (the fully observed and the missing ones). There are 16 covariates that are fully observed in the main study including age, sex, race, eligibility for Medicaid, computerized tomography (CT) scan status, Magnetic resonance imaging (MRI) status, as well as a variety of comorbid conditions. The covariates available only in SEER-Medicare include marital status, Glioblastoma, income, and various covariates regarding the severity and location of the tumors leading to seven variables that are not observed in Medicare. Variables such as tumor size and location are of particular concern as they are likely related to surgical decisions and patient outcomes, but are missing in the main study. For this analysis, we specify the outcome as a binary indicator of 30 day survival, and our treatment is a binary indicator of surgical resection versus biopsy. We set 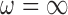 , to provide extra protection against excluding important confounders from the analysis. Convergence of posterior distributions was assessed via visual inspection of trace plots and calculation of the potential scale reduction factor (Gelman and others, 2014). We analyze the data using the following approaches: (i) GBAC(
, to provide extra protection against excluding important confounders from the analysis. Convergence of posterior distributions was assessed via visual inspection of trace plots and calculation of the potential scale reduction factor (Gelman and others, 2014). We analyze the data using the following approaches: (i) GBAC(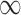 ), (ii) GBAC(1), (iii) CPSs, (iv) MI, and (v) the validation only approach that only examines the SEER-Medicare data.
), (ii) GBAC(1), (iii) CPSs, (iv) MI, and (v) the validation only approach that only examines the SEER-Medicare data.
Table 1.
Patient characteristics and posterior inclusion probabilities for covariates into the treatment and outcome models under GBAC(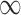 ). Binary variables are reported as number of patients (percentage), and continuous covariates are reported as mean (standard deviation). Bold terms represent covariates with a posterior probability greater than 0.5 of entering into both the treatment and outcome models
). Binary variables are reported as number of patients (percentage), and continuous covariates are reported as mean (standard deviation). Bold terms represent covariates with a posterior probability greater than 0.5 of entering into both the treatment and outcome models
| Covariate | Biopsy | Resection | 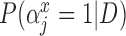 |
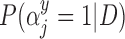 |
|
|---|---|---|---|---|---|
| Main data | 75  Age Age  85 85 |
1919 (0.41) | 2717 (0.34) | 1.00 | 1.00 |
| + validation | Age  85 85 |
445 (0.09) | 453 (0.06) | 1.00 | 1.00 |
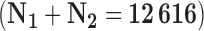 |
Female | 2339 (0.5) | 3637 (0.46) | 0.00 | 0.00 |
| White | 4352 (0.92) | 7313 (0.93) | 0.75 | 0.78 | |
| Head CT scan done | 373 (0.08) | 490 (0.06) | 0.00 | 0.00 | |
| Brain MRI done | 423 (0.09) | 821 (0.1) | 0.00 | 0.00 | |
| Dual eligible | 387 (0.08) | 637 (0.08) | 0.00 | 0.00 | |
| Chronic Atherosclerosis | 1045 (0.22) | 1494 (0.19) | 0.00 | 0.00 | |
| Substance abuse | 335 (0.07) | 624 (0.08) | 0.00 | 0.00 | |
| Hypertension | 2912 (0.62) | 4650 (0.59) | 0.25 | 0.25 | |
| Chronic Obstructive Pulmonary Disease | 520 (0.11) | 996 (0.13) | 0.03 | 0.99 | |
| Dementia | 511 (0.11) | 660 (0.08) | 0.02 | 0.68 | |
| Depression | 366 (0.08) | 511 (0.06) | 0.00 | 0.00 | |
| Seizure disorder | 937 (0.2) | 1604 (0.2) | 0.00 | 0.00 | |
| Valvular and rheumatic heart disease | 293 (0.06) | 423 (0.05) | 0.00 | 0.00 | |
| Diabetes | 913 (0.19) | 1387 (0.18) | 0.00 | 0.01 | |
| Validation only | Married | 395 (0.59) | 1011 (0.65) | 0.00 | 0.03 |
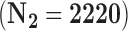 |
Glioblastoma | 461 (0.69) | 1362 (0.88) | 1.00 | 1.00 |
Number of tumors (1 tumor/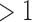 tumor) tumor) |
575 (0.87) | 1385 (0.89) | 0.00 | 0.07 | |
| Tumor location (Supratentorial/other) | 440 (0.66) | 1256 (0.81) | 1.00 | 1.00 | |
Tumor size (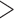 3cm) 3cm) |
345 (0.52) | 960 (0.62) | 0.01 | 0.05 | |
| Income (High/Low) | 244 (0.37) | 514 (0.33) | 0.00 | 0.05 | |
| Tumor stage (Localized/other) | 435 (0.66) | 1315 (0.85) | 1.00 | 1.00 |
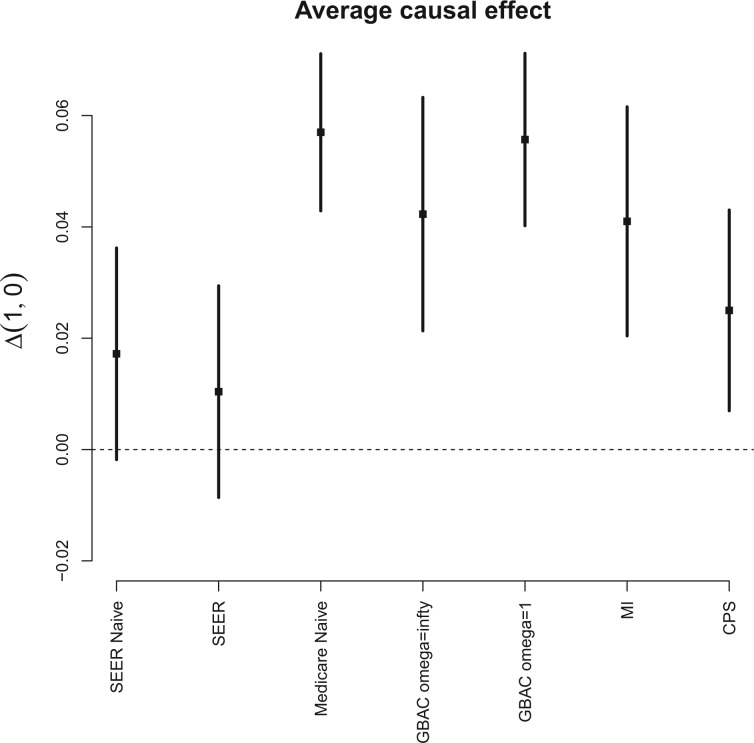
To gauge the potential for biased effect estimates, Figure 3 shows the resulting estimates of the AEC of surgical resection on the probability of 30 day survival under several approaches that use varying amounts of information from the main and validation studies. In all cases, we see that surgical resection is beneficial, mirroring results seen in Chaichana and others (2011), though the estimated effects differ across the estimation approaches. Ignoring the covariates only available in SEER-Medicare and analyzing the entire 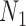 subjects in Medicare (Medicare Naive) leads to a naive estimate of 0.056 (0.044, 0.068). When we fit the same model in the SEER-Medicare data only and ignore the additional covariates (SEER Naive), we obtain an estimate of 0.017 (-0.002, 0.037). The substantial difference between these two estimates suggests that the effect of surgical resection on the probability of 30 day survival is different in the two populations. Only analyzing SEER-Medicare, but with all available covariates (SEER), leads to a causal effect estimate of 0.010 (-0.001, 0.030) which is a 41% decrease from the estimate obtained by the SEER-Naive approach, which suggests important confounding from the additional covariates only available in SEER-Medicare.
subjects in Medicare (Medicare Naive) leads to a naive estimate of 0.056 (0.044, 0.068). When we fit the same model in the SEER-Medicare data only and ignore the additional covariates (SEER Naive), we obtain an estimate of 0.017 (-0.002, 0.037). The substantial difference between these two estimates suggests that the effect of surgical resection on the probability of 30 day survival is different in the two populations. Only analyzing SEER-Medicare, but with all available covariates (SEER), leads to a causal effect estimate of 0.010 (-0.001, 0.030) which is a 41% decrease from the estimate obtained by the SEER-Naive approach, which suggests important confounding from the additional covariates only available in SEER-Medicare.
Fig. 3.
Estimates and 95% posterior credible intervals for the average causal effect of surgical resection on the probability of 30 day survival in the Medicare population.
We can apply the aforementioned approaches aimed at adjusting for the unmeasured confounders in the main data set. GBAC(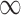 ) gives an estimate of 0.042 (0.021, 0.063) for the effect of surgical resection on the probability of 30 day survival, which differs from the naive estimate of 0.056 that results from ignoring the additional covariates from SEER-Medicare. The fully Bayesian MI gives a similar estimate of 0.041 (0.020, 0.062), while GBAC(1) gives an estimate of 0.056 (0.040, 0.071). The fully Bayesian MI includes all covariates with probability 1, so if there is confounding by variables from SEER, then the estimate obtained should account for the confounding assuming the imputation models are correct. GBAC(1) on the other hand, does not include all the covariates and it is possible it is ignoring important confounders in the final effect estimate. Table 2 shows the posterior inclusion probabilities for GBAC(
) gives an estimate of 0.042 (0.021, 0.063) for the effect of surgical resection on the probability of 30 day survival, which differs from the naive estimate of 0.056 that results from ignoring the additional covariates from SEER-Medicare. The fully Bayesian MI gives a similar estimate of 0.041 (0.020, 0.062), while GBAC(1) gives an estimate of 0.056 (0.040, 0.071). The fully Bayesian MI includes all covariates with probability 1, so if there is confounding by variables from SEER, then the estimate obtained should account for the confounding assuming the imputation models are correct. GBAC(1) on the other hand, does not include all the covariates and it is possible it is ignoring important confounders in the final effect estimate. Table 2 shows the posterior inclusion probabilities for GBAC(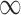 ) and GBAC(1). GBAC(
) and GBAC(1). GBAC(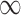 ) always selects Glioblastoma, tumor location, and tumor stage into the outcome model, while GBAC(1) almost never includes them. This is due to the dependence on the treatment variable as all three of these covariates are strongly associated with the treatment as indicated by high
) always selects Glioblastoma, tumor location, and tumor stage into the outcome model, while GBAC(1) almost never includes them. This is due to the dependence on the treatment variable as all three of these covariates are strongly associated with the treatment as indicated by high 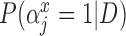 estimates. It’s possible that these variables are weakly associated with the outcome and therefore GBAC(
estimates. It’s possible that these variables are weakly associated with the outcome and therefore GBAC(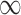 ) rightly includes them into the outcome model.
) rightly includes them into the outcome model.
Table 2.
Posterior inclusion probabilities for covariates that are only available in SEER-Medicare for both GBAC(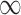 ) and GBAC(1)
) and GBAC(1)
GBAC(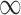 ) ) |
GBAC(1) | |||
|---|---|---|---|---|
| variables | 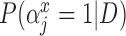 |
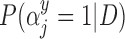 |
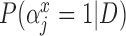 |
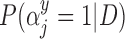 |
| Married | 0.00 | 0.03 | 0.06 | 0.02 |
| Glioblastoma | 1.00 | 1.00 | 1.00 | 0.05 |
Number of tumors (1 tumor/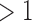 tumor) tumor) |
0.00 | 0.06 | 0.03 | 0.05 |
| Tumor location (Supratentorial/other) | 1.00 | 1.00 | 1.00 | 0.03 |
Tumor size (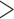 3cm) 3cm) |
0.01 | 0.05 | 0.61 | 0.05 |
| Income (High/Low) | 0.00 | 0.05 | 0.02 | 0.04 |
| Tumor stage (Localized/other) | 1.00 | 1.00 | 1.00 | 0.06 |
6. Discussion
In this article, we have combined ideas of Bayesian variable selection and missing data imputation to estimate the effect of a treatment on an outcome when there are missing confounders in the data set, but auxiliary information on the confounders is available through a validation data set. Our proposed method has advantages particularly when the effect of the treatment on the outcome differs between the main and validation study, and when the number of missing covariates in the main study is large relative to the sample size of the validation study. In these settings, reducing the dimension to only those covariates which are required for valid effect estimation is a desirable feature. Through simulation we showed that our proposed approach performs comparatively well to or better than existing approaches to utilizing validation data to control for confounding. Finally, we illustrated our approach by combining data from SEER-Medicare and Medicare. We found that there was likely unmeasured confounding bias from covariates missing in Medicare. Our approach attenuated the naive estimate of the effect of surgical resection on 30 day survival by 30% indicating that the original estimate may have been confounded.
Our proposed method combines and extends many different ideas from the missing data and confounder selection literature. We have applied the prior distribution from Wang and others (2012) that facilitates selection of confounders in model averaging to a setting with large amounts of missing data in the confounders. We have adopted ideas from the missing data literature to impute these covariates within a fully Bayesian framework, while simultaneously selecting those required for valid effect estimation. Due to the modeling structure we have proposed, we are able to handle any treatment or outcome variable that falls within the GLM framework making it more flexible than propensity score based approaches that require binary treatments. We have also allowed for the effect of the treatment on the outcome to differ in the two studies. This is an important point as we do not expect the effects to be shared across populations, and we saw in our analysis of SEER-Medicare that the effects did appear to differ. This differs from the model calibration literature (Breslow and others, 2009; Chatterjee and others, 2015), which also addresses the question of missing covariates when validation data is available, because those approaches assume that the relationships between the covariates and outcome are the same across data sets.
While the results of our simulation study suggest that our method is very useful in controlling for confounding in the validation data setting, there are some limitations. In particular, the proposed methods rely on correct specification of models for both 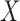 and
and 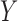 , as well as models for missing covariates, all of which determine the ultimate imputation of covariates in the main study. Thus, while the prioritization of only genuine confounders via specification for
, as well as models for missing covariates, all of which determine the ultimate imputation of covariates in the main study. Thus, while the prioritization of only genuine confounders via specification for 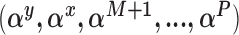 can protect against some threats to model misspecification by focusing inference only on the most salient covariates, such danger persists. This is in contrast to, for example, the use of propensity scores to estimate causal effects, which are less reliant on the correct specification of an outcome model. While the proposed methods do not share many of the advantages of traditional propensity-score methods, the parametric models used here permit consideration of non-binary treatments and the ability to imbed effect estimation within the mechanics of model averaging and confounder selection. These issues are particularly advantageous in high-dimensional settings where propensity scores can be difficult to implement.
can protect against some threats to model misspecification by focusing inference only on the most salient covariates, such danger persists. This is in contrast to, for example, the use of propensity scores to estimate causal effects, which are less reliant on the correct specification of an outcome model. While the proposed methods do not share many of the advantages of traditional propensity-score methods, the parametric models used here permit consideration of non-binary treatments and the ability to imbed effect estimation within the mechanics of model averaging and confounder selection. These issues are particularly advantageous in high-dimensional settings where propensity scores can be difficult to implement.
Our approach also necessitates the selection of 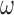 , which controls the strength of protection against missing an important confounder. Throughout the manuscript we have recommended a large value of
, which controls the strength of protection against missing an important confounder. Throughout the manuscript we have recommended a large value of 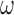 , which comes with the undesirable feature of including instruments only associated with
, which comes with the undesirable feature of including instruments only associated with 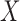 with higher posterior probability than if
with higher posterior probability than if 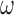 were small. While these variables can increase the variability of our estimate of the ACE, we believe this to be smaller than the potential increase in bias caused by omitting confounders. If one is not comfortable with setting
were small. While these variables can increase the variability of our estimate of the ACE, we believe this to be smaller than the potential increase in bias caused by omitting confounders. If one is not comfortable with setting 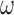 to a large value, they can adopt ideas from Lefebvre and others (2014a), that aim to find a value of
to a large value, they can adopt ideas from Lefebvre and others (2014a), that aim to find a value of 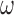 that optimizes the bias-variance trade-off associated with increasing
that optimizes the bias-variance trade-off associated with increasing 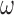 . Another approach could be to extend ideas from Hahn and others (2016) to scenarios with missing data. Their approach re-parameterizes the exposure and outcome models in a way that prevents the need for selecting a tuning parameter to dictate the strength of protection against confounder control.
. Another approach could be to extend ideas from Hahn and others (2016) to scenarios with missing data. Their approach re-parameterizes the exposure and outcome models in a way that prevents the need for selecting a tuning parameter to dictate the strength of protection against confounder control.
In general, our approach makes a variety of assumptions and we recommend assessing sensitivity to a number of these specifications. Assessing the sensitivity to the aforementioned 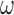 tuning parameter is important, but we also recommend assessing the sensitivity to the other prior distributions such as the inverse gamma priors for variance parameters. Studies involving main and validation data sets are usually large and therefore not likely to be sensitive to this prior specification, however, if the variance is small then the selection of the inverse gamma hyper parameters can play an important role. One can adopt ideas from Gelman (2006) and use a uniform prior on the standard deviation, which generally reflects a lack of prior information and compare with an inverse gamma prior.
tuning parameter is important, but we also recommend assessing the sensitivity to the other prior distributions such as the inverse gamma priors for variance parameters. Studies involving main and validation data sets are usually large and therefore not likely to be sensitive to this prior specification, however, if the variance is small then the selection of the inverse gamma hyper parameters can play an important role. One can adopt ideas from Gelman (2006) and use a uniform prior on the standard deviation, which generally reflects a lack of prior information and compare with an inverse gamma prior.
In summary, we have proposed a procedure to control for confounding in the presence of missing confounders when validation data is available. The proposed procedure utilizes a fully probabilisitic, Bayesian approach, which accounts for the uncertainty in the selection of confounders and in missing data imputations into the final effect estimates.
7. Supplementary Material
Details of the posterior calculation and additional simulation results can be found in the Supplementary Material available online at http://biostatistics.oxfordjournals.org R Software is available at https://github.com/jantonelli111/Guided-BAC
Supplementary Material
Acknowledgments
Conflict of Interest: None declared.
Funding
This work was supported by grants from the National Institutes of Health (ES000002, ES024332, ES007142, ES026217 P01CA134294, R01GM111339, R35CA197449, P50MD010428), U.S. Environmental Protection Agency (83587201-0), and the Health Effects Institute (4953-RFA14-3/16-4). Its contents are solely the responsibility of the grantee and do not necessarily represent the official views of the USEPA. Further, USEPA does not endorse the purchase of any commercial products or services mentioned in the publication.
References
- Albert, J. H. and Chib, S. (1993). Bayesian analysis of binary and polychotomous response data.. Journal of the American Statistical Association, 88, 669–679. [Google Scholar]
- Breslow, N. E, Lumley, T., Ballantyne, C. M., Chambless, L. E. and Kulich, M. (2009). Improved Horvitz–Thompson estimation of model parameters from two-phase stratified samples: applications in epidemiology.. Statistics in Biosciences, 1, 32–49. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carroll, R. J, Ruppert, D., Stefanski, L. A and Crainiceanu, C. M. (2006). Measurement Error in Nonlinear Models: A Modern Perspective. Boca Raton, Florida: CRC Press. [Google Scholar]
- Chaichana, K. L, Garzon-Muvdi, T., Parker, S., Weingart, J. D, Olivi, A., Bennett, R., Brem, H. and Quinones-Hinojosa, A. (2011). Supratentorial glioblastoma multiforme: the role of surgical resection versus biopsy among older patients.. Annals of Surgical Oncology, 18, 239–245. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chatterjee, N., Chen, Y. H., Maas, P. and Carroll, R. J. (2015). Constrained maximum likelihood estimation for model calibration using summary-level information from external big data sources.. Journal of the American Statistical Association, 111, 1–32. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cooper, G. S., Virnig, B., Klabunde, C. N., Schussler, N., Freeman, J. and Warren, J. L. (2002). Use of SEER-Medicare data for measuring cancer surgery.. Medical Care, 40, IV–43. [DOI] [PubMed] [Google Scholar]
- Crainiceanu, C. M., Dominici, F. and Parmigiani, G. (2008). Adjustment uncertainty in effect estimation.. Biometrika, 95, 635–651. [Google Scholar]
- Gelman, A., King, G. and Liu, C. (1998). Not asked and not answered: multiple imputation for multiple surveys.. Journal of the American Statistical Association, 93, 846–857. [Google Scholar]
- Gelman, A. (2006). Prior distributions for variance parameters in hierarchical models (comment on article by Browne and Draper).. Bayesian Analysis, 1, 515–534. [Google Scholar]
- Gelman, A., Carlin, J. B, Stern, H. S. and Rubin, D. B. (2014). Bayesian Data Analysis, vol. 2 Boca Raton, Florida: Taylor & Francis. [Google Scholar]
- Hahn, P. R., Carvalho, C. and Puelz, D. (2016). Bayesian regularized regression for treatment effect estimation from observational data.. Available at SSRN, https://arxiv.org/pdf/1602.02176v3.pdf.
- Hiraki, L. T., Joshi, A. D., Ng, K., Fuchs, C. S., Ma, J., Hazra, A., Peters, U., Karlson, E. W., Giovannucci, E., Kraft, P. and Chan, A. T. (2014). Joint effects of colorectal cancer susceptibility loci, circulating 25-hydroxyvitamin D and risk of colorectal cancer.. PloS ONE, 9, e92212. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jackson, C. H., Best, N. G. and Richardson, S. (2009). Bayesian graphical models for regression on multiple data sets with different variables.. Biostatistics, 10, 335–351. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lefebvre, G., Atherton, J. and Talbot, D. (2014a). The effect of the prior distribution in the Bayesian Adjustment for Confounding algorithm.. Computational Statistics & Data Analysis, 70, 227–240. [Google Scholar]
- Lefebvre, G., Delaney, J. A. and McClelland, R. L. (2014b). Extending the Bayesian Adjustment for Confounding algorithm to binary treatment covariates to estimate the effect of smoking on carotid intima-media thickness: the Multi-Ethnic Study of Atherosclerosis.. Statistics in Medicine, 33, 2797–2813. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Little, R. J. A. and Rubin, D. B. (2014). Statistical Analysis with Missing Data. Hoboken, New Jersey: John Wiley & Sons. [Google Scholar]
- McCandless, L. C., Richardson, S. and Best, N. (2012). Adjustment for missing confounders using external validation data and propensity scores.. Journal of the American Statistical Association, 107, 40–51. [Google Scholar]
- Mitra, R. and Dunson, D. (2010). Two-level stochastic search variable selection in GLMs with missing predictors.. The International Journal of Biostatistics, 6: Article 33. [DOI] [PubMed] [Google Scholar]
- Murray, J. S. and Reiter, J. P. (2016). Multiple imputation of missing categorical and continuous values via Bayesian mixture models with local dependence.. Journal of the American Statistical Association. [Google Scholar]
- Raftery, A. E. (1995). Bayesian model selection in social research.. Sociological Methodology, 25, 111–164. [Google Scholar]
- Raghunathan, T. E., Lepkowski, J. M., Van Hoewyk, J. and Solenberger, P. (2001). A multivariate technique for multiply imputing missing values using a sequence of regression models.. Survey Methodology, 27, 85–96. [Google Scholar]
- Rässler, S. (2004). Data fusion: identification problems, validity, and multiple imputation.. Austrian Journal of Statistics, 33, 153–171. [Google Scholar]
- Reiter, J. P. (2012). Bayesian finite population imputation for data fusion.. Statistica Sinica, 22, 795–811. [Google Scholar]
- Rosenbaum, P. R. and Rubin, D. B. (1983). The central role of the propensity score in observational studies for causal effects.. Biometrika, 70, 41–55. [Google Scholar]
- Spiegelman, D., Rosner, B. and Logan, R. (2000). Estimation and inference for logistic regression with covariate misclassification and measurement error in main study/validation study designs.. Journal of the American Statistical Association, 95, 51–61. [Google Scholar]
- Stürmer, T., Schneeweiss, S., Avorn, J. and Glynn, R. J. (2005). Adjusting effect estimates for unmeasured confounding with validation data using propensity score calibration.. American Journal of Epidemiology, 162, 279–289. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stürmer, T., Schneeweiss, S., Rothman, K. J., Avorn, J. and Glynn, R. J. (2007). Performance of propensity score calibrationÑa simulation study.. American Journal of Epidemiology, 165, 1110–1118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vansteelandt, S., Bekaert, M. and Claeskens, G. (2012). On model selection and model misspecification in causal inference.. Statistical Methods in Medical Research, 21, 7–30. [DOI] [PubMed] [Google Scholar]
- Wang, C., Parmigiani, G. and Dominici, F. (2012). Bayesian effect estimation accounting for adjustment uncertainty.. Biometrics, 68, 661–671. [DOI] [PubMed] [Google Scholar]
- Wang, C., Dominici, F., Parmigiani, G. and Zigler, C. M. (2015). Accounting for uncertainty in confounder and effect modifier selection when estimating average causal effects in generalized linear models.. Biometrics, 71, 654–665. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Warren, J. L., Klabunde, C. N., Schrag, D., Bach, P. B. and Riley, G. F. (2002). Overview of the SEER-Medicare data: content, research applications, and generalizability to the United States elderly population.. Medical Care, 40, IV–3. [DOI] [PubMed] [Google Scholar]
- Wilson, A. and Reich, B. J. (2014). Confounder selection via penalized credible regions.. Biometrics, 70, 852–861. [DOI] [PubMed] [Google Scholar]
- Yang, X., Belin, T. R. and Boscardin, W. J. (2005). Imputation and variable selection in linear regression models with missing covariates.. Biometrics, 61, 498–506. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.