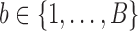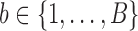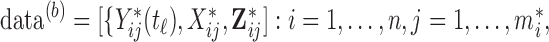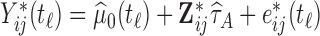SUMMARY
We propose simple inferential approaches for the fixed effects in complex functional mixed effects models. We estimate the fixed effects under the independence of functional residuals assumption and then bootstrap independent units (e.g. subjects) to conduct inference on the fixed effects parameters. Simulations show excellent coverage probability of the confidence intervals and size of tests for the fixed effects model parameters. Methods are motivated by and applied to the Baltimore Longitudinal Study of Aging, though they are applicable to other studies that collect correlated functional data.
Keywords: Bootstrap/resampling, Functional data, Measurement error, Smoothing and nonparametric regression
1. Introduction
Rapid advancement in technology and computation has led to an increasing number of studies that collect complex-correlated functional data. In response to these studies research in structured functional data analysis (FDA) has witnessed rapid development. A major characteristic of these data is that they are strongly correlated, as multiple functions are observed on the same observational unit. Many new studies have functional structures including multilevel (Morris and others, 2003; Morris and Carroll, 2006; Di and others, 2009; Crainiceanu and others, 2009), longitudinal (Greven and others, 2010; Chen and Müller, 2012; Scheipl and others, 2015), spatially aligned (Baladandayuthapani and others, 2008; Staicu and others, 2010; Serban and others, 2013), or crossed (Aston and others, 2010; Shou and others, 2015).
While these types of data can have highly complex dependence structures, one is often interested in simple, population-level, questions for which the multi-layered structure of the correlation is just an infinite-dimensional nuisance parameter. For example, the Baltimore Study of Aging (BLSA), which motivated this article, collected physical activity levels from each of many participants at the minute level for multiple consecutive days. Thus, the BLSA activity data exhibit complex within-day and between-day correlations. However, the most important questions in the BLSA tend to be simple; in particular, one may be interested in how age affects the daily patterns of activity or whether the effect is different by gender. In this context, the high complexity and size of the data are just technical inconveniences.
Such simple questions are typically answered by estimating fixed effects in complex functional mixed effects models. Our proposed approach avoids complex modeling and implementation by: (i) estimating the fixed (population-level) effects under the assumption of independence of functional residuals; and (ii) using a nonparametric bootstrap of independent units (e.g. subjects) to construct confidence intervals and conduct tests. A natural question is whether efficiency is lost by ignoring the correlation. While the loss of efficiency is well documented in longitudinal studies with few observations per subject and small dimensional within-subject correlation, little is known about inference when there are many observations per subject with an unknown large dimensional within-subject correlation matrix. An important contribution of this article is to evaluate the performance of bootstrap-based inferential approaches in this particular context. Our view is that estimating large dimensional covariance matrices of functional data may hurt fixed effects estimation by wasting degrees of freedom. Indeed, a covariance matrix for an  by
by  matrix of functional data (
matrix of functional data (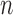 = number of subjects and
= number of subjects and 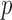 = number of subject-specific observations) would require estimation of
= number of subject-specific observations) would require estimation of 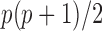 matrix covariance entries when the covariance matrix is unstructured. When
matrix covariance entries when the covariance matrix is unstructured. When 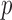 is moderate or large this is a difficult problem. Moreover, the resulting matrix has an unknown low rank and is not invertible.
is moderate or large this is a difficult problem. Moreover, the resulting matrix has an unknown low rank and is not invertible.
We will consider cases when multiple functional observations are observed for the same subject. This structure is inspired by many current observational studies, but we will focus on the BLSA, where activity data are recorded at the minute level over multiple consecutive days, resulting in daily activity profiles (each as a function of time of the day) observed for each participant over multiple days. Specifically, we will focus on data from 332 female BLSA participants with age varying between 50 and 90. A total of 1580 daily activity profiles were collected (an average of 4.7 monitoring days per person), where each daily profile consists of 1440 activity counts measured at the minute level. Thus, the activity data considered in this paper is stored in a 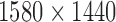 dimensional matrix. Our primary interest is to conduct inference on the fixed effects of covariates, such as age and body mass index (BMI), on daily activity profiles. Because data from each participant were collected on consecutive days in a short period (about a week on average), age and BMI in the BLSA data are subject-specific but visit-invariant.
dimensional matrix. Our primary interest is to conduct inference on the fixed effects of covariates, such as age and body mass index (BMI), on daily activity profiles. Because data from each participant were collected on consecutive days in a short period (about a week on average), age and BMI in the BLSA data are subject-specific but visit-invariant.
While our covariates are time-invariant, we propose methods that can accommodate both time-invariant and time-dependent covariates. Assume that the observed data is of the form 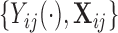 , where
, where 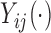 is the
is the 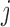 th unit functional response (e.g.
th unit functional response (e.g. 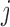 th visit) for the
th visit) for the 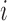 th subject, and
th subject, and 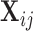 is the corresponding vector of covariates. This general form applies to all types of functional data discussed above: multilevel, longitudinal, spatially correlated, crossed, etc. The main objective is to make statistical inference for the population-level effects of interest using repeatedly observed functional response data.
is the corresponding vector of covariates. This general form applies to all types of functional data discussed above: multilevel, longitudinal, spatially correlated, crossed, etc. The main objective is to make statistical inference for the population-level effects of interest using repeatedly observed functional response data.
A naïve approach to analyze data with such a complex structure is to ignore the dependence over the functional argument 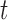 , but to account for the dependence across the repeated visits. That is, by assuming that the responses
, but to account for the dependence across the repeated visits. That is, by assuming that the responses 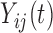 are correlated over
are correlated over 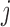 and independent over
and independent over 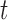 . Longitudinal data analysis literature offers a wide variety of models and methods for estimating the fixed effects and their uncertainty, and for conducting tests (see for example Laird and Ware (1982); Liang and Zeger (1986); Fitzmaurice and others (2012)). These methods allow to account for within-subject correlation, incorporate additional covariates, and make inference about the fixed effects. However, extending these estimation and inferential procedures to functional data is difficult. In the literature this has been addressed by modeling the within- and between-curve dependence structure using functional random effects. These approaches are highly computationally intensive, require inverting high dimensional covariances matrices, and make implicit assumptions about the correlation structures that may not be easy to transport across applications.
. Longitudinal data analysis literature offers a wide variety of models and methods for estimating the fixed effects and their uncertainty, and for conducting tests (see for example Laird and Ware (1982); Liang and Zeger (1986); Fitzmaurice and others (2012)). These methods allow to account for within-subject correlation, incorporate additional covariates, and make inference about the fixed effects. However, extending these estimation and inferential procedures to functional data is difficult. In the literature this has been addressed by modeling the within- and between-curve dependence structure using functional random effects. These approaches are highly computationally intensive, require inverting high dimensional covariances matrices, and make implicit assumptions about the correlation structures that may not be easy to transport across applications.
Another possible approach is to completely ignore the dependence across the repeated visits 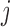 , but account for the functional dependence. That is, assume
, but account for the functional dependence. That is, assume 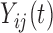 are dependent over
are dependent over 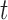 , but independent over
, but independent over 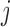 . Function on scalar/vector regression models can be used to estimate the fixed effects of interest; see for example Faraway (1997); Jiang and others (2011). In this context, testing procedures for hypotheses on fixed effects are available. For example, Shen and Faraway (2004) proposed the functional F statistic for testing hypotheses related to nested functional linear models. Zhang and others (2007) proposed
. Function on scalar/vector regression models can be used to estimate the fixed effects of interest; see for example Faraway (1997); Jiang and others (2011). In this context, testing procedures for hypotheses on fixed effects are available. For example, Shen and Faraway (2004) proposed the functional F statistic for testing hypotheses related to nested functional linear models. Zhang and others (2007) proposed 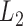 norm based test for testing the effect of a linear combination of time-varying coefficients, and approximate the null sampling distribution using resampling methods. However, failing to account for dependence across visits results in tests with inflated type I error.
norm based test for testing the effect of a linear combination of time-varying coefficients, and approximate the null sampling distribution using resampling methods. However, failing to account for dependence across visits results in tests with inflated type I error.
In contrast, development of statistical inferential methods for correlated functional data has received less attention. Fully Bayesian inference has been previously considered in the literature for complex designs; see, for example, Morris and Carroll (2006), Morris and others (2006), Morris and others (2011), Zhu and others (2011), and Zhang and others (2016). These approaches take into account both between- and within-function correlations using MCMC simulations of the posterior distribution. In contrast, we focus on a frequentist approach to inference that avoids modeling of the complex correlation structures. In the frequentist framework, Crainiceanu and others (2012) discussed bootstrap-based inferential methods for the difference in the mean profiles of correlated functional data. Staicu and others (2014) proposed a likelihood-ratio type testing procedure, while Staicu and others (2015) considered 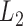 norm-based testing procedures for testing that multiple group mean functions are equal. Horváth and others (2013) developed inference for the mean function of a functional time series. However, these approaches focus on testing the effect of a categorical variable, and do not handle inference on fixed effects in full generality.
norm-based testing procedures for testing that multiple group mean functions are equal. Horváth and others (2013) developed inference for the mean function of a functional time series. However, these approaches focus on testing the effect of a categorical variable, and do not handle inference on fixed effects in full generality.
Here we consider a modeling framework that is a direct generalization of the linear mixed model framework from longitudinal data analysis, where scalar responses are replaced with functional ones. We propose to model the fixed effect of a scalar covariate either parametrically or nonparametrically while the error covariance is left unspecified to avoid model complexity. We estimate the fixed effects under the working independence and account for all known sources of data dependence by bootstrapping over subjects. Based on this procedure, we propose confidence bands and 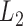 norm-based testing for fixed effects parameters. An important contribution of this article is to investigate and confirm the performance of the bootstrap-based inferential approaches when data have a complex functional dependence structure.
norm-based testing for fixed effects parameters. An important contribution of this article is to investigate and confirm the performance of the bootstrap-based inferential approaches when data have a complex functional dependence structure.
2. Modeling framework and estimation
Consider the case when each subject is observed at 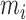 visits, and data at each visit consist of a functional outcome
visits, and data at each visit consist of a functional outcome 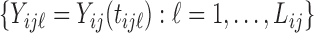 and a vector of covariates including a scalar covariate of interest,
and a vector of covariates including a scalar covariate of interest, 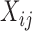 , and additional
, and additional 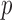 -dimensional vector of covariates,
-dimensional vector of covariates, 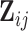 . We assume that
. We assume that 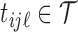 , where
, where 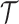 is a compact and closed domain; take
is a compact and closed domain; take 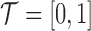 for simplicity. For convenience, we assume a balanced regular sampling design, i.e.
for simplicity. For convenience, we assume a balanced regular sampling design, i.e. 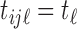 and
and 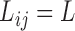 , though all methods apply to general sampling designs. Furthermore, we assume that
, though all methods apply to general sampling designs. Furthermore, we assume that 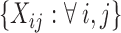 is a dense set in the closed domain
is a dense set in the closed domain 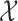 ; this assumption is needed when the fixed effect of
; this assumption is needed when the fixed effect of 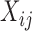 is modeled nonparametrically (Ruppert and others, 2003; Fitzmaurice and others, 2012). A common approach for the study of the effect of the covariates on
is modeled nonparametrically (Ruppert and others, 2003; Fitzmaurice and others, 2012). A common approach for the study of the effect of the covariates on 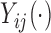 is to posit a model of the type
is to posit a model of the type
| (2.1) |
where 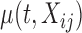 is a time-varying smooth fixed effect of the covariate of interest,
is a time-varying smooth fixed effect of the covariate of interest, 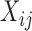 , and
, and 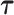 is a
is a 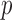 -dimensional parameter quantifying the linear additive fixed effect of the covariate vector,
-dimensional parameter quantifying the linear additive fixed effect of the covariate vector, 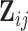 .
. 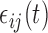 is a zero-mean random deviation that incorporates both the within- and between-subject variability.
is a zero-mean random deviation that incorporates both the within- and between-subject variability. 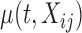 can be modeled either parametrically or nonparametrically; see Section 6 (F2.) for some possible mean structures. While technically more difficult to implement, nonparametric smoothing is useful when limited information about the mean structure is available.
can be modeled either parametrically or nonparametrically; see Section 6 (F2.) for some possible mean structures. While technically more difficult to implement, nonparametric smoothing is useful when limited information about the mean structure is available.
Here we present the most complex case where the mean structure for 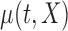 is an unknown bivariate smooth function. We construct a bivariate basis using the tensor product of two univariate B-spline bases,
is an unknown bivariate smooth function. We construct a bivariate basis using the tensor product of two univariate B-spline bases, 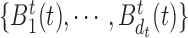 , and
, and 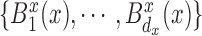 , defined on
, defined on 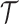 and
and 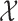 respectively. The unspecified mean is then expressed as
respectively. The unspecified mean is then expressed as 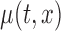
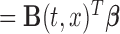 , where
, where 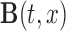 is the
is the 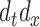 -dimensional vector of
-dimensional vector of 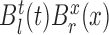 ’s and
’s and 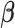 is the vector of parameters
is the vector of parameters 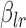 . Typically, the number of basis functions is chosen sufficiently large to capture the maximum complexity of the mean function and smoothness is induced by a quadratic penalty on the coefficients. There are several penalties for bivariate smoothing; see, for example, Marx and Eilers (2005), Wood (2006), and Xiao and others (2013, 2016). In this article we used the following estimation criterion
. Typically, the number of basis functions is chosen sufficiently large to capture the maximum complexity of the mean function and smoothness is induced by a quadratic penalty on the coefficients. There are several penalties for bivariate smoothing; see, for example, Marx and Eilers (2005), Wood (2006), and Xiao and others (2013, 2016). In this article we used the following estimation criterion
| (2.2) |
with a penalty matrix 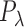 described in Wood (2006) and a vector of smoothing parameters,
described in Wood (2006) and a vector of smoothing parameters, 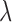 . Specifically, we used
. Specifically, we used 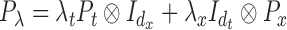 and
and 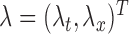 , where
, where 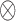 denotes the tensor product, and
denotes the tensor product, and 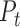 and
and 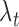 are the marginal second order difference matrix and the smoothing parameter for the
are the marginal second order difference matrix and the smoothing parameter for the 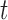 direction, respectively;
direction, respectively; 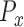 and
and 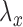 are defined similarly for the
are defined similarly for the 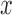 direction. Here
direction. Here  and
and 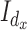 are the identity matrices of dimensions
are the identity matrices of dimensions 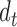 and
and 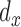 , respectively. For a fixed smoothing parameter,
, respectively. For a fixed smoothing parameter, 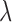 , the minimizer of (2.2) has the form
, the minimizer of (2.2) has the form 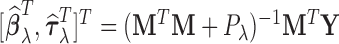 where
where 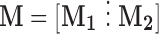 with
with 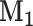 the matrix with rows B
the matrix with rows B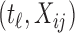 and
and 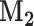 the matrix obtained by row-stacking of
the matrix obtained by row-stacking of 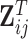 , while the estimated mean is
, while the estimated mean is 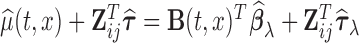 . In this article, the generalized cross validation (GCV) is used to select the optimal smoothing parameters, while other criteria such as the restricted maximum likelihood can be used; relevant literatures on selection of the smoothing parameter include Wahba (1990) and Ruppert and others (2003).
. In this article, the generalized cross validation (GCV) is used to select the optimal smoothing parameters, while other criteria such as the restricted maximum likelihood can be used; relevant literatures on selection of the smoothing parameter include Wahba (1990) and Ruppert and others (2003).
Estimation of the fixed effects in model (2.1) under the working independence assumption is not new; see for example Scheipl and others (2015) and Chen and Müller (2012). However, our approach to inference for the population level fixed effects in the context of structured functional data has not been studied. The novelty of this article consists precisely in filling this gap in the literature. We consider an estimation approach of fixed effects under working independence and a bootstrap of independent units approach to appropriately account for complex correlation.
3. Confidence bands for 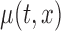
We now discuss inference for 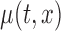 using confidence bands and formal hypothesis testing. Without loss of generality, assume that the mean structure is
using confidence bands and formal hypothesis testing. Without loss of generality, assume that the mean structure is 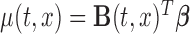 , where
, where 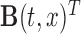 can be as simple as
can be as simple as 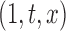 or as complex as a vector of prespecified basis functions. The mean estimator of interest is
or as complex as a vector of prespecified basis functions. The mean estimator of interest is 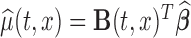 . One could study pointwise variability for every pair
. One could study pointwise variability for every pair 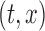 , that is
, that is 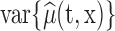 , or the joint variability for the entire domain
, or the joint variability for the entire domain 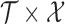 , that is
, that is 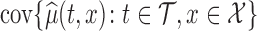 . Irrespective of the choice, the variability is fully described by the variability of the parameter estimator
. Irrespective of the choice, the variability is fully described by the variability of the parameter estimator 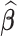 .
.
3.1. Bootstrap algorithms
We consider a flexible dependence structure for 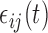 that describes both within- and between-subject variability. We make minimal assumption that
that describes both within- and between-subject variability. We make minimal assumption that 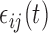 is independent over
is independent over 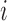 but correlated over
but correlated over 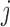 and
and 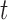 , though we do not specify the form of this correlation. Deriving the analytical expression for the sampling variability of the estimator
, though we do not specify the form of this correlation. Deriving the analytical expression for the sampling variability of the estimator 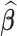 in such contexts is challenging. Instead, we propose to use two bootstrap algorithms: bootstrap of subject-level data and bootstrap of subject-level residuals. These approaches have already been studied and used in nonparametric regression for independent measurements; see, for example, Härdle and Bowman (1988), Efron and Tibshirani (1994), and Hall and others (2013) among many others. Bootstrap of functional data for fixed effects has also been considered, including by Politis and Romano (1994) for weakly dependent processes in Hilbert space, by Cuevas and others (2006) for independent functional data, and by Crainiceanu and others (2012) for paired samples of functional data. However, studying these bootstrap algorithms for functional data with complex correlation is new.
in such contexts is challenging. Instead, we propose to use two bootstrap algorithms: bootstrap of subject-level data and bootstrap of subject-level residuals. These approaches have already been studied and used in nonparametric regression for independent measurements; see, for example, Härdle and Bowman (1988), Efron and Tibshirani (1994), and Hall and others (2013) among many others. Bootstrap of functional data for fixed effects has also been considered, including by Politis and Romano (1994) for weakly dependent processes in Hilbert space, by Cuevas and others (2006) for independent functional data, and by Crainiceanu and others (2012) for paired samples of functional data. However, studying these bootstrap algorithms for functional data with complex correlation is new.
The subject-level bootstrap algorithm for correlated functional data is provided below.
Algorithm 1 Bootstrap of the subject-level data [uncertainty estimation]
1: for
do
2: Re-sample the subject indexes from the index set
with replacement.
Let
be the resulting sample of
subjects.
3: Define the
th bootstrap data by:
.
4: Using
fit the model (2.1) with the mean structure of interest modeled by
, by employing criterion (2.2). Let
be the corresponding estimate of the parameter of interest; similarly define
. end for
5: Calculate the sample covariance of
; denote it by
.
The bootstrap of subject-level data is more generally applicable, while the bootstrap of subject-level residuals approach relies on two important assumptions: (i) the covariates do not depend on visit, that is 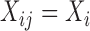 and
and 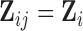 ; and (ii) both the correlation and the error variance are independent of covariates. These assumptions ensure that sets of subject-level errors, i.e.
; and (ii) both the correlation and the error variance are independent of covariates. These assumptions ensure that sets of subject-level errors, i.e. 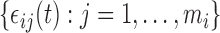 for
for 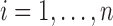 , can be resampled over subjects without affecting the sampling distribution. These assumptions are reasonable when covariates are independent of the visit, as is the case in the BLSA application. Indeed, in BLSA we consider age and BMI, which are time-invariant because repeated measures per subject were collected within a week.
, can be resampled over subjects without affecting the sampling distribution. These assumptions are reasonable when covariates are independent of the visit, as is the case in the BLSA application. Indeed, in BLSA we consider age and BMI, which are time-invariant because repeated measures per subject were collected within a week.
Similarly, we introduce the algorithm for bootstrapping residuals. We start by fitting the model (2.1) with the mean structure of interest modeled by 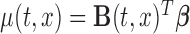 , using the estimation criterion described in (2.2), and calculating the residuals
, using the estimation criterion described in (2.2), and calculating the residuals 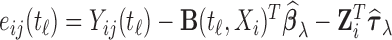 .
.
Algorithm 2 Bootstrap of the subject-level residuals [uncertainty estimation]
1: for
2: Re-sample the subject indexes from the index set
with replacement. Let
be the resulting sample of subjects. For each
denote by
the number of repeated time-visits for the
th subject selected in
.
3: Define the
th bootstrap sample of residuals
.
4: Define the
th bootstrap data by:
, where
.
5: Using
fit the model (2.1) with the mean structure of interest modeled by
, by employing criterion (2.2). Let
be the corresponding estimate of the parameter of interest; similarly define
. end for
6: Calculate the sample covariance of
; denote it by
.
Based on our numerical investigation (see Section 6) the bootstrap of subject-level residuals has excellent performance and is recommended when the necessary assumptions are satisfied, though the bootstrap of subjects is a good alternative.
3.2. Bootstrap-based inference
For fixed 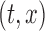 , the variance of the estimator
, the variance of the estimator 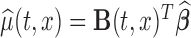 can be estimated as
can be estimated as 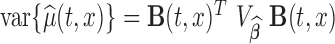 , by using the bootstrap-based estimate of the covariance of
, by using the bootstrap-based estimate of the covariance of 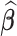 . A
. A 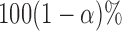 pointwise confidence interval for
pointwise confidence interval for 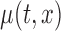 can be calculated as
can be calculated as 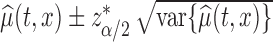 , using normal distributional assumption for the estimator
, using normal distributional assumption for the estimator 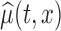 , where
, where 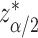 is the
is the 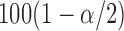 percentile of the standard normal. An alternative is to use the pointwise
percentile of the standard normal. An alternative is to use the pointwise 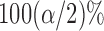 and
and 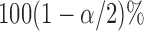 quantiles of the bootstrap estimates
quantiles of the bootstrap estimates 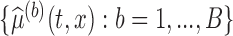 .
.
In most cases, it makes more sense to study the variability of 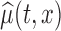 , and draw inference about the entire true mean function
, and draw inference about the entire true mean function 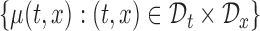 . Thus, we focus our study on constructing a joint (or simultaneous) confidence band for
. Thus, we focus our study on constructing a joint (or simultaneous) confidence band for 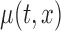 . Constructing simultaneous confidence bands for univariate smooths has already been discussed in the nonparametric literature. For example, Degras (2009), Ma and others (2012), and Cao and others (2012) proposed asymptotically correct simultaneous confidence bands for different estimators, when data are independently sampled curves; Crainiceanu and others (2012) proposed bootstrap-based joint confidence bands for univariate smooths in the case of functional data with complex error processes. Here, we present an extension of the approach considered by Crainiceanu and others (2012) to bivariate smooth function estimation for general functional correlation structures.
. Constructing simultaneous confidence bands for univariate smooths has already been discussed in the nonparametric literature. For example, Degras (2009), Ma and others (2012), and Cao and others (2012) proposed asymptotically correct simultaneous confidence bands for different estimators, when data are independently sampled curves; Crainiceanu and others (2012) proposed bootstrap-based joint confidence bands for univariate smooths in the case of functional data with complex error processes. Here, we present an extension of the approach considered by Crainiceanu and others (2012) to bivariate smooth function estimation for general functional correlation structures.
Let 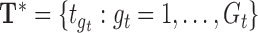 and
and 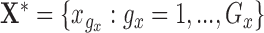 be the evaluation points that are equally spaced in the domains
be the evaluation points that are equally spaced in the domains 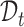 and
and 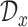 , respectively. We evaluate the bootstrap estimate
, respectively. We evaluate the bootstrap estimate 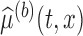 of one bootstrap sample at all pairs
of one bootstrap sample at all pairs 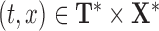 , and denote by
, and denote by 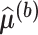 the
the 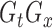 -dimensional vector with components
-dimensional vector with components  . Let
. Let 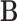 be the
be the 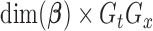 -dimensional matrix obtained by column-stacking
-dimensional matrix obtained by column-stacking 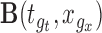 for all
for all 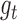 and
and 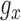 . Let
. Let 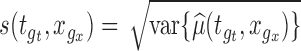 as defined above. After adjusting for the bivariate structure of the problem, the main steps of the construction of the joint confidence bands for
as defined above. After adjusting for the bivariate structure of the problem, the main steps of the construction of the joint confidence bands for 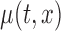 follow similarly to the ones used in Crainiceanu and others (2012) for univariate smooth parameter functions.
follow similarly to the ones used in Crainiceanu and others (2012) for univariate smooth parameter functions.
Step 1. Generate a random variable 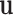 from the multivariate normal with mean
from the multivariate normal with mean 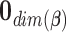 and covariance matrix
and covariance matrix 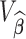 ; let
; let 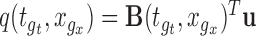 for
for 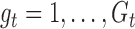 and
and 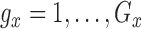 .
.
Step 2. Calculate 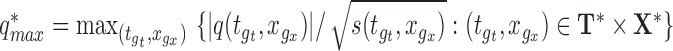 .
.
Step 3. Repeat Step 1. and Step 2. for 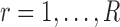 , and obtain
, and obtain 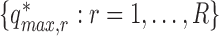 . Determine the
. Determine the 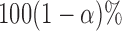 empirical quantile of
empirical quantile of 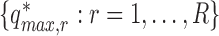 , say
, say 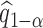 .
.
Step 4. Construct the 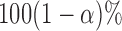 joint confidence band by:
joint confidence band by: 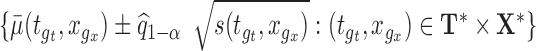 . Here
. Here 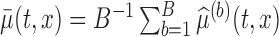 .
.
The joint confidence band, in contrast to the pointwise confidence band, can be used as an inferential tool for formal global tests about the mean function, 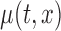 . For example, one can use the joint confidence band for testing the null hypothesis,
. For example, one can use the joint confidence band for testing the null hypothesis, 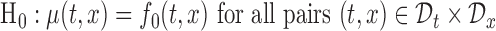 and for some prespecified function
and for some prespecified function 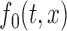 , by checking whether the confidence band
, by checking whether the confidence band 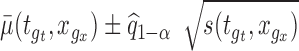 contains
contains 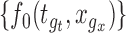 for all
for all 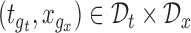 . If the confidence band does not contain
. If the confidence band does not contain 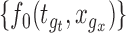 for some
for some 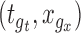 , then we conclude that there is significant evidence that the true mean function is the prespecified function
, then we conclude that there is significant evidence that the true mean function is the prespecified function 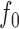 .
.
4. Hypothesis testing for 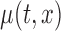
Next, we focus on assessing the effect of the covariate of interest 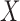 on the mean function. Consider the general case when the model is (2.1) and the average effect is an unspecified bivariate smooth function,
on the mean function. Consider the general case when the model is (2.1) and the average effect is an unspecified bivariate smooth function, 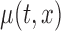 . Our goal is to test if the true mean function depends on
. Our goal is to test if the true mean function depends on 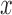 , that is testing:
, that is testing:
| (4.1) |
for some unknown smooth function 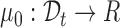 against
against 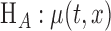 varies over
varies over 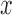 for some
for some 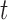 .
.
To the best of our knowledge, this type of hypothesis, where the mean function is nonparametric both under the null and alternative hypotheses, has not been studied in FDA. The problem was extensively studied in nonparametric smoothing, where the primary interest centered on significance testing of a subset of covariates in a nonparametric regression model; see, for example, Fan and Li (1996), Lavergne and Vuong (2000), Delgado and Manteiga (2001), Gu and others (2007), and Hall and others (2007). However, all these methods are based on the assumption that observations are independent across sampling units; in our context requiring independence of 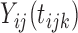 over
over 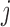 and
and 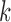 is unrealistic and failing to account for this dependence leads to inflated type I error rates.
is unrealistic and failing to account for this dependence leads to inflated type I error rates.
To test hypothesis (4.1) we propose a test statistic based on the 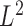 distance between the mean estimators under the null and alternative hypotheses. Specifically we define it as:
distance between the mean estimators under the null and alternative hypotheses. Specifically we define it as:
| (4.2) |
where 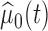 and
and 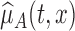 are the estimates of
are the estimates of 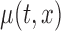 under the null and alternative hypotheses, respectively. In particular,
under the null and alternative hypotheses, respectively. In particular, 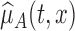 is estimated as in Section 2. The estimator
is estimated as in Section 2. The estimator 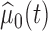 is obtained by modeling
is obtained by modeling 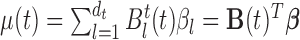 for the
for the 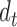 -dimensional vector
-dimensional vector 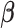 and by estimating the mean parameters
and by estimating the mean parameters 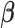 based on a criterion similar to (2.2).
based on a criterion similar to (2.2).
Deriving the finite sample distribution of the test statistic 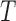 under the null hypothesis is challenging and we propose to approximate it using the bootstrap. As in Section 3, the smoothing parameter selection is repeated for each bootstrap sample and model,
under the null hypothesis is challenging and we propose to approximate it using the bootstrap. As in Section 3, the smoothing parameter selection is repeated for each bootstrap sample and model, 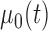 and
and 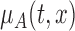 .
.
Algorithm 3 Bootstrap approximation of the null distribution of the test statistic,
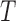
1: for
2: Re-sample the subject indexes from the index set
with replacement. Let
be the obtained sample of subjects. For each
denote by
the number of repeated time-visits for the
th subject selected in
.
3: Define the
th bootstrap sample of pseudo-residuals
. For each
let
the corresponding sample of the nuisance covariates for the
th subject selected in
. Similarly define
.
4: Define the
th bootstrap data by:
, where
5: Using
fit two models. First, fit model (2.1) with the mean structure modeled by
and estimate
. Second, fit model (2.1) with the mean model
and estimate
. Calculate the test statistic
using (4.2). end for
6: Approximate the tail probability
by the
, where
is obtained using the original data and
is the indicator function.
When the covariates 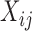 and
and 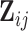 do not depend on visit, i.e.
do not depend on visit, i.e. 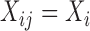 and
and 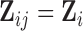 , the algorithm can be modified along the lines of the ‘bootstrap of the subject-level residuals’ algorithm.
, the algorithm can be modified along the lines of the ‘bootstrap of the subject-level residuals’ algorithm.
5. Application to physical activity data
Physical activity measured by wearable devices such as accelerometers provides new insights into the association between activity and health outcomes (Schrack and others, 2014); the complexity of the data also poses serious challenges to current statistical analysis. For example, accelerometers can record activity at the minute level for many days and for hundreds of individuals. Here we consider the physical activity data from the BLSA (Stone and Norris, 1966). Each female participant in the study wore the Actiheart portable physical activity monitor (Brage and others 2006) for 24 h a day for a number of consecutive days; visit duration varied among participants with an average of 4.7 days. Activity counts were measured in 1-min epochs and each daily activity profile has 1440 minute-by-minute activity counts measurements. Activity counts are proxies of activity intensity. Activity counts were log-transformed (more precisely, 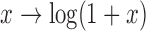 ) because they are highly skewed and then averaged in 30-min intervals. For simplicity, hereafter we refer to the log-transformed counts as log counts. Here we focus on 1580 daily activity profiles from a single visit of 332 female participants who have at least two days of data. Women in the study are aged between 50 and 90 years. Further details on the BLSA activity data can be found in Schrack and others (2014) and Xiao and others (2015).
) because they are highly skewed and then averaged in 30-min intervals. For simplicity, hereafter we refer to the log-transformed counts as log counts. Here we focus on 1580 daily activity profiles from a single visit of 332 female participants who have at least two days of data. Women in the study are aged between 50 and 90 years. Further details on the BLSA activity data can be found in Schrack and others (2014) and Xiao and others (2015).
Our objective is to conduct inference on the marginal effect of age on women’s daily activity after adjusting for BMI. We model the mean log counts as 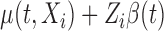 , where
, where 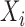 and
and 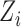 are the age and BMI of the
are the age and BMI of the 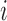 th woman during the visit,
th woman during the visit, 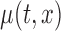 is the baseline mean log counts for time
is the baseline mean log counts for time 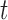 within the day for a woman who is
within the day for a woman who is 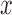 -years old, and
-years old, and 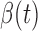 is the association of BMI with mean log counts for time
is the association of BMI with mean log counts for time 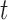 within the day. We test whether
within the day. We test whether 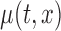 varies solely with
varies solely with 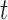 . We use the proposed testing statistic,
. We use the proposed testing statistic, 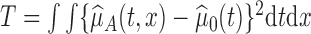 as detailed in Section 4. The estimate
as detailed in Section 4. The estimate 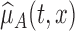 is based on the tensor product of
is based on the tensor product of 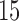 cubic basis functions in
cubic basis functions in 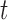 and
and 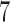 cubic basis functions in
cubic basis functions in 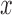 and the estimate
and the estimate  is based on
is based on 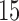 cubic basis functions. Goodness of fit is studied by comparing the observed data with simulated data from the fitted model; see Figure S6 of the supplementary materials available at Biostatistics online. Figure S1 of supplementary material available at Biostatistics online shows the null distribution of the statistic
cubic basis functions. Goodness of fit is studied by comparing the observed data with simulated data from the fitted model; see Figure S6 of the supplementary materials available at Biostatistics online. Figure S1 of supplementary material available at Biostatistics online shows the null distribution of the statistic 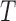 . The observed test statistic is
. The observed test statistic is 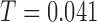 and the corresponding p-value is less than
and the corresponding p-value is less than 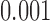 based on
based on 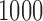 MC samples. This indicates that there is strong evidence that daily activity profiles in women vary with age.
MC samples. This indicates that there is strong evidence that daily activity profiles in women vary with age.
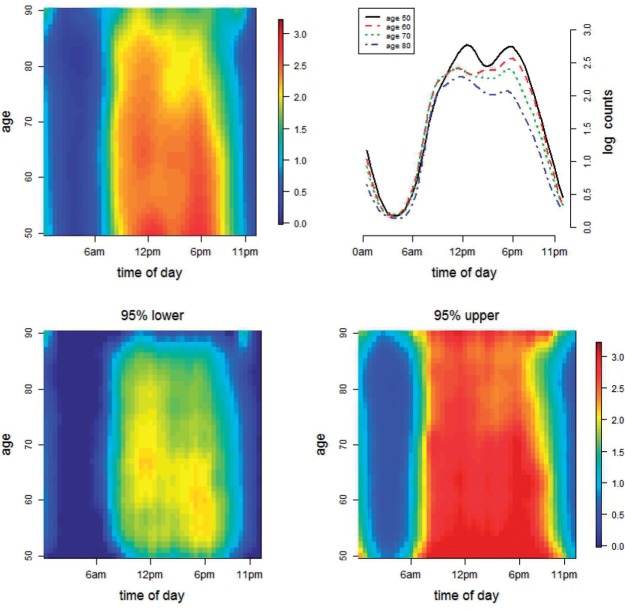
Figure 1 displays the estimated baseline activity profile as a function of age, 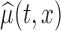 , using the average of all bootstrap estimates. The plot indicates that the average log counts is a decreasing function of age for most times during the day. Furthermore, it depicts two activity peaks, one around 12 pm and the other around 6 pm. The 6-pm peak seems to decrease faster with age, indicating that afternoon activity is more affected by age than morning activity. We use joint confidence band to evaluate the sampling variability of
, using the average of all bootstrap estimates. The plot indicates that the average log counts is a decreasing function of age for most times during the day. Furthermore, it depicts two activity peaks, one around 12 pm and the other around 6 pm. The 6-pm peak seems to decrease faster with age, indicating that afternoon activity is more affected by age than morning activity. We use joint confidence band to evaluate the sampling variability of 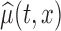 . The joint lower and upper
. The joint lower and upper 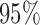 confidence limits based on methods described in Section 3 are displayed in the bottom plots of Figure 1; the plots show that across all ages, the estimated low average activity at night has relatively small variability while the estimated high-average activity during the day has relatively high variability. To visualize the results, we display the estimated activity profile for 60-years-old women,
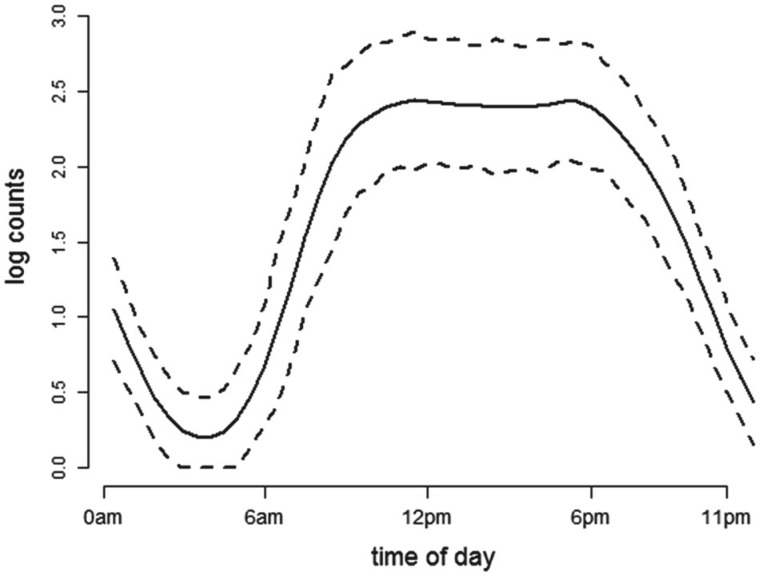
confidence limits based on methods described in Section 3 are displayed in the bottom plots of Figure 1; the plots show that across all ages, the estimated low average activity at night has relatively small variability while the estimated high-average activity during the day has relatively high variability. To visualize the results, we display the estimated activity profile for 60-years-old women, 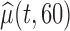 , and the corresponding
, and the corresponding 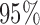 joint confidence band in Figure 2. Figure S2 of supplementary material available at Biostatistics online displays the estimated association of BMI with mean log counts as a function of time of day; it suggests that women with higher BMI have less activity during the day and evening, albeit more activity at late night and in early morning.
joint confidence band in Figure 2. Figure S2 of supplementary material available at Biostatistics online displays the estimated association of BMI with mean log counts as a function of time of day; it suggests that women with higher BMI have less activity during the day and evening, albeit more activity at late night and in early morning.
Fig. 1.
Heat map of average of bootstrap estimates of log counts as a bivariate function of time of day and age (top left panel); average of bootstrap estimates of log counts for five different age groups (top right panel); and heat maps of joint confidence bands for the estimate in the top left panel (bottom panels). The legend on the right applies to both of the bottom plots.
Fig. 2.
Average of bootstrap estimates of log counts as a function of time of day at age 60 and the associated joint confidence bands.
5.1. Validating the testing results via simulation study
We conducted a simulation study designed to closely mimic the BLSA data structure. Specifically, we generated data from model (2.1) with 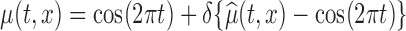 , where
, where 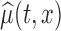 is the estimated mean log counts, and
is the estimated mean log counts, and 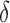 is a parameter quantifying the distance from the null and alternative hypotheses. When
is a parameter quantifying the distance from the null and alternative hypotheses. When 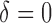 the true mean profile
the true mean profile 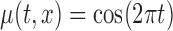 , whereas when
, whereas when 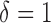 then
then 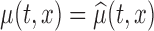 . The errors
. The errors 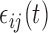 are generated with a covariance structure that closely mimics that of the residuals from the BLSA data. Specifically we use the model
are generated with a covariance structure that closely mimics that of the residuals from the BLSA data. Specifically we use the model 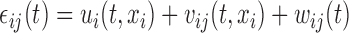 and the associated model estimates from Xiao and others (2015), where
and the associated model estimates from Xiao and others (2015), where 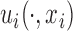 and
and 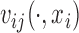 are subject-specific and subject- and visit-specific random processes with mean zero and
are subject-specific and subject- and visit-specific random processes with mean zero and 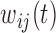 is white noise.
is white noise. 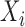 and
and 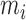 are generated uniformly from
are generated uniformly from 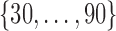 and
and 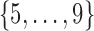 , respectively. Sample size is set to be the number of female participants in the BLSA. Estimation is done exactly the same as in our data analysis. Table 1 shows the rejection probabilities in 1000 simulations when
, respectively. Sample size is set to be the number of female participants in the BLSA. Estimation is done exactly the same as in our data analysis. Table 1 shows the rejection probabilities in 1000 simulations when 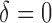 and indicates that the empirical size is close to the nominal levels. Figure S3 of supplementary material available at Biostatistics online displays the power in 500 simulations, when
and indicates that the empirical size is close to the nominal levels. Figure S3 of supplementary material available at Biostatistics online displays the power in 500 simulations, when 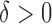 . When the true
. When the true 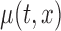 is the estimated bivariate mean log counts of the BLSA data, i.e.
is the estimated bivariate mean log counts of the BLSA data, i.e. 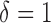 , the rejection probability reaches 1.
, the rejection probability reaches 1.
Table 1.
Empirical type I error of the test statistic 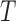 based on the
based on the 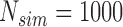 MC samples; Mean function is
MC samples; Mean function is 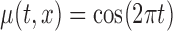 ,
, 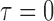
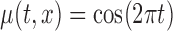 , , 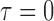
| ||
|---|---|---|
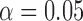
|
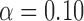
|
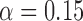
|
| 0.06 | 0.11 | 0.16 |
| (0.01) | (0.01) | (0.01) |
Standard errors are presented in parentheses.
6. Simulation Study
We evaluate the performance of the proposed inferential methods. Data are simulated using the model (2.1) where 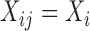 ,
, 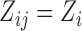 . The errors
. The errors 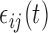 are generated from the model
are generated from the model 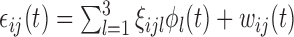 , where for each
, where for each 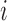 and
and 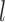 the basis coefficients
the basis coefficients 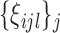 are generated from a multivariate normal distribution with mean zero and covariance
are generated from a multivariate normal distribution with mean zero and covariance 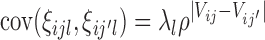 , where
, where 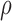 is a correlation parameter and
is a correlation parameter and 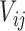 is the actual time of visit at which
is the actual time of visit at which 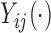 is observed; a similar dependence structure has been considered in simulation studies by Park and Staicu (2015) and Islam and others (2016). The residuals
is observed; a similar dependence structure has been considered in simulation studies by Park and Staicu (2015) and Islam and others (2016). The residuals 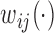 are mutually independent with zero mean and variance
are mutually independent with zero mean and variance 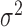 . The number of repeated measures is fixed at
. The number of repeated measures is fixed at 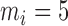 ,
, 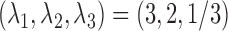 , and the functions
, and the functions 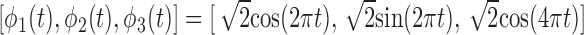 . The subject-specific covariates
. The subject-specific covariates 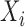 and
and 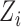 are generated from a Uniform
are generated from a Uniform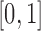 . The grid of points
. The grid of points 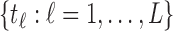 is set as
is set as 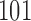 equally spaced points in
equally spaced points in 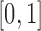 . The variance of the white noise process
. The variance of the white noise process 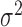 is set to
is set to 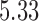 , which provides a signal to noise ratio SNR
, which provides a signal to noise ratio SNR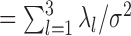 equal to
equal to 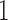 .
.
We consider different combinations of the following factors: F1. number of subjects: (a) 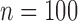 , (b)
, (b) 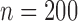 , and (c)
, and (c)  ; F2. bivariate mean function: (a)
; F2. bivariate mean function: (a) 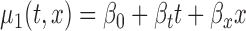 for
for 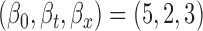 , (b)
, (b) 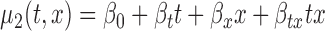 for
for 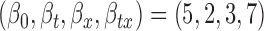 , (c)
, (c)  , and (d)
, and (d) 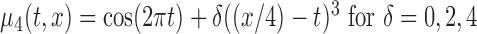 , and
, and 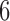 , with/without the addition of linear effect of nuisance covariate
, with/without the addition of linear effect of nuisance covariate 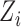 , i.e.
, i.e. 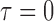 (no effect) and
(no effect) and 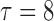 ; lastly, F3. between-curves correlations: (a)
; lastly, F3. between-curves correlations: (a) 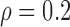 (weak) and (b)
(weak) and (b) 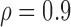 (strong).
(strong).
Confidence bands for model parameters are evaluated in two ways. First, we model the data by assuming the correct model and by evaluating the accuracy of the inferential procedures. Second, we model the data using a bivariate mean, 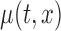 , and evaluate the performance of the confidence bands of
, and evaluate the performance of the confidence bands of 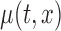 for covering the true mean even when the true mean has a simpler structure, i.e. F2 i.(a)–(c). The results for the first case are included in Section B of the supplementary material available at Biostatistics online, whereas those for the second case are presented below, because in the BLSA we used bivariate nonparametric fitting. Estimation is done as detailed in Section 2. We use
for covering the true mean even when the true mean has a simpler structure, i.e. F2 i.(a)–(c). The results for the first case are included in Section B of the supplementary material available at Biostatistics online, whereas those for the second case are presented below, because in the BLSA we used bivariate nonparametric fitting. Estimation is done as detailed in Section 2. We use 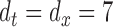 cubic B-spline basis functions, and select the smoothing parameters via GCV; specifically, for the bivariate smooth,
cubic B-spline basis functions, and select the smoothing parameters via GCV; specifically, for the bivariate smooth, 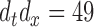 basis functions are used.
basis functions are used.
The performance of the pointwise and joint confidence bands is evaluated in terms of average coverage probability (ACP), and average length (AL) of the confidence intervals. Specifically, let 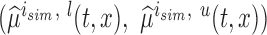 be the
be the 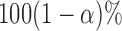 pointwise confidence interval of
pointwise confidence interval of 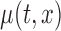 obtained at the
obtained at the 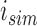 Monte Carlo generation of the data, then
Monte Carlo generation of the data, then
where 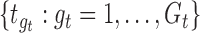 and
and 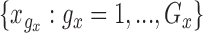 are equi-distanced grid points in the domains
are equi-distanced grid points in the domains 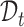 , and
, and 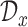 , respectively. Next, let
, respectively. Next, let 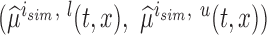 be
be 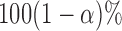 joint confidence interval. The AL is calculated as above, while the ACP is calculated as:
joint confidence interval. The AL is calculated as above, while the ACP is calculated as:
The performance of the test statistic 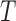 is evaluated in terms of its size for the nominal levels
is evaluated in terms of its size for the nominal levels 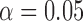 ,
, 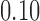 , and
, and 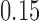 , and power at
, and power at 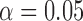 . The results for the size are based on
. The results for the size are based on 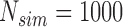 MC samples, while the results for ACP and AL of the confidence bands, and power of the test are based on
MC samples, while the results for ACP and AL of the confidence bands, and power of the test are based on 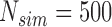 MC samples. For each MC simulation we use
MC samples. For each MC simulation we use 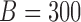 bootstrap samples.
bootstrap samples.
Table 2 shows the ACP and AL for the 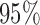 confidence bands based on the bootstrap of subject-level residuals when the sample size
confidence bands based on the bootstrap of subject-level residuals when the sample size 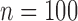 and when
and when 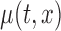 is modeled nonparametrically regardless of the true mean structure; the results for other nominal coverages (
is modeled nonparametrically regardless of the true mean structure; the results for other nominal coverages (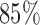 and
and 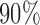 ) are included in Section A of the supplementary material available at Biostatistics online. Overall, the pointwise/joint confidence bands achieve the nominal coverage for all of the mean structures considered. The confidence bands tend to be wider when the between-curves correlation is strong (
) are included in Section A of the supplementary material available at Biostatistics online. Overall, the pointwise/joint confidence bands achieve the nominal coverage for all of the mean structures considered. The confidence bands tend to be wider when the between-curves correlation is strong (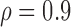 ).
).
Table 2.
Simulation results for 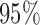 confidence bands based on the bootstrap of subject-level residuals when a nonparametric bivariate function is fitted for
confidence bands based on the bootstrap of subject-level residuals when a nonparametric bivariate function is fitted for 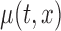 ; results are based on
; results are based on 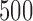 MC samples
MC samples
| Case | True mean function |
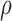
|
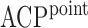
|
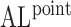
|
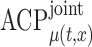
|
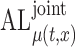
|
||||
|---|---|---|---|---|---|---|---|---|---|---|
| (a) |
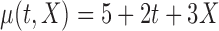
|
0.20 | 0.94 | (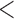 0.01) 0.01) |
1.65 | (0.01) | 0.94 | (0.01) | 3.22 | (0.01) |
| 0.90 | 0.94 | (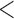 0.01) 0.01) |
2.17 | (0.02) | 0.93 | (0.01) | 4.24 | (0.01) | ||
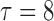
|
0.20 | 0.93 | (0.01) | 0.14 | (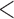 0.01) 0.01) |
|||||
| 0.90 | 0.93 | (0.01) | 0.14 | (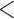 0.01) 0.01) |
||||||
| (b) |
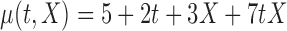
|
0.20 | 0.94 | (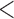 0.01) 0.01) |
1.65 | (0.01) | 0.94 | (0.01) | 3.22 | (0.01) |
| 0.90 | 0.94 | ( 0.01) 0.01) |
2.17 | (0.02) | 0.93 | (0.01) | 4.24 | (0.01) | ||
|
0.20 | 0.93 | (0.01) | 0.14 | ( 0.01) 0.01) |
|||||
| 0.90 | 0.93 | (0.01) | 0.14 | ( 0.01) 0.01) |
||||||
| (c) |
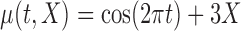
|
0.20 | 0.94 | (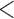 0.01) 0.01) |
1.65 | (0.01) | 0.93 | (0.01) | 3.23 | (0.01) |
| 0.90 | 0.94 | (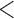 0.01) 0.01) |
2.18 | (0.02) | 0.93 | (0.01) | 4.25 | (0.01) | ||
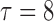
|
0.20 | 0.93 | (0.01) | 0.14 | ( 0.01) 0.01) |
|||||
| 0.90 | 0.93 | (0.01) | 0.14 | ( 0.01) 0.01) |
||||||
| (d) |
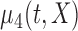
|
0.61 | 0.94 | ( 0.01) 0.01) |
1.65 | (0.01) | 0.93 | (0.01) | 3.23 | (0.01) |
| 0.90 | 0.94 | (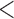 0.01) 0.01) |
2.18 | (0.02) | 0.93 | (0.01) | 4.26 | (0.01) | ||
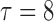
|
0.20 | 0.93 | (0.01) | 0.14 | (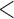 0.01) 0.01) |
|||||
| 0.90 | 0.94 | (0.01) | 0.14 | (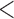 0.01) 0.01) |
||||||
Standard errors are presented in parentheses.
We also investigate the performance of the confidence band when the correct structure of 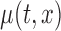 is used; the corresponding results for the bootstrap of subject-level residuals and observations are included in Section B and Section C of the supplementary material available at Biostatistics online. The results show the good coverage of the pointwise/joint confidence bands based on the bootstrap of residuals by subjects for all of the mean structures considered. The bootstrap of observations by subjects leads to equally good coverage when the true effect of the covariate
is used; the corresponding results for the bootstrap of subject-level residuals and observations are included in Section B and Section C of the supplementary material available at Biostatistics online. The results show the good coverage of the pointwise/joint confidence bands based on the bootstrap of residuals by subjects for all of the mean structures considered. The bootstrap of observations by subjects leads to equally good coverage when the true effect of the covariate 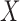 is linear (cases F2 i.(a)–(c)), whereas it leads to slight under–coverage when the true effect of
is linear (cases F2 i.(a)–(c)), whereas it leads to slight under–coverage when the true effect of 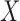 is nonlinear (case F2 i.(d)). However, in the case of a visit-varying covariate
is nonlinear (case F2 i.(d)). However, in the case of a visit-varying covariate 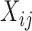 the joint confidence band maintains nominal coverage even when the effect of
the joint confidence band maintains nominal coverage even when the effect of 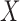 is nonlinear; see Table S9 of the supplementary material available at Biostatistics online. These results indicate that for a time-invariant covariate,
is nonlinear; see Table S9 of the supplementary material available at Biostatistics online. These results indicate that for a time-invariant covariate, 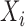 , the bootstrap of subject-level residuals is narrower and has better coverage. In terms of computational cost, fitting a nonparametric model is much slower than fitting a parametric model. For example when the true mean F2 i. (c) is used to generate the data, fitting a nonparametric model for
, the bootstrap of subject-level residuals is narrower and has better coverage. In terms of computational cost, fitting a nonparametric model is much slower than fitting a parametric model. For example when the true mean F2 i. (c) is used to generate the data, fitting a nonparametric model for 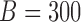 bootstrap samples takes 337 s whereas the same procedure for a parametric model takes 50 s; the results are based on
bootstrap samples takes 337 s whereas the same procedure for a parametric model takes 50 s; the results are based on 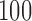 MC samples on a computer with a 3.60 Hz processor.
MC samples on a computer with a 3.60 Hz processor.
Table 3 shows the empirical size of the proposed testing procedure for testing 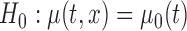 , where
, where 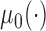 is a smooth effect depending on
is a smooth effect depending on 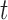 only. Results indicate that, as sample size increases, the size of the test gets closer to the corresponding nominal levels. In the simulation settings considered, the test attains the correct sizes with sample size
only. Results indicate that, as sample size increases, the size of the test gets closer to the corresponding nominal levels. In the simulation settings considered, the test attains the correct sizes with sample size 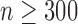 , which is the case in our motivating BLSA data application. Including an additional covariate in the model seems to have no effect on the performance of the testing procedure. Figure S4 of supplementary material available at Biostatistics online illustrates the power curves, when the true mean structure deviates from the null hypothesis. It presents the power as a function of the deviation from the null that involves both
, which is the case in our motivating BLSA data application. Including an additional covariate in the model seems to have no effect on the performance of the testing procedure. Figure S4 of supplementary material available at Biostatistics online illustrates the power curves, when the true mean structure deviates from the null hypothesis. It presents the power as a function of the deviation from the null that involves both 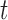 and
and 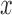 ,
, 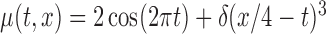 . Here
. Here 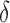 quantifies the departure from the null hypothesis. As expected, for
quantifies the departure from the null hypothesis. As expected, for 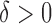 rejection probabilities increase as the departure from the null hypothesis increases, irrespective of the direction in which it deviates. As expected, rejection probabilities increase with the sample size. Our investigation indicates that the strength of the correlation between the functional observations corresponding to the same subject affect the rejection probability: the weaker the correlation, the larger the power. There is no competitive testing method available for this null hypothesis. Lastly we conducted a simulation study to evaluate the robustness of the proposed methods to non-Gaussian error distributions and obtained similar results with those from the Gaussian case; see Section D of the supplementary material available at Biostatistics online.
rejection probabilities increase as the departure from the null hypothesis increases, irrespective of the direction in which it deviates. As expected, rejection probabilities increase with the sample size. Our investigation indicates that the strength of the correlation between the functional observations corresponding to the same subject affect the rejection probability: the weaker the correlation, the larger the power. There is no competitive testing method available for this null hypothesis. Lastly we conducted a simulation study to evaluate the robustness of the proposed methods to non-Gaussian error distributions and obtained similar results with those from the Gaussian case; see Section D of the supplementary material available at Biostatistics online.
Table 3.
Empirical Type I error of the test statistic 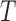 based on the
based on the 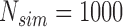 MC samples
MC samples
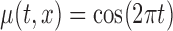 , , 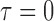
|
|||||||
|---|---|---|---|---|---|---|---|
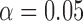
|
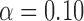
|
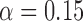
|
|||||
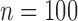
|
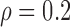
|
0.08 | (0.01) | 0.14 | (0.01) | 0.21 | (0.01) |
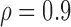
|
0.09 | (0.01) | 0.14 | (0.01) | 0.20 | (0.01) | |
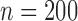
|
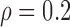
|
0.07 | (0.01) | 0.13 | (0.01) | 0.17 | (0.01) |
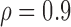
|
0.08 | (0.01) | 0.12 | (0.01) | 0.18 | (0.01) | |
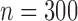
|
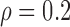
|
0.06 | (0.01) | 0.11 | (0.01) | 0.16 | (0.01) |
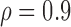
|
0.06 | (0.01) | 0.12 | (0.01) | 0.16 | (0.01) | |
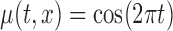 , , 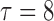
|
|||||||
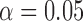
|
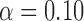
|
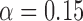
|
|||||
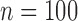
|
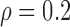
|
0.07 | (0.01) | 0.15 | (0.01) | 0.20 | (0.01) |
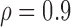
|
0.08 | (0.01) | 0.15 | (0.01) | 0.21 | (0.01) | |
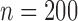
|
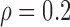
|
0.07 | (0.01) | 0.13 | (0.01) | 0.17 | (0.01) |
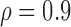
|
0.08 | (0.01) | 0.12 | (0.01) | 0.18 | (0.01) | |
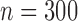
|
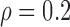
|
0.06 | (0.01) | 0.11 | (0.01) | 0.16 | (0.01) |
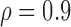
|
0.06 | (0.01) | 0.12 | (0.01) | 0.16 | (0.01) | |
Supplementary Material
Supplementary Material
Supplementary material is available online at http://biostatistics.oxfordjournals.org. Conflict of Interest: None declared.
Acknowledgments
Conflict of Interest: None declared.
Funding
NSF (DMS 1007466 and DMS 1454942 to A.M.S.); NIH (R01 NS085211 and R01 MH086633 to A.M.S); NIH (R01 NS085211, R01 NS060910, R01 HL123407), NIA contracts (HHSN27121400603P and HHSN27120400775P) to C.M.C Data for these analyses were obtained from the Baltimore Longitudinal Study of Aging, performed by the National Institute on Aging.
References
- Aston J. A., Chiou J.-M. and Evans J. P. (2010). Linguistic pitch analysis using functional principal component mixed effect models. Journal of the Royal Statistical Society: Series C (Applied Statistics) 59, 297–317. [Google Scholar]
- Baladandayuthapani V., Mallick B. K, Young H., Mee L., Joanne R. T., Nancy D. and Carroll R. J. (2008). Bayesian hierarchical spatially correlated functional data analysis with application to colon carcinogenesis. Biometrics 64, 64–73. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brage S., Brage N., Ekelund U., Luan J., Franks P. W., Froberg K. and Wareham N. J. (2006). Effect of combined movement and heart rate monitor placement on physical activity estimates during treadmill locomotion and free-living. European Journal of Applied Physiology 96, 517–524. [DOI] [PubMed] [Google Scholar]
- Cao G., Yang L. and Todem D. (2012). Simultaneous inference for the mean function based on dense functional data. Journal of Nonparametric Statistics 24, 359–377. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen K. and Müller H.-G. (2012). Modeling repeated functional observations. Journal of the American Statistical Association 107, 1599–1609. [Google Scholar]
- Crainiceanu C. M., Staicu A.-M. and Di C.-Z. (2009). Generalized multilevel functional regression. Journal of the American Statistical Association 104, 1550–1561. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Crainiceanu C. M., Staicu A.-M., Ray S. and Punjabi N. (2012). Bootstrap-based inference on the difference in the means of two correlated functional processes. Statistics in Medicine 31, 3223–3240. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cuevas A., Febrero M. and Fraiman R. (2006). On the use of the bootstrap for estimating functions with functional data. Computational Statistics & Data Analysis 51, 1063–1074. [Google Scholar]
- Degras D. A. (2011). Simultaneous confidence bands for nonparametric regression with functional data. Statistica Sinica, 21, 1735–1765. [Google Scholar]
- Delgado M. A. and Manteiga W. G. (2001). Significance testing in nonparametric regression based on the bootstrap. Annals of Statistics, 29, 1469–1507. [Google Scholar]
- Di C.-Z., Crainiceanu C. M., Caffo B. S and Punjabi N. M. (2009). Multilevel functional principal component analysis. The Annals of Applied Statistics 3, 458. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Efron B. and Tibshirani R. J. (1994). An Introduction to the Bootstrap. Boca Raton, Florida: CRC press. [Google Scholar]
- Fan Y. and Li Q. (1996). Consistent model specification tests: omitted variables and semiparametric functional forms, Econometrica 64, 865–890. [Google Scholar]
- Faraway J. J. (1997). Regression analysis for a functional response. Technometrics 39, 254–261. [Google Scholar]
- Fitzmaurice G. M., Laird N. M. and Ware J. H. (2012). Applied Longitudinal Analysis, Volume 998 Hoboken, NJ: John Wiley & Sons. [Google Scholar]
- Greven S., Crainiceanu C., Caffo B. and Reich D. (2010). Longitudinal functional principal component analysis. Electronic Journal of Statistics 4, 1022–1054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gu J., Li D. and Liu D. (2007). Bootstrap non-parametric significance test. Journal of Nonparametric Statistics 19, 215–230. [Google Scholar]
- Hall P. and Horowitz J. (2013). A simple bootstrap method for constructing nonparametric confidence bands for functions. The Annals of Statistics 41, 1892–1921. [Google Scholar]
- Hall P., Li Q. and Racine J. S. (2007). Nonparametric estimation of regression functions in the presence of irrelevant regressors. The Review of Economics and Statistics 89, 784–789. [Google Scholar]
- Härdle W. and Bowman A. W. (1988). Bootstrapping in nonparametric regression: local adaptive smoothing and confidence bands. Journal of the American Statistical Association 83, 102–110. [Google Scholar]
- Horváth L., Kokoszka P. and Reeder R. (2013). Estimation of the mean of functional time series and a two-sample problem. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 75, 103–122. [Google Scholar]
- Islam M. N., Staicu A.-M. and van Heugten E. (2016). Longitudinal dynamic functional regression. arXiv preprint arXiv:1611.01831. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ivanescu A. E., Staicu A.-M., Scheipl F. and Greven S. (2015). Penalized function-on-function regression. Computational Statistics 30, 539–568. [Google Scholar]
- Jiang C.-R. and Wang J.-L. (2011). Functional single index models for longitudinal data. The Annals of Statistics 39, 362–388. [Google Scholar]
- Laird N. M. and Ware J. H. (1982). Random-effects models for longitudinal data. Biometrics 38, 963–974. [PubMed] [Google Scholar]
- Lavergne P. and Vuong Q. (2000). Nonparametric significance testing. Econometric Theory 16, 576–601. [Google Scholar]
- Liang K.-Y. and Zeger S. L. (1986). Longitudinal data analysis using generalized linear models. Biometrika 73, 13–22. [Google Scholar]
- Ma S., Yang L. and Carroll R. J. (2012). A simultaneous confidence band for sparse longitudinal regression. Statistica Sinica 22, 95. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marx B. D. and Eilers P. H. (2005). Multidimensional penalized signal regression. Technometrics 47, 13–22. [Google Scholar]
- Morris J. S., Arroyo C., Coull B. A., Ryan L. M., Herrick R. and Gortmaker S. L. (2006). Using wavelet-based functional mixed models to characterize population heterogeneity in accelerometer profiles: a case study. Journal of the American Statistical Association 101, 1352–1364. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morris J. S, Baladandayuthapani V., Herrick R. C, Sanna P. and Gutstein H. (2011). Automated analysis of quantitative image data using isomorphic functional mixed models, with application to proteomics data. The Annals of Applied Statistics 5, 894. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morris J. S. and Carroll R. J. (2006). Wavelet-based functional mixed models. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 68, 179–199. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morris J. S., Vannucci M., Brown P. J. and Carroll R. J. (2003). Wavelet-based nonparametric modeling of hierarchical functions in colon carcinogenesis. Journal of the American Statistical Association 98, 573–583. [Google Scholar]
- Park S. Y. and Staicu A.-M. (2015). Longitudinal functional data analysis. Stat 4, 212–226. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Politis D. N. and Romano J. P. (1994). The stationary bootstrap. Journal of the American Statistical association 89, 1303–1313. [Google Scholar]
- Ruppert D., Wand M. P and Carroll R. J. (2003). Semiparametric regression, Number 12 Cambridge, UK: Cambridge university press. [Google Scholar]
- Scheipl F., Staicu A.-M. and Greven S. (2015). Functional additive mixed models. Journal of Computational and Graphical Statistics 24, 477–501. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schrack J. A., Zipunnikov V., Goldsmith J., Bai J., Simonsick E. M., Crainiceanu C. M. and Ferrucci L. (2014). Assessing the “physical cliff”: detailed quantification of aging and patterns of physical activity. The Journals of Gerontogoly Series A: Biological Sciences and Medical Sciences. 69, 973–979. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Serban N., Staicu A.-M. and Carroll R. J. (2013). Multilevel cross-dependent binary longitudinal data. Biometrics 69, 903–913. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shen Q. and Faraway J. (2004). An f test for linear models with functional responses. Statistica Sinica 14, 1239–1258. [Google Scholar]
- Shou H., Zipunnikov V., Crainiceanu C. M. and Greven S. (2015). Structured functional principal component analysis. Biometrics 71, 247–257. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Staicu A.-M., Crainiceanu C. M. and Carroll R. J. (2010). Fast methods for spatially correlated multilevel functional data. Biostatistics 11, 177–194. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Staicu A.-M., Lahiri S. N. and Carroll R. J. (2015). Significance tests for functional data with complex dependence structure. Journal of Statistical Planning and Inference 156, 1–13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Staicu A.-M., Li Y., Crainiceanu C. M and Ruppert D. (2014). Likelihood ratio tests for dependent data with applications to longitudinal and functional data analysis. Scandinavian Journal of Statistics 41, 932–949. [Google Scholar]
- Stone J. L. and Norris A. H. (1966). Activities and attitudes of participants in the Baltimore Longitudinal Study. Journal of Gerontology 21, 575–580. [DOI] [PubMed] [Google Scholar]
- Wahba G. (1990). Spline Models for Observational Data, Volume 59 Philadelphia, PA: Siam. [Google Scholar]
- Wood S. N. (2006). Low-rank scale-invariant tensor product smooths for generalized additive mixed models. Biometrics 62, 1025–1036. [DOI] [PubMed] [Google Scholar]
- Xiao L., Huang L., Schrack J. A, Ferrucci L., Zipunnikov V. and Crainiceanu C. M. (2015). Quantifying the lifetime circadian rhythm of physical activity: a covariate-dependent functional approach. Biostatistics 16, 352–367. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xiao L., Li Y. and Ruppert D. (2013). Fast bivariate p-splines: the sandwich smoother. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 75, 577–599. [Google Scholar]
- Xiao L., Zipunnikov V., Ruppert D. and Crainiceanu C. (2016). Fast covariance estimation for high-dimensional functional data. Statistics and Computing 26, 409–421. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang J.-T. and Chen J. (2007). Statistical inferences for functional data. The Annals of Statistics 35, 1052–1079. [Google Scholar]
- Zhang L., Baladandayuthapani V., Zhu H., Baggerly K. A, Majewski T., Czerniak B. A. and Morris J. S. (2016). Functional car models for large spatially correlated functional datasets. Journal of the American Statistical Association 111, 772–786. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu H., Brown P. J and Morris J. S. (2011). Robust, adaptive functional regression in functional mixed model framework. Journal of the American Statistical Association 106, 1167–1179. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.