Empirical Null Estimation using Zero-inflated Discrete Mixture Distributions and its Application to Protein Domain Data

Summary

In recent mutation studies, analyses based on protein domain positions are gaining popularity over gene-centric approaches since the latter have limitations in considering the functional context that the position of the mutation provides. This presents a large-scale simultaneous inference problem, with hundreds of hypothesis tests to consider at the same time. This paper aims to select significant mutation counts while controlling a given level of Type I error via False Discovery Rate (FDR) procedures. One main assumption is that the mutation counts follow a zero-inflated model in order to account for the true zeros in the count model and the excess zeros. The class of models considered is the Zero-inflated Generalized Poisson (ZIGP) distribution. Furthermore, we assumed that there exists a cut-off value such that smaller counts than this value are generated from the null distribution. We present several data-dependent methods to determine the cut-off value. We also consider a two-stage procedure based on screening process so that the number of mutations exceeding a certain value should be considered as significant mutations. Simulated and protein domain data sets are used to illustrate this procedure in estimation of the empirical null using a mixture of discrete distributions. Overall, while maintaining control of the FDR, the proposed two-stage testing procedure has superior empirical power.

1. Introduction

Interest towards multiple testing procedures has been growing rapidly in the advent of the so-called genomic age. With the breakthrough in large-scale methods to purify, identify and characterize DNA, RNA, proteins and other molecules, researchers are becoming increasingly reliant on statistical methods for determining the significance of biological findings (Pollard et al., 2005). Gene-based analyses of cancer data are classic examples of studies which present thousands of genes for simultaneous hypothesis testing. However, Nehrt et al. (2012) reported that gene-centric cancer studies are limited since the functional context that the position of the mutation provides is not considered. In lieu of this, Nehrt et al. (2012) have shown that protein domain level analyses of cancer somatic variants can identify functionally relevant somatic mutations where traditional gene-centric methods fail by focusing on protein domain regions within genes, leveraging the modularity and polyfunctionality of genes.

In protein domain-centric studies, somatic mutations from sequenced tumor samples are mapped from their genomic positions to positions within protein domains, enabling the comparison of distant genomic regions that share similar structure and amino acid composition (Peterson et al., 2013). In the analysis of sequenced tumor samples, it is assumed that the mutational distribution will consist of many “passenger” mutations, which are non-functional randomly distributed background mutations, in addition to rare functional “driver” mutations that reoccur at specific sites within the domain and contribute to the initiation or progression of cancer (Parmigiani et al., 2007). The major interest is in a single domain, how to identify the highly mutated positions compared to the background where the number of positions in a domain can be as large as several hundreds.

Motivated by the aforementioned domain-level analyses, we propose a methodology for identifying significant mutation counts while controlling the rate of false rejections. Dudoit et al. (2003) reported that much of the statistics microarray literature is focused on controlling the probability of a Type I error, a “false discovery”. A traditional approach is to control the family-wise error rate (FWER), the probability of making at least one false discovery. However, with the collection of simultaneous hypothesis tests in the hundreds or thousands, trying to limit the probability of even a single false discovery leads to lack of power. Alternatively, in a seminal paper, Benjamini and Hochberg (1995) introduced a multiple hypothesis testing error measure called False Discovery Rate (FDR). This quantity is the expected proportion of false positive findings among all the rejected hypotheses. Among the FDR-controlling test methods, Efron et al. (2001) developed an empirical Bayes approach where they established a close connection between the estimated posterior probabilities and a local version of the FDR.

A key step in controlling the local false discoveries is to estimate the null distribution of the test statistics. Efron (2004) stated that the test statistics in large-scale testing may not accurately follow the theoretical null distribution. Instead, the density of the null distribution is estimated from the large number of genes. In these microarray experiments, Efron (2005) employed a normal mixture model and proposed maximum likelihood and mode matching to estimate the empirical null distribution. Park et al. (2011) proposed a local FDR estimation procedure based on modeling the null distribution with a mixture of normal distributions. However, these existing methods are based on the assumption that the null is a mixture of continuous distributions. In the case of domain-level analyses, the data is characterized as mutation counts among N positions in the domain. This indicates that the available methods in the estimation of the empirical null should be extended to a mixture of discrete distributions.

The rest of the paper is organized as follows. In Section 2, we discuss the problem in detail and review two existing multiple testing procedures, namely Efron’s Local FDR procedure and Storey’s procedure. In Section 3, we introduce the estimation procedure for f₀, f and π₀, where the null distribution is assumed to be a zero-inflated model. Also, a novel two-stage multiple testing procedure is presented in this section. In Section 4, the performance of the new procedure is studied via simulations and the results for real data sets are presented. Some concluding remarks will be presented in Section 5.

2. Multiple Testing Procedures controlling FDR

In this section, we briefly discuss the motivating example and review the existing procedures for analysis. The collection of the original dataset is a = (a₁, a₂, …, a_N)′, where a_i is the number of mutations in the ith position of the specific domain with N positions. We define 𝒜 as the set of the unique values of a, K = max(a), and L is the cardinality of 𝒜 where L ≤ K + 1. Some relevant features of a follow. A large proportion of positions do not have any mutation, a_i = 0. Also, L is relatively small compared to N, which means that the number of mutations in many positions are tied. Since our goal is to identify the positions with extra disease mutation counts, it is only reasonable to have the same conclusion for positions wherein the number of mutations are tied. Therefore, we transform the data into the observed “histograph” of positions over “mutation counts”. We define n_j =| {i : a_i = j} |, as the number of positions with j mutations, j ∈ 𝒜, where 𝒜 ≡ {j : j ≥ 0, n_j > 0} and $\sum _{j\le K}{n}_j=N$. The ordered data x_N can be represented as a partition of the unique values of a, that is,

$${\mathbf{x}}_N^{\prime }=({\mathbf{x}}_0^{\prime },{\mathbf{x}}_1^{\prime },\dots ,{\mathbf{x}}_K^{\prime })=\underset{{\mathbf{x}}_0^{\prime }}{\underbrace{(0,0,\dots ,0}},\underset{{\mathbf{x}}_1^{\prime }}{\underbrace{1,1,\dots ,1}}\dots ,\underset{{\mathbf{x}}_K^{\prime }}{\underbrace{K,K,\dots ,K)}}$$

where x_j is the column vector containing n_j of js.

For any single domain of interest, a total of L mutation counts can be decomposed into two groups, 𝒜₀ and 𝒜₁, where 𝒜₀ is the collection of small number of mutation counts which is considered to be non-significant and 𝒜₁ is the set of large number of mutation counts which consists of significantly mutated positions. Let the prior probabilities of the two groups be π₀ or π₁ = 1 − π₀, and assume corresponding densities, f₀ or f₁. Define f₀ to be the null distribution and f₁ to be the alternative distribution. Therefore, we consider the problem of testing L null hypotheses simultaneously, H_0j is true for j ∈ 𝒜, |𝒜| = L, where H_0j is stated as the number of mutations j is generated from f₀.

For a given position, the number of mutations follow one of the two distributions f₀ or f₁, so the probability density function of the mixture distribution can be represented as

$$f(a_i)={\pi }_0{f}_0(a_i)+(1-{\pi }_0)f_1(a_i)$$ (1)

and our goal is to identify the positions which have significantly different patterns from the null. For continuous data, Efron (2005) introduced the idea of “zero assumption” where observations around the central peak of the distribution consists mainly of null cases. Using this assumption, f₀ is estimated using Gaussian quadrature which is based on derivative at the mode. However, such a procedure is not applicable to discrete data. In our problem on discrete data, we introduce the following assumption on the null distribution which plays a key role throughout this paper.

Assumption on f₀:

$$f(a_i)={\pi }_0{f}_0(a_i)\mathit{\text{ for }}{a}_i\le C\mathit{\text{ for some integer }}C$$ (2)

From the assumption, a_i ≤ C are guaranteed to be from f₀ and a_i > C are generated from the mixture of f₀ and f₁. We will discuss more details about how to choose the value of C in the next section. We do not have the issue of identifiability in the mixture model (1) since f₁ has a different support from that of f₀ from the assumption (2), so any parametric model for f₀ considered in our paper is uniquely identified.

Benjamini and Hochberg (1995) employed a sequential p-value method to determine r that tells us to reject p₍₁₎, p₍₂₎, …, p_(r), where p₍₁₎, p₍₂₎, …, p_(K) are the ordered observed p-values. Storey (2002) improved the Benjamini-Hochberg (BH) procedure with the inclusion of the estimator of the null proportion, π̂₀, which indicates that we reject p₍₁₎, p₍₂₎, …, p_(ℓ) such that

$$\ell =\text{max }\{i:p_{(i)}\le \frac{\alpha \sum _{j\ge i}{n}_j}{N{\hat{\pi }}_0}\}$$

The BH procedure and Storey’s procedure are equivalent, that is r = ℓ, if we take π̂₀ = 1. The details about the estimation of π₀ is provided in the next section. Moreover, following Efron (2007), we define the local FDR at any mutation count, say t, as

$$\mathit{\text{fdr}}(t)=\frac{{\pi }_0{f}_0(t)}{f(t)}$$ (3)

which indicates that fdr(t) is the posterior probability of a true null hypothesis at t. The interpretation of the local FDR value is analogous to the frequentist’s p-value wherein local FDR values less than a specified level of significance provide stronger evidence against the null hypothesis.

3. Methodology

3.1 Model Specification

Depending on the application, we assume that the mutation counts follow a zero-inflated model in order to account for the true zeros in the count model and the excess zeros. For example, the zero-inflation observed in protein domain data is due to the negative selection of mutations that can not occur in either a healthy cell or a cancer cell. Biologically, zero-inflation is expected due to of the many protein positions that are crucial for proper function, often leading to a cell that can not perform the functions necessary for life. The class of models considered is the Generalized Poisson (GP) distribution introduced by Consul and Jain (1970), with an additional zero-inflation parameter. Let T be a nonnegative integer-valued random variable where relative to Poisson model, it is overdispersed with variance to mean ratio exceeding 1. If T ~ GP(λ, θ), then the probability mass function can be written as

$$P(T=t)=g(t)=\frac{\lambda {(\lambda +\theta t)}^{t-1}}{t!}{e}^{-\lambda -\theta t}$$ (4)

where 0 ≤ θ < 1 and λ > 0. If zero is observed with a significantly higher frequency, we can include a zero-inflation parameter in (4) to characterize the distribution. Then X ~ ZIGP(η, λ, θ) and the probability that X = j, denoted by f₀(j), is

$$f_0(j)=\eta I_{\{0\}}(j)+(1-\eta )g(j)I_{\{0,1,2,\dots \}}(j)$$

where j is a nonnegative integer, 0 ≤ η < 1, 0 ≤ θ < 1 and λ > 0. The indicator function I_𝒮(j) is equal to 1 if j ∈ 𝒮 and 0 otherwise. Recently, ZIGP models have been found useful for the analysis of heavy-tailed count data with a large proportion of zeros (Famoye and Singh (2006)). The ZIGP model reduces to Zero-Inflated Poisson (ZIP) distribution when θ = 0, Generalized Poisson distribution (GP) when η = 0 and Poisson distribution when η = 0 and θ = 0. The ZIP model, first introduced by Lambert (1992), is applied when the count data possess the equality of mean and variance property while taking into consideration the structural zeros and zeros which exist by chance. Meanwhile, the Zero-Inflated Negative Binomial (ZINB) model is widely used for handling data with population heterogeneity which may be caused by the occurrence of excess zeros and the overdispersion due to unobserved heterogeneity (Phang and Loh, 2013). The rationale for choosing ZIGP as a model for f₀ was provided by Joe and Zhu (2005). They showed that ZIGP provides a better fit than ZINB when there is a large fraction of zeros and the data is heavily right-skewed. They compared the probabilistic properties of the zero-inflated variations of NB and GP distributions, such as probability mass and skewness, while keeping the first two moments fixed. Using this result, it is worthwhile to consider ZIGP rather than ZINB given that the mutation count data exhibited both features.

3.2 Estimation of f₀, f and π₀

From (3), the local FDR formulation consists of unknown quantities f₀, f, and π₀ which must be estimated accordingly. We follow the idea of “zero assumption” in Efron (2005) where f₀ is assumed to be normally distributed and Park et al. (2011) which modeled f₀ as a mixture of normal distributions.

However, since f₀ is unknown in practice, four count models will be compared in order to come up with estimates for the parameters of the null distribution. These models belong to the class of ZIGP distribution, namely, (i) ZIGP (ii) ZIP (iii) Generalized Poisson and (iv) Poisson distribution. If the true f₀ is ZIGP and the model used to estimate f₀ is ZIGP then we expect superior results compared to the other three distributions. Moreover, if the true null distribution is ZIP, then we expect better results for ZIP and ZIGP distribution compared to GP and Poisson distribution. This suggests that since ZIGP can characterize overdispersion, even if there is none such as the case of ZIP, it should still be able to capture the behavior of f₀ accurately.

To estimate the parameters of f₀ for any of these four count models, the EM Algorithm proposed by McLachlan and Jones (1988) will be utilized. For truncated data sets described in (2), fitting the model using EM algorithm is not straightforward as when all data points are available. The details of the EM Algorithm are provided in Web Appendix A.

Moreover, it is straightforward to estimate f(j) by using relative frequency given by f̂(j) = n_j/N. Using the assumption on f₀, for j ≤ C, f(j) from (1) reduces to π₀f₀(j). Hence, $\sum _{j\le C}{\pi }_0{f}_0(j)=\sum _{j\le C}f(j)$. Finally, the estimate of π₀ is min(1, π̂₀) where π̂₀ can be computed as

$${\hat{\pi }}_0=\frac{\sum _{j\le C}\hat{f}(j)}{\sum _{j\le C}{\hat{f}}_0(j)}$$

using f̂(j) = n_j/N and the estimate of f₀ after plugging in Θ̂ resulting from the EM algorithm.

3.3 Choice of the Cut-off C

In our model, we assume that we can identify a cut-off C, wherein positions with number of mutations greater than C contain more mutations than what would be expected in the null model. The choice of the cut-off C is of paramount importance since the estimation of f₀ and π₀ depend on C. It is more realistic to assume that C is unknown, so such a predetermined C may affect the result of local FDR procedure seriously. In particular, if C is predetermined and is chosen to be larger than the true value, the null distribution is estimated based on observations from alternative hypothesis as well as null hypothesis, so the estimated null distribution is contaminated by the alternative distribution. This will cause insensitivity of local FDR procedure in detecting the alternative hypothesis. On the other hand, if C is chosen to be smaller, then the null distribution is estimated only based on small values, so the estimation of the null distribution especially at the tail part is less reliable. Empirically, the FDR procedure yields liberal results in that there are too many rejections resulting in failure in controlling a given level of FDR.

The estimation of the cut-off C has been formulated using the likelihood function. Define the index sets 𝒜 = {j : j ≥ 0, n_j > 0}, 𝒜(C) = {j : 0 ≤ j ≤ C, n_j > 0, f₁(j) = 0}. Note that 𝒜(C₁) ⊂ 𝒜(C₂) for C₁ < C₂ and f(j) = π₀f₀(j) when j ∈ 𝒜(C). The likelihood function of (0, n₀), …, (K, n_K) for a given 𝒜(ν) is

$$L({\mathrm{\Theta }}^{\ast },f)=\prod _{j\le K}f{(j)}^{n_j}=\prod _{j\le \nu }{({\pi }_0{f}_0(j))}^{n_j}\prod _{j\ge \nu +1}f{(j)}^{n_j}$$

where π₀f₀ depends on Θ* = (π₀, η, θ, λ) = {π₀} ∪ Θ. The log likelihood is also

$$\text{log }L({\mathrm{\Theta }}^{\ast },f)={\ell }_{\nu }({\mathrm{\Theta }}^{\ast },f)\equiv \sum _{j\le \nu }{n}_j\text{ log}({\pi }_0{f}_0(j))+\sum _{j\ge \nu +1}{n}_j\text{ log }f(j)$$

since f(j) = π₀f₀(j) for j ∈ 𝒜(ν). This leads to

$${\ell }_{\nu }({\mathrm{\Theta }}^{\ast },f)\equiv \sum _{j\le \nu }{n}_j\text{ log}\frac{{\pi }_0{f}_0(j)}{f(j)}+\underset{{\ell }_0}{\underbrace{\sum _{j\le K}{n}_j\text{ log }f(j)}}$$

We adopt the idea of sequential testing to detect the change point in which the observations are generated from the mixture distribution f. More specifically, suppose we observed (0, n₀), (1, n₂), …, (K, n_K) sequentially from f₀(0), f₀(1), …, f₀(C), f(C + 1), …, f(K) where distribution is changed from f₀ to f at C + 1. Our goal is to detect the change point C based on assuming that we observe 0, 1, 2, …, K sequentially. For a given ν, we define S_ν(Θ, f) as

$$S_{\nu }(\mathrm{\Theta },f)=\sum _{j\le \nu }{n}_j\text{ log }{f}_0(j)+\sum _{j\ge \nu +1}{n}_j\text{ log }f(j)=\sum _{j\le \nu }{n}_j\text{ log}\frac{f_0(j)}{f(j)}+\sum _{j\le K}{n}_j\text{ log }f(j).$$

Maximizing S_ν(Θ, f) is equivalent to the CUSUM(cumulative sum) $\sum _{j\le \nu }{n}_j\text{ log}\frac{f_0(j)}{f(j)}$. Since the parameters Θ is estimated from EM algorithm and $\hat{f}(j)=\frac{n_j}{N}$, our procedure is

$$\hat{C}=\text{arg}\underset{\nu =1,2,\dots ,K}{\text{max}}{S}_{\nu }({\hat{\mathrm{\Theta }}}_{\nu })$$

where Θ̂_ν is the estimator from the EM algorithm with the value of C set to ν. One may consider the full likelihood of all observations and find out some connection between S_ν and the full likelihood presented as follows:

$$S_{\nu }({\mathrm{\Theta }}^{\ast },f)={\ell }_{\nu }({\mathrm{\Theta }}^{\ast },f)-N_{\nu }\text{ log }{\pi }_0=\sum _{j\le \nu }{n}_j({\text{lr}}_j({\mathrm{\Theta }}^{\ast },f)-\text{log }{\pi }_0)+{\ell }_0$$

where $N_{\nu }=\sum _{j\le \nu }{n}_j$ and ${\text{lr}}_j({\mathrm{\Theta }}^{\ast },f)=\text{log}\frac{{\pi }_0{f}_0(j)}{f(j)}$.

Sheetlin et al. (2011) offer an objective-change point method that can replace the subjective approaches performed by eye-balling the data. Their proposed method resembles the change-point regression and robust regression but it is tailored to estimate the change point from a transient to an asymptotic regime. Given a tuning parameter c and a criterion function ρ, depending on β, the estimator for the change point k* is defined as

$$k^{\ast }=\text{arg }\underset{k=0,1,\dots ,n}{\text{min}}(\underset{\beta }{\text{min}}\sum _{i=k+1}^n(\rho (e_i)-c))$$ (5)

where ρ(e_i) is the estimated least-squares normalized residual. In (5), there is a tuning parameter c which should be given ahead. The value of c plays the role of penalty for adding terms ρ(e_i) in (5), so the predetermined value of c affects k* arbitrarily. We see that our proposed estimation of C is related to the form (5). We estimate C via

$${\hat{C}}_1=\text{arg}\underset{\nu =1,2,\dots ,K}{\text{min}}(-S_{\nu }({\hat{\mathrm{\Theta }}}_{\nu }^{\ast },\hat{f}))=\text{arg}\underset{\nu =1,2,\dots ,K}{\text{min}}\sum _{j\in 𝒜(C)}{n}_j({\rho }_j({\hat{\mathrm{\Theta }}}_{\nu }^{\ast },\hat{f})-{\hat{c}}_{\nu })$$ (6)

where ${\hat{\mathrm{\Theta }}}_{\nu }^{\ast }=({\hat{\pi }}_{0,\nu },{\hat{\eta }}_{\nu },{\hat{\theta }}_{\nu },{\hat{\lambda }}_{\nu })$ is obtained from the EM algorithm discussed in the previous section, $\hat{f}(j)=n_j/N,{\rho }_j({\hat{\mathrm{\Theta }}}_{\nu }^{\ast },\hat{f})=-{\text{lr}}_j({\hat{\mathrm{\Theta }}}_{\nu }^{\ast },\hat{f})$ and ĉ_ν = −log π̂_0,ν. In (5), c is a predetermined value, however we don’t need to predetermine any parameter in (6). The proposed criterion (6) is related to the penalized model selection such as AIC and BIC. When we use the information that $n=\sum _{j\le C}{n}_j$ observed values are generated from $f_0,-\sum _{j\le \nu }{n}_j{\text{lr}}_j({\mathrm{\Theta }}^{\ast },f)$ is increasing in ν, there is a compromise term c = −log π₀ for each observation to compensate adding additional terms. There is a total of N_ν positions, so when we use the assumption ν = C, we consider N_ν log π₀ penalty to the log likelihood function ℓ_ν. Most of well known model selection criteria have similar forms where the penalty terms are related to penalize the complexity of models. In our context, the term −log π₀ gives penalty to using the information that j for j ≤ ν are generated from f₀. For a small value of π₀, the corresponding penalty (−log π₀) is large since a large penalty should be given to a low chance of f₀. On the other hand, if π₀ is close to 1, there becomes small risk from assuming observations are from the null hypothesis.

For the second method, we consider the extension of the methodology proposed by Efron (2007) which explicitly uses the zero assumption. This stipulates that the non-null density f₁ is supported outside some set {0, 1, …, C}. The likelihood function for x_n = (x₀, …, x_C) is defined as

$$L({\hat{\mathrm{\Theta }}}_{\nu }^{\ast }|{\mathbf{x}}_n)={\xi }^n{(1-\xi )}^{N-n}\prod _{j\le \nu }(f_0{(j))}^{n_j}$$

where $\xi ={\pi }_0\sum _{j\le C}{f}_0(j)$. The cut-off can be computed as

$${\hat{C}}_2=\text{arg}\underset{\nu =1,2,\dots ,K}{\text{min}}(-\text{log }L({\hat{\mathrm{\Theta }}}_{\nu }^{\ast }|{\mathbf{x}}_n))$$ (7)

3.4 Modification of local FDR by truncation

In practice, if a given domain position has a large number of mutations, then these mutations are expected to be significant. In many cases, there are relatively few positions in a protein domain where large values of mutations can be observed. This indicates that for large values of j, estimation of f based on relative frequency is not accurate due to the sparse data in the tail part. Consequently, the estimated local FDR is not reliable since it depends on the estimator of f. Rather than testing significance based on inaccurate local FDRs from large mutation counts, we consider a screening process so that the number of mutations exceeding a certain value should be considered as significant mutations. Such a critical value will be decided depending on the estimated null distribution. When we have observations a_i for 1 ≤ i ≤ N generated from the null distribution, we are interested in figuring out D_N such that

$$P_{H_0}(\underset{1\le i\le N}{\text{max}}{a}_i<D_N)\to 1$$ (8)

as N → ∞. Once a sequence D_N is identified, a_i(≥ D_N) is hardly observed under the null hypothesis, so the corresponding null hypothesis is rejected directly rather than making decision based on local FDR procedure. There are many choices of D_N, but a smaller sequence of D_N satisfying (8) is of our interest since any sequence B_N satisfying B_N > D_N also satisfies the property. The details of the calculation of D_N are provided in Web Appendix B.

The calculation of D_N when f₀ is modeled using ZIGP or Generalized Poisson is similar since the derivation will eventually yield leading terms which does not involve η. Likewise, the calculation of D_N when f₀ is modeled using either ZIP or Poisson is the same. On the other hand, since the true values of the parameters λ and θ are unknown, we calculate D_N using the estimates λ̂ and θ̂. Hence, D_N can be calculated as

$$D_N=\lceil \text{max }({𝒟}_1,{𝒟}_2)\rceil$$ (9)

where ⌈x⌉ is the smallest integer greater than or equal to x(x > 0). 𝒟₁ and 𝒟₂ are presented in Web Supplementary Materials (Web Appendix B) where 𝒟₁ is a function of λ̂ and θ̂ and 𝒟₂ is a function of θ̂ when f₀ is modeled using ZIGP or Generalized Poisson distribution. When f₀ is modeled using ZIP or Poisson distribution, 𝒟₁ is a function of λ̂ only while 𝒟₂ does not depend on any parameter estimate. Finally, the proposed Two-Stage procedure can be summarized into two stages:

Two-Stage Procedure

1. Stage 1(Screening Step): Based on Ĉ (either Ĉ₁ in (6) or Ĉ₂ in (7), estimate ${\hat{\mathrm{\Theta }}}_{\hat{C}}^{\ast }$ and compute D̂_N in (9). To incorporate this condition in the formulation of D_N, we have

   $$D_N(\hat{C})=\lceil \text{max }(D_N,\hat{C}+1)\rceil .$$ (10)

   We reject the H_0j if j ≥ D_N (Ĉ) and do not reject if j ≤ Ĉ.
2. Stage 2 (Testing step): For Ĉ + 1 ≤ j < D_N (Ĉ), we calculate the local FDR given by

   $$\widehat{\mathit{\text{fdr}}}(j)=\frac{{\hat{\pi }}_{0,\hat{C}}{\hat{f}}_0(j;{\hat{\mathrm{\Theta }}}_{\hat{C}})}{\hat{f}(j)}.$$ (11)

   We reject the H_0j if $\widehat{\mathit{\text{fdr}}}(j)\le \alpha$.

Note that D̂_N (Ĉ) in (10) shows Ĉ + 1 ≤ D_N (Ĉ). In particular, the Stage 2 of testing step is not necessary when D_N (Ĉ) = Ĉ + 1.

4. Numerical Studies

4.1 Simulation Studies

To gain insights regarding the robustness of the proposed procedures in the presence of model misspecification, we perform some simulation studies. The comparison is based on four simulation boundaries: (i) model for the estimation of f₀; (ii) method used in the choice of the cut-off C; (iii) true null distribution; and (iv) non-null distribution used in data generation. There are four models compared for the estimation of f₀ as discussed in Section 3.2. Also, there are two methods presented in Section 3.3 for the choice of cut-off C. The true null distributions considered are Zero-Inflated Poisson (ZIP) and Zero-Inflated Generalized Poisson (ZIGP) distribution. Both distributions account for the excessive number of zeros which is a characteristic of the mutation count data. Following the key assumption on f₀, the support of f₁ does not contain values in [0, C]. Hence, f₁ can be expressed as f₁ = C + 1 + W where W follows another count model. For the model specification of W, Geometric(p = 0.08) and Binomial(n = 250, p = 0.20) distribution are utilized. They exhibit the pattern of the mutation count observed in the real data set.

Using these model specifications in terms of the true f₀ and f₁, there are 15 mixture models considered for data generation as presented in Web Table 1. For each of the specification of f₀, Ĉ is calculated and the corresponding set of parameter estimates ${\hat{\mathrm{\Theta }}}_{\hat{C}}^{\ast }=({\hat{\eta }}_{\hat{C}},{\hat{\lambda }}_{\hat{C}},{\hat{\theta }}_{\hat{C}},{\hat{\pi }}_{0,\hat{C}})$ from EM Algorithm are obtained. Results show that regardless of the true null distribution, if f₀ is modeled using the ZIGP distribution, then Ĉ produces the most accurate estimate for C in terms of the bias and standard error. This validates the robustness of ZIGP as a model for f₀, that is, even if the true null distribution is ZIP, the most accurate estimate of Ĉ can still be observed when f₀ is modeled using ZIGP. The bias of the parameter estimates for each of these specifications are presented in Web Tables 2 – 5 in the Supplementary Materials.

A total of L hypotheses tests were performed for independent random variables n_j over 1000 replications. For each replication, the proportion of n_j from the null distribution is set to be π₀ and the total number of positions N is specified to be 1000. To calculate the False Discovery Rate, $\widehat{\mathit{\text{FDR}}}$, for the kth generated data, k = 1, 2, …, 1000, we compute the False Discovery Proportion (FDP) which is defined by

$${\mathit{\text{FDP}}}_k=\frac{V_k}{R_k}I(R_k>0)$$

where V_k and R_k are the number of falsely rejected hypotheses (false discoveries) and the total number of rejected hypotheses in the kth generated data, respectively. FDR is the expected value of the false discovery proportion and can be computed empirically as

$$\widehat{\mathit{\text{FDR}}}=\frac{1}{1000}\sum _{k=1}^{1000}\frac{V_k}{R_k}I(R_k>0)$$

In our simulations, the decision rule is to reject the null H_0j if $\widehat{\mathit{\text{fdr}}}(j)={\hat{\pi }}_0{\hat{f}}_0(j)/\hat{f}(j)\le \alpha$. Throughout the simulations, we consider the level of significance α = 0.05. The True Positive Rate, $\widehat{\mathit{\text{TPR}}}$ is computed empirically as

$$\widehat{\mathit{\text{TPR}}}=\frac{1}{1000}\sum _{k=1}^{1000}\left(\frac{S_k}{S_k+T_k}\right)$$

where S_k and T_k are the number of correctly rejected hypotheses (true discoveries) and the number of falsely accepted hypotheses (false non-discoveries) in the kth generated data, respectively. Three procedures are compared in terms of controlling $\widehat{\mathit{\text{FDR}}}$ and the value of $\widehat{\mathit{\text{TPR}}}$, namely the one-stage local FDR procedure, the proposed two-stage procedure and Storey’s procedure. The results which yields the superior $\widehat{\mathit{\text{TPR}}}$ while controlling FDR are highlighted using bold face quantities.

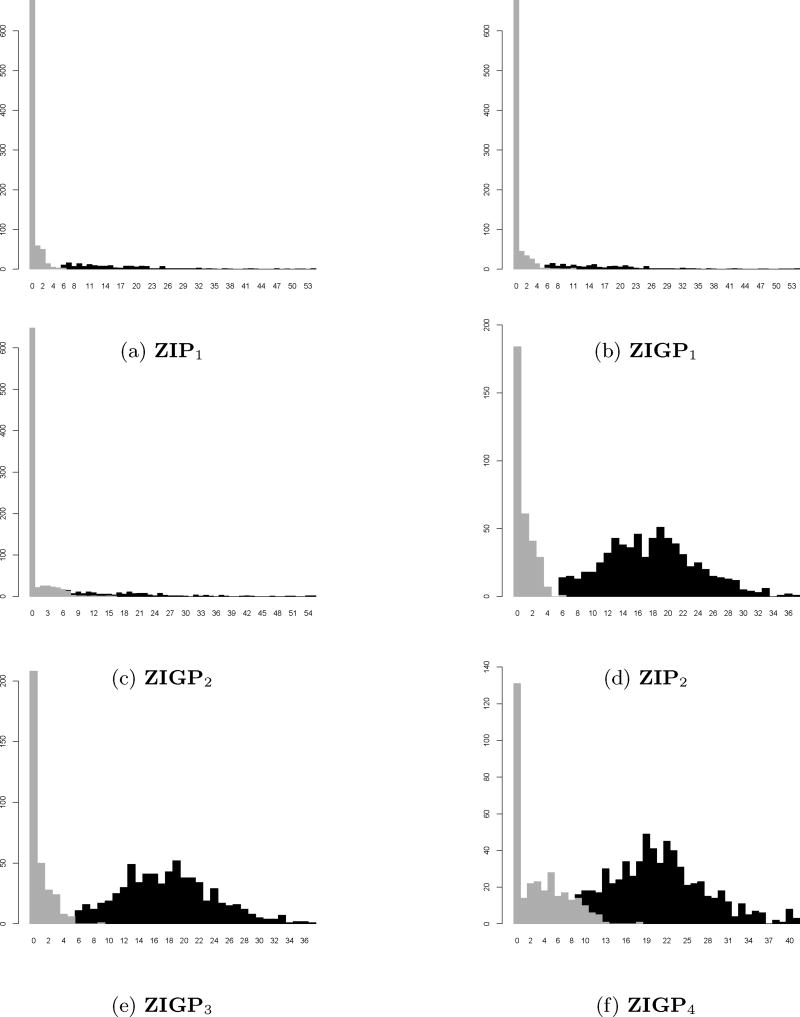
As displayed in Figure 1 (a)–(c), the non-null distribution is Geometric, the proportion of null cases is 0.80 and the fraction of zeros is 0.80. The degree to which the null model is mixed with the non-null model is described using the three cases. ZIP₁ represents the well-separated case, ZIGP₁ is the moderately mixed case while ZIGP₂ can be described as the heavily mixed case. The corresponding numerical comparison is shown in Table 1.

Figure 1.

Histogram of different scenarios for comparison when C = 5. (a) The first panel in the first row: f₀ is ZIP₁(η = 0.80, λ = 1.5) which represents the well-separated case, f₁ is shifted Geometric(p = 0.08), π₀ = 0.80 (b) The second panel in the first row: f₀ is ZIGP₁(η = 0.80, λ = 1.5, θ = 0.3) which represents the moderately mixed case, f₁ is shifted Geometric(p = 0.08), π₀ = 0.80 (c) The first panel in the third row: f₀ is ZIGP₂(η = 0.80, λ = 3, θ = 0.3) which represents the heavily mixed case, f₁ is shifted Geometric(p = 0.08), π₀ = 0.80 (d) The second panel in the second row: f₀ is ZIP₂(η = 0.40, λ = 1.5) which represents the well-separated case, f₁ is shifted Binomial(n = 250, p = 0.20), π₀ = 0.35 (e) The first panel in the third row: f₀ is ZIGP₃(η = 0.40, λ = 1, θ = 0.20) which represents the moderately mixed case, f₁ is shifted Binomial(n = 250, p = 0.20), π₀ = 0.35 (f) The second panel in the third row: f₀ is ZIGP₄(η = 0.40, λ = 3, θ = 0.20) which represents the heavily mixed case, f₁ is shifted Binomial(n = 250, p = 0.20), π₀ = 0.35.

Table 1.

Numerical Comparison when f₁ is shifted Geometric(p = 0.08), π₀ = 0.80 and C = 5. ZIP₁ (η = 0.80, λ = 1.5) represents the well-separated case, ZIGP₁ (η = 0.80, λ = 1.5, θ = 0.3) represents the moderately mixed case, and ZIGP₂ (η = 0.80, λ = 3, θ = 0.3) represents the heavily mixed case. The number in (·) corresponds to the standard error.

			Two-Stage Procedure			One-Stage Procedure			Storey’s FDR
True f0	Choice of C	Model for f0	R	$\widehat{\mathit{\text{FDR}}}$	$\widehat{\mathit{\text{TPR}}}$	R	$\widehat{\mathit{\text{FDR}}}$	$\widehat{\mathit{\text{TPR}}}$	R	$\widehat{\mathit{\text{FDR}}}$	$\widehat{\mathit{\text{TPR}}}$
ZIP1	Ĉ1	ZIGP	200.91 (12.86)	0.0042 (0.0064)	1.000 (0.000)	187.88 (13.58)	0.0009 (0.0023)	0.938 (0.025)	182.91 (13.90)	0.0005 (0.0017)	0.914 (0.037)
		ZIP	198.27 (14.20)	0.0027 (0.0040)	0.988 (0.024)	198.25 (14.23)	0.0027 (0.0040)	0.988 (0.024)	191.89 (14.65)	0.0017 (0.0035)	0.957 (0.037)
		GP	0.16 (4.93)	0.0000 (0.0000)	0.001 (0.032)	0.14 (4.46)	0.0000 (0.0000)	0.001 (0.029)	0.14 (4.46)	0.0000 (0.0000)	0.001 (0.029)
		P	236.75 (20.21)	0.1513 (0.0623)	1.000 (0.000)	236.75 (20.21)	0.1513 (0.0623)	1.000 (0.000)	219.30 (13.99)	0.0864 (0.0486)	1.000 (0.000)
	Ĉ2	ZIGP	198.76 (14.51)	0.0041 (0.0058)	0.989 (0.027)	182.28 (15.11)	0.0005 (0.0017)	0.911 (0.037)	174.85 (13.99)	0.0003 (0.0013)	0.874 (0.038)
		ZIP	195.41 (14.47)	0.0023 (0.0038)	0.974 (0.032)	194.73 (15.05)	0.0023 (0.0038)	0.971 (0.039)	188.65 (15.78)	0.0014 (0.0034)	0.942 (0.049)
		GP	0.16 (5.03)	0.0189 (0.0000)	0.001 (0.032)	0.14 (4.46)	0.0000 (0.0000)	0.001 (0.029)	0.14 (4.46)	0.0000 (0.0000)	0.001 (0.029)
		P	236.75 (20.21)	0.1513 (0.0623)	1.000 (0.000)	236.75 (20.21)	0.1513 (0.0623)	1.000 (0.000)	219.30 (13.99)	0.0864 (0.0486)	1.000 (0.000)
ZIGP1	Ĉ1	ZIGP	194.00 (39.02)	0.0420 (0.0207)	0.928 (0.175)	179.77 (36.31)	0.0278 (0.0153)	0.878 (0.164)	170.23 (31.40)	0.0202 (0.0125)	0.834 (0.144)
		ZIP	208.30 (15.30)	0.0523 (0.0211)	0.986 (0.027)	208.12 (15.58)	0.0521 (0.0213)	0.986 (0.028)	198.94 (16.93)	0.0416 (0.0200)	0.952 (0.044)
		GP	0.00 (0.00)	0.0000 (0.0000)	0.000 (0.000)	0.00 (0.00)	0.0000 (0.0000)	0.000 (0.000)	0.00 (0.00)	0.0000 (0.0000)	0.000 (0.000)
		P	258.86 (17.02)	0.2255 (0.0472)	1.000 (0.000)	258.86 (17.02)	0.2255 (0.0472)	1.000 (0.000)	242.28 (16.01)	0.1728 (0.0463)	1.000 (0.000)
	Ĉ2	ZIGP	185.10 (53.98)	0.0393 (0.0217)	0.887 (0.250)	171.67 (50.08)	0.0262 (0.0158)	0.840 (0.235)	163.25 (43.65)	0.0192 (0.0125)	0.801 (0.207)
		ZIP	207.31 (15.76)	0.0513 (0.0215)	0.982 (0.030)	206.48 (16.89)	0.0507 (0.0222)	0.979 (0.038)	197.00 (18.50)	0.0399 (0.0206)	0.944 (0.053)
		GP	0.00 (0.00)	0.0000 (0.0000)	0.000 (0.000)	0.00 (0.00)	0.0000 (0.0000)	0.000 (0.000)	0.00 (0.00)	0.0000 (0.0000)	0.000 (0.000)
		P	258.86 (17.02)	0.2255 (0.0472)	1.000 (0.000)	258.86 (17.02)	0.2255 (0.0472)	1.000 (0.000)	242.28 (16.01)	0.1728 (0.0463)	1.000 (0.000)
ZIGP2	Ĉ1	ZIGP	50.36 (72.57)	0.0184 (0.0341)	0.237 (0.335)	50.23 (72.40)	0.0182 (0.0339)	0.237 (0.335)	58.05 (62.16)	0.0148 (0.0274)	0.279 (0.290)
		ZIP	227.11 (19.67)	0.1581 (0.0361)	0.954 (0.032)	211.90 (32.17)	0.1340 (0.0532)	0.916 (0.072)	192.28 (26.79)	0.1032 (0.0428)	0.858 (0.073)
		GP	19.35 (71.88)	0.3140 (0.0401)	0.068 (0.252)	16.45 (61.04)	0.1946 (0.0264)	0.068 (0.252)	14.35 (53.25)	0.1483 (0.0228)	0.063 (0.232)
		P	313.13 (16.02)	0.3606 (0.0349)	1.000 (0.000)	313.14 (16.00)	0.3605 (0.0349)	1.000 (0.000)	310.41 (15.11)	0.3553 (0.0296)	1.000 (0.000)
	Ĉ2	ZIGP	43.52 (70.04)	0.0161 (0.0324)	0.204 (0.323)	43.40 (69.87)	0.0159 (0.0321)	0.204 (0.323)	51.71 (60.28)	0.0129 (0.0261)	0.248 (0.281)
		ZIP	226.97 (19.68)	0.1579 (0.0360)	0.953 (0.032)	206.83 (35.94)	0.1266 (0.0580)	0.901 (0.086)	188.93 (29.37)	0.0987 (0.0461)	0.846 (0.083)
		GP	19.66 (72.92)	0.3258 (0.0258)	0.068 (0.252)	16.45 (61.04)	0.1946 (0.0264)	0.068 (0.252)	14.35 (53.25)	0.1483 (0.0228)	0.063 (0.232)
		P	313.13 (16.02)	0.3606 (0.0349)	1.000 (0.000)	313.14 (16.00)	0.3605 (0.0349)	1.000 (0.000)	310.41 (15.11)	0.3553 (0.0296)	1.000 (0.000)

Based upon the results of Table 1, since null and non-null distribution is moderately mixed for ZIGP₁, the resulting $\widehat{\mathit{\text{TPR}}}$ for all three procedures is substantially higher than the $\widehat{\mathit{\text{TPR}}}$ for ZIGP₂, regardless of the model used for the estimation of f₀. Given that $\widehat{\mathit{\text{FDR}}}$ is controlled in all procedures, if the model for f₀ is ZIGP, then the Two-Stage procedure yields the highest $\widehat{\mathit{\text{TPR}}}$.

This suggests that the proposed procedure is better than the other existing procedures. Meanwhile, due to the “well-separation” if the true null is ZIP₁, then the $\widehat{\mathit{\text{TPR}}}$ for ZIP₁ is slightly higher than the $\widehat{\mathit{\text{TPR}}}$ for ZIGP₁. Moreover, the $\widehat{\mathit{\text{FDR}}}$ for all three procedures for ZIP₁ are noticeably lower than the $\widehat{\mathit{\text{FDR}}}$ for ZIGP₁. This means that the number of rejections for ZIGP₁ and ZIP₁ are almost the same but there are more erroneous rejections for ZIGP₁. This result can be explained by the presence of overdispersion in ZIGP₁, thereby suggesting that the presence of overdispersion in the data could lead to erroneous rejections. Overall, there are more rejections using Ĉ₁ as a cut-off compared to Ĉ₂. Also, even if Ĉ₁ yields more rejections, it still controls the value of FDR demonstrating the superiority of Ĉ₁ as a cut-off method.

Figure 1 (d) – (f) also presents the histograms when the non-null distribution is Binomial, the proportion of null cases is 0.35 and the fraction of zeros is 0.40. Unlike the parametrization of the Geometric non-null distribution which appears to be skewed to the right, this f₁ exhibits near symmetry. In terms of the mixing of the null and non-null distribution, ZIP₂ represents the well-separated case, ZIGP₃ is the moderately mixed case while ZIGP₄ can be described as the heavily mixed case. The numerical comparison is shown in Table 2.

Table 2.

Numerical Comparison when f₁ is shifted Binomial(n = 250, p = 0.20), π₀ = 0.35 and C = 5. ZIP₂ (η = 0.40, λ = 1.5) is the well-separated case, ZIGP₃ (η = 0.40, λ = 1, θ = 0.30) represents the moderately mixed case, and ZIGP₄ (η = 0.40, λ = 4, θ = 0.30) represents the heavily mixed case. The number in (·) represents the standard error.

			Two-Stage Procedure			One-Stage Procedure			Storey’s FDR
True f0	Choice of C	Model for f0	R	$\widehat{\mathit{\text{FDR}}}$	$\widehat{\mathit{\text{TPR}}}$	R	$\widehat{\mathit{\text{FDR}}}$	$\widehat{\mathit{\text{TPR}}}$	R	$\widehat{\mathit{\text{FDR}}}$	$\widehat{\mathit{\text{TPR}}}$
ZIP2	Ĉ1	ZIGP	643.15 (15.32)	0.0015 (0.0016)	1.000 (0.001)	631.41 (16.20)	0.0003 (0.0007)	0.983 (0.007)	632.95 (16.00)	0.0003 (0.0008)	0.985 (0.007)
		ZIP	635.66 (16.68)	0.0006 (0.0012)	0.989 (0.007)	635.62 (16.71)	0.0006 (0.0012)	0.989 (0.007)	638.45 (16.96)	0.0009 (0.0013)	0.993 (0.008)
		GP	1.85 (9.24)	0.0000 (0.0000)	0.003 (0.014)	1.85 (9.24)	0.0000 (0.0000)	0.003 (0.014)	123.76 (39.52)	0.0000 (0.0000)	0.192 (0.060)
		P	644.35 (15.21)	0.0033 (0.0046)	1.000 (0.000)	644.35 (15.21)	0.0033 (0.0046)	1.000 (0.000)	646.02 (15.23)	0.0058 (0.0039)	1.000 (0.000)
	Ĉ2	ZIGP	620.41 (99.01)	0.0018 (0.0022)	0.964 (0.152)	608.78 (96.45)	0.0002 (0.0006)	0.948 (0.148)	614.49 (78.24)	0.0003 (0.0007)	0.956 (0.119)
		ZIP	636.53 (16.41)	0.0007 (0.0012)	0.990 (0.008)	635.35 (17.29)	0.0007 (0.0012)	0.988 (0.011)	637.63 (16.87)	0.0009 (0.0015)	0.992 (0.010)
		GP	0.37 (3.96)	0.0000 (0.0000)	0.001 (0.006)	0.37 (3.96)	0.0000 (0.0000)	0.001 (0.006)	106.13 (35.67)	0.0000 (0.0000)	0.165 (0.054)
		P	644.79 (15.23)	0.0039 (0.0049)	1.000 (0.000)	644.79 (15.23)	0.0039 (0.0049)	1.000 (0.000)	646.31 (15.22)	0.0063 (0.0039)	1.000 (0.000)
ZIGP3	Ĉ1	ZIGP	636.30 (58.87)	0.0098 (0.0046)	0.981 (0.087)	622.87 (56.55)	0.0054 (0.0033)	0.965 (0.084)	623.14 (60.60)	0.0057 (0.0034)	0.965 (0.091)
		ZIP	642.91 (16.71)	0.0086 (0.0048)	0.993 (0.008)	642.87 (16.73)	0.0086 (0.0048)	0.993 (0.008)	643.98 (16.84)	0.0090 (0.0047)	0.994 (0.008)
		GP	0.14 (2.55)	0.0000 (0.0000)	0.000 (0.004)	0.14 (2.55)	0.0000 (0.0000)	0.000 (0.004)	77.54 (27.75)	0.0000 (0.0000)	0.120 (0.042)
		P	659.04 (15.45)	0.0259 (0.0111)	1.000 (0.000)	659.04 (15.45)	0.0259 (0.0111)	1.000 (0.000)	657.95 (15.54)	0.0243 (0.0098)	1.000 (0.000)
	Ĉ2	ZIGP	506.01 (185.12)	0.0064 (0.0061)	0.782 (0.283)	497.86 (178.91)	0.0036 (0.0037)	0.772 (0.276)	509.59 (158.92)	0.0037 (0.0040)	0.790 (0.244)
		ZIP	648.00 (15.92)	0.0110 (0.0056)	0.998 (0.005)	647.92 (15.97)	0.0110 (0.0056)	0.998 (0.005)	649.10 (16.06)	0.0125 (0.0063)	0.998 (0.005)
		GP	0.00 (0.00)	0.0000 (0.0000)	0.000 (0.000)	0.00 (0.00)	0.0000 (0.0000)	0.000 (0.000)	68.95 (25.35)	0.0000 (0.0000)	0.107 (0.038)
		P	659.07 (15.49)	0.0259 (0.0111)	1.000 (0.000)	659.07 (15.49)	0.0259 (0.0111)	1.000 (0.000)	658.00 (15.60)	0.0244 (0.0098)	1.000 (0.000)
ZIGP4	Ĉ1	ZIGP	256.82 (230.14)	0.0086 (0.0157)	0.390 (0.345)	256.80 (230.15)	0.0086 (0.0157)	0.390 (0.345)	352.65 (163.87)	0.0092 (0.0155)	0.538 (0.241)
		ZIP	671.07 (33.70)	0.0724 (0.0264)	0.964 (0.026)	582.86 (34.91)	0.0257 (0.0125)	0.877 (0.061)	588.60 (38.89)	0.0271 (0.0112)	0.888 (0.052)
		GP	0.04 (1.20)	0.0000 (0.0000)	0.000 (0.002)	0.04 (1.20)	0.0000 (0.0000)	0.000 (0.002)	90.70 (27.57)	0.0001 (0.0013)	0.140 (0.042)
		P	794.02 (15.34)	0.1876 (0.0184)	1.000 (0.000)	794.02 (15.34)	0.1876 (0.0184)	1.000 (0.000)	772.11 (16.62)	0.1645 (0.0179)	1.000 (0.000)
	Ĉ2	ZIGP	132.44 (147.29)	0.0024 (0.0094)	0.203 (0.221)	132.41 (147.28)	0.0024 (0.0094)	0.203 (0.221)	257.84 (108.30)	0.0028 (0.0096)	0.397 (0.160)
		ZIP	712.98 (16.66)	0.1051 (0.0122)	0.989 (0.010)	650.62 (40.86)	0.0585 (0.0239)	0.949 (0.046)	645.79 (38.80)	0.0546 (0.0199)	0.946 (0.039)
		GP	0.00 (0.00)	0.0000 (0.0000)	0.000 (0.000)	0.00 (0.00)	0.0000 (0.0000)	0.000 (0.000)	79.22 (27.18)	0.0001 (0.0014)	0.123 (0.041)
		P	794.02 (15.34)	0.1876 (0.0184)	1.000 (0.000)	794.02 (15.34)	0.1876 (0.0184)	1.000 (0.000)	772.11 (16.62)	0.1645 (0.0179)	1.000 (0.000)

According to Table 2, when f₀ is modeled using ZIGP, using Ĉ₁ as a cut-off yielded many more rejections, regardless of the procedure used. This suggests that the extension of Efron’s method is conservative and would miss significant positions. The difference between Ĉ₁ and Ĉ₂ is further highlighted for ZIGP₄, where the true null distribution is heavily mixed with the non-null distribution and overdispersion is present. For scenarios where $\widehat{\mathit{\text{FDR}}}$ is controlled for ZIP₂ and ZIGP₃, using Two-Stage procedure leads to the highest $\widehat{\mathit{\text{TPR}}}$. However, for ZIGP₄ where overdispersion is evident and f₀ is heavily mixed with f₁, the value of $\widehat{\mathit{\text{TPR}}}$ is substantially higher using Storey’s procedure, while keeping the $\widehat{\mathit{\text{FDR}}}$ controlled.

Another scenario considered is when the true non-null distribution is Geometric, the proportion of null cases is 0.85 but the fraction of zeros is 0.40. Unlike the scenario presented in Table 1 and Figure 1, the specified proportion of zeros is reduced to half. The interest is to determine whether there would be a change in pattern should there be a significant decrease in the number of positions without a mutation. The histograms and the corresponding numerical comparison are presented in Web Figure 1 and Web Table 6 in the Supplementary section. It can be noted that regardless of the magnitude of the fraction of zeros, a similar pattern can be observed in terms of the superiority of Ĉ₁ as a method for choosing C. Among the procedures, the $\widehat{\mathit{\text{TPR}}}$ is consistently highest for the Two-Stage procedure, given that the $\widehat{\mathit{\text{FDR}}}$ is controlled. Also, even if the true model is ZIP, using ZIGP to model f₀ produced better results in terms of $\widehat{\mathit{\text{TPR}}}$, while keeping $\widehat{\mathit{\text{FDR}}}$ controlled.

Finally, the last scenario considered is when the non-null distribution is Binomial, the fraction of zeros is still 0.40 but the proportion of null cases is increased to 0.80. When the true f₀ exhibits near symmetry, the goal is to determine whether there would be a change in pattern should there be a significant increase in the number of positions without a mutation. The histograms and the corresponding numerical comparison are presented in Web Figure 2 and Web Table 7 in the Supplementary section. Results revealed that the difference between Ĉ₁ and Ĉ₂ is apparent when there is overdispersion and f₀ is heavily mixed with f₁. If ZIGP is the model used for the estimation of f₀, the value of $\widehat{\mathit{\text{TPR}}}$ is substantially higher using Ĉ₁, while keeping the $\widehat{\mathit{\text{FDR}}}$ controlled. Moreover, the resulting $\widehat{\mathit{\text{TPR}}}$ for the moderately mixed case is substantially higher than the $\widehat{\mathit{\text{TPR}}}$ for the heavily mixed case, regardless of the model used for the estimation of f₀ and the procedure employed. However, given that $\widehat{\mathit{\text{FDR}}}$ is controlled by specifying either of the two models, using ZIGP leads to a higher $\widehat{\mathit{\text{TPR}}}$ than when the true model ZIP is specified. This result implies using ZIGP would yield satisfactory results even under model misspecification.

Taking everything into account, for the well-separated and moderately mixed case, if the null model is correctly specified and $\widehat{\mathit{\text{FDR}}}$ is controlled, using the Two-Stage procedure yields $\widehat{\mathit{\text{FDR}}}$ closest to the nominal level α. Consequently, the Two-Stage procedure is superior in terms $\widehat{\mathit{\text{TPR}}}$ in most cases. If the true null model is ZIGP and the null model is correctly specified, $\widehat{\mathit{\text{FDR}}}$ is controlled in all procedures. However, the Two-Stage procedure is better than the local FDR procedure and Storey’s procedure in terms of $\widehat{\mathit{\text{TPR}}}$. It can also be noted that if the true model is ZIP and ZIGP is used to model the null distribution, then the Two-Stage Procedure still yields the closest $\widehat{\mathit{\text{FDR}}}$ to α and leads to higher $\widehat{\mathit{\text{TPR}}}$ as compared to the other procedures. This implies using the Two-Stage Procedure when the null model is misspecified would still produce satisfactory results. Moreover, regardless of the shape of the non-null distribution, the Two-Stage Procedure yields better results than the other procedures.

Additionally, the condition (2) can be weakened so that mutation counts belonging in [0, C] can be contaminated by f₁ with probability close to zero. In fact, if there are alternative observations below C, then the true C is changed to be a smaller value (say C′) where all observations below C′ are actually from f₀. Intuitively, we can posit that this may affect the estimates of null parameters and the TPR. To address this concern, we perform additional simulation studies using C = 1 which represents that small values of data can be observed from the alternative. The bias and standard error of the parameter estimates are provided in Web Tables 8 to 11. Results show that the estimates of null parameters tend to have large biases and standard errors compared to those for C = 5 in Web Tables 2 to 7. Furthermore, the corresponding numerical comparisons of FDR and TPR were also provided in Web Tables 12 to 15. When there are alternative observations for a small value of C, the situations become more heavily mixed case, so this results in lower TPR while FDRs are still controlled.

4.2 Application to Protein Domain Data

In the study of cancer at the molecular level, it is important to understand which somatic mutations contribute to tumor initiation or progression in order to develop new treatments or to identify patients for which a given treatment will be effective. In this field, some researchers focus on the patterns of somatic variants on protein domains due to the well-defined function and structure of these units, which can lead to a better understanding of how these functions are disrupted in cancer (Nehrt et al., 2012; Peterson et al., 2010). Here, one interesting issue is identifying “protein domain hotspots”, or positions within domains that are found to be mutated frequently (Peterson et al., 2012). It is among a fixed number of positions in a single domain, which ones are significantly different from the majority.

In application to cancer, Peterson et al. (2012) discovered that known cancer variants tended to cluster at specific positions more than variants involved with unrelated diseases, suggesting that protein domain hotspots could be useful in understanding the molecular mechanisms involved with cancer. It is a novel solution for the application of protein domain hotspots to somatic variants in sequenced tumor samples, which has the potential to distinguish between driver variants that contribute to cancer and passenger variants that do not contribute and are assumed to be distributed randomly.

As an example, we analyze the mutation data obtained from the tumors of 5,848 patients from The Cancer Genome Atlas (TCGA) data portal (http://tcga-data.nci.nih.gov/tcga/, Collins and Barker, 2007). These were mapped to specific positions within protein domain models to identify clusters. TCGA MAF files were obtained for 20 cancer types.

Among several hundreds of domains, we focus on six functionally well-known domains to identify the hotspots of somatic variants in TCGA sequenced tumor samples. We start with the hotspots on growth factors (cd00031), which are known to harbor reoccurring somatic mutations involved with clonal expansion, invasion across tissue barriers, and colonization of distant niches (Jeanes et al., 2008). Furthermore, protein kinases (cd00180) and RAS-Like GTPase family of genes (cd00882) are well-known for their role in regulating pathways important to cancer (Tsatsanis and Spandidos, 2000). Genes with kinases or RAS-like GTPases are expected to harbor driver mutations that reoccur at specific sites since they are classic examples of proto-oncogenes that mutate into oncogenes, contributing to cancer (Anderson et al., 1992). Additionally, we identify hotspots on ankyrin domains (cd00204), which play a role in mediating protein-protein interactions important in cancer (Imaoka et al., 2014). Also, we find hotspots on transmembrane domains of proteins that are known to be involved with signal transduction, which is relevant in controlling processes involved with cancer (Sever and Brugge, 2015) and experimental evidence confirms the important regulatory role played by membrane proteins in cancer Neuhaus et al., 2009).

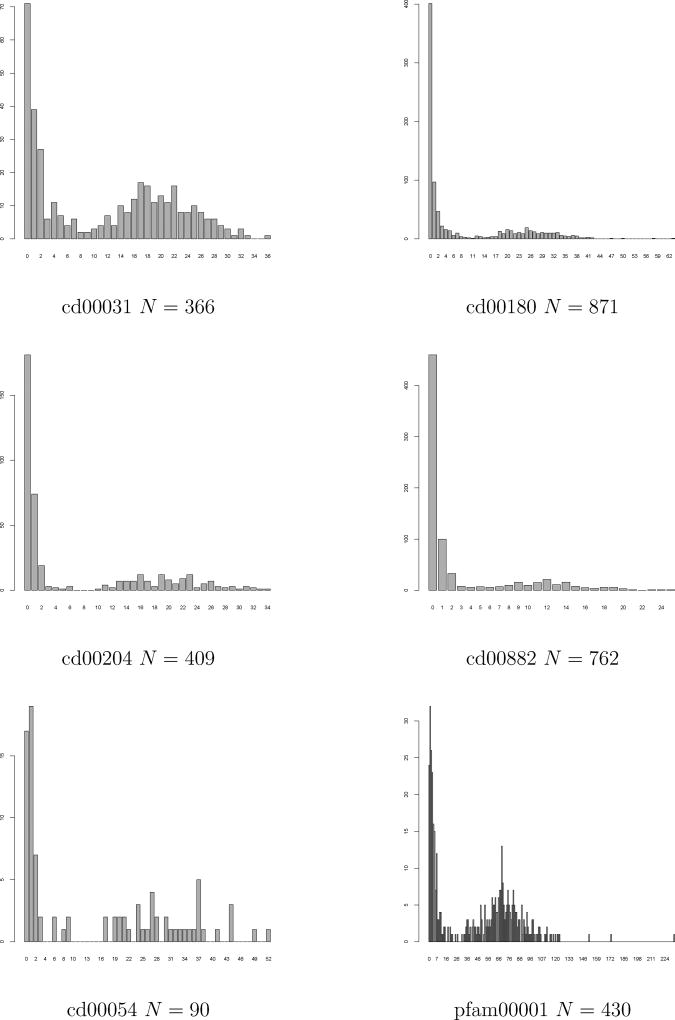
Since the mutation counts are discrete, we apply our proposed method based on various discrete models, such as ZIGP, ZIP, Generalized Poisson and Poisson distribution for f₀. The estimated parameters based on those models are reported in Web Table 16 in the Supplementary Section. Figure 2 shows the distribution of each protein domain and its total number of positions. In order to assess the general goodness-of-fit using these different parametric models, we estimate the probabilities for a_i ≤ Ĉ and compared these estimated values with relative frequencies. The results are presented in Web Figures 7 to 12 in the Web Supplementary Materials.

Figure 2.

Histogram of Protein Domain Data

The identified number of positions which are mutated differently from expected are in Table 3. For example, when assume that f₀ follows ZIGP, the results show that the identified hotspots on growth factor domain (cd00031) based on One-stage and Two-stage procedures are 143 positions among a total of 366 positions, using Ĉ₂. On the other hand, the local FDR with Ĉ₁ identifies more hotspots for Two-stage procedure (201) than One-stage (191) and Storey’s procedure (200). The rest of the domains can be analyzed in the similar manner.

Table 3.

Comparison of Number of Rejections for Protein Domain Data

		One-Stage Procedure				Two-Stage Procedure				Storey’s FDR
Data	Method	ZIGP	ZIP	GP	P	ZIGP	ZIP	GP	P	ZIGP	ZIP	GP	P
cd00031	Ĉ1	191	212	140	212	201	212	141	212	200	211	154	211
	Ĉ2	143	205	16	212	143	205	17	212	162	204	85	211
cd00054	Ĉ1	45	45	42	45	45	45	42	45	25	25	25	25
	Ĉ2	45	45	26	45	45	45	26	45	25	25	20	25
cd00180	Ĉ1	254	288	0	304	268	288	1	304	254	270	5	284
	Ĉ2	63	288	0	304	63	288	1	304	122	284	0	284
cd00204	Ĉ1	129	130	19	130	129	130	20	130	125	128	60	128
	Ĉ2	129	130	12	130	130	130	13	130	125	128	52	128
cd00882	Ĉ1	148	155	148	169	155	155	155	169	147	154	147	160
	Ĉ2	148	155	148	169	161	155	155	169	147	154	147	160
pfam00001	Ĉ1	255	340	253	341	255	405	253	403	242	206	240	204
	Ĉ2	55	340	57	341	55	405	57	403	177	206	174	204

Results from Table 3 revealed that using Ĉ₁ yields more rejections. This suggests that the data analysis for the real data shows the same pattern as the simulation results presented previously. Moreover, two domains can be highlighted in terms of the difference in the number of rejections, namely, cd00180 and pfam00001. The number of rejections using Ĉ₁ is almost four times higher if the model used for f₀ is ZIGP and the procedure employed is either local FDR or Two-stage method. For both of these data sets, the number of rejections using Ĉ₁ is almost twice compared to Ĉ₂ given that the model for f₀ is ZIGP and using Storey’s FDR. Overall, the results for the real data analysis is consistent with the simulation studies.

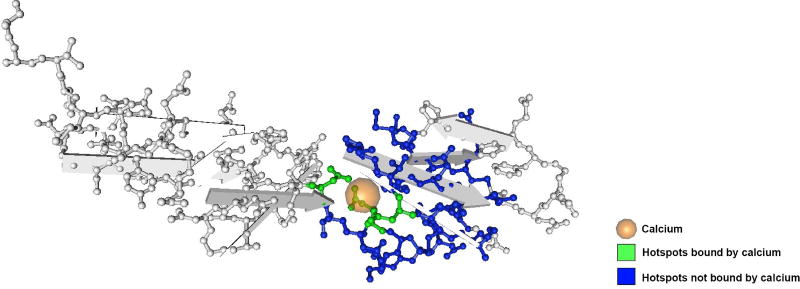
These results recapitulate much of what is known about how protein domain families contribute to the initiation or progression of cancer and are useful to biologists studying the molecular mechanisms underlying cancer. For instance, hotspots identified on the calcium-binding domain of epidermal growth factors (cd00054) are mapped to the 1EMN structure in Figure 3. Here, all three residues known to bind to calcium are also identified as hotspots, confirming the known importance of this binding pocket in cancer. In addition, we identify 42 other residues on the domain as hotspots that do not bind with calcium but tend to occur around the binding pocket and are present in many patients, suggesting their importance in cancer.

Figure 3.

Patterns of Protein Domain Hotspots on the Calcium-Binding Domain of Epidermal Growth Factors (cd00054). This figure appears in color in the electronic version of this article.

5. Conclusion

In this paper, our primary interest is to select significant mutation counts for a specific protein domain, while controlling a given level of Type I error via False Discovery Rate (FDR) procedures. For the ith position, the number of mutations a_i follow one of the two distributions f₀ or f₁, namely, the null or alternative distribution, respectively. With π₀ and 1 − π₀ representing the prior probabilities of the two groups, the probability density function of the mixture distribution can be represented as f(a_i) = π₀f₀(a_i) + (1 − π₀)f₁(a_i). We assume that if the number of mutations a_i ≤ C, then a_i is guaranteed to be from the null model, for some positive integer C, i = 1, 2, …, N. We propose a method for identify a cut-off C and show that this is superior to the cut-off developed by extending Efron’s proposal. In addition, after the selection of this cut-off, we consider a screening process so that the number of mutations exceeding a certain value D_N (Ĉ) (Ĉ + 1 ≤ D_N (Ĉ)) should be considered as significant mutations.

The proposed two-stage procedure in the selection of C and D_N yielded a testing procedure which is superior in terms $\widehat{\mathit{\text{TPR}}}$ in most cases. For the well-separated and moderately mixed case, if the null model is correctly specified, then using the Two-Stage procedure yields $\widehat{\mathit{\text{FDR}}}$ closest to the nominal level α and the highest $\widehat{\mathit{\text{TPR}}}$. It can be noted that if the true model is ZIP and ZIGP is used to model f₀, then the Two-Stage Procedure still yields the closest $\widehat{\mathit{\text{FDR}}}$ to α and leads to highest $\widehat{\mathit{\text{TPR}}}$. This means that even when the null model is misspecified, the Two-Stage procedure would still produce satisfactory results. Also, regardless of the shape of the alternative distribution, the Two-Stage Procedure yields better results than the other procedures. Furthermore, results from six chosen protein domain data sets revealed that using the proposed cut-off for C yielded more rejections. In general, the results for the real data analysis is consistent with the simulation studies. These results sum up how protein domain families contribute to the initiation or progression of cancer and are useful to biologists studying the molecular mechanisms underlying cancer.