Dynamic patterns of cortical expansion during folding of the preterm human brain

Significance

The human brain exhibits complex folding patterns that emerge during the third trimester of fetal development. Minor folds are quasi-randomly shaped and distributed. Major folds, in contrast, are more conserved and form important landmarks. Disruption of cortical folding is associated with devastating disorders of cognition and emotion. Despite decades of study, the processes that produce normal and abnormal folding remain unresolved, although the relatively rapid tangential expansion of the cortex has emerged as a driving factor. Accurate and precise measurement of cortical growth patterns during the period of folding has remained elusive. Here, we illuminate the spatiotemporal dynamics of cortical expansion by analyzing MRI-derived surfaces of preterm infant brains, using a unique strain energy minimization approach.

Abstract

During the third trimester of human brain development, the cerebral cortex undergoes dramatic surface expansion and folding. Physical models suggest that relatively rapid growth of the cortical gray matter helps drive this folding, and structural data suggest that growth may vary in both space (by region on the cortical surface) and time. In this study, we propose a unique method to estimate local growth from sequential cortical reconstructions. Using anatomically constrained multimodal surface matching (aMSM), we obtain accurate, physically guided point correspondence between younger and older cortical reconstructions of the same individual. From each pair of surfaces, we calculate continuous, smooth maps of cortical expansion with unprecedented precision. By considering 30 preterm infants scanned two to four times during the period of rapid cortical expansion (28–38 wk postmenstrual age), we observe significant regional differences in growth across the cortical surface that are consistent with the emergence of new folds. Furthermore, these growth patterns shift over the course of development, with noninjured subjects following a highly consistent trajectory. This information provides a detailed picture of dynamic changes in cortical growth, connecting what is known about patterns of development at the microscopic (cellular) and macroscopic (folding) scales. Since our method provides specific growth maps for individual brains, we are also able to detect alterations due to injury. This fully automated surface analysis, based on tools freely available to the brain-mapping community, may also serve as a useful approach for future studies of abnormal growth due to genetic disorders, injury, or other environmental variables.

During the final weeks of fetal or preterm development, the human brain undergoes crucial changes in connectivity and cellular maturation (1, 2). The cerebral cortex also rapidly increases in surface area, coinciding with the formation of complex folds (Fig. 1). Physical simulations suggest that cortical folding may result from mechanical instability, as the outer gray matter grows faster than underlying white matter (3, 4). Such models accurately predict stress patterns within folds and explain abnormal folding conditions such as polymicrogyria and pachygyria. However, even recent models that consider uniform cortical growth on a realistic brain geometry do not accurately reproduce the conserved (primary) patterns of folding observed in the human brain (4). This discrepancy suggests a role for other hypothesized factors such as axon tension in white matter (5), regional differences in material properties, or regional differences in growth (6).

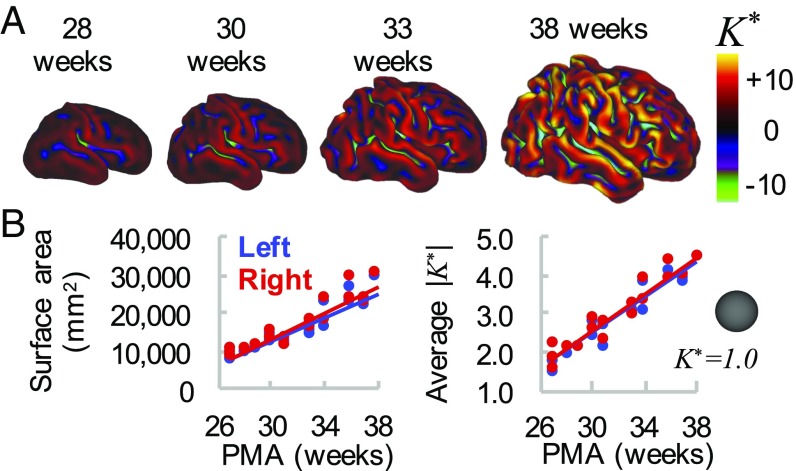
Fig. 1.

Global measures of cortical surface area and folding increase over time. (A) Cortical midthickness surfaces for individual hemisphere at 28 wk, 30 wk, 33 wk, and 38 wk PMA. Color overlay represents nondimensional curvature, $K\text{*}$, a useful metric of the degree of folding. (B) Total cortical surface area (Left) and average magnitude of $K\text{*}$ (Right) increase with time. However, these global measures do not provide information about regional variations in maturation and morphology.

Advances in magnetic resonance imaging (MRI) and cortical reconstruction have enabled detailed quantification of brain structure and connectivity during brain development (7–9). Nonetheless, measuring patterns of physical growth over time presents a unique challenge, requiring precise identification of corresponding points between multiple scans. To date, clinical studies often rely on global measures of shape or total surface expansion (8) despite evidence of important regional differences (10). Primary sensory and motor regions exhibit earlier maturation and folding than other areas (2, 7). Furthermore, even subtle or localized abnormalities in folding have been linked to disorders such as epilepsy, autism, and schizophrenia (11–13).

To attain more detailed measures of cortical growth, several groups have segmented the brain into user-delineated regions of interest (ROIs) for analysis (14–16). However, manual definition of ROIs may introduce bias or error and typically requires labor-intensive editing. A priori parcellation can also lead to skewed or weakened conclusions if the true effect does not fall neatly within the assumed area.

In this study, we use an ROI-independent approach to estimate spatiotemporal patterns of cortical growth over the course of human brain folding. Harnessing recent developments in anatomical multimodal surface matching (aMSM) (17, 18), we achieve physically guided point correspondence between cortical surfaces of the same individual across multiple time points. This was accomplished by automatically matching common features (gyri and sulci) within a spherical framework and penalizing physically unlikely (energy-expensive) deformations on the anatomical surface, an approach first described in ferret models (19, 20). While alternative methods have been proposed to match anatomical surfaces (21, 22), none provide MSM’s flexibility in terms of data matching (17) or use penalties inspired by physical behavior of brain tissue (19). Our approach produces smooth, regionally varying maps of surface expansion for each subject analyzed. By considering right and left hemispheres from 30 preterm subjects, scanned at different intervals from approximately 28–38 wk postmenstrual age (PMA), we observe consistent, meaningful patterns of differential growth that change over time.

This study provides a comprehensive, quantitative analysis of cortical expansion dynamics during human brain folding. We report statistically significant regional differences consistent with established patterns of cellular maturation and the emergence of new folds. These findings, which suggest that prenatal cortical growth is not uniform, may guide future studies of regional maturation and more accurate simulations of cortical folding. Furthermore, since our tools are freely available to the neuroscience community (9, 17, 23, 24), the approach presented here can be widely applied to future studies of development and disease progression.

Results

To visualize changes in cortical growth over the course of brain folding, we analyzed right and left hemispheres from 30 very preterm infants (born <30 wk PMA, 15 male, 15 female) scanned two to four times leading up to term equivalent (36–40 wk PMA). Six subjects were excluded from group analysis due to injury (see Materials and Methods for criteria), but all were analyzed longitudinally for individual growth patterns.

aMSM Produces Accurate Point Correspondence and Smooth Growth Estimation Across the Cortex of Individual Subjects.

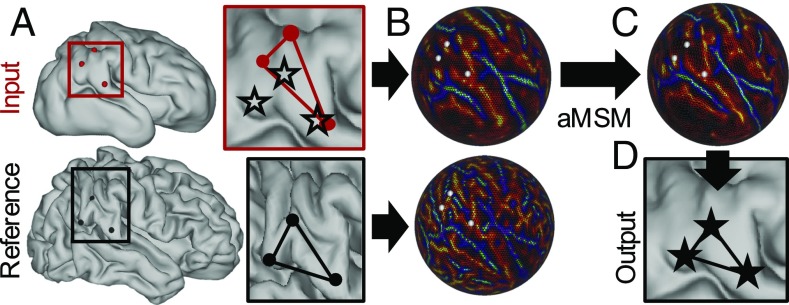
MSM uses a flexible spherical framework to align surfaces based on a range of available surface data (17). As shown in Fig. 2, anatomical surfaces (Fig. 2A) and corresponding data (e.g., univariate patterns of curvature, Fig. 1A) are projected to a spherical surface to provide a simpler mathematical framework for registration (Fig. 2B). Spherical registration shifts points on the input sphere until data are optimally aligned with those of the reference sphere (Fig. 2C), such that reprojection onto the input anatomical surface reveals accurate point correspondence with the reference surface (Fig. 2D).

Fig. 2.

Longitudinal (intrasubject) registration with aMSM. (A) Cortical midthickness surfaces (ordered sets of vertices in 3D) were generated at multiple time points for each individual. After resampling to a “standard mesh,” vertices on the input surface (red dots) do not correspond to the same locations on the reference surface (black dots). Red and black boxes outline a region of interest, in which black stars represent plausible locations for point correspondence. (B) Mean curvatures (generated from original topologies, Fig. 1A), along with deformations (generated from area-normalized input and reference anatomical surfaces), are projected to a spherical framework to drive registration. (C) aMSM moves points on the input sphere to (i) optimize curvature matching and (ii) minimize deformations between the anatomical surfaces. (D) Projection of shifted vertices reveals new anatomical locations with plausible alignment and reduced deformations.

In this study, we use mean surface curvature ($K$), calculated at the cortical midthickness, to drive initial matching. To reduce unrealistic distortions induced by both curvature matching and spherical projection, we further refine our registration to minimize physical strain energy (Eq. 1) between the input and reference anatomical surfaces (18). Unlike other spherical registration methods, which reduce distortions on the sphere, this allows us to explicitly minimize deformations that are energetically unfavorable (and thus unlikely), greatly reducing artifacts associated with the spherical projection process. (See Supporting Information for examples and validation.) Local expansion can then be estimated for each individual mesh face as the ratio of older to younger surface area.

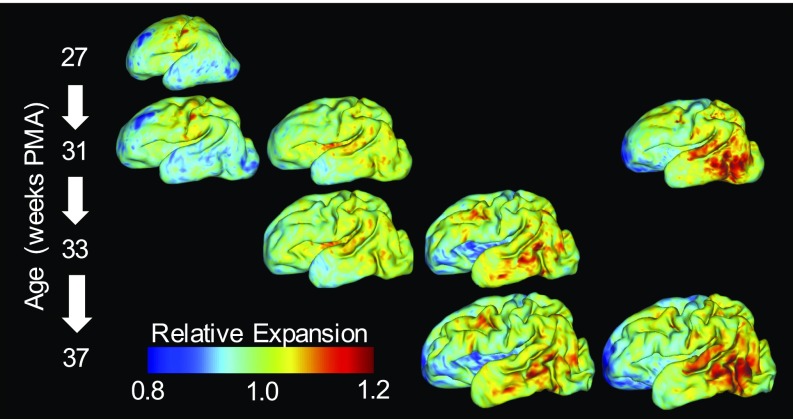
Using aMSM, we were able to obtain physically justified point correspondence and smooth maps of cortical expansion at the individual level. Fig. 3 shows results for a representative subject at multiple developmental periods: 27–31 wk, 31–33 wk, 33–37 wk, and directly from 31 wk to 37 wk PMA. Qualitatively, plotting the same color map on registered younger (Fig. 3, Top) and older (Fig. 3, Bottom) geometries reveals accurate point correspondence for each time period. Quantitative analysis confirmed significant improvements in curvature correlation and strain energy due to aMSM registration (Table S1). As illustrated in Fig. 3, direct registration from 31 wk to 37 wk was also similar to registration from 31 wk to 33 wk and then from 33 wk to 37 wk. (See Fig. S5 for group-wise comparison.)

Fig. 3.

Gradients of cortical expansion are evident in an individual brain. Relative cortical expansion (local surface expansion normalized by total hemisphere expansion) is shown for each developmental period. For each column, the same map is overlaid on a younger (Top) and an older (Bottom) surface to visualize point correspondence after longitudinal registration. From Left to Right, relative expansion is estimated for growth from 27 wk to 31 wk PMA, 31 wk to 33 wk PMA, and 33 wk to 37 wk PMA. Far Right shows direct registration from 31 wk to 37 wk PMA, as considered for group analysis in Fig. 4. True cortical expansion is equal to relative expansion (plotted) multiplied by global cortical expansion of 1.26, 1.37, 1.70, or 2.33, respectively.

Spatial Patterns of Preterm Growth Are Consistent Across Subjects and Correspond to Folding Regions.

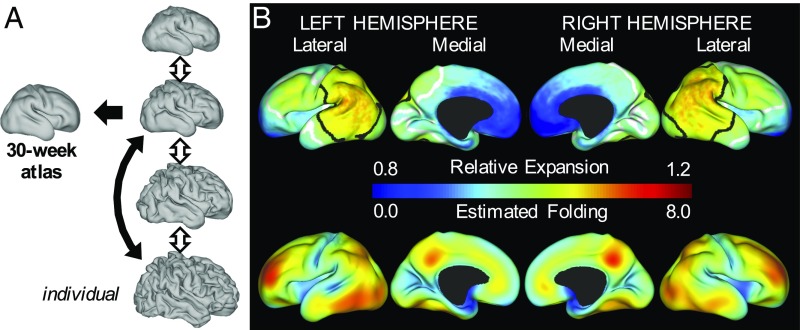
For statistical comparisons, individuals were also registered to a 30-wk atlas generated from our cohort (Fig. 4A; see Atlas Generation for details). Since folding patterns (primary sulci) are similar across individuals at 30 wk PMA (7), and because most subjects were scanned near 30 wk PMA, this atlas served as an appropriate reference for group analyses. Once registration was established between 30-wk individual surfaces and the 30-wk atlas (intersubject registration, black arrow in Fig. 4A), individual growth metrics determined by intrasubject registration were transformed to the atlas, facilitating statistical analysis across individuals and time points.

Fig. 4.

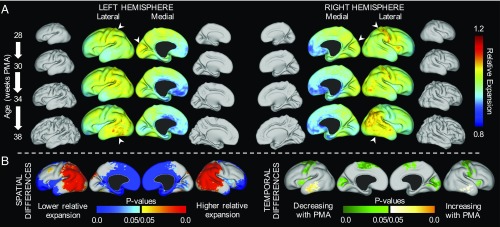
Gradients of cortical expansion and folding are consistent across subjects. (A) Correspondence between individual surfaces (closest to 30 wk, black arrow) and the 30-wk atlas was determined by aMSM registration. Using intrasubject correspondence from aMSM (double arrows), individual growth patterns from each period were registered to the 30-wk atlas for intersubject statistics. (B) For the period from 30 wk to 38 wk PMA (black double arrow in A), relative area expansion (Top) and regional folding (Bottom) were highest in the lateral parietal–temporal–occipital region and lateral frontal lobe (n = 20). Black and white contours enclose regions where relative expansion is significantly higher and lower than the global average.

To determine whether regional differences in cortical expansion are conserved across individuals, we first considered the period from 30 $\pm$ 1 wk to 38 $\pm$ 2 wk PMA (n = 20 subjects without significant injury). Permutation analysis of linear models (PALM) with threshold-free cluster enhancement (24) revealed significantly higher cortical expansion in the lateral parietal, occipital, and temporal regions and significantly lower cortical expansion in medial and insular regions (Fig. 4B, Top). These patterns were consistent across right and left hemispheres.

At the individual level, we observed highest cortical expansion in areas undergoing the most dramatic folding (Fig. 3), consistent with previous reports in ferrets (20, 25–27). To quantify change in preterm folding, we analyzed nondimensional mean curvature, defined as $K^{\ast }=KL$, where $L=\sqrt{SA/4\pi }$ and $SA$ = total cortical surface area (20). As shown in Fig. 1B, Right, $K^{\ast }=1$ across a spherical surface, and the global average of $|K^{\ast }|$ increases for more convoluted surfaces. Local folding was estimated as the difference between $|K^{\ast }|$ on the older and younger surfaces after one iteration of Gaussian kernel smoothing ($\sigma =4$ mm) on the atlas. As shown in Fig. 4B, regions of highest cortical folding were similar, but not identical, to those of highest cortical expansion (Pearson’s correlation = 0.46 and 0.42 for left and right hemispheres).

Cortical Growth Changes Regionally and Dynamically During Folding.

From individuals with scans less than 6 wk apart (n = 27 measurements from 15 subjects), we also investigated temporal variations in regional growth. As shown in Fig. 5A, relative expansion initially appears highest in the early motor, somatosensory, and visual cortices, as well as the insula, but lower near term equivalent (n = 4 with four sequential scans). By contrast, relative growth appears to increase with age in lateral parietal, temporal, and frontal regions. To determine whether these dynamic shifts were statistically significant, we considered the effect of midpoint PMA (midpoint between younger and older scan PMAs) as a covariate. PALM revealed mean spatial patterns (Fig. 5B, Left, mean PMA = 33 wk) similar to those for 30–38 wk (Fig. 4B, mean PMA = 34 wk). Importantly, temporal analysis revealed significant decreases in relative expansion of the insula and early motor, somatosensory, and visual cortices (initially fast-expanding regions slow over time relative to other regions), as well as increases in the lateral temporal lobe (Fig. 5B).

Fig. 5.

Regions of highest cortical expansion change over time. (A) Maps of average relative expansion are shown for brief windows of development, denoted on Left. For subjects in which three distinct periods of growth could be measured (n = 4), regions of maximum expansion (white arrowheads) appear to shift over time. For illustration, average midthickness surfaces are also shown to scale for each time point. (B) Regions of statistically significant differences relative to global growth were observed based on 27 growth measurements (15 subjects) over the third trimester equivalent (temporal resolution <6 wk, mean PMA = 33 wk). (B, Left) Relative expansion is higher in the lateral parietal, temporal, occipital, and frontal regions (red) and lower in the medial frontal and insular regions (blue). (B, Right) Relative expansion in the primary motor, sensory, and visual cortices, as well as in the insula, decreases over time (green). By contrast, relative expansion increases in the temporal lobe over time (yellow).

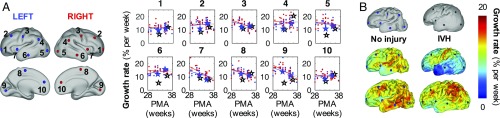
We also examined dynamic changes in terms of growth rate, defined as local percentage of increase in cortical area per week. By plotting vertex values vs. midpoint PMA (Fig. 6A), we quantified the rate and acceleration of cortical growth at specific locations over time. For noninjured individuals (Fig. 6A, blue and red dots), growth rates were generally higher at younger ages. Note that growth decelerates significantly (P < 0.05) in the initially fast-growing primary cortices (3, 8, 9) and insula (7), but it remains fairly constant in frontal (1–2, 10), temporal (6), and lateral parietal–occipital (4–5) vertices. Linear fit and statistics are shown in Table S2.

Fig. 6.

Growth rate decreases in initially fast-growing cortical areas. (A) To quantify changes over time, local growth rates (n = 27 measurements from 15 noninjured subjects) are plotted against midpoint PMA at 10 vertices on left (blue) and right (red) hemispheres. Growth rate decreases with PMA at vertices 3, 8, and 9 (early motor, somatosensory, and visual cortices) and 7 (insula). By contrast, vertices 1–2, 4–6, and 10 remain relatively constant. (B) Individual growth rates were also compared between a noninjured subject (Left) and a subject with bilateral grade III/IV IVH (Right). From Top to Bottom, surfaces are shown at approximately 30 wk, 34 wk, and 38 wk PMA. Growth rate from 30 wk to 34 wk is plotted on the 34-wk surface, and growth rate from 34 wk to 38 wk is plotted on the 38-wk surface. For the subject with IVH, growth rate is initially reduced in occipital (5, 9) and temporal (6) lobes, but later recovers to near noninjured levels. Rates at locations 1–10 in these specific individuals are denoted in A by blue stars (no injury) or black stars (IVH).

Local Growth Estimation Detects Abnormalities Associated with Preterm Injury.

Since our technique produces continuous estimates of cortical growth for individual subjects, we also analyzed cortical surfaces of infants identified to have grade III/IV intraventricular hemorrhage (IVH) and/or ventriculomegaly during their neonatal intensive care unit course (n = 6). For illustration, Fig. 6B compares a subject with no injury (same subject as in Fig. 3) to one diagnosed with bilateral grade III/IV IVH. Reduction in growth rate is particularly evident in the temporal and occipital lobes of the subject with IVH (Fig. 6B, Middle). We also note that growth rate “recovered” to near noninjured levels during the period from 34 wk to 38 wk PMA in this individual (Fig. 6B, Bottom and black open stars in Fig. 6A).

Discussion

In this work, we implemented an automated, quantitative method for analyzing regional growth in longitudinal studies of cortical maturation. Individual registration with aMSM not only produced accurate alignment of gyri and sulci, but also effectively minimized distortions on the cortical surface (Fig. 3 and Table S1). This shift in focus—regularizing the physical anatomical mesh instead of the abstract spherical mesh—offers a significant improvement for longitudinal registration using spherical techniques, which have been plagued by artifactual deformations that obscure real trends and limit interpretation of cortical growth maps (18). Furthermore, our mechanics-inspired regularization penalty (strain energy density, Eq. 1) is physically justified for longitudinal registration and has been shown to outperform other mathematical approaches (18).

Other registration techniques have been proposed to control distortion via spectral matching or varifolds (21, 22), but they have not been integrated into widely used analysis pipelines (9, 28, 29) or produced smooth, meaningful maps of cortical surface expansion. By contrast, spherical registration provides an efficient, versatile framework for inter- and intrasubject analysis based on a variety of imaging modalities (17, 30). While this study matched curvatures, an intrinsic feature of any cortical reconstruction, MSM allows registration based on multimodal data, which may further improve the accuracy of registration (9). Future studies may exploit additional data, such as myelin content and fMRI contrasts, to establish or improve correspondence.

The current approach provides continuous maps of local expansion for each individual, enabling continuous statistical analysis across the surface. Without the limitations of ROIs (14–16), spatiotemporal trends presented here offer unique insight into the trajectory of cortical growth and maturation. In many respects, these patterns are consistent with those in past literature: Diffusion tensor imaging and histological analyses have reported mature dendritic branching in the primary motor and sensory cortices before the visual cortex, which in turn matures earlier than the frontal cortex (1, 2). Similar patterns have been reported for regional folding in the preterm brain (7). The dynamic measures of cortical surface expansion reported here offer a bridge between these metrics, supporting the idea that biological processes (neuronal migration and dendritic branching) contribute to physical expansion of the cortex (constrained regional growth), which leads to mechanical instability and folding in different areas at different times.

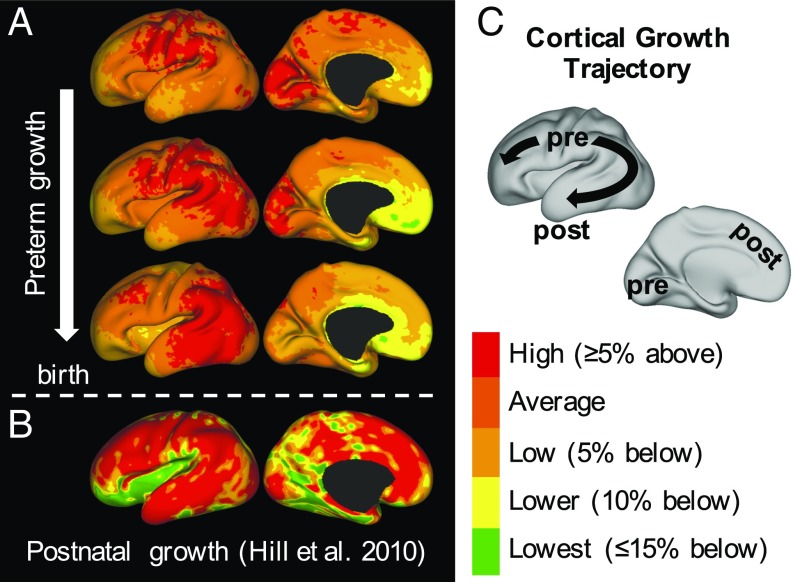
As shown in Fig. 7, the patterns we report for preterm growth (third trimester equivalent) may also link existing studies of cortical growth during the late second trimester and childhood. A volumetric study of fetal MRIs found maximum cortical growth at the central sulcus, which increased between 20–24 wk and 24–28 wk, as well as above-average growth near the insula, cingulate, and orbital sulcus (31). Similarly, we observe a trajectory in which the area of maximum growth migrates outward from the central sulcus at 28–30 wk (Fig. 7A, Top) toward the parietal and then temporal and frontal lobes while dissipating from the medial occipital lobe (Fig. 7C). As shown in Fig. 7B, this is generally consistent with reported patterns of postnatal expansion (term to adult in human, also proposed for human evolution) (10).

Fig. 7.

Trajectory of preterm growth may continue after term. (A) We observe that regions of highest expansion (“hot spots”) migrate smoothly from the central sulcus and nearby regions (Top) into parietal (Middle) and then, finally, frontal and temporal regions (Bottom). Growth slows gradually in the primary visual cortex. (B) Reported postnatal trends appear to continue this trajectory, maintaining high growth in the parietal, temporal, and frontal lobes (10). Expansion is lowest in the insula and visual cortex after birth (although still a minimum of twofold, data from ref. 10). (C) Schematic illustrating the trajectory of the maximum growth region from primary motor, sensory, and visual cortices—areas highly conserved across species and critical for basic survival—into regions highly developed in humans, particularly after birth. Pre, prenatal/preterm; post, postnatal.

One limitation of our study is the use of preterm infant data rather than fetal scans. With the advent of improved motion correction tools (32), fetal scans have become feasible and may reveal faster or different growth patterns (33). Although our results appear consistent with second trimester and postnatal trends, future studies should assess potential differences in preterm vs. healthy growth as in utero longitudinal scans become available with sufficient temporal resolution. Furthermore, the current approach may not fully characterize within-fold differences, such as gyri-specific growth (34); higher-resolution matching data may be needed to resolve growth patterns at subgyral scales.

We also note some conflicting results with past studies using manually defined ROIs. For example, a recent study of preterm infants (30 wk PMA to term equivalent) analyzed growth by dividing the brain into its major lobes (14). Authors reported high expansion in the parietal and occipital lobes, in agreement with our results, but low expansion in the temporal lobe. We speculate that this discrepancy stems from inclusion of the insula and medial temporal surface in their temporal lobe ROI. Relatively low expansion of these regions (Fig. 4B) may be sufficient to “cancel out” the high expansion we observed in the lateral temporal region. Another recent study used ROIs to relate regional surface expansion and cellular maturation in the developing rhesus macaque brain (16). This ROI analysis did not reveal a clear relationship, whereas our current approach in humans (Fig. 6) (1, 2) and ferrets (20) suggests a connection between the two. We speculate that a priori definition of ROIs may diminish the ability to detect such relationships.

Finally, we note that, for infants with high-grade IVH and/or ventriculomegaly, our analysis was able to clearly detect alterations in local growth. Fig. 6B provides an example of grade III/IV IVH, where abnormal folding is evident at all time points. However, as illustrated in Fig. 4B, folding may not serve as a perfect representation of underlying growth. Our method revealed reduced growth rate in specific regions, followed by recovery to near-normal levels. These areas and effects would be difficult to pinpoint with global measures or even local measures of folding. Just as we were able to detect subtle differences in preterm growth, future studies may apply this approach to detect differences related to specific injury mechanisms, genetic disorders, or environmental variables.

Materials and Methods

Recruitment, MRI Acquisition, and Surface Generation.

Preterm infants in this study were born at <30 wk gestation and were recruited from St. Louis Children’s Hospital. The Washington University Institutional Review Board approved all procedures related to the study, and parents or legal guardians provided informed, written consent. Images were obtained using a turbo-spin echo T2-weighted sequence (repetition time = 8,500 ms; echo time = 160 ms; voxel size = 1 × 1 × 1 mm³) on a Siemens 3T Trio scanner. T2-weighted images were processed, and cortical segmentations were generated at the midthickness of the cortex using previously documented methods (35). These segmentations were then used to generate cortical surface reconstructions, including midthickness and spherical surfaces, for each hemisphere using methods previously reported (35).

Preterm infants with moderate to severe cerebellar hemorrhage, grade III/IV IVH, cystic periventricular leukomalacia, or ventriculomegaly on MRI were identified and analyzed separately (36, 37). Clinical and demographic information for included and excluded subjects is available in Table S3. Three of 26 included subjects exhibited noncystic white matter injuries. These details, as well as PMA for each individual scan, are available in Table S4.

Longitudinal Surface Alignment and Theory.

To obtain point correspondence across time, individual surfaces (“input” and “reference”) were projected to a sphere and registered with aMSM (18) (Fig. 2). This tool systematically moves points on the input spherical surface to maximize similarity of a specified metric and minimize strain energy between the anatomical input and reference surfaces. Mean curvatures, generated in Connectome Workbench (23), were used for matching data and cortical midthickness surfaces, rescaled to the same total surface area, were used as the anatomical input and reference surfaces.

Inspired by studies that have modeled brain tissue as a hyperelastic material (3, 4, 6, 38), we define surface strain energy as

$$W=\frac{\mu }{2}\left(R+\frac{1}{R}-2\right)+\frac{\kappa }{2}\left(J+\frac{1}{J}-2\right),$$ [1]

where $R={\lambda }_1/{\lambda }_2$ represents change in shape, $J={\lambda }_1{\lambda }_2$ represents change in size, and ${\lambda }_1$and ${\lambda }_2$ represent in-plane anatomical stretches in the maximum and minimum principal directions, respectively. This form corresponds to a modified, compressible neo-Hookean material in 2D, and here we define bulk modulus, $\kappa$, to be 10 times greater than shear modulus, $\mu$. To prevent bias associated with the direction of registration (39), average results were calculated for aMSM registration performed from both older to younger and younger to older surfaces (Fig. S3). Additional details on theory and implementation of aMSM, as well as parameter effects of bulk-to-shear ratio, are described in Anatomical Mesh Regularization with aMSM, aMSM Validation, and aMSM Implementation Details and ref. 18. Other parameter effects have been described previously (17, 18).

Group Statistics.

To analyze trends in growth, individual metric maps were compared on the 30-wk group atlas by applying point correspondences described in Fig. 4. Atlas generation details can be found in Supporting Information. Individual-to-atlas alignment was accomplished with aMSM, using one surface from each individual as input (time point closest to 30 wk PMA). PALM was performed with threshold-free cluster enhancement (TFCE) (24), using 1,000 iterations and a medial wall mask. Single-group t tests were performed on the log transform of relative surface expansion to obtain a normally distributed metric centered at zero. Atlas midthickness surfaces and vertex areas were used for TFCE surface area computations.

Significance of correlations was assessed using Pearson’s correlation coefficient, and total strain energy was calculated by integrating Eq. 1 with respect to cortical surface area (MATLAB; The MathWorks, Inc.) (19). Significant improvements due to aMSM were assessed by comparing total correlation and energy values before and after registration with paired t tests (Table S1).

Data from this study are available at https://balsa.wustl.edu/study/show/K65Z.