Genome-wide genetic heterogeneity discovery with categorical covariates

Abstract

Motivation

Genetic heterogeneity is the phenomenon that distinct genetic variants may give rise to the same phenotype. The recently introduced algorithm Fast Automatic Interval Search (FAIS) enables the genome-wide search of candidate regions for genetic heterogeneity in the form of any contiguous sequence of variants, and achieves high computational efficiency and statistical power. Although FAIS can test all possible genomic regions for association with a phenotype, a key limitation is its inability to correct for confounders such as gender or population structure, which may lead to numerous false-positive associations.

Results

We propose FastCMH, a method that overcomes this problem by properly accounting for categorical confounders, while still retaining statistical power and computational efficiency. Experiments comparing FastCMH with FAIS and multiple kinds of burden tests on simulated data, as well as on human and Arabidopsis samples, demonstrate that FastCMH can drastically reduce genomic inflation and discover associations that are missed by standard burden tests.

Availability and Implementation

An R package fastcmh is available on CRAN and the source code can be found at: https://www.bsse.ethz.ch/mlcb/research/bioinformatics-and-computational-biology/fastcmh.html

Supplementary information

Supplementary data are available at Bioinformatics online.

Introduction

Genome-wide association studies (GWASs) typically test the association of individual markers, such as SNPs, with a phenotypic trait of interest (Wellcome Trust Case Control, 2007). Genetic heterogeneity, the fact that multiple genomic markers might affect the phenotype in a similar way (Burrell et al., 2013), can be leveraged to improve statistical power in GWAS. Indeed, the individual signal carried by each marker is often too weak to be discovered in a single SNP study. However, genetic heterogeneity motivates aggregating multiple neighboring markers to obtain a stronger signal that is easier to detect. This naturally leads to the problem of testing the association of genomic regions with a phenotype of interest. Since the number of genomic regions scales quadratically with the number of markers in the dataset, testing all genomic regions for association is extremely challenging both computationally and statistically. To give a sense of scale, in a typical GWAS dataset with a million SNPs, one would need to perform approximately 500 billion association tests. Because of this, most existing approaches such as gene tests or burden tests are in practice limited to test only a reduced number of arbitrarily predefined genomic regions, e.g. exons or genes or to test fixed-size genomic windows (Lee et al., 2014). Therefore, these methods are unable to discover signals that do not significantly overlap with some of the genomic regions defined prior to inspecting the data.

In a recent study, Llinares-López et al. (2015a) presented FAIS, an approach to find all genomic regions associated to a phenotype of interest under a model of genetic heterogeneity. The proposed method solves both the statistical and computational challenges derived from the sheer number of association tests to be performed through the concept of testability, originally proposed by Tarone (1990). The key idea in Tarone’s trick is that there are untestable hypotheses, which can never achieve statistical significance, and thus can be ignored in the multiple testing correction procedure without causing more false-positives to be found. While Tarone’s trick has lead to algorithms that combine statistical power with computational efficiency, none of the related methods could correct for covariates such as age, gender, or population stratification. Ignoring these may lead to many false-positive associations (Vilhjálmsson and Nordborg, 2013), limiting the applicability of FAIS in GWASs. Papaxanthos et al. (2016) proposed a significant pattern mining algorithm that can account for categorical covariates. They consider the general problem of itemset mining, which aims at finding arbitrary combinations of features in a dataset of interest. In that setting, the number of association tests to be performed scales exponentially with the number of features, making the approach unsuitable for genome-wide analyses.

We here present FastCMH, a novel method that combines both the search strategy of FAIS and pattern mining with categorical covariates. Compared to FAIS, FastCMH gains the key ability to correct for confounding without sacrificing scalability to genome-wide data.

We performed exhaustive experiments on simulated data, a study of COPD and five Arabidopsis thaliana datasets. We show that FastCMH inherits the computational efficiency and high statistical power of FAIS, while dramatically decreasing the amount of false positives due to confounding. An exhaustive comparison with multiple kinds of burden tests reveals that, by testing all possible genomic regions instead of a small set of predefined candidates or of fixed-size genomic regions, our approach can discover associated genomic regions that would otherwise be missed. In the COPD study, we find three significant genomic regions that are associated with the disease and are supported by the literature, none of which are discovered by either single-marker tests or the burden tests that we performed.

2 Problem statement

In this section, we provide the necessary background for the remainder of this article. In Section 2.1, we precisely state the problem we solve: discovering genomic regions that are significantly associated with a binary phenotype of interest. Then, in Sections 2.2 and 2.3, we introduce the Cochran–Mantel–Haenszel (CMH) test and Tarone’s trick, respectively.

2.1 Overview

Consider a dataset consisting of n individuals subdivided into n₁ cases and $n_2=n-n_1$ controls according to a binary phenotype y. For each individual $i\in \{1,\dots ,n\}$, we assume a genotypic representation in the form of an ordered sequence of l binary genomic markers, ${\mathbf{g}}_i=({\mathbf{g}}_i[1],{\mathbf{g}}_i[2]\dots ,{\mathbf{g}}_i[l])$ with ${\mathbf{g}}_i[t]\in \{0,1\}$. For example, these binary markers could be the result of a dominant/recessive/over-dominant encoding of SNPs or be obtained based on external information such as functional annotations. Furthermore, for each individual $i\in \{1,\dots ,n\}$, we record a categorical covariate c with k states, i.e. $c_i\in \{1,2,\dots ,k\}$.

Under a model of genetic heterogeneity, several genomic markers in close proximity might have evolved to affect the phenotype in the same manner. However, their individual effect sizes might be too weak to reach significance in a single-marker GWAS. Assuming that most individual markers in a genomic region $t\in 〚t_s,t_e〛$, where $〚t_s,t_e〛=\{t_s,t_s+1,\dots ,t_e\}$, have the same direction of effect motivates aggregating them into a new genomic meta-marker$g_i(〚t_s,t_e〛)=\max ({\mathbf{g}}_i[t_s],{\mathbf{g}}_i[t_s+1],\dots ,{\mathbf{g}}_i[t_e])$ for the entire region. This is equivalent to defining $g_i(〚t_s,t_e〛)=1$ if the genomic region $〚t_s,t_e〛$ for individual i contains any genomic marker encoded as 1 (typically minor alleles or risk alleles under the model of choice), and $g_i(〚t_s,t_e〛)=0$ if it only contains genomic markers encoded as 0. We refer the reader to Supplementary Section S1.3 for a generalized definition of the meta-marker. For genomic regions in which these assumptions apply, the region meta-marker $g(〚t_s,t_e〛)$ will exhibit a stronger signal than any of the individual markers, allowing the discovery of novel genome-wide significant multivariate associations. This situation is illustrated in Figure 1, where the markers contained in regions $〚t_{s,1},t_{e,1}〛$ (green) and $〚t_{s,2},t_{e,2}〛$ (red) are all weakly associated with the phenotype y. In contrast, their respective meta-markers $g_i(〚t_{s,1},t_{e,1}〛)$ and $g_i(〚t_{s,2},t_{e,2}〛)$ exhibit a much stronger association.

Fig. 1.

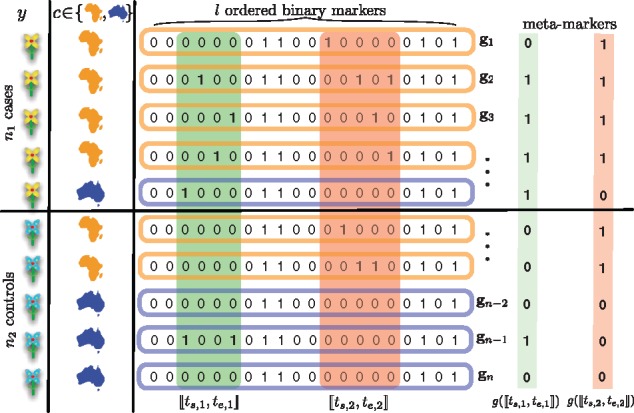
Schematic illustration of how individually weak signals inside a genomic region can be reinforced in meta-markers. In this example, $n_1=n_2=5$, l = 20 and k = 2

Nevertheless, significant associations in a GWAS often originate merely as the result of confounding by external covariates such as gender, age, population structure or environmental factors. It is essential to account for these covariates in any method that tries to assess the association between genotype and phenotype. This is also represented in Figure 1. The association with the phenotype y of the meta-marker of region $〚t_{s,2},t_{e,2}〛$ (in red) is a spurious association exclusively mediated by the covariate c (origin of the sample), whereas the meta-marker of region $〚t_{s,1},t_{e,1}〛$ (in green) remains associated after correcting for the effect of the covariate.

Existing methods can either (i) correct for covariates, but only test individual markers or highly constrained, predefined sets of markers such as entire genes or fixed-size windows (Listgarten et al., 2013) or (ii) test all possible genomic regions without constraints on location or size, without allowing covariates to be taken into account (Llinares-López et al., 2015a).

In this article, we present FastCMH, the first algorithm able to find all genomic regions$〚t_s,t_e〛,1\le t_s\le t_e\le l$, such that their corresponding meta-marker$g_i(〚t_s,t_e〛)$is significantly associated with the case/control phenotype y given the effect of a covariate c, while strictly correcting for multiple hypothesis testing under family-wise error rate (FWER) control.

To achieve its goal, FastCMH combines the scheme proposed by Llinares-López et al. (2015a) to explore the search space consisting of all possible genomic regions with the novel approach presented by Papaxanthos et al. (2016) to correct for categorical covariates in significant pattern mining. In the remainder of this section we introduce the CMH test and Tarone’s trick, the two fundamental concepts on which FastCMH relies. A full description of FastCMH is provided in the next section.

2.2 Testing the association of discrete random variables given a covariate using the CMH test

For each genomic region $〚t_s,t_e〛$, we need to test whether its meta-marker $g_i(〚t_s,t_e〛)$ and the phenotype y are statistically associated given the covariate c. Mathematically, this means testing the conditional statistical dependence of two binary random variables (the meta-marker and the case/control phenotype), given the value of a categorical random variable with k categories (the covariate).

The CMH test (Cochran, 1954; Mantel and Haenszel, 1959) is based on contingency tables, in the same way as Fisher’s exact test (Fisher, 1922) and Pearson’s χ² test (Pearson, 1900) are. However, unlike these methods, the CMH test does not build a single contingency table, but rather builds k tables, where each one corresponds to a different category of the confounder. For each 2 × 2 contingency table h, with $h=1,\dots ,k$, cell counts are computed based on all individuals for which $c_i=h$:

Variables	$g_i(〚t_s,t_e〛)=1$	$g_i(〚t_s,t_e〛)=0$	Row totals
$y=\text{case}$	ah	$n_{1,h}-a_h$	$n_{1,h}$
$y=\text{control}$	$x_h-a_h$	$n_{2,h}-x_h+a_h$	$n_{2,h}$
Col. totals	xh	$n_h-x_h$	nh

Here, n_h is the number of individuals with $c_i=h$, divided into $n_{1,h}$ cases and $n_{2,h}$ controls. Similarly, x_h is the number of individuals with $c_i=h$ for which the meta-marker $g_i(〚t_s,t_e〛)$ takes value 1, a_h of which are cases and $x_h-a_h$ controls. Using the cell counts ${\{n_h,n_{1,h},x_h,a_h\}}_{h=1}^k$, we can compute the P-value $p(〚t_s,t_e〛)$ for genomic region $〚t_s,t_e〛$ under the CMH test as explained in Supplementary Section S1.2.1. A genomic region $〚t_s,t_e〛$ is found to be significantly associated with the phenotype y given the covariate c if $p(〚t_s,t_e〛)\le \delta$, where δ is the adjusted significance threshold. In this study, we compute δ according to Tarone’s trick, presented in Section 2.3.

2.3 FWER control using Tarone’s trick

As discussed in Section 1, one of the main challenges in significant pattern mining is a consequence of the enormous number of association tests that need to be performed. In our setup, in a dataset with l genomic markers, $\frac{l(l-1)}{2}=O(l^2)$ genomic regions would need to be tested for association with the phenotype. For example, a typical GWAS dataset with $l={10}^6$ SNPs would result in approximately 500 billion association tests. Besides the computational challenge, this creates a large multiple hypothesis testing problem which, if unaccounted for, would lead to millions of false-positives being reported. For this reason, we correct for multiple hypothesis testing using FWER control, a criterion that places an upper bound on the probability of making any false discoveries (the FWER) by a user-defined target threshold α.

The most common approach to control the FWER is the Bonferroni correction (Dunn, 1961), which uses an adjusted significance threshold ${\delta }_{bon}=\alpha /b$, with b being the total number of association tests performed. However, in our setup, $b=O(l^2)$ is too large, resulting in very low statistical power. Instead, state-of-the-art methods in significant pattern mining obtain the adjusted significance threshold using Tarone’s trick, as it tends to greatly outperform Bonferroni correction in terms of statistical power while retaining strict FWER control.

The key concept behind Tarone’s trick is that, for certain association tests based on contingency tables, a minimum attainable P-value p_min can be computed as a function of the table margins. Examples of these association tests are Fisher's exact test or Pearson’s χ² test. If an association test has a minimum attainable P-value p_min greater than the adjusted significance threshold δ, the test can never be significant, and thus it can never cause a false-positive. In Tarone’s terminology, these tests are said to be untestable. Tarone showed that, in order to control the FWER, the adjusted significance threshold only needs to account for testable association tests.

To apply Tarone’s trick in our setup, we define ${\mathcal{R}}_T(\delta )=\{〚t_s,t_e〛\hspace{0.17em}|\hspace{0.17em}{p}_{min}(〚t_s,t_e〛)\le \delta \}$ as the set of testable genomic regions at significance level δ. Any regions not contained in ${\mathcal{R}}_T(\delta )$ are untestable and do not contribute to the FWER. Tarone’s trick chooses the adjusted significance threshold as ${\delta }_{tar}=\max \{\delta \hspace{0.17em}|\hspace{0.17em}\delta \le \alpha /|{\mathcal{R}}_T(\delta )|\}$. In real-world datasets, usually $|{\mathcal{R}}_T({\delta }_{tar})|\ll b$, making Tarone’s trick far less conservative than Bonferroni correction.

Tarone’s trick has been recently applied to (i) itemset mining (Terada et al., 2013; Minato et al., 2014; Llinares-López et al., 2015b), (ii) subgraph mining (Sugiyama et al., 2015), and (iii) to mine associated genomic regions with the previously mentioned FAIS algorithm (Llinares-López et al., 2015a). However, none of these methods were able to incorporate covariates to correct for confounding. In the next section, we show how to overcome this fundamental limitation of FAIS by combining it with the novel approach for pattern mining with categorical covariates.

Method

In this section, we introduce FastCMH, the first algorithm able to discover, with high statistical power and efficiency, all genomic regions exhibiting a statistically significant association with a case/control phenotype under strict FWER control while conditioning on a categorical covariate. In Section 3.1, we provide a high-level description of FastCMH. Next, Section 3.2 describes how to efficiently perform its key step of identifying all genomic regions that are deemed testable.

3.1 The FastCMH algorithm

High-level pseudocode of FastCMH is shown in Algorithm 1. Additional implementation details can be found in Supplementary Section S1.1. Conceptually, our method involves three main steps.

Algorithm 1.

FastCMH

Input: Dataset $\mathcal{G}={\{{\mathbf{g}}_i,y_i,c_i\}}_{i=1}^n$, desired FWER α

Output: Set of non-overlapping conditionally associated    genomic regions ${\mathcal{R}}_{sig,filt}=\{〚t_s,t_e〛\hspace{0.17em}|\hspace{0.17em}p(〚t_s,t_e〛)\le {\delta }_{tar}\}$

1: $({\delta }_{tar},{\mathcal{R}}_T({\delta }_{tar}))\leftarrow \mathrm{get\_testable\_regions}(\mathcal{G},\alpha )$

2: ${\mathcal{R}}_{sig,raw}\leftarrow \{〚t_s,t_e〛\in {\mathcal{R}}_T({\delta }_{tar})\hspace{0.17em}|\hspace{0.17em}p(〚t_s,t_e〛)\le {\delta }_{tar}\}$

3: ${\mathcal{R}}_{sig,filt}\leftarrow \mathrm{filter\_overlapping\_regions}({\mathcal{R}}_{sig,raw})$

4: Return ${\mathcal{R}}_{sig,filt}$

First, in Line 1, we invoke the routine $\mathrm{get\_testable\_regions}$ to compute Tarone’s adjusted significance threshold δ_tar and retrieve the corresponding set of testable genomic regions ${\mathcal{R}}_T({\delta }_{tar})$ under the CMH test. The enormous number of candidate genomic regions, often in the order of hundreds of billions, or even trillions, makes the routine $\mathrm{get\_testable\_regions}$, described in detail in Algorithm 2, the most challenging and crucial part of FastCMH.

Second, in Line 2, P-values $p(〚t_s,t_e〛)$ obtained from CMH tests are evaluated for all testable genomic regions $〚t_s,t_e〛\in {\mathcal{R}}_T({\delta }_{tar})$. Since a large proportion of all candidate genomic regions are not testable, and thus can never be significant, Tarone’s trick allows us to greatly reduce the computational burden of this step without causing any additional false negatives. Those testable regions $〚t_s,t_e〛\in {\mathcal{R}}_T({\delta }_{tar})$ whose P-values $p(〚t_s,t_e〛)$ are below Tarone’s adjusted significance threshold δ_tar are deemed significant and stored in ${\mathcal{R}}_{sig,raw}$.

Third, while all genomic regions in ${\mathcal{R}}_{sig,raw}$ are significantly associated with the phenotype—given the effect of the covariate—both the exhaustive nature of the search and linkage disequilibrium tend to generate disjoint clusters of significant genomic regions that have a high overlap with each other. To eliminate this redundancy which might otherwise complicate the analysis of the results, we invoke the routine $\mathrm{filter\_overlapping\_regions}$ in Line 3. This procedure groups all significant genomic regions in ${\mathcal{R}}_{sig,raw}$ into disjoint clusters of overlapping regions, generating a new set ${\mathcal{R}}_{sig,filt}$ containing only the most significant genomic region for each cluster and discarding the rest (see Supplementary Section S1.1.1 for additional details). Finally, the set ${\mathcal{R}}_{sig,filt}$ is returned as FastCMH’s output.

3.2 Getting testable regions in FastCMH

As mentioned before, efficiently finding Tarone’s adjusted significance threshold δ_tar and the set of testable genomic regions ${\mathcal{R}}_T({\delta }_{tar})$ is the key algorithmic step in FastCMH. A naive enumeration approach, which would require computing the minimum attainable P-value $p_{min}(〚t_s,t_e〛)$ for all $\frac{l(l-1)}{2}=O(l^2)$ candidate regions, would not scale to the number of genomic markers l in typical GWAS datasets. For this reason, the routine $\mathrm{get\_testable\_regions}$ of FastCMH combines the branch-and-bound approach used by its predecessor FAIS with the novel search space pruning criterion developed for the CMH test in Papaxanthos et al. (2016).

Algorithm 2.

$\mathrm{get\_testable\_regions}$

Input: Dataset $\mathcal{G}={\{{\mathbf{g}}_i,y_i,c_i\}}_{i=1}^n$, desired FWER α

Output: Tarone’s adjusted significance threshold δ_tar and set of testable genomic regions ${\mathcal{R}}_T({\delta }_{tar})$

1:  $\delta \leftarrow 1,\hspace{0.17em}{\mathcal{R}}_T(\delta )\leftarrow \varnothing$

2:  ${\mathcal{R}}_{cand}\leftarrow \{〚t_s,t_e〛\hspace{0.17em}|\hspace{0.17em}1\le t_s\le t_e\le l\}$

3:  for$〚t_s,t_e〛\in {\mathcal{R}}_{cand}$do ▹ Regions in ${\mathcal{R}}_{cand}$ enumerated firstly in increasing order of length and then starting position

4:   if$p_{min}(〚t_s,t_e〛)\le \delta$then

5:    ${\mathcal{R}}_T(\delta )\leftarrow {\mathcal{R}}_T(\delta )\cup \{〚t_s,t_e〛\}$

6:    while$\delta >\alpha /|{\mathcal{R}}_T(\delta )|$do

7:     Decrease δ

8:     $\mathcal{P}\leftarrow \{〚t_s,t_e〛\in {\mathcal{R}}_T(\delta )\hspace{0.17em}|\hspace{0.17em}{p}_{min}(〚t_s,t_e〛)>\delta \}$

9:     ${\mathcal{R}}_T(\delta )\leftarrow {\mathcal{R}}_T(\delta )\mathcal{P}$

10:   if$\mathrm{pruning\_condition}(〚t_s,t_e〛)$then

11:    Remove all $〚t_s^{\prime },t_e^{\prime }〛\supset 〚t_s,t_e〛$ from ${\mathcal{R}}_{cand}$

12:  Return ${\delta }_{tar}\leftarrow \delta$ and ${\mathcal{R}}_T({\delta }_{tar})={\mathcal{R}}_T(\delta )$

The routine $\mathrm{get\_testable\_regions}$ initializes the adjusted significance threshold δ to 1, the largest value it could possibly attain, and initializes the set of testable genomic regions ${\mathcal{R}}_T(\delta )$ to the empty set, as shown in Line 1 of Algorithm 2. In Line 2, the search space of genomic regions ${\mathcal{R}}_{cand}$ is initialized to contain all possible candidate genomic regions, i.e. ${\mathcal{R}}_{cand}=\{〚t_s,t_e〛\hspace{0.17em}|\hspace{0.17em}1\le t_s\le t_e\le l\}$.

After initialization, in Line 3, the algorithm enumerates the genomic regions in ${\mathcal{R}}_{cand}$ in the same order as the FAIS algorithm in Llinares-López et al. (2015a): enumerating first in increasing order of region length, i.e. smaller regions first, and then, among all regions having the same length, in increasing order of starting position. For each genomic region $〚t_s,t_e〛$ being processed, we perform the steps described below.

First, in Line 4, we compute the minimum attainable P-value for the CMH test, $p_{min}(〚t_s,t_e〛)$, using the closed-form expression shown in Supplementary Section S1.2.2. Then, we check whether the region is testable at the current significance threshold δ, i.e. if $p_{min}(〚t_s,t_e〛)\le \delta$. If it is, the region is added to the set of testable regions ${\mathcal{R}}_T(\delta )$ in Line 5 and Tarone’s condition $\alpha /|{\mathcal{R}}_T(\delta )|$ is checked in the following line. If the condition is found to be violated, it means that the current significance threshold δ is too large and must be decreased (Line 7). By decreasing δ, some already processed genomic regions that were found to be testable, i.e. $p_{min}(〚t_s,t_e〛)\le \delta$ for a larger value of δ, might now become untestable. Those genomic regions are retrieved and removed from ${\mathcal{R}}_T(\delta )$ in Lines 8 and 9, an operation that can be implemented in O(1) time if an appropriate data structure is used for storing ${\mathcal{R}}_T(\delta )$ in memory.

The last step in processing a candidate genomic region $〚t_s,t_e〛$ is also the most relevant for computational efficiency: the pruning step in Line 10 of Algorithm 2. If the pruning condition evaluates to True for region $〚t_s,t_e〛$, in Line 11, we remove from the search space ${\mathcal{R}}_{cand}$ all candidate genomic regions $〚t_s^{\prime },t_e^{\prime }〛$ that contain the region $〚t_s,t_e〛$ currently being processed. This step can dramatically reduce the size of ${\mathcal{R}}_{cand}$, allowing our method to be many orders of magnitude faster than a naive enumeration. As illustrated in Supplementary Figure S2, by storing ${\mathcal{R}}_{cand}$ as a tree, the removal of pruned candidates can be performed in O(1) time. Due to the use of the CMH test for association testing, the pruning condition can no longer be based solely on the minimum attainable P-value $p_{min}(〚t_s,t_e〛)$ of the region $〚t_s,t_e〛$ currently being processed, as for FAIS and other significant pattern mining approaches which do not take covariates into account. Instead, FastCMH uses the pruning criterion proposed by Papaxanthos et al. (2016), which computes a lower bound ${\tilde{p}}_{min}(〚t_s,t_e〛)\le p_{min}(〚t_s,t_e〛)$ for the minimum attainable P-value $p_{min}(〚t_s,t_e〛)$ of each candidate genomic region $〚t_s,t_e〛$. In their study, the authors show that ${\tilde{p}}_{min}(〚t_s,t_e〛)>\delta$ is a valid pruning condition for the CMH test and provide an $O(k\hspace{0.17em}\text{log}\hspace{0.17em}k)$ algorithm to evaluate ${\tilde{p}}_{min}(〚t_s,t_e〛)$, which we use in Line 10 of Algorithm 2. Pseudocode of the algorithm used to evaluate the pruning condition, as well as mathematical details of its derivation in the context of mining associated genomic regions can be found in Supplementary Section S1.2.3.

The routine $\mathrm{get\_testable\_regions}$ naturally terminates when all candidate regions in ${\mathcal{R}}_{cand}$ have either been pruned or processed. At that point, the algorithm has converged and we can return δ_tar and ${\mathcal{R}}_T({\delta }_{tar})$ as the final values of δ and ${\mathcal{R}}_T(\delta )$.

4 Experiments

In this section, we empirically evaluate the performance of FastCMH in different scenarios, assessing its power, speed and ability to correct for confounders. Our analyses are performed on simulated datasets, on data from the COPDGene study and of the model organism A. thaliana. We then compare the results of FastCMH with those obtained from performing a set of burden tests, which are a common method to conduct association mapping.

4.1 Simulation study

We conducted a wide range of simulation analyses to evaluate the performance of FastCMH, as well as to compare it with other methods and algorithms. Two of these analyses are presented in this section, and the remaining ones have been included in the Supplementary Material.

4.1.1 Assessing power, false detection proportion and speed

Comparison partners:

We compare FastCMH, our proposed method, with two alternative approaches: (i) FAIS-χ², a version of the method proposed by Llinares-López et al. (2015a) using Pearson’s χ² test, which uses Tarone’s trick but cannot account for confounding and (ii) BonfCMH, which does not use Tarone’s trick, but does use the CMH test.

Data generation:

A dataset is generated so that there is exactly one truly significant genomic region and one confounded genomic region, that is, a region whose genomic meta-marker is highly correlated with the (confounding) covariate c, with c itself being correlated with the phenotype y. In our experiments, both regions contain $\ell =5$ markers each. The parameter $p_{\mathrm{s}}\in [0,1]$ controls the strength of the signal in the truly significant region; when $p_{\mathrm{s}}$ is closer to 1, then the truly significant regions are easier to find. On the other hand, the parameter ${\rho }_{\text{con}}\in [0,1]$ controls the strength of association between the confounding covariate and the phenotype; when ${\rho }_{\text{con}}$ is close to 1, then the level of confounding is very high. The significant and confounded regions are then generated based on $p_{\mathrm{s}}$ and ${\rho }_{\text{con}}$. Additional details can be found in Supplementary Section S2.1.1.

Power and false-detection proportion:

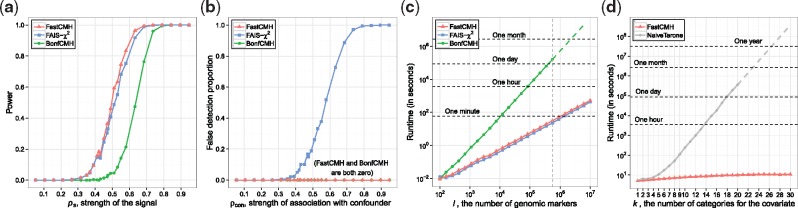
There are two complementary situations where FastCMH has improved performance. First, it has improved detection performance of truly significant regions, due to its use of Tarone’s testability criterion, when compared to BonfCMH. In Figure 2a, both FastCMH and FAIS-χ² have higher power than BonfCMH for $p_{\mathrm{s}}\in [0.3,0.8]$ and FastCMH has slightly higher power than FAIS-χ². Second, it will often (correctly) omit regions that appear to be significant, but are actually highly correlated with the covariate rather than the phenotype. Figure 2b shows that FastCMH and BonfCMH do not detect these confounded genomic regions, whereas FAIS-χ² does. We consider the detection of these regions to be false-positives. The Type I error rate obtained in these experiments is shown in Supplementary Section S3.1.1, proving that both FastCMH and its comparison partners satisfy FWER control. In Supplementary Section S3.1.2, a variation of this experiment is performed in which we show that the power and false discovery proportion of FastCMH are mostly unaffected by the number of categories, provided the resulting contingency tables have enough observations.

Fig. 2.

(a) A comparison of the power of FastCMH, FAIS-χ² and BonfCMH for detecting true significant regions, as $p_{\mathrm{s}}$ varies. The parameters are chosen as: n = 500, $l={10}^6$, k = 2 and $p_{\mathrm{s}}={\rho }_{\text{con}} \in [0.05,0.95]$. (b) The proportion of confounded significant regions falsely detected by each of those three algorithms. The parameters have the same values as for (a). (c) A comparison of the runtimes for the three methods, where the dashed section for BonfCMH represents approximated values. Both axes are plotted on the log-scale. The set of parameters is as follows: n = 500, k = 4, $l\in [{10}^2,{10}^7]$. (d) The difference in runtime between FastCMH and a naive implementation of a procedure combining Tarone’s trick and the CMH test. The dashed section of the naive method represents approximated values. We chose: n = 500, $l={10}^5,\hspace{0.17em}k\in \{1,2,\dots ,30\}$

Speed:

Figure 2c shows that FastCMH is also dramatically faster than BonfCMH for large l. For example, BonfCMH would take over 24 hr to process a dataset with $l\approx 5\times {10}^5$ (vertical grey dashed line), whereas FastCMH would take less than a minute. Moreover, FastCMH is virtually as fast as FAIS-χ², showing that our method can correct for confounders with negligible runtime overhead. Supplementary Section S3.1.3 also contains experiments that show that the runtime of FastCMH scales linearly with the number of samples n. In addition to the methods described above, we show in Figure 2d that our implementation of FastCMH is several orders of magnitude faster that a naive implementation of Tarone’s trick applied to CMH. In fact, the computation time of this naive method increases exponentially as k increases, whereas FastCMH increases only almost linearly, in $O(k\hspace{0.17em}\text{log}\hspace{0.17em}k)$. This empirically confirms the theoretical result by Papaxanthos et al. (2016) regarding the scalability of their search space pruning condition for the CMH test.

4.1.2 Comparison with burden tests

Burden tests are methods aimed at identifying genomic regions of contiguous markers that are significantly associated with a phenotype. The regions tested by the burden tests must always be defined a priori. As an example, the gene-based burden tests rely on biological knowledge about the location of the coding regions of genes, and only test markers located within those regions. Another example is the partitioning of the genome in windows of fixed length, followed by the execution of burden tests on each window.

To allow for a fair comparison to FastCMH, we performed simulations using burden tests with window-based approaches as these perform a genome-wide scan and thus analyze all genomic markers. We considered two different types of windows: non-overlapping and sliding windows.

First, we conducted burden tests on non-overlapping windows of a fixed length w. In this approach, it is known that the statistical power strongly depends on the relative location of the window boundaries with respect to the associated genomic regions (Schmid and Yang, 2008).

To overcome this limitation, we also conducted burden tests on sliding windows with a stride (or shift) of one marker between two consecutive windows. In this way, the sliding windows cover several potential alignments of the window boundaries with respect to the starting locations of the associated genomic regions. This ensures that the power of the burden tests does not depend on the (random) partitioning of the associated regions induced by the tested windows (Lee et al., 2014).

We therefore conducted several simulations to illustrate how the choice of the window length w, prior to the execution of the burden tests, and the choice of the stride affect the power of the burden tests. We then compared the performance of the burden tests to that of FastCMH, which is more flexible as it screens all possible (and testable) windows.

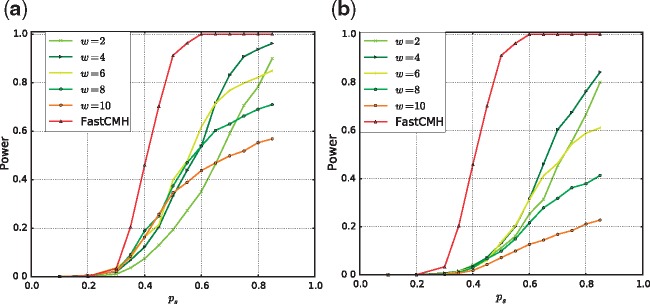
The data generation process is an extension of the one described in Section 4.1: the dataset contains n = 500 samples and $l={10}^5$ markers. The phenotype y is a binary variable. We introduced a confounding covariate c with k = 2 categories. Each dataset includes seven truly associated genomic regions of lengths $\ell \in [2,4,6,8,10,12,14]$ and seven confounded genomic regions with the same lengths. We compared our approach to five different settings of window-based burden tests, each of them testing a different window size $w\in [2,4,6,8,10]$. The starting position of each window was either separated from the starting position of its neighboring window by a stride (or shift) of one genomic marker—sliding windows—or by the length w of the window—non-overlapping windows (see Supplementary Section S1.5.1 for more details). The results were averaged over 200 iterations.

Figure 3 shows the power of the burden tests with Encoding (II) (see Supplementary Section S1.5), and the power of FastCMH as a function of the strength of the association $p_{\mathrm{s}}$ between the associated genomic regions and the phenotype. The figure illustrates the results for both non-overlapping windows (Figure 3a) and for sliding windows (Figure 3b). The power of the burden tests represents the proportion of truly associated genomic regions that are retrieved by the tests.

Fig. 3.

A comparison of the power between FastCMH and several burden tests with (a) non-overlapping windows and (b) sliding windows. The burden tests were performed for various windows sizes (w) and used the encoding that counts all minor alleles in the window. Refer to Supplementary Section S1.5 for more details

In both cases, we observe that FastCMH achieves better power than both window-based tests, regardless of the size of the tested windows. This is mainly due to the flexibility of our method FastCMH, which is able to simultaneously detect associated regions of different lengths, combined with an efficient correction for multiple hypothesis testing. In contrast, the window-based tests exhibit low power for all window sizes. This is due to the fact that the associated genomic regions are split over several tested windows, which are in general weakly correlated with the phenotype as they combine part of the associated markers with non-associated ones. Moreover, as soon as the correlation between the signal and the phenotype is large enough, i.e. larger than $p_{\mathrm{s}}=0.6$, FastCMH’s statistical power remains very close to 1. Additional results, described in Supplementary Section S3.1.5, show that FastCMH efficiently controls the FWER and corrects for covariates. Supplementary Section S3.1.5 also illustrates the influence of the length of the associated genomic regions on the results of window-based burden tests. Except for some extreme (unrealistic) cases, FastCMH achieves better power.

Overall, we show that FastCMH outperforms the burden tests with non-overlapping and sliding windows, in terms of statistical power, when the ground truth—the true lengths and locations of the associated genomic regions—is unknown to the method. FastCMH is therefore efficient in retrieving the associated genomic regions in exploratory analysis when the biological prior knowledge is weak or non-existent. Additional simulations show that FastCMH also outperforms gene-based burden tests, as explained in Supplementary Section S3.1.5.

4.1.3 Additional simulation experiments

The Supplementary Material contains a set of additional experiments that offer further insights into the performance of FastCMH. In Supplementary Section S3.1.4, we show that FastCMH outperforms single-marker testing under a simulation model in which there is a single, unmeasured causal marker in linkage disequilibrium with multiple other measured markers in the region. In Supplementary Section S3.1.7, we investigate the performance of FastCMH when the method is extended to control the false discovery rate (FDR) instead of the FWER. As our results show, this extension leads to increased statistical power, as FDR is a less conservative criterion than FWER, but at the expense of also increasing the absolute number of false-positives.

4.2 Experiments on COPDGene and A. thaliana

In this section, we present the datasets that we use to evaluate FastCMH: (i) a case/control study of association with COPD in humans and (ii) five plant datasets of the model organism A. thaliana involving different binary phenotypic traits.

4.2.1 Description of the datasets and preprocessing

Human data:

We analyzed samples from the COPDGene study (Regan et al., 2011) whose goal is to identify genetic risk factors for COPD. Participants of the study belong to two different ethnic groups: African-Americans and non-Hispanic whites. The samples of the two populations were combined and 615 906 SNPs found in the intersection were kept. The combined dataset contains 7993 samples of which 3633 are cases and 4360 are controls (see Supplementary Section S2.2 and Supplementary Table S2 for more details). Finally, each SNP was binarized according to a dominant encoding. That is, homozygous major SNPs were encoded as 0, whereas heterozygous and homozygous minor SNPs were encoded as 1. In this way, significantly associated genomic regions can be interpreted as regions for which the presence/absence of any number of minor alleles in the region is associated with disease risk for COPD.

Plant data :

We analyzed a widely used A. thaliana GWAS dataset by Atwell et al. (2010) from the easyGWAS online resource (Grimm et al., 2016). This dataset contains a large collection of 107 phenotypes, 21 of which are dichotomous. We kept five phenotypes: LY and LES (lesioning or yellowing leaves traits) and avrB, avrPphB and avrBpm1 (hypersensitive-response traits). Each of the five A. thaliana datasets contains between 84 and 95 inbred samples and approximately 214 050 homozygous SNPs (see Supplementary Section S2.3 and Supplementary Table S3 for more details about the chosen phenotypes). We encoded homozygous major SNPs as 0 and homozygous minor SNPs as 1.

4.2.2 Definition of the covariates

In a GWAS, spurious associations between genotype and the trait of interest are often found due to confounding factors such as gender, age or population structure (Marchini et al., 2004). The ability of FastCMH to handle categorical covariates can be used to correct for such confounding variables. In the COPD study, defining the covariate is straightforward: we define the categorical covariate c as the (known) genetic ancestry of the individuals, namely African-Americans or non-Hispanic whites. To illustrate both the ability of FastCMH to cope with several covariates simultaneously and to handle a large number of categories k for each covariate, we also consider ‘height’ (Cho et al., 2014) as an additional covariate. For each of the A. thaliana datasets, the categorical covariate c on which we condition to correct for population structure was defined using k-means clustering on the three principal components of the empirical kinship matrix (Price et al., 2006), with k optimized to minimize genomic inflation. Details about how the covariates were selected and encoded can be found in Supplementary Section S2.4.

4.3 Results

Here, we discuss the results we obtained when analyzing the human and plant data. We first present our findings with respect to the correction of confounding factors, followed by a presentation of the significant genomic regions that our method discovered. Finally, we provide a comparison with burden tests (Lee et al., 2014).

Population structure correction:

In Table 1, we show that the results of FAIS-χ² for all five A. thaliana datasets exhibit a moderate-to-severe degree of genomic inflation (Devlin and Roeder, 1999), i.e. λ ranging between 1.53 and 2.51. FastCMH significantly reduces inflation due to population structure, resulting in λ ranging between 1.13 and 1.30.

Table 1.

Comparison of the results obtained using our proposed method (FastCMH) and the previous state-of-the-art algorithm (FAIS-χ²), which cannot correct for covariates

Dataset and phenotype	Samples n	Cases %	k	FAIS-χ2		FastCMH
				λ	Hits	λ	Hits
COPDGene
$▹$COPD	7993	45.4	20	16.70	88 403	1.05	3
A. thaliana
$▹$avrB	87	63.2	3	1.66	14	1.17	11
$▹$avrRpm1	84	66.7	3	1.53	15	1.13	13
$▹$avrPphB	90	51.1	4	1.70	6	1.22	5
$▹$ LES	95	22.1	3	2.05	20	1.21	3
$▹$ LY	95	30.5	5	2.51	26	1.30	1

For each method, the columns λ and “Hits” refer to the genomic inflation factor and the resulting number of non-overlapping genomic regions deemed significant, respectively. The value of λ is computed based on the P-values of all testable regions.

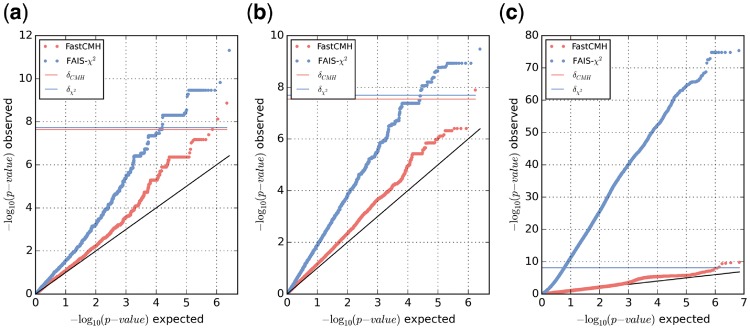
The ability of FastCMH to account for population structure becomes even more evident with the results from COPDGene. First, there are marked genetic differences between individuals of African-American and non-Hispanic white ancestry (see Supplementary Figure S6). This coupled together with the shift in the ratio of cases/controls across populations (30.81% for African-Americans versus 52.81% for non-Hispanic whites) causes an extreme level of inflation that FAIS-χ² is unable to cope with. With a genomic inflation factor of $\lambda =16.70$, any hit reported by FAIS-χ² is completely unreliable. In contrast, FastCMH eliminates the inflation almost entirely by reducing it to $\lambda =1.05$. To further illustrate the effects of population structure correction when using FastCMH versus FAIS-χ², in Figure 4, we show QQ-plots of P-values for all testable genomic regions in three selected datasets: two A. thaliana datasets (LES and LY) and the COPDGene study. Based on Figure 4, it is evident that FastCMH can successfully reduce severe levels of genomic inflation. The QQ-plots for the remaining A. thaliana datasets can be found in Supplementary Section S3.3.1. Additionally, we investigated the possibility of further correcting for population structure in the COPDGene study by defining the categorical covariate using k-means on the top p principal components of the empirical kinship matrix, as we did when analyzing the A. thaliana datasets. This analysis, which considers all 81 possible combinations of p and k in the range $〚2,10〛$, lead to a further decrease in genomic inflation ($\lambda =1.01$) without affecting the significant genomic regions discovered by FastCMH, as shown in Supplementary Section S3.2.1.

Fig. 4.

Comparison of the QQ-plots for the P-values of all testable genomic regions obtained with FastCMH (red) and the previous state-of-the-art FAIS-χ² (blue) for three datasets: (a) A. thaliana LES, (b) A. thaliana LY, (c) COPDGene. Horizontal lines show the adjusted significance thresholds

Finally, we studied the impact of k, the number of categories of the covariate, on the runtime of FastCMH (see Supplementary Section S3.2.2). We analyzed the COPDGene data with different levels of discretization of the covariate ‘height’. Our results are consistent with the trend observed in Figure 2d: the runtime of FastCMH scales smoothly with k, while approaches based on naive evaluations of the pruning criterion scale exponentially with k. This severely limits their applicability, being only feasible for k < 16, a limitation not present for FastCMH.

Significantly associated genomic regions:

In Table 1, we also show the number of non-overlapping genomic regions deemed statistically significant (hits) by our method, FastCMH, and our comparison partner, FAIS-χ². Both algorithms were run with a target FWER of $\alpha =0.05$.

Across all five A. thaliana datasets, we observe that FastCMH systematically retrieves less genomic regions (33 in total) than FAIS-χ² (81 in total). Moreover, the decrease in the number of hits is larger for those datasets with stronger genomic inflation. For instance, in LY ($\lambda =2.51$ for FAIS-χ²), our method retrieves a single genomic region, whereas FAIS-χ² retrieves 26. Similarly, in LES ($\lambda =2.05$ for FAIS-χ²), our method has three hits whereas FAIS-χ² reports 20. Based on the results presented in the previous section, and the correlation in the decrease of the number of hits with genomic inflation, it is plausible to conclude that the results of FAIS-χ² can be inflated by population structure, while FastCMH successfully reduces such inflation. Finally, it is worth noting that out of the 33 significantly associated genomic regions retrieved by FastCMH in the A. thaliana datasets, 17 of them did not contain any SNPs that were deemed significant by a single-SNP association study, illustrating how mining genomic regions can lead to the discovery of novel associations. The most significant genomic regions and their respective P-values are shown in Supplementary Table S6.

Our results for the COPDGene study also clearly demonstrate the need to correct for population structure while mining significant genomic regions. FAIS-χ² reports a very large number of hits (88 403), mainly due to the extreme genomic inflation ($\lambda =16.70$). In contrast, FastCMH reports only three significantly associated genomic regions. Each of the three regions overlaps with a different gene in the gene cluster known as the (CHRNA5–CHRNA3–CHRNB4) nicotinic acetylcholine receptor, located on chromosome 15q25.1. Independent studies have reported individual and joint association of some of these genes to COPD (Cho et al., 2010, 2014). Our results are remarkable in that the three regions detected by FastCMH are formed by SNPs, each of which do not seem to have an association to COPD, but their joint effect across genetically different populations is strongly associated to the disease.

Details about the SNPs involved, their locations, and individual as well as region-based P-values are shown in Supplementary Table S4. When analyzing both populations independently with FAIS-χ², no significant region was found in the African-American cohort, whereas only one region was reported for the non-Hispanic whites (see Supplementary Section S3.2.4). With this, we conclude that the main advantage of our method relies on attaining statistical power, not only through an efficient mechanism that avoids testing untestable regions but also by allowing the analysis of larger datasets with samples of mixed populations thanks to a reliable and computationally efficient correction of confounding factors.

Comparison with burden tests:

To illustrate the usefulness of exploring all genomic regions, as FastCMH does, instead of a small set of predefined regions, we ran different kinds of burden tests for all five A. thaliana datasets and for the COPDGene study. Here, we provide a brief description of the results. For additional details on the experimental setup and results, we refer the reader to Supplementary Sections S1.5, S3.2.5 and S.3.3.3.

First, we ran gene-based burden tests. For both plant and human studies, we considered all genes as candidate genomic regions, resulting in 24 426 regions for A. thaliana and 17 817 regions for COPDGene. Each region includes markers at a distance smaller than 10 kb from the gene boundary. As a result for A. thaliana, 45% of all the SNPs discovered by FastCMH are not inside genes and, as a consequence, were not discovered by the burden tests. FastCMH also leads to results that are complementary to those of the burden tests at the gene level (see Supplementary Tables S6 and S8): 21% of the genes reported by any of the burden tests are also found by FastCMH, including the most significant ones. This number is artificially decreased by the high variability of the results across burden tests and by the high inflation factor of some of them (see Supplementary Table S7). At last, 40% of all the significant genes are only found by FastCMH. Concerning the COPD dataset, none of the three genes (CHRNA5–CHRNA3–CHRNB4) found by FastCMH was significant using any of the burden tests. Taking the smallest P-value across all burden tests performed, only CHRNB4 was close to significance (P-value $5.72·{10}^{-6}$), whereas CHRNA5 and CHRNA3 had P-values 0.24 and 0.41, respectively. While each of the three significantly associated genomic regions found by FastCMH overlaps with one gene in the cluster (CHRNA5–CHRNA3–CHRNB4), the significant regions do not span the entire gene.

Second, in both the A. thaliana datasets and the COPDGene study, we performed burden tests by splitting the genome into non-overlapping windows of sizes 500 kb and 1 Mb (see Supplementary Section S1.5). The experiments in the COPDGene dataset and in the A. thaliana datasets show that this approach does not retrieve the SNPs found by FastCMH but only some of those of the gene-based tests. While these results are complementary to those of FastCMH, they are potentially harder to interpret because a larger number of SNPs are combined together.

In summary, FastCMH should not be considered as a substitute for burden tests, but rather as a complementary approach that allows testing a much broader range of hypotheses, allowing the discovery of novel associations that would otherwise be missed by burden tests.

5 Conclusions and outlook

In this article, we have proposed FastCMH, an algorithm to discover genomic regions exhibiting genetic heterogeneity. We present the first method capable of testing all genomic regions for association with a phenotype of interest while correcting for covariates, without sacrificing statistical power or computational efficiency. Our experiments on simulated, COPDGene and A. thaliana data show that FastCMH combines improved detection performance with superior computational power when compared to approaches that use naive multiple testing correction procedures or do not take covariates into account.

FastCMH combines variants in a genomic region—assuming homogeneous effect signs—in the same way as its predecessor FAIS-χ² and most non-adaptive burden tests. Therefore, this makes FastCMH a valuable method for exhaustive analyses in rare-variant association testing. When we focus on common variants, if the variants within a region of interest have different directions of effect, FastCMH can potentially miss this region. Adaptive burden tests tackle this problem by estimating the effect signs of the variants before combining them, an approach that requires permutation testing to assess significance. These methods can afford permutation testing because, as mentioned before, burden tests in general require an a priori specification of the genomic regions to analyze. In our setting, and due to the fact that all possible regions are considered, the computational considerations make it extremely challenging to naively apply permutation testing. Nevertheless, combining FastCMH with the approach proposed in Llinares-López et al. (2015b), which uses Tarone’s method as a way to speed-up permutation testing, would be an interesting topic for future work. Enhancing FastCMH with permutation testing would also have additional benefits, such as taking into account the dependence between test statistics to obtain less stringent significance thresholds, thereby increasing statistical power.

Due to the use of Tarone’s method, FastCMH relies on all data being discrete. Developing an alternative, computationally efficient framework for large-scale association testing, which is able to handle continuous variables, constitutes an important topic for future research.

Funding

This work was supported in part by the SNSF Starting Grant “Significant Pattern Mining” (to K.B., F.L.L.) and the Marie Curie ITN MLPM2012 [316861 to K.B., F.L.L]. The COPDGene project was supported by award number R01HL089897 and award number R01HL089856 from the National Heart, Lung, And Blood Institute (refer to Supplementary S5 for a complete list of COPDGene investigators). The COPDGene project is also supported by the COPD Foundation through contributions made to an Industry Advisory Board composed of AstraZeneca, Boehringer Ingelheim, Novartis, Pfizer, Siemens, GlaxoSmithKline, and Sunovion.

Conflict of Interest: none declared.