Modelling haplotypes with respect to reference cohort variation graphs

Abstract

Motivation

Current statistical models of haplotypes are limited to panels of haplotypes whose genetic variation can be represented by arrays of values at linearly ordered bi- or multiallelic loci. These methods cannot model structural variants or variants that nest or overlap.

Results

A variation graph is a mathematical structure that can encode arbitrarily complex genetic variation. We present the first haplotype model that operates on a variation graph-embedded population reference cohort. We describe an algorithm to calculate the likelihood that a haplotype arose from this cohort through recombinations and demonstrate time complexity linear in haplotype length and sublinear in population size. We furthermore demonstrate a method of rapidly calculating likelihoods for related haplotypes. We describe mathematical extensions to allow modelling of mutations. This work is an important incremental step for clinical genomics and genetic epidemiology since it is the first haplotype model which can represent all sorts of variation in the population.

Availability and Implementation

Available on GitHub at https://github.com/yoheirosen/vg.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Background

Statistical modelling of individual haplotypes within population distributions of genetic variation dates back to the Kingman (1982)n-coalescent. In general, the coalescent and other models describe haplotypes as generated from some structured state space via recombination and mutation events.

Although coalescent models are powerful generative tools, their computational complexity is unsuited to inference on chromosome length haplotypes. Therefore, the dominant haplotype likelihood model used for statistical inference is the Li and Stephens (2003) model (LS) and its various modifications. LS closely approximates the more exact coalescent models but admits implementations with rapid runtime.

Orthogonal to statistical models, another important frontier in genomics is the development of the variation graph, as described in Paten et al. (2014). This is a structure which encodes the wide variety of variation found in the population, including many types of variation which cannot be represented by conventional models. Variation graphs are a natural structure to represent reference cohorts of haplotypes since they encode haplotypes in a canonical manner: as node sequences embedded in the graph (see Novak et al., 2016).

Dilthey et al. (2015) demonstrate the benefit of incorporating a graph representation of population information into a model for genome inference. However, their model does not account for haplotype phasing. In this paper, we present the first statistical model for haplotype modelling with respect to graph-embedded populations.

We also describe an efficient algorithm for calculating haplotype likelihoods with respect to large reference panels. The algorithm makes significant use of the graph positional Burrows-Wheeler transform (gPBWT) index of haplotypes described by Novak et al. (2016).

2 Materials and methods

2.1 Encoding the full set of human variation

Haplotypes in the Kingman (1982)$n$-coalescent and Li and Stephens (2003) models are represented as sequences of values at linearly ordered, non-overlapping binary loci. Some authors model multiallelic loci (for example, single base positions taking on values of A, C, T, G or gap) as in Lunter (2016), but all assume that the entirety of genetic variation can be expressed by values at linearly ordered loci.

However, many types of genetic variation cannot be represented in this manner. Copy number variations, inversions or transpositions of sequence create cyclic paths which cannot be totally ordered. Large population cohorts such as the 1000 Genomes Project Consortium et al. (2015) project data contain simple insertions, deletions and substitution at a sufficient density that these variants sometimes overlap or nest into structures not representable by linearly ordered sites. Two examples of this phenomenon from 1000 Genomes data [Phase 3 Variant Call Format file (VCF)] for chromosome 22 are pictured in Figure 1.

Fig. 1.

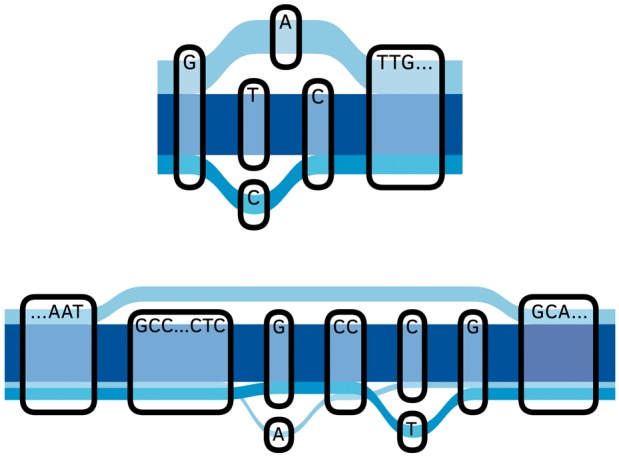
Two examples of non-linearly orderable loci in a graph of 1000 Genomes variation data for chromosome 22 which form overlapping or nested sites

In order to represent these more challenging types of variation, we use a variation graph. This is a type of sequence graph—a mathematical graph in which nodes represent elements of sequence, augmented with 5′ and 3′sides, and edges are drawn between sides if the adjacency of sequence is observed in the population cohort (see Paten et al., 2017). Haplotypes are embedded as paths through oriented nodes in the graph. We are able to represent novel recombinations, deletions, copy number variations or other structural events by adding paths with new edges to the graph, and novel inserted sequence by paths through new nodes.

2.2 Adapting the recombination component of LS to graphs

The Li and Stephens (2003) model (LS) can be described by an HMM with a state space consisting of previously observed haplotypes and observations consisting of the haplotypes’ alleles at loci. Recombinations correspond to transitions between states and mutations are modelled within the emission probabilities. Since variation graphs encode full nucleic acid sequences rather than lists of sites we extend the model to allow recombinations at base-pair resolution rather than just between loci.

Let $G$ denote a variation graph. Let $\mathcal{S}\left(G\right)$ be the set of all possible finite paths visiting oriented nodes of $G$. A path $h$ in $\mathcal{S}\left(G\right)$ encodes a potential haplotype. A variation graph posesses an embedded population reference cohort$H$ which is a multiset of haplotypes $p\in \mathcal{S}\left(G\right)$. Given a pair $(G,H)$, we seek the likelihood $P\left(h\right|G,H)$ that $h$ arose from haplotypes in $H$ via recombinations.

Recall that every oriented node of $G$ is labelled with a nucleic acid sequence. Therefore, every path $h\in \mathcal{S}$ corresponds to a nucleic acid sequence $seq\left(h\right)$ formed by concatenation of its node labels. We represent recombinations between haplotypes by assembling subsequences of these sequences $seq\left(h\right)$ for $h\in H$. We call a concatenation of such subsequences a recombination mosaic. This is pictured in Figure 2.

Fig. 2.

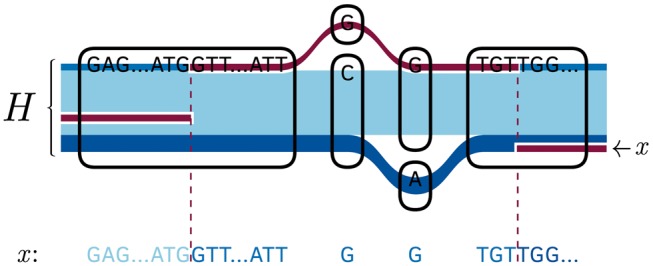
The labelled path shows the recombination mosaic $x$ superimposed on the embedded haplotypes $H$ in our 1000 Genomes project chr 22 graph; below, $x$ is mapped onto its nucleic acid sequence

Fig. 3.

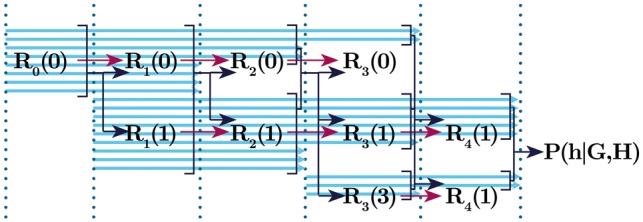
A sketch of the flow of information in the likelihood calculation algorithm described. Blue arrows a represent the rectangular decomposition, $R_{·}(·)$ are prefix likelihoods

We can assign a likelihood to a mosaic $x$ by analogy with the recombination model from LS. Assume that nucleotide in $x$ has precisely one successor in each $p\in H$ to which it could recombine. Then, between each base pair, we assign a probability ${\pi }_r$ of recombining to a given other $p\in H$, and therefore a probability $(1-(\left|H\right|-1\left){\pi }_r\right)$ of not recombining. Write ${\pi }_c$ for $(1-(\left|H\right|-1\left){\pi }_r\right)$.

By the same argument underlying the LS recombination model, we then we have a probability of a given mosaic having arisen from $(G,H)$ through recombinations:

$$P\left(x\right|G,H)={\pi }_r^{R\left(x\right)}{\pi }_c^{\left|x\right|-R\left(x\right)}$$ (1)

where $\left|x\right|$ is the length of $x$ in base pairs and $R\left(x\right)$ the number of recombinations in $x$. We will use this to determine the probability $P\left(h\right|G,H)$ for a given $h\in \mathcal{S}\left(G\right)$, noting that multiple mosaics $x$ can correspond to the same node path $h\in \mathcal{S}\left(G\right)$.

Given a haplotype $h\in \mathcal{S}\left(G\right)$, let $\chi \left(h\right)$ be the set of all mosaics involving the same path through the graph as $h$. The law of total probability gives

$$P\left(h\right|G,H)={\sum }_{x\in \chi \left(h\right)}P(x|G,H)$$ (2)

$$={\sum }_{x\in \chi \left(h\right)}{\pi }_c^{\left|h\right|-R\left(x\right)}{\pi }_r^{R\left(x\right)}={\pi }_c^{\left|h\right|}{{\sum }_{x\in \chi \left(h\right)}\left(\frac{{\pi }_r}{{\pi }_c}\right)}^{R\left(x\right)}$$ (3)

Let $\rho :=\frac{{\pi }_r}{{\pi }_c}$; then $P\left(h\right|G,H)$ is proportional to a ${\rho }^{R\left(x\right)}$-weighted enumeration of $x\in \chi \left(h\right)$.

We can extend this model by allowing recombination rate $\pi \left(n\right)$ and effective population size $\left|H{|}_{\text{eff}}\right(n)$ to vary across the genome according to node $n\in G$ in the graph. Varying the effective population size allows the model to remain sensible in regions traversed multiple times by cycle-containing haplotypes. In our basic implementation we will assume that $\pi \left(n\right)$ is constant and $\left|H{|}_{\text{eff}}\right(n)=|H|$; however varying these parameters does not add to the computational complexity of the model.

2.3 A linear-time dynamic programming for likelihood calculation

We wish to calculate the sum ${\sum }_{x\in \chi \left(h\right)}{\rho }^{R\left(x\right)}$ efficiently. (See (3) above) We will achieve this by traversing the node sequence $h$ left-to-right, computing the sum for all prefixes of $h$. Write $h_b$ for the prefix of $h$ ending with node $b$.

Definition 1. A subinterval$s$ of a haplotype $h$ is a contiguous subpath of $h$. Two subintervals $s_1,s_2$ of haplotypes $h_1,h_2$ are consistent if $s_1=s_2$ as paths, however we distinguish them as separate objects.

Definition 2. Given a indices $a,b$ of nodes of a haplotype $h$, $S_b^a$ is the set of subintervals $s^{*}$ of $p\in H$ such that

1. there exists a subinterval $s$ of $h$ which begins with $a$, ends with $b$ and is consistent with $s^{*}$

2. there exists no such subinterval of $p$ which begins with $a-1$, the node before $a$ in $h$(left-maximality)

Definition 3. For a given prefix $h_b$ of $h$ and a subinterval $s^{*}$ of a haplotype $p\in H$, define the subset $\chi {\left(h\right)}_{s^{*}}\subseteq \chi \left(h\right)$ as the set of all mosaics whose rightmost segment arose as a subsequence of $s^{*}$.

The following result is key to being able to efficiently enumerate mosaics:

Claim 1. If $s_1,s_2\in S_b^a$ for some $a$, then there exists a recombination-count preserving bijection between $\chi {\left(h_b\right)}_{s_1}$ and $\chi {\left(h_b\right)}_{s_2}$.

Proof. See Supplementary Material.

Corollary 1. If we define

$$R_b\left(s_i\right):={\sum }_{x\in \chi {\left(h_b\right)}_{s_i}}{\rho }^{R\left(x\right)}$$ (4)

then $R_b\left(s_1\right)=R_b\left(s_2\right)$ if $s_1,s_2\in S_b^a$ for some $a$. Call this shared value $R_b\left(a\right)$.

Definition 4. $A_b$ is the set of all nodes $a\in G$ such that $S_b^a$ is nonempty.

Using these results, the likelihood $P\left(h_b\right|G,H)$ of the prefix $h_b$ ending at index $b$ can be written as

$$P\left(h_b\right|G,H)={\pi }_c^{\left|h_b\right|}{\sum }_{s_i}{R}_b(s_i)={\pi }_c^{\left|h_b\right|}{\sum }_{a\in A_b}\left|S_b^a{R}_b\right(a)$$ (5)

Let $b-1$ represent the node preceding $b$ in $h$; we wish to show that if we know $R_{b-1}\left(a\right)$ for all $a\in A_{b-1}$, we can calculate $R_b\left(a\right)$ for all $a\in A_b$ in constant time with respect to $\left|h\right|$. This can be recognized by inspection of the following linear transformation:

$$R_b\left(a\right)=\rho f_s(w,\ell )(A+B)+$$

$$1_{a\ne b}(1-\rho )\left(f_t\right(\ell \left)R_{b-1}\right(a)+$$

$$\frac{f_s(w,\ell )+f_t(\ell )}{w}A)$$ (6)

where $w={\sum }_a\left|S_b^a\right|$, $f_s(w,\ell ):={(1+(w-1)\rho )}^{\ell -1}$, $f_t(\ell ):={(1-\rho )}^{\ell -1}$, and $A,B$ are the $\left|A_{b-1}\right|$-element sums

$$A:={\sum }_{a\in A_{b-1}}\left|S_b^a\right|R_{b-1}\left(a\right),$$ (7)

$$B :={\sum }_{a\in A_{b-1}}\left[\right|S_{b-1}^a|-|S_b^a\left|\right]R_{b-1}\left(a\right)$$ (8)

Proof that (6) computes $R_b(·)$ from $R_{b-1}(·)$ is straightforward but lengthy and therefore deferred to the Supplementary Material.

If we assume memoization of the polynomials $f_s(h,\ell ),f_t(\ell )$, and knowledge of $w,\ell$ and all $\left|S_b^a\right|$’s, then all $R_b\left(a\right)$_’s can be calculated together in two shared $\left|A_{b-1}\right|$-element sums (to calculate $A$ and $A+B$) followed by a single sum per $R_b\left(a\right)$. Therefore, by computing increasing prefixes $h_b$ of $h$, we can compute $P\left(h\right|G,H)$ in time complexity which is $\mathcal{O}(n·m)$ in $n=\left|h\right|$, and $m={\text{max}}_b\left|A_b\right|$. The latter quantity is bounded by $\left|H\right|$ in the worst theoretical case; we will show experimentally that runtime is asymptotically sublinear in $\left|H\right|$.

2.4 Using the gPBWT to enumerate equivalence classes in linear time

The gPBWT index described by Novak et al. (2016) is a succinct data structure which allows for linear-time subpath search in a variation graph. This is graph analogue of the positional Burrows Wheeler transform by Durbin (2014) which is used in the Lunter (2016) fast implementation of the Viterbi algorithm in the LS model. Like other Burrows-Wheeler transform variants, the gPBWT possesses a subsequence search function which returns intervals in a sorted path index.

Novak et al. (2016) prove that the gPBWT allows $\mathcal{O}\left(n\right)$ query of the number of subintervals from a set of graph-embedded paths containing a sequence of length $n$. Therefore, for any indices $a,b$ in a path $h$ we can compute the following quantity in $\mathcal{O}(b-a)$ time.

Definition 5. $J_b^a:=$ the number of subpaths in $H$ matching $h$ between nodes $a$ and $b$.

Since we can cache the search interval used to compute $J_b^a$ from the gPBWT, we can also calculate $J_b^a$ in $\mathcal{O}\left(1\right)$ time given that we have already computed $J_{b-1}^a$. This is important because

Claim 2. $\left|S_b^a\right|=J_b^a-J_b^{a-1}$

Proof.

By straightforward manipulation of definitions 2 and 5.

And therefore, if we have already calculated $\left\{\right|S_{b-1}^a|:a\in A_{b-1}\}$, then in order to compute $\left\{\right|S_b^a|:a\in A_b\}$, we need only perform $\left|A_{b-1}\right|$$\mathcal{O}\left(1\right)$ extensions of the gPBWT search intervals used to compute the $\left|S_{b-1}^a\right|$’s and one additional $\mathcal{O}\left(1\right)$ query to compute $\left|S_b^b\right|$.

Therefore, we can compute all nonzero values $\left|S_b^a\right|$, for indices $a\le b$ of $h$, using $\left|A_{b-1}\right|+1$$\mathcal{O}\left(1\right)$ gPBWT search interval extensions for each node $b\in h$. This makes the calculation of all such nonzero $\left|S_b^a\right|$’s calculable in $\mathcal{O}(n·m)$ time overall, where $n=\left|h\right|$ and $m={\text{max}}_b\left|A_b\right|$. This result, combined with the results of Section 2.3, show that we can calculate $P\left(h\right|G,H)$ in $\mathcal{O}(n·m)$ time, for $n=\left|h\right|$ and $m={\text{max}}_b\left|A_b\right|$.

2.5 Modelling mutations

We can assign to two haplotypes $h,h\prime$ the probability $P_m\left(h\right|h\prime )$ that $h$ arose from $h\prime$ through a mutation event. As in LS model, we can assume conditional independence properties such that

$$P_{\text{tot}}\left(h\right|G,H)={\sum }_{h\prime \in seq\left(G\right)}{P}_m(h|h\prime )P_r(h\prime |G,H)$$ (9)

It is reasonable to make the simplifying assumption that $P_m\left(h\right|h\prime )=0$ unless $h\prime$ differs from $h$ exclusively at short, non-overlapping substitutions, indels and cycles since more dramatic mutation events are vanishingly rare. This assumption is implicitly contained in the n-coalescent and LS models by their inability to model more complex mutations.

Detection of all simple sites in the graph traversed by $h$ can be achieved in linear time with respect to the length of $h$. The number of such paths remains exponential in the number of simple sites. However, our model allows us to perform branch-and-bound type approaches to exploring these paths. This is possible since we can calculate upper bounds for likelihood from either a prefix, or from interval censored haplotypes where we do not specify variants within encapsulated regions in the middle of the path.

Furthermore, it is evident from our algorithm that if two paths share the same prefix, then we can reuse the calculation over this prefix. If two paths share the same suffix, in general we only need to recompute the $\left|S_b^a\right|$ values for a small number of nodes. This is demonstrated in Section 4.2.

3 Implementation

We implemented the algorithms described in C ++, building on the variation graph toolkit vg by Garrison (2016). This is found in the ‘haplotypes’ branch at https://github.com/yoheirosen/vg. No comparable graph-based haplotype models exist, so we could not provide comparative performance data; absolute performance on a single machine is presented instead.

4 Results

4.1 Runtime for individual haplotype queries

We assessed time complexity of our likelihood algorithm using the implementation described above. Tests were run on single threads of an Intel Xeon X7560 running at 2.27 GHz.

To assess for time dependence on haplotype length, we measured runtime for queries against a 5008 haplotype graph of human chromosome 22 built from the 1000 Genomes Phase 3 VCF on the hg19 assembly created using vg and 1000 Genomes Project Consortium et al. (2015) project data. Starting nodes and haplotypes at these nodes were randomly selected, then walked out to specific lengths. In our graph, 1 million nodes correspond, on average, to 16.6 million base pairs. Reported runtimes are for performing both the rectangular decomposition and likelihood calculation steps (Fig. 4).

Fig. 4.

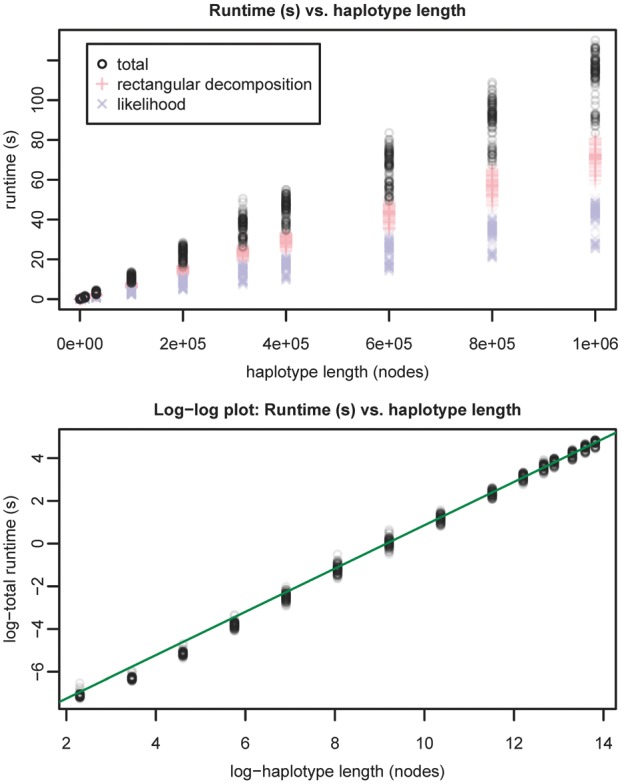
Runtime (s) versus haplotype length (nodes) for Chr 22 1000 Genomes data. Line with slope $1.01$ and $R^2=0.972$ was fitted to samples with length >50 000 nodes in the log-log plot. This supports a $\mathcal{O}(n)$ time complexity with respect to haplotype length

The observed relationship (see Fig. 4) of runtime to haplotype length is consistent with $\mathcal{O}\left(n\right)$ time complexity with respect to $n=\left|h\right|$.

We also assessed the effect of reference cohort size on runtime. Random subsets of the 1000 Genomes data were made using vcftools (Danecek et al., 2011) and our graph-building process was repeated. Five replicate subset graphs were made per population size with the exception of the full population graph of 2504 individuals.

We observe (see Fig. 5) an asymptotically sublinear relationship between runtime and reference cohort size.

Fig. 5.

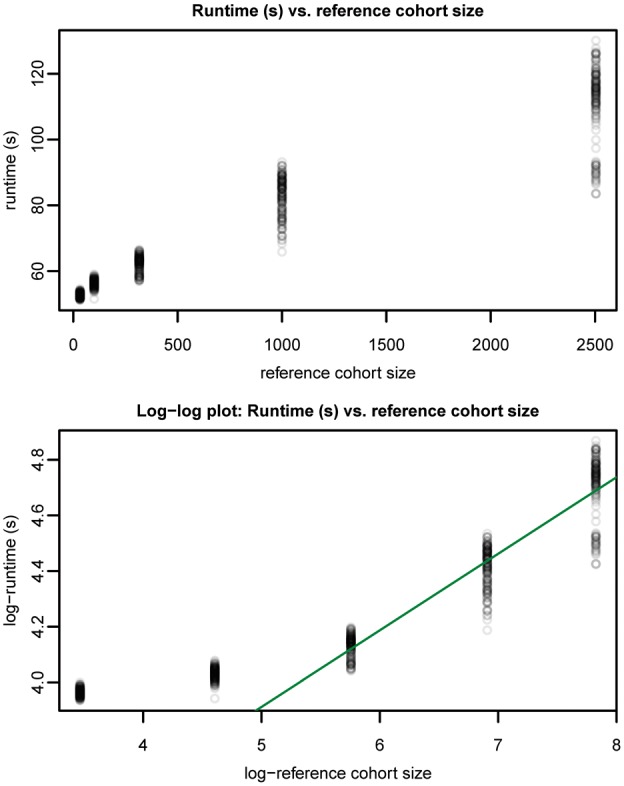
Runtime (s) versus reference cohort size (diploid individuals) for chromosome 22 1000 Genomes data. Line with slope $0.27$ and $R^2=0.888$ was fitted to samples with population size >300 individuals in the log-log plot. This supports an asymptotically sublinear time complexity with respect to reference cohort size

4.2 Time needed to compute the rectangular decomposition of a haplotype formed by a recombination of two previously queried haplotypes

The assessments described above are for computing the likelihood of a single haplotype in isolation. However, haplotypes are generally similar along most of their length. It is straightforward to generate rectangular decompositions for all haplotypes $h\in H$ in the population reference cohort by a branching process, where rectangular decompositions for shared prefixes are calculated only once. This will capture all variants observed in the reference cohort.

Haplotypes not in the reference cohort can then be generated through recombinations between the $h\in H$. If this produces another haplotype also in $H$, it suffices to recognize this fact. If not, then given that $h$ is formed by a recombination of $h_1$ and $h_2$, then $h$ must contain some sequence of nodes $c\to j$ contained in neither $h_1$ nor $h_2$. We only need to recalculate $S_b^a$ for $a\le j\le b$.

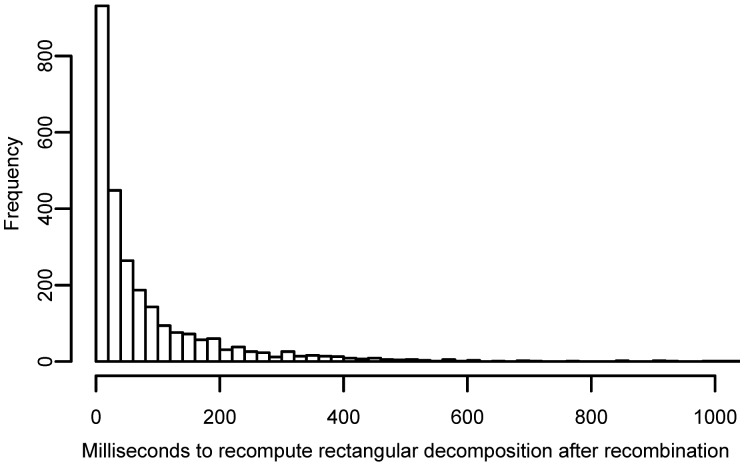
We have implemented methods to recognize these nodes and perform the necessary gPBWT queries to build the rectangular decomposition for $h$. The distribution of time taken (in milliseconds) to generate this new rectangular decomposition for randomly chosen $h_1,h_2$ and recombination point is shown in Figure 6.

Fig. 6.

Distribution of times (in milliseconds) required to recompute the rectangular decomposition of a haplotye given that it was formed by recombination of two haplotypes for which rectangular decompositions have been constructed. This graph omits 0.6% of observations which are outliers beyond 1 s of time

Mean time is 141 ms, median time 34 ms, first quartile time 12 ms and third quartile time 99 ms. To compute a rectangular decomposition from scratch mean time is 71 160 ms, first quartile time 68 690 ms and third quartile time 73 590 ms.

This rapid calculation of rectangular decompositions formed by recombinations of already-queried haplotypes is promising for the feasibility of a mutation model or of sampling the likelihoods of large numbers of haplotypes. Similar methods for the likelihood computation using this rectangular decomposition are a subject of our current research.

4.3 Qualitative assessment of the likelihood function’s ability to reflect rare-in-reference features in reads

We used vg to map the 1000 Genomes low coverage read set for individual NA12878 on chromosome 22 against the variation graph described previously. 1 476 977 reads were mapped. Read likelihoods were computed by treating each read as a short haplotype. These likelihoods were normalized to ‘relative log-likelihoods’ by computing their log-ratio against the maximum theoretical likelihood of a sequence of the same length. An arbitrary value of ${10}^{-9}$ was used for ${\pi }_{\text{recomb}}$.

We define a read to contain $n$ ‘novel recombinations’ if it is a subsequence of no haplotype in the reference, but it could be made into one using a minimum of $n$ recombination events. We define the prevalence of the rarest variant of a read to be the lowest percentage of haplotypes in the index which pass through any node in the read’s sequence.

We segregated our set of mapped reads according to these features. We make three qualitative observations, which can be observed in (Fig. 7). First, the likelihood of a read containing a novel recombination is lower than one without any novel recombinations. Second, this likelihood decreases as novel recombinations increase. Third, the likelihood of a read decreases with decreasing prevalence of its rarest variant.

Fig. 7.

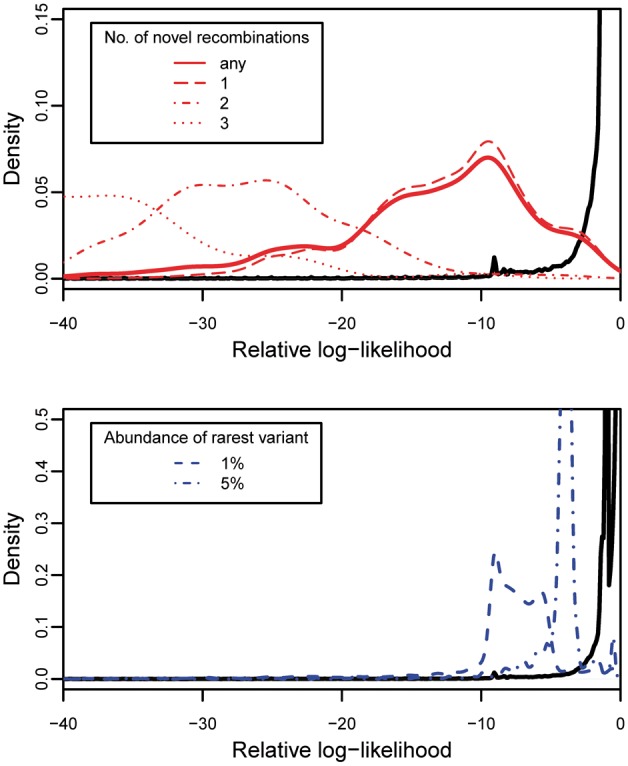
Left: density plot of relative log-likelihood of reads not containing variants below 5% prevalence or novel recombinations (black line) versus reads containing novel recombinations. Right, density plot of relative log-likelihood of reads not containing variants below 5% prevalence or novel recombinations (black line) versus reads containing variants present at under 5% prevalence and under 1% prevalence

A further comparison (Fig. 8) of these same mapped reads against reads which were randomly simulated without regard to haplotype structure shows that the majority of mapped reads from NA12878 score are assigned higher relative log-likelihoods than the majority of randomly simulated reads.

Fig. 8.

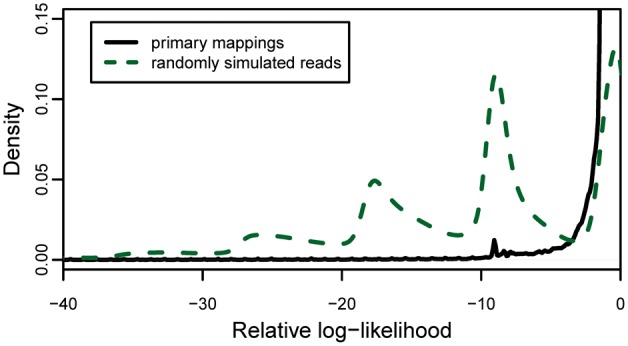
Density plot of relative log-likelihood of mapped reads versus randomly generated simulated haplotypes

5 Conclusions

We have introduced a method of describing a haplotype with respect to the sequence it shares with a variation graph-encoded reference cohort. We have extended this into an efficient algorithm for haplotype likelihood calculation based on the gPBWT described by Novak et al. (2016). We applied this method to a full-chromosome graph consisting of 5008 haplotypes from the 1000 Genomes data set to show that this algorithm can efficiently model recombination with respect to both long sequences and large reference cohorts. This is an important proof of concept for translating haplotype modelling to the breadth of genetic variant types and structures representable on variation graphs.

Our basic algorithm does not directly model mutation, however we describe an extension which does. Making this extension computationally tractable will depend on being able to very rapidly compute likelihoods of sets of similar haplotypes. We demonstrate that our algorithm can be modified to compute rectangular decompositions for haplotypes related by a recombination event in millisecond-range times. We have also devised mathematical methods for recomputing likelihoods of similar haplotypes which take advantage of analogous redundancy properties; however, they have yet to be implemented and tested. However, we anticipate that we will be able to compute likelihoods of large sets of related haplotypes on a time scale which makes modelling mutation feasible.