Abstract
Motivation
Current metagenomics approaches allow analyzing the composition of microbial communities at high resolution. Important changes to the composition are known to even occur on strain level and to go hand in hand with changes in disease or ecological state. However, specific challenges arise for strain level analysis due to highly similar genome sequences present. Only a limited number of tools approach taxa abundance estimation beyond species level and there is a strong need for dedicated tools for strain resolution and differential abundance testing.
Methods
We present DiTASiC (Differential Taxa Abundance including Similarity Correction) as a novel approach for quantification and differential assessment of individual taxa in metagenomics samples. We introduce a generalized linear model for the resolution of shared read counts which cause a significant bias on strain level. Further, we capture abundance estimation uncertainties, which play a crucial role in differential abundance analysis. A novel statistical framework is built, which integrates the abundance variance and infers abundance distributions for differential testing sensitive to strain level.
Results
As a result, we obtain highly accurate abundance estimates down to sub-strain level and enable fine-grained resolution of strain clusters. We demonstrate the relevance of read ambiguity resolution and integration of abundance uncertainties for differential analysis. Accurate detections of even small changes are achieved and false-positives are significantly reduced. Superior performance is shown on latest benchmark sets of various complexities and in comparison to existing methods.
Availability and Implementation
DiTASiC code is freely available from https://rki_bioinformatics.gitlab.io/ditasic.
Supplementary information
Supplementary data are available at Bioinformatics online.
1 Introduction
Rapid advances in next generation sequencing (NGS) technologies have revolutionized the field of metagenomics (Oulas et al., 2015; Wooley et al., 2010). Metagenomics enables the study of complex communities in environmental or human samples by direct analysis of whole shotgun metagenomes, without prior need for cultivation. Among others, two major goals in metagenomics profiling studies are pursued. One is to unravel the taxonomic composition of the community in a given sample, the second concerns the abundance change of taxa between different metagenomes (Neelakanta and Sultana, 2013).
Especially, differences occurring on strain level in microbiomes can be of high relevance for disease and health state (Nawy, 2015). Investigations on strain level have been proven to be crucial for the understanding of evolutionary processes, adaption, pathogenicity, drug resistance and transmission (Lieberman et al., 2014; Rosen et al., 2015; Shapiro et al., 2012; Snitkin et al., 2011). However, although importance of resolution on strain level is acknowledged, there are still only a limited number of tools focusing on accurate profiling beyond species level (Sczyrba et al., 2017).
Altogether, in this context, three main concepts are relevant: strain identification, abundance estimation and differential abundance assessment. Our objective in this work is to address all these steps by specifically focusing on strain level resolution and its arising challenges. In particular for differential abundance evaluation on the strain level, there is a need for novel tools. Here, we use the term strain level referring to the highest possible resolution available and always work on the exact genome level.
Many concepts have been pioneered for taxa identification and quantification, apart from assembly and binning methods, diverse metagenomics profiling tools have specialized on this task (Lindgreen et al., 2016; Sczyrba et al., 2017). In practice, these concern the assignment of the sequenced reads to taxa and corresponding inference of taxa abundance. Read assignment can be conducted either by the full alignment of reads to genome sequences or by using pseudo-alignment approaches (Wood and Salzberg, 2014). The latter is sufficient for many metagenomics quantification studies due to the fact that only the assignment of reads is required and not exact alignments. Another variant is to rely on marker genes instead of complete genome sequences (Segata et al., 2012; Scholz et al., 2016; Luo et al., 2015); however, a general drawback is the requirement of high-sequencing coverage contrasting typical metagenomics scenarios of many low abundant taxa (Li, 2015). One of the first and popular reference-based tools for read assignment in metagenomics was MEGAN (Huson et al., 2007), which assigns the reads to the lowest common ancestor in the taxonomic tree at which a unique alignment is achieved. However, this approach limits MEGAN to the identification and quantification of only higher taxonomic levels. A main characteristic on strain level is the presence of highly similar reference sequences, causing many reads to match to multiple genomes equally. A further common practice is to assign multiply mapped reads heuristically to reference genomes according to uniquely mapped read proportions (Liu et al., 2017; Nayfach et al., 2016). Yet, this can easily result in biased abundance estimates due to reference sequence similarities as observed e.g. by Liu et al., 2017. GRAMMy (Xia et al., 2011) and GASiC (Lindner and Renard, 2013) were the first tools to include reference genome similarities in a model for the resolution of ambiguously mapped reads. Since being based on read alignments, these methods can encounter computational limits in large sample sizes. A new era evolved by utilizing fast k-mer approaches, significantly accelerating read assignments, with Kraken being a popular representative (Wood and Salzberg, 2014), but showing reduced resolution power on strain level (Schaeffer et al., 2017). As a consequence, the importance of combining fast mapping approaches with methods for read ambiguity resolution was recognized. This was likewise applied in the field of RNA-Seq, resulting in the development of kallisto (Bray et al., 2016), which promises to also support metagenomics abundance analysis (Schaeffer et al., 2017). kallisto consists of two parts, a new fast pseudo-aligner based on k-mer hashing and an expectation–maximization (EM) algorithm on equivalence classes, which carries out the statistical resolution of read ambiguities.
In this work, we present DiTASiC (Differential Taxa Abundance including Similarity Correction) which relies on pseudo-alignments for mapping and is built on a novel generalized linear model (GLM) framework for read ambiguity resolution. Hereby, we significantly improve on our previous development in this field, GASiC. Our new model framework is developed to adapt more precisely to the characteristics of absolute mapping count data observed for taxa. Moreover, our method improves on existing pure abundance profiling strategies by including additional error terms in the model and capturing abundance estimation uncertainties.
The integration of variance of abundance estimates plays a crucial role for the differential abundance analysis. This variance reflects the uncertainty in the resolution of read mapping ambiguities in the presence of similar reference sequences. Hence, it is of particular importance on strain level to integrate this variance to enable accurate detections of differential or non-differential abundance of a taxon in co-existence of similar strains, most notably in the case of smaller changes.
Most approaches developed for identification of differential abundance in the field of comparative metagenomics focus exclusively on experimental sources of variance, namely on sample variance relevant within technical and biological replicates. A large variety of tools is available (Jonsson et al., 2016); amongst others, software packages implementing diverse parametric and non-parametric statistical standard tests (Karlsson et al., 2013; Parks et al., 2014; Parks and Beiko, 2010; Segata et al., 2011; White et al., 2009). Another group comprises zero-inflated models either combined with Gaussian mixture distribution (Paulson et al., 2013), log-normal distribution (Sohn et al., 2015), or beta-regression (Peng et al., 2015), concentrating on the potential sparsity in count data. Further, popular methods from RNA-Seq analysis such as edgeR (Robinson et al., 2010), DESeq2 (Love et al., 2014) and voom (Law et al., 2014) are also commonly applied in comparative metagenomics. Without doubt, the integration of experimental variance is of high necessity when comparing groups of samples. However, here, we want to emphasize and raise awareness for variance in abundance estimates and its impact on differential abundance analysis on strain level.
Further it should be noted that many methods treat the differential assessment of taxa and genes equivalently. However, assumptions such as the majority of features will show non-differential abundance, which has widely been proven for gene expression, are not necessarily valid for taxa abundance in a sample. Antibiotics treatment and other life influential factors have shown rapid changes of microbial compositions in human samples (David et al., 2014) and similar scenarios are found in ecological environments (Gibbons and Gilbert, 2015). Thus, commonly used assumptions cannot be easily transferred to composition change.
In summary, we present DiTASiC, which addresses abundance estimation as well as differential abundance of taxa specifically focusing on strain level. A new GLM framework is proposed for resolution of read mapping ambiguities and allows inference of highly accurate taxa abundance estimates. Second, a statistical framework, which integrates abundance estimate uncertainties, is built for differential abundance testing. Here, no prior assumptions on overall composition change are required. A resulting list of tested taxa is reported with estimated abundances, fold-changes and P-values to infer significance. The performance of DiTASiC is evaluated on different metagenomics data sets from four different data sources and in comparison to existing tools.
2 Materials and methods
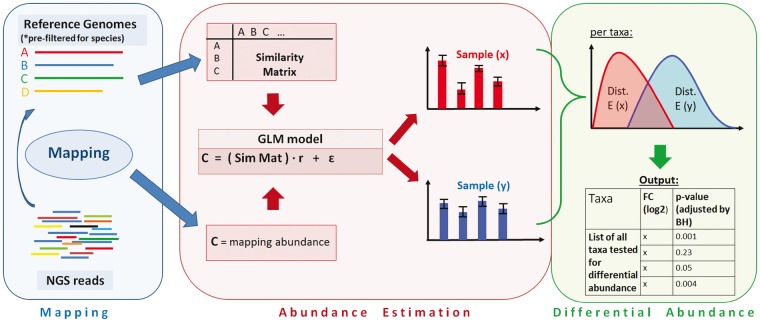
DiTASiC is designed as a comprehensive approach for abundance estimation and differential abundance assessment of individual taxa. Thereby, the main focus is on distinguishing on the strain level with highly similar sequences and its corresponding challenges. The steps of the DiTASiC workflow are illustrated in Figure 1, it consists of three main parts: mapping, abundance estimation and differential abundance assessment.
Fig. 1.
Workflow of DiTASiC. It consists of three main parts: (i) mapping, (ii) taxa abundance estimation and (iii) differential abundance assessment. (i) We rely on prior pre-filtering of species by external profiling tools such as Kraken or Mash. Reads are mapped to the given reference genome sequences and the number of matching reads per reference are counted (mapping abundance). A similarity matrix reflecting the genome similarities is constructed. (ii) Subsequently, a GLM is built for resolution of read count ambiguities, resulting in corrected abundance estimates along with standard errors. (iii) For the comparison of metagenomes, abundances are formulated as distributions and their divergence reflects differential events. A final list of tested taxa with fold change and adjusted P-values is reported
In the first two parts we built on some of the core ideas of our previously published tool GASiC (Lindner and Renard, 2013), while strongly improving on abundance quantification and introducing new methodology to address the critical aspects of variance of abundance estimates and differential abundance.
In a metagenomics sample measured by NGS technologies we face millions to billions of reads which are derived from diverse taxa. DiTASiC relies on a pre-filtering of species by fast profiling tools such as Kraken (Wood and Salzberg, 2014), CLARK (Ounit et al., 2015), Kaiju (Menzel et al., 2016), or by using Mash (Ondov et al., 2016), a genome distance calculator, to reduce the number of potential reference genomes and keep the main focus on species expected in the data. Here, we specifically aim at revealing the picture on the highest available strain levels. In the first mapping step, all reads are assigned to the given references as a first attempt to decipher their potential origin. The number of hits per reference genome is counted. We refer to it as mapping abundance of a taxon. In the next step of abundance estimation, a new generalized linear model (GLM) is introduced for the resolution of shared read counts, which are crucial on strain level. As a result, more accurate abundance estimates are obtained for the different strains along with standard errors for abundance uncertainty. In the last section, the focus is on the comparison of whole metagenomics samples and the assessment of differential abundance of taxa. Thereby, we concentrate on a method to integrate the variance of abundance estimates. Abundances are transformed into distributions, divergence of distributions is used to infer differential events and corresponding P-values are calculated.
The details of the three DiTASiC parts are explained in the following sections. The following notation is applied: different metagenomics samples are denoted as D = {Dk, k = 1,…, K}, each containing N = {Nk, k= 1,…, K} total input reads. A set of taxa S = {Si, i= 1,…, M} with known reference sequences is considered. Thereby, Si is synonymously used for both the taxa itself as well as its exact reference genome. Mapping and abundance estimation are addressed for each data set separately, while the last step of differential abundance estimation is defined on a pair of samples from D.
2.1 Mapping
To identify their origin, the assignment of reads is conducted by a competitive mapping approach, which means all selected reference genome sequences S are simultaneously offered to all reads of a sample D ϵ D for mapping. Particularly on strain level, reference sequences exhibit high sequence similarities, thus some reads are expected to match to different genome sequences equally well. These reads are defined as shared reads and we account for all their multiple hits. However, the exact matching position in a reference genome Si is not of importance and several position hits of one read on the same reference Si are counted as one. For the mapping itself, a pseudo-alignment approach provided as part of the kallisto implementation (Bray et al., 2016) is applied. As no exact alignments are required for our purpose, a pseudo-aligner is sufficient and proves to be much faster and accurate using a fast kmer-based approach. Here, we gain significant improvements over our previously published tool GASiC, which relied on individual reference alignments by Bowtie 2 (Langmead and Salzberg, 2012).
Altogether, we extract and count the number of read hits each reference genome receives and refer to it as mapping abundance ci of taxon Si. In case the data set D consists of mainly dissimilar references and is dominated by clearly unique mappings, the observed mapping abundances ci may already closely reflect the underlying true abundances of the taxa. However, if many similar references are present, which is a common scenario on strain level, a large bias is present due to multiple hits of shared reads. The sum of the mapping abundances of all taxa then drastically exceeds the number of input reads.
2.2 Abundance estimation
Following the idea introduced in GASiC, we rely on a simulation-based representation of reference genome similarities to resolve the effect of shared reads. A similarity matrix is constructed, which encodes the proportion of reads which are expected to be shared among all pairwise combinations of reference sequences considered. Reads are simulated using Mason (Holtgrewe, 2010) based on each reference sequence, and are subsequently mapped to all references following the same competitive mapping setup as applied to the reads of D in the step before. The key element is to imitate sequencing, read, and mapping characteristics as good as possible to reproduce the source of ambiguities. Parameters such as read length and mismatch probability are crucial for the simulation of reads, and are inferred from the raw reads of D. The square matrix A = (aij), i,j = 1,…,M, is computed column-wise for each reference, with aij referring to the count of reads simulated from reference j which map to reference i. Next, the matrix is normalized column-wise by the read count ajj, the number of simulated reads which are assigned back to their reference of origin. Thus, the matrix A = (aij/ajj), i,j = 1,…,M, holds values between zero and one.
Replacing the classic linear model of GASiC, we formulate a new GLM with the vector of absolute mapping abundances c and similarity matrix A to correct for the shared read biases. Aiming to recover the true, but unknown, abundances r of the taxa:
with A = (aij), i,j= 1,…,M, c = (c1, c2, …, cM)T, r = (r1, r2, …, rM)T with non-negativity constraint r ≥ 0, and error term ɛ.
The observed mapping count ci of taxon i corresponds to a summed mixture of the underlying true abundance ri of taxon i and a proportion of shared read counts rj due to the other references:
The GLM is defined by an identity link function as a linear relation of components holds to explain the observed mapping counts. However, in this setting of discrete counts the error ɛ is defined to follow a Poisson distribution. We expect and observed no overdispersion in the abundance estimates within a sample after ambiguity correction by the model (Supplementary Material). This is in contrast to measurements of replicate samples, which may display overdispersion and motivate a negative-binomial assumption (Anders and Huber, 2010). The GLM is internally solved by an ‘iteratively reweighted least squares’ to find the maximum likelihood estimates referring to the ‘true’ abundance estimates ri for each taxon i. Along with the abundance estimates, standard errors are computed which report the range of accuracy and reliability of the abundance estimates. Further, P-values are given for each taxa estimate as a measure of significance.
In case of high uncertainty about the presence of a crucial amount of taxa within the selected set of references, the application of an implemented filtering is possible. Thereby, P-values above a set threshold, commonly a value of 0.05, and estimates below a minimum number of assigned reads are used as indicators for false-positive estimates. The filtering step helps to numerically stabilize the equation system in case of many absent taxa and a re-optimization step is subsequently conducted.
2.3 Differential abundance
In this section, the focus is on comparing metagenomics samples. The objective is to identify which taxa significantly change their abundance from one metagenome sample to another as well as which hold a constant abundance. For the differential abundance assessment of similar strains the integration of the variance of their abundance estimates is crucial. Hence, in place of directly comparing abundance point estimates of taxa between samples, we make use of the estimates as well as their standard errors.
First, the comparison of different samples requires accounting for potentially different numbers of total input reads N. The number of input reads has a significant impact on the computed abundances r and standard error estimates. A linear dependence is clearly noticeable (see Supplementary Fig. S1) and is in agreement with theoretical derivations of the GLM framework. The abundance count estimate r scales linear with the number of reads whereas the standard error scales quadratic. This means the accuracy of abundance estimates improves with increased number of input reads as expected. Altogether, a normalization factor is required and a factor of Nx/Ny is correspondingly applied to samples Dx and Dy to achieve a comparable base between samples.
In the next step, we integrate abundance estimates and corresponding standard errors to infer an abundance distribution for each taxon in each sample. Here, it is assumed that the unknown true abundance count of a taxon underlies a Poisson distribution. The potential bias due to falsely assigned reads to taxa, after correction for read ambiguities by the GLM model, is not expected to exceed the variance of a Poisson distribution. But, an analytical approach is not feasible here, as the exact distribution is described in practice by a mixture of Poisson distributions. However, an empirical approach can be pursued, which is realized by a two-step sampling process: In the first step, we define intervals with abundance estimates ri ± their standard errors as boundaries for each listed taxon. We use a scale unit of one standard error, as this reflects the uncertainty interval which is expected to contain the abundance estimate. Subsequently, potential abundance point estimates are uniformly sampled from this interval. Concurrently each of these sampled values refers to a λ value of a Poisson distribution. In the second step, for each taxon and each potential λ of it, 500 values in a default setup are drawn from the corresponding defined Poisson distribution with parameter λ. This creates one empirical distribution based on a specific λ for the taxon. Pooling all empirical distributions, created by all the different λ which are assigned to the taxon, results in an overall empirical distribution comprising 50 000 Poisson draws by default setup. We refer to it as empirical abundance distribution of a taxon.
In order to assess whether taxa show differential abundance between two samples, their abundance distributions need to be compared. As we rely on empirical distributions here, no analytical form of standard differential testing is applicable. Yet, we can transfer the assessment of differential abundance to the question to which extent the corresponding abundance distributions overlap. Clearly separated distributions refer to a significant abundance change, while an increasing overlap points to smaller or no significant difference. Measuring the separation of the distributions is implemented by randomly drawing pairs of values from either distribution. The difference within each pair is computed and yields an overall distribution of differences as a result. Thereby, the location of the zero value related to the distribution of differences is meaningful. A zero value moving towards the center of the distribution reflects a higher previous overlap and corresponds to a less significant abundance change. An empirical P-value is correspondingly inferred by determining the quantile of the zero value within the distribution.
In case a taxon is only detected within one sample, while absent in the other, the single abundance distribution of the taxon is tested against a user-defined threshold corresponding to a minimum read count. The latter test yields the significance of taxa presence in this one sample.
Generally, P-values are calculated individually for all taxa considered in the samples of comparison, either to assess differential abundance of taxa present in both samples or to infer new appearance of taxa in only one sample. Thus, P-values need to be adjusted for multiplicity, which is performed by the method of Benjamini-Hochberg (Benjamini and Hochberg, 1995). A final report is provided listing all taxa tested for differential abundance along with normalized abundance estimates for each sample, log2 fold changes, and adjusted P-values.
2.4 Implementation
DiTASiC is implemented in Python3 and R (version ≥ 3.3.1), and is available from https://rki_bioinformatics.gitlab.io/ditasic. Further, a linked webpage and user manual provides easy guidance through the three main commands. DiTASiC is based on a flexible design and allows the integration of mapping algorithms and read simulators of choice. Our implementation uses the current state of the art pseudo-alignment algorithm provided within the kallisto framework (Bray et al., 2016), which can be individually called by the command kallisto pseudo. As a prerequisite, an overall index is built on selected reference sequences. Using the generated tsv and ec file formats, we extract the mapping counts of the contigs and merge them according to genomes. This allows circumventing the use of large SAM files. Further, read simulators need to be optimally adapted to capture the read characteristics. Here, the Mason simulator (Holtgrewe, 2010) serves as default.
3 Experimental setup
We tested DiTASiC and existing approaches on a variety of data sets from four different sources (Table 1), challenging the tools by number of taxa, total number of input reads, read characteristics, abundance complexity and degree of reference similarities.
Table 1.
Characteristics of the four data sources: CAMI, FAMeS, Illumina 100 data (i100) and the simulation setups (Sim (1), (2), (3))
| Source | CAMI | FAMeS | Sim (1) | Sim (2) | Sim (3) | i100 |
|---|---|---|---|---|---|---|
| Samples | Set 1-2 | LC, MC, HC | Set 1-3 | Set 4-9 | Set 10-11 | |
| References | 225 | 122 | 35 | 35 | 55 | 100 |
| Genera | 128 | 81 | 12 | 12 | 12 | 63 |
| Species | 199 | 108 | 22 | 22 | 26 | 85 |
| Reads (M) | ∼150 | ∼1.0 | 0.75a | 0.75a | 0.75a | 53.3 |
| Length (bp) | 100 | 110 | 100 | 100 | 100 | 75 |
| Abundance range | 0.0009–8% | 2–20% | 1–30% | 0.1–15% | 0.1–2% | 0.8–2.2% |
Note: Each reference set is defined by the union of references of the underlying samples. All read profiles follow Illumina characteristics (areads are simulated by Mason).
A comprehensive simulation setup is established to enable abundance estimation as well as differential evaluation on an exact ground truth at which taxa proportions are known. In total, we consider 11 different simulation sets characterized by many strain clusters (Supplementary Fig. S2-3), and distinguish between three groups: Group (1) serves to evaluate the abundance performance with different proportions of absent taxa, group (2) defined by all 35 taxa ensures an unbiased differential abundance evaluation in pairwise comparisons and group (3) focuses on the resolution of large and highly similar strain clusters as well as on the impact of missing strains. Further, we relied on the Illumina based FAMeS data set of Pignatelli and Moya (2011), evolved from the original set by Mavromatis et al. (2007), which covers low (LC), medium (MC) and high complexity (HC) metagenomics profiles (Supplementary Fig. S4). Additionally, we tested the popular Illumina 100 data sample (Mende et al., 2012), which serves as benchmark set in the latest relevant studies (Lu et al., 2017; Schaeffer et al., 2017). Last, we used two benchmark data sets of medium complexity from a current comparative metagenomics challenge, CAMI (Sczyrba et al., 2017). We further extended the CAMI sets by simulated spike-in data, adding 30 new strains of genera already present in the original set and 20 million reads per sample, to create an additional ground truth for differential assessment. Further details on the data sets and parameter settings are found in the Supplementary Material. In all presented data sets, ground truth of relative abundances of taxa is available. Comparing the samples, a ground truth to classify differentially or non-differentially abundant taxa is given for the simulation and CAMI study, while fold-change accuracy can be assessed in all data sources.
4 Results
In the following sections, we demonstrate the performance of DiTASiC on the presented data sets in comparison to existing tools. We separately investigate three aspects: (i) abundance estimation, (ii) absent and missing taxa and (iii) differential abundance. Evaluations focus on the accuracy of estimates of relative taxa abundance as well as fold change, and on sensitivity and specificity concerning detection of differentially abundant taxa.
4.1 Abundance estimation
In this first part, we address the quantification of taxa in a given metagenomics sample, aiming for the highest taxonomic level. We highlight the strength of our proposed GLM model for the resolution of shared read counts and subsequent inference of corrected abundance estimates for taxa considered.
We compare to our previously published tool GASiC (Lindner and Renard, 2013), which relies on individual reference alignments and a non-negative LASSO modelling approach for abundance estimation, and present significant improvements. Further we test against the most recently published tool for RNA-Seq analysis, kallisto (Bray et al., 2016; Schaeffer et al., 2017), which has also been shown to perform superior to other existing tools in the application to metagenomics. We also evaluate on the same benchmark data to allow further comparison of tools (see Supplementary Material). Although we compare against the full version of kallisto, it is important to note, that we use and integrate the pseudo-aligner of kallisto for mapping purpose, but not kallisto’s quantification and modelling framework. Yet our main focus in this work is the modeling and resolution of arising read ambiguities due to highly similar genome sequences considered. Hence, the comparison of DiTASiC to kallisto in this section refers to a comparison of our GLM model to the statistical EM framework of kallisto.
All tools are applied to each sample individually, in total we consider and evaluate 17 different samples from four data sources.
The output of all three tools are absolute read counts assigned to each taxa in the data set considered. Normalization is applied by dividing all absolute taxa counts by the total number of input reads of the corresponding sample. We receive an estimation of a quantitative taxa composition of a sample as a result.
All data sets described here provide a ground truth of taxa abundance proportions, enabling us to assess the difference between truth and estimate. As an error measure we apply the SSE (Sum of Squared Errors) to evaluate the accuracy of the given estimates, the SSE also penalizes abundance estimates obtained for absent taxa.
The resulting error measures of abundance estimation by DiTASiC, GASiC and kallisto, according to all different data sets are reported in Table 2. Overall, DiTASiC strongly reduces the error on all data sets compared with GASiC by several orders of magnitude. Further, DiTASiC shows either comparable and in many cases improved performance to kallisto. Generally, reported error values are dependent on data size and prevailing genome similarities. However, the presented values refer to a remarkably high accuracy of abundance estimates overall. Smallest divergences of estimates from the ground truth are found for the FAMeS data sets (Supplementary Fig. S5). This is expected due to less pronounced reference similarities within the data and moderate median abundance proportions, meaning less challenge for the resolution models. The CAMI data do pose a much greater challenge, considering 255 taxa for quantification with several strain clusters and some extremely small relative abundance values. Yet, highly accurate taxa estimates, apart from few small outliers, are obtained by DiTASiC; notably also for very low relative abundances below 0.01% (see also Supplementary Fig. S6). CAMI data were not analyzed with GASiC due to computational limitations. The commonly used i100 data set is characterized by shorter reads derived from different bacterial strain clusters. DiTASiC achieves an improved accuracy in comparison to kallisto, and also to further tools when compared with the values reported in a recent benchmark study of different abundance profiling tools on the i100 set (Schaeffer et al., 2017) (see Supplementary Material and Supplementary Fig. S7). The simulation data serves as a challenge with a high number of similar strains and a smaller number of reads available for assignment. In comparison, samples in CAMI hold 150 times more reads with only seven times more taxa. The results show that DiTASiC performs superior in all sets of simulation group (2), where all taxa are present, while errors are proportionally higher in sets of group (1), where taxa are absent. Group (1) is primarily defined by the absence of distant strains or entire strain clusters; the EM algorithm of kallisto proves to be slightly more accurate in these scenarios. However, sets in simulation group (3) are characterized by the absence of strains from highly similar clusters and by the presence of very large clusters of high sequence similarities. Here, DiTASiC demonstrates to be more powerful (Supplementary Fig. S8). Notably, we observe an increased error of abundance estimates in kallisto predominantly for highly similar strain sequences. In contrast, DiTASiC reveals its particular strength in the resolution of these strain clusters, it demonstrates to precisely distinguish abundances down to sub-strains with sequence similarities above 95%. Different examples are found for the CAMI, i100 and simulation data, considering diverse Escherichia coli cluster, Corynebacterium and Staphylococcus aureus cluster (Supplementary Fig. S9). Here, an accurate cluster resolution is obtained by DiTASiC, and common errors such as abundance interchange or equalization of similar sub-strains are avoided.
Table 2.
Accuracy of taxa abundance estimates by DiTASiC, kallisto and GASiC
| DiTASiC | kallisto | GASiC | ||
|---|---|---|---|---|
| CAMI | Set 1 | 6.98 e-02 | 1.05 e-01 | n.a. |
| Set 2 | 5.36 e-02 | 5.69 e-02 | n.a. | |
| i100 | i100 | 8.23 e-06 | 5.62 e-05 | 9.32 e-04 |
| FAMeS | LC | 6.87 e-06 | 1.73 e-08 | 3.18 e-04 |
| MC | 3.07 e-08 | 1.70 e-08 | 4.17 e-04 | |
| HC | 8.34 e-08 | 2.79 e-08 | 7.79 e-05 | |
| Simulation group (1) | Set 1 | 8.38 e-07 | 7.61 e-07 | 6.92 e-03 |
| Set 2 | 9.33 e-07 | 9.61 e-07 | 1.13 e-02 | |
| Set 3 | 4.37 e-07 | 2.59 e-07 | 9.73 e-03 | |
| Simulation group (2) | Set 4 | 2.54 e-06 | 4.09 e-05 | 6.10 e-03 |
| Set 5 | 1.85 e-06 | 5.94 e-05 | 8.54 e-03 | |
| Set 6 | 2.67 e-06 | 3.46 e-05 | 2.22 e-03 | |
| Set 7 | 3.41 e-06 | 2.84 e-04 | 6.55 e-03 | |
| Set 8 | 4.93 e-06 | 2.99 e-04 | 2.27 e-03 | |
| Set 9 | 4.15 e-06 | 5.37 e-05 | 1.63 e-03 | |
| Simulation group (3) | Set 10 | 3.94 e-06 | 5.43 e-05 | 1.84 e-02 |
| Set 11 | 3.39 e-05 | 5.07 e-04 | 7.29 e-03 |
Note: Accuracy is defined by the SSE between estimates and available ground truth. A significant error reduction is shown for DiTASiC compared with GASiC and a comparable performance is observed for kallisto (highest accuracy is depicted in bold print). GASiC was not run on CAMI data due to computational limitations.
Supplementary Figure S10 visualizes the taxa abundance estimates of the different tools in comparison to the observed mapping abundances, exemplary for three simulation sets of different complexity. It clearly demonstrates how the mapping abundance, biased due to read ambiguities, mainly overestimates the ground truth and further assigns abundance counts to absent taxa. GASiC shows some significant over- and underestimations, while the accuracy of DiTASiC and kallisto is consistently high. Further, a study of two replicate sets, defined by read sets simulated with the same abundance profile, proves robustness and precise reproducibility of results by DiTASiC as well as kallisto, with significant improvement over GASiC (Supplementary Fig. S11).
4.2 Absent and missing taxa
We recommend prior pre-filtering of references to focus on reference genomes of species expected in the data. Still, frequently we consider more references than taxa actually present in the data and an inclusion of all potentially abundant strains is advised.
Hence, in the simulation groups (1) and (3) and the FAMeS data, which hold different proportions of absent taxa, we tested the detection performance of DiTASiC. The internal filtering is conducted to infer potential false-positive taxa in the given sets. In the simulation group (1) the abundant taxa proportions of 28, 40 and 45%, respectively, are exactly detected with neither false-positive nor false-negative calls. In the FAMeS data, proportion of absent taxa based on the reference set corresponds to 8, 9 and 8% in the three samples. DiTASiC achieves sensitivity and specificity of 100% for the MC and HC data. In the LC set, a false-negative is caused by missing one abundant taxon, resulting in a decreased sensitivity of 99.1%. (Supplementary Table S1). In simulation group (3), set 10 serves to study the impact of absent strains from highly similar clusters and indicates un-biased abundance estimation of strains of the affected clusters by DiTASiC (refer to Supplementary Fig. S7). In another study, reads derived from 55 taxa are contrasted to a reduced reference set of 35 taxa to investigate the impact of missing taxa in a selected reference set. First, we observe that 11% of the reads are not aligned; second, it is shown that abundance estimates of some taxa are overestimated by DiTASiC. However, a closer look reveals that it concerns closely related strains which show an increased abundance due to missing strains within their cluster. The results propose that no overall abundance bias is caused (Supplementary Fig. S12).
4.3 Differential taxa abundance
Here, we evaluate pairwise comparisons of metagenomics samples, aiming to reveal the change of taxa compositions at the highest taxonomic level. We demonstrate how the entire process of read ambiguity resolution and incorporating the uncertainty of abundance estimates has a crucial impact on differential assessment on strain level. As a result, a more accurate detection of differential events is achieved, particularly in case of small changes. False-positives are significantly reduced.
In order to evaluate independent of technical and biological variance factors, we do not consider replicate samples and comparisons here. This way we can test our specifically addressed differential method and prove the validity and impact of the abundance variance without bias. We compare our approach to STAMP (Parks and Beiko, 2010; Parks et al., 2014), which is available for pairwise comparisons to exemplary demonstrate the importance of the issues of read ambiguities and abundance estimation uncertainties. The mapping abundances of the taxa serve as input for STAMP. STAMP is a software package providing several statistical tests for differential taxonomic and functional assessment and a user-friendly graphical interface. The recommended option of a G-test with Yates continuity correction followed by a Benjamini-Hochberg adjustment is selected.
Different metagenome comparisons are conducted within the presented data sources. Evaluations focus on correct detections of differentially abundant taxa and on accuracy of taxa fold changes.
For the simulation data and the CAMI spike-in data, ground truth is available for specific classification into differential and non-differential taxa, results are described by measures of sensitivity, specificity and accuracy as combined measure of correct detections. For the FAMeS and the original CAMI data, no classification is provided, here, the accuracy of fold changes is evaluated by using the SSE instead.
Different pairwise comparisons of the simulation data cover various scenarios of non-differential and differential events. A P-value cutoff of 0.05, adjusted for multiplicity, is used to define differentially abundant taxa. Evaluation results for the simulation data are presented in Table 3. For all scenarios, DiTASiC reports no false-positive hits, holding a false discovery rate (FDR) of zero and a resulting specificity of one. Further, in five out of eight comparisons also a sensitivity of 100% is achieved. In the other three cases, the detection of one known differentially abundant taxon fails resulting in one false-negative detection and corresponding sensitivities of 97%. Here, it concerns the differential detection of the sub-strain E.coli K12 MG1655, which holds accurate abundance estimates but fairly large standard errors, arising due to uncertainties because of high sequence similarity of 98% with another E.coli sub-strain DH10B. The known relative abundance decrease by 1% is very small and hereby falls in the abundance variance range, while an increase by 3% for sub-strain DH10B could be detected as well as differences below 1% for the other E.coli strains in the cluster. In general contrast are the results obtained for STAMP, showing a strong tendency of identifying non-differential taxa as differentially expressed, causing high numbers of false-positives. As abundance estimates underlie some variation, additionally biased due to read ambiguities, these results confirm how the inclusion of standard errors is crucial to identify taxa with consistent abundances. The FDR of STAMP ranges from 12 to 63% and the overall accuracy from 46 to 86%.
Table 3.
Evaluation of differential taxa abundance by DiTASiC and STAMP based on sample comparisons within the simulation data and the CAMI data set
| Data source | Samples compared | No. of non-differential events | No. of differential events | False positives (FPs) and False negatives (FNs) | FDR | Sensitivity | Specificity | Accuracy | ||||||
| DiTASiC | STAMP | DiTASiC | STAMP | DiTASiC | STAMP | DiTASiC | STAMP | ||||||
| FP | FN | FP | FN | ||||||||||
| CAMI spike-in data | Samples S1 versus S2 | ||||||||||||
| 15 | 15 | 0 | 0 | 15 | 0 | 0 | 0.50 | 1 | 1 | 1 | 0.5 | 1 | 0.5 | ||
| Simulation group (2): Pairwise sample comparisons of different simulation sets (numbered from 4 to 9) | set 4 versus set 5 | 35 | 0 | 0 | 0 | 0 | 0 | n.a. | n.a. | n.a. | 1 | n.a | 1 | 1 | 1 |
| set 5 versus set 9 | 28 | 7 | 0 | 0 | 12 | 0 | 0 | 0.63 | 1 | 1 | 1 | 0.7 | 1 | 0.66 | |
| set 5 versus set 6 | 18 | 17 | 0 | 1 | 18 | 2 | 0 | 0.51 | 0.94 | 1 | 0.89 | 0.5 | 0.97 | 0.43 | |
| set 6 versus set 7 | 17 | 18 | 0 | 0 | 16 | 0 | 0 | 0.47 | 1 | 1 | 1 | 0.51 | 1 | 0.54 | |
| set 7 versus set 8 | 10 | 25 | 0 | 0 | 7 | 0 | 0 | 0.22 | 1 | 1 | 1 | 0.59 | 1 | 0.8 | |
| set 6 versus set 8 | 6 | 29 | 0 | 0 | 4 | 0 | 0 | 0.12 | 1 | 1 | 1 | 0.6 | 1 | 0.89 | |
| set 4 versus set 7 | 5 | 30 | 0 | 1 | 5 | 0 | 0 | 0.14 | 0.97 | 1 | 1 | 0.5 | 0.97 | 0.86 | |
| set 4 versus set 8 | 5 | 30 | 0 | 1 | 5 | 0 | 0 | 0.14 | 0.97 | 1 | 1 | 0.5 | 0.97 | 0.86 | |
Note: A P-value cutoff of 0.05 is used to define differentially abundant taxa. In most scenarios, DiTASiC achieves exact detections, holding a FDR of zero and accuracy above 97% overall. A reduced accuracy performance by STAMP, using mapping abundances, confirms the significant impact of read ambiguities and abundance estimate uncertainties. In case of no differential events, FDR and sensitivity cannot be computed (n.a.).
A similar situation is observed for the CAMI spike-in data. DiTASiC correctly detects all 15 differential and 15 non-differential taxa. However, all 30 taxa are found to be differentially abundant by STAMP, resulting in an accuracy of only 50%. Considering the entire CAMI data set, fold changes, spanning from 0.0009 to 1024, are proven to be highly accurate for DiTASiC with an SSE 19 times smaller compared with the STAMP output. Further, the assigned P-values by DiTASiC clearly separate the spiked-in non-differential and differential taxa (Supplementary Fig. S13). All other taxa of the data set, holding fold change values greater than zero, also receive very small P-values stating differential abundance, but cannot be further confirmed.
Pairwise metagenome comparisons within the FAMeS data also exhibit high fold change accuracies, as consequence to the former highly accurate abundance estimates. Corresponding SSE values are two magnitudes smaller compared with the ones computed by STAMP (see Supplementary Table S2).
5 Discussion
Our work demonstrates the challenges concerning strain level resolution in metagenomics data and the need for dedicated methods for quantification and differential abundance testing. DiTASiC addresses these challenges and provides novel approaches.
The inference of taxa abundances by directly counting mapped reads is not suitable on strain level. Although read mappers have significantly improved in speed and mapping accuracy, they cannot resolve shared read assignments and thereby cannot directly output correct abundances. Our results show the bias introduced by the pseudo-aligner of kallisto (without its well working EM-based quantification framework): the abundances of most taxa are overestimated and many actually absent taxa are assigned positive abundances. This effect is due to shared read counts, caused by highly similar reference sequences of strains in a metagenomics sample. DiTASiC is based on a new GLM framework, adapted to characteristics of taxa data for the resolution of shared read counts. As a result, it provides highly accurate abundance estimates for taxa in different metagenomics samples. Thereby, DiTASiC proves excellent performance independent of abundance profile complexities and also shows reduced errors in comparison to existing tools on a recent benchmark study on the i100 data (Schaeffer et al., 2017). It enables accuracy in a large range of relative abundances from 0.001 to 30% present in the various data sets. Further, while generally the read coverage in a metagenomics sample is a critical factor for abundance estimation, the degree of reference similarities of present taxa means a greater challenge. Thus, on the FAMeS data set with 122 taxa, but many dissimilar species, all tools achieve overall higher abundance accuracy compared with the simulation sets with only 35 taxa holding almost the same number of input reads, but different challenging strain clusters. However, the GLM model of DiTASiC proves specific strength in highly accurate abundance resolution within strain clusters, as is shown for various examples in the i100, CAMI and simulation studies. In particular, it demonstrates to precisely distinguish abundances down to sub-strains which share sequence similarities above 95%. Whereas this is more challenging for kallisto, which was similarly reported in a benchmark study by McLoughlin (2016). An important point is that the similarity matrix used in DiTASiC is not necessarily symmetric. Hence, the simulated proportion of reads shared from reference i with reference j can differ from the proportion reference j shares with reference i. We observe these dissimilarities in the matrix e.g. for the E.coli clusters and hypothesize that this may explain the good performance of DiTASiC, as it allows capturing sub-strain sequences, which may be shorter, but highly similar to other longer strain sequences.
The framework of DiTASiC is also robust with increasing sequencing error, as the internal matrix simulations account for the error profiles found in the raw reads. However, as a consequence, misaligned reads in addition to shared reads will cause abundance bias, which poses another resolution challenge. Further, missing or unknown taxa in reference sets may introduce quantification bias. However, one of our studies indicates that closely related strains compensate for missing ones and not affected strain cluster remain stable. Overall, DiTASiC shows certain robustness on imperfect reference sets with either missing or false-positive taxa included. Nevertheless, explicitly accounting for non-mapped reads and their missed abundance proportion could be included in future work.
All in all, the accuracy of the abundance estimation has an immediate impact on the accuracy that can be achieved in the differential abundance analysis of the taxa. This is clearly observable in the comparisons of the FAMeS data sets, which result in highly accurate fold change estimates in consequence of the accurate abundance estimates that were obtained.
However, for differential abundance testing, in order to distinguish differentially and non-differentially abundant taxa, the uncertainty of the abundance estimates plays a crucial role. Especially on strain level, this variance reflects uncertainties in the underlying read ambiguity resolution in the presence of highly similar reference sequences. DiTASiC introduces a new statistical framework, which integrates the abundance variance and forms abundance distributions for differential testing sensitive to strain level.
Generally in comparative metagenomics, it is difficult to predict how a community of taxa in a sample will change, as there is a variety of influential factors involved. A study by (David et al., 2014), demonstrates how human actions can cause next-day abundance change in the microbiome. Hence, putting assumptions on data for composition change is complex. Further, although taxa abundance data and gene expression data share discrete count data characteristics, assumptions commonly made for gene expression for differential analysis cannot be easily transferred. One of the most common assumptions is that the majority of features will not be differentially changed. This is reasonable for genes in a cell as no global change of expression of all genes is biologically expected. In metagenomics studies though, antibiotics treatment has shown to cause rapid change of microbial compositions in human samples (Dethlefsen and Relman, 2011). Further, gene expression data in RNA-Seq studies are often characterized by overdispersion and correspondingly modelled by negative binomial distributions.
Different popular RNA-Seq tools as well as standard statistical tests are frequently applied to metagenomics gene data for differential analysis, however, have been shown to not capture the data well in all cases (Jonsson et al., 2016). Similar problems are observed when considering differential taxa abundance. In a study of plaque samples, DESeq and edgeR were also shown to not fit the data properly (Paulson et al., 2013). Hence overall, it is important to distinguish gene and taxa level and critically assess corresponding assumptions. Furthermore, defining assumptions to capture all diverse structures of metagenomics data might pose an almost impossible challenge. Here, we propose an independent statistical framework for differential testing of all individual taxa in the set, without putting any assumptions on overall composition change.
We evaluated our approach on diverse scenarios, covering sets with only non-differential events to sets with overall change, and can indicate overall correct detections. Further, the method is not dependent on the presence of a taxon in both samples of comparison, it also serves as test on taxa emergence or extinction.
In contrast, STAMP yields many false-positives, which reflects the importance of read ambiguity resolution and integration of abundance uncertainties for strain level analysis. In cases of extremely similar strain sequences, however, large standard errors for the estimates can occur, as shown for the two E.coli sub-strains, and can consequently cause a lower limit for the detection of very small fold-changes in DiTASiC.
Generally, DiTASiC is neither limited to bacteria nor any taxonomic level. Also its concept is applicable to any ambiguity resolution in which the similarities causing the ambiguities can be described. Further, variance of sample replicates pose another crucial variance source, integration could be achieved by not sampling from the mixture of Poisson distributions of one experiment, but across all replicates. DiTASiC is independent of specific databases or any additional data information, it simply relies on the raw reads and on a (pre-filtered) species reference set in fasta format, the latter can also contain assemblies or fragmented sequences.
6 Conclusion
This contribution focuses on the resolution on strain level in metagenomics data concerning taxa quantification and differential abundance assessment. We point out the challenges arising on strain level due to the presence of highly similar reference sequences. We present DiTASiC, which provides a new GLM framework for the resolution of shared read counts and introduce a statistical framework, which integrates abundance variances, for differential testing sensitive to strain level. As a result, highly accurate abundance estimates down to sub-strain level as well as detections of differentially abundant taxa are obtained. Evaluations are conducted on different data sources and in comparison to existing methods.
Supplementary Material
Acknowledgements
We thank Kathrin Trappe, Tobias Loka and Vitor Piro (Robert Koch Institute) for critical reading and helpful comments on the article as well as Martin S. Lindner for inspiring discussions.
Funding
We acknowledge financial support by Deutsche Forschungsgemeinschaft [grant number RE3474/2-1 to B.Y.R.].
Conflict of Interest: none declared.
References
- Anders S., Huber W. (2010) Differential expression analysis for sequence count data. Genome Biol., 11, R106.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Benjamini Y., Hochberg Y. (1995) Controlling the false discovery rate: a practical and powerful approach to multiple testing. J. R. Stat. Soc. Ser B (Methodological), 57, 289–300. [Google Scholar]
- Bray N.L. et al. (2016) Near-optimal probabilistic RNA-seq quantification. Nat. Biotechnol., 34, 525–527. [DOI] [PubMed] [Google Scholar]
- David L.A. et al. (2014) Host lifestyle affects human microbiota on daily timescales. Genome Biol., 15, R89.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dethlefsen L., Relman D.A. (2011) Incomplete recovery and individualized responses of the human distal gut microbiota to repeated antibiotic perturbation. Proc. Natl. Acad. Sci. USA, 108(Suppl 1), 4554–4561. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gibbons S.M., Gilbert J.A. (2015) Microbial diversity–exploration of natural ecosystems and microbiomes. Curr. Opin. Genet. Dev., 35, 66–72. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holtgrewe M. (2010) Mason – a read simulator for second generation sequencing data. Tech. Rep. FU Berl. [Google Scholar]
- Huson D.H. et al. (2007) MEGAN analysis of metagenomic data. Genome Res., 17, 377–386. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jonsson V. et al. (2016) Statistical evaluation of methods for identification of differentially abundant genes in comparative metagenomics. BMC Genomics, 17, 78.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Karlsson F.H. et al. (2013) Gut metagenome in European women with normal, impaired and diabetic glucose control. Nature, 498, 99–103. [DOI] [PubMed] [Google Scholar]
- Langmead B., Salzberg S.L. (2012) Fast gapped-read alignment with Bowtie 2. Nat. Methods, 9, 357–359. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Law C.W. et al. (2014) voom: Precision weights unlock linear model analysis tools for RNA-seq read counts. Genome Biol., 15, R29.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li H. (2015) Microbiome, metagenomics, and high-dimensional compositional data analysis. Annu. Rev. Stat. Appl., 2, 73–94. [Google Scholar]
- Lieberman T.D. et al. (2014) Genetic variation of a bacterial pathogen within individuals with cystic fibrosis provides a record of selective pressures. Nat. Gene., 46, 82–87. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lindgreen S. et al. (2016) An evaluation of the accuracy and speed of metagenome analysis tools. Sci. Rep., 6, 19233.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lindner M.S., Renard B.Y. (2013) Metagenomic abundance estimation and diagnostic testing on species level. Nucleic Acids Res., 41, e10.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu Y. et al. (2017) AFS: identification and quantification of species composition by metagenomic sequencing. Bioinformatics, 33, 1396–1398. [DOI] [PubMed] [Google Scholar]
- Love M.I. et al. (2014) Moderated estimation of fold change and dispersion for RNA-seq data with DESeq2. Genome Biol., 15, 550.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lu J. et al. (2017) Bracken: estimating species abundance in metagenomics data. PeerJ Comput. Sci., 3, e104. [Google Scholar]
- Luo C. et al. (2015) ConStrains identifies microbial strains in metagenomic datasets. Nat. Biotechnol., 33, 1045–1052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mavromatis K. et al. (2007) Use of simulated data sets to evaluate the fidelity of metagenomic processing methods. Nat. Methods, 4, 495–500. [DOI] [PubMed] [Google Scholar]
- McLoughlin K. (2016) Technical report: benchmarking for quasispecies abundance inference with confidence intervals from metagenomic sequence data. Tech. Rep., LLNL-TR-681108 [Google Scholar]
- Mende D.R. et al. (2012) Assessment of metagenomic assembly using simulated next generation sequencing data. Plos One, 7, e31386.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Menzel P. et al. (2016) Fast and sensitive taxonomic classification for metagenomics with Kaiju. Nat. Commun., 7, 11257.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nawy T. (2015) MICROBIOLOGY: the strain in metagenomics. Nat. Methods, 12, 1005.. [DOI] [PubMed] [Google Scholar]
- Nayfach S. et al. (2016) An integrated metagenomics pipeline for strain profiling reveals novel patterns of bacterial transmission and biogeography. Genome Res., 26, 1612–1625. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Neelakanta G., Sultana H. (2013) The use of metagenomic approaches to analyze changes in microbial communities. Microbiol. Insights, 6, 37–48. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ondov B.D. et al. (2016) Mash: fast genome and metagenome distance estimation using MinHash. Genome Biol., 17, 132.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oulas A. et al. (2015) Metagenomics: tools and insights for analyzing next-generation sequencing data derived from biodiversity studies. Bioinformatics Biol. Insights, 9, 75–88. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ounit R. et al. (2015) CLARK: fast and accurate classification of metagenomic and genomic sequences using discriminative k-mers. BMC Genomics, 16, 236.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pignatelli M., Moya A. (2011) Evaluating the fidelity of de novo short read metagenomic assembly using simulated data. PloS One, 6, e19984. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Parks D.H. et al. (2014) STAMP: statistical analysis of taxonomic and functional profiles. Bioinformatics, 30, 3123–3124. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Parks D.H., Beiko R.G. (2010) Identifying biologically relevant differences between metagenomic communities. Bioinformatics, 26, 715–721. [DOI] [PubMed] [Google Scholar]
- Paulson J.N. et al. (2013) Differential abundance analysis for microbial marker-gene surveys. Nat. Methods, 10, 1200–1202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peng X. et al. (2015) Zero-inflated beta regression for differential abundance analysis with metagenomics data. J. Comput. Biol., 23, 102–110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robinson M.D. et al. (2010) edgeR: a Bioconductor package for differential expression analysis of digital gene expression data. Bioinformatics, 26, 139–140. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rosen M.J. et al. (2015) Microbial diversity. Fine-scale diversity and extensive recombination in a quasisexual bacterial population occupying a broad niche. Science, 348, 1019–1023. [DOI] [PubMed] [Google Scholar]
- Schaeffer L. et al. (2017) Pseudoalignment for metagenomic read assignment. Bioinformatics, DOI: 10.1093/bioinformatics/btx106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scholz M. et al. (2016) Strain-level microbial epidemiology and population genomics from shotgun metagenomics. Nat. Methods, 13, 435–438. [DOI] [PubMed] [Google Scholar]
- Sczyrba A. et al. (2017) Critical Assessment of Metagenome Interpretation – a benchmark of computational metagenomics software. bioRxiv, 99127. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Segata N. et al. (2011) Metagenomic biomarker discovery and explanation. Genome Biol., 12, R60.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Segata N. et al. (2012) Metagenomic microbial community profiling using unique clade-specific marker genes. Nat. Methods, 9, 811–814. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shapiro B.J. et al. (2012) Population genomics of early events in the ecological differentiation of bacteria. Science, 336, 48–51. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Snitkin E.S. et al. (2011) Genome-wide recombination drives diversification of epidemic strains of Acinetobacter baumannii. Proc. Natl. Acad. Sci. USA, 108, 13758–13763. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sohn M.B. et al. (2015) A robust approach for identifying differentially abundant features in metagenomic samples. Bioinformatics, 31, 2269–2275. [DOI] [PMC free article] [PubMed] [Google Scholar]
- White J.R. et al. (2009) Statistical methods for detecting differentially abundant features in clinical metagenomic samples. PLoS Comput. Biol., 5, e1000352.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wood D.E., Salzberg S.L. (2014) Kraken: ultrafast metagenomic sequence classification using exact alignments. Genome Biol., 15, R46.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wooley J.C. et al. (2010) A primer on metagenomics. PLoS Comput. Biol., 6, e1000667.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xia L.C. et al. (2011) Accurate genome relative abundance estimation based on shotgun metagenomic reads. PloS One, 6, e27992.. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.