Incorporating interaction networks into the determination of functionally related hit genes in genomic experiments with Markov random fields

Abstract

Motivation

Incorporating gene interaction data into the identification of ‘hit’ genes in genomic experiments is a well-established approach leveraging the ‘guilt by association’ assumption to obtain a network based hit list of functionally related genes. We aim to develop a method to allow for multivariate gene scores and multiple hit labels in order to extend the analysis of genomic screening data within such an approach.

Results

We propose a Markov random field-based method to achieve our aim and show that the particular advantages of our method compared with those currently used lead to new insights in previously analysed data as well as for our own motivating data. Our method additionally achieves the best performance in an independent simulation experiment. The real data applications we consider comprise of a survival analysis and differential expression experiment and a cell-based RNA interference functional screen.

Availability and implementation

We provide all of the data and code related to the results in the paper.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

High-throughput genomic experiments allow for measurements to be taken on thousands of genes relating to particular biological processes such as gene expression or exhibition of a phenotype of interest. Such experiments generally concern an overly large number of genes and where ‘hit’ genes in the experiment, those with significant expression or scores, are subsequently identified for further analysis. The hit gene list is a smaller and more easily analysable subset of genes that is used to inform follow up studies and as a general aide for interpretation of the biological question of interest. One classical strategy is to decipher mechanisms of action between hit genes in the form of modelled cellular pathways (Wang et al., 2011).

Based on a mathematical graph object, genomic networks are made up of vertices corresponding to genes and edges between vertices possibly corresponding to physical, regulatory or signalling information, for example (Kim et al., 2016). Protein–protein interaction (PPI) networks, where there is an edge between vertices if the corresponding genes are known or inferred to have proteins that interact, have been previously used as the basis of network analysis of genomic screening data, including from RNA interference (RNAi) screens (Hao et al., 2013; Kumar et al., 2013).

Although there is a large body of work on biological network analysis in general (Pavlopoulos et al., 2011), overlaying additional genomic data leads to further considerations in the analysis. For example, an initial approach is to investigate the distribution of scores or hits within the PPI network to find structures or areas of interest (Kumar et al., 2013). Network-based tests for differential expression (Jacob et al., 2012) and extensions of Fisher exact tests for enrichment or depletion of functional/gene ontology (GO) annotations (Dong et al., 2016) have also been proposed, along with methods to quantify the clustering of functional/GO annotations in the network (Cornish and Markowetz, 2014). Further sophisticated approaches include network inference and gene functional prediction (Ma et al., 2014) and using a PPI network as the basis of a meta-analysis of multiple screening data sets (Amberkar and Kaderali, 2015; Hao et al., 2013; Kumar et al., 2013).

Our aim is to incorporate PPI networks and the observed genomic data to determine a network based hit list by making use of the ‘guilt by association’ assumption (Cornish and Markowetz, 2014; Ma et al., 2014; Wang et al., 2009). It has been commented on that by visualizing a PPI network overlaid with hit results from an RNAi screen, genes that are just below a simple hit threshold but connected to many other hit genes in the network could be fruitfully considered as a hit themselves (Kumar et al., 2013). Besides, to facilitate the interpretation of gene hit lists, taking into account known or inferred functional relations between proteins would help in deciphering gene relationships important in the phenotype of interest (Markowetz, 2010). There are a number of proposed approaches to turn this ad hoc notion into a mathematically formulated network determination of hit genes concerning RNAi screening data (Cornish and Markowetz, 2014; Jiang et al., 2015; Wang et al., 2009) as well as gene expression data (Beisser et al., 2010; Dittrich et al., 2008) among others.

The Knode (Cornish and Markowetz, 2014), NePhe (Wang et al., 2009) and NEST (Jiang et al., 2015) methods all calculate additional network based scores for each gene. Table 1 lists the proposed ways in which the PPI network is incorporated into these methods. Then the NePhe and NEST scores are simply calculated by summing or averaging the original scores weighted by the similarity matrix. For example, considering the ‘shortest paths’ similarity matrix and ‘average’ summation, the network score for each gene is the average of all the other original scores weighted by the inverse distance of the shortest path between the vertices. The summing procedure for the Knode method is based on a network adaptation of Ripley’s K-function (Ripley, 2004) and hence ‘Knode’. A hit list in these cases is a certain number of genes with the highest network based scores.

Table 1.

The proposed similarity matrices for calculating the Knode (Cornish and Markowetz, 2014), NePhe (Wang et al., 2009) and NEST (Jiang et al., 2015) scores

	Knode	NePhe	NEST
Adjacency		X	X
Common neighbours		X
Mean steps between	X
Shortest path	X	X
Diffusion kernel	X	X

The BioNet method (Beisser et al., 2010; Dittrich et al., 2008) aims to find a subgraph of hits. Compared to similar approaches (Chuang et al., 2007), BioNet is guaranteed to find the maximum-weight connected subgraph in the network. This subgraph is anticipated to be generally made up of the genes with the most significant scores but genes with non-significant scores may also be contained within the subgraph. That is, even though individual genes with non-significant scores will themselves contribute a suboptimal weight in the subgraph, they may allow for other more significantly scored genes to be included through their edges, which can give a more optimal overall weight. The list of genes in the maximum-weight connected subgraph can then be taken as the hit list of interest.

Our proposed approach is based on Markov random fields (MRFs), mathematical models where associations in the data can be considered in an efficient way. Such models have been previously used for network-based classification of gene expression data (Stingo and Vannucci, 2011), finding differentially expressed genes in specified pathways (Wei and Li, 2007) and modelling gene expression over a network (Wei and Pan, 2008, 2010). Instead of aiming to model genomic data and the underlying network, we broadly consider the same approach to using MRFs for digital image segmentation (Blake et al., 2011; Robinson et al., 2015). That is, the genomic data are not modelled over the network but rather ‘hit’ and ‘non-hit’ genes are labelled taking the network into account. In this way, we determine a network based hit list comparable to previously proposed methods (Beisser et al., 2010; Cornish and Markowetz, 2014; Dittrich et al., 2008; Jiang et al., 2015; Wang et al., 2009).

We consider a number of different data sets including from a simulated experiment, a lymphoma study with measurements based on differential expression and survival analysis, and from our own motivating RNAi screen. We compare to previously proposed methods to show that our MRF based method performs the best in a simulation study and is able to provide increased pathway enrichment and a greater determination of the hit genes in the previously analysed lymphoma study. For our motivating RNAi screening data, the MRF method is able to find pertinent network hits that are otherwise not discovered by thresholding the multivariate scores, suggesting useful possibilities for further analysis. We show that the major advantages of our MRF based method are that multivariate scores for genes as well as multiple hit labels are easily available in the method.

2 Materials and methods

2.1 Network scoring of hit genes

Consider that we have a collection of genes with an associated gene network and that each gene is indexed by a scalar i. Let the vertex set $\mathcal{V}$ be the set of gene indices and let the edge set $\mathcal{E}=\{e_{ij}\ge 0\hspace{0.17em}|\hspace{0.17em}{e}_{ij}=e_{ji}, \text{for} \text{all} i,j\in \mathcal{V}\}$ be the set of all edges between every pair of vertices where genes i and j are neighbours in the network if and only if e_ij > 0. Let the degree of gene/vertex i be

$${\partial }_i=\sum _{j\in \mathcal{V}}{e}_{ij}.$$

Note that if the graph is not weighted (that is $e_{ij}\in \{0,1\}$ for all $i,j\in \mathcal{V}$), then ${\partial }_i$ is just the number of neighbours of vertex i.

Let the (possibly multivariate) random variable Z_i be the data derived from the genomic experiment for gene i and let the random variable X_i be the unobserved label of interest. In the most general case, the labels will be ‘hit’ and ‘non-hit’ but it is also possible to have more than 2 hit labels. Let the collection of these random variables be a conditional MRF with the associated energy function

$$E\left(x\right)=\sum _i\sum _l{u}_{i;l}I\{x_i=l\}+\sum _{(i,j)}\sum _l\sum _k{w}_{ij;lk}I\{x_i=l,x_j=k\}$$ (1)

for vertices i and pairs of vertices (i, j) with labels l and k. The minimum energy labels are

$$\widehat{x}=\underset{x}{\text{argmin}}E\left(x\right).$$

The unary potentials u_i;l are defined to be

$$u_{i;l}=-\text{log}\hspace{0.17em}\left({\pi }_l\right(z_i\left)\right)$$ (2)

where z_i is the observed data for gene i and π_l is the probability density function corresponding to label l. The pairwise potentials w_ij;lk are defined to be

$$w_{ij;lk}=\beta \{\begin{array}{cc}{e}_{ij}& \text{if} l\ne k\\ 0& \text{if} l=k.\end{array}$$ (3)

When β = 0, the minimum energy labels are simply given by the unary potentials. That is, each gene i has minimum energy label based on the observed data z_i and unary potentials (Equation (2)) only, independent of the network. This is equivalent to labelling the genes based on thresholding the scores at the interception points of the densities corresponding to each label. When β > 0, the pairwise potentials (Equation (3)) impose a penalty in the energy function between pairs of neighbouring vertices without the same label. Hence neighbouring vertices are impelled to have the same label in order that the total labelling has the minimum possible energy. Although this is balanced against the unary potentials, there exists a value β* above which all of the vertices have the same minimum energy label. This ‘dominant’ label is the label such that the energy is minimized when all vertices are given this label compared to all other labels. That is, the dominant label l is the label such that ${\sum }_{i\in \mathcal{V}}{u}_{i;l}<\sum _{i\in \mathcal{V}}{u}_{i;k}$ for all other labels k. Note that a toy example is presented below.

In practice we need to set the value of β as well as the probability density function π_l for each label l. We first consider setting the value of β, while setting the underlying densities π_l for each label l is considered in Section 2.3. Let $\widehat{x}(\beta )$ be the minimum energy labels for a given value of β. We define the MRF score for vertex i under label l as

$$s_{i;l}={\partial }_i\sum _{\beta \in \mathcal{B}}I\left\{{\widehat{x}}_i\right(\beta )=l\}$$ (4)

where $\mathcal{B}=\{0,(1/n){\beta }^{*},(2/n){\beta }^{*},\dots ,{\beta }^{*}\}$, n is the resolution and β* is the minimum value of β such that the minimum energy labelling is the dominant label for all vertices. That is, the score for each vertex, for each label, is the number of values of β for which the vertex is assigned the label, scaled by the degree of the vertex. Since the value of β is bounded by 0 and β*, and the score is defined as a summation over a range of values of β between these bounds, we are not required to actually set the value of β.

2.2 Toy example

In order to explain the proposed score, Figure 1 presents a toy example. The graph seen in Figure 1a is made up of two complete subgraphs of nine vertices, each with an additional leaf vertex and a single edge bridging the two subgraphs. In this case, all of the edges have the same weight. The unobserved labels in the network are ‘blue’ and ‘red’, each with an associated Gaussian distribution centred at −1 and 1, respectively, with a standard deviation of 2 (Fig. 1b). The vertices $1,2,\dots ,10$ on the left of Figure 1a are true ‘blue’ vertices while the vertices $11,12,\dots ,20$ on the right are true ‘red’ vertices. The colour of the vertices in Figure 1a corresponds to the observed value from the associated distribution.

Fig. 1.

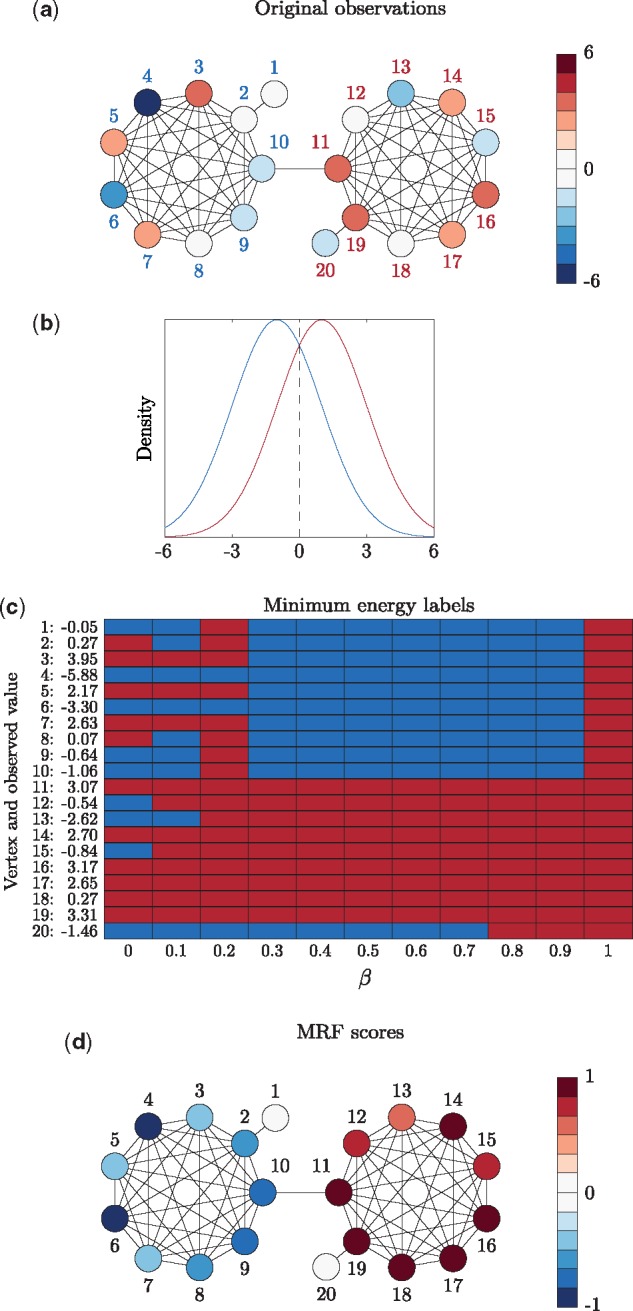
Toy example. (a) Original observations and underlying label (‘blue’ or ‘red’) for each vertex. The vertices $1,2,\dots ,10$ on the left are true ‘blue’ vertices while the vertices $11,12,\dots ,20$ on the right are true ‘red’ vertices, indicated in the vertex labels. The observed value for the vertex is indicated in the colour of the vertex itself. (b) Densities corresponding to both the ‘blue’ or ‘red’ labels. (c) Minimum energy labels for a range of values of β. (d) The MRF scores

Figure 1c shows the minimum energy labels for different values of β. When β = 0 there is no edge information in the energy function and each vertex is labelled as either ‘blue’ or ‘red’ based only on its observed value. That is, whether the observed value is above or below the intercept point of the two densities at 0 (Fig. 1b). For increasing values of β, the minimum energy labelling increasingly ‘smooths out’ up to the point where every vertex is assigned the ‘red’ label when $\beta ={\beta }^{*}=1$.

Figure 1d shows the scaled difference in MRF scores ($s_{i;‘\text{red}’}-s_{i;‘\text{blue}’}$) for each vertex. Comparing the final scores to the minimum energy labels for any single value of β, the MRF scores allow for greater determination of the labelling. For example, when $\beta =0.9$ the vertices $1,2,\dots ,10$ have the correct minimum energy label ‘blue’, but we can see in the final MRF scores that vertices 4 and 6 are the strongest ‘blue’. That is, rather than requiring the value of β be determined, we simultaneously sidestep this problem and increase the labelling information for each vertex.

In this toy example the densities associated to each label are symmetric and so it is just by chance that the dominant label is ‘red’. That is, it happened to be the case that ${\sum }_{i=1}^{20}{u}_{i;‘\text{red}’}<{\sum }_{i=1}^{20}{u}_{i;‘\text{blue}’}$. We can see that the leaf vertex 20 holds out from the dominant ‘red’ label much longer than the initially ‘blue’ vertex 13 with a higher observed value. This is because vertex 13 is much more connected than 20, which is on the periphery of the graph and will therefore hold onto its initial label much longer with increasing β. It is this tendency that we account for by scaling the MRF score by vertex degree. Hence both the leaf vertices 1 and 20 are labelled ‘blue’ for as many values of β as vertices 8 or 9 (Fig. 1c) but do not have as high a final MRF score since they are less connected in the graph. Although we considered other graph centrality measures such as betweenness, closeness, harmonic and eigenvector centrality (Pavlopoulos et al., 2011), none of them was as consistently suitable or were as computationally feasible as simply using vertex degree.

2.3 Setting the underlying densities

In the toy example of Figure 1, we knew the true densities associated to each label and so were able to use them whereas this is not the case in practice. However, in all of our applications the observed data are associated to a P-value as derived from a screen or other experiment. Hence for the ‘non-hit’ label, we use a standard uniform density and for the ‘hit’ label we use an exponential density. We chose an exponential density as it is peaked at 0 but does not asymptote at the y axis and decays much slower than a truncated Gaussian density. In the general ‘hit’ and ‘non-hit’ scenario we suggest an exponential density that intercepts the standard uniform density at 0.3 (Supplementary Fig. S1).

3 Results and discussion

3.1 The MRF method allows for the network analysis of multivariate RNAi data and finds pertinent functional/GO enrichment

We consider data from an RNAi screen aiming to identify genes implicated in DNA repair after induction of oxidative DNA damage (Guyon et al., 2015). Briefly, in the context of this screen, HeLa cells specifically engineered to express OGG1 [the initiating enzyme of the base excision repair (BER) of oxidized guanine] fused to a Green Fluorescent Protein (GFP), were systematically transfected with siRNAs targeting the ‘druggable’ subset of genes from human genome (3 siRNAs/gene; 7218 target genes). Three days post-transfection, 8-oxo-7,8-dihydro-guanine (8-oxoG) DNA base lesions were induced by cell exposure to potassium bromate (KBrO3) and the recruitment of chromatin-bound OGG1-GFP was quantified (subsequently the fluorescence intensity is averaged in each nucleus) by computer-assisted imaging performed on an automated epifluorescence microscope (Operetta, Perkin Elmer).

Each observation was converted to a $\Phi$-score (Guyon et al., 2015), which has a standard Gaussian distribution under the null hypothesis that we observe no phenotypic difference in the gene knock-down condition. We only consider the negative phenotype and hence a low P-value is associated to a negative siRNA score corresponding to a decrease of chromatin bound OGG1 upon siRNA transfection. For each gene, we converted either the known RefSeq gene ID or gene symbol to Entrez gene ID using bioDBnet (Mudunuri et al., 2009) (latest release bioDBnet 2.1; May 6, 2015), which was subsequently converted to STRING ID (Szklarczyk et al., 2014), resulting in 4006 genes. Hence our RNAi screening data set is made up of 4006 genes each with 3 scores/P-values (hereafter OGG1 data).

The STRING database (Szklarczyk et al., 2014) compiles known and inferred PPI information from experimental sources as well as text mining the literature. The strength of evidence for each interaction is calculated from these multiple sources (Von Mering et al., 2005) and is given as a weight on the corresponding edge. Table 2 gives the proportion of edges in the 4006 vertex ‘combined’ PPI network for the OGG1 data that have a contribution from each source. Also shown are the proportion of edges that have a unique contribution from a source although note that otherwise Table 2 does not give the extent of contribution, just that the source contributed.

Table 2.

Proportion of edges with contributions from different sources in the overall ‘combined’ PPI network for the OGG1 data

	Contribute	Uniquely contribute
Text mining	0.9268	0.5364
Experimental	0.3294	0.0295
Co-expression	0.1134	0.0095
Database	0.0722	0.0236
Neighbourhood	0.0161	0.0006
Co-occurrence	0.0119	0.0015
Fusion	0.0005	0.0000

Previous analysis has shown that a confounding factor between the way gene annotation is carried out and the construction of PPI networks has resulted in a ‘circular’ way of optimizing and validating algorithms for gene function prediction (Gillis and Pavlidis, 2011). In this case, considering functional/GO annotation enrichment will be problematic due to an ‘annotation bias’ (Gillis et al., 2014), where highly studied genes both have more known protein interactions (edges in the PPI network) as well as more functional/GO annotations.

Table 2 shows that ‘text mining’ is the most prominent source of interaction evidence, which is also the most likely source to be associated to an annotation bias. In this case, PPI evidence is automatically extracted from abstracts in the literature, which likely furthers the issue that well studied genes with many known functional/GO annotations have many known or inferred protein interactions and hence edges in the network. Not only does ‘text mining’ contribute to ∼93% of all edges, but it is the unique source of information for ∼54% of edges in the ‘combined’ network. Both ‘experimental’ and ‘database’ concern interaction information gathered from other PPI databases which are also likely to be affected by an ‘annotation bias’ among others (Gillis et al., 2014).

The ‘co-expression’ evidence concerns genes found to have been co-expressed in a variety of experiments and across a number of different species (Stuart et al., 2003; Von Mering et al., 2005). Conservation of co-expressed genes over multiple species implies a selective advantage and hence that the genes are functionally related (Xulvi-Brunet and Li, 2010). This is one source in the STRING database that we expect not to be influenced by an annotation bias (Gillis et al., 2014) and with a low unique contribution, this evidence additionally conforms to that from the other sources.

Supplementary Figure S2 shows the vertex degree and the number of functional/GO annotations from DAVID (Huang et al., 2009a, b) for the 4006 genes in both the ‘combined’ and ‘co-expression’ networks. In the combined network we can see a high linear correlation while in the co-expression network vertex degree does not seem to be correlated to the number of terms at all. Although it is known that some functional/GO annotation terms are inferred from expression patterns, this potential issue does not appear to be present in the same way as the ‘annotation bias’ (Supplementary Fig. S2) for the OGG1 data. Note that each edge in both networks is weighted by the strength of evidence for that interaction and hence vertex degree is not simply the number of neighbours. Hence, we use the co-expression PPI network for the network analysis of the OGG1 data. The network is made up of 4006 vertices and 43 097 weighted edges (density = 0.0054).

Recall that for the OGG1 data there are three scores and hence three P-values for each gene. However, there is no natural or intrinsic way to order the siRNAs for each gene so that the data can be considered as trivariate. Correspondent trivariate data are achieved by ordering the three P-values so that the first data dimension is the lowest P-value, the second data dimension is the median P-value and the third data dimension is the highest P-value for each gene. Figure 2 presents the density schematic for the OGG1 data. Here, there are four labels of interest, a given number of negative siRNAs, as well as the dominant ‘no negative siRNAs’ label. Note that the densities in each dimension intercept at increasingly significant P-values. This is necessary as due to the ordering of the P-values, the lowest are skewed towards 0 and require a lower intercept so that the ‘no negative siRNAs’ label remains the dominant label. Hence a gene is guaranteed to have a non-zero MRF score for the ‘1 negative siRNA’ label if its lowest P-value is below 0.1, the ‘2 negative siRNAs’ label if its lowest P-value is below 0.1 and its median P-value is below 0.2, and the ‘3 negative siRNAs’ label if its lowest P-value is below 0.1, its median P-value is below 0.2 and its highest P-value is below 0.3. It is the consideration of multiple siRNAs for each gene that aims to address the variability of the P-values. Then when we consider our MRF score, we consider all dimensions so that ‘hits’ have either 2 or 3 negative siRNAs.

Fig. 2.

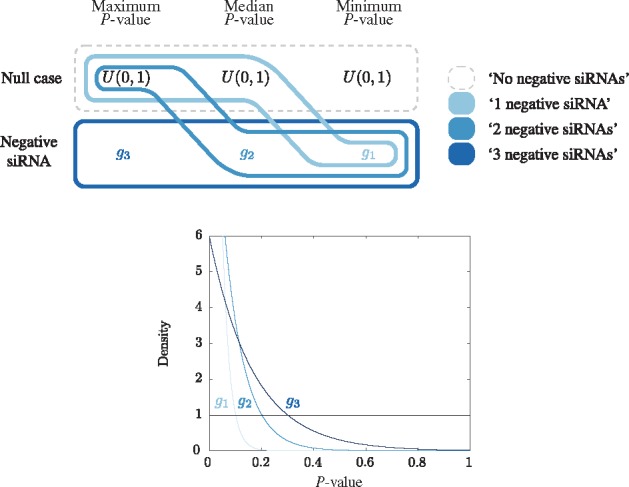
Schematic diagram of the construction of the trivariate densities corresponding to each label for the OGG1 data. In each dimension there are two possibilities and an associated univariate density: ‘null case’ (U(0, 1)) and ‘negative siRNA’ ($g_{·}$). Trivariate densities are defined for each of four labels of interest and are schematically represented by encompassing a single possibility in each dimension. The four labels are: ‘3 negative siRNAs’ (3 low P-values), ‘2 negative siRNAs’ (2 low P-values), ‘1 negative siRNA’ (1 low P-value) and ‘no negative siRNAs’ (no low P-values). Note that the ordering of the P-values limits the possible combinations of trivariate densities across the three dimensions in this case

Figure 3 shows the log₁₀(P-values) for Fisher exact tests of enrichment or depletion in functional/GO annotation terms for the top 200 hits for the MRF method ($s_{i;‘2 \text{negative} \text{siRNAs}’}+s_{i;‘3\text{negative} \text{siRNAs}’}$) against the top 200 hits obtained by ordering the genes by median P-value. These hit lists are comparable in that if the median P-value is below a certain threshold, at least 2 of the P-values are below the threshold and hence we consider both the ‘2 negative siRNAs’ and ‘3 negative siRNAs’ labels from the MRF method. A greater functional/GO enrichment can be generally observed in the MRF based hit lists.

Fig. 3.

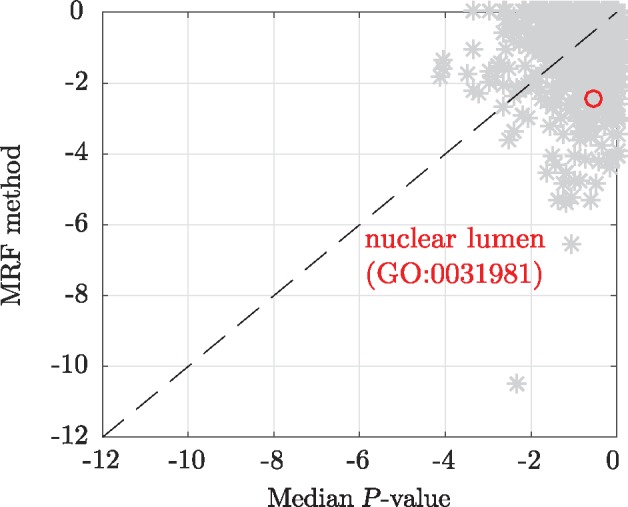
Log₁₀(P-values) for Fisher exact tests of enrichment or depletion in functional/GO annotations for the hits lists obtained from the MRF method and median P-value. The annotation term ‘nuclear lumen (GO:0031981)’ has been highlighted

Supporting the pertinence of the network based hits, we consider those with the increased enriched ‘nuclear lumen (GO:0031981)’ annotation (Fig. 3), where BER takes place. Nuclear lumen corresponds to the localization of genes comprised in the whole volume inside the nuclear inner membrane, including ‘nuclear chromosome (GO:0000228)’, ‘nucleoplasm (GO:0005654)’ and ‘nucleolus (GO:0005730)’. Figure 4 shows TOP3A and its neighbours that are also present in the MRF hit list. Genes with the ‘nuclear lumen (GO:0031981)’ annotation have diamond vertices. Neither TOP3A with P-values (0.03, 0.03, 0.05), nor POLR1C with P-values (0.01, 0.05, 0.12) are strong hits when ordered by their median P-value with ranks 500 and 576 respectively. However, both of these genes can be seen to be likely hits based on a consensus judgment of their P-values and are much more highly ranked with the MRF method.

Fig. 4.

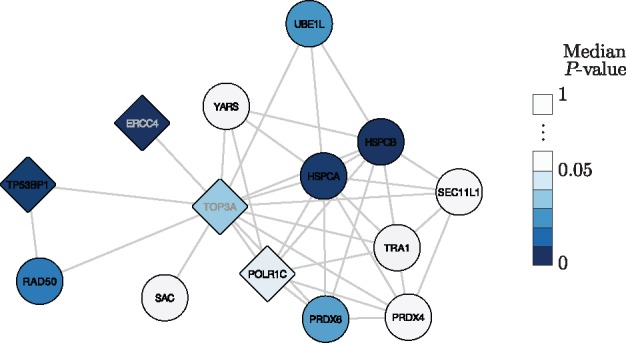
TOP3A and neighbours present in the top 200 MRF hits. Vertices are coloured based on median score/P-value. Diamond vertices correspond to the genes with the ‘nuclear lumen (GO:0031981)’ annotation. The network was visualized in Cytoscape 3.3.0 (Shannon et al., 2003) using the yFiles Organic layout

Neighbours of TOP3A also in the MRF hit list include other DNA repair proteins such as RAD50 and ERCC4, which belongs to a pathway previously shown to be involved in the repair of oxidized bases (Parlanti et al., 2012). The presence of TOP3A and POLR1C in this cluster, both proteins involved in transcription, supports the link between transcription and the repair of the oxidized guanine. Moreover, ERCC4 is known to participate in the repair of actively transcribed genes and more globally in transcription, consistent with the hypothesis of a preferential repair of 8-oxoguanine present in active regions of the genome (Amouroux et al., 2010).

We additionally investigated the functional/GO enrichment for hit lists based on vertex degree. Supplementary Table S1 shows that the vertices with the highest degree are indeed the most enriched in exceptional terms of interest such as ‘Pathways in cancer (hsa05200)’. However, for the co-expression network degree, these exceptional terms are not the most enriched but rather a number of terms associated with nucleotide and nucleoside binding in particular. This suggests that our choice to use the co-expression PPI network was well founded and allows us to avoid the previously identified annotation bias clearly present in the combined PPI network.

To investigate the extent of the influence of the network on the MRF hit list we permuted the gene scores (maintaining the co-expression PPI network structure) and considered which genes are present in the MRF hit list. This was carried out 100 times and Supplementary Figure S3 shows the proportion of times that each gene was present in the hit list plotted by its vertex degree. It appears that genes with a higher degree are generally more often present in the hit list and in the extreme case, genes with no neighbours will never be in the hit list. However, it is clear that simply because a vertex has a high degree, the corresponding gene is not automatically present in the hit list.

Here we have demonstrated the flexibility of our MRF based network scoring method that allows for multivariate densities corresponding to multiple labels of interest to be readily defined. We considered functional/GO enrichment as a guide for interpretation that has allowed for the formation of further relevant hypotheses for specifically identified genes. We took particular care to account for the previously observed annotation bias and also investigated the direct influence of the PPI network on our results.

3.2 The MRF method finds greater pathway enrichment and allows for more detailed determination of hit genes in a lymphoma study

We consider data from a study of diffuse large B-cell lymphoma previously analysed using both the BioNet and Knode methods. For each gene, risk association was obtained from a survival analysis and differential expression was measured between the lymphoma subtypes ABC and GCB (Beisser et al., 2010; Dittrich et al., 2008). Hence there are 2 P-values for each gene corresponding to survival analysis (S) and differential expression (T). A method for combining multiple P-values using order statistics was also proposed with BioNet (Dittrich et al., 2008; Beisser et al., 2010). As can be seen in Supplementary Figure S4, the low combined P-values are those that have both low S and T P-values and if one of the P-values is high, then the combined P-value is high.

The PPI network for the lymphoma data was sourced from the Human Protein Reference Database (Prasad et al., 2009), which is no longer maintained. We could have considered obtaining another PPI network from a more contemporary source and also attempted to account for the previously identified ‘annotation bias’. However, the aim of this section is not to analyse the lymphoma data for its own sake but rather to compare the MRF output to the previously published output from the BioNet and Knode methods. The PPI network is made up of 2034 vertices and 15 512 unweighted edges (density = 0.0038).

We consider the lymphoma data to show a general advantage of the MRF method in that we both find greater pathway enrichment and are able to more generally determine the hit genes as against the BioNet analysis. In this experiment, there are many genes with one high and one low P-value resulting in a high combined P-value (Supplementary Fig. S4). Assuming that interest lies not only when both P-values are low but when one or the other is, we can achieve such output with the MRF method by defining bivariate densities for these labels. Figure 5 shows the construction of the bivariate densities where the 4 labels are ‘S and T hit’, ‘S hits only’, ‘T hits only’ and ‘no hits’. The P-values in the T dimension are generally much lower (Supplementary Fig. S4b) and approximately half of them are below 0.2. In order that the ‘no hits’ label remains dominant, we set the intercept of the exponential density and the standard uniform in the T dimension to be 0.2 (Fig. 5).

Fig. 5.

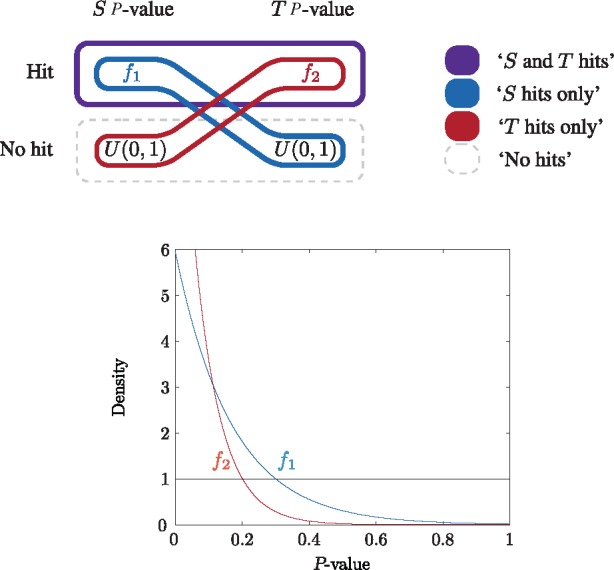
Schematic diagram of the construction of the bivariate densities corresponding to each label for the lymphoma data. In each dimension there are two possibilities and an associated univariate density: ‘non-hit’ (U(0, 1)) and ‘hit’ ($f_{·}$). Bivariate densities are defined for each of four labels of interest and are schematically represented by encompassing a single possibility in each dimension. The four labels are: ‘S and T hits’ (low P-value in both dimensions), ‘S hits only’ (low P-value in S dimension), ‘T hits only’ (low P-value in T dimension) and ‘no hits’ (no low P-value in either dimension)

Recall that the BioNet output is a binary labelling for each gene and the hit list is the list of genes in the maximum-weight connected subgraph. Since the subgraph obtained from BioNet contains 46 genes, following the Knode analysis (Cornish and Markowetz, 2014), we also consider the top 46 genes as the hit list for each other method. In this case, we obtain 3 hit lists from the MRF output based on ranking the genes for each of the three labels of interest, ‘S and T hit’, ‘S hits only’ and ‘T hits only’. Figure 6 shows the overlap in the top 46 genes for each method. Firstly, there is no overlap between the top 46 genes for each of the lists from the MRF method as expected. Similarly, the BioNet hit list does not intersect with either the ‘S hit only’ or ‘T hit only’ lists but does overlap with the ‘S and T hits’ list. This again makes sense since the ‘S and T hits’ label is the closest to BioNet since both P-values being low is necessary for the combined P-value used by BioNet to be low (Supplementary Fig. S4). There is reasonable overlap between the vertex degree hit list and all the other lists except ‘S hits only’. This makes sense for the MRF hit lists as vertex degree is explicitly present the MRF score (Equation (4)). This is also not surprising for BioNet since vertices with high degree are likely to be included in the maximum-weight connected subgraph since they allow access to the most number of other vertices through their edges.

Fig. 6.

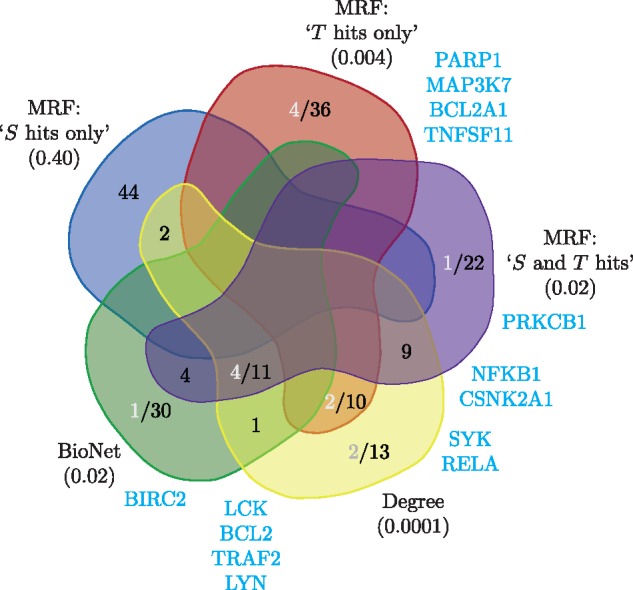
Venn diagram of the hit lists for the lymphoma data overlaid with genes associated with the NFκB pathway. There are 46 genes in each hit list (black) along with the genes associated with the NFκB pathway (grey and listed at the sides in blue). The NFκB annotation was obtained from KEGG (Kanehisa et al., 2016). Below each method is the P-value for the Fisher exact text for enrichment or depletion of the NFκB terms in the hit list. The Venn diagram is based on the layout from http://bioinformatics.psb.ugent.be/webtools/Venn/

Also shown in Figure 6 are genes associated with the carcinogenic NFκB pathway (Hoesel and Schmid, 2013), originally used to evaluate the BioNet output for the lymphoma data (Dittrich et al., 2008). We can see that most of the NFκB genes contained in the BioNet list are also present in the ‘S and T hits’ list, while there are additional such genes in the ‘T hits only’ list. The ‘S hits only’ list does not have any NFκB genes (although it is not significantly depleted) which is interesting in itself. Although the vertex degree hit list has eight NFκB genes in total, only two of them are exclusive and there are an additional five genes the MRF lists contain that are not in the degree list. Hence we are able to find additional enrichment in the NFκB pathway as previously reported for BioNet while gaining further insight into the lymphoma study by demarcating such genes as ‘S and T hits’ or ‘T hit only’, as well as that we find no NFκB genes for ‘S hit only’.

A general advantage of the MRF method that it readily allows for more than a single hit list for multiple labels of interest. The additional information available in this way is not possible to determine after the P-values have been combined as was done for input into the BioNet method. The output from Knode (Supplementary Fig. S5) generally conforms to the above discussion. Although multivariate P-values do not appear to be a problem in principle for either the BioNet or Knode methods, it is not clear how multiple labels beyond binary ‘hit’ and ‘non-hit’ could also be achieved. The output of the NePhe and NEST methods, as well as simply ordering by combined P-value is also provided in the supplementary MATLAB code.

3.3 The MRF method performs the best in an independent simulation experiment

We consider the simulation experiment used to evaluate the Knode method against BioNet (Cornish and Markowetz, 2014). A scale free network with 1000 vertices was simulated with 3 ‘clusters’ of designated hits resulting in a total of 30 ‘true hit’ vertices. The hit vertices have P-values simulated from a truncated Gaussian distribution centred at 0 while the non-hit vertices have P-values simulated from a standard uniform distribution. Rather than using the original standard deviation of ${10}^{-6}$ for the hit distribution, we consider a standard deviation of 0.05. This greatly increased value is necessary because under the original simulation set-up, the density was too peaked at 0 and simply taking the top 30 vertices ordered by lowest P-value finds the highest proportion of true hits (Supplementary Fig. S6).

For the MRF method, we used our general exponential density scheme (Supplementary Fig. S1), rather than the known densities since this information is not available for the other methods we are comparing to. For the BioNet method, the input FDR parameter was set to 0.8 in order that the maximum-weight connected subgraph could be found. The similarity matrix used for the Knode method was the diffusion kernel, the same as was used originally (Cornish and Markowetz, 2014). We considered the NePhe score with the shortest path similarity matrix and average summation method, the best performing pair of options. We additionally considered the NEST score (Jiang et al., 2015) along with simply ordering the vertices by vertex degree (highest) and P-value (lowest). The hit lists are the top 30 vertices obtained from each method.

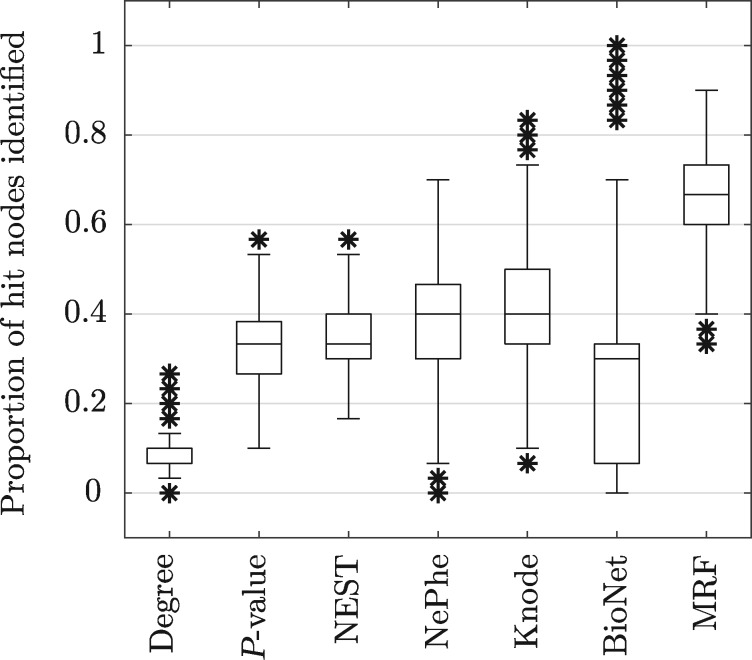
Figure 7 shows box plots of the proportion of true hits vertices for each method obtained over 1000 simulation runs. Since it is known that there are 30 true hits, as originally presented (Cornish and Markowetz, 2014), we consider the proportion of true hits in each hit list of size 30. We can see that simply ordering the vertices by degree performs very poorly, while ordering by P-value is better but still relatively poor. The NEST, NePhe and Knode scores perform quite similarly while BioNet has a lower median performance and a much greater spread. The MRF method clearly gives the best performance and when using the known true hit density rather than our general exponential scheme, the MRF method gives even better results, with a median proportion just below 0.8 and a similar spread (not shown).

Fig. 7.

Box plots of the proportion of true hit vertices identified for each method in the ‘3 cluster’ Knode simulation scheme (1000 simulation runs) (Cornish and Markowetz, 2014)

There were 30 simulated runs where BioNet obtained a proportion correct >0.8 and for 12 of those runs, the proportion correct was 1. However, for the BioNet method there is no guarantee that the maximum-weight connected subgraph contains only 30 vertices and in these cases, the minimum number of vertices in the returned subgraph was 43 while the median was 91. Overall, the median size of the BioNet hit list was 27 vertices (mean 39.53) with a maximum size of 251 vertices. So even without accounting for the false positives in the BioNet hit lists, the number of true positives found is still generally worse than other methods, which was also the case in the original simulation experiment (Supplementary Fig. S6).

Simulating a biological network is particularly difficult as even characterizing network topologies is a challenging problem (Pavlopoulos et al., 2011). Here, the simulated scale free networks were trees whereas this is an unlikely attribute of a 1000 vertex PPI network. Additionally, simulating genomic data are equally difficult and recent tools, for example to simulate gene expression based on RNA sequencing (Benidt and Nettleton, 2015; Frazee et al., 2015), do not then further consider the simulated data over a network. We have just used an independent simulation experiment to compare our MRF score to a number of other previously proposed methods. Such a comparison with known ‘true hits’ is otherwise not possible for any real data application.

3.4 Model fitting discussion

The intercept of the underlying densities in our general set-up (Supplementary Fig. S1) has an interpretation as the P-value below which genes are guaranteed to have a non-zero MRF score. We found that an intercept of 0.3 generally gave reasonable results. This value is near the maximum possible intercept point while still being reasonably peaked at 0 (Supplementary Fig. S1). Under this general scheme, all genes with P-values <0.3 will therefore be a ‘hit’ at β = 0 and hence will have a non-zero MRF score. Genes with P-values >0.3 may be a hit for some other value of β dependent on their P-value and neighbours, it is just not guaranteed they will have a non-zero score. The consideration here is that the intercept should be as high as possible so that many genes are scored, while maintaining that the ‘non-hit’ label is the dominant label and so the final MRF scores are therefore a measure of the strength of the hit. Note that the hit density is not a model for the observed ‘true hit’ P-values but simply a discriminative element in our MRF based method.

A general trade-off in a network based hit list is the loss of information relating to screening data that does not conform to the network. In the most extreme case, if a vertex does not have any neighbours then the corresponding gene cannot be a network based hit. This is equally true for any of the other previously proposed methods we have compared to. Hence the network based hit list should never be considered by itself but rather as an additional network ‘grouped’ or ‘smoothed’ hit list that is considered in relation to the original threshold hit list. In our case, by using a co-expression PPI network for the OGG1 data, our network based hit list favours functionally related (Stuart et al., 2003; Xulvi-Brunet and Li, 2010) moderate to strong hits at the expense of strong isolated hits. This directly facilitates the investigation of mechanisms of interest for the selected phenotype. The full ‘combined’ PPI network may also be of interest to investigate well studied groups of genes in other biological contexts. For example, co-expression PPI networks may not include important interactions such as those involving house-keeping genes. It would also be of interest to investigate PPI networks inferred from single specific studies (Huttlin et al., 2015; Rolland et al., 2014), rather than inferred from a collection of many disparate studies such as the PPI data collated by STRING.

PPI networks are the most common genomic networks utilized in such analysis. However, in general there are known issues with the accuracy of PPI network data (Mahdavi and Lin, 2007; Pan et al., 2015) as well as the fact that proteins that may not physically interact but that still act on the same cell or molecular function are not taken into consideration. Furthermore, as opposed to regulatory networks, it is not known whether any given interaction represents a positive or negative effect, for example. It is possible that such additional information could be incorporated within a network based analysis. More generally, such an approach could also be considered with directed network data from other sources, for example signalling or metabolic pathway information, and this could be a fruitful subject for future work.

3.5 Implementation in MATLAB and computational expense

The MATLAB code to reproduce the results presented in the paper is given as Supplementary Material. Our MRF based network scoring method was implemented in MATLAB on a mid-2012 MacBook Pro with a 2.6 GHz Intel Core i7 processor (quad-core) and 16 GB of RAM. The minimum energy labels were found using the α-expansion algorithm (Boykov et al., 2001; Boykov and Kolmogorov, 2004; Kolmogorov and Zabih, 2004). Running over n = 1000 values of β took ∼1.3 s for the simulated data (1000 vertices, 2 labels), ∼20 s for the lymphoma data (2034 vertices, 4 labels) and ∼70 s for the OGG1 data (4006 vertices, 4 labels). Due to the heterogeneous nature of the genomic data and networks, our MRF-based method is currently not suitable for a graphical user interface. For example, the flexibility to consider multivariate P-values as well as multiple labels of interest beyond just binary ‘hit’ and ‘non-hit’ is best achieved using a command line input as available in MATLAB.

4 Conclusion

We have proposed a network based method to determine hit genes using an MRF and have shown the effectiveness of the method using a broad range of different data sets. The multiple advantages of the MRF method are that it easily allows for multivariate gene scores in addition to multiple labels of interest beyond binary ‘hit’ and ‘non-hit’. The intercept of the underlying densities can be considered as a parameter with an interpretation and for which we have provided general advice on setting. We have provided the MATLAB code and data to reproduce the results presented in the paper, which is freely available for modification.

We have shown that our MRF method gave the best results in a simulation experiment originally used to evaluate Knode and BioNet. We have additionally shown that we were able to find greater pathway enrichment as well as further determine hit genes in a lymphoma study concerning survival analysis and gene expression, whereas the multiple observed P-values for each gene were combined for input into the BioNet method. For the OGG1 screening data we have shown that the MRF method allows for the analysis of the multivariate scores and is able to find relevant functional/GO annotation. For the study of genomic data with an associated network where the ‘guilt by association’ assumption is appropriate, we have shown that our proposed MRF based method gives an advantageous way to determine network based hit genes as against previously proposed methods.

We also noted a major pitfall using functional/GO enrichment for validation when it is strongly correlated with vertex degree in the PPI network and confounded by an ‘annotation bias’. We considered a network of only co-expression PPI evidence to account for this issue and also took this into consideration when evaluating our results. This issue does not appear to have been given enough attention in the literature, especially when there are so many papers utilizing both PPI networks as well as functional/GO enrichment analysis.