Abstract
Motivation
Meta-analysis is essential to combine the results of genome-wide association studies (GWASs). Recent large-scale meta-analyses have combined studies of different ethnicities, environments and even studies of different related phenotypes. These differences between studies can manifest as effect size heterogeneity. We previously developed a modified random effects model (RE2) that can achieve higher power to detect heterogeneous effects than the commonly used fixed effects model (FE). However, RE2 cannot perform meta-analysis of correlated statistics, which are found in recent research designs, and the identified variants often overlap with those found by FE.
Results
Here, we propose RE2C, which increases the power of RE2 in two ways. First, we generalized the likelihood model to account for correlations of statistics to achieve optimal power, using an optimization technique based on spectral decomposition for efficient parameter estimation. Second, we designed a novel statistic to focus on the heterogeneous effects that FE cannot detect, thereby, increasing the power to identify new associations. We developed an efficient and accurate p-value approximation procedure using analytical decomposition of the statistic. In simulations, RE2C achieved a dramatic increase in power compared with the decoupling approach (71% vs. 21%) when the statistics were correlated. Even when the statistics are uncorrelated, RE2C achieves a modest increase in power. Applications to real genetic data supported the utility of RE2C. RE2C is highly efficient and can meta-analyze one hundred GWASs in one day.
Availability and implementation
The software is freely available at http://software.buhmhan.com/RE2C.
Supplementary information
Supplementary data are available at Bioinformatics online.
1 Introduction
Genome-wide association studies (GWASs) have identified numerous single-nucleotide polymorphisms (SNPs) that are associated with human traits (Manolio, 2010; Welter et al., 2014). For many diseases, however, the identified variants explain only part of the known heritability, which indicates the existence of undetected variants with small effects (Evangelou and Ioannidis, 2013; Manolio, 2013). To scale up genetic discovery, meta-analysis of GWASs has become a popular tool to augment the sample size (Evangelou and Ioannidis, 2013; Fleiss, 1993; Zeggini and Ioannidis, 2009). Recently, the use of meta-analysis in GWASs has expanded to new research designs, such as combining different related diseases (Kiryluk et al., 2012; Lee et al., 2014; Perry et al., 2012), populations (Liu et al., 2015), environments (Kang et al., 2014), tissues (Sul et al., 2013) and cancer types (Bhattacharjee et al., 2012; Petersen et al., 2010). These differences between studies can manifest as heterogeneity, which refers to effect-size differences. When heterogeneity exists, the commonly used fixed effects model (FE) is not optimal. The traditional random effects model (RE) (DerSimonian and Laird, 1986) is also conservative and is not powerful (Han and Eskin, 2011). To overcome this challenge, we recently developed a modified RE (RE2) that has higher power under condition of heterogeneity (Han and Eskin, 2011). RE2 has been used widely in cross-population human disease analyses (Chimusa et al., 2014; Keller et al., 2014; Sapkota et al., 2014), cross-environment mouse trait analyses (Kang et al., 2014), cross-condition expression quantitative trait loci (eQTL) analyses (Sul et al., 2013; Ye et al., 2014), and cross-feature neuroimaging analyses (Hibar et al., 2012; Stein et al., 2012).
However, RE2 has some limitations. First, RE2 cannot perform meta-analysis of correlated statistics. Although the traditional assumption of independence of statistics has been valid in conventional study designs, it can be invalidated in new research designs. For example, in cross-disease meta-analyses, it is common that some controls are used in more than one study, which can cause correlations of statistics (Dichgans et al., 2014; Kar et al., 2016; Moskvina et al., 2013). Thus, in cross-disease analyses, both heterogeneity and correlations can occur. In a cross-tissue eQTL analysis (Sul et al., 2013), the intra-individual similarity of gene expression levels between different tissues can cause the correlations of statistics. To account for these correlations, Lin and Sullivan extended FE (Lin and Sullivan, 2009). However, for RE methods, no solutions have been suggested. Recently, Han et al. developed a decoupling approach that makes the statistics independent (Han et al., 2016). The transformed data can be used for RE2. However, the optimality of this approach has not been evaluated yet. The second limitation of RE2 is that the identified variants by RE2 and FE overlap substantially. This is because RE2 is designed as a stand-alone method that captures variants with and without heterogeneity. However, in most of the meta-analyses of GWASs, it is essential to apply FE before applying RE2, because detecting variants with homogeneous effects is of primary interest. To the best of our knowledge, all investigators who employed RE2 for meta-analyses of GWASs used RE2 coupled with FE. Considering this practical situation, the current implementation of RE2 could be suboptimal.
In the present study, we propose a new method, called RE2C, which increases the power of RE2 in two ways. First, we generalized the likelihood model of RE2 to account for correlations of statistics and to achieve optimal power. To estimate the maximum likelihood estimators of parameters efficiently, we developed an optimization procedure based on spectral decomposition of the variance-covariance matrix. Second, we modified the statistic to focus on the heterogeneous effects that cannot be detected by FE. This modification increased the power to identify new associations after the application of FE. The statistic does not follow a known asymptotic distribution; therefore, we developed an efficient and accurate P-value approximation procedure using analytical decomposition of the statistic. In our simulations, RE2C achieved a dramatic increase in power compared with competing approaches, such as the decoupling approach (71% vs. 21%) when the statistics were correlated. Even when the statistics were uncorrelated, RE2C achieved a modest increase in power. Applications to real genetic data demonstrated that RE2C improved the significances of the associated variants. RE2C is efficient and can meta-analyze one hundred GWASs within one day. The software is available at http://software.buhmhan.com/RE2C.
2 Materials and methods
2.1 Existing meta-analysis methods for independent statistics
2.1.1 Fixed effects model
The FE method assumes that the magnitude of the true effect is common or fixed in every study in the meta-analysis. The inverse-variance-weighted effect-size method (Cochran, 1954; de Bakker et al., 2008; Fleiss, 1993; Mantel and Haenszel, 1959) and the weighted sum-of-z-scores method (de Bakker et al., 2008; Han and Eskin, 2011; Zaykin, 2011) are used widely. We only describe the former, because the two methods are approximately equivalent (Lee et al., 2016). Let be the effect-size estimates, such as log odds ratios or regression coefficients, in independent studies.
Under the FE model, the observed effect of study i is the sum of the true common effect and the within-study error :
If the sample sizes of the studies are sufficiently large, is normally distributed. Let SE() be the standard error of and let = SE()2. It is common practice to use the estimated sample variance for . Let be the inverse variance. The inverse-variance-weighted effect-size estimator is the sum of weighted with weights :
| (1) |
The variance of is
It follows that the standard error of is . Note that is minimized only if the weights are inverse variances, which explains the method’s name (Cochran, 1954; Greene, 2012; Lee et al., 2016). We can then build a summary z-score,
which follows under the null hypothesis of no association . The P-value can be calculated as
where is the cumulative density function of the standard normal distribution.
2.1.2 Random effects model (traditional)
In contrast to FE, the RE method models heterogeneity explicitly and assumes that the true value of the effect size of each study is sampled from an underlying distribution. Suppose that the distribution has mean and variance 2. The observed effect is then the sum of the common effect and the deviation of the th study’s observed effect from , say (Cochran, 1954) such that
where the within-study error is uncorrelated with the true effect sizes . The variance in is the sum of the between-study variance and the within-study variance (Western and Bloome, 2009),
The most popular approach to estimate is the method of moments proposed by DerSimonian and Laird (DerSimonian and Laird, 1986, 2015). Given the estimated between-study variance , the RE effect size is calculated similarly to Equation (1):
where the weights are now instead of . Note that SE .
Similarly to FE, we can construct a z-score statistic
and the P-value is
The traditional RE approach is equivalent to a likelihood ratio test that assumes the same heterogeneity under both the null and the alternative hypotheses (Han and Eskin, 2011). This assumption can be conservative in GWASs; therefore, RE has limited power in GWASs (Han and Eskin, 2011).
2.1.3 RE2 (Han and Eskin)
Han and Eskin proposed a modified RE method (RE2) that has better power than RE or FE under conditions of effect size heterogeneity (Han and Eskin, 2011). The key difference between RE and RE2 is that the latter assumes no heterogeneity under the null hypothesis. This assumption is appropriate in many situations of GWASs where we expect that the effect sizes are all zero under the null hypothesis. The method is a likelihood ratio test that has the fixed parameters under the null hypothesis, as follows:
| (2) |
| (3) |
The roots of the partial derivatives of the equation (3) are not in a closed form; therefore, the maximum likelihood (ML) estimates and must be determined by using an iterative procedure. Hardy and Thompson suggested a simple and efficient procedure based on the Newton–Raphson method (Han and Eskin, 2011; Hardy and Thompson, 1996). Given and , the likelihood ratio statistic can be constructed as follows:
The value of is restricted to be non-negative; therefore, as shown by Self and Liang (Self and Liang, 1987), the statistic follows a 50:50 mixture of and asymptotically. Thus, the asymptotic P-value is
In practice, because of the small number of studies (N), a tabulated correction is necessary for an accurate P-value. We pre-calculated the P-value table and the P-value is
where is the small sample correction factor.
2.2 Existing meta-analysis methods for correlated statistics
2.2.1 The Lin-Sullivan method
Historically, meta-analysis methods focused mainly on summarizing independent estimates. However, in recent research design, the statistics are often correlated, for example, because of overlapping subjects, which is common in cross-disease meta-analysis. Lin and Sullivan (Lin and Sullivan, 2009) developed a meta-analysis solution to account for these correlations. First, they showed that the correlations of statistics could be calculated analytically. For example, in a case/control design, the correlation between statistics of studies i and j is approximated as
where , and are the total number of th and th studies and the number of overlapping subjects between the two (th and th), respectively. Subscripts 1 and 0 denote the case and control status. Let be the correlation matrix of . Given , one can easily calculate the variance-covariance matrix, Lin and Sullivan suggested a statistic:
where is an vector with ones. The variance is Therefore, one can obtain a z-score as well as a P-value (Lin and Sullivan, 2009). This method does not assume heterogeneity; therefore, it can be considered as an extension of FE to account for correlations.
2.2.2 The decoupling method
Recently, Han et al. (Han et al., 2016) proposed a method called "decoupling" that can transform correlated data into independent data. As Lin and Sullivan showed, in many situations, the correlation matrix C can be approximated analytically before the meta-analysis. Han et al. calculate a transformed covariance structure:
where s is the vector of standard errors, and diag(s) is a diagonal matrix whose diagonals are s. The updated standard errors then become
where denotes the th diagonal element of . The data become independent, and thus can be used for RE2 as well as FE. Han et al. showed that when the decoupled data are used for FE, the method is analytically equivalent to the Lin-Sullivan method. Han et al. also showed that under conditions of heterogeneity, RE2 with decoupling (Decoupling-RE2) shows a higher power than FE with decoupling. However, the optimality of Decoupling-RE2 has not been evaluated.
2.3 RE2C
In the present study, we propose RE2C, a powerful random effects method for meta-analysis of GWASs. RE2C is built upon RE2, but with two modifications that improve its power: (1) accounting optimally for correlations, and (2) focusing on heterogeneous effects conditioned on the application of FE. C in RE2C refers to both correlations and conditioning.
2.3.1 Optimizing for the meta-analysis of correlated datasets
We extended the RE2 model to include correlations between statistics. Let be the length n vector denoting the observed effect sizes. Then, we could build a model
where are random effects reflecting between-study heterogeneity and are random errors. Given the correlation of statistics C, which can be approximated analytically using the Lin-Sullivan approach (Lin and Sullivan, 2009), we have where is the vector of the standard errors. Then, the variance-covariance matrix of is
The likelihood functions under the null and alternative hypotheses become
To build a likelihood ratio test, we must find the maximum likelihood estimation (MLE) of the parameters and . Previously, for independent statistics, RE2 utilized an iterative procedure suggested by Hardy and Thompson (Hardy and Thompson, 1996). However, their method only considers independent statistics. Therefore, we developed an optimization procedure that can be applied efficiently for both independent and correlated statistics. We chose to use the technique developed for the restricted maximum likelihood (REML) framework. The key idea of our optimization procedure is to transform the two-dimensional search into a one-dimension search using the technique that was developed by Patterson and Thompson (Patterson and Thompson, 1971). A similar technique has been used previously to correct for population stratifications (Kang et al., 2008).
We decomposed the observations using a direct sum, where one of the decomposed observations is the observation for the REML function after integrating out the fixed effects. That is, we decomposed into two matrix-vector multiplications of and such as:
where is a transformation matrix of rank and is a transformation matrix of rank. The specific forms of and for our purpose are described below. The properties of the direct sum mean that the log-likelihood function of the mixed model can be decomposed into two log-likelihood functions of independent observations as follows:
The projection matrix is an idempotent and symmetrical matrix that integrates out the fixed effects (mean) of the observation . In our problem, matrix is:
Here, is a vector of ones of size n. The matrix satisfies , i.e. . Then, matrix becomes:
Matrix satisfies the conditions and . Next, we considered the full log-likelihood with the parameters of interest and as follows
is an orthogonal projection matrix; therefore, is in the form of , where is an matrix with orthonormal columns, such that . To reduce the complexity of the restricted likelihood function for , Harville (1974) suggested the use of the restricted likelihood function for , where the MLE for the two likelihood functions are the same. As Harville showed, the restricted likelihood can be shown as:
where . Let the orthogonal matrix, , be the eigenvectors of the matrix such that is diagonal. Let . The matrix then has the following properties: (i) , (ii) , (iii) and (iv) . Using the spectral decomposition framework, the symmetric matrix can be shown as:
| (4) |
where is the eigenvalues of the matrix , where at least one value is zero, and the ) matrix has the eigenvectors associated with as the columns. We use to refer to a vector of ones of size . Note that is equal to . Using the properties of the matrix and , we have
Here, we considered the full (not restricted) likelihood function whose is substituted with .
For our problem of finding the MLE, this modified function is sufficient, because it satisfies that at the MLE. Note that although we focused on the full likelihood function to build a likelihood ratio test, the same optimization procedure below can be applied to the restricted likelihood function. Following Equation (4), we could define the generalized inverse of the matrix , , which is
Next, we could transform into a simpler expression as follows:
Thus, the likelihood becomes
where the scalar value is the th eigenvalue of the matrix , and is the th component of the vector . Now, the transformation has reduced the number of parameters to one (). Thus, we can use a simple Newton-Raphson procedure to estimate the unknown parameter, . The first and the second derivatives of the transformed log-likelihood functions are:
In summary, using this optimization procedure, the parameter estimation needs only the application of the Newton-Raphson method to a single parameter, which is very efficient. Thus, we have a high chance of obtaining the global optimum using a grid search as the starting point for the Newton-Raphson procedure. After we find the MLE, we can build a likelihood ratio test statistic,
which follows a 50:50 mixture of and asymptotically.
2.3.2 Focusing on heterogeneous effects
We then modified the test procedure of RE2 to focus on heterogeneous effects. In most meta-analyses of GWASs, detecting variants with homogeneous effects is of primary interest. For this reason, it is often essential to apply FE before applying RE2, while accounting for the increased multiple testing burden. We surveyed the literature that cited and used RE2; at least in all the papers that we examined, the studies used RE2 coupled with FE. Thus, considering this unique situation of meta-analysis of GWASs, where the prior application of FE is mandatory, we can improve the power of RE2 by focusing on the heterogeneous effects that would not be identified by FE.
Specifically, we designed a statistic as follows,
In short, this statistic can become significant only if the RE2 P-value is more significant than the FE P-value. Although the statistic looks simple, calculating the P-value of this statistic is non-trivial. Obviously, unlike RE2, this statistic does not follow a known asymptotic distribution. One possible way is to use a resampling approach that samples null z-scores repeatedly. However, P-values typically observed in GWASs are extremely small . To estimate such a small P-value using resampling, a large number of samplings are required. Thus, in GWASs where millions of markers are analyzed, resampling can be very slow.
To approximate the P-value of the new method efficiently, we used the following strategy. Recall that the RE2 statistic is a likelihood ratio statistic that measures the difference between the two likelihoods: L0 in Equation (2) and L1 in Equation (3). We introduced an intermediate likelihood function,
which is similar to L1, but with a restriction of Then, the RE2 statistic can be decomposed into the sum of the difference between L0 and Lint and the difference between Lint and L1, as follows (Han and Eskin, 2011):
where Ø indicates an empty set. The first statistic, , is equal to the square of the FE statistic (). The second statistic, , tests for nonzero between-study variance, similar to the Cochran’s Q test. The two statistics are independent under the null hypothesis (Self and Liang, 1987). Asymptotically, follows , and follows a 50:50 mixture of 0 and . However, the conditions for them to follow their asymptotic distributions are different. Under the assumption that the effect size () follows a normal distribution due to a large sample in each study, which is the case in GWASs, follows regardless of the number of studies (N). However, even under the normality assumption, follows a 50:50 mixture of 0 and only if N is large. N is small in typical meta-analysis of GWAS; therefore, the true distribution of can deviate greatly from the asymptotic distribution. For our method, we approximated and tabulated the distribution of empirically for every possible N.
In the previous section, we extended the RE2 model to account for correlations between statistics. Equation (5) can also be decomposed into two parts,
where is the Lin-Sullivan estimator of μ, which is . is equivalent to the square of the z-score of the Lin-Sullivan method in this situation.
Now that the RE2 statistic can be decomposed into and whose null distributions are known, given an observed RE2 statistic, its P-value can be interpreted as an integral over a region in the two-dimensional space. Specifically, in Figure 1, the RE2 P-value is the volume of the region excluding the bottom left triangle (i.e. region ). However, in RE2C, we only consider the region where . Thus, for each , we can search for that would satisfy , or
Let this lower boundary of that satisfies be . This boundary is plotted as a dashed line in Figure 1. Then, given an observed RE2C statistic , we calculated the P-value as follows. We divided the range of into K small bins (e.g. 1000 bins in [0,50]), denoted as (). The approximated P-value is
where is the width of the bins. That is, we calculated the probability that would be large enough to satisfy for every bin of , and integrated them together. We took the maximum function because if is smaller than , then by definition. Thus, we calculated the volume of region A in Figure 1. As a result, it always satisfies the equation:
as long as , because we have removed region B in Figure 1. This shows that the RE2C P-value can never be less significant than the RE2 P-value when those methods are used coupled with FE, for the variants with . Note that the calculation of the P-value is efficient because we have pre-calculated for every x and N and the cumulative density function of for every N. Thus, the computational complexity is only O(K). Moreover, the complexity is not dependent on how small the P-value is, unlike in the resampling approaches.
Fig. 1.
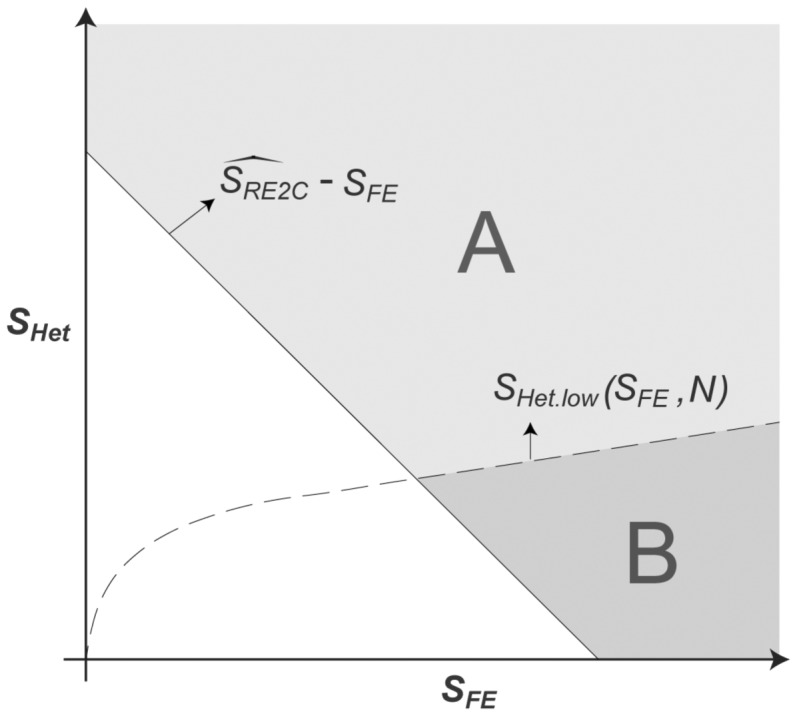
Two-dimensional representation of and . Given the observed statistic , is the probability in area A, while is the probability in areas A and B
3 Results
3.1 Simulations
We evaluated the performance of RE2C using simulations. We assumed seven studies, each of which comprised individuals, half of which were controls and half were cases. We assumed a SNP with a minor allele frequency (MAF) of 0.1, following the Hardy-Weinberg equilibrium.
3.1.1 False positive rate
We assumed the null hypothesis of no association and evaluated the false positive rate of RE2C. We repeated the null simulations 109 times and estimated the false positive rate as the proportion of the repeats whose P-value was , where . Table 1 shows that the false positive rates of RE2C were well calibrated. We then assumed that the statistics were correlated, with a correlation coefficient ρ = 0.4. The false positive rates for the correlated statistics were also controlled (Table 1). There was a slight conservative tendency, which was possibly caused by the errors in our approximation of P-values using bins. However, the discrepancies were very small.
Table 1.
False positive rates of RE2C
| 5.0·10−2 | 5.0·10−4 | 5.0·10−6 | 5.0·10−8 | |
|---|---|---|---|---|
| Independent input | 4.8·10−2 | 4.8·10−4 | 4.7·10−6 | 5.5·10−8 |
| Correlated input (ρ = 0.4) | 4.7·10−2 | 4.6·10−4 | 4.5·10−6 | 4.0·10−8 |
3.1.2 Power for independent statistics
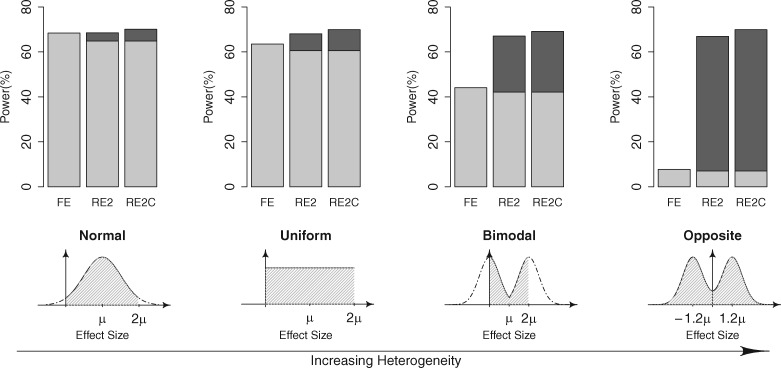
We compared the powers of FE, RE2 and RE2C. We generated 10 000 sets for meta-analysis, where we again assumed seven studies with sample size equal to 2000 and a MAF of 0.1. In our simulations, we considered the practical situations that FE was already applied before the application of RE2 or RE2C. Thus, we considered the combined use of RE2 (or RE2C) with FE where multiple tests were accounted. Specifically, the power of FE was the proportion of the sets whose P-value exceeded the genome-wide threshold . The power of RE2 (or RE2C) was the proportion of the sets whose FE or RE2 (RE2C) P-value exceeded . To model the effect size heterogeneity in our simulations, we assumed four different effect size distributions. Let μ be a specific, assumed target log odds ratio. The four distributions were as follows, in order of increasing amount of heterogeneity. First, we assumed a unimodal distribution that was a normal distribution with mean and standard error μ, truncated to [0, 2μ]. Second, we assumed a uniform distribution spanning . Third, we assumed a bimodal distribution that followed N(0, μ2) truncated to [0, μ] with one half probability, and N(2μ, μ2) truncated to [μ, 2μ] with another half probability. These three distributions all had mean μ. Finally, we assumed a distribution representing opposite effects, which followed N(-1.2μ, μ2) with one-half probability and N(1.2μ, μ2) with another half probability. Although opposite effects between studies can be rare in genetic studies of the same disease, they can occur in cross-disease meta-analyses or cross-tissue eQTL analyses. Once we assumed one of the distributions above, we randomly sampled , the log odds ratio in study , from the distribution. We then sampled the minor allele counts in control and case samples assuming the control and case MAF, respectively. The control MAF was assumed to be the same as the population MAF (0.1), assuming a very small prevalence, and the case MAF was . For effective comparisons of power, we adjusted for each distribution such that the power of the most powerful method was approximately 70%.
Figure 2 shows the power comparison results. The powers of RE2 and RE2C are shown as stacked bars. We assumed a prior application of FE to random effect methods; therefore, we applied a different color scheme to the proportion of datasets determined as significant by FE (light grey) and the proportion of datasets where the random effect methods newly identified as significant (dark grey). Note that the height of light grey bar is slightly shrunk in RE2/RE2C compared in FE, because the significance level was adjusted to one-half. As the heterogeneity increases, the combined use of the random effect methods with FE gave increasingly higher powers than compared with using FE alone, as expected. Under all tested scenarios of effect size distributions, RE2C was the most powerful. RE2C increased power of RE2 by 1.55, 1.85, 2.07 and 2.98% for unimodal, uniform, bimodal and opposite effects, respectively. Although the increase in the absolute amount of power was modest, the increase in relative power gain compared with FE was non-negligible. For example, in the unimodal distribution, the power gain of RE2C from FE was 1.71%, which was more than 10 times greater than that of RE2 (0.16%).
Fig. 2.
Power of FE, RE2 and our new RE2C method for the meta-analysis of independent statistics. Assuming the statistics are independent, we simulated various effect size distributions with differing amounts of heterogeneity. We considered the scenario that RE2 or RE2C is additionally applied to FE while accounting for multiple testing. The power of RE2 and RE2C are shown as two-color stacked bars, where we colored the proportion identified by FE as significant in light grey and the proportion that RE2/RE2C additionally identified as significant in dark grey
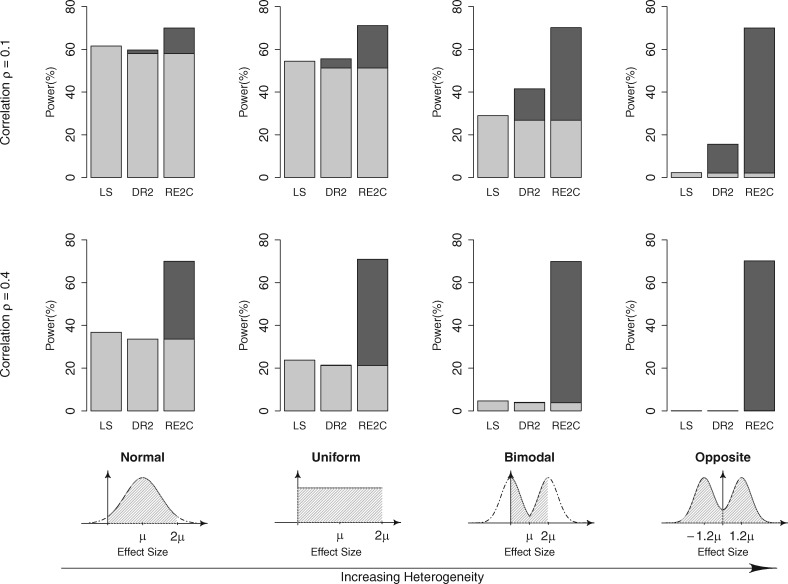
3.1.3 Power for correlated statistics
Using a similar simulation scheme, we evaluated the power of RE2C under the situation that the statistics were correlated. After we sampled the effect sizes of the studies, we generated the observed effect sizes assuming that they were correlated with correlation coefficient ρ. We assumed ρ = 0.1 and ρ = 0.4, and calculated the power for each setting. The value ρ = 0.4 was derived from assuming a cross-disease analysis with 2000 cases and 3000 shared controls (Wellcome Trust Case Control Consortium, 2007). The competing approaches in this simulation were the Lin-Sullivan (LS) and the Decoupling-RE2 (DR2) methods. As described in the Methods, the Lin-Sullivan method is an extended FE method to account for correlations. Decoupling-RE2 refers to the application of the transformed data by decoupling approach, which became independent, to RE2. Figure 3 shows that RE2C outperformed the other methods greatly in all scenarios of effect size distributions and correlations. For example, for the uniform distribution where ρ = 0.4, RE2C achieved 71% power while the power of Lin-Sullivan method and Decoupling-RE2 were only 23.8% and 21.4% respectively. Surprisingly, Decoupling-RE2 performed poorly even for large heterogeneity when the correlations were high (ρ = 0.4). This demonstrates that although the application of the decoupled data to RE2 is possible, it may not provide optimal power.
Fig. 3.
Power of Lin-Sullivan (LS), Decoupling-RE2 (DR2) and our new RE2C method for meta-analyzing correlated statistics. Assuming statistics are correlated with correlation coefficient ρ, we simulated various effect size distributions with differing amount of heterogeneity. We considered the scenario that DR2 or RE2C is additionally applied to LS while accounting for multiple testing. DR2 and RE2C power is shown as two-color stacked bars, where we colored the proportion that LS was significant in light grey and the proportion that DR2/RE2C additionally identified as significant in dark grey
3.2 Applications to real data
We wanted to evaluate the utility of RE2C for real data. To this end, we used the cross-disease analysis data of Moskvina et al. (Moskvina et al., 2013) who performed a meta-analysis of association results for the Alzheimer's disease (AD) and the Parkinson’s disease (PD). Moskvina et al. examined the meta-analysis P-values of 10 loci known to be associated with AD and 18 loci known to be associated with PD. The two diseases shared some controls; therefore, there were correlations between the statistics of the two diseases. To account for these correlations, Moskvina et al. used the Lin-Sullivan method. However, the same variant may have differing effects on the two diseases. Therefore, random effect methods might help in association tests. We obtained the reported effect sizes (OR) and P-values for these 28 loci from the table shown in their manuscript. We then calculated the standard errors from the OR and P-values, and used them for meta-analysis. We removed three loci whose OR was 1.00 (because the paper reported only two digits below zero), and applied RE2C to the remaining 25 loci.
Table 2 gives the details of the collected data and the meta-analysis results. Out of 25 loci, LS was the most significant in 13 loci. In all the remaining 12 loci, RE2C was the most significant. Note that for the 13 loci where LS was the most significant, RE2C P-values were completely non-significant (). This is because RE2C was designed to be used with FE (LS), but focusing only on loci with heterogeneity. We also show the results of an RE2C implementation with optimization for correlated statistics but without the technique for focusing on heterogeneous effects (denoted as RE2C*), which shows that focusing on heterogeneous effects improved P-values at these 12 loci. Overall, these results showed that if RE2C is used in combination with LS, a high association test power to detect both loci with and without heterogeneity is obtained. Interestingly, RE2C found two loci (rs4698413 and rs2263418) as genome-wide significant that were not identified by LS alone.
Table 2.
Cross-disease meta-analysis results of the Alzheimer’s disease and Parkinson’s disease based on the reported data from Moskvina et al.
| Methods |
||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Parkinson Disease |
Alzheimer Disease |
LS | DR2 | RE2C* | RE2C | |||||
| Chr | Base Pairs | SNP | OR | P | OR | P | P | P | P | P |
| Alzheimer Disease | ||||||||||
| 1 | 207 819 492 | 1-207819492 | 0.61 | 0.062 | 0.50 | 0.058 | 0.016 | 0.019 | 0.02389 | 1 |
| 2 | 127 892 810 | rs6733839 | 1.07 | 0.0098 | 1.23 | 5.2E-5 | 0.00029 | 0.00033 | 0.00017 | 3.0E-5 |
| 6 | 47 327 031 | rs9367271 | 1.11 | 0.0014 | 1.06 | 0.339 | 0.0017 | 0.0020 | 0.00279 | 1 |
| 7 | 143 106 884 | rs7806047 | 0.87 | 0.001 | 0.89 | 0.151 | 0.0007 | 0.0008 | 0.00118 | 1 |
| 8 | 27 466 181 | rs1532277 | 0.99 | 0.709 | 0.81 | 1.8E-6 | 0.024 | 0.0011 | 8.11E-05 | 1.5E-5 |
| 11 | 60 045 900 | rs7949816 | 0.95 | 0.073 | 0.82 | 0.00075 | 0.0084 | 0.010 | 0.00589 | 0.0012 |
| 11 | 85 677 094 | 11-85677094 | 1.20 | 0.0055 | 1.26 | 0.057 | 0.0019 | 0.002 | 0.00314 | 1 |
| 19 | 01 032 228 | rs56059558 | 0.86 | 0.0023 | 0.84 | 0.05 | 0.0008 | 0.0009 | 0.001302 | 1 |
| 19 | 45 392 254 | rs6857 | 0.95 | 0.154 | 5.55 | 4.4E-92 | 0.0002 | 2.9E-53 | 3.24E-94 | 1.6E-95 |
| 19 | 51 724 326 | rs200656 | 1.06 | 0.089 | 1.06 | 0.23713 | 0.055 | 0.06 | 0.07461 | 1 |
| Parkinson Disease | ||||||||||
| 1 | 155 135 036 | rs35749011 | 1.43 | 6.1E-5 | 1.02 | 0.938 | 0.00012 | 0.00014 | 0.00022 | 1 |
| 2 | 135 592 245 | rs6758044 | 1.12 | 1.2E-5 | 0.96 | 0.383 | 0.0005 | 0.0003 | 7.99E-05 | 1.5E-5 |
| 2 | 169 119 178 | rs13392079 | 1.14 | 1.1E-6 | 0.95 | 0.296 | 0.0001 | 3.2E-5 | 6.07E-06 | 1.0E-6 |
| 3 | 161 114 968 | rs336549 | 0.90 | 9.4E-6 | 1.05 | 0.275 | 0.0004 | 0.0002 | 4.68E-05 | 8.5E-6 |
| 3 | 182 760 073 | rs10513789 | 1.11 | 0.0007 | 1.01 | 0.921 | 0.001 | 0.0012 | 0.00164 | 1 |
| 4 | 15 737 882 | rs4698413 | 1.15 | 4.4E-9 | 0.98 | 0.651 | 5.6E-7 | 2.2E-7 | 5.38E-08 | 8.2E-9 |
| 4 | 77 146 751 | rs56275416 | 1.15 | 2.0E-6 | 1.01 | 0.84 | 3.8E-5 | 4.1E-5 | 2.80E-05 | 4.9E-6 |
| 4 | 90 646 886 | rs356165 | 0.76 | 1.2E-28 | 1.04 | 0.38 | 9.4E-21 | 8.0E-25 | 3.81E-28 | 3.2E-29 |
| 6 | 32 440 158 | rs7453703 | 1.10 | 0.0006 | 1.20 | 0.00021 | 1.4E-5 | 1.7E-5 | 2.68E-05 | 1 |
| 8 | 16 718 969 | rs587738 | 1.10 | 0.00015 | 1.02 | 0.616 | 0.0008 | 0.0009 | 0.00117 | 1 |
| 8 | 89 647 688 | 8-89647688 | 1.63 | 1.9E-5 | 1.50 | 0.078 | 1.2E-5 | 1.4E-5 | 2.26E-05 | 1 |
| 12 | 40 582 993 | rs2263418 | 1.24 | 1.5E-8 | 0.93 | 0.354 | 1.4E-6 | 5.6E-7 | 9.45E-08 | 1.5E-8 |
| 12 | 123 110 365 | rs6489158 | 0.91 | 0.00018 | 0.93 | 0.119 | 0.0001 | 0.0002 | 0.00023 | 1 |
| 16 | 31 103 796 | rs2359612 | 1.12 | 3.3E-6 | 1.08 | 0.073 | 2.8E-6 | 3.4E-6 | 5.55E-06 | 1 |
| 17 | 43 804 317 | rs9897399 | 0.75 | 1.5E-19 | 0.92 | 0.107 | 1.4E-16 | 4.6E-17 | 8.19E-18 | 8.3E-19 |
We compared the results of the Lin-Sullivan method (LS), Decoupling-RE2 (DR2) and RE2C. RE2C* refers to an RE2C implementation with optimization for correlated statistics but without the technique for focusing on heterogeneous effects. The most significant P-value among all methods is in bold-face.
We also performed additional real data analyses where statistics were uncorrelated, to demonstrate the performance of RE2C for combining independent datasets. The results are shown in Supplementary Materials (Supplementary Table S1).
3.3 Efficiency
We evaluated the efficiency of the methods (Table 3). To this end, we measured the running time of methods for the meta-analysis of differing numbers of studies (from 2 to 100). We timed how long it took to analyze 1 000 000 SNPs. We used the software R to run FE and RE2C, and Java to run RE2. RE2C was highly efficient. The estimated time to analyze a million SNPs in a meta-analysis combining 100 studies was 0.07 hours for RE2 and 0.44 hours for RE2C. Our results imply that RE2C is suitable for future large-scale meta-analyses, where the number of datasets to be combined is expected to grow.
Table 3.
Efficiency of RE2C
| 2 studies | 10 studies | 25 studies | 100 studies | |
|---|---|---|---|---|
| FE (R) | 25s | 52s | 93s | 297s |
| RE2 (Java) | 36s | 51s | 85s | 260s |
| RE2C (R) | 23s | 51s | 118s | 1615s (0.44h) |
4 Conclusion
We proposed a new random effects model meta-analysis method RE2C, which has an improved power for the detection of heterogeneous effects between studies. We optimized the statistic for meta-analyzing correlated statistics, and modified the statistics to only focus on heterogeneous effects. We expect that our method will be applied to a wide range of study designs in the future, such as cross-disease or cross-population studies, to help identify new associations.
Funding
This work was supported by the National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIP) [grant number 2016R1C1B2013126].
Conflict of Interest: none declared.
Supplementary Material
References
- Bhattacharjee S. et al. (2012) A subset-based approach improves power and interpretation for the combined analysis of genetic association studies of heterogeneous traits. Am. J. Hum. Genet., 90, 821–835. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chimusa E.R. et al. (2014) Genome-wide association study of ancestry-specific TB risk in the South African Coloured population. Hum. Mol. Genet., 23, 796–809. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cochran W.G. (1954) The Combination of Estimates from Different Experiments. Biometrics, 10, 101–129. [Google Scholar]
- de Bakker P.I.W. et al. (2008) Practical aspects of imputation-driven meta-analysis of genome-wide association studies. Hum. Mol. Genet., 17, R122–R128. [DOI] [PMC free article] [PubMed] [Google Scholar]
- DerSimonian R., Laird N. (2015) Meta-analysis in clinical trials revisited. Contemp. Clin. Trials, 45, 139–145. [DOI] [PMC free article] [PubMed] [Google Scholar]
- DerSimonian R., Laird N. (1986) Meta-analysis in clinical trials. Controlled Clin. Trials, 7, 177–188. [DOI] [PubMed] [Google Scholar]
- Dichgans M. et al. (2014) Shared genetic susceptibility to ischemic stroke and coronary artery disease: a genome-wide analysis of common variants. Stroke, 45, 24–36. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Evangelou E., Ioannidis J.P.A. (2013) Meta-analysis methods for genome-wide association studies and beyond. Nat. Rev. Genet., 14, 379–389. [DOI] [PubMed] [Google Scholar]
- Fleiss J. (1993) The statistical basis of meta-analysis. Stat. Methods Med. Res., 2, 121–145. [DOI] [PubMed] [Google Scholar]
- Greene William H. (2012) Econometric Analysis (7th ed.). Pearson Education. pp. 549–642. ISBN 9780131395381.
- Han B., Eskin E. (2011) Random-effects model aimed at discovering associations in meta-analysis of genome-wide association studies. Am. J. Hum. Genet., 88, 586–598. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Han B. et al. (2016) A general framework for meta-analyzing dependent studies with overlapping subjects in association mapping. Hum. Mol. Genet., 25, 1857–1866. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hardy R.J., Thompson S.G. (1996) A likelihood approach to meta-analysis with random effects. Statist. Med., 15, 619–629. [DOI] [PubMed] [Google Scholar]
- Harville D.A. (1974) Bayesian inference for variance components using only error contrasts. Biometrika., 61, 383–385. [Google Scholar]
- Hibar D.P. et al. (2012) Genome-wide association identifies genetic variants associated with lentiform nucleus volume in N = 1345 young and elderly subjects. Brain Imaging Behav., 7, 102–115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kang E.Y. et al. (2014) Meta-Analysis Identifies Gene-by-Environment Interactions as Demonstrated in a Study of 4,965 Mice. PLoS Genet, 10, e1004022–16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kang H.M. et al. (2008) Efficient control of population structure in model organism association mapping. Genetics, 178, 1709–1723. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kar S.P. et al. (2016) Genome-wide meta-analyses of breast, ovarian, and prostate cancer association studies identify multiple new susceptibility loci shared by at least two cancer types. Cancer Discov., 6, 1052–1067. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keller M.F. et al. (2014) Trans-ethnic meta-analysis of white blood cell phenotypes. Hum. Mol. Genet., 23, 6944–6960. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kiryluk K. et al. (2012) Geographic Differences in Genetic Susceptibility to IgA Nephropathy: GWAS Replication Study and Geospatial Risk Analysis. PLoS Genet., 8, e1002765–16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee C.H. et al. (2016) Comparison of Two Meta-Analysis Methods: Inverse-Variance-Weighted Average and Weighted Sum of Z-Scores. Genomics Inform., 14, 173–180. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee J.H. et al. (2014) Genetic susceptibility for chronic bronchitis in chronic obstructive pulmonary disease. Respir. Res., 15, 1–12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lin D.-Y., Sullivan P.F. (2009) Meta-analysis of genome-wide association studies with overlapping subjects. Am. J. Hum. Genet., 85, 862–872. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu J.Z. et al. (2015) Association analyses identify 38 susceptibility loci for inflammatory bowel disease and highlight shared genetic risk across populations. Nat. Genet., 47, 979–986. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Manolio T.A. (2013) Bringing genome-wide association findings into clinical use. Nat. Publishing Group, 14, 549–558. [DOI] [PubMed] [Google Scholar]
- Manolio T.A. (2010) Genomewide association studies and assessment of the risk of disease. N. Engl. J. Med., 363, 166–176. [DOI] [PubMed] [Google Scholar]
- Mantel N., Haenszel W. (1959) Statistical aspects of the analysis of data from retrospective studies of disease. JNCI J. Natl. Cancer Inst., 22, 719–748. [PubMed] [Google Scholar]
- Moskvina V. et al. (2013) Analysis of genome-wide association studies of Alzheimer disease and of parkinson disease to determine if these 2 diseases share a common genetic risk. JAMA Neurol., 70, 1268–1276. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Patterson H.D., Thompson R. (1971) recovery of inter-block information when block sizes are unequal. Biometrika, 58, 545–554. [Google Scholar]
- Perry J.R.B. et al. (2012) Stratifying Type 2 Diabetes Cases by BMI Identifies Genetic Risk Variants in LAMA1 and Enrichment for Risk Variants in Lean Compared to Obese Cases. PLoS Genet., 8, e1002741–14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Petersen G.M. et al. (2010) A genome-wide association study identifies pancreatic cancer susceptibility loci on chromosomes 13q22.1, 1q32.1 and 5p15.33. Nat. Genet., 42, 224–230. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sapkota Y. et al. (2014) Association between endometriosis and the interleukin 1A (IL1A) locus. Hum. Reprod., 30, 239–248. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Self S.G., Liang K.Y. (1987) Asymptotic properties of maximum likelihood estimators and likelihood ratio tests under nonstandard conditions. J. Am. Stat. Assoc., 82, 605–610. [Google Scholar]
- Stein J.L. et al. (2012) Identification of common variants associated with human hippocampal and intracranial volumes. Nat. Genet., 44, 552–563. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sul J.H. et al. (2013) Effectively identifying eQTLs from multiple tissues by combining mixed model and meta-analytic approaches. PLoS Genet., 9, e1003491–e1003413. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wellcome Trust Case Control Consortium. (2007) Genome-wide association study of 14,000 cases of seven common diseases and 3,000 shared controls. Nature, 447, 661–678. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Welter D. et al. (2014) The NHGRI GWAS Catalog, a curated resource of SNP-trait associations. Nucleic Acids Res., 42, D1001–D1006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Western B., Bloome D. (2009) Variance Function Regressions for Studying Inequality. Sociological Methodology., 39, 293–326. [Google Scholar]
- Ye C.J. et al. (2014) Intersection of population variation and autoimmunity genetics in human T cell activation. Science., 345, 1–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zaykin D.V. (2011) Optimally weighted Z-test is a powerful method for combining probabilities in meta analysis. J. Evol. Biol., 24, 1836–1841. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zeggini E., Ioannidis J.P. (2009) Meta-analysis in genome-wide association studies. Pharmacogenomics, 10, 191–201. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.