Subpicosecond conformational dynamics of small peptides probed by two-dimensional vibrational spectroscopy

Abstract

The observation of subpicosecond fluctuations in the conformation of a small peptide in water is demonstrated. We use an experimental method that is specifically sensitive to conformational dynamics taking place on an ultrafast time scale. Complementary molecular-dynamics simulations confirm that the conformational fluctuations exhibit a subpicosecond component, the time scale and amplitude of which agree well with those derived from the experiment.

Conformational fluctuations are an important property of proteins and peptides, and it seems likely that evolution has optimized not only the structure of proteins, but also their dynamics. It is well known that the dynamics of proteins occur on a wide range of time scales, extending from seconds to femtoseconds (1, 2). Ultrafast fluctuations of the backbone of peptides and proteins enable a rapid sampling of the highly dimensional configuration space of proteins, and hence promote the elementary steps of large-scale conformational changes, such as protein folding (3, 4). Furthermore, molecular dynamics (MD) studies have shown that ultrafast structural fluctuations can be essential for biological activity (5) and selectivity (6). As most experimental methods for studying conformational dynamics give very limited information on the (sub)picosecond component of these dynamics, our present knowledge of fast protein dynamics stems mainly from MD simulations.

Recently, two-dimensional (2D) IR spectroscopy has been demonstrated (7–12), a technique that has been discussed mostly in terms of the time-averaged structure of the investigated small peptides. In 2D NMR spectroscopy, incoherent population transfer between spin states is commonly used to investigate conformational fluctuations of peptides and proteins (13, 14), a technique known as nuclear Overhauser effect spectroscopy (NOESY). Transfer of excitation is related to conformational fluctuations, which give rise to a stochastic time dependence of the coupling between spin states. Because frequency splittings of spin transitions are typically on the order of MHz, NOESY is most sensitive to fluctuations taking place on a time scale of microseconds. Here, we show that IR double-resonance spectroscopy on vibrational transitions is capable of revealing information similar to that obtained with NOESY (15, 16). We measure the incoherent energy transfer of amide I vibrational excitations (which mainly involve the stretching of the peptide C⩵O bond) between the two coupled peptide units of the small peptide trialanine in aqueous solution. Just as in NOESY, the population transfer is related to conformational dynamics. However, because the typical frequency splittings between amide I states are on the order of 10–100 cm⁻¹, the method presented here has the important advantage of being specifically sensitive to conformational fluctuations taking place on a subpicosecond time scale. We study the small peptide trialanine, the two main degrees of freedom of which are the (φ,ψ) dihedral angles (see Fig. 4A), which also determine the backbone conformation of proteins. The experimental results are compared with the results of complementary MD simulations.

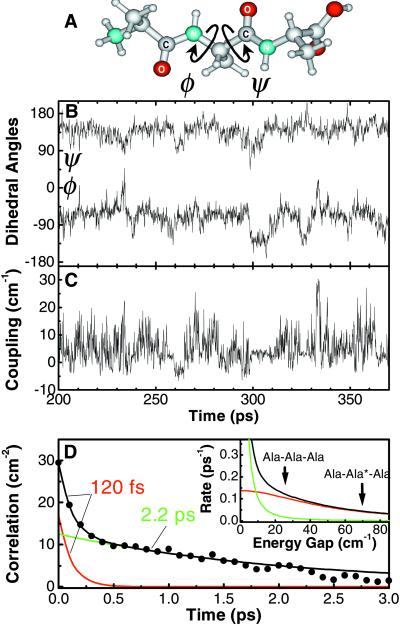
Figure 4.

(A) Molecular structure of trialanine. The central dihedral angles (φ,ψ) are indicated by arrows. (B) Trajectory of the dihedral angles φ(t) and ψ(t) of the central amino acid of trialanine as obtained from the MD simulation. (C) Instantaneous coupling β(t) computed from the trajectory. (D) Coupling correlation function 〈δβ(t)δβ(0)〉, the Fourier transform of which determines the cross relaxation rate (Inset). The arrows mark the frequency splittings of Ala-Ala-Ala and Ala-Ala*-Ala, respectively. The red and green curves represent the fast and slow components of the correlation function, respectively.

Experiment

Our laser setup has been described in detail elsewhere (17). Using a white-light seeded optical parametric amplifier pumped with the output of a commercial Ti:Sapphire amplifier, we generate mid-IR pulses tunable from 2 to 10 μm, with a duration of 100–150 fs, and an energy and bandwidth of 1 μJ and 200 cm⁻¹, respectively. A small fraction of the pulses is split off to obtain broadband probe and reference pulses. The remainder, which is used as the pump pulse, is passed through a computer-controlled Fabry-Perot filter. In this way, narrow-band pump pulses (bandwidth 11 cm⁻¹, pulse duration 750 fs full-width-half maximum)‖ are obtained, the center frequency of which can be tuned by adjusting the Fabry-Perot filter. We obtain 2D vibrational spectra by recording the absorption change of the sample as a function of the pump and probe frequencies.

Experiments were carried out on 0.15 M solutions of deuterated Ala-Ala-Ala and Ala-Ala*-Ala (where * denotes ¹³C substitution of the carbonyl carbon atom). ¹³C-Isotope-labeled and normal tri-l-alanine (purity > 95%) were purchased from Biosynthan (Berlin), and Bachem Biochemica (Heidelberg), respectively, and were lyophilized first from HCl solution to remove residual trifluoroacetic acid, then from D₂O to deuterate the NH groups. The samples were kept between 2-mm-thick CaF₂ windows separated by a 50-μm spacer. Experiments were carried out in D₂O, at pD = 1 to ensure that most (>95%) of the carboxylate groups are protonated, thereby minimizing the spectral overlap between the carboxylate CO-stretch and amide I modes.

The MD simulations were performed with the GROMOS96 simulation program package using the gromos force field 43A1 (18). Trialanine was placed in a periodic box containing 1263 SPC water molecules. The equation of motion was integrated by using a leapfrog algorithm with a time step of 0.002 ps and constraining covalent bond lengths. The solute and solvent were separately weakly coupled to temperature baths of 300 K and a pressure of 1 atm, respectively (19). Following a standard equilibration procedure, a 20-ns trajectory was recorded.

Results

The absorption spectrum of deuterated Ala-Ala*-Ala (Fig. 1A) exhibits two amide I bands, which correspond to the two peptide units of the molecule and are separated by a frequency splitting Δɛ of ≈70 cm⁻¹. In the case of Ala-Ala-Ala, the splitting is Δɛ = 25 cm⁻¹ (10). 2D-IR spectroscopy has recently been applied to Ala-Ala-Ala (10) and Ala-Ala*-Ala (11). From the intensity and the polarization dependence of the cross peaks of both samples, we were able to uniquely determine the coupling (6 cm⁻¹) and relative orientation (106°) between the two peptide C⩵O groups, and hence the time-averaged solution conformation of the peptide, for which we found (φ,ψ) ≈ (−60°, 140°) (10, 11). It should be noted that conventional (one-dimensional) IR spectroscopy of the amide I band, well known for its conformation sensitivity (20), does not contain sufficient information for such an unambiguous structure determination (10). Because the coupling β between the two peptide units is 6 cm⁻¹, both isotopomers are in the weak-coupling limit (β ≪ Δɛ), in which the excitations are strongly localized on either of the two peptide units.

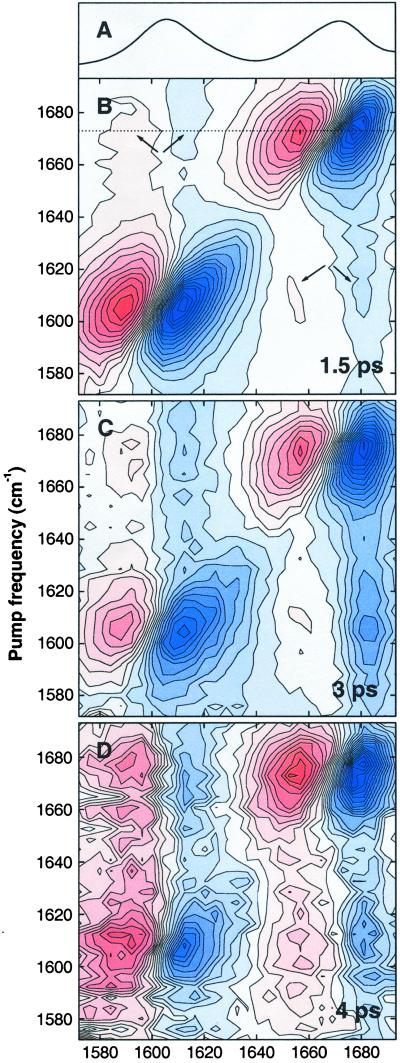
Figure 1.

(A) Linear absorption spectrum of deuterated Ala-Ala*-Ala dissolved in D₂O. (B–D) 2D spectra for perpendicular polarizations of the pump and probe pulses, showing the absorption change as a function of pump and probe frequency for mixing times of 1.5 ps (B), 3 ps (C), and 4 ps (D). Red denotes positive absorption change, blue denotes negative absorption change. The data have been scaled to eliminate the effect of T₁ relaxation.

Fig. 1B shows the 2D spectrum of Ala-Ala*-Ala for perpendicularly polarized pump and probe, at a pump-probe delay 1.5 ps, which is the earliest delay at which coherent effects due to temporal overlap of pump and probe are negligible. Along the diagonal of the 2D spectrum one observes the bleach and stimulated emission for each of the two amide I bands as the negative signal, and the excited-state absorption as the positive signal at lower probe frequency. The pump-probe signal is elongated along the diagonal, indicating that the amide I bands are inhomogeneously broadened (21). Because the two amide I modes are coupled, excitation of one gives rise to a spectral change of the other, which is observed as a cross peak in the off-diagonal region of the 2D spectrum (indicated by the arrows in Fig. 1B). These cross peaks represent a coherent effect as the molecular eigenstates are coherent superposition states of local excitations. In first-order approximation, the coupling between the amide I modes causes a frequency shift of the one when the other is populated. Because this shift is smaller than the linewidth of the transition, the cross peaks consist of a positive and negative part along the probe frequency direction. The intensity of the cross peak mirrors the strength of the coupling between the peptide units (8, 9), from which the time-averaged solution conformation of the peptide has been determined (10, 11).

To address the dynamics of the peptide conformation, we introduce a third dimension, the pump-probe delay or mixing time. Fig. 1 C and D shows the 2D spectra of Ala-Ala*-Ala at mixing times of 3 and 4 ps. Clearly, the 2D spectrum changes significantly with increasing mixing time. The diagonal peaks become less directed along the diagonal and more along the vertical axis, as a consequence of spectral diffusion (22). More importantly, the relative intensity of the cross peaks increases with increasing mixing time. This is caused by an incoherent population transfer of the vibrational excitation from the optically excited peptide unit to the other peptide unit. For the latter this gives rise to a negative absorption change at the v = 0→1 frequency and a positive absorption change at the v = 1→2 frequency, which is observed in the off-diagonal region of the 2D spectrum. This contribution to the cross peak has essentially the same shape as the coherent cross peak described before. Both contributions can, however, clearly be distinguished by their mixing-time dependence (13): the coherent contribution to the cross peak is independent of mixing time, whereas the contribution due to cross relaxation is initially zero, and increases with increasing mixing time.

The relative populations of the two amide I states as a function of mixing time can be determined by recording cross sections through the 2D spectrum for a series of mixing times. Fig. 2A shows such cross sections, obtained for a pump frequency resonant with the high-frequency amide I band (corresponding to the dotted line in Fig. 1B). To obtain the population ratio of the two amide I modes from these data, the ratio of the cross and diagonal peaks must be divided by an appropriate scaling factor, which is determined as follows. The two transition dipoles are at an average angle of θ = 106° (10). Hence, for perpendicularly polarized pump and probe, a population ratio of unity corresponds to a peak ratio of 2 − cos² θ = 1.92, and the experimentally observed peak ratio must be divided by this number to obtain the population ratio. This procedure was used for Ala-Ala*-Ala, where the cross and diagonal peaks are well separated, but could not be used for Ala-Ala-Ala, where they strongly overlap (10). However, for Ala-Ala-Ala the population transfer occurs sufficiently rapid that the peak ratio approaches its asymptotic value quite closely within the experimentally accessible delay range, so that the scaling factor could be derived by requiring that the observed population ratio should approach unity. The ratio of the populations of the two amide I states derived from the data are shown as a function of mixing time in Fig. 2B. Fitting the data yields for the cross-relaxation rates 0.07 ± 0.01 ps⁻¹ and 0.19 ± 0.02 ps⁻¹ for Ala-Ala*-Ala and Ala-Ala-Ala, respectively.

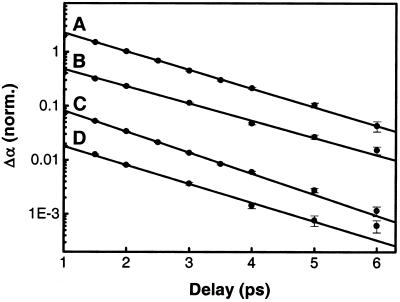
Figure 2.

(A) Transient spectra showing the absorption change as a function of probe frequency for a range of mixing times. The pump frequency is resonant to the higher frequency band (1,673 cm⁻¹), corresponding to the dotted line in Fig. 1B. The data have been scaled to eliminate the effect of T₁ relaxation. (B) Population ratio as a function of mixing time for Ala-Ala*-Ala (open points) and Ala-Ala-Ala (solid points), as obtained from the ratio of the cross and diagonal peaks observed in transient spectra recorded at different mixing times. The solid lines represent fits to the data, with cross-relaxation rates of 0.07 ps⁻¹ and 0.19 ps⁻¹ for Ala-Ala*-Ala and Ala-Ala-Ala, respectively.

The strong dependence of the cross-relaxation rate on the energy splitting between both amide I states provides strong evidence that the observed cross-relaxation is a direct process, rather than a indirect process through a reservoir of modes populated by the pumped state and back-populating the unpumped state. Relaxation out of the amide I states is considerably faster (T₁ ≈ 1.2 ps, see Fig. 3) than cross-relaxation between them. Nevertheless, relaxation out of the amide I states is essentially frequency-independent and varies by only ≈10% when shifting the frequency of one of the amide I state by 35 cm⁻¹ due to isotope labeling. The cross-relaxation rate, on the other hand, decreases by a factor of 2.7 upon isotope labeling. Because depopulation and backpopulation rates between amide I states and the reservoir would be connected by detailed balance, an indirect process as a mechanism for cross-relaxation can be excluded. On the other hand, we shall see in the next section that direct cross-relaxation caused by structural fluctuations of the backbone can explain the strong dependence of the cross-relaxation rate on the energy gap very well. Finally, the symmetric growth of both cross peaks in Fig. 1 verifies that the increasing cross peak, measured relative to the quickly decaying diagonal peak, is not just an effect of the relaxation rate out of one state being faster than that out of the other state.

Figure 3.

Pump-probe scans showing the normalized population decay of resonantly excited amide I states as a function of delay for the higher frequency band of Ala-Ala-Ala (1,675 cm⁻¹) (A) and Ala-Ala*-Ala (1,673 cm⁻¹) (B), and the lower frequency band of Ala-Ala-Ala (1,650 cm⁻¹) (C) and Ala-Ala*-Ala (1,605 cm⁻¹) (D). The lower frequency band is the one that shifts upon isotope labeling. In B–D, population decay has been determined from the decay of the anharmonically shifted v = 1→2 absorption, whereas in A, the bleach recovery was used instead, because the v = 1→2 absorption of the 1,675-cm⁻¹ band overlaps with the bleach of the 1,650-cm⁻¹ band. The lines are single-exponential fits corresponding to vibrational lifetimes of (A) 1.26 ps, (B) 1.37 ps, (C) 1.12 ps, and (D) 1.25 ps, respectively.

Discussion

A quantitative relation between the observed cross-relaxation and the conformational dynamics can be established by using a perturbational approach. To this end, we describe the system in a local site basis using the Hamiltonian (23)

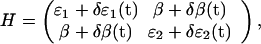1

where δɛ₁(t), δɛ₂(t), and δβ(t) are instantaneous deviations of the site energies and the couplings from their time-average values ɛ₁, ɛ₂, and β. Diagonalizing this Hamiltonian with respect to its time average, and using Fermi's Golden Rule, one obtains for the cross-relaxation rate between both eigenstates in the weak coupling limit (β ≪ Δɛ) (24)

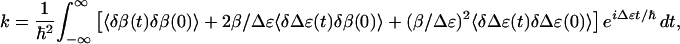2

where δΔɛ(t) = δɛ₁(t) − δɛ₂(t) and 〈… 〉 denotes ensemble averaging. The observed cross-relaxation rate is determined by the fluctuations of the coupling δβ(t) (first term in Eq. 2), the energy splitting δΔɛ(t) (third term), and the cross-correlation between both (second term). Owing to the prefactors β/Δɛ ≪ 1, the second and third terms are expected to be small in the weak coupling limit and are usually neglected in NMR spectroscopy. However, because for vibrational transitions the amplitude of the δΔɛ(t) fluctuations can be larger than that of the δβ(t) fluctuations, the relative magnitude of all terms in Eq. 2 must be carefully examined. The fluctuations δΔɛ(t) of the energy gap are caused by the forces of the fluctuating surroundings on the peptide groups associated with the two amide I modes. Because the amide I transition is anharmonic, these forces lead to a time-dependent frequency shift, which is determined by the surroundings (25) and can be calculated from the MD trajectory. We find that the dominant contribution to 〈δΔɛ(t)Δɛ(0)〉 is from a process with a 500-fs time scale, a time scale that is similar to that reported for the CN⁻ ion dissolved in water (25). Because the fluctuations of the transition frequencies also give rise to the pure dephasing of the amide I transitions, the experimentally determined pure dephasing rate T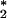≈1.5 ps [T₂≈0.9 ps and T₁≈1.2 ps (7, 10)] can be used to estimate the amplitude of the 〈δΔɛ(t)δΔɛ(0)〉 correlation function, which is difficult to obtain accurately from the MD simulations. These numbers lead to the conclusion that the third term in Eq. 2 contributes to the total cross-relaxation rate only on the order of 10% in the case of Ala-Ala-Ala and is entirely negligible in the case of Ala-Ala*-Ala. Furthermore, we find that the cross-correlation term 〈δΔɛ(t)δβ(0)〉 in Eq. 2 contributes less than 2% and can be neglected completely. This is to be expected, because the δΔɛ(t) and δβ(t) fluctuations relate to completely different parts of the system (namely, fluctuations of the water molecules surrounding the peptide units, and fluctuations of the backbone itself), and hence are essentially uncorrelated.

Hence, we conclude that vibrational cross-relaxation rate is dominated by the first term, i.e., the autocorrelation 〈δβ(t)δβ(0)〉 of the fluctuations of the coupling between the peptide units. Assuming that these fluctuations can be described as a Markovian process, 〈δβ(t)δβ(0)〉 = d²exp(−t/τ), we obtain for the relaxation rate

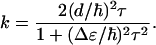3

This rate has been determined experimentally for two values of Δɛ by using the Ala-Ala-Ala and Ala-Ala*-Ala samples, which are chemically identical, but have a different energy gap Δɛ as a consequence of the ¹³C isotope substitution. From the two k values we obtain the amplitude of the coupling correlation function d = 5.2 ± 0.5 cm, and a correlation time τ = 110 ± 20 fs. Because the fluctuations in β directly mirror the fluctuations in the peptide dihedral angles (φ,ψ) (26), our measurements show that the conformation exhibits fluctuations that occur on a time scale of 100 fs.

It might seem surprising that a time constant on the order of 100 fs can be accurately determined by using pump pulses that are several times longer (750 fs, see Experiment). However, it should be noted that this time constant is not determined directly in a time-resolved pump-probe measurement, but derived (using Eq. 3) from the two cross-relaxation rates k, which are both very slow compared with the pump and probe pulse durations. In fact, it can be seen from Eq. 3 that the time scale to which the method presented here is most sensitive is given by the inverse of the frequency splitting between the coupled states, regardless of the duration of the pulses used in the experiment. The only requirement is that these durations be short enough to measure the cross-relaxation rates from which the time constant is derived. It should be noted that the indirect determination of dynamical time scales that are much faster than the pulse duration is also widely used in NOESY (14).

Interestingly, the simple relation between vibrational population transfer rates and microscopic dynamics, based on the classical correlation functions in Eq. 2, only holds if the frequency splitting Δɛ is less than kT. It has been convincingly shown that such a simple relation no longer exists if quantum effects have to be taken into account, which is the case when Δɛ ≫ kT (27). Because the latter condition generally applies for population relaxation from the first excited to the vibrational ground state, it would be very difficult to obtain dynamical information of the kind presented here from T₁ relaxation rates.

It is instructive to compare our experimental results to the theoretical predictions obtained from the 20-ns MD simulation of trialanine in water. Fig. 4B shows a representative example of the calculated time evolution of the dihedral angles φ(t) and ψ(t) pertaining to the central amino acid of trialanine (see Fig. 4A). The trajectory populates three free-energy minima, the lowest of which at (φ,ψ) = (−68°, 141°) is in very good agreement with the time-averaged conformation (φ,ψ)≈(−60°, 140°) obtained recently from the vibrational 2D spectrum of trialanine (10, 11). In view of the uncertainty in the values of free-energy minima calculated from MD, we restrict our further analysis to the experimentally confirmed minimum.

Fig. 4C shows the instantaneous coupling β(t), which was calculated from the (φ,ψ) trajectory with the aid of an ab initio-based map of β as a function of (φ,ψ) (26). By using this ab initio calculation, we avoid using the dipole approximation and include the higher-order multipole and through-bond contributions to the coupling. Fig. 4D shows the corresponding correlation function 〈δβ(t)δβ(0)〉, which is well approximated by a sum of two exponentially decaying components (shown as the red and green curves in Fig. 4D): an ultrafast inertial component with time constants τ₁ = 120 fs and a fluctuation amplitude d₁ = 4.1 cm and a slower, diffusive component with τ₂ = 2.2 ps and d₂ = 3.5 cm. From the MD data we also can calculate cross-relaxation rates. Because the MD simulation does not give the amide I frequencies, we use the experimental values (10, 11) for the time-averaged energy splittings Δɛ between the amide I eigenstates, on which the relaxation rate depends (see Eq. 2). We obtain values of 0.04 ps⁻¹ and 0.13 ps⁻¹ for the cross-relaxation rates of Ala-Ala*-Ala and Ala-Ala-Ala, respectively (Fig. 4D Inset), both very close to the experimentally observed values. It can be seen from Fig. 4D Inset that these rates are exclusively determined by the fast, subpicosecond component of the correlation function (red curve), the time constant and amplitude of which agree well with the values derived from the experiment (see Table 1). Fig. 4 B and D shows that this ultrafast component contributes significantly to the overall conformational dynamics of the peptide. It should be noted that the correlation function shown in Fig. 4D was obtained from the first 100 ps in Fig. 4B when the trajectory mainly populated the lowest free-energy minimum at (φ,ψ) = (−68°, 141°). Averaging over all conformations populated during the 20-ns trajectory, the amplitude d of the cross-relaxation correlation function decreases by 30%, whereas the correlation time τ stays approximately the same.

Table 1.

Comparison of experimental and MD results obtained for the peptide dihedral angles φ, ψ and the average transition coupling β, as well as for the correlation time τ and amplitude d of the cross-relaxation correlation function

	Structural parameters			Dynamical parameters
	φ (°)	ψ (°)	β (cm−1)	τ (fs)	d (cm−1)
Experiment	−60	140	6	110 ± 20	5.2 ± 0.5
Theory	−68	141	5	120	4.1

Conclusions

We have observed fluctuations in the dihedral angles (φ,ψ) of a small peptide in water, which take place on an ultrafast (100 fs) time scale. It seems likely that such fluctuations also will exist in certain parts of proteins, in particular those parts that have direct contact with the surrounding solvent, a situation that occurs during the initial stages of protein folding, and in the binding pocket of enzymes. The method presented here provides a unique way of investigating such ultrafast conformational dynamics. It can easily be extended to larger peptides, such as the cyclic pentapeptide for which the 2D-IR spectrum was reported (8), and in combination with site-specific isotope-labeling (28), to small proteins. The cross-relaxation between each pair of amide I modes will specifically mirror the fluctuations of those conformational degrees of freedom that determine the strength of the coupling between these two modes. In this way, it is possible to obtain a detailed, mode-specific picture of the subpicosecond conformational dynamics of the peptide or protein under study.

Abbreviations

2D

two-dimensional

MD

molecular dynamics

NOESY

nuclear Overhauser effect spectroscopy