Population Modeling of Tumor Kinetics and Overall Survival to Identify Prognostic and Predictive Biomarkers of Efficacy for Durvalumab in Patients With Urothelial Carcinoma

Abstract

Durvalumab is an anti‐PD‐L1 monoclonal antibody approved for patients with locally advanced or metastatic urothelial carcinoma (UC) that has progressed after platinum‐containing chemotherapy. A population tumor kinetic model, coupled with dropout and survival models, was developed to describe longitudinal tumor size data and predict overall survival in UC patients treated with durvalumab (NCT01693562) and to identify prognostic and predictive biomarkers of clinical outcomes. Model‐based covariate analysis identified liver metastasis as the most influential factor for tumor growth and immune‐cell PD‐L1 expression and baseline tumor burden as predictive factors for tumor killing. Tumor or immune‐cell PD‐L1 expression, liver metastasis, baseline hemoglobin, and albumin levels were identified as significant covariates for overall survival. These model simulations provided further insights into the impact of PD‐L1 cutoff values on treatment outcomes. The modeling framework can be a useful tool to guide patient selection and enrichment strategies for immunotherapies across various cancer indications.

Study Highlights.

WHAT IS THE CURRENT KNOWLEDGE ON THE TOPIC?

☑ Durvalumab is an anti‐PD‐L1 monoclonal antibody approved for patients with locally advanced or metastatic urothelial carcinoma (UC) that has progressed after platinum‐containing chemotherapy. Durvalumab treatment demonstrated favorable clinical activity in objective tumor response and overall survival (OS) in UC patients.

WHAT QUESTION DID THIS STUDY ADDRESS?

☑ This study analyzed the longitudinal tumor size data and OS in UC patients treated with durvalumab and identified prognostic and predictive biomarkers of clinical outcomes with a population‐based modeling approach.

WHAT THIS STUDY ADDS TO OUR KNOWLEDGE

☑ This study identified several prognostic or predictive biomarkers as significant covariates for tumor growth, immune cell‐mediated tumor killing, and/or OS after durvalumab treatment and provided insights into the impact of biomarker cutoff values on treatment outcomes.

HOW THIS MIGHT CHANGE CLINICAL PHARMACOLOGY OR TRANSLATIONAL SCIENCE

☑ This novel application of a pharmacometric modeling approach for biomarker identification can be adapted to other cancer immunotherapies. It can serve as a useful tool to guide patient selection and enrichment strategies and to optimize trial designs across various cancer indications.

Immune checkpoint inhibitors such as antibodies targeting PD‐1 and PD‐L1 have evolved as new treatment options for cancer patients and have demonstrated efficacy in reducing tumor size and prolonging survival in multiple cancer indications.1, 2, 3, 4 An important clinical question in the development of immuno‐oncology (IO) therapies is how to identify patients who are most likely to benefit from these therapies. Pharmacometric modeling provides a quantitative tool to address this question through mathematical modeling of clinical efficacy data with multivariate covariate testing. Although numerous reports of tumor kinetic models have been published for traditional chemotherapy or non‐IO therapies in cancer patients,5, 6, 7 few studies have modeled tumor dynamics after IO therapies.8 Further, no quantitative model has been published to date to link tumor kinetics to overall survival (OS) for IO therapeutics as a tool to identify and characterize prognostic and predictive biomarkers of efficacy outcomes.

Durvalumab is a human immunoglobulin G1 antibody that specifically binds human PD‐L1, blocking its interaction with PD‐1 or CD80 receptors expressed on activated T cells. Durvalumab (10 mg/kg q2w) has recently been approved as a treatment for patients with locally advanced or metastatic urothelial carcinoma (UC) that has progressed after platinum‐containing chemotherapy. Study 1108 (NCT01693562) was a phase I/II, open‐label expansion study of durvalumab in patients with advanced urothelial bladder cancer, in which durvalumab treatment demonstrated favorable clinical activity in objective tumor response and OS.3 The objectives of this analysis were to model survival data and longitudinal changes in target lesion size, to characterize the relationship between tumor kinetics and survival, and to evaluate prognostic and predictive biomarkers for efficacy outcomes in these patients.

RESULTS

Tumor kinetic model

A total of 186 UC patients who had been treated with durvalumab at 10 mg/kg q2w in study 1108 had tumor assessment by blinded independent central review according to RECIST v. 1.1 guidelines and were included in the population to be analyzed for the modeling. Of these 186 patients, 159 had postbaseline tumor size data. The observed individual tumor kinetic profiles from these patients showed large variability, with three distinct profile types: continued tumor progression throughout the study, immediate tumor shrinkage after the first dose, and delayed tumor response with initial stable tumor size or pseudoprogression followed by shrinkage (Figure 1 a,b). No tumor regrowth after regression was observed in any patients in the dataset. Each of these profiles were well captured by the tumor kinetic model, which describes tumor growth, killing, and delayed immune response after treatment (Figure 1 b).

Figure 1.

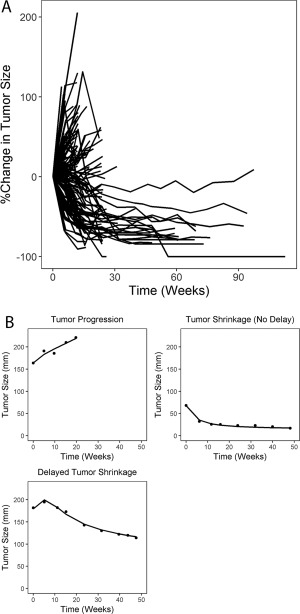
(a) Observed percent change in tumor size from baseline in all subjects; (b) typical types of individual tumor kinetic profiles, where dots represent observed data and lines represent individual prediction from the base tumor kinetic model.

A number of covariates were evaluated, including biomarkers, baseline characteristics, and disease factors, using a full covariate model (Table 1). Potential prognostic factors, including time since prior chemotherapy; baseline albumin, hemoglobin, and lactate dehydrogenase levels; neutrophil‐to‐lymphocyte (N:L) ratio; and Eastern Cooperative Oncology Group (ECOG) performance status were evaluated on tumor growth rate constant (k_g) and were chosen based on literature reports of prognostic factors affecting survival in UC patients receiving other salvage therapies.9, 10, 11 Intratumor PD‐L1 expression on tumor cell membrane (TC) and on tumor‐infiltrating immune cells (IC) has been evaluated as a predictive biomarker for other anti‐PD‐1/PD‐L1 therapies and was associated with efficacy in study 1108³; therefore, TC and IC were evaluated as covariates on killing rate constant (k_kill) only. Smoking history was also evaluated on k_kill due to its association with mutational burden.12 Factors that could be both prognostic and predictive, including baseline tumor size, liver metastasis, lymph node (LN)‐only disease, and line of therapy, were evaluated on either k_g or k_kill or both, depending on the significance of the univariate correlation between the individual post‐hoc parameter estimates and the parameters, where appropriate.

Table 1.

Summary of covariate distributions in UC patients

Continuous covariates
Covariate (units)	N	Mean (SD)	Median	Range
TC (%)	172	20.8 (32)	5	0–100
IC (%)	146	29 (26.6)	20	0–100
Baseline tumor (mm)	186	72.9 (49.4)	59.9	16.2–333
LDH (U/L)	178	316 (370)	227	89–4,260
Albumin (g/dL)	182	3.74 (0.529)	3.81	2–4.6
Hemoglobin (g/dL)	180	11.3 (1.55)	11.3	8–15.3
N:L ratio	178	6.22 (7.98)	3.91	0.872–72.3
Age (years)	186	66.2 (9.46)	67	34–88

Categorical covariates
Covariate	Category	N (%)
Duration from prior chemotherapy ≤3 months	No	106 (57)
	Yes	80 (43)
ECOG performance status	0	62 (33.3)
	1	124 (66.7)
Smoking history	Never	77 (41.4)
	Ever	109 (58.6)
Line of therapy	1	9 (4.8)
	2	113 (60.8)
	≥3	64 (34.4)
Liver metastasis	No	105 (56.5)
	Yes	81 (43.5)
LN‐only disease	No	173 (93)
	Yes	13 (7)

ECOG, Eastern Cooperative Oncology Group; IC, immune cell PD‐L1 expression; LDH, lactate dehydrogenase; N:L ratio, neutrophil‐to‐lymphocyte ratio; LN, lymph node; TC, tumor cell PD‐L1 expression.

The full covariate analysis results showed that the most influential covariate for k_g was liver metastasis, which caused a 46% increase in k_g (Figure 2 a). LN‐only disease also had a notable impact on k_g, which led to an average 30% decrease in k_g. This effect was not well estimated, however, because the confidence interval was large and crossed zero, probably due to the small number of subjects with LN‐only disease (n = 13). The most influential covariate for k_kill was baseline tumor size, followed by IC and then TC (Figure 2 b). A baseline tumor size of 21 mm (5^th percentile of the study population) led to an approximately 3‐fold increase in k_kill, whereas a TC or IC of 100% resulted in 27% and 86% increases in k_kill, respectively, compared to the median values, although the effect of TC was not well estimated.

Figure 2.

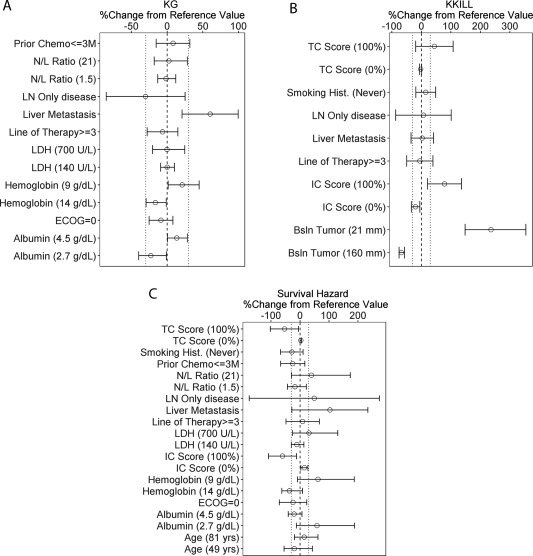
Forest plots of covariate effects on k_g (a) and k_kill (b) estimated from the full covariate tumor kinetic model and survival hazard (c) from the full covariate survival model. Circles represent the calculated percent change in the parameter value from the reference value at the indicated covariate values, using the point estimates of the respective covariate effects; error bars represent the 95% confidence intervals of the covariate effects based on the relative standard error estimates from NONMEM; dashed vertical lines represent the reference value; dotted lines represent the 30% change from reference value. For continuous covariates, the values in parentheses represent the 5^th and 95^th percentiles of each covariate in the study population (except for PD‐L1 expression on tumor cells and immune cells, which are the minimum and maximum values, respectively), and the reference value is the median of the study population. For categorical covariates, the following reference values were taken: prior chemotherapy ≤3 months = “no”; LN‐only disease = “no”; liver metastasis = “no”; line of therapy = 1 or 2; smoking history = “ever smoked”; ECOG = 1. ECOG, Eastern Cooperative Oncology Group performance status; IC, immune cell PD‐L1 expression; LDH, lactate dehydrogenase; LN, lymph node; N/L, neutrophil‐to‐lymphocyte ratio; TC, tumor cell PD‐L1 expression.

Further stepwise backward elimination yielded the final model, which included significant covariates of liver metastasis on k_g, and baseline tumor size and IC on k_kill. Most of the parameters in the final model were estimated with good precision (Table 2). The k_g in a typical patient (with liver metastasis, median baseline tumor size, and IC) was estimated to be 0.076 week⁻¹, which corresponds to a tumor doubling time of ∼9 weeks. Approximately 49% of patients were estimated to have delayed tumor killing, with a mean delay time of ∼4.5 weeks. The standard diagnostic plots comparing the individual and population model prediction and observed data, as well as residual plots, showed reasonably good fit of the final tumor kinetic model (Supplemental Figure S1).

Table 2.

Parameter estimates of the final tumor kinetic model

Parameter	Description	Estimate	% RSE	Bootstrap 95% CI	Shrinkage (%)
kg,TV (week−1)	Typical value of growth rate constant	0.076	11.1	0.0431, 0.0922
kkill,TV (week−1mm−1)	Typical value of killing rate constant	0.00145	12.4	0.000985, 0.00187
DTIMTV (weeks)	Typical value of delay time for subpopulation with delay in tumor killing	4.49	22.1	2.79, 6.49
PDTIM = 0	Probability of being in the subpopulation of DTIM = 0	0.489	20.4	0.128, 0.639
θLM∼kg	Relative change in kg in patients with liver metastasis (LM = 1)	0.616	21.9	0.307, 1.01
θIC∼kkill	Linear coefficient for effect of IC on kkill	1.08	37	0.249, 1.87
θTBSL∼kkill	Power exponent of effect of TBSL on kkill	−1.24	12.1	−1.58, −0.969
θ2,TBSL∼kkill (mm)	Maximum TBSL above which kkill is not affected by TBSL	145	40.4	98.4, 212
γ_ηkg	Box‐Cox parameter for BSV of kg	–2.63	35.8	−5.02, −0.162
γ_ηkkill	Box‐Cox parameter for BSV of kkill	0.033	362	–0.495, 0.613
ω2: kg	BSV of kg (variance)	0.465	56.8	0.192, 1.43	47.2%
ω2: kkill	BSV of kkill (variance)	0.778	18.4	0.398, 3.19	31.6%
ω2: DTIM	BSV of DTIM for subpopulation with DTIM > 0 (variance)	0.776	36.6	0.241,1.42	37.8%
Covariance kg∼kkill	Covariance between kg and kkill	0.368	40.2	0.115, 1.53
Covariance kg∼DTIM	Covariance between kg and DTIM	−0.282	69.7	−0.617, 0.0245
ɛadd (mm)	Additive residual error	3.6	1.4	2.76, 4.42	17.8%

BSV, between‐subject variability; CI, confidence interval; DTIM, mean transit time for delay in immune response; IC, immune cell PD‐L1 expression; LM, liver metastasis; RSE, relative standard error (based on NONMEM output); TBSL, baseline tumor size.Final covariate equations for k_g and k_kill: $k_g=k_{g,TV}\times \left(1+{\theta }_{LM\sim kg}\times \text{LM}\right)$; $k_{kill}=k_{kill,TV}\times \left(1+{\theta }_{IC\sim kkill}\times \left(\text{IC}-{\text{IC}}_{med}\right)\right)\times {\left(\frac{\min \left({\text{TBSL},\theta }_{2,TBSL\sim kkill}\right)}{{\text{TBSL}}_{med}}\right)}^{{\theta }_{TBSL\sim kkill}}$.

Survival and dropout models

At the time of the data cutoff date, 100 of 186 subjects had dropped out of the study (67 of them were due to death). As is typical of oncology trials, the risk of patient dropout was strongly influenced by treatment response. Patients with rapid tumor progression dropped out early, whereas those whose disease improved had longer follow‐up times (Figure 1). To accurately simulate the longitudinal tumor response in the trial, the model had to account for correlation between dropout and response. A dropout model was therefore developed in which the model‐predicted tumor response from the final tumor kinetic model was used as time‐varying covariates in the dropout hazard. Similarly, given the observed relationship between OS and tumor response (Figure 3), a survival model was developed to predict OS, using the model‐predicted tumor response as a time‐varying covariate.

Figure 3.

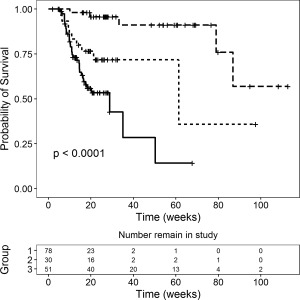
Kaplan‐Meier curves of overall survival stratified by best percent change in tumor size from baseline: ≥0% (solid line, Group 1); <0% and ≥–30% (dotted line, Group 2); and <–30% (dashed line; Group 3). P‐value is based on Cox proportional hazard regression.

The effect of covariates on survival and dropout hazard were further evaluated with a full covariate modeling approach. The results suggested that the average baseline survival hazard decreased by 54% and 61% in patients with 100% TC and IC, respectively, compared to the median values, and increased by 103% in patients with liver metastasis (Figure 2 c). In addition, the baseline survival hazard increased by 62% and 59% in patients with low (5^th percentile of the study population) hemoglobin and albumin levels, respectively, and by 39% in those with high (95^th percentile) N:L ratios compared to the median values (Figure 2 c). There was also a trend of increased survival hazard with LN‐only disease, but this effect was poorly estimated due to small sample size. Further stepwise backward elimination yielded the final model, which included TC, IC, hemoglobin and albumin levels, and liver metastasis as significant covariates for OS. The parameter estimates for the final survival and dropout models are presented in Supplemental Tables S1, S2.

Model validation and simulations

Visual predictive checks (VPCs) showed that the final tumor kinetic model, coupled with the final dropout and survival models, predicted the central tendency and variability in tumor dynamics (Figure 4 a), as well as OS (Figure 4 b). Similar to the observed data, the model predicted generally shorter follow‐up times in the simulated fast progressors than in responders and those with stable disease (Figure 4 c), suggesting that the dropout model adequately described the relationship between tumor response and dropout. Further, VPC stratified by tumor response categories showed that the models described the longitudinal tumor size changes, OS, and dropout in responders (with or without delay) and nonresponders reasonably well (Supplemental Figure S2).

Figure 4.

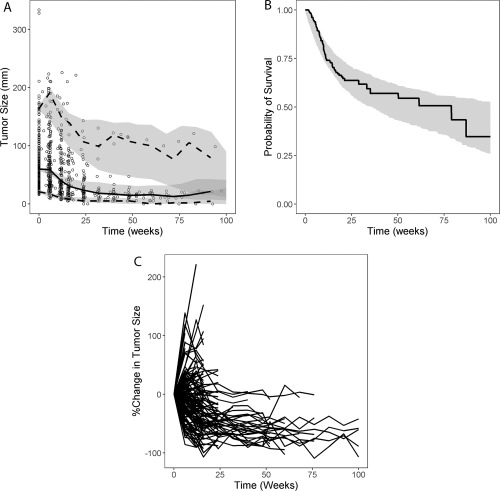
(a) Visual predictive check for tumor kinetics; (b) visual predictive check for survival; (c) simulated individual tumor kinetic profiles including dropout from one representative simulated trial. (a) Circles represent the observed individual data; solid line represents the observed median; dashed lines represent the observed 5^th and 95^th percentiles; shaded areas show 95% confidence intervals of model‐predicted median, 5^th and 95^th percentiles based on 500 visual predictive check runs incorporating between‐subject variability and residual variability. (b) Solid line and shaded area represent observed and 95% confidence interval of model‐predicted Kaplan–Meier curve for overall survival, respectively.

To predict the covariate effects on tumor response rates and survival, trial simulations were performed to predict the 1‐year survival rate and the percentage of patients with greater than 30% reductions in tumor size from baseline by various covariate categories. The predicted trends were generally consistent with the observed data, although the model did not account for disease progression due to nontarget lesions and slightly overpredicted the true objective response rate (Figure 5). The model predicted that a higher IC cutoff would lead to a better rate of tumor response (12%, 18%, and 33% increases with ICs of ≥25%, ≥50%, and ≥75%, respectively, compared with all‐comers), whereas no effect of TC was predicted (Figure 5 , top). These data translated to a similar trend for OS (Figure 5 , bottom), where the model predicted averages of 12%, 15%, and 32% increases in 1‐year survival rate with ICs of ≥25%, ≥50%, and ≥75%, respectively, but no apparent trend with TC. The observed survival rate was lower than predicted for an IC of ≥75%, which may be due to the limited number of patients in this group (n = 12); hence, the large uncertainty in the observed data. The models also predicted that patients with lower baseline tumor burden and N:L ratio, higher albumin and hemoglobin levels, and LN‐only disease or no liver metastasis would have greater tumor response rate and longer survival, which was generally consistent with the observed trends (Figure 5).

Figure 5.

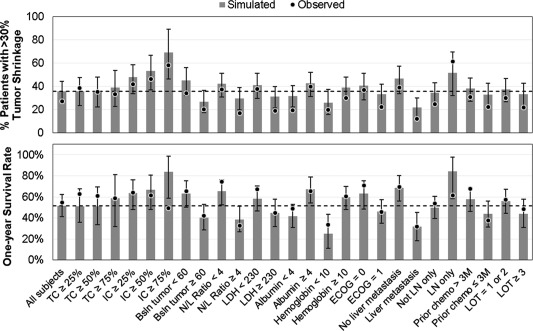
Simulated and observed tumor response (top) and 1‐year survival rate (bottom) by covariate subgroups. Dots represent the observed data; gray bars represent the simulated data; error bars represent the 95% confidence intervals of the simulated data based on 500 trial simulations incorporating parameter uncertainty, between‐subject variability, and residual variability; dashed horizontal lines represent the simulated response/survival rate in the overall study population. The number of subjects in each covariate subgroup in the observed data are presented in Table 1 and Supplemental Table S9. Bsln, baseline; ECOG, Eastern Cooperative Oncology Group performance status; IC, immune cell PD‐L1 expression; LDH, lactate dehydrogenase; LN, lymph node; LOT, line of therapy; N/L, neutrophil‐to‐lymphocyte ratio; TC, tumor cell PD‐L1 expression.

DISCUSSION

We developed a population‐based tumor kinetic model to describe the longitudinal tumor dynamics in UC patients after durvalumab treatment. The predicted tumor dynamics were then used to model OS and time to dropout in the same population. Covariate analyses identified patient baseline characteristics, disease‐related factors, and biomarkers as potential prognostic or predictive factors for tumor growth or shrinkage and for survival. This approach allowed tumor kinetics to be linked to survival and dropout while enabling systematic and multivariate study of the effect of prognostic or predictive covariates on both tumor response and OS for IO therapeutics.

Our results suggest that liver metastasis is the most influential and statistically significant covariate for tumor growth. This finding is consistent with recent reports showing that liver metastasis is associated with poor prognosis in various cancers.13, 14, 15, 16, 17 We also showed that baseline tumor size and IC are the most influential and significant covariates for tumor killing after durvalumab treatment. This observation of faster tumor killing rate with smaller baseline tumor size could be explained by the greater accessibility of smaller tumors to immune cell infiltration and antibody penetration, which leads to a higher killing rate. High PD‐L1 expression has been shown to predict better response to durvalumab and other PD‐L1‐ and PD‐1‐targeting therapies.2, 3, 4 In study 1108, “PD‐L1 high” was defined as either a TC or an IC score above a cutoff of 25%.3 In the present study, the effect of IC was more pronounced than that of TC in UC tumors, of which the latter did not show statistical significance. Although this finding could reflect the mechanism of action and the differential role of immune cells and tumor cells in this particular cancer type, it may also be confounded by the overall low (median 5%) TC distribution in the study population, which makes it difficult to detect a significant effect of TC in this population.

For OS, both TC and IC, as well as liver metastasis and levels of hemoglobin and albumin, were identified as significant covariates after accounting for the effect of tumor size. The effects of TC and IC on OS suggests that intratumoral PD‐L1 expression is predictive not only of tumor response, but also of OS independently of tumor response, after durvalumab treatment. The effects of liver metastasis and hemoglobin and albumin levels on OS are consistent with literature reports on UC patients and supports our conclusion that the population modeling approach can accurately identify prognostic and predictive biomarkers in a multivariate framework.10, 18 In a recent pooled study across multiple phase II trials in patients receiving salvage systemic therapy for advanced UC, a five‐factor prognostic model was proposed for patients receiving salvage systemic therapy for advanced UC.10 Three of these prognostic factors (liver metastasis, and hemoglobin and albumin levels) were also identified in our analysis, suggesting that they are also applicable to patients receiving durvalumab treatment and that their prognostic value for OS is retained after accounting for tumor response.

One advantage of using the pharmacometrics approach, as compared with the traditional statistical approach, to study the effects of predictive and prognostic factors on clinical endpoints is the ability to perform simulations to predict clinical outcomes along a continuum of biomarker levels, taking into consideration their correlation with other risk factors in a multivariate fashion. When evaluating dichotomous predictive biomarker cutoffs (biomarker high or low) in univariate analyses, imbalances in other predictive or prognostic factors within the biomarker strata can potentially confound interpretation of the appropriate cutoff. In our study, the model simulations predicted that increased IC cutoff (from 25% to 50% or 75%) may lead to higher tumor response rate and OS, whereas the effect of TC cutoff was not clear. However, our results may have been confounded by the scarcity of available data at high IC or TC ranges (11% with TC of ≥75%, 6.5% with IC of ≥75%). Another limitation of our analysis is the lack of a comparator cohort to clearly differentiate between prognostic and predictive biomarkers. Although TC and IC have been tested on k_kill as potential predictive factors, PD‐L1 expression has also been shown to have a prognostic effect in solid tumors (unpublished data). Post‐hoc analysis with the final tumor kinetic model confirmed the absence of any remaining correlations between k_g and TC or IC, suggesting that PD‐L1 expression is likely to be predictive rather than prognostic in UC patients.

The results of this analysis provided useful insights to optimize future clinical trial designs by identifying patient subgroups that are likely to respond better to treatment. Model simulations predicted that patients with no liver metastasis, higher immune cell PD‐L1 expression, smaller tumor size, higher albumin and hemoglobin levels, and lower neutrophil‐to‐lymphocyte ratio at baseline were associated with increased tumor response rate as well as prolonged survival following durvalumab treatment (Figure 5 ; Supplemental Figures S3, S4). These biomarkers and the associated cutoff values can be used as patient stratification variables and will be further validated in future trials. It is worth noting that some of these biomarkers are correlated, e.g., liver metastasis is generally associated with larger tumor size, and albumin and hemoglobin levels are correlated. In addition, an optimal balance between response rate and population prevalence needs to be considered. For example, an increased IC cutoff is predicted to result in greater response, but leads to a reduced prevalence and would exclude some patients who could still benefit from therapy. Therefore, the appropriate set of factors and the associated cutoff values for patient stratification should be carefully selected and practical considerations need to be taken into account.

In this analysis, drug exposure or clearance was not formally tested as a covariate in the model. It has been reported that clearance of therapeutic antibodies may be associated with disease severity in cancer patients and correlates with other known prognostic factors, such as albumin level.19 In addition, improved disease status in cancer patients after treatment has been associated with decreased clearance of anti‐PD‐L1 and PD‐1 therapeutics, including durvalumab, over time.20, 21, 22, 23 Therefore, the covariate analysis for drug exposure would be confounded by its correlation with disease severity and time‐varying clearance as disease improves after treatment. In this analysis, although drug exposure was not included in the full covariate models, adding durvalumab clearance (at baseline or steady state) to the final tumor kinetic, OS or dropout models did not result in a significant improvement in model fit (P > 0.05). This is consistent with the results from an exposure–response analysis previously conducted with data from study 1108, which showed that, at the 10‐mg/kg q2w dose, no exposure–efficacy relationship was observed after adjustment for confounding risk factors.24

In a previous study, a population pharmacokinetic‐pharmacodynamic model was developed to describe tumor dynamics in pembrolizumab‐treated advanced melanoma.8 Our model was different in several key aspects. First, the previous model assumed first‐order kinetics for both tumor growth and killing, whereas our model assumed a second‐order kinetics for tumor killing to allow the system to reach steady state. This characteristic of our model explained the durable tumor responses observed in many patients without a requirement for a very low growth rate constant, resulting in a greatly improved model fit (Supplemental Table S3) and a realistic estimate of tumor doubling time, and is consistent with a previously proposed tumor‐killing model for IO therapy that takes into account tumor and immune cell competition.25 Second, we incorporated a mixed‐population transit compartment model for tumor killing in our model to better describe the delayed tumor response observed in some patients, which resulted in a large improvement in model fit (Supplemental Table S3). The delayed drug effect on tumor killing may be explained by interpatient variability in the time it takes for the immune system to be activated in response to PD‐L1 blockade and enhance effector T‐cell function in the tumor microenvironment. Third, the pembrolizumab model assumed two tumor compartments to represent tumor volume, i.e., “accessible” or “not accessible” to treatment, whereas in our model, a single tumor compartment was sufficient to describe the observed tumor growth or shrinkage profiles, given the absence of tumor regrowth in the study population. Finally, we incorporated dropout in our model to account for the relationship between tumor response and dropout, which allowed better prediction of tumor kinetics over time in a clinical trial. The VPC plots showed that our tumor kinetic model, coupled with the dropout model, adequately predicted the population mean as well as variability in the longitudinal tumor size data in the UC population.

A number of published studies have modeled OS based on tumor kinetics in cancer patients treated with traditional chemotherapy or non‐IO therapies.6, 26, 27, 28, 29 Our study is the first reported study that linked tumor kinetics to OS by using quantitative modeling for IO therapeutics. In contrast to previous studies, our model utilized the entire longitudinal tumor kinetic profile rather than a single timepoint or derived variable (e.g., time to tumor growth) as a predictor of OS. This allowed a more accurate assessment of the relationship between tumor response and survival and enabled a model‐based extrapolation of missing data, thus allowing a better prediction of OS and a more reliable evaluation of covariate effects on survival independently of their effect on tumor dynamics. The model reasonably predicted the OS curve and the effect of key covariates on survival rate in UC patients treated with durvalumab.

In conclusion, we developed a population tumor kinetic model linked to a dropout and survival model to describe both the longitudinal change in tumor size and OS to identify potential predictive or prognostic biomarkers for tumor growth, shrinkage, and OS in UC patients treated with durvalumab. This modeling approach provides a useful framework to study tumor response and its correlation with OS, in which the effect of multiple prognostic and predictive biomarkers can be evaluated in a multivariate analysis. Therefore, this modeling approach can be used to guide patient selection and enrichment strategies and to optimize clinical trial designs for IO therapies across various cancer indications.

METHODS

Study design and analysis data

Study 1108 (NCT01693562) is an ongoing phase I/II study to evaluate the safety, tolerability, and pharmacokinetics of durvalumab in patients with advanced solid tumors. The dose‐expansion phase of the study enrolled patients with locally advanced and metastatic UC who had disease progression on, were ineligible for, or refused prior chemotherapy and who received durvalumab 10 mg/kg q2w via intravenous infusion.3 Data on tumor size (sum of longest diameter) and OS from UC patients in the expansion study, with a cutoff date of October 2016, were used in this analysis. Tumor measurements were done at weeks 6, 12, and 16 after first dose and then every 8 weeks afterward. Tumor assessments were performed by blinded independent central review, using RECIST v. 1.1 criteria.

Tumor kinetic model development

A nonlinear mixed‐effects model was developed to describe longitudinal tumor data in UC patients after durvalumab treatment. The model assumes that the dynamics of tumor size are governed by k_g and k_kill, ensuring a steady‐state tumor size as the competition between tumor growth and killing reaches an equilibrium:

$$TS\left(t\right)\prime =k_g\times TS\left(t\right)-k_{kill}\times TS{\left(t\right)}^2\times R_{im}\left(t\right)$$ (1)

where TS(t) is the tumor size at time t; k _g and k _kill are tumor growth and killing constants, respectively; and R _im(t) is a delay function representing the delay time in immune response, modeled using a transit compartment model (see Supplementary Material). The mean transit time for the delay, DTIM, is modeled by using a mixture model consisting of two mixture populations, one with no delay (DTIM = 0) and the other with a nonzero delay time.

Between‐subject variability was included for k_g, k_kill, and DTIM (for the subpopulation with nonzero DTIM). Various between‐subject variability and residual error models, as well as variance‐covariance matrix structures, were explored and evaluated based on the objective function value and model stability. The selected base model assumes log‐normal distribution for the between‐subject variability of DTIM and Box‐Cox distributions for the between‐subject variability of k_g and k_kill, using the following eta‐transformation function:

$${\tilde{\eta }}_i=\frac{{\left(e^{{\eta }_i}\right)}^{\gamma }-1}{\gamma }$$ (2)

where η_i is a normally distributed random variable, ${\tilde{\eta }}_i$ is the transformed random variable, and γ is the Box‐Cox parameter. The residual errors were described using an additive error model.

Dropout and survival model development

The time to death and time to dropout from study were modeled with parametric hazard models, using the model‐predicted tumor size over time as covariates in the model. Different model structures were evaluated, including different probability distribution assumptions (exponential, Weibull, and Gompertz‐Makeham) for survival and dropout times, as well as different combinations of tumor kinetic variables (e.g., baseline tumor size, percent change in tumor size over time, and absolute tumor size over time) as covariates in the model. The best model selected was an exponential model with predicted absolute tumor size and percent change in tumor size over time as time‐varying covariates for both OS and dropout, as well as predicted disease progression status and time since progression as additional covariates for dropout:

$$h_{OS}\left(t\right)=h_{0\_OS}\times \exp \left({\theta }_{TS\_OS}\times TS\left(t\right)+{\theta }_{PC\_OS}\times PC\left(t\right)\right)$$ (3)

$$\begin{array}{l}{h}_{DO}\left(t\right)=h_{0\_DO}\times \exp ({\theta }_{TS\_DO}\times TS\left(t\right)+{\theta }_{PC\_DO}\times PC\left(t\right)+{\theta }_{PD\_DO}\times PD\left(t_{prev}\right)+{\theta }_{TPD\_DO}\times TPD\left(t\right))\end{array}$$ (4)

where h _OS(t) and h _DO(t) are the hazard of death and dropout at time t, respectively; h _{0_OS} and h _{0_DO} are the corresponding baseline hazard; TS(t) is the model‐predicted tumor size at time t for each individual; PC(t) is the percent change in tumor size from baseline to time t, calculated as (TS(t)/TS(0) – 1) × 100; PD(t _prev) is the predicted disease progression status at the previous visit (= 1 if >20% and >5‐mm increase in tumor size from last nadir, 0 otherwise); and TPD(t) is the duration since last time when PD is switched from 0 to 1 when the current PD status is 1; and θ_{TS_OS}, θ_{TS_DO}, θ_{PC_OS}, θ_{PC_DO}, θ_{PD_DO}, and θ_{TPD_DO} are the respective covariate coefficients.

Model fitting

The tumor kinetic and OS/dropout models were fitted sequentially. First, the parameters of the tumor kinetic model were estimated by fitting the model to the longitudinal tumor size data. Then the individual parameters estimated from the final tumor kinetic model were used as input to the OS/dropout model to simulate the longitudinal tumor size over time, which is used as covariates in the models, and the corresponding parameters were estimated by fitting the models to the OS and dropout data. All model parameters were estimated using NONMEM v. 7.3 (Icon Development Solutions, Ellicott City, MD).

Covariate analysis

Covariate analyses were performed on the tumor kinetic, OS, and dropout models to evaluate the effects of various potential prognostic and predictive factors on tumor kinetic parameters, survival, and dropout hazards. The covariate selection for the full model was based on theoretical plausibility and understanding of the mechanism of action of the drug. For continuous covariates, power functions or linear function, where appropriate, were used to describe the covariate effects. For categorical covariates, the covariate effect was modeled as the relative change in the parameter value compared with the reference value. Full covariate models for tumor kinetics and for dropout or survival were constructed by including all covariates of interest on the corresponding parameters, and all covariate effects were estimated simultaneously from the full models. Covariate forest plots were constructed by calculating the relative changes in parameter values at the extreme values (5^th to 95^th percentiles or full range) of each continuous covariate or at the alternative values of each categorical covariate, using the estimated covariate effects and associated confidence intervals based on standard error estimates from NONMEM. Stepwise backward elimination was conducted on the full covariate models to identify significant covariates (P < 0.001 for tumor kinetics and P < 0.05 for overall survival and dropout models) to be included in the final models, using the SCM routine in PsN (Peal‐speaks‐NONMEM). Nonparametric bootstraps (500 runs) were conducted to estimate the confidence intervals of the parameter estimates from the final models.

Model evaluation and validation

The model performance was evaluated by standard goodness‐of‐fit plots, precision of parameter estimation based on NONMEM covariance run or bootstrap, and VPCs. Five hundred VPC runs were simulated by using the final tumor kinetic, OS, and dropout models, using the covariate information from study 1108 UC population (with the same sample size as the original dataset in each VPC run) and the between‐subject variability and residual errors randomly sampled from the distributions estimated from the tumor kinetic model. The time to death and time to dropout were simulated by using the predicted tumor size over time, as well as the baseline characteristics in each simulated individual in each VPC run. The simulated tumor size data were censored by the simulated dropout time and the actual data cutoff time in each individual and compared with the observed tumor kinetic data from UC patients in study 1108.

Model simulations

To predict the percentage of patients with greater than 30% best tumor shrinkage and the 1‐year survival rate, 500 trial simulations were conducted with 500 patients in each trial randomly resampled from the UC patient population in study 1108. In each simulated trial, parameter uncertainties were incorporated by resampling from 500 bootstrap runs of the tumor kinetic, OS, and dropout models. The simulation results for tumor shrinkage and 1‐year survival rate were summarized across all simulated trials to calculate the mean and 95% confidence intervals of the predictions.

CONFLICT OF INTEREST/DISCLOSURE

Y.Z., R.N., C.J., P.G.B., A.G., P.M., B.W.H., and L.R. are employees of MedImmune or AstraZeneca and own stock and/or stock interests in AstraZeneca; Y.B., X.J., and B.W. were employees of MedImmune or AstraZeneca and owned stock and/or stock interests in AstraZeneca at the time of the research; B.W. has received personal consulting fees from MedImmune outside of this work.

FUNDING

This study was sponsored by MedImmune, the global R&D biologics arm of AstraZeneca.

AUTHOR CONTRIBUTIONS

Y.Z., R.N., and L.R. wrote the article; L.R., R.N., and Y.Z. designed the research; Y.Z., C.J., P.G.B., X.J., A.G., Y.B., B.W., P.M., and B.W.H. performed the research; Y.Z., C.J., P.G.B., X.J., A.G., Y.B., B.W., P.M., and B.W.H. analyzed the data.

Supporting information

Supplemental Information ‐ Model Equations

Supplemental Figures and Tables