A novel mechanism for mechanosensory-based rheotaxis in larval zebrafish

Abstract

When flying or swimming, animals must adjust their own movement to compensate for displacements induced by the flow of the surrounding air or water¹. These flow-induced displacements can most easily be detected as visual whole-field motion with respect to the animal’s frame of reference². In spite of this, many aquatic animals consistently orient and swim against oncoming flows (a behavior known as rheotaxis) even in the absence of visual cues^3,4. How animals achieve this task, and its underlying sensory basis, is still unknown. Here we show that in the absence of visual information, larval zebrafish (Danio rerio) perform rheotaxis by using flow velocity gradients as navigational cues. We present behavioral data that support a novel algorithm based on such local velocity gradients that fish use to efficiently avoid getting dragged by flowing water. Specifically, we show that fish use their mechanosensory lateral line to first sense the curl (or vorticity) of the local velocity vector field to detect the presence of flow and, second, measure its temporal change following swim bouts to deduce flow direction. These results reveal an elegant navigational strategy based on the sensing of flow velocity gradients and provide a comprehensive behavioral algorithm, also applicable for robotic design, that generalizes to a wide range of animal behaviors in moving fluids.

In order to describe the behavioral mechanisms of flow navigation in larval zebrafish, we built a system consisting of a horizontal transparent tube in which controlled laminar flow can be induced, and the behavior of the fish monitored, in three-dimensional space (Fig.1a–c). We observed that, as previously shown, 5-7 day-old larval zebrafish perform rheotaxis by orienting (Fig.1d,f,g) and swimming (Fig.1e,h,i) against the direction of the water flow⁵; even in the absence of any visual references^6,7 (Fig.1f–i).

Figure1. Larval zebrafish perform rheotaxis in the absence of visual cues.

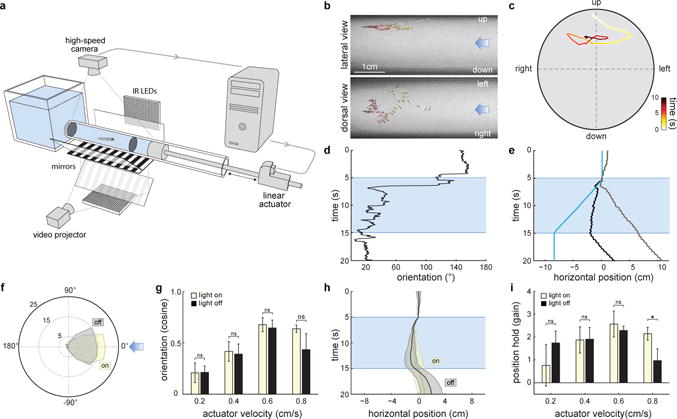
a, Schematics of the setup. b, Time-projection of a zebrafish larva performing rheotaxis in the dark. Light blue arrows represent flow direction. c, Cross-sectional view of the trial shown in (b). d-e, Behavioral features of the trial shown in (b-c). Light blue indicates water flow stimulus is on. d, Fish orientation in relation to water flow. e, Fish position in the axis of the water flow from the observer’s (black trace) and the fish’s (grey trace) point of view. Blue trace corresponds to the displacement of the water column. f-i, Rheotaxis in the presence and absence of visual cues. f, Polar plot of fish orientation in the axis of the flow during stimulation. Light blue arrow represents flow direction. g, Cosine of the mean orientation (see Methods) for fish presented with different actuator velocities. h, Fish position (from the observer’s point of view) in the axis of the water flow. i, gain (see Methods) for fish presented with different actuator velocities. n = 6 fish subjected to 12 trials at each actuator velocity (288 trials total). Data is shown as means ± s.e.m. ns = p>0.05; * = p>0.01&<0.05; Monte Carlo permutation test.

It is important to point out that under these conditions the flow cannot be directly sensed by the animal if it is being dragged by a homogeneous current. In this scenario, the fish navigates within the reference frame of the constantly moving body of water and all rules of physics are invariant under such a velocity transformation⁸. From the fish’s perspective there is no oncoming water flow and, if the flow is truly homogeneous, it is physically impossible to detect it in the absence of cues from an external frame of reference^2,8. Contact with the wall or linear acceleration detected by the inner ear might provide such cues^9,10. However, given that fish perform rheotaxis away from the chamber walls (Fig.1b–c, Extended Data Video 1 and Extended Data Fig.1a,b) and semicircular canals are not functional at larval stages¹¹, both touch and angular acceleration are unlikely to play a role in our setup. To test the role of linear acceleration, we mounted the entire behavioral setup on rails, and accelerated it using the same actuator as used for flow induction. We observed no orientation and position-holding behavior at all acceleration values tested, even at those significantly exceeding the ones used during rheotaxis experiments (Extended Data Fig.1c–f).

Thus, we hypothesized that the navigational information required for vision– independent rheotaxis had to be provided by border-induced non-homogeneities within the flow. In order to precisely measure such flow conditions, we used Particle Image Velocimetry (PIV), and observed a radially symmetric flow profile that develops within approximately five seconds and reaches steady state thereafter (Fig.2a, Extended Data Fig.2a). To investigate the importance of such velocity gradients for flow navigation, we performed experiments across steep, medium and shallow gradient regimes (Fig.2b) and observed that the ability of fish to orient and hold position consistently improved with increasing gradient magnitudes (Fig.2c,d). Trivially, when exposed to a zero-gradient regime, fish did not perform rheotaxis (Fig.2c,d)⁸. Thus, in the absence of visual references, flow velocity gradients represent the main cue for rheotaxis in larval zebrafish.

Figure2. Flow velocity gradients are the stimulus for rheotaxis in larval zebrafish.

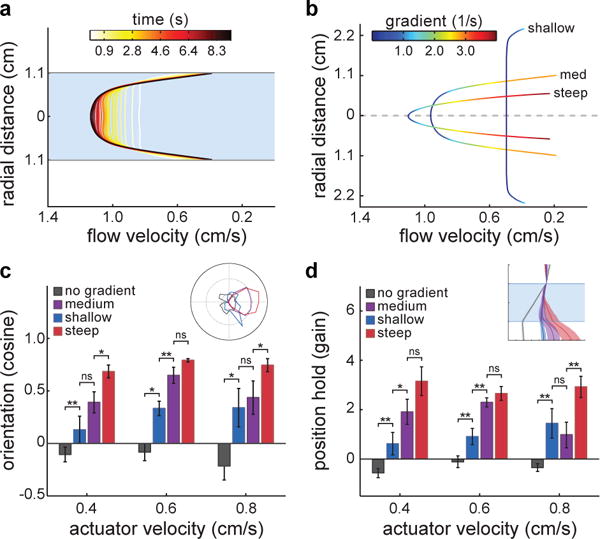
a, Development of the flow velocity profile obtained through Particle Image Velocimetry in the behavioral chamber. b, Flow velocity profiles and gradient magnitudes in different diameter tubes (see Methods). c, Cosine of the mean orientation for fish presented with different gradient conditions. Inset: Polar plot of fish orientation during flow stimulation. d, Gain for fish in each of the gradient conditions. Inset: Horizontal positions of fish from the observer’s point of view. n = 6 fish subjected to 6 trials at each actuator velocity (108 trials) for each gradient condition (432 trials total). Medium gradient values are the same as in Fig.1g,i. Data is shown as means ± s.e.m. ns = p>0.05; * = p>0.01&<0.05; ** = p<0.01; Monte Carlo permutation test.

As any solid body drifting in a fluid containing velocity gradients, a larval zebrafish will experience a rotational flow field (or shear) around its perimeter. The predicted spinning of an object in such a rotational flow-field can be observed in the case of a paralyzed fish shown in Extended Data Video 2 and Extended Data Fig.2b,c. This rotational flow field is directly related to the local curl of the water volume ( $=\nabla \times \overrightarrow{V}$) and the two values are mathematically linked by Stokes’ Theorem, which states that the integrated curl over the area occupied by the fish’s body (S) can be measured by a line integral around the animal’s perimeter:

$$\int {\int }_S(\nabla \times \overrightarrow{V})\cdot d\overrightarrow{a}={\oint }_C\overrightarrow{V}\cdot d\overrightarrow{s}$$ (1)

Thus, in our setup fish could estimate the local curl in the water at its current position by calculating a line integral of the relative water flow around the circumference of its body (Fig.3a). We will show below that the lateral line, a collection of mechanosensory organs distributed along the surface of the body in fish and amphibians¹², is well suited to perform such measurements (the lateral-line integral) and that these measurements provide an elegant and accurate method of estimating local gradient values.

Fig.3. A behavioral algorithm for rheotaxis in larval zebrafish.

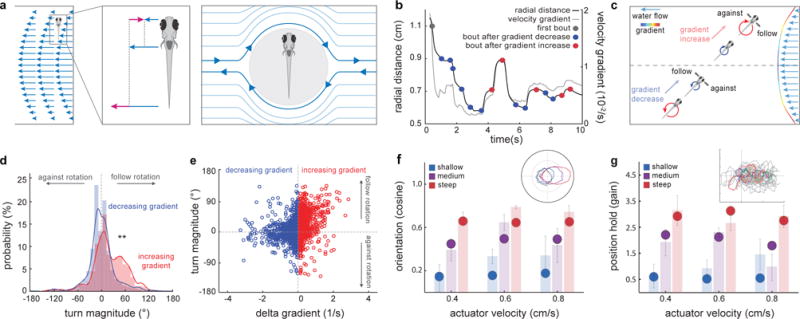
a, Schematics of gradient-induced rotational flow fields. A fish in a gradient will drift at the flow velocity in its center of mass (left). As a consequence, the differences between fish velocity and the rest of the flow velocities (center) will induce a local rotational flow field around the animal (right). b, Radial distance (grey trace) and velocity gradient (black trace) experienced by a single fish during a trial. Swim bouts occur after increases (red dots) or decreases (blue dots) in gradient magnitude. Data corresponds to the example shown in Fig.1b–e. c, Graphical representation of bout types during rheotaxis. d, Histogram for turn magnitudes during rheotaxis. ** = p<0.01. Kolmogorov-Smirnov test, n = 13 fish, 341 trials. e, Scatter plot of turn magnitude vs delta gradient. n = 13 fish, 2762 bouts. f, g, model fish perform rheotaxis. Comparison of cosine of the mean orientation (f) and gain (g) between model (circles) and real (shaded bars, data as in Fig.2b,d) fish. Insets: f, Polar plot of model fish orientation under different gradient conditions and g, trajectories of one hundred (grey) modeled fish facing a virtual flow towards the left. Five examples are colored for clarity.

We next focused on the behavioral mechanisms of rheotaxis. Since fish cover a large range of radial distances from the center of the tube, they experience significant changes in gradient magnitude during each trial, extending from a flat (zero) gradient at the center to maximal gradient values close to the border (Fig.2b and Fig.3b–c). As larval zebrafish swim in discrete periods of motor activity (swim bouts)¹³ separated by longer inactive inter-bout periods, each swim bout will necessarily elicit a change in the gradient experienced by the fish (delta gradient) that will define the conditions in which the subsequent bout will occur. Thus, during rheotaxis, swim bouts can be grouped into bouts that occur after increases (Fig.3b–e, red) and bouts that occur after decreases (Fig.3b–e, blue) in gradient magnitude, where the former generally occur when the fish swims towards the high gradient regime of the wall and the latter when it swims away from it. Importantly, we found that while bouts occurring after decreases in gradient magnitude showed a symmetric distribution of low magnitude turns with no obvious directionality (Fig.3d, blue), the distribution of bouts occurring after increases in gradient magnitude was strongly skewed towards high magnitude turns that followed the direction of the rotational vector field (Fig.3d, red). These results unveil a simple rheotactic algorithm in which a larval zebrafish, after experiencing a decrease in gradient magnitude, primarily swims straight. On the contrary, after experiencing an increase in gradient magnitude, it performs a high magnitude turn in the direction of flow field rotation (Fig.3d, Extended Data Fig. 3a). This algorithm relies on small changes in gradient magnitude (Extended Data Fig.4a–c), occurs mostly in the left-right axis, i.e. the yaw, of the fish (Extended Data Fig.4d–f), is independent of both flow direction (Extended Data Fig.4g–i) and passive rotations of the animal’s body¹⁴ (Extended Data Fig.2d,e) and, most importantly, allows the fish to both orient and swim against oncoming water flow (Extended Data Fig. 3b–i).

Next, we generated a simple model to test whether our algorithm is sufficient to explain the observed rheotactic behavior. In this simulation, a particle moves randomly in a virtual flow field which is matched to our experimental conditions (Extended Data Fig. 5a; See Methods). Importantly, we found that this simple algorithm is sufficient to elicit rheotaxis with remarkable robustness (Fig.3 f–g, Extended Data Video 3). In addition, our behavioral experiments also showed that over the course of a trial, fish swim increasingly closer to the center of the tube (Extended Data Video 1 and Extended Data Fig.6a–c). This phenomenon, also faithfully reproduced by the model (Extended Data Fig. 6d), is strongly reminiscent of the biased random walk during bacterial chemotaxis¹⁵ and automatically leads to the avoidance of high gradient regions near the walls. Interestingly, since high velocity gradients will consistently develop around any obstacles in flowing bodies of water, an algorithm that guides the animal away from a strong gradient will automatically assist in avoiding such obstacles. Somewhat paradoxically, this ‘gradient avoidance’ effect will eventually lead the fish to veer away from the shore to the center of the stream, where gradient is lowest and flow velocity is highest. As a consequence, we believe that our algorithm selectively applies to animals whose natural habitat is largely restricted to the vicinity of the shore, the reef or generally to small rivers, brooks and rivulets, where they are confined to the strong gradients near wall regions^16,17.

Another main feature of natural currents is the presence of turbulence and vortices of varying magnitude. To explore how our proposed algorithm would perform under such disorderly conditions, we added Karman vortex streets^16–19 to the laminar flow profile used in our simulations (Extended Data Fig.5a–c). Remarkably, although rheotactic performance invariably decayed with increases in turbulence, it remained consistently robust even when conditions became distinctly unstable (Extended Data Fig.5d–g, Extended Data Fig.6d, Extended Data Video 3). Interestingly, we also observed that while gain and orientation values depended quite linearly on vortex density (Extended Data Fig.5f), model performance showed a much more delicate sensitivity to minute changes in vortex intensity (Extended Data Fig.5g). These extended simulations show that our algorithm is surprisingly robust to mild and moderate turbulence and can even sustain a minimal baseline performance once fully turbulent flow¹⁹ is established. We propose that the robustness of this effect arises from the consecutive and cumulative integration of many turn angle choices that together average out the random perturbations induced by local vortices.

Finally, we searched for the sensory basis of gradient–dependent rheotaxis. This question, and the role of the lateral line (LL) system¹², has been the subject of a continuous debate^3,4,9,10,20. In the larval zebrafish, the LL system consists of a series of mechanosensory organs (the neuromasts) located along multiple stripes in the fish’s head (the anterior LL) or in single stripes along each side of the fish’s tail (the posterior LL²¹). To assess its importance in gradient-induced rheotaxis, we performed chemical ablations of all neuromast hair cells using copper sulfate^4,9 (Extended Data Fig. 7a–a′) and observed that turn distributions for bouts occurring after increases or decreases in gradient magnitude almost completely lost their asymmetry (Fig.3d and Fig.4a,b). Consequently, the fish’s ability to orient against oncoming water flows was severely reduced (Fig. 4c; Extended Data Video 4). Unilateral and bilateral laser ablations of the anterior or the posterior LL nerves (Extended Data Fig.7b–d′) showed that the lack of the posterior, but not the anterior LL system induced a significant decrease in the fish’s orienting performance (Fig.4c), which is in agreement with the predominantly left-right component of fish turns during rheotaxis (Extended Data Fig.4d–f) and the primarily antero-posterior receptive fields of the posterior LL neuromasts^22,23. Furthermore, we found that behavioral loss was comparable in unilaterally- as well as bilaterally-ablated fish (Extended Data Fig.7e), suggesting that fish need to integrate the flow over both sides of their body in order to estimate the curl of local rotational flow fields^24,25.

Fig.4. The mechanosensory lateral line system acts as a gradient sensor during larval zebrafish rheotaxis.

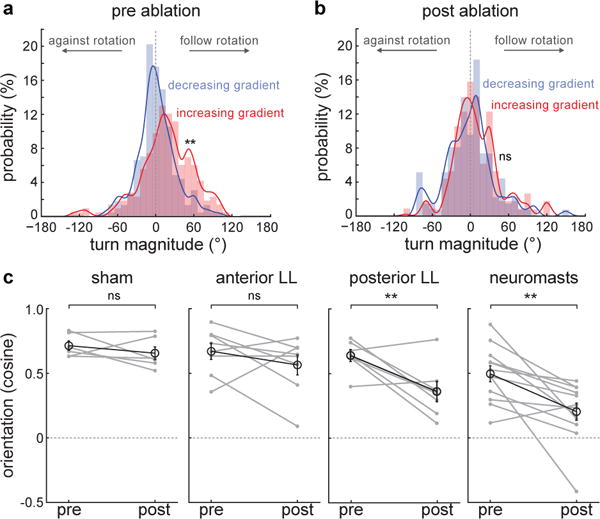
a–b, Turn magnitude histogram before (a) and after (b) copper-induced chemical ablation of all neuromast hair cells. ** = p<0.01; Kolmogorov-Smirnov test. n = 12 fish. c, Mean orientation of fish subjected to different experimental conditions. Mean and s.e.m. of the population (black) and means of individual fish (grey) before and after treatment are shown. n = sham, 6 fish; anterior lateral line ablation, 8 fish; posterior lateral line ablation, 7 fish; chemical neuromast ablation, 12 fish. All fish were subjected to 6 trials before and after manipulations. ns = p>0.05, ** = p<0.01; Monte Carlo permutation test.

In summary, our experiments show that a relatively complex behavior such as rheotaxis can emerge from a surprisingly simple behavioral algorithm that relies on the detection of gradient-induced rotational flow fields. Velocity gradients in natural environments will be present at the interface between flows and any kind of surface; thus the ecological relevance of our algorithm encompasses both rheotaxis as well as obstacle avoidance. Since flow navigation is a fundamental feature of all animals that fly or swim¹, the description of its elementary rules and sensory basis will be essential to unveil its underlying neural circuits, understand the evolution of this conserved behavior and provide robust algorithms for robot navigation.

Methods

Animals

5–7 days-post-fertilization (dpf) wild-type zebrafish of the WIK strain were used for all behavioral experiments, unless indicated. Animal handling and experimental procedures were approved by the Harvard University Standing Committee on the Use of Animals in Research and Training. No statistical methods were used to predetermine sample size.

Behavioral Chamber

A 45 cm long polycarbonate tube (1.27, 2.22 or 4.76-cm inner diameter, 0.31 cm wall thickness) was attached to a water reservoir and filled with aquarium water. Two 140 μm mesh filters were used to contain single zebrafish larvae in a 13 cm long behavioral section while two infrared (IR) LED arrays provided illumination from below and from the sides of the tube. A high-speed camera (Pike F-032B, Allied Vision Technologies) fitted with a macro-lens (Sigma DG, USA) and a visible-light-blocking filter (to block visual cues in light-on experiments) recorded fish behavior at 200 frames per second (fps) directly from above the behavioral section and from the reflection of a lateral IR reflecting mirror (hot mirror, Edmund Optics, USA). For experiments in which visual cues were present, stationary black & white stripes (0.5 cm wide) from a mini projector (Dell M109S, USA) were reflected upward on a visible light-reflecting mirror (cold mirror, Edmund Optics, USA) into a diffusive screen underneath the behavioral section. Laminar water flow was created by the displacement of a custom-made plunger attached to the rod of a computer-controlled linear actuator (Servotube Actuator STA1112, Copley Controls). For acceleration and water displacement experiments, the behavioral section of the rig was mounted on rails and attached to the actuator’s rod. Behavioral trials were controlled using software custom-written in LabView (National Instruments, Austin, TX) and consisted of 5s of no stimulus, 0.1s acceleration, 9.8s water flow/water displacement stimulus, 0.1s de-acceleration and another 5s of no stimulus. For acceleration experiments, trials consisted of 2.5s of no stimulus, 1s of acceleration, 1s of water displacement, 1s of de-acceleration and another 2.5s of no stimulus. All experiments were performed by randomly moving the plunger towards or away from the water reservoir.

Behavioral Analysis

All behavioral analyses were performed using custom-written Matlab code (MathWorks Inc.). Rheotactic orientation was calculated as the mean of the cosines of all fish orientations during stimulus presentation. Thus, cosine = 1 represents perfect alignment against flow direction (0 degrees fish orientation) while cosine = -1 represents perfect alignment in the direction of the flow (180 degrees fish orientation). To quantify the ability to hold position against incoming flows, we calculated a relation between the velocity of the fish and the velocity of the incoming water flow (the ‘gain’) through the formula (fish velocity – water velocity)/water velocity. Thus, gain < 1 means fish actively swim in the direction of the flow, gain = 0 represents passive drift, gain = 1 means perfect position holding, and gain > 1 means overcompensation. This metric was used for individual bout types (i.e., Extended Data Fig.3i) or, by calculating their mean, for a whole behavioral trial (i.e., Fig1i). Since flow stimulus onset and direction were always randomized, both cosine and whole-trial gain were calculated from a similar number of experiments in which the fish faced towards or against the direction of the flow at the beginning of the stimulus. For paralyzed fish experiments, larval zebrafish were incubated in 1mg/ml of α-bungarotoxin and then directly released into the behavioral chamber while water flow was induced. With the exception of minor necessary modifications (i.e. swimming vs paralyzed fish), all analyses were performed using the same code, independently of the experiment type.

Statistics

Kolmogorov-Smirnoff tests were performed through embedded functions while Monte Carlo permutation tests were custom written in Matlab (MathWorks Inc.). For the latter, we calculated the difference between the means of the two distributions to be compared; then both distributions were shuffled and a new difference in means was calculated. This was repeated through 10000 iterations and the p-value was calculated as the probability of finding the original difference of the means. No variance analyses were performed.

Water Flow Analysis

Particle Image Velocimetry (PIV) was performed as previously described²⁶. Water velocity profiles were calculated at 50 fps (Davis software version 7.2.2, LaVision Inc., Goettingen, Germany) and analyzed using custom software written in Matlab (The MathWorks Inc.). Different flow profiles were created by the displacement of actuator-attached plugs into small (1.27-cm), medium (2.22-cm) and large (4.76-cm) diameter polycarbonate tubes. For behavioral analyses, flow stimulus direction was always taken as leftwards and all the time points (except for the initial acceleration) during flow development were used. As the average horizontal position of the fish during rheotaxis was 6.5 ± 0.7cm away from the flow source (either the plunger or the water reservoir), behavioral analyses were performed using the flow profile obtained at 5-7cm away from the source (Fig.2a, Extended Data Fig.2a). All time points in the development of the flow profile were matched to the time points in the behavioral videos. Since both flow profile and rheotactic behavior between experiments in which the flow was induced towards or away from the water reservoir was similar (Figure S4 g–i), all trials were included in the analyses.

Modeling

Modeling of the rheotactic algorithm was made using software custom-written in LabView (National Instruments, Austin, TX). In brief, our simulations consist in a particle randomly moving in a virtual flow field that matches our experimental conditions with the following constraints: the path-length of each iterative step corresponds to the average bout distance travelled by a larval zebrafish, the time taken for each step is set to the average bout frequency, and turn angles are drawn from the distributions described in Fig.3d. Finally, delta gradient values were obtained by the change in position of the particle within the measured flow field described in Fig.2a. Additionally, under high velocity conditions, the fixed bout length of the model fish was gradually up-regulated during the course of a successful trial to account for similar observations under experimental conditions (data not shown). In order to add turbulence to the model, we equipped our simulation platform with the ability to add Karman vortex streets to the laminar flow profile described in Extended Data Fig.5. The maximum value (100%) of the rotational speed of each individual vortex (intensity) was set to the maximal absolute velocity of the parabolic velocity profile of the stream. The vortex density was defined by the relative spacing of hexagonally arranged vortices with respect to each other.

Lateral Line Ablations

For chemical neuromast ablations, 5-7 dpf WIK larvae were used. Fish were subjected to six trials at a single actuator velocity (0.6 cm/s), incubated in 1 mM copper sulfate for 85 minutes and allowed to rest in fish water for 60 minutes before being subjected to six more trials. Only fish that showed a complete neuromast ablation (assessed by DiASP staining²⁷) and a constant swimming activity were included in the analysis. For 2-photon lateral line nerve ablations, 6 dpf HGn93D zebrafish larvae²⁸ were subjected to six trials at a single actuator velocity (0.6 cm/s) and embedded in low-melting-point agarose with one of their otic vesicles looking upwards. An image stack of the GFP-labeled lateral line (LL) nerve in the HGn93D strain was acquired and then 1-3 850nm laser pulses of 1ms duration were targeted on the anterior or the posterior central projection of the LL nerve. For sham ablations, the same treatment was performed on a single neighboring nerve innervating a dorsal neuromast. Fish were then released from the agarose and allowed to rest for 24hs to allow the regeneration of the neuromast cupula after being damaged during agarose release. In the case of bilateral LL ablations, fish were immediately mounted and ablated on their opposite side after being released from the agarose and allowed to rest for 24hs. The next day, fish were subjected to another six trials, re-embedded in agarose and another stack of the LL nerve was acquired. Only fish with normal buoyancy, constant swim activity and with clear damage to the LL nerve targeted in the treatment were included in the analysis. All experiments were analyzed using the same code, independently of the ablation type.

Data Availability

All codes and video data that support the findings of this study are available from the corresponding authors upon request.

Extended Data

Extended Data Fig.1. Touch and acceleration do not explain rheotaxis in larval zebrafish.

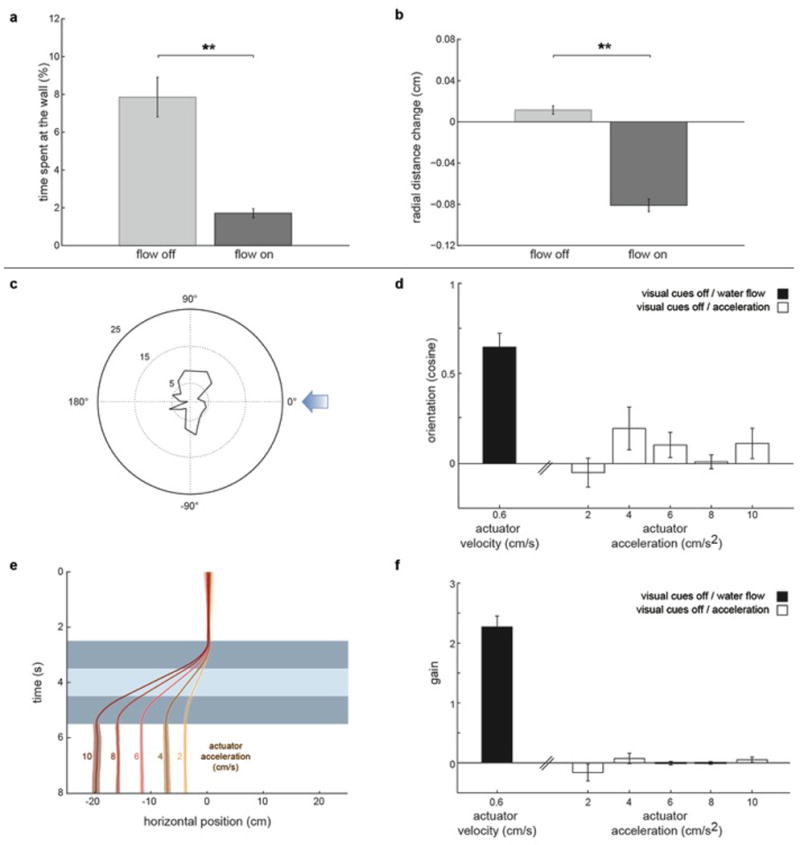
a, Percentage of time fish spend at the wall; n = 13 fish, 341 trials. b, Mean radial distance change for bouts occurring in close proximity to the wall (<0.36cm, 1/3 of the tube radius). n = 13 fish, 1364 bouts. c-f, Rheotactic metrics for larval zebrafish exposed to a series of acceleration/water displacement/de-acceleration stimulus. c, Polar plot of fish orientation in the axis of the stimulation. Blue arrow represents stimulus direction. d, cosine of the mean orientation for fish presented with different acceleration regimes. Black bar represents cosine of the mean orientation for fish exposed to water flow in the dark (Fig.1g). e, Fish position (from the observer’s point of view) in the axis of the stimulus. Dark blue represent acceleration/de-acceleration periods while light blue represents water displacement. f, Gain for fish presented with different acceleration regimes. Black bar represents gain for fish exposed to water flow in the dark (Fig.1i). n = 6 fish subjected to 6 trials at each acceleration regime (180 trials total). All data is shown as means ± s.e.m. ** = p<0.01; Monte Carlo permutation test.

Extended Data Fig.2. Gradient-dependent rotation of the larval zebrafish body.

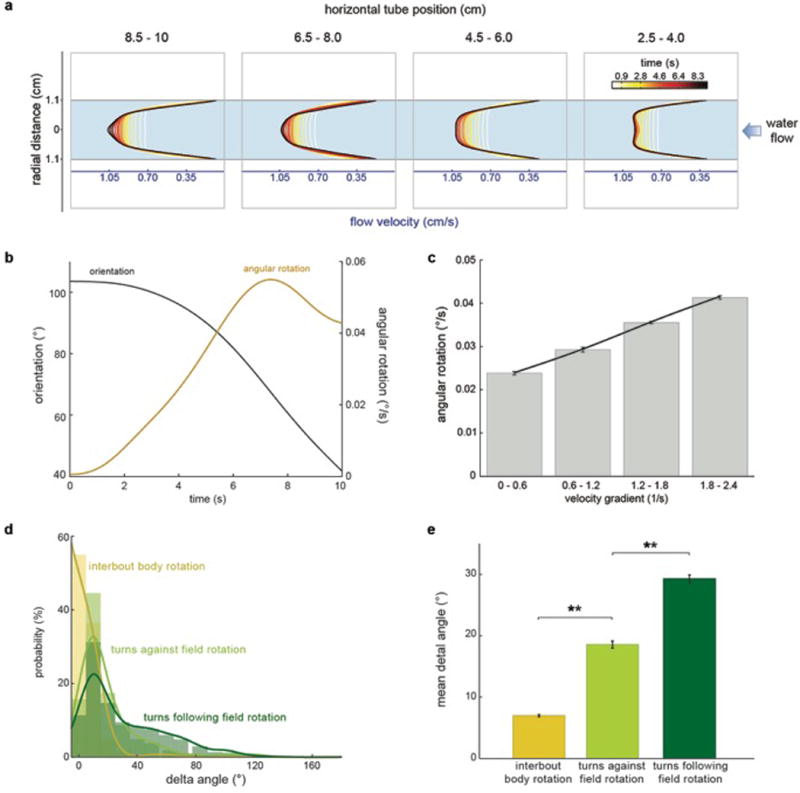
a, Development of flow velocity profiles obtained through Particle Image Velocimetry at different points in the horizontal axis of the tube (see Methods). b, Orientation (black) and angular rotation (brown) changes in a single paralyzed larval zebrafish in water flow. Data corresponds to the example shown in Extended Data Movie 2. c, Mean angular rotational velocities for different velocity gradient magnitudes. n = 3 fish, 18 trials. d, Inter-bout body rotation (yellow) and turn magnitude histogram for bouts going against (light green) and following (dark green) flow rotational fields. Histograms and fitted lines for each distribution are shown. n = 13 fish, 341 trials. e, Mean delta angle for inter-bout body rotation and turns following/going against flow field rotation. n = 3840 inter-bout periods, 2831 bouts. Means and ± s.e.m. (c,e) and bars and fitted lines (d) are shown. ** = p<0.01; Monte Carlo permutation test.

Extended Data Fig.3. The rheotactic algorithm allows the fish to orient and swim against incoming water flows.

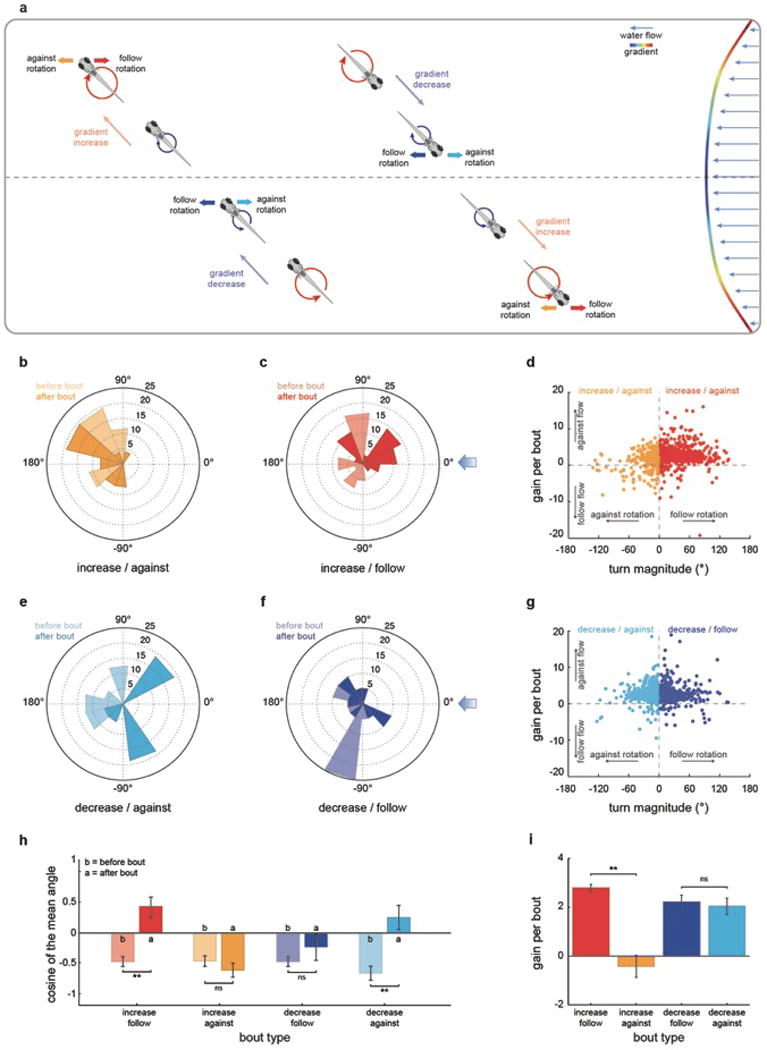
a, Graphical representation of bout types during rheotaxis. b, c, e, f, Polar plots of fish orientation before (light color) and after (dark color) high magnitude (>45 degrees) turns that start when fish is facing away from the flow. n = 98 bouts. d, g, Scatter plots of turn magnitude vs gain for bouts occurring after increases (d) or decreases (g) in gradient magnitude. n = 2598 bouts. h, Cosine of the mean orientation for the data shown in (b, c, e, f). i, Gain for high magnitude turns extracted from the data shown in (d, g). n = 508 bouts. Data is shown as means ± s.e.m. * = p>0.01&<0.05; ** = p<0.01, Monte Carlo permutation test.

Extended Data Fig.4. The rheotactic algorithm depends on delta velocity gradients, is mainly composed of lateral turns and is independent of flow direction.

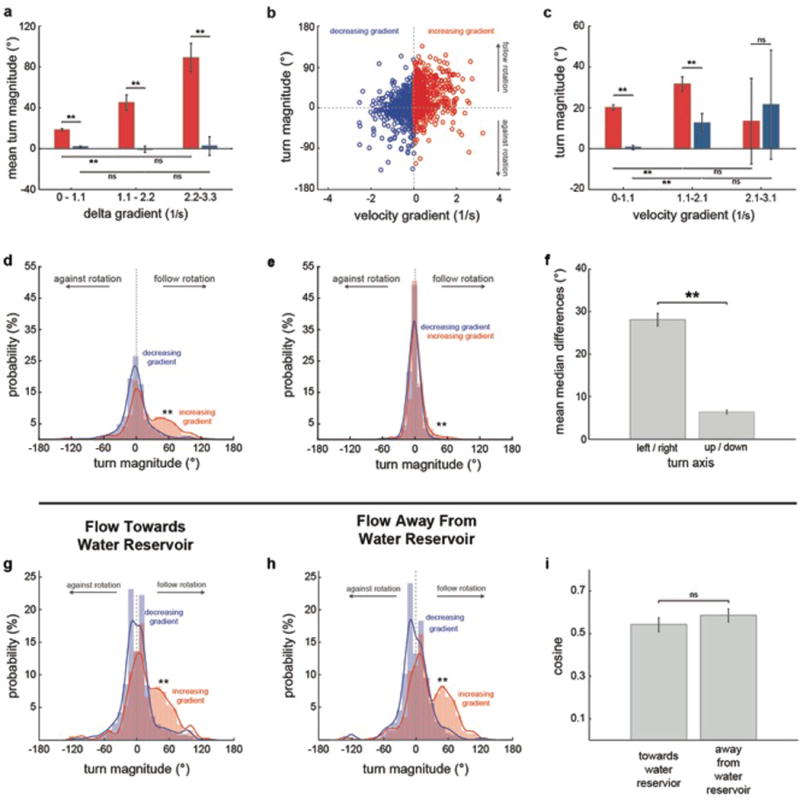
a, Mean turn magnitude for bouts occurring after increases or decreases in gradient magnitude, grouped by delta gradient. Data is the same as in Fig3, e. b, Scatter plot of absolute velocity gradient versus turn magnitude for bouts occurring at intermediate tube regions (0.36-0.74cm away from the walls) that can be reached from both low and high gradient areas. n = 13 fish, 1691 bouts. c, Mean turn magnitude for bouts following increases or decreases in gradient magnitude, grouped by absolute velocity gradient. Data is the same as in (b). d-e, Turn magnitude histogram for left/right (d) and up/down (e) turns. n = 13 fish, 341 trials. f, Mean difference between the medians of increasing and decreasing gradient turn distributions. Data is the same as in (d,e). g–i, Turn magnitude histogram for experiments in which water flowed towards (g) or away (h) from the water reservoir (ftwr and fawr conditions, respectively). n = 13 fish; 170 and 171 trials for ftwr and awr experiments, respectively. i, Cosine of the mean orientation for ftwr and fawr experiments. Data is the same as in (g,h). Means and ± s.e.m. (a,c,f,i) and bars and fitted lines (d,e,g,h) are shown. ns = p>0.05; ** = p<0.01; Kolmogorov- Smirnov (d,e,g,h) and Monte Carlo permutation (a,c,f,i) tests.

Extended Data Fig.5. Model fish perform rheotaxis in a virtual turbulent flow.

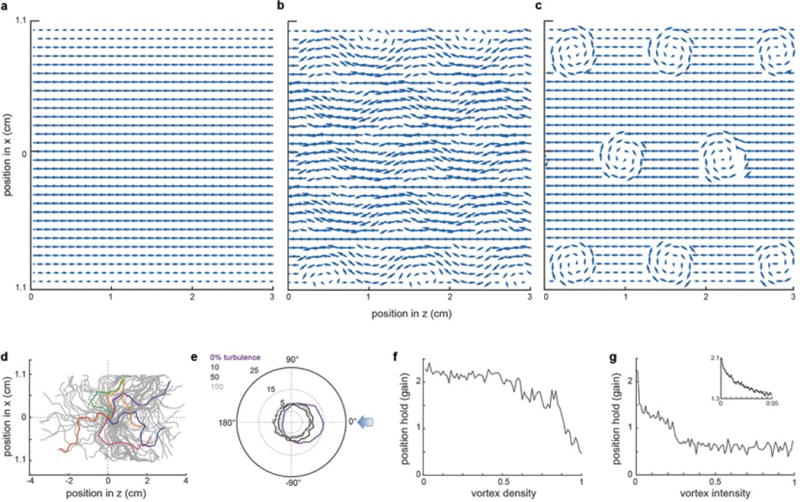
a, Virtual laminar flow profile used for modeling rheotactic behavior (Fig.3 f–g). b, Flow profile in (a) after the addition of Karman vortex streets to (a) at 50% intensity and 100% density. c, Flow profile in (a) after the addition of static vortices set to 100% intensity and 100% density. d, Trajectories of one hundred (grey) modeled fish facing a virtual turbulent flow towards the left. Five examples are colored for clarity. e, Polar plot of model fish orientation under different turbulence strengths. f, Gain of model fish as a function of increasing vortex density at a constant 100% vortex intensity. g, Gain of model fish as a function of increasing vortex intensity at a constant 100% vortex density. Inset is an expanded view of the initial gain drop.

Extended Data Fig.6. Larval zebrafish swims towards the center of the tube during rheotaxis.

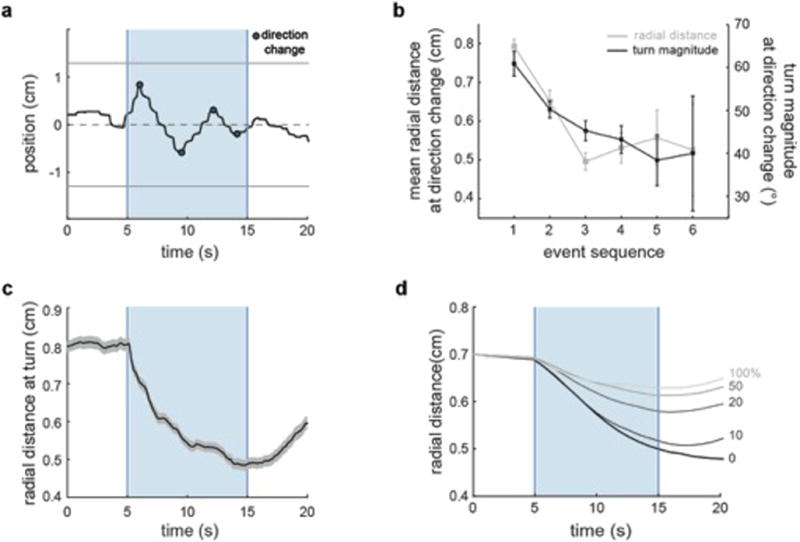
a, Horizontal (left/right) positions of a single fish during rheotaxis. Light blue indicates water flow stimulus and dark blue dots indicate direction change events. Data corresponds to the example shown in Fig.1b–e. b, Radial distance and turn magnitude at consecutive swim direction changes. n = 774 direction change events. c, Radial distance over time. n = 13 fish, 341trials. d, Radial distance over time for a modeled particle following the rheotactic algorithm at different vortex densities. Data is shown as means ± s.e.m. ** = p<0.01; Monte Carlo permutation test.

Extended Data Fig.7. Bilateral Lateral Line stimulation is required for rheotaxis in larval zebrafish.

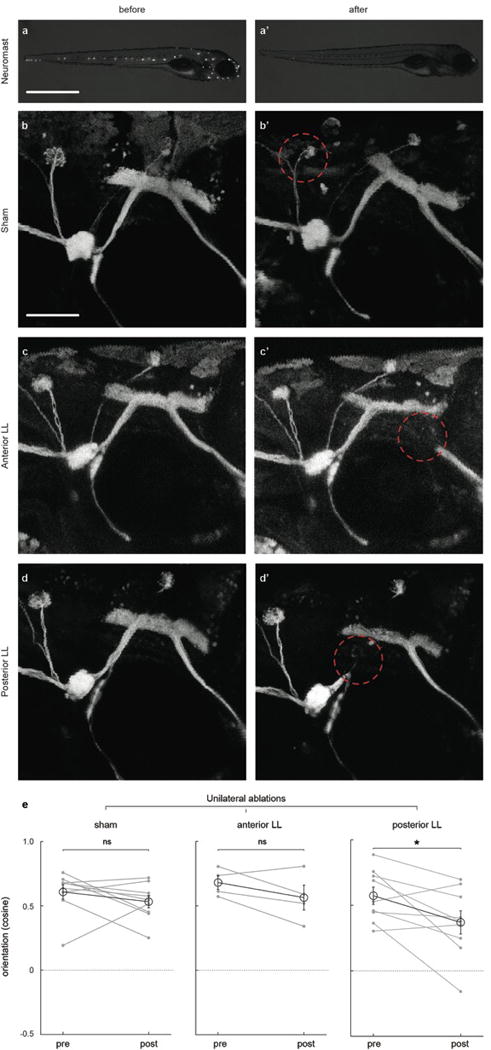
a–d, Representative examples of copper-mediated chemical neuromast (a-a’) and 2-photon laser sham (b-b’), anterior (c-c’) and posterior (d-d’) LL nerve ablations before (left column) and after (right column) treatment. DiasP stained (a-a’) and GFP-expressing Tg(HGn93D) fish shown. Red dotted circles indicate the region in which laser power was focused. e, Cosine of the mean orientation for fish subjected to unilateral laser ablations of the LL nerve. Mean and SEM of the population (black) and means of individual fish (grey) before and after treatment are shown. n = sham, 9 fish; Anterior LL ablation, 4 fish; Posterior LL ablation, 9 fish. All fish were subjected to 6 trials before and after manipulations. ns = p>0.05, * = p<0.05&>0.01; Monte Carlo permutation test.