Summary
Combinations of multiple drugs are an important approach to maximize the chance for therapeutic success by inhibiting multiple pathways/targets. Analytic methods for studying drug combinations have received increasing attention because major advances in biomedical research have made available large number of potential agents for testing. The preclinical experiment on multi-drug combinations plays a key role in (especially cancer) drug development because of the complex nature of the disease, the need to reduce development time and costs. Despite recent progresses in statistical methods for assessing drug interaction, there is an acute lack of methods for designing experiments on multi-drug combinations. The number of combinations grows exponentially with the number of drugs and dose-levels and it quickly precludes laboratory testing. Utilizing experimental dose-response data of single drugs and a few combinations along with pathway/network information to obtain an estimate of the functional structure of the dose-response relationship in silico, we propose an optimal design that allows exploration of the dose-effect surface with the smallest possible sample size in this paper. The simulation studies show our proposed methods perform well.
Keywords: Experimental design, Dose-response, Drug combinations, Functional ANOVA, Signaling network
1. Introduction
Multi-drug combination is an important therapeutic approach for diseases such as cancer, viral or microbial infections, hypertension and other diseases involving complex biological pathways. Synergistic drug combinations, which are more effective than expected from summing effects of individual drugs, offer the potential for improved therapeutic index. The past decade has seen significant progresses in developing proper design and analysis methods for two/three-drug combination studies, which have increased the chances of identifying optimized combinations for further therapeutic opportunities (Tan et al., 2003, 2009; Kong and Lee 2006; Fang et al. 2008, 2015) as well as adaptive phase I clinical trial designs that attempt to identify the best possible maximum tolerated doses through modeling of the joint dose-toxicity relationship (see, e.g., Yuan and Yin, 2008; Yin and Yuan, 2009a, 2009b; Tan et al., 2016; Yang et al., 2016).
However, combination drug therapy targeting just a few gene products may be ineffective (Chen and Dancey, 2008; Jones, et al., 2008; Parson et al., 2008). Increasing the number of agents in a combination has been another strategy for increasing the level or type of interaction produced. In the past decade, the approach to cancer therapy has been revolutionized by the identification of a variety of novel signal transduction targets amenable to therapeutic intervention. These targets were identified based on improved understanding of the molecular mechanisms of action of second messengers, other components of signal transduction pathways, and systems biology. These advances have also made available large number of potential agents and call for new quantitative approaches for combination therapy (Fitzgerald et al., 2006; Hopkins, 2008; Xavier and Sander, 2010). Despite the changing paradigm to target multiple pathways, methodological advances in accurately identifying drug interactions have fallen behind, as shown by a paucity of literature on the design and analysis of multi-drug combinations.
The design of multi-drug combination experiment presents exceptional challenges and a high dimensional statistical problem. The number of combinations reaches 59049 for a study of 10 drug combinations with only 3 dose-levels for each drug. Since the number of combinations grows exponentially with dose-levels, it quickly precludes laboratory testing. In spite of the biological advances mentioned above and the significance of multi-agent combinations, current methods remain to be descriptive, thus, fail to address dimensionality and often violate statistical assumptions. As a result, many multi-drug combination studies are designed suboptimally by studying only pairwise combinations while fixing the dose of one or more drugs.
To determine the interaction among multi-drugs, the dose-response surface provides a comprehensive description on dose effects. For estimating the high dimensional dose-response surface, experimental designs are required that provide selected concentrations or dose-levels of combinations, which allow exploration of the dose-effect surface with high accuracy at reasonable sample sizes. Recently, we developed a novel method to screen the large number of combinations and identify the functional structure of the dose-response relationship by using the dose-response data of single drugs and pathway/network knowledge (Fang et al., 2016). That is, data from experiments of single drugs and a few combinations as well as existing signaling network knowledge from sources such as KEGG are utilized to develop a statistical re-scaling model to describe the effects of drugs on network topology. The system comprises a series of statistical models with biological considerations, such as Hill equations, generic enzymatic rate equations and a regression model, to represent the cumulative effect of genes implicated in activation of the cell death machinery. In other words, a quantitative model can be established upon existing network topology along with meaningful signal propagation rules, and the significant drug interactions as well as the single drug effects are expected to “hide” in such a model. How to extract the significant drug interactions and single drug effects from the model will be described in Section 2. The method of Fang et al. (2016) is highly beneficial in bringing forth a statistical framework for selecting drug interactions, and developing experimental designs and statistical analysis to estimate the high dimensional dose-response surface.
The purpose of this article is to derive designs of combinations of multi-drugs based on the functional structure of the dose-response relationship. The remainder of this paper is organized as follows. Section 2 briefly describes model formulation for the dose-response of multi-drug combinations. The experimental design of maximizing the posterior information on the dose-response is proposed in Section 3. Section 4 gives the design construction algorithm and sample size calculation. Simulation studies are conducted in Section 5. Concluding remarks and further discussions in Section 6 close this paper.
2. Model Formulation
Consider a combination study of s drugs A1, A2, …, As inhibiting some cell line or against some cancer tumor. Assume the dose-response surface to be
| (1) |
where xi is the dose-level of drug Ai, y is the dose-effect scaled to be a viability (proportion of cells surviving) or a tumor volume (with some transformation), and 𝔇 is the dose region. Without loss of generality, we assume that 𝔇 = Cs = [0, 1]s in this paper. Using the functional ANOVA decomposition (see, Sobol’, 2001), the dose-response y(x) has the following unique decomposition,
| (2) |
where g0 = ∫Cs y (x)dx is the overall mean of y(x), and
| (3) |
| (4) |
Eq.(3) implies that the terms on the right-hand side of Eq.(2) are centered, whereas Eq.(4) implies that the terms on the right-hand side of Eq.(2) are mutually orthogonal. Furthermore, if we denote and DI = ∫Cs [gI(xI)]2dx for I ⊂ {1, …, s}, then due to Eqs.(3) and (4) it follows
| (5) |
Therefore, the influence of gI on y(x) can be measured by the ratio SI = DI / D, which is called the global sensitivity index and satisfies
| (6) |
The variances D and DI’s and, hence, the global sensitivity indices can be approximated by the quasi Monte Carlo method (Fang, Li and Sudijianto 2006).
The global sensitivity indices are often used to rank the importance of the gI(xI)’s appearing on the right-hand side of Eq.(2). The larger the index SI is, the more significant the effect of gI(xI) in the dose-response is. Thus, the functional structure of y(x) can be studied by calculating the indices. Since there are 2s terms on the right-hand side of Eq.(2), the estimation of the corresponding coefficients of those terms will not be possible, with limited sample size and/or wrong design settings. Recently, Fang et al. (2016) proposed a novel procedure to identify the most significant gI(xI)’s by utilizing data from experiments of single drugs (and a few combinations) and existing signaling network knowledge. The simulation studies showed that most contributions of single drugs and drug-interactions in the dose-response yielding a total of global sensitivity indices over 85%, are consistent with those from the true dose-response. Denote the vector of the dominating terms (e.g., those terms with their total global sensitivity indices more than 80%) by z(x) = [1, z1(x), …, zp(x)]⊤, where 1 corresponds to the overall mean and each of the functions zi corresponds to some gI, and the corresponding vector of regression coefficients is denoted by θ = (θ0, θ1, …, θp)⊤. Then the dose-response Eq.(1) becomes as
| (7) |
where f(x) is an unknown function and its global sensitivity index should be less than 20%. Since gI(xI) is determined by integrating y(x) with respect to some specific coordinates (see, Santner, Williams and Notz 2003, pages 193–194; Fang, Li and Sudjianto 2006, pages 193–194), it typically has no closed form representation. As a result, a reduced form needs to be specified for the corresponding zi(x). Throughout this paper zi(x) is taken to be the product of the centered variables involved to represent the corresponding drug interaction. The purpose of variable centralization is to make Eqs.(3) and (4) being satisfied among zi(x)’s and it will not change the meanings of zi(x)’s. In this case, f(x) is interpreted as the effects that cannot be captured by the zi(x)’s. Below is a simple illustration.
Example 1
Suppose that s = 3 and y(x) with x = (x1, x2, x3) is the in silico model describing the does-effects on the response. Then by the functional ANOVA one can obtain that
where each gI(xI) is uniquely determined by integrating y(x) with respect to some specific coordinates (please see, Santner, Williams and Notz 2003, pages 193–194; Fang, Li and Sudjianto 2006, pages 193–194, for details). Furthermore, if the sensitivity indices of g1(x1), g12(x1, x2) and g123(x1, x2, x3) are the largest three and their total sensitivity indices is more that 80%, y(x) is then re-written as
where f(x) is interpreted as the effects that cannot be captured by z1(x) = (x1 − 0.5), z2(x) = (x1 − 0.5)(x2 − 0.5) and z3(x) = (x1 − 0.5)(x2 − 0.5)(x3 − 0.5). It is easy to check that Eqs.(3) and (4) are satisfied among z1(x), z2(x) and z3(x).
As will be seen in the next section, Eq.(7) is served as the model basis for the combination experiments. Notice that according to the functional structure obtained from functional ANOVA, the function f(x) should satisfy
| (8) |
The orthogonality requirement in (8) makes many conventional nonparametric methods such as spline technique and multivariate kernel smoothing not convenient to use. In fact, another way of thinking about the orthogonality is to use it to guarantee the identifiability of the regression parameter θ (Wiens 1991; Tan, Fang and Tian 2009). Finding a function that is orthogonal to each of the regression functions, however, may be too restricted. Our take is that a function that can address the identifiability problem is more general than the one that is exactly orthogonal to the regression functions.
3. Experimental Design
If the interest is the estimation of regression coefficients, the D-optimal design (Wu and Hamada, 2009) and Bayesian D-optimal design (Chaloner and Verdinelli, 1995) may be useful. Since the purpose of a drug combination study is to discover the promising dose-level combinations among the agents (e.g., identify the synergistic dose region), a prediction-based design appears to be more desirable. In this section, a maximum entropy design is proposed for the combination experiments.
Let 𝒳 = {x1, …, xk} be the candidate set of design points in the experimental domain, e.g., 𝒳 is typically chosen to be a set of lattice points over the experimental domain. The aim is to choose n points (n ≪ k) from 𝒳 as the experimental points such that the prediction variability at un-experimental points, conditionally on the experimental points, is minimized. Based on Eq.(7), the dose-response can be formulated as
| (9) |
where Yj(xi) is the response value of the jth replication at the point xi, is the measurement error and ni is the number of replications at xi. The unknown function f(x) is modeled as a Gaussian random function with zero-mean and global covariance matrix . In other words, F𝒳 = [f(x1), …, f(xk)]⊤ is regarded as a realization of f(x). Similarly, a Gaussian prior is placed on the regression parameters, i.e., . Generally, we need the following assumptions.
Assumption 1: and for i = 1, …, k, j = 1, …, ni.
Assumption 2: zi(x) is the product of the centered variables involved, i = 1, …, p.
Assumption 3: The distributions of θ, F𝒳 and εij’s are independent.
The above assumptions allow the experimenter to write down the model as follows
| (10) |
where W = diag{n1, …, nk} is a diagonal matrix defining the replications on each of the candidate design points. In applications, the prior knowledge regarding which candidate design point is more important is typically unavailable, setting the same number of replications for each candidate design point, say n1 = ⋯ nk = m, is a fair practice. The number m is called hereafter as the number of replications for simplicity and its value may be determined by knowledge about the run-to-run variation. For example, if the variation among the animals is known to be substantial, the number of replications may need to be a relatively large one. It is worthwhile to note that the model in (10) is defined at all candidate design points, i.e., no matter whether the point xi is actually selected as the design point or not, a number of replications is assigned to it before the experiment starts.
3.1 Design Criterion
In this section a design criterion is proposed under the special case that the model parameters and are known. This setting allows us to demonstrate why the proposed design criterion is desirable without cluttering the discussion with estimation issues, which are resolved in Section 3.2. Without loss of generality, let e be a n-run experiment selected from 𝒳 = {x1, …, xk}, i.e., e has n distinct support points selected from 𝒳. Denote Ye as the vector of response values at e, Yē as the vector of response values at ē = 𝒳 − e. In other words, e is the set of experimental points whereas ē is the set of un-experimental points such that e ∪ ē = 𝒳 and e ∩ ē = ∅. Let pZ(·) be the probability density function of the random vector Z, the entropy of Z is then defined by
Entropy is a measure of unpredictability of a random vector, i.e., the larger the value of Ent(Z), the more uniform the distribution of the random vector Z—which in turns implies that the more unpredictable Z is likely to be (Shewry and Wynn 1987). The standard formula from information theory suggests that (cf., Lindley, 1956)
| (11) |
where Y𝒳 = (Ye, Yē) and the expectation is with respect to the marginal distribution of Ye. Obviously, it is desirable for a combination experiment to minimize the second term on the right-hand side of Eq.(11) because this term represents the average prediction variability of the unsampled vector given the experimental design. By the model in (10), Y𝒳 is a k-dimensional Gaussian vector with mean and covariance matrix being
respectively. Also, for a Gaussian random vector Γ ~ Nn(μΓ, ΣΓ) one can verify
| (12) |
which implies that Ent(Y𝒳) is a constant. Therefore, minimizing the value of EYe{Ent(Yē|Ye)} is equivalent to maximizing the value of Ent(Ye). The optimal design, denoted by e*, obtained by solving the following optimization problem
| (13) |
is referred to as the maximum entropy design in the literature (Santner, Williams and Notz 2003; Fang, Li and Sudijianto 2006). That is, by using the experimental design obtained from Eq.(13), the average prediction variability at un-experimental design points is minimized.
Further denoting and . Then, by the model in (10) Ye is a n-dimensional Gaussian vector with mean and covariance matrix being
respectively, where is a submatrix of , determined by the experiment e, and We is diagonal matrix also determined by e. According to Eqs. (12) and (13), the proposed design criterion is to find a design e* such that
| (14) |
It is easy to see that the maximum entropy design criterion only depends on the experimental design points. This feature makes it convenient to use. In contrast, conventional prediction-based criteria, such as c-optimality, E-optimality, G-optimality, Q-optimality, I-optimality and their Bayesian versions, not only depend on the experimental design points but also on the points to be predicted. Consequently, their closed form representations are usually not easy to obtain for high dimensional cases or only target some very special points to be predicted. It shall be pointed out that only exact designs are considered here because ni’s (they are set to be the same in this paper) are required to be integer-valued for drug combination experiments. Continuous designs, which relax the requirement for ni’s to be integer-valued and may regard any probability measure as a design, are beyond the scope of this paper and readers are referred to Kiefer (1959) and Fang, Liu and Zhou (2011) for detailed treatments of this topic.
3.2 Parameter Estimation
The maximum entropy design criterion (14) is relative to the variance ratios and the correlation matrix of the random function . As mentioned in Section 2, the total global sensitivity indices of the dominating terms is usually more than 80%, whereas the global sensitivity index of f(x) is less than 20%. This suggests that the variance ratio . As is shown at the end of this section, the value of the ratio is also convenient to specify. Then, the primary matter is to estimate the correlation matrix .
The idea to estimate is to use the single drug dose-effect curves which are estimated from the experimental data of single drugs. Let the covariance function between f(xi) and f(xj) be defined by , where xi and xj are two design points and R(xi, xj) is the correlation function. The most commonly-used correlation function is the power exponential correlation (Cressie, 1993; Santner, Williams and Notes, 2003),
| (15) |
where xiu is the uth element of xi, ϕu > 0 and 0 < pu ≤ 2, u = 1, …, s. In order to alleviate the computational complexity and make the design easier to interpret, the value of pu is here considered to be fixed and given as 2, and ϕ1 = ⋯ = ϕs = ϕ is specified. The correlation in Eq.(15) is hence defined by the parameter ϕ.
Denote the set of design points by , where each has at least one component not equivalent to 0, and the vector of observed response values by . Using the Gaussian assumption on f(x), the log-likelihood is proportional to
| (16) |
where and . Given ϕ, the maximum likelihood estimator (MLE) for θ is given by
| (17) |
and the MLE for is given by
| (18) |
Substituting Eqs.(17) and (18) into Eq.(16), one can obtain that the maximum of the likelihood over θ and is
which depends on ϕ alone. Thus the MLE of ϕ is given by
| (19) |
where is given by (18). Hence, the correlation in the design criterion (14) can be estimated by the parameter ϕ̂ obtained from Eq.(19). At this point, the value of can be readily specified: on one hand, the value of is already estimated by Eq.(18); on the other hand, the measurement error variance can be estimated by the pooled variance from the single drug experimental data (Tan et al., 2003, 2009; Fang et al., 2008, 2015).
4. Computational Algorithms
According to the maximum entropy design criterion in (14), we propose a computational algorithm for design construction in this section. An algorithm for sample size determination is also given. As noted in Section 3, the number of replications m is often determined by knowledge about the run-to-run variation. Therefore, the determination of the sample size essentially relies upon the determination of the number of design points.
4.1 Computational Algorithm for Design Construction
Recall that 𝒳 = {x1, …, xk} is the candidate set of the design points. In order to cover the dose region 𝒞s thoroughly, the lattice method is often used to construct 𝒳 (Fang, Li and Sudijianto 2006). That is, q equidistant dose-levels are first selected for each single drug, then all the level-combinations among the single drugs constitute 𝒳. The n-run maximum entropy design e* is selected from 𝒳 by solving the optimization problem (14). Typically, q is not a small number so n ≪ k = qs, which means that candidate-set dependent algorithms such as row exchange algorithm may be time-consuming. We use the candidate-set free coordinate exchange algorithm, as described by Meyer and Nachtsheim (1995), to address the optimization problem (14).
At the beginning, a n × s starting design is randomly generated in the dose region Cs. That is, each entry of the starting design is randomly generated from the interval (0, 1). The starting design is improved by sequentially updating its entries. For each entry, the algorithm evaluates the effect of changing that entry to the q levels. If the objective function in (14) improves for at least one of these operations, then the current entry is updated with the level that results in the maximum entropy. After the first pass through each entry in the design matrix, the algorithm takes a second pass. If any entry of the design changes in the second pass, then the algorithm performs another pass. This process continues until there are no changes in any pass through the design or when a maximum iteration limit is reached. For practical purpose, a step-by-step algorithm for design construction is provided in Table 1.
Table 1.
Algorithm 1 [Design Construction]
| Initialize an n × s matrix D with each entry generated from (0, 1), a large positive integer T (e.g., T = 1000), the number of dose-levels q and t = 1. | |
| Denote the entries of D by d(1), …, d(n × s) using a row-by-row order, and for simplicity, denote D = {d(1), …, d(n × s)}. | |
| 1: | while t ≤ T do |
| 2: | for (i in 1 : n × s) |
| 3: | for (j in 0 : : 1) |
| 4: | D* = {d(1), …, d(i − 1), j, d(i + 1), …, d(n × s)}; |
| 5: | if Ent(D*) > Ent(D) |
| 6: | D = D*; |
| 7: | end if |
| 8: | end for |
| 9: | end for |
| 10: | t = t + 1; |
| 11: | end while |
| 12: | Output D as the optimal design. |
The resulting design D from Table 1 may be local optimal with respect to the maximum entropy criterion, so multiple random starting designs may be used.
It is noteworthy that the number of replications, irrespective of whether it is the same or not for each candidate design point, needs to be preassigned for Algorithm 1. This is because if the number of replications changes, so dose the value of Ent(Y𝒳) that appears on the left-hand side of Eq.(11). As discussed in Section 3.1, Ent(Y𝒳) needs to be kept as a constant to justify the proposed maximum entropy design. Preassigning a number of replications at each candidate design point is the limitation of the proposed design. Also, an approach to verify whether the resulting design is optimal with respect to the maximum entropy criterion may need further study. For instance, a tight upper bound may exist for the entropy value given the number of replications. If one can find a tight upper bound of the entropy over the design region, this upper bound can be served as a benchmark for construction of the maximum entropy design and may speed up the searching process.
4.2 Computational Algorithm for Sample Size Determination
For any n, the maximum entropy design can be constructed via Algorithm 1. However, an exact value of n shall be determined before the combination experiments. In this section, we first propose a criterion for sample size determination. Similar to the practice used in Section 3.1, it is tentatively assumed that parameters θ, ϕ, and are known. Such a practice would facilitate the derivation of the sample size criterion without cluttering the discussion with estimation issues. It turns out that only the parameters ϕ, and need to be estimated, which is the same requirement for the design criterion in (14).
Consider the estimation of Y (x0) = z(x0)⊤θ + f(x0) at any x0 ∈ ē. By Assumptions 1–3 and the model in (10), follows a Gaussian distribution with mean and covariance matrix being
respectively, where is the experiment and . It is known that the MSE-optimal predictor of Y (x0), conditional on the experiment e, is given by E [Y (x0)|Ye] (see, for example, page 40 of Shao (2003)). Let Ŷe(x0) = E [Y (x0)|Ye], then according to the property of multivariate normal distribution (see, for example, page 248 of Fang, Li and Sudijianto (2006)) the closed form expression of Ŷe(x0) is given by
| (20) |
and the MSE of Ŷe(x0) is
The detailed derivation of the MSE is provided in Web Appendix A for interested readers. Define the relative MSE (RMSE) as to be
and the average RMSE (ARMSE) as
It is easy to see that 0 < ARMSE(e; n) < 1, thus our idea for sample size determination is to find the smallest number of design points, say n*, such that
where 0 < δ < 1 is a user-specified targeted precision, en is the n-run maximum entropy design constructed by Algorithm 1. The ARMSE depends on the parameters ϕ, and . As discussed in Section 3.2, ϕ and can be respectively estimated through Eqs.(19) and (18), whereas the measurement error variance can be estimated by the pooled variance from the single drug experimental data. Once ϕ, and are estimated from the previous studies, the empirical MSE-optimal predictor can be obtained by plugging θ̂(ϕ) in Eq.(17) or, alternatively, the posterior mean E[θ|Ye] into Eq.(20). Such a predictor is more general than the regression predictor z(x0)⊤θ̂ (ϕ) (or z(x0)⊤E[θ|Ye]) when the random function f(x) is presented in the dose-response model, as it not only accounts for the regression predictor but also the “correction” caused by the random function f(x).
The computational algorithm we use for sample size determination is a root-finding algorithm, which proceeds as follows. For given m, let nmin and nmax be respectively the minimum and maximum numbers of design points that can be afforded. First of all, calculate ARMSE(emin; nmin), where emin is an nmin-run maximum entropy design. If ARMSE(emin; nmin) ≤ δ, output n = nmin; otherwise increase nmin by Δ (e.g., Δ = 10) and calculate ARMSE(e1; nmin+Δ), where e1 is an (nmin + Δ)-run maximum entropy design. If ARMSE(e1; nmin + Δ) ≤ δ, output n = nmin + Δ; otherwise continue increasing the number of design points until the ARMSE no larger than δ or nmax is reached.
5. Numerical Illustration
In this section, we revisit one numerical experiment of Fang et al. (2016) to demonstrate how to construct the proposed maximum entropy design for a given multi-drug combination study and compare its efficiency with some other conventional designs. We use the example of Fang et al. (2016) as illustration because functional ANOVA, which is introduced in Section 2, had been applied to their in silico model. Based on our experience, the establishment of an in silico model upon a signaling network requires some carefully selected combination data and is computationally demanding. To save the efforts for data collection and computation time, the sensitivity indices calculated by Fang et al. (2016) are directly presented here.
In the numerical experiment of Fang et al. (2016), 10 single drugs, denoted by A1, …, A10, were considered and their single drug curves are provided in Web Appendix B. Using the single drug information plus some combination data, Fang et al. (2016) established an in silico model based on the apoptosis signaling network (hsa04210). Then, functional ANOVA was applied to this in silico model. Their results showed that A1, A1A2A3, A1A2A3A4A5 and A1A2A3A4A5A6A7 are significant single drug effect and interaction effects whose total sensitivity indices is about 80%. As a result, z(x) = (x1 − 0.5, (x1 − 0.5)(x2 − 0.5)(x3 − 0.5), (x1 − 0.5)(x2 − 0.5)(x3 − 0.5)(x4 − 0.5)(x5 − 0.5), (x1 − 0.5)(x2 − 0.5)(x3 − 0.5)(x4 − 0.5)(x5 − 0.5)(x6 − 0.5)(x7 − 0.5)) is taken for this example.
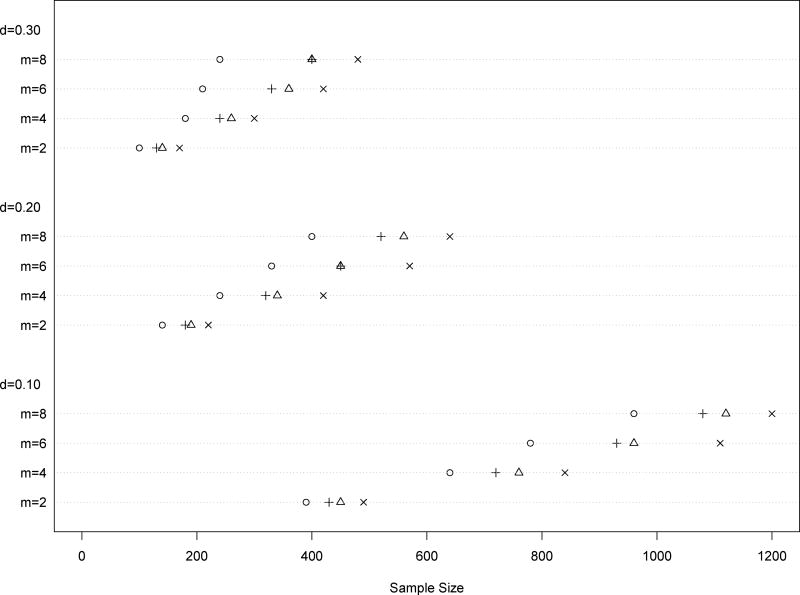
To estimate the correlation matrix , 8 equidistant dose-levels are selected from the interval [0.01, 0.99] for each single drug curve. The data generated from the single drug curves are provided in Web Table 1. Using the data in Web Table 1, the maximum likelihood estimates of the correlation parameter and the random function variance are ϕ̂ = 1.5515 and , respectively. In addition, the measurement error variance (pooled variance) is estimated to be . Based on these estimates, one can use the design criterion (14) (with ) and the computational algorithms described in Section 4 to construct the maximum entropy designs and determine the corresponding sample sizes. In particular, three values of δ = 0.30, 0.20, 0.10 and four values of m = 2, 4, 6, 8 are examined. Under each tuple of (δ, m), the sample sizes are plotted in Figure 1 with mark “◦”. As expected, for given number of replications, the sample size increases as δ becomes small. In addition, for given δ the more replications are, the more is the sample size. We stress that for different drug combination studies, the sample sizes and the corresponding experimental designs may vary significantly. However, one can always follow our approach to determine the sample sizes and the corresponding experimental designs and, then, an appropriate tuple of (δ, m) may be selected for the combination experiments. For instance, if the sample size could not be more than 300 in a study, the tuple (δ, m) = (0.20, 4) might be selected because this choice yields the highest precision with the largest sample size ≤ 300.
Figure 1.
Sample sizes of the compared designs: “◦”–the proposed maximum entropy design; “+”–the Bayesian D-optimal design; “△”–the D-optimal design; “×”–the design under criterion (21). To facilitate the comparison, Δ = 5, nmin = 50 and nmax = 1500 are used in the computational algorithm for sample size determination.
To assess the effectiveness of using the design criterion (14), consider another design criterion below
| (21) |
The above criterion represents the case where no regression terms are identified for the dose-response. Based on criterion (21) and the estimates previously obtained, the sample sizes under various tuples of (δ, m) are plotted in Figure 1 with mark “×”. By comparing the sample sizes marked with “◦” and those marked with “×”, it is easy to see that for any given (δ, m) the sample size determined from criterion (21) is considerably larger than that determined from criterion (14). This indicates that by incorporating significant regression terms into the design criterion, the sample size for achieving a given model accuracy can be significantly reduced. Furthermore, the sample sizes of the D-optimal design (marked with “△”), which maximizes , and the Bayesian D-optimal design (marked with “+”), which maximizes , are also plotted in Figure 1 for comparison purpose. In summary, the Bayesian D-optimal design is a bit more efficient than the D-optimal design and both of them are clearly more efficient than the design under criterion (21). However, the proposed maximum entropy design performs the best across all tuples of (δ, m).
From the simulation study, we have
-
To give the experimenters an impression that how the design points distribute over the design region, bivariate projections of the compared designs with (n, m) = (50, 2) are presented in Figures 2 and 3. The bivariate projections of the design under criterion (21) (see Figure 2 (a)) look similar for any pair of variables. This is due to the isotropy (i,e., ϕ1 = ⋯ = ϕs = ϕ) specified for the correlation function (15). The bivariate projections of the Bayesian D-optimal design (see Figure 2 (b)) show that more and more no-extreme levels tends to emerge as the variable subscript increases. This indicates that the less frequent a variable appears in the regression functions the more no-extreme levels it tends to take. The bivariate projections of the proposed maximum entropy design (see Figure 2 (c)) can be viewed as a compromise between Figures 2 (a) and (b) in the sense that the less frequent a variable appears in the regression functions the more no-extreme levels it tends to take, but the design still tries to keep the projections similar especially for the first a few variables. In fact, by using the standard formula det(A + BC) = det(A) det(I + CA−1B) one can obtain that
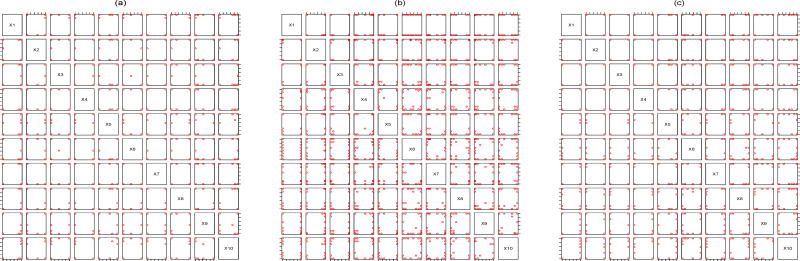
(22) This means that the criterion value of the proposed maximum entropy design is the product of the criterion value in (21) and that of the Bayesian D-optimal design. As a result, Figure 2 (c) looks like a compromise between Figures 2 (a) and (b). Finally, the D-optimal design (see Figure 3 (a)) pushes the variables appearing in the regression functions towards their extreme levels while allows the remaining variables to take many non-extreme levels. The driver for the higher number of levels on drugs 8, 9 and 10 is that the regression functions currently do not include drugs 8, 9 and 10, such that all information on them may only be acquired via the correlation function of f(x). The bivariate projections under other values of (n, m) are similar so the details are omitted.
A sensitivity analysis for the variance ratio may be needed if its value is suspicious not to be around 4. For large Eq.(22) indicates that the design criterion value behaves like which is D-optimality, whereas a small means that the design criterion value behaves like that in Eq.(21). Figures 3 (b) and (c) present the bivariate projections of the maximum entropy design with and (50, 2, 100), respectively. It is not difficult to see that Figure 3 (b) is similar to Figure 2 (a) while Figure 3 (c) looks similar to Figure 3 (a). Although only two values are examined here, such a sensitivity analysis demonstrates that how the distribution of design points varies as the value of changes.
Increasing the number of replications may not significantly reduce the number of design points. For example, the sample size of m = 4 almost doubles that of m = 2. As pointed out by one referee, the number of required drugs and doses to estimate the regression parameters is relatively small and they will provide no information from the model on drugs 8, 9 and 10. Doubling the number of replications adds information to the model. However, as the regression predictor will not forward much information to drugs 8, 9 and 10, the number of design points would not significantly decrease, as design points are still needed to cover much of the design region for the modeling via the correlation function of f(x).
Figure 2.
(a): Bivariate projections of the design under criterion (21) with (n, m) = (50, 2). (b): Bivariate projections of the Bayesian D-optimal design with (n, m) = (50, 2). (c): Bivariate projections of the maximum entropy design with (n, m) = (50, 2).
Figure 3.
(a): Bivariate projections of the D-optimal design with (n, m) = (50, 2). (b): Bivariate projections of the maximum entropy design with . (c): Bivariate projections of the maximum entropy design with .
6. Concluding Remarks and Discussions
The proposed novel combination of functional ANOVA with maximum entropy designs utilizes both the biological pathway and single drug data for the selection of optimal drug combinations in multi-drug combination studies. The proposed study designs for drug-combinations provide a basis for future developments on statistical methods and experimental designs for complex multi-drug dose-finding problems. The simulation studies showed that the proposed experimental design (dose-level selection and sample size determination) is efficient for combination studies and statistical procedures to fit the high dimensional dose-response surface.
7. Supplementary Materials
Web Appendices A, B and Web Table 1 referenced in Sections 4–5 are available with this paper at Biometrics website on Wiley Online Library.
Supplementary Material
Acknowledgments
The authors thank the editor, the associate editor and two reviewers for their constructive comments which improved the manuscript significantly. Huang’s research was completed at Georgetown University where he was a post-doctoral research fellow. This work was partially supported by the National Cancer Institute (NCI) grant R01CA164717 and the National Natural Science Foundation of China (Grant No. 11701109).
References
- Chen HX, Dancey JE. Combinations of Molecular-Targeted Therapies: Opportunities and Challenges. In: Kaufman HL, Wadler S, Antman K, editors. Molecular Targeting in Oncology. Totowa, New Jersey: Humana Press; 2008. pp. 693–705. [Google Scholar]
- Cressie NAC. Statistics for Spatial DATA. New York: Wiley; 1993. [Google Scholar]
- Chaloner K, Verdinelli I. Bayesian experimental design: a review. Statistical Science. 1995;10:273–304. [Google Scholar]
- Fang HB, Huang H, Clarke R, Tan M. Predicting multi-drug inhibition interactions based on signaling networks and single drug dose-response information. Journal of Computational Systems Biology. 2016;2:101. [Google Scholar]
- Fang HB, Ross DD, Sausville E, Tan M. Experimental design and interaction analysis of combination studies of drugs with log-linear dose responses. Statistics in Medicine. 2008;27:3071–3083. doi: 10.1002/sim.3204. [DOI] [PubMed] [Google Scholar]
- Fang HB, Chen XR, Pei XY, Grant S, Tan M. Experimental design and statistical analysis for three-drug combination studies. Statistical Methods in Medical Research. 2017;26:1261–1280. doi: 10.1177/0962280215574320. [DOI] [PubMed] [Google Scholar]
- Fang KT, Li R, Sudjianto A. Design and Modeling for Computer Experiments. New York: Chapman & Hall/CRC; 2006. [Google Scholar]
- Fang KT, Liu MQ, Zhou YD. Design and Modeling of Experiments. Beijing: Higher Education Press; 2011. [Google Scholar]
- Fitzgerald JB, Schoeberl B, Nielsen UB, Sorger PK. Systems biology and combination therapy in the quest for clinical efficacy. Nature Chemical Biology. 2006;2:458–466. doi: 10.1038/nchembio817. [DOI] [PubMed] [Google Scholar]
- Hopkins AL. Network pharmacology: the next paradigm in drug discovery. Nature Chemical Biology. 2008;4:682–690. doi: 10.1038/nchembio.118. [DOI] [PubMed] [Google Scholar]
- Lindley DV. On a measure of information provided by an experiment. Annals of Mathematical Statistics. 1956;27:986–1005. [Google Scholar]
- Jones S, et al. Core signaling pathways in human pancreatic cancers revealed by global genomic analysis. Science. 2008;321:1801–1806. doi: 10.1126/science.1164368. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kiefer J. Optimum experimental designs (with discussion) Journal of the Royal Statistical Society B. 1959;21:272–319. [Google Scholar]
- Kong M, Lee JJ. A generalized response surface model with varying relative potency for assessing drug interaction. Biometrics. 2006;62:986–995. doi: 10.1111/j.1541-0420.2006.00579.x. [DOI] [PubMed] [Google Scholar]
- Meyer RK, Nachisheim CJ. The coordinate-exchange algorithm for constructing exact optimal experimental designs. Technometrics. 1995;37:60–69. [Google Scholar]
- Parsons DW, et al. An integrated genomic analysis of human glioblastoma multiforme. Science. 2008;321:1807–1812. doi: 10.1126/science.1164382. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Santner TJ, Williams BJ, Notz WI. The Design and Analysis of Computer Experiments. New York: Springer; 2003. [Google Scholar]
- Shao J. Mathematical Statistics. 2. New York: Springer; 2003. [Google Scholar]
- Shewry MC, Wynn HP. Maximum entropy sampling. Journal of Applied Statistics. 1987;14:165–170. [Google Scholar]
- Sobol’ IM. Global sensitivity indices for nonlinear mathematical models and their Monte Carlo estimates. Mathematics and Computers in Simulation. 2001;55:271–280. [Google Scholar]
- Tan M, Fang HB, Huang H, Yang Y. Design and statistical analysis of multidrug combinations in preclinical studies and clinical trials. In: Lin J, Wang B, Hu X, Chen K, Liu R, editors. Statistical Applications from Clinical Trials and Personalized Medicine to Finance and Business Analytics. Springer; New York & Switzerland: 2016. pp. 215–234. [Google Scholar]
- Tan M, Fang HB, Tian GL, Houghton PJ. Experimental design and sample size determination for testing synergy in drug combination studies based on uniform measures. Statistics in Medicine. 2003;22:2091–2100. doi: 10.1002/sim.1467. [DOI] [PubMed] [Google Scholar]
- Tan M, Fang HB, Tian GL. Dose and sample size determination for multidrug combination studies. Statistics in Biopharmaceutical Research. 2009;1:301–316. [Google Scholar]
- Wiens DP. Designs for approximately linear regression: two optimality properties of uniform designs. Statistics & Probability letters. 1991;12:217–221. [Google Scholar]
- Wu CFJ, Hamada M. Experiments: Planning, Analysis, and Optimization. 2. New York: Wiley; 2009. [Google Scholar]
- Xavier JB, Sander C. Principle of System Balance for Drug Interactions. The New England Journal of Medicine. 2010;362:1339–1340. doi: 10.1056/NEJMcibr1001270. [DOI] [PubMed] [Google Scholar]
- Yang Y, Fang HB, Roy A, Tan M. An adaptive Bayesian dose finding approach for drug combinations with drug-drug interaction. Statistics and Its interface. 2017 (In press) [Google Scholar]
- Yin G, Yuan Y. A latent contingency table approach to dose finding for combinations of two agents. Biometrics. 2009a;65:866–875. doi: 10.1111/j.1541-0420.2008.01119.x. [DOI] [PubMed] [Google Scholar]
- Yin G, Yuan Y. Bayesian dose finding in oncology for drug combinations by copula regression. Journal of the Royal Statistical Society: Series C (Applied Statistics) 2009b;58:211–224. [Google Scholar]
- Yuan Y, Yin G. Sequential continual reassessment method for two-dimensional dose finding. Statistics in medicine. 2008;27:5664–5678. doi: 10.1002/sim.3372. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.