Estimation and Evaluation of Linear Individualized Treatment Rules to Guarantee Performance

SUMMARY

In clinical practice, an informative and practically useful treatment rule should be simple and transparent. However, because simple rules are likely to be far from optimal, effective methods to construct such rules must guarantee performance, in terms of yielding the best clinical outcome (highest reward) among the class of simple rules under consideration. Furthermore, it is important to evaluate the benefit of the derived rules on the whole sample and in pre-specified subgroups (e.g., vulnerable patients). To achieve both goals, we propose a robust machine learning method to estimate a linear treatment rule that is guaranteed to achieve optimal reward among the class of all linear rules. We then develop a diagnostic measure and inference procedure to evaluate the benefit of the obtained rule and compare it with the rules estimated by other methods. We provide theoretical justification for the proposed method and its inference procedure, and we demonstrate via simulations its superior performance when compared to existing methods. Lastly, we apply the method to the Sequenced Treatment Alternatives to Relieve Depression (STAR*D) trial on major depressive disorder and show that the estimated optimal linear rule provides a large benefit for mildly depressed and severely depressed patients but manifests a lack-of-fit for moderately depressed patients.

1. Introduction

Heterogeneity in patient response to treatment is a long-recognized challenge in the clinical community. For example, in adults affected by major depression, only around 30% of patients achieve remission with a single acute phase of treatment (Trivedi et al., 2006; Rush et al., 2004); the remaining 70% of patients require augmentation of the current treatment or a switch to a new treatment. Thus, a universal strategy that treats all patients by the same treatment is inadequate, and individualized treatment strategies are required to improve response in individual patients. In this regard, rapid advances in technologies for collecting patient-level data have made it possible to tailor treatments to individual patients based on specific characteristics, thereby enabling the new paradigm of personalized medicine.

Statistical methods have been proposed to estimate optimal individualized treatment rules (ITR) (Lavori and Dawson, 2004) using predictive and prescriptive clinical variables that manifest quantitative and qualitative treatment interactions, respectively (Carini et al., 2014; Gunter et al., 2011). Q-learning (Watkins, 1989; Qian and Murphy, 2011) and A-learning (Murphy, 2003; Blatt et al., 2004) are proposed to identify an optimal ITR. Q-learning estimates an ITR by directly modelling the Q-function. A-learning only requires posited models for contrast functions and uses a doubly robust estimating equation to estimate the contrast functions. This makes A-learning more robust to model misspecification than Q-learning and provides a consistent estimation of an ITR (Schulte et al., 2014). Other proposed approaches include semiparametric methods and machine learning methods (Zhang et al., 2012; Foster et al., 2011; Zhao et al., 2012; Chakraborty and Moodie, 2013). For example, the virtual twins approach (Foster et al., 2011) uses tree-based estimators to identify subgroups of patients who show larger than expected treatment effects. Zhang et al. (2012, 2013) estimated the optimal ITR by directly maximizing the value function over a specified parametric class of treatment rules through augmented inverse probability weighting. In contrast, Zhao et al. (2012) proposed outcome weighted learning (O-learning), which utilizes weighted support vector machine to maximize the value function. More recently, Huang and Fong (2014) proposed a robust machine learning method to select the ITR that minimizes a total burden score. Interactive Q-learning (Laber et al., 2014) models two ordinary mean-variance functions instead of modeling the predicted future optimal outcomes. Fan et al. (2016) proposed a concordance function for prescribing treatment, where a patient is more likely to be assigned to a treatment than another patient if s/he has a greater benefit than the other patient.

In clinical practice, simple treatment rules such as linear rules, are preferred due to their transparency and convenience for interpretation. However, when only linear rules are in consideration, many existing methods including semiparametric models and some machine learning methods may not yield a rule with optimal performance, because they focus on optimization of a surrogate objective function of treatment benefit. Using surrogate objective functions may only guarantee the optimality when there is no restriction on the functional form of the treatment rules. For example, with O-learning, the objective function is a weighted hinge-loss, which yields the optimal rule among nonparametric rules, but may not be optimal when the candidate rules are restricted to the linear form. Therefore, learning algorithms are desired to derive a treatment rule with guaranteed performance when constraints are placed on the class of candidate rules.

An additional consideration is the need to evaluate, through diagnostics, any approach for rule estimation. However, less emphasis has been placed on the evaluation of the estimated ITR in the context of personalized medicine. Residual plots were used to evaluate model fit for G-estimation (Rich et al., 2010) and Q-learning (Ertefaie et al., 2016). In the recent work by Wallace et al. (2016), a dynamic treatment regime (DTR) is estimated by G-estimation and double robustness is exploited for model diagnosis. How to evaluate the optimality of an ITR in general remains an open research question.

The purpose of this paper is two-fold: we first develop a general approach to identify a linear ITR with guaranteed performance; we then propose a diagnostic method to evaluate performance of any derived ITR including the proposed one. Our two-stage approach separates the estimation of the ITR from its evaluation and the sample used in each stage. Specifically, in the first stage, we propose ramp-loss-based (McAllester and Keshet, 2011; Huang and Fong, 2014) learning for the estimation and we show that this approach guarantees the derived linear ITR to be asymptotically optimal within the class of all linear rules. We refer our method as Asymptotically Best Linear O-learning, ABLO. For the second stage, in practice, it is infeasible to expect that an ITR that benefits each individual can be identified due to the unknown treatment mechanism and the likely omission of some prescriptive variables. Thus, we propose a practical solution to calibrate the average ITR effect in the population given the observed variables, or in pre-specified important subgroups (e.g., patients in most severe state). Specifically, to obtain an ITR evaluation criterion, we define the benefit of a candidate ITR as the average difference in the value function between those who follow the ITR and those who do not. We then use the ITR benefit as a diagnostic measure to evaluate its optimality. Our method exploits the fact that if an ITR is truly optimal for all individuals, then for any given patient subgroup, the average outcome for patients who are treated according to the ITR should be greater than for those who are not treated according to the ITR. On the contrary, if the average outcome of the ITR is worse for some patients who follow the ITR than for those who do not, then the ITR is not optimal on this subgroup.

Compared to the existing literature, two main contributions of this work are to propose a benefit function to calibrate an ITR, and a diagnostic procedure to evaluate optimality of a derived ITR, while most of the existing work focuses on the estimation of ITR/DTR. A third contribution is to prove asymptotic properties of ITR estimated under the ramp loss (Huang and Fong, 2014). Asymptotic results in the existing literature (e.g., Zhao et al., 2012) are obtained for the hinge loss. Due to these theoretical results, we can provide valid statistical inference procedure for testing optimality of an ITR using asymptotic normality.

In the remainder of this paper, we show that ABLO consistently estimates the ITR benefit for a class of candidate rules regardless of two potential pitfalls: 1) the consistency of benefit estimator is maintained even though the functional form of the rule is misspecified; 2) the rule does not include all prescriptive/tailoring variables and thus the true global optimal rule is not in the specified class. We further derive the asymptotic distribution for the proposed diagnostic measure. We conduct simulation studies to demonstrate finite sample performance and show advantages over existing machine learning methods. Lastly, we apply the method to the Sequenced Treatment Alternatives to Relieve Depression (STAR*D) trial on major depressive disorder (MDD), where substantial treatment response heterogeneity has been documented (Trivedi et al., 2006; Huynh and McIntyre, 2008). Our analyses estimate an optimal linear ITR, and we demonstrate a large benefit in mildly depressed and severely depressed patients but a lack-of-fit among moderately depressed patients.

2. Methodology

Let R denote a continuous variable measuring clinical response after treatment (e.g., reduction of depressive symptoms). Without loss of generality, assume a large value of R is desirable. Let X denote a vector of subject-specific baseline feature variables, and let A = 1 or A = −1 denote two alternative treatments being compared. Assume that we observe (A_i, X_i, R_i) for the ith subject in a two-arm randomized trial with randomization probability P(A_i = a|X_i = x) = π(a|x), for i = 1, …, n.

An ITR, denoted as $\mathcal{D}(\mathit{X})$, is a binary decision function that maps X into the treatment domain A = {−1, 1}. Let $P_{\mathcal{D}}$ denote the distribution of (A, X, R) in which $\mathcal{D}$ is used to assign treatments. The value function of $\mathcal{D}$ satisfies

$$V(\mathcal{D})=E^{\mathcal{D}}(R)={\displaystyle \int Rd{P}^{\mathcal{D}}={\displaystyle \int R\frac{d{P}^{\mathcal{D}}}{dP}}}=E\left\{\frac{RI(A=\mathcal{D}(\mathit{X}))}{\pi (A|\mathit{X})}\right\}.$$ (1)

In most applications, $\mathcal{D}(\mathit{X})$ is determined by the sign of a function, f(X), which is referred to as the ITR decision function. That is, $\mathcal{D}(\mathit{X})=\text{sign}(f(\mathit{X}))$. In general settings, $f\in ℱ$ can take any form, either a parametric function or a non-parametric function. To quantify the benefit of an ITR, a measure related to the value function is a natural choice. The mean difference is widely used to compare the average effect of two treatments. Analogously, we define the benefit function corresponding to an ITR as the difference in the value function between two complementary strategies: one that assigns treatments according to $\mathcal{D}(\mathit{X})$ and the other assigns according to the complementary rule $-\mathcal{D}(\mathit{X})$ for any given feature variables X. That is, the benefit function for $\mathcal{D}(\mathit{X})=\text{sign}(f(\mathit{X}))$ is

$$\delta (f(\mathit{X}))=E\left\{R|A=\text{sign}(f(\mathit{X})),\mathit{X}\right\}-E\left\{R|A=-\text{sign}(f(\mathit{X})),\mathit{X}\right\}.$$ (2)

2.1 Estimating Optimal Linear Treatment Rule

To obtain a practically useful and transparent ITR, we consider a class of linear ITR decision functions, denoted by $ℒ$, and estimate the optimal linear function $f_L^{\ast }\in ℒ$, that maximizes the value function (1) among this class. To this end, following the original idea of Liu et al. (2014), we note that maximizing $V(\mathcal{D})$ is equivalent to minimizing a residual-weighted misclassification error given as

$$E\left[|R-r(\mathit{X})|\frac{I\{A\text{sign}(R-r(\mathit{X}))\ne \mathcal{D}(\mathit{X})\}}{\pi (A|\mathit{X})}\right],$$

where r(X) is any function of X, taken as an approximation to the conditional mean of R given X. Thus, we aim to minimize the empirical version of the above quantity, given as

$$\frac{1}{n}{\displaystyle \sum _i\frac{|W_i|I(A_i{Z}_i\ne \mathcal{D}({\mathit{X}}_i))}{\pi (A_i|{\mathit{X}}_i)}}=\frac{1}{n}{\displaystyle \sum _i\frac{|W_i|I(A_i{Z}_{i}f({\mathit{X}}_i)<0)}{\pi (A_i|{\mathit{X}}_i)}}$$

for $f\in ℒ$, where $W_i=R_i-\hat{r}({\mathit{X}}_i)$, Z_i = sign(W_i), and $\hat{r}(\mathit{X})$ is obtained from a working model by regressing R_i on X_i (Liu et al., 2014).

The above optimization with zero-one loss is a non-deterministic polynomial-time hard (NP-hard) problem (Natarajan, 1995). To avoid this computational challenge, the zero-one loss was replaced by some convex surrogate loss in existing methods, for instance, the squared loss or hinge loss. Let f^∗ denote the global optimal decision function corresponding to the optimal treatment rule among any decision functions. That is, f^∗(X) = E(R|A = 1, X) − E(R|A = −1, X). When $ℒ$ consists of linear decision functions that are far from the global optimal rule such that $f^{\ast }\notin ℒ$, estimating optimal linear rule by minimizing the surrogate loss (e.g., hinge loss or squared loss) no longer guarantees that the induced value or benefit is maximized among the linear class.

In order to obtain the best linear ITR with guaranteed performance, we propose to use an authentic approximation loss that will converge to zero-one loss, referred to as the ramp loss (McAllester and Keshet, 2011; Huang and Fong, 2014), for value maximization. The ramp loss, as plotted in Figure A.1 in the Supplementary Material, has been used in the machine learning literature to provide a tight bound on the misclassification rate (McAllester and Keshet, 2011; Collobert et al., 2006). Mathematically, this function can be expressed as

$$h_s(u)=I(u\le -\frac{s}{2})-\frac{u-s}{2s}I(-\frac{s}{2}<u<\frac{s}{2})$$ (3)

where s is a tuning parameter to be chosen in a data-adaptive fashion. Clearly, when s converges to zero, the ramp loss function converges to the zero-one loss; thus, we expect that the estimated rule from this loss function should approximately maximize the value function among class $ℒ$.

Specifically, with the ramp loss (3), we propose to estimate the optimal linear ITR decision function, $f_L^{\ast }(\mathit{X})$, by minimizing the penalized weighted sum of ramp loss of a linear decision function f(X) = β₀ + X^T β,

$$L(f)=C{\displaystyle \sum _{i=1}^n\frac{|W_i|h_s(Z_i{A}_{i}f({\mathit{X}}_i))}{\pi (A_i|{\mathit{X}}_i)}}+\frac{1}{2}{\Vert \mathit{\beta }\Vert }^2,$$ (4)

where C is the cost parameter. Because the ramp loss is not convex, we solve the optimization by the difference of convex functions algorithm (DCA) (An et al., 1996). First, we express h_s(u) as the difference of two convex functions, $h_s(u)=h_{1,s}(u)-h_{2,s}(u)={(\frac{1}{2}-\frac{u}{s})}_{+}-{(-\frac{1}{2}-\frac{u}{s})}_{+}$, where function (x)₊ denotes the positive part of x. Let η_i denote Z_iA_if(X_i). With the DCA, starting from an initial value for η, the minimization in (4) can be carried out iteratively, and denote the solution as

$$\hat{\mathit{\beta }}=\text{agr}min{\displaystyle \sum _{i=1}^{n}C\frac{|W_i|\{h_{1,s}({\eta }_i)-{\hat{h}}_{2,s}({\eta }_i,{\eta }_i^0)\}}{\pi (A_i|{\mathit{X}}_i)}}+\frac{1}{2}{\Vert \mathit{\beta }\Vert }^2,$$ (5)

where ${\hat{h}}_{2,s}({\eta }_i,{\eta }_i^0)=h_{2,s}({\eta }_i^0)+h_{2,s}^{\prime }({\eta }_i^0){\eta }_i$, and $h_{2,s}^{\prime }(u)=-I(u/s<-1/2)/s$. The iteration stops when the change in the objective function is less than a pre-specified threshold. Detailed steps in estimating β are provided in Section A1 of the Supplementary Materials.

We denote the optimal linear decision function obtained by the above procedure as $\widehat{f_L^{\ast }}(\mathit{X})={\hat{\beta }}_0+{\mathit{X}}^T\hat{\mathit{\beta }}$ and denote the optimal ITR as $\text{sign}(\widehat{f_L^{\ast }}(\mathit{X}))$. In the Supplementary Materials (Section A2), we show that $\widehat{f_L^{\ast }}$ converges to the true best linear rule, $f_L^{\ast }$, asymptotically, at a slower rate than the usual root-n rate. We refer the proposed estimation procedure as Asymptotically Best Linear O-learning, ABLO. We also prove the asymptotic normality of $\hat{\mathit{\beta }}$ and the estimated benefit function, which provides justification of the inference procedures proposed in the next two sections.

2.2 Performance Diagnostics for the Estimated ITR

ABLO guarantees that the optimal value among the class $ℒ$ is achieved asymptotically. Nevertheless, the optimal linear rule $f_L^{\ast }(\mathit{X})$ may still be far from the global optimal, f^∗, such that for some important subgroups, $f_L^{\ast }(\mathit{X})$ may be non-optimal or even worse than the complementary treatment rule. Therefore, an empirical measure must be constructed to evaluate the performance of an estimated ITR.

To develop a practically feasible diagnostic method for any estimated ITR, given by $\text{sign}(\hat{f}(\mathit{X}))$ we note that if $\hat{f}(\mathit{X})$ is truly optimal among any decision functions in $ℱ$, i.e., $\hat{f}(\mathit{X})$ has the same sign as f^∗(X), then for any subgroup defined by $\mathit{X}\in \mathcal{C}$ for a given set $\mathcal{C}$ in the domain of X, the value function for those subjects whose treatments are the same as $\text{sign}(\hat{f}(\mathit{X}))$. should always be larger than or equal to the value function for those subjects with the same $\mathit{X}\in \mathcal{C}$, but whose treatments are opposite to $\text{sign}(\hat{f}(\mathit{X}))$. This is because

$$\begin{gathered} E\left[\frac{RI\left\{A=\text{sign}(\hat{f}(\mathit{X}))\right\}}{\pi (A|\mathit{X})}|\mathit{X}\right] \\ -E\left[\frac{RI\left\{A=-\text{sign}(\hat{f}(\mathit{X}))\right\}}{\pi (A|\mathit{X})}|\mathit{X}\right]=I(f^{\ast }(\mathit{X})>0)E(R|A=1,\mathit{X})+I(f^{\ast }(\mathit{X})\le 0)E(R|A=-1,\mathit{X})-I(f^{\ast }(\mathit{X})>0)E(R|A=-1,\mathit{X})-I(f^{\ast }(\mathit{X})\le 0)E(R|A=1,\mathit{X})=|f^{\ast }(\mathit{X})|⩾0. \end{gathered}$$

It then follows that the group-average benefit for $\hat{f}$, defined as

$${\delta }_{\mathcal{C}}(\hat{f})\equiv E\left[\frac{RI\left\{A=\text{sign}(\hat{f}(\mathit{X}))\right\}}{\pi (A|\mathit{X})}|\mathit{X}\in \mathcal{C}\right]-E\left[\frac{RI\left\{A=-\text{sign}(\hat{f}(\mathit{X}))\right\}}{\pi (A|\mathit{X})}|\mathit{X}\in \mathcal{C}\right],$$

should be non-negative. On the other hand, if ${\delta }_{\mathcal{C}}(\hat{f})⩾0$ holds for any subset $\mathcal{C}$, then the above derivation also indicates that $\hat{f}(\mathit{X})$ must have the same sign as f^∗(X), i.e., $\hat{f}(\mathit{X})$ is the optimal treatment rule for subjects in $\mathcal{C}$.

These observations suggest a diagnostic measure ${\delta }_{\mathcal{C}}(\hat{f})$ for any subgroup $\mathcal{C}$. Specifically, we propose an empirical ITR diagnostic measure as

$$\begin{gathered} {\hat{\delta }}_{\mathcal{C}}(\hat{f})= \\ \frac{{\displaystyle {\sum }_{i=1}^n\left[I\left\{{\mathit{X}}_i\in \mathcal{C},A_i=\text{sign}(\hat{f}({\mathit{X}}_i))\right\}-I\left\{{\mathit{X}}_i\in \mathcal{C},A_i=-\text{sign}(\hat{f}({\mathit{X}}_i))\right\}\right]R_i/\pi (A_i|{\mathit{X}}_i)}}{{\displaystyle {\sum }_{i=1}^{n}I({\mathit{X}}_i\in \mathcal{C})}}. \end{gathered}$$

Because ${\hat{\delta }}_{\mathcal{C}}(\hat{f})$ approximates ${\delta }_{\mathcal{C}}(\hat{f})$ the measure ${\hat{\delta }}_{\mathcal{C}}(\hat{f})$ is expected to be positive with a high probability if $\hat{f}(\mathit{X})$ is close to the global true optimal. Furthermore, the evidence that ${\hat{\delta }}_{\mathcal{C}}(\hat{f})$ is positive for a rich class of subsets $\mathcal{C}$ will support the approximate optimality of $\hat{f}$ in the class. However, because it is infeasible to exhaust all subgroups, we suggest a class of pre-specified subgroups ${\mathcal{C}}_1,\dots ,{\mathcal{C}}_m$ and calculate the corresponding ${\hat{\delta }}_{{\mathcal{C}}_1}(\hat{f}),\dots ,{\hat{\delta }}_{{\mathcal{C}}_m}(\hat{f})$. An aggregated diagnostic measure is $\hat{\mathrm{\Delta }}(\hat{f})=min\left\{{\hat{\delta }}_{{\mathcal{C}}_1}(\hat{f}),\dots ,{\hat{\delta }}_{{\mathcal{C}}_m}(\hat{f})\right\}$. A positive value of $\hat{\mathrm{\Delta }}(\hat{f})$ implies approximate optimality of $\hat{f}$ when m is large enough. In practice, we consider ${\mathcal{C}}_k$ to be pre-specified groups or the sets determined by the tertiles of each component of X, for example, the jth component of X below its first tertile, between the first and the second tertiles, or above the second tertile. Moreover, using the proposed diagnostic measure, by examining the subsets $\mathcal{C}$ (or tertiles defined by variables) with negative or close to zero values of ${\hat{\delta }}_{\mathcal{C}}(\hat{f})$, we can identify subgroups or components of X for which the estimated rule $\hat{f}$ may not be sufficiently optimal. Thus, we can further improve the rule estimation in this subgroup to obtain an improved ITR.

If the same data are used for estimating the optimal ITR and performing diagnostics, the latter may not be an honest measure of performance (Athey and Imbens, 2016). Thus, we suggest the following sample-splitting scheme. Divide the data into K folds, and denote ${\hat{f}}^{(-k)}$ as the optimal ITR obtained using data without the kth-fold. Next, each ${\hat{f}}^{(-k)}$ is calibrated on the kth-fold data using the diagnostic measure and then averaged. Let n_k denote the sample size of the kth-fold, and let I_k index subjects in this fold. The honest diagnostic measure for subgroup $\mathcal{C}$ is estimated by ${\hat{\delta }}_{\mathcal{C}}(\hat{f})=\frac{1}{K}{\displaystyle {\sum }_{k=1}^K{\hat{\delta }}_{\mathcal{C}}^{(k)}}$, where

$${\hat{\delta }}_{\mathcal{C}}^{(k)}=\frac{1}{n_k}{\displaystyle \sum _{\{i:i\in I_k\}}\left[I\left\{A_i=\text{sign}({\hat{f}}^{(-k)}({\mathit{X}}_i))\right\}-I\left\{A_i=-\text{sign}({\hat{f}}^{(-k)}({\mathit{X}}_i))\right\}\right]}{R}_i/\pi (A_i{\mathit{X}}_i).$$

We will implement this scheme in subsequent analysis.

2.3 Inference Using the Diagnostic Measure

The proposed diagnostic measure, ${\hat{\delta }}_{\mathcal{C}}(\hat{f})$, can be used to compare different ITRs and non-personalized rules, make comparisons within certain subgroups, and assess heterogeneity of ITR benefit (HTB) across subgroups. Hypotheses of interest may include:

• Test significance of the optimal linear rule compared to the non-personalized rule in the overall sample, i.e., $H_0:\delta (f_L^{\ast })-{\delta }_0=0$, v.s. $H_1:\delta (f_L^{\ast })-{\delta }_0>0$, where δ₀ is the average treatment effect of a non-personalized rule (difference in the mean response between treatment groups). For this purpose, we can construct the test statistic based on ${\hat{\delta }}_{\mathcal{C}}(\hat{f})-{\delta }_0$, where $\hat{f}$ is obtained from any method, and $\mathcal{C}$ is the whole population. We reject the null hypothesis at a significance level of α if the (1−α)-confidence interval with ∞ as the upper bound for ${\hat{\delta }}_{\mathcal{C}}(\hat{f})-{\delta }_0$ does not contain 0.

• Test significance of the optimal linear rule compared to the non-personalized rule in a subgroup k, i.e., $H_0:{\delta }_{{\mathcal{C}}_k}(f_L^{\ast })-{\delta }_{0k}=0$ v.s., $H_1:{\delta }_{{\mathcal{C}}_k}(f_L^{\ast })-{\delta }_{0k}>0$ where δ_0k is the average treatment effect in the subgroup. The same test statistic as the previous one can be used but with $\mathcal{C}={\mathcal{C}}_k$.

• Test the HTB across subgroups $\{{\mathcal{C}}_1,\cdots ,{\mathcal{C}}_K\}$, i.e., $H_0:{\delta }_{{\mathcal{C}}_k}(f_L^{\ast })-{\delta }_{{\mathcal{C}}_K}(f_L^{\ast })=0,k=1,\cdots ,K-1$. We propose the HTB test statistic $T={\hat{\mathbf{\Delta }}}_{\mathcal{C}}^T{\{\mathrm{cov}({\hat{\mathbf{\Delta }}}_{\mathcal{C}})\}}^{-1}{\hat{\mathbf{\Delta }}}_{\mathcal{C}}$, where ${\hat{\mathbf{\Delta }}}_{\mathcal{C}}^T=({\hat{\delta }}_{{\mathcal{C}}_1}(\hat{f})-{\hat{\delta }}_{{\mathcal{C}}_K}(\hat{f}),\cdots ,{\hat{\delta }}_{{\mathcal{C}}_{K-1}}(\hat{f})-{\hat{\delta }}_{{\mathcal{C}}_K}(\hat{f}))$. It can be shown that T asymptotically follows ${\chi }_{K-1}^2$ under H₀, so we reject H₀ when T is larger than the (1 − α)-quantile of ${\chi }_{K-1}^2$.

• Test the non-optimality of the best linear rule $f_L^{\ast }$ in a subgroup $\mathcal{C}$ by evaluating $H_0:{\delta }_{\mathcal{C}}(f_L^{\ast })⩾0$ v.s. $H_1:{\delta }_{\mathcal{C}}(f_L^{\ast })<0$. For this purpose, we can directly use ${\hat{\delta }}_{\mathcal{C}}(\hat{f})$ and reject the null hypothesis if the confidence interval with lower bound of −∞ does not contain zero.

The asymptotic properties of $\hat{\mathit{\beta }}$ and ${\hat{\delta }}_{\mathcal{C}}(\hat{f})$ are required to perform inference above. Based on the theoretical properties (asymptotic normality) given in the Supplementary Materials (Section A2), we propose a bootstrap method to compute confidence interval for the diagnostic measure. We denote the bth bootstrap sample as $({\stackrel{\sim }{A}}_i^{(b)},{\stackrel{\sim }{\mathit{X}}}_i^{(b)},{\stackrel{\sim }{R}}_i^{(b)})$, where i = 1, 2, ⋯, n, and re-estimate residuals as ${\stackrel{\sim }{W}}_i^{(b)}$ in (5). Next, we re-fit treatment rule ${\stackrel{\sim }{f}}^{(b)}$ and obtain ${\stackrel{\sim }{\delta }}_{\mathcal{C}}^{(b)}({\stackrel{\sim }{f}}^{(b)})$. The 95% confidence interval for ${\hat{\delta }}_{\mathcal{C}}(\hat{f})$ is constructed from the empirical quantiles of ${\stackrel{\sim }{\delta }}_{\mathcal{C}}^{(b)}({\stackrel{\sim }{f}}^{(b)}),b=1,2,\cdots ,B$.

3. Simulation Studies

3.1 Simulation Design

For all simulation scenarios, we first generated four latent subgroups of subjects based on 10 feature variables X = (X¹, ⋯, X¹⁰) informative of optimal treatment choice from a pattern mixture model. Treatment A = 1 has a greater average effect for subjects in subgroups 1 and 2, and the alternative treatment −1 has a greater average effect in subgroups 3 and 4. Within each subgroup, X were independently simulated from a normal distribution with different means and standard deviation of one. Two settings were considered. In Setting 1, the means of the feature variables for subjects in the four subgroups were (1, 0.5, −1, −0.5), respectively. In Setting 2, the means were (1, 0.3, −1, −0.3). Five noise variables U = (U¹, ⋯, U⁵) not contributing to R were independently generated from the standard normal distribution and included in the analyses in order to assess the robustness of each method in the presence of noise features. The treatments for each subject were randomly assigned to 1 or −1 with equal probability, and the number of subjects in each subgroup was equal.

Three additional feature variables W, V, and S were generated to be directly associated with the clinical outcome R. Here, W is an observed prescriptive variable informative of the optimal treatment, V is a prognostic variable predictive of the outcome but not the optimal treatment, and S is an unobserved prescriptive variable not available in the analysis. The clinical outcome for subjects in the kth subgroup was generated by

$$R=1+I(A=1)({\delta }_{1k}+{\alpha }_{1k}\ast W+{\beta }_{1k}\ast S)+I(A=-1)({\delta }_{2k}+{\alpha }_{2k}\ast W+{\beta }_{2k}\ast S)+V+e,$$

where e ∼ N(0, 0.25), V, W, and S are i.i.d. and follow the standard normal distribution, $\mathit{\delta }={[{\delta }_{lk}]}_{2\ast 4}=\left[\begin{array}{cccc}1& 0.3& 0& 0\\ 0& 0& 1& 0.3\end{array}\right],\mathit{\alpha }={[{\alpha }_{lk}]}_{2\ast 4}=\left[\begin{array}{cccc}1& 0.6& 0.5& 0.3\\ 0.5& 0.3& 1& 0.6\end{array}\right]$, and β =2α within each group k, there is a qualitative interaction between treatment and W. Additional visualization of the simulation setting is provided in the Supplementary Materials (Figure A.2).

The benefit function of the theoretical global optimal ITR decision function, denoted as f^∗, was computed numerically by simulating the clinical outcome R under treatment 1 or −1, using all observed feature variables (i.e., X, W, and V), and taking the average difference of R under the true optimal and non-optimal treatments using a large independent test set of N = 100, 000. In practice, this global optimum may not be attained by a linear rule due to the unknown and potentially nonlinear true optimal treatment rule. The theoretical optimal linear rule $f_L^{\ast }$ was computed numerically using the observed variables and maximizing the value function in the class of all linear rules under each simulation model (details in the Supplementary Materials; Section A3). The benefit of $f_L^{\ast }$ was then computed with a large independent test set of N = 50, 000.

For each simulated data set, predictive modeling (PM), Q-learning, O-learning, and ABLO were applied to estimate the optimal ITR. For PM, we considered a random forest-based prediction related to the virtual twins approach of Foster et al. (2011). PM first applies random forest on R, including all observed feature variables Z = (X, U, W, V) and treatment assignments. It next predicts the outcome for the ith subject given (Z_i, A_i = 1) and (Z_i, A_i = −1), denoted as ${\hat{R}}_{1i}$ and ${\hat{R}}_{-1i}$, respectively. The optimal treatment for the subject is $\text{sign}({\hat{R}}_{1i}-{\hat{R}}_{-1i})$. Q-learning was implemented by a linear regression including all the observed feature variables, treatment assignments, and their interactions. Benefit of the estimated optimal ITR under each method and was computed by ${\hat{\delta }}_{\mathcal{C}}(\hat{f})$ in Section 2.2.

In the simulations, observed feature variables Z were used in all methods, while the unobserved prescriptive variable S and latent subgroup membership were not included. Linear kernel was used for O-learning and ABLO. Five-fold cross validation was used to select the tuning parameters C and s. For each method, the optimal treatment selection accuracy and ITR benefit were estimated using two-fold cross validation with equal size of training and testing sets. The training set was used to estimate the ITR and the testing set was used to estimate the ITR benefit and accuracy. Bootstrap was used to estimate the confidence interval of the ITR benefit under the estimated rule. Coverage probabilities were reported to evaluate the performance of the inference procedure. To evaluate performance on subgroups, we partitioned W, V, X¹, and U¹ into three groups based on values in the intervals (−∞, −0.5), [−0.5, 0.5], or (0.5, ∞). We calculated the HTB test for the candidate variables and tested the difference between the estimated rules and the overall non-personalized rules.

3.2 Simulation Results

Results from 500 replicates are summarized in Table 1, 2, 3, Figure 1 and 2. For both simulation settings, ABLO with linear kernel has the largest optimal treatment selection accuracy regardless of the sample size, and it is also close to the maximal accuracy rate based on the theoretical best linear rule. In addition, ABLO estimates the ITR benefit closest to the true global maximal value of 0.678 on the overall sample, and it is almost identical to the benefit estimated by the theoretical best linear rule when the sample size is large (= 800 training, 800 testing). PM, Q-learning, and O-learning all underestimate the ITR benefit, especially when the sample size is smaller (N = 400 training, 400 testing), and thus they do not attain the maximal value of the theoretical optimal linear rule. Based on the empirical standard deviation, we also observe that ABLO is more robust than all other methods. For all methods, as the sample size increases, the treatment selection accuracy increases and the estimated mean benefit is closer to the true optimal value. Furthermore, the estimated ITR benefit increases as the accuracy rate increases. The coverage probability of the overall benefit of the best linear rule is close to the nominal level of 95% using ABLO, but less than 95% using other methods. The coverages are not nominal for O-learning, Q-learning, and PM, since their benefit estimates are biased when the candidate rules are misspecified (e.g., true optimal rule is not linear). This is because they use a surrogate loss function that does not guarantee convergence to the indicator function in the benefit function ${\delta }_{\mathcal{C}}(\hat{f})$.

Table 1.

Simulation results: mean and standard deviation of the accuracy rate, mean ITR benefit, and coverage probability for estimation of the benefit of the optimal ITR. PM: predictive modeling by random forest; Q-learning: Q-learning with linear regression; O-learning: improved single stage O-learning (Liu et al., 2014); ABLO: asymptotically best linear O-learning.

Setting 1. Four region means = (1, 0.5, −1, −0.5).
		Overall Benefit		W < −0.5		W ∈ [−0.5, 0.5]		W > 0.5
	Accuracy rate	Mean (sd)	Coverage	Mean (sd)	Coverage	Mean (sd)	Coverage	Mean (sd)	Coverage
N = 800
PM	0.71 (0.04)	0.37 (0.17)	0.69	0.08 (0.23)	0.97	0.36 (0.23)	0.82	0.67 (0.30)	0.72
Q-learning	0.76 (0.03)	0.45 (0.17)	0.80	0.17 (0.22)	0.97	0.46 (0.23)	0.89	0.73 (0.29)	0.78
O-learning	0.77 (0.05)	0.46 (0.18)	0.82	0.17 (0.24)	0.97	0.46 (0.24)	0.89	0.76 (0.30)	0.80
ABLO	0.83 (0.04)	0.65 (0.14)	0.94	0.30 (0.23)	0.92	0.64 (0.20)	0.96	1.01 (0.24)	0.93
N = 1600
PM	0.75 (0.03)	0.44 (0.12)	0.64	0.11 (0.17)	0.96	0.43 (0.17)	0.80	0.79 (0.20)	0.71
Q-learning	0.81 (0.02)	0.52 (0.11)	0.86	0.18 (0.16)	0.97	0.53 (0.15)	0.92	0.86 (0.19)	0.82
O-learning	0.84 (0.02)	0.57 (0.11)	0.93	0.19 (0.15)	0.97	0.57 (0.16)	0.95	0.94 (0.19)	0.90
ABLO	0.86 (0.02)	0.63 (0.09)	0.96	0.22 (0.15)	0.97	0.63 (0.15)	0.95	1.04 (0.17)	0.94
Best linear rule†	0.890	${\delta }_{\mathcal{C}}^l=0.629$		${\delta }_{\mathcal{C}}^l=0.192$		${\delta }_{\mathcal{C}}^l=0.621$		${\delta }_{\mathcal{C}}^l=1.071$

Setting 2. Four region means = (1, 0.3, −1, −0.3).
		Overall Benefit		W < −0.5		W ∈ [−0.5, 0.5]		W > 0.5
	Accuracy rate	Mean (sd)	Coverage	Mean (sd)	Coverage	Mean (sd)	Coverage	Mean (sd)	Coverage
N = 800
PM	0.68 (0.04)	0.34 (0.17)	0.67	0.10 (0.24)	0.95	0.34 (0.24)	0.83	0.59 (0.30)	0.71
Q-learning	0.74 (0.03)	0.43 (0.16)	0.85	0.16 (0.23)	0.97	0.44 (0.22)	0.92	0.70 (0.28)	0.82
O-learning	0.73 (0.04)	0.42 (0.17)	0.84	0.16 (0.21)	0.98	0.43 (0.24)	0.90	0.68 (0.29)	0.79
ABLO	0.78 (0.03)	0.62 (0.13)	0.95	0.30 (0.21)	0.96	0.62 (0.21)	0.96	0.94 (0.25)	0.92
N = 1600
PM	0.72 (0.03)	0.42 (0.12)	0.69	0.12 (0.17)	0.95	0.42 (0.17)	0.84	0.72 (0.20)	0.73
Q-learning	0.78 (0.02)	0.51 (0.11)	0.89	0.19 (0.16)	0.96	0.52 (0.15)	0.94	0.81 (0.18)	0.85
O-learning	0.79 (0.02)	0.52 (0.11)	0.91	0.19 (0.16)	0.95	0.53 (0.16)	0.93	0.85 (0.19)	0.89
ABLO	0.82 (0.02)	0.61 (0.10)	0.94	0.25 (0.16)	0.94	0.61 (0.15)	0.95	0.96 (0.17)	0.95
Best linear rule†	0.850	${\delta }_{\mathcal{C}}^l=0.593$		${\delta }_{\mathcal{C}}^l=0.200$		${\delta }_{\mathcal{C}}^l=0.583$		${\delta }_{\mathcal{C}}^l=0.996$
Best global rule†		${\delta }_{\mathcal{C}}=0.678$		${\delta }_{{\mathcal{C}}_1}=0.285$		${\delta }_{{\mathcal{C}}_2}=0.647$		${\delta }_{{\mathcal{C}}_3}=1.109$

^*The theoretical best linear rule for both settings is sign(X_s), where X_s = X¹ + X² + ⋯ + X¹⁰.

^†The true value of the best linear rule and best global rule is computed from a large independent test data set.

Table 2.

Simulation results: probability of rejecting the null hypothesis that the treatment benefit across subgroups is equivalent by the HTB test.

Setting 1. Four region means = (1, 0.5, −1, −0.5).
	W	X1	V	U1
N = 800
PM	0.16	0.05	0.03	0.02
Q-learning	0.18	0.06	0.03	0.03
O-learning	0.21	0.05	0.03	0.03
ABLO	0.42	0.07	0.05	0.06
N = 1600
PM	0.52	0.05	0.05	0.02
Q-learning	0.61	0.05	0.04	0.02
O-learning	0.71	0.04	0.04	0.02
ABLO	0.84	0.05	0.05	0.03
Setting 2. Four region means = (1, 0.3, −1, −0.3).
N = 800
PM	0.12	0.03	0.02	0.02
Q-learning	0.17	0.04	0.03	0.04
O-learning	0.15	0.03	0.03	0.03
ABLO	0.34	0.06	0.04	0.05
N = 1600
PM	0.42	0.06	0.04	0.03
Q-learning	0.56	0.07	0.04	0.03
O-learning	0.57	0.07	0.03	0.03
ABLO	0.74	0.10	0.04	0.05

^*W has strong signal; X¹ has weak signal; V and U¹ have no signal.

Table 3.

Simulation results: Comparison of the ITR to the non-personalized universal rule. The proportion of rejecting the null that the ITR has the same benefit as the universal rule^∗ are reported for the overall sample and by subgroups.

	Setting 1. Four region means = (1, 0.5, −1, −0.5).
	Overall	W < −0.5	W ∈ [−0.5, 0.5]	W > 0.5
N = 800
PM	0.22	0	0.09	0.33
Q-learning	0.37	0.02	0.20	0.40
O-learning	0.39	0.02	0.20	0.43
ABLO	0.86	0.07	0.47	0.78
N = 1600
PM	0.76	0.02	0.38	0.83
Q-learning	0.92	0.05	0.59	0.90
O-learning	0.95	0.06	0.67	0.94
ABLO	0.99	0.08	0.79	0.98
	Setting 2. Four region means = (1, 0.3, −1, −0.3).
N = 800
PM	0.18	0.01	0.07	0.27
Q-learning	0.35	0.03	0.17	0.37
O-learning	0.31	0.03	0.17	0.35
ABLO	0.82	0.07	0.43	0.74
N = 1600
PM	0.72	0.03	0.38	0.75
Q-learning	0.88	0.05	0.57	0.86
O-learning	0.90	0.07	0.59	0.86
ABLO	0.99	0.12	0.77	0.97

^*For Setting 1, the mean difference (sd) of the universal rule is 0.09(0.08) for N = 800 and 0.07(0.05) for N = 1600.

For Setting 2, the mean difference (sd) of the universal rule is 0.11(0.08) for N = 800 and 0.08(0.05) for N = 1600.

Figure 1.

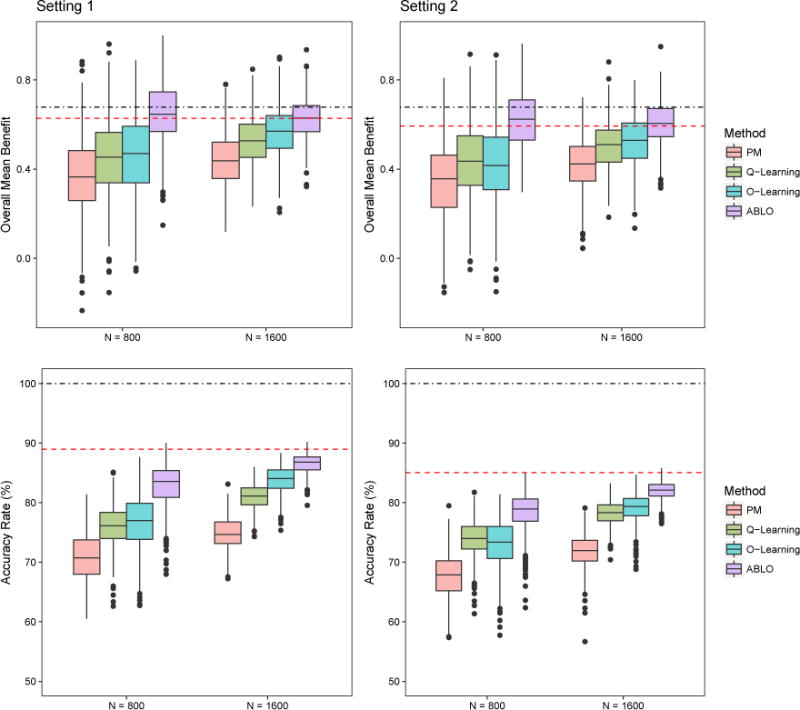
Simulation results: Overall ITR benefit and optimal treatment accuracy rates for the four methods. Dotted-dashed lines represent the benefit (top panels) and accuracy (bottom panels) under the theoretical global optimal treatment rule f^∗. Dashed lines represent the benefit and accuracy under the theoretical optimal linear rule $f_L^{\ast }$. The methods being compared are (from left to right): PM: predictive modeling by random forest; Q-learning: Q-learning with linear regression; O-learning: improved single stage O-learning (Liu et al., 2014); ABLO: asymptotically best linear O-learning. This figure appears in color in the electronic version of this article.

Figure 2.

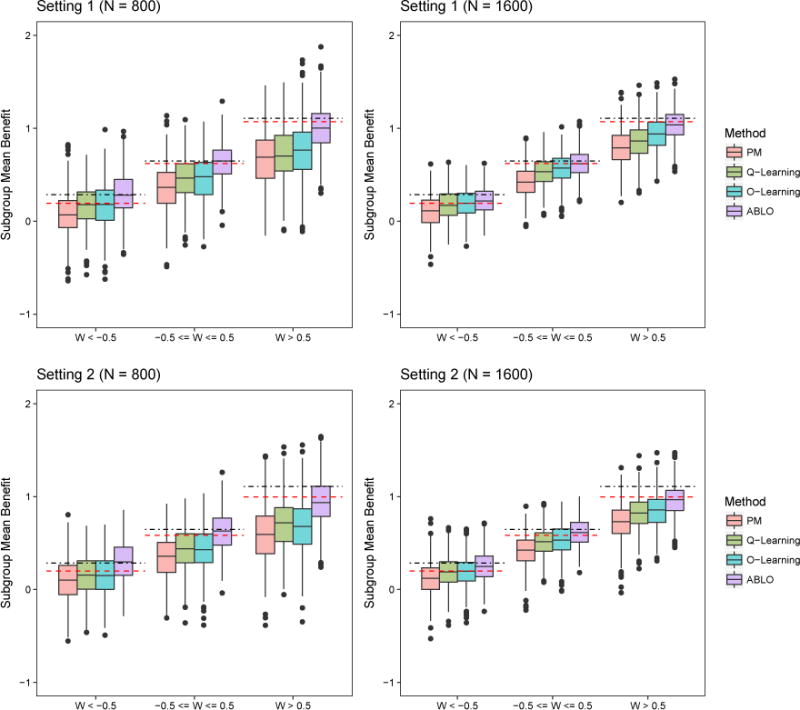
Simulation results: Subgroup ITR benefit for the four methods. Dotted-dashed lines represent the benefit under the theoretical global optimal treatment f^∗. Dashed lines represent the benefit under the theoretical optimal linear rule $f_L^{\ast }$. The methods being compared are (from left to right): PM: predictive modeling by random forest; Q-learning: Q-learning with linear regression; O-learning: improved single stage O-learning (Liu et al., 2014); ABLO: asymptotically best linear O-learning. This figure appears in color in the electronic version of this article.

The performance of estimation of the subgroup ITR benefit shows similar results, whereby ABLO outperforms O-learning, Q-learning, and PM in both settings, especially when W ∈ [−0.5, 0.5], and W > 0.5. Table 2 reports the probability of rejecting $H_0:{\delta }_{{\mathcal{C}}_k}(f_L^{\ast })-{\delta }_{{\mathcal{C}}_3}(f_L^{\ast })=0$, k= 1 or 2, using the HTB test with a null distribution of ${\chi }_2^2$. The rejection rates of the HTB tests of V and U¹ that do not have a difference in ITR benefit across subgroups correspond to the type I error rate. The type I error rates of ABLO are close to 5%, but conservative for the other three methods. To examine the power, we test the effect of W on the benefit across subgroups defined by discretizing W at −0.5 and 0.5. The power of ABLO is much greater than the other three methods especially when the sample size is small. The other three methods underestimate the benefit function, and thus the HTB test is conservative and less powerful.

Lastly, we test the difference in the benefit between the ITRs and the non-personalized rule in the overall sample and the subgroups. Table 3 shows that with a sample size of 800, ABLO is the only method that provides a significantly better benefit than the non-personalized rule with a large power (> 80%). When the sample size is large (N = 1600), ABLO, Q-learning, and O-learning have a power of ⩾ 88%. As for the subgroups, the ITR estimated by ABLO is more likely to outperform the non-personalized rule on the subgroups showing a larger true benefit (i.e., when W > 0.5).

Additional simulation results varying the strength of the prescriptive feature variable W are described in the Supplementary Materials (Section A4).

4. Application to the STAR*D Study

STAR*D (Rush et al., 2004) was conducted as a multi-site, multi-level, randomized controlled trial designed to compare different treatment regimes for major depressive disorder when patients fail to respond to the initial treatment of Citalopram (CIT) within 8 weeks. The primary outcome, Quick Inventory of Depressive Symptomatology (QIDS) score (ranging from 0 to 27), was measured to assess the severity of depression. A lower QIDS score indicates less symptoms and thus reflects a better outcome. Participants with a total QIDS score under 5 were considered to experience a clinically meaningful response to the assigned treatment and were therefore remitted from future treatments.

The trial had four levels of treatments (e.g., see Figure 2.3 in Chakraborty and Moodie (2013)); we focused on the first two levels. At the first level, all participants were treated with CIT for a minimum of 8 weeks. Participants who had clinically meaningful response were excluded from level-2 treatment. At level-2, participants without remission with level-1 treatment were randomized to level-2 treatment based on their preference to switch or augment their level-1 treatment. Patients who preferred to switch treatment were randomized with equal probability to bupropion (BUP), cognitive therapy (CT), sertraline (SER), or venlafaxine (VEN). Those who preferred augmentation were randomly assigned to CIT+BUP, CIT+buspirone (BUS), or CIT+CT. If a patient had no preference, s/he was randomized to any of the above treatments.

The clinical outcome (reward) is the QIDS score at the end of level-2 treatment. There were 788 participants with complete feature variable information included in our analysis. We compared two categories of treatments: 1) treatment with selective serotonin reputake inhibitors (SSRIs, alone or in combination): CIT+BUS, CIT+BUP, CIT+CT, and SER; and 2) treatment with one or more non-SSRIs: CT, BUP, and VEN. Feature variables used to estimate the optimal ITR included the QIDS scores measured at the start of level-2 treatment (level 2 baseline), the change in the QIDS score over the level-1 treatment phase, patient preference regarding level-2 treatment, and demographic variables (gender, age, race), and family history of depression. As the randomization to treatment was based on patient preference, we estimated π(A_i|X_i) using empirical proportions based on preferring switching or no preference, because patients who preferred augmentation were all treated with an SSRI and were excluded from the analysis.

We applied four methods to estimate the optimal ITR for patients with MDD who did not achieve remission with 8 weeks of treatment with CIT. For all methods, we randomly split the sample into a training and testing set with a 1:1 ratio and repeated the procedure 500 times. The value function and ITR benefits were evaluated on the testing set. PM, Q-learning, O-learning, and ABLO are compared in Figure 3. The non-personalized rules yield a QIDS score of 10.16 for SSRI and 9.60 for non-SSRI, with a difference of 0.56. The ITR estimated by ABLO yields a QIDS score of 9.32 (sd = 0.23), which is smaller than PM (9.69, sd = 0.38), Q-learning (9.50, sd=0.35), and O-leaning (9.55, sd = 0.41). The overall ITR benefit estimated by ABLO (1.11, sd = 0.46) is much larger than PM (0.38, sd = 0.76), Q-learning (0.77, sd = 0.70), and O-leaning (0.66, sd = 0.82). The ITR benefit based on ABLO is also larger than the non-personalized rule (1.11 versus 0.56). The final ITR estimated by ABLO is reported in Supplementary Materials (Section A5).

Figure 3.

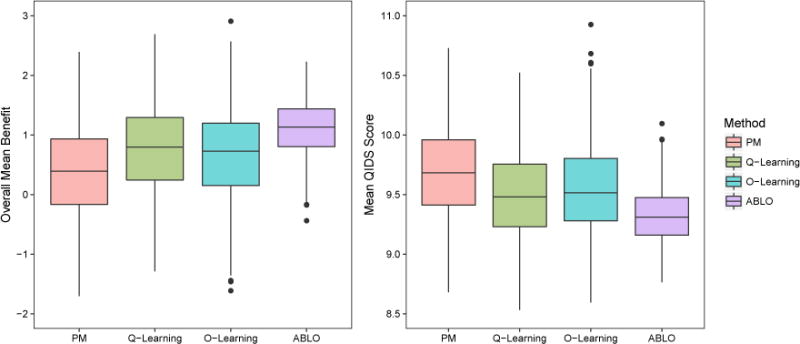
STAR*D analysis results: Distribution of the estimated ITR benefit (the higher the better) and QIDS score (the lower the better) at the end of level-2 treatment for the four methods (based on 500 cross-validation runs). The methods being compared are (from left to right): PM: predictive modeling by random forest; Q-learning: Q-learning with linear regression; O-learning: improved single stage O-learning (Liu et al., 2014); ABLO: asymptotically best linear O-learning. This figure appears in color in the electronic version of this article.

Clinical literature suggests that the baseline MDD severity may be a moderator for treatment response (Bower et al., 2013). In addition, baseline MDD severity is highly associated with suicidality; thus, patients with severe baseline MDD (QIDS ⩾ 16) represent an important subgroup. We partitioned patients into mild (QIDS ≤ 10), moderate (QIDS ∈ [11, 15]), and severe (QIDS ⩾ 16) MDD subgroups. Using ABLO and the HTB test, baseline QIDS score was found to be significantly associated with ITR benefit: two subgroups show a large positive ITR benefit (2.22 for the mild group and 2.02 for the severe group), whereas the moderate subgroup shows no benefit (ITR benefit = −0.18). This result indicates that patients with mild or severe baseline depressive symptoms (high or low QIDS score) might benefit from following the estimated linear ITR. For patients who are moderately depressed (QIDS ∈ [11, 15]), the linear ITR estimated from the overall sample does not adequately fit the data and does not outperform a non-personalized rule. Thus, we re-fit a linear rule using ABLO for the moderate subgroup only. The re-estimated ITR yields a lower average QIDS score of 8.93 (sd = 0.35), with a much improved subgroup ITR benefit of 0.60 (sd = 0.70). This analysis demonstrates the advantage of the ITR benefit diagnostic measure, the HTB test, and the value of re-fitting the ITR on subgroups showing a lack-of-fit.

5. Discussion

In this work, we propose a diagnostic measure (benefit function) to compare candidate ITRs, a machine learning method (ABLO) to estimate the optimal linear ITR, and several tests for goodness-of-fit. In practice, often not all predictive and prescriptive variables that influence heterogeneous responses to treatment are known and collected. Thus, it is unrealistic to expect that an ITR that benefits each and every individual can be identified. Our practical solution proposes to evaluate the average ITR effect over the entire population and on vulnerable or important subgroups. Although we focus on linear decision functions here, it is straightforward to extend ABLO to other simple decision functions such as polynomial rules by choosing other kernel functions (i.e., polynomial kernel). ABLO can also be applied to observational studies using propensity scores to replace π(A|X) under the assumption that the propensity score model is correctly specified. We prove the asymptotic properties of ABLO and identify a condition to avoid the non-regularity issue (in Supplementary Material Section A2). In practice, when such issue is of concern, adaptive inference (Laber and Murphy, 2011) can be used to construct confidence intervals.

ABLO can consistently estimate the ITR benefit function regardless of misspecification of the rule by drawing a connection with the robust machine learning approach for approximating the zero-one loss. We provide an objective diagnostic measure for assessing optimization. In our method, prescriptive variables mostly contribute to the estimation of the optimal treatment rule while predictive variables mostly contribute to the development of the diagnostic measure and assessment of the benefit of the optimal rule. Future work will consider methods to distinguish these two sets of variables, which potentially overlap.

ABLO is slower than O-learning because it involves iterations of quadratic programming when applying the DCA. In addition, certain simulations show that the algorithm can be slightly sensitive to the initial values in extreme cases (examples provided in Figure A.5 in the Supplementary Materials). However, our numeric results show that O-learning estimators serve as adequate initial values leading to fast convergence of the DCA. Another limitation is that the current methods only apply to single-stage trials. ABLO can be extended to multiple stage setting following a similar backward multi-stage O-learning in Zhao et al. (2015). The objective function in multi-stage O-learning will be replaced by the ramp loss and the benefit function will be extended with some attention to subjects whose observed treatment sequences are partially consistent with the predicted optimal treatment sequences.