Probing DNA Translocations with Inplane Current Signals in a Graphene Nanoribbon with a Nanopore

Abstract

Many theoretical studies predict that DNA sequencing should be feasible by monitoring the transverse current through a graphene nanoribbon while a DNA molecule translocates through a nanopore in that ribbon. Such a readout would benefit from the special transport properties of graphene, provide ultimate spatial resolution because of the single-atom layer thickness of graphene, and facilitate high-bandwidth measurements. Previous experimental attempts to measure such transverse inplane signals were however dominated by a trivial capacitive response. Here, we explore the feasibility of the approach using a custom-made differential current amplifier that discriminates between the capacitive current signal and the resistive response in the graphene. We fabricate well-defined short and narrow (30 nm × 30 nm) nanoribbons with a 5 nm nanopore in graphene with a high-temperature scanning transmission electron microscope to retain the crystallinity and sensitivity of the graphene. We show that, indeed, resistive modulations can be observed in the graphene current due to DNA translocation through the nanopore, thus demonstrating that DNA sensing with inplane currents in graphene nanostructures is possible. The approach is however exceedingly challenging due to low yields in device fabrication connected to the complex multistep device layout.

Nanopores have proven to be powerful biomolecular sensors as they allow detection and characterization of even single molecules solely via an electronic readout with no need for amplification or labels. In nanopore sensing, the molecule of interest is pulled by an electric field through a nanometer-sized hole in a thin membrane in a head-to-tail fashion while structural features of the molecule can be consecutively read.¹ The traversal of a DNA molecule leads to a blockade in the ionic current through the nanopore that is monitored, that is, what is commonly measured as the sensing signal. DNA sequencing using biological nanopores within a lipid membrane has successfully been shown² and recently even commercialized.^3,4

Solid-state nanopores⁵ present some advantages over biological pores, such as their robustness, thermal, mechanical, and chemical versatility, and potential for device integration in wafer-scale integrated circuits.⁶ Whereas solid-state nanopores have enabled numerous interesting biophysics studies of proteins and nucleic acids,^7,8 calling individual bases along a DNA molecule traversing through such a nanopore—a prerequisite for sequencing—remains to be shown yet. Conventional solid-state nanopores suffer from poor spatial resolution, as the length of these nanopores is set by the thickness of the membranes used, typically 10–30 nm, resulting in an ionic current blockade that is constituted by ∼100 bases that collectively reside in the pore. For that reason, the use of a two-dimensional membrane material, such as graphene, is clearly appealing, as only one or a few bases can occupy the pore volume at the same time. Various attempts have been reported on the use of graphene and related layered materials to probe DNA, with partial success.⁹⁻²⁰ Individual DNA molecules could well be distinguished but challenges remain. For example, detailed features were hard to resolve because the ionic currents through these nanopores exhibited high levels of 1/f-noise.²¹ Furthermore, the fast translocation speed of the DNA molecules (0.01–1 μs/base) sets a need for >MHz sampling rates, at which the noise is too high to resolve the blockade signals, let alone sequence information.

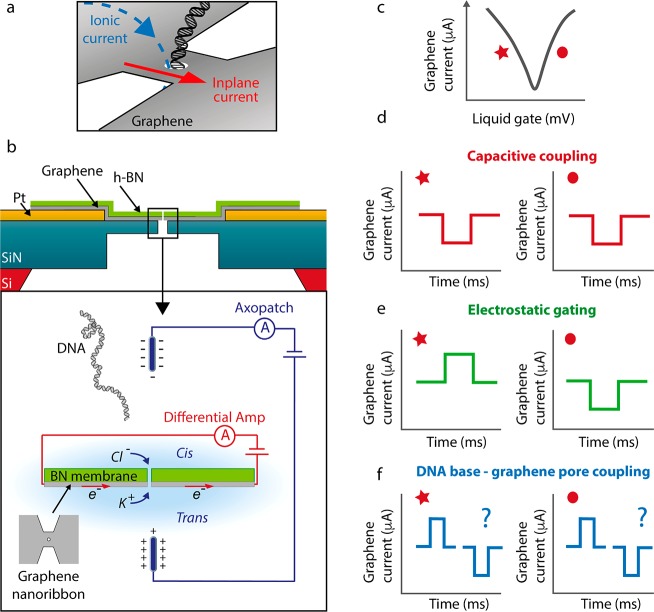
Since graphene is a conducting material,²² an interesting alternative to the ionic-current readout is the measurement of the transverse (i.e., perpendicular to the DNA molecule) current through a graphene nanoribbon with a nanopore through that ribbon, see Figure 1a. Many theoretical and computational studies on transport in graphene nanoribbons (GNRs) and graphene quantum point contacts with a nanopore have shown that the presence of the DNA bases inside the nanopore can lead to base-specific modulations in the electronic current through the graphene nanostructure, thus in principle enabling measurement of the DNA sequence as the molecule passes through the nanopore.²³⁻³⁴ These studies show that non-electrostatic base-specific interactions between the DNA bases and the graphene nanoribbon result in alterations of the local density of states around the nanopore leading to resistive changes of the nanoribbon that can be measured in the inplane current running through the ribbon. An important advantage of this approach is the relatively large current magnitude in these nanoribbons (μA) and the flat frequency response to high megahertz frequencies,^35,36 facilitating high-bandwidth measurements, that is, opening up the possibility to sequence at the translocation speed that is typically observed with solid-state nanopores.

Figure 1.

Transverse current measurement for DNA detection. (a) Concept of the experiment: Both the inplane current through a graphene nanoribbon and an ionic current through the nanopore are measured, while a DNA molecule translocates through a nanopore in that ribbon. (b) Schematic representation (not to scale) of the device (top) and measurement setup (bottom). A silicon chip with a silicon nitride membrane and platinum electrodes acts as substrate for the graphene nanoribbon, which is covered by a top-layer of h-BN, with a nanopore drilled through the BN/graphene stack. The graphene nanoribbon is exposed to the liquid on the trans side (bottom). In the experiment, both the ionic current through a nanopore and the graphene transverse electronic current are measured. The ionic voltage probes that are used to drag the DNA through the nanopore are concurrently used to gate the nanostructure. (c) With the liquid gate, the potential of the graphene can be sweeped such that the Dirac curve is obtained, revealing the ambipolar nature of the charge carriers in graphene. The DC operating point of the graphene device can be tuned to the left wing of the Dirac curve (star), representing negative transconductance, and to the right wing (circle), representing positive transconductance value. Three different types of signals can be measured: (d) Capacitive signals, which will always be of the same sign and will be independent of the Fermi level of the graphene. (e) Electrostatic interactions either due to the negative charge of the DNA backbone or due to a potential change at the nanopore caused by DNA translocation. These will result in different signals on both sides of the Dirac curve: A current increase when the current is carried by holes (left wing), and a current decrease when electrons are the dominant carriers (right wing). (f) Current fluctuations due to non-electrostatic local interactions between the DNA bases and the graphene nanopore, which can lead to current enhancements or decreases. The question mark denotes that the sign of this signal is not a priori known, as different theories predict different outcomes, depending on device parameters.

A simplified schematic of the proposed experiment is presented in the Figure 1b. The traversal of DNA through a nanopore in a graphene nanoribbon is monitored by the inplane current measurement. The voltage that is applied to the ionic current electrodes to drive DNA through the nanopore simultaneously acts as an electrolytic gate that modulates the current through the graphene nanoribbon. The graphene current dependence on the gate voltage, the so-called Dirac curve (Figure 1c), yields the transconductance g_m that indicates the sensitivity of the graphene conductance to external voltage fluctuations. Similar approaches have been reported before with wider graphene nanoribbons^37,38 and silicon nanowires³⁹ for DNA detection. Importantly, the current signals measured with these systems were shown to originate in a capacitive coupling of the potential change at the nanopore that occurs during DNA translocation to the local capacitance of the sensor at the nanopore.³⁹ These capacitive signals were studied in detail and were shown to increase with smaller pore diameters and thinner membranes and can be maximized through the introduction of a buffer salt gradient.³⁷⁻⁴¹ Importantly, while this capacitive signal reveals the local presence of DNA in the nanopore, it does not represent the theoretically predicted resistive modulation in the graphene current discussed above. In this study, we aim to elucidate whether or not it is feasible to measure a non-capacitive response of DNA translocations in the transverse current through a graphene nanoribbon.

What signals can be expected in the graphene transverse current due to the presence of DNA in the nanopore? We distinguish between three different types of signals, which are schematically shown in Figure 1d–f. First, as mentioned above, we expect to measure a capacitive signal (Figure 1d), which is expected to be similar irrespective of the choice of the DC operating point on the Dirac curve (indicated by * and • in Figure 1c), and its magnitude should be independent of the bias voltage applied to the graphene.³⁸ This signal can be defined as 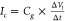, where ΔV_l the local potential change at the nanopore due to DNA translocation, Δt the time scale over which this change is realized, and C_g the capacitance of the graphene to the electrolyte at the nanopore. Second, we expect that electrostatic interactions will modify the Fermi level of the graphene nanostructure (Figure 1e). Current modulations will depend on the type of carriers, where transport dominated by holes will lead to negative transconductance g_m (left wing of Dirac curve in Figure 1c), and transport dominated by electrons will result in positive transconductance g_m (right wing of Dirac curve in Figure 1c). This electrostatic signal can be defined as I_e = g_mΔV_e, where ΔV_e is a potential change that can have two possible origins. The first originates in the negative charge of the DNA backbone 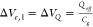, where Q_eff is the effective charge of the DNA.⁴² Second, a contribution ΔV_e,2 = ΔV_l due to a local potential change is evoked by a perturbation in the electric field at the nanopore due to insertion of DNA into the nanopore, as already mentioned above.³⁹ Third, we expect current signals due to non-electrostatic DNA base-graphene interactions (Figure 1f). As calculated in a great number of theoretical reports,²³⁻³⁴ the presence of a DNA base can lead to substantial current modulations that increase with the bias voltage applied to the graphene. However, the magnitude and sign of the current change that is induced depend on multiple factors, including the width of the structure, the position and size of the nanopore, the edge structure of the ribbon (zigzag or armchair), and the Fermi level of the graphene, and is therefore not known a priori.

The particular size of the graphene nanostructure that probes the presence of the DNA in the nanopore is of great importance. While previous theoretical work focused on sub-10 nm wide ribbons, early experiments probed the transport only for 600–1000 nm long and 50–200 nm wide ribbons.^37,38 Here we measure on short and narrow graphene nanoribbons (minimum width w) to maximize the sensitivity for effects near the nanopore. We also argue that short ribbon lengths (L) are beneficial, because long ribbons are more prone to edge damage. Previous studies have shown that roughness and disorder along the edges may result in transport that is characterized by a series of quantum dots rather than by a single nanoribbon.^43,44 In addition, shorter nanoribbons feature a higher conductance. Therefore, we realized short and narrow nanoribbons of 30 × 30 nm that were as small as experimentally feasible while explicitly also striving for a minimal amount of defects, which is non-trivial since most top-down patterning strategies (e.g., focused ion beams or etching/e-beam lithography)⁴³ lead to defect layers of tens of nanometers near the edges.

Results and Discussion

Fabrication Workflow and Device Characterization

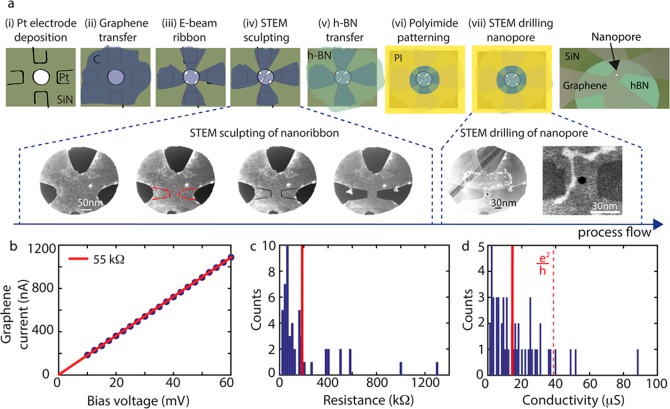
We first describe the extensive fabrication protocol of our devices. The workflow is indicated in Figure 2a. Device fabrication is started with a wafer of silicon chips, with 500 nm-thick SiN membranes containing embedded platinum heaters. We spraycoated e-beam resist from the backside and employed through-membrane e-beam lithography, to RIE etch 5 × 5 μm windows of 100 nm thickness in the silicon nitride membranes.⁴⁵ Platinum electrodes were deposited on top of the membranes, in which we patterned 400 nm holes (panel i in Figure 2a) to suspend graphene, which later enables sculpting of freestanding graphene. An exfoliated graphene flake (typically 10 × 10 μm) is transferred on top of the SiN membrane (panel ii). Subsequently, the graphene is patterned using e-beam lithography and oxygen plasma etching into a 200 × 200 nm square with four leads that each contact a platinum electrode (panel iii). This layout ensures that currents run nowhere else than through the graphene nanostructure. Then, a 30 × 30 nm graphene nanoribbon is sculpted using high-temperature STEM at 300–600 °C with high precision⁴⁶ (panel iv). At such high temperatures, carbon adatoms knocked out by the e-beam or originating from C-rich contaminations in the environment diffuse at high rates and instantly reoccupy vacancies in the graphene lattice, preventing carbon deposition and, importantly, preserving the crystallinity of the graphene.⁴⁷ The bottom row in Figure 2a presents an example of the consecutive sculpting steps performed in the STEM, where the graphene (gray) can be distinguished from vacuum (black). An automated script is used to move the electron beam along predefined paths to make cutting lines (see Methods section for details), visualized by the dark lines in the STEM images. In between the sculpting, we switch to imaging for which we use a fast scanning e-beam with short dwell times (μs) to be able to correct for drift in the microscope. A thin flake (3–7 layers) of h-BN is subsequently transferred on top of the nanoribbon as a support and, more importantly, to represent the membrane for the nanopore experiments, that is, to enforce the DNA to translocate through the nanopore and not next to the sides of the graphene square. To prevent parasitic electrochemical currents during the nanopore measurements, a thick (1.5 μm) layer of polyimide is placed on top of the stack to coat the electrodes (panel vi). A 5 × 5 μm area is exposed using e-beam lithography, such that after development a circular area with a diameter of approximately 10 μm at the nanostructure uncovered. Finally, a 5 nm nanopore is drilled with STEM at the center of the nanoribbon-BN stack (panel vii). Note that, using STEM imaging, the graphene can still be distinguished from the h-BN.

Figure 2.

Fabrication procedure and device characterization. (a) Process work flow of the device fabrication. Top: schematic images showing the sequential patterning steps. Bottom: STEM images of a single nanoribbon device, where gray represents the graphene and black is vacuum. In the second image, the cutting lines that are to be made with STEM are marked with a red dotted line. When the cutting lines are subsequently connected, the graphene is removed. After the BN transfer, some wrinkles of the h-BN flake are visible. After the polyimide patterning, a 5 nm nanopore is drilled through the stack of graphene and h-BN. (b) Example of a current–voltage measurement. (c) Ribbon resistances as measured directly after sculpting at room temperature. We find an average resistance of 194 ± 35 kΩ (±s.e.m.) (indicated by the vertical red line), deduced from 51 ribbons. (d) Conductivity of the graphene nanostructures, as calculated from 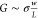for 51 STEM ribbons. The average conductivity measured in this study was 17 ± 2 μS (±s.e.m.) (indicated by the vertical red line). For reference, the red dotted line indicates 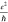∼ 38 μS.

The resistances of the graphene nanoribbons were measured in a two-probe configuration immediately after STEM sculpting (Figure 2b). The structures demonstrated linear current–voltage characteristics (Figure 2b) featuring an average resistance of R = 194 ± 35 kΩ (mean ± s.e.m.) (Figure 2c). After high-temperature patterning in TEM, the contact resistances between the platinum and graphene were found to be low (∼1 kΩ) and therefore not accounted for in the resistance determination. The graphene conductivity σ can be deduced from the conductance G, using the relation 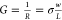(see supplemental Figure S1 for the conductance versus conductivity for our devices). The theoretical planar conductivity of graphene⁴⁸ is 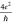, where e is the electron charge and ℏ is Planck’s constant. However, experimental studies on graphene nanoribbons so far revealed conductivities closer to 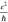, with narrower ribbons typically exposing (much) lower conductivities,^49,50 which likely can be attributed to damage in the graphene induced during nanopatterning. Figure 2d shows the data for our graphene nanoribbons (N = 51), with a highest conductivity of 89 μS (2.3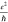) and a median of 17 ± 2 μS (±s.e.m.) (0.44 ).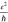

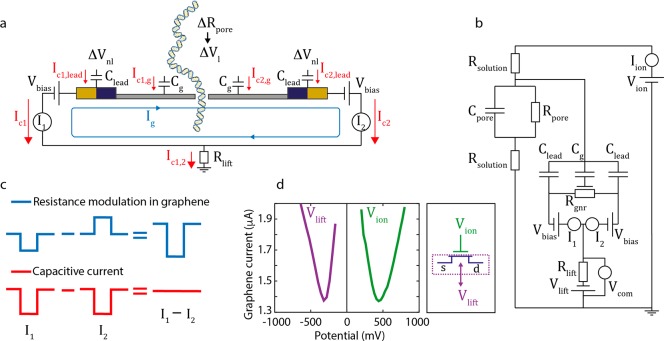
Decoupling of Capacitive Signals Using a Differential Current Amplifier

We developed a custom-made differential current amplifier to be able to discriminate between signals in the graphene current generated by capacitive coupling and signals due to electrostatic gating or modulations in the density of states. As explained in Figure 3a, capacitive currents I_C1,2 are created when temporal potential fluctuations couple to capacitances between the electrolyte and the conducting channel of the sensor, where the index 1,2 indicates the coupling to the left and right electrode of the graphene device, respectively. Here we distinguish between two relevant capacitance terms: first, the capacitance between the electrolyte and the graphene right at the nanopore (C_g) and, second, the capacitances that couple within the several micrometers range distance from the nanopore. The latter are represented by the capacitance between the electrolyte and the graphene that extends from the nanoribbon connecting the electrodes and between the electrolyte and the electrodes, which we combine in one term C_lead (see Figure 3a). Any local change of the potential ΔV_l at the nanopore couples to the sensor’s capacitance C_g to constitute a current 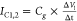. Potential fluctuations that are not strongly localized at the nanopore, ΔV_nl, for instance due to a jump in the applied gate potential, will couple non-locally to both C_g and C_lead: 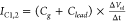. Capacitive currents are inherent to all nanopore sensors that are combined with a second electronic readout, such as transverse or tunneling currents. Our differential amplifier applies opposite potentials to the two electrodes connected to the graphene nanoribbon, see Figure 3ab, (+) to electrode 1 on the left and (−) to electrode 2 on the right, with respect to the ground potential of the liquid. All capacitive currents are independent of the electrode potential, and thus of equal sign at both electrodes, while, by contrast, any resistance modulation leading to a current signal in the graphene nanostructure (I_g in Figure 3a) will be of opposite sign at each voltage electrode (Figure 3c). The differential current amplifier is designed such that we detect only current contributions that are dissimilar at the two measurement electrodes, while all induced signals that are equal in sign will be subtracted (see Figure 3c).

Figure 3.

Capacitive coupling and the differential current amplifier. (a) Potential fluctuations couple to the graphene signal through the capacitance C_g between the electrolyte and the graphene nanosensor (gray), which is in parallel with the lead capacitance C_lead between the electrolyte and the graphene leads contacting the electrodes (dark blue) and to the electrodes themselves (yellow)). We distinguish local potential fluctuations ΔV_p that are induced by DNA translocations, from non-local potential fluctuations ΔV_nl due to modulations in the gate voltage. On the two electrodes (electrode 1 on the left and electrode 2 on the right), a voltage of opposite sign but equal magnitude is applied (V_bias). Resistive current modulations in the graphene I_g = g_mΔV are indicated in blue. (b) Equivalent circuit diagram of the setup. V_ion is the applied potential during DNA measurements which simultaneously gates the graphene; V_lift is used as extra “knob” to tune the gate voltage to a favorable point on the Dirac curve; V_bias sets the bias potential at the electrodes; I_ion represents the ionic current (Axopatch 200B); I₁ and I₂ are the lead graphene currents that are used in the differential graphene current measurement; and V_com measures the DC potential of the graphene. (c) Principle of the differential current measurement. Due to the opposite potentials at the two electrodes, resistive modulations in the graphene will yield currents I₁ and I₂ of opposite polarity. The capacitive currents are, however, independent of the electrode potentials and thus hold the same polarity. Subtraction of the two current measurements I₁ and I₂ leads to the differential measurement, where the capacitive-current contribution vanishes, whereas the graphene resistance modulations are maintained. (d) Graphene current versus applied gate potential. The purple trace was obtained by sweeping V_lift at V_ion = 0 mV; the green trace was acquired by sweeping V_ion while V_lift = 0 mV. During the experiments, V_lift and V_ion are both used to gate the graphene, and the effective gate potential can be expressed as V_gate = V_ion – V_lift.

Through this differential measurement, we thus eliminate all capacitive contributions to the inplane current while retaining any contributions due to resistive modulations of the graphene nanoribbon current. To show the principle of the differential current measurement, we performed SPICE simulations (Figure S2). DNA events were simulated by 1 ms-duration voltage steps of 100 mV, and graphene resistance modulations were simulated by 1 ms-duration resistance increases. The current at each electrode was measured by a separate op-amp, each obtaining a unique signal. After the subtraction of the two current signals measured at the two electrodes, the differential current signal solely represented the resistance modulation in the graphene, while the addition of the two responses yielded the capacitive signal (see Figure S2). In reality, the amplifier eliminates the capacitive component from the inplane current signals, while also measuring the common mode DC potentials of the graphene conducting channel with respect to ground at the two electrodes. From this common-mode potential measurement in V_com we can deduce the capacitive currents, which are related to all potential fluctuations, local and non-local, where C_lead is in parallel with C_g.

As it is exposed to the electrolyte solution, the graphene nanoribbon is gated by the applied voltage V_ion on the trans ionic reservoir. Since V_ion thus has a dual role, viz., it is necessary for controlling DNA translocations as well as changes the DC operating point of the graphene nanoribbon, we equipped the amplifier with additional “knob” to adjust the gate voltage, V_lift, which lifts the DC operating potential of the graphene nanostructure with respect to ground (Figure 3b). As both V_ion and V_lift affect the transconductance of the nanoribbon (Figure 3d), the effective gating potential at the graphene nanostructure can be defined as V_gate = V_ion – V_lift. This is advantageous, since this provides the ability to gate the sensor through V_lift, readjusting the operating point to optimize g_m each time that the V_ion potential changed. As V_lift acts opposite to V_ion, the Dirac curves measured as a function of V_lift or V_ion are mirrored about the y-axis (Figure 3d). The combination of the DC bias voltage V_bias, which sets the in-plane current in the graphene nanoribbon, and V_ion and V_lift can be chosen such that we perform the DNA measurements at the highest transconductance. Finally, we note that the V_com readout can also be used to monitor any leakage of the transverse current channel to the liquid, which could occur through unintentional electrochemical processes at the electrodes or on the graphene surface. In the ideal case, the measured common mode potential of the graphene should equal the V_lift applied potential. An offset between the two indicates that there is a leakage. Using this approach, we showed that electrochemical leakage currents of tens of nanoamperes can arise if electrodes on the device are only partly coated, while an intact polyimide layer on the chip resulted in zero leakage currents (Figure S4).

Proof-of-Principle Experiments

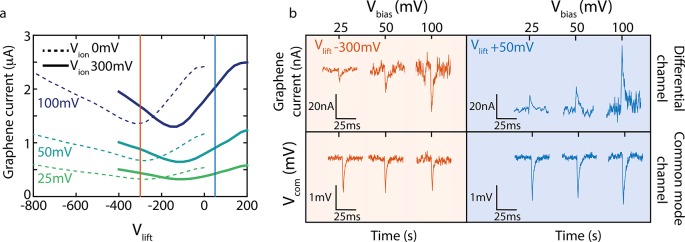
We benchmarked our amplifier and graphene devices by first performing a series of control measurements. We simulated DNA translocations by voltage pulses ΔV_ion (−20 mV, 1 ms) applied to the ionic voltage channel (V_ion = 300 mV) and detected the response in the graphene transverse current ΔI_g. Furthermore, we probed the current signals in the graphene at three different values of V_bias (25, 50, and 100 mV) and tuned the DC operating point to either side of the Dirac curve such that the conductance was dominated by either p- or n-type carriers (V_lift = 300 mV (n-type) versus +50 mV (p-type) (indicated by the orange and blue lines that cross the solid lines measured at V_ion = 300 mV in Figure 4a), leading to a g_m of different sign. As shown in Figure 4a, we measured, as expected, a near-linear V_bias dependence of the graphene current signals (see Figure S5).

Figure 4.

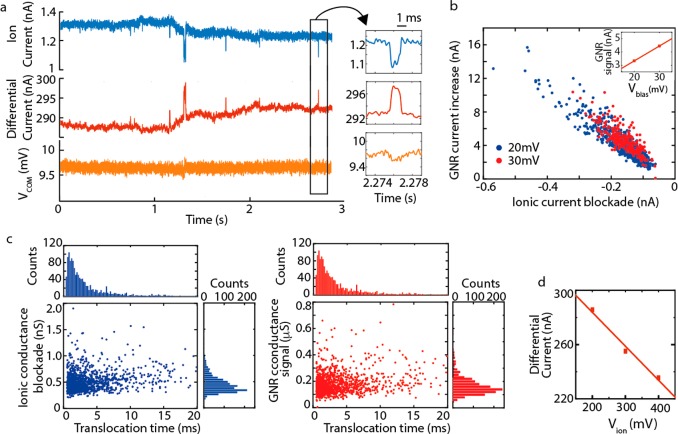
Proof-of-principle. (a) Mapping of the graphene current response to a sweep in V_lift gate potential, at different V_bias (25 mV, green, 50 mV, turquoise, and 100 mV, purple), and for two values of V_ion (0 mV, dotted line, and 300 mV, solid line). The orange and blue lines indicate the V_lift gate potentials at which we measure the pulses displayed in panel b (i.e., V_lift= −300 mV and +50 mV, respectively). (b) Response from the differential current amplifier to −20 mV pulses of 1 ms in V_ion. The positive probe (V_ion= 300 mV) is located on the graphene side (i.e., trans side) of the membrane. The response in the graphene current is, as expected, different on both sides of the Dirac curve: We observe current dips (orange) for V_lift = −300 mV and current peaks (blue) for V_lift = +50 mV. Measurements were done at three values for the bias voltage, 25, 50, and 100 mV. As expected, larger signals are measured in the graphene current for higher bias voltages. The common mode channel presents the capacitive signals, and as expected, these do not change sign or magnitude, as these do not depend on the gate voltage nor the bias voltage. A signal amplitude of 1 mV corresponds to a current of 200pA.

The most noteworthy result is presented in the top panels of Figure 4b, where we measured a different-sign response of the graphene current to the gate voltage, depending on the choice of the operating point: downward spikes for V_lift = −300 mV and upward spikes for V_lift = +50 mV (Figure 4c). The values of transconductance derived from the Dirac curves (g_m = −1.1 nA/mV and 0.7 nA/mV, respectively) were in good agreement with ones obtained from graphene current responses to the V_ion pulses (g_m = −1.1 nA/mV and 1 nA/mV, see Figure S5b). At the same time, the currents induced by capacitive couplings are measured in the common-mode channel (bottom panels Figure 4b). As expected, these signals (i) remain of the same sign at any V_lift and (ii) do not increase in magnitude with increasing V_bias. This clearly asserts that our differential amplifier separates, as designed, the transverse current response due to gating of the graphene sensor, recorded in the differential channel, from signals caused by capacitive coupling which are picked up in the common mode channel of the amplifier.

Probing DNA Translocations

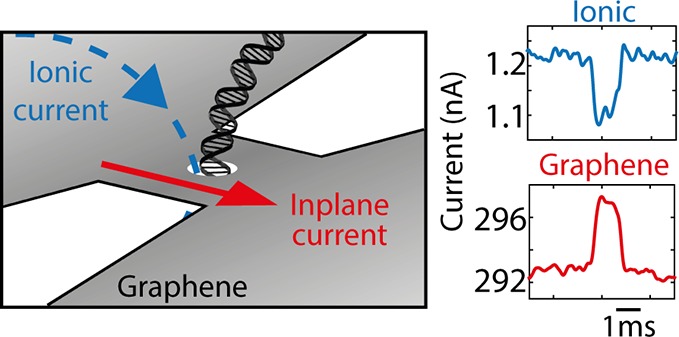
Finally, we performed DNA translocation experiments with our graphene nanostructure devices, where we simultaneously recorded the time traces of the ionic nanopore current and the graphene transverse current, using the setup shown in Figure 1a. It proved to be extremely challenging to perform such experiments successfully, because of constraints in the extensive fabrication protocol and additionally because it was very difficult to wet the nanopores. The latter is likely caused by the hydrophobic nature of the graphene. Note that the samples cannot be treated with oxygen plasma or piranha solution as this will remove the graphene. Attempts to wet the pores through ethanol flushing often resulted in breaking of the nanostructure. These effects rather unfortunately reduced our yield of successful experiments dramatically. However, we managed to obtain consistent data with one sample (out of 180 devices that we started fabricating) with a good enough signal-to-noise ratio to study the signals in detail.

After addition of 20kb plasmid DNA, we detected current blockades in the current trace of the ion flow through the graphene nanopore as well as simultaneous current signals in the electronic current running through the graphene nanostructure. An example trace of such events is shown in Figure 5a (and more example events are presented in Figure S6). Clearly, the signals were fully synchronized in time as for 99.9% of the events in the ionic current (N = 1429) we also observed a very clear signature in the graphene current. Furthermore, an anticorrelation is observed in the sign of both signals: a decrease of the ion current, which unambiguously signals the translocation of DNA at these high-salt conditions, corresponds to an increase in the current measured through the graphene nanoribbon. In other words: The passage of the DNA leads to a temporarily lowered resistance of the graphene nanoribbon.

Figure 5.

DNA translocation through a nanopore in a graphene nanostructure. (a) Example traces (filtered at 2 kHz) that are simultaneously collected in three channels: the ionic current (blue), graphene current (red), and the common mode voltage channel (yellow). The right panel shows a zoom of one DNA event in the three different channels. (b) Scatterplot showing the ion current signals versus the graphene current, for 20 mV (blue) and 30 mV bias voltage (red). The ionic potential was held constant at 300 mV. All events were detected at V_lift = 0 mV. Larger current blockades in the ionic current (i.e., more negative values) correspond to larger upward peaks in the graphene current (more positive). Inset: Medians of graphene current signals versus bias voltages. (c) Ionic conductance blockades (blue) and graphene conductance signals (red) versus DNA translocation time. The median of the translocation time distribution is 2.3 ± 8.9 ms (±s.d.). The ionic conductance blockade observed is 0.46 ± 0.2 nS (median ± s.d.), and the graphene conductance signal measured is 0.16 ± 0.08 μS (median ± s.d.). (d) Graphene current measured versus V_ion (at V_lift = 0 mV), recorded prior to the DNA experiments. From the slope of the fit, we deduce a transconductance of −0.25 nA/mV.

About 1400 of these events were measured, as presented in the scatterplots in Figure 5b,c. The data in Figure 5b show that the correlation also holds for the magnitude of the current deviations in both channels, viz., a larger current dip in the ionic current corresponds to a larger current increase in the graphene current. The magnitude of the signal in graphene channel furthermore scaled with the bias voltage (inset Figure 5b), while the ionic current signals remained unchanged (Figure S7b). The signal-to-noise ratio (SNR) in the graphene current is comparable to the SNR in the ionic current (see Figure S7c) (SNR = 4.2–4.5 for the graphene current versus 3.8–5.4 for the ionic current at 20–30 mV bias voltage). Figure 5c displays the ionic conductance blockades (0.46 ± 0.19 nS (median ± s.d.)) and the graphene conductance signals (0.16 ± 0.08 μS (median ± s.d.)) versus the observed translocations times. The distribution of the observed translocation time (top of Figure 5c) has a median of 2.3 ± 8.9 ms (±s.d.). The widespread of translocation times shows that a substantial amount of events is much longer, which may be due to interactions between the DNA molecule and the graphene. Interestingly, the subset of events with longer translocations times (all >2.5 ms) showed a 16% larger graphene current signal. The transconductance recorded prior to the measurements was −0.25 nA/mV (see Figure 5d), at the potentials at which we performed the measurements. For the large majority of the events, no signal was detected in the common mode channel (see Figure 5a for a typical example). For a small minority of the events (3.5%), we measured a correlated signature in common mode channel of ∼100 μV magnitude, corresponding to transient currents of approximately 10pA. Eventually, after about 30 min of measurement time, the nanostructure broke, and the current was lost in the graphene nanostructure. Although the nanopore current had significantly increased to 16 nA, indicating a much increased pore size, events could still be detected in the ionic current, but the signatures in the graphene current were lost.

Data Interpretation

To interpret these signals, we first consider that we measured on the left wing of the Dirac curve with V_lift = 0 mV and V_ion = 300 mV, that is, with p-type conduction in graphene. Electrostatic interactions in this case would yield, as observed, a current enhancement in the graphene when the DNA molecule translocates through the nanostructure. Electrostatic gating by the negative charge of the DNA backbone and gating due to a change in the local potential at the nanopore during DNA translocation will both induce a current enhancement through I_g = g_mΔV. From the measured transconductance g_m = −0.25 nA/mV (see Figure 5d) and the median of the graphene current signals I_g = 3.8 nA measured at 20 mV V_bias (see inset Figure 5b), we deduce a ΔV ≅ −15 mV.

What underlies this induced voltage change? We first discuss the potential change that the charge of the DNA backbone can generate through 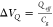. We consider that the Debye screening length at 1 M KCl is approximately 0.3 nm and that at any distance further than that no charge is probed. The maximum charge of the DNA as seen from the nanopore rim in 1 M KCl is approximated to be 2e or a fraction of that (as the DNA basepairs each carry an effective charge of 0.5e⁵¹ and as the effective graphene length is approximately 0.6 nm,¹⁰ see SI-9 for details). To approximate a value for the relevant capacitance of the graphene, we consider a ring of 1 nm extending from the nanopore rim, to find C_g ≅ 5 × 10^–19 F (see SI-8), yielding an estimate of ΔV_Q ranging between −30 mV and −600 mV. It must be noted, however, that the capacitance value extracted from the measured transconductance is substantially smaller, which would correspond to much higher ΔV_Q values. Second, we examine the potential change at the nanopore that occurs due to the insertion of DNA in the nanopore. With the use of an analytical relation,^38,40,42 we approximate the potential change at the nanopore to be about −50 mV, based on our nanopore geometry and DNA plasmid analyte (see SI-9 and Figure S9), which can be an overestimation because surface charges are not accounted for in this relation.³⁸

From these estimates, we conclude that the measured response signals in the graphene current can be explained as due to the local potential change and DNA charge. The approximations discussed above show that both effects can induce a ΔV in the order of tens of mV, which is close to what we measure here (−15 mV). Furthermore, it is possible that the graphene current signals are partly due to a non-electrostatic coupling between the nanopore and the DNA bases,²³⁻³⁴ leading to a modulation in the density of states which causes a change in the graphene nanoribbon conductance. Unfortunately, different theories provide rather conflicting predictions regarding the signal sign and magnitude, which hinders comparison to our data.

Finally, we comment on those rare (3.5%) events where we measured ∼100 μV signals in the common mode channel, which correspond to ∼20pA transient capacitive currents. The local capacitance between the electrolyte and the graphene at the nanopore is simply too small to induce such currents through 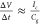(see SI-9). From this relation, it can be conceived that pA currents rather correspond to capacitances in the order of pF. The capacitance of the area exposed to liquid was measured to be ∼20 pF (see SI-9). Therefore, we attribute these events to non-local interactions ΔV_nl to the capacitances of the leads C_lead (i.e., to the graphene capacitance at a distance from the nanopore). This is supported by Spice simulations that show a 100 μV response in the common mode channel to 10 mV voltage steps when the capacitance at the nanopore is increased to 20 pF, see SI-9 for details.

Conclusions

In this paper, we have shown that it is possible to fabricate freestanding 30 × 30 nm graphene nanoribbons with a 5 nm nanopore in its center, which allow to measure resistive modulations in the inplane graphene current due to DNA translocation through the nanopore. Due to our high-temperature STEM sculpting approach, in combination with transfer techniques to assembled stacked structures of 2D materials, we were able to make graphene nanostructures that are significantly smaller than what was studied before. With our custom-made differential current amplifier, we presented a method that enables to discriminate between resistive modulations in the graphene current and signals due to capacitive coupling. Despite this success, we also have to note that, unfortunately, the fabrication procedure and protocol for DNA measurements were overly challenging, yielding an unacceptably low yield (as we successfully obtained dual signals in only 1 out of 180 devices; see Methods for details). In future studies, a more scalable approach could be explored, such as e-beam lithography with ion beam milling⁵² instead of TEM sculpting, leading to a higher device yield. Furthermore, other 2D materials, such as MoS₂ and WS₂^18,19 that can be oxygen-plasma treated to render the pore hydrophilic, could provide interesting alternatives to graphene, using the same approach of inplane current detection toward high-bandwidth DNA sequencing.

Methods

Fabrication Procedure

Devices were built on top of a silicon wafer, diced into silicon chips with 500 nm-thick silicon nitride membranes with embedded platinum heater coils, which were used to locally heat the graphene during STEM sculpting. Windows were etched in the backside of the “heaterchips” using backside spraycoating of e-beam resist, through membrane e-beam lithography, followed by RIE etching to obtain windows to 100 nm thickness.⁴⁵ Platinum electrodes were deposited on the topside of the chips using e-beam lithography (200 nm CSAR 6200.09 resist) and metal evaporation (10 nm Ti, 60 nm Pt). Next, 400 nm holes were patterned using e-beam lithography (800 nm resist layer CSAR 6200.18) and RIE etching (50W, 25:25 sccm Ar:CHF₃, 80 μbar). Monolayer graphene flakes were exfoliated onto silicon wafers with 90 nm SiO₂ and transferred onto the chips with platinum electrodes and holes in the membranes using the wedging transfer.⁵³ To prevent leakage currents on the membrane, and because sculpting with a transmission electron microscope (TEM) is difficult and time-consuming on supported graphene, graphene structures consisting of a 200 × 200 nm square with leads were prepatterned using e-beam lithography (200 nm PMMA A4) and oxygen plasma etching (40 s, 20 W, 20 sccm, 800 μbar), and the PMMA was removed through soaking in room-temperature acetone overnight. To prevent polymer residues after lithography, fresh stocks of PMMA were used. Subsequently, a 30 × 30 nm graphene nanostructure was sculpted using high-temperature STEM, as detailed below. After this high-temperature patterning in the TEM, the contact resistances were low (∼1 kΩ). To support the freestanding sculpted nanoribbon and to cover the cavities next to the ribbon (in order to make the nanopore the only possible way for the DNA to pass), we transferred thin (3–7 layer) flakes of h-BN on top of the nanoribbon using wedging transfer. Relatively free of dangling bonds, h-BN is a good insulator, has an atomically smooth surface, and has a lattice that is very similar to that of graphene, which makes it a good material to make stacked structures with graphene.⁵⁴ h-BN flakes were exfoliated onto silicon wafers with 90 nm SiO₂, and the flake thickness was determined using optical microscopy. In order to do this transfer, a glass mask was placed on top of the target device with the graphene nanostructure during the oxygen plasma cleaning step. The deposition of a very thick polyimide layer (1.5 μm) on top of the electrodes proved to be the only strategy to overcome electrochemical leakage during our nanopore measurements. Before patterning, samples were prebaked at 100 °C, and an adhesion layer vm651/vm652 0.1% in H₂O was spin-coated (3000 rpm) on top and baked for 2 min at 120 °C. Next, the layer of polyimide was spun on top (PI-2545) at 5000 rpm to obtain a thickness of 1.5 μm. The polymer was soft baked at 90 °C on a hot plate for 10 min. Finally, a 200 nm layer of PMMA (A4 4000 rpm) was spin-coated on top and baked at 90 °C on the hot plate for 5 min. A small area of 5 × 5 μm² at the nanostructure was exposed to the e-beam. After the development of the PMMA toplayer in MIBK (25% in IPA) and solvation of the exposed PI in diluted tetramethylammonium hydroxide (Mf321, 25% and 10%), a circular area with diameter ∼10 μm was cleared, and the PMMA was subsequently removed in room temperature acetone overnight. Finally, the nanopore was drilled in STEM mode, while using Joule heating to overcome carbon contamination. Before nanopore measurements were performed, the samples were baked at 180 °C for 5 min on a hot plate, to cure the polyimide.

STEM Sculpting of Nanoribbons and Nanopores

Sculpting of graphene nanoribbons and nanopores was performed using the focused electron beam of a TEM, model FEI Titan 80-300, operated in scanning mode (STEM). The fine probe of the electron beam (0.1 nm spot size, 0.15 nA beam current, 5 ms dwell time, doses ranging between 10⁷–10⁸ e/atom), combined with the 300 keV electron energy, allowed us to knock off single carbon atoms from the graphene lattice, so that we could “sculpt” graphene according to our needs.⁴⁶ Immediate feedback on the sculpting process was easily obtained by switching the microscope to imaging mode (5 μs dwell time and doses ranging between 10⁴–10⁵ e/atom). During sculpting, the electron beam decomposed the hydrocarbons which were adsorbed on graphene surface (originating from the TEM vacuum chamber and organic residues from solvents used during sample preparation), causing carbon atoms to “stick” near the illuminated area and grow into a thin amorphous carbon layer. Such carbon deposition was minimized by (1) the high temperatures (>300 °C), at which the surface diffusion of carbon adatoms is enhanced preventing adatom accumulation in the spot where the e-beam illuminates the sample, while graphene lattice recrystallization or “self-repair” is induced at high temperatures (∼500 °C),^46,47,55 and (2) the high vacuum (∼10^–8 mbar), as a lower total pressure implies a lower rate of impinging carbon atoms on the surface. For Joule heating, the Pt electrodes on the membrane were used to pass a high current densities (∼10⁸ A/cm²) through the graphene ribbon, to locally reach a very high temperature.⁵⁵ After polyimide deposition, the devices could not be heated above 300 °C, as the polymer would turn conductive at such temperatures. We therefore aimed for high vacuum to prevent carbon contamination and kept the samples in the TEM vacuum chamber for 12–24 h, until the vacuum reached ∼5 × 10^–8 mbar.

Device Yield

The elegancy of our approach is that it allows exquisite control of the graphene nanostructure properties, but its downside is that the device fabrication is extremely challenging, leading to a low device yield. In total, we started the fabrication procedure on about 180 devices, of which 51 graphene nanostructures were sculpted with STEM, 15 of which survived the h-BN transfer, polyimide passivation, and nanopore drilling. It showed to be very difficult to establish a decent nanopore current, likely due to the hydrophobic nature of the graphene. Attempts to wet the nanopores by ethanol flushing frequently resulted in breaking of the nanostructures. We managed to perform DNA translocation measurements on a few devices, but with only two devices we measured clear DNA signals in the ionic current channel, of which in one device, we managed to measure clear resistive modulations in the graphene current due to DNA, occurring simultaneously with the ionic current events. Comparison of the transconductances, noise levels, and ionic signals of the two samples are given in Table S1. In the sample where we did not resolve graphene signals, the sensitivity was lower, and the noise levels were higher.

Nanopore Experiments

The samples were mounted in a PEEK flowcell that fits a dedicated holder to insert Ag/AgCl probes in the flow chambers and to connect the electrodes to the electrode pads. The V_ion gate potential is set with the use of an Axopatch 200B patchclamp amplifier, connected to two Ag/AgCl electrodes on each side of the membrane. The positive electrode was located on the graphene side (trans) of the membrane. The platinum electrode pads on the chip were contacted by PoGo pins connected to the differential preamplifier, such that the amplifier is in close proximity to the graphene nanostructure (minimizing input capacitances). Nanopore measurements were performed with 1 M KCl, 10 mM Tris-HCl buffer solution (pH 8.1), and 3 ng/μL 20kb DNA plasmids dissolved in the same buffer. We measured the transconductance by sweeping V_ion in the range of the voltages that were used during the DNA measurements (in our case 200–400 mV) at selected V_lift gate potentials. Typically, the measured sensitivities ranged between 0.1 and 2 nA/mV (varying per device). Due to the presence of the graphene nanostructure, we were not able to oxygen plasma or piranha clean the samples, making it difficult to wet the nanopore during DNA measurements. Attempts to wet the nanopores by flushing ethanol and buffer often resulted in breaking of the nanoribbons. The events were extracted from the ionic current traces using Tranzalyser,⁵⁶ and the corresponding time traces in the differential and common mode channels were analyzed with Matlab.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acsnano.7b08635.

• Experimental data, simulations and calculations, including SPICE simulations, prevention of electrochemical leakage, transconductance and sensitivity of proof-of-principle measurement, examples DNA translocation events, sensitivity of the graphene nanoribbon, graphene capacitance determination, data interpretation, and transconductance, signal and noise details of samples (PDF)

Author Contributions

S.J.H. performed the nanofabrication, the experiments and analyzed the data. L.V. and H.Z. conceived the STEM work, L.V. carried out the STEM work. R.S. designed and developed the differential amplifier. S.J.H, S.P. and C.D. conceived and discussed the work and wrote the paper.

The authors declare no competing financial interest.