Stabilized supralinear network can give rise to bistable, oscillatory, and persistent activity

Significance

Many fundamental neural computations from normalization to rhythm generation emerge from the same cortical hardware, but they often require dedicated models to explain each phenomenon. Recently, the stabilized supralinear network (SSN) model has been used to explain a variety of nonlinear integration phenomena such as normalization, surround suppression, and contrast invariance. However, cortical circuits are also capable of implementing working memory and oscillations which are often associated with distinct model classes. Here, we show that the SSN motif can serve as a universal circuit model that is sufficient to support not only stimulus integration phenomena but also persistent states, self-sustained network-wide oscillations along with two coexisting stable states that have been linked with working memory.

Abstract

A hallmark of cortical circuits is their versatility. They can perform multiple fundamental computations such as normalization, memory storage, and rhythm generation. Yet it is far from clear how such versatility can be achieved in a single circuit, given that specialized models are often needed to replicate each computation. Here, we show that the stabilized supralinear network (SSN) model, which was originally proposed for sensory integration phenomena such as contrast invariance, normalization, and surround suppression, can give rise to dynamic cortical features of working memory, persistent activity, and rhythm generation. We study the SSN model analytically and uncover regimes where it can provide a substrate for working memory by supporting two stable steady states. Furthermore, we prove that the SSN model can sustain finite firing rates following input withdrawal and present an exact connectivity condition for such persistent activity. In addition, we show that the SSN model can undergo a supercritical Hopf bifurcation and generate global oscillations. Based on the SSN model, we outline the synaptic and neuronal mechanisms underlying computational versatility of cortical circuits. Our work shows that the SSN is an exactly solvable nonlinear recurrent neural network model that could pave the way for a unified theory of cortical function.

Understanding the mechanisms underlying cortical function is the main challenge facing theoretical neuroscience. Nonlinear responses such as normalization, contrast invariance, and surround suppression are often encountered in the cortex, particularly in the visual cortex (1, 2). At the same time, working memory about a transient stimulus, persistent activity in decision-making tasks, and generation of global rhythms represent fundamental computations which have been linked to cognitive functions (3–5). Whether these computations arise from common or different mechanisms is an open question.

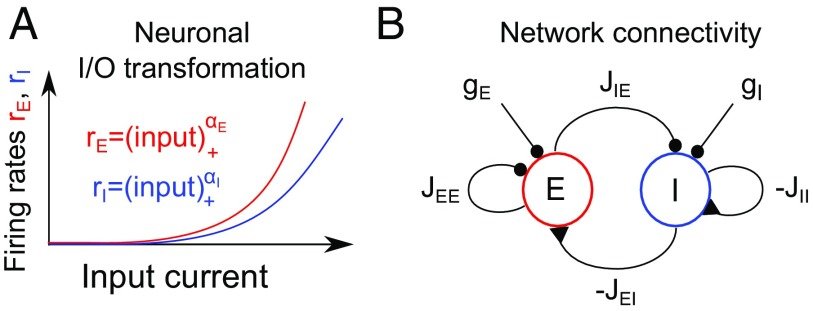
Previous work showed that the response of in vivo cortical neurons is well described by a power law (6) (Fig. 1). Experiments and theory indicate that low firing rates and high variability reported in the cortex are associated with a power-law activation function and noise-driven firing (6–9). Furthermore, a power law is mathematically the only function that permits precise contrast invariance of tuning given input that has contrast-invariant tuning (8, 9). Recent work (1, 2, 10) proposed the stabilized supralinear network (SSN) as a mechanism for normalization, contrast invariance, and surround suppression. While the SSN model is powerful in the context of stimulus integration, its role for other cortical computations remains to be clarified (11).

Fig. 1.

Firing-rate transformation and network wiring. (A) Threshold power-law transfer function determines the relationship between input current and the firing rate of excitatory and inhibitory neurons. (B) Populations of power-law neurons are recurrently connected and receive excitatory external inputs. E, excitatory; I, inhibitory.

Working memory is the ability to remember a transient input long enough for it to be processed (3). It is often implemented as a stimulus-induced switch in a bistable system (12). Persistent activity is thought to be critical for neural implementation of decision making (3, 4). Mechanistically, it is firing observed in the absence of any stimulus between the cue and the go signal in decision-making tasks. Persistent activity was first recorded in the early 1970s in the prefrontal cortex of behaving monkeys (13) and has since been found in other cortical areas (3). Finally, generation of synchronous network-wide rhythms is also a fundamental cortical feature that has been suggested to mediate communication between cortical areas and may be needed for attention, feature integration, and motor control (5).

Here, we investigate whether the SSN motif is sufficient to give rise to network multistability, persistent activity, and global rhythms. Seminal articles have proposed that working memory is a result of network multistability (12). To explain multistability, mechanisms that involve either S-shaped neuronal activation function in combination with a suitably strong excitatory feedback or S-shaped synaptic nonlinearity have been proposed (14–16). Likewise, a persistent state which occurs in the decision-making process has been modeled using synaptic nonlinearities (17). The SSN framework, however, lacks both ingredients: it does not exhibit an S-shaped neural activation function and lacks synaptic plasticity. It is also currently unclear whether the SSN motif alone supports the emergence of stable global oscillations. If oscillations can emerge in the SSN, it would be important to determine the conditions for connectivity and neural power-law exponents when this occurs. On the other hand, if the SSN motif is not sufficient for the emergence of oscillations, it would be necessary to understand what sets it apart from models that can support global rhythms (14, 18, 19).

To investigate whether and when the SSN model can support multistability and persistent and oscillatory activity we need to understand its dynamics systematically. Since the SSN is a nonlinear model, mathematical methods to obtain exact solutions are challenging. Previous studies used the functional shape of nullclines to determine their possible crossings and derive the number of steady states in the Wilson–Cowan model with an S-shaped activation function (14, 15). Here, we aim to explain how location and multiplicity of steady states are influenced by specific parameter choices for which information on the shape of nullclines is not always mathematically tractable. To this end, we developed an analytical method that allows us to map the steady states of the 2D SSN model to the zero crossings of a 1D characteristic function. We determine multiplicity and stability of the SSN steady states for all possible parameter regimes. In particular, we show that the SSN model supports the following three effects. First, we outline network configurations corresponding to a bistable regime that could serve as a substrate for working memory. Second, we show that the SSN model can lead to dynamically stable persistent activity and derive the corresponding connectivity requirements. Third, we prove the occurrence of stable global oscillations in the SSN and provide methods for how to tune the oscillatory frequency to a desired value. Our article is organized as follows. First, we analyze the multiplicity and stability of the SSN steady states and show the existence of a unique mapping between zero crossings of a characteristic function and steady states. Second, we prove for equal-integer power-law exponents that the model has at most four coexisting steady states and at most two steady states can be stable. Finally, we present parameter regimes for which a stable persistent state and global oscillations exist.

Results

We consider a recurrent network as illustrated in Fig. 1 and model the activity of excitatory and inhibitory populations $r_E$ and $r_I$ using the following equations often referred to as the SSN model (2, 10):

$$\begin{array}{c}{\tau }_E{\dot{r}}_E=-r_E+{(J_{EE}{r}_E-J_{EI}{r}_I+g_E)}_{+}^{{\alpha }_E},\\ {\tau }_I{\dot{r}}_I=-r_I+{(J_{IE}{r}_E-J_{II}{r}_I+g_I)}_{+}^{{\alpha }_I}.\end{array}$$ [1]

Here, $g_E$ and $g_I$ are the nonnegative constant inputs to the respective populations, and ${\tau }_E$ and ${\tau }_I$ denote the time constants. $J_{XY}>0$ is the effective synaptic strength from the population $Y$ to the population $X$, where $X,Y\in \{E,I\}$. By $J$ we denote the connectivity matrix where the first row is $J_{EE}$, $-J_{EI}$, and the second row is $J_{IE}$, $-J_{II}$. The susceptibility of a neuronal population to currents is expressed using the power-law activation functions with the exponents ${\alpha }_E,{\alpha }_I\ge 2$, where ${(x)}_{+}=\max \{x,0\}$. The power-law dependence is based on experimental and theoretical studies (6, 8, 9). Here, let us briefly comment on our choice of units. Throughout the article, we use unitless quantities for all parameters including firing rates because the values of connectivities and inputs can be rescaled by any number to match the desired firing-rate range. See Rescaling the Connectivity and Input Constants to Match a Desired Firing-Rate Range for details on the rescaling procedure.

To characterize the SSN activity states, it is crucial to understand how location, multiplicity, and dynamical stability of the SSN steady states depend on connectivity, inputs, and activation functions of neuronal populations. The steady-state firing rates $r_E$ and $r_I$ are described by

$$\begin{array}{c}{r}_E={(J_{EE}{r}_E-J_{EI}{r}_I+g_E)}_{+}^{{\alpha }_E},\\ r_I={(J_{IE}{r}_E-J_{II}{r}_I+g_I)}_{+}^{{\alpha }_I}.\end{array}$$ [2]

While a steady state can be easily found in the case of ${\alpha }_{E,I}=1$, the nonlinear case ${\alpha }_{E,I}\ge 2$ currently lacks analytical solution strategies. Here, we present a unique approach for finding and analyzing the steady states in Eq. 1. We show that the 2D system of nonlinear equations in Eq. 2 can be reduced to a single 1D equation for a nonlinear characteristic function. Specifically, we have identified a one-to-one correspondence between the 2D steady states and the 1D zero crossings of a characteristic function such that the steady-state search algorithm is reduced to a lower-dimensional problem.

Reducing the Dimensionality via a Characteristic Function.

To solve the two nonlinear equations presented in Eq. 2, we take the following steps. We first apply a variable substitution replacing $r_X$ with $z_X=J_{XE}{r}_E-J_{XI}{r}_I+g_X$, $X\in \{E,I\}$ as detailed in Materials and Methods. Now, we can simplify the problem by eliminating the variable $z_I$ for $detJ\ge 0$ and $z_E$ for $detJ<0$. We denote the remaining variable by $z$ and show that the solutions of Eq. 2 are uniquely mapped to the zero crossings of the characteristic function $\mathcal{F}$ which depends on $z$. For $detJ\ge 0$, this function is given by

$$\mathcal{F}(z)=J_{EE}{(z)}_{+}^{{\alpha }_E}-J_{EI}{(P(z))}_{+}^{{\alpha }_I}-z+g_E,$$ [3]

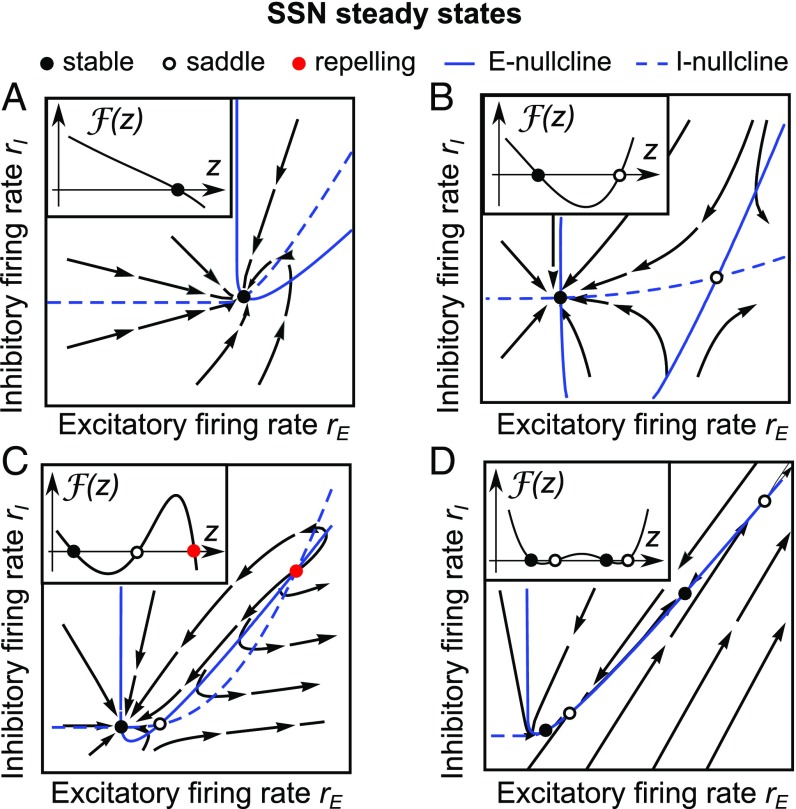
where $P(z)=J_{EI}^{-1}(detJ\cdot {(z)}_{+}^{{\alpha }_E}+J_{II}(z-g_E)+J_{EI}{g}_I)$. The steady-state $r_E$, $r_I$ corresponding to the zero-crossing $z$ is given by $r_E={(z)}_{+}^{{\alpha }_E}$ and $r_I={(P(z))}_{+}^{{\alpha }_I}$. A similar form of $\mathcal{F}$ and $P$ exists for $detJ<0$ (Materials and Methods and Characteristic Function). In the following, we refer to the function $\mathcal{F}$ as a characteristic function. Mathematically, the nullcline crossings in Eq. 2 that define the steady states are now mapped to the zero crossings of a 1D function $\mathcal{F}$. This transformation significantly enhances the mathematical tractability because steady states are now intersection points of a 1D function with a coordinate axis and are no longer intersections of two complex nonlinear nullclines. In Fig. 2, we depict the zero crossings of $\mathcal{F}$ and the corresponding steady states for four representative classes of solutions. Additionally, in Location of SSN Steady States Is Preserved in the Presence of Firing-Rate Saturation and Fig. S2 we show that these steady states remain at the same location if activation functions saturate at high firing rates. Saturation of activation functions provides boundedness of all solution trajectories; however, it can introduce additional steady states.

Fig. 2.

Steady states and characteristic functions. Steady states are related to zero crossings of the characteristic function $\mathcal{F}$ (A–D, Insets). Black flowlines represent trajectories starting from different initial points. (A) A single steady state can exist only for $detJ\ge 0$. (B) Two SSN steady states can coexist for $detJ\le 0$. Zero crossings of $\mathcal{F}$ with a positive derivative correspond to saddles. (C) Three steady states are possible if $detJ\ge 0$. Dependent on the sign in Eq. 5 zero crossings with the negative derivative can correspond to either stable or repelling steady states. (D) Four steady states can coexist only for $detJ<0$. Parameters are as in Table 2.

Stability Conditions.

The characteristic functions in Fig. 2 exhibit zero crossings with positive derivatives which correspond to saddles, while those with negative derivatives correspond to either stable or repelling steady states. To support this finding mathematically, we consider the eigenvalues ${\lambda }_1$ and ${\lambda }_2$ of the Jacobian matrix at the steady state of interest. We find that $\mathcal{F}\prime$ at the zero-crossing $z$ is related to the negative product of the eigenvalues at the corresponding steady state:

$${\lambda }_1{\lambda }_2=-{\tau }_E^{-1}{\tau }_I^{-1}\mathcal{F}\prime (z).$$ [4]

Notably, Eq. 4 is similar to the relation derived in ref. 20 where a 2D system of equations corresponding to a conductance-based model was reduced to a 1D function whose derivative coincided with the determinant of the Jacobian. A steady state is a saddle if the eigenvalues are real and have opposite signs. This can occur if and only if $\mathcal{F}\prime$ is positive at the zero-crossing $z$ (Fig. 2). Stable steady states require that both $\mathcal{F}\prime$ and the sum of the eigenvalues are negative (18). The sum of the eigenvalues is negative only if

$$0<{\tau }_I\left(1-J_{EE}{\alpha }_E{r}_E^{1-{\alpha }_E^{-1}}\right)+{\tau }_E\left(1+J_{II}{\alpha }_I{r}_I^{1-{\alpha }_I^{-1}}\right).$$ [5]

Thus, the stability of a steady state is equivalent to the requirements that $\mathcal{F}\prime$ is negative at the zero crossing and that the condition Eq. 5 is fulfilled. We note that if $\mathcal{F}\prime$ is negative, then Eq. 5 can always be fulfilled by choosing ${\tau }_I/{\tau }_E$ to be sufficiently small. Interestingly, we have found that if $detJ\le 0$ and ${\tau }_I\le {\tau }_E$, then the sign of $\mathcal{F}\prime$ directly determines the stability of the steady state. If $\mathcal{F}\prime (z)<0$ in this case, then Eq. 5 is automatically fulfilled and the steady state is stable. If $\mathcal{F}\prime (z)>0$, then the corresponding steady state is a saddle (Stability Conditions).

Determining the Number of Coexisting Steady States.

We now determine how many steady states can coexist for a given synaptic connectivity and inputs. First, let us note that previous work (14, 15) reported up to five steady states in the Wilson–Cowan model with an S-shaped activation for positive $J_{XY}$ and nonnegative $g_X$ or up to nine if $J_{XY}$ and $g_X$ are allowed to be negative. Here, we aim to find how many steady states emerge from a power-law activation function and determine exactly the possible number of steady states for a given combination of inputs, exponents, and connectivity. To obtain exact results, we consider a situation where the excitatory and the inhibitory populations have the same integer exponents, such that ${\alpha }_E={\alpha }_I=n\in \mathbb{N}$ and $n\ge 2$. Here, it is plausible to assume that the characteristic function, which now contains a polynomial of degree up to $n^2$, could have $n^2$ zero crossings leading to $n^2$ steady states. If the number of steady states was indeed dependent on the steepness of the activation function and grew proportional to $n^2$, then networks of neurons with steep activation functions and higher exponents $n$ would likely have a fractured phase space with many coexisting steady states. The steady state assumed by the network could then be highly dependent on the initial condition. Since such networks have not yet been biologically observed, it is likely that the number of steady states remains bounded even if the steepness of the activation function $n$ increases. Thus, we decided to check our initial intuition that the number of steady states grows with $n$. Surprisingly, it turned out not to be the case.

To study the multiplicity of the SSN steady states, we partition the parameter space of the SSN model into nine classes. Such partition makes the problem more accessible for mathematical analysis. For details we refer to Materials and Methods. First, we identify three classes according to the sign of $detJ$ (Table 1). Second, we further separate each of three $detJ$ classes into three parameter subsets according to the sign of the constants $C_{+}=-J_{EI}^{-1}{J}_{II}{g}_E+g_I$ for $detJ\ge 0$ and $C_{-}=-J_{IE}^{-1}{J}_{EE}{g}_I+g_E$ for $detJ<0$ (Table 1 and Materials and Methods). To determine the multiplicity of steady states for each of the nine parameter classes presented in Table 1, we follow the steps outlined in Materials and Methods and Multiplicity of Steady States. We find that there can be at most four steady states and this number does not grow with $n$. For $n=2$ there are at most three steady states (Multiplicity of Steady States). For $n\ge 2$, we show that at most two stable steady states can coexist (Fig. 2 and Table 1).

Table 1.

Multiplicity of SSN steady states for ${\alpha }_E={\alpha }_I=n$, whereby $n\mathbf{\in }\mathrm{N}$ and $n\mathbf{\ge }2$

	$C_{-}<0$	$C_{-}=0$	$C_{-}>0$
$n>2$, $detJ<0$	2(1)/0	2(1)/0	4(2)/2(1)/0
$n=2$, $detJ<0$	2(1)/0	2(1)/0	2(1)/0
	$C_{+}<0$	$C_{+}=0$	$C_{+}>0$
$n>2$, $detJ=0$	3(2)/2(1)/1(1)/0	2(1)/1(1)/0	2(1)/1(1)/0
$n=2$, $detJ=0$	2(1)/1(1)/0	2(1)/1(1)/0	2(1)/1(1)/0
$n\ge 2$, $detJ>0$	3(2)/1(1)	3(2)/1(1)	3(2)/1(1)

For each class, we give the possible numbers of steady states (in parentheses is the maximal number of stable states, which is for example possible for sufficiently small ${\tau }_I$, Eq. 5). All alternative steady-state configurations are indicated with “/”. In cases where results for $n=2$ and $n>2$ differ, we show them on a separate line. Parameter sets supporting bistability are highlighted in boldface type. Ordered by the distance to the origin, the first and the third steady states always correspond to the zero crossings of the characteristic function with negative derivative $\mathcal{F}\prime (z)<0$ and dependent on the sign in Eq. 5 are either stable or repelling. The second and the fourth steady states always correspond to the zero crossings with the positive derivative $\mathcal{F}\prime (z)>0$ and represent saddles. For completeness, let us note that we have ignored nongeneric cases (destroyed by any perturbation of parameters) in which there is a steady state with a zero eigenvalue.

Taken together, our results indicate that the power-law–type networks with equal integer exponents can support two coexisting stable states, but no more than two stable states can occur at a time. The ability of a circuit to support bistability has been suggested as a substrate for working memory where the circuit transitions from the lower to the upper state follow the presentation of a brief stimulus. The emergence of bistability has so far been confirmed in neural networks with S-shaped synaptic or neuronal nonlinearities (16). However, our results show that neither synaptic nonlinearities nor S-shaped activation functions are prerequisites for bistability in a network. Two coexisting steady states can simply emerge in a network with a globally convex power-law activation.

Persistent State.

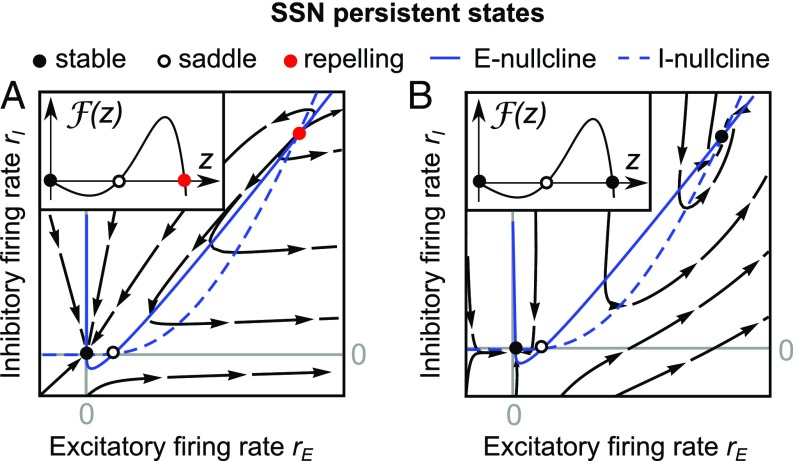
One of the hallmarks of nonlinear systems is the ability to sustain a response after the input is switched off. Such response is referred to as a persistent state. We ask whether it is possible to observe a persistent state in a system described by Eq. 1 with the exponents ${\alpha }_E,{\alpha }_I\ge 2$. Here, we consider the same integer exponents ${\alpha }_E={\alpha }_I=n\ge 2$ of the excitatory and the inhibitory populations. To approach this question, we examined the characteristic function for zero inputs $g_E$ and $g_I$ and looked for its positive zero crossings with the negative derivative. We note that only a zero crossing with the negative derivative can lead to a stable steady state. In absence of inputs, we derived the following necessary condition for the existence of such zero crossing which can be directly verified for $J$ and $n$:

$$0<detJ<\frac{n}{n+1}\left(J_{EE}^{\frac{n+1}{n}}{J}_{EI}^{\frac{n-1}{n}}-J_{II}{J}_{EE}\right)$$ [6]

(Materials and Methods and Existence of Persistent States). The inequality on the left side of Eq. 6 implies that a persistent state in the network described by Eq. 1 is possible only when the cross-population connectivity $J_{EI}{J}_{IE}$ dominates the connectivity $J_{EE}{J}_{II}$ within the individual populations. Moreover, the excitability $n$ of individual neurons has to fulfill the inequality on the right side of Eq. 6. We note that a stable persistent state does not exist outside the parameter set specified by the inequality Eq. 6 (see Materials and Methods for further details). To guarantee that a given persistent steady state is stable and can thus be reached dynamically, the time constants ${\tau }_E$ and ${\tau }_I$ need to meet the stability condition Eq. 5 presented above. Fig. 3 A and B shows examples of a stable and repelling persistent state. If the existence of a positive zero crossing with negative derivative in absence of inputs has been established, ${\tau }_I$ can be chosen sufficiently small (or ${\tau }_E$ large) such that the persistent state fulfills the stability condition Eq. 5.

Fig. 3.

Persistent state in the SSN model. The nonzero persistent state can be stable (black solid circle) or repelling (red solid circle). If Eq. 5 is not satisfied, the persistent state is repelling (A); otherwise it is stable (B). Parameters are as in Table 2.

Table 2.

Synaptic and neuronal parameters in Figs. 2–4

	Fig. 2				Fig. 3		Fig. 4
Parameters	A	B	C	D	A	B	A	B
$J_{EE}$	1.1	1.5	1.1	2.25	1.5	1.5	1.5	1.5
$J_{EI}$	0.9	1	1	44.4	1	1	1	1
$J_{IE}$	2	0.5	0.5	1	0.5	0.5	10	10
$J_{II}$	1	1	0.1	20	0.1	0.1	1	1
$g_E$	0.4	0.1	0.2	0.2808	0	0	0.7	5
$g_I$	0.3	0.1	0.01	0.015	0	0	0.01	0.01
${\tau }_E$	1	1	1	1	1	15	0.1	0.1

For all figures, we use ${\alpha }_E={\alpha }_I=3$ and ${\tau }_I=1$.

Emergence of Oscillations.

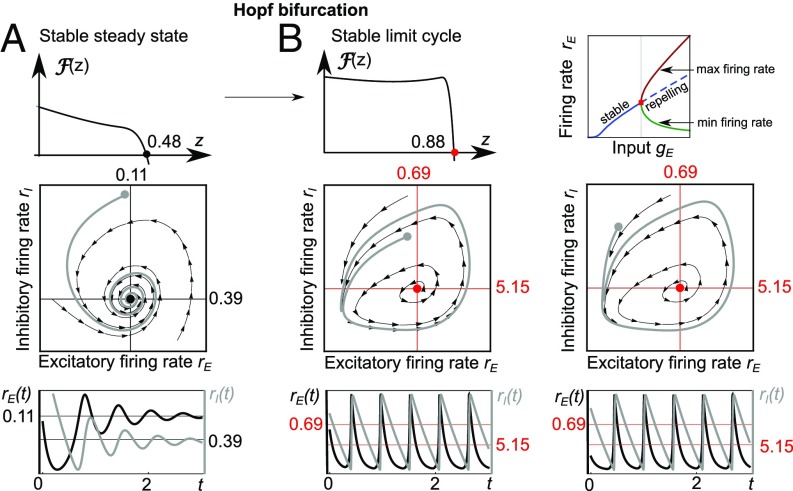
Periodic fluctuations of neural activity are a common occurrence across the cortex and have been associated with many information-processing tasks (5). Some cognitive disorders are also reportedly accompanied by a change in the oscillatory cortical activity (21). In some instances, the oscillatory activity has been explained by the amplification of selected input frequencies (22) while in others, it has been proposed to arise from intrinsic, self-sustained oscillations originating for example from a Hopf bifurcation (18). Here, we study whether the SSN can support global oscillations arising from a Hopf bifurcation and if so which synaptic or neuronal parameters can lead to oscillations and which ones control the oscillatory frequency. An extensive analysis of the Hopf bifurcation for the Wilson–Cowan model with an S-shaped activation function can be found in ref. 23. A Hopf bifurcation occurs when the complex conjugate eigenvalues corresponding to a stable steady state cross the imaginary axis when the input current or other parameter values are varied. In this way, the initial frequency of the global oscillation corresponds to the imaginary part of the eigenvalues (18). To determine when the steady-state eigenvalues in the SSN can become complex and when the limit cycle is stable, we have followed the steps outlined in Existence of Global Oscillations and in ref. 24. If $detJ>0$, then it is always possible to find inputs and time constants for which the eigenvalues become purely imaginary. Moreover, for $detJ\le 0$ a Hopf bifurcation in the SSN can occur only for ${\tau }_I>{\tau }_E$, because our stability analysis implies that for ${\tau }_I\le {\tau }_E$ eigenvalues are always real. When a Hopf bifurcation occurs, the emergent oscillation frequency is $f={(2\pi )}^{-1}\sqrt{-{\tau }_E^{-1}{\tau }_I^{-1}\mathcal{F}\prime (z)}$. We note that $f$ can be tuned to any value; e.g., decreasing the time constants ${\tau }_E$ or ${\tau }_I$ will result in an increasing oscillatory frequency. The stability of the limit cycle can be determined using the Lyapunov coefficient; see Existence of Global Oscillations and the code accompanying this article. In Fig. 4 we present the example of a stable limit cycle emerging from a supercritical Hopf transition.

Fig. 4.

Emergence of oscillations in the SSN model. (A) A steady state corresponding to the zero crossing of $\mathcal{F}$ at $z=0.48$ (Top) is located at $r_E=0.11$, $r_I=0.39$ (Middle). Initializing the network at $r_E(0)=0.1$, $r_I(0)=0.6$ leads to a converging spiral (Middle and Bottom). (B) If the input $g_E$ to the excitatory population is increased, the steady state becomes repelling (bifurcation diagram, Top Right). The zero crossing of $\mathcal{F}$ is shifted to $z=0.88$ (Top Left). The corresponding steady-state $r_E=0.69$, $r_I=5.15$ is repelling, and a stable limit cycle can be observed (Middle row). The initial conditions located inside (B, Left) and outside (B, Right) both converge to the limit cycle orbit. Parameters are as in Table 2.

Discussion

Multipurpose models that explain more than just the functions they are designed for are currently in short supply. Here, we show that the SSN can serve as a universal circuit model that can support rhythm generation and working-memory features such as bistability and persistent states along with many stimulus integration rules as well as contrast invariance, normalization, and surround suppression (2, 6, 8, 9). Importantly, we provide a unique analytical method to obtain exact solutions for the SSN model that are valid for all parameter regimes. This makes the SSN model a nonlinear, yet exactly solvable, recurrent neural network model. Remarkably, the computational versatility of the SSN model emerges from the nonlinear activation function and does not require synaptic plasticity, delay tuning, or specific ion channel models. The characteristic function method we derived here allows us to show that the connectivity regime where the product of cross-connectivities $J_{IE}{J}_{EI}$ dominates the recurrent connections $J_{II}{J}_{EE}$ ($detJ>0$) is particularly efficient and supports all three of the fundamental activity types: bistability, persistent state, and oscillations. In our work, we derived exact conditions that describe how to control the frequency of global rhythms and determined when persistent activity emerges and when two coexisting states with finite firing rates can subserve working memory. For example, we found that persistent activity in the SSN model can occur only if $detJ>0$ and if the power-law steepness is carefully matched to the connectivity matrix (Eq. 6). Our work thus provides an important step toward a unified theory of cortical function by identifying connectivity regimes supporting working memory and network oscillations and uniting these fundamental computations via the SSN.

Materials and Methods

Correspondence Between the Steady States and the Zero Crossings of a Characteristic Function.

We show how the SSN steady states can be unambiguously mapped to the zero crossings of a characteristic function $\mathcal{F}$, a correspondence which we illustrate in Fig. 2. Here, we derive $\mathcal{F}$ for $detJ>0$. Using similar arguments, we derive $\mathcal{F}$ in Characteristic Function for $detJ\le 0$ and summarize both in Eq. 15.

As a first step toward $\mathcal{F}$ for $detJ>0$ we substitute

$$z_E=J_{EE}{r}_E-J_{EI}{r}_I+g_E,z_I=J_{IE}{r}_E-J_{II}{r}_I+g_I.$$ [7]

Now the equilibrium equations in Eq. 2 can be written as

$$r_E={(z_E)}_{+}^{{\alpha }_E},\hspace{1em}{r}_I={(z_I)}_{+}^{{\alpha }_I}.$$ [8]

Since $detJ\ne 0$, we now express the old variables $r_E$, $r_I$ using the new variables $z_E$, $z_I$ by inverting Eq. 7. We obtain

$$\begin{array}{c}{r}_E={(detJ)}^{-1}(-J_{II}{z}_E+J_{EI}{z}_I-C_{+}{J}_{EI}),\\ r_I={(detJ)}^{-1}(-J_{IE}{z}_E+J_{EE}{z}_I+C_{-}{J}_{IE}),\end{array}$$ [9]

where $C_{+}=-J_{EI}^{-1}{J}_{II}{g}_E+g_I$ and $C_{-}=-J_{IE}^{-1}{J}_{EE}{g}_I+g_E$. Our next goal is to eliminate $r_E$ and $r_I$ from the above equations. To this end, we substitute Eq. 8 into Eq. 9 and obtain

$$detJ\cdot J_{EI}^{-1}\cdot {(z_E)}_{+}^{{\alpha }_E}+J_{EI}^{-1}{J}_{II}{z}_E+C_{+}=z_I,$$ [10]

$$-detJ\cdot J_{IE}^{-1}\cdot {(z_I)}_{+}^{{\alpha }_I}+J_{IE}^{-1}{J}_{EE}{z}_I+C_{-}=z_E.$$ [11]

Now, the above equations contain only the new variables $z_E$ and $z_I$. Our next goal is to eliminate the variable $z_I$ from the system Eqs. 10 and 11 and reduce the system to 1D. To this end, we introduce an abbreviation for the left side of Eq. 10:

$$P(z_E)=detJ\cdot J_{EI}^{-1}\cdot {(z_E)}_{+}^{{\alpha }_E}+J_{EI}^{-1}{J}_{II}{z}_E+C_{+}.$$ [12]

Now, Eq. 10 can be written as $P(z_E)=z_I$. We substitute $z_I=P(z_E)$ into Eq. 11 and obtain

$$J_{EE}{(z_E)}_{+}^{{\alpha }_E}-J_{EI}{(P(z_E))}_{+}^{{\alpha }_I}-z_E+g_E=0.$$ [13]

For $detJ>0$, we denote by $\mathcal{F}$ the left side of Eq. 13,

$$\mathcal{F}(z_E)=J_{EE}{(z_E)}_{+}^{{\alpha }_E}-J_{EI}{(P(z_E))}_{+}^{{\alpha }_I}-z_E+g_E$$ [14]

with $P$ defined by Eq. 12. We thereby have shown that if $r_E$, $r_I$ is a steady state for $detJ>0$, then $z_E=J_{EE}{r}_E-J_{EI}{r}_I+g_E$ satisfies $\mathcal{F}(z_E)=0$ with the functions $P$ and $\mathcal{F}$ given by Eqs. 12 and 14, respectively. Next, we show that no spurious zeros of $\mathcal{F}$ exist that do not correspond to steady states. To this end, we consider a real number $z^{\ast }$ such that $\mathcal{F}(z^{\ast })=0$ where $\mathcal{F}$ is as defined by Eq. 14 for $detJ>0$. We define $r_E={(z^{\ast })}_{+}^{{\alpha }_E}$, $r_I={(P(z^{\ast }))}_{+}^{{\alpha }_I}$, in which $P$ is given by Eq. 12, and insert these variables into $\mathcal{F}(z^{\ast })=0$. Thereby we obtain the first steady-state relation from Eq. 2. Next, we use the relation $r_I={(P(z^{\ast }))}_{+}^{{\alpha }_I}$ to obtain the second relation in Eq. 2. This shows that our definition of $\mathcal{F}$ establishes a bijective mapping between $r_E$, $r_I$, and the zero crossings of $\mathcal{F}$.

In summary, the steps outlined above for $detJ>0$ and those in Characteristic Function for $detJ\le 0$ lead to the following form of $\mathcal{F}$:

$$\mathcal{F}(z)=\{\begin{array}{cc}{J}_{EE}{(z)}_{+}^{{\alpha }_E}-J_{EI}{(P(z))}_{+}^{{\alpha }_I}-z+g_E,\hfill & detJ\ge 0,\hfill \\ J_{IE}{(P(z))}_{+}^{{\alpha }_E}-J_{II}{(z)}_{+}^{{\alpha }_I}-z+g_I,\hfill & detJ<0.\hfill \end{array}$$ [15]

Here, the function $P$ is given by

$$P(z)=\{\begin{array}{cc}detJ\cdot J_{EI}^{-1}\cdot {(z)}_{+}^{{\alpha }_E}+J_{EI}^{-1}{J}_{II}z+C_{+},\hfill & detJ\ge 0\hfill \\ -detJ\cdot J_{IE}^{-1}\cdot {(z)}_{+}^{{\alpha }_I}+J_{IE}^{-1}{J}_{EE}z+C_{-},\hfill & detJ<0\hfill \end{array}$$

with the constants $C_{+}$ and $C_{-}$ defined above.

Notably, we obtain a bijective mapping such that if $r_E$, $r_I$ is a steady state of Eq. 1, then $\mathcal{F}(z)=0$ whereby

$$z=\{\begin{array}{cc}{J}_{EE}{r}_E-J_{EI}{r}_I+g_E,\hfill & detJ\ge 0\hfill \\ J_{IE}{r}_E-J_{II}{r}_I+g_I,\hfill & detJ<0.\hfill \end{array}$$

And vice versa, if $\mathcal{F}(z)=0$, then the steady state of Eq. 1 is

$$r_E=\{\begin{array}{cc}{(z)}_{+}^{{\alpha }_E},\hfill & detJ\ge 0\hfill \\ {(P(z))}_{+}^{{\alpha }_E},\hfill & detJ<0\hfill \end{array},\hspace{1em}{r}_I=\{\begin{array}{cc}{(P(z))}_{+}^{{\alpha }_I},\hfill & detJ\ge 0\hfill \\ {(z)}_{+}^{{\alpha }_I},\hfill & detJ<0.\hfill \end{array}$$

We note that using different $P$ functions for $detJ\ge 0$ and $detJ<0$ as in Eq. 15 is necessary for calculating the number of zero crossings of $\mathcal{F}$ later (it is critical to the Descartes rule of signs and other statements) (Multiplicity of Steady States). When applying the same $P$ and $\mathcal{F}$ for all values of $detJ$ one would also obtain a bijective mapping but multiplicity statements would no longer be readily available.

Stability of Steady States.

In the previous paragraph, we presented the method of finding the steady states using the characteristic function in Eq. 15. Next, we derive exact stability conditions for the steady states. Our goal is to relate stability of steady states to the behavior of the characteristic function in the vicinity of its zero crossings. To this end, we first move the time constants to the right side of Eq. 1 and consider the resulting dynamical system $({\dot{r}}_E,{\dot{r}}_I)=G(r_E,r_I)$. Its Jacobian $DG(r_E,r_I)$ is given by

$$DG=\left(\begin{array}{cccccccccc}\hfill {\tau }_E^{-1}(J_{EE}{\alpha }_E{(z_E)}_{+}^{{\alpha }_E-1}-1)\hfill & \hfill -{\tau }_E^{-1}{J}_{EI}{\alpha }_E{(z_E)}_{+}^{{\alpha }_E-1}\hfill & & & & & & & & \\ \hfill {\tau }_I^{-1}{J}_{IE}{\alpha }_I{(z_I)}_{+}^{{\alpha }_I-1}\hfill & \hfill -{\tau }_I^{-1}(1+J_{II}{\alpha }_I{(z_I)}_{+}^{{\alpha }_I-1})\hfill & & & & & & & & \end{array}\right),$$

where $z_E=J_{EE}{r}_E-J_{EI}{r}_I+g_E$ and $z_I=J_{IE}{r}_E-J_{II}{r}_I+g_I$. Remarkably, we find that $detDG(r_E,r_I)$ and $\mathcal{F}\prime$ are related and always have opposite signs:

$$det\hspace{0.17em}DG(r_E,r_I)=-{\tau }_E^{-1}{\tau }_I^{-1}\mathcal{F}\prime (z).$$ [16]

Here, $z=J_{EE}{r}_E-J_{EI}{r}_I+g_E$ for $detJ\ge 0$ and $z=J_{IE}{r}_E-J_{II}{r}_I+g_I$ for $detJ<0$. Since the product of the eigenvalues ${\lambda }_1$ and ${\lambda }_2$ of the Jacobian $DG$ is equal to $detDG$ and their sum coincides with the trace of $DG$, we obtain Eqs. 4 and 5.

For completeness, we note that a previous study (10) showed that if $r_E$, $r_I$ is a stable state for ${\tau }_I=0$ and $detJ>0$, then $r_E$, $r_I$ is also stable for all ${\tau }_I>0$ that satisfy Eq. 5. Here, we significantly expanded this result and revealed the full SSN stability repertoire.

Multiplicity of Steady States.

In the previous two paragraphs, we demonstrated how to determine the location of steady states and to characterize their stability using the characteristic function. Here, we build on these findings and use the characteristic function to derive the multiplicity of possible steady states. To provide exact results, we limit our analysis to integer power-law exponents ${\alpha }_E={\alpha }_I=n$ with $n\ge 2$. The numerical study in Fig. S1 indicates that integer exponents are a good starting point to understand the expected location and multiplicity of the SSN steady states. In Multiplicity of Steady States, we detailed why the maximal number of coexistent steady states with equal integer exponents is four and that at most two can be stable simultaneously. This proves that bistability is supported by the SSN model.

To determine the multiplicity of steady states, we need to find the number of $\mathcal{F}$ zero crossings. To this end, we separate the parameter space into nine distinct classes as indicated in Table 1 and determine possible multiplicity configurations of zero crossings in each class. The goal of parameter separation is to simplify the equation for the characteristic function Eq. 15 in each class and make it more accessible for mathematical analysis. We distinguish three subsets of the parameter space according to the sign of $detJ$, because they lead to different functions in Eq. 15. Further, we separate parameter space based on the sign of $C_{\pm }$.

To understand why, consider the expressions ${(P(z))}_{+}$ and ${(z)}_{+}$ which enter the definition of the characteristic function $\mathcal{F}$. As long as $z$ is negative, the expression ${(z)}_{+}$ is zero. If $z$ is positive, then ${(z)}_{+}=z$. The critical point for ${(z)}_{+}$ is $z=0$. Similarly, since $P$ is a monotonically increasing function, there is a unique critical point $z_0$ for $P$; i.e., ${(P(z))}_{+}=P(z)$ for $z>z_0$ and zero for $z\le z_0$. The parameter, which determines whether the critical point $z_0$ is above or below the critical point 0, is the sign of $C_{\pm }$. Specifically, we have $z_0<0$, $z_0=0$, or $z_0>0$, if $C_{\pm }>0$, $C_{\pm }=0$, or $C_{\pm }<0$, respectively. Thus, different signs of $C_{\pm }$ lead to different separations of the $z$ axis into subintervals, where $\mathcal{F}$ coincides with an usual polynomial. Taken together, we partition the parameter space into nine classes that correspond to different signs of $detJ$ and $C_{\pm }$ as presented in Table 1. Following the steps outlined in Multiplicity of Steady States, we determine possible stability and multiplicity configurations of steady states in each class. The parameter classes in which two stable steady states can coexist are indicated in boldface type in Table 1. The constants $C_{+}$ and $C_{-}$ are modifications of the constants ${\mathrm{\Omega }}_E=J_{II}{g}_E-J_{EI}{g}_I$ and ${\mathrm{\Omega }}_I=J_{IE}{g}_E-J_{EE}{g}_I$ introduced in ref. 10.

Persistent Stable State.

A persistent state is a stable positive steady state for zero input. To guarantee its existence, it is necessary to show two features. First, we show the existence of a positive zero-crossing $z$ with $\mathcal{F}\prime (z)<0$ for zero input $g_E=g_I=0$ because only such zero crossing can lead to a positive stable steady state. Second, we verify that this steady state is indeed stable (see Eq. 5). Using the steps outlined in Existence of Persistent States, we show that a required positive zero crossing of the characteristic function with the negative derivative exists in absence of inputs if and only if $detJ$ is constrained as

$$0<detJ<(J_{EE}-J_{EI}^{1-n}{x}_0^n)(x_0-J_{II}).$$ [17]

Here, $x_0$ is the unique solution of the equation

$$(n+1)x_0^n-J_{II}n{x}_0^{n-1}-J_{EI}^{n-1}{J}_{EE}=0$$ [18]

in the interval $(J_{II},J_{EI}^{\frac{n-1}{n}}{J}_{EE}^{\frac{1}{n}})$.

Based on this result, we derived an easy-to-verify necessary condition Eq. 6 for the existence of a stable persistent state. For $n=2$, the explicit solution of Eq. 18 can be directly inserted in the inequality Eq. 17; see Existence of Persistent States for more details.