Metastability and avalanche dynamics in strongly correlated gases with long-range interactions

Significance

Most structured matter, whether in the form of solids or macromolecules, is found in metastable states. Metastability, as well as the transition processes between metastable states, is ubiquitous in nature, but challenges our tools to describe such complex quantum systems. Using a quantum gas, we assemble a synthetic quantum many-body system featuring metastability. The essential ingredient is a global interaction that couples superfluid shells of the system with a metastable Mott insulator in its core. We study in real time the self-induced switching of the core to a different density configuration, a process reminiscent of the folding between discrete structures encountered in the study of macromolecules.

Abstract

We experimentally study the stability of a bosonic Mott insulator against the formation of a density wave induced by long-range interactions and characterize the intrinsic dynamics between these two states. The Mott insulator is created in a quantum degenerate gas of 87-Rubidium atoms, trapped in a 3D optical lattice. The gas is located inside and globally coupled to an optical cavity. This causes interactions of global range, mediated by photons dispersively scattered between a transverse lattice and the cavity. The scattering comes with an atomic density modulation, which is measured by the photon flux leaking from the cavity. We initialize the system in a Mott-insulating state and then rapidly increase the global coupling strength. We observe that the system falls into either of two distinct final states. One is characterized by a low photon flux, signaling a Mott insulator, and the other is characterized by a high photon flux, which we associate with a density wave. Ramping the global coupling slowly, we observe a hysteresis loop between the two states—a further signature of metastability. A comparison with a theoretical model confirms that the metastability originates in the competition between short- and global-range interactions. From the increasing photon flux monitored during the switching process, we find that several thousand atoms tunnel to a neighboring site on the timescale of the single-particle dynamics. We argue that a density modulation, initially forming in the compressible surface of the trapped gas, triggers an avalanche tunneling process in the Mott-insulating region.

When found in a metastable state or phase, a system resides in a condition differing from its state of least energy for an extended period. Examples for long-lived metastable phases are found in magnetized materials, glasses, and crystals like diamond, as well as in macromolecules 1–3). In many solid-state systems, metastability can be described by a first-order phase transition (4), yet the less accessible switching dynamics and their associated timescales are crucial to gain insights into the mechanisms of structure formation.

Ultracold atoms emerge as a promising tool to study questions related to metastability in quantum many-body systems, due to the precise knowledge and high level of control over the underlying Hamiltonian. Indeed, metastable states, many-body localization, and first-order phase transitions have recently attracted theoretical (5–10) and experimental interest (11–16). The presence of long-range interactions is of particular importance to induce and influence metastability, since it makes decay processes like nucleation and phase separation energetically costly, resulting in increased lifetimes of higher-energy states, as recently observed in Rydberg excitation clusters (17). The consequences are even more severe in systems with long-range interactions decaying slower than $1/r^d$, where $r$ is the interparticle distance and $d$ is the dimensionality of the system, as a separation into independent clusters is no longer possible. The lifetime of metastable phases then scales with the system size and diverges in the thermodynamic limit (18, 19).

Here we study a trapped bosonic quantum gas with strong short-range interactions in which all atoms are also coupled to each other through global-range interactions. Increasing the strength of the global coupling triggers a switching process that results in a rearranged atomic distribution and self-consistent potential. The timescale during which this process takes place is intrinsically determined by the many-body dynamics of the gas and is continuously monitored in the experiment.

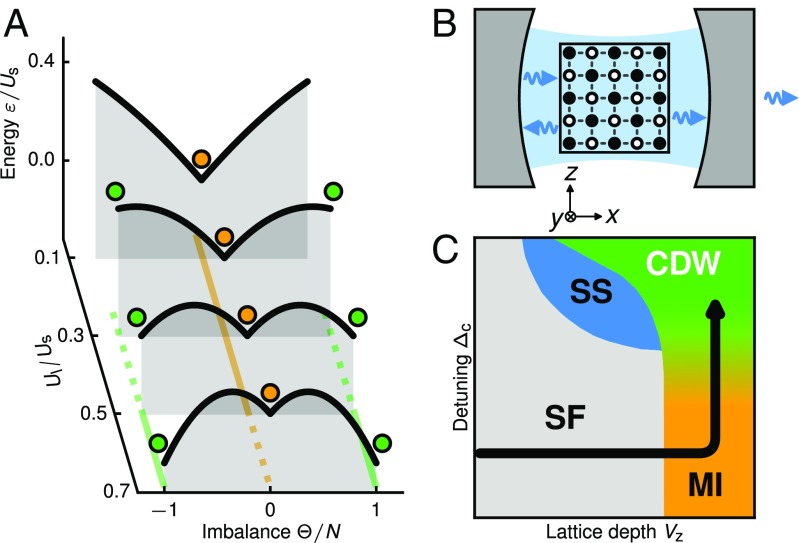
In our experiment the global interactions arise from the coupling of a Bose–Einstein condensate (BEC) to a single mode of an optical high-finesse cavity (20, 21). With the atomic gas trapped in a 3D optical lattice we can simultaneously control short-range interactions and push the system into a strongly correlated regime (Fig. 1B). The phase diagram of the system is schematically shown in Fig. 1C. It was recently determined experimentally (22, 23) and studied theoretically (24–32). In the thermodynamic limit a first-order phase transition from a Mott insulator (MI) (33, 34) to a charge-density wave (CDW) state has been predicted (27, 28, 30, 32).

Fig. 1.

Metastability and system overview. (A) Mean-field results from the toy model. In the presence of short-range interactions $U_{\text{𝗌}}$ and global-range interactions $U_{\text{𝗅}}$ atoms placed in a lattice potential can show metastable behavior. States (indicated by circles) can be protected by an energy barrier and the present state of the system depends on its history, leading to hysteresis. The Mott insulator (orange line) and the charge density wave (green lines) are stable (solid), metastable (dashed), or unstable. (B) Our system consists of a Bose–Einstein condensate coupled to a single mode of an optical resonator in the presence of 3D optical lattices. The atoms can create a particle imbalance $\mathrm{\Theta }$ by arranging in a checkerboard pattern which maximizes scattering of photons from a z lattice (not shown) into the resonator mode. (C) Schematic phase diagram of the system with a superfluid (SF, gray), a lattice supersolid (SS, blue), a Mott insulator (MI, orange), and a charge-density wave (CDW, green) phase. The shaded region between the MI and CDW indicates a region of hysteresis between the phases. The black arrow illustrates the experimental sequence: We prepare the atoms in the SF phase and ramp up the 3D optical lattices to increase $U_{\text{𝗌}}$, which brings the system into the MI phase. Subsequently, we carry out a detuning ramp toward cavity resonance which increases $U_{\text{𝗅}}$.

Toy Model

To achieve a basic understanding of our system we study a toy model with Hamiltonian $\widehat{\mathcal{H}}=\frac{1}{2}{U}_{\text{𝗌}}{\sum }_{i\in e,o}{\widehat{n}}_i\left({\widehat{n}}_i-1\right)-\frac{1}{K}{U}_{\text{𝗅}}{\widehat{\mathrm{\Theta }}}^2$, i.e., an extended Bose-Hubbard model where we have neglected tunneling for simplicity. We consider the situation of a fixed number of atoms $N$ in a box potential, with $K=N$ lattice sites and an average filling per lattice site of $⟨{\widehat{n}}_i⟩=1$. $U_{\text{𝗌}}$ and $U_{\text{𝗅}}$ denote the strength of short- and global-range interactions, respectively. The global-range interaction term favors a particle imbalance between even and odd lattice sites. It is characterized by the imbalance operator $\widehat{\mathrm{\Theta }}={\sum }_{i\in e}{\widehat{n}}_i-{\sum }_{i\in o}{\widehat{n}}_i$, where ${\widehat{n}}_i$ counts the number of atoms on lattice site $i$ and the subindexes $e$ and $o$ denote even and odd lattice sites, respectively.

We obtain the average ground-state energy per particle $\epsilon =<\widehat{\mathcal{H}}>/N$ as a function of the imbalance $\mathrm{\Theta }=<\widehat{\mathrm{\Theta }}>$ for varying $U_{\text{𝗅}}$/$U_{\text{𝗌}}$ (Fig. 1A and Derivation of the Extended Bose–Hubbard Toy Model). When global-range interactions are weak ($U_{\text{𝗅}}/U_{\text{𝗌}}<0.25$), the free-energy landscape has a single global minimum at imbalance $\mathrm{\Theta }=0$ corresponding to an MI with exactly one atom on every lattice site. For $U_{\text{𝗅}}/U_{\text{𝗌}}>0.5$ global-range interactions dominate and we find an insulating ground state with a modulated density distribution which we denote CDW. Since the discrete even-odd symmetry of the lattice is broken, the energy landscape shows two global minima at $\mathrm{\Theta }/N=\pm 1$. In the region around $U_{\text{𝗅}}/U_{\text{𝗌}}\approx 0.5$ this model shows metastable behavior (31, 32). Here the MI state is a local minimum in the free-energy landscape, separated from the CDW states by an energy barrier, which results from the competition between strong interactions of short- and global-range character.

System Description

We load a BEC of $(15-25)\times {10}^3$ ⁸⁷Rb atoms into a harmonic potential centered at the position of the cavity mode. The cloud is split into about $70$ weakly coupled 2D layers using an optical lattice of (26.2–30.7) $E_{\text{𝖱}}^{\text{𝟨𝟩𝟣}}$ depth along the $y$ axis at wavelength ${\lambda }_{\text{𝗒}}=671.0$ nm (Calculation of Atomic Density Distributions). We specify lattice depths in units of the recoil energy $E_{\text{𝖱}}^{\lambda }=h^2/(2m{\lambda }^2)$ for the wavelength $\lambda$, where $h$ denotes Planck’s constant and $m$ is the atomic mass of ⁸⁷Rb. The 2D layers are exposed to a square lattice composed of a free-space lattice in the $z$ direction and an intracavity optical standing wave along the $x$ direction which is externally applied through the cavity mirrors (Fig. 1B) at wavelengths ${\lambda }_{\text{𝗑}}={\lambda }_{\text{𝗓}}=784.7$ nm. In all experiments, the depths of these lattices are tuned simultaneously such that $V_{\text{𝗑}}\approx V_{\text{𝗓}}$ (Lattice Calibrations), but due to the special role of the $z$ lattice we refer to $V_{\text{𝗓}}$ throughout the paper. The $z$ lattice mediates global-range atom-atom interactions of tunable strength $U_{\text{𝗅}}\propto V_{\text{𝗓}}/{\mathrm{\Delta }}_{\text{𝖼}}$ via off-resonant scattering into the optical resonator mode (21) (Strength of Effective Atom–Atom Interactions of Global Range). Here ${\mathrm{\Delta }}_{\text{𝖼}}$ is the detuning of the frequency of the laser forming the $z$ lattice from cavity resonance. We estimate a final filling of at most two atoms per lattice site at the center of the cloud in the MI phase. We monitor in real time the flux of photons leaking out of the cavity, using a heterodyne detector (35). The flux is converted into an imbalance $\mathrm{\Theta }\propto \sqrt{n_{\text{𝗉𝗁}}}$, where $n_{\text{𝗉𝗁}}$ represents the mean intracavity photon number. For further information on the system see ref. 23 and Supporting Information.

Metastability and Hysteresis

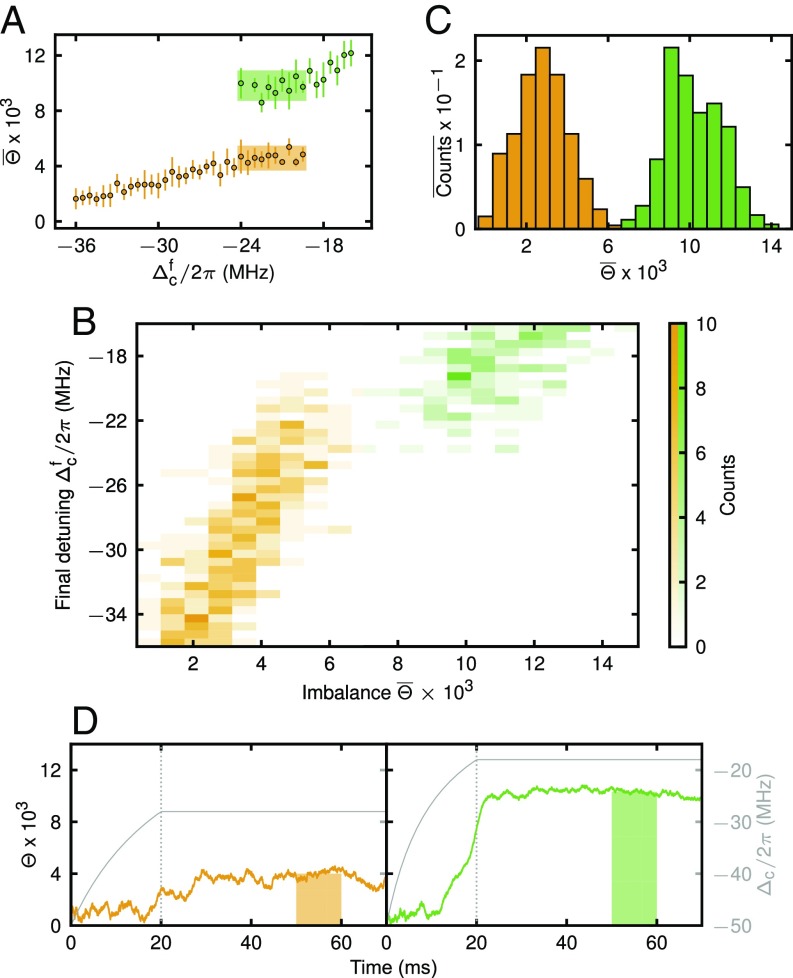
A common method to probe a system for the presence of metastable states is to prepare it in a well-defined state, to provide excess energy, and to observe which states it relaxes to. We accordingly implement such a metastability measurement where we prepare the cloud in an MI state by slowly ramping up the lattices at an initial detuning ${\mathrm{\Delta }}_{\text{𝖼}}/2\pi =-50$ MHz that corresponds to a negligible strength of global-range interactions $U_{\text{𝗅}}$. Subsequently, to provide energy to the system, we quench the initial detuning within $20$ ms to a variable endpoint of ${\mathrm{\Delta }}_{\text{𝖼}}^{\text{𝖿}}$ closer to cavity resonance. The quench increases $U_{\text{𝗅}}$ while $U_{\text{𝗌}}$ stays unchanged. Following the quench the system evolves while all experimental parameters are kept constant. A schematic of this sequence is shown in Fig. 1C. We observe that the imbalance $\mathrm{\Theta }$ rises during or after the quench until it settles at a steady-state level $\overline{\mathrm{\Theta }}$, defined as an average over 10 ms taken 30 ms after finishing the quench (Fig. 2D).

Fig. 2.

Metastability measurement. Shown is the observation of two distinct steady-state imbalances $\overline{\mathrm{\Theta }}$, shown in orange and green, and exemplary time traces. We prepare an MI and then quench the detuning from ${\mathrm{\Delta }}_{\text{𝖼}}/2\pi =-50$ MHz to ${\mathrm{\Delta }}_{\text{𝖼}}^{\text{𝖿}}$ closer to resonance within $20$ ms, increasing $U_{\text{𝗅}}$. (A) Mean values of the imbalance $\overline{\mathrm{\Theta }}$. Errors are SD. The imbalance $\overline{\mathrm{\Theta }}$ is separated by a gap of $5.2(1.4)\times {10}^3$ atoms into two levels. (B) Histogram as a function of $\overline{\mathrm{\Theta }}$ and ${\mathrm{\Delta }}_{\text{𝖼}}^{\text{𝖿}}$ with bin sizes of $700$ atoms in $\overline{\mathrm{\Theta }}$ and $0.5$ MHz in ${\mathrm{\Delta }}_{\text{𝖼}}^{\text{𝖿}}$. (C) Histogram of the normalized sum of all counts with respect to $\overline{\mathrm{\Theta }}$. For the normalization see Evaluation of the Metastability Measurement. (D) Exemplary time traces for quenches ending at ${\mathrm{\Delta }}_{\text{𝖼}}^{\text{𝖿}}/2\pi =-28$ MHz (Left) and ${\mathrm{\Delta }}_{\text{𝖼}}^{\text{𝖿}}/2\pi =-18$ MHz (Right). The shaded regions indicate where the averaged imbalance $\overline{\mathrm{\Theta }}$ is extracted. This experiment was performed with $25(2)\times {10}^3$ atoms at maximum lattice depths of $(V_{\text{𝗑}},V_{\text{𝗒}},V_{\text{𝗓}})=(17.3E_{\text{𝖱}}^{\text{𝟩𝟪𝟧}},30.7E_{\text{𝖱}}^{\text{𝟨𝟩𝟣}},11.1E_{\text{𝖱}}^{\text{𝟩𝟪𝟧}})$.

Repeating the experiment, we measure the imbalance $\overline{\mathrm{\Theta }}$ as a function of the final detuning ${\mathrm{\Delta }}_{\text{𝖼}}^{\text{𝖿}}$ (Fig. 2 A–C). Far from resonance (${\mathrm{\Delta }}_{\text{𝖼}}^{\text{𝖿}}/2\pi <-24$ MHz), where the strength of global-range interactions is weak, the system consistently ends up at low imbalances (orange) in an interval of $0<\overline{\mathrm{\Theta }}<7\times {10}^3$ atoms. Quenching the detuning closer to resonance (${\mathrm{\Delta }}_{\text{𝖼}}^{\text{𝖿}}/2\pi \ge -19.5$ MHz), where the strength of global-range interactions is higher, the system is never found to end up within this imbalance interval. We now observe consistently higher imbalances (green) of $\overline{\mathrm{\Theta }}>7\times {10}^3$ atoms. The two well-separated imbalance intervals (Fig. 2A) coexist for final detunings in an intermediate region ($-24$ MHz $\le {\mathrm{\Delta }}_{\text{𝖼}}^{\text{𝖿}}/2\pi \le -19.5$ MHz) where the system ends up in a state either of low or of large average imbalance $\overline{\mathrm{\Theta }}$ (Evaluation of the Metastability Measurement).

We attribute the observation of two distinct imbalance distributions in our system to the existence of two metastable states. Their separation signals the presence of an energy barrier between the states which does not allow for a continuous connection between them. Our observation of a constant imbalance level after equilibration (Fig. 2D) shows that the final state is long-lived and hence can be either metastable or stable. Monte Carlo simulations for the closed version of the system indeed predict metastable states (32). We observe that this metastability is preserved in our system despite its open character due to the dissipative cavity, which could lead to a fast decay of metastable states.

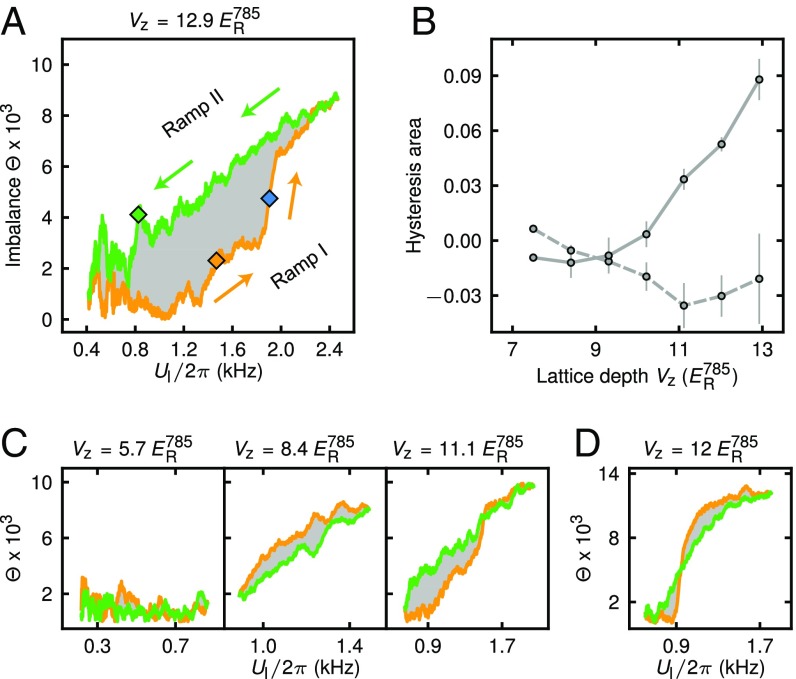
Metastable behavior in a many-body system is usually associated with hysteresis at phase transitions. When a control parameter is slowly varied back and forth across a critical point, the final state of the system depends on its history. The direct observation of hysteresis provides an indication for the stability of metastable states with respect to parameter changes. We perform such a hysteresis measurement by preparing our system in the MI phase at a lattice depth of $V_{\text{𝗓}}=12.9$ $E_{\text{𝖱}}^{\text{𝟩𝟪𝟧}}$ and again at a detuning where global-range interactions are negligible. Afterward, the detuning is swept during $80$ ms across the phase transition toward resonance (Fig. 3A, ramp I) and subsequently back to the starting point, again within $80$ ms (Fig. 3A, ramp II). We choose a detuning ramp which varies $U_{\text{𝗅}}$ linearly in time, starting from ${\mathrm{\Delta }}_{\text{𝖼}}/2\pi =-53$ MHz to ${\mathrm{\Delta }}_{\text{𝖼}}/2\pi =-13$ MHz and back to ${\mathrm{\Delta }}_{\text{𝖼}}/2\pi =-53$ MHz, while $U_{\text{𝗌}}$ is kept constant (Hysteresis Measurement: Lattice and Detuning Ramps and Fig. S2). During ramp I an imbalance is created that increases with increasing $U_{\text{𝗅}}$ (orange line in Fig. 3A). During ramp II the imbalance decreases again until it fully vanishes (green line in Fig. 3A). The observed evolution of the imbalance is path dependent and describes a hysteresis loop across the phase transition.

Fig. 3.

Hysteresis measurement. (A) We prepare an MI and then sweep the detuning toward cavity resonance and subsequently back to the starting point. The imbalance created during ramp I is shown in orange and the imbalance during ramp II is shown in green. Arrows indicate the ramp directions. We quantify the amount of hysteresis created by the area highlighted in gray. Diamonds signal where we deduce the threshold for the creation (orange) and the disappearance (green) of an imbalance $\mathrm{\Theta }$ and where the center of an imbalance jump is located (blue) (Hysteresis Loops: Data Evaluation and Comparison of Different Ramp Times). (B) We study the hysteresis area (Hysteresis Loops: Data Evaluation and Comparison of Different Ramp Times) as a function of the final lattice depth $V_{\text{𝗓}}$; the data are shown by the solid line. The dashed line represents the case where the $y$ lattice is switched off to reduce $U_{\text{𝗌}}$. (C) Exemplary traces of the imbalance $\mathrm{\Theta }$ as a function of $U_{\text{𝗅}}$ for different lattice depths $V_{\text{𝗓}}$. These experiments were performed with $17(2)\times {10}^3$ atoms at maximum lattice depths of $(V_{\text{𝗑}},V_{\text{𝗒}},V_{\text{𝗓}})=(14.5E_{\text{𝖱}}^{\text{𝟩𝟪𝟧}},26.2E_{\text{𝖱}}^{\text{𝟨𝟩𝟣}},12.9E_{\text{𝖱}}^{\text{𝟩𝟪𝟧}})$. (D) Exemplary trace with the $y$ lattice switched off. Here we prepare $15(1)\times {10}^3$ atoms at $V_{\text{𝗑}}=12.4$ $E_{\text{𝖱}}^{\text{𝟩𝟪𝟧}}$ and $V_{\text{𝗓}}=12.0$ $E_{\text{𝖱}}^{\text{𝟩𝟪𝟧}}$ (Lattice Calibrations). Error bars are SD (Hysteresis Loops: Data Evaluation and Comparison of Different Ramp Times).

A natural question in our system is the connection between the strength of short-range interactions and the emergence of a hysteresis loop. We therefore repeat the experiment at different $V_{\text{𝗓}}$ to vary $U_{\text{𝗌}}/t$, where $t$ is tunneling. Sample traces are shown in Fig. 3C. We quantify the amount of hysteresis by integrating the area of imbalance with respect to $U_{\text{𝗅}}$ (gray area in Fig. 3 A and C). The hysteresis area is growing with increasing $V_{\text{𝗓}}$ (solid line in Fig. 3B), indicating that the metastable states become increasingly robust against a change in $U_{\text{𝗅}}$. In the case where we repeat the experiment with the $y$ lattice switched off, such as to significantly reduce $U_{\text{𝗌}}$, we, however, observe barely any hysteresis area (dashed line in Fig. 3B); an exemplary trace is shown in Fig. 3D. Our findings suggest that the emergence of a hysteresis loop is linked to the system being in a regime where both interactions are strong.

So far we have neglected the influence of nonadiabaticity when crossing the phase transition point as well as heating effects. Nonadiabaticity which stems from short ramp times leads to a delayed reaction of the system with respect to a change of the detuning (36). Consequently, during ramp I, the imbalance buildup is delayed while during ramp II the imbalance vanishes at a later point, leading to an increase in the observed hysteresis area. Heating on the other hand leads to a reduction of the imbalance over time, resulting in a decreased hysteresis area which can thus also become negative (Fig. 3B). The full comparison between the hysteresis area and thermodynamic states is challenging due to these effects. A detailed study of the dependence of the observed hysteresis on the ramp time is provided in Hysteresis Loops: Data Evaluation and Comparison of Different Ramp Times and Fig. S3. Independent of the ramp time, we always observe a larger hysteresis area when $U_{\text{𝗌}}$ is high compared with the case where $U_{\text{𝗌}}$ is reduced by switching off the $y$ lattice. Reverting the order of ramps I and II to start in a CDW state would have the effect that both heating and nonadiabaticity increase the observed hysteresis area.

Imbalance Dynamics

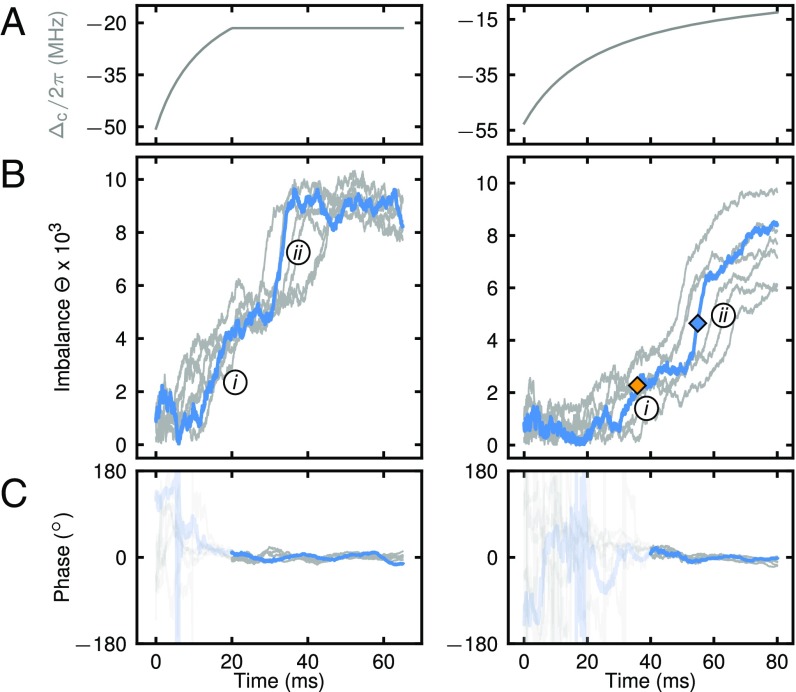
Our findings in the previous two experiments, the metastability measurement and the hysteresis measurement, are based on changes of the imbalance $\mathrm{\Theta }$ when varying the detuning ${\mathrm{\Delta }}_{\text{𝖼}}$ in time. Such a change in the imbalance corresponds to a reordering of the atomic density distribution via tunneling in the lattice potential. Our real-time access unveils nontrivial dynamics of the imbalance in the same data. We observe an initial imbalance buildup (i) followed by a fast jump (ii) (Fig. 4B). Both features are present in the case of a detuning quench and the case of a slow detuning ramp. To be independent of the quench time, we postselect the quench data based on the condition that the imbalance jump (ii) happens after experimental parameters are kept constant (Imbalance Dynamics: Data Evaluation). From these data we measure a height of the jump of $\mathrm{\Delta }\mathrm{\Theta }=3.5(9)\times {10}^3$ atoms and an upper bound of the duration $\mathrm{\Delta }T$ of $4.3(6)$ ms (Imbalance Dynamics: Data Evaluation). It is comparable to the tunneling time in a double well along the $x[z]$ direction of $11.8[3.1]$ ms, defined as $\pi /(2\sqrt{2}{t}_{x[z]})$ (Imbalance Dynamics: Data Evaluation). We interpret this jump as a collective tunneling of several thousand atoms, and a possible microscopic description of this process is given in the following section. The timescale of the initial imbalance buildup (i) depends on the ramp time, while the jump (ii) has a comparable duration in all datasets.

Fig. 4.

Time traces of the dynamics of the system. (A–C, Left) Data from the metastability measurement. (A–C, Right) Data from the hysteresis measurement. (A) Ramps in the detuning ${\mathrm{\Delta }}_{\text{𝖼}}$. (B) Imbalance dynamics. Starting from a state with almost zero imbalance $\mathrm{\Theta }$, we first observe a slow increase in $\mathrm{\Theta }$ (i) followed by a sudden jump (ii). (A–C, Left) After quenching the detuning ${\mathrm{\Delta }}_{\text{𝖼}}$ in the MI phase toward cavity resonance, we hold all experimental parameters constant. We observe dynamics in the imbalance $\mathrm{\Theta }$ during and after the detuning quench. The exemplary trace of $\mathrm{\Theta }$ as a function of time at a final detuning of ${\mathrm{\Delta }}_{\text{𝖼}}^{\text{𝖿}}/2\pi =-21$ MHz is shown in blue, while several repetitions of the experiment at ${\mathrm{\Delta }}_{\text{𝖼}}^{\text{𝖿}}/2\pi =-23\mathsf{\text{to}}-20$ MHz are shown in gray. (A–C, Right) We sweep the detuning ${\mathrm{\Delta }}_{\text{𝖼}}$ within $80$ ms from the MI phase toward cavity resonance. An exemplary trace of $\mathrm{\Theta }$ as a function of time is shown in blue where we observe dynamics in the imbalance during the sweep. Multiple repetitions of the experiment with the same parameters are shown in gray, here $V_{\text{𝗓}}=12.9$ $E_{\text{𝖱}}^{\text{𝟩𝟪𝟧}}$. Diamonds signal where we deduce the threshold for the creation of an imbalance $\mathrm{\Theta }$ (orange) and where the center of the imbalance jump (ii) is located (blue) (Hysteresis Loops: Data Evaluation and Comparison of Different Ramp Times). (C) Phase of the light field indicating a broken ${\mathbb{Z}}_2$ symmetry. We observe a constant phase after an imbalance is created throughout the slow increase (i) and jump (ii) in $\mathrm{\Theta }$ (Imbalance Dynamics: Data Evaluation). In the shaded region, the signal is dominated by technical noise due to low photon flux.

In contrast to our toy model, the experimental system is at nonzero tunneling, at finite temperature, and exposed to a harmonic trapping potential. Accordingly we expect the MI, in which we initially prepare the system, to form a wedding-cake structure consisting of an insulating bulk surrounded by superfluid shells at the surface. Such an inhomogeneous finite-size system can exhibit a first-order phase transition of the bulk material (the MI), which is triggered by a second-order phase transition that took place previously on the system’s surface (37, 38). The superfluid surface atoms possess a higher mobility than the insulating bulk (39). When the detuning ${\mathrm{\Delta }}_{\text{𝖼}}$ is swept toward cavity resonance, these atoms break the underlying ${\mathbb{Z}}_2$ symmetry once global-range interactions overcome kinetic energy and the trapping potential. This emerging imbalance then determines the parity of the CDW state, indicated by a well-defined and constant phase of the measured light field (40), shown in Fig. 4C. We attribute the initial imbalance increase (i) to a rearrangement of surface atoms. From the experimental parameters of the metastability measurement, we theoretically estimate a number of surface atoms of $N_{\text{surf}}\approx (4-8)\times {10}^3$ (Calculation of Atomic Density Distributions), which is in agreement with the initial imbalance increase (i). Photons scattered at these atoms into the cavity mode generate an energy offset ${\delta }_{\text{off}}$ between even and odd sites (Fig. 5B). This offset eventually drives the bulk system from a metastable MI to a CDW state, which we link to the fast imbalance jump (ii). However, we do not observe an imbalance jump when ramping the detuning back to the starting value in ramp II (Fig. 3), which we mainly attribute to the cloud being heated.

Fig. 5.

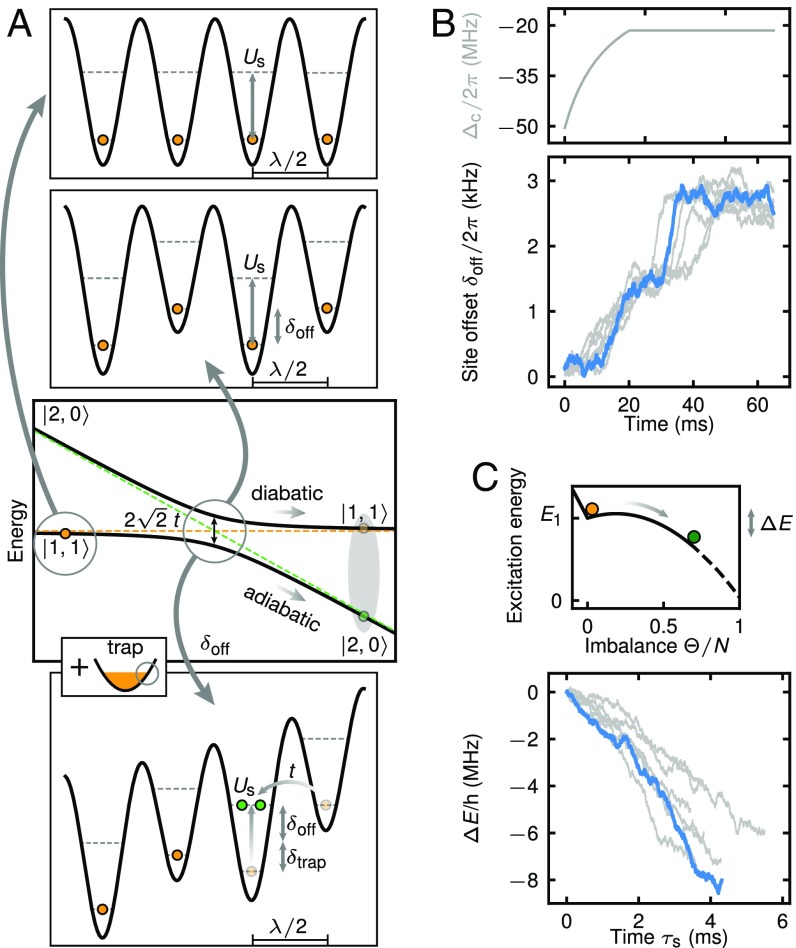
Microscopic dynamics and energy redistribution of the system. (A) Microscopic description of the system dynamics following the detuning quench, in terms of a Landau–Zener transition. One-dimensional lattice potentials are shown for a normal lattice (Top), a dynamic superlattice with site offset ${\delta }_{\text{off}}$ generated by superfluid surface atoms (Middle), and a tilted dynamic superlattice with spatially varying site offset ${\delta }_{\text{off}}+{\delta }_{\text{trap}}$ as encountered at the edge of the harmonic trap (Bottom). Colored circles represent atoms in the states $|\mathrm{1,1}⟩$ (orange) or $|\mathrm{2,0}⟩$ (green). Resonant nearest-neighbor tunneling is allowed when the site offset ${\delta }_{\text{off}}+{\delta }_{\text{trap}}$ equals the short-range interaction strength $U_{\text{𝗌}}$. (B) Dynamics of the site offset ${\delta }_{\text{off}}$ in the metastability measurement. (C, Top) Sketch of the excitation energy of the bulk atoms. Superfluid surface atoms add a symmetry-breaking field to the toy model. During the imbalance jump (ii), the highly excited system reduces the initial excitation energy $E_1$ via an avalanche of inherently nonadiabatic Landau-Zener transitions by an amount of $\mathrm{\Delta }E$. Colored circles represent the state of the system, where the MI state (orange) results from all bulk atoms in the $|\mathrm{1,1}⟩$ state and the CDW state (green) from atoms being in a superposition of $|\mathrm{1,1}⟩$ and $|\mathrm{2,0}⟩$ states. Accordingly, the relative imbalance saturates at $\mathrm{\Theta }/N<1$, indicated by the dashed line. (C, Bottom) Reduction of $\mathrm{\Delta }E$ as a function of time ${\tau }_{\text{s}}$ during the imbalance jump (ii). (B and C) Exemplary traces use the same data as shown in Fig. 4. ${\delta }_{\text{off}}$ and $\mathrm{\Delta }E$ are inferred from the photon flux leaking from the cavity.

Microscopic Dynamics and Energy Redistribution During the Imbalance Jump

A simplified microscopic picture of the imbalance dynamics following the detuning quench is sketched in Fig. 5A, where the system is broken into a collection of coupled double wells. In the initial MI state, bulk atoms occupy both sites of each double well. This state is labeled $|\mathrm{1,1}⟩$, where $|n_{\text{e}},n_{\text{o}}⟩$ denotes the filling on the even and odd sites, respectively. Here, on-site interactions of strength $U_{\text{𝗌}}/2\pi =2.2(1)$ kHz provide an energy barrier for neighboring atoms, thus suppressing tunneling into a $|\mathrm{2,0}⟩$ state. The barrier softens but persists as surface atoms generate an imbalance $\mathrm{\Theta }$ and a site offset ${\delta }_{\text{off}}$. Monitoring the flux of photons leaking from the cavity, we observe ${\delta }_{\text{off}}/2\pi =1.6(2)$ kHz just before the imbalance jump (ii) happens (Extraction of the Even–Odd Particle Imbalance Θ and Site Offset δ_off from the Measured Photon Flux). The harmonic trapping potential causes an additional site offset of $0\text{kHz}\le {\delta }_{\text{trap}}/2\pi \le {\delta }_{\text{trap}}^{\text{max}}/2\pi =0.6\text{kHz}$, increasing from the center outward. When ${\delta }_{\text{off}}+{\delta }_{\text{trap}}^{\text{max}}\approx U_{\text{𝗌}}$, the outermost bulk atoms start resonantly tunneling to their neighboring lattice sites. They further increase $\mathrm{\Theta }$ and ${\delta }_{\text{off}}$, successively allowing more and more atoms to resonantly tunnel. The imbalance jump (ii) thus results from an avalanche of resonant tunneling processes of bulk atoms which stops only once ${\delta }_{\text{off}}-{\delta }_{\text{trap}}^{\text{max}}>U_{\text{𝗌}}$. Indeed, we find ${\delta }_{\text{off}}/2\pi =2.7(3)$ kHz at the end of the jump.

We describe each resonant tunneling process by a Landau–Zener transition, shown in Fig. 5A. The $|\mathrm{1,1}⟩$ and $|\mathrm{2,0}⟩$ states are coupled with strength $\sqrt{2}t$, where the tunneling $t$ is bosonically enhanced by a factor of $\sqrt{2}$. We find an upper bound for the probability of adiabatic Landau-Zener transfer of about $60$%, which is determined by the measured rate of change of ${\delta }_{\text{off}}$ during the imbalance jump, shown in Fig. 5B. As all experimental parameters are held constant after the quench, the site offset ${\delta }_{\text{off}}$ is solely tuned by the reordering atoms. The timescale and (non)adiabaticity of the Landau–Zener transitions is thus inherently determined by the system evolving nonlinearly due to the presence of the global-range interactions.

At the beginning of the imbalance jump (ii), the ground state of the system is the CDW state. The bulk is, however, still in the MI state, which is now a highly excited state of energy $E_1$. During the imbalance jump (ii) each double well in the bulk evolves via nonadiabatic Landau–Zener transfers to a superposition of $|\mathrm{1,1}⟩$ and $|\mathrm{2,0}⟩$ states. On top of the imbalance created previously by superfluid surface atoms, the redistributing bulk increases the imbalance further, allowing the system to lower the excitation energy by $\mathrm{\Delta }E$. We infer $\mathrm{\Delta }E=7.7(2.1)$ MHz from the imbalance jump (ii) in the metastability measurement (Extraction of the Change in Excitation Energy ΔE from the Measured Photon Flux) (Fig. 5C). This process is sketched using our toy model, where a symmetry-breaking field is present due to the imbalance created by superfluid surface atoms.

To study the energy budget of the system we consider two scenarios. If the system was closed, the total energy could not change, and the reduction in excitation energy $\mathrm{\Delta }E$ would be balanced by an increase in kinetic energy of the system. Since our system is inherently open, the energy could also be dissipated by leaking cavity photons. We make use of the spectrum of these photons to distinguish the two cases. We estimate the number of scattered photons during the imbalance jump (ii) to be about $12(3)\times {10}^3$ (Number of Photons Scattered During the Imbalance Jump), where each photon would have to dissipate at least $0.6(3)$ kHz of energy. This would leave a notable signature in the photon spectrum, which is not observed. While our heterodyne detection cannot rule out processes where only few photons dissipate all of the energy, such a collective scattering process seems unlikely. Hence we conclude that the excitation energy released during the jump (ii) remains in the system and is transformed into kinetic and interaction energy (Energy Stored in the Superfluid Surface and the Insulating Bulk During the Imbalance Jump).

Phase Diagram

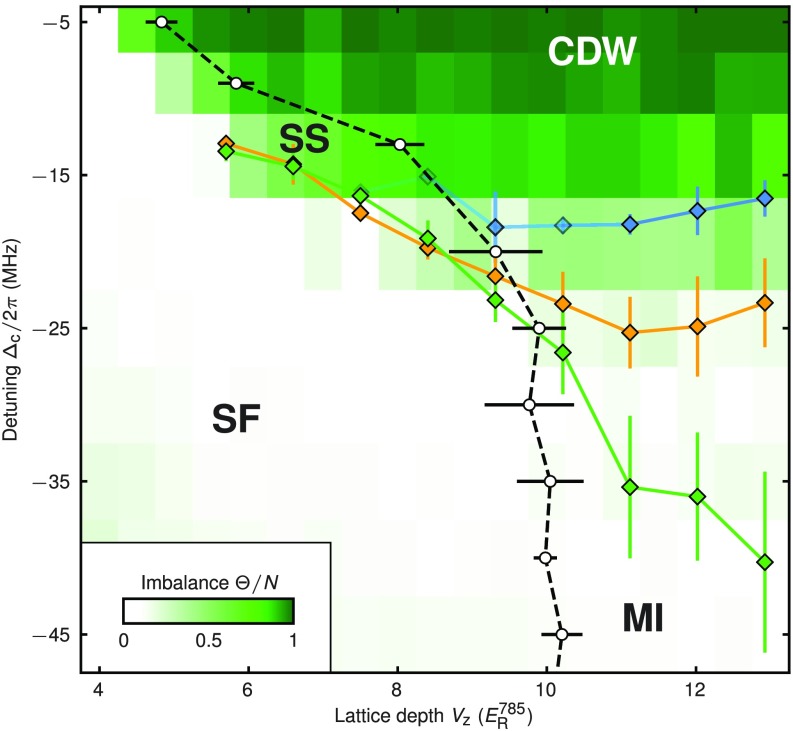
The observation of metastable states, a coexistence of phases, and a jump in the order parameter are typical features of first-order phase transitions. We thus want to relate our observations to a phase diagram of the system measured as in ref. 23 (Fig. 6). Here, we superimpose the thresholds extracted in the hysteresis measurement on the phase diagram.

Fig. 6.

Previously extracted transition points superimposed on a phase diagram of the system. Results from the hysteresis measurement: Orange and green diamonds indicate the thresholds where an imbalance is created and where it vanishes during detuning ramps, respectively. The center of the imbalance jump is shown in blue, where transparency indicates the probability of occurrence of the jump. For details on the measurement of the phase diagram, see Phase Diagram Measurement: Data Evaluation. White data points and the associated black dashed line indicated the loss of coherence, from left to right, which we infer from the measured BEC fraction, and green tiles indicate states with nonzero imbalance. We identify a superfluid (SF), a lattice supersolid (SS), an MI, and a CDW phase. This experiment was performed with $16(1)\times {10}^3$ atoms at maximum lattice depths of $(V_{\text{𝗑}},V_{\text{𝗒}},V_{\text{𝗓}})=(15.7E_{\text{𝖱}}^{\text{𝟩𝟪𝟧}},26.2E_{\text{𝖱}}^{\text{𝟨𝟩𝟣}},12.9E_{\text{𝖱}}^{\text{𝟩𝟪𝟧}})$. For further details see ref. 23 and Phase Diagram Measurement: Data Evaluation. Error bars are SD (Phase Diagram Measurement: Data Evaluation and Fig. S4).

The threshold for the creation of an imbalance (orange diamonds in Fig. 6) coincides with the appearance of an imbalance in the phase diagram (green tiles in Fig. 6). The center position of the fast jump (blue diamonds in Fig. 6) is located within a region of intermediate imbalance present in the phase diagram at ${\mathrm{\Delta }}_{\text{𝖼}}/2\pi \approx -20$ MHz (light green tiles in Fig. 6). The threshold for the disappearance of an imbalance (green diamonds in Fig. 6) extends deep into the MI region (white tiles in Fig. 6). The associated blue and green lines enclose an area where the MI and the CDW phases can coexist and where hysteresis is observed. In addition, we find the parameter regime where the system can fall into either of the two final states in the metastability measurement (Fig. 2A) to lie close to the blue line (Fig. 6).

Conclusion and Outlook

Using the unique real-time access of our experiment, we observed long-lived metastable phases and hysteretic behavior at a first-order quantum phase transition between an MI and a CDW phase. Owing to the nonlinearity stemming from the global-range interactions, the system develops its own timescale when quenched across the phase transition. The resulting dynamics of spatially reordering atoms point to an avalanche of resonant tunneling processes taking place, which render the transition out of the metastable state inherently nonadiabatic. The observed lack of energy dissipation during the transition poses questions about the thermalization of the final state. Our work provides a unique approach to study dynamics and thermalization processes in open quantum many-body systems.