Network Reconstruction From High-Dimensional Ordinary Differential Equations

Abstract

We consider the task of learning a dynamical system from high-dimensional time-course data. For instance, we might wish to estimate a gene regulatory network from gene expression data measured at discrete time points. We model the dynamical system nonparametrically as a system of additive ordinary differential equations. Most existing methods for parameter estimation in ordinary differential equations estimate the derivatives from noisy observations. This is known to be challenging and inefficient. We propose a novel approach that does not involve derivative estimation. We show that the proposed method can consistently recover the true network structure even in high dimensions, and we demonstrate empirical improvement over competing approaches. Supplementary materials for this article are available online.

1. Introduction

Ordinary differential equations (ODEs) have been widely used to model dynamical systems in many fields, including chemical engineering (Biegler, Damiano, and Blau 1986), genomics (Chou and Voit 2009), neuroscience (Izhikevich 2007), and infectious diseases (Wu 2005). A system of ODEs takes the form

$$X\prime (t;\theta )\equiv \left[\begin{array}{c}\frac{d{X}_1(t;\theta )}{dt}\\ ⋮\\ \frac{d{X}_p(t;\theta )}{dt}\end{array}\right]=\left[\begin{array}{c}{f}_1(X(t;\theta ),\theta )\\ ⋮\\ f_p(X(t;\theta ),\theta )\end{array}\right]\equiv f(X(t;\theta ),\theta );t\in [0,1],$$ (1)

where X(t; θ) = (X₁(t; θ), …, X_p(t; θ))^T denotes a set of variables, and the form of the functions f = (f₁, …, f_p)^T may be known or unknown. In (1), t indexes time. Typically, there is also an initial condition of the form X(0; θ) = C, where C is a p-vector. In practice, the system (1) is often observed on discrete time points subject to measurement errors. Let Y_i ∈ ℝ^p be the measurement of the system at time t_i such that

$$Y_i=X(t_i;{\theta }^{\ast })+{\epsilon }_i,i=1,\dots ,n,$$ (2)

where θ^∗ denotes the true set of parameter values and the random p-vector ε_i represents independent measurement errors. In what follows, for notational simplicity, we sometimes suppress the dependence of X(t; θ) on θ, that is, X(t) ≡ X(t; θ) in (1) and X^∗(t) ≡ X(t; θ^∗) in (2).

In the context of high-dimensional time-course data arising from biology, it can be of interest to recover the structure of a system of ODEs—that is, to determine which features regulate each other. If f_j in (1) is a function of X_k, then we say that X_k regulates X_j in the sense that X_k controls the changes of X_j through its derivative $X_j^{\prime }$. For instance, biologists might want to infer gene regulatory networks from noisy time-course gene expression data. In this case, the number of variables p exceeds the number of time points n; we refer to this as the high-dimensional setting.

In high-dimensional statistics, sparsity-inducing penalties such as the lasso (Tibshirani 1996) and the group lasso (Yuan and Lin 2006) have been well-studied. Such penalties have also been extensively used to recover the structure of probabilistic graphical models (e.g., Yuan and Lin 2007; Friedman, Hastie, and Tibshirani 2008; Meinshausen and Bühlmann 2010; Voorman, Shojaie, and Witten 2014). However, model selection in high-dimensional ODEs remains a relatively open problem, with the exception of some notable recent work (Lu et al. 2011; Henderson and Michailidis 2014; Wu et al. 2014). In fact, the tasks of parameter estimation and model selection in ODEs from noisy data are very challenging, even in the classical statistical setting where n > p (see, e.g., Ramsay et al. 2007; Brunel 2008; Liang and Wu 2008; Qi and Zhao 2010; Xue, Miao, and Wu 2010; Gugushvili and Klaassen 2012; Hall and Ma 2014; Zhang, Cao, and Carroll 2015). Moreover, the problem of high-dimensionality is compounded if the form of the function f in (1) is unknown, leading to both statistical and computational issues.

In this article, we propose an efficient procedure for structure recovery of an ODE system of the form (1) from noisy observations of the form (2), in the setting where the functional form of f is unknown. In Section 2, we review existing methods. In Section 3, we propose a new structure recovery procedure. In Section 4, we study the theoretical properties of our proposal. In Section 5, we apply our procedure to simulated data. In Section 6, we apply it to in silico gene expression data generated by GeneNetWeaver (Schaffter, Marbach, and Floreano 2011) and to calcium imaging data. We conclude with a discussion in Section 7. Proofs and additional details are provided in the supplementary material.

2. Literature Review

In this section, we review existing statistical methods for parameter estimation and/or model selection in ODEs. Most of the methods reviewed in this section are proposed for the low-dimensional setting. Even though they may not be directly applicable to the high-dimensional setting, they lay the foundation for the development of model selection procedures in high-dimensional additive ODEs.

2.1. Notation

Without loss of generality, assume that 0 = t₁ < t₂ < ⋯ < t_n = 1. We let Y_ij indicate the observation of the jth variable at the ith time point, t_i. We use $\mathcal{X}(h)$ to denote a nonparametric class of functions on [0, 1] indexed by some smoothing parameter(s) h. We use Z(·) to represent an arbitrary function belonging to $\mathcal{X}(·)$. We use ‖·‖₂ to denote the ℓ₂-norm of a vector or a matrix, and ||| f ||| to denote the ℓ₂-norm of a function f on the interval [0, 1], that is, $|||f||{|}^2\equiv {\displaystyle {\int }_0^1{f}^2(t)dt}$. We use an asterisk to denote true values—for instance, θ^∗ denotes the true value of θ in (1). We use Λ_min(A) and Λ_max(A) to denote the minimum and maximum eigenvalues of a square matrix A, respectively.

2.2. Methods that Assume a Known Form of f

2.2.1. Gold Standard Approach

To begin, we suppose that the function f in (1) takes a known form. Benson (1979) and Biegler, Damiano, and Blau (1986) proposed to estimate the unknown parameter θ^∗ in (2) by solving the problem

$${\widehat{\theta }}^{\text{gold}}=\underset{\theta }{\arg min}{\displaystyle \sum _{i=1}^n\Vert Y_i-X(t_i;\theta ){\Vert }_2^2}$$ (3a)

$$\text{subject to }X\prime (t;\theta )=f(X(t;\theta ),\theta ),t\in [0,1].$$ (3b)

Note that X(·; θ) in (3) is a fixed function given θ, although an analytic expression may not be available. The resulting estimator ${\widehat{\theta }}^{\text{gold}}$ has appealing theoretical properties: for instance, when the measurement errors ε_i in (2) are Gaussian, then ${\widehat{\theta }}^{\text{gold}}$ is the maximum likelihood estimator, and is $\sqrt{n}-\text{consistent}$. In this sense, (3) can thus be considered the gold standard approach. However, solving (3) is often computationally challenging.

2.2.2. Two-Step Collocation Methods

To overcome the computational challenges associated with solving (3), collocation methods have been employed by a number of authors (Varah 1982; Ellner, Seifu, and Smith 2002; Ramsay et al. 2007; Brunel 2008; Cao and Zhao 2008; Liang and Wu 2008; Cao, Wang, and Xu 2011; Lu et al. 2011; Gugushvili and Klaassen 2012; Brunel, Clairon, and d’Alché Buc 2014; Hall and Ma 2014; Henderson and Michailidis 2014; Wu et al. 2014; Dattner and Klaassen 2015; Zhang, Cao, and Carroll 2015).

The two-step collocation procedure first proposed by Varah (1982) involves fitting a smoothing estimate $\widehat{X}(·;h)$ to the observations Y₁, …,Y_n in (2) with a smoothing parameter h, and then plugging $\widehat{X}(·;h)$ and its derivative with respect to t into (1) to estimate θ. This amounts to solving the optimization problem

$${\widehat{\theta }}^{\text{TS}}=\underset{\theta }{\arg min}{\displaystyle {\int }_0^1\Vert \widehat{X}\prime (t;h)-f(\widehat{X}(t;h),\theta ){\Vert }_2^{2}dt,}$$ (4a)

where

$$\widehat{X}(·;h)=\underset{Z(·)\in \mathcal{X}(h)}{\arg min}{\displaystyle \sum _{i=1}^n\Vert Y_i-Z(t_i){\Vert }_2^2}.$$ (4b)

The two-step procedure (4) has a clear advantage over the gold standard approach (3) because the former decouples the estimation of θ and X. However, this advantage comes at a cost: due to the presence of $\widehat{X}\prime$ in (4a), the properties of the estimator ${\widehat{\theta }}^{\text{TS}}$ in (4) rely heavily on the smoothing estimates obtained in (4b), and $\sqrt{n}-\text{consistency}$ has only been shown for certain values of the smoothing parameter h that are hard to choose in practice (Brunel 2008; Liang and Wu 2008; Gugushvili and Klaassen 2012).

Dattner and Klaassen (2015) proposed an improvement to (4) for a special case of (1). To be more specific, they assume that f_j(X(t), θ) in (1) is a linear function of θ, which leads to

$$X\prime (t)\equiv \left[\begin{array}{c}\frac{d{X}_1(t)}{dt}\\ ⋮\\ \frac{d{X}_p(t)}{dt}\end{array}\right]=\left[\begin{array}{c}{g}_1^{\mathrm{T}}(X(t))\theta \\ ⋮\\ g_p^{\mathrm{T}}(X(t))\theta \end{array}\right]\equiv g(X(t))\theta ;t\in [0,1],$$ (5)

where g(X(t)) is a known function of X(t). Integrating both sides of (5) gives

$$X(t)=\left\{{\displaystyle {\int }_0^{t}g(X(u))du}\right\}\theta +C,$$ (6)

where C ≡ X(0; θ). The unknown parameter θ^∗ is estimated by solving

$${\widehat{\theta }}^{\text{LM}}=\underset{\theta }{\arg min}{\displaystyle {\int }_0^1{\Vert \widehat{X}(t;h)-\left\{{\displaystyle {\int }_0^{t}g(\widehat{X}(u;h))du}\right\}\theta -C\Vert }_2^{2}dt},$$ (7a)

where

$$\widehat{X}(·;h)=\underset{Z(·)\in \mathcal{X}(h)}{\arg min}{\displaystyle \sum _{i=1}^n\Vert Y_i-Z(t_i){\Vert }_2^2}.$$ (7b)

The optimization problem (7a) has an analytical solution, given the smoothing estimates from (7b). Compared with the two-step procedure (4), this approach requires an estimate of the integral, ${\displaystyle {\int }_0^{t}g(\widehat{X}(u;h))du}$ in (7a), rather than an estimate of the derivative, $\widehat{X}\prime (t;h)$. This has profound effects on the asymptotic behavior of the estimator ${\widehat{\theta }}^{\text{LM}}$. $\sqrt{n}-\text{consistency}$ of ${\widehat{\theta }}^{\text{LM}}$ has been established under mild conditions, and it has been found that the choice of smoothing parameter h is less crucial than for other methods (Gugushvili and Klaassen 2012).

Recently, Brunel, Clairon, and d’Alché Buc (2014) and Hall and Ma (2014) had considered alternatives to the loss function in (4a). Let ℂ¹(0, 1) be the set of functions that are first-order differentiable on (0, 1) and equal zero on the boundary points 0 and 1. Then (1) implies that, for any ϕ ∈ ℂ¹(0, 1),

$${\displaystyle {\int }_0^{1}f(X(t),\theta )\varphi (t)dt+{\displaystyle {\int }_0^{1}X(t)\varphi \prime (t)dt}}=0.$$ (8)

Equation (8) is referred to as the variational formulation of the ODE. A least-square loss based on (8) takes the form

$${\widehat{\theta }}^{\mathrm{V}}=\underset{\theta }{\arg min}\frac{1}{L}{\displaystyle \sum _{l=1}^L\Vert {\displaystyle {\int }_0^{1}f(\widehat{X}(t;h),\theta ){\varphi }_l(t)dt}}{+{\displaystyle {\int }_0^1\widehat{X}(t;h){\varphi }_l^{\prime }(t)dt}\Vert }_2^2,$$ (9)

where $\widehat{X}(t;h)$ is defined in (4b) and {ϕ_l, l = 1, …, L} is a finite set of functions in ℂ¹(0, 1) (Brunel, Clairon, and d’Alché Buc 2014). In Hall and Ma (2014), the loss function is the sum of the loss functions in (4b) and (9), so that θ and the optimal bandwidth h are estimated simultaneously. It is immediately clear that the derivative X′ (·; θ) is not needed in (9), which can lead to substantial improvement compared to the two-step procedure in (4). A minor drawback of (9) is that the variational formulation (8) is enforced on a finite set of functions {ϕ_l, l = 1, …, L} rather than on the whole class ℂ¹(0, 1). Under suitable assumptions, the estimator ${\widehat{\theta }}^{\mathrm{V}}$ is $\sqrt{n}-\text{consistent}$ (Brunel, Clairon, and d’Alché Buc 2014; Hall and Ma 2014).

2.2.3. The Generalized Profiling Method

Another collocation-based method is the generalized profiling method of Ramsay et al. (2007). Instead of the smoothing estimate $\widehat{X}(·;h)$ in (4b), the generalized profiling method uses a smoothing estimate $\check{X}(·;h,\theta )$ that minimizes the weighted sum of a data-fitting loss and a model-fitting loss for any given θ. In greater detail,

$${\widehat{\theta }}_{\lambda }^{\text{GP}}=\underset{\theta }{\arg min}{{\displaystyle \sum _{i=1}^n\Vert Y_i-\check{X}(t_i;h,\theta )\Vert }}_2^2,$$ (10a)

where

$$\check{X}(·;h,\theta )=\underset{Z(·)\in \mathcal{X}(h)}{\arg min}\frac{1}{n}{\displaystyle \sum _{i=1}^n\Vert Y_i-Z(t_i){\Vert }_2^2}+\lambda {\displaystyle {\int }_0^1\Vert Z\prime (t)-f(Z(t),\theta ){\Vert }_2^{2}dt}.$$ (10b)

In Ramsay et al. (2007), the authors solve (10a) iteratively for a nondecreasing sequence of λ’s in (10b). $\sqrt{n}-\text{consistency}$ of the limiting estimator was later established by Qi and Zhao (2010). Zhang, Cao, and Carroll (2015) proposed a model selection procedure by applying an ad hoc lasso procedure (Wang and Leng 2007) to the estimates from (10).

2.3. Methods that do not Assume the Form of f

A few authors have recently considered modeling large-scale dynamical systems from biology using ODEs (Henderson and Michailidis 2014; Wu et al. 2014), under the assumption that the right-hand side of (1) is additive,

$$X_j^{\prime }(t)={\theta }_{j0}+{\displaystyle \sum _{k=1}^p{f}_{jk}(X_k(t)),}{\theta }_{j0}\in \mathrm{ℝ}.$$ (11)

Henderson and Michailidis (2014) and Wu et al. (2014) approximated the unknown f_jk with a truncated basis expansion. Consider a finite basis, ψ(x) = (ψ₁(x), …, ψ_M(x))^T, such that

$$f_{jk}(a_k)=\psi {(a_k)}^{\mathrm{T}}{\theta }_{jk}+{\delta }_{jk}(a_k),{\theta }_{jk}\in {\mathrm{ℝ}}^M,$$ (12)

where δ_jk(a_k) denotes the residual. Using (12), a system of additive ODEs of the form (11) can be written as

$$X_j^{\prime }(t)={\theta }_{j0}+{\displaystyle \sum _{k=1}^p\psi {(X_k(t))}^{\mathrm{T}}{\theta }_{jk}}+{\displaystyle \sum _{k=1}^p{\delta }_{jk}(X_k(t)),j=1,\dots ,p}.$$ (13)

Henderson and Michailidis (2014) and Wu et al. (2014) considered the problem of estimating and selecting the nonzero elements θ_jk in (13). Roughly speaking, they proposed to solve optimization problems of the form

$${\widehat{\theta }}_j^{\text{NP}}=\underset{{\theta }_{j0}\in \mathrm{ℝ},{\theta }_{jk}\in {\mathrm{ℝ}}^M}{\arg min}{\displaystyle {\int }_0^1{\Vert {\widehat{X}}_j^{\prime }(t;h)-{\theta }_{j0}-{\displaystyle \sum _{k=1}^p\psi }{({\widehat{X}}_k(t;h))}^{\mathrm{T}}{\theta }_{jk}\Vert }_2^{2}dt}+{\lambda }_n{{\displaystyle \sum _{k=1}^p\left[{\displaystyle {\int }_0^1{\{\psi {({\widehat{X}}_k(t;h))}^{\mathrm{T}}{\theta }_{jk}\}}^{2}dt}\right]}}^{1/2},$$ (14a)

for j = 1, …, p, where

$$\widehat{X}(·;h)=\underset{Z(·)\in \mathcal{X}(h)}{\arg min}{\displaystyle \sum _{i=1}^n\Vert Y_i-Z(t_i){\Vert }_2^2}.$$ (14b)

In (14a), a standardized group lasso penalty forces all elements in θ_jk to be either zero or nonzero when λ_n is large, thereby providing variable selection.

The proposals by Henderson and Michailidis (2014) and Wu et al. (2014) are slightly more involved than (14): an extra ℓ₂-penalty is applied to the θ_jk’s in (14a) in Henderson and Michailidis (2014), whereas in Wu et al. (2014) (14a) is followed by tuning parameter selection using Bayesian information criterion (BIC), an adaptive group lasso regression, and a regular lasso. We refer the reader to Henderson and Michailidis (2014) and Wu et al. (2014) for further details.

3. Proposed Approach

We consider the problem of model selection in high-dimensional ODEs. As in Henderson and Michailidis (2014) and Wu et al. (2014), we assume an additive ODE model (11). We use a finite basis ψ(·) to approximate the additive components f_jk as in (12), leading to an ODE system that is linear in the unknown parameters (13). Following the example by Dattner and Klaassen (2015), we exploit this linearity by integrating both sides of (13), which yields

$$X_j(t)=X_j(0)+{\theta }_{j0}t+{\displaystyle \sum _{k=1}^p{\mathrm{\Psi }}_k{(t)}^{\mathrm{T}}{\theta }_{jk}}+{\displaystyle \sum _{k=1}^p{\displaystyle {\int }_0^t{\delta }_{jk}(X_k(u))du,}}$$ (15)

where Ψ_k(t) denotes the integrated basis such that

$$\begin{array}{c}{\mathrm{\Psi }}_k(t)={({\mathrm{\Psi }}_{k1}(t),\dots ,{\mathrm{\Psi }}_{kM}(t))}^{\mathrm{T}}\\ ={\displaystyle {\int }_0^t\psi (X_k(u))du,k=1,\dots ,p,}\end{array}$$ (16)

and Ψ₀(t) = t. Our method, called graph reconstruction via additive differential equations (GRADE), then solves the following problem for j = 1, …, p:

$$\begin{gathered} {\widehat{\theta }}_j=\underset{C_{j0}\in \mathrm{ℝ},{\theta }_{j0}\in \mathrm{ℝ},{\theta }_{j1,\dots ,}{\theta }_{jp}\in {\mathrm{ℝ}}^M}{\arg min}\frac{1}{2n} \\ \times {\displaystyle \sum _{i=1}^n{\left\{Y_{ij}-C_{j0}-{\theta }_{j0}{\widehat{\mathrm{\Psi }}}_0(t_i)-{\displaystyle \sum _{k=1}^p{\theta }_{jk}^{\mathrm{T}}{\widehat{\mathrm{\Psi }}}_k(t_i)}\right\}}^2} \\ +{\lambda }_{n,j}{{\displaystyle \sum _{k=1}^p\left[\frac{1}{n}{\displaystyle \sum _{i=1}^n{\{{\theta }_{jk}^{\mathrm{T}}{\widehat{\mathrm{\Psi }}}_k(t_i)\}}^2}\right]}}^{1/2}, \end{gathered}$$ (17a)

where

$$\widehat{X}(·;h)=\underset{Z(·)\in \mathcal{X}(h)}{\arg min}{\displaystyle \sum _{i=1}^n\Vert Y_i-Z(t_i){\Vert }_2^2},$$ (17b)

and

$${\widehat{\mathrm{\Psi }}}_0(t)=t;{\widehat{\mathrm{\Psi }}}_k(t)={\displaystyle {\int }_0^t\psi ({\widehat{X}}_k(u;h))du,k=1,\dots ,p}.$$ (17c)

In (17a), λ_n,j is a nonnegative sparsity-inducing tuning parameter. We may sometimes use λ_n,j ≡ λ_n for j = 1, …, p for simplicity. If the true function $f_{jk}^{\ast }$ in (11) is nonzero, we say that the kth variable $X_k^{\ast }$ is a true regulator of $X_j^{\ast }$. We let $S_j\equiv \{k:\Vert f_{jk}^{\ast }{\Vert }_2\ne 0,k=1,\dots ,p\}$ denote the set of true regulators. We let the estimated index set of regulators be ${\widehat{S}}_j\equiv \{k:\Vert {\widehat{\theta }}_{jk}{\Vert }_2\ne 0,k=1,\dots ,p\}$. We then reconstruct the network using Ŝ_j, j = 1, …, p.

Both (17a) and (17b) can be implemented efficiently using existing software (see, e.g., software methods in Loader 1999; Meier, van de Geer, and Bühlmann 2008). In our theoretical analysis in Section 4, we use local polynomial regression to obtain the smoothing estimate in (17b). We use generalized cross-validation (GCV) on the loss (17b) to select the smoothing tuning parameter h. We use BIC to select the number of bases M for ψ and $\widehat{\mathrm{\Psi }}$ in (17c), and the sparsity tuning parameter λ_n in (17a).

In some studies, time-course data are collected from multiple samples, or experiments. Let R denote the total number of experiments, and Y^(r) the observations in the rth experiment. We assume that the same ODE system (13) applies across all experiments with the same true parameter ${\theta }_{jk}^{\ast }$. We allow a different set of initial values for each experiment. Assume that each experiment consists of measurements on the same set of time points. This leads us to modify (17) as follows:

$$\begin{gathered} {\widehat{\theta }}_j=\underset{C_{j0}^{(r)}\in \mathrm{ℝ},{\theta }_{j0}\in \mathrm{ℝ},{\theta }_{j1,\dots ,}{\theta }_{jp}\in {\mathrm{ℝ}}^M}{\arg min}\frac{1}{2Rn}\sum _{r=1}^R\sum _{i=1}^n \\ \times {\left\{Y_{ij}^{(r)}-C_{j0}^{(r)}-{\theta }_{j0}{\widehat{\mathrm{\Psi }}}_0(t_i)-{\displaystyle \sum _{k=1}^p{\theta }_{jk}^{\mathrm{T}}{\widehat{\mathrm{\Psi }}}_k^{(r)}(t_i)}\right\}}^2 \\ +{\lambda }_n{\displaystyle \sum _{k=1}^p{\left[\frac{1}{Rn}{\displaystyle \sum _{r=1}^R{\displaystyle \sum _{i=1}^n{\{{\theta }_{jk}^{\mathrm{T}}{\widehat{\mathrm{\Psi }}}_k^{(r)}(t_i)\}}^2}}\right]}^{1/2}}, \end{gathered}$$ (18)

where

$$\begin{gathered} {\widehat{X}}^{(r)}(·;h)=\underset{Z(·)\in \mathcal{X}(h)}{\arg min}{\displaystyle \sum _{i=1}^n\Vert Y_i^{(r)}-Z(t_i){\Vert }_2^2,r=1,\dots ,R,} \\ {\widehat{\mathrm{\Psi }}}_0(t)=t;{\widehat{\mathrm{\Psi }}}_k^{(r)}(t)={\displaystyle {\int }_0^t\psi ({\widehat{X}}_k^{(r)}(u;h))du,k=1,\dots ,p.} \end{gathered}$$

In Sections 4, 5.1, and 5.2, we will assume that only one experiment is available, so that our proposal takes the form (17). In Sections 5.3 and 6, we will apply our proposal to data from multiple experiments using (18).

Remark 1

To facilitate the comparison of GRADE (17) with other methods, we introduce an intermediate variable,

$${\stackrel{\sim }{X}}_j(t;h,\theta )\equiv C_{j0}+{\theta }_{j0}t+{\displaystyle \sum _{k=1}^p{\theta }_{jk}^{\mathrm{T}}{\widehat{\mathrm{\Psi }}}_k(t)},$$ (19)

following from (15). Plugging (19) into the loss function in (17a) yields ${\displaystyle {\sum }_{i=1}^n{\{Y_{ij}-{\stackrel{\sim }{X}}_j(t_i;h,\theta )\}}^2}$. In the gold standard (3), the ODE system (1) is strictly satisfied due to the constraint in (3b). In the two-step procedure (4a) and (14a), the smoothing estimate $\widehat{X}(·;h)$ does not satisfy (1). GRADE stands in between: the initial estimate $\widehat{X}(·;h)$ in (17b) is solely based on the observations, while the intermediate estimate $\stackrel{\sim }{X}(·;h,\theta )$ is calculated by plugging $\widehat{X}(·;h)$ into the additive ODE (13).

4. Theoretical Properties

In this section, we establish variable selection consistency of the GRADE estimator (17). Technical proofs of the statements in this section are available in Section A in the supplementary material. We use s_j to denote the cardinality of S_j, and set s = max_j{s_j}. For ease of presentation, we let $S_j^0=\{0\}\cup S_j$, so that ${\mathrm{\Psi }}_{S_j^0}(t)={({\mathrm{\Psi }}_0(t),{\mathrm{\Psi }}_{S_j}^{\mathrm{T}}(t))}^{\mathrm{T}}={(t,{\mathrm{\Psi }}_{S_j}^{\mathrm{T}}(t))}^{\mathrm{T}}$ is an (s_jM + 1)-vector.

The proposed method (17) differs from the standard sparse additive model (Ravikumar et al. 2009) in that the regressors ${\widehat{\mathrm{\Psi }}}_k(t)$ in (17c) are estimated from smoothing estimates $\widehat{X}(·;h)$ (17b) instead of the true trajectories X^∗ in (2). We use local polynomial regression to compute $\widehat{X}(·;h)$ in (17b) (see, e.g., eq. (1.67) of Tsybakov 2009 for details on parameterization). To establish variable selection consistency, it is necessary to obtain a bound for the difference between $\widehat{X}(·;h)$ and X^∗. This is addressed in Theorem 1. Using the bound in Theorem 1, we then establish variable selection consistency of the estimator in (17) for high-dimensional ODEs in Theorem 2.

In this study, we assume that the measurement errors in (2) are normally distributed. Generalizations to bounded or sub-Gaussian errors are straightforward.

Assumption 1

The measurement errors in (2) are independent, and ε_ij ∼ N(0, σ²), i = 1, …, n, j = 1, …, p.

We also require the true trajectories $X_j^{\ast }$ in (2) to be smooth.

Assumption 2

Assume that the solutions $X_j^{\ast }$, 1 ≤ j ≤ p, belong to a Hölder class Σ(β₁, L₁), where β₁ ≥ 3.

In addition, we need some regularity assumptions to hold for the smoothing estimation (17b). These assumptions are common and not crucial to this study, and are hence deferred to Section A.2 in the supplementary material (or see sec. 1.6.1 in Tsybakov 2009). We arrive at the following concentration inequality for $|||\widehat{X}-X^{\ast }|||$.

Theorem 1

Suppose that Assumptions 1–2 and S1–S3 in the supplementary material are satisfied. Let ${\widehat{X}}_j$ in (17b) be the local polynomial regression estimator of order ℓ= ⌊β₁⌋ with bandwidth

$$h_n\propto n^{(\alpha -1)/(2{\beta }_1+1)}$$ (20)

for some positive α < 1. Then, for each j = 1, …, p,

$$|||{\widehat{X}}_j-X_j^{\ast }||{|}^2\le C_2{n}^{\frac{2{\beta }_1}{2{\beta }_1+1}(\alpha -1)}$$ (21)

holds with probability at least 1 − 2 exp{−n^α/(2C₃σ²)}, for some constants C₂ and C₃.

The concentration inequality in Theorem 1 is derived using concentration bounds for Gaussian errors (Boucheron, Lugosi, and Massart 2013). Using Theorem 1, we see that the bound (21) holds uniformly for j = 1, …, p with probability at least 1 − 2p exp{−n^α/(2C₃σ²)}. The bound in Theorem 1 thus holds uniformly for j = 1, …, p with probability converging to unity if p = o(exp{n^α/(2C₃σ²)}).

For the methods outlined in (14) (Henderson and Michailidis 2014; Wu et al. 2014), variable selection consistency depends on the convergence of $|||{\widehat{X}}^{\prime }-(X^{\ast })\prime |||$ and $|||\widehat{X}-X^{\ast }|||$. In contrast, our method depends only on the convergence rate of $|||\widehat{X}-X^{\ast }|||$. It is known that the convergence of $|||\widehat{X}\prime -(X^{\ast })\prime |||$ is slower than that of $|||\widehat{X}-X^{\ast }|||$, see, for example, Gugushvili and Klaassen (2012). As a result, the rate of convergence of ${\widehat{\theta }}_{jk}$ from (14) is slower than that of our proposed method (17).

To establish the main result, we need the following additional assumptions. Recall the definition of Ψ_j(t) from (16); for convenience, we suppress the dependence of Ψ(t) on t in what follows.

Assumption 3

For j = 1, …, p, $(X_j^{\ast })\prime$ is an additive function of $X_k^{\ast }$, k = 1, …, p. In other words,

$$(X_j^{\ast })\prime (t)={\theta }_{j0}^{\ast }+{\displaystyle \sum _{k=1}^p{f}_{jk}^{\ast }(X_k^{\ast }(t))},{\theta }_{j0}^{\ast }\in \mathrm{ℝ},j=1,\dots ,p,$$ (22)

where ${\displaystyle {\int }_0^1{f}_{jk}^{\ast }(X_k^{\ast }(t))dt=0}$ for all j, k. Furthermore, the functions $f_{jk}^{\ast }(1\le j,k\le p)$ belong to a Sobolev class W (β₂, L₂) on a finite interval with β₂ ≥ 3.

Assumption 4

The eigenvalues of ${\displaystyle {\int }_0^1{\mathrm{\Psi }}_{S_j^0}{\mathrm{\Psi }}_{S_j^0}^{\mathrm{T}}dt}$ are bounded from above by C_max and bounded from below by a positive number C_min, and for $k\cancel{\in }{S}_j^0$, the eigenvalues of ${\displaystyle {\int }_0^1{\mathrm{\Psi }}_k{\mathrm{\Psi }}_k^{\mathrm{T}}dt}$ are bounded from below by C_min. In other words,

$$\begin{gathered} 0<C_{min}\le {\mathrm{\Lambda }}_{min}\left({\displaystyle {\int }_0^1{\mathrm{\Psi }}_{S_j^0}}{\mathrm{\Psi }}_{S_j^0}^{\mathrm{T}}dt\right) \\ \le {\mathrm{\Lambda }}_{max}\left({\displaystyle {\int }_0^1{\mathrm{\Psi }}_{S_j^0}{\mathrm{\Psi }}_{S_j^0}^{\mathrm{T}}dt}\right)\le C_{max}, \end{gathered}$$ (23)

and

$$C_{min}\le {\mathrm{\Lambda }}_{min}\left({\displaystyle {\int }_0^1{\mathrm{\Psi }}_k{\mathrm{\Psi }}_k^{\mathrm{T}}dt}\right),\text{for }k\cancel{\in }{S}_j^0.$$ (24)

Assumption 5

Assume that

$$\underset{k\cancel{\in }{S}_j^0}{max}{\Vert \left({\displaystyle {\int }_0^1{\mathrm{\Psi }}_k{\mathrm{\Psi }}_{S_j^0}^{\mathrm{T}}dt}\right){\left({\displaystyle {\int }_0^1{\mathrm{\Psi }}_{S_j^0}}{\mathrm{\Psi }}_{S_j^0}^{\mathrm{T}}dt\right)}^{-1}\Vert }_2\le \xi .$$ (25)

The first part of Assumption 4 ensures identifiability among the s_j + 1 elements in the set $\{t,X_{S_j}^{\ast }\}$, and the second part ensures that Ψ_k is nondegenerate for $k\cancel{\in }{S}_j^0$. Assumption 5 restricts the association between the elements in the set $\{t,X_{S_j}^{\ast }\}$ and the elements in the set $X_{S_j^c}^{\ast }$. Note that in order for the parameters in an additive model such as (13) to be identifiable, there must be no concurvity among the variables (Buja, Hastie, and Tibshirani 1989). This is guaranteed by Assumptions 4 and 5, which appear often in the literature of lasso regression (Meinshausen and Bühlmann 2006; Zhao and Yu 2006; Ravikumar et al. 2009; Wainwright 2009; Lee, Sun, and Taylor 2013). We refer the readers to Miao et al. (2011) for a detailed discussion of the identifiability of the parameters in an ODE model.

The next assumption characterizes the relationships between the quantities in Assumptions 4 and 5 and the sparsity tuning parameter λ_n in (17a). Similar assumptions have been made in lasso-type regression (Meinshausen and Bühlmann 2006; Zhao and Yu 2006; Ravikumar et al. 2009; Wainwright 2009; Lee, Sun, and Taylor 2013).

Assumption 6

Assume that

$$f_{min}>{\lambda }_n\frac{4\sqrt{2s{C}_{max}}}{C_{min}}\text{and}\xi <\frac{1}{4}\sqrt{\frac{C_{min}}{s{C}_{max}}},$$

where $f_{min}\equiv {min}_{k\in S_j}{\{{\displaystyle {\int }_0^1{[f_{jk}^{\ast }(X_k^{\ast }(t))]}^{2}dt}\}}^{1/2}$ is the minimum regulatory effect.

Furthermore, we impose some regularity conditions on the bases ψ(·); these are deferred to Assumption S4 in the supplementary material.

We arrive at the following theorem.

Theorem 2

Suppose that Assumptions 1–6 and S1–S4 in the supplementary material hold, and let

$$\begin{gathered} h_n\propto n^{(\alpha -1)/(2{\beta }_1+1)},M\propto n^{\frac{2{\beta }_1(1-\alpha )}{(2{\beta }_1+1)(2{\beta }_2+1)}}, \\ {\lambda }_n\propto n^{-\frac{{\beta }_1(2{\beta }_2-1)(1-\alpha )}{(2{\beta }_1+1)(2{\beta }_2+1)}+2\gamma }, \end{gathered}$$

where 0 < α < 1, 0 < γ < H₁(β₁, β₂, α), and H₁(β₁, β₂, α) is a constant that depends only on β₁, β₂ and α. Then as n increases, the proposed procedure (17) correctly recovers the true graph, that is, Ŝ_j = S_j for all j = 1, …, p, with probability converging to 1, if s = O(n^γ) and pn exp(−C₄n^α/σ²) = o(1) for some constant C₄.

Because the regressors $\widehat{\mathrm{\Psi }}$ are estimated, establishing variable selection consistency requires extra attention. To prove Theorem 2, we must first establish variable selection consistency of group lasso regression with errors in variables. This generalizes the recent work on errors in variables for lasso regression (Loh and Wainwright 2012). Theorem 2 ensures that the proposed method is able to recover the true graph exactly, given sufficiently dense observations in a finite time interval if the graph is sparse. The number of variables in the system can grow exponentially fast with respect to n, which means that the result holds for the “large p, small n” scenario.

Theorem 2 does not provide us with practical guidance for selecting the bandwidth h_n for the local polynomial regression estimator ${\widehat{X}}_j$. The next result mirrors Theorem 2 for the bandwidths selected by cross-validation or GCV, which converge to $h_n\propto n^{-1/(2{\beta }_1+1)}$ asymptotically (see Xia and Li 2002; Tsybakov 2009 for details).

Proposition 1

Suppose that Assumptions 1–6 and S1–S4 in the supplementary material hold, and let

$$\begin{gathered} h_n\propto n^{-1/(2{\beta }_1+1)},M\propto n^{\frac{1}{2{\beta }_2+1}(\frac{2{\beta }_1}{2{\beta }_1+1}-\alpha )},\text{and} \\ {\lambda }_n\propto n^{-\frac{2{\beta }_2-1}{4{\beta }_2+2}(\frac{2{\beta }_1}{2{\beta }_1+1}-\alpha )+2\gamma }, \end{gathered}$$

where $0<\alpha <\frac{2{\beta }_1}{2{\beta }_1+1}$, 0 < γ < H₂(β₁, β₂, α), and H₂(β₁, β₂, α) is a constant that depends only on β₁, β₂, and α. Then as n increases, the proposed procedure (17) correctly recovers the true graph, that is, Ŝ_j = S_j for all j = 1, …, p, with probability converging to 1, if s = O(n^γ) and pn exp(−C₄n^α/σ²) = o(1) for some constant C₄.

We note that selecting the values of M and λ_n that yield the rate specified in Proposition 1 is challenging in practice. The rate of convergence of the sparsity tuning parameter λ_n is slower in Proposition 1 compared to Theorem 2. This results in an increase in the minimum regulatory effect f_min because of the relation between f_min and λ_n in Assumption 6.

5. Numerical Experiments

We study the empirical performance of our proposal in three different scenarios in the following subsections. In what follows, given a set of initial conditions and a system of ODEs, numerical solutions of the ODEs are obtained using the Euler method with step size 0.001. Observations are drawn from the solutions at an evenly spaced time grid {iT/n; i = 1, …, n} with independent N(0, 1) measurement errors, unless specified otherwise. To facilitate the comparison of GRADE with other methods, we fit the smoothing estimates $\widehat{X}$ in (17b) using smoothing splines with bandwidth chosen by GCV. We use cubic splines with two internal knots as the basis functions in (17c) in Sections 5.1 and 5.3. Linear basis functions are used in Section 5.2. The integral ${\widehat{\mathrm{\Psi }}}_k(t)={\displaystyle {\int }_0^t\psi ({\widehat{X}}_k(u;h))}du$ in (17c) is calculated numerically with step size 0.01.

5.1. Variable Selection in Additive ODEs

In this simulation, we compare GRADE with NeRDS (Henderson and Michailidis 2014) and SA-ODE (Wu et al. 2014) described in (14). We consider the following system of additive ODEs, for k = 1, …, 5:

$$\{\begin{array}{l}{X}_{2k-1}^{\prime }(t)={\theta }_{2k-1,0}+\psi {(X_{2k-1}(t))}^{\mathrm{T}}{\theta }_{2k-1,2k-1}+\psi {(X_{2k}(t))}^{\mathrm{T}}{\theta }_{2k-1,2k}\hfill \\ X_{2k}^{\prime }(t)={\theta }_{2k,0}+\psi {(X_{2k-1}(t))}^{\mathrm{T}}{\theta }_{2k,2k-1}+\psi {(X_{2k}(t))}^{\mathrm{T}}{\theta }_{2k,2k}\hfill \end{array},t\in [0,20]$$ (26)

where ψ(x) = (x, x², x³)^T is the cubic monomial basis. The parameters and initial conditions are chosen so that the solution trajectories are identifiable under an additive model (Buja, Hastie, and Tibshirani 1989). Detailed specification of (26) can be found in Section C of the supplementary material.

After generating data according to (26) and introducing noise, we apply GRADE, NeRDS, and SA-ODE to recover the directed graph encoded in (26). Both NeRDS and SA-ODE are implemented using code provided by the authors. NeRDS and SA-ODE use smoothing splines to estimate $\widehat{X}$ and ${\widehat{X}}^{\prime }$ in (14b), and cubic splines with two internal knots as the basis ψ in (14a). As mentioned briefly in Section 2, NeRDS applies an additional smoothing penalty that amounts to an ℓ₂ penalty on θ_jk in (14a), controlled by a parameter selected using GCV (Henderson and Michailidis 2014). We apply GRADE using the same smoothing estimates and basis functions as NeRDS and SA-ODE. To facilitate a direct comparison to NeRDS, we apply GRADE both with and without an additional ℓ₂-type penalty on the θ_jk’s in (17a). We apply all methods for a range of values of the sparsity-inducing tuning parameter (e.g., λ_n in (17a)), to yield a recovery curve of varying sparsity.

We summarize the simulation results in Figure 1, where the numbers of true edges selected are displayed against the total numbers of selected edges over a range of sparsity tuning parameters. We see that GRADE outperforms the other two methods, which corroborates our theoretical findings in Section 4 that our proposed method is more efficient than methods such as NeRDS and SA-ODE, which involve derivative estimation (see, e.g., comments below Theorem 1).

Figure 1.

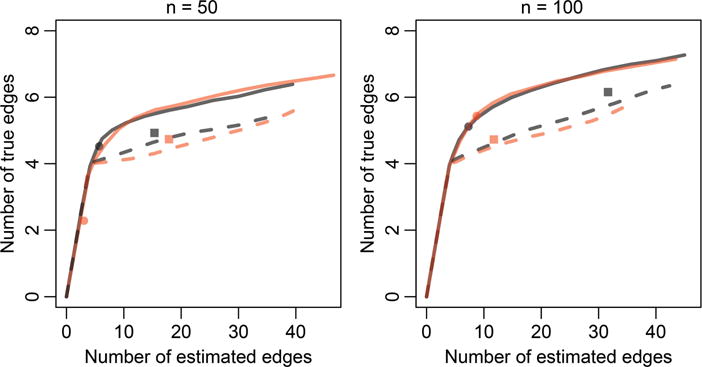
Performance of network recovery methods on the system of additive ODEs in (26), averaged over 400 simulations. The four curves represent SA-ODE (dashed, red line), NeRDS (dashed, gray line), and GRADE without (solid, red line) and with (solid, gray line) the additional smoothing penalty in (17a) used by NeRDS. Each point on the curves corresponds to average performance for a given sparsity tuning parameter λ_n in (14a) or (17a). The symbols indicate the sparsity tuning parameter λ_n selected using BIC (SA-ODE, red square, and GRADE, red circle and gray circle) or GCV (NeRDS, gray square).

5.2. Variable Selection in Linear ODEs

In this simulation, we compare GRADE to two recent proposals by Brunel, Clairon, and d’Alché Buc (2014) and Hall and Ma (2014). Recall from Section 2.2.2 that Brunel, Clairon, and d’Alché Buc (2014) and Hall and Ma (2014) proposed to estimate a few unknown parameters in an ODE system of known form. Hence, we consider a simple linear ODE system, for k = 1, …, 4,

$$\{\begin{array}{l}{X}_{2k-1}^{\prime }(t)=2k\pi X_{2k}(t)\hfill \\ X_{2k}^{\prime }(t)=-2k\pi X_{2k-1}(t)\hfill \end{array},t\in [0,1].$$ (27)

For each k = 1, …, 4, we set the initial condition to be (X_2k−1(0), X_2k(0)) = (sin(y_k), cos(y_k)) where y_k ∼ N(0, 1). The solutions to (27) take the form of sine and cosine functions of frequencies ranging from 2π to 8π. The graph corresponding to (27) is sparse, with only eight directed edges out of 64 possible edges. We fit the model

$$X\prime (t)=\mathrm{\Theta }X(t)+C,$$ (28)

where Θ is an unknown 8 × 8 matrix and C is an 8-vector. We apply the method in Brunel, Clairon, and d’Alché Buc (2014) using the code provided by the authors. We implement the method in Hall and Ma (2014) in R based on the authors’ code in Fortran. Because the loss function in Hall and Ma (2014) is not convex, we use five sets of random initial values and report the best performance. Since both Brunel, Clairon, and d’Alché Buc (2014) and Hall and Ma (2014) yielded dense estimates for Θ in (28), to examine how well these methods recover the true graph, we threshold the estimates at a range of values to obtain a variable selection path. We apply GRADE using the linear basis function ψ(x) = x.

Results are shown in Figure 2. We can see that GRADE outperforms the methods in Brunel, Clairon, and d’Alché Buc (2014) and Hall and Ma (2014). This is likely because GRADE exploits the sparsity of the true graph with a sparsity-inducing penalty. In principle, Brunel, Clairon, and d’Alché Buc (2014) and Hall and Ma (2014) could be generalized to include penalties on the parameters. We leave this to future research.

Figure 2.

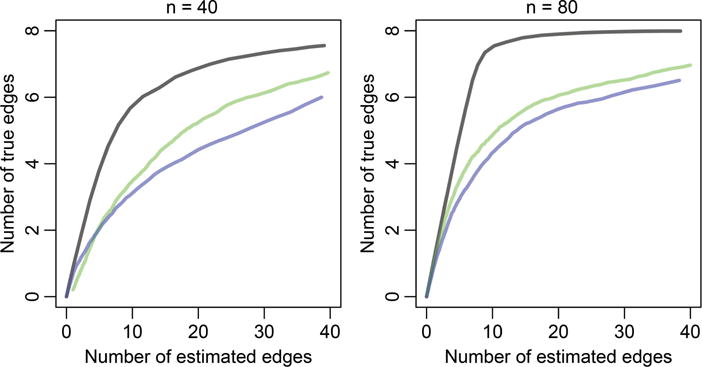
Network recovery on the system of linear ODEs (27), averaged over 200 simulated datasets. The three curves represent GRADE (gray line), Hall and Ma (2014) (blue line), Brunel, Clairon, and d’Alché Buc (2014) (green line).

5.3. Robustness of GRADE to the Additivity Assumption

The GRADE method assumes that the true underlying model is additive (Assumption 3). However, in many systems, the additivity assumption is violated; for instance, multiplicative effects may be present in gene regulatory networks (Ma et al. 2009). In this subsection, we investigate the performance of GRADE in a setting where the true model is nonadditive. We consider the following system of ODEs, for k = 1, …, 5,

$$\{\begin{array}{l}{X}_{2k-1}^{\prime }(t)=f_{2k-1}(X_{2k-1}(t),X_{2k}(t))\equiv 2X_{2k-1}(t)-v{X}_{2k-1}(t)X_{2k}(t)\hfill \\ X_{2k}^{\prime }(t)=f_{2k}(X_{2k-1}(t),X_{2k}(t))\equiv v{X}_{2k-1}(t)X_{2k}(t)-2X_{2k}(t)\hfill \end{array},t\in [0,5],$$ (29)

where v is a positive constant. For each k = 1, …, 5, the pair of Equation (29) is a special case of the Lotka–Volterra equations (Volterra 1928), which represent the dynamics between predators (X_2k) and prey (X_2k−1). The parameter v defines the interaction between the two populations. For v ≠ 0, both $X_{2k-1}^{\prime }$ and $X_{2k}^{\prime }$ are nonadditive functions of X_2k−1 and X_2k. We define two types of directed edges, where ℰ₁ ≡ {(X_j, X_j), j = 1, …, 10} and ℰ₂ ≡ {(X_2k−1, X_2k), (X_2k, X_2k−1), k = 1, …, 5} represent the self-edges and nonself-edges, respectively. Figure 3(a) contains an illustration of the graph and edge types for each pair of equations. In what follows, we investigate how well GRADE recovers these two types of edges as we change the parameter v, that is, as the additivity assumption is violated.

Figure 3.

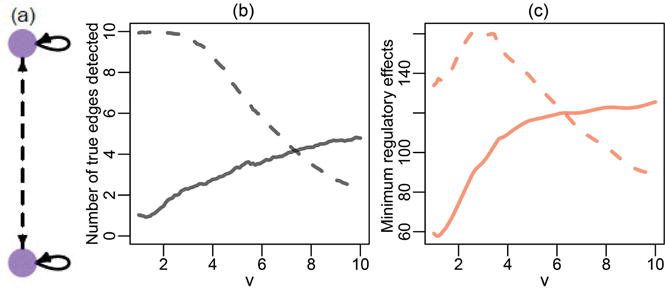
(a) The graph encoded by a pair of Lotka-Volterra equations as given in (29). Self-edges (solid, gray line) and nonself-edges (dashed, gray line) are shown. (b) Self-edge (solid, gray line) and nonself-edge (dashed, gray line) recovery of GRADE, averaged over 200 simulated datasets. (c) Minimum signals defined in (31), for self-edges, D⁽¹⁾(·) (solid, red line), and nonself-edges, D⁽²⁾(·) (dashed, red line).

Since measurement error is not essential to the current discussion, we generate data according to (29) without adding noise. To ensure that the trajectories are identifiable, we generate R = 2 sets of random initial values drawn from N₁₀(0, 2I₁₀), where I₁₀ is a 10 × 10 identity matrix. To quantify the amount of signal in an edge that GRADE can detect, we introduce the quantity

$$D_{j,k}(v)=\mathbb{E}\left[R{\displaystyle {\int }_0^T{\left\{\frac{\partial f_j}{\partial X_k}(t;X(0))\right\}}^{2}dt}\right],$$ (30)

where the expectation is taken with respect to the random initial values X(0) and R is the number of initial values. The measure D_j,k in (30) is a loose analogy to ${\{{\displaystyle {\int }_0^1{[f_{jk}^{\ast }(X_k^{\ast }(t))]}^{2}dt}\}}^{1/2}$ used in Assumption 6. Note that if no edge is present from X_k to X_j, then ∂f_j/∂X_k ≡ 0 and hence D_j,k(v) = 0. One immediately notes that, as R increases, the regulatory effect for a true edge increases proportionally to R, while the regulatory effect of a nonedge remains zero. For the self-edges in ℰ₁ and the nonself-edges in ℰ₂, we can define D⁽¹⁾(v) and D⁽²⁾(v) as

$$\begin{gathered} D^{(1)}(v)=\underset{k=1,\dots ,10}{min}{D}_{k,k}(v),\text{and} \\ {D}^{(2)}(v)=\underset{k=1,\dots ,5}{min}\{D_{2k-1,2k}(v),D_{2k,2k-1}(v)\}, \end{gathered}$$ (31)

where we use the minimum because variable selection is limited by the minimum regulatory effect (see Assumption 6). With a slight abuse of definition, we refer to (31) as the minimum regulatory effects in a nonadditive model.

We apply GRADE using the formulation in (18). The sparsity parameter λ is chosen so that there are 20 directed edges in the estimated network. We record the number of estimated edges that are in ℰ₁ and ℰ₂. The edge recovery performance is shown in Figure 3(b). In Figure 3(c), we display the minimum regulatory effects defined in (31). Edge recovery and minimum regulatory effects show a similar trend as a function of r in (29). This suggests that (31), and thus (30), is a reasonable measure of the additive components of the regulatory effect of the edges. The slight deviation between the trends reflects the fact that the measure defined in (30) is not a direct counterpart of ${\{{\displaystyle {\int }_0^1{[f_{jk}^{\ast }(X_k^{\ast }(t))]}^{2}dt}\}}^{1/2}$ in a nonadditive model. The edge recovery improves when a larger value of R is used, though these results are omitted due to space constraints. Our results indicate that GRADE can recover the true graph even when the additivity assumption is violated, provided that the regulatory effects (30) for the true edges are sufficiently large.

6. Applications

6.1. Application to in Silico Gene Expression Data

GeneNetWeaver (GNW) provides an in silico benchmark for assessing the performance of network recovery methods (Schaffter, Marbach, and Floreano 2011), and was used in the third DREAM challenge (Marbach et al. 2009). GNW is based upon real gene regulatory networks of yeast and E. coli. It extracts sub-networks from the yeast or E. coli gene regulatory networks, and assigns a system of ODEs to the extracted network. This system of ODEs is nonadditive, and includes unobserved variables (Marbach et al. 2010). Therefore, the assumptions of GRADE are violated in the GNW data.

To mimic real-world laboratory experiments, GNW provides several data generation mechanisms. In this study, we consider data from the perturbation experiments. The perturbation experiments are similar to the data-generating mechanisms used in Section 5.3, where initial conditions of the ODE system are perturbed to emulate the diversity of trajectories from multiple independent experiments.

We investigate 10 networks from GNW that have been previously studied by Henderson and Michailidis (2014), of which five have 10 nodes and five have 100 nodes. For each network, GNW provides one set of noiseless gene expression data consisting of R perturbation experiments where the trajectories are measured at n = 21 evenly spaced time points in [0, 1]. Here R = 10 for the five 10-node networks and R = 100 for the five 100-node networks. As in Henderson and Michailidis (2014), we add independent N (0, 0.025²) measurement errors to the data at each timepoint.

We apply NeRDS as described in Henderson and Michailidis (2014). We apply GRADE using the formulation (18) to handle observations from multiple experiments, with the smoothing estimates $\widehat{X}$ in (17b) fit using smoothing splines with bandwidth chosen by GCV, and using cubic splines with two internal knots as the basis functions in (17c). The integral ${\widehat{\mathrm{\Psi }}}_k(t)={\displaystyle {\int }_0^t\psi }({\widehat{X}}_k(u;h))du$ in (17c) is calculated numerically with step size 0.01. Finally, we apply an additional ℓ₂-type penalty to the θ_jk’s in (18) to match the setup of NeRDS. The tuning parameter for this penalty is set to be 0.1.

Results are shown in Table 1. Recall that the data-generating mechanism violates crucial assumptions for both NeRDS and GRADE. We see in Table 1 that NeRDS outperforms GRADE in one network, while GRADE outperforms NeRDS in the other nine networks. This suggests that GRADE is a competitive exploratory tool for reconstructing gene regulatory networks.

Table 1.

Area under ROC curves for NeRDS and GRADE.

	p = 10		p = 100
	NeRDS	GRADE	NeRDS	GRADE
Ecoli1	0.450 (0.438, 0.462)	0.545 (0.534, 0.557)	0.624 (0.622, 0.627)	0.670 (0.667, 0.673)
Ecoli2	0.512 (0.502, 0.523)	0.643 (0.634, 0.653)	0.637 (0.635, 0.640)	0.653 (0.650, 0.656)
Yeast1	0.486 (0.476, 0.495)	0.679 (0.666, 0.691)	0.610 (0.607, 0.612)	0.636 (0.635, 0.638)
Yeast2	0.525 (0.518, 0.532)	0.607 (0.600, 0.613)	0.568 (0.566, 0.569)	0.584 (0.582, 0.585)
Yeast3	0.467 (0.460, 0.474)	0.576 (0.566, 0.587)	0.617 (0.616, 0.619)	0.567 (0.566, 0.568)

NOTES: The average area under the curves and 90% confidence intervals, over 100 simulated datasets. Networks and data-generating mechanisms are described in Section 6.1. Boldface indicates the method with larger AUC.

6.2. Application to Calcium Imaging Recordings

In this section, we consider the task of learning regulatory relationships among populations of neurons. We investigate the calcium imaging recording data from the Allen Brain Observatory project conducted by the Allen Institute for Brain Science (available at http://observatory.brain-map.org.). Here, we investigate one of the experiments in the project. In this experiment, calcium fluorescence levels (a surrogate for neuronal activity) are recorded at 30 Hz on a region of the primary visual cortex while the subject mouse is shown 40 visual stimuli. The 40 visual stimuli are combinations of eight spatial orientations and five temporal frequencies. Each stimulus lasts for 2 sec and is repeated 15 times. The recorded videos are processed by the Allen Institute to identify individual neurons. In this particular experiment, there are 575 neurons. Each neuron’s activity is defined as the average calcium fluorescence level of the pixels that it covers in the video.

It is known that the activities of individual neurons are noisy and sometimes misleading (Cunningham and Byron 2014). As an alternative, neuronal populations can be studied (see, e.g., Part Three of Gerstner, Kistler, Naud, and Paninski 2014). We define 25 neuronal populations by dividing the recording region into a 5 × 5 grid, where each population contains roughly 20 neurons. We use GRADE to capture the functional connectivity among the 25 neuronal populations. Note that functional connectivity is distinct from physical connectivity. Functional connectivity involves the relationships among neuronal populations that can be observed through neuron activities and may change across stimuli, whereas physical connectivity consists of synaptic interactions.

We estimate the functional connectivity corresponding to three different but related stimuli, consisting of frequencies of 1 Hz, 2 Hz, and 4 Hz, each at a spatial orientation of 90°. For each stimulus, we have calcium fluorescence levels of the p = 25 neuronal populations for each of R = 15 repetitions. Since each repetition spans 2 sec and the calcium fluorescence is recorded at 30 Hz, there are 60 timepoints per repetition. We apply GRADE using the formulation in (18) to reconstruct the functional connectivity under each of the three stimuli. We use smoothing splines with bandwidth h selected with GCV to estimate $\widehat{X}$ in (17b), and use cubic splines with four internal knots as the basis functions ψ(·) in (17c). The sparsity parameter λ_j,n for each nodewise regression in (18) is selected using BIC for each j = 1, …, 25. For ease of visualization, we prefer a sparse network, and so we fit GRADE using tuning parameter values α(λ_1,n, …, λ_p,n), where the scalar α is selected so that each of the estimated networks contains approximately 25 edges.

Estimated functional connectivities are shown in Figure 4. We see that, in all three networks, the 24th neuronal population regulates many other neuronal populations, indicating that this region may contain neurons that are sensitive to this spatial orientation. Furthermore, we see that the adjacent connectivity networks in Figure 4 are somewhat similar to each other, whereas the networks at 1 Hz and 4 Hz have few similarities. This agrees with the observation in neuroscience that neurons in the mouse primary visual cortex are responsive to a somewhat narrow range of temporal frequencies near their peak frequencies (see, e.g., Gao, DeAngelis, and Burkhalter 2010).

Figure 4.

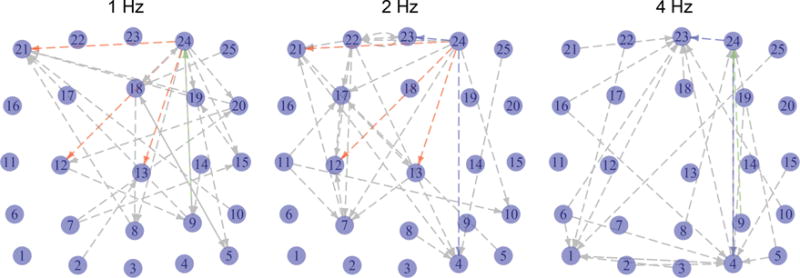
Estimated functional connectivities among neuronal populations from the calcium imaging data described in Section 6.2. Each node is positioned near the center of the neuronal population it represents, with jitter added for ease of display. The three red edges are shared between the estimated networks at 1 Hz and 2 Hz; the two blue edges are shared between estimated networks at 2 Hz and 4 Hz; the single green edge is shared between the estimated networks at 1 Hz and 4 Hz. For reference, given two Erdös-Rènyi graphs consisting of 25 nodes and 25 edges, the probability of having three or more shared edges is 0.07, and the probability of having two or more shared edges is 0.26.

7. Discussion

In this article, we propose a new approach, GRADE, for estimating a system of high-dimensional additive ODEs. GRADE involves estimation of an integral rather than a derivative. We show that estimating the integral is superior to estimating the derivatives both theoretically and empirically. We leave an extension of our work to nonadditive ODEs to future research.

In this article, we have not addressed the issue of experimental design. Given a finite set of resources, one may choose to design an experiment to measure n observations on a very dense time grid, or on a coarse time grid. Alternatively, one might choose to measure n/R observations for R distinct experiments from a single ODE system (1), each with a different initial condition. This presents a trade-off that is especially interesting in the context of ODEs: using a dense time grid improves the quality of the smoothing estimates $\widehat{X}$, as seen in Sections 5.1 and 5.2, while running multiple experiments enhances the identifiability of the true structure, as seen in Section 5.3. We leave a more detailed treatment of these issues to future work.