Hexahydrated Mg²⁺ Binding and Outer-Shell Dehydration on RNA Surface

Abstract

The interaction between metal ions, especially Mg²⁺ ions, and RNA plays a critical role in RNA folding. Upon binding to RNA, a metal ion that is fully hydrated in bulk solvent can become dehydrated. Here we use molecular dynamics simulation to investigate the dehydration of bound hexahydrated Mg²⁺ ions. We find that a hydrated Mg²⁺ ion in the RNA groove region can involve significant dehydration in the outer hydration shell. The first or innermost hydration shell of the Mg²⁺ ion, however, is retained during the simulation because of the strong ion-water electrostatic attraction. As a result, water-mediated hydrogen bonding remains an important form for Mg²⁺-RNA interaction. Analysis for ions at different binding sites shows that the most pronounced water deficiency relative to the fully hydrated state occurs at a radial distance of around 11 Å from the center of the ion. Based on the independent 200 ns molecular dynamics simulations for three different RNA structures (Protein Data Bank: 1TRA, 2TPK, and 437D), we find that Mg²⁺ ions overwhelmingly dominate over monovalent ions such as Na⁺ and K⁺ in ion-RNA binding. Furthermore, application of the free energy perturbation method leads to a quantitative relationship between the Mg²⁺ dehydration free energy and the local structural environment. We find that $\text{ΔΔ}{G}_{\text{hyd}},$ the change of the Mg²⁺ hydration free energy upon binding to RNA, varies linearly with the inverse distance between the Mg²⁺ ion and the nearby nonbridging oxygen atoms of the phosphate groups, and $\text{ΔΔ}{G}_{\text{hyd}}$ can reach −2.0 kcal/mol and −3.0 kcal/mol for an Mg²⁺ ion bound to the surface and to the groove interior, respectively. In addition, the computation results in an analytical formula for the hydration ratio as a function of the average inverse Mg²⁺-O distance. The results here might be useful for further quantitative investigations of ion-RNA interactions in RNA folding.

Introduction

The folding of RNA involves metal-ion-binding to RNA to neutralize the RNA backbone charge and screen Coulomb repulsion between the backbone charges (1, 2, 3, 4, 5, 6). The ion atmosphere of bound ions around the nucleic acid plays a critical role in stabilizing the three-dimensional structure of RNA and carrying out RNA-based enzymatic catalysis (7, 8, 9, 10, 11, 12, 13, 14). In particular, the Mg²⁺ ion, which shows unusually high efficiency in stabilizing RNA tertiary structures (11, 15, 16), is essential for the proper folding and stabilization of these structures (8, 17, 18, 19).

Metal ions around an RNA helix accumulate around the major and minor grooves (distance within 8 Å from the central axis) and the surface region (10–15 Å from the RNA surface). Furthermore, an RNA structure often involves multiple bound Mg²⁺ ions in the RNA grooves and/or other sites on the RNA surface (20, 21, 22). Such an ion accumulation effect can lower the overall electrostatic energy of the system and help stabilize the structure (15, 17, 23).

A number of theoretical approaches, such as the Poisson-Boltzmann theory (24), the counterion condensation model (25, 26, 27), the tightly bound ion (TBI) model (28, 29, 30, 31, 32), the three-dimensional reference interaction site model (33, 34), and all-atom molecular dynamics (MD) simulation methods (23, 35, 36, 37, 38, 39, 40, 41, 42), have been developed to predict the ion distribution around RNA. Among these methods, MD simulation has the unique advantage of providing detailed atomistic and dynamic descriptions for ion binding (37, 38). Recently, MD simulations and anomalous small-angle x-ray scattering experiments showed an interesting radial distance-concentration relationship for Mg²⁺ binding around the RNA surface (37, 38, 43). Moreover, MD simulations can adapt to various force field parameters (38, 44, 45, 46) and, depending on the force field and the sampling algorithm, can provide more detailed and accurate predictions (35, 36, 37, 38, 43) for ion distributions around nucleic acids than the nonlinear Poisson-Boltzmann equation calculations.

The TBI model has the advantage of accounting for ion correlation and fluctuation effects. These effects are potentially important for multivalent ions such as Mg²⁺ ions (7). However, neither the original coarse-grained TBI model nor the more recent Monte Carlo TBI model (47), the new generation model based on atomistic ion distributions and Monte Carlo sampling of the ion distribution, can treat the dehydration effect. To include ion dehydration effects in the TBI/Monte Carlo TBI and other models, we need quantitative understanding of the dehydration states of the bound ions at the different RNA sites and a dehydration free-energy function for ions bound at the different sites. In this study, we derive such an energy function through MD simulation.

Despite the critical role of Mg²⁺-RNA interaction in RNA folding, predicting Mg²⁺ binding sites remains a significant challenge. Studying Mg²⁺ distribution around RNA using traditional x-ray diffraction and solution NMR methods can be challenging because of RNA flexibility and the mobility of Mg²⁺ ions in the solution. In addition, ion-ion correlation, ion and RNA dehydration, the interplay between the specific and nonspecific ion-RNA interactions, and the different force field parameters for metal ion-RNA interaction further challenge the computational predictions for ion distribution and ion binding sites. Recently, using the grand canonical Monte Carlo sampling combined with MD simulations, Lemkul et al. (35) investigated the Mg²⁺ ion distribution around four representative RNA structures and observed inner-sphere and outer-sphere ion binding sites. The study represents a significant advance in studying Mg²⁺ distribution around RNA with an explicit solvent. In another recent important study, by combining combined the enhanced sampling techniques with the parameterization for Mg²⁺-related interactions, Cunha and Bussi (36) developed a modified version of bias-exchange metadynamics simulation method. The simulation provided detailed information about the binding affinity of Mg²⁺ on the possible binding sites for a four-base-pair RNA duplex (36). The results showed significant improvements in the applicability of the bias-exchange metadynamics method for the calculation of complex free-energy landscapes as well as the affinities for an Mg²⁺-RNA system. Furthermore, the results of the study indicated a reduced divalent ion binding because of RNA conformational flexibility and the competition from other ions.

According to the hydration state, Mg²⁺-RNA interaction can be classified into direct and indirect interactions. For direct interaction, such as Mg²⁺ binding to certain sites on rRNA fragments (48) and 23S RNA (49), the Mg²⁺ ion interacts with the RNA (phosphate group) as part of the inner-shell coordination sphere of Mg²⁺. For indirect interaction, Mg²⁺ retains a hydration shell in the “ion atmosphere” around RNA (37, 38), and ion-RNA interaction is mediated by the water molecule in the hydration shell (23, 39). Mg²⁺ ions are fully hydrated in the bulk solution. A hydrated Mg²⁺ ion has a relatively robust innermost hydration shell with six bound water molecules and a second hydration layer (50, 51). As a fully hydrated Mg²⁺ ion binds to RNA from bulk solution, the hydration state of the Mg²⁺ ion can be changed by the structural and electrostatic environment around the ion binding site (23, 39). Specifically, as a hydrated Mg²⁺ ion moves closer to specific binding sites on an RNA surface or in the grooves (52, 53), the ion may become dehydrated. Such an RNA-induced ion dehydration would result in a change in ion-RNA interactions and significantly influence RNA stability and biological functions.

Efficient and accurate computations for the hydration free energy for a solute molecule or charged ion can be challenging (54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66). Explicit solvent models can give accurate hydration free-energy results but often require exceedingly long computing time (66, 67, 68). On the other hand, implicit solvent-based models such as the nonlinear Poisson-Boltzmann model (56, 59, 69), Born solvent model (70, 71, 72), and the weight surface area method (73, 74, 75, 76, 77) are computationally efficient, but the accuracy of the results may be inconsistent. Recently, using an adaptive molecular boundary and the corresponding force field, Fennell et al. (78, 79, 80) developed a new approach, semiexplicit assembly (SEA), based on the improved field-SEA water models to compute the solvation free energy of nonpolar, polar, and charged solutes. The improved field-SEA algorithm can predict the solvation free energy of charged monovalent ions, and the results are consistent with those predicted from the explicit solvent model (80). For the highly charged Mg²⁺ ions, the asymmetry of its dehydration states in the different binding sites on the RNA surface would affect the ion-RNA contact form (18, 81, 82). Because Mg²⁺ ions can bind at different locations around the RNA structure, such as the major and minor grooves, and interact with the phosphate group through strong electrostatic attraction, the hydration free energy of Mg²⁺ ions requires a separate, careful evaluation.

In this study, we use MD simulation to investigate the coordinated distribution of water molecules around Mg²⁺ at the different binding locations and calculate the hydration free energy $\text{Δ}{G}_{\text{hyd}}$ of Mg²⁺ using the free energy perturbation (FEP) method in explicit TIP3P solvent. Our simulations show long-time binding of ions and water-mediated Mg²⁺-RNA interactions at different locations. Using the FEP method, we compute the change of the hydration free energy $\text{ΔΔ}{G}_{\text{hyd}}$ as an Mg²⁺ ion moves from the bulk solvent to the RNA surface. We find an average change of hydration free energy of around −2.0 kcal/mol for ions bound to the surface and an additional −3.0 kcal/mol free-energy change for those bound to the deep groove. Furthermore, our data indicate that ion dehydration energy varies linearly with the hydration ratio (HR), the ratio of the number of (bound) water molecules between the dehydration and the hydration states. From the simulation results for ions bound at the different locations on RNA, we derive an analytical formula for the average dehydration energy for ions in the different structural environments of RNA. The analytical formula may provide a useful and efficient estimation for the dehydration of the bound ions.

Materials and Methods

MD simulation

We select three representative RNA structures to investigate Mg²⁺ hydration properties upon RNA binding; see Table 1 for the Protein Data Bank (PDB) identifiers of the structures and the solution conditions in the simulation. In the presimulation treatment, we add hydrogen atom coordinates using the psfgen plugin of Visual Molecular Dynamics (VMD) (Theoretical and Computational Biophysics Group, Urbana-Champaign, IL) (83). The RNA structure is embedded in the respective explicit TIP3P water box. We set the minimal distance between RNA and the box boundary as 25 Å. To simulate the experimental conditions (84, 85, 86), salt (NaCl or KCl) and Mg²⁺ ions are added to the water boxes. All the metal ion parameters are obtained from a CHARMM36 force field (MacKerell Lab, University of Maryland, Baltimore, MD) (87, 88), and their coordinates are randomly placed by using VMD (Theoretical and Computational Biophysics Group). The minimal distance among Mg²⁺ ions is 5 Å. To highlight the Mg²⁺ binding property, we let the Mg²⁺ ions neutralize the RNA charge. The whole system is kept electrically neutral with additional ions and the added Cl⁻ ions. The procedure above is completed with the Solvate and Add Ions plugins of VMD (Theoretical and Computational Biophysics Group), using atomic parameters given by the CHARMM36 force field (MacKerell Lab) (87, 88); see Table 1 for the information about the RNA-water-ion solution systems for the three RNA structures.

Table 1.

Three Representative RNA Models and the Corresponding Simulation Conditions

PDB ID	Description	Nucleotide No.	Experiment Method	Resolution (Å)	Mg2+ No.	System Size (Å3)	[Mg2+] (mM)	[Na+/K+] (mM)
1TRA	tRNA	76	x ray	3.0	38	100$\times$89$\times$121	20	100 Na+
2TPK	mRNA	36	NMR	N/A	18	75$\times$78$\times$102	20	150 K+
437D	BWYV	27	x ray	1.6	12	93$\times$81$\times$80	15	100 Na+

The RNA coordinates are downloaded from the PDB, and the solution simulation systems are constructed by VMD (Theoretical and Computational Biophysics Group) (83). ID, identifier.

For each of the above RNA solution systems, using the NAMD 2.10 package (Theoretical and Computational Biophysics Group) (89), we first run minimization for 10,000 steps, with 1 fs time step for the first 1 ns and 2 fs for the subsequent time period. The total simulation time for each RNA solution system is 200 ns. During the simulation, the RNA may translate and drift in the solution. To localize the RNA at the center of the simulation box, we restrict the two backbone C4′ and C3′ atoms near the box center by applying a harmonic potential with a force constant of 5 kcal/mol $\cdot$ Ų. All the other RNA atoms are allowed to move. In the simulation, nonbonded interactions are calculated using the Verlet cutoff scheme, and the cutoff is set to be 12 Å. Long-range electrostatic interactions are treated with the particle mesh Ewald method. All atoms of the system are in the isobaric-isothermal ensemble. The isotropic pressure is maintained at 1 atm, and Langevin dynamics and Langevin piston methods are used. The MD simulation temperature is in accordance with the experimental conditions (298.15 K for tRNA and BWYV, 310 K for mRNA). All the MD simulations are performed on a GPU NVIDIA Tesla C2075 (NVIDIA, Santa Clara, CA).

FEP calculation for Mg²⁺ hydration free energy

Based on the equilibrated system after the 200 ns simulation, we determine the hydration free energy of an Mg²⁺ ion using the FEP method integrated in the NAMD 2.10 package (Theoretical and Computational Biophysics Group) (65, 90, 91, 92). In the FEP calculation, we charge a bare Lennard-Jones particle into an Mg²⁺ ion using the dual-topology paradigm. The dual-topology approach has the benefit of improving the convergence while perturbing only the electrostatic component of the nonbonded potential without changing the Lennard-Jones terms (52, 93). The Mg²⁺ ion hydration energy change is treated as a transformation from the noncharged state (reference state, ion-RNA coupling transformation parameter λ = 0) to the fully charged state on the RNA surface (target state, λ = 1). The free-energy difference between the target state and the reference state is the hydration energy $\text{Δ}{G}_{\text{hyd}}$ of the ion.

When evaluating the free-energy difference between two states, variable λ-values correspond to the different Hamiltonian in the thermodynamic integration. The variation of λ between 0 and 1 allows interconversion between two states during MD simulation (93). During the ion-charging process that connects the reference state to the target state, a stratification strategy is used. If there are N states (including $N\mathrm{-}2$ intermediate states) in the stratification process, the Hamiltonian of coupling parameter λ is

$$H\left({\lambda }_i\right)={\lambda }_i{H}_1+\left(1\mathrm{-}{\lambda }_i\right)H_0=H_0+{\lambda }_i\text{Δ}H,$$ (1)

where $\text{Δ}H$ is the perturbation term in the target Hamiltonian and $H_1\mathrm{-}{H}_0$ is the net change of the Hamiltonian in the process. The i-th $\text{Δ}H$ is obtained from

$$\text{Δ}{H}_i=H\left({\lambda }_{i+1}\right)-H\left({\lambda }_i\right)=\left({\lambda }_{i+1}-{\lambda }_i\right)\text{Δ}H=\text{Δ}{\lambda }_i\text{Δ}H,$$ (2)

and the total free-energy difference is

$$\text{Δ}A=-\frac{1}{\beta }\sum _{i=1}^{N-1}\text{ln}{\langle e^{-\beta \text{Δ}{\lambda }_i\text{Δ}H}\rangle }_{{\lambda }_i},$$ (3)

where β is 1/$k_{\text{B}}T,$ $k_{\text{B}}$ is the Boltzmann constant, and T is the temperature. For a given ionic solution system, integrating out the kinetic energy term in the Hamiltonian leads to the following change in the hydration free energy $\left(\lambda =0\to 1\right)$ for an Mg²⁺ ion:

$$\text{Δ}{G}_{\text{hyd}}=-\frac{1}{\beta }\sum _{i=1}^{N-1}\text{ln}{\langle e^{-\beta \text{Δ}{\lambda }_i\text{Δ}U}\rangle }_{{\lambda }_i},$$ (4)

where $\text{Δ}U$ denotes the potential energy change from state i to state $i+1$.

To enhance the sampling quality for the hydration free-energy calculation, we run both ion-charging $\left(\lambda =0\to 1\right)$ and discharging $\left(\lambda =1\to 0\right)$ processes for the FEP calculation. Each charging/discharging process is divided into 16 equally spaced simulation windows ($\text{Δ}\lambda$ = ± 0.0625, $N=17$ in Eq. 1). For each interval $\text{Δ}\lambda$, we run 20,000 MD steps with 2 fs for each step, including the first 5000 equilibration steps. Thus, the total simulated time for calculating the hydration free energy of an Mg²⁺ ion is 20,000 (steps) $\times$ 2 (fs/step) $\times$ [16 (charging) + 16 (discharging)] = 1.28 ns. A soft-core potential for the ions is used to remove the singularity in the van der Waals potential caused by Mg²⁺-solvent contact (94, 95). In the final analysis of the FEP calculation, we use Bennett’s acceptance ratio method (the ParseFEP plugin in VMD (Theoretical and Computational Biophysics Group)) to estimate the Mg²⁺ ion hydration free-energy differences both in the charging and the discharging processes of the alchemical transformation (96). For each Mg²⁺ binding site, we run 10 independent FEP calculations and calculate the average as well as the standard deviations (SD) over these 10 FEP results. The FEP calculations are performed on Intel Xeon CPU E5-2650 v3 computer clusters (Intel, Santa Clara, CA).

Results and Discussion

Distribution of bound ions

The simulations for the three RNA-water-ion systems show significant Mg²⁺ ion binding in the major grooves as well as the other regions on the RNA surface. Mg²⁺ ions, which carry higher charges than monovalent ions, are more competitive in RNA binding than Na⁺ or K⁺ ions (see Fig. 1). Physically, charge neutralization requires fewer divalent ions than monovalent ions. Less ion binding means less ion entropic decrease upon RNA binding. Therefore, divalent ions are preferred over monovalent ions in RNA binding (31, 32, 48). To investigate the distribution of the “bound” ions, we focus on the metal ions within 5 Å from the RNA surface. For the tRNA system, there are on average 20 bound Mg²⁺ ions in the region. In contrast, there are only ∼15 Na⁺ ions and 1 Cl⁻ in the same “bound” region. The result shows that Mg²⁺ has a much stronger tendency to accumulate around the RNA structure than Na⁺ (15, 17, 19, 23, 39).

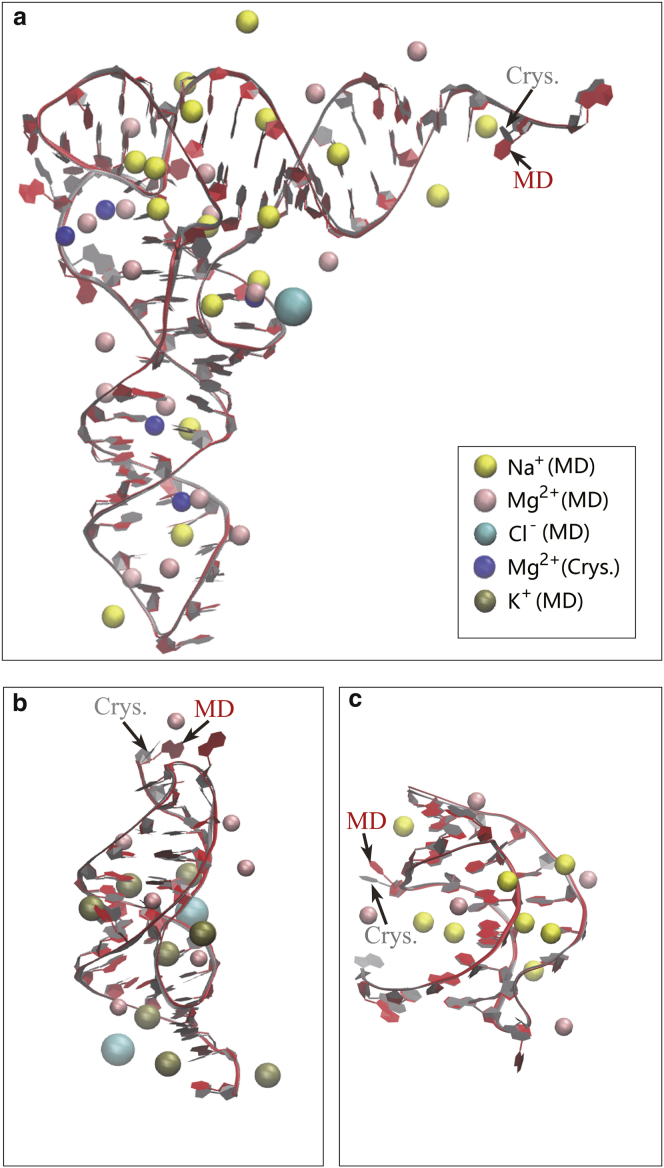
Figure 1.

Comparison between the PDB crystal structure and MD snapshot structures of the three RNA models: (a) the yeast phenylalanine tRNA (PDB: 1TRA); (b) a gene 32 messenger RNA pseudoknot of bacteriophage T2 (PDB: 2TPK); and (c) BWYV, a ribosomal frameshifting viral pseudoknot (PDB: 437D). The RNA contour structures are drawn using NewRibbons of VMD (Theoretical and Computational Biophysics Group) (83). The crystal structure (Crys.) and the MD simulated structure (MD) are very close except for the orientations of a few bases. The figure shows the simulated distributions of the different metal ions: Na⁺, K⁺, Mg²⁺ (MD), and Cl⁻. Also shown in (a) are the five Mg²⁺ ions (Crys.) observed in the crystal structures. To see this figure in color, go online.

As shown in Fig. 1 a, the simulation can predict stable ion binding sites (pink for Mg²⁺ ions) with long residence time, including sites in close agreement with those observed in the crystallographic structure (e.g., Fig. 1 a, the five sites marked in blue) as well as additional potential sites not shown in the crystallographic structure. The coordinate fluctuations of the bound ions during the 200 ns MD simulation (see Fig. S1) indicate that about half of all the bound ions reside inside or around the entrance of the major grooves. During the simulation, the RNA structures do not experience large conformational changes except for the fluctuations in base orientations.

The bound-ion distribution and the specific ion binding sites can be sensitive to the structural constraint and the backbone charge distribution of RNA. Because the phosphate group of the RNA structure carries a negative charge, Mg²⁺ ions tend to bind to RNA around the phosphate groups, and such an ion-RNA binding can be further stabilized by a water-mediated hydrogen bond network (see Fig. 2). Another important factor that can influence ion binding is the geometric shape of the RNA surface, particularly in the major and minor grooves. The different widths and depths of the grooves determine the different accessibility for ion binding. For example, a hydrated Mg²⁺ ion can only bind to the surface (instead of the interior) of the minor groove because the groove is not deep enough. Specifically, since the major groove in an A-form RNA helix is deep and narrow and the minor groove is wide and shallow, a fully hydrated Mg²⁺ ion cannot enter the major groove, which is too narrow for it. This steric effect competes against the electrostatic effect, since the high local charge density around the major groove can cause a strong attraction for the Mg²⁺ ion. The interplay between the geometric accessibility and the ion-RNA electrostatic force plays an important role in determining the dehydration states for ions binding to the RNA structure at different sites.

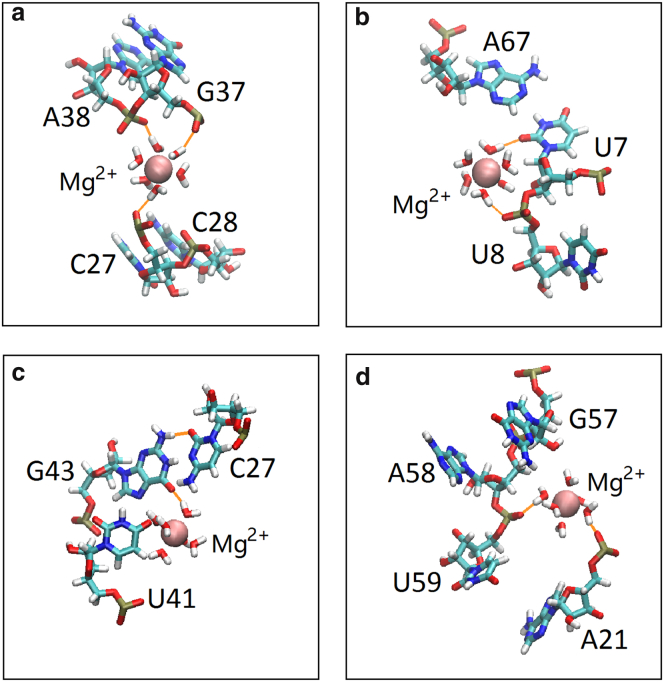
Figure 2.

(a–d) Four hexahydrated Mg²⁺ ions inside the major grooves of a tRNA structure (PDB: 1TRA). Each ion is stabilized by a hydrogen bond network between the hexahydrated Mg²⁺ ions and the RNA. The nucleotides of RNA are represented by the backbone model. The spheres represent Mg²⁺ ions. To see this figure in color, go online.

Dehydration of Mg²⁺ ions upon binding to RNA

In the bulk solvent away from the RNA surface, Mg²⁺ ions are fully hydrated with six tightly bound water molecules in the first hydration shell and more water molecules in the second hydration layer. Due to the strong attraction between the Mg²⁺ ion and the hexahydrated water molecules in the first hydration shell, full dehydration of the first hydration shell is rare for Mg²⁺ ions (18). As a result, water-mediated contact becomes the major form for the interaction between RNA and bound Mg²⁺ ions. The most important water-mediated interaction is hydrogen bonding between the first water shell and the phosphate group or the bases in the RNA. Sampling of the ion distributions in our MD simulation showed that dehydration mostly occurs for Mg²⁺ ions located inside the major (deep and narrow) grooves. This is because the narrow, deep groove causes a high charge density to attract the Mg²⁺ ions, and the water molecules around the Mg²⁺ ion must be removed for the ion to enter the narrow groove.

To further characterize water-mediated interactions, we select four representative bound Mg²⁺ ions corresponding to the Mg²⁺ ions observed in the experimentally determined crystal structure. For example, in the tRNA structure, our simulation shows four hexahydrated Mg²⁺ ions inside the major grooves, where each ion is stabilized by a hydrogen bond network between the hexahydrated Mg²⁺ ions and the RNA (see Fig. 2). The variation of the hydrogen bond number from one to three may indicate the different stabilities for the Mg²⁺-RNA interactions. Mg²⁺-RNA binding not only neutralizes the negative charges on RNA but also stabilizes the specific RNA tertiary interactions through the water-mediated hydrogen bond network. Once the hydrogen bonds are formed, the water-mediated ion-RNA interactions will stabilize the Mg²⁺ ion with a long residence time (see Fig. S1 for the data). To further characterize the bound-ion distribution, we calculate the distance between the Mg²⁺ ion and the nearest oxygen atom on RNA. In most cases, the distance varies between 3.9 and 4.5 Å. The short distance indicates a strong binding of the Mg²⁺ ion in the major groove.

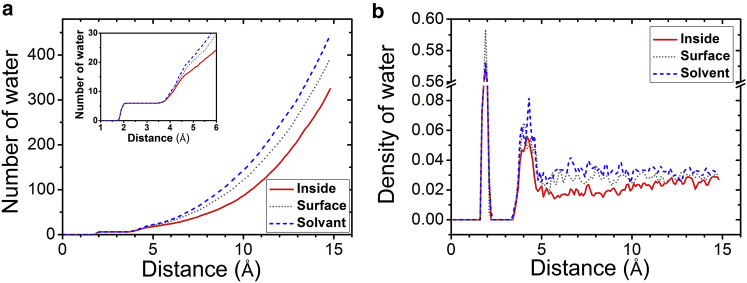
To illustrate the water distribution around the Mg²⁺ ions, we calculate the number and the distribution of water molecules around bound Mg²⁺ ions at the different binding sites. Fig. 3 a shows that because of the strong electrostatic attraction between Mg²⁺ and water, the first water shell (∼2 Å from Mg²⁺ to the oxygen (O) atom of water molecule) is very stable. In contrast, the second water layer (from four to five Å from the Mg²⁺ ion) undergoes a variety of different levels of dehydration when Mg²⁺ approaches the RNA structure. This finding is consistent with the water density distribution in Fig. 3 b, which shows that the first hydration shell is robust, and the dehydration starts from the second hydration shell.

Figure 3.

Water distributions around the highly positively charged Mg²⁺ ions. The total number of water molecules (a) and the density distribution around the Mg²⁺ ions (b) are plotted in different situations. The dashed line represents the Mg²⁺ ions in the bulk solvent. The dotted and solid lines represent Mg²⁺ ions located on the external surface and inside the major groove, respectively. To see this figure in color, go online.

According to the distance between the Mg²⁺ ion and the different atoms on the RNA structure, we can classify three types of Mg²⁺ binding sites: inside the major grooves (“groove sites”), on the surface of RNA (“surface sites”), and in the bulk solvent. As shown in Fig. 3, Mg²⁺ ions bound at the different types of locations show distinct levels of dehydration. Specifically, we find that Mg²⁺ ions bound inside the major grooves and folded loop structures on the RNA surface show stronger dehydration.

We quantify the level of dehydration using the HR parameter. HR at distance r from the center of the ion is defined as HR$\left(r\right)=N\left(r\right)/N_0\left(r\right),$ where $N\left(r\right)$ is the number of water molecules inside the sphere of radius r around a dehydrated ion and $N_0\left(r\right)$ is the number of water molecules in the same sphere for a fully hydrated ion. HR is between 0.0 and 1.0 with one for the fully hydrated state and zero for the fully dehydrated states in the reference state. Therefore, HR measures the degree of dehydration for an ion. Large and small HR values correspond to weak and strong dehydration, respectively. As an Mg²⁺ ion binds to RNA, the dehydration states of the Mg²⁺ ion and the corresponding phosphate group are coupled and often occur concomitantly. Water molecules around an originally fully hydrated Mg²⁺ ion will be rejected into the solution because of geometry restriction and the strong Mg²⁺-RNA electrostatic attraction, resulting in a reduced HR.

Fig. 4 shows the HR$\left(r\right)$ for a bound Mg²⁺ ion as a function of the radial distance r. The HR shows a nonmonotonic behavior with a minimum at $r\simeq 11$ Å. The nonmonotonic behavior of HR$\left(r\right)$ can be understood as follows. As shown in Fig. 3 b, the dehydration occurs predominantly in the region between $r\simeq 4$ Å (∼second hydration shell) and $r\simeq 11$ Å. Therefore, HR$\left(r\right)$ decreases in the above range. However, for distant regions further away from the ion ($r>11$ Å), the dehydration effect is weak (see Fig. 3 b), and thus the overall relative water deficiency within a large radius $r>11$ Å is less pronounced, resulting in an increase in HR$\left(r\right)$. This result is mainly caused by the steric restriction of the RNA surface.

Figure 4.

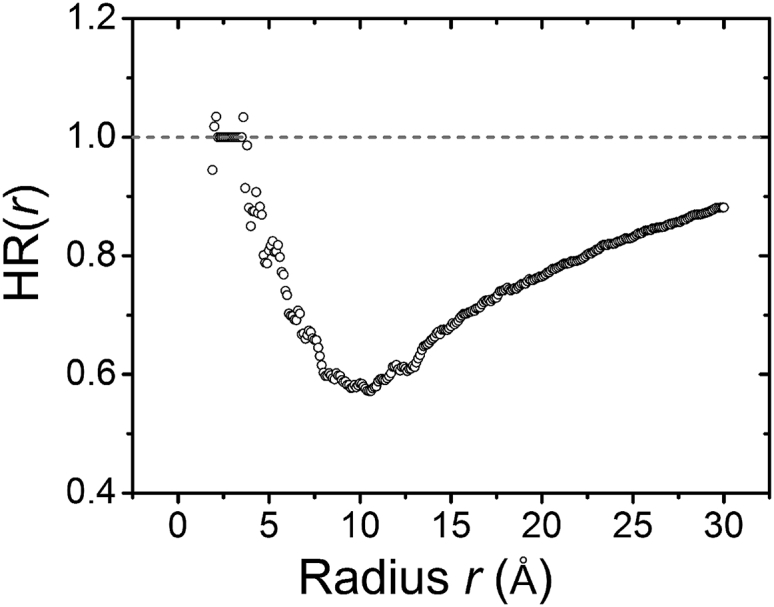
HR (circles) as a function of the radial distance r from the Mg²⁺ ion. The dotted reference line represents the fully hydrated Mg²⁺ ion in the bulk solution.

Ion dehydration free energy associated with ion-RNA binding

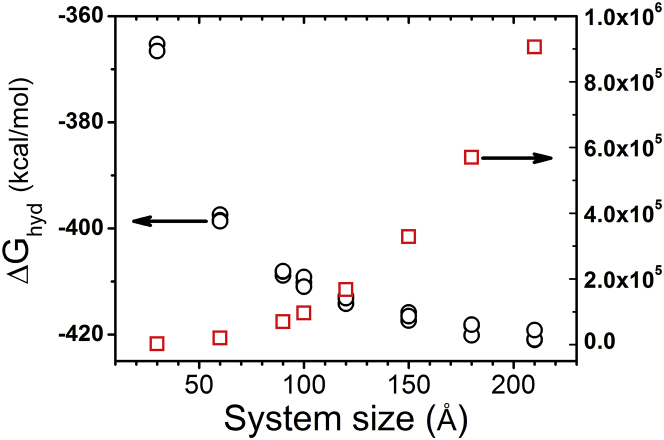
To understand and predict ion binding, it is important to accurately calculate the free-energy change for dehydration. We employ the FEP method to compute the hydration free energy $\text{Δ}{G}_{\text{hyd}}$ for Mg²⁺ ions bound at different locations. For small simulation boxes (52), the results for $\text{Δ}{G}_{\text{hyd}}$ can be dependent on the size of the box. To examine the size-dependence of the hydration free energy, we perform the simulations based on a series of different box sizes ranging from $L=30$ to 210 Å, with an Mg²⁺ ion placed at the center of the $L\times L\times L$ box. The results in Fig. 5 show the rapid increase in the number of atoms in the system and the MD simulation time with the box size. Taking box size with 210 Å as an example, the system contains 906,301 atoms, and simulating every 1 ns can cost 3 days in a GPU cluster NVIDIA Tesla C2075 (NVIDIA). The hydration free energy decreases with the box size and reaches a stable value if the box is large enough (such as 210 Å in Fig. 5). In the tRNA simulation system, the total atom number is 97,424, and the system size corresponds to a $100\times 100\times 100{\text{Å}}^3$ cubic box. The simulation gives the hydration free energy for a free Mg²⁺ ion in the simulation system as about −412.0 kcal/mol. In the mRNA or BWYV RNA systems, however, the simulation system corresponds to a $85\times 85\times 85{\text{Å}}^3$ cubic box, and $\text{Δ}{G}_{\text{hyd}}$ is about −407.0 kcal/mol. Thus the $\text{Δ}{G}_{\text{hyd}}$ results for an unbound Mg²⁺ ion in the different RNA systems are similar to those with the same box size shown in Fig. 5.

Figure 5.

The dependence of the hydration free energy of Mg²⁺ ion on the size of the simulation system. The circles and squares represent the hydration free energy and the number of atoms for the different system sizes, respectively. To see this figure in color, go online.

Ions binding to the different sites on RNA can have different dehydration states for the ions. Therefore, the hydration free energy $\text{Δ}{G}_{\text{hyd}}$ for a bound Mg²⁺ ion is dependent on the RNA structural environment around the binding site. Fig. 6 shows the dehydration free-energy change of Mg²⁺ ions in the tRNA-water-ion system. Because O atoms carry the most negative charges of the RNA structure (87), the strong interaction between Mg²⁺ and RNA can cause the Mg²⁺ ion and the O atoms to form a short-range ordered configuration. The Mg²⁺-O distance can significantly influence the ion-RNA binding strength. As shown in Fig. 4, the minimal HR, namely, overall maximal dehydration, occurs at an Mg²⁺-O distance of around 11 Å. Therefore, to parameterize the hydration free-energy change, we consider the sum of the inverse Mg²⁺-O distance within 11 Å. As shown in Fig. 6, $\text{Δ}{G}_{\text{hyd}}$ for a bound Mg²⁺ ion decreases with the sum of inverse Mg²⁺-O distance, $1/R_{\text{O}-{\text{Mg}}^{2+}}$. Analysis of the FEP-predicted $\text{Δ}{G}_{\text{hyd}}$ for Mg²⁺ ions bound at the different sites on RNA gives the following quantitative relationship:

$$\text{Δ}{G}_{\text{hyd}}=-\frac{0.67}{R_{\text{O}-{\text{Mg}}^{2+}}}-411.78,$$

where $R_{\text{O}-{\text{Mg}}^{2+}}$ and $\text{Δ}{G}_{\text{hyd}}$ are in the units of Å and kcal/mol, respectively. The SD is ∼1.39 kcal/mol.

Figure 6.

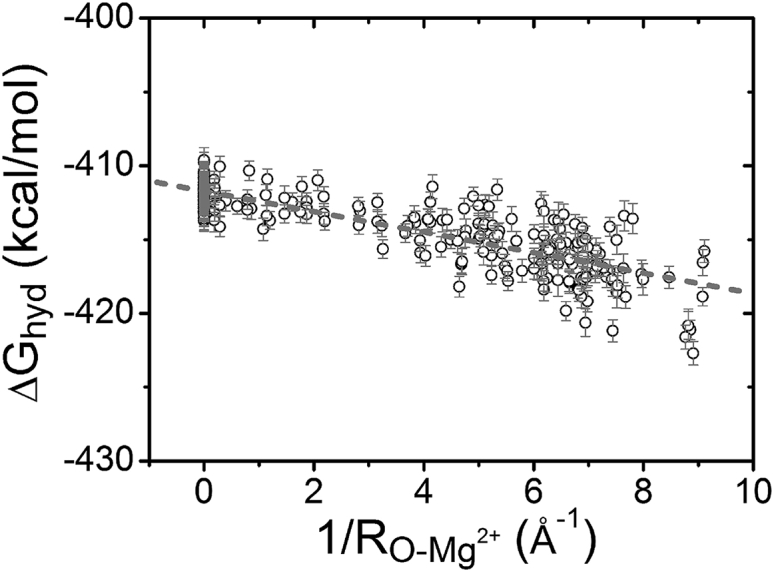
The hydration free energy for Mg²⁺ ions bound at different binding sites. The dotted line shows the fitted formula (SD 1.39 kcal/mol): $\text{Δ}{G}_{\text{hyd}}$ = −0.67/$R_{\text{O}-{\text{Mg}}^{2+}}$−411.78.

The above formula quantifies the Mg²⁺ hydration free energy as a function of bound ion sites. It is important to note that the above free-energy function effectively accounts for not only the dehydration of the ion but also that of the RNA. The formula gives a low hydration free energy for Mg²⁺ ions located in the grooves of the RNA structure, in which case $1/R_{\text{O}-{\text{Mg}}^{2+}}$ can be larger than 5.0 Å⁻¹. Another important result from the above formula is the linear dependence of $\text{Δ}{G}_{\text{hyd}}$ on $1/R_{\text{O}-{\text{Mg}}^{2+}}$. The large value of $1/R_{\text{O}-{\text{Mg}}^{2+}}$ corresponds to closer Mg²⁺ proximity to RNA and hence greater magnitude of the hydration free energy. Furthermore, the results from Fig. 6 and the above analytical formula indicate that 1) $\text{Δ}{G}_{\text{hyd}}$ is lowered by 0.67 kcal/mol as $1/R_{\text{O}-{\text{Mg}}^{2+}}$ is increased by 1.0 Å⁻¹, and 2) $\text{Δ}{G}_{\text{hyd}}$ is approximately equal to −411.78 kcal/mol for a fully hydrated Mg²⁺ ion in the bulk solution of the tRNA-water-ion system. This conclusion is consistent with the results in Fig. 5 with a box size of 100 Å.

Mg²⁺ hydration at different binding sites

According to the binding positions and the corresponding hydration free energies, we find Mg²⁺ binding scenarios can be classified into the aforementioned three types: Mg²⁺ binding inside the grooves (“groove sites”), on the RNA surface (“surface sites”), and Mg²⁺ in the bulk solvent. We find that Mg²⁺ binding inside the major groove is accompanied by a large HR and small coordinate fluctuation of the bound ion. Table 2 shows the results for Mg²⁺ ion hydration free energies and the dependence on the different binding positions from bulk solution to deep major grooves. The results indicate that the maximal $\text{Δ}{G}_{\text{hyd}}$ for Mg²⁺ ion is about −5.0 kcal/mol, corresponding to the change in the hydration free energy for transferring an Mg²⁺ ion from the bulk solution to the deep inside of the major groove. Our detailed analysis of the simulation results suggests that the total free-energy change (−5.0 kcal/mol) can be decomposed into two parts: −2.0 kcal/mol for the binding to the RNA external surface, and −3.0 kcal/mol for moving from the RNA external surface to the inside of the groove.

Table 2.

The Change of an Mg²⁺ Ion Hydration Free Energy $\text{Δ}{G}_{\text{hyd}}$ as the Ion Moves from the Bulk Solution to the Major Groove of an RNA Helix

Categories	Bulk Solution	Peripheral Surface	Deep Inside
1/${\mathrm{R}}_{O-M{g}^{2+}}$(Å−1)	0.0	3.0	8.0
$\text{Δ}{G}_{\text{hyd}}$ (kcal/mol)	−412.0 (0.6)	−414.0 (0.7)	−417.0 (0.7)
$\text{ΔΔ}{G}_{\text{hyd}}$ (kcal/mol)	0.0	−2.0	−5.0

In addition to the relationship between $1/R_{\text{O}-{\text{Mg}}^{2+}}$ and the hydration free energy $\text{Δ}{G}_{\text{hyd}}$, there also exists a correlation between $1/R_{\text{O}-{\text{Mg}}^{2+}}$ and the dehydration ratio. Since HR$\left(r\right)$ as a function of the distance r to the Mg²⁺ ion shows a minimal HR around $r\simeq 11$Å (see Fig. 4), we investigate the relationship between the HR and $1/R_{\text{O}-{\text{Mg}}^{2+}}$ for $r\le 11\text{Å}$. Fig. 7 shows a roughly linear relationship between HR and $1/R_{\text{O}-{\text{Mg}}^{2+}}$ with a slope equal to −15.44 Å^–1. A low HR such as 0.45 corresponds to a situation in which a large number (more than 50%) of the water molecules are rejected from the Mg²⁺ hydration shell by RNA atoms. Usually stronger water-mediated interactions between the Mg²⁺ ion and RNA atoms cause a larger $1/R_{\text{O}-{\text{Mg}}^{2+}}$ and a lower HR (stronger dehydration).

Figure 7.

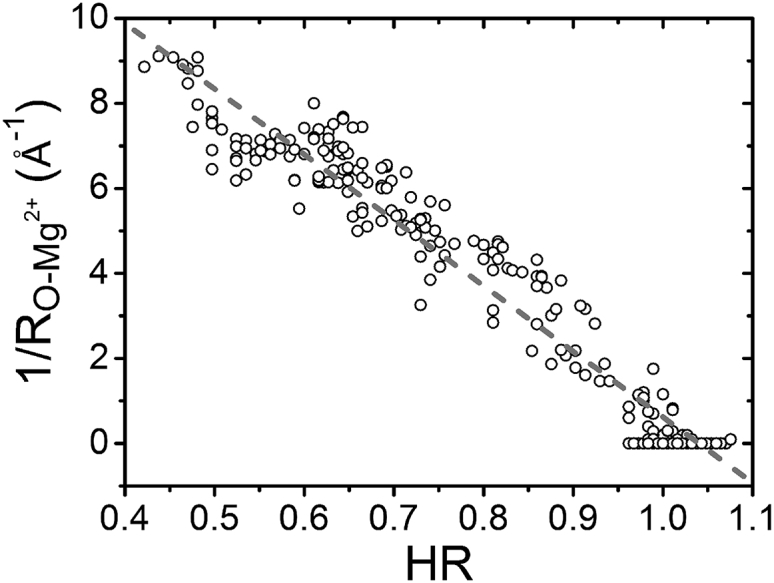
Relationship between HR and the Mg²⁺-RNA distance. The dotted line is fitted by the following equation (SD 0.69): 1/$R_{\text{O}-M{g}^{2+}}$ = −15.44 HR + 16.06.

Ion dehydration upon RNA binding: monovalent vs divalent ions

Due to the different charges carried by monovalent and divalent ions, Na⁺ and Mg²⁺ surrounding an RNA structure can have very different dehydration state and binding modes. We calculate the hydration free-energy change of Na⁺ ion at different binding sites using FEP. As shown in Fig. 8, compared with Mg²⁺ (Fig. 6), Na⁺ has two main different features in $\text{Δ}{G}_{\text{hyd}}$. First, Na⁺ ion binding involves a much smaller $\text{Δ}{G}_{\text{hyd}}$ than Mg²⁺, with a ratio of 1:4.63. We find that the hydration free energy changes nonlinearly with the charge of the metal ion. Second, unlike Mg²⁺, the $\text{Δ}{G}_{\text{hyd}}$ of Na⁺ does not change linearly with $1/R_{\text{O}-{\text{Na}}^{+}}$ (see Fig. 8). For Na⁺ ions bound to the deep inside of the grooves (sum of the $1/R_{\text{O}-{\text{Na}}^{+}}>7.0$), the hydration free energy decreases rapidly. Detailed analysis for the hydration state of the Na⁺ ion in the RNA grooves indicates that, unlike the Mg²⁺ ion with its robust first hydration shell, the first hydration shell of the bound Na⁺ can be disrupted. The different hydration states between Na⁺ and Mg²⁺ arise from the fact that the lower charge of Na⁺ leads to a weaker ion-water attraction, causing a less stable hydration shell. The disruption of the first hydration shell leads to direct contact between the ion and RNA, resulting in a steep decrease in the free energy. In contrast, because of the much stronger Mg²⁺-water attraction, despite the ion binding site, the first shell of water molecules around the Mg²⁺ ion remains nearly intact.

Figure 8.

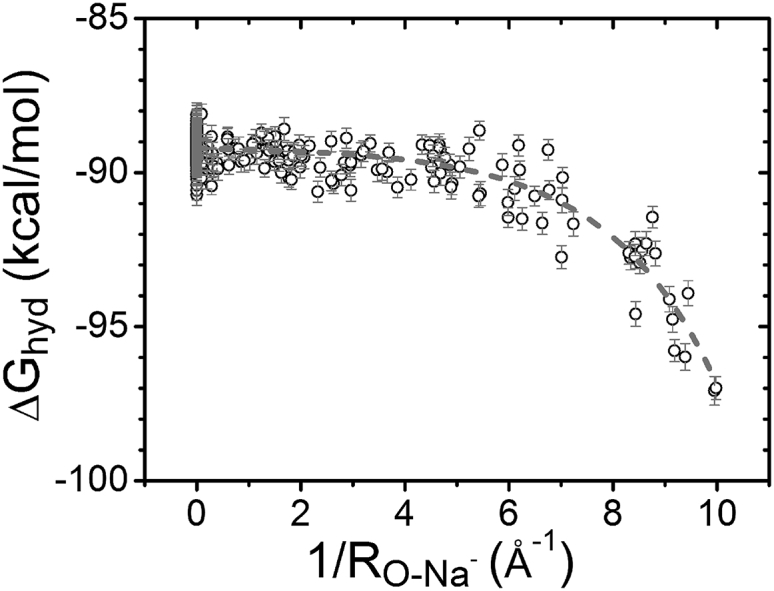
Hydration free energy of Na⁺ at different binding sites. The curve shows the trend of the hydration free-energy change.

Conclusions

When an Mg²⁺ ion diffuses from the bulk solution to the RNA surface and binds to RNA, especially inside the grooves, the fully hydrated ion may become dehydrated so that water molecules originally bound to the ion are removed from the hydration shell and released into the bulk solution. Through MD simulation with explicit solvent, we investigated the distribution of bound Mg²⁺ ions and the change in the ion hydration state at the different binding sites. This study leads to several conclusions:

• 1)Our MD simulation shows that ions at the experimentally observed binding sites exhibit low fluctuation and long dwell time. Moreover, combined with the coordinate fluctuation analysis, the simulation also predicts additional potential Mg²⁺ binding sites in the major groove not shown in the crystal structure. More extensive theoretical and experimental structural studies may provide further information to examine the accuracy of the predicted binding sites.
• 2)The dehydration state of the first water shell was not observed in the limited multiple trajectory 200 ns MD simulations, suggesting a high energy barrier for inner sphere dehydration. Meanwhile, we find that water-mediated hydrogen bonding remains an important form of Mg²⁺-RNA interaction.
• 3)Using the HR—defined as the ratio of the number of (bound) water molecules between the dehydration and the fully hydrated states—as a measure for ion dehydration, we find the overall minimal hydration (maximal dehydration relative to the fully hydrated state) occurs at a radial distance of 11.0 Å around the Mg²⁺ ion. This result suggests that the strong Mg²⁺-water attraction holds the first hydration shell nearly intact during the simulation. Therefore, for the observed binding sites, Mg²⁺-RNA interactions involve water-mediated hydrogen bonding.
• 4)Ions bound to RNA at the different sites show different dehydration ratios; in particular, Mg²⁺ ions binding deeply into the major groove have the lowest HR (i.e., highest dehydration ratio).
• 5)An important result of this study is the analytical formula for the relationship between Mg²⁺ ion dehydration energy and RNA structure around the binding site. The FEP calculation gives the hydration free-energy change $\text{ΔΔ}{G}_{\text{hyd}}$ as a linear function of the inverse distance between the Mg²⁺ ion and the surrounding O atoms, $1/R_{\text{O}-{\text{Mg}}^{2+}}$. $\text{ΔΔ}{G}_{\text{hyd}}$ decreases by −0.67 kcal/mol as $1/R_{\text{O}-{\text{Mg}}^{2+}}$ increases by 1 Å⁻¹. Our analysis indicates that $\text{ΔΔ}{G}_{\text{hyd}}$ can reach −2.0 kcal/mol for Mg²⁺ ions bound to the RNA exterior surface and −3.0 kcal/mol for those bound to the groove.
• 6)We find a similar linear dependence of the HR as a function of $1/R_{\text{O}-{\text{Mg}}^{2+}}$. Putting together the results here suggests that the dehydration of a Mg²⁺ ion bound to RNA may be predominantly determined by the geometric constraints of the RNA surface and the electrostatic attraction between Mg²⁺ and RNA.

The current study has several limitations. First, the metal ion force field is crucial for the simulation. In future model development, it is important to test the results by using different force fields. Second, it may be necessary to test the sampling effect by either running multiple trajectories and/or a longer time simulation (35, 36). Third, in the future, it would be useful to run systematic tests for a series of RNA structures on the ion binding sites and compare them with experiments.

An in vivo environment is much more complicated than the solution conditions studied here. However, the ion effects investigated based on simple systems may be useful for understanding in vivo RNA functions. For example, a recent study on the effects of Mg²⁺ in RNA folding showed that the high concentration of Mg²⁺ in liver may play a critical role in promoting the formation of an RNA kissing complex, a structure essential for efficient hepatitis C viral replication. This result suggests that Mg²⁺-dependent structural equilibrium may be an adaptive property of the hepatitis C genomic RNA (97, 98, 99). Furthermore, the results from the current study, including the analytical formulas for the dehydration free energy, may serve as a useful starting point for a systematic development of the dehydration free energy as a function of the structure environment of the binding site. Such an energy function can provide a useful tool for quantitative estimation of the ion dehydration probabilities and the metal ion effects on RNA folding stability.

Author Contributions

S.-J.C. designed the research. T.Y. performed the simulations. T.Y. and S.-J.C. performed the analysis. Both authors contributed to writing the article.

Editor: Tamar Schlick.